$D^+ \rightarrow K_s^0 \pi ^+ \eta$ reaction and $a_0(980)^+$

Abstract

We study the $D^+ \rightarrow {\bar{K}}^0 \pi ^+ \eta$ reaction where the $a_0(980)$ excitation plays a dominant role. We consider mechanisms of external and internal emission at the quark level, hadronize the $q {\bar{q}}$ components into two mesons and allow these mesons to undergo final state interaction where the $a_0(980)$ state is generated. While the $a_0(980)$ production is the dominant term, we also find other terms in the reaction that interfere with this production mode and, through interference with it, lead to a shape of the $a_0(980)$ significantly different from the one observed in other experiments, with an apparently much larger width.

1 Introduction

The $D^+ \rightarrow K_s^0 \pi ^+ \eta$ reaction measured by the BESIII collaboration in Ref. [1], and more recently in Ref. [2] with more precision and an amplitude analysis, has turned into an ideal reaction to isolate the $a_0(980)$ contribution. The reaction is actually $D^+ \rightarrow {\bar{K}}^0 \pi ^+ \eta$, and the ${\bar{K}} ^0$ is observed as a $K_s^0$ state. It might look at a simple sight that this reaction is just a copy of the $D^0 \rightarrow K^- \pi ^+ \eta$ reaction measured by the Belle collaboration [3]. Indeed, one goes from the first reaction to the second by changing a ${\bar{d}} \rightarrow {\bar{u}}$ quark. Yet, the differences are striking as we shall see in the present work, comparing it with the theoretical study of the $D^0 \rightarrow K^- \pi ^+ \eta$ reaction in Ref. [4]. The key point to see these striking differences is the fact that the $K^- \pi ^+$ in the $D^0 \rightarrow K^- \pi ^+ \eta$ reaction can come from ${\bar{K}}^{*0}$ excitation, but ${\bar{K}}^0 \pi ^+$ with positive charge and an s quark cannot come from ${\bar{K}}^{*0}, K^{*-}$. Hence, there is no ${\bar{K}}^*$ contribution in the $D^+ \rightarrow {\bar{K}}^0 \pi ^+ \eta$ reaction which makes cleaner the $a_0(980)$ production as seen in the experiment [2].

The differences in the mass distributions in the $D^0 \rightarrow K^- \pi ^+ \eta$ and $D^+ \rightarrow {\bar{K}}^0 \pi ^+ \eta$ reactions are striking. Indeed, in the $D^0 \rightarrow K^- \pi ^+ \eta$ reaction the $K^- \pi ^+$ mass distribution is dominated by the ${\bar{K}}^{*0}$ contribution, with a sharp peak at the ${\bar{K}}^{*0}$ mass, while in the $D^+ \rightarrow {\bar{K}}^0 \pi ^+ \eta$ reaction the ${\bar{K}}^0 \pi ^+$ mass distribution is rather structureless. This is not all, because the $\pi ^+ \eta$ mass distribution in the $D^0 \rightarrow K^- \pi ^+ \eta$ reaction, shows indeed a peak for the $a_0(980)$ production but has large strength at low and high invariant masses which are replicas of the $\bar{K}^{*0}$ resonance in the $K^- \pi ^+$ channel. Even more striking is the shape of the $K^- \eta$ mass distribution which has a double hump shape created again by the presence of the ${\bar{K}}^{*0}$ resonance in the $K^- \pi ^+$ channel. By contrast, the $\pi ^+ \eta$ mass distribution in the $D^+ \rightarrow {\bar{K}}^0 \pi ^+ \eta$ reaction has a mass distribution where the $a_0(980)$ dominates the spectrum and the ${\bar{K}}^0 \eta$ mass distribution has also very different shape.

It is worth mentioning that the related $D^0 \rightarrow K_s^0 \pi ^+ \pi ^-, {\bar{K}}_s^0 \pi ^0 \eta$ reactions were studied prior to the experiments, paying attention to the $\pi ^+\pi ^-$ and $\pi ^0\eta$ mass distributions, predicting that a clear signal of the $a_0(980)$ should be seen in these experiments [5].

Fig. 1

Mechanism with external emission at the quark level, $D^+ \rightarrow \pi ^+ s {\bar{d}}$

Fig. 2

a Hadronization of the $s{\bar{d}}$ component adding a ${\bar{q}}q$ pair producing two mesons. b Hadronization of the ${\bar{d}} u$ component in external emission

Fig. 3

Diagrams for $D^+ \rightarrow {\bar{K}}^0 \pi ^+ \eta$ coming from external emission: a tree level; b $\eta \pi ^+$ rescattering; c ${\bar{K}}^0 \pi ^+$ rescattering

Our purpose in the present work is to try to understand the spectrum from the perspective that the $a_0(980)$ is a dynamically generated state from the interaction of the $\pi \eta , K{\bar{K}}$ channels, which is well described by the chiral unitary approach [6,7,8,9]. For this we shall investigate the reaction mechanism of external and internal emission [10] at the quark level, and see how the hadronization of $q{\bar{q}}$ pairs can lead to the production of the final state.

2 Formalism

We study the $D^+ \rightarrow {\bar{K}}^0 \pi ^+ \eta$ reaction and look at the mechanisms for external and internal emission.

2.1 External emission

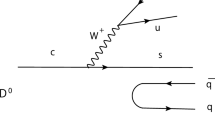
In Fig. 1, we show the mechanism of external emission, Cabibbo favoured, and in Fig. 2a the $s{\bar{d}}$ pair is hadronized in the following way

$$\begin{aligned} s{\bar{d}} \rightarrow \sum _i s\;{\bar{q}}_i q_i\; {\bar{d}}, \end{aligned}$$

(1)

which is easily interpreted writing the $q_i {\bar{q}}_j$ matrix in terms of pseudoscalar mesons, $\mathcal {P}_{ij}$, which in the standard $\eta -\eta '$ mixing of Ref. [11] is given by

$$\begin{aligned} \mathcal {P} = \left( \begin{array}{ccc} \frac{\pi ^0}{\sqrt{2}} + \frac{\eta }{\sqrt{3}} + \frac{\eta '}{\sqrt{6}} &{} \pi ^+ &{} K^+ \\ \pi ^- &{} -\frac{\pi ^0}{\sqrt{2}} + \frac{\eta }{\sqrt{3}} + \frac{\eta '}{\sqrt{6}} &{} K^0 \\ K^- &{} \bar{K}^0 &{} -\frac{\eta }{\sqrt{3}} + \sqrt{\frac{2}{3}} \eta ^{\prime } \\ \end{array} \right) .\nonumber \\ \end{aligned}$$

(2)

We ignore the $\eta ^{\prime }$ in our calculations as well as in Ref. [4] since it plays no role in the reaction due to the large mass.

Hence,

$$\begin{aligned} s{\bar{d}} \rightarrow \sum _i \;\mathcal {P}_{3i} \; \mathcal {P}_{i2}=\left( \mathcal {P}^2\right) _{32}=K^-\pi ^+-{\bar{K}}^0 \,\dfrac{\pi ^0}{\sqrt{2}}, \end{aligned}$$

(3)

where the ${\bar{K}}^0 \eta$ component has cancelled.

The combination of Eq. (3), together with the $\pi ^+$ of Fig. 1, does not lead to the desired final state $\bar{K}^0 \pi ^+ \eta$. However, through rescattering the $K^-\pi ^+$ and ${\bar{K}}^0 \pi ^0$ could lead to ${\bar{K}}^0 \eta$. Yet, the threshold of ${\bar{K}}^0 \eta$ is $1040\text { MeV}$, which is about $300\text { MeV}$ above the peak of the $K^*_0(700)$ (the kappa), where the $K^- \pi ^+ \rightarrow \bar{K}^0 \eta$ amplitude has a reduced strength, and because of that we shall disregard this contribution, as it was also done in Ref. [4].

Next, with the same mechanism of Fig. 1, we look at the hadronization of the ${\bar{d}} u$ component, as shown in Fig. 2b. We have now

$$\begin{aligned} u{\bar{d}} \rightarrow \sum _i u \;{\bar{q}}_i q_i \;{\bar{d}}= & {} \sum _i \;\mathcal {P}_{1i} \; \mathcal {P}_{i2}=\left( \mathcal {P}^2\right) _{12} \nonumber \\= & {} \dfrac{2}{\sqrt{3}}\, \eta \pi ^+ + K^+ {\bar{K}}^0, \end{aligned}$$

(4)

where now the $\pi ^0\pi ^+$ component has cancelled.

Hence we have now the combination

$$\begin{aligned} H=\left( \frac{2}{\sqrt{3}}\, \eta \pi ^+ + K^+ {\bar{K}}^0 \right) \, {\bar{K}}^0. \end{aligned}$$

(5)

However, there is a subtlety here concerning the $K^+ {\bar{K}}^0$ production (see discussion in page 3 of Ref. [12]) because for dynamical reasons the $WK^+{\bar{K}}^0$ vertex goes as the difference of energies of $K^+{\bar{K}}^0$ which vanishes in the average. However, due to the different masses of $\eta \pi ^+$ this cancellation does not occur, and consequently we keep the $\eta \pi ^+$ term and disregard the $K^+{\bar{K}}^0$ one.

We can see that the term H in Eq. (5) already contains the ${\bar{K}}^0 \pi ^+ \eta$ state at the tree level. In addition we can have rescattering of the $\eta \pi ^+$ and also of the ${\bar{K}}^0 \pi ^+$. Once again, we disregard the $\eta {\bar{K}}^0$ rescattering for the reasons given before. Then, the picture that we have for ${\bar{K}}^0 \pi ^+ \eta$ production is shown in Fig. 3, including tree level and rescattering.

Analytically we have for these terms originating from external emission

$$\begin{aligned} t^{(ee)}= & {} \mathcal {C} \Bigg \{h_{\eta \pi ^+ {\bar{K}}^0} \nonumber \\{} & {} + \left. h_{\eta \pi ^+ {\bar{K}}^0} \left[ G_{\eta \pi ^+} (M_\textrm{inv}(\eta \pi ^+)) \cdot t_{\eta \pi ^+, \, \eta \pi ^+} (M_\textrm{inv}(\eta \pi ^+)) \right. \right. \nonumber \\{} & {} + \left. \!\!G_{{\bar{K}}^0 \pi ^+} (M_\textrm{inv} (\bar{K}^0 \pi ^+)) \cdot t_{{\bar{K}}^0 \pi ^+, {\bar{K}}^0 \pi ^+}(M_\textrm{inv}({\bar{K}}^0 \pi ^+)) \right] \Bigg \},\nonumber \\ \end{aligned}$$

(6)

where $h_{\eta \pi ^+ {\bar{K}}^0}$ is the weight of the $\eta \pi ^+ {\bar{K}}^0$ component in Eq. (5),

$$\begin{aligned} h_{\eta \pi ^+ {\bar{K}}^0}= \dfrac{2}{\sqrt{3}}, \end{aligned}$$

(7)

and $G_{i}, t_{ij}$ are the loop functions of two mesons and the scattering matrices for the transition of channel i to channel j, taken as in Ref. [4]. $\mathcal {C}$ in Eq. (6) is a global constant that will be used to get the normalization of the data.

2.2 Internal emission

For internal emission we have the diagrams of Fig. 4, which account for the hadronization of quark pairs.

Fig. 4

Diagrams for internal emission: a hadronization of the $s{\bar{d}}$ pair; b hadronization of the $u{\bar{d}}$ pair

Fig. 5

Diagrams for $\eta \pi ^+ {\bar{K}}^0$ production coming from internal emission: a tree level; b $\pi ^+ \eta$ rescattering; c $\pi ^+ {\bar{K}}^0$ rescattering; d $K^+ {\bar{K}}^0$ rescattering

Following the path of subsection 2.1, we have now for the hadronization

$$\begin{aligned} s{\bar{d}}\rightarrow & {} \sum _i s \;{\bar{q}}_i q_i \;{\bar{d}} =\sum _i \;\mathcal {P}_{3i} \; \mathcal {P}_{i2}=\left( \mathcal {P}^2\right) _{32} \nonumber \\= & {} K^- \pi ^+ -\dfrac{1}{\sqrt{2}}\, \pi ^0 {\bar{K}}^0, \end{aligned}$$

(8)

where the ${\bar{K}}^0 \eta$ terms have cancelled, and

$$\begin{aligned} u{\bar{d}}\rightarrow & {} \sum _i u \;{\bar{q}}_i q_i \;{\bar{d}} =\sum _i \;\mathcal {P}_{1i} \; \mathcal {P}_{i2}=\left( \mathcal {P}^2\right) _{12} \nonumber \\= & {} \dfrac{2}{\sqrt{3}}\, \eta \pi ^+ + K^+ {\bar{K}}^0, \end{aligned}$$

(9)

where the $\pi ^+ \pi ^0$ terms have cancelled. Summing the two terms we have, including the $\pi ^+$ in Fig. 4a and $\bar{K}^0$ in Fig. 4b,

$$\begin{aligned} H'= & {} K^- \pi ^+ \pi ^+ -\dfrac{1}{\sqrt{2}}\; \pi ^0 \pi ^+ {\bar{K}}^0 + \dfrac{2}{\sqrt{3}}\; \eta \pi ^+ {\bar{K}}^0\nonumber \\{} & {} + K^+ {\bar{K}}^0 {\bar{K}}^0. \end{aligned}$$

(10)

Once again we have a tree level $\eta \pi ^+ {\bar{K}}^0$ production and the other terms can lead to this final state through rescattering, as shown in Fig. 5.

In Fig. 5 we have disregarded the possible rescattering of $K^- \pi ^+ \rightarrow {\bar{K}}^0 \eta$, ${\bar{K}}^0 \pi ^0 \rightarrow {\bar{K}}^0 \eta$, ${\bar{K}}^0 \eta \rightarrow {\bar{K}}^0 \eta$ for the same reasons as in the former subsection. We have checked numerically that these terms are, indeed, negligible.

Analytically we have for the diagrams of Fig. 5 corresponding to internal emission

$$\begin{aligned} t^{(ie)}= & {} \beta \mathcal {C} \left\{ {\bar{h}}_{\eta \pi ^+ {\bar{K}}^0} \right. \nonumber \\{} & {} + \left. {\bar{h}}_{\eta \pi ^+ {\bar{K}}^0} \left[ G_{\eta \pi ^+} (M_\textrm{inv}(\eta \pi ^+)) \cdot t_{\eta \pi ^+, \, \eta \pi ^+} (M_\textrm{inv}(\eta \pi ^+)) \right. \right. \nonumber \\{} & {} + \left. G_{\pi ^+ {\bar{K}}^0} (M_\textrm{inv} (\pi ^+ {\bar{K}}^0)) \cdot t_{\pi ^+ {\bar{K}}^0, \, \pi ^+ {\bar{K}}^0}(M_\textrm{inv}(\pi ^+ {\bar{K}}^0)) \right] \nonumber \\{} & {} + 2 \left. {\bar{h}}_{K^+ {\bar{K}}^0 {\bar{K}}^0} \; G_{K^+ \bar{K}^0}(M_\textrm{inv}(\pi ^+ \eta )) \right. \\{} & {} \left. \ \ \cdot t_{K^+ {\bar{K}}^0, \pi ^+ \eta } (M_\textrm{inv}(\pi ^+ \eta )) \right\} , \end{aligned}$$

(11)

where the weights ${\bar{h}}_i$ are now

$$\begin{aligned} {\bar{h}}_{\eta \pi ^+ {\bar{K}}^0}= \dfrac{2}{\sqrt{3}};\quad {\bar{h}}_{K^+ {\bar{K}}^0 {\bar{K}}^0}=1, \end{aligned}$$

(12)

and the factor 2 multiplying ${\bar{h}}_{K^+ {\bar{K}}^0 {\bar{K}}^0}$ in Eq. (11) accounts for the two ${\bar{K}}^0$ identical particles. In Eq. (11) we have put a weight $\beta \mathcal {C}$, conserving the global factor $\mathcal {C}$. The $\beta$ should be a factor of the order of $\frac{1}{N_c}$ ($N_c$ number of colors) which one expects from the ratio of terms from internal emission to those of external emission.

The total amplitude for the process is now given by

$$\begin{aligned} t=t^{(ee)} + t^{(ie)}. \end{aligned}$$

(13)

2.3 $K^*_0(1430)$ contribution

In Ref. [2] it was found that the scalar $K^*_0(1430)$ [$I\, (J^P)=\frac{1}{2}\, (0^+)$] state contributed to the process and showed up in the $K\eta$ mass distribution. The process can proceed as shown in Fig. 6.

Fig. 6

Diagrammatic representation of $D^+ \rightarrow \pi ^+ \bar{K}^*_0(1430) \rightarrow \pi ^+ {\bar{K}}^0 \eta$

We take into account this contribution phenomenologically by means of the amplitude

$$\begin{aligned} t^*= \mathcal {D} \, e^{i \phi }\; \dfrac{M_D^2}{s_{13}-M^2_{K^*_0}+i M_{K^*_0}\, \Gamma _{K^*_0}}, \end{aligned}$$

(14)

where $\mathcal {D}$ and $\phi$ will be chosen as free parameters and $s_{13}=(p_{{\bar{K}}^0}+p_\eta )^2$ taking the order of the particles ${\bar{K}}^0 (1), \pi ^+ (2), \eta (3)$. The factor $M_D^2$ is put to have $\mathcal {D}$ dimensionless.

One may wonder whether the consideration of the $K^*_0(1430)$ as we do here could lead to double counting with the other components that we consider in the work. From the point of view that we do not generate this resonance from the pseudoscalar–pseudoscalar interaction that we have implemented, there cannot be double counting. Thus, if the resonance is produced in the reaction, we should implement it empirically in addition to what we have done. We can justify that this resonance is not generated for the pseudoscalar–pseudoscalar interaction, because it was generated from the vector–vector interaction in Ref. [13]. Yet, the mass was shifted somewhat with respect to the experimental one. Its implementation by producing vectors and considering their interaction, as we have done here for the pseudoscalar mesons, is possible, but there is no gain in reducing the number of parameters and, as mentioned, the properties of this resonance obtained in Ref. [13] are not too accurate. Thus, the empirical implementation of the resonance, as done here, is preferable.

The final amplitude will now be

$$\begin{aligned} t=t^{(ee)} + t^{(ie)} + t^*. \end{aligned}$$

(15)

Then in order to calculate the mass distributions, we use the PDG standard formula [14]

$$\begin{aligned} \dfrac{\textrm{d}^2 \Gamma }{\textrm{d}s_{12}\; \textrm{d}s_{23}} = \dfrac{1}{(2\pi )^3}\; \dfrac{1}{32\, M^3_D}\; |t|^2. \end{aligned}$$

(16)

We can integrate over the limits of the PDG formula [14] to get $\textrm{d} \Gamma / \textrm{d} s_{12}$ integrating over $s_{23}$. Then, by cyclical permutations in the formulas we can get $\textrm{d} \Gamma / \textrm{d}s_{13}$, $\textrm{d} \Gamma / \textrm{d}s_{23}$ and compare with experiment [2].

2.4 Scattering amplitudes

We need the amplitudes

$$\begin{aligned} t_{\eta \pi ^+, \, \eta \pi ^+}, ~~ t_{{\bar{K}}^0 \pi ^+, \, {\bar{K}}^0 \pi ^+}, ~~ t_{{\bar{K}}^0 K^+, \, \pi ^+ \eta }. \end{aligned}$$

We use the results of Ref. [15] (Eq. (A.4) of Ref. [15]), which considers explicitly the $\eta -\eta '$ mixing, and for the channels $K^+ K^- (1), K^0 {\bar{K}}^0 (2), \pi ^0 \eta (3)$ one finds the matrix elements of the potential

$$\begin{aligned} V_{11}&=-\dfrac{s}{2f^2},&\quad \quad&V_{12}= -\dfrac{s}{4f^2}, \nonumber \\ V_{13}&= -\dfrac{3s-2m^2_K-m^2_\eta }{3\sqrt{6}f^2},&\quad \quad&V_{22}=-\dfrac{s}{2f^2}, \nonumber \\ V_{23}&= -\dfrac{3s-2m^2_K-m^2_\eta }{3\sqrt{6}f^2},&\quad \quad&V_{33}= -\dfrac{2m^2_\pi }{3f^2}. \end{aligned}$$

(17)

By evaluating the coupled channel T matrix

$$\begin{aligned} T= [1-VG]^{-1}\, V, \end{aligned}$$

(18)

we find, considering that $|\pi ^+\rangle =-|11\rangle$ of isospin,

$$\begin{aligned} t_{\eta \pi ^+, \, \eta \pi ^+} = t_{\eta \pi ^0, \, \eta \pi ^0}. \end{aligned}$$

(19)

Then, taking into account that $K^+K^-$ in term of $|I,\, I_3\rangle$ is

$$\begin{aligned} K^+K^- = - \left( \dfrac{1}{\sqrt{2}} | 10 \rangle + \dfrac{1}{\sqrt{2}} | 00 \rangle \right) , \end{aligned}$$

(20)

we find that

$$\begin{aligned} t_{{\bar{K}}^0 K^+, \, \pi ^+ \eta } = \sqrt{2}\; t_{K^+ K^-,\, \pi ^0 \eta }. \end{aligned}$$

(21)

We also need the $K\pi \rightarrow K\pi$ amplitudes, which we take from the Appendix of Ref. [4], using the channels $\pi ^- K^+ (1), \pi ^0 K^0 (2), \eta K^0 (3)$. Once again, using isospin coefficients and C parity $C {\bar{K}}^0 \pi ^+ = K^0 \pi ^-$, we obtain

$$\begin{aligned} t_{{\bar{K}}^0 \pi ^+, \, {\bar{K}}^0 \pi ^+} = \dfrac{2}{3}\, T_{22} + \dfrac{1}{3} \, T_{11} + \dfrac{2\sqrt{2}}{3} \, T_{12}. \end{aligned}$$

(22)

Note that this amplitude has $I=3/2$ and hence does not contain the $K^*_0(700)$.

3 Results

We have four parameters, $\mathcal {C}$, $\beta$, $\mathcal {D}$, and $\exp (i \phi )$, in our theoretical model. To determine these parameters, we perform a best fit to the three mass distributions of ${\bar{K}}^0 \pi ^+$, ${\bar{K}}^0 \eta$, and $\pi ^+ \eta$ with the experimental data of Ref. [2]. The parameter set obtained from the fit is shown in Table 1. The parameter $\mathcal {C}$ provides a global normalization for external and internal emission. The parameter $\beta$ gives the relative weight of the internal emission mechanism to the external emission, while $\mathcal {D}$ quantifies the strength of the $K_0^*(1430)$ contribution. Additionally, the phase $\exp (i \phi )$ corresponds to the interference between the $K_0^*(1430)$ and other contributions, influencing the non-trivial shapes of the various mass distributions under consideration. In Figs. 7, 8, 9, 10, 11, 12, we illustrate the mass distribution results obtained with the parameters from Table 1. It is evident that our theoretical calculations closely replicate the experimental data.

Table 1 Values of the parameters from the fit

Fig. 7

The $\pi ^+ \eta$ mass distribution $\textrm{d} \Gamma /\textrm{d} M_{\pi ^+ \eta }$. The total theoretical result is shown in the red line. The contributions of the $a_0(980)$, the ${\bar{K}}^0 \pi ^+$ scattering terms, and the $K^*_0(1430)$ are shown in the blue, green, and magenta lines, respectively. The experimental data, shown by points, are taken from Ref. [2]

Fig. 8

The contributions of the external emission $t^{(ee)}$, the internal emission $t^{(ie)}$, and the $K^*_0(1430)$ ($t^*$) are shown for the same total theoretical result of the $\pi ^+ \eta$ mass distribution $\textrm{d} \Gamma /\textrm{d} M_{\pi ^+ \eta }$ as in Fig. 7. The $a_0(980)$ contributions of the external emission $t^{(ee)}$ and the internal emission $t^{(ie)}$ are also shown

Fig. 9

The ${\bar{K}}^0 \eta$ mass distribution $d\Gamma /dM_{{\bar{K}}^0 \eta }$. The same as Fig. 7 but for the ${\bar{K}}^0 \eta$ mass distribution

Fig. 10

The contributions of the external emission $t^{(ee)}$, the internal emission $t^{(ie)}$, and the $K^*_0(1430)$ ($t^*$) are shown for the same total theoretical result of the $\bar{K}^0 \eta$ mass distribution $\textrm{d}\Gamma /\textrm{d} M_{{\bar{K}}^0 \eta }$ as in Fig. 9

In Fig. 7, we can see a clear peak dominating the $\pi ^+\eta$ spectrum around $1.0\text { GeV}$, corresponding to the $a_0(980)$ resonance, which, in our model, is encoded in the t-matrix elements $t_{\eta \pi ^+,\,\eta \pi ^+}$, and $t_{\bar{K}^0 K^+,\, \eta \pi ^+}$, defined in Eqs. (19) and (21), respectively. In contrast, both the $\bar{K}^0\pi ^+$ scattering term in Eq. (22) and the contributions from $K_0^*(1430)$ have relatively small strengths compared to the $a_0(980)$ resonance, particularly around $1.0\text { GeV}$, where their corresponding strengths are 8–9 times smaller. Consequently, we can claim that the peak observed in the experiment can be identified as the $a_0(980)$ state. Furthermore, it is crucial to note that due to interference with other contributions, particularly with the tree level in Eqs. (6) and (11), the lineshape of the $a_0(980)$ is broader than those observed in other reactions. Indeed, the apparent width of approximately $150\text { MeV}$ exceeds the range of 50–100 $\text { MeV}$ as stated in the PDG [14], or the width observed in the $\chi _{c 1} \rightarrow \eta \pi ^{+} \pi ^{-}$ decay [16] (see also Ref. [17]).

Fig. 11

The ${\bar{K}}^0 \pi ^+$ mass distribution $\textrm{d} \Gamma /\textrm{d} M_{{\bar{K}}^0 \pi ^+}$. The same as Fig. 7 but for the ${\bar{K}}^0 \pi ^+$ mass distribution

Fig. 12

The contributions of the external emission $t^{(ee)}$, the internal emission $t^{(ie)}$, and the $K^*_0(1430)$ ($t^*$) are shown for the same total theoretical result of the $\bar{K}^0 \pi ^+$ mass distribution $\textrm{d}\Gamma /\textrm{d}M_{{\bar{K}}^0 \pi ^+}$ as in Fig. 11

In Fig. 8, we also show the contributions of the external emission $t^{(ee)}$ of Eq. (6), the internal emission $t^{(ie)}$ of Eq. (11), and the $K^*_0(1430)$ ($t^*$) of Eq. (14) for the total theoretical result of the $\pi ^+ \eta$ mass distribution $\textrm{d}\Gamma /\textrm{d} M_{\pi ^+ \eta }$ which is the same as in Fig. 7. We can see that the internal emission $t^{(ie)}$ has a large contribution in our calculation, even if the parameter $\beta$ is introduced as a factor of the order of 1/$N_c$ in the internal emission. This is because of the different contributions of the $a_0(980)$ in the external and internal emissions, which are shown in the same figure of Fig. 8. We can also understand the reason from Eqs. (11) and (6). The $a_0(980)$ contribution of the internal emission $t^{(ie)}$ comes from two terms in Eq. (11), one is the second term, $\beta \mathcal {C} \; {\bar{h}}_{\eta \pi ^+ {\bar{K}}^0} G_{\eta \pi ^+} \cdot t_{\eta \pi ^+, \, \eta \pi ^+}$, and the other one is the last term, $\beta \mathcal {C} \; 2 \; {\bar{h}}_{K^+ {\bar{K}}^0 {\bar{K}}^0} \; G_{K^+ {\bar{K}}^0} \cdot t_{K^+ {\bar{K}}^0, \pi ^+ \eta }$. The latter has a larger contribution due to the factor 2. On the other hand, the external emission $t^{(ee)}$ has only one term contributing to the $a_0(980)$, $\mathcal {C} h_{\eta \pi ^+ {\bar{K}}^0} G_{\eta \pi ^+} \cdot t_{\eta \pi ^+, \, \eta \pi ^+}$, which is the second term in Eq. (6).

In Fig. 9, we reproduce a double hump structure in the ${\bar{K}}^0 \eta$ mass distribution. The $K^*_0(1430)$ spectrum has a peak structure at $M_{{\bar{K}}^0 \eta } = M_{K^*_0} = 1425\text { MeV}$ with the width $\Gamma _{K^*_0} = 270\text { MeV}$ as seen in Eq. (14). The hump structure comes from the interference between the $K^*_0(1430)$ and $a_0(980)$ contributions. Thus, the phase exp$(i\phi )$ in Table 1 is required to be negative. The contributions of the external emission $t^{(ee)}$, the internal emission $t^{(ie)}$, and the $K^*_0(1430)$ ($t^*$) are shown in Fig. 10. Because of the large contribution of $a_0(980)$ as discussed above, the internal emission $t^{(ie)}$ has a large contribution.

Figure 11 shows no distinct peak structure in the $\bar{K}^0\pi ^+$ mass distribution, except for a broad bump around $1.25\text { GeV}$. The $\bar{K}^0\pi ^+$ spectrum also exhibits a relatively large contribution, with a discontinuity at $1.05\text { GeV}$. This behavior arises from the cut-off mass $M_{\text {cut}}$ applied to the contribution from the products $G\cdot t$ in Eqs. (6) and (11), following the prescription discussed in Refs. [4, 18]. The introduction of this cut is essential for extrapolating Gt to high energies, given that the two-body amplitudes from the chiral unitary approach are applicable up to about $1200\text { MeV}$. Furthermore, it is worth noting that, as discussed in Refs. [4, 18], the overall results exhibit minimal dependence on the parameters associated with these cuts. In this study, we adopt $M_{\text {cut}} = 1050\text { MeV}$ and $\alpha = 0.0037\text { MeV}^{-1}$. According to our findings, the impact of $M_{\text {cut}}$ is noticeable only in the $\bar{K}^0\pi ^+$ distribution. Moreover, when exploring different values for the $M_{\text {cut}}$, such as $1150\text { MeV}$ as shown in Sect. 3.1, we observe no significant influence on the distribution lineshapes, except in the $\bar{K}^0\pi ^+$ spectrum, where the dip shifts from $1050\text { MeV}$ to $1150\text { MeV}$. Thus, we conclude that the dip in our model is not physical, and we could have a smooth curve in that region. The relevant thing is that this change in $M_\textrm{cut}$ has little repercussion in the ${\bar{K}}^0 \eta$ mass distribution and in particular in the $\pi ^+ \eta$ distribution, where the effects are negligible. The latter one is the most relevant channel in the present work, where we are concerned about the effect of the $a_0(980)$ in this reaction, and, hence, the conclusions that we draw about the effect of the $a_0(980)$ are not affected by the mentioned uncertainties.

The contributions of the external emission $t^{(ee)}$, the internal emission $t^{(ie)}$, and the $K^*_0(1430)$ ($t^*$) for the ${\bar{K}}^0 \pi ^+$ mass distribution $\textrm{d} \Gamma /\textrm{d} M_{{\bar{K}}^0 \pi ^+}$ are shown in Fig. 12.

3.1 Theoretical uncertainties

In this subsection, we show the results of several tests to determine some uncertainties of our theoretical models to the three mass distributions.

3.1.1 Effect of the cut mass $M_\textrm{cut}$

Figure 13 shows the results for the considered distributions with $M_{\text {cut}}$ fixed at $1150\text { MeV}$. Following a new fit in this setting, we obtain the parameters $\mathcal {C}= 532.04$, $\mathcal {D} = 90.28$, $\beta = 0.70$, and $\phi = -2.07$ radians. As a result, while there are noticeable changes in the strengths of individual contributions, the lineshapes for the first two distributions show only minimal differences, especially in the $\pi ^+\eta$ distribution where the $a_0(980)$ peak is evident. Conversely, the dip in the $\bar{K}^0\pi ^+$ spectrum has shifted to $1150\text { MeV}$ compared to its position in Fig. 11. As discussed earlier, this dip is directly influenced by the parameter $M_{\text {cut}}$. Nevertheless, we observe only slight changes in the strength and shape of the $\bar{K}^0\pi ^+$ distribution.

Fig. 13

The mass distributions of $\pi ^+ \eta$ (left), ${\bar{K}}^0 \eta$ (middle), and ${\bar{K}}^0 \pi ^+$ (right) with fixed $M_\textrm{cut}=1150\text { MeV}$. The parameters $\mathcal {C}= 532.04$, $\mathcal {D} = 90.28$, $\beta = 0.70$, and $\phi = -2.07$ radians are used

3.1.2 Effect of the parameter $\beta$

The parameter $\beta$ gives the relative weight of the internal emission mechanism to the external emission. The value of the parameter $\beta$ might be expected to be of the order of $1/N_c$. Here we restrict the value of the $\beta$ within $[-0.33:0.33]$ and we make a fit. In Fig. 14, we show the three mass distributions with $\beta =0.33$ which is obtained from the best fit. The parameters obtained from the fit are $\mathcal {C}= 691.80$, $\mathcal {D} = 71.29$, $\beta = 0.33$, and $\phi = -2.29$ radians. Once again, we see that the changes are not significant.

Fig. 14

The mass distributions of $\pi ^+ \eta$ (left), ${\bar{K}}^0 \eta$ (middle), and ${\bar{K}}^0 \pi ^+$ (right) with fixed $M_\textrm{cut}=1050\text { MeV}$. The parameters $\mathcal {C}= 691.80$, $\mathcal {D} = 71.29$, $\beta = 0.33$, and $\phi = -2.29$ radians are used

3.1.3 Effect of the $K_0^*(1430)$ mass

The mass of the $K_0^*(1430)$ has a relatively large uncertainty, $M_{K^*_0} = 1425 \pm 50\text { MeV}$ [14]. Here we take $M_{K^*_0} = 1385\text { MeV}$, which is consistent within the error bars, and then we perform the same calculations for the three invariant mass distributions. The parameters obtained from the fit are $\mathcal {C}= 473.34$, $\mathcal {D} = 57.27$, $\beta = 0.70$, and $\phi = -2.39$ radians. We show the three mass distribution in Fig. 15. The resulting calculation of the $\bar{K}^0 \pi ^+$ mass distribution is in better agreement with the data because the peak position of $K^*_0(1430)$ has moved a bit to the left from Fig. 9.

Fig. 15

The mass distributions of $\pi ^+ \eta$ (left), ${\bar{K}}^0 \eta$ (middle), and ${\bar{K}}^0 \pi ^+$ (right) with fixed $M_{K^*_0} = 1385\text { MeV}$ and fixed $M_\textrm{cut}=1050\text { MeV}$. The parameters $\mathcal {C}= 473.34$, $\mathcal {D} = 57.27$, $\beta = 0.70$, and $\phi = -2.39$ radians are used

In conclusion, we can see the clear peak of the $a_0(980)$ contribution even considering the uncertainties. We found that the $D^+ \rightarrow {\bar{K}}^0 \pi ^+ \eta$ reaction is a good reaction to see the peak structure of $a_0(980)$ in the $\pi ^+ \eta$ mass distribution. Yet, we also explained why the observed shape and width do not correspond to those seen in other experiments, through the interference with other terms that appear necessarily linked to the $a_0(980)$ production in our theoretical approach.

4 Conclusions

We have performed an analysis of the $D^+ \rightarrow {\bar{K}}^0 \pi ^+ \eta$ reaction based on the picture of the $a_0(980)$ resonance as dynamically generated from the interaction of the $\pi \eta$, $K {\bar{K}}$ channels, which emerges from the study of the chiral unitary approach and has been tested in many previous reactions. We show that this reaction is drastically different from the apparently analogous one $D^0 \rightarrow K^- \pi ^+ \eta$, and we trace it to the absence of a $K^*$ contribution in the $D^+ \rightarrow {\bar{K}}^0 \pi ^+ \eta$ reaction, while it is the driving term in the $D^0 \rightarrow K^- \pi ^+ \eta$ one. This leads to a much cleaner signal of the $a_0(980)$ excitation in the $D^+ \rightarrow {\bar{K}}^0 \pi ^+ \eta$ reaction as seen in the experiment.

In our study, we begin by looking at the dominant weak decay modes of external and internal emission at the quark level. Then we proceed with the hadronization of the $q {\bar{q}}$ pairs into two mesons and finally we allow the meson pairs to interact. We also take into account the contribution of the ${\bar{K}}^*_0(1430)$ as done in the experimental analysis and fit it to the data. Up to this empirical information and a global normalization constant, our framework only depends on the relative strength of the internal emission mechanism to the external emission one, which is also a fit parameter, and we get a result barely consistent with the expected large $N_c$ reduction. With this framework, we obtain a fair reproduction of the three mass distributions and we observe that the driving term in this reaction is the excitation of the $a_0(980)$. Yet, we note that the shape obtained has a much larger width than the one observed in other experiments, and we trace back this feature to the interference of the dominant $a_0(980)$ excitation with the other mechanisms that are also generated in the final state interaction of the mesons produced, together with the $\bar{K}^*_0(1430)$ excitation. This explanation is important to prevent taking the present shape of the $a_0(980)$ as a measure of the width of the $a_0(980)$ state, and reconcile the findings of the $D^+ \rightarrow {\bar{K}}^0 \pi ^+ \eta$ reaction with the shapes of the $a_0(980)$ seen in other experiments.