The $D_s^+ \rightarrow \pi ^+ K_S^0 K_S^0$ reaction and the $I=1$ partner of the $f_0(1710)$ state

Abstract

We have identified the decay modes of the $D_s^+ \rightarrow \pi ^+ K^{*+} K^{*-} , \pi ^+ K^{*0} \bar{K}^{*0}$ reactions producing a pion and two vector mesons. The posterior vector–vector interaction generates two resonances that we associate to the $f_0(1710)$ and the $a_0(1710)$ recently claimed, and they decay to the observed $K^+ K^-$ or $K_S^0 K_S^0$ pair, leading to the reactions $D_s^+ \rightarrow \pi ^+ K^+ K^- , \pi ^+ K_S^0 K_S^0$. The results depend on two parameters related to external and internal emission. We determine a narrow region of the parameters consistent with the large $N_c$ limit within uncertainties which gives rise to decay widths in agreement with experiment. With this scenario we make predictions for the branching ratio of the $a_0(1710)$ contribution to the $D_s^+ \rightarrow \pi ^0 K^+ K_S^0$ reaction, finding values within the range of $(1.3 \pm 0.4)\times 10^{-3}$. Comparison of these predictions with coming experimental results on that latter reaction will be most useful to deepen our understanding on the nature of these two resonances.

1 Introduction

The $f_0(1710)$ is a well established meson in the RPP (Review of Particle Physics) [1]. In the relativized quark model of Godfrey and Isgur [2] it appears as an $I^G(J^{PC})=0^+({0^{++}})$ state at 1780 MeV with the 2 $^3P_1$ configuration. In the same work a state with the same mass and configuration appears for $I=1$. Similar results are also reported in [3]. The $f_0(1710)$ is also obtained in [4] with the same configuration, but no mention is made of the possible $I=1$ partner. These models consider the excitation of u, d quarks. However, the fact that the $f_0(1710)$ decays mostly in $K{\bar{K}}, \eta \eta$ with only about $4\%$ branching ratio to $\pi \pi$ decay [1] indicates that this state should have large components of $s{\bar{s}}$ quarks.

A different picture for the $f_0(1710)$ comes from the work of [5], where the interaction of vector mesons studied in [6] for the $\rho \rho$ case is extended to the SU(3) space. The $f_0(1710)$ is found around 1726 MeV and couples mostly to $K^* {\bar{K}}^*$, but also to $\omega \phi$, $\phi \phi$, $\omega \omega$, $\rho \rho$ in that order. The vector–vector interaction is taken from the local hidden gauge approach [7,8,9,10], which stems from a contact term plus vector exchange. Considering box diagrams with intermediate two pseudoscalar mesons, decay rates to $K{\bar{K}}, \eta \eta , \pi \pi$ were evaluated in [5] and found consistent with experimental data. Interestingly, in [5] a partner state of the $f_0(1710)$ with $1^-({0^{++}})$ $a_0$ state is also found at 1780 MeV with $\Gamma \sim 130$ MeV. This state couples mostly to $K^* {\bar{K}}^*$ but also to $\rho \omega$ and $\rho \phi$. The picture of [5] for the $f_0(1710)$ has been tested in different processes. In [11] the $\gamma \gamma$ decay rate is evaluated and found consistent with the RPP information [1]. In [12] it is also suggested that the peak observed at the $\phi \omega$ threshold in the $\phi \omega$ mass distribution of the $J/\psi \rightarrow \gamma \phi \omega$ decay [13] is due to the $f_0(1710)$ resonance. Predictions for other decay modes, and rates for $f_0(1710)$ production are done in [14,15,16,17,18,19].

The success of the predictions for other vector–vector molecules obtained in [5] discussed in the former references gives us confidence in that model and concretely about the existence of the $I=1$ partner of the $f_0(1710)$ state, which we will call the $a_0(1710)$ by analogy to the $f_0(1710)$. A different formalism to deal with the unitarity in coupled channels in the vector–vector interaction, using the same kernels for the interaction, is presented in [20] based upon the use of dispersion relations. The regions of validity and limitations of that approach were discussed in [21], but it is interesting to note that in the region of validity of the approach, both a $0^+(0^{++})$ state with mass [1.58–1.76 GeV] and a $1^-(0^{++})$ state with mass [1.75–1.79 GeV] were found, in good agreement with the results of [5], 1.73 GeV for the mass of the $0^+(0^{++})$ state and 1.78 GeV  for the mass of the $1^-(0^{++})$ state. Hence, both approaches predict the existence of an $a_0$ state with mass around 1.78 GeV. Yet, this state is not reported in the RPP [1]. The situation has changed recently with the appearance of two works showing evidence for this state. One of these works is the clear observation of a peak around 1710 MeV in the $\pi ^+ \eta$ mass distribution in the $\eta _c \rightarrow \eta \pi ^+ \pi ^-$ decay [22]. The other work is the study of the $D_s^+ \rightarrow \pi ^+ K_S^0 K_S^0$ decay [23] showing a peak around 1710 MeV in the $K_S^0 K_S^0$ mass distribution with an abnormally large strength compared to the one of a similar peak seen in the $D_s^+ \rightarrow \pi ^+ K^+ K^-$ decay [24]. This cannot be explained from a $K{\bar{K}}$ state in $I=0$, implying that there must also be an $I=1$ state with a similar mass. The $I=0$ and $I=1$ states have relative opposite sign in the $K^+ K^-$ or $K^0 {\bar{K}}^0$ components and the contribution of the two states around 1710 MeV will give differences in the $K^+ K^-$ or $K^0 {\bar{K}}^0$ production rates.

Our aim in the present work is to show that from the perspective of Refs. [5, 20] for the $f_0(1710)$ and $a_0(1710)$ it is natural to reproduce the experimental data on $K{\bar{K}}$ production in the $D_s^+ \rightarrow \pi ^+ K {\bar{K}}$ decay. At the same time we can make predictions for the rate of the $I=1$ $a_0(1710)$ production in the $K^+ K_S^0$ invariant mass distribution of the $D_s^+ \rightarrow \pi ^0 K^+ K_S^0$ reaction, which, as mentioned in [23] is in the process of being analyzed at BESIII.

2 Formalism

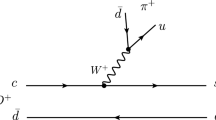
We look at the mechanism for $D_s^+ \rightarrow \pi ^+ K {\bar{K}}$ production at the quark level starting from the dominant external emission process and then considering the internal emission, both in the Cabibbo-favored mode [25]. The external emission with $\pi ^+$ production is shown in Fig. 1.

Fig. 1

Cabibbo-favored decay mode of $D_s^+$ at the quark level with external emission (a); Hadronization of the $s{\bar{s}}$ component (b); hadronization of the ${\bar{d}}u$ component (c)

Since we wish to have three mesons in the final state we must hadronize a pair of quarks introducing an extra ${\bar{q}}q$ with the vacuum quantum numbers $({\bar{q}}q={\bar{u}}u+{\bar{d}}d+{\bar{s}}s)$. Also, the hadronization must produce a pair of vector mesons, such that their interaction can produce the $f_0(1710)$ and $a_0(1710)$ resonances. Then, hadronizing $s{\bar{s}}$ we will have

$$\begin{aligned} s{{\bar{s}}} \rightarrow \sum _i s\, {{\bar{q}}}_i q_i \, {{\bar{s}}} = V_{3i} V_{i3} = (V^2)_{33}, \end{aligned}$$

(1)

where V is the $q_i {{\bar{q}}}_j$ matrix written in terms of the vector meson

$$\begin{aligned} V = \left( \begin{array}{ccc} \frac{\rho ^0 }{\sqrt{2}}+ \frac{\omega }{\sqrt{2}} &{} \rho ^+ &{} K^{*+} \\ \rho ^- &{} -\frac{\rho ^0 }{\sqrt{2}}+ \frac{\omega }{\sqrt{2}} &{}K^{*0} \\ K^{*-} &{} {\bar{K}}^{*0} &{} \phi \\ \end{array} \right) \,. \end{aligned}$$

(2)

Then we have the hadronic state

$$\begin{aligned} H_1=(V^2)_{33}\pi ^+=( K^{*-} K^{*+} + {\bar{K}}^{*0} K^{*0} +\phi \phi ) \, \pi ^+ \,. \end{aligned}$$

(3)

With the implicit isospin phase convention of this matrix, with the $(K^{*+},K^{*0})$, $({\bar{K}}^{*0}, -K^{*-})$ isospin doublets, the former combination represents $K^* {\bar{K}}^*$ in isospin $I=0$, as it should be, plus $\phi \phi$, also $I=0$, since originally we had the $I=0$ $s{{\bar{s}}}$ state.

The two isospin states of $K^* {\bar{K}}^*$ are given by

$$\begin{aligned} |K^* {\bar{K}}^*, I=0\rangle= & {} -\frac{1}{\sqrt{2}} \big (K^{*+} K^{*-} \, + \, K^{*0}{\bar{K}}^{*0} \big ) \,,\nonumber \\ |K^* {\bar{K}}^*, I=1,I_3=0\rangle= & {} -\frac{1}{\sqrt{2}} \big (K^{*+} K^{*-} - K^{*0}{\bar{K}}^{*0} \big ) \,,\nonumber \\ |K^* {\bar{K}}^*, I=1,I_3=1\rangle= & {} K^{*+}{\bar{K}}^{*0}\,. \end{aligned}$$

(4)

For later use we also write the $K{\bar{K}}$ wave functions

$$\begin{aligned} |K {\bar{K}}, I=0\rangle= & {} -\frac{1}{\sqrt{2}} \big (K^{+} K^{-} \, + \, K^{0}{\bar{K}}^{0} \big ) \,,\nonumber \\ |K {\bar{K}}, I=1,I_3=0\rangle= & {} -\frac{1}{\sqrt{2}} \big (K^{+} K^{-} - K^{0}{\bar{K}}^{0} \big ) \,,\nonumber \\ |K {\bar{K}}, I=1,I_3=1\rangle= & {} K^{+}{\bar{K}}^{0}\,. \end{aligned}$$

(5)

We could also think of hadronizing the $u{\bar{d}}$ pair with VV but then $s{\bar{s}}$ should be a pseudoscalar, in this case a combination of $\eta$ and $\eta '$, and we do not get the $\pi ^+ K {\bar{K}}$ mode. Note that if we wish to have $\pi ^+ K {\bar{K}}$, we could also have the $s{\bar{s}}$ as the $\phi$ meson and then $\phi \rightarrow K {\bar{K}}$, but the invariant mass of $K {\bar{K}}$ will peak at the $\phi$ mass and we are only concerned about the vicinity of 1710 MeV, where the $f_0(1710)$ and $a_0(1710)$ resonances appear. This decay mode and the $K^+ K^- \pi ^+$ spectrum at low $K^+ K^-$ invariant mass has been studied in detail in [26]. We shall concentrate here only in the region of $f_0(1710)$ and $a_0(1710)$ production.

We have then another possibility which is to hadronize the $u{\bar{d}}$ component with VP or PV (P for pseudoscalar meson). Similarly to Eq. (2) we have the $q_i {{\bar{q}}}_j$ matrix for pseudoscalars

$$\begin{aligned} P = \left( \begin{array}{ccc} \frac{\pi ^0 }{\sqrt{2}}+ \frac{\eta }{\sqrt{3}} &{} \pi ^+ &{} K^+ \\ \pi ^- &{} -\frac{\pi ^0 }{\sqrt{2}}+ \frac{\eta }{\sqrt{3}} &{} K^0 \\ K^- &{} {\bar{K}}^0 &{} -\frac{\eta }{\sqrt{3}}\\ \end{array} \right) \,, \end{aligned}$$

(6)

where we have used the $\eta$ and $\eta '$ mixing of Ref. [27] and neglected the $\eta '$ which does not play any role here. The mixing of Ref. [27] corresponds to

$$\begin{aligned} \eta =\cos \theta _p \eta _8 -\sin \theta _p \eta _1\,, \qquad \eta '=\sin \theta _p \eta _8 +\cos \theta _p \eta _1 \,, \end{aligned}$$

where $\eta _1, \eta _8$ are the singlet and octet state of SU(3) with $I=0$, with $\cos \theta _p=2\sqrt{2}/3$, $\sin \theta _p=-1/3$. These results are close to the empirical numbers used in [28], with $\theta _p=-14.47 ^\circ$. The use of one or the other mixing angles leads to results with negligible differences in observables [29].

In this case we obtain the contribution

$$\begin{aligned} u{{\bar{d}}} \rightarrow \sum _i u\, {{\bar{q}}}_i q_i \, {{\bar{d}}} = M_{1i} M'_{i2} = (MM')_{12}\,, \end{aligned}$$

(7)

but now $M,M'$ can be vector or pseudoscalar. Hence, we obtain the combinations

$$\begin{aligned} (VP)_{12}= & {} \bigg (\frac{\rho ^0 }{\sqrt{2}}+ \frac{\omega }{\sqrt{2}} \bigg )\,\pi ^+ \,+\, \rho ^+ \bigg ( \frac{-\pi ^0 }{\sqrt{2}}+ \frac{\eta }{\sqrt{3}}\bigg )\nonumber \\&+ K^{*+}{\bar{K}}^0 \end{aligned}$$

(8)

$$\begin{aligned} (PV)_{12}= & {} \bigg ( \frac{\pi ^0 }{\sqrt{2}}+ \frac{\eta }{\sqrt{3}}\bigg ) \rho ^+ \,+\, \pi ^+ \bigg (\frac{-\rho ^0 }{\sqrt{2}}+ \frac{\omega }{\sqrt{2}} \bigg ) \nonumber \\&+ K^+ {\bar{K}}^{*0}\,, \end{aligned}$$

(9)

and the $s{\bar{s}}$ pair will provide the $\phi$ meson.

We aim at getting $\pi ^+ f_0(1710)$ and $\pi ^+ a_0(1710)$ which have G-parity negative and positive respectively. Neither VP or PV of Eqs. (8), (9) have good G-parity but the combinations $VP \pm PV$ have. Thus, we construct

$$\begin{aligned} H_2= & {} \phi [(VP)_{12}+(PV)_{12}]\nonumber \\= & {} \bigg [2 \frac{\omega }{\sqrt{2}}\pi ^+ \,+\,\frac{2}{\sqrt{3}}\rho ^+ \eta \,+\, K^{*+}{\bar{K}}^0 \,+\, K^+ {\bar{K}}^{*0} \bigg ]\phi \end{aligned}$$

(10)

$$\begin{aligned} H_3= & {} \phi [(VP)_{12}-(PV)_{12}]\nonumber \\= & {} \bigg [2 \frac{\rho ^0}{\sqrt{2}}\pi ^+ \,-\,\frac{2}{\sqrt{2}}\rho ^+ \pi ^0 \,+\, K^{*+}{\bar{K}}^0 \,-\, K^+ {\bar{K}}^{*0} \bigg ]\phi \,. \end{aligned}$$

(11)

The combination of Eq. (10) has G-parity positive while the case of Eq. (11) has G-parity negative.¹ With the latter combination we are able to reach the $\pi ^+ f_0(1710)$ state, while from Eq. (10) we can produce $\pi ^+ a_0(1710)$.

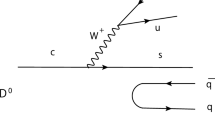
So far we have relied upon external emission. Suppressed by a color factor $\frac{1}{N_c}$ we have internal emission, which is depicted in Fig. 2. We could hadronize the $s{\bar{d}}$ or $u{\bar{s}}$ components with VV but then we neither get a pion nor the VV combination to give the nonstrange $f_0(1710)$ or $a_0(1710)$. We must hadronize with VP and PV combinations and we get

Fig. 2

Internal emission. (a) With hadronization of the $s{\bar{d}}$ pair; (b) with hadronization of the $u{\bar{s}}$ pair

$$\begin{aligned} (VP)_{32}= & {} K^{*-}\pi ^+ \,+\, {\bar{K}}^{*0} \bigg ( \frac{-\pi ^0 }{\sqrt{2}}+ \frac{\eta }{\sqrt{3}}\bigg ) + \phi {\bar{K}}^0 \nonumber \\ (PV)_{32}= & {} K^-\rho ^+ \,+\, {\bar{K}}^0 \bigg (\frac{-\rho ^0 }{\sqrt{2}}+ \frac{\omega }{\sqrt{2}} \bigg )-\frac{\eta }{\sqrt{3}} {\bar{K}}^{*0} \nonumber \\ (VP)_{13}= & {} \bigg (\frac{\rho ^0 }{\sqrt{2}}+ \frac{\omega }{\sqrt{2}} \bigg ) K^+ \,+\, \rho ^+ K^0- K^{*+}\frac{\eta }{\sqrt{3}} \nonumber \\ (PV)_{13}= & {} \bigg ( \frac{\pi ^0 }{\sqrt{2}}+ \frac{\eta }{\sqrt{3}}\bigg ) K^{*+} \,+\, \pi ^+ K^{*0} \,+\, K^+\phi \,. \end{aligned}$$

(12)

We must form the good G-parity combinations from the former terms and we find

$$\begin{aligned} H_4= & {} K^{*+} (VP)_{32}+ {\bar{K}}^{*0} (PV)_{13} \nonumber \\= & {} \pi ^+ (K^{*+} K^{*-} + {\bar{K}}^{*0}K^{*0}) \,+\,\frac{2}{\sqrt{3}} \eta K^{*+} {\bar{K}}^{*0} \nonumber \\&+ \phi (K^{*+}{\bar{K}}^0+ {\bar{K}}^{*0}K^+) \end{aligned}$$

(13)

$$\begin{aligned} H_5= & {} K^{*+} (VP)_{32}- {\bar{K}}^{*0} (PV)_{13} \nonumber \\= & {} \pi ^+ (K^{*+} K^{*-} - {\bar{K}}^{*0}K^{*0}) \,-\,\sqrt{2} \pi ^0 K^{*+} {\bar{K}}^{*0} \nonumber \\&+ \phi (K^{*+}{\bar{K}}^0 - {\bar{K}}^{*0}K^+) \,. \end{aligned}$$

(14)

Note that $(PV)_{32}$ and $(VP)_{13}$ combinations have no pions and do not lead to our desired final state. We see again that $H_4$ has G-parity negative and can lead to $\pi ^+ f_0(1710)$, while $H_5$ has G-parity positive and can lead to $\pi ^+ a_0(1710)$. The different mechanisms have different weights and we shall give weights:

$$\begin{aligned} H_1:A \, \qquad H_2:A \alpha \, \qquad H_3:A \beta \, \qquad H_4:A \gamma \, \qquad H_5:A \delta \,. \end{aligned}$$

From this hadronic combinations we select the terms that have a $\pi ^+$ state. In this way we only have one VV interaction leading to the resonances $f_0(1710)$ and $a_0(1710)$. We hence discard other possibilities that would require extra interactions to produce the required $\pi ^+ VV$ modes. Any extra interaction weakens the amplitude, and even more if it is of the PV type which has no particular strength in the final $K{\bar{K}}$ peaks. The same can be said about producing $K{\bar{K}}$ instead of $K^* {\bar{K}}^*$ pairs, since we require again an extra $K{\bar{K}} \rightarrow K^* {\bar{K}}^*$ interaction and this is weak compared to the $K^* {\bar{K}}^* \rightarrow K^* {\bar{K}}^*$ that produce the resonances (see Appendix B of Ref. [30], also reflected in the very small real parts of the box diagrams in [5, 6]).

We will evaluate ratios of $\pi ^+ K_S^0 K_S^0$ and $\pi ^+ K^+ K^-$ production and the global factor A disappears. Then we have 4 parameters to adjust an experimental ratio, which seems an excessive freedom, but we will see that in practice we have only two effective free parameters, which facilitates the study.

The hadronic states $H_i$ $(i=1,2,3,4,5)$ do not have $K{\bar{K}}$ in the final state. We must produce the $f_0(1710)$ and $a_0(1710)$ and then let them decay into $K{\bar{K}}$ . The mechanisms for $K{\bar{K}}$ decay are explained in [5]. The $K{\bar{K}}$ decay widths of the states were obtained via box diagrams as depicted in Fig. 3, which were added to the potential stemming from vector exchange and used as kernel in the Bethe-Salpeter equation. However, here we are interested in interference of amplitudes and then we have to look explicitly into the amplitudes generated by the $VV \rightarrow K{\bar{K}}$ transitions depicted in Fig. 4.

Fig. 3

Box diagrams considered in [5] to evaluate the width of the vector–vector molecular states

Fig. 4

$K^* {\bar{K}}^* \rightarrow K{\bar{K}}$ transitions driven by $\pi$ exchange (a) and $\phi (\rho ,\omega ,\phi ) \rightarrow K{\bar{K}}$ transitions driven by K exchange (b)

Table 1 Couplings of $f_0(1710)$ and $a_0(1710)$ to VV channels. All quantities are in units of MeV

We can see how the different $H_i$ terms contribute to $\pi ^+ f_0(1710)$, $\pi ^+ a_0(1710) (I_3=0)$ and $\pi ^+ a_0(1710) (I_3=1)$.

$$\begin{aligned} \left\{ \begin{array}{ll} H_1:&{} \pi ^+ f_0(1710) ~\mathrm{with} ~\pi ^+ K^*{\bar{K}}^* {~\mathrm and~} \pi ^+\phi \phi {~\mathrm terms}. \\ H_2:&{} \pi ^+ f_0(1710) ~\mathrm{with} ~ \omega \phi \pi ^+ {~\mathrm term}. \\ H_3:&{} \pi ^+ a_0(1710)~(I_3=0)~\mathrm{with} ~ \pi ^+ \rho ^0 \phi {~\mathrm term}; \\ &{} \pi ^+ a_0(1710)~(I_3=1)~\mathrm{with} ~ \pi ^0 \rho ^+ \phi {~\mathrm term}. \\ H_4:&{} \pi ^+ f_0(1710) ~\mathrm{with~} \pi ^+ K^* {\bar{K}}^* {~\mathrm term}. \\ H_5:&{} \pi ^+ a_0(1710)~(I_3=0)~\mathrm{with} ~ \pi ^+ K^* {\bar{K}}^* {~\mathrm term}; \\ &{} \pi ^+ a_0(1710)~(I_3=1)~\mathrm{with} ~ \pi ^0 K^* {\bar{K}}^* {~\mathrm term}. \end{array} \right. \end{aligned}$$

(15)

The mechanism for $f_0(1710)$ and $a_0(1710)$ production and $K{\bar{K}}$ final state are depicted in Fig. 5.

Fig. 5

Mechanisms for $D_s^+ \rightarrow \pi ^+ K^+ K^- (K^0 {\bar{K}}^0)$ and $D_s^+ \rightarrow \pi ^0 K^+ {\bar{K}}^0$. For $\pi ^+ f_0(1710)$ production $V_i V'_i\equiv K^*{\bar{K}}^*,\omega \phi ,\phi \phi$; for $\pi ^+ a_0(1710) ~(I_3=0)$ production $V_i V'_i\equiv K^*{\bar{K}}^*,\rho ^0 \phi$;  for $\pi ^+ a_0(1710) ~(I_3=1)$ production $V_i V'_i\equiv K^*{\bar{K}}^*,\rho ^+ \phi$

All this said, and with the weights of the different mechanisms, we can write

$$\begin{aligned} {{\tilde{t}}_{f_0}}= & {} A \bigg \lbrace -\sqrt{2}\,(1+ {\gamma })\, G_{K^* {\bar{K}}^*}(M_{\mathrm{inv}})\, g_{f_0,K^* {\bar{K}}^*}\nonumber \\&+ 2 \,\times \frac{1}{2} G_{\phi \phi }(M_{\mathrm{inv}})\sqrt{2}\, g_{f_0,\phi \phi } \nonumber \\&+ \sqrt{2}\,{\alpha } \,G_{\omega \phi }(M_{\mathrm{inv}})\, g_{f_0,\omega \phi }\bigg \rbrace \end{aligned}$$

(16)

$$\begin{aligned} {{\tilde{t}}_{a_0}}(I_3=0)= & {} A \bigg \lbrace \sqrt{2}\,{\beta }\, G_{\rho \phi }(M_{\mathrm{inv}})\, g_{a_0,\rho \phi }\nonumber \\&-\sqrt{2}\,{\delta } \,G_{K^* {\bar{K}}^*}(M_{\mathrm{inv}})\, g_{a_0,K^* {\bar{K}}^*}\bigg \rbrace \end{aligned}$$

(17)

$$\begin{aligned} {{\tilde{t}}_{a_0}}(I_3=1)= & {} A \bigg \lbrace \sqrt{2}\,{\beta }\, G_{\rho \phi }(M_{\mathrm{inv}})\, g_{a_0,\rho \phi }\nonumber \\&-\sqrt{2}\,{\delta } \,G_{K^* {\bar{K}}^*}(M_{\mathrm{inv}})\, g_{a_0,K^* {\bar{K}}^*}\bigg \rbrace \,, \end{aligned}$$

(18)

where we have taken into account the $K^* {\bar{K}}^*$ wave functions of Eq. (4), and, considering the isospin multiplet $(-\rho ^+,\rho ^0,\rho ^-)$, the $\rho \phi$ wave functions

$$\begin{aligned} |\rho \phi ; I=1,I_3=0\rangle= & {} \rho ^0 \phi \nonumber \\ |\rho \phi ; I=1,I_3=1\rangle= & {} -\rho ^+ \phi \,. \end{aligned}$$

(19)

The G functions in Eqs. (16), (17), (18) are the loop functions for pairs of vector mesons, which are calculated using a cutoff method with $q_{\mathrm{max}} =960$ MeV, giving similar results as those found in [5], where dimensional regularization was used.

Since in all mechanisms we started from $s{\bar{d}}$, $u{\bar{s}}$, this state is $I=1,I_3=1$. Considering the phase of $\pi ^+$ (($-\pi ^+, \pi ^0,\pi ^-$) isospin multiplet), the components $\pi ^+ a_0$ $(I_3=0)$ and $\pi ^0 a_0$ $(I_3=1)$ have the same weights, which means that Eqs. (17), (18) should be the same, which is indeed the case.

The $G_{\omega \phi }$ and $G_{\rho \phi }$ loop functions are remarkably similar to $G_{K^* {\bar{K}}^*}$ given the proximity of the $\omega \phi , \rho \phi , K^* {\bar{K}}^*$ thresholds. This allows us to rewrite Eqs. (16), (17), (18) by

$$\begin{aligned} {{\tilde{t}}_{f_0}}= & {} A \bigg \lbrace -\sqrt{2}\, G_{K^* {\bar{K}}^*}(M_{\mathrm{inv}})\, g_{f_0,K^* {\bar{K}}^*} + G_{\phi \phi }(M_{\mathrm{inv}})\sqrt{2}\, g_{f_0,\phi \phi } \nonumber \\&- \sqrt{2}\, \big (\gamma - \alpha \, \frac{g_{f_0,\omega \phi }}{g_{f_0,K^* {\bar{K}}^*}} \big ) \, G_{K^* {\bar{K}}^*}(M_{\mathrm{inv}} )\, g_{f_0,K^* {\bar{K}}^*} \bigg \rbrace \nonumber \\= & {} A \bigg \lbrace -\sqrt{2}\, G_{K^* {\bar{K}}^*}(M_{\mathrm{inv}})\, g_{f_0,K^* {\bar{K}}^*} + G_{\phi \phi }(M_{\mathrm{inv}})\sqrt{2}\, g_{f_0,\phi \phi } \nonumber \\&- \sqrt{2}\, \gamma ' \, G_{K^* {\bar{K}}^*}(M_{\mathrm{inv}})\, g_{f_0,K^* {\bar{K}}^*} \bigg \rbrace \end{aligned}$$

(20)

$$\begin{aligned} {{\tilde{t}}_{a_0}}= & {} -A \sqrt{2}\, \,G_{K^* {\bar{K}}^*}(M_{\mathrm{inv}})\, g_{a_0,K^* {\bar{K}}^*} \bigg \lbrace \delta - \beta \frac{g_{f_0,\rho \phi }}{g_{a_0,K^* {\bar{K}}^*}} \bigg \rbrace \nonumber \\= & {} -A \sqrt{2}\, \delta ' \,G_{K^* {\bar{K}}^*}(M_{\mathrm{inv}})\, g_{a_0,K^* {\bar{K}}^*} \end{aligned}$$

(21)

And now we have only two effective parameters

$$\begin{aligned} \gamma ' = \gamma - \alpha \, \frac{g_{f_0,\omega \phi }}{g_{f_0,K^* {\bar{K}}^*}}\,, \qquad \delta ' =\delta - \beta \frac{g_{f_0,\rho \phi }}{g_{a_0,K^* {\bar{K}}^*}} \,. \end{aligned}$$

(22)

We do not know the values of $\gamma$, $\alpha$, $\delta$, $\beta$, but since external emission is color enhanced by a factor $N_c$, taking $|\alpha |$, $|\beta |$ equal 1 and $|\gamma |$, $|\delta |$ of the order of equal 1/3 (we take 2/3 to have a bigger margin of freedom), and considering the couplings of Table 1 (we neglect the relatively smaller imaginary parts), we obtain a range for the parameters:

$$\begin{aligned} \gamma ' \in [-1,1]\,; \qquad \delta ' \in [-1.3,1.3]\,. \end{aligned}$$

(23)

The strategy to follow is to find a band of allowed values of $\gamma ',\delta '$ within the range of Eq. (23) that agree with the $K^+ K^-$ and $K^0 {\bar{K}}^0$ experimental branching ratios, and then predict the branching ratio for the $K^+ K^0_S$ production corresponding to the $a_0$ excitation.

We need one more step to construct the $K^+ K^-$, $K^0 {\bar{K}}^0$ amplitudes. So far we have the amplitudes that produce the R resonances, $f_0$, $a_0$ in Fig. 5. Next we need to see how the resonances $f_0$, $a_0$ decay into $K{\bar{K}}$, the last vertex in Fig. 5. This requires to use the dynamics employed in Ref. [5] applied to the transitions of Fig. 4. The decay of a resonance made of $VV'$ coupled channels proceeds as shown in Fig. 6.

Fig. 6

Amplitude for $R \rightarrow K{\bar{K}}$ for a resonance build up from the $V_i,V_i'$ channels. Diagrams with ${\bar{K}}K$ instead of $K {\bar{K}}$ in the final state appear with $\rho ,\omega ,\phi$ vector mesons but not for the $V_i,V_i' \equiv K^* {\bar{K}}^*$

We need the Lagrangian for $V \rightarrow PP$ given by

$$\begin{aligned} \mathcal{{L}}_{VPP}= & {} -ig \,\langle [P, \partial _\mu P] V^\mu \rangle \,, \\ g= & {} \frac{M_V}{2\,f}, ~~(M_V=800 \text { MeV},~f=93 \text { MeV}). \nonumber \end{aligned}$$

(24)

Following [31], we can proceed factorizing the $VV' \rightarrow K{\bar{K}}$ transition on shell for $VV' \rightarrow K{\bar{K}}$ and performing the loop function for the two vector mesons. One can see indeed that the pion or the kaon exchanged are very far off shell which justifies that factorization. Indeed, the $q^2$ for the $\pi$, K exchanged evaluated at the $K^* {\bar{K}}^*$ threshold is ($2\omega _K=2 M_{K^*}$)

$$\begin{aligned} q^2= & {} (p_{K^*}-p_K)^2 =M^2_{K^*}+m^2_K-2 M_{K^*} \omega _K\\= & {} -M^2_{K^*}+m^2_K \,, \end{aligned}$$

and the $\pi$ or K propagators are

$$\begin{aligned} D_{\pi }=\frac{1}{-M^2_{K^*}+m^2_K-m^2_{\pi }}\,, \quad D_K=\frac{1}{-M^2_{K^*}} \,, \end{aligned}$$

(25)

which shows that $D_K$ is suppressed with respect to $D_{\pi }$²

Since we are only interested in ratios of production rates and the $K{\bar{K}}$ final momenta are the same for all the channels, in the region of the resonances where we are concerned we do not need to evaluate explicitly the amplitudes but have enough with the coefficients that are different for the different channels. Thus, using Eq. (24) we obtain the weights $\widetilde{W_i}$

$$\begin{aligned} I= & {} 0 ~~ \left\{ \begin{array}{ll} K^* {\bar{K}}^* \rightarrow K{\bar{K}}\,, &{}~~~ {\widetilde{W}}=\frac{3}{2} \, D_{\pi }\, \\ \phi \omega \rightarrow K{\bar{K}}\,, &{}~~~ {\widetilde{W}}=2 \,D_{K}\, \\ \phi \phi \rightarrow K{\bar{K}}\,, &{}~~~ {\widetilde{W}}=- 2 \,D_{K}\, \\ \rho \rho \rightarrow K{\bar{K}}\,, &{}~~~ {\widetilde{W}}=\sqrt{3} \, D_{K}\, \\ \omega \omega \rightarrow K{\bar{K}}\,, &{}~~~ {\widetilde{W}}=- D_{K} \end{array} \right. \,~~~~ \end{aligned}$$

(26)

$$\begin{aligned} I= & {} 1 ~~ \left\{ \begin{array}{ll} K^* {\bar{K}}^* \rightarrow K{\bar{K}}\,, &{}~~~ {\widetilde{W}}=-\frac{1}{2} \, D_{\pi }\, \\ \phi \rho \rightarrow K{\bar{K}}\,, &{}~~~ {\widetilde{W}}= 2 \,D_{K}\, \\ \omega \rho \rightarrow K{\bar{K}}\,, &{}~~~ {\widetilde{W}}=-\sqrt{2} \, D_{K}\,, \end{array} \right. \,,~~~~ \end{aligned}$$

(27)

where the unitary normalization, as used in [5], is taken for the states with two identical particle ($\frac{1}{\sqrt{2}} \omega \omega$, etc). Then the weights for $f_0$ or $a_0$ production are given by

$$\begin{aligned} W_{f_0}= & {} \sum _i g_{f_0,i} \, {\widetilde{W}}_i \, G_i(M_{\mathrm{inv}})\,, \nonumber \\ W_{a_0}= & {} \sum _i g_{a_0,i} \, {\widetilde{W}}_i \, G_i(M_{\mathrm{inv}}) \,, \end{aligned}$$

(28)

where the sum over i goes over the channels of $I=0$ and $I=1$ of Eqs. (26), (27), respectively.

We see that $|W_{f_0}/W_{a_0}|^2$ around $1710\text { MeV}$, which gives the relative weight of $\Gamma _{K{\bar{K}}}$ for the two resonances, is about a factor of two. This is consistent with what was found in [5]. Indeed in [32] one finds that $\Gamma _{K{\bar{K}}}/\Gamma _{\mathrm{tot}}\simeq 55\%$ for $f_0$ and about $27\%$ for $a_0$. Taking the value of $\Gamma _{\mathrm{tot}}$ in the real axis for the two resonances, one finds that $\Gamma _{K{\bar{K}}}(f_0)/\Gamma _{K{\bar{K}}}(a_0)\simeq 1.83$.

Considering the weights of Eqs. (28) of the resonances to $K{\bar{K}}$ and the wave functions of Eqs. (5) , we can then write:

$$\begin{aligned} t_{K^+ K^-}= & {} -{{\tilde{t}}_{f_0}} \frac{1}{M^2_{\mathrm{inv}}-M^2_{f_0}+i M_{f_0} \Gamma _{f_0}} \, W_{f_0}\, \frac{1}{\sqrt{2}}\,g_{K{\bar{K}}}\nonumber \\&-{{\tilde{t}}_{a_0}} \frac{1}{M^2_{\mathrm{inv}}-M^2_{a_0}+i M_{a_0} \Gamma _{a_0}} \, W_{a_0} \,\frac{1}{\sqrt{2}}\,g_{K{\bar{K}}} \nonumber \\ t_{K^0 {\bar{K}}^0}= & {} - {{\tilde{t}}_{f_0}} \frac{1}{M^2_{\mathrm{inv}}-M^2_{f_0}+i M_{f_0} \Gamma _{f_0}} \, W_{f_0}\, \frac{1}{\sqrt{2}}\,g_{K{\bar{K}}}\nonumber \\&+ {{\tilde{t}}_{a_0}} \frac{1}{M^2_{\mathrm{inv}}-M^2_{a_0}+i M_{a_0} \Gamma _{a_0}} \, W_{a_0}\, \frac{1}{\sqrt{2}}\,g_{K{\bar{K}}} \nonumber \\ t_{K^+ {\bar{K}}^0}= & {} {{\tilde{t}}_{a_0}} \frac{1}{M^2_{\mathrm{inv}}-M^2_{a_0}+i M_{a_0} \Gamma _{a_0}} \, W_{a_0} \,g_{K{\bar{K}}} \nonumber \\ t_{K^+ K_S^0}= & {} -\frac{1}{\sqrt{2}}t_{K^+ {\bar{K}}^0}\,, \end{aligned}$$

(29)

where in the last equation we have taken into account that $K_S^0=\frac{1}{\sqrt{2}}(K^0-{\bar{K}}^0)$.

We can see how ${{\tilde{t}}_{f_0}}$, ${{\tilde{t}}_{a_0}}$ appear with opposite relative signs in $K^+ K^-$ or $K^0 {\bar{K}}^0$ production, which explains why there can be differences in these production rates. We should note that Eqs. (29) contain much dynamics from the assumed vector–vector nature of the $f_0$ and $a_0$ resonances and their decay modes into $K{\bar{K}}$.

Finally we have to calculate the differential decay width given by

$$\begin{aligned} \frac{d\Gamma _i}{dM_{\mathrm{inv}}(K{\bar{K}})}=\frac{1}{(2\pi )^3}\,\frac{1}{4 M^2_{D_s}} \, p_{\pi } \, {\tilde{p}}_k \, |t_i|^2 \end{aligned}$$

(30)

for $i=\pi ^+ K^+ K^-, \pi ^+ K^0 {\bar{K}}^0, \pi ^0 K^+ K_S^0$, with

$$\begin{aligned} p_{\pi }= & {} \frac{\lambda ^{1/2}(M^2_{D_s},m^2_{\pi },M^2_{\mathrm{inv}}(K{\bar{K}}))}{2M_{D_s}}\,,\nonumber \\ {\tilde{p}}_k= & {} \frac{\lambda ^{1/2}(M^2_{\mathrm{inv}}(K{\bar{K}}),m^2_{K},m^2_{K})}{2M_{\mathrm{inv}}(K{\bar{K}})} \,. \end{aligned}$$

(31)

We integrate from $M_{\mathrm{inv}}=1600$ MeV to 1870 MeV to obtain the integrated width into $\pi f_0$,$\pi a_0$ and use the data of the RPP for the $f_0(1710)$ and from [5] for the $a_0$,

$$\begin{aligned} M_{f_0}= & {} 1732~ \mathrm{MeV};\quad \Gamma _{f_0}=147~ \mathrm{MeV} \nonumber \\ M_{a_0}= & {} 1777~ \mathrm{MeV};\quad \Gamma _{a_0}=148~ \mathrm{MeV}. \end{aligned}$$

(32)

3 Results

We must evaluate $\Gamma _i$ for the different channels in terms of the parameters $A,\gamma ',\delta '$. We define the ratio

$$\begin{aligned} R_1=\frac{\Gamma (D_s^+ \rightarrow \pi ^+ K^0 {\bar{K}}^0)}{\Gamma (D_s^+ \rightarrow \pi ^+ K^+ K^-)} \,, \end{aligned}$$

(33)

using the results of Eqs. (29) and (30). Similarly we also define

$$\begin{aligned} R_2=\frac{\Gamma (D_s^+ \rightarrow \pi ^0 K^+ K_S^0)}{\Gamma (D_s^+ \rightarrow \pi ^+ K^+ K^-)}\,, \end{aligned}$$

(34)

and we integrate $d\Gamma /dM_{\mathrm{inv}}$ over the range of $M_{\mathrm{inv}}\in [1600-1870]~\mathrm{MeV}$.

We should compare our results with experiment. Recalling the discussion in Ref. [23], we see that ${\mathrm {Br}}[D_s^+ \rightarrow \pi ^+ f_0(1710)]$ from [24] is³

$$\begin{aligned}&{\mathrm {Br}}[D_s^+ \rightarrow \pi ^+ ``f_0(1710){\text {''}};~``f_0(1710)){\text {''}} \rightarrow K^+ K^-]\nonumber \\&\quad =(1.0 \pm 0.2\pm 0.3)\times 10^{-3} \,, \end{aligned}$$

(35)

and from [23]

$$\begin{aligned}&{\mathrm {Br}}[D_s^+ \rightarrow \pi ^+ ``f_0(1710)){\text {''}};~ ``f_0(1710)){\text {''}} \rightarrow K_S^0 K_S^0]\nonumber \\&\quad =(3.1 \pm 0.3\pm 0.1)\times 10^{-3} \,, \end{aligned}$$

(36)

This gives

$$\begin{aligned} R_1=2\times \frac{\Gamma (D_s^+ \rightarrow \pi ^+ K_S^0 K_S^0)}{\Gamma (D_s^+ \rightarrow \pi ^+ K^+ K^-)} =6.20 \pm 0.67 \,, \end{aligned}$$

(37)

where we have added experimental errors in quadrature. We have a bracket of experimental values of $R_1 \in [5.57-6.83]$.

To evaluate theoretically the width we proceed in the following way. $R_1$ is evaluated as a function of $\gamma ',\delta '$ and we take a band of values $\gamma ',\delta '$ inside the rectangle of Eqs. (23) that gives $R_1$ between 5.5 and 6.9. This band is shown in Fig. 7.

Fig. 7

Shaded area: overlap of the region $-1< \gamma ' < 1$, $-1.3< \delta ' < 1.3$, giving $R_1$ between 5.5 and 6.9. The two near straight lines correspond to the experimental lower and upper limits of $R_1=5.5$ (a) and $R_1=6.9$ (b)

Fig. 8

Mass distributions $d\Gamma /dM_{\mathrm{inv}}$ for the cases of Eq. (39)

We also plot in the figure the values of $\gamma ',\delta '$ that lead to the experimental lower and upper limits of $R_1$. The accepted value of $\gamma ',\delta '$ with these constraints are those in the shaded overlap region of Fig. 7. We observe then that it is possible to explain the experimental value of $R_1$ with our theory with values of $\gamma ',\delta '$ consistent with the large $1/N_c$ limit within uncertainties.

The challenge of the approach is now to make predictions for the $D_s^+ \rightarrow \pi ^0 K^+ K_S^0$ reaction to be contrasted with coming results from BESIII. For this purpose we take random numbers of $\gamma ', \delta '$ in the overlap region of Fig. 7 and evaluate $R_2$ for each of them. We find results in the range

$$\begin{aligned} R_2^{theo}\in [1.20, 1.60] \,. \end{aligned}$$

We also evaluate the average and the dispersion and find

$$\begin{aligned} R_2^{theo} \simeq 1.31 \pm 0.12 \,. \end{aligned}$$

We can convert this result into a branching ratio using the experimental branching ratio of Eq. (35). Adding the three errors in quadrature we obtain

$$\begin{aligned}&{\mathrm {Br}}[D_s^+ \rightarrow \pi ^0 a_0(1710); a_0(1710)\rightarrow K^+ K_S^0]\nonumber \\&\quad \simeq (1.3 \pm 0.4)\times 10^{-3} \,, \end{aligned}$$

(38)

the largest source of error coming from the experimental branching ratio of Eq. (35).

To finalize our study we plot in Fig. 8 the results of $d\Gamma /dM_{\mathrm{inv}}(K{\bar{K}})$ of Eq. (30) with the different amplitudes $t_i$ of Eq. (29), with

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathrm{1)}~ t_i={{\tilde{t}}_{f_0}} \mathrm{~part~ of~} t_{K^+ K^-} \\ \mathrm{2)}~ t_i={{\tilde{t}}_{a_0}} \mathrm{~part~ of~} t_{K^0 {\bar{K}}^0} \\ \mathrm{3)}~ t_i=t_{K^+ K^-} \\ \mathrm{4)}~ t_i=t_{K^0 {\bar{K}}^0}\,. \end{array}\right. } \end{aligned}$$

(39)

We show the distributions with a global normalization in arbitrary units for a value of the parameters $\gamma ' =-0.5$, $\delta ' =-0.75$, in the middle of the allowed region of Fig. 7. The strength of the distributions for other parameters in the allowed band can change about a factor of two, but the relative strengths are practically unaltered. This allows us to reach some conclusions from there.

As we can see, the differential mass distribution for the case of only the $f_0(1710)$ contribution has a bigger strength than the one with only the $a_0(1710)$ contribution. The peak of the $a_0$ contribution is displaced to the right relative to the $f_0$ contribution because we use the theoretical mass of [5] for the $a_0$ [see Eq. (32)]. This distribution should be the same seen in the $D_s^+ \rightarrow \pi ^0 K^+ K_S^0$ reaction around the peak. It will be most interesting to see the peak position in the coming experiment of the $D_s^+ \rightarrow \pi ^0 K^+ K_S^0$ decay. Note that uncertainties of $30-40$ MeV in the predicted position of the resonance are normal in the approach of [5]. The sharp peak seen in some curves correspond to cusp at the $K^* {\bar{K}}^*$ threshold, indicating the major role played by this channel in the reactions. It would be washed out if we take into account the width of the $K^*$, but we avoid doing this exercise, since we only wish to show the main effect of the interference of the amplitudes.

What is clear from the figure is that in the $K^0 {\bar{K}}^0$ mass distribution there has been a constructive interference of the $f_0$ and $a_0$ resonances, while in the $K^+ K^-$ mass distribution the interference has been destructive. This is exactly the reason suggested in the analysis of the $D_s^+ \rightarrow \pi ^+ K^+ K^-$ and $D_s^+ \rightarrow \pi ^+ K_S^0 K_S^0$ reactions [23] to justify the existence of the $a_0(1710)$ resonance, which should give the same $K^+ K^-$ or $K^0 {\bar{K}}^0$ mass distributions should there be only the $f_0(1710)$ state.

4 Conclusions

The appearance of the $D_s^+ \rightarrow \pi ^+ K_S^0 K_S^0$ experiment [23] contrasting the results with those observed in the $D_s^+ \rightarrow \pi ^+ K^+ K^-$ reaction in [24] and claiming the existence of an $a_0$ resonance around 1710 MeV, the isospin parter of the $f_0(1710)$ (with mass 1735 MeV in the RPP), motivated us to perform this work, since indeed such a resonance had been predicted in Ref. [5] as a molecular state of $K^* {\bar{K}}^*$ and other vector–vector coupled channels, and was corroborated in the work of Ref. [20] .

We looked into the possible ways that the $f_0(1710)$ and $a_0(1710)$ could be produced in the $D_s^+ \rightarrow \pi ^+ K^+ K^-, \pi ^+ K^0 {\bar{K}}^0, \pi ^0 K^+ {\bar{K}}^0$ decays and we identified five different modes in which they could be produced. Three of them associated with external emission, to which we gave weights $A, A\alpha , A \beta$ and two modes associated with internal emission with weights $A\gamma , A \delta$. The value of A is irrelevant since it is related to the global strength and disappears when we perform ratios of rates at the peak of the $K{\bar{K}}$ distributions. While it might look like we have four free parameters, this is not the case, and we showed that taking $A=1$, we could write the amplitudes in terms of two effective free parameters $\gamma ', \delta '$ with a range of values restricted by the large $N_c$ constraints. We calculated the ratio of the $D_s^+ \rightarrow \pi ^+ K^0 {\bar{K}}^0$ and $D_s^+ \rightarrow \pi ^+ K^+ K^-$ decay widths $R_1$, as a function of $\gamma ', \delta '$ and looked for the overlap region of the $\gamma '$ and $\delta '$ parameters that give the experimental band for this ratio with the constraint $|\gamma '| <1$, $|\delta '|<1.3$. The overlap region with these constraints allowed us to determine the $\gamma ',\delta '$ parameters within a reasonable range. In this way we have shown that the picture of [5, 20] for the $a_0(1710)$ state provides results for the ratio $R_1$ in agreement with the findings of the experiment.

Another interesting result of our study is that we make predictions for the branching ratio of the, yet, unknown results for the $D_s^+ \rightarrow \pi ^0 K^+ K_S^0$ reaction. We calculated this branching fraction using values of $\gamma ',\delta '$ randomly chosen from the allowed region for the ratio of $R_1$, and counting different uncertainties we found a branching ratio for this reaction of $(1.3 \pm 0.4)\times 10^{-3}$. This is a prediction of our theoretical approach which is only tied to the theoretical couplings of the $f_0(1710)$ and $a_0(1710)$ resonances found in [5] to the different coupled channels that build up the resonance, their decay amplitudes to $K{\bar{K}}$, and to the experimental value of the ratio of branching ratios of $D_s^+ \rightarrow \pi ^+ K_S^0 K_S^0$ and $D_s^+ \rightarrow \pi ^0 K^+ K^-$ found in [23] at the peak of the $f_0$, $a_0$ $K{\bar{K}}$ distributions. An agreement of the coming results of the $D_s^+ \rightarrow \pi ^0 K^+ K_S^0$ reaction with the predictions made here would give a boost to the molecular interpretation on the nature of these two resonances. The present work makes then very valuable the expected results for the $D_s^+ \rightarrow \pi ^0 K^+ K_S^0$ reaction.