1 Introduction

The existence of black holes is an important prediction of the theory of general relativity. It has been confirmed frequently through the detection of gravitational waves by LIGO [1] and the observations of the shadow images of supermassive black holes M87* and Sgr A* by the Event Horizon Telescope (EHT) [2]. However, the theory of general relativity does not admit the emergence of dark energy responsible for the apparent accelerating expansion of the Universe. To cure the limits of general relativity, modified or extended gravity theories are necessarily given. Some of them are scalar-tensor theories [3,4,5], Einstein-æther theories [6,7,8], quantum gravity theories [9, 10] and Einstein-scalar-Gauss–Bonnet theories [11].

Several observations support the presence of magnetic fields around astrophysical black holes [12,13,14]. A possible generation of magnetic fields is due to the dynamo mechanism in the plasma of accretion disks around the central black holes [12]. The magnetic fields in the vicinity of the black holes is generally believed to transfer the energy from the accretion disc to relativistic jets. In this sense, they are helpful for one to understand the formation and energetics of the black hole jets. However, the supermassive black hole at the centre of the Galaxy is surrounded by a strong magnetic field independent of an accretion disc [14]. In spite of the different claim, the existence of an asymptotically uniform test magnetic field in the vicinity of a black hole was shown at large enough distance to the magnetar [15]. The obtainment of such an external, large-scale electromagnetic field is based on a Wald solution [16,17,18,19]. The Wald solution requires that the black hole should be uncharged like the Kerr background black hole or the Schwarzschild one. In addition to this requirement, the external magnetic field should be such a weak field that its strength is much smaller than \(10^{19}M_{\odot }/M\) Gauss [20], where \(M_{\odot }\) and M respectively correspond to the masses of the Sun and black hole. When the black hole is electrically charged, nonvacuum like the Kerr–Newman black hole or the Reissner–Nordström (RN) one, the Wald vector potential does not exactly satisfy the source-less Maxwell equations, as was claimed by Azreg–Aïnou [21]. This result is also suitable for the case of a uniform magnetic field near a nonvacuum black hole of modified gravity with extra fields. To satisfy the source-less Maxwell equations in the two cases, the Wald vector potential has to be modified appropriately. Although relatively weak external magnetic fields have a negligible effect on the spacetime background, they can strongly influence the motion of charged particles in the vicinity of the black hole horizon. The charged particle chaotic motions induced by the magnetic fields have appeared in a number of studies [22,23,24,25,26,27,28,29,30,31,32,33]. If the external magnetic fields have their strengths close to \(10^{19}M_{\odot }/M\) Gauss, they not only change the metric tensor of the black hole spacetime [34,35,36,37] but also influence the motion of neutral or charged particles in the vicinity of the black hole horizon. The chaotic motion of neutral particles can be found in several references [38,39,40,41,42,43].

Although a Hamiltonian system for the description of neutral or charged particle motion in the vicinity of a black hole immersed in an external electromagnetic field is inseparable and exhibits chaotic character in most cases, it or its time-transformed version may have more than two explicitly integrable splitting pieces. This brings a chance for the construction of explicit symplectic integrators in curved spacetimes [44,45,46,47,48,49,50]. The symplectic integrators preserve the symplectic structures of Hamiltonian dynamics, and show no secular drifts in errors of the integrals of motion [51, 52]. Thus, they are particularly adapted to mimicking the long-term dynamical evolution of Hamiltonian systems. The explicit symplectic methods have an advantage over the implicit ones [53, 54] in computational efficiency.

In addition to reliable numerical integration methods such as the symplectic integrators, efficient chaos detection methods are necessary to discriminate between order and chaos of Hamiltonian dynamics. The Poincaré map is a common chaos detection method applied to a conservative system with two degrees of freedom. The maximal Lyapunov exponent (mLE) is also a common chaos detection method used in a system with any dimensions. The fast Lyapunov indicator (FLI) [55] as a variant of the mLE is a quicker indicator to detect the chaotical behaviour. The mLE and FLI were developed as those independent of the choice of spacetime coordinates in general relativity [56, 57]. There are other chaos detection methods, which include the smaller alignment index (SALI) [58] and its generalized alignment index (GALI) [59], the 0–1 binary test correlation method [60], the recurrence plot (RP) method based on the recurrence quantification analysis [23, 61,62,63,64] and so on. Although these techniques have been shown to be very efficient to detect the chaos onset in many Newtonian gravitational systems, they have few applications in the context of relativistic gravitational problems. The RP method was applied to identify the transition between different dynamical regimes in the Kerr black hole background immersed in a weak, asymptotically uniform magnetic field [23, 63]. The SALI was used to trace the chaotic motion of charged particles around a deformed Schwarzschild black hole with an external magnetic field [65]. Recently, the 0–1 binary test correlation method was employed to identify chaos in magnetized Kerr–Newman spacetimes [43].

In the present paper, we use the RP method combined with an explicit symplectic method to study the chaotic dynamics of charged test particles around a hairy black hole with an external magnetic field in the Horndeski gravity [66]. Because the Horndeski gravity is a very general scalar-tensor theory belonging to a theory of modified gravity [67,68,69], we give the vector potential of electromagnetic field by modifying the Wald vector potential in Sect. 2. Then we explore the dynamical properties of charged test particles in Sect. 3. Finally, our main results are concluded in Sect. 4.

2 Electromagnetic field of hairy black hole in Horndeski gravity

There have been many interesting solutions describing hairy black holes in literature (see e.g. [66,67,68,69,70,71,72,73]). Here, we focus on a hairy black hole spacetime in Horndeski gravity [66,67,68,69]. Above all, the expressions for the vector potential and electromagnetic field around the hairy black hole are given.

2.1 Hairy black hole solution in sqrt quartic Horndeski gravity

Horndeski gravity [66] is a very general scalar-tensor theory, which belongs to a theory of modified gravity. A scalar field \(\phi \) in the theory has a shift symmetry \(\phi \rightarrow \phi + \text {const}\). We focus on one black hole solution in the class of Horndeski theory, which is obtained from the action [67,68,69]

$$\begin{aligned} S=\int \textrm{d}^4 x \sqrt{-g}\left( {\mathcal {L}}_2+{\mathcal {L}}_4\right) , \end{aligned}$$
(1)

where \(\textrm{d}^4 x\) is products of infinitesimal spacetime coordinate elements (such as dt, dx, dy and dz, or dt, dr, \(d\theta \) and \(d\varphi \)), and g is the determinant of a metric matrix \(g_{\alpha \beta }\). In addition, \({\mathcal {L}}_2\) and \({\mathcal {L}}_4\) are two Lagrangian terms:

$$\begin{aligned} {{{\mathcal {L}}}}_2= & {} G_2(X), \end{aligned}$$
(2)
$$\begin{aligned} {{{\mathcal {L}}}}_4= & {} G_4(X) R + G_{4,X} \left[ (\Box \phi )^2 -(\nabla _\mu \nabla _\nu \phi )^2 \right] . \end{aligned}$$
(3)

Here, \(G_2\) and \(G_4\) are two arbitrary functions of a canonical kinetic term \(X =-\partial ^\mu \phi \partial _\mu \phi / 2\). \(G_{4,X}\) corresponds to a derivative of \(G_4\) with respect to X, and R stands for the Ricci scalar. \((\Box \phi )^2=\left( \partial _{\mu } \partial ^{\mu }\phi \right) ^2\), and \(\left( \nabla _\mu \nabla _\nu \phi \right) ^2 = \nabla _\mu \nabla _\nu \phi \nabla ^\nu \nabla ^\mu \phi \). For example, \(G_2\) and \(G_4\) are chosen as

$$\begin{aligned} G_2=\eta X, \quad G_4=1 / (16 \pi )+\beta \sqrt{-X}, \end{aligned}$$
(4)

where \(\eta \) and \(\beta \) represent two dimensionless parameters. It is clear that \(G_2\) depends on the canonical kinetic term only. \(G_4\) has the constant term \(1/(16 \pi )\) associated with an Einstein–Hilbert piece in the action and the X-dependence term yielding a contribution to the Noether current that is independent of the scalar field \(\phi \). Because of the expression of the Lagrangian term \({\mathcal {L}}_4\), the theory given by the action (1) was referred to as a “sqrt quartic Horndeski gravity” in [67, 68].

Using the action (1), the authors of [67, 68] wrote a hairy black hole solution in Boyer–Lindquist coordinates as

$$\begin{aligned} ds^{2}= & {} g_{\mu \nu }dx^{\mu }dx^{\nu } \nonumber \\= & {} -(1-\frac{2M}{r}-\frac{8\pi \rho _{\textrm{eff}}}{r^2})dt^{2} \nonumber \\{} & {} +(1-\frac{2M}{r}-\frac{8\pi \rho _{\textrm{eff}}}{r^2})^{-1} dr^{2}\nonumber \\{} & {} +r^{2}d \theta ^{2} +r^{2}\sin ^{2} \theta d \varphi ^2, \end{aligned}$$
(5)

where \(\rho _{\textrm{eff}} = \beta ^2 / \eta \) is a scalar hairy parameter. If the hairy parameter satisfies the condition

$$\begin{aligned} \rho _{\textrm{eff}}\ge -M^2/(8\pi ), \end{aligned}$$
(6)

the black hole solution has one or two event horizons \(r_{\pm }=M\pm \sqrt{M^2+8\pi \rho _{eff}}\). For \(\rho _{\textrm{eff}}=- M^2/(8\pi )\), the metric (5) corresponds to the black hole with one horizon \(r=M\). When \(-M^2/(8\pi )<\rho _{\textrm{eff}}<0\), the metric is the RN-like black hole with two event horizons, where \(Q_{sc}=\sqrt{-8\pi \rho _{\textrm{eff}}}\) is a scalar charge [74]. Although it is not an electric charge of the black hole, it has a physical behaviour like the electric charge effect of the black hole. If the hairy parameter \(\rho _{\textrm{eff}}\) is nonzero, it yields an extra force for the neutral black hole. When \(\rho _{\textrm{eff}}<0\), the extra force leads to the acceleration of positively charged particles in the increasing \(\varphi \) direction, but to the deceleration of negatively charged particles. In a word, the effect should be considered in the vicinity of the event horizon. For \(\rho _{\textrm{eff}}=0\), the metric becomes the Schwarzschild spacetime with one horizon \(r=2M\). If \(\rho _{\textrm{eff}}>0\), the metric is unlike the RN black hole but has two event horizons. However, the metric is no longer any black hole solution when \(\rho _{\textrm{eff}}< -M^2/(8\pi )\) because no event horizon can exist in this case. Throughout this paper, the constant of gravity G and the speed of light c take one geometric unit, \(G=c=1\).

The hairy black hole spacetime (5) is spherically symmetric and asymptotically flat. There are two Killing vectors \(\xi ^{\mu }_{t}=(1,0,0,0)\) and \(\xi ^{\mu }_{\varphi }=(0,0,0,1)\). They determine the conserved energy \({\bar{E}}\) and orbital angular momentum \({\bar{L}}\) per unit mass of a test particle:

$$\begin{aligned} {\bar{E}}= & {} -u^{\mu }\xi _{t\mu }=-u^{\mu }g_{\mu \nu }\xi ^{\nu }_{t} =-g_{tt}{\dot{t}}=-{\bar{P}}_t, \end{aligned}$$
(7)
$$\begin{aligned} {\bar{L}}= & {} u^{\mu }\xi _{\varphi \mu }=u^{\mu }g_{\mu \nu }\xi ^{\nu }_{\varphi } = g_{\varphi \varphi }{\dot{\varphi }}={\bar{P}}_{\varphi }, \end{aligned}$$
(8)

where the dots denote the derivatives of the coordinates t and \(\varphi \) with respect to the proper time \(\tau \), i.e. two components of the 4-velocity \(u^{\mu }={\dot{x}}^{\mu }\). \({\bar{P}}_t\) and \({\bar{P}}_{\varphi }\) are two components of the generalized 4-momentum \({\bar{P}}_{\mu }=g_{\mu \nu }{\dot{x}}^{\nu }\). For the test particle with mass m around the black hole, its motion can be described by a Hamiltonian system

$$\begin{aligned} H= & {} \frac{1}{2m} g^{\mu \nu }P_{\mu }P_{\nu } \nonumber \\= & {} -\frac{\text {E}^2}{2m \left( 1-\frac{2M}{r}-\frac{8\pi \rho _{\text {eff}}}{r^2}\right) }+\frac{L^2 \csc ^2\theta }{2m r^2} \nonumber \\{} & {} +\frac{P^2_r}{2m} \left( 1-\frac{2M}{r}-\frac{8\pi \rho _{\text {eff}}}{r^2}\right) +\frac{P_{\theta }^2}{2m r^2}, \end{aligned}$$
(9)

where \(P_{\mu }=m{\bar{P}}_{\mu }\), \(E=m{\bar{E}}\) and \(L=m{\bar{L}}\). This Hamiltonian is a conserved quantity

$$\begin{aligned} H=-\frac{m}{2}, \end{aligned}$$
(10)

which is due to the rest mass relation \(g_{\mu \nu }{\dot{x}}^{\mu }{\dot{x}}^{\nu }=-1\). There is a fourth constant of motion, which is obtained from the separation of variables in the Hamilton–Jacobi equation of the Hamiltonian system (9). The fourth constant reads

$$\begin{aligned} C_k= & {} \frac{r^2\text {E}^2}{m \left( 1-\frac{2M}{r}-\frac{8\pi \rho _{\text {eff}}}{r^2}\right) }-mr^2 \nonumber \\{} & {} -\frac{r^2P^2_r}{m} \left( 1-\frac{2M}{r}-\frac{8\pi \rho _{\text {eff}}}{r^2}\right) \nonumber \\= & {} \frac{P_{\theta }^2}{m}+\frac{L^2 \csc ^2\theta }{m}, \end{aligned}$$
(11)

where \(C_k\) is the Carter-like constant. Thus, the Hamiltonian system (9) is integrable and has formally analytical solutions.

For simplicity, we give dimensionless operations to the Hamiltonian system (9) via scale transformations: \(t\rightarrow Mt\), \(\tau \rightarrow M\tau \), \(r\rightarrow Mr\), \(\rho _{\text {eff}}\rightarrow M^2 \rho _{\text {eff}}\), \(E\rightarrow mE\), \(L\rightarrow mML\), \(P_r\rightarrow mP_r\), \(P_{\theta }\rightarrow mMP_{\theta }\), \(H\rightarrow mH\) and \(C_k\rightarrow mM^2C_k\). In this way, the mass factors m and M are eliminated in all the above expressions. That is, \(P_{\mu }={\bar{P}}_{\mu }\), \(E={\bar{E}}\), \(L={\bar{L}}\), \(\cdots \). Hereafter, the scaled quantities are still represented in terms of \(P_{\mu }\), E, L, \(\rho _{\text {eff}}\) and so on for convenience. These operations give not only the simple expressions but also the links between the practical quantities and the scaled ones. For instance, the transformation \(\rho _{\text {eff,pra}}\rightarrow M^2 \rho _{\text {eff,sca}}\) means that the scaled value of the hairy parameter \(\rho _{\textrm{eff, sca}}\) corresponds to its practical value \(\rho _{\text {eff,pra}}\) equal to \(M^2\rho _{\textrm{eff, sca}}\).

2.2 Electromagnetic field around the hairy black hole

Wald [16] considered the solution for an electromagnetic field of a vacuum, stationary, axisymmetric black hole immersed in a uniform magnetic field aligned with the axis of symmetry of the black hole. The solution is described by the vector potential

$$\begin{aligned} A^{\mu } =C_{t}(B)\xi ^{\mu }_{t}+C_{\varphi }(B)\xi ^{\mu }_{\varphi }, \end{aligned}$$
(12)

where coefficients \(C_{t}\) and \(C_{\varphi }\) depend on the magnetic field strength B. When the black hole is neutral, the coefficients obtained from the Wald’s solution are

$$\begin{aligned} C_{t}=aB, \quad C_{\varphi }=\frac{B}{2}, \end{aligned}$$
(13)

where a is the rotation angular momentum of the black hole. If the black hole has an electric charge Q, the coefficients are

$$\begin{aligned} C_{t}=aB+\frac{Q}{2M},\quad C_{\varphi }=\frac{B}{2}. \end{aligned}$$
(14)

Azreg–Aïnou [21] pointed out that the potential (12) given by the coefficients (13) in the Kerr background metric (including the Schwarzschild one) is an exact solution of the source-less Maxwell equations

$$\begin{aligned}{} & {} F_{\alpha \beta ;\gamma }+F_{\gamma \alpha ;\beta }+F_{\beta \gamma ;\alpha }=0, \end{aligned}$$
(15)
$$\begin{aligned}{} & {} J^{\mu }=F^{\mu \nu }_{;\nu }=0, \end{aligned}$$
(16)

where \(F_{\mu \nu }=A_{\nu ,\mu }-A_{\mu ,\nu }\) is the electromagnetic field tensor. However, the potential (12) given by the coefficients (14) in the Kerr–Newman metric (including the RN one) does not exactly satisfy Eq. (16) because the electric charge density \(J^t\) and the current density \(J^{\varphi }\) are nonvanishing for the charged, nonvacuum black hole metric. This thing also occurs in the case of nonvacuum black holes under theories of modified gravity. Extra sources are included in the theories of modified gravity, therefore, the coefficients (12) or (13) based on the vacuum black holes are not suitable for the nonvacuum ones in general. It is necessary to give extensions to Wald’s coefficients (12) or (13) for black holes in Hořava–Lifshitz gravity [75] and in a braneworld [76]. If the coefficients \(C_{t}\) and \(C_{\varphi }\) are assumed to be functions of the coordinates r and \(\theta \), the potential may be solved from the source-less Maxwell field equations (15) and (16). Following this idea, Azreg–Aïnou modified the coefficients (13) as

$$\begin{aligned} C_{t}=aB+c_t, \quad C_{\varphi }=\frac{B}{2}+c_{\varphi }, \end{aligned}$$
(17)

where \(c_t\) and \(c_{\varphi }\) are functions of the coordinates r and \(\theta \) and the parameters a and B. In the Gürses–Gürsey metric [77], Eq. (12) with Eq. (17) can satisfy Eq. (15) and two equations \(J^{r}=J^{\theta }=0\) of Eq. (16). When the black hole is nonrotating and spherically symmetrical, \(c_t\) and \(c_{\varphi }\) do not depend on \(\theta \). If \(g_{tt}=-\left[ 1-2(f_1r+f_2)/r^2\right] =-1/g_{rr}\), \(c_t\) solved from the equation \(J^{t}=0\) is

$$\begin{aligned} c_{t}=-\frac{\kappa _{1}}{rg_{tt}}-\frac{\kappa _{2}}{g_{tt}}, \end{aligned}$$
(18)

where \(\kappa _{1}\) and \(\kappa _{2}\) are integration constants. In principle, the two constants can be chosen arbitrarily. However, they must be \(\kappa _{1}=Q\) and \(\kappa _{2}=0\) for the black hole with an electric Q, and \(\kappa _{1}=\kappa _{2}=0\) for the black hole that is neutral. Such choices are determined by the Coulomb potential \(-Q/r\), which corresponds to a nonzero covariant component of the four-vector electromagnetic potential \(A_t=-(\kappa _{1}/r)-\kappa _{2}\). The equation \(J^{\varphi }=0\) yields

$$\begin{aligned} c_{\varphi }=\frac{Bf_2}{r^2}. \end{aligned}$$
(19)

In light of the results of Azreg–Aïnou, we can easily write the expression for the vector potential of electromagnetic field around the hairy black hole (5) as a particular form of the Gürses–Gürsey metric [77]. Here, \(Q=0\), \(f_1=M\) and \(f_2=4\pi \rho _{\textrm{eff}}\). Considering Eqs. (12), (17)–(19), we have the vector potential

$$\begin{aligned} A^{\alpha }&=\left( \frac{4 \pi }{r^2}B \rho _{\text {eff}}+\frac{B}{2}\right) \xi ^{\alpha }_{\varphi }, \end{aligned}$$
(20)

which is equivalent to the following expression

$$\begin{aligned} A_{\varphi }=\frac{1}{2}B\left( r^2+8\pi \rho _{\text {eff}}\right) \sin ^2\theta . \end{aligned}$$
(21)

This vector potential is an exact solution of the source-less Maxwell field equations (15) and (16). Note that the vector potential should have been \(A_{\varphi }=\frac{1}{2}Br^2\sin ^2\theta \) based on the Wald potential, but such a vector potential satisfies Eq. (15) and the two equations \(J^{r}=J^{\theta }=0\) of Eq. (16) except the other equations \(J^{t}=J^{\varphi }=0\) of Eq. (16).

In order to obtain nonzero orthonormal components of the electromagnetic field, we introduce four orthogonal basis vectors in an observer’s reference frame. The observer basis \(\{e_{\hat{t}}, e_{\hat{r}}, e_{\hat{\theta }}, e_{\hat{\varphi }}\}\) is expressed in the coordinate basis \(\{\partial _{ t},\partial _{ r}, \partial _{\theta }, \partial _{\varphi }\}\) as

$$\begin{aligned} e_{\hat{\mu }}=e_{\hat{\mu }}^{\nu }\partial _{\nu }, \end{aligned}$$
(22)

where the transform matrix \(e_{\hat{\mu }}\) satisfies the relation \(g_{\mu \nu }e_{\hat{\alpha }}^{\mu }e_{\hat{\beta }}^{\nu }=\eta _{\hat{\alpha }\hat{\beta }}\). \(\eta _{\hat{\alpha }\hat{\beta }}\) is the metric of Minkowski spacetime. For the hairy black hole metric (5), a simple choice of the basis is given as follows:

$$\begin{aligned} \begin{matrix} \\ e_{\hat{\mu }}^{\nu }=\\ \\ \end{matrix} \begin{bmatrix} \sqrt{-g^{tt}} &{} 0 &{} 0 &{} 0\\ 0 &{}\sqrt{g^{rr}} &{} 0&{} 0\\ 0 &{} 0 &{}\sqrt{g^{\theta \theta }}&{} 0\\ 0 &{} 0 &{} 0&{}\sqrt{g^{\varphi \varphi }}\\ \end{bmatrix}. \end{aligned}$$
(23)

The 4-velocity of the rest observer \(U^{\alpha }\) at the reference frame is

$$\begin{aligned} U^{\alpha }= & {} \sqrt{-g^{tt}}(1,0,0,0), \end{aligned}$$
(24)
$$\begin{aligned} U_{\alpha }= & {} \sqrt{-g_{tt}}(-1,0,0,0). \end{aligned}$$
(25)

The components of the electric and magnetic fields in the frame read

$$\begin{aligned} E_{\alpha }= & {} F_{\alpha \beta }U^{\beta }, \end{aligned}$$
(26)
$$\begin{aligned} B_{\alpha }= & {} \frac{1}{2}\epsilon _{\beta \alpha \mu \nu }F^{\mu \nu }U^{\beta }, \end{aligned}$$
(27)

where \(\epsilon _{\beta \alpha \mu \nu }\) is the Levi–Civita tensor. Thus, the nonvanishing orthonormal components of the electromagnetic field measured by the zero angular momentum observer are

$$\begin{aligned} B_{\hat{r}}= & {} B_{r}e_{\hat{r}}^{r}=B(1+\frac{8\pi \rho _{\text {eff}}}{r^{2}})\cos \theta , \end{aligned}$$
(28)
$$\begin{aligned} B_{\hat{\theta }}= & {} B_{\theta }e_{\hat{\theta }}^{\theta }=-B\sin \theta \sqrt{1-\frac{2}{r}-\frac{8\pi \rho _{\text {eff}}}{r^2}}. \end{aligned}$$
(29)
Fig. 1
figure 1

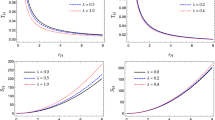
Magnetic configurations of the hairy black hole. a The total magnetic field \(B_{tot}\) with \(B=1\) and \(\theta =\pi /4\) for three positive values of the hairy parameter \(\rho _\text {{eff}}\). b The total magnetic field \(B_{tot}\) for three negative values of the hairy parameter \(\rho _\text {{eff}}\). c The total magnetic field \(B_{tot}\) with \(B=1\) and \(\rho _\text {{eff}}=0.01\) for different observational angles \(\theta \). d Magnetic field lines in the vicinity of the hairy black hole in the \(x-z\) plane, where \(B=1\), \(\rho _\text {{eff}}=0.001\) for blue lines, and \(\rho _\text {{eff}}=0.01\) for pink lines

Full size image

The total magnetic field is \(B_{tot}=\sqrt{B_{\hat{r}}^{2}+B_{\hat{\theta }}^{2}}\). In Fig. 1, we plot \(B_{tot}\) varying with the parameter \(\rho _\text {{eff}}\) or the radial distance r. It is clear that the magnetic field increases with an increases of the parameter \(|\rho _{\text {eff}}|\), but decreases with an increases of \(\theta \).

3 Motions of charged particles around hairy black holes in external magnetic fields

Suppose that a particle with a charge q moving around the hairy black hole with the external magnetic field (21). The momentum in Eq. (9) is \(P_{\mu }=p_{\mu }-qA_{\mu }\). The charged-particle motion is described by the super-Hamiltonian

$$\begin{aligned} K= & {} \frac{1}{2}g^{\mu \nu }(p_{\mu }-qA_{\mu })(p_{\nu } -qA_{\nu }) \nonumber \\= & {} -\frac{1}{2}\left( 1-\frac{2}{r}-\frac{8\pi \rho _{\text {eff}}}{r^2}\right) ^{-1} E^{2} \nonumber \\{} & {} +\frac{1}{2}\left( 1-\frac{2}{r} -\frac{8 \pi \rho _{\text {eff}}}{r^2}\right) p^{2}_{r} +\frac{1}{2}\frac{p^{2}_{\theta }}{r^2} \nonumber \\{} & {} +\frac{1}{2r^2\sin ^2\theta }\left[ L-\frac{b}{2}\left( r^2+8\pi \rho _{\text {eff}}\right) \sin ^{2}\theta \right] ^{2}, \end{aligned}$$
(30)

where \(b=qB\). The scale transformations in K are similar to those in H. In addition, \(q\rightarrow mq\) and \(B\rightarrow B/M\) are used. Similar to H, K still satisfies the constraint

$$\begin{aligned} K=-\frac{1}{2}. \end{aligned}$$
(31)

However, the external magnetic field leads to the absence of the fourth constant (11). As a result, the Hamiltonian (30) is nonintegrable. This fact shows that the weak electromagnetic field can exert an influence on the charged particle dynamics although it gives no contribution to the geometry of spacetime.

3.1 Explicit symplectic integrators

Symplectic schemes are naturally viewed as the most appropriate solvers for long-term integration of the Hamiltonian system (30) because they preserve the symplectic structure of Hamiltonian dynamics. Explicit symplectic methods are less than implicit ones at the expense of computational time. The Hamiltonian is not directly split into two explicitly integrable pieces and then explicit symplectic integrators become useless. However, they are still variable when the Hamiltonian is split into more than two explicitly integrable parts. In fact, the construction of explicit symplectic schemes based on the multi-part splitting method has appeared in recent literature [44,45,46,47,48,49,50].

The Hamiltonian (30) is separated in the form

$$\begin{aligned} K=K_1+K_2+K_3+K_4+K_5, \end{aligned}$$
(32)

where all sub-Hamiltonians are written as follows:

$$\begin{aligned} K_1= & {} \frac{1}{2r^2\sin ^2\theta }\left[ L-\frac{b}{2}(r^2+8\pi \rho _{\text {eff}})\sin ^{2}\theta \right] ^{2} \nonumber \\{} & {} -\frac{{E}^{2}}{2}\left( 1-\frac{2}{r}-\frac{8\pi \rho _\text {eff}}{r^2}\right) ^{-1}, \end{aligned}$$
(33)
$$\begin{aligned} K_{2}= & {} \frac{1}{2}p^{2}_{r}, \end{aligned}$$
(34)
$$\begin{aligned} K_{3}= & {} -\frac{1}{r}p^{2}_{r}, \end{aligned}$$
(35)
$$\begin{aligned} K_{4}= & {} \frac{p^{2}_{\theta }}{2r^2}, \end{aligned}$$
(36)
$$\begin{aligned} K_{5}= & {} -\frac{4\pi \rho _\text {eff}}{r^2}p^{2}_{r}. \end{aligned}$$
(37)

It is easy to check that each of the five parts has an analytical solution as an explicit function of the proper time \(\tau \). Solvers for the sub-Hamiltonians \(K_1\), \(K_2\), \(K_3\), \(K_4\), and \(K_5\) are termed \(\varkappa _1\), \(\varkappa _2\), \(\varkappa _3\), \(\varkappa _4\) and \(\varkappa _5\), respectively.

Setting h as a time step, we have a second-order explicit symplectic integrator

$$\begin{aligned} S2 (h)= \chi ^*(\frac{h}{2})\times \chi (\frac{h}{2}), \end{aligned}$$
(38)

where two first-order solvers are

$$\begin{aligned} \chi (h)= & {} \varkappa _5(h)\times \varkappa _4(h)\times \varkappa _3(h)\times \varkappa _2(h)\times \varkappa _1(h), \end{aligned}$$
(39)
$$\begin{aligned} \chi ^*(h)= & {} \varkappa _1(h)\times \varkappa _2(h)\times \varkappa _3(h)\times \varkappa _4(h)\times \varkappa _5(h). \end{aligned}$$
(40)

Composing three second-order methods, we obtain a fourth-order explicit symplectic algorithm

$$\begin{aligned} S4=S2(\gamma h)\times S2(\delta h)\times S2(\gamma h), \end{aligned}$$
(41)

where \(\gamma =1/(1-\root 3 \of {2}) \) and \(\delta =1-2\gamma \). The construction is that of Yoshida [78]. By the component of more first-order operators \(\chi \) and \(\chi ^*\), an optimized fourth-order partitioned Runge–Kutta (PRK) symplectic algorithm was given in [49, 50] by

$$\begin{aligned} PRK_64= & {} \chi ^* (\alpha _{12} h)\times \chi (\alpha _{11} h)\times \cdots \nonumber \\{} & {} \times \chi ^* (\alpha _2 h) \times \chi (\alpha _1 h), \end{aligned}$$
(42)

where time coefficients are

$$\begin{aligned} \alpha _1= & {} \alpha _{12}= 0.079203696431196, \\ \alpha _2= & {} \alpha _{11}= 0.130311410182166, \\ \alpha _3= & {} \alpha _{10}= 0.222861495867608, \\ \alpha _4= & {} \alpha _9=-0.366713269047426, \\ \alpha _5= & {} \alpha _8= 0.324648188689706, \\ \alpha _6= & {} \alpha _7= 0.109688477876750. \end{aligned}$$
Fig. 2
figure 2

a, b Hamiltonian errors \(\varDelta K=K+1/2\) for several explicit symplectic algorithms integrating Orbits 1 and 2, which have common parameters \(E=0.996\), \(L=4.6\), \(\rho _\text {{eff}}=0.001\) and initial conditions \(r=16\), \(\theta =\pi /2\), but different magnetic parameters b. c Poincaré sections of the two orbits. d FLIs of the two orbits. e, f RPs of the two orbits. Here, i corresponds to the time \(\tau _i=i\times 10000\). Many diagonal lines parallel to the main diagonal \(j=i\) show the regular dynamics of Orbit 1, whereas no diagonal lines parallel to the main diagonal describe the chaotic dynamics of Orbit 2. That is, the dynamical features of Orbits 1 and 2 described by the RPs are consistent with those given by the techniques of Poincaré sections and FLIs

Full size image
Fig. 3
figure 3

a Effective potentials for uncharged test particles moving at three different planes, where common parameters are \(L=4\) and \(\rho _\text {{eff}}=0.001\). b Stable circular orbits at the three different planes. c RP of the circular orbit at the plane \(\theta =\pi /4\) corresponding to \(E=0.98\) and the radius \(r=28.62\). d RP of the circular orbit at the plane \(\theta =\pi /2\) corresponding to \(E=0.96\) and the radius \(r=11.95\)

Full size image
Fig. 4
figure 4

a FLI describing a dynamical transition to chaos with the energy E increasing, where the initial conditions are \(r=16\), \(\theta =\pi /2\), and the other parameters are \(L=4.6\), \(b=0.0001\), \(\rho _\text {{eff}}=0.0001\). Chaos occurs at \(E=0.9977\) and \(0.9992\le E<1\). b Poincaré sections for four values of the energy E. c–f RPs for four values of the energy E. The RPs in (c) and (d) correspond to strong chaos. The RP in (e) seems to exhibit a symmetrical structure with diagonal lines parallel to the main diagonal, while corresponds to weak chaos. The RP in (f) shows the regular dynamics

Full size image
Fig. 5
figure 5

a FLI describing a dynamical transition to chaos with the angular momentum L increasing, where the initial conditions are \(r=16\), \(\theta =\pi /2\), and the other parameters are \(E=0.996\), \(b=0.0006\), \(\rho _\text {{eff}}=0.0001\). The transition to the regular dynamics from the chaotic dynamics at \(L=4.07\). b Poincaré sections for four values of the angular momentum L. c–f RPs for four values of the angular momentum L. The RPs in (c) and (d) correspond to chaos, while the RPs in (e) and (f) show the regular dynamics

Full size image

Let us take \(h=1\), \(E=0.996\), \(L=4.6\) and \(\rho _\text {{eff}}=0.001\). The initial conditions are \(r=16\), \(\theta =\pi /2\) and \(p_r=0\). The initial value \(p_{\theta }>0\) is given by Eqs. (29) and (30). The magnetic field parameters are \(b=10^{-4}\) for Orbit 1 and \(b=10^{-3}\) for Orbit 2. When the integration time reaches \(10^{7}\), the three methods S2, S4 and \(PRK_64\) give no secular drifts to Hamiltonian errors \(\varDelta K=K+1/2\) for integrations of the two orbits in Fig. 2a, b. They exhibit an advantage of symplectic methods in the energy conservation. It is also shown that S4 is four orders of magnitude better than S2 but two orders of magnitude poorer than \(PRK_64\) in accuracy. Thus, the algorithm \(PRK_64\) is employed in later computations.

3.2 Chaos detection methods

The phase space structures of Orbits 1 and 2 in Fig. 2a, b can be described through the Poincaré map in the two dimensional \(r-p_r\) plane. In fact, these points \((r,p_r)\) obtained from the Poincaré map are intersections of the particles’ orbits with the surface of section \(\theta =\pi /2\) and \(p_{\theta }>0\). Orbit 1 is regular and nonchaotic because the intersection points form a closed curve in Fig. 2c. However, Orbit 2 is chaotic because the intersection points behave in a random distribution way. The Poincaré map method is useful to classify whether a number of orbits in a conservative system with four-dimensional phase space are regular or chaotic.

Fig. 6
figure 6

a FLI describing a dynamical transition to chaos with the magnetic parameter b increasing, where the initial conditions are \(r=10\), \(\theta =\pi /2\), and the other parameters are \(E=0.996\), \(L=4.4\), \(\rho _\text {{eff}}=0.0001\). Chaos exists at \(b=-0.0008,0.0003,0.0006\) and \(0.0008\le b\le 0.001\). b Poincaré sections for four values of the magnetic parameter b. c–f RPs for four values of the magnetic parameter b. The RPs in (c) and (d) correspond to chaos, while the RPs in (e) and (f) show the regular dynamics

Full size image
Fig. 7
figure 7

a FLI describing a dynamical transition to chaos with the hairy parameter \(\rho _\text {{eff}}\) increasing, where the initial conditions are \(r=16\), \(\theta =\pi /2\), and the other parameters are \(E=0.996\), \(L=4.6\), \(b=0.00088\). Chaos occurs when \(\rho _\text {{eff}}\ge 0.005\). b Poincaré sections for three values of the hairy parameter \(\rho _\text {{eff}}\). The RPs in (c) and (d) correspond to chaos

Full size image
Fig. 8
figure 8

Same as Fig. 7, but the initial conditions are \(r=9\), \(\theta =\pi /2\), and the other parameters are \(E=0.999\), \(L=4.6\), \(b=0.0001\). Chaos exists at \(-0.01\le \rho _\text {{eff}}\le -0.003\) and \(\rho _{\text {eff}}=0,0.005,0.006\)

Full size image
Fig. 9
figure 9

Same as Fig. 7, but the initial conditions are \(r=6\), \(\theta =\pi /2\), and the other parameters are \(E=0.996\), \(L=4.1\), \(b=-0.0008\). There is the chaotic dynamics when \(\rho _\text {{eff}}\ge -0.006\)

Full size image

The maximum Lyapunov exponent (mLE) is also a common tool to distinguish between regular motions and irregular ones. It is often used to quantify the rate of divergence between nearby orbits. If a bounded orbit has a positive Lyapunov exponent, it is chaotic; If the mLE of a bounded orbit vanishes, this orbit is ordered. It takes a very long time to calculate the mLE in a weakly chaotic orbit. The fast Lyapunov indicator (FLI) of Froeschlé et al. [55] is a quicker chaos indicator to investigate such a weak chaotic property. It was developed as a relativistic invariant form of two nearby orbits [56] from a modified version of the relativistic invariant Lyapunov exponent with two nearby orbits [57]. The linear growth of FLI with time shows the regularity of Orbit 1 in Fig. 2d, whereas the exponential growth of FLI indicates the chaoticity of Orbit 2.

Compared with the techniques of Poincaré map, mLE and FLI, the recurrence analysis method [23, 61,62,63,64] is rarely used to detect chaos from order in relativistic astrophysics. The method relates to the description of recurrence plots (RPs), which measure the recurrences of an orbit into the vicinity of previously reached phase-space points in terms of the recurrence quantification analysis. The method is described as follows. For a given phase-space variable \({{\textbf {x}}}(\tau )\) of an orbit at time \(\tau \) in a dynamical system, the recurrence matrix is defined as

$$\begin{aligned} {\textbf{R}}_{ij}(\varepsilon )=\varTheta (\varepsilon -||{{\textbf {x}}}(i)-{{\textbf {x}}}(j)||) \quad (i,j=1,\ldots ,N). \end{aligned}$$
(43)

Here, \(\varTheta \) is the Heaviside function: \(\varTheta (\vartheta )=0\) for \(\vartheta <0\) and \(\varTheta (\vartheta )=1\) for \(\vartheta \ge 0\). \(\varepsilon \) stands for a pre-defined threshold parameter. N represents the sampling number. When T is the total integration time, one of the sampling number corresponds to the time T/N. In this sense, i denotes the time \(\tau _i=iT/N\). \(||.\;||\) is the Euclidean norm \(L^2\). A visual plot of the recurrence matrix \({\textbf{R}}_{ij}\) is made of points (i, j), which correspond to the binary values 0 and 1. A black dot represents the pair (i, j) for \({\textbf{R}}_{ij}=1\) and a white dot denotes the pair (i, j) for \({\textbf{R}}_{ij}=0\). Because \({\textbf{R}}_{ij}={\textbf{R}}_{ji}\), the visual is symmetric with respect to the main diagonal, i.e. the line of identity \(j=i\). The visual behaviour of points (i, j) about the presence or absence of diagonal structures can contain wealth of dynamical information. If there are many diagonal lines parallel to the main diagonal, the considered orbit is regular. If there are short, disrupted diagonal features or no diagonal lines parallel to the main diagonal, the motion is chaotic. In a word, the RP behaves in regular diagonal structures for the nonchaotic case, but has more complicated, irregular structures for the chaotic case. The regular or chaotic dynamics of an orbit can be characterized via the visual behaviour of points (i, j) corresponding to the binary values 0 and 1 in a two-dimensional plane.

We take \(N=1000\), \(T=10^{7}\) and \(\varepsilon =k\sigma \), where \(\sigma \) is the standard mean deviation of the given data set and k is a proportionality constant [62]. Although \({{\textbf {x}}}(\tau )\) is taken as the phase-space variables \((r,\theta ,p_r,p_{\theta })\), any one of the phase-space variables is admissible. For example, r is given to \({{\textbf {x}}}(\tau )\). We draw the RPs of Orbits 1 and 2 in Fig. 2e, f. The presence of a number of diagonal lines parallel to the main diagonal shows the regularity of Orbit 1. The absence of diagonal lines parallel to the main diagonal determines the chaoticity of Orbit 2. The RP method is an efficient tool to identify the dynamical features of Orbits 1 and 2, as the techniques of Poincaré surfaces of section and FLIs are.

The visual plot of \({\textbf{R}}_{ij}\) for the quasiperiodic orbit 1 is shown in Fig. 2e. What is a visual for a periodic orbit? In order to answer this question, we choose some circular orbits of particles in the system (9). Based on Eq. (11) with \(P_r=P_{\theta }=0\), the effective potential for particles moving at the plane \(\theta \) is

$$\begin{aligned} V_{eff}= & {} E^2=\left( 1+\frac{C_k}{r^2}\right) \left( 1-\frac{2}{r}-\frac{8\pi \rho _{\text {eff}}}{r^2}\right) , \end{aligned}$$
(44)
$$\begin{aligned} C_k= & {} L^2 \csc ^2\theta . \end{aligned}$$
(45)

When \(L=4\) and \(\rho _{\text {eff}}=0.001\) are given, the effective potentials at the three planes \(\theta =\pi /4,~\pi /3,~\pi /2\) are shown in Fig. 3a. The conditions for stable circular orbits at the planes \(\theta \) are \(dV_{eff}/dr=0\) and \(d^2V_{eff}/dr^2\ge 0\). The stable circular orbits in Fig. 3b correspond to their parameters and radii as follows: \(E=0.98\) and \(r=28.62\) for the circular orbit 1 at the plane \(\theta =\pi /4\); \(E=0.97\) and \(r=17.68\) for the circular orbit 2 at the plane \(\theta =\pi /3\); \(E=0.96\) and \(r=11.95\) for the circular orbit 3 at the plane \(\theta =\pi /2\). When the circular orbit conditions and the algorithm \(PRK_64\) are applied to the Hamiltonian (30) with \(b=0\), we plot the visuals of \({\textbf{R}}_{ij}\) for these stable circular orbits. The visual for the circular orbit 1 has diagonal lines parallel to the main diagonal and numerous square lattices in Fig. 3c. The visual for the circular orbit 3 in Fig. 3d looks like that for the quasiperiodic orbit 1 in Fig. 2e and has a series of diagonal lines parallel to the main diagonal. This fact shows that the RPs of periodic orbits and those of quasiperiodic orbit are not strictly distinguishable.

3.3 The effect of varying one parameter on a transition from regular to chaotic regime

We use the method of FLIs to study the effect of varying one parameter on the transition from regular to chaotic regime in the Hamiltonian (30) with \(b\ne 0\). For comparison, the methods of Poincaré surfaces of section and RPs are also employed.

Taking the parameters \(L=4.6\), \(b=0.0001\), \(\rho _\text {{eff}}=0.0001\) and the initial conditions \(r=16\), \(\theta =\pi /2\), we estimate the FLIs of 30 trajectories with the energy running over the interval \(E\in [0.9970,0.9999]\). The FLIs in Fig. 4a show the occurrence of abrupt transitions to chaos at \(E=0.9977\) and \(E=0.9992\). Each of the FLIs is obtained after the integration time arrives at \(\tau =2\times 10^{6}\). All FLIs larger than (or equal to) 15 correspond to the onset of chaos, but those less than this value indicate the regular dynamics. The FLIs at \(E\le 0.9976\) indicate the regular dynamics. The trajectory for the energy \(E=0.9976\) is a torus on the Poincaré surface of section in Fig. 4b, and its regularity is also confirmed through the RP with diagonal lines parallel to the main diagonal in Fig. 4f. When \(E=0.9977\), the weak chaoticity is shown by the methods of Poincaré map and FLI in Fig. 4a, b. The RP in Fig. 4e seems to have diagonal line structures that are slightly disrupted. The regular dynamics exists for \(0.9978\le E\le 0.9992\), but the chaotic dynamics does for \(E\ge 0.9993\). Especially for \(E=0.9996\) and \(E=0.9998\), the chaotic behaviours are described in Fig. 4b, and are also shown by the RPs in Fig. 4c, d. The RPs have complex large-scale torus structures unlike diagonal line structures. Figure 4 shows that the degree of chaos increases when the energy increases in the interval \(0.9992\le E\le 0.9996\). In fact, the degree of chaos is strengthened with the energy increasing from a global phase-space structure under appropriate conditions.

Now, we consider the effect of the angular momentum on the chaotic motion. When the parameters \(E=0.996\), \(b=0.0006\), \(\rho _\text {{eff}}=0.0001\) and the initial conditions \(r=16\), \(\theta =\pi /2\) are given, L ranges from 4.0 to 4.2. The FLIs in Fig. 5a show that the transition from chaotic to regular regime occurs at the angular momentum \(L=4.07\). It is seen clearly that the extent of chaos decreases with the angular momentum increasing. The Poincaré maps in Fig. 5b and the RPs without complete diagonal line structures in Fig. 5c, d give chaotic dynamical information for \(L=4.03\), 4.05. Although the diagonal lines seem to be present for \(L=4.05\), they are shorter and then indicate the weak chaoticity. The trajectories are ordered for \(L=4.07\), 4.10, as shown via the Poincaré maps in Fig. 5b and the RPs with diagonal line structures in Fig. 5e, f.

Then, let the magnetic field parameter b be varied in the interval \(b\in [-0.001,0.001]\), where the other parameters are \(E = 0.996\), \(L = 4.4\), \(\rho _\text {{eff}}== 0.0001\) and the initial separation is \(r = 10\). The FLIs in Fig. 6a have abrupt changes at \(b=-0.0008\), 0.0003, 0.0006, 0.0008. As claimed below Eq. (31), the external magnetic field destroys the existence of a fourth constant in the Hamiltonian system (30), and thus, it should be responsible for chaotic dynamics of charged particles. Even the small values of the magnetic parameter such as \(b=-0.0008\), 0.0008 can exert strong chaotic effects on the trajectories of charged particles in Fig. 6b. The chaotic behaviours at \(b=-0.0008\), 0.0008 are also described via the RPs in Fig. 6c, d.

Finally, we investigate the dependence of regular and chaotic dynamics on varying the hairy parameter \(\rho _\text {{eff}}\). In various simulations, the hairy parameter is constrained in the interval \(\rho _\text {{eff}}\in [-0.1, 0.1]\), which comes from the limits of \(\rho _\text {{eff}}\) based on the Event Horizon Telescope (EHT) observations of Sagittarius A\(^*\) (Sgr A\(^*\)) [68]. The other parameters are \(E=0.996\), \(L=4.6\), \(b=0.00088\) and the initial conditions are \(r=16\), \(\theta =\pi /2\). Chaos exists for \(\rho _\text {{eff}}\ge 0.005\) in Fig. 7a about the FLIs depending on \(\rho _\text {{eff}}\). The chaoticness of charged-particle motions for \(\rho _\text {{eff}}=0.005\), 0.01 is checked by the Poincaré maps in Fig. 7b and the RPs without diagonal line structures in Fig. 7c, d. If the parameters and one of the initial conditions are altered as \(E=0.999\), \(b=0.00001\) and \(r=9\), the FLIs in Fig. 8a correspond to chaos for \(-0.001\le \rho _\text {{eff}}\le -0.003\) and \(\rho _\text {{eff}}=0,~0.005,~0.006\). The regular dynamics is also shown for \(\rho _\text {{eff}}=-0.002, -0.001\), \(0.001\le \rho _\text {{eff}}\le 0.004\), and \(0.007\le \rho _\text {{eff}}\le 0.01\). The chaoticity for \(\rho _\text {{eff}}=0\) and the regularity for \(E=0.01\) can be observed from the RPs in Fig. 8c, d. When the parameters and one of the initial conditions become \(E=0.996\), \(L=4.1\), \(b=-0.00008\) and \(r=6\), there is an abrupt transition to chaos when \(\rho _\text {{eff}}\) exceeds \(-\) 0.006, as is seen from the FLIs in Fig. 9a. Figure 9b-d describe the regular dynamics at \(\rho _\text {{eff}}=-0.01\) and the chaotic dynamics at \(\rho _\text {{eff}}=0.005\). Because of different choices of the initial conditions and other parameters in Figs. 7a, 8a and 9a, there is no universal rule for the dependence of chaotic dynamics on the hairy parameter \(\rho _\text {{eff}}\).

The above demonstrations completely support the results of [23]. The results are summarized here. The visuals of RPs for periodic or quasiperiodic orbits exhibit typical regular structures on the diagonal lines parallel to the main diagonal, as shown in Figs. 2e,  3c, d, 4f, 5e, f, 8d and 9d. The visuals of RPs for weakly chaotic orbits still have the contour of diagonal line structures, but the structures are short or slightly disrupted. Thus, no strict diagonal line structures are present, as shown in Figs. 4e and 5c, d. There are no diagonal line structures or complex, irregular large-scale torus structures unlike diagonal line structures in the visuals of RPs for the existence of strong chaos, as shown in Figs. 2f, 4c, d,  6c, d, 7c, d, 8c and 9c.

4 Conclusions

The Horndeski gravity is a theory of modified gravity based on a very general scalar-tensor theory. A hairy black hole solution in the Horndeski gravity is spherically symmetric and asymptotically flat. It is the RN-like black hole solution for a negative value of the hairy parameter. An asymptotically uniform magnetic field in the vicinity of the hairy black hole is so weak that it has a negligible effect on the spacetime background but exerts a large influence on the motion of charged test particles. The vector potential of electromagnetic field in the context of modified gravity must be a modified version of the Wald potential derived from the vacuum background. Such a modified vector potential can strictly satisfy the source-less Maxwell equations.

Explicit symplectic integrators exhibit excellent long-term behaviour in simulating the motion of charged particles around the hairy black hole immersed in the external magnetic field. Chaos indicators such as the methods of Poincaré surfaces of section, FLIs and RPs are used to investigate the regular and chaotic dynamics of charged particles. The RP method is the recurrence quantification analysis method, which measures the recurrences of an orbit into the vicinity of previously reached phase-space points. A visual plot of the recurrence matrix with or without diagonal structures parallel to the main diagonal can contain wealth of dynamical information. The presence of diagonal structures means the regular dynamics, but the absence of diagonal structures or the existence of short, disrupted diagonal features shows the chaotic dynamics. The RP method is efficient to detect chaos from order, as the methods of Poincaré surfaces of section and FLIs are.