1 Introduction

The physics of black holes is becoming one of the most active branches of modern physics. This dynamic is constantly evolving with the collection of new data. At the same time, different theories have been developed in order to explain and model these data, attracting attention to the exploration of these mystical objects of the universe [1]. The optical properties of black holes have sparked significant interest in the scientific community, particularly with the historic achievement of the first black hole image by the Event Horizon Telescope (EHT) [2,3,4]. This image has opened new perspectives for studying black holes and prompted researchers to explore solutions beyond the general relativity framework [5]. The image has reinforced confidence in Einstein’s general relativity predictions but also raised questions about its limits in extreme environments. This has led to a deeper exploration of black hole properties, exploring theoretical models beyond general relativity [6], and stimulating scientific debates on the fundamental nature of space-time in extreme conditions. The EHT’s captivating image has marked the beginning of a passionate era of discoveries and questions, propelling the understanding of black holes to new horizons [7].

The study of black holes is progressing due to the complexity of their relationship with the equations of general relativity. The apparent problems associated with black holes depend on the conceptual framework in which these solutions are treated. This led to the development of modified relativity, which aims to overcome the limitations of general relativity in the context of black holes [8]. This new theoretical approach explores the possible modifications of the laws of gravity at important scales, expanding our understanding of fundamental physics [9]. This exploration represents a bold extension of black hole research, offering a new perspective that could potentially reveal unexpected aspects of space-time in extreme cosmic regions.

From theoretical as well as observational aspects, the gravitational field features of a black hole, such as its gravitational lensing and shadow can be determined by studying the null geodesics around the black hole. Gravitational lensing features around black holes have been explored in a plethora of scenarios, such as the Schwarzschild black hole [10], naked singularity and horizonless ultracompact objects [11, 12], AdS/dS black holes [13, 14], etc. In 2008, Gibbons and Werner reformed the standard perspective by proposing a new geometrical approach to deduce the deflection angle in the weak field limit using the Gauss–Bonnet theorem (GBT) [15] for the static and asymptotically flat spacetimes [16]. This method was then applied to stationary spacetimes using a Finsler metric of Randers type [17, 18]. In 2016, this method was further developed by Ishihara et. al. for source and observer at finite distances employed to both static as well as stationary black hole solutions [19]. For asymptotically non-flat black hole solutions, study of gravitational lensing features can be found in the Refs. [20, 21]. For black hole spacetimes in modified gravity theories, studies on the deflection angle of light using GBT are also reported in [22,23,24,25]. Additionally, after the successful release of the black hole images by the EHT, exploring the shadow cast by a black hole has attracted the scientific minds [26,27,28,29,30,31,32,33,34,35]. Such investigations can also aid in differentiating the features of various gravity theories [22, 24, 36]. Another observable phenomenon which has also gained interest is the emission rate of particles around the black hole and studies have been reported in the Refs. [37,38,39,40,41].

Motivated by the elements mentioned above, our research approach continues with perseverance within the framework of the Einstein–Gauss–Bonnet theory [42,43,44,45,46,47,48,49,50], inspired by noncommutative geometry [51,52,53,54,55,56,57,58,59,60]. Following on from our previous investigations [61,62,63], we present a new part of our work in this ambitious scientific context. More precisely, our attention is focused on a careful analysis of the optical properties of the noncommutative inspired charged 4D-AdS-EGB solution that we have established previously in [64]. This investigation aims to unveil the subtleties of light interactions in the specific context of this solution, highlighting the implications of noncommutative geometry on the propagation of light near dense gravitational structures.

The organization of the paper is as follows: In Sect. 2, we explain the framework in which we will work throughout the document. In Sect. 3, we calculate the shadow of our studied black hole. In Sect. 4, we discuss the constraints on black hole shadow from EHT observations. The energy emission rate is studied in Sect. 5. In Sect. 6, we explore the deflection angle. In the last Sect. 7, we summarize our results.

2 Noncommutative inspired charged 4D-AdS-EGB black hole

In this section, we explicitly present the metric solution of our charged black hole, elaborated within the framework of the 4D-AdS-EGB model and inspired by noncommutative geometry. For more detailed information about this solution, please refer to the reference [64]. To do this, we start by giving the action of such a theory

$$\begin{aligned} S=\frac{1}{2}\int d^{D}x\sqrt{-g}\big [R-2\Lambda +\frac{\alpha }{D-4}\mathcal {L }_{GB}+F_{\mu \nu }F^{\mu \nu }\big ],\nonumber \\ \end{aligned}$$
(2.1)

where g is the metric determinant, R is the Ricci scalar, \(\alpha \) is the GB coupling constant which has a dimension of \(lenght^2\), \(\mathcal {L} _{GB}\) is the GB term given by

$$\begin{aligned} \mathcal {L}_{GB}=R^{\mu \nu \lambda \sigma }R_{ \mu \nu \lambda \sigma }-4R^{\mu \nu }R_{\mu \nu }+R^{2} \end{aligned}$$
(2.2)

and \(F_{\mu \nu }\) is the electromagnetic tensor defined by \(F_{\mu \nu }=\delta _{0[\mu |}\delta _{r| \nu ]}E(r)\). The field equations are obtained by varying the action (2.1) with respect to the metric tensor \(g_{\mu \nu }\).

$$\begin{aligned} R_{\mu \nu }-\frac{1}{2}g_{\mu \nu }R+\Lambda g_{\mu \nu }+ \frac{\alpha }{D-4} H_{\mu \nu } =\mathcal {T}_{\mu \nu }, \end{aligned}$$
(2.3)

where \(\mathcal {T}_{\mu \nu }\) is the total energy-momentum tensor and \( H_{\mu \nu }\) is the Lanczos tensor defined by

$$\begin{aligned} H_{\mu \nu }{} & {} =2\Big (RR_{\mu \nu }-2R_{\mu \lambda } R_{\nu }^{\lambda }-2R_{\mu \lambda \nu \sigma }R^{\lambda \sigma }-R_{\mu \lambda \sigma \rho }R_{\nu }^{\lambda \sigma \rho }\Big )\nonumber \\{} & {} \quad -\frac{1}{2}\mathcal {L} _{GB}g_{\mu \nu }. \end{aligned}$$
(2.4)

In the right-hand side of Eq. (2.3), it is widely recognized that the Gauss–Bonnet term in a 4-dimension is generally considered to be a total derivative, thus suggesting a significant non-participation in gravitational dynamics. However, various efforts have been undertaken to solve this problem. In particular, the recent proposal by Glavan and Lin is based on a clever redefinition of the Gauss–Bonnet coupling constant, denoted \(\alpha \), where \(\alpha \rightarrow \frac{\alpha }{D-4}\) and in a four-dimensional theory, the Gauss–Bonnet term regains significant relevance by taking the \(D\rightarrow 4\) limit at the level of Einstein’s field equations. This regularization method thus allows the Gauss–Bonnet term to provide a significant contribution to the dynamics of the system, thus modifying our understanding of its role in the gravitational context.

In the context of noncommutativity, a reformulation of Einstein’s equations is conceivable to take into account this newly introduced feature in the background. Although, so far, such a formulation is not available, an alternative approach based on the results of [52, 53] suggests that the noncommutativity of the spacetime coordinates, denoted \([x_{\mu }, x_{\nu }] =i\theta _{\mu \nu }\), can be incorporated into the spacetime content as the noncommutativity is an intrinsic property of the manifold itself. This makes it possible to express the matter and the electrical sources in the form of smeared distributions rather than localized sources. As a result, spacetime acquires a certain indeterminacy, and the notion of point structure loses its relevance. In other words, a minimum distance cannot be less than \(\sqrt{\theta }\). This modification of the nature of the sources is implemented mathematically by replacing the Dirac delta function with a Gaussian distribution. Thus, the left part of Einstein’s equation (2.3) is adjusted by integrating a new energy-momentum, which takes into account the effect of non-commutativity. Nevertheless, the geometric sector of Eq. (2.3) remains unchanged, thus preserving the spherical symmetry of the required solution [46].

Using the regularization method mentioned above, our objective is to derive a static spherical solution by solving Eq. (2.3) when the matter and the electrical sources are represented by Gaussian distributions [59]. These Gaussian distributions, defined by

$$\begin{aligned}{} & {} \rho _{matt}(r)=\frac{m}{(4\pi \theta )^{\frac{3}{2}}}\exp \Bigg (-\frac{r^2}{4\theta }\Bigg ),\nonumber \\{} & {} \rho _{ele}(r)=\frac{Q}{(4\pi \theta )^{\frac{3}{2}}}\exp \Bigg (-\frac{r^2}{4\theta }\Bigg ) \end{aligned}$$
(2.5)

where m is the barre mass and Q is the total electrical charge [60].

Subsequently, countless studies were undertaken exploring different forms of matter distributions, such as Gaussian, non-Gaussian, Lorentzian, etc. These investigations aimed to understand how different characteristics of matter distributions influence the geometry of spacetime in the context of general relativity. These various approaches have made it possible to explore the flexibility and implications of the theory, paving the way for a deeper understanding of the gravitational phenomena associated with specific configurations of matter.

The supposed form of the metric is as follows:

$$\begin{aligned} ds^{2}=-f(r)dt^{2}+\frac{dr^{2}}{f(r)}+r^{2}(d\vartheta ^{2}+\sin ^{2}(\vartheta )d\phi ^{2}). \end{aligned}$$
(2.6)

In accordance with [51], if we assume that \(g_{00}=\frac{1}{g_{rr}}\) and employ (2.5), the temporal and radial components of the total energy-momentum tensor are assumed by the following form:

$$\begin{aligned} \mathcal {T}_{t}^{t}{} & {} =\mathcal {T}_{r}^{r}=\rho _{\theta }(r)=\rho _{matt}(r)+\rho _{ele}(r)\nonumber \\{} & {} =\frac{m+Q}{(4\pi \theta )^{\frac{3}{2}}}\exp {\left( \frac{-r^{2}}{4\theta }\right) }. \end{aligned}$$
(2.7)

Moreover, the other two components, which remain the same due to spherical symmetry, must also be determined. Utilizing the requirement that the total energy-momentum tensor has zero divergence, \(\mathcal {T}^{\mu \nu }{;\nu }\), where the semicolon indicates covariant differentiation [55], assists in achieving this and results in:

$$\begin{aligned} \mathcal {T}_{\vartheta }^{\vartheta }=\mathcal {T}_{\phi }^{\phi }=\rho _{\theta }(r)+\frac{r}{2}\partial _{r}\rho _{\theta }(r), \end{aligned}$$
(2.8)

By combining Eqs. (2.7) and (2.8) and subsequently substituting them into (2.3), and using the same approach as described in [60] to connect m with the integration constants and the total mass M of the black hole, we arrive at a static spherically symmetric charged solution inspired by noncommutative geometry in 4D-AdS-EGB gravity

$$\begin{aligned} f(r)= & {} 1+\frac{r^2}{2\alpha }\nonumber \\{} & {} \times \quad \Bigg [1-\sqrt{1+\frac{16\alpha M}{\sqrt{\pi }r^3}\gamma (\frac{3}{2},\frac{r^2}{4\theta })-\frac{4\alpha Q^2}{\pi r^4} \mathcal {F}(r)+\frac{4\alpha \Lambda }{3}}\Bigg ],\nonumber \\ \end{aligned}$$
(2.9)

with

$$\begin{aligned} \mathcal {F}(r){} & {} =\gamma ^2\left( \frac{1}{2},\frac{r^2}{4\theta }\right) -\frac{r}{\sqrt{2\theta }} \gamma \left( \frac{1}{2},\frac{r^2}{2\theta }\right) \nonumber \\{} & {} \quad +\sqrt{\frac{2}{\theta }}r\gamma \left( \frac{ 3}{2},\frac{r^2}{4\theta }\right) , \end{aligned}$$
(2.10)

and \(\gamma \) is the lower incomplete gamma function defined by

$$\begin{aligned} \gamma \Bigg (\frac{a}{b},x\Bigg )=\int _{0}^{x}\frac{dt}{t}t^{\frac{a}{b}}\exp (-t). \end{aligned}$$
(2.11)

In Eq. (2.9) the quantities \(\alpha \), M, \(\theta \), Q and \(\Lambda \) are the Gauss–Bonnet coupling constant, the black hole mass, the noncommutative parameter, the electric charge and the Cosmological constant respectively.

In what follows from our study, we restrict our analysis to the impact of the electric charge Q and the noncommutative parameter \(\theta \). Indeed, the effect of the Gauss–Bonnet coupling constant \(\alpha \) has already been the subject of numerous investigations in the scientific literature [67]. We, therefore, focus our attention on the specific aspects of the electric charge and the noncommutative parameter to deepen our understanding of these influences on our model.

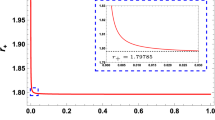
It is widely recognized that the first thing to compute for an established black hole solution is the event horizon radius. To do so, we have to find the roots of the equation \(f(r_{+})=0\). Unfortunately, this equation lacks an analytical solution, prompting us to look for an alternative method, which is the numerical one. In Fig. 1, we depict the metric function for various values of the noncommutative parameter \(\theta \) and the electrical charge Q against the event horizon radius \(r_{+}\). It becomes evident that three distinct cases can be identified: i) two event horizons; ii) one degenerate event horizon. ii) No event horizon radius.

For more details about (2.9), such as asymptotic behavior at large distances and its convergence to the standard solutions of general relativity, you can see [64].

Fig. 1
figure 1

The metric function vs event horizon radius for various values of electrical charge Q (a) and noncommutative parameter \(\theta \) (b) with \(M=1\), \(\alpha =0.01\) and \(\Lambda =-0.02\)

Full size image

3 Shadow

Here, we demonstrate how noncommutativity and electric charge affect the black hole shadow’s size since the metric function provides a static solution; the shape is perfectly circular. When a black hole is placed between an observer and a light source, the image that results is known as the black hole’s shadow. Thus, it seems that the shadow of the black hole brings us to study the geodesics followed by the photons in the curved space-time. To do this, we start with the Lagrangian given by

$$\begin{aligned} \mathcal {L}=\frac{1}{2}g_{\mu \nu }\dot{x}^{\mu }\dot{x}^{\nu }, \end{aligned}$$
(3.1)

where \(g_{\mu \nu }\) is the metric tensor and the over dot is the derivative with respect to an affine parameter along the geodesics \(\sigma \).

To determine the photon orbits, we use the Hamilton-Jacobi method and the Carter approach

$$\begin{aligned} \frac{1}{2}g^{\mu \nu }\frac{d \mathcal {S}}{d x^{\mu }}\frac{d \mathcal {S}}{d x^{\nu }}+\frac{d \mathcal {S}}{d \sigma }=0, \end{aligned}$$
(3.2)

where \(\mathcal {S}\) is the Hamilton-Jacobi action, which we assume to take the following form: where \(\sigma \) denotes the affine parameter along the geodesics and \(\mathcal {S}\) is the Hamilton-Jacobi action which takes the form

$$\begin{aligned} \mathcal {S}=-Et+L_{\phi }\phi +\mathcal {S}_{r}(r)+\mathcal {S}_{\vartheta }(\vartheta ), \end{aligned}$$
(3.3)

where E is identified with the energy of the photon and \(L_{\phi }\) with the angular momentum, \(\mathcal {S}_r\) and \(\mathcal {S}_\vartheta \) are r and \(\vartheta \) functions, respectively. Using Eqs. (3.2)–(3.3), the functions of r and \(\vartheta \) can be separated as follows:

$$\begin{aligned}&r^{2}f(r)\Big (\frac{d\mathcal {S}_{r}(r)}{dr}\Big )^{2}-\frac{r^{2}E^{2}}{f(r)}+\frac{L_{\phi }^{2}}{\sin ^{2}\vartheta }=\mathcal {X} \end{aligned}$$
(3.4)
$$\begin{aligned}&\Big (\frac{d\mathcal {S}_{\vartheta }(\vartheta )}{d\vartheta }\Big )^{2}+ L_{\phi }^{2}\cot ^{2}\vartheta =-\mathcal {X} \end{aligned}$$
(3.5)

where \(\mathcal {X}\) is the Carter constant. Based on the Hamilton-Jacobi approach, photon motion is governed by the following equations:

$$\begin{aligned} \frac{dt}{d\sigma }&=\frac{E}{f(r)} \end{aligned}$$
(3.6)
$$\begin{aligned} r^{2}\frac{dr}{d\sigma }&=\pm \sqrt{\mathcal {R}}\end{aligned}$$
(3.7)
$$\begin{aligned} r^{2}\frac{d\vartheta }{d\sigma }&=\pm \sqrt{\Phi }\end{aligned}$$
(3.8)
$$\begin{aligned} \frac{d\phi }{d\sigma }&=\frac{L_{\phi }}{r^{2}\sin ^{2}\vartheta } \end{aligned}$$
(3.9)

where \(\mathcal {R}\) and \(\Phi \) take the following forms

$$\begin{aligned} \mathcal {R}&=E^{2}r^{4}-r^{2}f(r)\big (\mathcal {X}+L_{\phi }^{2}\big )\end{aligned}$$
(3.10)
$$\begin{aligned} \Phi&=\mathcal {X}-L_{\phi }^{2}\cot ^{2}\vartheta \end{aligned}$$
(3.11)

The radial null geodesic Eq. (3.7) can be rewritten to take the form

$$\begin{aligned} \Big (\frac{dr}{d\sigma }\Big )^{2}+V_{eff}(r)=0 \end{aligned}$$
(3.12)

where \(V_{eff}(r)\) is the effective radial potential given by

$$\begin{aligned} V_{eff}=\frac{f(r)}{r^{2}}\big (\mathcal {X}+L_{\phi }^{2})-E^{2} \end{aligned}$$
(3.13)

In order to determine the unstable circular orbits that limit the visible shape of a black hole’s shadow, we take advantage of the effective potential by imposing the following conditions:

$$\begin{aligned} V_{eff}(r)\big |_{r=r_{p}}=\frac{dV_{eff}(r)}{dr}\big |_{r=r_{p}}=0, \end{aligned}$$
(3.14)

where \(r_{p}\) denotes the radius of the photon sphere. The radius of the photon sphere \(r_{p}\) is provided by the solution of the equation \(V_{eff}(r_{p}) = 0\). The obtained \(r_{p}\) is subsequently put into the equation \(V'_{eff}(r_{p}) = 0\) to check if the constraint \(V''_{eff}(r_{p})<0\) is satisfied in order to get the unstable photon orbits. Conditions (3.14) for determining the radius of the photon sphere can be put together to be

$$\begin{aligned} rf'(r)\big |_{r=r_{p}}-2f(r)\big |_{r=r_{p}}=0. \end{aligned}$$
(3.15)

The above Eq. (3.15) cannot be solved analytically. Alternately, we are moving towards a numerical solution where the results are summarized in Table 1.

Table 1 The photon sphere radius and event horizon radius for variations in electrical charge Q and noncommutative parameter \(\theta \) with \(M=1, \alpha =0.01\) and \(\Lambda =-0.02\)
Full size table

At this point, we want to produce the visible shape of the black hole’s shadow, which may be obtained by using the celestial coordinates X and Y, which are defined as follows:

$$\begin{aligned} X&=\lim _{r_{0}\rightarrow \infty }\bigg (-r_{0}^{2}\sin \vartheta _{0}\frac{d\phi }{dr}\bigg |_{\vartheta =\vartheta _{0}}\bigg ),\end{aligned}$$
(3.16)
$$\begin{aligned} Y&=\lim _{r_{0}\rightarrow \infty }\bigg (r_{0}^{2}\frac{d\vartheta }{dr}\bigg |_{\vartheta =\vartheta _{0}}\bigg ) \end{aligned}$$
(3.17)

where \((r_{0},\vartheta _{0})\) are the observer coordinates at infinity. Using the Eqs. (3.6)–(3.7) we get the following results

$$\begin{aligned} \frac{d\vartheta }{dr}&=\frac{\sqrt{\mathcal {X}-L_{\phi }^{2}\cot ^{2}\vartheta \tan ^{2}\vartheta }}{\sqrt{E^{2}r^{4}-r^{2}f(r)\big (\mathcal {R}+L_{\phi }^{2}\big )}}\end{aligned}$$
(3.18)
$$\begin{aligned} \frac{d\phi }{dr}&=\frac{L_{\phi }}{\sin ^{2}\vartheta \sqrt{E^{2}r^{4}-r^{2}f(r)\big (\mathcal {R}+L_{\phi }^{2}\big )}}. \end{aligned}$$
(3.19)

Taking the limit \(r\rightarrow \infty \) for the above expressions, the celestial coordinates are reduced to

$$\begin{aligned} X&=-\frac{\eta \csc \vartheta }{\sqrt{1-\frac{\big (\varrho +\eta ^2\big )\big (1-\sqrt{1+\frac{4\alpha \Lambda }{3}}\big )}{2\alpha }}}\end{aligned}$$
(3.20)
$$\begin{aligned} Y&=\pm \sqrt{\frac{\varrho -\eta ^2\cot ^{2}\vartheta }{1-\frac{\big (\varrho +\eta ^2\big )\big (1-\sqrt{1+\frac{4\alpha \Lambda }{3}}\big )}{2\alpha }}} \end{aligned}$$
(3.21)

where the impact parameters are defined by

$$\begin{aligned} \varrho =\frac{\mathcal {X}}{E^{2}},\qquad \eta =\frac{L_{\phi }}{E},\qquad . \end{aligned}$$
(3.22)

To investigate the apparent shape of the shadow, we combine the coordinates X and Y and derive an equation that represents a circle with radius \(R_s\) in the celestial plane X-Y, as given by

$$\begin{aligned} X^{2}+Y^{2}=\eta ^{2}+\varrho =R_{s}^{2} \end{aligned}$$
(3.23)

The observer is assumed to be in the equatorial plane, as imposed by \((\vartheta =\frac{\pi }{2})\). Also, we use the condition \(V_{eff}(r)=0\), which implies that \(\frac{r_p^2}{f(r_p)}=\varrho +\eta ^2\). Therefore, we get the shadow radius

$$\begin{aligned} R_{sh}^{2}=\frac{\frac{r_{p}^{2}}{f(r_{p})}}{1-\frac{r_{p}^{2}}{f(r_{p})}\bigg (\frac{1-\sqrt{1+\frac{4\alpha \Lambda }{3}}}{2\alpha }\bigg )}. \end{aligned}$$
(3.24)
Fig. 2
figure 2

Black hole shadow in celestial plane \((X-Y)\) for various values of noncommutative parameter \(\theta \) with \(M=1\), \(\alpha =0.01\) and \(\Lambda =-0.02\)

Full size image

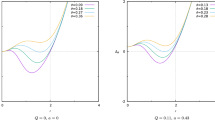
A depiction of the shadow cast by the noncommutative charged 4D-AdS EGB black hole is provided in Fig. 2. It is evident from this figure that the shadow has a perfectly circular form, and it’s noteworthy to notice that the radius of the shadow is sensitive to variations in two different parameters: the noncommutative parameter \(\theta \) and the electric charge Q. Figure 4a provides a clear demonstration of this link, showing that a large reduction in the shadow’s radius is induced by an increase in electric charge Q. Similarly, looking at Fig. 4b, it is clear that the noncommutative parameter \(\theta \) changes and the shadow’s radius is inversely proportional, highlighting the significance of these two elements in the shadow’s configuration.

It is relevant to emphasize that the tiny influence of the noncommutative parameter arises from the quantum nature of spacetime at extremely small scales, such as those associated with the Planck or String scales, where quantum effects prevail [65]. At these energy levels, quantum fluctuations induce fundamental alterations in the geometry and the very constitution of spacetime. Developments in advanced theories such as string theory suggest that this noncommutativity is intrinsic to the deep structure of reality at quantum scales [66]. The careful exploration of these corrections at microscopic scales offers crucial information on the nature of spacetime and its interaction with particles and quantum fields, thus contributing to a thorough understanding of the universe.

One of the main features of this black hole solution is the investigated black hole’s shadow radius sensitivity to changes in the different parameters. This characteristic opens up a useful application of these data for astrophysics observations, allowing constraints on the shadow observables captured by objects like M87* and Sgr A*. Whether or not these items are connected to rotating black holes does not affect their usefulness [68, 69].

By the same token, the effect of the correspondence between the electric charge and the noncommutative parameter has already been noted in the literature [61, 63, 64]. By way of illustration, reference [80] has demonstrated a close relationship between the electric charge and the noncommutative parameter, in particular with regard to the thermodynamic properties. In order to deepen this relationship from an optical angle, a thorough understanding of these two quantities in light of the Event Horizon Telescope (EHT) data.

4 Observational constraints on shadow from EHT

In this section, we shall discuss the constraints on the model parameters Q and \(\theta \) from the black hole shadow observational data. Using the distance \(D\) between the supermassive black hole (SMBH) and the galactic center, the shadow’s size \(d_\text {sh}\) of a black hole can be found using the arclength equation as given below:

$$\begin{aligned}d_\text {sh} = \frac{D \theta _\text {sh}}{M}.\end{aligned}$$

For the case of M87\(^\star \), the shadow diameter is given by \(d^\text {M87*}_\text {sh} = (11 \pm 1.5)M\) [71, 72]. These results can be used to constrain the theory using arclength. However, this study uses uncertainties from Event Horizon Telescope (EHT) following Refs. [73, 74] to limit or constrain the possible values of black hole charge \(Q\), which are more precise than those from the arclength equation. The focus here is on determining the \(1\sigma \) boundaries of the considered black hole parameters Q and \(\theta \) using data from M87\(^\star \) and Sgr. A\(^\star \). Further details on the methodology and confidence levels can be found in the referenced works. One may note that the properties of black hole shadows are significantly affected by model parameters in a modified theory of gravity [75,76,77,78,79]. Hence observational constraints on the model parameters from shadow observations can provide us with feasibility and a better understanding of the theory in light of EHT data.

Fig. 3
figure 3

\(1\sigma \) constraints on the black hole shadow using Sgr A\(^\star \) with \(M=1,\) \(\alpha = 0.01\) and \(\Lambda = -0.02\)

Full size image
Fig. 4
figure 4

\(1\sigma \) constraints on the black hole shadow using M87\(^\star \) with \(M=1,\) \(\alpha = 0.01\) and \(\Lambda = -0.02\)

Full size image
Table 2 \(1\sigma \) constraints on Q and \(\theta \) based on the shadow radii of Sgr. A* and M87* as depicted in Figs. 3 and 4 with \(M=1,\) \(\alpha = 0.01\) and \(\Lambda = -0.02\)
Full size table

In Figs. 3 and 4, we have shown the \(1\sigma \) constraints on the model parameters Q and \(\theta \) from EHT data associated with M87* and Sgr A* and the constrained model parameter values are shown in Table 2. One may observe that both observations suggest that the Q value less than 1 is preferable. The other parameter \(\theta \) is also well constrained and has a lower and upper bound from EHT data. Constraints on both Q and \(\theta \) from Sgr. A* are more stringent in comparison to the constraints obtained from M87*.

Another apparent observation is the correspondence between charge Q and the non-commutative parameter \(\theta \) from the shadow observations for smaller values of \(\theta \). Such a correspondence is also reported in Ref. [80]. It is seen from our investigation that with an increase in the value of both Q and \(\theta \), the shadow of the black hole decreases initially. This correspondence is found to be valid for smaller values of \(\theta \) only. On the contrary, we observe that for the higher values of \(\theta \), both parameters have opposite impacts on black hole shadow. However, it is evident that Q has a more distinct impact on the shadow radius of the black hole. Observational constraints on both the parameters in this section showed that Q has a larger feasible parameter space in comparison to \(\theta \). From the complete scenario of feasible parameter space, the important aspect is that the non-commutative parameter, in most cases, supports a larger black hole shadow. On the other hand, the presence of charge results in a smaller black hole shadow.

5 Energy emission rate

Hawking has demonstrated that, due to quantum effects, black holes can radiate. This radiation is expressed by what is called the energy emission rate, which measures the amount of energy emitted per unit of time. The energy emission rate is expressed as follows [28]

$$\begin{aligned} \frac{d^{2}E(\varpi )}{dtd\varpi }=\frac{2\pi ^{3}R_{sh}^{2}}{\exp (\frac{\varpi }{T_{H}})-1} \end{aligned}$$
(5.1)

where \(\varpi \) is the emission frequency and \(T_{H}\) is Hawking temperature given by

$$\begin{aligned} T_{H}&=\frac{1}{12 \pi ^2 r_+ \left( 2 \alpha +r_+^2\right) }\Bigg [-3 \left( Q^2 \left( \mathcal {F}(r_+)-r_+ \mathcal {F}^{\prime }(r_+)\right) \right. \nonumber \\&\quad \left. +\pi \left( \alpha +\Lambda r_+^4-r_+^2\right) \right) \nonumber \\&\quad \times r_+ \left( -3 Q^2 \mathcal {F}(r_+)+\pi \Lambda r_+^4-3 \pi \left( \alpha +r_+^2\right) \right) \frac{\gamma ^{\prime }(\frac{3}{2},\frac{ r_+^2}{4\theta })}{\gamma (\frac{3}{2},\frac{r_+^2}{4\theta })}\Bigg ].\nonumber \\ \end{aligned}$$
(5.2)
Fig. 5
figure 5

The energy emission rate variation vs frequency \(\varpi \) for different values of electric charge Q and noncommutative parameter \(\theta \)

Full size image

The energy emission rate of the charged noncommutative 4D-AdS EGB black hole is plotted against frequency \(\varpi \) for a variety of electric charge Q values and a noncommutative parameter \(\theta \) in Fig. 5. This graphic illustrates a broad pattern in the energy emission rate’s evolution, which is marked by growth that rises before declining until complete extinction. It is especially noteworthy that this final point, shown by the peak in Fig. 5, turns out to be sensitive to changes in the properties that the black hole in question contains.

To describe it even more precisely, it is clear that the rise in electric charge directly affects the peak’s magnitude, as shown on the graph. Put another way, the energy emission rate approaches a decreasing peak as the electric charge rises; this variation may be seen on the curve (Fig. 5a). This phenomenon points to an inherent relationship between the electric charge and the energy emitted by the black holes in this specific configuration.

Likewise, the same pattern reproduces when the variation of the noncommutative parameter is observed. The energy emission rate’s peak (Fig. 5b) declines in direct proportion to this noncommutative parameter’s increase. As a result, the dynamics of the energy release rate of the black holes under study are significantly influenced by the electric charge and the noncommutative parameter.

Finally, Fig. 5 sheds light on how these parameters influence the behavior of the energy emission rate of black holes by showing how their variation can modify the height of the peak, which contributes substantially to our understanding of the complex phenomena surrounding these celestial objects.

6 Deflection angle

The bending angle of light is a key parameter in the investigation of the beautiful phenomenon called gravitational lensing. In this section, we shall deduce the deflection angle for the noncommutative charged 4D-AdS EGB black hole (2.6) in order to investigate how the noncommutative parameter and the charge of the black hole affects the angle at which light is bent as it approaches the gravitational field of the black hole. To this end, we consider the approach followed by Ishihara et al. for asymptotically non-flat spacetimes depicted in Ref. [19]. This method utilizes the Gauss–Bonnet Theorem (GBT) [16] to calculate the deflection angle. Out of the many formulations of the GBT, the most straightforward one postulates that the total Gaussian curvature within an enclosed triangle can be represented in terms of the total geodesic curvature of the boundary and the jump angles formed at the corners. As demonstrated in Fig. 6, if an orientable surface T in two dimensions is considered, then the boundaries of the surface which are differentiable curves are expressed as \(\partial T_a\) (\(a=1,2,\ldots ,N\)) with \(\beta _a\) as the jump angles formed between the curves. Following this, the GBT can be mathematically expressed as [15]

$$\begin{aligned} \int \int _T \mathcal {K} dS + \sum ^{N}_{a\,=\,1} \int _{\partial T_a} \kappa _g dl + \sum ^{N}_{a\,=\,1} \beta _a = 2\pi , \end{aligned}$$
(6.1)

where \(\mathcal {K}\) is the Gaussian curvature of the surface T, \(\kappa _g\) is the geodesic curvature of the boundaries \(\partial T_a\) with an infinitesimal line element dl along the boundary. The sign of dl is chosen such that it is consistent with the orientation of the surface with \(dl>0\) for prograde motion and \(dl<0\) for retrograde motion of photons.

Fig. 6
figure 6

Schematic representation for the GBT [19]. The inner angle is \(\varepsilon _a\) and the jump angle is \(\beta _a\) (\(a =1,2,\ldots ,N\))

Full size image

Light rays follow the null condition for which \(ds^2 = 0\). Hence, the black hole metric can be rewritten as

$$\begin{aligned} dt^2 = \gamma _{ij} dx^i dx^j = \frac{1}{f(r)^2}\, dr^2 + \frac{r^2}{f(r)}\, d\Omega ^2, \end{aligned}$$
(6.2)

where \(\gamma _{ij}\) is usually referred to as the optical metric, which specifies a 3D Riemannian space denoted by \(\mathcal {M}^{(3)}\). A ray of light in this manifold is considered as a spatial curve. The non-vanishing components of this metric are

$$\begin{aligned} \gamma _{rr} = \frac{1}{f(r)^2},\;\; \gamma _{\phi \phi } = \frac{r^2}{f(r)}. \end{aligned}$$
(6.3)

The impact parameter is of utmost importance in the analysis of the gravitational bending of light which is given by Eq. (3.22) and can be recast as

$$\begin{aligned} \eta \equiv \frac{L_\phi }{E} = \frac{r^2}{f(r)} \frac{d\phi }{dt}. \end{aligned}$$
(6.4)

The unit vector in the radial direction from the center of the lens can be written as \(e_{rad} = (f(r), 0)\), and the unit vector along the angular direction can be obtained as \(e_{ang} = (0, f(r)/r)\). Again, the components of the unit tangent vector \(\textbf{K} \equiv d\textbf{x}/dt\) along the photon orbit are obtained as [19]

$$\begin{aligned} (K^r, K^\phi ) = \frac{\eta f(r)}{r^2} \left( \frac{dr}{d\phi }, 1\right) . \end{aligned}$$
(6.5)

In the above relation, the term \(dr/d\phi \) leads to the orbit equation expressed as

$$\begin{aligned} \left( \frac{dr}{d\phi }\right) ^{\!2} = -\, r^2 f(r) + \frac{r^4}{\eta ^2}. \end{aligned}$$
(6.6)

If \(\Psi \) is assumed to be the angle between the radial component of the tangent vector and the radial vector, i.e. the angle formed by the light ray in the radial direction, then we arrive at

$$\begin{aligned} \cos \Psi = \frac{\eta }{r^2} \frac{dr}{d\phi }. \end{aligned}$$
(6.7)

It consequently results in,

$$\begin{aligned} \sin \Psi = \frac{\eta \sqrt{f(r)}}{r}. \end{aligned}$$
(6.8)

Assuming a new variable \(u = 1/r\), the orbit Eq. (6.6) can be rewritten in the form

$$\begin{aligned} \left( \frac{du}{d\phi }\right) ^2 = F(u), \end{aligned}$$
(6.9)

where we obtain the function \(F(u) = -\,u^2\,f(u) + 1/\eta ^2\).

Fig. 7
figure 7

Illustrative description for the quadrilateral \({\mathop {R}\limits ^{\infty }}\!\square \!{\mathop {S}\limits ^{\infty }}\) enclosed in a curved space [21]

Full size image

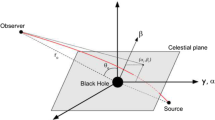
Portrayed in Fig. 7 is the black hole which behaves as a lens (L) with the source (S) and the receiver (R) situated at finite distance from the lens. Considering the equatorial plane (\(\vartheta = \pi /2\)), the bending angle of light arriving from the source can be expressed as [19, 81]

$$\begin{aligned} \hat{\Theta } = \Psi _R - \Psi _S + \phi _{RS}, \end{aligned}$$
(6.10)

where \(\Psi _R\) and \(\Psi _S\) are the angles of light estimated with respect to L at the positions of S and R respectively. The separation angle between R and S is denoted by \(\phi _{RS} = \phi _R - \phi _S\) where \(\phi _R\) and \(\phi _S\) are the longitudes of R and S respectively.

The quadrilateral \({\mathop {R}\limits ^{\infty }}\!\square \!{\mathop {S}\limits ^{\infty }}\) illustrated in Fig. 7 is enclosed in a curved space \(\mathcal {M}^{(3)}\). \({\mathop {R}\limits ^{\infty }}\!\square \!{\mathop {S}\limits ^{\infty }}\) contains light rays considered as spatial curves with two outgoing radial lines from S and R positions, and a fragment of the circular arc \(C_r\) with the coordinate radius \(r_C\) (\(r_C \rightarrow \infty \)). It is evident from Fig. 7 that within the asymptotically Minkowskian spacetime, \(\kappa _g \rightarrow 1/r_C\) and \(dl \rightarrow r_C\, d\phi \) as \(r_C \rightarrow \infty \) [16]. Consequently, the gravitational bending angle of light in the domain \({\mathop {R}\limits ^{\infty }}\!\square \!{\mathop {S}\limits ^{\infty }}\) can be defined as

$$\begin{aligned} \hat{\Theta } = \Psi _R - \Psi _S + \phi _{RS} = - \int \int _{{\mathop {R}\limits ^{\infty }}\square {\mathop {S}\limits ^{\infty }}} \mathcal {K}\, dS \end{aligned}$$
(6.11)

Integration of Eq. (6.9) results in the separation angle \(\phi _{RS}\) as

$$\begin{aligned} \phi _{RS} = 2\int _{0}^{u_0}\frac{du}{\sqrt{F(u)}}, \end{aligned}$$
(6.12)

where \(u_0\) is the inverse of the distance of the closest approach. In accordance with the approach demonstrated by Ishihara et al.  if S and R positions are considered to be at finite distances from the black hole, then the angle of deflection of light can be expressed as

$$\begin{aligned} \hat{\Theta } = \Psi _R - \Psi _S + \int _{u_R}^{u_0} \frac{du}{\sqrt{F(u)}} + \int _{u_S}^{u_0} \frac{du}{\sqrt{F(u)}}. \end{aligned}$$
(6.13)

Now, implementing Eq. (6.8) into the black hole spacetime (2.6), we obtain

$$\begin{aligned}{} & {} \Psi _R - \Psi _S \approx \arcsin (\eta u_R) + \arcsin (\eta u_s)\nonumber \\{} & {} \quad - \pi + \left( \eta M - \frac{2\eta M\alpha \Lambda }{3}\right) \left( \frac{u_R^2}{\sqrt{1 - \eta ^2 u_R^2}} + \frac{u_S^2}{\sqrt{1 - \eta ^2 u_S^2}}\right) \nonumber \\{} & {} \quad +\left( \frac{\eta Q^2}{2\sqrt{2}\pi \theta } - \frac{\eta M}{\sqrt{\pi \theta }} - \frac{\eta Q^2 \alpha \Lambda }{3\sqrt{2}\pi \theta } + \frac{2\eta M\alpha \Lambda }{3\sqrt{\pi \theta }}\right) \nonumber \\{} & {} \quad \times \left( \frac{u_R}{\sqrt{1 - \eta ^2 u_R^2}} + \frac{u_S}{\sqrt{1 - \eta ^2 u_S^2}}\right) \nonumber \\{} & {} \quad - \left( \frac{\eta Q^2}{2} - \frac{\sqrt{2}\eta MQ^2\alpha }{(\pi \theta )^{3/2}} - \frac{\eta Q^2\alpha \Lambda }{3}\right) \nonumber \\{} & {} \quad \times \left( \frac{u_R^3}{\sqrt{1 - \eta ^2 u_R^2}} + \frac{u_S^3}{\sqrt{1 - \eta ^2 u_S^2}}\right) + \left( \frac{\eta \Lambda }{6} - \frac{\eta \alpha \Lambda ^2}{18}\right) \nonumber \\{} & {} \quad \times \left( \frac{u_R^{-1}}{\sqrt{1 - \eta ^2 u_R^2}} + \frac{u_S^{-1}}{\sqrt{1 - \eta ^2 u_S^2}}\right) - \left( \frac{\eta M\Lambda }{6} - \frac{\eta M\Lambda }{6\sqrt{\pi \theta }}\right) \nonumber \\{} & {} \quad \times \left[ \frac{1}{(1 - \eta ^2 u_R^2)^{3/2}} + \frac{1}{(1 - \eta ^2 u_S^2)^{3/2}}\right] \nonumber \\{} & {} \quad -\left( \frac{\eta MQ^2}{2\sqrt{2}(\pi \theta )^{3/2}} + \frac{\eta Q^2\Lambda }{12}\right. \nonumber \\{} & {} \quad \left. - \frac{\eta MQ^2\alpha \Lambda }{\sqrt{2}(\pi \theta )^{3/2}} + \frac{\eta ^3 Q^2\Lambda }{6\sqrt{2}\pi \theta } - \frac{\eta ^3 M\Lambda }{3\sqrt{\pi \theta }}\right) \nonumber \\{} & {} \quad \times \left[ \frac{u_R}{(1 - \eta ^2 u_R^2)^{3/2}} + \frac{u_S}{(1 - \eta ^2 u_S^2)^{3/2}}\right] \nonumber \\{} & {} \quad -\left( \frac{\eta ^3 M\Lambda }{3} + \frac{\eta MQ^2\alpha \Lambda }{\sqrt{2}\pi \theta }\right) \nonumber \\{} & {} \quad \times \left[ \frac{u_R^2}{(1 - \eta ^2 u_R^2)^{3/2}} + \frac{u_S^2}{(1 - \eta ^2 u_S^2)^{3/2}}\right] \nonumber \\{} & {} \quad +\left( \frac{\eta ^3 MQ^2}{\sqrt{2}(\pi \theta )^{3/2}} + \frac{\eta MQ^2}{2\sqrt{\pi \theta }} + \frac{\eta ^3 Q^2\Lambda }{6}\right. \nonumber \\{} & {} \quad \left. - \frac{\sqrt{2}\eta ^3 MQ^2\alpha \Lambda }{(\pi \theta )^{3/2}} - \frac{\eta MQ^2\alpha \Lambda }{\sqrt{\pi \theta }}\right) \nonumber \\{} & {} \quad \times \left[ \frac{u_R^3}{(1 - \eta ^2 u_R^2)^{3/2}} + \frac{u_S^3}{(1 - \eta ^2 u_S^2)^{3/2}}\right] \nonumber \\{} & {} \quad + \left( \frac{\eta Q^2\Lambda }{12\sqrt{2}\pi \theta } - \frac{\eta M\Lambda }{6\sqrt{\pi \theta }}\right) \nonumber \\{} & {} \quad \times \left[ \frac{u_R^{-1}}{(1 - \eta ^2 u_R^2)^{3/2}} + \frac{u_S^{-1}}{(1 - \eta ^2 u_S^2)^{3/2}}\right] \end{aligned}$$
(6.14)

It is clear that the above expansion becomes divergent at infinite distances of the source and the receiver, i.e. \(u_R \rightarrow 0\) and \(u_S \rightarrow 0\). This is an outcome of the fact that the black hole under study is an asymptotically non-flat spacetime.

Next, we compute the separation angle as

$$\begin{aligned}{} & {} \phi _{RS} \approx \pi - \arcsin (\eta u_R) - \arcsin (\eta u_S)\nonumber \\{} & {} \quad + \left( \frac{2M}{\eta } + \frac{32MQ^2\alpha }{5\eta ^5} - \frac{8\sqrt{2}MQ^2\alpha }{3\eta ^3 \pi \theta } - \frac{4M\alpha \Lambda }{3\eta }\right) \nonumber \\{} & {} \quad \times \left( \frac{1}{\sqrt{1 - \eta ^2 u_R^2}} + \frac{1}{\sqrt{1 - \eta ^2 u_S^2}}\right) \nonumber \\{} & {} \quad - \left( \frac{u_R}{\sqrt{1 - \eta ^2 u_R^2}} + \frac{u_S}{\sqrt{1 - \eta ^2 u_S^2}}\right) \nonumber \\{} & {} \quad \times \left( \frac{3Q^2}{4\eta } - \frac{3MQ^2\alpha }{\sqrt{2}\eta (\pi \theta )^{3/2}} - \frac{\eta Q^2}{2\sqrt{2}\pi \theta } + \frac{\eta M}{\sqrt{\pi \theta }} \right. \nonumber \\{} & {} \quad \left. + \frac{15MQ^2\alpha }{4\eta ^3 \sqrt{\pi \theta }} - \frac{\eta ^3\Lambda }{6} - \frac{Q^2\alpha \Lambda }{2\eta } + \frac{\eta Q^2\alpha \Lambda }{3\sqrt{2}\pi \theta } + \frac{\eta ^3 \alpha \Lambda ^2}{18}\right) \nonumber \\{} & {} \quad -\left( \eta M + \frac{16MQ^2\alpha }{5\eta ^3} - \frac{4\sqrt{2}MQ^2\alpha }{3\eta \pi \theta } - \frac{2\eta M\alpha \Lambda }{3}\right) \nonumber \\{} & {} \quad \times \left( \frac{u_R^2}{\sqrt{1 - \eta ^2 u_R^2}} + \frac{u_S^2}{\sqrt{1 - \eta ^2 u_S^2}}\right) \nonumber \\{} & {} \quad +\left( \frac{\eta Q^2}{4} - \frac{\eta MQ^2\alpha }{\sqrt{2}(\pi \theta )^{3/2}} + \frac{5MQ^2\alpha }{4\eta \sqrt{\pi \theta }} - \frac{\eta Q^2\alpha \Lambda }{6}\right) \nonumber \\{} & {} \quad \times \left( \frac{u_R^3}{\sqrt{1 - \eta ^2 u_R^2}} + \frac{u_S^3}{\sqrt{1 - \eta ^2 u_S^2}}\right) \nonumber \\{} & {} \quad -\left( \frac{8MQ^2}{\eta ^3} - \frac{2\sqrt{2}MQ^2}{\eta \pi \theta } - \frac{\eta M\Lambda }{3}\right. \nonumber \\{} & {} \quad \left. - \frac{16MQ^2\alpha \Lambda }{\eta ^3} + \frac{4\sqrt{2}MQ^2 \alpha \Lambda }{\eta \pi \theta }\right) \nonumber \\{} & {} \quad \times \left[ \frac{1}{(1 - \eta ^2 u_R^2)^{3/2}} + \frac{1}{(1 - \eta ^2 u_S^2)^{3/2}}\right] \nonumber \\{} & {} \quad - \left[ \frac{u_R}{(1 - \eta ^2 u_R^2)^{3/2}} + \frac{u_S}{(1 - \eta ^2 u_S^2)^{3/2}}\right] \nonumber \\{} & {} \quad \times \left( \frac{3\eta MQ^2}{2\sqrt{2}(\pi \theta )^{3/2}} - \frac{15MQ^2}{4\eta \sqrt{\pi \theta }} + \frac{\eta Q^2\Lambda }{4}\right. \nonumber \\{} & {} \quad \left. - \frac{3\eta MQ^2\alpha \Lambda }{\sqrt{2}(\pi \theta )^{3/2}} + \frac{15MQ^2\alpha \Lambda }{2\eta \sqrt{\pi \theta }}\right) \nonumber \\{} & {} \quad +\left( \frac{12MQ^2}{\eta } - \frac{3\sqrt{2}\eta MQ^2}{\pi \theta } - \frac{\eta ^3 M\Lambda }{2} \right. \nonumber \\{} & {} \quad \left. - \frac{24MQ^2\alpha \Lambda }{\eta } + \frac{6\sqrt{2}\eta MQ^2\alpha \Lambda }{\pi \theta }\right) \nonumber \\{} & {} \quad \times \left[ \frac{u_R^2}{(1 - \eta ^2 u_R^2)^{3/2}} + \frac{u_S^2}{(1 - \eta ^2 u_S^2)^{3/2}}\right] \nonumber \\{} & {} \quad + \left[ \frac{u_R^3}{(1 - \eta ^2 u_R^2)^{3/2}} + \frac{u_S^3}{(1 - \eta ^2 u_S^2)^{3/2}}\right] \nonumber \\{} & {} \quad \times \left( \frac{\sqrt{2}\eta ^3 MQ^2}{(\pi \theta )^{3/2}} - \frac{5\eta MQ^2}{\sqrt{\pi \theta }} + \frac{\eta ^3Q^2\Lambda }{3} \right. \nonumber \\{} & {} \quad - \frac{2\sqrt{2}\eta ^3 MQ^2\alpha \Lambda }{(\pi \theta )^{3/2}} \nonumber \\{} & {} \quad \left. - \frac{\eta ^5 Q^2\Lambda }{12\sqrt{2}\pi \theta } + \frac{\eta ^5 M\Lambda }{6\sqrt{\pi \theta }} + \frac{10\eta MQ^2\alpha \Lambda }{\sqrt{\pi \theta }}\right) \end{aligned}$$
(6.15)

Consequently, for the noncommutative charged black hole under study, combining Eqs. (6.14) and  (6.15) yields the deflection angle of light presented as

Fig. 8
figure 8

Deflection angle as a function of the impact parameter \(\eta \) for various values of the noncommutative parameter \(\theta \) and the electric charge Q with \(M=1\), \(\alpha =0.01\) and \(\Lambda =-0.02\)

Full size image
$$\begin{aligned} \hat{\Theta }{} & {} = \left( \frac{32 \alpha M Q^2}{5 \eta ^5}-\frac{8 \sqrt{2} \alpha M Q^2}{3 \pi \eta ^3 \theta }-\frac{4 \alpha \Lambda M}{3\eta }+\frac{2 M}{\eta }\right) \nonumber \\{} & {} \quad \times \left( \frac{1}{\sqrt{1-\eta ^2 u_R^2}} + \frac{1}{\sqrt{1-\eta ^2 u_S^2}}\right) \nonumber \\{} & {} \quad + \left[ \frac{\eta ^3 \Lambda (3-\alpha \Lambda )}{18} +\frac{\left( \frac{1}{\sqrt{2} \pi \theta }-\frac{5}{4 \eta ^2}\right) 3 \alpha M Q^2}{\eta \sqrt{\pi \theta }}\right. \nonumber \\{} & {} \quad \left. -\frac{2 \eta M (3-2 \alpha \Lambda )}{3 \sqrt{\pi \theta }}+\frac{\eta Q^2 (3-2 \alpha \Lambda )}{3 \sqrt{2} \pi \theta }-\frac{Q^2 (3-2 \alpha \Lambda )}{4 \eta }\right] \nonumber \\{} & {} \quad \times \left( \frac{u_R}{\sqrt{1-b^2 u_R^2}} + \frac{u_S}{\sqrt{1-\eta ^2 u_S^2}}\right) \nonumber \\{} & {} \quad + \left( \frac{4 \sqrt{2} \alpha M Q^2}{\pi \theta }-\frac{16 \alpha M Q^2}{5 \eta ^3}\right) \nonumber \\{} & {} \quad \times \left( \frac{u_R^2}{\sqrt{1-\eta ^2 u_R^2}} + \frac{u_S^2}{\sqrt{1-\eta ^2 u_S^2}}\right) \nonumber \\{} & {} \quad -\left[ \frac{\eta Q^2}{12}(3-2 \alpha \Lambda )-\frac{\alpha \eta M Q^2}{\sqrt{2} (\pi \theta )^{3/2}}-\frac{5 \alpha M Q^2}{4 \eta \sqrt{\pi \theta }}\right] \nonumber \\{} & {} \quad \times \left( \frac{u_R^3}{\sqrt{1-\eta ^2 u_R^2}} + \frac{u_S^3}{\sqrt{1-\eta ^2 u_S^2}}\right) \nonumber \\{} & {} \quad -\left[ \frac{8 M Q^2}{\eta ^3}+\frac{\eta \Lambda M}{6 \sqrt{\pi \theta }}-\frac{\eta \Lambda M}{2}\right. \nonumber \\{} & {} \quad \left. -\frac{(1-2 \alpha \Lambda )2 \sqrt{2} M Q^2}{\pi \eta \theta }-\frac{16}{3}\alpha \Lambda M Q^2\right] \nonumber \\{} & {} \quad \times \left[ \frac{1}{(1 - \eta ^2 u_R^2)^{3/2}} + \frac{1}{(1 - \eta ^2 u_S^2)^{3/2}}\right] \nonumber \\{} & {} \quad - \left[ \frac{u_R}{(1 - \eta ^2 u_R^2)^{3/2}} + \frac{u_S}{(1 - \eta ^2 u_S^2)^{3/2}}\right] \nonumber \\{} & {} \quad \times \left[ \frac{\eta ^3 \Lambda Q^2}{6 \sqrt{2} \pi \theta }-\frac{\eta ^3 \Lambda M}{3 \sqrt{\pi \theta }}+\frac{(1-2 \alpha \Lambda )2 \eta M Q^2}{\sqrt{2} (\pi \theta )^{3/2}}\right. \nonumber \\{} & {} \quad \left. -\frac{(1-2 \alpha \Lambda )15 M Q^2}{4 \eta \sqrt{\pi \theta }}+\frac{1}{3} \eta \Lambda Q^2\right] \nonumber \\{} & {} \quad -\left[ \frac{5}{6} \eta ^3 \Lambda M+\frac{(1-2 \alpha \Lambda )11 \eta M Q^2}{2\sqrt{2} \pi \theta }-\frac{(1-2\alpha \Lambda )12 M Q^2}{\eta }\right] \nonumber \\{} & {} \quad \times \left[ \frac{u_R^2}{(1 - \eta ^2 u_R^2)^{3/2}} + \frac{u_S^2}{(1 - \eta ^2 u_S^2)^{3/2}}\right] \nonumber \\{} & {} \quad +\left[ \frac{\eta ^5 \Lambda M}{6 \sqrt{\pi \theta }}-\frac{\eta ^5 \Lambda Q^2}{12 \sqrt{2} \pi \theta }+\frac{(1-2 \alpha \Lambda )3 \eta ^3 M Q^2}{\sqrt{2} (\pi \theta )^{3/2}}+\frac{3}{6} \eta ^3 \Lambda Q^2\right. \nonumber \\{} & {} \quad \left. -\frac{(1-2 \alpha \Lambda )9 \eta M Q^2}{2 \sqrt{\pi \theta }}\right] \nonumber \\{} & {} \quad \times \left[ \frac{u_R^3}{(1 - \eta ^2 u_R^2)^{3/2}} + \frac{u_S^3}{(1 - \eta ^2 u_S^2)^{3/2}}\right] + \left( \frac{\eta \Lambda }{6}-\frac{\alpha \eta \Lambda ^2}{18}\right) \nonumber \\{} & {} \quad \times \left( \frac{u_R^{-1}}{\sqrt{1-\eta ^2 u_R^2}} + \frac{u_S^{-1}}{\sqrt{1-\eta ^2 u_S^2}}\right) \nonumber \\{} & {} \quad +\left( \frac{\eta \Lambda Q^2}{12 \sqrt{2} \pi \theta }-\frac{\eta \Lambda M}{6 \sqrt{\pi \theta }}\right) \nonumber \\{} & {} \quad \times \left[ \frac{u_R^{-1}}{(1 - \eta ^2 u_R^2)^{3/2}} + \frac{u_S^{-1}}{(1 - \eta ^2 u_S^2)^{3/2}}\right] \end{aligned}$$
(6.16)

It can be seen from the above equation that similar to Eq. (6.14), this expression also has few terms that tend to diverge in the far distance limit \((u_R \rightarrow 0, u_S \rightarrow 0)\). Also, the effect of the noncommutative parameter and the elctric charge of the black hole on the bending angle can be clearly observed from the above expression. Furthermore, if the noncommutative parameter \(\theta \), charge Q, the GB coupling constant \(\alpha \) and the cosmological constant \(\Lambda \) are to vanish, it would result in

$$\begin{aligned} \hat{\Theta } \approx \frac{2M}{\eta }\left( \frac{1}{\sqrt{1-\eta ^2 u_R^2}} + \frac{1}{\sqrt{1-\eta ^2 u_S^2}}\right) \end{aligned}$$
(6.17)

which in the far distance limit \((u_R \rightarrow 0, u_S \rightarrow 0)\) reduces to

$$\begin{aligned} \hat{\Theta } \approx \frac{4M}{\eta } \end{aligned}$$
(6.18)

The gravitational bending angle of light formed in the vicinity of the gravitational field of this noncommutative charged 4D-AdS EGB black hole is portrayed in Fig. 8 as a function of the impact parameter. The first illustration is for different values of the noncommutative parameter \(\theta \) and the second one is for different values of electric charge Q. We have assumed \(u_R = u_S = 0.5/\eta \). Further, each plot is compared with that of the Schwarzschild case. It can be seen from the figure that the behaviour of the bending angle for the black hole under study is similar to that of the Schwarzschild case up to a particular value of the impact parameter. However, with increasing impact parameter, unlike the Schwarzschild case, the deflection angle for the noncommutative charged black hole further decreases and becomes negative. For the first figure, with rising values of the noncommutative parameter, the value of the deflection angle also increases. Again, with an increase in the charge of the black hole, the value of the deflection angle becomes smaller. This indicates that the properties of the black hole under consideration have significant effect on the behaviour of the deflection of light around the black hole. It can be said that for higher impact parameters, the photons are repelled by the gravitational field of the black hole thereby resulting in a negative deflection angle. In fact, such a negative deflection angle gives us an idea about the gravitational nature of the black hole under study. Here, it should be remarked that negative deflection angle has also been obtained in various literature [19, 22, 81,82,83] and in modified gravity theories with exotic matter and energy [84, 85].

7 Conclusion

In summary, our article takes an in-depth look at the optical features of a charged 4D-AdS-EGB black hole, inspired by noncommutative geometry. Such a black hole solution was derived in the framework of 4D-EGB with a negative cosmological constant. The recent regularization proposed by Glavan and Lin has been used to restore the dynamic component of the Gauss–Bonnet term in a 4D context. In addition, the influence of the non-commutativity of space-time has been incorporated by characterizing the source of matter and charge by Gaussian distributions.

To investigate the shadow of the black hole, we applied the Hamilton-Jacobi technique and the Carter separation method to integrate the geodesic equation and calculate the radius of the shadow. The equations of the system do not have an analytical solution. Alternately, we used the numerical method to find the solution.. Our results highlight the influence of the framework of the noncommutative geometry on the radius of the shadow, showing an inverse relationship with the variation of the noncommutative parameter \(\theta \). This trend is also observed with the variation of the electric charge Q. Therefore, the examination of the restrictions imposed on the parameters of the model by the observations of the shadows could not only increase the feasibility but also improve our understanding of the theory by illuminating our perspective, thanks to the data of the EHT.

Subsequently, given that the radius of the shadow is directly related to the rate of energy emission, we analyzed the impact of the electric charge and noncommutativity on this physical quantity. Our results demonstrate that the increase in the electric charge, or the noncommutative parameter, leads to a decrease in the energy emission rate (EER).

Furthermore, we have investigated the deflection angle of the black hole. To this end, the GBT is employed. The effect of the parameters of the black hole on the deflection angle is analyzed. For a change in the charge or the noncommutative parameter of the black hole, the deflection angle is found to decrease and become negative after a certain impact parameter. Specifically, for a rise in the charge of the black hole, the angle becomes smaller whereas for an increasing noncommutative parameter, the deflection angle becomes larger. This outcome gives us an idea about the nature of the gravitational field of the black hole. A few other optical features related to lensing by the noncommutative 4D-AdS-EGB black hole can also be investigated in future work.