Abstract
We extend the anholonomic frame and connection deformation method, AFCDM, for constructing exact and parametric solutions in general relativity, GR, to geometric flow models and modified gravity theories, MGTs, with nontrivial torsion and nonmetricity fields. Following abstract geometric or variational methods, we can derive corresponding systems of nonmetric gravitational and matter field equations which consist of very sophisticate systems of coupled nonlinear PDEs. Using nonholonomic frames with dyadic spacetime splitting and applying the AFCDM, we prove that such systems of PDEs can be decoupled and integrated in general forms for generic off-diagonal metric structures and generalized affine connections. We generate new classes of quasi-stationary solutions (which do not depend on time like coordinates) and study the physical properties of some physically important examples. Such exact or parametric solutions are determined by nonmetric solitonic distributions and/or ellipsoidal deformations of wormhole hole configurations. It is not possible to describe the thermodynamic properties of such solutions in the framework of the Bekenstein–Hawking paradigm because such metrics do not involve, in general, certain horizons, duality, or holographic configurations. Nevertheless, we can always elaborate on associated Grigori Perelman thermodynamic models elaborated for nonmetric geometric flows. In explicit form, applying the AFCDM, we construct and study the physical implications of new classes of traversable wormhole solutions describing solitonic deformation and dissipation of non-Riemannian geometric objects. Such models with nontrivial gravitational off-diagonal vacuum are important for elaborating models of dark energy and dark matter involving wormhole configurations and solitonic-type structure formation.
Similar content being viewed by others
1 Introduction, motivations and objectives
The standard approach to the gravity theory and general relativity, GR (i.e. Einstein’s gravity theory) is formulated in the framework of pseudo-Riemannian geometry, see [1,2,3,4] as typical monographs and reviews of physically important exact solutions. In GR, a four dimensional, 4-d, curved spacetime V is modelled as a Lorentz manifold endowed with metric structure, \(g=\{g_{\alpha \beta }\},\) when the Levi-Civita, LC-connection \(\nabla =\{\ ^{\nabla }\Gamma _{\ \beta \gamma }^{\alpha }\}\) is uniquely determined by coefficients \(g_{\alpha \beta }\) following two conditions: (1) zero nonmetricity (i. e. metric compatibility), \(Q:=\nabla g=0\) and (2) zero torsion, \(\ ^{\nabla }T=0.\)Footnote 1 The Einstein relativity theory has a remarkable success and deep influence both in physics and mathematics. Nevertheless, various alternatives and modifications of GR were elaborated when instead of standard Lorentz manifolds there are considered metric-affine spaces determined by some general metric and (independent) affine/linear connection structures, \((g,D=\{\Gamma _{\ \beta \gamma }^{\alpha }\}).\) Such non-Riemannian spaces can be characterized by nonzero torsion, \(T=\{T_{\ \beta \gamma }^{\alpha }\},\) and/or nontrivial nonmetricity, \(Q:=Dg=\{Q_{\alpha \beta \gamma }:= D_{\alpha }g_{\beta \gamma }\},\) fields. We cite [5] as an early review of metric-affine gravity theories. For applications in modern cosmology, various generalizations of such geometric and gravity models are formulated as modified gravity theories, MGTs, when the gravitational and matter field Lagrangians in GR are changed into some functionals \(F(R,T,Q,\ ^{tr}T),\) where R is the Ricci scalar for D, and \(\ ^{tr}T\) is the trace of the energy-momentum tensor for matter [6, 7].Footnote 2
Generalizations of the Einstein equations with geometric distortions of linear connections, \(\nabla \rightarrow D\), can be written in some effective forms:
In such formulas, \(\varkappa \) is defined by the gravitational constant and the energy-momentum tensors contain respective labels [br], for barionic matter (which can be written also \(T_{\mu \nu }^{[m]});\) [DM] is for dark matter models with some scalar, \(\phi ,\) spinor, \(\psi ,\) and other type fields. The label [DE] is used for respective dark energy terms. The tensor \(T_{\mu \nu }^{[geom]}\) is a functional of different geometric and physical values including classical and quasi-classical and/or extra dimension contributions, string terms contributions, distortions of mater fields Lagrange densities, \(\mathcal {L}^{[m]},\) and corresponding traces of energy-momentum tensors, \(T^{[m]}\). In some MGTs, there are considered nonlocal terms of type \(\square R\) and/or \(\square T,\) where \(\square \) is a corresponding variant of d’Alambert (wave operator) for respective curved spacetime etc. The modified Einstein tensor \(E_{\mu \nu }\) and respective (effective) barionic matter terms \(T_{\mu \nu }\approx T_{\mu \nu }^{[br]}+...\) can be derived from a corresponding action
Typically, such formulas define a four-dimensional, 4-d, spacetime model which is distorted in the symbolic form \(D=\nabla +Z[g,T,Q,...],\) where Z is the distortion tensor. Physical motivations and details on such MGTs and dark gravity/matter/energy formalism are presented in [6,7,8] and references therein ( there are studied also certain applications in modern acceleration cosmology and DM and DE physics).
Modified Einstein equations of type (1) consist of very sophisticate systems of coupled nonlinear partial differential equations, PDEs. It is very difficult to find exact/parametric solutions for such dynamical equations using standard methods elaborated in GR [4], when for some higher symmetry and diagonal ansatz form metrics, nonlinear PDEs transform into certain nonlinear systems of ordinary differential equations, ODEs. For instance, it is not clear how to construct black hole, BH, like solutions for nontrivial Q-terms, for generic off-diagonal \(g_{\alpha \beta };\) and how to define extensions of the Einstein-Dirac equations. Such problems were discussed in detail in [9, 10], (in a general form for Finsler modifications of gravity theories). Similar problems exist for metric-affine distortions of physical models elaborated on Lorentz manifolds. The DM and DE coupling theories and various MGTs involve constructions with nonminimal coupling between geometry and matter. The equations (1) lead to the “nonconservation” of matter energy-momentum tensor which makes more sophisticate the physical interpretation of such models and solutions of dynamical or evolution equations. Nevertheless, we can elaborate on a nonholonomic deformation formalism with adapted distortions \(\nabla \rightarrow D,\) when “nonconservation” is related to certain (equivalently, anholonomic, i.e. nonintegrable) constraints like in nonholonomic mechanics. By introducing integration constants, then solving the constraint equations and redefining the effective Lagrangians, we can formulate some types of modified conservation laws.
The main goal of this work is to prove that modified Einstein equations of type (1) can be decoupled and integrated in some general forms for \(Q\ne 0\). We shall provide explicit examples for generic off-diagonal solutions defining Q-deformations of gravitational solitonic hierarchies and wormhole configurations. Such methods for generating exact/parametric solutions of physically important systems of nonlinear PDEs are not contained in standard monographs on GR and various MGTs reviews [1,2,3,4,5,6,7,8]. During the last 30 years, it was elaborated the anholonomic frame and connection deformation method, AFCDM, for constructing exact and parametric off-diagonal solutions of physically important systems of nonlinear PDEs. We cite [9,10,11,12] for a review of main results and methods, examples and applications. Here we note that the AFCDM involves nonholonomic distributions of geometric objects and nonholonomic frames, with respective types 2 + 2 + 2 +\(\cdots \), 3+1 and (3 + 1) + (2 + 2), 3 + 2 + 2 +\(\cdots \) (correspondingly, for 4-d, and extra dimension spacetimes). Then, it is important to construct an auxiliary connection \(\widehat{\textbf{D}}=\nabla + \widehat{\textbf{Z}}\) when equations of type (1) with redefined linear connections, \(\nabla \rightarrow \widehat{\textbf{D}}\) can be decoupled and integrated in certain general forms. In the next section, we shall provide the necessary definitions and explicit formulas.
Our nonholonomic geometric approach to generating solutions in gravity theories should not be confused with the well-known Cartan moving frame method, Neuman-Penrose formalism or other nontrivial string torsion generalizations and/or equivalent constructions involving various types of tetradic, dyadic, and Arnowit–Deser–Wheeler, ADM, formalisms. Main geometric and analytic constructions related to GR are summarized in [4]). The main difference of the AFCDM from other ones is that it involves deformations both of the frame and linear connection structures which are adapted to certain canonical nonholonomic distributions. In such nonholonomic adapted variables, physically important systems of nonlinear PDEs can be decoupled and integrated in certain general forms, when the technique of constructing solutions is not restricted only to special diagonal ansatz transforming systems of nonlinear PDEs into systems of nonlinear ODEs. For generic off-diagonal ansatz, we can prescribe some special symmetries with Killing vectors and/or Lie algebra structure, for spherical, cylindrical, toroid or other type configurations. Such solutions also posses certain nonlinear symmetries. We can prescribe necessary symmetries of solutions, and compute certain deformations (for instance, by nonmetricity fields) for some physically important classes of solutions. Usually, it is possible to extract LC configurations if there are imposed additional nonholonomic constraints on the nonlinear and linear connection structures, and respective generating and integration functions. For some models, the off-diagonal terms of metrics and the nontrivial nonholonomic structure may encode nonmetricity contributions even for constraints to LC models.
This paper is a generalization to nonmetric geometric flows providing a metric-affine development of the methods reviewed in [10,11,12]. Such geometric constructions can be performed for nonassociative and noncommutative geometric flow and gravity theories [13], when the constructions are performed for star product R-flux deformations in metric compatible forms but including nonsymmetric metrics. In this work, we consider associative and commutative metric-affine structures with symmetric metrics when the nonholonomic deformations and nonmetricity fields are related both to nonmetricity-induced torsion fields and canonically induced torsions. For this work, we state three general objectives:
The first objective (Obj1, in Sect. 2) is to provide an introduction to theories of geometric flow and gravity including nonmetricity. The 4-d metric–affine geometry is formulated in an N-connection adapted form with (dyadic) nonholonomic (2+2)-splitting. We define Q-modified (for Riemannian metrics introduced by G. Perelman [15]) F- and W-functionals and sketch how they can be derived from respective Hamilton-Friedan geometric flow equations with nonmetricity. Nonmetric Ricci solitons and related modified Einstein equations are derived as self-similar nonholonomic geometric flow configurations for a fixed flow parameter.
The second objective, Obj2, stated for Sect. 3, is to construct and analyse solitonic deformations of exact/parametric quasi-stationary geometric flow solutions encoding nonmetricity fields, which for fixed flow parameters and LC-configurations define solutions of modified Einstein equations (1) and their nonholonomic deformations. Such systems of nonlinear PDEs are extended in certain forms encoding nonmetric geometric flow data. We provide necessary examples of solitonic distributions defined in quasi-stationary geometric form and study models with locally anisotropic wormhole solutions encoding nonmetricity. Nonmetric quasi-stationary deformations of 4-d wormhole metrics in GR are constructed for general and small parametric off-diagonal and nonmetric gravitational polarizations.
The third objective, Obj3, is stated for Sect. 4. It consists of a study of Q-modified Grigori Perelman thermodynamics and its applications for quasi-stationary configurations. We show how to define and compute (using integration functions and nonlinear symmetries to some flow-running cosmological constants) respective volume elements. This allows us to compute thermodynamic variables with running cosmological constants and nonmetricity. For nonmetric modified wormhole configurations and their solitonic deformations, we show that, in principle, we can construct two thermodynamic models: a ‘l’a Perelman’ and/or do not follow the Bekenstein–Hawking approach because the last one is applicable only for solutions with conventional horizons, holographic models and similar. Modified Perelman thermodynamic models can be formulated for all classes of nonholonomic geometric flow theories, including theories with Q-deformations.
In this article and a series of further partner works on nonmetric geometric flow and gravity theories we follow the Hypothesis: Metric-affine geometric flow models can be exploited as alternatives for describing DE and DM effects and elaborating new physical theories. Such approaches can be elaborated in self-consistent and solvable forms using nonholonomic variables with conventional \(2(3) + 2 + \cdots \) splitting which allows to decouple and integrate of physically important systems of nonlinear PDEs for such theories. The solutions with conventional \(\tau \)-running effective cosmological constants physics can be used for modelling DE physics when nonlinear symmetries relate such configurations to models of DM physics. Generic off-diagonal metrics are determined by respective generating functions and effective matter sources which encode nonmetric Q-deformations and describe DE and DM off-diagonal interactions or geometric evolution scenarios. Corresponding systems of Q–deformed geometric flow/gravitational and (effective) matter field equations admit exact and parametric solutions describing certain quasi-stationary (BH, wormhole etc.) configurations and (locally anisotropic and inhomogeneous) cosmological scenarios. For well-defined nonholonomic geometric constraints, such models can be defined almost equivalently in canonical metric compatible backgrounds with effective N-connection structure, when generalized conservation laws and nonlinear symmetries are well-defined. In such cases, we can formulate self-consistent nonmetric modifications of classical gravity and quantum gravity theories, quantum mechanical models and quantum field theories, which can be unified as thermodynamic information theories in the framework of respective geometric and quantum information models.
In Appendix A, we revise in a nonmetric quasi-stationary form all formulas which are necessary for general decoupling and integration of Q-modified nonholonomic Ricci flow/ soliton equations. Details and proofs for general metric compatible canonical d-connections are provided in [10,11,12,13]. In this work, abstract and N-adapted coefficient formulas are re-defined by Q-deformations and Q-generating sources. A summary of basic concepts and formulas for generating solitonic hierarchies via d-metrics and nonmetricity effective sources is presented in Appendix B.
2 Metric noncompatible geometric flows and MGTs
This section contains an introduction to the geometry of four dimensional, 4-d, metric-affine spaces with nontrivial torsion and nonmetricity fields. The approach is formulated in canonical nonholonomic variables with (2+2)-splitting defined by a nonlinear connection, N-connection, structure stating dyadic frame decompositions. We consider N-adapted distortions of linear connections and fundamental geometric objects. The constructions are performed in such forms that physically important systems of nonlinear PDEs (such as nonmetric geometric flow evolution and modified Einstein equations) can be decoupled and integrated in certain general off-diagonal forms. Necessary concepts and additional technical formulas for the nonmetric anholonomic frame and connection deformation method, AFCDM, are outlined in Appendix A. Such a nonholonomic geometric formalism was elaborated for (co) tangent bundles, see reviews of results and methods in [10, 12]. In this section, we develop the approach in a form which allows to construct exact and parametric solutions with nonmetricity for gravity theories of type in [5,6,7,8]. The Grigori Perelman functionals [15] (see [16] for recent developments related to GR, MGTs and quantum information flow theories) are modified in nonmetric forms. For self-similar configurations (i.e. for nonholonomic Ricci solitons) such models encode the action functionals for gravity theories with nontrivial Q-fields [6].
2.1 Geometric preliminaries on metric-affine spaces and nonholonomic deformations
In this work, the background geometric arena consists from a Lorentz spacetime manifold V enabled with standard geometric data \((V, \textbf{g,}\nabla ).\) Such a (primary) spacetime is defined as a 4-d pseudo-Riemannian manifold of necessary smooth/differentiability class, when the symmetric metric tensor \(\textbf{g}\) is of signature \((+++-)\) and can be written in the form
using the tensor product \(\otimes \) of general co-frames \(e^{\alpha ^{\prime }}\), which are dual to frame bases \(e_{\alpha ^{\prime }}.\) In general form, the geometric and physical constructions are performed for metric-affine spaces (target ones) determined by geometric data \((V,\textbf{g,}D),\) when \( \nabla \rightarrow D\) and, in general, the nonmetricity field is nontrivial, \(Q:=D\textbf{g}\ne 0.\) To elaborate theories of geometric flows [15, 16] one considers families of metrics \(\textbf{g}(\tau )=\{g_{\alpha \beta }(\tau ,u)\},\) where \(\tau \) is a temperature like parameter considered for an interval \(0\le \tau \le \tau _{1},\) or \(\tau =\tau _{0}\) for a fixed value. Frame vectors can be prescribed to depend, or not, on \(\tau \)-parameter, i.e. \(e_{\alpha ^{\prime }}(\tau ),\) or \( e_{\alpha ^{\prime }}.\) For simplicity, we shall write only \(g_{\alpha \beta }(\tau )\) instead of \(g_{\alpha \beta }(\tau ,u)\) if that will not result in ambiguities.
2.1.1 N-adapted metric-affine structures with nonholonomic (2+2) splitting
We introduce a nonlinear connection, N-connection, structure as a Whitney sum:
which is globally defined on V and its tangent bundle TV. A \(\textbf{N}\) defines a conventional horizontal and vertical splitting ( h- and v–decomposition) into respective 2-d and 2-d subspaces, hV and vV. In local coordinate form, a N-connection is defined by a set of coefficients \( N_{i}^{a}(u)\) when \(\textbf{N}=N_{i}^{a}(x,y)dx^{i}\otimes \partial /\partial y^{a}.\)Footnote 3
N–elongated/adapted local bases, \(\textbf{e}_{\nu },\) and co-bases (N–differentials), \(\textbf{e}^{\mu },\) are defined
to be linear on \(N_{i}^{a}.\) The term nonholonomic (equivalently, anholonomic) is used because, for instance, a N-elongated basis (4) satisfies certain nonholonomy relations
with nontrivial anholonomy coefficients
In these formulas, \(\Omega _{ij}^{a}\) define the coefficients of N-connection curvature. If all \(W_{ia}^{b}\) (7) are zero for a \( \textbf{e}_{\alpha },\) such a N-adapted base is holonomic and we can write it as a partial derivative \(\partial _{\alpha }\) with \(N_{i}^{a}=0.\) In curved local coordinates, the coefficients \(N_{j}^{a}\) may be nontrivial even all \(W_{\alpha \beta }^{\gamma }=0\) and we may chose a holonomic base.Footnote 4
The geometric objects on a nonholonomic manifold \(\textbf{V}\) enabled with a N-connection structure \(\textbf{N}\) (and on extensions to tangent, \(T\textbf{ V,}\) and cotangent, \(T^{*}\textbf{V}\), bundles; and their tensor products, for instance, \(T\mathbf {V\otimes }T^{*}\textbf{V}\)) are called distinguished (in brief, d-objects, d-vectors, d-tensors etc) if they are adapted to the N–connection structure via corresponding decompositions with respect to frames of type (4) and (5). For instance, we write a d–vector as \(\textbf{X}=(hX,vX)\).
Any spacetime metric \(\textbf{g}=(hg,vg)\) (2) can be represented equivalently as a d–metric,Footnote 5 when
Ad–connection \(\textbf{D}=(hD,vD)\) is defined as a linear connection preserving under parallelism the N–connection splitting (3). In N-adapted coefficient form with respect to frames (4) and (5), we can write decompositions of \(\textbf{D}\) in terms of h- and v-indices,
We define a nonholonomic metric-affine space by geometric data \((\textbf{ V,N,g,D}).\)
2.1.2 Geometric objects adapted to a N-connection structure and nonmetricity
The fundamental geometric d-objects of nonholonomic metric-affine space are defined:
The N-adapted coefficient formulas involving (8), (9) and (10) are provided and computed in [10,11,12]. Here we only present, respectively, their 4-d N-adapted coefficient representations,
In geometric flow and gravity theories, there are also another important geometric d-objects:
where we uses the inverse d-tensor \(\{\textbf{g}^{\alpha \beta }\}\) of a d-metric (8).
Using a d-metric \(\textbf{g}\) (8), we can define two important linear connection structures:
In this paper, “hat” labels are used for geometric d-objects defined by a \( \widehat{\textbf{D}}.\) Such an auxiliary d-connection defines a canonical distortion relation
when the canonical distortion d-tensor, \(\widehat{\textbf{Z}}\), and \(\nabla [\textbf{g}]\) are determined by the same metric structure \(\mathbf {g.} \)Footnote 6
The coefficients of the canonical fundamental geometric d-objects (11) are labeled by “hat” symbols, for instance, \(\widehat{\mathcal {R} }=\{\widehat{\textbf{R}}_{\ \beta \gamma \delta }^{\alpha }\}.\) Similar fundamental geometric objects can be defined and computed for \(\nabla ,\) for instance, \({}_{\nabla }\mathcal {R}=\{{}_{\nabla }R_{\ \beta \gamma \delta }^{\alpha }\}\) (in such cases, boldface indices are not used). Considering the canonical distortion relation for linear connections (13), we can compute respective canonical distortions of fundamental geometric d-objects (11). Such formulas relate, for instance, two different curvature tensors, \({}_{\nabla }\mathcal {R}=\{{}_{\nabla }R_{\ \beta \gamma \delta }^{\alpha }\}\) and \(\widehat{\mathcal {R}}=\{\widehat{ \textbf{R}}_{\ \beta \gamma \delta }^{\alpha }\}\) etc.
An arbitrary d-connection \(\mathbf {D=\{\varvec{\Gamma }}_{\ \alpha \beta }^{\gamma }\}\) with nontrivial nonmetric d-tensor \(\textbf{Q}_{\gamma \alpha \beta }\) can be expressed via distortion d-tensors with respect to \( \nabla =\{\breve{\Gamma }_{\ \alpha \beta }^{\gamma }\}\) or \(\widehat{\textbf{ D}}=\{\widehat{{\varvec{\Gamma }}}_{\ \alpha \beta }^{\gamma }\},\)
In these formulas, for instance, for (T, Q)-deformations of LC-configurations, we use and construct such distortion tensors:
where \(Q_{\alpha \beta \gamma }:=D_{\alpha }g_{\beta \gamma }\) and \(T_{\ \beta \gamma }^{\alpha }\) is computed for any \(D=\{\Gamma _{\ \alpha \beta }^{\gamma }\}\) which can an arbitrary affine connection (with coefficients in coordinate or arbitrary frames). The torsion d-tensor \(\textbf{T}_{\ \beta \gamma }^{\alpha }\) can be computed for an arbitrary d-connection \( \textbf{D}=\{{\Gamma }_{\ \alpha \beta }^{\gamma }\},\) using N-adapted bases. Such objects are defined with respect to coordinate or N-adapted frames and used for introducing three scalar values considered in the Weyl–Cartan geometry:
For the nonholonomic Weyl-Cartan geometry, corresponding scalar values are defined for \(\textbf{D}=\{{\Gamma }_{\ \alpha \beta }^{\gamma }\}\) and \( \textbf{Q}_{\alpha \beta \gamma }:=\textbf{D}_{\alpha }\textbf{g}_{\beta \gamma }\) as distortions (13) of \(\widehat{\textbf{D}}=\{\widehat{ \Gamma }_{\ \alpha \beta }^{\gamma }\}\) and can be written
MGTs with torsion and nonmetricity are modelled for actions of type
where the gravitational Lagrange density is a functional \(\ ^{g}\mathcal {L} =F(R,\ ^{s}T,Q,T^{[m]})\) and \(\ ^{m}\mathcal {L}[\phi ]\) is the Lagrange density for conventional matter fields \(\phi .\) Such a model is studied in [6] but, in this work, we follow a different system of notations considered, for instance, in [11] (for instance, we write F(...) instead of f(...)). The gravitational and matter field equations of type (1) derived variationally from an action (15) consist sophisticate coupled systems of nonlinear PDEs. It is very difficult to find exact/parametric solutions in such MGTs even, for instance, certain cosmological and DE and DM models were studied in [6,7,8].
In this work, we shall consider MGTs of type (15) written in canonical d-variables \((\textbf{g,D}=\widehat{\textbf{D}}+\widehat{\textbf{K} }+\ ^{q}\widehat{\textbf{Z}}),\) see distortions (14), and following a N-adapted variational calculus for actions of type
where \(\delta ^{4}u\) is the volume element defined with N-elongated differentials (5), \(\ ^{g}\widehat{\mathcal {L}}=F(\widehat{\textbf{ R}}sc,\ ^{s}\widehat{T},T^{[m]})\) is computed as \(\ ^{g}\mathcal {L}\) from ( 15) when \(\nabla \rightarrow \widehat{\textbf{D}},\) for \( \widehat{\textbf{Q}}_{\alpha \beta \gamma }=0\); \(\ ^{e}\widehat{\mathcal {L}}( \textbf{Q}_{\alpha \beta \gamma },\widehat{\textbf{D}},\phi )\) includes distortions of geometric d-objects and Lagrangians deformations for \( \widehat{\textbf{D}}\rightarrow \textbf{D}\) is nontrivial \(\textbf{Q} _{\alpha \beta \gamma };\) and \(\ ^{m}\widehat{\mathcal {L}}(\textbf{g} _{\alpha \beta },\phi ,\widehat{\textbf{D}})\) if \(\ ^{m}\mathcal {L} (g_{\alpha \beta },\phi ,\nabla ),\) or (we can consider some simplified models) when \(\ ^{m}\widehat{\mathcal {L}}(\textbf{g}_{\alpha \beta },\phi )=\ ^{m}\mathcal {L}(\textbf{g}_{\alpha \beta },\phi ).\)
In a series of works [11,12,13, 16], we proved that geometric flow and gravitational field equations in MGTs with \( \textbf{D}=\widehat{\textbf{D}}\) or \(\mathbf {D\rightarrow }\widehat{\textbf{D }}\rightarrow \nabla \) can be decoupled and integrated in certain general off-diagonal forms using the AFCDM. The general goal of this article is to show how those methods can be generalized for nontrivial \(\textbf{Q} _{\alpha \beta \gamma }(\tau )\) and applied for research of the relativistic Ricci flows of nonholonomic metric-affine structures, or corresponding nonholonomic Ricci soliton equations for any \(\tau _{0}.\)
2.2 Relativistic geometric flows encoding nonmetricity fields
The theory of Ricci flows has a high scientific impact in modern mathematics and physics after Grigori Perelman proved [15] the famous Poincaré–Thurston conjecture, see original works [19] and [17, 18] and monographs [20,21,22] for reviews of mathematical results and methods. A crucial step in elaborating such theories consisted in definition of the so-called \(\mathcal {F}\)- and \(\mathcal {W}\)-functionals from which the geometric flow equations (called also as R. Hamilton or Hamilton-Friedan equations) can be proved in variational form. It is not clear how mathematically can be formulated and proved relativistic variants of such conjectures and generalizations for nonmetric/supersymmetric/nonassociative/noncommutative/Finsler like geometries. Nevertheless, generalizations of \(\mathcal {F}\)- and \(\mathcal {W}\)-functionals allow to prove modified versions of geometric flow equations and solve such systems of nonlinear PDEs using the AFCDM. The results of a series of recent papers [16, 23] demonstrate that Perelman like information thermodynamics may play an important role in the theory of quantum geometric and information, QGIF, flows. In this work, we show how such constructions can be performed for nonmetric geometric flows for families \(\tau \)-evolving metric-affine data \((\textbf{g}(\tau ),\textbf{D}(\tau ))\) and Lagrange densities \(\ ^{g}\widehat{\mathcal {L}}(\tau )+\ ^{e}\mathcal {L}(\tau )+\ ^{m} \widehat{\mathcal {L}}(\tau ).\)
2.2.1 Q-modified Perelman’s F- and W-functionals in canonical nonholonomic variables
The modified Perelman’s functionals for nonmetric geometric flows are postulated in the form
where the condition \(\int _{t_{1}}^{t_{2}}\int _{\Xi _{t}}\left( 4\pi \tau \right) ^{-2}e^{-f(\tau )}\sqrt{|\textbf{g}|}d^{4}u=1\) is imposed on the normalizing function \(f(\tau )=f(\tau ,u).\) The difference from the original F- and W-functionals [15] introduced for 3-d Riemannian \(\tau \) -flows \((g(\tau ),\nabla (\tau ))\) is that in this work we study geometric flows of canonical geometric data \((\textbf{g}(\tau ),\) \(\textbf{N}(\tau ), \textbf{D}(\tau ))\) for Q-deformations of nonholonomic Lorentz manifolds.
We can compute relativistic effective functionals (17) and (18) for any 3+1 splitting with 3-d closed hypersurface fibrations \(\widehat{\Xi }_{t}\) and considering nonholonomic canonical d-connections and respective geometric variables. In general, it is possible to work with any class of normalizing functions \(f(\tau )\). Such a function can be fixed by some constant values or some parametrization conditions simplifying corresponding systems of nonlinear PDEs. Such \(f(\tau )\) define respective integration measures which may be important, or not, for elaborating topological and/or geometric models. The \(\mathcal {W}\) -functional possess the properties of “minus” entropy. This can be stated by choosing corresponding nonholonomic configurations along some causal curves taking values \(\mathcal {W}(\tau )\) on \(\widehat{\Xi }_{t}.\) Using N-adapted variations, we can derive nonmetric geometric flow evolution equations which can be solved using the AFCDM for metrics with pseudo-Euclidean signature even analogs of Poincaré–Thurston conjecture have not been formulated and proven in modern mathematics.
2.2.2 Hamilton-Friedan geometric flow equations with nonmetricity
There are two possibilities to derive geometric flow equations from functionals \(\mathcal {F}(\tau )\) (17) and \(\mathcal {W} (\tau )\) (18). In the first case, we can use \(\textbf{D} (\tau )\) instead of \(\nabla (\tau )\) and reproduce in N-adapted form all covariant differential and integral calculus from [15, 20,21,22]. This would consist proofs on some hundred of pages.
We can follow geometric abstract principles [1] when all geometric and physically important objects and fundamental physical equations are derived by corresponding generalizations of Riemannian geometry to certain nonholonomic metric-affine geometries with \(\nabla (\tau )\rightarrow \textbf{D }(\tau )=\widehat{\textbf{D}}(\tau )+\widehat{\textbf{K}}(\tau )+\ ^{q} \widehat{\textbf{Z}}(\tau )\) respective generalizations of Ricci, torsion, and energy-momentum d-tensors. Such an abstract geometric calculus allows to prove for some primary data \((\textbf{g}=\{\textbf{g}_{\mu \nu }=[g_{ij},g_{ab}]\}, \textbf{N}= \{ N_{i}^{a}\},\textbf{D},\ ^{tot}\widehat{ \mathcal {L}}= \ ^{e}\mathcal {L} + \ ^{m}\widehat{\mathcal {L}}),\) see definitions related to formulas (16) the nonholonomic geometric flow evolution equations:
In these formulas, there are used such geometric d-objects and N-adapted operators: \(\widehat{\square }(\tau )=\widehat{\textbf{D}}^{\alpha }(\tau ) \widehat{\textbf{D}}_{\alpha }(\tau )\) when the conditions \(\widehat{\textbf{ R}}_{ia}=\widehat{\textbf{R}}_{ai}=0\) for the Ricci tensor \(\widehat{R}ic[ \widehat{\textbf{D}}]=\{\widehat{\textbf{R}}_{\alpha \beta } = [\widehat{R} _{ij},\widehat{R}_{ia},\widehat{R}_{ai},\widehat{R}_{ab,}]\}\) are necessary if we want to keep the metric \(\textbf{g}(\tau )\) to be symmetric under nonholonomic Ricci flow evolution. Such constraints are not obligatory, for instance, in nonassociative geometric flow theory with nonsymmetric metrics [13].
The definition of \(\ ^{tot}\widehat{\Upsilon }_{ab}(\tau )\) from (19) will be discussed in Sect. 2.3 for \( \tau =\tau _{0}.\) Here we note that such equations describe nonmetric geometric flow evolution of d-metrics \(\textbf{g}_{\mu \nu }(\tau )\) described in nonholonomic canonical variables. Alternatively, such equations can be introduced as relativistic generalizations and nonholonomic canonical deformations of the R. Hamilton [19] and D. Friedan [17, 18] Ricci flow equations for \(\nabla (\tau ).\)
The normalizing function \(f(\tau )\) can be re-defined in such a way that it compensates certain Q-deforms, or other type nonholonomic distortions, when \(\widehat{f}(\tau )\rightarrow f(\tau )\) for
Such an equation involves nonlinear partial differential operators and usually it is not possible to solve it in an explicit form and define the evolution of topological configurations determined, for instance, by nontrivial nonmetric structures. Nevertheless, we can fix a variant of \( \widehat{f}(\tau )\) which together with some off-diagonal ansatz for metrics we can solve the nonholonomic system of nonlinear PDEs (19) in certain general/parametric forms and then to re-define the constructions in for arbitrary systems of reference, other types of distortions of connections and normalizing functions. The formulas for nonholonomic frame/coordinate/normalizing transforms could be found in certain series/recurrent form when the solutions of geometric flow equations are generated in explicit form.
2.3 Nonmetric Ricci solitons and modified Einstein equations
A nonholonomic and nonmetric Ricci soliton configuration is a self-similar one for the geometric flow equations (19). For Riemannian metrics, such configurations homothetically strink, remain steady or expand under geometric flow evolution, see details in [15, 19,20,21,22], and can be respectively studied for a fixed point \(\tau =\tau _{0}\). Considering relativistic and torsion and nonmetricity modified nonlinear systems with \(\partial _{\tau } \textbf{g}_{\mu \nu }=0\) and for a specific choice of the normalizing geometric flow function f, the Eq. (19) transform into nonholonomic Ricci soliton equations encoding Q-distortions into effective sources. Such systems of nonlinear PDEs are equivalent to modified Einstein equations in nonholonomic metric-affine gravity for corresponding definitions of effective sources \(\ ^{tot}\widehat{\Upsilon }_{\alpha \beta }(\tau _{0})=[\ ^{tot}\widehat{\Upsilon }_{ij},\ ^{tot}\widehat{ \Upsilon }_{ab}],\)
The effective sources in (20) are can be parameterized as for the effective Lagrangians (16)
where \(\varkappa \) is determined in standard form by the Newton gravitational constant G,
For the full system relating nonholonomic Ricci solitons to modified gravity, the effective energy-momentum d-tensor is computed for
when
Choosing \(F(\ ^{s}R)=\ ^{s}R\) and the Levi-Civita connection \(\textbf{D} \rightarrow \nabla ,\) we can relate above formulas to GR.
2.3.1 Connecting nonholonomic solitons to nonmetric modified gravitational equations
The gravitational field equations in Weyl-Cartan MGT can be constructed by considering variations of the action on a metric-affine manifold determined by geometric objects using such values constructed for the affine connection \(\textbf{D}\) expressed as a canonical distortion (14) from \( \widehat{\textbf{D}}\) involving \(\ ^{e}\widehat{\textbf{T}}_{\mu \nu }\) as an effective source containing nontrivial contributions from \(\textbf{Q} _{\alpha \beta \gamma }:\)
Such values can be constructed in terms of \(\widehat{{\varvec{\Gamma } }}_{\ \mu \nu }^{\alpha }\) and/or \({\varvec{\Gamma }}_{\ \mu \nu }^{\alpha }.\) In coordinate bases and in non N-adapted form, such results are presented, for instance by formulas (23)–(26) in [6].
In this work, we consider a model of nonholonomic nonmetric Ricci solitons with a Weyl d-vector \(\textbf{q}_{\alpha },\) when \(\textbf{Q}_{\alpha \beta \gamma }=\textbf{q}_{\alpha }\textbf{g}_{\beta \gamma }\) and nontrivial d-torsion \(\textbf{T}_{\mu \nu \alpha }=\textbf{A}_{\nu }\textbf{g}_{\mu \alpha }-\textbf{A}_{\alpha }\textbf{g}_{\mu \nu },\) for \(\textbf{A}_{\mu }=q \textbf{q}_{\mu }, q=const.\) For such approximations considering \(\frac{ \partial F}{\partial T}=1/2q\frac{\partial F}{\partial Q},\) the variational N-adapted gravitational field equations with \(\widehat{\textbf{D}}\) can be written in the form:
for effective Q-source
We defined the system of constraints and nonlinear PDEs (23)–(25) in a form that for \(\widehat{\textbf{D}}\rightarrow \nabla \) it transforms into respective Eqs. (37) and (38) in [6]. For such nonholonomic Ricci soliton equations, we can decouple and integrate in certain general forms the modified Einstein equations (24) if the Q-source (25) is generated by two effective sources (see below). It is not possible to decouple such equations for generic off-diagonal \(\textbf{g}_{\beta \gamma }\) if it is considered only the LC-connection \(\nabla \) and/or general nonmetricity fields.
2.3.2 Generating sources for \(\tau \)-running quasi-stationary effective matter fields and nonmetricity deformations
In this work, we shall construct and study physical implications of quasi-stationary solutions of nonmetric geometric flow equations (19) when the metric (2) (in equivalent form, the d-metric (8)) is determined by N-adapted coefficients \(\textbf{g} (\tau )=[g_{i}(\tau ),g_{a}(\tau ),N_{i}^{a}(\tau )],\) when such coefficients do not depend on variable \(y^{4}=t\) and can be parameterized in the form
Let us consider effective sources \(\ ^{tot}\widehat{\Upsilon }_{ab}(\tau )\) from (19) which via N–adapted frames can be parameterized in the form
In these formulas, there are considered \(\tau \)-families of vierbein transforms \(\textbf{e}_{\ \mu ^{\prime }}^{\mu }(\tau )=\textbf{e}_{\ \mu ^{\prime }}^{\mu }(\tau ,u^{\gamma })\) and their dual \(\textbf{e}_{\nu }^{\ \nu ^{\prime }}(\tau ,u^{\gamma })\), when \(\textbf{e}_{\ }^{\mu }{=}\textbf{e} _{\ \mu ^{\prime }}^{\mu }du^{\mu ^{\prime }}.\) The values \([{}_{h}^{tot}\Upsilon (\tau ,{x}^{k}),\ ^{tot}\Upsilon (\tau ,x^{k},y^{3})]\) can be fixed as generating functions for (effective) matter sources imposing nonholonomic frame constraints on quasi-stationary distributions of (effective) matter fields. In particular, we can change \(\ ^{tot}\Upsilon _{\mu ^{\prime }\nu ^{\prime }}(\tau )\rightarrow \ ^{q}\widehat{\Upsilon } _{\alpha \beta }(\tau )\) for modeling nonholonomic flow evolution of a Q -source (25), when the generating sources are written in the form
In Appendix A, we show how nonlinear systems of PDEs (19) can be decoupled in general forms for any quasi-stationary ansatz (26) and any variant of generating sources (27) or (28). For certain classes of nonholonomic constraints and small parametric deformations, we are able to change symbolic data \([{}_{h}^{q}\Upsilon ,\ ^{q}\Upsilon ]\) into some approximations of (25) and study in explicit form for contributions from any \(\frac{\partial F}{\partial \ ^{s}R_{}},\frac{\partial F }{\partial \ ^{m}T}\) and/or q-term. In general, we can consider that \([{}_{h}^{tot}\Upsilon ,~\ ^{tot}\Upsilon ]\) or \([{}_{h}^{q}\Upsilon ,\ ^{q}\Upsilon ]\) impose certain nonholonomic constraints on respective geometric evolution/dynamical field generating sources which allow to generate solutions with nontrivial canonical d-torsion \(\widehat{\textbf{T}} _{\ \alpha \beta }^{\gamma }(\tau ,x^{k},y^{3}).\) Such nonholnomic values can be eliminated by additional nonholonomic constraints \(\widehat{\textbf{D} }[\textbf{g}]\rightarrow \nabla [\textbf{g}]\) even the d-torsion \( \textbf{T}_{\mu \nu \alpha }=\textbf{A}_{\nu }\textbf{g}_{\mu \alpha }- \textbf{A}_{\alpha }\textbf{g}_{\mu \nu },\) for \(\textbf{A}_{\mu }=q\textbf{q }_{\mu },q=const,\) can be nonzero because of nonmetricity.
3 Off-diagonal quasi-stationary solutions encoding nonmetricity
In this section, we construct and analyze physical properties of two classes of respective nonholonomic geometric flow and Ricci soliton equations encoding quasi-stationary nonmetricity effects. First, we consider examples of nonmetric solitionic hierarchies. Then, we generate wormhole solutions determined by nonmetric fields and study generic off-diagonal deformations, ellipsoidal deformations and embedding into nonmetric backgrounds determined by solitonic hierarchies with general or small parametric polarizations. In Appendix B, we provide necessary formulas for bi-Hamilton structures and solitonic hierarchies.
3.1 Effective nonmetric and \(\tau \)-running Einstein equations
Let us consider a system of nonlinear PDEs (19), for nonmetric Ricci flows, or (20), for nonmetric Ricci solitons, with generating sources of nonmetric type \([{}_{h}^{q}\Upsilon (\tau ), \ ^{q}\Upsilon (\tau )]\) (28). Such effective sources can be substituted by formulas of type \([{}_{h}^{tot}\Upsilon (\tau ),\ ^{tot}\Upsilon (\tau )]\) (27) involving additional effective sources \(\frac{1}{2}\partial _{\tau }\textbf{g}_{\mu \nu }(\tau ).\) Such conditions involve a more special class of nonholonomic constraints on the geometric evolution and dynamics of effective sources which allows to decouple the nonlinear systems of PDEs in general form. For elaborating evolution scenarios in explicit forms, we can consider product parameterizations of type \(\textbf{g}_{\mu \nu }(\tau ,x^{k},y^{3})= \ ^{1} \textbf{g}_{\mu \nu }(\tau )\times \ ^{2}\textbf{g}_{\mu \nu }(x^{k},y^{3})\). In this work, we shall write the general form only parametric solutions in terms of generating functions and generating sources without discussing particular details on how we may apply methods with separation of variables. In abstract geometric form, any quasi-stationary d-metric generated by a \(\ ^{q}\varvec{\Upsilon }_{\ \nu }^{\mu }(\tau )\) and respective generating functions and nonlinear symmetries to effective cosmological constants, see details in Appendix A.2.2, can be transformed by frame and connection deformations into a more general \(\varvec{\Upsilon }_{\ \nu }^{\mu }(\tau ).\) Different types of nonholonomic deformations determined by a \(\ ^{q}\varvec{\Upsilon }_{\ \nu }^{\mu }\) or a general type \(\mathbf { \Upsilon }_{\ \nu }^{\mu }\), and their physical properties and implications in physical theories can be studied using Perelman thermodynamic variables as we shall consider in Sect. 4.
With respect to N-adapted frames (4) and (5), we can write the modified Einstein equations (20) in \(\tau \) -parametric form for nonmetric sources (28) and using the canonical d-connection \(\widehat{\textbf{D}},\)
Equation (30) do not involve zero conditions for another types of torsion which may be present in theory, for instance, of type \( \textbf{T}_{\mu \nu \alpha }=\textbf{A}_{\nu }\textbf{g}_{\mu \alpha }- \textbf{A}_{\alpha }\textbf{g}_{\mu \nu }.\) Such a torsion is induced by a nontrivial nonmetricity d-vector \(\textbf{A}_{\nu }\) for a d-metric \(\textbf{ g}_{\mu \alpha }\) defined as a solution of (29).
We note that, in general, for above considered systems of nonmetric gravitational and matter fields,
which is typical for nonholonomic systems. In some similar forms, such nonholonomic configurations are modeled in nonholonomic mechanics when the conservation laws are not formulated in a standard form. For mechanical systems, there are introduced the so-called Lagrange multiples associated to certain classes of nonholonomic constraints. Solving the constraint equations, it is possible to re-define the variables. Such nonholonomic variables allow us to introduce new effective Lagrangians and, finally, to define conservation laws in certain standard form if \(\textbf{Q}_{\alpha \beta \gamma }=0.\) In explicit general forms, such constructions can be performed only for some “toy” models. Using distortions of connections, we can rewrite (29) in terms of \(\nabla ,\) when \(\nabla ^{\beta }E_{\ \ \beta }^{\alpha }=\nabla ^{\beta }T_{\ \ \beta }^{\alpha }=0\) for \(\textbf{ Q}_{\alpha \beta \gamma }\rightarrow 0.\)
In Appendix B, we show how using the AFCDM the Eqs. (29) and (30) can be decoupled and integrated in general quasi-stationary forms for certain prescribed nonmetric effective sources (28).
3.2 Nonmetric solitonic hierarchies
Nonholonomic geometric flow models with solitonic hierarchies, in metric compatible form, are studied in Sects. 4 and 5 of [16] for constructing theories of geometric information flows of nonholonomic Einstein systems. Similar geometric models can be elaborated for solutions of \(\tau \)-modified Einstein equations (29), when the effective source \(\ ^{q}\varvec{\Upsilon }_{\ \ \beta }^{\alpha }(\tau )\) is determined by nonmetricity fields as we considered in previoussubsection. The physical interpretation of such off-diagonal solutions involving solitonic wave/distributions and describing geometric evolution flow processes is different. In this work, the nonmetricity is encoded into effective generating sources. We present a brief summary on the theory of quasi-stationary solitonic hierarchies and their nonmetric \(\tau \)-evolution in Appendix B. The goal of this subsection is to provide explicit formulas for general off-diagonal solutions defining nonmetric geometric flow equations determined by solitonic distributions for generating functions and/or generating sources written in solitonic functional form, for instance, as \([{}_{1}^{q}\Upsilon [\varvec{\wp } ],{}_{2}^{q}\Upsilon [\varvec{\wp }]]\), see formulas (B.5).
3.2.1 \(\tau \)-running quasi-stationary generating functions with solitonic hierarchies
We show how \(\tau \)-evolution of quasi-stationary solitonic configurations can be defined by respective classes of generating functions when the nonmetricity generating source \(\ ^{q}\varvec{\Upsilon }_{\ \ \beta }^{\alpha }(\tau )\) is an arbitrary one (i.e. it is not obligatory of solitonic nature). For instance, we consider that \(\Phi [\varvec{\wp }]\) is any functional on a solitonic hierarchy \(\wp (\tau ,x^{i},y^{3})\) as we stated for d-metrics \(\textbf{g}(\tau )=(g_{i}[\varvec{\wp }],g_{a}[\varvec{\wp }])\) (B.4). Using nonlinear symmetries (A.14), we can consider as a generating function any coefficient
We can also express
and use such a Q-deformed (by a generating source \({}_{2}^{q}\Upsilon (\tau )\)) solitonic configuration \(\Psi (\tau )\) as a new generating function. For simplicity, the integration function \(h_{4}^{[0]}(\tau ,x^{i})\) can be approximated to some \(\tau \)-running values or constants when the generating functions are some functionals of type \(h_{4}[\varvec{\wp }],\Psi [\varvec{\wp }]\) and \(\Phi [\varvec{\wp }].\)
We can express above quadratic element in three equivalent forms:

In these formulas, there are used respective generating data: \(\{{h} _{4}{[\wp ],\ }_{2}^{q}{\Upsilon (\tau ),\ }_{2}^{q}{\Lambda (\tau )}\}\) from (A.11); \(\{{\Psi [\wp ],\ }_{2}^{q}{\Upsilon (\tau )}\}\) from (A.7); and \(\{ {\Phi [\wp ],\ }_{2}^{q}{\Lambda (\tau ),\ }_{2}^{q} {\Upsilon (\tau )}\}\) from (A.10).
The solutions (31) can be re-defined for \(\eta (\tau )\) -polarizations in a form (A.16) (for instance, with functionals \(\eta _{4}[\varvec{\wp }]\)) or considering \(\kappa \)-parametric deformations to \(\tau \)–families of quasi-stationary d-metrics with \(\chi \) -generating functions for solutions of type (A.18) (with functionals \(\chi _{4}[\varvec{\wp }]\)). The prime metrics can be taken of any nature (being or not solutions of some modified gravitational equations, or some quasi-periodic/solitonic configurations) and than subjected to nonmetric quasi-stationary solitonic deformations via generating/ gravitational polarization functions. In such cases, the target solutions will define a mixture of solitonic distributions under \(\tau \)-evolution and respective prescribed geometric data for primary d-metrics and effective nonmetric generating sources.
3.2.2 Nonmetric quasi-stationary generating sources with solitonic hierarchies
We can generate a different class of generic off-diagonal solitonic solutions of nonmetric geometric flow equations (29) when the generating source is of type \(\ ^{q}\varvec{\Upsilon }_{\ \nu }^{\mu }(\tau )= [{}_{h}^{q}\Upsilon [\varvec{\wp }], \ ^{q}\Upsilon [\mathbf { \wp }]]\) (B.5) but the d-metric coefficients of \(\textbf{g} (\tau )=(g_{i}(\tau ),g_{a}(\tau ))\) are computed via corresponding nonholonomic deformations of nonmetric sources. The respective quadratic elements are written in the form,

In d-metrics (32), the corresponding generating data for (A.11), (A.7), and (A.10) are stated in such forms: \(\{{h}_{4}(\tau )={h}_{4}(\tau ,x^{i},y^{3}){,\ ^{q} \varvec{\Upsilon } [\varvec{\wp }]\,\ }_{2}^{q}{\Lambda (\tau )}\};\) \(\{{\Psi (\tau ),\, \,{}^{q}\varvec{\Upsilon }[\varvec{\wp }]\ }\}\) from (A.7); and \(\{{\Phi (\tau ),\ }_{2}^{q}{\Lambda (\tau ),\, \,{}^{q}\varvec{\Upsilon } [\varvec{\wp }]\ }\}.\)
3.2.3 Interacting \(\tau \)-running solitonic hierarchies for generating functions with respective solitonic hierarchies for nonmetric sources
The generic off-diagonal solutions (31) or (32) can be generalized for \(\tau \)-running configurations when a set of solitionic hierarchies \({}_{1}{\varvec{\wp }}\) is prescribed for generating functions and another set \({}_{2}{\varvec{\wp }}\) is generated for generating functions of nonmetric origin. For a prime d-metric \(\mathring{\textbf{g}}\) (A.12) of arbitrary nature, we generate a target quasi-stationary d-metric double generating function/source solitonic hierarchies,
In such nonlinear quadratic elements, we can prescribe \(\mathring{\textbf{g}} \) to define, for instance, a black hole, BH, solution in GR or a MGT like in [11, 16]. Nonmetric soltionic deformations of type (33) do not preserve, in general, the primary BH character. Nevertheless, for small parametric deformations like in (A.18), we can generate \(\tau \)-families of quasi-stationary d-metrics with \(\chi \)-generating functions for solutions with generating functionals \(\chi _{4}[{}_{1}\varvec{\wp }]\) and/or \({}_{2}^{q}\mathbf { \Upsilon }[{}_{2}\varvec{\wp }].\) Various variants with ellipsoid and solitonic deformations, for instance, for black ellipsoids, BE, with additional solitonic modifications (of physical constants, or embedding into certain solitonic gravitational vacuum) can be modelled. We do not study in this work solutions for BHs, or BEs, solitonic \(\tau \)-running but concentrate only on nonmetric wormhole-soliton configurations.
3.3 Nonmetric wormhole solutions and their solitonic deformations
The goal of this subsection is to construct analyze physical properties of wormhole solutions and their solitonic deformations in nonmetric geometric flow and gravity theories with \(\tau \)-modified Einstein equations (29). As prime d-metric configurations, we shell consider certain curve coordinate transforms of the Morris–Thorne and generalized Ellis–Bronnikov wormholes to certain trivial off-diagonal configurations which allow to apply the AFCDM. We cite [25,26,27,28, 31, 33] for details and a recent review of results on wormhole solutions. Then, we shall construct new classes of quasi-stationary solutions as target metrics, for certain gravitational polarizations determined by additional nonmetricity source, and study their possible traversable nonmetric properties. Necessary technical results are summarized in Appendix A, containing a brief summary of the AFCDM adapted to nonmetric gravity, and Appendix B, for necessary formulas on solitoinic hierarchies.
3.3.1 Prime metrics for 4-d metric compatible wormhole configurations
Let us consider a prime d-metric
where the (tortoise) coordinates \(u^{\alpha }=(r,\theta ,\varphi ,t)\) are defined for \(r(l)=(l^{2k}+{}_{0}b^{2k})^{1/2k}\) and the cylindrical angular coordinate \(\phi \in [0,2\pi )\) is called parallel. In such coordinates, \(-\infty<l<\infty \) which is different from the standard cylindrical radial coordinate \(\rho ,\) when \(0\le \rho <\infty .\) We can fix \(\check{g}_{1}=1,\check{g}_{2}=r^{2}(l),\check{g}_{3}=r^{2}(l)\sin ^{2}\theta \) and \(\check{g}_{4}=-1\) and can consider frame transforms to a parametrization with trivial N-connection coefficients \(\check{N}_{i}^{a}= \check{N}_{i}^{a}(u^{\alpha }(l,\theta ,\varphi ,t))\) and \(\check{g} _{\beta }(u^{j}(l,\theta ,\varphi ),u^{3}(l,\theta ,\varphi )),\) when new coordinates are \(u^{1}=x^{1}=l,u^{2}=\theta ,\) and \(u^{3}=y^{3}=\varphi +\ ^{3}B(l,\theta ),u^{4}=y^{4}=t+\ ^{4}B(l,\theta ),\) for
for \(\mathring{N}_{i}^{3}=-\partial \ ^{3}B/\partial x^{i}\) and \(\mathring{N} _{i}^{4}=-\partial \ ^{4}B/\partial x^{i}.\)
We consider a prime d-metric (34) which is related via coordinate transforms to the generic Morris-Thorne wormhole solution [25],
where \(e^{2\Phi (r)}\) is a red-shift function and b(r) as a shape function defined in spherically polar coordinates \(u^{\alpha }=(r,\theta ,\varphi ,t). \) We can also parameterize this metric to get usual Ellis–Bronnikov, EB, wormholes which are defined for \(\Phi (r)=0\) and \(b(r)={}_{0}b^{2}/r\) characterizing a zero tidal wormhole with \({}_{0}b\) the throat radius. A generalized EB is characterized additionally by even integers 2k (with \( k=1,2,...\)) This allows us to define a prime metric
when
Generic off-diagonal nonholonomic deformations of prime metrics (34) can be analyzed for effective sources of type (25) when the Q-deformations are stated to be zero. For such quasi-stationary diagonalizable solutions, the effective sources are of type \(\ ^{tot} \widehat{\varvec{\Upsilon }}_{\mu \nu }\) (21) when \(\ ^{m} \widehat{\textbf{T}}_{\mu \nu }\) in (22) is taken for a energy-momentum tensor for matter fields. For generating off-diagonal deformations of wormhole solutions, we shall consider generating sources of type (27) or (28). Corresponding classes of generating and integration functions are related via nonlinear symmetries (A.8) or (A.9), when a class of solutions for \(({}_{2}^{tot}\varvec{\Upsilon }(\tau )\leftrightarrow {}_{2}^{tot}\Lambda (\tau ))\) can be distinguished from another class of solutions for \(({}_{2}^{q}\varvec{\Upsilon }(\tau )\leftrightarrow {}_{2}^{q}\Lambda (\tau )).\) In general, such \(\tau \)-running or nonholonomic Ricci flow configurations are characterized by different types of thermodynamic variables as we shall prove in Sect. 4.
3.3.2 Nonholonomic quasi-stationary gravitational polarizations of wormholes
Nonmetric off-diagonal quasi-stationary deformations of wormhole d-metrics (34) can be generated by introducing \(\left( \check{g}_{\beta }, \check{N}_{i}^{a}\right) \) instead of primary geometric data \(\mathbf { \mathring{g}}=[\mathring{g}_{\alpha },\ \mathring{N}_{i}^{a}]\) (A.12) in (A.16) using some generating sources \({}_{2}^{q}\varvec{\Upsilon }(\tau )\) and/or \(_{2}^{q}\Lambda (\tau ).\) We generate new classes of a target \(\tau \)-family of d-metrics \(\textbf{g} (\tau )\) determined by nonmetric geometric flows and respective \(\eta \) -polarization functions, when \(\check{\textbf{g}}\rightarrow \textbf{g} (\tau )= [g_{\alpha }(\tau )=\eta _{\alpha }(\tau )\check{g} _{\alpha },N_{i}^{a}(\tau )= \eta _{i}^{a}\ (\tau )\check{g}_{i}^{a}].\) Corresponding quadratic linear elements
This class of solutions are determined by respective generating function \( \eta _{4}(\tau )=\eta _{4}(\tau ,l,\theta ,\varphi )\) and integration functions \({}_{1}n_{k}(\tau ,l,\theta )\) and \({}_{2}n_{k}(\tau ,l,\theta ).\) The \(\tau \)-family of functions \(\psi (\tau ,l,\theta )\) are defined as a solution of a respective family of 2-d Poisson equations, \(\partial _{11}^{2}\psi (\tau )+\partial _{22}^{2}\psi (\tau )=2{}_{1}^{q} \varvec{\Upsilon }(\tau ,l,\theta )\),
when the horizontal generating effective sources, \({}_{1}^{q}\mathbf { \Upsilon }(\tau ,l,\theta ),\) can be different from the vertical ones which may depend on a vertical coordinate, \({}_{2}^{q}\varvec{\Upsilon } (\tau ,l,\theta ,z).\)
For families of off-diagonal solutions (35), we can fix \({}_{1}^{q}\Lambda (\tau )={}_{2}^{q}\Lambda (\tau )\) and analyze quasi-stationary configurations with running cosmological constants. We suppose that such effective \(\tau \)-families of cosmological constants can be expressed in additive form
where \({}_{2}^{tot}\Lambda (\tau )\) model metric compatible configurations and \({}_{2}^{1}\Lambda (\tau )\) describe possible additional nonmetric contributions. The three terms with left labels m, F, e in these formulas correspond to (effective) energy-momentum tensors (22). We can consider nonlinear symmetries of type (A.14) relating \(\mathbf { \Upsilon }_{\ \nu }^{\mu }(\tau )\simeq \) \([~{}_{h}^{tot}\Upsilon ,~\ ^{tot}\Upsilon ]\) (27) to a \(\tau \)-family \({}_{s}^{tot}\Lambda (\tau ),\) for \(s=1,2,\) and \(\ ^{q}\varvec{\Upsilon }_{\ \nu }^{\mu }(\tau )\simeq [{}_{h}^{q}\Upsilon ,~\ ^{q}\Upsilon ]\) (28) to another family \({}_{2}^{q}\Lambda (\tau )={}_{2}^{q}\Lambda [\tau ,{}_{2}^{tot}\Lambda (\tau )]\) which may be a nonlinear functional on \({}_{2}^{tot}\Lambda (\tau ).\) In this work, we elaborate on models with nontrivial nonmetricity effective sources and additional type functionals (36) for cosmological constants.
The class of quasi-stationary nonmetric deformed wormholes (35) can be written in terms of generating data \(\left[ \Phi (\tau ),{}_{2}^{tot}\Lambda (\tau )+{}_{2}^{1}\Lambda (\tau )\right] \) as in (32),
In such a form, the data for a prime wormhole metric are “hidden” into generating functions and the equations for nonlinear symmetries.
The target d-metrics (35) or (37) do not describe wormhole configurations for general classes of generating and integrating data. There are necessary additional assumptions on polarization functions and integration functions which allows us to provide certain physical interpretation of such generic off-diagonal solutions. Typically, we can prescribe some generating data for solitonic waves, or some small deformations of wormhole configurations. For instance, to elaborate cosmological scenarios with acceleration and quasi-periodic structure, or to transform quasi-stationary d-metrics into locally anisotropic cosmological ones, we have to consider other types of gravitational polarization and generating data.
3.3.3 Off-diagonal quasi-stationary solitonic deformations of wormhole d-metrics
We can generate a class of d-metrics (33) when the prime d-metric \(\mathring{\textbf{g}}\) (A.12) changed into a wormhole one (34) with space coordinates \((l,\theta ,\varphi ).\) Such a target d-metric is of type (35) when off-diagonal deformations are determined by a generating function \(\eta _{4}(\tau )=\eta _{4}[\wp ],\) where \(\wp =\wp (\tau ,x^{i}),\) \(=\wp (\tau ,x^{1},y^{3}),\) or \(=\wp (\tau ,x^{2},y^{3})\) is any solution for \(\tau \)-running solitonic configurations ( B.3).Footnote 7 The quadratic linear element for \(\wp (\tau ,x^{1},y^{3})\)–solitonic deformations of wormhole metrics is constructed
Such solutions describe nonmetric nonholonomic dissipations of a prime wormhole metric into certain \(\tau \)-running generic off-diagonal solitonic distributions. Nonlinear symmetries of type (A.8) or (A.9) involve additive decompositions of running cosmological constants, \({}_{2}^{m}\Lambda (\tau )+{}_{2}^{F}\Lambda (\tau )+{}_{2}^{e}\Lambda (\tau )\), and a nonmetric source \({}_{2}^{q}\varvec{\Upsilon }(\tau )\) which can be of non-solitonic character.
3.3.4 Small parametric off-diagonal quasi-stationary deformations of wormhole d-metrics
We can generate new classes of solutions which preserve wormhole character under nonmetric geometric flow evolution scenarios of a prime d-metric \(\check{\textbf{g}}\) (34) if we consider small \(\varepsilon \) -parametric deformations of type (A.18). The generating functions can be linearized on \(\varepsilon \) as in (A.17) when in terms of \(\chi \)-polarization functions, the quadratic linear elements (35) can be expressed
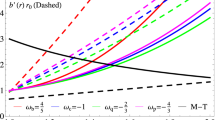
We can model elliptic deformations of the wormhole throat as a particular case of d-metrics of type (38) if we chose a generating function of type
as for cylindric configurations with \(\varphi \)-anisotropic deformations and \(\tau \)-running small deformations. Such classes of solutions describe nonmetric \(\tau \)-evolution of some ellipsoidal wormholes.
If in (38) we take a vacuum profile with \(\zeta _{4}=[{}_{1}\wp ]\) i.e. as a functional of a solitonic distribution \({}_{1}\wp ={}_{1}\wp (l,\theta ,\varphi )\) as in (B.2) but with correspondingly re-defined coordinates, the wormhole ellipsoidal configuration is modelled as a \(\tau \)-evolution in such nonmetric gravitational vacuum. Instead of ellipsoidal configurations (39), we can consider small solitonic \(\chi \)-deformations. For such classes of generic off-diagonal solutions, we can consider any \(\chi _{4}(\tau ,l,\theta ,\varphi )\) defined as functional \(\chi _{4}[\wp ]\) of a \(\wp =\wp (\tau ,x^{i}),\) \(=\wp (\tau ,x^{1},y^{3}),\) or \(=\wp (\tau ,x^{2},y^{3}),\) of some solitonic \(\tau \) -waves (B.3).
The class of nonmetric locally anisotropic wormhole solutions (38) may possess a multiple solitonic wave or solitionic distribution character even the generating source \({}_{2}^{q}\varvec{\Upsilon }(\tau )\) can be non-solitonic. Nonlinear symmetries allow to associate to such configurations certain effective \(\tau \)-running cosmological constants of type (36). Considering, for instance, zero values of \({}_{2}^{e}\Lambda (\tau ),\) we can model some metric compatible locally anisotropic wormholes and then to extend the constructions for nonmetric configurations with nontrivial \({}_{2}^{e}\Lambda (\tau ).\)
3.3.5 On traversable nonmetric wormholes
Wormhole solutions in GR and MGTs are considered as hypothetical geometric structures that link two distinct regions of the same spacetime. References [25,26,27,28,29] contain reviews of results and methods of constructing wormhole solutions. Standard wormhole solutions in GR are not traversable because for various classes of such solutions it is not possible to send causal light signals through it throat faster than we can send it through outside. The first wormhole model of the so-called Einstein-Rosen bridge was elaborated using as a vacuum solution of gravitational field equations [30]. That solution was derived as a modification of the Schwarzschild BH when the corresponding wormhole model is not traversable because of singularity of such solutions. Latter, a static and spherically symmetric wormhole configuration with a traversable throat at the center was constructed in [25]. Various classes of wormhole metrics were found in the framework of GR and MGTs [27, 28, 31]. The existence of such solutions demands the presence of some exotic matter and additional geometric distortions for which the null energy condition, NEC, is violated in order to achieve a stable and traversable structure.
Let us remember in brief how traversable wormholes require a violation of the so-called average null energy condition, ANEC, and how such conditions are modified in the framework of MGTs with nonmetricity. The ANEC states that the energy-momentum tensor for matter fields, \(T_{\mu \nu },\) for a local quantum field theory, QFT, along a complete achronal null geodesic, there are satisfied the conditions \(\int T_{\mu \nu }k^{\mu }k^{\nu }d\lambda \ge 0,\) where \(k^{\mu }\) is a tangent d-vector and \(\lambda \) is an affine parameter. For elaborating quantum gravity, QG, models, such conditions have to be considered for certain effective matter field and distortion of geometric objects. Here we note that in classical theories the violation of the ANEC is prevented by the null energy conditions, NEC, \( T_{\mu \nu }k^{\mu }k^{\nu }d\lambda \ge 0.\) It is considered that such conditions must be valid for any physically reasonable theory at least for classical and semi-classical configurations. Additionally, there are considered other important criteria on causality, topological censorship, absence of singularities etc.
Due to problems with transversability, many authors excluded wormholes to be considered as reliable astrophysical objects. In another turn, a number of authors concluded that there are possibilities to realize wormholes without considering exotic matter but modifying GR. In various cosmological models, there are used solutions with NECs. One supposes that such theories are not experimentally prohibited in the condition when MGTs are involved and due to ideas on existence of particles beyond the standard model.
However, for elaborating explicit physical models and applications in modern cosmology and astrophysics, it is admitted that QM and distortions of geometric effects may induce negative null energy, leading to violations of some NECs and/or ANECs. For nonholonomic systems, the variational and conservation laws are different from those stated for unconstrained ones. For diagonal traversable systems, to sustain a traversable wormhole there are introduced certain negative null energy and various nonlocal/nonachronal constructions. The matter fields are considered as quantum ones, but the gravitational field is treated classically. In such models, there are solved some semi-classical Einstein’s equations with an effective source \(<T_{\mu \nu }>\) computed as the expectation value of the stress-energy tensor in a given quantum state. For certain classes of wormhole solutions, the 1-loop expectation value of the stress-energy tensor satisfy in some spacetime regions the conditions \(\int<T_{\mu \nu }>k^{\mu }k^{\nu }d\lambda <0\). Such configurations allows us to construct traversable Einstein-Rosen bridges with certain interesting physical properties.
Quantum effects and wormhole solutions are studied in various MGTs and quantum information theories. For elaborating quantum computing models, this provides the possibility to transfer information between the two asymptotic spacetime boundaries. Such a process can be viewed as a teleportation protocol, see details and references in [32]. Here we note that wormholes seem to be traversable for qubits [33,34,35].
In this work, we follow an approach to constructing wormhole solutions with off-diagonal deformations of some prime wormhole metrics in 4-d theories (see also generalizations for higher dimensions and MGTs [36,37,38,39,40,41]). Such solutions can be constructed using the AFCDM and extended to nonmetric geometric flow and gravity theories as we have shown in previous subsections. The generating sources \(\ ^{q}\varvec{\Upsilon }_{\ \ \beta }^{\alpha }(\tau )\simeq [{}_{h}^{q}\Upsilon (\tau ), \ ^{q}\Upsilon (\tau )]\) (28) for Q-modified Einstein equations(29) can be prescribed in such a form that \(\int \ ^{q}\varvec{\Upsilon }_{\mu \nu }k^{\mu }k^{\nu }d\lambda <0 \) even using the matter energy-momentum d-tensor from (22), we have \(\ ^{m}\widehat{\textbf{T}}_{\mu \nu }k^{\mu }k^{\nu }d\lambda \ge 0.\) This means that certain types of nonmetric geometric flow and off-diagonal deformations resulting in certain locally anisotropic wormhole solutions result in traversable conditions even at the classical level. Such conditions can be valid even for locally anisotropic wormhole solutions in GR because of additional generic off-diagonal terms. This is also a result of nonholonomic modifications of the spacetime structure.
4 Perelman thermodynamics for nonmetric quasi-stationary configurations
The parametric solutions constructed in previous section describe nonmetric geometric flow and solitonic deformations of wormhole metrics. They are characterized by respective Perelman statistical/ geometric thermodynamic variables [15]. The Bekenstein–Hawking thermodynamic paradigm is not applicable to such solutions because, in general, they do not involve certain hypersurface configurations. We cite [16, 23] for details on relativistic generalizations and MGTs. For geometric flows and metric and nonmetric gravity theories, the W-functional (18) can be treated as a “minus” entropy. The goal of this section is to show how nonmetric geometric flow thermodynamic variables can be defined and computed for quasi-stationary off-diagonal solutions of type (37).
4.1 Statistical thermodynamic variables for Q-deformed relativistic geometric flows
Let us consider nonmetric geometric flow equations (29). They can be derived in geometric or variational form, following the methods outlined in Sects. 3.1 and 5 of [15],Footnote 8 from the W-functional,
In this formula, the normalizing function \(\widehat{f}(\tau ,u)\) and the parameter \(\tau \) are such way re-defined that corresponding geometric flow equations and normalizing conditions formulas contributions from possible matter fields, F- and Q-distortions of the geometric data \( (g(\tau ),\nabla (\tau ))\) to canonical ones, \((\textbf{g}(\tau ), \textbf{N} (\tau ),\widehat{\textbf{D}}(\tau )).\) We use different integration measures and nonlinear symmetries for (40) comparing to \(\mathcal {W}(\tau )\) ( 18). The effects of nonmetricity will be emphasized below when there will be used solutions of (29) determined by respective \( \tau \)–running generating sources (28) or effective cosmological constants (36).
On a metric-affine space \(\mathcal {M}\) endowed with canonical geometric data and an additional nonholonomic (3+1) splitting,Footnote 9 we introduce the statistical partition function
where the volume element is defined and computed as
We use a left label q because nonmetric Q-contributions can be encoded in \(\textbf{g}(\tau ).\) Such a label will be omitted in formulas below if that will not result in ambiguities. Here we note that a a statistical thermodynamic model can be constructed using a partition function \(Z=\int \exp (-\beta E)d\omega (E)\) for a canonical ensemble at temperature \(\beta ^{-1}=\tau \) and when the measure is stated as the density of states \(\omega (E).\) The thermodynamical variables are computed as the average energy, \( \left\langle E\right\rangle :=-\partial \log Z/\partial \beta ,\) the entropy \(S:=\beta \left\langle E\right\rangle +\log Z\) and the fluctuation parameter \(\sigma :=\left\langle \left( E-\left\langle E\right\rangle \right) ^{2}\right\rangle = \partial ^{2}\log Z/\partial \beta ^{2}.\)
Using \(\widehat{Z}\) (41) and \(\widehat{\mathcal {W}}(\tau )\) (40) and following for canonical variables a variational procedure on a closed region of \(\mathcal {M}\) as in Sect. 5 of [15], we can define and compute respective thermodynamic variables:
We note that such a thermodynamic systems can be associated to solution of the nonholonomic nonmetric geometric flow equations (19). In particular, we can fix conventionally the temperature and consider such data for nonmetric Ricci solitons characterized by \(\left[ \ ^{q}\widehat{ \mathcal {E}}(\tau _{0}),\ ^{q}\widehat{\mathcal {S}}(\tau _{0}),\ ^{q} \widehat{\sigma }(\tau _{0})\right] .\) Certain classes of solutions can be not well-defined in the framework of such a statistical and geometric thermodynamic approach, for instance, if \(\ ^{q}\widehat{\mathcal {S}}(\tau _{0})<0.\) We have to restrict certain classes of nonholonomic frames/distributions/distortions in order to generate physically viable solutions. The nonmetric Q-deformations may have different sign contributions comparing to certain metric compatible classes of solutions determined by corresponding \(\left[ \widehat{\mathcal {E}}(\tau ),\widehat{\mathcal {S}} (\tau ),\widehat{\sigma }(\tau )\right] .\)
4.2 Thermodynamic variables for nonmetric deformations of wormhole solutions
We compute in explicit form the variables \(\widehat{Z}\) (41), and \(\ ^{q}\widehat{\mathcal {E}}\ (\tau ), \ ^{q}\widehat{S}(\tau )\) from (43) for quasi-stationary off-diagonal solutions (37).Footnote 10 The simplest way is to consider that
choosing such a normalizing function when \(\widehat{\textbf{D}}_{\alpha }\ \widehat{f}=0\) and approximating \(\widehat{f}\approx 0.\) Such conditions can be considered for a frame/coordinate system and then the results can be redefined for arbitrary bases and normalizing functions. Correspondingly, we obtain
To compute the volume form \(\delta \ ^{q}\mathcal {V}(\tau )\) (42) is better to consider the equivalent d-metric (35) with \(\eta \) –polarization functions, or (38) for \(\eta \)–polarization functions, and including data for nonmetric generating sources. Respectively, we can write
For simplicity, we shall elaborate on nonholonomic evolution models with trivial integration functions \({}_{1}n_{k}=0\) and \({}_{2}n_{k}=0.\) Introducing formulas (45) in (42), then separating terms with shell \(\tau \)-running cosmological constants, we express:
where \(\delta {}_{\eta }\mathcal {V}=\ \delta {}_{\eta }^{1}\mathcal {V}\times \delta {}_{\eta }^{2}\mathcal {V}\).
In these formulas, we use the functionals:
where numeric coefficients were used for re-defining the generating functions. We note that we can define \(\widetilde{\psi }(\tau )\) as a \(\tau \) –family of solutions of 2-d Poisson equations with effective source \({}_{1}^{tot}\Lambda (\tau )+{}_{1}^{1}\Lambda (\tau ),\) or use \(\psi (\tau )\) for a respective source \({}_{h}^{q}\Upsilon (\tau ).\) Integrating on a closed hypersurface \(\widehat{\Xi }\) such products of h- and v-forms, we obtain a running phase space volume functional
determined by prescribed classes of generating \(\eta \)-functions, effective generating sources \(\left[ _{h}^{q}\Upsilon (\tau ),\ ^{q}\Upsilon (\tau ) \right] ,\) coefficients of a prime s-metric \(\ \mathring{g}_{\alpha }\) and nonholonomic distributions defining the hyper-surface \(\widehat{\Xi }.\) The explicit value of \({}_{\eta }^{\shortmid }\mathcal {\mathring{V}}(\tau )\) depends on the data we prescribe for \(\widehat{\Xi }\) the type of Q -deformations (via \(\eta \)- or \(\zeta \)-polarizations) we use for deforming a prime wormhole d-metric into quasi-stationary ones as we considered in Sect. 3. We emphasize that it is always possible to compute \({}_{\eta }^{\shortmid }\mathcal {\mathring{V}}(\tau )\) for certain nonlinear solitonic waves/distributions and some general Q-deformations. The thermodynamic variables depend on the \(\tau \)-running effective cosmological constants.
5 Conclusions and open questions
In this work we elaborated on the nonmetric geometric flow theory of metric-affine spaces and applied it to modified gravity theories, MGT, as in [5,6,7,8, 10]. The approach was generalized in nonholonomic form [11, 13, 16] with the aim to apply the anholonomic frame and connection deformation method, AFCDM, for constructing physically important exact and parametric solutions in geometric flow and gravity theories with nonmetricity. Such solutions are defined by generic off-diagonal metrics and generalized (non) linear connections and, in general, do not possess hypersurface/duality/holographic configurations which would allow to treat them in the framework of Bekenstein–Hawking paradigm [42,43,44,45]. In another turn, as we have shown in this paper, the G. Perelman statistical and geometric thermodynamic paradigm [15] can be applied for all types of solutions in MGTs including nonmetric geometric flow evolution models as we considered in the previous section. In addition to gaining a more complete understanding of gravity theories with nonmetricity, we also studied in this article certain new classes of wormhole and solitonic solutions encoding nonmetric data. This included such new and original results:
-
1.
In Sect. 2.1, the metric-affine geometry was formulated in nonholonomic dyadic variables for nonmetric Q-deformed 4-d Lorentz manifolds. Such a formulation allows us to prove general decoupling and integration properties of nonmetric geometric flow equations and modified Einstein equations in MGTs as we outlined in Appendix A.
-
2.
The Obj1 of this work was completed in Sect. 2.2 where Lyapunov type F- and W-functionals are defined for nonholonomic variables encoding Q-deformations. This allowed us to formulate nonmetric geometric flow models, which for self-similar configurations define nonmetric Ricci solitons containing as particular cases, for instance, nonmetric gravitational equations studied in [6, 7, 10].
-
3.
In Sect. 3, we solved the goals of Obj2 by constructing in explicit form two classes of physically important quasi-stationary solutions of nonmetric geometric flow equations which for fixed flow parameters define Q-deformed Einstein spaces. We proved that such generic off-diagonal solutions can be described in general form by respective solitonic hierarchies and solitonic distributions (see Sect. 3.2, when the necessary concepts and formulas are outlined in Appendix B).
-
4.
Wormhole solutions present an important tool for testing MGTs and applications in modern quantum computer science as we show by constructing and analyzing possible nonmetric effects in Sect. 3.3. Such configurations can be with nonholonomic solitonic Q-deformations and gravitational polarizations, locally anisotropic, in particular, ellipsoid deformations of throats, when nonmetricity makes such configurations to be transversable.
-
5.
In general, the quasi-stationary solutions encoding nonmetricity do not involve hypersurface/holographic configurations or certain duality conditions when the concept of Bekenstein–Hawking entropy could be applicable. As in GR and other MGTs, general classes of exact/parametric solutions can be characterized thermodynamically in the framework of corresponding generalization of G. Perelman paradigm with W-entropy. In Sect. 4, we show how such constructions can be performed for Q-deformations, which presents a solution of Obj3.
The quasi-stationary solutions constructed in this work are characterized by a \(\tau \)-family of Weyl d-vectors \(\textbf{q}_{\alpha }(\tau )\) subjected to conditions of type (23). For such nonholonomic configurations, we can computed respectively induced \(\tau \)-families of nonmetricity d-tensors, \(\textbf{Q}_{\alpha \beta \gamma }(\tau )=\textbf{q}_{\alpha }(\tau )\textbf{g}_{\beta \gamma }(\tau )\), and d-torsion, \(\textbf{T}_{\mu \nu \alpha }(\tau )=\textbf{A}_{\nu }(\tau )\textbf{g}_{\mu \alpha }(\tau ) -\textbf{A}_{\alpha }(\tau )\textbf{g}_{\mu \nu }(\tau ),\) for \(\textbf{A}_{\mu }(\tau )= q\textbf{q}_{\mu }(\tau ),\) when \(q=const\) or depend on \(\tau .\) Such a q can be chosen as a small parameter (like \(\varepsilon \) in (A.17)) for Q-deformations which allow to construct parametric deformations of physically important solutions in GR.
Let us discuss the legacy of using Q-deformed Perelman’s F- and W-functionals to formulate and prove analogues of Poincaré–Thorston conjecture [15, 20,21,22] for nonmetric geometric flows. For general Q-deformations this is an un-defined mathematical problem similar to those for an infinite number of noncommutative/nonassociative differential and integral calculuses and geometric theories, see discussions and respective variants of solutions in [13, 16, 23]. For metric-affine spaces, an infinite number of topological and nonmetric geometric models can be formulated because of an infinite number of nonlinear and linear connection structures that can be used. So, it is not possible to formulate a general mathematical framework involving only some fundamental topological theories and nonmetric geometric analysis. Nevertheless, self-consistent generalizations of the statistic and nonmetric geometric thermodynamics are possible if there are used Q-deformations as in Sects. 2.2.1 and 4. They encode nonmetric geometric data and result in nonholonomic Ricci soliton configurations and Q-modified Einstein equations. Such systems of nonlinear PDEs can be solved in some general forms as we show in Appendix A and provide explicit examples in Sect. 3. For instance, we can associate and compute for such generic off-diagonal solutions respective Perelman-like nonmetric geometric thermodynamic variables, see respective formulas (43), (44) and (??). Thus, such nonmetric geometric flow and MGTs and their associated thermodynamic theories can be formulated in a self-consistent form as \(\tau \)-parametric Q-deformations of Lorentz manifolds geometries, and this is possible even if we are not able to formulate in general form a rigorous version of metric-affine Poincarè hypothesis. Here we also note that the concept of Bekenstein–Hawking entropy is not applicable for the classes of nonmetric solitonic and wormholes solutions considered in Sect. 3. However, the concepts of Perelman’s W-entropy and related statistical thermodynamics can be generalized for various classes of nonmetric theories and their solutions.
The results of this work support the Hypothesis from the Introduction section in such senses:
-
1.
We constructed in explicit form certain models of metric-affine geometric flow and MGTs which are exactly/parametric solvable in certain general off-diagonal forms in nonholonomic dyadic variables.
-
2.
The solutions with \(\tau \)-running effective cosmological constants can be used for modelling DE physical effects and other type configurations with generating sources for effective matter (all such solutions encoding nonmetricity data) for modelling DM physics.
-
3.
In this paper, we elaborated only on nonmetric quasi-stationary configurations which can be described as solitonic hierarchies or nonmetric wormhole solutions and certain nonlinear Q-deformations of such generic off-diagonal solutions subjected to respective nonlinear symmetries.
-
4.
Perelman type nonmetric geometric thermodynamic variables were defined and computed in explicit form for the mentioned classes of quasi-stationary solutions.
Nevertheless, there is a series of important fundamental problems that should be investigated and solved in future works. Here we outline four of the most important open questions on nonmetric geometric and information flow theories and gravity (QNGIFG) and cite some relevant previous works:
-
QNGIFG1: To elaborate full and viable classical and quantum theories on metric-affine spacetimes we have to formulate a theory of spinors and Q-deformed Dirac operators, which is not possible in general form for arbitrary nonmetric structures. This problem is discussed in more general forms in [9, 12] for phase or Finsler-Lagrange-Hamilton theories on (co) tangent Lorentz bundles. Corresponding conceptual and technical difficulties exist for metric-affine generalizations of Lorentz manifolds. Certain solutions can be found as Q-deformed off-diagonal Einstein-Dirac systems, see previous results [14].
-
QNGIFG2: One of the next steps is to study models of Q-deformed Einstein-Yang-Mills-Higgs systems. If such systems are derived as star-product R-flux deformations in string theory, the obtain nonholonomic geometric structures with nonsymmetric metrics and Q-deformed Einstein-Eisenhart-Moffat theories, see details and references to [10, 13].
-
QNGIFG3: Q-deformed off-diagonal cosmological systems can be considered as certain dual ones to quasi-stationary configurations as stated in [11]. Such solutions involve, for instance, various quasi-periodic (cosmological time quasi-crystals etc.) and time-solitonic hierarchies which can be exploited for modelling DE and DM effects.
-
QNGIFG4: Finally, we point to the possibility to extend the geometric and quantum information flow theory [16, 23] to certain Q-deformed versions with nonmetric qubits, nonmetric entanglement and respective generalizations of conditional entropies with Q-modified Perelman’s functionals.
We shall report on progress to answers for above questions in future works.
Data Availability Statements
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: Data sharing does not apply to this article as no datasets were generated or analysed during the current study.].
Notes
In our approach, we use the signature \((+++-)\), when coordinate indices \(\alpha ,\beta ,....\) run values 1,2,3,4; in general, indices may be abstract ones; we use also certain left/up labels for geometric/physical objects; local coordinates are labelled \(u=\{u^{\alpha }\}\) and the Einstein summation rule on up-low indices is used. All necessary notation conventions and definitions of geometric/physical objects are defined in the next sections and appendices. We assume that readers are familiar with standard results and methods outlined in the mentioned monographs and understand basic ideas and motivations for how to extend the geometric constructions to modern modified gravity theories, MGTs, and accelerating cosmology.
Readers may find in the cited works many references with chronological historical remarks, criticism, and applications in modern cosmology and astrophysics. In this paper, we do not provide a comprehensive review on nonmetricity and MGTs but concentrate on elaborating new geometric methods for constructing exact and parametric solutions in nonmetric geometric flow and gravity models. In our works, we write F(R, T, ...) instead of f(, R, T, ...) used in papers by other authors.
We can always define local coordinates \(u=\{u^{\alpha }=(x^{i},y^{a})\}\) involving a conventional \(2+2\) splitting into h-coordinates, \(x=(x^{i}),\) and v-coordinates, \(y=(y^{a}),\) for indices \(j,k,...=1,2\) and \( a,b,c,...=3,4, \) when \(\alpha ,\beta ,...=1,2,3,4.\) Using partial derivatives, local coordinate basis and a co-base are computed respectively as \(e_{\alpha }=\partial _{\alpha }=\partial /\partial u^{\beta }\) and \( e^{\beta }=du^{\beta }.\) Transforms to arbitrary frames (tetrads/vierbeinds) are defined as \(e_{\alpha ^{\prime }}=e_{\ \alpha ^{\prime }}^{\alpha }(u)e_{\alpha }\) and \(e^{\alpha ^{\prime }}=e_{\alpha \ }^{\ \alpha ^{\prime }}(u)e^{\alpha }.\) Usually, such (co) bases are orthonormalized by the conditions \(e_{\alpha \ }^{\ \alpha ^{\prime }}e_{\ \alpha ^{\prime }}^{\beta }=\delta _{\alpha }^{\beta },\) where \(\delta _{\alpha }^{\beta }\) is the Kronecker symbol. On Lorentz manifolds, a N-connection (3) states a nonholonomic distribution defining a fibred 2+2 structure. We use the term nonholonomic Lorentz/pseudo-Riemannian manifold when a conventional h-v-splitting is considered. Typically, “boldface” symbols are used to emphasize that certain spaces or geometric objects are enabled (adapted) with (to) a N-connection structure.
For instance, we define and write a d–vector in N-adapted form as \(\textbf{X }=(hX,vX)\). The geometric objects on a nonholonomic manifold \(\textbf{V}\) enabled with a N-connection structure \(\textbf{N}\) are called distinguished (i.e d-objects, d-vectors, d-tensors etc) if they are adapted to the N–connection structure via corresponding decompositions with respect to frames of type (4) and (5).
Introducing coefficients of (5) into (8) and regrouping with respect to the coordinate dual basis, we obtain the formulas for the coefficients in (9),
$$\begin{aligned} \underline{g}_{\alpha \beta }=\left[ \begin{array}{cc} g_{ij}+N_{i}^{a}N_{j}^{b}g_{ab} &{} N_{j}^{e}g_{ae} \\ N_{i}^{e}g_{be} &{} g_{ab} \end{array} \right] . \end{aligned}$$A metric \(\textbf{g}=\{\underline{g}_{\alpha \beta }\}\) is generic off–diagonal if the anholonomy coefficients \(W_{\alpha \beta }^{\gamma }\) are not identical to zero. For 4-d spacetimes, such a matrix can’t be diagonalized via coordinate transforms.
A canonical d-connection (12) is defined by N-adapted coefficients \(\widehat{\textbf{D}}=\{\widehat{\varvec{\Gamma }}_{\ \alpha \beta }^{\gamma } =(\widehat{L}_{jk}^{i},\widehat{L}_{bk}^{a},\widehat{C}_{jc}^{i}, \widehat{C}_{bc}^{a})\},\) for
$$\begin{aligned} \widehat{L}_{jk}^{i}= & {} \frac{1}{2}g^{ir}(\textbf{e}_{k}g_{jr}+\textbf{e} _{j}g_{kr}-\textbf{e}_{r}g_{jk}),\widehat{L}_{bk}^{a}=e_{b}(N_{k}^{a})\\{} & {} +\frac{ 1}{2}g^{ac}(\textbf{e}_{k}g_{bc}-g_{dc}\ e_{b}N_{k}^{d}-g_{db}\ e_{c}N_{k}^{d}), \\ \widehat{C}_{jc}^{i}= & {} \frac{1}{2}g^{ik}e_{c}g_{jk},\ \widehat{C}_{bc}^{a}= \frac{1}{2}g^{ad}(e_{c}g_{bd}+e_{b}g_{cd}-e_{d}g_{bc}). \end{aligned}$$We can consider \(\wp \) as any solitonic hierarchy considered in Appendix B.1 and re-defined in coordinates \((\tau ,l,\theta ,\varphi ).\)
In this work, we consider 4-d Lorentz manifols which correspond to dimension \(n=4\), which a conventional changing to Riemannian signature; Perelman’s formulas for deriving geometric flows and thermodynamic variables can be used for arbitrary dimension \(n\ge 3\) and signature but such formulas can’t be used for formulations/ proofs of analogs of Poincare–Thorston conjectures in non-Riemannian cases.
Such a conventional splitting is necessary for introducing thermodynamic variables, when the nonholonomic 2+2 decompositions is important for generating off-diagonal solutions.
We omit more cumbersome calculations for \(\ ^{q}\widehat{\sigma }(\tau ).\)
References
C. W. Misner, K. S. Thorn, J. A. Wheeler, Gravitation (Freeman, 1973)
S. W. Hawking, C.F. R. Ellis, The Large Scale Structure of Spacetime (Cambridge University Press, 1973)
R.W. Wald, General Relativity (Universtiy of Chicago Press, Chicago, IL, 1984)
D. Kramer, H. Stephani, E. Herdlt, M. A. H. MacCallum, Exact Solutions of Einstein’s Field Equations, 2d edition (Cambridge University Press, 2003)
F.W. Hehl, J.D. McCrea, E.W. Mielke, Y. Ne’eman, Metric-affine gauge theory of gravity: Field equations, Noether identities, world spinors, and breaking of dilaton invariance. Phys. Rept. 258, 1–171 (1995). arXiv:gr-qc/9402012
T. Harko, N. Myrzakulov, R. Myrzakulov, S. Shahidi, Non-minimal geometry-matter coupling in Weyl-Cartan space-tiems: f(R, T, Q, Tm) gravity. Phys. Dark Univ. 34, 100886 (2021)
D. Iosifidis, R. Myrzakulov, L. Ravera, G. Yergaliyeva, K. Yerzhanov, Metric-affine vector-tensor correspondence and implications in F(R, T, Q, T, D) gravity. Phys. Dark Univ. 37, 101094 (2022)
W. Khyllep, J. Dutta, E. Saridakis, K. Yesmakhanova, Cosmology in f(Q) gravity: A unified dynamical systems analysiso of the background and perturbations. Phys. Rev. D 107, 044022 (2023). arXiv:2207.02610
S. Vacaru, Critical remarks on Finsler modifications of gravity and cosmology by Zhe Chang and Xin Li. Phys. Lett. B 690, 224–228 (2010). arXiv:1003.0044v2
R. Clifford, Finsler Structures in Geometric Mechanics and Gravity, Selected Works, by S. Vacaru, P. Stavrinos, E. Gaburov and D. Gonta. Differential Geometry - Dynamical Systems, Monograph 7 (Geometry Balkan Press, 2006). www.mathem.pub.ro/dgds/mono/va-t.pdf and gr-qc/0508023
L. Bubuianu, S. Vacaru, Deforming black hole and cosmological solutions by quasiperiodic and/or pattern forming structures in modified and Einstein gravity. Eur. Phys. J. C 78, 393 (2018). arXiv:1706.02584
S. Vacaru, On axiomatic formulation of gravity and matter field theories with MDRs and Finsler-Lagrange-Hamilton geometry on (co) tangent Lorentz bundles, [with historical remarks in Appendix B]; the axiomatic part was published: L. Bubuianu and S. Vacaru, Axiomatic formulations of modified gravity theories with nonlinear dispersion relations and Finsler-Lagrange-Hamilton geometry. Eur. Phys. J. C 78, 969 (2018). arXiv:1801.06444
L. Bubuianu, S. Vacaru, E, V. Veliev, Nonassociative Ricci flows, star product and R-flux deformed black holes, and swampland conjectures. Fortschr. Phys. 71, 2200140 (2023). arXiv:2305.20014
S. Vacaru, Spinors and field interactions in higher order anisotropic spaces. JHEP 09(011), 1–49 (1998). arXiv:hep-th/9807214
G. Perelman, The entropy formula for the Ricci flow and its geometric applications. arXiv:math.DG/0211159
I. Bubuianu, S. Vacaru, E. Veli Veliev, Quantum geometric information flows and relativistic generalizations of Grigory Perelman thermodynamics for nonholonomic Einstein systems with black holes and stationary solitonic hierarchies. Quant. Inf. Proc. QINP 21, 51 (2022). arXiv:1907.03541
D. Friedan, Nonlinear models in \(2+\varepsilon \) dimensions. Phys. Rev. Lett. 45, 1057–1060 (1980)
D. Friedan, Ricci flows. Nonlinear models in \( 2+\varepsilon \) dimensions. Ann. Phys. 163, 318–419 (1985)
R.S. Hamilton, Three-manifolds with postive Ricci curvature. J. Diff. Geom. 17, 255–306 (1982)
H.-D. Cao, H.-P. Zhu, A complete proof of the Poincaré and geometrization conjectures - application of the Hamilton-Perelman theory of the Ricci flow. Asian J. Math. 10, 165–495 (2006)
J. W. Morgan, G. Tian, Ricci flow and the Poincaré conjecture, AMS, Clay Math.Monog. v.3 (2007)
B. Kleiner, J. Lott, Notes on Perelman’s papers. Geom. Topol. 12, 2587–2855 (2008)
S. Iuliana, V. Bubuianu, E.V. Veliev, Entropy functionals and thermodynamics of geometric flows, stationary quasi-periodic Ricci solitons, and gravity. Ann. Phys. NY 423, 168333 (2020). arXiv:1903.04920v4
S. Vacaru, Generic off-diagonal solutions and solitonic hierarchies in Einstein and modified gravity. Mod. Phys. Lett. A 30, 1550090 (2015). arXiv:1308.6180
M.S. Morris, K.S. Thorne, Wormhole in spacetime and their use for interstellar travel: a tool for teaching general relativity. Am. J. Phys. 56, 395–412 (1988)
S. Kar, S.N. Minwalla, D. Mishra, D. Sahdev, Resonances in the transmission of massless scalar waves in a class of wormholes. Phys. Rev. D 51, 1632–1638 (1994)
P.D. Roy, S. Aneesh, S. Kar, Revisiting a family of wormholes: geometry, matter, scalar quasinormal modes and echoes. Eur. Phys. J. 80, 850 (2020). arXiv:1910.08746
T. F. de Souza, A. C. A Ramos, R. N. Costa Filho, J. Furtado, Generalized Ellis-Bronnikov graphene wormhole. arXiv:2208.06869
S. Kar, Wormholes with a warped extra dimension? arXiv:2203.1463
A. Einstein, N. Rosen, The particle problem in the general theory of relativity. Phys. Rev. 48, 73–77 (1935)
A. Kundu, Wormholes and holography: an introduction. Eur. Phys. J. C 82, 447 (2022). arXiv:2110.14958
P. Gao, D.L. Jafferis, A transversable wormhole teleportation protocol in the SYK model. JHEP 07, 097 (2021). arXiv:1911.07416
A. R. Brown, H. Gharibyan, S. Leichenauer, H. W. Lin, S. Neami, G. Satlon, L. Sussking, B. Swingle, M. Walter, Quantum gravity in the lab: teleportation by size and transversable wormholes, PRX Quantum 4, 010320 (2023). arxiv:1911.06314
S. Nezami, H. W. Lin, A. R. Brown, H. Gharibyan, S. Leichenauer, G. Salton, L. Susskind, B. Swingle, M. M. Walter, Quantum gravity in the lab: teleportation by size and transversable wormholes, part II, PRX Quantum 4, 010321 (2023). arxiv:2102.01064
D. Jafferis, A. Zlokapa, J.D. Lykken, D.K. Kolchmeyer, S.I. Davis, N. Lauk, H. Neven, M. Spiropulu, Transversable wormhole dynamics on a quantum processor. Nature 612, 51–55 (2022)
S. Vacaru, D. Singleton, V. Botan, D. Dotenco, Locally anisotropic wormholes and flux tubes in 5D gravity, Phys. Lett. B 519, 249-258 (2001). arXiv: gr-qc/0103058
S. Vacaru D. Singleton, Ellipsoidal, cylindrical, bipolar and toroidal worm holes in 5D gravity, J. Math. Phys. 43, 2486-2504 (2002). arXiv:hep-th/0110272
S. Vacaru, D. Singleton, Warped, anisotropic wormhole / soliton configurations in vacuum 5D gravity, Class. Quant. Grav. 19, 2793-2811 (2002). arXiv: hep-th/0111045
T. Harko, F.S.N. Lobo, M.K. Mak, S.V. Sushkov, Modified-gravity wormholes without exotic matter. Phys. Rev. D 87, 067504 (2013). arXiv:1301.6878
S. Vacaru, Wormholes and off-diagonal solutions in f(R,T), Einstein and Finsler gravity theories, in: (eds.) A. Garcia-Parrado, F. C. Mena, F. Moura. E. Vaz, Progress in Mathematical Relativity, Gravitation and Cosmology, Springer Proceedings in Mathematics & Statistics, 60 (2014) 439-443 [Proceedings of Spanish Relativity Meeting ERE2012, Univ. Minho, Guimaraes, Portugal, Sep 3-7, 2012, ISBN:978-3-642-40156-5; https://doi.org/10.1007/978-3-642-40157-2_67; arXiv:1303.3515
S. Vacaru, Exact solutions in modified massive gravity and off-diagonal wormhole deformations Eur. Phys. J. C 74, 2781 (2014). arXiv:1403.1815
J.D. Bekenstein, Black holes and entropy. Phys. Rev. D 7, 2333–2346 (1973)
J.D. Bekenstein, Generalized second law of thermodynamics in black hole physics. Phys. Rev. D 9, 3292–3300 (1974)
S. W. Hawking, Particle creation by black holes. Commun. Math. Phys. 43, 199–220 (1975) [Erratum: 46 (1976) 2006]
S.W. Hawking, Black holes and thermodynamics. Phys. Rev. D 13, 191–197 (1976)
Acknowledgements
SV activity on nonmetric geometry and constructing off-diagonal solutions in MGTs was inspired by many discussions during 1986-1988 with Ascar Aringazin, Sergei Ponomarenko and Anatolii Mikhailov who were postgraduate students of Prof. G. A. Asanov at the department of theoretical physics of M. Lomonosov Moscow State University. Those ideas and nonholonomic geometric formalism resulted in elaborating the AFCDM in a series of works by SV and his students from R. Moldova, for metric affine Finsler-Lagrange- Hamilton geometry and nonmetric locally anisotropic gravity theories [10], see Introduction, Conclusion and Appendix B to [12] for historical remarks, main references and reviews of results. This research on nonmetric geometric flows and applications extends SV and AZ visit programs, supported respectively by Fulbright USA-Romania and the Ministry of Education and Science of the Republic of Kazakhstan, at the physics department at California State University at Fresno, USA. The program on the AFCDM for theories with effective sources encoding nonmetricity consists also a generalization of some objectives for a SV’s visiting program at CAS LMU in Munich, Germany. Co-affiliations for the universities in Germany, Ukraine and USA are motivated by the mentioned fellowships. Authors are grateful to Prof. D. Lüst, Prof. D. Singleton and Dr. Lena Bouman for respective support of their research activity.
Author information
Authors and Affiliations
Corresponding author
Additional information
S. I. Vacaru: Address for post correspondence in 2022–2023 as a visitor senior researcher at YF CNU Ukraine: Vokzal’na street, 37-3, Chernivtsi, 58008, Ukraine.
Appendices
Decoupling and integrability of nonmetric quasi-stationary geometric flow equations
In this appendix, we summarize necessary formulas which allow us to prove some general decoupling and integration properties of nonmetric geometric flow equations (19) with generating sources (28). There are studied generic off-diagonal solutions parameterized by a quasi-stationary ansatz (26). Details on nonholonomic geometric methods can be found in generalized Finsler-Lagrange-Hamilton and metric–affine forms in [10,11,12].
1.1 Decoupling of nonlinear PDEs with nonmetricity fields
We provide formulas for \(\tau \)-depending coefficients of fundamental geometric objects describing nonmetric geometric flows in such a form that for any fixed \(\tau _{0}\) we shall generate solutions for nonmetric Ricci solitons.
1.1.1 The coefficients of quasi-stationary ansatz and canonical Ricci d-tensor
To generate quasi-stationary \(\tau \)-evolving solutions of the system of nonlinear PDEs (29) we consider a generic off-diagonal ansatz with N-adapted coefficients of type (26), when the nonlinear quadratic element is
This d-metric possess a Killing symmetry on the time like coordinate \(\partial _{4}=\partial _{t}\). Such d-metric and N-connection coefficients are functions of necessary smooth class on respective coordinates. We put a “hat” label for a family of d-metrics \(\hat{\textbf{g}}(\tau )\) in order to emphasize that such d-metrics are with Killing symmetry on \(\partial _{t}.\) It is supposed that such a parametrization can be obtained for corresponding classes of frame/coordinate transforms for a general family \(\hat{\textbf{g} }(\tau ,u)\) depending on all spacetime coordinates for other systems of references.
Tedious computations of N-adapted coefficients of the canonical d-connection and respective Ricci d-tensors for (A.1) result in such formulas for the system of nonlinear PDEs (29):
For simplicity, we use brief notations of partial derivatives when, for instance, \(\partial _{1}q(u^{\alpha }):=q^{\bullet }, \partial _{2}q(u^{\alpha }):=q^{\prime }, \partial _{3}q(u^{\alpha }):=q^{*}\) for an arbitrary function \(q(u^{\alpha }).\) In abstract geometric form, such formulas are written in similar forms as in various MGTs but in this work the generating sources encode nonmetricity terms as we explained for (28).
1.1.2 Decoupling of nonmetric geometric flow equations
Let us express \(g_{i}(\tau )\,{=}\,e^{\psi (\tau ,x^{k})}\) and introduce the coefficients \(\alpha _{i}(\tau )\,{=}\,h_{4}^{*}\partial _{i}[\varpi (\tau )], \beta (\tau )\,{=}\,h_{4}^{*}(\tau )[\varpi (\tau )]^{*}\), \(\gamma (\tau )\,{=}\,(\ln |h_{4}(\tau )|^{3/2}/|h_{3}(\tau )|)^{*}\), for \(\varpi (\tau )\,{=}\,\ln |h_{4}^{*}(\tau )/\sqrt{|h_{3}(\tau )h_{4}(\tau )}|;\) and considering \(\ \Psi (\tau )=\exp [\varpi (\tau )]\) as a family of generating functions. Equation (A.2) transform into:
where the explicit dependence of coefficients on respective \((\tau ,x^{k})\) or \((\tau ,x^{k},y^{3})\) is omitted. This system of equations together with the previous one possess an explicit decoupling property. In brief, this means that \(g_{i}(\tau )\) are related to a \(\tau \)-family of 2-d Poisson equations (A.3); then \(h_{3}(\tau )\) and \(h_{4}(\tau )\) are related via nontrivial \(\varpi (\tau )\) and \({}_{2}^{q}\varvec{\Upsilon } (\tau )\) as in (A.4). Finding any solution for \(h_{a}(\tau ),\) we can compute the families of coefficients \(\beta (\tau )\) and \(\alpha _{i}(\tau )\) and solve respective linear equations for \(w_{j}(\tau )\) from (A.5). To find solutions for \(n_{k}(\tau )\) we have to integrate two times on \( y^{3} \) in (A.6) when \(\gamma (\tau )\) is determined by \(h_{3}(\tau )\) and \(h_{4}(\tau ).\)
1.2 Off-diagonal solutions for nonmetric quasi-stationary configurations
We can generate \(\tau \)-families of solutions of nonmetric geometric flow equations by integrating recurrently the decoupled system of nonlinear PDEs (A.3)–(A.6). Any generic off-diagonal metric (A.1) (if the N-coefficients vanish for certain coordinate transforms, we generate diagonal metrics) is determined by respective families of generating function \(\varpi (\tau )\) (equivalently, \(\Psi (\tau )\)) and two generating sources \({}_{1}^{q}\varvec{\Upsilon }(\tau )\) and \({}_{2}^{q}\mathbf { \Upsilon }(\tau ).\) The explicit form of such solutions depends on the type of parameterizations of generating functions and generating sources and how such values are related to some integration functions.
1.2.1 Generating functions and sources for nonmetric quasi-stationary off-diagonal solutions
By straightforward computations, we can check that exact solutions are defined by such generic off-diagonal quasi-stationary \(\tau \)-families of d-metrics,
If for such d-metrics there are considered parametric decompositions as in (25), we generate recurrently certain classes of parametric solutions.
With respect to coordinate dual frames, the d-metrics (A.7) can be represented in the form
when the off-diagonal metrics are parameterized in the form
where we omit respective dependencies of coefficients on \((\tau ,x^{k},y^{3}) \) are omitted.
Finally, we note that \(\tau \)-families of quasi-stationary solutions (A.7) are general in the sense that they are determined by some general generating function \(\Psi (\tau ,x^{k},y^{3}),\) two generating effective sources \({}_{1}^{q}\varvec{\Upsilon }(\tau ,x^{k})\) (encoded as a solution \( \psi (\tau ,x^{k})\) of 2-d Poisson equation (A.3)) and \({}_{2}^{q} \varvec{\Upsilon }(\tau ,x^{k},y^{3})\), and integration functions \({}_{1}n_{i}(\tau ,x^{k}),{}_{2}n_{i}(\tau ,x^{k})\) and \(h_{4}^{[0]}(\tau ,x^{k}).\)
1.2.2 Nonlinear symmetries of nonmetric quasi-stationary off-diagonal solutions
The \(\tau \)-family of solutions (A.7) posses important nonlinear shell symmetries which allow us to define in explicit form certain transforms of generating functions and effective sources into other types of generating functions and effective cosmological constants. Such formulas allow to change the generating data, \((\Psi (\tau ), {}_{2}^{q}\varvec{\Upsilon }(\tau ))\leftrightarrow (\Phi (\tau ),{}_{2}^{q}\Lambda (\tau )=const\ne 0,\) for \(\tau _{0}),\) using the formulas
Such nonlinear symmetries can be defined for other types of effective sources. For instance, we can consider effective matter sources \(\ ^{tot} \widehat{\textbf{T}}_{\mu \nu }\) (22), for (27) as in (20), when \(\tau \)-running effective cosmological constants are parameterized in the form \({}_{2}^{m}\Lambda (\tau )+{}_{2}^{F}\Lambda (\tau )+{}_{2}^{e}\Lambda (\tau ).\) Corresponding nonlinear symmetries can be considered for generating new classes of off-diagonal solutions and in order to compare their physical implications defined by different types of effective cosmological constants. For nonmetric effective sources and running cosmological constants, we use the left label q when \({}_{2}^{q}\Lambda (\tau )=0\) is taken for metric compatible configurations.
We conclude that any quasi-stationary solution (A.7) possess important nonlinear symmetries of type (A.8) and (A.9). As a result, the nonlinear quadratic element for quasi-stationary solutions (A.7) can be written in the form
for indices: \(i,j,k,\ldots =1,2;a,b,c,\ldots =3,4;\) generating functions \(\psi (\tau ,x^{k})\) and\(\ \Phi (\tau ,x^{k_{1}}y^{3});\) generating sources \({}_{2}^{q} \varvec{\Upsilon }(\tau ,x^{k})\) and \({}_{2}^{q}\varvec{\Upsilon }(\tau , x^{k_{1}},y^{3});\) effective cosmological constants \({}_{1}^{q}\Lambda (\tau )\) and \({}_{2}^{q}\Lambda (\tau );\) and integration functions \({}_{1}n_{k}(\tau ,x^{j}),{}_{2}n_{k}(\tau ,x^{j})\) and \(g_{4}^{[0]}(\tau , x^{k}).\)
1.2.3 Using some d-metric coefficients as generating functions and nonmetricity
Formulas (A.10) allow us to write \(h_{4}^{*}(\tau )=-[\Psi ^{2}(\tau )]^{*}/4{}_{2}^{q}\) \(\varvec{\Upsilon }(\tau )\) and to compute up to certain integration functions a value of \(\ \Psi (\tau )\). We have to integrate \([\Psi ^{2}(\tau )]^{*}=\int dy^{3}{}_{2}^{q}\mathbf { \Upsilon }(\tau )h_{4}^{*}(\tau )\) for any prescribed \(h_{4}(\tau )\) and \({}_{2}^{q}\varvec{\Upsilon }(\tau ).\) So, considering generating data \( (h_{4}(\tau ), {}_{2}^{q}\varvec{\Upsilon }(\tau ))\), we can write the \(\tau \) -families of quasi-stationary d-metric (A.7) in such equivalent forms,
In a similar form using the nonlinear symmetries (A.8) and (A.9) and expressing \(\Phi ^{2}(\tau )=-4{}_{2}^{q}\Lambda (\tau )h_{4}(\tau ),\) we can eliminate \(\Phi (\tau )\) from the nonlinear quadratic element in (A.10). We construct a \(\tau \)-family of solutions of type (A.11) determined by some generating data \((h_{4}(\tau );{}_{2}^{q}\Lambda (\tau ),{}_{2}^{q}\varvec{\Upsilon } (\tau )).\)
1.2.4 Gravitational nonmetric polarizations
We can consider deformations of a prime d-metric on a metric affine manifold
Such a \(\mathring{\textbf{g}}\) can be an arbitrary one, a solution of some equations in GR or a MGTs, or defined as a \(\tau \)-family. In this subsection, we study transforms of a (family) primary d-metric into a a family of target d-metrics \(\textbf{g}(\tau )\) defined a quasi-stationary solutions of type (A.1), when
Such transforms are defined by some values \(\eta _{\alpha }(\tau ,x^{k},y^{3}) \) and \(\eta _{i}^{a}(\tau ,x^{k},y^{3})\) called \(\tau \) -running gravitational polarization (\(\eta \)-polarization) functions.
Target d-metrics \(\textbf{g}(\tau )\) can be constructed as quasi-stationary solutions of type (A.7), or (A.10), when the nonholonomic deformations are determined by respective generating functions, generating sources and effective cosmological constants,
where \({}_{2}^{q}\Lambda (\tau )\) is an effective cosmological constant in the v-subspace, \(\varepsilon \) is a small parameter \(0\le \varepsilon <1,\) with some \(\zeta _{\alpha }(\tau ,x^{k},y^{3})\) and \(\chi _{\alpha }(\tau ,x^{k},y^{3}).\)
For families of \(\eta \)- and/or \(\chi \)-polarizations, the nonlinear symmetries (A.9) are defined in the form:
Generating functions for families of off-diagonal \(\eta \)-transforms of type (A.13) can be parameterized for \(\eta \)-polarizations,
Such generating functions can be used for defining \(\tau \)-families of quasi-stationary nonlinear quadratic elements of type (A.11),
For \(\Phi ^{2}(\tau )=-4{}_{2}^{q}\Lambda h_{4}(\tau ),\) we can transform (A.10) in a variant of (A.16) with \(\eta \) -polarizations determined by the generating data \((h_{4}(\tau );{}_{2}\Lambda ,\ (\tau )).\) For general \(\eta \)- and Q-deformations, it is difficult to understand if such off-diagonal metrics have certain physically important interpretation even the primary data possess certain important physical meaning. Nevertheless, even in such cases certain quasi-periodic, solitonic, or another type structures can be generated. It is possible always to compute respective Perelman thermodynamic variables and solve the issue if certain configurations with a prescribed \({}_{2}^{q}\mathbf { \Upsilon }(\tau ),\) or \({}_{2}^{q}\Lambda (\tau ),\) can be thermodynamically more optimal than other ones with some prescribed effective \({}_{2}^{m}\Lambda (\tau )+{}_{2}^{F}\Lambda (\tau )+{}_{2}^{e}\Lambda (\tau ),\) see formulas (36).
1.2.5 Generating solutions with small parametric decompositions encoding nonmetricity
For a small parameter \(\varepsilon ,\) we can construct \(\varepsilon \)-linear functions for \(\eta \)-polarizations in (A.16) and study small nonholonomic deformations of a prime d-metric \(\mathring{\textbf{g}}\) into so-called \(\varepsilon \)-parametric \(\tau \)-families of solutions with \( \zeta \)- and \(\chi \)-coefficients. Corresponding parametric decompositions are of type
where \(\psi (\tau )\) and \(\eta _{2}(\tau )=\ \eta _{1}(\tau )\) are such way chosen to be determined by solutions of the 2-d Poisson equation \(\partial _{11}^{2}\psi (\tau )+\partial _{22}^{2}\psi (\tau )= 2{}_{1}^{q}\mathbf { \Upsilon }(\tau ,x^{k}),\) see (A.3). For other type signatures of d-metrics, it can be a 2-d wave equation with respective source and certain \( \tau \)-evolving scenarios.
Parameterizations of type (A.17) allow to compute \( \varepsilon \)-parametric deformations to \(\tau \)-families of quasi-stationary d-metrics with \(\chi \)-generating functions,
Such off-diagonal parametric solutions allow us to define, for instance, ellipsoidal deformations of BH metrics into BE ones and to provide realistic interpretation of nonmetric deformations under geometric flows or for off-diagonal modifications. Quasi-stationary d-metrics of type (A.18) can be generated for by certain small parametric deformations with generating data \((\Phi (\tau ),{}_{2}^{q}\Lambda (\tau )).\)
1.2.6 Extracting Levi–Civita configurations
The generic off–diagonal quasi-stationary solutions considered in previous subsections were constructed for canonical d–connections \(\widehat{\textbf{D }}(\tau ).\) In general, such solutions are characterized by nonholonomically induced d–torsion coefficients \(\ \widehat{\textbf{T}}_{\ \alpha \beta }^{\gamma }(\tau )\) (such values are completely defined by the N–connection and d–metric structures) and contain Q-deformations related to nontrivial d-torsions \(\textbf{T}_{\mu \nu \alpha }(\tau )=\textbf{A}_{\nu }(\tau ) \textbf{g}_{\mu \alpha }(\tau ) - \textbf{A}_{\alpha }(\tau )\textbf{g}_{\mu \nu }(\tau )\), see formulas (25). We can extract zero torsion LC-configurations for q-distortions of \(\nabla (\tau )\) if we impose additionally the conditions (30). By straightforward computations for quasi-stationary configurations, we can verify that all canonical d-torsion coefficients \(\widehat{\textbf{T}}_{\ \alpha \beta }^{\gamma }(\tau )\) vanish if the coefficients of N–adapted frames and v –components of \(\tau \)-families of d–metrics are subjected to respective conditions,
The solutions for necessary type of w- and n-functions depend on the class of vacuum, non–vacuum, Q-deformed and other type metrics which we attempt to generate. We may follow such steps for finding solutions subjected to conditions (A.19):
Prescribing a generating function \(\Psi (\tau )=\check{\Psi } (\tau ,x^{i_{1}},y^{3}),\) for which \([\partial _{i}({}_{2}\check{\Psi })]^{*}=\partial _{i}({}_{2}\check{\Psi })^{*},\) we solve the equations for \(w_{j}\) from (A.19) in explicit form if \({}_{2}^{q} \varvec{\Upsilon }=const,\) or if such an effective source can be expressed as a functional \({}_{2}^{q}\varvec{\Upsilon }(\tau ,x^{i},y^{3})= {}_{2}^{q} \varvec{\Upsilon }[{}_{2}\check{\Psi }(\tau )].\) The conditions \(\partial _{i}w_{j}(\tau )=\partial _{j}w_{i}(\tau ),\) are solved by any generating function \(\check{A}=\check{A}(\tau ,x^{k},y^{3})\) for which
The equations for n-functions in (A.19) are solved for any \( n_{i}(\tau )=\partial _{i}[\ ^{2}n(\tau ,x^{k})].\)
Putting together above formulas for respective classes of generating functions, we construct a nonlinear quadratic element for quasi-stationary solutions with zero canonical d-torsions, (A.7),
Finally, we note that d-metrics (A.20) define LC-configurations for \( \nabla (\tau )\) that involve also nonmetricity contributions encoded into \( _{2}^{q}\varvec{\Upsilon }(\tau ).\) This is an example when using nonlinear symmetries we encode nonmetricity data into, in general, generic off-diagonal pseudo-Riemannian metric for an effective Einstein gravity with “exotic” effective energy-momentum sources.
Generating nonmetric solitonic hierarchies via solitonic metrics and effective sources
Let us consider the formulas for nonmetric geometric evolution of a d-metric \(\textbf{g}(\tau )\) constructed as a solution of (29): We associate a non–stretching curve \(\gamma (\tau ,\textbf{l}) \) on a nonholonomic Lorentz manifold \(\textbf{V}\) and use \(\tau \) both as a curve running real parameter and a geometric flow parameter. The value \( \textbf{l}\) is the arclength of a curve on \(\textbf{V}\) which is defined by an evolution d–vector \(\textbf{Y}=\varsigma _{\tau }\) and tangent d–vector \(\textbf{X}=\varsigma _{\textbf{l}}\) that \(\mathbf {g(X,X)=}1\). Any curve \( \varsigma (\tau ,\textbf{l})\) defines a two–dimensional surface in \( T_{\varsigma (\tau ,\textbf{l})}\textbf{V}\subset T\mathbf {V.}\) In [24], there are given details on metric compatible curve flows. In this work, the approach is generalized for nonmetric deformations. To any dual basis (5) a coframe \(\textbf{e} \in T_{\varsigma }^{*}\textbf{V}_{\textbf{N}}\otimes (h\mathfrak {p\oplus }v\mathfrak {p})\) can be associated. It is a N–adapted \(\left( SO(n) \mathfrak {\oplus }SO(m)\right) \)–parallel basis along \(\varsigma .\)
1.1 Preliminaries on geometric models and solitons
We can associate a canonical d-connection \(\widehat{\textbf{D}}\) (13) with a linear connection 1–form parameterized as \(\widehat{ \varvec{\Gamma }}\in T_{\varsigma }^{*}\textbf{V}_{\textbf{N}}\otimes ( \mathfrak {so}(n)\mathfrak {\oplus so}(m)).\) The frame bases are 1-forms \( \textbf{e}_{\textbf{X}}=\textbf{e}_{h\textbf{X}}+\textbf{e}_{v\textbf{X}}\) defined by N-adapted frames (4), which (for \((1,\overrightarrow{0})\in \mathbb {R}^{n},\overrightarrow{0}\in \mathbb {R}^{n-1}\) and \((1, \overleftarrow{0})\in \mathbb {R}^{m}, \overleftarrow{0}\in \mathbb {R} ^{m-1}), \) can be parameterized by respective matrices,
Such d-operators act on the spaces of curves on \(\textbf{V}\).
For a N-connection (3), we can construct a corresponding h- and v-splitting of canonical d-connections 1-forms, \(\widehat{\varvec{\Gamma }} =\left[ \widehat{\varvec{\Gamma }}_{h\textbf{X}},\widehat{\varvec{\Gamma }}_{v \textbf{X}}\right] ,\) parameterizing
Using the canonical d–connection \(\widehat{\textbf{D}},\) we can define some d-matrices being decomposed with respect to the flow direction: in the h–direction,
and
Then, we introduce similar parameterizations for the v–direction,
and
We summarize and adapt for nonmetric geometric flows and gravity three important results proven in [24] for parameterizations related to nonholonomic canonical geometric flows of 4-d Lorentzian metrics:
For any solution of N-adapted Hamilton-Friedan equations in canonical variables (19), or for relativistic nonholonomic Ricci soliton equations (29), there is a canonical hierarchy of N–adapted flows of curves \(\varsigma (\tau ,\textbf{l})=h\varsigma (\tau , \textbf{l})+ v\varsigma (\tau ,\textbf{l})\) described by nonholonomic geometric map equations encoding nonmetric sources:
-
The 0 flows are convective (travelling wave) maps \(\varsigma _{\tau }=\varsigma _{\textbf{l}}\) distinguished as \(\left( h\varsigma \right) _{\tau }=\left( h\varsigma \right) _{h\textbf{X}}\) and \(\left( v\varsigma \right) _{\tau }=\left( v\varsigma \right) _{v\textbf{X}}\). The classification of such maps depend on the type of d-connection structure.
-
There are +1 flows defined as non–stretching mKdV maps
$$\begin{aligned} -\left( h\varsigma \right) _{\tau }= & {} \widehat{\textbf{D}}_{h\textbf{X} }^{2}\left( h\varsigma \right) _{h\textbf{X}} +\frac{3}{2}|\widehat{\textbf{D }}_{h\textbf{X}}\left( h\varsigma \right) _{h\textbf{X}}|_{h\textbf{g}}^{2} \left( h\varsigma \right) _{h\textbf{X}}, \nonumber \\ -\left( v\varsigma \right) _{\tau }= & {} \widehat{\textbf{D}}_{v\textbf{X} }^{2}\left( v\varsigma \right) _{v\textbf{X}}+\frac{3}{2}|\widehat{\textbf{D} }_{v\textbf{X}}\left( v\varsigma \right) _{v\textbf{X}}|_{v\textbf{g} }^{2}~\left( v\varsigma \right) _{v\textbf{X}}, \nonumber \\ \end{aligned}$$(B.1)and the +2,... flows as higher order analogs.
-
Finally, the -1 flows are defined by the kernels of the canonical recursion h–operator,
$$\begin{aligned} h\widehat{{\mathfrak {R}}}\!=\!\widehat{\textbf{D}}_{h\textbf{X}}\left( \widehat{\textbf{D}}_{h\textbf{X}}\!+\!\widehat{\textbf{D}}_{h\textbf{X}}^{-1}\left( \overrightarrow{v}\cdot \right) \overrightarrow{v}\right) \!+\!\overrightarrow{v} \rfloor \widehat{\textbf{D}}_{h\textbf{X}}^{-1}\left( \overrightarrow{v} \wedge \widehat{\textbf{D}}_{h\textbf{X}}\right) , \end{aligned}$$and of the canonical recursion v–operator,
$$\begin{aligned} v\widehat{{\mathfrak {R}}}=\widehat{\textbf{D}}_{v\textbf{X}}\left( \widehat{\textbf{D}}_{v\textbf{X}}+\widehat{\textbf{D}}_{v\textbf{X}}^{-1}\left( \overleftarrow{v}\cdot \right) \overleftarrow{v}\right) +\overleftarrow{v} \rfloor \widehat{\textbf{D}}_{v\textbf{X}}^{-1}\left( \overleftarrow{v} \wedge \widehat{\textbf{D}}_{v\textbf{X}}\right) , \end{aligned}$$inducing non–stretching maps \(\widehat{\textbf{D}}_{h\textbf{Y} }\left( h\varsigma \right) _{h\textbf{X}}=0\) and \(\widehat{\textbf{D}}_{v \textbf{Y}}\left( v\varsigma \right) _{v\textbf{X}}=0\).
The canonical recursion d-operator \(\widehat{{\mathfrak {R}}}=(h\widehat{{ \mathfrak {R}}},v\widehat{{\mathfrak {R}}})\) is related to respective bi-Hamiltonian structures for curve flows (in our case, determined by geometric flows and respective solitonic models).
1.2 Examples of solitonic space like stationary distributions and nonlinear waves
To generate quasi-stationary solutions of nonmetric geometric flow and gravity equations we can consider \(\tau \)-running of fixed \(\tau _{0}\) space distributions which can anisotropic on certain angular type coordinates \( (\vartheta ,\varphi ).\)
1.2.1 Quasi-stationary solitonic distributions
We shall use distributions \(\ \wp =\wp (r,\vartheta ,\varphi )\) as solutions of a respective six classes of solitonic 3-d equations
for \(\epsilon =\pm 1\). To construct in explicit form solutions of such nonlinear PDEs is a very difficult task. Nevertheless, their physical properties are well known from the theory of solitonic hierarchies. We can take any \(\wp (u)\) as a parametric, or exact solution of an equation (B.2) and consider as a generating function and/or generating source which does not depend on the time coordinate. These equations and their solutions can be redefined via frame/coordinate transforms for stationary generating functions parameterized in non-spherical coordinates and labeled in the form \(\wp =\wp (x^{i},y^{3})\). We can use such functions as generating functions and/or generating sources for nonmetric Ricci solitons (20) when the constructions can be extended for quasi-stationary geometric flows.
1.2.2 Generating nonlinear solitonic waves on temperature like parameter
Stationary geometric flow evolution on a Lorentz manifold can be characterized by 3-d solitonic waves with explicit dependence flow parameter \(\tau \) defined by functions \(\wp (\tau ,u)\) as solutions of such nonlinear PDEs:
Applying general frame/coordinate transforms on respective solutions (B.3), we construct solitonic waves parameterized by functions labeled in the form \(\ \wp =\wp (\tau ,x^{i}),\) \(=\wp (\tau ,x^{1},y^{3}),\) or \(=\wp (\tau ,x^{2},y^{3}).\)
1.2.3 Ansatz for quasi-stationary geometric flows and solitonic hierarchies
We can consider different types of solitonic stationary configurations determined, for instance, by sine-Gordon (using \(\tau \)-derivatives) and various types of nonlinear temperature like wave configurations characterized by nonholonomic geometric curve flows. Any such solitonic hierarchy configuration, nonlinear wave and solitonic distribution of type \( \wp (\tau ,u)\) (B.3) or (B.2) can be can be used as generating functions for quasi-stationary d-metrics of type (A.1),
In terms of polarization functions (A.16) determined by solitonic hierarchies, we write \(\eta _{i}(\tau )=\eta _{i}(\tau ,x^{k})=\eta _{i}[\varvec{\wp }],\eta _{a}(\tau )=\eta _{a}(\tau ,x^{k},y^{b})=\eta _{a}[\varvec{\wp }]\) and \(\eta _{i}^{a}(\tau )=\eta _{i}^{a}(\tau ,x^{k},y^{b})=\eta _{i}^{a}[\varvec{\wp }].\) In general, a functional dependence \([\varvec{\wp }]\) can be defined by a superpositions of some solitonic hierarchies of type (B.1) (we can mix also configurations of type (B.3) and/or (B.2)). This can be written, for instance, in the form \([\varvec{\wp }]=[{}_{1}\varvec{\wp },{}_{2}\varvec{\wp },...]\) where the left label is for numbering the solitonic hierarchies.
Solitonic hierarchies can be used for modeling nonholonomic flow evolution of a Q-source (25), when the generating sources (28) are determined by some functionals
The \(\tau \)-modified Einstein equations (29) with such nonmetricity sources and written in canonical nonholonomic variables transform into functional equations \(\widehat{\textbf{R}}_{\ \ \beta }^{\alpha }(\tau )=\ ^{q}\varvec{\Upsilon }_{\ \ \beta }^{\alpha }(\wp ).\) We can extract LC-configurations by imposing conditions (30), when \(\widehat{ \textbf{T}}_{\ \alpha \beta }^{\gamma }=0,\)for \(\nabla .\) For such nonmetric geometric flow configurations, the nonmetricity field \(\textbf{Q} _{\alpha \beta \gamma }(\wp )\) and d-torsion \(\textbf{T}_{\mu \nu \alpha }(\wp )=\textbf{A}_{\nu }\textbf{g}_{\mu \alpha }(\wp )-\textbf{A}_{\alpha } \textbf{g}_{\mu \nu }(\wp )\) are determined by solitonic hierarchies.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3.
About this article
Cite this article
Bubuianu, L., Vacaru, S.I., Veliev, E.V. et al. Dark energy and dark matter configurations for wormholes and solitionic hierarchies of nonmetric Ricci flows and \(F(R,T,Q,T_{m})\) gravity. Eur. Phys. J. C 84, 211 (2024). https://doi.org/10.1140/epjc/s10052-024-12530-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-024-12530-1