1 Introduction

In modern cosmology, the phenomenon of accelerated cosmic expansion and its possible causes, as confirmed by numerous astronomical probes, have become a focus of interest for the researchers [1,2,3]. In this respect, the first attempt was made by Einstein, by introducing a well-known \(\Lambda CDM\) model; but in spite of its all beauty and success, this model cannot be proved to be problem free [4]. Later on, a bulk of different proposals have been presented by the researchers that can be grouped into two kinds: modified matter proposals and modified curvature proposals. The tachyon model, quintessence, the Chaplygin gas and its different versions, phantom, quintom etc., are all obtained by introducing some extra terms in the matter section and hence are members of the modified matter proposal group [5,6,7,8,9,10,11,12,13,14,15]. The other idea is to modify curvature sector of Einstein’s general relativity (GR) by including some extra degrees of freedom there. One of the primary alterations was the speculation of the Einstein–Hilbert Lagrangian density with an arbitrary function f(R) instead of the Ricci scalar R. This theory has been widely used in the literature [16] to examine the dark energy (DE) and its resulting speedy cosmic expansion. Moreover, f(R) theory of gravitation provides a unified picture of early stages of cosmos (inflation) as well as the late stages of accelerated cosmos. Some other well-known examples include Brans–Dicke gravity, generalized scalar–tensor theory, \(f(\tau )\) gravity, where \(\tau \) is a torsion, Gauss–Bonnet gravity and its generalized forms like f(G) gravity, f(R, G) gravity, and \(f(\tau , \tau _G)\) theory, etc. [17,18,19,20,21,22,23,24,25,26].

Another significant modification of Einstein gravity namely f(R, T) gravity was proposed by Harko et al. [27] almost five years ago. In this formulation, a generic function f(R, T), representing the coupling of the Ricci scalar and energy-momentum tensor trace, replaces the Ricci scalar R for the possible modification of curvature sector. Using metric formalism, they derived the associated field equations for some specific cases. In [28,29,30,31,32], some interesting cosmological f(R, T) models have been developed by employing various scenarios namely, auxiliary scalar field, dark energy models and anisotropic universe models. In literature [33,34,35,36,37,38,39,40,41,42,43,44,45,46,47], different cosmological applications of f(R, T) gravity have been discussed like energy conditions, thermodynamics, exact and numerical solutions of field equations with different matter content, phase space perturbation, compact stars and stability of collapsing objects etc.

The existence and construction of the wormhole solutions is one of the most fascinating topics in modern cosmology. Wormholes are topological passage-like structures connecting two distant parts of the same universe or different universes together through a shortcut called tunnel or bridge. Generally, in nature, wormholes are categorized into two sorts namely static wormholes and dynamic wormholes [48]. For the development of wormhole structures, an exotic fluid (hypothetical form of matter) is required which violates the null energy condition (NEC) in GR. This violation of energy condition is regarded as one of the basic requirements for wormhole construction. The existence of the wormhole solutions in GR has always been a great challenge for the researchers. Although GR allows the existence of wormholes but it is necessary to first modify the matter sector by including some extra terms (as the ordinary matter satisfies the energy bounds and hence violates the basic criteria for existence of the wormhole). These extra terms are responsible for energy bound violation and hence permits the existence of wormhole in GR. In 1935, Einstein and Rosen [49] discussed the mathematical criteria of wormholes in GR and they obtained the wormhole solutions known as Lorentzian wormholes or Schwarzchild wormholes. In 1988, it was shown [50] that wormholes could be large enough for humanoid travelers and even permit time travel. In the literature [51,52,53,54,55,56,57,58,59] numerous authors constructed wormholes by including different types of exotic matter like quintom, scalar field models, non-commutative geometry and electromagnetic field etc. and obtained different interesting and physically viable results. Some important and interesting results regarding the stable wormhole solutions without inclusion of any exotic matter are discussed in [60, 61]. In Ref. [62], the existence of the wormhole solutions and its different properties in f(R, T) theory gravity has been discussed.

“On a D-brane, the coordinates may be treated as non-commutative operators”, this is one of the most interesting aspect of non-commutative geometry of string theory, providing a mathematical way to explore some important concepts of quantum gravity [63, 64]. Basically, non-commutative geometry is an effort to construct a unified platform where one can take the spacetime gravitational forces as a combined form of weak and strong forces with gravity. Non-commutativity has the important feature of replacing point-like structures by smeared objects and hence corresponds to spacetime discretization, which is due to the commutator defined by \([x^{\alpha }, x^{\beta }] = i\theta ^{\alpha \beta }\), where \(\theta ^{\alpha \beta }\) is an anti-symmetric second-order matrix. This smearing effect can be modeled by including a Gaussian distribution and a Lorentzian distribution of minimal length \(\sqrt{\theta }\) instead of the Dirac delta function. The spherically symmetric, static particle-like gravitational source representing the Gaussian distribution of non-commutative geometry with total mass M has an energy density given by [65,66,67]

$$\begin{aligned} \rho (r)=\frac{M}{(4\pi \theta )^{\frac{3}{2}} }e^{-\frac{r^{2}}{4\theta }}, \end{aligned}$$

while, with reference to Lorentzian distribution, we can take the density function of particle-like mass M as follows:

$$\begin{aligned} \rho (r)=\frac{M \sqrt{\theta }}{\pi ^{2}(r^{2}+\theta )^{2}}. \end{aligned}$$

Here the total mass M can be considered as wormhole, a type of diffused centralized object and clearly, \(\theta \) is the non-commutative parameter. The Gaussian distribution source has been utilized by Sushkov to model phantom-energy upheld wormholes [68]. Also, Nicolini and Spalluci [69] used this distribution to demonstrate the physical impacts of short-separation changes of non-commutative coordinates in the investigation of black holes.

Motivated by this literature, in this manuscript, we will construct spherically symmetric static wormholes in the presence of curvature–matter coupling with non-commutative geometry. In the next section, we will describe the basic mathematical formulation of f(R, T) gravity and the corresponding field equations for static spherically symmetric spacetime. In Sect. 3, we shall discuss the wormhole solutions for both Gaussian and Lorentzian distributions of non-commutative geometry by taking the linear model of f(R, T) gravity, i.e., \(f(R,T)=R+\lambda T\). Section 4 provides wormhole solutions for both these distributions of non-commutative geometry where the model \(f(R,T)=R+\alpha R^{2}+\gamma R^{n}+\lambda T\) will be taken into account. In Sect. 5, the stability of these obtained wormhole solutions will be discussed through graphs. Section 6 will be devoted to an investigation of the gravitational lensing phenomenon for the exact model of Sect. 3 by exploring deflection angle at the wormhole throat. The last section will summarize the whole discussion by highlighting the major achievements.

2 Field equations of f(R, T) gravity and spherically symmetric wormhole geometry

In this section, we shall discuss the basic formulation of f(R, T) gravity and its corresponding field equations for spherically symmetric spacetime in the presence of ordinary matter. For this purpose, we take the following action of this modified gravity [27]:

$$\begin{aligned} S=\frac{1}{16\pi }\int f(R,T)\sqrt{-g}\mathrm{d}^{4}x+\int L_{m}\sqrt{-g}\mathrm{d}^{4}x, \end{aligned}$$
(1)

where f(R, T) is an arbitrary function of the Ricci scalar R and the trace of the energy-momentum tensor \(T=g^{\mu \nu }T_{\mu \nu }\). Here \(L_{m}\) represents the Lagrangian density of ordinary matter. By taking the variation of the above action, we have

$$\begin{aligned}&8\pi T_{\mu \nu }-f_{T}(R,T)T_{\mu \nu }-f_{T}(R,T)\Theta _{\mu \nu }=f_{R}(R,T)R_{\mu \nu }\nonumber \\&\quad -\frac{1}{2}f(R,T)g_{\mu \nu } +(g_{\mu \nu }\Box -\nabla _{\mu }\nabla _{\nu })f_{R}(R,T). \end{aligned}$$
(2)

By contracting the above equation, we have a relation between the Ricci scalar R and the trace T of the energy-momentum tensor as follows:

$$\begin{aligned}&8\pi T-f_{T}(R,T)T-f_{T}(R,T)\Theta =f_{R}(R,T)R\nonumber \\&\quad +\, 3\Box f_{R}(R,T)-2f(R,T). \end{aligned}$$
(3)

These two equations involves covariant derivative and d’Alembert operator denoted by \(\nabla \) and \(\Box \), respectively. Furthermore, \(f_{R}(R,T)\) and \(f_{T}(R,T)\) correspond to the function derivatives with respect to R and T, respectively. Also, the term \(\Theta _{\mu \nu }\) is defined by

$$\begin{aligned} \Theta _{\mu \nu }=\frac{g^{\alpha \beta }\delta T_{\mu \nu }}{\delta g^{\mu \nu }}=-2T_{\mu \nu }+g_{\mu \nu }L_{m}-2g^{\alpha \beta }\frac{\partial ^{2}L_{m}}{\partial g^{\mu \nu }\partial g^{\alpha \beta }}. \end{aligned}$$

The energy-momentum tensor for an anisotropic fluid is given by

$$\begin{aligned} T_{\mu \nu }=(\rho +p_{t})V_{\mu }V_{\nu }-p_{t}g_{\mu \nu }+(p_{r}-p_{t})\chi _{\mu }\chi _{\nu }, \end{aligned}$$

where \(V_{\mu }\) is the 4-velocity vector of the fluid given by \(V^{\mu }=e^{-a}\delta ^{\mu }_{0}\) and \(\chi ^{\mu }=e^{-b}\delta ^{\mu }_{1}\), which satisfy the relations \(V^{\mu }V_{\mu }=-\chi ^{\mu }\chi _{\mu }=1\). Here we choose \(L_{m}=\rho \), which leads to the following expression for \(\Theta _{\mu \nu }\):

$$\begin{aligned} \Theta _{\mu \nu }=-2T_{\mu \nu }-\rho g_{\mu \nu }. \end{aligned}$$

We relate the trace equation (3) with Eq. (2), then the Einstein field equations take the form given by

$$\begin{aligned} f_{R}(R,T)G_{\mu \nu }= & {} (8\pi +f_{T}(R,T))T_{\mu \nu }+[\nabla _{\mu }\nabla _{\nu }f_{R}(R,T) \nonumber \\&-\, \frac{1}{4}g_{\mu \nu } \{(8\pi +f_{T}(R,T))T\nonumber \\&+\, \Box f_{R}(R,T)+f_{R}(R,T)R)\}]. \end{aligned}$$
(4)

The spherically symmetric wormhole geometry is defined by the spacetime:

$$\begin{aligned} \mathrm{d}s^2=-e^{2\Phi (r)}\mathrm{d}t^2+\frac{\mathrm{d}r^2}{1-b(r)/r}+r^{2}(\mathrm{d}\theta ^{2}+\mathrm{sin}^{2}\theta \mathrm{d}\Phi ^{2}), \end{aligned}$$
(5)

where \(\Phi (r)\) and b(r) both are functions of radial coordinate r and represent redshift and shape functions, respectively [50, 70]. In the subsequent discussion, we shall assume the red shift function to be constant, i.e., \(\Phi '(r)=0\). Here the radial coordinate r is non-monotonic as it decreases from infinity to a minimum value \(r_{0}\), representing the location of wormhole throat, i.e., \(b(r_{0})=r_{0}\), then it increases back from \(r_{0}\) to infinity. The most important condition for existence of the wormhole is the flaring out property where the shape function satisfies the inequality: \((b-b^{'}r)/b^{2}>0\), while at the wormhole throat, it satisfies \(b(r_{0})=r_{0}\). Further, the property \(b^{'}(r_{0})<1\), is also a necessary condition to be satisfied for the wormhole solutions. Basically these conditions lead to NEC violation in classical GR. Furthermore, another condition that needs to be satisfied for wormhole solutions is \(1-b(r)/r>0\). All these conditions collectively provide basic criteria for the existence of a physically realistic wormhole model.

In order to find the relations for \(\rho ,~p_{r}\) and \(p_{t}\), we substitute the corresponding quantities for the metric (5) in Eq. (4) and then by rearranging the resulting equations, we have

$$\begin{aligned}&\frac{b^{'}}{r^2}=\frac{(8\pi +f_{T}(R,T))}{f_{R}(R,T)}\rho +\frac{H}{f_{R}(R,T)}, \end{aligned}$$
(6)
$$\begin{aligned}&-\frac{b}{r^3}=\frac{(8\pi +f_{T}(R,T))}{f_{R}(R,T)}p_{r}+\frac{1}{f_{R}(R,T)}\left( 1-\frac{b}{r}\right) \nonumber \\&\times \,\left[ \left( f^{''}_{R}(R,T) -f^{'}_{R}(R,T) \frac{(b^{'}r-b)}{2r^{2}\left( 1-b/r\right) }\right) \right] \nonumber \\&-\,\frac{H}{f_{R}(R,T)}, \end{aligned}$$
(7)
$$\begin{aligned} -\frac{b^{'}r-b}{2r^3}= & {} \frac{(8\pi +f_{T}(R,T))}{f_{R}(R,T)}p_{t}+\frac{1}{f_{R}(R,T)}\nonumber \\&\times \,\left( 1-\frac{b}{r}\right) \frac{f^{'}_{R}(R,T)}{r} -\frac{H}{f_{R}(R,T)}, \end{aligned}$$
(8)

where

$$\begin{aligned} H= & {} H(r)=\frac{1}{4}(f_{R}(R,T)R\nonumber \\&+\,\Box f_{R}(R,T)+(8\pi +f_{T}(R,T))T). \end{aligned}$$
(9)

The curvature scalar R is given by

$$\begin{aligned} R=\frac{2b^{'}}{r^2} \end{aligned}$$
(10)

and \(\Box f_{R}(R,T)\) obeys the following expression:

$$\begin{aligned} \Box f_{R}(R,T)= & {} \left( 1-\frac{b}{r}\right) \bigg [f^{''}_{R}(R,T)-f^{'}_{R}(R,T)\nonumber \\&\times \, \frac{(b^{'}r-b)}{2r^{2}(1-b/r)}+\frac{2f^{'}_{R}(R,T)}{r}\bigg ]. \end{aligned}$$
(11)

Since the above system, involving higher-order derivatives with many unknowns, is very complicated to solve for the quantities \(\rho ,\;p_{r}\) and \(p_{t}\) therefore, for the sake of simplicity in calculations, we assume a particular form of the function f(R, T) given by the relation \(f(R,T)=f_{1}(R)+f_{2}(T)\) with \(f_{2}(T)=\lambda T\), where \(\lambda \) is a coupling parameter. After inserting this form of f(R, T) and then by simplifying the corresponding Eqs. (6)–(8), we get

$$\begin{aligned} \rho= & {} \frac{b^{'}f_{R}}{r^{2}(8\pi +\lambda )}, \end{aligned}$$
(12)
$$\begin{aligned} p_{r}= & {} -\frac{b f_{R} }{r^3(8\pi +\lambda )}+\frac{f^{'}_{R}}{2r^{2}(8\pi +\lambda )}(b^{'}r-b)\nonumber \\&-\,\left( 1-\frac{b}{r}\right) \frac{f^{''}_{R}}{(8\pi +\lambda )}, \end{aligned}$$
(13)
$$\begin{aligned} p_{t}= & {} -\frac{f^{'}_{R}}{r(8\pi +\lambda )}\left( 1-\frac{b}{r}\right) +\frac{f_{R}}{2r^{3}(8\pi +\lambda )}(b^{'}r-b). \end{aligned}$$
(14)
Fig. 1
figure 1

This shows the behavior of the shape function b(r) and \(\frac{b(r)}{r}\) versus r for the Gaussian distribution. Here, we fix the free parameters as \(\theta =4,~M=0.0001,~C_1=0.2\) and \(\lambda =2\)

Full size image
Fig. 2
figure 2

This indicates the development of \(b(r)-r\) and \(b^{'}(r)\) versus r for the Gaussian distribution. Here, we choose some specific values of the free parameters as \(\theta =4, M=0.0001, C_1=0.2\) and \(\lambda =2\)

Full size image
Fig. 3
figure 3

This shows the graphical illustration of \(\rho \) and \(\rho +p_{t}\) versus r for the Gaussian distribution. Here, we used these values of free parameters \(\theta =4, M=0.0001, C_1=0.2\) and \(\lambda =2\)

Full size image

3 Wormhole solutions: Gaussian and Lorentzian distributions for \(f_1(R)=R\) model

In this section, we shall consider a specific and interesting f(R) model [71, 72] that is given by the linear function of the Ricci scalar:

$$\begin{aligned} f_1(R)=R. \end{aligned}$$
(15)

Using this relation in Eqs. (12)–(14) and after doing some simplifications, we get the following set of field equations:

$$\begin{aligned} \rho= & {} \frac{b^{'}}{r^{2}(8\pi +\lambda )}, \end{aligned}$$
(16)
$$\begin{aligned} p_{r}= & {} -\frac{b }{r^3(8\pi +\lambda )}, \end{aligned}$$
(17)
$$\begin{aligned} p_{t}= & {} \frac{(b-b^{'}r)}{2r^{3}(8\pi +\lambda )}. \end{aligned}$$
(18)

Here we include the smearing effect mathematically by substituting Gaussian distribution of insignificant width \(\sqrt{\theta }\) in place of the Dirac delta function, where \(\theta \) is a non-commutative parameter of Gaussian distribution. Here we consider the mass density of a static, spherically symmetric, smeared, particle-like gravitational source given by

$$\begin{aligned} \rho (r)=\frac{M}{(4\pi \theta )^{\frac{3}{2}} }e^{-\frac{r^{2}}{4\theta }}. \end{aligned}$$
(19)

The particle mass M, rather than being splendidly restricted at the point, diffused on a region of the direct estimate \(\sqrt{\theta }\). This is because of the fact that the uncertainty is encoded in the coordinate commutator.

Comparing Eqs. (16) and (19), and then solving the resulting differential equation, we get the shape function b(r) in terms of error function as follows:

$$\begin{aligned} b(r)=m_{0}\left[ -2r\theta e^{-\frac{r^{2}}{4\theta }}+2 \theta ^{\frac{3}{2}}\pi ^{\frac{1}{2}}erf\left\{ \frac{r}{2\sqrt{\theta }}\right\} +C_1\right] , \end{aligned}$$
(20)

where

$$\begin{aligned} m_{0}= \frac{M(8\pi +\lambda )}{8\pi ^{\frac{3}{2}}\theta ^{\frac{3}{2}}} \end{aligned}$$

and

$$\begin{aligned} erf(\theta )=\frac{2}{\sqrt{\pi }}\int ^{\theta }_{0}e^{-t^{2}}\mathrm{d}t. \end{aligned}$$

Here \(C_1\) is a constant of integration. Also, \(\lambda \ne -8\pi \) which clearly leads to \(b(r)=0\). Using Eq. (20) in (16)–(18), we get the following relations for the ordinary energy density, tangential and radial pressures, which will be helpful to discuss the energy bounds:

$$\begin{aligned} \rho= & {} \frac{M e^{-\frac{r^2}{4 \theta }}}{8 \pi ^{3/2} \theta ^{3/2}}, \end{aligned}$$
(21)
$$\begin{aligned} p_{r}= & {} -\frac{{C}_1+\frac{M(\lambda +8 \pi )erf\left( \frac{r}{2 \sqrt{\theta }}\right) }{4 \pi }-\frac{M(\lambda +8 \pi ) re^{-\frac{r^2}{4 \theta }}}{4 \pi ^{3/2} \sqrt{\theta }}}{(\lambda +8 \pi ) r^3}, \end{aligned}$$
(22)
$$\begin{aligned} p_{t}= & {} \frac{2 \sqrt{\pi } \left( \frac{4 \pi {C}_1}{\lambda +8 \pi }+erf\left( \frac{r}{2 \sqrt{\theta }}\right) M\right) -\frac{r e^{-\frac{r^2}{4 \theta }} \left( 2 \theta +r^2\right) M}{\theta ^{3/2}}}{16 \pi ^{3/2} r^3}. \end{aligned}$$
(23)

In the case of non-commutative geometry with reference to the Lorentzian distribution, we take the density function as follows:

$$\begin{aligned} \rho (r)=\frac{M \sqrt{\theta }}{\pi ^{2}(r^{2}+\theta )^{2}}, \end{aligned}$$
(24)

where M is a mass which is diffused centralized object such as a wormhole and \(\theta \) is a non-commutative parameter. Comparing (16) and (24) and then solving the resulting differential equation, we get the following form of the shape function:

$$\begin{aligned} b(r)=\frac{(\lambda +8 \pi ) M \left( (\theta +r^2) \tan ^{-1}\left( \frac{r}{\sqrt{\theta }}\right) -\sqrt{\theta } r\right) }{2 \pi ^2 (\theta +r^2)}+C_2,\nonumber \\ \end{aligned}$$
(25)

where \(C_2\) is an integration constant. Again using Eq. (25) in (16) and (18), we get a new set of equations which help us to discuss the energy conditions for the existence of wormhole structure. In this case, the expressions for energy density, radial and tangential pressures are given by

$$\begin{aligned} \rho= & {} \frac{\sqrt{\theta } M}{\pi ^2 (\theta +r^2)^2}, \end{aligned}$$
(26)
$$\begin{aligned} p_{r}= & {} -\frac{C_2+\frac{(\lambda +8 \pi ) M \left( \left( \theta +r^2\right) \tan ^{-1}\left( \frac{r}{\sqrt{\theta }}\right) -\sqrt{\theta } r\right) }{2 \pi ^2 \left( \theta +r^2\right) }}{(\lambda +8 \pi ) r^3}, \end{aligned}$$
(27)
$$\begin{aligned} p_{t}= & {} -\frac{\sqrt{\theta } M}{2 \pi ^2 \left( \theta +r^2\right) ^2}\nonumber \\&+\,\frac{C_2+\frac{(\lambda +8 \pi ) M \left( \left( \theta +r^2\right) \tan ^{-1}\left( \frac{r}{\sqrt{\theta }}\right) -\sqrt{\theta } r\right) }{2 \pi ^2 \left( \theta +r^2\right) }}{2 (\lambda +8 \pi ) r^3}. \end{aligned}$$
(28)

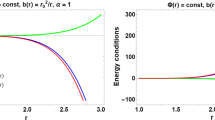
Now we will present the graphical illustration of the obtained shape functions as well as the conditions that need to be fulfilled for existence of the wormhole. For this purpose, we take different suitable choices for the involved free parameters. Firstly, we check the behavior of the shape function b(r) for the Gaussian distribution where the red shift function has been taken as a constant. The left graph of Fig. 1 indicates the positive increasing behavior of the shape function and its right graph corresponds to the behavior of the shape function ratio to radial coordinate, i.e., \(\frac{b(r)}{r}\) which shows that as the radial coordinate gets larger values, the ratio \(\frac{b(r)}{r}\) approaches zero, and hence confirms the asymptotic behavior of the shape function. The left part of Fig. 2 indicates the behavior of \(b(r)-r\), which shows that the wormhole throat for this model is located at \(r_0=0.2\) where \(b(r_0)=r_0\). In the right part of this figure, we check the flaring out condition for this model by plotting \(b^{'}(r)\). It shows that at the wormhole throat \(r_0=0.2\), clearly the condition \(b^{'}(r_0)<1\) is satisfied. The graphical behavior of density function as well as the null energy conditions \(\rho \,+\,p_r\) and \(\rho \,+\,p_t\) are shown in Figs. 3 and 4, respectively. It is clear from these graphs that the energy density function and the function \(\rho +p_t\) indicate the positive but decreasing behavior versus radial coordinate while \(\rho \,+\,p_r\) shows negative and increasing behavior and hence violates the NEC. Thus it can be concluded that the obtained wormhole solutions are acceptable in this modified gravity.

Fig. 4
figure 4

This corresponds to the development of \(\rho +p_{r}\) versus r for the Gaussian distribution. Here, we choose \(\theta =4, M=0.0001, C_1=0.2\) and \(\lambda =2\)

Full size image
Fig. 5
figure 5

This indicates the behavior of b(r) and \(\frac{b(r)}{r}\) versus r for the Lorentzian distribution. Here, we choose the free parameters as \(\theta =0.9, M=0.0001, C_2=0.1\) and \(\lambda =2\)

Full size image
Fig. 6
figure 6

This illustrates the development of \(b(r)-r\) and \(b^{'}(r)\) versus r for the Lorentzian distribution. Here, we fix the free parameters as \(\theta =0.9, M=0.0001, C_2=0.1\) and \(\lambda =2\)

Full size image
Fig. 7
figure 7

This shows graph of \(\rho \) and \(\rho +p_{t}\) versus r for the Lorentzian distribution. Here, \(\theta =0.9, M=0.0001, C_2=0.1\) and \(\lambda =2\)

Full size image
Fig. 8
figure 8

This shows \(\rho +p_{r}\) versus r for the Lorentzian distribution. Here, we fix \(\theta =0.9, M=0.0001, C_2=0.1\) and \(\lambda =2\)

Full size image
Fig. 9
figure 9

This corresponds to the development of b(r) and \(\frac{b(r)}{r}\) versus r for the Gaussian distribution. Here, we take \(\theta =10, M=0.01, n=3, \alpha =2.5, \gamma =2.5\) and \(\lambda =2\)

Full size image

In the case of the wormhole solution with a Lorentzian distribution, the graphical behavior of the shape function as well as its corresponding properties is given in Figs. 5, 6 and 7. The left curve of Fig. 5 corresponds to the behavior of the shape function while the right graph shows the behavior of \(\frac{b(r)}{r}\). It is clear from the curves that the shape function is positive and increasing satisfying the asymptotic flatness condition as \(r\rightarrow 0\). Figure 6 indicates the location of wormhole throat and the flaring out condition. It is seen that the wormhole throat is located at \(r_0=0.1\) where the function \(b(r)-r\) crosses the radial coordinate axis. Also, at this wormhole throat, the flaring out condition \(b^{'}(r_0)<1\) is satisfied for this case as shown in the right part of Fig. 6. The behavior of the energy density profile and the functions \(\rho +p_r\) and \(\rho +p_t\) is presented in Figs. 7 and 8. These show that the energy density remains positive and increasing with increasing values of r. Similarly, the function \(\rho +p_t\) indicates the positive but decreasing behavior whereas the function \(\rho +p_r\) shows the negative increasing behavior versus r. This confirms the violation of NEC in this case and hence allows the existence of the wormhole. Thus in both cases, all necessary and important characteristics of the shape function for the existence of the wormhole are satisfied and thus it can be concluded that the obtained solutions are physically viable.

4 Wormhole solutions: Gaussian and Lorentzian distributions for \(f_{1}(R)=R+\alpha R^{2}+\gamma R^{n}\) model

In this segment, we will consider another specific \(f_{1}(R)\) model [73, 74] which is given by the relation

$$\begin{aligned} f_{1}(R)=R+\alpha R^{2}+\gamma R^{n}, \end{aligned}$$
(29)

where \(\alpha \) and \(\gamma \) are arbitrary constants while \(n\ge 3\). Using the model (29) in Eqs. (12)–(14), we get the following set of equations for energy density, and the radial and tangential pressures:

$$\begin{aligned} \rho= & {} \frac{b'(r)\left( \gamma 2^{n-1} n \left( \frac{b'(r)}{r^2}\right) ^{n-1}+\frac{4 \alpha b'(r)}{r^2}+1\right) }{r^2(8 \pi +\lambda )}, \end{aligned}$$
(30)
$$\begin{aligned} p_r= & {} \frac{1}{4 r^5 (8 \pi +\lambda ) (b'(r))^3}(-8 r \alpha b'(r)^3 (-8 r b''(r)\nonumber \\&+\, b'(r)\, (12+2 b'(r)-\, r b''(r))+2 r^2 b^{(3)}(r))\nonumber \\&-\,2^n (-1+n) n r^5 \gamma \left( \frac{b'(r)}{r^2}\right) ^n \bigg (2 (b'(r))^3+2 \nonumber \\&\times \, (-2+n) r^2 (b''(r)^2+(b'(r))^2 (-4+8 n-r b''(r))\nonumber \\&+\,2 r b'(r) (-4 (-1+n) b''(r)+r b^{(3)}(r)))\nonumber \\&+\,b(r) \bigg (2^n n r^4 \gamma \left( \frac{b'(r)}{r^2}\right) ^n (2 n\times \, (-5+4 n) \nonumber \\&\times \,b'(r)^2+2 (-2+n) (-1+n) r^2 b''(r)^2\nonumber \\&-\,(-1+n) r b'(r) ((-7+8 n) b''(r)\nonumber \\&-\,2 r b^{(3)}(r)))+4 (b'(r))^3 (24 \alpha b'(r)\nonumber \\&+\,r (-r-\,18 \alpha b''(r)+4 r \alpha b^{(3)}(r)))\bigg )\bigg ), \end{aligned}$$
(31)
$$\begin{aligned} p_t= & {} -\frac{1}{4 r^5 (8 \pi +\lambda ) (b'(r))^2}\bigg (2^n n r^4 \gamma \left( \frac{b'(r)}{r^2}\right) ^n \nonumber \\&\times \,(b'(r) ((-5+4 n) b(r)+r (4-4 n+b'(r))) \nonumber \\&+\,2 (-1+n) r (r-b(r)) b''(r))+\,2 (b'(r))^2 (r (b'(r)\nonumber \\&- \,(r^2-16 \alpha +4 \alpha b'(r))+8 r \alpha b''(r))-b(r) \nonumber \\&\times \,(-12 \alpha b'(r)+r (r+8 \alpha b''(r))))\bigg ). \end{aligned}$$
(32)

A comparison of Eqs. (19) and (30) (Gaussian distribution) yields the following non-linear differential equation:

$$\begin{aligned} \frac{b'(r) \left( \gamma 2^{n-1} n \left( \frac{b'(r)}{r^2}\right) ^{n-1}+\frac{4 \alpha b'(r)}{r^2}+1\right) }{(\lambda +8 \pi ) r^2}=\frac{M e^{-\frac{r^2}{4 \theta }}}{(4 \pi \theta )^{3/2}}, \end{aligned}$$

which is complicated and hence we solve it numerically for the shape function b(r).

Fig. 10
figure 10

This shows the graphs of \(b(r)-r\) and \(b^{'}(r)\) versus r for the Gaussian distribution. Here, \(\theta =10, M=0.01, n=3, \alpha =2.5, \gamma =2.5\) and \(\lambda =2\)

Full size image
Fig. 11
figure 11

This indicates the behavior of \(\rho \) and \(\rho +p_{t}\) versus r for the Gaussian distribution. Here, \(\theta =0.5, M=0.01, n=3, \alpha =2.5, \gamma =2.5\) and \(\lambda =2\)

Full size image

In a similar way, by comparing Eqs. (24) and (30) (Lorentzian distribution), we get the following non-linear differential equation:

$$\begin{aligned} \frac{b'(r) \left( \gamma 2^{n-1} n \left( \frac{b'(r)}{r^2}\right) ^{n-1}+\frac{4 \alpha b'(r)}{r^2}+1\right) }{(\lambda +8 \pi ) r^2}=\frac{M\sqrt{\theta } }{\pi ^2 (\theta +r^2)^2} \end{aligned}$$

whose analytic solution is also not possible, thus we evaluate the possible form of the shape function by solving this equation numerically.

Now we will discuss the behavior of the shape functions that are obtained by numerical approach as well as their corresponding important and necessary properties for the existence of wormhole structure for both Gaussian and Lorentzian distributions. For this purpose, we utilize a fixed value \(n=3\) for the modified model (29) which results in the cubic form given by \(f(R)=R+\alpha R^{2}+\gamma R^{3}\). For the other higher values, i.e., \(n>3\), it is observed that the resulting form of the shape function is not physically viable. For graphical illustration of the shape functions and their other properties, we will take different feasible values of the free parameters. The left part of Fig. 9 indicates that the shape function remains positive and increasing for the Gaussian distribution (obtained numerically), while its right part shows behavior of the function \(\frac{b(r)}{r}\) versus radial coordinate. Clearly, it indicates that as the radial

Fig. 12
figure 12

This provides the development of \(\rho +p_{r}\) versus r for a Gaussian distribution with the same values of the involved parameters

Full size image
Fig. 13
figure 13

This shows the behavior of b(r) and \(\frac{b(r)}{r}\) versus r. Here, we choose the free parameters as \(\theta =0.5, M=0.0001, n=3, \alpha =2, \gamma =2\) and \(\lambda =2\)

Full size image

coordinate increases, the function tends to zero and hence leads to the asymptotic behavior of the shape function. In Fig. 10, the left curve corresponds to the function \(b(r)-r\), which provides the location of wormhole throat at \(r_0=0.001\) where it cuts the r-axis. Its right curve provides information as regards the flaring out condition, i.e., \(b^{'}(r_0)<1\) which is clearly compatible at the obtained wormhole throat. Furthermore, the graphical illustration of energy density, tangential and radial pressures is given in Figs. 11 and 12. The left part of Fig. 11 corresponds to the energy density which shows a positive but decreasing behavior, while the right curve shows the graph of \(\rho +p_t\), which is also positive decreasing. Figure 12 indicates the behavior of \(\rho +p_r\), which is clearly negative and increasing versus r and hence violates the NEC. Thus all the conditions are satisfied allowing the existence of physically viable wormhole solution.

Fig. 14
figure 14

This corresponds to the development of \(b(r)-r\) and \(b^{'}(r)\) versus r for Lorentzian distribution with the same choices of free parameters

Full size image
Fig. 15
figure 15

This indicates the graphs of \(\rho \) and \(\rho +p_{t}\) versus r for the Lorentzian distribution with the same free parameters choices

Full size image
Fig. 16
figure 16

This shows the development of \(\rho +p_{r}\) versus r for the Lorentzian distribution

Full size image

Similarly, for the Lorentzian distribution, the graphical behavior of the shape function and its properties like asymptotic behavior, wormhole throat and the flaring out condition are shown in Figs. 13 and 14. It can easily be observed that the obtained shape function is positive increasing and is compatible with all conditions. Further, the graphs for the resulting density profile, \(\rho +p_{t}\) and \(\rho +p_{r}\), are given in Figs. 15 and 16, respectively, which confirm the violation of NEC for this wormhole model. Thus it can be concluded that the obtained wormhole solutions for this cubic polynomial \(f_1(R)\) model are physically interesting for both non-commutative distributions.

Fig. 17
figure 17

This shows the graphical illustration of \(F_{af}\) and \(F_{hf}\) forces versus r for the Gaussian and Lorentzian distribution when \(f_1(R)=R\) in the left and right panels, respectively. Here, \(\theta =0.5, M=0.01, n=3, \alpha =2.5, \gamma =2.5\) and \(\lambda =2\)

Full size image
Fig. 18
figure 18

This shows the development of the \(F_{af}\) and \(F_{hf}\) forces versus r for the Gaussian and Lorentzian distributions when \(f(R)=R+\alpha R^{2}+\gamma R^{3}\). Here, we fix \(\theta =0.5, M=0.01, n=3, \alpha =2.5, \gamma =2.5\) and \(\lambda =2\)

Full size image

5 Equilibrium condition

In this segment, we explore the stability of obtained solutions using equilibrium conditions in the presence of Gaussian and Lorentzian distributions of non-commutative geometry. For this purpose, we take the Tolman–Oppenheimer–Volkov equation [59], which is given by

$$\begin{aligned} \frac{\mathrm{d}p_{r}}{\mathrm{d}r}+\frac{\sigma ^{'}}{2}(\rho +p_{r})+\frac{2}{r}(p_{r}-p_{t})=0, \end{aligned}$$
(33)

where \(\sigma (r)=2\Phi (r)\). This equation determines the equilibrium state of configuration by taking the gravitational, hydrostatic as well as the anisotropic forces (arising due to anisotropy of matter) into account. These forces are defined by the following relations:

$$\begin{aligned} F_{gf}=-\frac{\sigma ^{'}(\rho +p_{r})}{2},\quad F_{hf}=-\frac{\mathrm{d}p_{r}}{\mathrm{d}r}, \quad F_{af}=2\frac{(p_{t}-p_{r})}{r}, \end{aligned}$$

and thus Eq. (33) takes the form given by

$$\begin{aligned} F_{af}+F_{gf}+F_{hf}=0. \end{aligned}$$

Since we assumed the red shift function to be a constant so that \(\Phi '(r)=0\), we have \(F_{gf}=0\) and hence the equilibrium condition reduces to the following form:

$$\begin{aligned} F_{af}+F_{hf}=0. \end{aligned}$$

We shall discuss the stability condition for both exact and numerical solutions in the presence of both distributions of non-commutative geometry. Firstly, we calculate \(F_{af}\) and \(F_{hf}\) for the Gaussian distribution as follows:

$$\begin{aligned} F_{af}= & {} \frac{6 \sqrt{\pi } \left( \frac{4 \pi {C1}}{8 \pi +\lambda } +erf\left( \frac{r}{2 \sqrt{\theta }}\right) M\right) -\frac{M r e^{-\frac{r^2}{4 \theta }} \left( 6 \theta +r^2\right) }{\theta ^{3/2}}}{8 \pi ^{3/2} r^4},\\ F_{hf}= & {} \frac{6 \sqrt{\pi } \left( -\frac{4 \pi {C1}}{8 \pi +\lambda }- erf\left( \frac{r}{2 \sqrt{\theta }}\right) M\right) +\frac{M r e^{-\frac{r^2}{4 \theta }} \left( 6 \theta +r^2\right) }{\theta ^{3/2}}}{8 \pi ^{3/2} r^4}, \end{aligned}$$

while, for a Lorentzian distribution, these are given by

$$\begin{aligned} F_{af}= & {} \frac{6 \pi ^2 C_2 (\theta +r^2)^2-\sqrt{\theta } (8 \pi +\lambda ) M r (3 \theta +5 r^2) +3M (8 \pi +\lambda ) (\theta +r^2)^2 \tan ^{-1}\left( \frac{r}{\sqrt{\theta }}\right) }{2 \pi ^2 (8 \pi +\lambda ) r^4 (\theta +r^2)^2},\\ F_{hf}= & {} \frac{-6 \pi ^2 C_2 (\theta +r^2)^2+\sqrt{\theta } (8 \pi +\lambda ) M r (3 \theta +5 r^2) -3M (8 \pi +\lambda ) (\theta +r^2)^2 \tan ^{-1}\left( \frac{r}{\sqrt{\theta }}\right) }{2 \pi ^2 (8 \pi +\lambda ) r^4 (\theta +r^2)^2}. \end{aligned}$$

The graphical behavior of these forces is given in Figs. 17 and 18. The left graph indicates the behavior of these forces for the Gaussian distribution while the right graph corresponds to Lorentzian distribution for simple \(f_1(R)\) model. It is clear from the graph that both these forces show the same but opposite behavior and hence cancel each other’s effect and thus leaving a stable wormhole configuration. Similarly, we investigate the stability of numerical solutions for modified cubic f(R) model using both the Gaussian and the Lorentzian distributions. The graphical behavior of resulting forces is given by Fig. 18. Its left part corresponds to behavior of these forces for the Gaussian distribution whereas the right graph provides the behavior for the Lorentzian distribution which clearly indicates that these forces are also balancing each other’s effect and thus leading to a stable wormhole structure.

6 Gravitational lensing effect of wormhole for simple \(f(R)=R\) model

In this section, we will explore the possible detection of traversable wormhole through gravitational lensing phenomena. For this purpose, we consider the static spherical symmetric metric involving \(x=\frac{r}{2M}\) representing the radius in Schwarzschild units and given by

$$\begin{aligned} \mathrm{d}s^2=-A(x)\mathrm{d}t^2+B(x)\mathrm{d}x^2+C(x)(\mathrm{d}\theta ^2+\sin ^2\theta \mathrm{d}\phi ^2). \end{aligned}$$
(34)

Here the closest path taken by the light ray is \({\hat{x}}=\frac{{\hat{r}}}{2M}\). Here we will consider the obtained exact form of the shape function in the case of a simple linear \(f_1(R)=R\) model (Sect. 3). The integration of this shape function from the wormhole throat \(r_{0}\) to r is given as follows:

$$\begin{aligned} b(r)= & {} \frac{(\lambda +8\pi )M\sqrt{\theta }}{2\pi ^2}\bigg [\frac{1}{\sqrt{\theta }} \arctan \bigg (\frac{r}{\sqrt{\theta }}\bigg )-\, \frac{r}{(r^2+\theta )}\nonumber \\&-\,\frac{1}{\sqrt{\theta }} \arctan \bigg (\frac{r_{0}}{\sqrt{\theta }}\bigg )-\frac{r_{0}}{(r_{0}^2+\theta )}\bigg ]+r_{0}. \end{aligned}$$
(35)

Here clearly the coupling constant satisfies \(\lambda \ne -8\pi \). Basically, we consider the form of static spherically symmetric wormhole metric (5) where \(e^{2\Phi (r)}=(\frac{r}{b_0})^m\) where \(b_0\) is an integration constant while \(m=2(v^{\phi })^2\), where \(v^{\phi }\) indicates the rotational velocity. In [75,76,77,78], it is pointed out that \(m=0.000001\), which is a very small value (nearly zero) and hence leaving the red shift function as a constant (as we assumed in previous sections). A comparison of these metrics leads to the following relations:

$$\begin{aligned} A(x)=\left( \frac{r}{b_0}\right) ^m,\quad B(x)=\left( 1-\frac{b(r)}{r}\right) ^{-1}, \quad C(x)=r^2.\nonumber \\ \end{aligned}$$
(36)

The deflection angle for the light ray is given by

$$\begin{aligned} \alpha ({\hat{x}})=-\ln \left( \frac{2d}{3}-1\right) -0.8056+I({\hat{x}}). \end{aligned}$$
(37)

Here d represents the mouth of wormhole because of exterior Schwarzschild line element, while the internal metric contribution is provided by \(I({\hat{x}})\), which implies that the closest path taken by the ray of light is bigger than the mouth of the wormhole. This is defined by the relation

$$\begin{aligned} I({\hat{x}})=\int ^{\infty }_{{\hat{x}}}\frac{2\sqrt{B(x)\mathrm{d}x}}{\sqrt{C(x)\sqrt{\frac{C(x)A({\hat{x}})}{C({\hat{x}})A(x)}}-1}}. \end{aligned}$$
(38)

In our case, this integral take the following form:

$$\begin{aligned} I({\hat{x}})=\int ^{d}_{{\hat{x}}}G(x)\mathrm{d}x \end{aligned}$$
(39)

representing the closest approach for the light ray to be inside the mouth of the wormhole. Here the function G(x) is given by

$$\begin{aligned} G(x)=\frac{2}{\sqrt{x^2\left[ 1-\frac{1}{x}\left( \frac{\lambda +8\pi }{4\pi ^2}\right) \left( \arctan \left( \frac{x}{\sqrt{\theta }}\right) -\frac{x\sqrt{\theta }}{(x^2+\theta )}-\arctan \left( \frac{x_{0}}{\sqrt{\theta }}\right) +\frac{x_{0}\sqrt{\theta }}{(x^2_{0}+\theta )}\right) +x_{0}\right] }\sqrt{\frac{x^{2-m}}{{\hat{x}}^{2-m}}-1}}. \end{aligned}$$
(40)

In order to investigate the convergence/divergence of this integral, we can redefine the variable as \(y=\frac{x}{{\hat{x}}}\) for the sake of simplicity in calculations. Thus the integral takes the following form:

$$\begin{aligned} I({\hat{x}})=\int ^{d/{\hat{x}}}_{1}\frac{2}{\sqrt{\left[ 1-\frac{1}{{\hat{x}}y}\left( \frac{\lambda +8\pi }{4\pi ^2}\right) \left( \arctan \left( \frac{{\hat{x}}y}{\sqrt{\theta }}\right) -\frac{{\hat{x}}y\sqrt{\theta }}{({\hat{x}}^2y^2+\theta )}-\arctan \left( \frac{{\hat{x}}y_{0}}{\sqrt{\theta }}\right) +\frac{{\hat{x}}y_{0}\sqrt{\theta }}{({\hat{x}}^2y_{0}^2+\theta )}\right) +{\hat{x}}y_{0}\right] }\sqrt{y^{4-m}-y^2}}. \end{aligned}$$
(41)

In the integrand of the above integral, we can assume that \(H(y)=f(y)(y^{4-m}-y^2)\), where

$$\begin{aligned} f(y)= & {} 1-\frac{1}{{\hat{x}}y}\bigg (\frac{\lambda +8\pi }{4\pi ^2}\bigg )\bigg [\arctan \bigg (\frac{{\hat{x}}y}{\sqrt{\theta }}\bigg ) -\frac{{\hat{x}}y\sqrt{\theta }}{({\hat{x}}^2y^2+\theta )}\nonumber \\&-\, \arctan \bigg (\frac{{\hat{x}}y_{0}}{\sqrt{\theta }}\bigg )+\frac{{\hat{x}}y_{0}\sqrt{\theta }}{({\hat{x}}^2y_{0}^2+\theta )}\bigg ] +{\hat{x}}y_{0}. \end{aligned}$$
(42)

Taylor’s series can be used to expand the function H(y) around \(y=1\) as follows:

$$\begin{aligned} H(y)= & {} s(2-m)f(1)(y-1)+\bigg [\frac{1}{2}(5-m)(2-m)f(1)\nonumber \\&+\, (2-m)f'(1)\bigg ](y-1)^2+O(y-1)^3. \end{aligned}$$
(43)

Here we truncate the Taylor expansion up to second order where \(O(y-1)^3\) indicates the cubic and higher-order terms of factor \((y-1)\). It can easily be observed that the integral \(I({\hat{x}})\) converges or diverges because of the leading term in the above expression. Integral can be convergent if the first \((y-1)^{1/2}\) leads the expression where \(g(1)\ne 0\). If \(g(1)=0\), then second term will lead the expression and whose integration will be \(\ln (y-1)\). Since \(y=1\), it turns out be undefined there and hence the integral diverges. If we choose the nearest approach of light ray as the wormhole throat, i.e., \({\hat{r}}=r_{0}\), then consequently, we have \(y_{0}=\frac{x_{0}}{{\hat{x}}}\) and thus \(y_{0}=1\). Using these values in f(y), it can easily be verified that \(f(1)=0\). Hence a photon sphere with radius \({\hat{r}}\) (closest path taken by the light ray) equal to radius of the throat \(r_0\), can be found.

7 Conclusions

The existence and construction of the wormhole solutions in GR with some exotic matter has always been of great interest for the researchers. The presence of exotic matter is one of the most important requirement for wormhole construction as it leads to NEC violation and hence permits the existence of the wormhole. In the case of modified theories, construction of wormholes has become more fascinating topic as these include the effective energy-momentum tensor that violates NEC without inclusion of any exotic matter separately. In the present paper, we have constructed spherically symmetric wormhole solutions in the presence of two interesting Gaussian and Lorentzian distributions of non-commutative geometry in f(R, T) modified gravity. For this purpose, in order to make system of equations closed, we assumed the function \(f(R,T)=f_1(R)+\lambda T\) with two different forms of \(f_1(R)\), i.e., the linear form \(f_1(R)=R\) and \(f_{1}(R)=R+\alpha R^{2}+\gamma R^{n},~n\ge 3\).

Firstly, we talked about the possible wormhole construction for the linear \(f_1(R)\) model with both Gaussian and Lorentzian distributions. For Lorentzian and Gaussian distribution, we found the exact solution. In order to examine the physical behavior of these obtained solutions, we plotted b(r) versus radial coordinate. It is observed that shape functions show positive increasing behaviors for both these non-commutative distributions. Further we found the location of wormhole throats and analyzed some important characteristics of the shape functions namely asymptotic behavior, the flaring out condition and the violation of NEC using graphs. This discussion has been given in Figs. 1, 2, 3, 4, 5, 6, 7 and 8. It is concluded from these graphs that the obtained shape functions show asymptotic behavior, i.e., \(\frac{b(r)}{r}\rightarrow 0\) as \(r\rightarrow \infty \). Also, for both cases, wormhole throats are located at \(r_0=0.2\) and \(r_0=0.1\). Furthermore, the obtained shape functions are compatible with the flaring out condition and NEC as the function \(\rho +p_r\) indicated negative behavior for both distributions. Thus the obtained solutions are viable permitting wormhole to exist in non-commutative f(R, T) gravity.

Secondly, we checked the existence of the wormhole for model \(f_{1}(R)=R+\alpha R^{2}+\gamma R^{n},~n\ge 3\) by taking both non-commutative distributions into account. In this case, we obtained very complicated non-linear differential equations for b(r) whose analytic solutions are not possible, therefore we solved them numerically. It is worthwhile to mention here that we fixed \(n=3\) for numerical solutions and their graphical behaviors as it is found that, for \(n>3\), the obtained solutions are not physically interesting (not meeting the necessary criteria for existence of the wormhole). In the left parts of Figs. 9 and 13, it is shown that the numerical solutions for b(r) indicate increasing positive behavior. Other necessary conditions like asymptotic behavior of the shape function, flaring out condition as well as NEC have been given in Figs. 9, 10, 11, 12, 13, 14, 15 and 16. The wormhole throat for solutions in both distributions are located at \(r_0=0.001\). Also, \(\rho +p_r\) shows negative behavior and hence NEC is incompatible for this solution. Thus it is concluded that all the conditions are satisfied for the chosen specific values of free parameters and hence the obtained wormhole solutions are viable. It is also interesting to mention here that, for a different selection of free parameters \(\theta ,~M,~\lambda \) etc. (other than the used values in the present paper), all the functions show a similar graphical behavior as presented in the figures. Thus all the necessary conditions for existence of the wormhole will also be satisfied in these cases and hence the wormhole solution still exist.

Further, we examined the stability of obtained solutions using equilibrium condition given by Tolman–Oppenheimer–Volkov equation. Here we explored the stability for both models of \(f_1(R)\) in the presence of Gaussian and Lorentzian distributions. After evaluating the possible expressions of anisotropic and hydrostatic forces for these cases, we examined them graphically as shown in Figs. 17 and 18. It can easily be observed from the graphs that these forces are almost equal in magnitude but opposite in behavior, therefore canceling each other’s effect and hence leaving a balanced final wormhole configuration. Furthermore, we explored the possible detection of photon sphere at the wormhole throat. For this purpose, we followed the procedure given in Refs. [75,76,77,78] and explored the convergence of deflection angle. It is observed that, for the obtained exact solution for \(f_1(R)=R\), the resulting integral diverges at wormhole throat and hence it is concluded that a photon sphere, with radius \(r_0\) (closest path taken by the light ray) equal to radius of the throat, can be detected.