1 Introduction

The Einstein field equations (EFEs), which connect space-time’s geometry and physics, provide the foundation of general theory of relativity. Because these equations are nonlinear, finding their exact solutions is quite challenging. Imposing some symmetry constraints is one method for finding EFE solutions. Since these symmetry restrictions are very helpful in figuring out the precise solutions of EFEs, they have a special place in Einstein’s theory of general relativity (GR). One of the most significant types of symmetry is killing symmetry, which occurs when the Lie derivative of a metric tensor vanishes. The concept of a conformal killing vector (CKV), denoted as \(\xi \), as a vector field on a manifold is established. This vector field possesses the remarkable property that when the metric undergoes displacement along the curves generated by \(\xi \), its Lie derivative exhibits proportionality to itself. It is well recognised that employing killing symmetry to determine the natural connection between geometry and matter via the EFEs is significant. The symmetry under CKV can be written as

$$\begin{aligned} L_\xi g_{ik}=\psi g_{ik},\,\,\,\,\ i,k=1,2,3,4,5. \end{aligned}$$
(1)

The conformal factor, denoted by \(\psi \), is an arbitrary function of both r and t. The Lie derivative of the metric tensor g, which describes how a compact star’s internal gravitational field relates to the vector field \(\xi \), is represented by the L. The vector \(\xi \) generates the conformal symmetry, facilitating the conformal transformation of the metric g onto itself along \(\xi \). Importantly, both \(\xi \) and \(\psi \) need not be static, even in the context of a static metric [1, 2]. Notably, Eq. (1) produces the Killing vector for \(\psi =0\), a homothetic vector when \(\psi =constant\), and a conformal vector when \(\psi =\psi (x,t)\). The presence of \(\psi =\psi (x,t)\) always gives rise to a conformal vector [3].

The conformal motion are widely used in the study of compact objects (COs). The research explores the presence of a one-parameter group of conformal motions in the context of anisotropic matter. The study reveals that the EFEs, corresponding to both isotropic and anisotropic matter, distinctly determine the equation of state. Notably, both solutions exhibit seamless compatibility with the Schwarzschild exterior metric and possess positive energy density surpassing the stresses throughout the entire spherical region [4]. The EFEs for spherically symmetric distributions of isotropic and an-isotropic matter are solved using conformal motions. Solutions are compatible with the Schwarzschild exterior metric, with a surface potential equal to 1/3. Two families of solutions describe expanding and contracting spheres, and oscillating black holes are described by a third family of solutions. Each solution has a positive energy density that is greater than the stress everywhere [5, 6]. In both perfect and anisotropic fluids, analytical solutions to the static Einstein-Maxwell equations have been found, provided that spherical symmetry and a one-parameter group of conformal motions are presented. Connected to the Reissner–Nordström metric, these solutions always show positive energy density, exceeding the sphere’s total stresses [7]. Different solutions to the EFEs for a spherically symmetric distribution of anisotropic matter are presented. Although the stresses and energy density remain inside the sphere, these solutions are alignable with flat spacetime at the matter’s boundary [8].

The research illustrates an instance of a perfect fluid within an Friedmann–Robertson–Walker (FRW) space-time, highlighting that CKV don’t map the fluid flow lines onto each other. Furthermore, the investigation explores the dynamic characteristics of special CKV in a fluid exhibiting anisotropic pressure and zero energy flux, as dictated by EFEs. Additionally, the study examines the relationship between anisotropic pressure components and energy density, with the dynamic outcomes contingent on the absence of the energy flux vector [9]. The study of radiating anisotropic spheres with a one-parameter conformal motion approach reveals two stress equation-based models. The first model integrates the system of equations by using luminosity as a function of timelike coordinates, whereas the second model infers luminosity from the stress equation. Both models are numerically integrated and analysed in terms of potential astrophysical applications [10]. This research investigates the interplay between perfect fluid matter and nonsingular aligned electromagnetic fields. The findings uncover that the existence of non-vanishing shear serves as a symmetry condition, contributing significantly to timelike conformal collineations. These outcomes have broad applicability to diverse physical scenarios and offer a coherent counterpart to space-times devoid of shear [11].

Anisotropic fluids that admit a generalization of conformal motion, called conformal collineation, are taken into consideration in GR [12]. The results of the study, provided spacetimes that are axially and reflection symmetric and have a conformal motion group with one parameter on \(S^2\). Minkowski is the only physically significant solution to the Einstein vacuum field equations [13]. The research looks into the concept of a proper CKV in fluid spacetimes, with a focus on synchronous spacetimes. Other than FRW spacetimes, orthogonal synchronous perfect fluid spacetimes do not admit proper inherited CKV. The study also considers generalizations to non-moving perfect fluid and comoving but non-perfect fluid synchronous spacetimes. Proper CKV spacetimes are extremely rare, and determining them all is of interest. It is suggested that a non-existence finding may be valid when generalised to non-synchronous spacetimes [14]. The work examines solutions to the Einstein–Maxwell equations for charged imperfect fluids in static spheres while taking space-time geometry conformal symmetry into account. It allows nonsingular solutions at the centre and generalises earlier work to nonstatic conformal symmetry. For charged spheres, two regular solutions are given; further generalisation for conformally symmetric stable accurate stellar models is proposed [15].

In GR, variables and constraints define kinematics and dynamics. One important restriction is symmetry, which is divided into two categories: curvature collineations and killing vectors. The CKV are used to simplify the EFEs for general spacelike collineations and matter. Applications to matter described by perfect or anisotropic fluids, as well as spacelike CKVs, are discussed. We extend the idea of symmetry inheritance to conformal Killing vectors, demonstrating that matter does not inherit symmetry [16]. In the thin-wall approximation, scalar soliton stars are described by two families of time-dependent solutions to the Einstein equation. The development of second-order phase transitions is supported by the selfsimilarity of the space-time inside the star. Values for the maximum and minimum surface potential are discovered [17]. The study compares every possible scenario of evolution with particular solutions to the differential equation controlling the time evolution of self-similar scalar soliton star models provided in [18]. Static spherically symmetric spacetimes contain the conformal Killing equation, which unifies and generalises particular scenarios. Non-con-formally flat spacetimes have three classes, one or both noninheriting conformal Killing vectors, and a maximum of two proper conformal motions. Conformally flat spacetimes with eleven valid conformal Killing vectors are classified into three classes, including the Schwarzschild interior metric [19]. The vector of conformal symmetry is derived within static and spherically symmetric spacetimes, taking into account integrability conditions and metric constraints. Some conformal symmetries are found as specific instances within this framework [20].

This work examines self-similarity in GR, with a focus on the first type of similarity, which relates to spacetimes with a homothetic vector. It investigates numerous self-similar solutions to EFEs, with a focus on spatially homogeneous and spherically symmetric solutions, possibly asymptotic states, and applications in astrophysics and cosmology. It also investigates broader self-similar models [21].

They explored the configuration of charged strange quark matter connected to a string cloud within spherically symmetric spacetime that allows for a one-parameter group of conformal motions. To achieve this, we solve EFEs for spherically symmetric spacetime, accounting for the attachment of strange quark matter to the string cloud through conformal motions. Additionally, we discuss the characteristics of the solutions obtained [22]. They conduct a general investigation into axially symmetric, static fluids with a CKV. The physical significance of this type of symmetry is highlighted. Following that, they analyse all possible repercussions that arise from the implementation of such symmetry. The issue of symmetry inheritance receives special consideration [23]. The research investigates non-static spherically symmetric fluids with a CKV and develops numerous exact analytical solutions for various CKV choices in both dissipative and adiabatic regimes. Additional requirements are added, such as eliminating complexity factor and quasi-homologous evolution. The study deals with the applications of the results in astrophysical contexts as well as other ways for finding new solutions [24]. Recently, Herrera et al. [4] discovered that the stiff equation of state \(p=\rho \) is unique for specific conformal motions if the generating conformal vector field is orthogonal to the four-velocity. They deal with this problem using conformal collineations, demonstrating that the stiff equation of state isn’t specifically intended for particular conformal collineations [25].

This study investigates fluid space-times in GR, with an emphasis on metric symmetry and conformal collineation. It highlights the importance of conformal collineation symmetry for smooth transitions at fluid pattern alterations. The research is applicable to the radiation-like viscous fluid FRW model, which has a conformal collineation symmetry vector parallel to the tilted velocity vector. Significant material curves in fluids as they evolve are revealed by the results [26]. The research looks at viscous heat-conducting fluid and anisotropic fluid space-times with a particular CKV and demonstrates general theorems concerning symmetry inheritance linked with the special CKV. It demonstrates that if the special CKV maps fluid flow lines, the special CKV symmetry is inherited by all physical components of the energy-momentum tensor. Furthermore, symmetry inheritance happens when the Lie derivative along a specific CKV is zero. A unique CKV cannot exist in ideal fluid space-times [27]. The research looks at ideal fluid spherically symmetric spacetimes with a proper inherited CKV. The only known spacetimes are conformal FRW spacetimes, static Schwarzschild interior spacetimes, and generalized Gutman-Be’spalko Wesson spacetimes with a constrained form and conformal factor. The nonexistence of such spacetimes is demonstrated, confirming a general non-existence conjecture [28].

In recent years, there has been a lot of interest in applying GR to higher dimensions. Rahaman et al. [29] examined the following four scenarios that were part of the solar system experiments in order to assess the feasibility of GR with larger dimensions: gravitational time delay, gravitational redshift, bending of light, and perihelion shift. Liu and Overduin [30] conducted some additional investigations about greater dimensions for the motion of a test particle. The D-dimensional gravstars are studied by Rahaman et al. [31].

Rahaman et al. investigated the novel class of four-dimensional interior solutions that accept conformal motion for anisotropic compact stars [32]. Rahaman et al. [33] also investigated fluids in higher and lower dimensions using noncommutative geometry and a Gaussian energy density distribution. They demonstrated that any spherically symmetric stellar system can only have a stable configuration in four dimensions.

The underlying matter distribution of CO is typically believed to be homogeneous and isotropic, or a perfect fluid that obeys the Tolman–Oppenheimer–Volkoff (TOV) equation [34, 35]. This method is frequently applied to the characterization of CO, including neutron stars, and polytropic objects like white dwarfs [36]. Theoretical developments show that pressure within a CO does not have to be completely isotropic, and that a variety of causes can contribute to pressure anisotropy [37]. The truth is that anisotropic fluids have been thoroughly investigated in the past, with the intent of determining sustainable anisotropy sources. A thorough analysis of anisotropic fluids may be found in [38], which also provides an extensive list of physical phenomena that may be in play when pressure anisotropy emerges. Anisotropic fluids exhibit two separate pressure components: the radial pressure, denoted as \(p_r\), and the transverse pressure, denoted as \(p_t\), which acts in the opposite direction to \(p_r\). The anisotropic factor, defined as \(\Delta =p_t-p_r\), becomes significant. When \(\Delta >0\) or, equivalently, when \(p_t>p_r\), the anisotropic force \((\frac{2\Delta }{r})\) manifests as both repulsive and attractive in nature.Therefore, it seems sense to take pressure anisotropy into account when developing the model under study. It is demonstrated that the presence of a repulsive force facilitates the construction of CO in the case of an anisotropic fluid [39].

In this paper, we investigated the five-dimensional non-static spherically symmetric distribution in Schwarzchild-like non-comoving coordinates with an energy density profile as shown in [40, 41]. The Eqs. (15) and (16) that appeared in the set of Eqs. (15–17) are similar to equations in four dimensions. We can demonstrate that compact stars can exist even in higher dimensional non-static spherical symmetry using this method. The following is the outline for this article: We reported the EFEs for the anisotropic star’s internal spacetime in Sect. 2. Section 3 employs the Particular density profile found in Equation (21) to solve the EFEs. We presented the five-dimensional exact solution in Sect. 4 to study the physical parameters. In Sect. 5, we studied the model’s characteristics, stability conditions, and graphical plot in the fifth dimension. In Sect. 6, we provide our final views for concluding the paper.

2 The Einstein field equations in higher dimension

The line element consedered have represents five-dimensional Schwarzschild-like coordinate dynamic system, which characterized the non-static spherically symmetric spacetime in five dimensions [42] as follows:

$$\begin{aligned} ds^2{=}e^{\nu (r,t)} dt^2{-}e^{\lambda (r,t)} dr^2{-}r^2(d\theta ^2{+}sin^2d\phi ^2){-}e^{\mu (r,t)} dw^2,\nonumber \\ \end{aligned}$$
(2)

The spacetime coordinates are \(x^0=t, x^1=r, x^2=\theta , x^3=\phi , x^4=w\). We will use geometries units i.e., \(c=G=1\). The inner matter distribution is anisotopic written as [43].

$$\begin{aligned} T^{\mu }_{\nu }=(\rho +p_r)u^\mu u_\nu -p_r g^{\mu }_{\nu }+(p_t-p_r) \eta ^\nu \eta _\mu . \end{aligned}$$
(3)

Here \(\rho \), \(p_r\), \(p_t\), \(u^\mu \), and \(\eta ^\mu \) represents the density, radial pressure, transverse pressure, fluid five velocity and unit space like vectors respectively. For line element Eq. (2) and energy momentum tensor in Eq. (3) the EFEs in five dimension are [44]

$$\begin{aligned} 8\pi \rho= & {} -\frac{1}{r^2}{+}e^{-\lambda } \Bigg (\frac{1}{r^2}{+}\frac{(\mu _{,r}{-}\lambda _{,r})}{r}{+}\frac{\big ((\mu _{,r})^2{-}\mu _{,r}\lambda _{,r}\big )}{4}\nonumber \\{} & {} +\frac{\mu _{,rr}}{2}\Bigg )+e^{-\nu }\Bigg (\frac{{\mu _{,t}}{\lambda _{,t}}}{4}\Bigg ),\end{aligned}$$
(4)
$$\begin{aligned} 8\pi p_r= & {} -\frac{1}{r^2}+e^{-\lambda }\Bigg (\frac{1}{r^2}+\frac{(\nu _{,r}+\mu _{,r})}{r}+\frac{\mu _{,r}\nu _{,r}}{4}\Bigg ) \nonumber \\{} & {} -\frac{e^{-\nu }}{4}\Bigg (2{ \mu _{,tt}}+{({\mu _{,t}})^2}-{\mu _{,t}} {\nu _{,t}} \Bigg ), \end{aligned}$$
(5)
$$\begin{aligned} 8\pi p_t= & {} \frac{e^{-\nu }}{4}\Bigg (2\big (\mu _{,tt}+\lambda _{,tt}\big )+\mu _{,t}\big (\mu _{,t}-\nu _{,t}+\lambda _{,t}\big )\nonumber \\{} & {} +\lambda _{,t}\big (\lambda _{,t}-\nu _{,t}\big )\Bigg )-\Bigg \{\frac{e^{{-}\lambda }}{4}\Bigg (2\big (\nu _{,rr}{+}\mu _{,rr}\big )+(\nu _{,r})^2\nonumber \\{} & {} +(\mu _{,r})^2-\nu _{,r}\lambda _{,r}-\mu _{,r}\big (\lambda _{,r}+\nu _{,r}\big )\Bigg ) \nonumber \\{} & {} +\frac{2}{r}\Bigg (\nu _{,r}-\lambda _{,r}+\mu _{,r}\Bigg )\Bigg \}, \end{aligned}$$
(6)
$$\begin{aligned} 8\pi T^{0}_{1}= & {} \Bigg (\frac{\mu _{,r}\mu _{,t}}{4}-\frac{\mu _{,t} \nu _{,r}}{4}-\frac{\mu _{,r}\lambda _{,t}}{4}+\frac{\mu _{,tr}}{2}-\frac{\lambda _{,t}}{r}\Bigg ).\nonumber \\ \end{aligned}$$
(7)

Here subscripts r and t represent the partial derivative with respect to the radial and temporal coordinates respectively.

3 Conformal killing vector in five dimension

The metric tensor of a spacetime remain invariant during conformal motions, commonly referred to as CKVs, up to a scale factor. An everywhere differentiable vector field denoted as \(\xi \) on a manifold \(\beta \) is termed a conformal vector field. This vector field satisfies a specific property with respect to the metric \(g_{ab}\) in any given coordinate system on \(\beta \). The property is expressed as \(\xi _{a;b} = \psi g_{ab} + F_{ab}\), where \(\psi : \beta \rightarrow {R}\) is a smooth function called the conformal function associated with the vector field \(\xi \), and \(F_{ab}\) represents the conformal bivector linked to x. This definition can also be expressed as \(L_{\xi }g_{ik} = \psi g_{ik}\), where \(L_\xi \) denotes the Lie derivative along the vector field \(\xi \). The CKV provide a more in-depth understanding of spacetime geometry. The CKVs make it easier to generate exact solutions to EFEs. Physically, it is crucial to understand conformal motions in spacetime because this could result in conservation laws, which are then used to create spacetime classification systems. The EFEs exhibit significant nonlinearity, the utilization of CKVs offers a method to transform PDEs into linear ODEs. The precise properties of compact stars and electron structures, which bear resemblance to fundamental particles, continue to be uncertain for theoretical physicists. Thus, let us explore a case where a one-parameter group of conformal motion is allowed to exist in a non-static, spherically symmetric spacetime. The CKV can be stated in a more practical form than that found in Eq. (1):

$$\begin{aligned} L_\xi g_{mn}=\xi _{m;n}+\xi _{n;m}=\psi g_{mn}, \end{aligned}$$
(8)

where \(m, n=1, 2, 3, 4, 5\). Here orbit group is denoted by \(\xi \), while \(\psi \) is an arbitrary function of both r and t. When considering \(\xi _i\), the metric \(g_{ij}\) undergoes a conformal transformation unto itself. Furthermore, let’s extend the assumption that the orbit of the group is orthogonal to the vector field representing the velocity of the fluid.

$$\begin{aligned} \xi ^\mu u_\mu =0. \end{aligned}$$
(9)

The spherical symmetry from Eq. (9) leads to the following:

$$\begin{aligned} \xi ^1=\xi ^3=....=\xi ^{n+1}=0. \end{aligned}$$

By using the CKV on the line element (2) yields the subsequent set of equations:

$$\begin{aligned} \nu _{,r}\xi ^2= & {} \psi , \end{aligned}$$
(10)
$$\begin{aligned} -e^{\lambda }\xi ^2_{,1}= & {} 0, \end{aligned}$$
(11)
$$\begin{aligned} \lambda _{,r}\xi ^2+2\xi ^2_{,2}= & {} \psi , \end{aligned}$$
(12)
$$\begin{aligned} \xi ^2= & {} \frac{\psi r}{2}, \end{aligned}$$
(13)
$$\begin{aligned} \mu _{,r}\xi ^2= & {} \psi . \end{aligned}$$
(14)

The result of the equations in the previous set is

$$\begin{aligned} e^\nu= & {} r^2C^2_{1}, \end{aligned}$$
(15)
$$\begin{aligned} e^{\lambda }= & {} \frac{C^2_{2}}{\psi ^2}, \end{aligned}$$
(16)
$$\begin{aligned} e^\mu= & {} r^2C^2_{3} \end{aligned}$$
(17)

where \(C_1\), \(C_2\), and \(C_3\) represent the integration constants. Substituting Eqs. (15)–(17) into the EFEs (4)–(6), we obtain:

$$\begin{aligned} 8\pi \rho= & {} \frac{1}{r^2}\Bigg (1-\frac{3\psi ^2}{C^2_{2}}\Bigg )-\frac{3\psi \psi _{,r}}{rC^2_{2}} \end{aligned}$$
(18)
$$\begin{aligned} 8\pi p_r= & {} -\frac{1}{r^2}\Bigg (1-\frac{6\psi ^2}{C^2_{2}}\Bigg ) \end{aligned}$$
(19)
$$\begin{aligned} 8\pi p_t= & {} -\frac{\psi _{,t}}{r^2 \psi C^2_{1}}-\frac{\psi _{,t}^2}{2\psi ^2 r^2 C^2_{1}}-\frac{2\psi \psi _{,r}}{r C^2_{2}}+\frac{\psi ^2}{r^2C^2_{2}}\nonumber \\{} & {} -\frac{2}{r^2}-\frac{\psi _{,r}}{r\psi } \end{aligned}$$
(20)

The above system of non-linear differential equations have four dependent variables \(\rho \), \(p_r\), \(p_t\), and \(\psi \) and two independent variables r and t. As a result, we end up with three distinct equations, namely Eqs. (18)–(20), involving the four unknowns: \(\rho \), \(p_r\), \(p_t\), and \(\psi \). Therefore, we have four unknowns and three equations, so we will use the density profile for balancing the equations, which is given in [34] as

$$\begin{aligned} \rho =\frac{1}{8\pi }\Big (\frac{a}{r^2}+3b\Big ) \end{aligned}$$
(21)

Here, the constants a and b yield different star configurations. Therefore, by substituting Eq. (21) into Eq. (18), we get

$$\begin{aligned} 3\psi ^2-\psi ^3=2(1-a)C^2_{2}-2bC^2_{2}r^2+\frac{2C}{r} \end{aligned}$$
(22)

In Eq. (22) C is the integration constant, we get

$$\begin{aligned} \psi= & {} -1+\frac{3\times 2^{1/3}}{A}+\frac{A}{3\times 2^{1/3}} \end{aligned}$$
(23)

where

$$\begin{aligned} A= & {} \Bigg (-54+54C^2_{2}-54a C^2_{2}+\frac{54C}{r}-54b C^2_{2}r^2\nonumber \\{} & {} {+}\sqrt{{-}2916{+}\big ({-}54{+}54C^2_{2}{-}54a C^2_{2}{+}\frac{54C}{r}{-}54b C^2_{2}r^2}\big )^2\Bigg )^{1/3}\nonumber \\ \end{aligned}$$
(24)

4 Model’s exact analytical solution

The exact analytical solution can be obtained as

$$\begin{aligned} e^{\lambda }=\frac{C^2_{2}}{\Big ({-1+\frac{3\times 2^{1/3}}{A}+\frac{A}{3\times 2^{1/3}}}\Big )^2} \end{aligned}$$
(25)

The two pressure are obtained as

$$\begin{aligned} p_r= & {} \frac{3\big (-1+\frac{3\times 2^{1/3}}{A}+\frac{A}{3\times 2^{1/3}}\big )^2}{4\pi r^2C^2_{2}}-\frac{1}{8\pi r^2} \end{aligned}$$
(26)
$$\begin{aligned} p_t= & {} \frac{1}{8\pi }\left[ -\frac{2}{r^2}+\frac{\Bigg (\frac{2^{1/3}\big (\alpha +\frac{\alpha \beta }{\gamma }\big )}{\big (\beta +\gamma \big )^{4/3}}- \frac{\Big (\alpha +\frac{\alpha \beta }{\gamma }\Big )}{9\times 2^{1/3}\big (\beta +\gamma \big )^{2/3}}\Bigg )}{\Bigg (r\bigg (-1+\frac{3\times 2^{1/3}}{\big (\beta +\gamma \big )^{1/3}} +\frac{\big (\beta +\gamma \big )^{1/3}}{3\times 2^{1/3}}\bigg )\Bigg )}\right. \nonumber \\{} & {} \left. -\frac{2}{(C^2_{2})^2r}\Bigg (-\frac{2^{1/3}\big (\alpha +\frac{\alpha \beta }{\gamma }\big )}{\big (\beta +\gamma \big )^{4/3}}+ \frac{\Big (\alpha +\frac{\alpha \beta }{\gamma }\Big )}{9\times 2^{1/3}\big (\beta +\gamma \big )^{2/3}}\Bigg )\right. \nonumber \\{} & {} \left. \times \Bigg (-1+\frac{3\times 2^{1/3}}{\big (\beta +\gamma \big )^{1/3}}+\frac{\big (\beta +\gamma \big )^{1/3}}{3\times 2^{1/3}}\Bigg ) \right. \nonumber \\{} & {} \left. +\Bigg (-1+\frac{3\times 2^{1/3}}{\big (\beta +\gamma \big )^{1/3}}+\frac{\big (\beta +\gamma \big )^{1/3}}{3\times 2^{1/3}}\Bigg )\right] \end{aligned}$$
(27)

where \(\alpha =(\frac{-54C}{r^2}-108bC^2_{2}r)\), \(\beta =(-54+54C^2_{2}-54aC^2_{2}+\frac{54}{C}{r}-54bC^2_{2}r^2)\), and \(\gamma =\sqrt{-2916+\beta ^2}\).

5 Analysis of model

Now, we will proceed with a comparative investigation of the physical properties. Several approaches can be adopted for this purpose. However, in our current study, we will focus on two main aspects. Firstly and most importantly, we will evaluate the models’ stability in five dimensions. Second, to acquire more insights, we will examine variations in various physical parameters such as \(\rho \), \(p_r\), \(p_t\), \(\Delta \), conformal parameter, pressure gradient, and metric potential. The five dimensional TOV equation is defined as

$$\begin{aligned} -\frac{M_G(r)(\rho +p_r)}{r^2}e^{\frac{\nu -\mu }{2}}-\frac{dp_r}{dr}+\frac{2}{r}(p_t-p_r)=0. \end{aligned}$$
(28)

Here, the gravitational mass contained in a sphere of radius r is denoted by \(M_G(r)\), whose expression is as follows:

$$\begin{aligned} M_G(r)=\frac{1}{2}r^2(\nu _{,r}+\mu _{,r})e^{\frac{\mu -\nu }{2}} \end{aligned}$$
(29)

Substituting (29) into (28), we obtain

$$\begin{aligned} -\frac{(\nu _{,r}+\mu _{,r})}{2})(\rho +p_r)-\frac{dp_r}{dr}+\frac{2}{r}(p_t-p_r)=0. \end{aligned}$$
(30)

The aforementioned TOV equation can be expressed in the following way since it describes the equilibrium of the star configuration under the influence of the forces of gravity \(F_g\), hydrostatic force \(F_h\), and anisotropic stress \(F_a\):

$$\begin{aligned} F_g+F_h+F_a=0, \end{aligned}$$
(31)

where

$$\begin{aligned} F_g= & {} -\frac{(\nu _{,r}+\mu _{,r})}{2}(\rho +p_r), \end{aligned}$$
(32)
$$\begin{aligned} F_h= & {} -\frac{dp_r}{dr}, \end{aligned}$$
(33)
$$\begin{aligned} F_a= & {} \frac{2}{r}(p_t-p_r). \end{aligned}$$
(34)

5.1 Energy conditions

We now determine whether or not all of the energy conditions have been satisfied. We will take into account the following inequalities given in [45]:

  • Null energy conditions: \(\rho \ge 0,\)

  • Weak energy conditions: \(\rho +p_r\ge 0\), \(\rho +p_t\ge 0\),

  • Strong energy conditions: \(\rho +p_r+2p_t\ge 0\).

The model’s properties are depicted graphically in Figs. 1, 2, 3, 4, 5, 6, 7, 8 and 9.

Fig. 1
figure 1

Energy conditions for \(a=0.1\), \(a=0.2\), \(a=0.3\), \(b=0.03\), \(C=0.5\) and \(C_{2}=0.1\)

Full size image
Fig. 2
figure 2

The conformal factor \(\psi \) for \(b=0.03\), \(C=0.5\) and \(C_{2}=0.1\)

Full size image
Fig. 3
figure 3

Variation of metric coefficient \(e^\lambda \) for \(b=0.03\), \(C=0.5\) and \(C_{2}=0.1\)

Full size image
Fig. 4
figure 4

Anisotropy factor for \(b=0.03\), \(C=0.5\) and \(C_{2}=0.1\)

Full size image
Fig. 5
figure 5

Variation of radial pressure against for \(b=0.03\), \(C=0.5\) and \(C_{2}=0.1\)

Full size image
Fig. 6
figure 6

Variation of transverse pressure for \(b=0.03\), \(C=0.5\) and \(C_{2}=0.1\)

Full size image
Fig. 7
figure 7

Anisotropy force for \(b=0.03\), \(C=0.5\) and \(C_{2}=0.1\)

Full size image
Fig. 8
figure 8

The density profile \(\rho \) for \(b=0.03\)

Full size image
Fig. 9
figure 9

The three different forces and sum of forces for \(b=0.03\), \(C=0.5\) and \(C_{2}=0.1\)

Full size image

6 Discussion

In this work, we examined a novel framework for anisotropic stars that allow conformal motion in a dynamical spherical system with five dimensions. The EFEs are solved using this spacetime geometry by selecting a specific density distribution function. It is widely acknowledged that the density within a compact star can surpass nuclear density, potentially leading to the emergence of anisotropy within the star. To model a compact star effectively, featuring a substantially anisotropic matter distribution, a relativistic approach is required.

A spherically symmetric fluid distribution is envisioned for the anisotropic star. The fluid’s overall pressure is separated into two independent components here: radial pressure and transverse pressure. The difference between the two measures the surface tension of the star in relation to its core stiffness. Here, we have presented a novel analytical solutions characterising anisotropic stars that admit conformal motion. These are derived by using energy density.

These concise and well-defined solutions provide a valuable resource for developing into the physical dynamics of compact anisotropic celestial bodies. Investigating the behaviors of key physical attributes such as energy density, force parameter, the equilibrium of the stellar configuration of the star is crucial for attaining a stable solution and deeper comprehension. The behavior of the model’s parameters is shown in Figs. 1, 2, 3, 4, 5, 6, 7, 8 and 9.

  • The interior region of five-dimensional spacetime satisfies the energy conditions shown in Fig. 1.

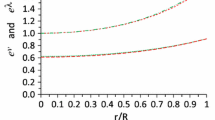
  • The plots in Figs. 2 and 3 depict conformal factor and metric potential variations.

  • If \(p_t>p_r\), or \(\Delta >0\), the anisotropy will be directed outward; otherwise, it will be directed inward when \(p_t<p_r\), or \(\Delta <0\). The \(\Delta >0\) implies a repulsive anisotropic force, whereas the curve in Figs. 4, 5 and 6 shows that \(\Delta <0\), i.e., \(p_t<p_r\) and anisotropic force, are attractive in nature.

  • The force caused by the star’s anisotropic nature is represented as \(\frac{\Delta }{r}\). If \(\frac{\Delta }{r}>0\), i.e., \(p_t>p_r\), this force will be repulsive; otherwise, it will be attractive. Figure 7 indicates that the force parameter’s behavior is attractive in nature.

  • The energy density has a positive characteristic as presented in Fig. 8 of the energy density depicts a stable configuration.

  • The three forces \(F_g\), \(F_h\), \(F_a\), which contributes towards stability of system from TOV equation and their sum \(F_g+F_h+F_a\) profiles for our chosen source are demonstrated in Fig. 9. Since the sum of pressure anisotropy, gravitational forces, and hydrostatic forces is zero, so system is in the state of equilibrium and TOV is satisfied.

On the basis of above discussion and the results presented here, leads us towards possible existence of compact stars in higher dimensions. With the incorporation of a specific density profile for higher-dimensional spacetime, the behavior of model parameters such as metric potential, conformal factor, pressure, anisotropy, and energy conditions is investigated. All of these parameters are well-behaved for the solution of higher dimensions. The chosen energy density distribution clearly demonstrates the presence of CO in higher dimensions. We can also employ alternative energy density profiles for the higher dimensions of spherically symmetric spacetime to investigate stellar structure.