$\nu$ Electroweak baryogenesis: the scalar singlet strikes back

Abstract

We perform a comprehensive scan of the parameter space of a general singlet scalar extension of the Standard Model to identify the regions which can lead to a strong first-order phase transition, as required by the electroweak baryogenesis mechanism. We find that taking into account bubble nucleation is a fundamental constraint on the parameter space and present a conservative and fast estimate for it so as to enable efficient parameter space scanning. The allowed regions turn out to be already significantly probed by constraints on the scalar mixing from Higgs signal strength measurements. We also consider the addition of new neutrino singlet fields with Yukawa couplings to both scalars and forming heavy (pseudo)-Dirac pairs, as in the linear or inverse Seesaw mechanisms for neutrino mass generation. We find that their inclusion does not alter the allowed parameter space from early universe phenomenology in a significant way. Conversely, there are allowed regions of the parameter space where the presence of the neutrino singlets would remarkably modify the collider phenomenology, yielding interesting new signatures in Higgs and singlet scalar decays.

1 Introduction

The origin of the observed Baryon Asymmetry of the Universe (BAU) is one of the fundamental open problems of the Standard Model (SM) of particle physics and one of the few precious pieces of experimental evidence for physics beyond the SM together with the existence of neutrino masses and dark matter. The generation of the BAU in the early Universe requires satisfying the three Sakharov conditions [1]: baryon number violation, C and CP violation, and departure from thermal equilibrium. In principle the SM itself could address the origin of the BAU via the electroweak baryogenesis (EWBG) mechanism [2,3,4,5,6,7]. However, the SM three-family quark mixing encoded in the Cabibbo–Kobayashi–Maskawa (CKM) matrix does not provide enough CP violation to generate a sufficient asymmetry [8,9,10], and the early Universe transition from the electroweak (EW) symmetric phase to the EW broken phase in the SM is a smooth crossover [11, 12], rather than the strongly first-order transition required by the out-of-equilibrium Sakharov condition.

Nevertheless, simple extensions of the SM could solve these issues and make EWBG viable. In particular, extending the scalar sector of the SM by just a real singlet field could allow for a first-order EW phase transition (see e.g. [13,14,15,16,17]). This new scalar singlet may not be alone, but rather be part of an extended dark sector to which it couples. A particularly motivated such scenario is the extension of the SM by (heavy) fermion singlets, i.e. right-handed neutrinos, able to account for the observed pattern of neutrino masses and mixings in Nature. Remarkably, it was shown in Refs. [18, 19] that the new sources of CP violation that arise in this extension of the SM, from the simultaneous presence of Yukawa interactions of the heavy neutrinos with the singlet scalar and with the Higgs doublet and SM neutrinos, could lead to successful EWBG depending on the evolution of the scalar sector during the phase transition (a scenario referred to as $\nu$-EWBG in [19]).

In this work we aim to clarify the conditions on the singlet scalar dynamics during the EW phase transition that possibly allows for EWBG in the above setup. Our scope is however more general, and we study the regions of parameter space of the real singlet scalar extension of the SM yielding a strong first-order phase transition (SFOPT), exploring the correlations among different model parameters, and emphasizing those that might arise between measurable quantities. The aim here is not a high-precision computation of the various thermodynamic quantities of the phase transition, which would be numerically challenging if combined with a thorough scan of the model parameter space. Rather, we focus on exploring the parameter space as efficiently as possible, covering broad areas of the multidimensional space via a number of approximations. Even if these approximations are not suitable to obtain highly-accurate results for the SFOPT quantities, they allow to pinpoint the regions of the parameter space with the desired features and test whether they are presently allowed, for subsequent analyses to concentrate in these regions. We pay particular attention to the SFOPT requirement of bubble nucleation for a successful completion of the EW phase transition, for which we provide conservative and fast estimate for assessing if nucleation would take place. While the nucleation dynamics has been studied previously [20] in the context of a ${\mathbb {Z}}_2$-symmetric singlet scalar extension of the SM, here we aim at a more general study without the additional constraint of additional symmetries. To the best of our knowledge, this is the first full scan exploring all the different correlations of the parameter space of the scalar singlet extension of the SM aiming to identify the regions where a SFOPT could take place. In addition, we investigate the impact of the heavy neutrinos on the SFOPT dynamics: while previous studies indicate that sizable values of the neutrino Yukawa interactions with the scalar singlet can strengthen the first-order phase transition [21], we find that large values of the neutrino Yukawas, unless compensated by other parameters, can also have the effect of destabilizing the EW broken minimum and are thus generally disfavoured. However, their inclusion does not alter significantly the allowed regions of the parameter space as compared to the singlet-only case.

Finally, we also discuss the phenomenological impact of the existence of such heavy neutrinos as compared to the minimal singlet scalar extension of the SM, finding that the phenomenology can be altered dramatically with respect to the latter model. Specifically, we find that the singlet-like scalar will dominantly decay into right-handed neutrinos (if allowed by phase space), instead of directly decaying into SM particles. These heavy neutrinos may then subsequently decay into SM particles either promptly or via displaced vertexes, depending on the size of their mixing $\theta$ with the active SM neutrinos. Since the production of the right-handed neutrinos from the scalar singlet decay is unrelated to the strongly constrained mixing $\theta$, this heavy neutrino production process could well be the dominant one at colliders like the LHC. Besides, the mixing between the scalar singlet and the Higgs would also lead to exotic Higgs decays into right-handed neutrinos (if these are light enough), which can be probed via Higgs signal strength measurements and also in direct searches for such exotic Higgs decays (see e.g. [22]) at the LHC.

This paper is organized as follows. In Sect. 2 we introduce the real singlet scalar extension of the SM with the addition of heavy neutrinos, and discuss the details of the scalar potential in the early Universe relevant for our SFOPT analysis. Then, in Sect. 3 we analyze the experimental constraints on the model, as well as the possible new combined probes of the existence of the singlet and the heavy neutrinos. In Sect. 4 we give details of our model parameter scan, and we discuss its results in Sect. 5. We finally conclude in Sect. 6.

2 The scalar singlet extension of the SM with heavy neutrinos

The simplest extension of the SM scalar sector is the inclusion of a real scalar singlet s that may mix with the Higgs boson. This small addition to the SM may however significantly alter the scalar sector phenomenology. In particular, it can allow for a SFOPT even at tree-level [13, 15], re-opening the possibility of explaining the origin of the observed matter–antimatter asymmetry of the Universe in the context of EWBG if new sources of CP violation beyond the SM are also present.

More interestingly, the scalar singlet field s could be a window to a dark sector capable of addressing some of the other open problems of the SM. Indeed, given its singlet nature, renormalizable (and therefore less suppressed) couplings are expected between the scalar and both the SM and the extended dark sector. Such scenarios could for example account for the observed dark matter of the Universe [23] (see also [24,25,26,27,28,29,30,31]) or the simultaneous origin of neutrino masses and the BAU [18, 19]. Motivated by the latter, but easily generalizable, in this work we will consider a dark sector that comprises the real scalar field s and n new Dirac neutrinos, $N'=(N'_{L}, N'_{R})$, singlets under the SM gauge group and with lepton number $+1$. In order to have an accessible extended neutrino sector with masses around the EW scale that may play a non-trivial role in the SFOPT and the baryogenesis process, we consider low-scale realizations of the Seesaw mechanism [32,33,34,35] with an approximate lepton number conservation so as to protect and ensure the lightness of neutrino masses [36,37,38]. Indeed in the so-called inverse [39, 40] or linear [41, 42] Seesaw mechanisms the new heavy neutrinos arrange in Dirac pairs while the SM neutrinos remain massless if the lepton number symmetry is exact. Upon softly breaking this symmetry, the SM neutrinos will acquire small masses and the mass degeneracy of the two members of each Dirac pair will be slightly broken [43]. Neglecting the small lepton-number-violating terms (which are suppressed by the tiny SM neutrino masses), the most general lepton-number-conserving interaction Lagrangian among the dark sector fields s, $N'$ and the SM fields is:

$$\begin{aligned} {\mathcal {L}}&\supset \left( -\overline{L_L}{\tilde{\Phi }}Y_{\nu }N'_R-\overline{N'_L}\,s Y_N N'_R+h.c.\right) \nonumber \\&\quad +V\left( \Phi ^{\dagger }\Phi ,s\right) , \end{aligned}$$

(2.1)

where $\Phi$ is the $SU(2)_L$ doublet Higgs field, ${\tilde{\Phi }} = i\sigma _{2} \Phi ^{*}$, $L_L$ is the $SU(2)_L$ lepton doublet and $Y_{\nu }$ and $Y_{N}$ are general $3\times n$ and $n\times n$ Yukawa matrices, respectively. Without loss of generality we will work in the basis where $Y_N$ is diagonal.

The most general Lagrangian scalar potential for the Higgs doublet $\Phi$ and the singlet scalar s is given by (see e.g. [15])

$$\begin{aligned} V\left( \Phi ^{\dagger }\Phi ,s\right)= & {} -{\tilde{\mu }}_h^2 \Phi ^{\dagger }\Phi +\lambda _h (\Phi ^{\dagger }\Phi )^2\nonumber \\{} & {} +\frac{1}{2}{\tilde{\mu }}_s^2 s^2+ \frac{1}{4}\lambda _s s^4\nonumber \\{} & {} + \frac{1}{2} \mu _m s \Phi ^{\dagger }\Phi +\frac{1}{2} \lambda _m s^2 \Phi ^{\dagger }\Phi \nonumber \\{} & {} +{\tilde{\mu }}_1^3 s+\frac{1}{3}\mu _3 s^3. \end{aligned}$$

(2.2)

By writing $\Phi = (h^{+}, (h + i \chi )/\sqrt{2})$, the scalar potential for the neutral fields h and s, relevant for EW symmetry breaking, is found to be

$$\begin{aligned} V (h,s)&= -\frac{1}{2} {\tilde{\mu }}_h^2 h^{2} +\frac{1}{4} \lambda _h h^{4}+\frac{1}{2}{\tilde{\mu }}_s^2 s^{2}+\frac{1}{4}\lambda _s s^{4}\nonumber \\&\quad + \frac{1}{4} \mu _m s h^{2}+\frac{1}{4} \lambda _m s^2 h^{2}+{\tilde{\mu }}_1^3 s+\frac{1}{3}\mu _3 s^3\, . \end{aligned}$$

(2.3)

In the rest of this work, we will denote the (zero-temperature) vacuum expectation values (vevs) of the Higgs and singlet fields stemming from the potential (2.3) by $v_{EW}$ and $\omega _{EW}$, respectively. We note that all parameters from V(h, s) are real, which means that the only sources of CP violation beyond the SM would arise from the Yukawa couplings in Eq. (2.1), in the absence of further new physics contributions.

In general, to study the early Universe dynamics of the scalar sector and the possibility to have a SFOPT, zero-temperature loop corrections (at 1-loop, this corresponds to the so-called Coleman–Weinberg contribution [44]) as well as finite-temperature contributions to the scalar potential [45, 46], should be taken into account. These corrections, however, introduce gauge dependence [47] and renormalization scale dependence in the effective potential of the theory, leading to important theoretical uncertainties [48, 49].¹ Nevertheless, the scalar potential of the singlet scalar extension of the SM may already lead to the generation of a tree-level barrier between the EW symmetric and broken minima [15] and, in such a case, an analysis based on the tree-level potential (2.3) supplemented by the leading ($\sim T^2$) thermal corrections in a high-temperature approximation, which do not depend on the choice of the gauge, captures the most relevant features needed for the study of the SFOPT. At the same time, working at this level of approximation allows to study the relevant features of the phase transition analytically, as advocated in Ref. [15]. This is very advantageous in order to efficiently scan the parameter space of the model. We have verified the generic validity of this approximation concerning the results of our global parameter scan, as we discuss in more detail in Sect. 4. The finite-temperature effective potential $V_T$ can in this case be written as:

$$\begin{aligned} V_T\left( h, s,T\right)= & {} -\frac{1}{2}\mu _h^2 h^2+\frac{1}{4}\lambda _h h^4+\frac{1}{2}\mu _s^2 s^2+\frac{1}{4}\lambda _s s^4 \nonumber \\{} & {} + \frac{1}{4}\mu _m s h^2+\frac{1}{4}\lambda _m s^2 h^2 +\mu _1^3 s +\frac{1}{3}\mu _3 s^3\nonumber \\{} & {} +\left[ \frac{1}{2}c_h h^2+\frac{1}{2}c_s s^2+m_3 s\right] (T^2-T_c^2). \nonumber \\ \end{aligned}$$

(2.4)

The explicit appearance as a free parameter in Eq. (2.4) of the critical temperature $T_c$, at which the EW symmetric and broken minima are degenerate in energy, proves very convenient in a scan of the model parameter space requiring the presence of a SFOPT. Indeed, when imposing that at $T=T_c$ the two minima are degenerate, an analytical condition among the other potential parameters in Eq. (2.4) is obtained, effectively trading its freedom for $T_c$ and allowing to explore only potentials for which the two-degenerate-minima condition is fulfilled (see Appendix A for details). The parameters in Eq. (2.4), defined at $T=T_c$, are related to those of Eq. (2.3), defined at $T=0$, by ${\tilde{\mu }}_{h}^{2} \equiv \mu _{h}^{2} + c_{h}T_{c}^{2}$, ${\tilde{\mu }}_{s}^{2} \equiv \mu _{s}^{2} - c_{s} T_{c}^{2}$, and ${\tilde{\mu }}_{1}^{3} \equiv \mu _{1}^{3} - m_{3} T_{c}^{2}$. The constants $c_h$, $c_s$ and $m_3$ are given by

$$\begin{aligned} c_h= & {} \frac{1}{48}\left[ 9g^2+3g^{\prime 2}+2(6 Y_t^2+12\lambda _h+\lambda _m+2 {\mathcal {Y}}_{\nu }^2)\right] ,\nonumber \\ c_s= & {} \frac{1}{12}\left[ 2\lambda _m+3\lambda _s+2{\mathcal {Y}}_{N}^2\right] , \nonumber \\ m_3= & {} \frac{1}{12}\left[ \mu _3+\mu _m\right] , \end{aligned}$$

(2.5)

where g and $g'$ are respectively the $SU(2)_L$ and $U(1)_Y$ gauge couplings, $Y_t$ is the top Yukawa coupling, and ${\mathcal {Y}}_{\nu }^{2}$, ${\mathcal {Y}}_{N}^{2}$ are defined as ${\mathcal {Y}}_{\nu }^2\equiv \textrm{tr}\left( Y_{\nu }^{\dagger }Y_{\nu }\right)$, ${\mathcal {Y}}_{N}^2\equiv \textrm{tr}\left( Y_{N}^{\dagger }Y_{N}\right)$.

For the study of the temperature evolution of the scalar potential minima and the SFOPT, it is also convenient to rewrite the potential $V_T$ from Eq. (2.4) in terms of the temperature-dependent vevs $v_T\equiv \langle h\rangle (T)$ and $\omega _T\equiv \langle s \rangle (T)$ in the broken minimum as [15]

$$\begin{aligned} V_T\left( h,s,T\right)= & {} \frac{m_h^2}{8v_T^2}\left( h^2-v_T^2\right) ^2\nonumber \\{} & {} +\frac{m_{sh}^2}{2v_T}\left( h^2-v_T^2\right) \left( s-\omega _T\right) \nonumber \\{} & {} +\frac{1}{4}\left[ 2m_s^2+\lambda _m\left( h^2-v_T^2\right) \right] \left( s-\omega _T\right) ^2\nonumber \\{} & {} +\frac{v_T}{2m_h^2}\left( \lambda _m m_{sh}^2+4m_{*}\right) \left( s-\omega _T\right) ^3\nonumber \\{} & {} +\frac{v_T^2}{8m_h^2} \left( 4\lambda ^2+\lambda _m^2\right) \left( s-\omega _T\right) ^4, \end{aligned}$$

(2.6)

where all dimensionful parameters have an implicit dependence on the temperature T. The mass parameters $m_{h}^{2}$, $m_{s}^{2}$, and $m_{sh}^{2}$ are defined as

$$\begin{aligned} m_h^2\equiv & {} \frac{\partial ^2V}{\partial h\partial h} \Biggl |_{\left( v_T,\omega _T\right) }, \quad m_s^2\equiv \frac{\partial ^2V}{\partial s\partial s}\Biggl |_{\left( v_T,\omega _T\right) },\nonumber \\ m_{sh}^2\equiv & {} \frac{\partial ^2V}{\partial h\partial s} \Biggl |_{\left( v_T,\omega _T\right) }, \end{aligned}$$

(2.7)

evaluated at the EW broken minimum at T. The effective coupling $\lambda ^2$ and mass $m_{*}$ in Eq. (2.6) are defined as

$$\begin{aligned} \lambda ^2\equiv & {} \lambda _h \lambda _s-\frac{1}{4}\lambda _m^2, \quad m_{*}\equiv \lambda ^2\omega _T\nonumber \\{} & {} +\frac{1}{3}\lambda _h \mu _3-\frac{1}{8}\lambda _m\mu _m. \end{aligned}$$

(2.8)

Furthermore, in the parameter scans in Sect. 4 we will eventually trade $m_{sh}^2$ for the quantity $\omega _p$, defined as

$$\begin{aligned} \omega _p\equiv \omega _T-\frac{m_{sh}^2}{\lambda _m v_T} = \frac{-\mu _m}{2 \lambda _m}, \end{aligned}$$

(2.9)

which has the advantage of being temperature-independent. The parametrization (2.6) explicitly shows that a shift in the field $s\rightarrow s+\sigma$ keeps the finite-temperature scalar potential $V_T$ invariant with a redefinition of $\omega _T\rightarrow \omega _T+\sigma$. The relations between the new parameters in Eq. (2.6) and the coefficients in Eq. (2.3) are found in Ref. [15].

The starting point of our analysis of SFOPT scenarios is the finite-temperature potential $V_T$ from Eq. (2.4) at $T = T_c$, with two degenerate minima located in general at $(0, \omega _{0})$ and $(v, \omega ) \equiv (v_{T_c}, \omega _{T_c})$ in the two-dimensional field space. We will require that both the Higgs and the singlet field acquire a vev in the EW broken phase, in order to generate masses for the heavy neutrinos after the phase transition. Furthermore, in Ref. [19] it was shown that successful baryogenesis in the present scenario favours the heavy neutrinos to be approximately massless at the onset of the SFOPT. We will thus make use of the shift symmetry of the potential via $\omega _T\rightarrow \omega _T+\sigma$ discussed above to set $\omega _0=0$ at the critical temperature $T_c$ (this corresponds to setting $\mu _1 = 0$ in Eq. (2.4)), and mainly focus on phase transitions from $(\langle h \rangle , \langle s \rangle ) = (0,\,0)\rightarrow (v,\,\omega )$. For studies on other phase transition scenarios in the singlet scalar extension of the SM, we refer the reader to Refs. [17, 20, 49, 55,56,57,58,59,60,61,62,63]. Following [15], we can use Eq. (2.6) to conveniently parametrize the finite-temperature potential at the critical temperature as

$$\begin{aligned} V_T(h,s,T_c)&= \frac{v^{2} m_{h}^{2}}{8}\Biggl \lbrace \left( \frac{h^2}{v^2} - 1\right) ^{2}+\left( \frac{s}{\omega } -1\right) ^{3} \left( 1 + \frac{3 s}{\omega }\right) \nonumber \\&\quad +2 \frac{\lambda _{m} \omega ^2}{m_h^2}\left( \frac{s}{\omega } - 1\right) ^{2} \left( \frac{h^2}{v^2} - \frac{s^2}{\omega ^2}\right) \nonumber \\&\quad +\frac{4 m_s^2}{ m_h^2} \frac{s^2}{v^2} \left( \frac{s}{\omega }-1\right) ^{2} + \frac{4 m_{sh}^2\omega }{ m_h^2 v}\left( \frac{s}{\omega } - 1\right) \nonumber \\&\quad \times \left[ \frac{h^2}{v^2} + \frac{s^2}{\omega ^2} \left( \frac{2 s}{\omega } - 3\right) \right] \Biggr \rbrace . \end{aligned}$$

(2.10)

The set of parameters of Eq. (2.4) at $T = T_{c}$ can be recovered from the new parametrization given in Eq. (2.10) (together with $\mu _1 = 0$) via the following relations²:

$$\begin{aligned} \mu _{h}^{2}&= \frac{1}{2} \left( m_{h}^{2} - \lambda _{m} \omega ^2 + 2 \frac{\omega m^2_{sh}}{v} \right) , \end{aligned}$$

(2.11)

$$\begin{aligned} \lambda _{h}&= \frac{1}{2} \frac{m_{h}^{2}}{v^{2}}, \end{aligned}$$

(2.12)

$$\begin{aligned} \mu _{s}^{2}&= \frac{1}{2} \frac{ v^{2}}{\omega ^{2}} \left( 3 m_{h}^{2} - \lambda _{m} \omega ^2 + 2 \frac{\omega ^2 m^2_s}{v^2} + 6 \frac{\omega m^2_{sh}}{v} \right) , \end{aligned}$$

(2.13)

$$\begin{aligned} \lambda _{s}&= \frac{1}{2} \frac{v^{2}}{\omega ^{4}} \left( 3 m_{h}^{2} -2 \lambda _{m} \omega ^2 + 4 \frac{\omega ^2 m^2_s}{v^2} + 8 \frac{\omega m^2_{sh}}{v} \right) , \end{aligned}$$

(2.14)

$$\begin{aligned} \mu _{m}&= -2 \left( \omega \lambda _{m} - \frac{m_{sh}^2}{v} \right) , \end{aligned}$$

(2.15)

$$\begin{aligned} \mu _{3}&= - \frac{3}{2} \frac{ v^{2}}{\omega ^{3}} \left( 2 m_{h}^{2} - \lambda _{m} \omega ^2 + 2 \frac{\omega ^2 m^2_s}{v^2} + 5 \frac{\omega m^2_{sh}}{v} \right) \, . \end{aligned}$$

(2.16)

Then, the set of parameters $\{\omega ,\omega _{p},v,m_{h}^{2}, m_{s}^{2}, \lambda _{m} \}$ evaluated at $T = T_c$ is enough to fully characterize the scalar potential with two degenerate minima at (0, 0) and $(v,\omega )$.³ Together with $T_{c}$, this set of parameters allows us to specify the finite-temperature potential as a function of T in the singlet scalar extension of the SM, in the high-T approximation. When considering the addition of extra heavy Dirac neutrinos, we also need to add ${\mathcal {Y}}_{\nu }$ and ${\mathcal {Y}}_{N}$ as free parameters in our analysis, since they appear in the thermal corrections of the potential $V_T$, see Eq. (2.5).

Fig. 1

Shape of the scalar potential for the example point in parameter space specified in Table 1 at the critical temperature $T_c$ (left panel) and at $T=0$ (right panel). The color bar denotes the value of the scalar potential, $V_T$. The purple diamonds denote the location of the minima, which are degenerate at $T_c$. The red dot denotes the location of the saddle point, which is close to the field trajectory for bubble nucleation (the bounce solution) at the nucleation temperature $T_N$ (see Sect. 4 for details)

Table 1 Parameter set at $T=0$ corresponding to the scalar potential shown in Fig. 1. This parameter set gives rise to a SFOPT with successful nucleation and satisfying all the bounds from Higgs phenomenology, including those on the scalar mixing (see Sect. 3 for details)

Figure 1 illustrates an example of the type of scalar potentials that would lead to a SFOPT with the characteristics described above, with the specific values of the corresponding potential parameter set at $T=0$ given in Table 1. In the left panel of Fig. 1, the potential $V_T(h,s,T)$ is shown at $T = T_c$ with the two degenerate minima, represented by the purple diamonds. The red dot indicates the location of the saddle point yielding a potential barrier between both minima. In the right panel we show the potential at $T=0$ where the EW breaking minimum ($v_{EW},\omega _{EW}$) is now the true vacuum and also the real singlet has an ${\mathcal {O}}(100\,\,\textrm{GeV})$ vev that generates EW-scale masses for the heavy neutrinos.

In general, the potential $V_T$ from Eq. (2.10) characterized by a random set of parameters $\{\omega ,\omega _{p},v,m_{h}^{2}, m_{s}^{2}, \lambda _{m} \}$ at $T_c$ satisfying the conditions in Appendix A from Ref. [15], despite satisfying the desired property of featuring two degenerate minima at (0, 0) and ($v,\omega$), will not reproduce the correct value for the EW symmetry breaking vev at $T=0$, $v_{EW} =246.22$ GeV, obtained from the measurement of the Fermi constant via the muon decay width [64]. In addition, upon diagonalization of the scalar mass matrix at $T = 0$,

$$\begin{aligned} {\mathcal {M}}^{0}_{s}=\begin{pmatrix} m_h^2 &{}\quad m_{sh}^2\\ m_{sh}^2 &{}\quad m_s^2 \end{pmatrix}\Bigg |_{T=0}, \end{aligned}$$

(2.17)

with $m_h^2$, $m_s^2$ and $m_{sh}^2$ defined in Eq. (2.7) and evaluated in the $T = 0$ EW broken minimum $\left( v_{EW},\,\omega _{EW}\right)$, the eigenvalue $M_H$ for the mostly-doublet mass eigenstate will generally not reproduce the measured value for the Higgs boson mass $M_{H}=125.10$ GeV. Satisfying these two physical requirements at $T=0$ is rather non-trivial in our setup, and considerably reduces the allowed parameter space: given the high accuracy of the $v_{EW}$ and $M_H$ measurements, two combinations of the free parameters in the scalar potential are effectively determined. In Sect. 4 we will discuss how these requirements are implemented in our numerical scan of the parameter space of the model.

Finally, we also need to consider the existing constraints on the mixing $\xi$ between the Higgs doublet and the scalar singlet, arising from the diagonalisation of the $T = 0$ scalar mass matrix, ${\mathcal {M}}^0_{s}$. We have

$$\begin{aligned} \begin{aligned} h&= v_{EW}+\cos {\xi }\, H +\sin {\xi }\, S,\\ s&= \omega _{EW}-\sin {\xi } \, H +\cos {\xi }\, S, \end{aligned} \end{aligned}$$

(2.18)

where S (H) is the mass eigenstate corresponding to the mostly-singlet (doublet) scalar combination with a mass $M_S$ ($M_H = 125.10$ GeV). In the next section we will discuss the present experimental constraints on the ($T=0$) model parameters, affecting in particular the possible allowed values of the mixing $\xi$, which will also be applied to our parameter scan in Sect. 4.

3 Experimental constraints and phenomenological probes

In this section we discuss the relevant experimental limits on the singlet scalar extension of the SM, making emphasis on how the possible presence of the extra heavy singlet neutrinos can affect them. These experimental constraints will translate into bounds on the parameters of the potential from Eq. (2.4) at $T = 0$. We also discuss the main phenomenological probes of the model, particularly in connection with both the structure of the scalar potential and the presence of the heavy neutrinos in comparison with the minimal singlet scalar extension of the SM.

3.1 SM-heavy neutrino mixing

The new Dirac neutrinos with components $N'_R$ and $N'_L$ introduced in Eq. (2.1) mix with the SM neutrinos after spontaneous symmetry breaking (SSB) and may participate in the generation of light neutrino masses. The mixing matrix between the SM active and the heavy sterile neutrinos is given by

$$\begin{aligned} \theta \equiv \frac{v_{EW}}{\sqrt{2}\,\omega _{EW}}Y_{\nu }Y_N^{-1}, \end{aligned}$$

(3.1)

with the Yukawa matrices $Y_N$ and $Y_\nu$ for singlet and SM neutrinos (see Eq. (2.1) for details), respectively. Thus, neglecting all small L-violating parameters that would eventually lead to the generation of the masses of the mostly SM-like light neutrinos, the heavy neutrinos have Dirac masses $M_{N_i}\simeq \omega _{EW} Y_{Ni}$ and the two chiralities of the mass eigenstates $N_i$ are given by

$$\begin{aligned} N_R = N'_R, \quad N_L \simeq N'_L - \theta ^\dagger \nu _L. \end{aligned}$$

(3.2)

For sterile neutrinos with masses $M_{N_i} > M_W$, the active-sterile neutrino mixing is bounded from above by a combination of EW precision tests⁴ and flavour observables [67, 68]

$$\begin{aligned} \textrm{tr}\left( \theta \theta ^{\dagger }\right) < 0.0048 \quad (2 \sigma ). \end{aligned}$$

(3.3)

For lighter sterile neutrinos ($M_{N_i} < M_W$), direct searches at colliders and beam dump experiments as well as searches for peaks and distortions in the decay products of mesons, leptons and beta decays set much more stringent constraints on the active-sterile neutrino mixing, and we refer the reader to Refs. [69, 70] for a comprehensive list of these limits.

The bound (3.3) will be used as a $\chi ^2$ contribution added to the weight function that we construct to guide our scan of the parameter space (see Appendix A). To constrain ${\mathcal {Y}}^2_{\nu } = \textrm{tr}\left( Y_{\nu }^{\dagger }Y_{\nu }\right)$ in our parameter scan, we use that

$$\begin{aligned} \textrm{tr}\left( \theta \theta ^{\dagger }\right) \le \frac{v_{EW}^2}{2\,\omega _{EW}^2}{\mathcal {Y}}_{\nu }^2\,\textrm{tr}\left( Y_N^{-2}\right) , \end{aligned}$$

(3.4)

since $\textrm{tr}\left( A B\right) \le \textrm{tr}\left( A\right) \textrm{tr}\left( B\right)$. Thus, when imposing the present bound on $\textrm{tr}\left( \theta \theta ^{\dagger }\right)$ to the right-hand side of Eq (3.4), a conservative bound is implemented since $\textrm{tr}\left( \theta \theta ^{\dagger }\right)$ will always be smaller than this quantity. In practice, because we only have access to ${\mathcal {Y}}_N$ and not the individual values of the Yukawas, when constraining ${\mathcal {Y}}_\nu$ we assume a degenerate spectrum such that $\textrm{tr}\left( Y_N^{-2}\right) =n^2{\mathcal {Y}}_N^{-2}$. Any other choice would translate into smaller values for ${\mathcal {Y}}_\nu$.

3.2 LHC Higgs signal strengths

The latest measurements of the 125 GeV Higgs boson signal strength by the ATLAS [71] and CMS [72] collaborations provide an important constraint on deviations of Higgs couplings from their SM values. In the singlet scalar extension of the SM, all SM couplings to the Higgs-like mass eigenstate H become rescaled relative to the SM values by $\cos {\xi }$, which, in the absence of exotic Higgs decays (see discussion below), yields an overall suppression of Higgs signal strength given by

$$\begin{aligned} \mu \equiv \frac{\sigma \cdot BR}{\left( \sigma \cdot BR\right) _{SM}}=\cos ^2{\xi }. \end{aligned}$$

(3.5)

This allows to constrain the singlet-doublet scalar mixing via Higgs measurements (see [73,74,75,76]). We use the latest measurements of the Higgs signal strength from ATLAS, $\mu = 1.05 \pm 0.06$ [77] and CMS, $\mu = 1.002 \pm 0.057$ [78], and combine them to derive a bound on $\cos {\xi }$ following the Feldman–Cousins [79] prescription.⁵ We find $\mu \ge 0.94$ at the $95\%$ C.L. which translates into $\left| \sin {\xi }\right| < 0.245$, as shown in Fig. 2. This is in fairly good agreement with other recent analyses (see e.g. [76]) where Feldman–Cousins is however not applied in general.

Fig. 2

Existing 95% C.L. constraints on the singlet-doublet scalar mixing $\sin {\xi }$ as a function of $M_S$ from EWPO (solid green), from LHC Higgs signal strength measurements (red) with $\textrm{BR}_{H \rightarrow \textrm{BSM}} \equiv \textrm{BR}_X = 0$ (solid) and $\textrm{BR}_X = 0.04$ (dash-dotted), from direct searches for $p p \rightarrow S \rightarrow Z Z$ by ATLAS [83] (ocher), with $\textrm{BR}_{S\rightarrow H H} + \textrm{BR}_{S\rightarrow \textrm{BSM}} \equiv \textrm{BR}_{H+X} = 0$ (dashed) and $\textrm{BR}_{H+X} = 0.9$ (dash-dotted), and from LEP searches for light scalars (blue) respectively assuming $\textrm{BR}_{S \rightarrow \textrm{BSM}} \equiv \textrm{BR}_{X} = 0$ (dashed), $\textrm{BR}_{X} = 0.9$ with visible BSM decays (dash-dotted) and $\textrm{BR}_{X} = 0.9$ with invisible BSM decays (dotted)

In the presence of an exotic Higgs branching fraction into beyond-the-SM (BSM) states $\textrm{BR}_{H\rightarrow \textrm{BSM}}$, the Higgs signal strength modifier $\mu$ in Eq. (3.5) becomes

$$\begin{aligned} \mu = \Bigl (1 - \textrm{BR}_{H\rightarrow \textrm{BSM}} \Bigr ) \cos ^2{\xi } \end{aligned}$$

(3.6)

since $\cos {\xi }$ and $\textrm{BR}_{H\rightarrow \textrm{BSM}}$ now yield a combined dilution of the global Higgs signal strength with respect to the SM. Thus, the presence of exotic Higgs decays yield a tighter bound on $\cos ^2{\xi }$ from Higgs signal strengths, as shown in Fig. 2 for the specific value $\textrm{BR}_{H\rightarrow \textrm{BSM}} \equiv \textrm{BR}_X = 0.04$⁶. In particular, the interactions in Eq. (2.1) between the Higgs boson H and the extra heavy neutrino states $N_i$ could lead to $H\rightarrow N_i{\bar{N}}_i$ if $M_{N_i}<M_{H}/2$, with the heavy neutrino masses $M_{N_i} \simeq Y_{N_i}\,\omega _{EW}$. This occurs via $Y_{N}$ in Eq. (2.1), through the singlet-doublet scalar mixing, or via $Y_{\nu }$, through the active-sterile neutrino mixing. In addition, the interaction $Y_{\nu }$ may also mediate $H \rightarrow \nu {\bar{N}}_i, \, {\bar{\nu }} N_i$ decays [80, 81]. Since the singlet-doublet scalar mixing is much more weakly constrained than the active-sterile neutrino mixing, the leading interaction (assuming $\theta ^2 \ll \sin ^2{\xi }$) after EW symmetry breaking between the scalar states and the $N_i$ ($i = 1,\ldots , n$), which is induced by the Lagrangian from Eq. (2.1), would be

$$\begin{aligned} {\mathcal {L}} \supset \frac{1}{\omega _{EW}} (\cos {\xi }\, S - \sin {\xi }\, H )\sum _i {\bar{N}}_i M_{N_i} N_i. \end{aligned}$$

(3.7)

The $H\rightarrow N_i{\bar{N}}_i$ decay channel is then driven by the scalar mixing, $\Gamma _{H \rightarrow N_i {\bar{N}}_i} \propto \sin ^2{\xi }$, while in minimal seesaw scenarios the heavy neutrinos are produced via mixing with the SM neutrinos, leading to $\Gamma _{H \rightarrow N_i {\bar{N}}_i} \propto \theta ^4$ and $\Gamma _{H \rightarrow \nu N_i} \propto \theta ^2$. In our scenario these generally correspond to subleading effects (the corrections for both H and S interactions in Eq. (3.7) are ${\mathcal {O}}(\theta ^2)$), and we concentrate in the following on the leading interaction from Eq. (3.7).

The decay $H\rightarrow N_i {\bar{N}}_i$ can have a significant impact on the LHC bounds on the Higgs signal strength. From the latest $\mu$ measurements performed by ATLAS [77] and CMS [78] and discussed above, we set the bound⁷

$$\begin{aligned} \left( 1- \sum _{i} \textrm{BR}_{H\rightarrow N_i{\bar{N}}_i} \right) \cos ^2\xi \ge 0.94. \end{aligned}$$

(3.8)

The total rate of the Higgs-like boson with a mass of 125 GeV decaying into $N_i$ states is given by

$$\begin{aligned} \Gamma _{H\rightarrow N{\bar{N}}}\equiv & {} \sum _{i=1}^{k} \Gamma _{H\rightarrow N_{i}{\bar{N}}_{i}} \simeq \frac{\sin ^2{\xi }}{8\pi }M_{H} \nonumber \\{} & {} \times \sum _{i=1}^{k} Y_{N_i}^2\left( 1-\frac{4\,\omega ^2_{EW}}{M^2_{H}}Y_{N_i}^2\right) ^{3/2}, \end{aligned}$$

(3.9)

where $k \le n$ is the number of kinematically accessible heavy neutrinos. The maximum possible value of $\Gamma _{H\rightarrow N{\bar{N}}}$ (occurring for $k=n$) is given by

$$\begin{aligned} \Gamma _{\text {max}}= & {} n\,\frac{\sin ^{2}\xi }{80\, \pi } \left( \frac{3}{5}\right) ^{3/2} \frac{M_{H}^{3}}{\omega _{EW}^{2}} \simeq 10^{-2}\,\textrm{GeV} \nonumber \\{} & {} \times \left( \frac{n}{3}\right) \, \left( \frac{\sin ^2{\xi }}{0.05}\right) \,\left( \frac{200\,\textrm{GeV}}{\omega _{EW}}\right) ^2, \end{aligned}$$

(3.10)

which is achieved for $Y_{N_i}^2=M_H^2/(10\,\omega _{EW}^2)$ with $i=1, 2,\ldots n$, and may well be comparable to the SM Higgs boson total width $\Gamma _{\textrm{SM}} = 0.00412$ GeV [82] if the mixing $\sin {\xi }$ is not too suppressed. For a given value of ${\mathcal {Y}}^2_{N} = \sum _{i=1}^{n} Y_{N_i}^2$, which is the relevant combination of neutrino Yukawa couplings affecting the thermal history of the scalar sector, the following two “Cases” are possible:

• 1. ${\varvec{{\mathcal {Y}}_N^2\, \omega _{EW}^2 < (M_H/2)^2}}$: Then all neutrinos are kinematically accessible and $k = n$ in Eq. (3.9) so that the 125 GeV Higgs boson decays into all n heavy neutrinos. For a fixed ${\mathcal {Y}}^2_{N}$ the maximum value of $\Gamma _{H\rightarrow N{\bar{N}}}$ is achieved when all Yukawa couplings are equal ($Y_{N_i}^2={\mathcal {Y}}_N^2/n$ with $i=1, 2,\ldots n$), while the minimum value is obtained when the rate is dominated by a single heavy neutrino contribution ($Y_{N_1}^2\approx {\mathcal {Y}}_N^2 \gg Y_{N_i}^2$ with $i=2,\ldots n$).

• 2. ${\varvec{{\mathcal {Y}}_N^2\, \omega _{EW}^2 > (M_H/2)^2}}$: The decay of the 125 GeV Higgs boson into at least one heavy neutrino may be kinematically forbidden.⁸ Therefore, for a given value of ${\mathcal {Y}}_N^2$, the decay rate can be arbitrarily suppressed depending on the value of the individual Yukawas $Y_{N_i}$ (e.g. in the limit $Y_{N_1}^2 \rightarrow {\mathcal {Y}}_N^2,\, Y_{N_i}^2 \rightarrow 0$ for $i=2,\ldots n$) and no lower bound on $\Gamma _{H\rightarrow N{\bar{N}}}$ exists. Still, sizable Higgs boson branching ratios into sterile neutrinos are also possible (even reaching $\Gamma _{H\rightarrow N{\bar{N}}} = \Gamma _{\text {max}}$) in this case for a fixed value of ${\mathcal {Y}}_N^2$.

The inclusion of the exotic $H \rightarrow N {\bar{N}}$ decay channel on the Higgs signal strength bound (recall Eq. (3.8)) allows to exclude a significant fraction of the parameter space in which a SFOPT is possible in the present scenario, as we will show explicitly in Sect. 5. Finally, we stress that the heavy neutrinos produced in the decays of the 125 GeV Higgs bosons may themselves decay visibly inside the detector via active-heavy neutrino mixing, leaving a prompt or displaced vertex signal in the detector depending on the value of $\theta ^2$. In particular, if the heavy neutrinos $N_i$ are long-lived, they can lead to a two-displaced-vertices signal in the LHC detectors, which would be a very powerful probe of the model [84, 85].

3.3 Electroweak precision observables

The properties of the singlet field are also constrained by EW precision observables (EWPO), which limit the value of the mixing $\sin {\xi }$ as a function of the scalar mass $M_S$ in the singlet scalar extension of the SM (see e.g. [86, 87]). This is a result of the shift induced by the presence of the singlet scalar on the EW oblique parameters S, T, U[88] with respect to the SM. A global fit to EWPO measurements yields the respective values of the shifts on the oblique parameters with respect to their SM predictions [89]

$$\begin{aligned}{} & {} S \; = \; 0.04 \pm 0.11, \; T \; = \; 0.09 \pm 0.14, \nonumber \\{} & {} U = -0.02 \pm 0.11, \end{aligned}$$

(3.11)

with the following correlation coefficients: $+0.92$ between S and T, $-0.68$ between S and U and $-0.87$ between T and U. Explicit expressions for S, T, U in the singlet scalar extension of the SM are given in [87] as a function of $\sin {\xi }$ and $M_S$. Using these, we obtain the 95% C.L. limits on the ($M_S, \, \left| \sin {\xi }\right|$) plane from a $\chi ^2$ fit to the S, T, U measurements from Eq. (3.11). These are shown in Fig. 2, highlighting that for values of $M_S$ below a TeV, the bound from Higgs signal strength discussed in the previous section is stronger than that of EWPO.

Notice, however, that the same EWPO used to constrain S, T and U and, from there, derive constraints on $\sin {\xi }$ are affected already at tree level and used to derive the bounds on the heavy-active neutrino mixing $\theta$ as outlined above [67]. In principle, the two contributions should be studied together to derive a consistent set of constraints. The interplay between new physics contributions to the EWPO through S, T, U and the presence of heavy neutrinos was studied in detail in Refs. [90,91,92,93]. In particular, it was realized that most observables depend on the same combination of elements of $\theta$ and T and that, if a cancellation between these two contributions is present, the bounds on both sources of new physics would weaken significantly. Nevertheless, for this situation to take place, negative and sizable values of T are required [93]. The scalar singlet contribution to T does indeed become negative for masses above the mass of the Higgs (see e.g. [87]). For lighter singlet masses, no cancellation is possible and the two effects would rather reinforce each other, leading to slightly stronger constraints. Nevertheless, since the bounds from Higgs signal strength are more stringent, the potential contribution of the singlet is small and does not alter significantly the constraints on heavy-active neutrino mixing derived in [93]. Conversely, for a scalar singlet heavier than the Higgs, the bound $\textrm{tr}\left( \theta \theta ^{\dagger }\right) \le 0.0048$ would weaken if $-2 \alpha T \sim 0.0048$. However, given the bounds on $\sin {\xi }$ from the LHC Higgs signal strength measurements (see Sect. 3.2), this is never achieved for sub-Planckian scalar masses. Thus, for the parameter space under study, the possible interplay between the heavy neutrino and scalar singlet contributions to EWPO can be safely neglected.

3.4 Searches for singlet-like scalars at LEP and LHC

Under the assumption that the singlet-like scalar decays into SM particles (i.e. its decay is driven by the singlet-doublet mixing), the null results from LEP searches for Higgs-like particles yield strong upper limits on $\left| \sin {\xi }\right|$ for singlet-like scalar masses below $M_S \simeq 115$ GeV (see e.g. [73]). These limits are at the level of $\left| \sin {\xi }\right| \lesssim 0.2$ (or below) for masses $M_S < 100$ GeV. At the same time, LHC searches for BSM scalars decaying to WW, ZZ or HH pairs also constrain the doublet admixture of the singlet-like scalar S for $M_S > M_H$. For $M_S > 200$ GeV the strongest such limits are obtained by ATLAS in the $Z Z \rightarrow 4\ell$ and $Z Z \rightarrow 2\ell \, 2\nu$ final states [83].⁹ In Fig. 2 we show the corresponding bounds on the ($M_S,\,\left| \sin {\xi }\right|$) plane from both LEP and LHC searches for new scalars, under the assumption $\textrm{BR}_{S\rightarrow H H} + \textrm{BR}_{S\rightarrow \textrm{BSM}} \equiv \textrm{BR}_{H+X} = 0$ (dashed lines).

Nevertheless, compared to the minimal singlet extension of the SM, here the presence of the heavy neutrinos may lead to much less stringent bounds on $\sin {\xi }$ from direct scalar searches. Indeed, the interactions of S with the heavy neutrinos $N_i$ in Eq. (3.7) will induce the decay $S \rightarrow N_i {\bar{N}}_i$ if available by phase space. The corresponding partial width $\Gamma ^S_{N {\bar{N}}} \propto \cos ^2{\xi }$, in contrast to the partial decay widths of S into SM states, $\Gamma ^S_{\textrm{SM}} \propto \sin ^2{\xi }$. Thus, $S \rightarrow N_i {\bar{N}}_i$ will generally be the dominant decay channel for the singlet-like scalar in the limit $\left| \sin {\xi }\right| \ll 1$ (as favoured by LHC Higgs signal strength measurements, see Sect. 3.2):

• For light singlets ($M_S \lesssim 100$ GeV), the $S\rightarrow N_i {\bar{N}}_i$ decay channel would significantly relax constraints on $\sin {\xi }$ from LEP searches for Higgs bosons decaying visibly (into SM particles), and we show the corresponding dilution of the limits when $\textrm{BR}_X = \textrm{BR}_{S\rightarrow N_i {\bar{N}}_i} = 0.9$ in Fig. 2. Nonetheless, if the heavy neutrinos $N_i$ are long-lived (e.g. for very small neutrino mixing) and would have escaped the LEP detectors, limits from LEP searches for invisibly decaying Higgses [96,97,98,99] would apply. We also depict the bounds from such searches on $\sin {\xi }$ in Fig. 2, showing that they become very strong for rather light scalars. We nevertheless re-stress that these only apply under specific conditions (very long-lived $N_i$, leading to invisible S decays), which depend on the details of the neutrino sector of the model.

• For $M_S \gtrsim 200$ GeV, the presence of the $S \rightarrow N_i {\bar{N}}_i$ decay would weaken the LHC limits on $\sin {\xi }$ from $p p \rightarrow S \rightarrow Z Z$ searches, as shown explicitly in Fig. 2 for $\textrm{BR}_{H+X} = 0.9$.¹⁰ At the same time, this BSM decay would open a new avenue to probe the existence of S and $N_i$ at the LHC, either when the $N_i$ decay products are resolved in the ATLAS/CMS detector or merge into a single reconstructed object (for $M_S \gg M_{N_i}$, producing a “neutrino jet” [103, 104]). Yet, current LHC searches for heavy neutrinos generally consider $N_i$ production modes (e.g. Drell–Yan or $W\gamma$ fusion, see [105] for a discussion) which yield kinematic properties of the $N_i$ rather different from those of $S \rightarrow N_i {\bar{N}}_i$ decays,¹¹ and as such present LHC limits (see [107, 108] for reviews) are difficult to extrapolate to our scenario. Moreover, the possibility that the $N_i$ yield displaced decays (for $\theta ^2 \ll 1$) would dramatically reduce the sensitivity of those existing searches, providing at the same time a new avenue for discovery in long-lived particle searches to be explored in the future.

3.5 Higgs self-coupling

Finally, the existence of the singlet scalar would induce a deviation on the Higgs boson trilinear self-coupling $\lambda _{HHH}$ from its SM value. This is currently being searched for at the LHC [109,110,111] via non-resonant di-Higgs production, albeit with limited precision at present. At tree-level, we find

$$\begin{aligned} \lambda _{HHH}= & {} \lambda _h\,v_{EW}\, c_{\xi }^3-\frac{2\,\lambda _m \,\omega _{EW} + \mu _m}{4}c_{\xi }^2s_\xi \nonumber \\{} & {} +\frac{\lambda _m\,v_{EW}}{2}c_{\xi }s_{\xi }^2-\frac{3\,\lambda _s \,\omega _{EW}+ \mu _3}{3}s_{\xi }^3, \end{aligned}$$

(3.12)

with $\cos {\xi }\,(\sin {\xi })=c_{\xi }\,(s_{\xi })$. Additionally, and particularly relevant in the $\left| \sin {\xi }\right| \ll 1$ limit, the one-loop corrections to the trilinear self-coupling coupling should be taken into account, as they contain terms that do not vanish even when $\sin {\xi } \rightarrow 0$. The one-loop contribution reads, in the $\left| \sin {\xi }\right| \ll 1$ limit [17]

$$\begin{aligned} \Delta \lambda _{HHH}^{\mathrm {1-loop}}= & {} \frac{1}{16\pi ^2}\left( \lambda _m^3\frac{v_{EW}^3}{2\,M_S^2}+27\frac{M_H^4}{v_{EW}^3}+3\lambda _m^2\frac{\mu _3\,v_{EW}^2}{M_S^2}s_{\xi }\right) . \nonumber \\ \end{aligned}$$

(3.13)

We parametrize the deviation with respect to the SM as

$$\begin{aligned} \kappa _\lambda \equiv \frac{\lambda _{HHH}+\Delta \lambda _{HHH}^{\mathrm {1-loop}}}{\lambda _{HHH}^{SM}}, \end{aligned}$$

(3.14)

with $\lambda _{HHH}^{SM}=M_H^2/(2v_{EW})$ the tree-level value of the SM Higgs boson self-coupling.¹² The most stringent constraint on $\kappa _\lambda$ has been recently set by the ATLAS Collaboration [111] to be

$$\begin{aligned} -1.0 \le \kappa _\lambda \le 6.6\;\;(95\%\,\mathrm{C.L.}). \end{aligned}$$

(3.15)

We note that the measurements of $\lambda _{HHH}$ at the LHC via non-resonant di-Higgs production can be significantly altered by the presence of a resonant contribution to the di-Higgs signature (see [113, 114] for a discussion), appearing in the singlet scalar extension of the SM via the $p p \rightarrow S \rightarrow H H$ process. Still, depending on the singlet-like scalar mass $M_S$, it should be possible to exploit the di-Higgs invariant mass distribution $m_{HH}$ to measure the self-coupling $\lambda _{HHH}$ [113] from the non-resonant part of the distribution (with the resonant part properly identified and subtracted), achieving comparable precision to the scenario with no resonant $S \rightarrow H H$ contribution. A detailed analysis of this issue is however beyond the scope of the present work. Moreover, as we will see in Sect. 5 this observable barely deviates from its SM value in the interesting regions of the parameter space and is therefore not a relevant probe of the scenario under study.

4 Parameter scan

In this section we describe our procedure to scan the parameter space of the model and collect the sets of parameters which fulfill the various necessary conditions for a SFOPT. As described in Sect. 2, in general a potential characterized by a random set of parameters $\{\omega , \omega _{p}, v, m_{h}^{2}, m_{s}^{2}, \lambda _{m}, T_{c}, {\mathcal {Y}}_{\nu }, {\mathcal {Y}}_{N}\}$ at $T = T_{c}$ will not yield the correct values of the Higgs vev and Higgs mass at $T=0$, namely $v_{EW} = v_{EW}^\text {exp} \equiv 246.22$ GeV and $M_{H} = M_{H}^\text {exp} \equiv 125.10$ GeV. The first condition $v_{EW} = 246.22$ GeV can always be imposed starting from any given set of parameters by shifting all the parameters $\eta$ with dimension of mass (including $T_{c}$) as $\eta \rightarrow (v_{EW}^\text {exp}/v_{EW})\, \eta$. To satisfy the second condition, $M_{H}=M_{H}^{\text {exp}}$, we solve for $m_{h}^{2}$ for each generated set $\vec {w} = \{\omega , \omega _{p}, v, m_{s}^{2}, \lambda _{m}, T_{c}, {\mathcal {Y}}_{\nu }, {\mathcal {Y}}_{N}\}$ to find values which reproduce the correct Higgs boson mass: in practice, for a given set $\vec {w}$ we scan $m_{h}^{2}$ imposing $v_{EW}/M_{H} = v_{EW}^\text {exp} / M_{H}^\text {exp}$ before the aforementioned shift of the mass dimensionful parameters $\eta$, which guarantees $M_{H} = M_{H}^\text {exp}$ after it. A solution does not always exist depending on the actual values of $\vec {w}$. In this way, we obtain the sets of parameters which have two degenerate minima at $T=T_{c}$ and also reproduce the correct Higgs vev and mass at $T=0$.

Following Ref. [15], we bias our scan towards the parameter sets that satisfy the necessary conditions for a SFOPT.¹³ For this purpose, we have defined an ad-hoc weight function to rate how well the selected points satisfy these conditions, in order to prioritize the parameter regions to which the points belong in our scan. We then use this weight function in place of the log-likelihood for a Markov Chain MonteCarlo (MCMC) using the standard Metropolis Hastings algorithm to sample the interesting regions of the parameter space with MonteCUBES [115]. The conditions for a SFOPT and the weight function used in the MCMC are explicitly defined in Appendix A. Our procedure of the parameter scan is summarized in Fig. 3.

Fig. 3

Flowchart for the selection of parameter sets generating the correct Higgs vev and mass at $T=0$ and satisfying all necessary conditions to potentially have a SFOPT from Ref. [15]

Finally, we have verified the validity of the high-T approximation adopted in Sect. 2 through a comparison of the value of $T_c$ obtained in this approximation with the one obtained from a potential with the same parameters at $T=0$ but implementing the temperature evolution with the full 1-loop thermal potential (see e.g. [116]). The comparison has been performed for points passing all viability criteria, as discussed below. Both values of $T_c$ agree within $5\%$ accuracy for the vast majority of the points scanned (a few outliers extend to $\sim 10 \%$). Then, even though in some cases the value for the scalar singlet mass $M_S$ found in the scan is of the same order as $T_c$, the high-T approximation can remain suitable for our purposes (a fast efficient scan of the parameter space). In addition, we impose a stringent perturbativity condition on the scalar quartic couplings, $\lambda _i\le 2$ (see below), which favours that radiative corrections are not significant.

The parameter sets output of our MCMC scan are further classified according to the following viability criteria:

• Points with the scalar potential quartic couplings $\lambda _i\le 2$ to ensure perturbativity.

• Points that lead to a sufficiently strong first-order phase transition (if the phase transition occurs). As a rough estimate, we ask for the ratio $v/T_c>1$.

  This is required to make EW baryogenesis possible by decoupling sphaleron processes in the EW broken phase.

• Points for which the bubbles of the EW broken phase can actually nucleate and the phase transition does take place. Although the conditions summarized in Fig. 3 are needed to realize a SFOPT, they are not sufficient to guarantee it. It is important to study whether a nucleation temperature $T_N < T_c$ exists for which the bubbles of the EW broken phase (the true vacuum for $T<T_{c}$) successfully grow [17, 60, 62, 117, 118] (and the Universe does not become trapped in the false vacuum). In our scan of parameters, we gauge the nucleation of EW bubbles as follows:

  The transition probability from the false to the true vacuum is proportional to $e^{-S_3/T}$, with $S_3$ the three-dimensional bounce action.

  At temperatures slightly below $T_c$, in the so-called thin-wall regime for which the two minima are almost degenerate, the action $S_3$ diverges for $T \rightarrow T_c$ [119, 120] and thus no transition is possible in this regime. As the Universe cools down from $T_c$ to the nucleation temperature $T_N$, away from the thin-wall limit, the computation of the bounce action becomes more involved. It requires to solve the equations of motion for the background fields to find the bounce solution. This is usually done via numerical solvers like CosmoTransitions [121], BubbleProfiler [122] or FindBounce [123]. Nucleation will be possible if there exists a temperature $T_N > 0$ at which $S_3/T_N\sim 140$ [124,125,126,127], for which the nucleation rate is comparable to the Hubble expansion rate during radiation domination.

  In order to estimate the bounce action and thus the nucleation temperature $T_N$, instead of computing the bounce solution along the path that minimizes the tunneling action, we approximate the solution by calculating the bounce action along a straight path in field space, which connects both minima at $T_N$. The action for such a field configuration, $S_3^{\text {app}}$, will by construction be larger than the tunneling solution [128,129,130], $S_3\le S_3^{\text {app}}$. We find that there is good agreement between the true action $S_3$ and our estimation for the cases of interest, and thus successful nucleation for points in parameter space is expected to occur when $S_3^{\text {app}}/T_N\lesssim 140$, which in turn represents a conservative estimate. In practice, we rewrite the scalar potential in terms of a linear combination of h and s along the straight line connecting the minima at a given T, $\phi _{\parallel }$, and the orthogonal one, $\phi _{\perp }$, as prescribed in Ref. [131]. By taking $\phi _{\perp }\rightarrow 0$ one can quickly find the bounce solution along the straight line using the overshoot-undershoot method in one dimension with, for example, FindBounce. In this manner, the action $S_3^{\text {app}}$ can be computed at the temperature T. The temperature at which $S_3^{\text {app}}/T\sim 140$ defines the nucleation temperature $T_N$. As an example of our approximation, we compare in Fig. 4 the approximated and the actual bounce trajectories in field space with the set of parameters given in Table 1. This approximation allows us to efficiently scan the parameter space. In the results shown in the following section, the boundaries between the nucleating and non-nucleating points should therefore be understood as an approximated result and somewhat conservative. In Sect. 5 we will perform a comparison between the regions of parameter space selected by our nucleation criteria and those found using CosmoTransitions, finding good agreement between both methods.

• Points with the scalar mixing $\xi$ at $T=0$ allowed by collider searches as described in the previous section.

In the next section, we will show the impact of each of these conditions in the parameter space to reveal the correlations among the parameters and the preference for particular parameter regions. As we will see, the condition of the bubble nucleation will prove to be the most constraining one [17, 60, 62, 118], which greatly reduces the allowed parameter space.

Fig. 4

The same as Fig. 1 but at the nucleation temperature $T_N$. The blue line corresponds to the straight path in the field configuration space which we use as an approximation to estimate the action and judge if nucleation may happen, while the purple curve corresponds to the actual bounce solution passing closer to the saddle point (red dot) between the two minima (purple diamonds)

5 Results

Fig. 5

Results of the parameter scan in the scalar mass, $M_S$, and mixing, $\sin {\xi }$, plane. In the right (left) panel the scan was performed with(out) the addition of the heavy Dirac neutrinos. The pink stars correspond to points with non-perturbative couplings, the purple crosses to points for which sphaleron transitions would not decouple in the broken phase. The light blue dots (dark blue pluses) additionally do (not) satisfy the nucleation condition as described in the text. The grey-shaded region corresponds to the bounds on the scalar mixing described in Sect. 3. In the right panel, we do not show the bounds that depend on the parameters in each point

In this section we present and analyze the results from the parameter scan described in Sect. 4 where the different constraints and conditions described in the previous section have been implemented. While the scan is performed over all parameters (at $T = T_c$) in $\vec {w} = \{\omega , \omega _{p}, v, m_{s}^{2}, \lambda _{m}, T_{c}, {\mathcal {Y}}_{\nu }, {\mathcal {Y}}_{N}\}$ with $m^2_h$ fixed so as to reproduce the correct Higgs mass, the constraint in the active-heavy neutrino mixing $\textrm{tr}\left( \theta \theta ^{\dagger }\right) |_{\text {exp}}\le 0.0048$ [67] implies ${\mathcal {Y}}_{\nu }^2$ will have a negligible impact on the scalar potential. We will therefore not show this parameter in the following. Instead we will mainly focus on parameters which have a direct connection to experimental observables, and thus refer the reader to Figs. 9 and 10 in Sect. 6 for results on the complete set of parameters at $T_c$, $\left\{ \vec {w},\,m_{h}^{2}\right\}$, and $T=0$ respectively, as a summary of our results.

In Fig. 5 we show the points collected in our parameter scan in the plane of the mass and mixing of the scalar singlet ($M_S$, $\left| \textrm{sin} \xi \right|$). We study and compare the scenarios with(out) the addition of the heavy Dirac neutrinos in the right (left) panels. All the points have been selected according to the algorithm summarized in Fig. 3 and, therefore, satisfy the conditions from Ref. [15] for a SFOPT and have the correct Higgs mass and vev at $T=0$. The points with different colours and symbols are classified by the conditions listed in Sect. 4. The pink stars are discarded since they have at least one very large scalar coupling ($\lambda _{i} > 2$).¹⁴ For the purple crosses, this perturbativity condition is satisfied, but the first-order phase transition is not strong enough to decouple the sphaleron process in the EW broken phase ($v/T_{c}<1$), even if the bubbles of the broken phase may nucleate. The dark blue crosses labeled with “No $T_{N}$” have $\lambda _{i}<2$ and $v/T_{c} >1$ but the nucleation condition $S_{3}^{\text {app}}/T \lesssim 140$ is not satisfied at any $T<T_{c}$ (and therefore, there is no $T_{N}$). Finally, the light blue dots labeled with “$T_{N}$” have $\lambda _{i} <2$ and $v/T_{c} >1$ and also fulfill the nucleation condition. Grey-shaded areas in the left panel represent the values of the scalar mixing ruled out by LHC Higgs signal strength measurements (assuming $\textrm{BR}_{X} = 0$) as described in Sect. 3.2, or by direct searches for Higgs-like particles at LEP for $M_S\lesssim 100$ GeV and at ATLAS for $M_S>200$ GeV (assuming $\textrm{BR}_{S\rightarrow H H} = 0$). On the right panel we only display the conservative Higgs signal strength bound in the absence of exotic Higgs decays, since the bounds from direct scalar searches at LEP and LHC may be diluted when heavy Dirac neutrinos are included, depending on the values of neutrino couplings as discussed in Sect. 3.4. As can be seen from the plots, these constraints are quite relevant and a big portion of the parameter space is ruled out by them, so that only small values of $\sin {\xi }$ are still allowed. Moreover, we also find that the condition of successful bubble nucleation considerably reduces the size of the viable parameter space, as pointed out in Refs. [117, 118] for other scenarios. Thus, only the light blue dots below the grey-shaded regions are successful candidates for a SFOPT satisfying all phenomenological constraints listed in the previous section. From Fig. 5 we can also see that the Universe may undergo an EW SFOPT only if the mass of the singlet scalar S is $M_{S} \lesssim 300$ GeV. Generally speaking, higher values of $M_S$ would also imply larger $\omega$ and hence a significant distance between the two minima, in general too large to allow for bubble nucleation. The apparent exception to this rule by the few points clustered around $M_S \sim 500{-}1000$ GeV can be understood through a closer inspection of their thermal evolution. Indeed, in these cases we find a SFOPT only in the singlet direction at $T\gg {\mathcal {O}}(100)$ GeV. After this transition, both the Higgs and the singlet vevs roll towards their values at $T=0$, $v_{EW}$ and $\omega _{EW}$, respectively, with $\omega _{EW}\gg v_{EW}$.

Fig. 6

Correlations between different parameters in the scan with non-zero neutrino Yukawa coupling. The allowed regions are very similar for the scan without neutrino Yukawas (see also Fig. 10). The color coding is the same as in Fig. 5 with the grey diamonds indicating the parameter space which can undergo successful nucleation but are excluded by their value of the scalar mixing $\xi$. In all panels the parameters are represented at $T=T_c$ except for the bottom-right panel with the trilinear Higgs coupling at $T=0$

Through the comparison between the left and right panels of Fig. 5, we can study the impact of the presence of heavy Dirac neutrinos. While we find new nucleating regions characterized by large $\omega$ and sizeable and negative $\lambda _m$ (as can be seen in Fig. 10), these are largely ruled out by the constraints from Higgs signal strength measurements, as shown in Fig. 9. Indeed, as shown in the upper-left panel of Fig. 6, the points that pass the criteria for the case including the heavy neutrinos cluster at small values of ${\mathcal {Y}}_{N}$ or small $\omega$. The condition that leads to the (hyperbola-like) correlation shown in this panel is the requirement of the stability of the EW broken minimum imposed in Eq. (A.3), in particular that $m_s^2 >0$ at $T=0$. Since ${\mathcal {Y}}_{N}$ induces a negative evolution of $m_s^2$ from $T_c$ down to $T = 0$, values of ${\mathcal {Y}}_{N} > 1$ are constrained in the scan unless $T_c$ is small and/or $\lambda _m$ is negative to cancel its effect in Eq. (2.5). This can be seen explicitly in the corresponding panels of Fig. 9. Such a cancellation is however prevented by the bounds on the scalar mixing, as indicated by the grey points in Fig. 9. Thus, from now on, we will only present the results of our scan with ${\mathcal {Y}}_{N} \ne 0$, i.e. in the presence of heavy Dirac neutrinos. However, the allowed regions should also be considered generally valid for the ${\mathcal {Y}}_{N}=0$ scenario without the heavy neutrinos, with the caveat that direct scalar searches at LEP and ATLAS further constrain the parameter space.

We present the distribution of scan points in various other interesting slices of the parameter space in Fig. 6. For information on the distributions under the other parameters of the scan, we refer the reader to Fig. 9. The color coding and symbols is the same as for Fig. 5, but in addition to them, we now have the grey diamonds (labeled with “$T_N+{\cos {\xi }\!\!\!\!\!\!\!\!/}$”) indicating the parameter space points which can undergo successful nucleation but are excluded by their value of the scalar mixing $\sin {\xi }$. They correspond to the blue dots covered by the grey-shaded area in the right panel of Fig. 5. In the upper right panel of Fig. 6 we show the correlations found in our scan between the two scalar vevs at $T=T_c$. As can be seen, the most significant constraint is the requirement of a sufficiently strong EW phase transition, $v/T_c > 1$. When imposing this together with $v_{EW}= v_{EW}^\textrm{exp}$ and $M_H=M_H^\textrm{exp}$, values of v below $\sim 100$ GeV are ruled out. Besides this constraint, we find that large values of $\omega$, beyond $\sim 200$ GeV, are disfavored by the requirement of successful nucleation. Indeed, we generally find that, if $\omega$ were too large, the field distance between the two minima would be too big to allow for bubble nucleation despite satisfying the rest of the requirements. Even though we find regions of parameter space successfully nucleating for singlet vevs as large as $\omega \sim 1000$ GeV at $T_c$, a detailed study of these regions shows that these transitions at $T_N$ occur from $(0,\omega -\Delta \omega )\rightarrow (0,\omega )$, with $\Delta \omega \ll \omega$, such as the distance travelled in field space is not qualitatively larger than for the region with $\omega \lesssim 200$ GeV.

In the lower left panel of Fig. 6 we show the distribution of scan points in the $\omega -\lambda _m$ plane at $T=T_c$. We find that the light-blue dots, which pass all requirements and in particular the nucleation condition, display an anticorrelation between these two parameters. Additionally, the bounds on $\sin {\xi }$ rule out most of the points with $\lambda _m<0$ unless $|\lambda _m|\ll 1$. These trends can be understood from the hyperbolic shape of the correlation between $\lambda _m$ and $\omega _p$, which is found in the corresponding panel of Fig. 9. Indeed, from Eq. (2.9) this behavior is expected if $\mu _m$ is negative. Analyzing the accepted samples, we find that negative $\mu _m$ is preferred in order to satisfy our condition for successful nucleation. In fact, negative $\mu _m$ decreases the barrier between the two degenerate minima and thus we find no nucleating samples for positive $\mu _m$. Finally, the area with negative $\lambda _m<0$ and negative $\omega _p$ is ruled out by the constraints on the scalar singlet mixing since, as expected from Eq. (2.9), $-m^2_{sh}$ would become too large.

We have further analyzed the non-trivial correlation found between $\omega$ and $\lambda _m$ when imposing our criteria for nucleation, comparing these results with points that successfully nucleate according to the tunneling module from CosmoTransitions. As can be seen in Fig. 7, for a subset of our sample featuring successful nucleation, the areas found by both our approximate estimate (light-blue points) and CosmoTransitions (black octagons for a first-order EW phase transition) generally agree well. The two exceptions we identify are: (i) the region with negative $\lambda _m$ and large $\omega$, where CosmoTransitions finds successfully tunneling points which are not found by our approximation.¹⁵ This region corresponds to significantly more curved trajectories than those depicted in Fig. 4, not-well approximated by our straight-line assumption. Nevertheless, this whole area of the parameter space also leads to too large scalar singlet-doublet mixing (as described above) and is experimentally excluded. (ii) The points for which CosmoTransitions does not find an EW phase transition, whereas our nucleation proxy does, i.e. the red squares and the blue points with no counterpart (neither red square, green pentagon or black octagon) in Fig. 7. This should a priori never happen, since our criterium for nucleation is conservative. A careful investigation of such points reveals that the phase-tracking module of CosmoTransitions does not produce numerically reliable results in such cases.¹⁶ We thus conclude that neither of these exceptions is meaningful, and our estimate for nucleation agrees well with the results from CosmoTransitions for the values of the parameters for which CosmoTransitions yields a reliable numerical result, thus representing an efficient and fast alternative for scans of the parameter space discriminating in a conservative way if nucleation could happen.

Fig. 7

Sample comparison between the results obtained with our proxy (light blue circles) and CosmoTransitions (CT) in the $\omega -\lambda _{m}$ plane for successfully nucleating points. According to CT, red squares correspond to non-nucleating points, green pentagons to those giving a $2^{\textrm{nd}}$ order phase transition (OPT) and black octagons to successfully nucleating points

Fig. 8

Bounds on the regions of parameter space giving rise to successful nucleation. The left panel correspond to the plane ${\mathcal {Y}}_N$ against $\omega _{EW}$ at $T=0$, with the color legend giving the size of $\textrm{BR}_{H\rightarrow N{\bar{N}}}$ for $n=3$ degenerate heavy neutrinos. The solid red line corresponding to $\, \omega _{EW}{\mathcal {Y}}_N = (M_H/2)$ separates the cases where the decay is always allowed (below) and where it depends strongly on the assumptions on the neutrino Yukawas $Y_{N_i}$ (above). The dashed black line yields the boundary of kinematically allowed $H\rightarrow N_i\bar{N_i}$ decay for the $n= 3$ degenerate neutrino case. The right panel shows the excluded parameter space at $95\%$ C.L. from Higgs signal strength measurements, in which red points are excluded while blue ones comply with the bounds, and is independent of n

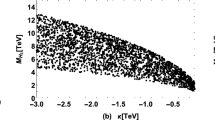
As discussed in Sect. 3, the inclusion of the singlet scalar causes a deviation of the Higgs trilinear coupling from its SM value, which can be parametrized as in Eq. (3.14). The distributions of $\kappa _{\lambda }$ as a function of $\omega _{EW}$ at $T=0$ is shown in the bottom-right panel of Fig. 6, together with the current bounds from collider searches, which are given by Eq. (3.15) and shown by the grey-shaded regions. We find that the light-blue points satisfying all conditions tend to cluster in a narrow range around $\kappa _{\lambda }\sim 1$. Thus, given the sensitivity to $\kappa _\lambda \sim 2.2$ [132] of future probes such as the HL-LHC, no deviations caused by a singlet scalar responsible for a SFOPT are to be expected in this observable.

Finally, in Fig. 8 we show the regions of the parameter space which are constrained by the possible new decay channel of the Higgs-like state H into heavy neutrinos using Eqs. (3.8) and (3.9) as described in Sect. 3.2, for points which pass all the constraints (i.e. light-blue in Fig. 6) in our parameter scan. In the left panel we show the contribution to the corresponding branching ratio assuming a degenerate heavy neutrino spectrum ($Y_{N_i}^2={\mathcal {Y}}_N^2/n$) with $n=3$, for which $\Gamma _{H \rightarrow N {\bar{N}}}$ can be comparable to or even exceed the SM Higgs boson total width $\Gamma _{\textrm{SM}}$ in an important part of the parameter space. The solid red line separates “Case 1” and “Case 2” as discussed in Sect. 3.2. Note that in the region above the solid red line (“Case 2”), a different combination of $Y_{N_i}$ Yukawa couplings (yielding the same value of ${\mathcal {Y}}_N^2$) could arbitrarily reduce the value of $\hbox {BR}_{H\rightarrow N{\bar{N}}}$ by making all neutrinos either too heavy for the Higgs to decay into or with negligible couplings. From this panel we can also infer that the heavy Dirac neutrinos are in general lighter than $\sim 300$ GeV. In the right panel of Fig. 8 we instead show the minimum possible value of $\hbox {BR}_{H\rightarrow N{\bar{N}}}$ for each parameter point. Notice that for the points corresponding to “Case 1” (region below the solid red line in the left panel) the exclusion limits from Higgs signal strength measurements, shown in grey, are unavoidable and rule out a significant region of the parameter space, while for “Case 2” the $\hbox {BR}_{H\rightarrow N{\bar{N}}}$ can be made arbitrarily small and thus the bound can always be evaded. In Fig. 9 we show in red the points excluded by $BR_{H\rightarrow N{\bar{N}}}$ in the different relevant planes in parameter space. Even though these constraints are important, as seen in Fig. 8, they do not exclude particular regions of parameter space.

6 Summary and conclusions

In this work we have explored the parameter space of the scalar singlet extension of the SM with the aim of identifying the regions in which a SFOPT, as required to explain the puzzle to the origin of the observed baryon asymmetry through the EWBG mechanism, can take place. The main goal of the study is to contribute to the predictability of the scenario by relating the areas where a SFOPT can happen with potentially testable observables or correlations among them.

Previous studies [15] showed the conditions that need to be met by the extended scalar potential in order to develop two degenerate minima at some critical temperature $T_c$. Together with the requirement of reproducing the correct mass and vacuum expectation value of the SM-like Higgs and of the required strength of the transition ($v/T_c > 1$), these set of constraints already impose stringent and non-trivial conditions of the allowed parameter space.

Nevertheless, as advocated by [17, 60, 62, 117, 118], we find that the requirement that bubble nucleation may actually take place between the two minima is the most constraining requirement, reducing drastically the allowed parameter space. Furthermore, testing explicitly this condition is not possible in a fast and analytical way and relying on the numerical solvers available [121,122,123] necessarily limits the speed of the scan hindering the exploration of large parameter spaces. Moreover, given the complexity of the problem, for some points in the parameter space we find that some numerical solvers fail to find one of the phases, and hence the corresponding transition, or are unable to produce a result. For this reason we have adopted a fast and conservative approximation to the three-dimensional action of the bounce solution, $S_3^{\text {app}}$, that controls the transition rate between the two minima and requires $S_3^{\text {app}}/T_N\sim 140$ at some nucleation temperature $T_N$. We find that for most of the sampled points in the parameter space that satisfy this criteria, CosmoTransitions does indeed find a first order phase transition (with a small fraction of second order transitions, something we did not explicitly discriminate), thus validating our approach. We also point out that, for many of the points that passed our selection criteria, CosmoTransitions did not provide an output. Thus, larger regions of the parameter space may be explored in a fast and efficient way through the approximation adopted, although it should be taken as a conservative estimate and not as an exact result.

In our scan of the parameter space we find that the regions with the correct mass and vev for the Higgs and successful nucleation are mainly characterized by values of the singlet vev $\omega _{EW} \lesssim 300$ GeV. Indeed, if $\omega _{EW}$ is too large, the two minima tend to be too far apart in field space¹⁷ and nucleation may not happen. This in turn translates into values of the scalar singlet mass that cluster around $M_S\lesssim 300$ GeV. The exception to this rule is a clustering of allowed points with large $\omega$ and values of $M_S$ in the 500–1000 GeV range, which in any case do not produce an EW phase transition given that v(T) smoothly goes from 0 to $v_{EW}$ as the Universe expands. We have verified that for these points the actual jump in $\omega$ during the phase transition is also small. Regarding the most constraining observables, we find that the bounds on the singlet-doublet mixing from Higgs signal strength measurements by ATLAS and CMS are already ruling out important regions of the parameter space. Direct searches for the singlet scalar when its decays are SM Higgs-like both at LEP and at LHC are also relevant.

We have also investigated how this picture is affected when the scalar singlet is not alone, but part of larger dark sector it may interact with. As a particularly motivated scenario, we considered as case study the addition of extra sterile neutrino singlets of both chiralities. These new states will have Yukawa couplings $Y_{N}$ to the scalar singlet, which would induce Dirac masses around the EW scale for these heavy neutral leptons. Furthermore, a Yukawa coupling $Y_{\nu }$ among the SM Higgs doublet, the SM neutrinos and the heavy neutrinos would generally also be allowed. The simultaneous presence of $Y_N$ and $Y_\nu$ implies a new source of CP-violation that may be enough to induce the BAU via EWBG [18, 19] (the so-called $\nu$-EWBG scenario [19]). Furthermore, if a small source of lepton-number violation is introduced, the presence of $Y_\nu$ would induce small neutrino masses able to explain the neutrino oscillation phenomenon in the manner of the low-scale symmetry-protected seesaws like the inverse or linear seesaw variants.

Fig. 9

Triangle plot for non-zero Yukawas, only for points successfully nucleating. The grey diamonds correspond to regions of parameter space excluded by constraints on the scalar mixing while red dots are excluded by the constraint from $H \rightarrow N{\bar{N}}$. The blue points satisfy all phenomenological bounds. We note the very strong correlation between the singlet vev $\omega$ and $\omega _p$ at $T_c$ for blue points, as well as between $\lambda _m$ and $\omega _p$

Fig. 10

Triangle plot comparing the successfully nucleating points for the singlet scalar alone (orange pentagons) and including the neutral fermions (blue dots), without imposing any phenomenological bound, at $T=0$ for the parameters defined in Eq. (2.3). In the singlet-scalar-only case we have ${\mathcal {Y}}_{\nu (N)}=0$ and it is not shown in the plot

Previous studies [21] showed that the presence of the heavy neutrinos increases the strength of the transition by enhancing $v/T_c$. We reproduce this result, but find that sizable $Y_N$, unless accompanied by small $\omega$, can also destabilize the broken minimum. Thus, when our criteria for nucleation and stability are imposed, for the allowed values of the Yukawa couplings the regions of the scalar potential parameter space are comparable to the scenario without heavy neutrinos. Hence the early universe phenomenology regarding the possibility of a SFOPT of both scenarios is very similar, as summarized in Figs. 9 and 10. Even if new areas appear when including the neutrinos, we observe in Fig. 9 that they are excluded by Higgs signal strength measurements. The small values of the Yukawa couplings and the scalar singlet vev $\omega$ preferred, seem to make the generation of the BAU via EWBG difficult according to the findings of [19], but a dedicated analysis would be required to confirm or rule out its viability.

Conversely, the presence of the heavy sterile neutrinos may significantly affect the collider phenomenology of the scalar singlet extension. Indeed, while very large values of $Y_N$ could hinder vacuum stability, values around $Y_N \sim {\mathcal {O}}(1)$ are perfectly allowed. Such a sizable coupling would on the one hand imply that the scalar singlet decays would be overwhelmingly dominated to the heavy sterile neutrino channel, given that the singlet-doublet mixing is more strongly constrained and the smaller SM Yukawa couplings. This would in turn invalidate the bounds on the scalar mixing derived from direct searches of the singlet with SM-like decays at LEP and LHC. On the other hand, dedicated searches for this new decay channel should be considered.

Furthermore, if allowed by phase space, the decay to heavy sterile neutrinos could also be sizable for the SM-like Higgs scalar via its mixing with the singlet. We have found that this in fact strengthens the Higgs signal strength constraints in significant portions of the parameter space, corresponding to the red points in Fig. 8. Interestingly, the possibility that this is the dominant channel to produce and test for the heavy neutrinos at collider searches also remains open in parts of the parameter space. Indeed, the mixing of the heavy neutrinos with their active counterparts induced by $Y_\nu$ is more strongly constrained from flavour and electroweak precision observables, as well as collider searches via Drell–Yan production. Thus, if $Y_N$ is more sizable than $Y_\nu$, the heavy neutrinos would be more easily produced via Higgs or singlet decays. For small enough values of $Y_\nu$, the decays of the heavy neutrinos themselves would not be prompt and may induce interesting signatures with displaced vertexes. We thus find that the viable parameter space allows for very striking and non-standard collider phenomenology which will be interesting to pursue in future dedicated studies.

Parameter scan with weight function

We describe in this section the ad-hoc weight function used for the parameter scan and also show the distribution of the parameter points that satisfy the nucleation condition in the full parameter space at Fig. 9.

A set of necessary conditions for a successful SFOPT were identified, analytically, in Ref. [15], and can be found in Table 1 therein. They fall into the following three categories:

• Conditions to have degenerate minima at $T=T_c$:

  In order for the two minima to be stable we impose

  $$\begin{aligned} \begin{gathered} \det ({\mathcal {M}}_s) - \frac{v^2}{\omega ^2}(m_h^2|_0)m_h^2>0,\\ m_h^2|_0, \; m_h^2, \; m_s^2 >0, \end{gathered} \end{aligned}$$

  (A.1)

  with $m_h^2|_0\equiv (\omega /2)[\lambda _m-m_h^2/\omega ^2-2m_{sh}^2/(v\omega )]$. These expressions are valid under the assumption that the symmetric minimum sits at (0, 0), which we can assume without loss of generality thanks to the shift symmetry present in the potential.

• Matching conditions at $T_c$:

  Once a viable degenerate potential is found at $T_c$ with the reduced set of parameters $\lbrace \omega ,\omega _p,v,m_h^2,m_s^2,\lambda _m\rbrace$, we need to set the parameters $\lambda ^2$, $m_{*}$ (given by Eq. (2.8)) and $m_{sh}^2$ to particular values so as to have the general potential from Eq. (2.6). In this step we ensure that the running of the potential according to temperature change makes the broken minimum the deepest one by imposing

  $$\begin{aligned} \frac{d(V_{T,b}-V_{T,s})}{dT^2}\Bigg |_{T_c}=c_h v^2+\omega (c_s \omega +2m_3)>0, \end{aligned}$$

  (A.2)

  where $V_{T,b(s)}$ correspond to the potential in the broken (symmetric) minimum. Notice that in this step the neutrino Yukawa couplings ${\mathcal {Y}}_{\nu (N)}$ may play an important role as they enter into the $c_h$ and $c_s$ constants which set the running of the potential with the temperature.

• Conditions for potential at $T\le T_c$:

  We require that the potential is bounded from below, and the broken minimum is the global minimum and stable, which are translated into the following conditions on the parameters at $T=0$.

  $$\begin{aligned} \begin{gathered} {\left\{ \begin{array}{ll} \lambda ^{2}> 0, &{}\quad \text {for}\quad \lambda _{m} \le 0, \\ \lambda ^{2} + \frac{1}{4}\lambda _{m}^{2}> 0, &{}\quad \text {for}\quad \lambda _{m}> 0, \end{array}\right. } \\ \det ({\mathcal {M}}_{s}^{2}), \; m_h^2, \; m_s^2>0, \\ \lambda ^2 - \frac{4 m_{*}^{2} v^{2}}{\det ({\mathcal {M}}_{s}^{2})} \ge 0. \end{gathered} \end{aligned}$$

  (A.3)

  Notice that, as seems to be the case in the SM, the electroweak minimum could be metastable at $T=0$ with a lifetime longer than the age of the Universe. Thus, this condition is more restrictive than strictly necessary. Nevertheless, it is convenient since it allows to efficiently scan the potential without the need of computing the lifetime of the vacuum.

All the conditions listed above take the form “$C_X >0$” with $C_X$ a given function of the parameters in the potential. In order to guide our scan towards the areas where these conditions are met we construct the following weight function

$$\begin{aligned} {\mathcal {W}}=\sum _X W_{X}, \end{aligned}$$

(A.4)

with $W_X$ defined as

$$\begin{aligned} W_X = {\left\{ \begin{array}{ll} (10^{6} C_{X})^{2}, &{}\quad \text {if}\quad C_X\le 0 \\ \text {0,} &{}\quad \text {if}\quad C_X>0. \\ \end{array}\right. } \end{aligned}$$

(A.5)

The factor $10^6$ is a penalty to the points that do not satisfy one of the conditions, with which we can make sure any point accepted in the MCMC satisfies all the necessary conditions for the SFOPT. We also add a Gaussian $\chi ^2$ term for the Higgs mass as well as for the constraint on ${\mathcal {Y}}_\nu$ from Eq. (3.3) as Gaussian priors to ${\mathcal {W}}$

$$\begin{aligned} {\mathcal {W}}= & {} \sum _X W_{X} +\left( \frac{M_H-M_{H}^\text {exp}}{ \sigma _{M_{H}^\text {exp}}}\right) ^2\nonumber \\{} & {} +\left( \frac{\frac{n^2v_{EW}^2}{2\omega _{EW}^2{\mathcal {Y}}_N}{\mathcal {Y}}^2_\nu -\textrm{tr}\left( \theta \theta ^{\dagger }\right) _\text {exp}}{ \sigma _{\textrm{tr}\left( \theta \theta ^{\dagger }\right) }}\right) ^2, \end{aligned}$$

(A.6)

where $M_{H}^\text {exp}=125.10$ GeV and $\sigma _{M_{H}^\text {exp}}=0.17$ GeV is its uncertainty [64] and $\textrm{tr}\left( \theta \theta ^{\dagger }\right) _\text {exp}=0.0014$ with $\sigma _{\textrm{tr}\left( \theta \theta ^{\dagger }\right) }=0.0014$ [67, 68], and we take $n=3$.