The flavor-dependent $U(1)_F$ model

Abstract

A flavor-dependent model (FDM) is proposed in this work. The model extends the Standard Model by an extra $U(1)_F$ local gauge group, two scalar doublets, one scalar singlet and two right-handed neutrinos, where the additional $U(1)_F$ charges are related to the particles’ flavor. The new fermion sector in the FDM can explain the flavor mixings puzzle and the mass hierarchy puzzle simultaneously, and the nonzero Majorana neutrino masses can be obtained naturally by the Type I see-saw mechanism. In addition, the B meson rare decay processes ${\bar{B}} \rightarrow X_s\gamma ,$ $B_s^0 \rightarrow \mu ^+\mu ^-,$ the top quark rare decay processes $t\rightarrow ch,$ $t\rightarrow uh$ and the $\tau$ lepton flavor violation processes $\tau \rightarrow 3e,$ $\tau \rightarrow 3\mu ,$ $\mu \rightarrow 3e$ predicted in the FDM are analyzed.

1 Introduction

The Standard Model (SM) achieves great success in describing the interactions of fundamental particles, and most of the observations coincide well with the SM predictions. However, the Yukawa couplings in the SM are still enigmatic, because the flavor mixings of quarks described by the Cabibbo–Kobayashi–Maskawa (CKM) matrix [1, 2] are not predicted from first principles in the SM, which is the so-called flavor puzzle. And the fermions of the three families have largely distinct masses

$$\begin{aligned}{} & {} \frac{m_t}{m_c}\approx 104,\;\frac{m_c}{m_u}\approx 773,\;\frac{m_b}{m_s}\approx 51,\;\frac{m_s}{m_d}\approx 20,\nonumber \\{} & {} \frac{m_\tau }{m_\mu }\approx 17,\;\frac{m_\mu }{m_e}\approx 207. \end{aligned}$$

(1)

It exhibits the large hierarchical structure of masses across the three families while they share common SM gauge group quantum numbers, which is the so-called mass hierarchy puzzle. Meanwhile, the nonzero neutrino masses and mixings observed at the neutrino oscillation experiments [3] make the so-called flavor puzzle in the SM more acutely. All of these indicate that explaining the observed fermionic mass spectrum and mixings is one of the most enigmatic questions in particle physics, which may help understand the flavor nature and seek possible new physics (NP).

In literatures, there are some attempts to explain the fermionic mass hierarchies and flavor mixings. For example, the authors of Refs. [4,5,6,7,8] try to explain the fermionic flavor mixings by imposing the family symmetries, some proposals to explain the fermionic mass hierarchies can be found in Refs. [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25]. The three-Higgs doublet model is motivated to account for the flavor structure with three generations of fermions [26,27,28,29,30,31,32,33,34], in which the number of Higgs doublets is three and has a flavor symmetry. A flavor-dependent U(1) extension of the SM is proposed in Ref. [35], the authors explained the small mixing at quark sector by introducing a NP cut-off scale parameter. Weinberg proposed a new mechanism in which only the third generation of quarks and leptons achieve the masses at the tree level, while the masses for the second and first generations are produced by one-loop and two-loop radiative corrections respectively [20]. However, his analysis indicated that the ratios of the masses of the second and third generations fermions are independent of various masses of the third generation, i.e.

$$\begin{aligned} \frac{m_c}{m_t}=\frac{m_s}{m_b}=\frac{m_\mu }{m_\tau }\quad \textrm{or}\quad \frac{m_c}{m_t^3}=\frac{m_s}{m_b^3}=\frac{m_\mu }{m_\tau ^3}, \end{aligned}$$

which is not true of observed masses as shown in Eq. (1). Hence, he pointed out in his work that “this kind of NP models are not realistic for some reasons” [20]. In addition, Weinberg was the first to propose the Type I see-saw mechanism to give the tiny neutrino masses naturally [36], which provides one of the most popular mechanisms so far to give the tiny Majorana neutrino masses.

In this work, we adopt the Weinberg’s idea “only the third generation of fermions achieve the masses at the tree level”, but abandon “the masses for the second and first generations are produced by one-loop and two-loop radiative corrections respectively”. Instead, we propose to obtain the masses for the second and first generations by the “see-saw mechanism” (which is proposed by Weinberg to give the tiny Majorana neutrino masses as mentioned above), i.e. the masses for the second and first generations are produced by mixing with the third generation. In this case, the ratios of the masses of the second and third generations fermions depend on the tree-level mixing parameters of fermions, and we propose a flavor-dependent model (FDM) to realize this mechanism. The model extends the SM by an extra $U(1)_F$ local gauge group which relates to the particles’ flavor, two scalar doublets, one scalar singlet and two right-handed neutrinos. The new fermion sector in the FDM relates the fermionic flavor mixings to the fermionic mass hierarchies, which provides a new understanding about the mass hierarchy puzzle and the flavor mixing puzzle. In addition, the nonzero neutrino masses can be obtained naturally in the FDM by the Type I see-saw mechanism.

The paper is organized as follows: The structure of the FDM including particle content, scalar sector, fermion masses and gauge sector are collected in Sect. 2. The numerical results of CKM matrix and Higgs masses predicted in the FDM are presented in Sect. 3. The processes mediated by the flavor changed neutral currents (FCNCs) in the FDM are analyzed in Sect. 4. The summary is made in Sect. 5.

2 The flavor-dependent model

Table 1 Matter content in the FDM, where the nonzero constant z denotes the extra $U(1)_F$ charge

The gauge group of the FDM is $SU(3)_C\otimes SU(2)_L\otimes U(1)_Y\otimes U(1)_F,$ where the extra $U(1)_F$ local gauge group is related to the particles’ flavor. In the FDM, the third generation of fermions obtain masses through the tree-level couplings with the SM scalar doublet, and the first two generations of fermions achieve masses through the tree-level mixings with the third generation as mentioned above. Hence, two additional scalar doublets are introduced in the FDM to realize the tree-level mixings of the first two generations and the third generation. In addition, to coincide with the observed neutrino oscillations, two right-handed neutrinos and one scalar singlet are introduced. Then the right-handed neutrinos obtain large Majorana masses after the scalar singlet achieving large vacuum expectation value (VEV), and the tiny neutrino masses and neutrino flavor mixings can be obtained by the Type I see-saw mechanism.

All fields in the FDM and the corresponding gauge symmetry charges are presented in Table 1, where $\Phi _3$ corresponds to the SM Higgs doublet, the nonzero constant z denotes the extra $U(1)_F$ charge. It can be noted in Table 1 that there are only two generations of right-handed neutrinos in the FDM, because both $U(1)_F$ and $U(1)_Y$ charges of the third generation of right-handed neutrinos $\nu _{R_3}$ are zero, which is trivial. In addition, it is obvious that the chiral anomaly cancellation can be guaranteed for the fermionic charges presented in Table 1.

2.1 The scalar sector of the FDM

The scalar potential in the FDM can be written as

$$\begin{aligned} V= & {} -M_{\Phi _1}^2 \Phi _1^\dagger \Phi _1-M_{\Phi _2}^2 \Phi _2^\dagger \Phi _2\nonumber \\{} & {} -M_{\Phi _3}^2 \Phi _3^\dagger \Phi _3-M_{\chi }^2\chi ^*\chi +\lambda _{\chi } (\chi ^*\chi )^2+\lambda _1 (\Phi _1^\dagger \Phi _1)^2\nonumber \\{} & {} +\lambda _2 (\Phi _2^\dagger \Phi _2)^2+\lambda _3 (\Phi _3^\dagger \Phi _3)^2+\lambda '_4 (\Phi _1^\dagger \Phi _1)(\Phi _2^\dagger \Phi _2)\nonumber \\{} & {} +\lambda _4'' (\Phi _1^\dagger \Phi _2)(\Phi _2^\dagger \Phi _1)\nonumber \\{} & {} +\lambda _5' (\Phi _1^\dagger \Phi _1)(\Phi _3^\dagger \Phi _3)+\lambda _5'' (\Phi _1^\dagger \Phi _3)(\Phi _3^\dagger \Phi _1)\nonumber \\{} & {} +\lambda _6' (\Phi _2^\dagger \Phi _2)(\Phi _3^\dagger \Phi _3)+\lambda _6'' (\Phi _2^\dagger \Phi _3)(\Phi _3^\dagger \Phi _2)\nonumber \\{} & {} +\lambda _7 (\Phi _1^\dagger \Phi _1)(\chi ^*\chi )+\lambda _{8} (\Phi _2^\dagger \Phi _2)(\chi ^*\chi )\nonumber \\{} & {} +\lambda _{9} (\Phi _3^\dagger \Phi _3)(\chi ^*\chi )+[\lambda _{10} (\Phi _3^\dagger \Phi _1)(\Phi _3^\dagger \Phi _2)\nonumber \\{} & {} +\kappa (\Phi _1^\dagger \Phi _2)\chi +h.c.], \end{aligned}$$

(2)

where

$$\begin{aligned}{} & {} \Phi _1=\left( \begin{array}{c}\phi _1^{+}\\ \frac{1}{\sqrt{2}}(i A_1{+}S_1{+}v_1)\end{array}\right) ,\Phi _2{=}\left( \begin{array}{c}\phi _2^{+}\\ \frac{1}{\sqrt{2}}(i A_2{+}S_2{+}v_2)\end{array}\right) ,\nonumber \\{} & {} \Phi _3=\left( \begin{array}{c}\phi _3^+\\ \frac{1}{\sqrt{2}}(i A_3+S_3+v_3)\end{array}\right) ,\nonumber \\{} & {} \chi =\frac{1}{\sqrt{2}}(i A_{\chi }+S_{\chi }+v_\chi ), \end{aligned}$$

(3)

and $v_i\;(i=1,\;2,\;3),\;v_\chi$ are the VEVs of $\Phi _i,\;\chi$ respectively.

Based on the scalar potential in Eq. (2), the tadpole equations in the FDM can be written as¹

$$\begin{aligned} M_{\Phi _1}^2= & {} \lambda _1v_1^2+\frac{1}{2}\Big [(\lambda _4'+\lambda _4'') v_2^2+(\lambda _5'+\lambda _5'') v_3^2\nonumber \\{} & {} +\frac{v_2}{v_1}v_3^2 {\textrm{Re}}(\lambda _{10})+\sqrt{2}\frac{v_2}{v_1} v_\chi {\textrm{Re}}(\kappa )+\lambda _7v_\chi ^2\Big ],\nonumber \\ M_{\Phi _2}^2= & {} \lambda _2v_2^2+\frac{1}{2}\Big [(\lambda _4'+\lambda _4'') v_1^2+(\lambda _6'+\lambda _6'') v_3^2\nonumber \\{} & {} +\frac{v_1}{v_2}v_3^2 {\textrm{Re}}(\lambda _{10})+\sqrt{2}\frac{v_1}{v_2} v_\chi {\textrm{Re}}(\kappa )+\lambda _8v_\chi ^2\Big ],\nonumber \\ M_{\Phi _3}^2= & {} \lambda _3v_3^2+{\textrm{Re}}(\lambda _{10})v_1v_2\nonumber \\{} & {} +\frac{1}{2}[(\lambda _5'+\lambda _5'') v_1^2+(\lambda _6'+\lambda _6'') v_2^2+\lambda _9 v_c^2],\nonumber \\ M_{\chi }^2= & {} \lambda _\chi v_\chi ^2+\frac{1}{2}\Big [\lambda _7 v_1^2+\lambda _8 v_2^2+\lambda _9 v_3^2+\sqrt{2}\frac{v_1v_2}{v_\chi } {\textrm{Re}}(\kappa )\Big ].\nonumber \\ \end{aligned}$$

(4)

On the basis $(S_1,\;S_2,\;S_3,\;S_\chi ),$ the CP-even Higgs squared mass matrix in the FDM is

$$\begin{aligned}{} & {} M_{h}^2=\left( \begin{array}{*{20}{cccc}} M_{h,11}^2 \quad &{} M_{h,12}^2 \quad &{} M_{h,13}^2\quad &{} M_{h,14}^2 \\ M_{h,12}^2\quad &{} M_{h,22}^2\quad &{} M_{h,23}^2\quad &{} M_{h,24}^2 \\ M_{h,13}^2\quad &{} M_{h,23}^2\quad &{} M_{h,33}^2\quad &{} M_{h,34}^2 \\ M_{h,14}^2\quad &{} M_{h,24}^2\quad &{} M_{h,34}^2 \quad &{} M_{h,44}^2 \\ \end{array}\right) , \end{aligned}$$

(5)

where

$$\begin{aligned}{} & {} M_{h,11}^2=2\lambda _1v_1^2-\frac{v_2}{2v_1}\Big [v_3^2 {\textrm{Re}}(\lambda _{10})+\sqrt{2} v_\chi {\textrm{Re}}(\kappa )\Big ],\nonumber \\{} & {} M_{h,22}^2=2\lambda _2v_2^2-\frac{v_1}{2v_2}\Big [v_3^2 {\textrm{Re}}(\lambda _{10})+\sqrt{2} v_\chi {\textrm{Re}}(\kappa )\Big ],\nonumber \\{} & {} M_{h,33}^2=2\lambda _3v_3^2,\;\;M_{h,44}^2=2\lambda _\chi v_\chi ^2-\frac{\sqrt{2}v_1v_2}{2v_\chi } {\textrm{Re}}(\kappa ),\nonumber \\{} & {} M_{h,12}^2=(\lambda _4'+\lambda _4'') v_1v_2+\frac{1}{2}{\textrm{Re}}(\lambda _{10})v_3^2+\frac{\sqrt{2}}{2}{\textrm{Re}}(\kappa )v_\chi ,\nonumber \\{} & {} M_{h,13}^2=(\lambda _5'+\lambda _5'')v_1v_3+{\textrm{Re}}(\lambda _{10})v_2v_3,\nonumber \\{} & {} M_{h,14}^2=\lambda _7v_1v_\chi +\frac{\sqrt{2}}{2}{\textrm{Re}}(\kappa )v_2,\nonumber \\{} & {} M_{h,23}^2=(\lambda _6'+\lambda _6'')v_2v_3+{\textrm{Re}}(\lambda _{10})v_1v_3,\nonumber \\{} & {} M_{h,24}^2=\lambda _8v_2v_\chi +\frac{\sqrt{2}}{2}{\textrm{Re}}(\kappa )v_1,\nonumber \\{} & {} M_{h,34}^2=\lambda _9v_3v_\chi . \end{aligned}$$

(6)

The tadpole equations in Eq. (4) are used to obtain the matrix elements above.

Then, on the basis $(A_1,\;A_2,\;A_3,\;A_\chi ),$ the squared mass matrix of CP-odd Higgs in the FDM can be written as

$$\begin{aligned} M_{A}^2=\left( \begin{array}{*{20}{cccc}} M_{A,11}^2\quad &{} M_{A,12}^2\quad &{} M_{A,13}^2\quad &{} M_{A,14}^2 \\ M_{A,12}^2\quad &{} M_{A,22}^2\quad &{} M_{A,23}^2\quad &{} M_{A,24}^2 \\ M_{A,13}^2\quad &{} M_{A,23}^2\quad &{} M_{A,33}^2 \quad &{} M_{A,34}^2 \\ M_{A,14}^2\quad &{} M_{A,24}^2\quad &{} M_{A,34}^2\quad &{} M_{A,44}^2 \\ \end{array}\right) , \end{aligned}$$

(7)

where

$$\begin{aligned}{} & {} M_{A,11}^2=-\frac{v_2}{2v_1}[{\textrm{Re}}(\lambda _{10})v_3^2+\sqrt{2} v_\chi {\textrm{Re}} (\kappa )],\nonumber \\{} & {} M_{A,33}^2=-2{\textrm{Re}}(\lambda _{10})v_1v_2,\nonumber \\{} & {} M_{A,22}^2=-\frac{v_1}{2v_2}[{\textrm{Re}}(\lambda _{10})v_3^2+\sqrt{2} v_\chi {\textrm{Re}} (\kappa )],\nonumber \\{} & {} M_{A,44}^2=-\frac{\sqrt{2} v_1v_2}{2v_\chi }{\textrm{Re}} (\kappa ),\nonumber \\{} & {} M_{A,12}^2=\frac{\sqrt{2}}{2} v_\chi {\textrm{Re}} (\kappa )-\frac{1}{2}{\textrm{Re}}(\lambda _{10})v_3^2,\nonumber \\{} & {} M_{A,13}^2={\textrm{Re}}(\lambda _{10})v_2v_3,\nonumber \\{} & {} M_{A,14}^2=\frac{\sqrt{2}}{2} v_2 {\textrm{Re}} (\kappa ),\;\;M_{A,23}^2={\textrm{Re}}(\lambda _{10})v_1v_3,\nonumber \\{} & {} M_{A,24}^2=-\frac{\sqrt{2}}{2} v_1 {\textrm{Re}} (\kappa ),\nonumber \\{} & {} M_{A,34}^2=0. \end{aligned}$$

(8)

On the basis $(\phi _1^+,\;\phi _2^+,\;\phi _3^+)$ and $(\phi _1^-,\;\phi _2^-,\;\phi _3^-)^T,$ the squared mass matrix of singly charged Higgs in the FDM can be written as

$$\begin{aligned} M_{H^\pm }^2=\left( \begin{array}{*{20}{ccc}} M_{H^\pm ,11}^2 &{} M_{H^\pm ,12}^2 &{} M_{H^\pm ,13}^2 \\ (M_{H^\pm ,12}^2)^* &{} M_{H^\pm ,22}^2 &{} M_{H^\pm ,23}^2 \\ (M_{H^\pm ,13}^2)^* &{} (M_{H^\pm ,23}^2)^* &{} M_{H^\pm ,33}^2 \\ \end{array}\right) , \end{aligned}$$

(9)

where

$$\begin{aligned}{} & {} M_{H^\pm ,11}^2=-\frac{v_2}{2v_1}[{\textrm{Re}}(\lambda _{10})v_3^2+\sqrt{2} v_\chi {\textrm{Re}} (\kappa )]\nonumber \\{} & {} \quad \quad \quad \qquad -\frac{1}{2}(\lambda _4'' v_2^2+\lambda _5'' v_3^2),\nonumber \\{} & {} M_{H^\pm ,22}^2=-\frac{v_1}{2v_2}[{\textrm{Re}}(\lambda _{10})v_3^2+\sqrt{2} v_\chi {\textrm{Re}} (\kappa )]\nonumber \\{} & {} M_{H^\pm ,33}^2=-{\textrm{Re}}(\lambda _{10})v_1v_2-\frac{1}{2}(\lambda _5'' v_1^2+\lambda _6'' v_2^2),\nonumber \\{} & {} M_{H^\pm ,12}^2=\frac{\sqrt{2}}{2}v_\chi \kappa +\frac{1}{2}\lambda _4'' v_1 v_2,\nonumber \\{} & {} M_{H^\pm ,13}^2=\frac{1}{2}v_3(\lambda _5'' v_1+\lambda _{10}^*v_2),\nonumber \\{} & {} M_{H^\pm ,23}^2=\frac{1}{2}v_3(\lambda _6'' v_2+\lambda _{10}^*v_1). \end{aligned}$$

(10)

It is easy to verify that there are two neutral Goldstones and one singly charged Goldstone in the FDM.

2.2 The fermion masses in the FDM

Based on the matter content listed in Table 1, the Yukawa couplings in the FDM can be written as

$$\begin{aligned} {\mathcal {L}}_Y= & {} Y_u^{33}{\bar{q}}_3 \tilde{\Phi }_3 u_{R_3}+Y_d^{33}{\bar{q}}_3 \Phi _3 d_{R_3}\nonumber \\{} & {} +Y_u^{32}{\bar{q}}_3 \tilde{\Phi }_1 u_{R_2}+Y_u^{23}{\bar{q}}_2 \tilde{\Phi }_1 u_{R_3}+Y_d^{32}{\bar{q}}_3 \Phi _2 d_{R_2}\nonumber \\{} & {} +Y_d^{23}{\bar{q}}_2 \Phi _2 d_{R_3}+Y_u^{21}{\bar{q}}_2 \tilde{\Phi }_3 u_{R_1}\nonumber \\{} & {} +Y_u^{12}{\bar{q}}_1 \tilde{\Phi }_3 u_{R_2}+Y_d^{21}{\bar{q}}_2 \Phi _3 d_{R_1}+ Y_d^{12}{\bar{q}}_1 \Phi _3 d_{R_2}\nonumber \\{} & {} +Y_u^{31}{\bar{q}}_3 \tilde{\Phi }_2 u_{R_1}+Y_u^{13}{\bar{q}}_1 \tilde{\Phi }_2 u_{R_3}\nonumber \\{} & {} +Y_d^{31}{\bar{q}}_3 \Phi _1 d_{R_1}+Y_d^{13}{\bar{q}}_1 \Phi _1 d_{R_3}\nonumber \\{} & {} +Y_e^{33}{\bar{l}}_3 \Phi _3 e_{R_3}+Y_e^{32}{\bar{l}}_3 \Phi _2 e_{R_2}\nonumber \\{} & {} +Y_e^{23}{\bar{l}}_2 \Phi _2 e_{R_3}+Y_e^{21}{\bar{l}}_2 \Phi _3 e_{R_1}+ Y_e^{12}{\bar{l}}_1 \Phi _3 e_{R_2}\nonumber \\{} & {} +Y_e^{31}{\bar{l}}_3 \Phi _1 e_{R_1}+Y_e^{13}{\bar{l}}_1 \Phi _1 e_{R_3}\nonumber \\{} & {} +Y_R^{11}{\bar{\nu }}^c_{R_1}\nu _{R_1}\chi +Y_R^{22}{\bar{\nu }}^c_{R_2}\nu _{R_2} \chi ^*+Y_D^{21}{\bar{l}}_2 \tilde{\Phi }_3 \nu _{R_1}\nonumber \\{} & {} +Y_D^{12}{\bar{l}}_1 \tilde{\Phi }_3 \nu _{R_2}+Y_D^{31}{\bar{l}}_3 \tilde{\Phi }_2 \nu _{R_1}\nonumber \\{} & {} +Y_D^{32}{\bar{l}}_3 \tilde{\Phi }_1 \nu _{R_2}+h.c. \end{aligned}$$

(11)

Then the mass matrices of quarks and leptons can be written as

$$\begin{aligned}{} & {} m_q{=}\left( \begin{array}{ccc} 0 &{} m_{q,12} &{} m_{q,13}\\ m_{q,12}^* &{} 0 &{} m_{q,23}\\ m_{q,13}^* &{} m_{q,23}^* &{} m_{q,33}\end{array}\right) ,m_e{=}\left( \begin{array}{ccc} 0 &{} m_{e,12} &{} m_{e,13}\\ m_{e,12}^* &{} 0 &{} m_{e,23}\\ m_{e,13}^* &{} m_{e,23}^* &{} m_{e,33}\end{array}\right) ,\nonumber \\{} & {} m_\nu =\left( \begin{array}{cc} 0 &{} M_D^T\\ M_D &{} M_R\end{array}\right) , \end{aligned}$$

(12)

where $q=u,d,$ the parameters $m_{q,33}$ and $m_{e,33}$ are real, $M_D$ is $2\times 3$ Dirac mass matrix and $M_R$ is $2\times 2$ Majorana mass matrix (the nonzero neutrino masses are obtained by the Type I see-saw mechanism). The elements of the matrices in Eq. (12) are

$$\begin{aligned}{} & {} m_{u,11}=m_{u,22}=0,\;m_{u,33}=\frac{1}{\sqrt{2}}Y_u^{33}v_3,\nonumber \\{} & {} m_{u,12}=\frac{1}{\sqrt{2}}Y_u^{12}v_3,\;m_{u,13}=\frac{1}{\sqrt{2}}Y_u^{13}v_1,\nonumber \\{} & {} m_{u,23}=\frac{1}{\sqrt{2}}Y_u^{23}v_2, \end{aligned}$$

(13)

$$\begin{aligned}{} & {} m_{d,11}=m_{d,22}=0,\;m_{d,33}=\frac{1}{\sqrt{2}}Y_d^{33}v_3,\nonumber \\{} & {} m_{d,12}=\frac{1}{\sqrt{2}}Y_d^{12}v_3,\;m_{d,13}=\frac{1}{\sqrt{2}}Y_d^{13}v_1,\nonumber \\{} & {} m_{d,23}=\frac{1}{\sqrt{2}}Y_d^{23}v_2, \end{aligned}$$

(14)

$$\begin{aligned}{} & {} m_{e,11}=m_{e,22}=0,\;m_{e,33}=\frac{1}{\sqrt{2}}Y_e^{33}v_3,\nonumber \\{} & {} m_{e,12}=\frac{1}{\sqrt{2}}Y_e^{12}v_3,\;m_{e,13}=\frac{1}{\sqrt{2}}Y_e^{13}v_1,\nonumber \\{} & {} m_{e,23}=\frac{1}{\sqrt{2}}Y_e^{23}v_2, \end{aligned}$$

(15)

$$\begin{aligned}{} & {} M_{D,11}=M_{D,22}=0,\;\;M_{D,12}=\frac{1}{\sqrt{2}}Y_D^{12}v_3,\nonumber \\{} & {} M_{D,31}=\frac{1}{\sqrt{2}}Y_D^{31}v_1,\nonumber \\{} & {} M_{D,32}=\frac{1}{\sqrt{2}}Y_D^{32}v_2,\;M_{R,12}=M_{R,21}=0,\nonumber \\{} & {} M_{R,11}=\frac{1}{\sqrt{2}}Y_R^{11}v_\chi ,\;M_{R,22}=\frac{1}{\sqrt{2}}Y_R^{22}v_\chi . \end{aligned}$$

(16)

2.3 The gauge sector of the FDM

Due to the introducing of an extra $U(1)_F$ local gauge group in the FDM, the covariant derivative corresponding to $SU(2)_L\otimes U(1)_Y\otimes U(1)_F$ is defined as

$$\begin{aligned} D_\mu= & {} \partial _\mu +i g_2 T_j A_{j\mu }+i g_1 Y B_\mu \nonumber \\{} & {} +i g_{_F} F B'_\mu +i g_{_{YF}} Y B'_\mu ,\quad (j=1,\;2,\;3), \end{aligned}$$

(17)

where $(g_2,\;g_1,\; g_{_F}),$ $(T_j,\;Y,\;F),$ $(A_{j\mu },\;B_\mu ,\; B'_\mu )$ denote the gauge coupling constants, generators and gauge bosons of groups $(SU(2)_L,\;U(1)_Y,\;U(1)_F)$ respectively, $g_{_{YF}}$ is the gauge coupling constant arises from the gauge kinetic mixing effect which presents in the models with two Abelian groups. Then the W boson mass can be written as

$$\begin{aligned}{} & {} M_W=\frac{1}{2}g_2 (v_1^2+v_2^2+v_3^2)^{1/2}, \end{aligned}$$

(18)

where $(v_1^2+v_2^2+v_3^2)^{1/2}=v\approx 246\;{\textrm{GeV}}$ and we have $v_1,\;v_2 < v_3$ in the FDM. The $\gamma ,$ Z and $Z'$ boson masses in the FDM can be written as

$$\begin{aligned} M_\gamma =0,\;M_Z\approx \frac{1}{2}(g_1^2+g_2^2)^{1/2} v,\;M_{Z'}\approx 2|zg_{_F}| v_\chi , \end{aligned}$$

(19)

and

$$\begin{aligned}{} & {} \gamma =c_W B+s_W A_3,\;Z=-s_W B+c_W A_3+s'_W B',\nonumber \\{} & {} Z'=s_W'(s_WB-c_W A_3)+c'_W B', \end{aligned}$$

(20)

where $\gamma ,\;Z,\;Z'$ are the mass eigenstates, $c_W\equiv \cos \theta _W,\;s_W \equiv \sin \theta _W$ with $\theta _W$ denoting the Weinberg angle, $s_W'\equiv \sin \theta '_W,$ $c_W'\equiv \cos \theta '_W$ with $\theta _W'$ representing the $Z-Z'$ mixing effect.

3 CKM matrix and Higgs masses in the FDM

The quark sector in the FDM are redefined and the additional two scalar doublets, one scalar singlet modify the scalar potential of the model, hence we focus on the quark sector and scalar sector of the model in this section.

3.1 CKM matrix

The analysis in our previous work [37] shows that the quark mass matrices obtained in the FDM can fit the measured CKM matrix well. In this work, we perform a $\chi ^2$ test to explore the best fit describing the quark masses and CKM matrix in the model. Generally, the $\chi ^2$ function can be constructed as

$$\begin{aligned} \chi ^2=\sum _1 \Bigg (\frac{O_i^{\textrm{th}}-O_i^{\textrm{exp}}}{\sigma _i^{\textrm{exp}}}\Bigg )^2, \end{aligned}$$

(21)

where $O_i^{\textrm{th}}$ denotes the i-th observable computed theoretically, $O_i^{\textrm{exp}}$ is the corresponding experimental value and $\sigma _i^{\textrm{exp}}$ is the uncertainty in $O_i^{\textrm{exp}}.$ Taking into account 10 observables including 6 quark masses, 3 mixing angles and a phase in the CKM matrix, we scan the parameter space

$$\begin{aligned}{} & {} |m_{u,13}|=(0.0\sim 1.0)~{\textrm{GeV}},\;|m_{d,13}|=(0.0\sim 0.1)~{\textrm{GeV}},\nonumber \\{} & {} \theta _{q,ij}=(-\pi ,\pi ) \end{aligned}$$

(22)

with $m_{q,ij}=|m_{q,ij}|e^{i\theta _{q,ij}},$ $q=u,d,$ $ij=12,13,23.$ Then we obtain the best fit solution corresponding to $\chi ^2=0.0072,$ the results of this fit are listed in Table 2 where various $O_i^{\textrm{exp}}$ we use are listed in the third column and $\sigma _i^{\textrm{exp}}$ are take from PDG [3]. The parameters for the best fit listed in Table 2 are

Table 2 The results obtained for the best fit corresponding to $\chi ^2={\mathbf {0.0072}}$

$$\begin{aligned}{} & {} |m_{u,13}|=0.3152~{{\textrm{GeV}}},\;\theta _{u,12}=-0.8248\pi ,\nonumber \\{} & {} \theta _{u,13}=0.1231\pi ,\;\theta _{u,23}=-0.1129\pi ,\nonumber \\{} & {} |m_{d,13}|=7.235~{\textrm{MeV}},\;\theta _{d,12}=0.6705\pi ,\nonumber \\{} & {} \theta _{d,13}=-0.3622\pi ,\;\theta _{d,23}=-0.06389\pi , \end{aligned}$$

(23)

and $|m_{q,12}|,\;|m_{q,23}|,\;m_{q,33}\;(q=u,\;d)$ can be obtained by²

$$\begin{aligned} m_{q,33}= & {} m_{q_3}-m_{q_1}-m_{q_2},\nonumber \\ |m_{q,23}|= & {} [(m_{q_1}+m_{q_2})m_{q,33}-|m_{q,13}|^2]^{1/2},\nonumber \\ |m_{q,12}|= & {} \frac{|m_{q,13}||m_{q,23}|}{|m_{q,33}|} \cos (\theta _{q,12}+\theta _{q,23}-\theta _{q,13})\nonumber \\{} & {} +\Bigg \{\Bigg [\frac{|m_{q,13}||m_{q,23}|}{|m_{q,33}|^2}\cos (\theta _{q,12}+\theta _{q,23}-\theta _{q,13})\Bigg ]^2\nonumber \\{} & {} +\frac{m_{q_1}m_{q_2}}{|m_{q,33}|^2}\Bigg \}^{1/2}|m_{q,33}|, \end{aligned}$$

(24)

with $m_{q_k}$ being the $k-$generation quark q mass.

It is obvious that there are additional CP phases in the obtained CKM matrix by taking the parameters in Eq. (23) as inputs, but we do not list the observed CP phase in the CKM matrix in Table 2. Because the CKM matrix is defined as

$$\begin{aligned} V_{\textrm{CKM}}=(U_L^{u}U_L^{d\dagger })^*, \end{aligned}$$

(25)

where $U_L^{u},$ $U_L^{d}$ are the unitary matrices which diagonalize the quark matrices in Eq. (12)

$$\begin{aligned} m_u^{\textrm{diag}}=U_L^{u*}m_uU_R^{u\dagger },\;m_d^{\textrm{diag}}=U_L^{d*}m_dU_R^{d\dagger }. \end{aligned}$$

(26)

Equation (26) is invariant under

$$\begin{aligned}{} & {} U_L^{u}\rightarrow \textrm{diag}(e^{-i \theta _u},e^{-i \theta _c},e^{-i \theta _t})\cdot U_L^{u},\nonumber \\{} & {} U_R^{u}\rightarrow \textrm{diag}(e^{i \theta _u},e^{i \theta _c},e^{i \theta _t})\cdot U_R^{u},\nonumber \\{} & {} U_L^{d}\rightarrow \textrm{diag}(e^{i \theta _d},e^{i \theta _s},e^{i \theta _b})\cdot U_L^{d},\nonumber \\{} & {} U_R^{d}\rightarrow \textrm{diag}(e^{-i \theta _d},e^{-i \theta _s},e^{-i \theta _b})\cdot U_R^{d}, \end{aligned}$$

(27)

so there are six free parameters $\theta _u,\;\theta _c,\;\theta _t,\;\theta _d,\;\theta _s,\;\theta _b$ which can absorb the extra CP phases in the obtained CKM matrix, these parameters are not observable. As a result, the observed CP phase in the CKM matrix can be obtained by defining appropriate $\theta _u,\;\theta _c,\;\theta _t,\;\theta _d,\;\theta _s,\;\theta _b.$ This fact is always valid because there are also six possible CP violation parameters at the quark sector in the model.

3.2 Perturbative unitary bounds

The scalar sector of the FDM is extended by two scalar doublets and one scalar singlet, additional new couplings are also introduced correspondingly. Therefore, the tree-level perturbative unitary should be applied to the scalar elastic scattering processes in this model [38]. The zero partial wave amplitude

$$\begin{aligned} a_0=\frac{1}{32\pi }\sqrt{\frac{4p_f^{\textrm{CM}}p_i^{\textrm{CM}}}{s}}\int _{-1}^{+1}T_{2\rightarrow 2}d\cos \theta \end{aligned}$$

(28)

must satisfy the condition $|{\textrm{Re}}(a_0)|\le \frac{1}{2},$ where s is the centre of mass (CM) energy, $T_{2\rightarrow 2}$ denotes the matrix element for $2\rightarrow 2$ processes, $\theta$ is the incident angle between two incoming particles, $p_i^{\textrm{CM}}$ and $p_f^{\textrm{CM}}$ are the initial and final momenta in the CM system respectively.

The possible two particle states of $2\rightarrow 2$ scattering processes at the scalar sector in the FDM are $S_1S_1,$ $S_2S_2,$ $S_3S_3,$ $S_\chi S_\chi ,$ $S_1S_2,$ $S_1S_3,$ $S_1S_\chi ,$ $S_2S_3,$ $S_2S_\chi ,$ $S_3S_\chi .$ Considering the limit $s\gg M_{S_1}^2,\;M_{S_2}^2,\;M_{S_3}^2,\;M_{S_\chi }^2,$ we have

$$\begin{aligned}{} & {} a_0^{S_1S_1\rightarrow S_1S_1}\approx \frac{1}{16\pi }(6\lambda _1),\;a_0^{S_2S_2\rightarrow S_2S_2}\approx \frac{1}{16\pi }(6\lambda _2),\nonumber \\{} & {} a_0^{S_3S_3\rightarrow S_3S_3}\approx \frac{1}{16\pi }(6\lambda _3),\;a_0^{S_\chi S_\chi \rightarrow S_\chi S_\chi }\approx \frac{1}{16\pi }(6\lambda _\chi ),\nonumber \\{} & {} a_0^{S_1S_1\rightarrow S_2S_2}\approx \frac{1}{16\pi }(\lambda _4'+\lambda _4''),\;a_0^{S_1S_2\rightarrow S_1S_2}\nonumber \\ {}{} & {} \approx \frac{1}{16\pi }(\lambda _4'+\lambda _4''),\nonumber \\{} & {} a_0^{S_1S_1\rightarrow S_3S_3}\approx \frac{1}{16\pi }(\lambda _5'+\lambda _5''),\;a_0^{S_1S_3\rightarrow S_1S_3}\nonumber \\ {}{} & {} \approx \frac{1}{16\pi }(\lambda _5'+\lambda _5''),\nonumber \\{} & {} a_0^{S_2S_2\rightarrow S_3S_3}\approx \frac{1}{16\pi }(\lambda _6'+\lambda _6''),\;a_0^{S_2S_3\rightarrow S_2S_3}\nonumber \\ {}{} & {} \approx \frac{1}{16\pi }(\lambda _6'+\lambda _6''),\nonumber \\{} & {} a_0^{S_1S_1\rightarrow S_\chi S_\chi }\approx \frac{1}{16\pi }(\lambda _7),\;a_0^{S_1S_\chi \rightarrow S_1S_\chi }\approx \frac{1}{16\pi }(\lambda _7),\nonumber \\{} & {} a_0^{S_2S_2\rightarrow S_\chi S_\chi }\approx \frac{1}{16\pi }(\lambda _8),\;a_0^{S_2S_\chi \rightarrow S_2S_\chi }\approx \frac{1}{16\pi }(\lambda _8),\nonumber \\{} & {} a_0^{S_3S_3\rightarrow S_\chi S_\chi }\approx \frac{1}{16\pi }(\lambda _9),\;a_0^{S_3S_\chi \rightarrow S_3S_\chi }\approx \frac{1}{16\pi }(\lambda _9),\nonumber \\{} & {} a_0^{S_3S_3\rightarrow S_1 S_2}\approx \frac{1}{16\pi }[2{\textrm{Re}}(\lambda _{10})], \nonumber \\{} & {} a_0^{S_1S_3\rightarrow S_2 S_3}\approx \frac{1}{16\pi }[2{\textrm{Re}}(\lambda _{10})]. \end{aligned}$$

(29)

Requiring $|{\textrm{Re}}(a_0)|\le \frac{1}{2}$ for each individual process, we have

$$\begin{aligned}{} & {} |\lambda _1|,\;|\lambda _2|,\;|\lambda _3|,\;|\lambda _\chi |\le \frac{4\pi }{3},\;|{\textrm{Re}}(\lambda _{10})|\le 4\pi ,\nonumber \\{} & {} |\lambda _4'+\lambda _4''|,\;|\lambda _5'+\lambda _5''|,\;|\lambda _6'+\lambda _6''|,\;|\lambda _7|,\;|\lambda _8|,\;|\lambda _9|\le 8\pi .\nonumber \\ \end{aligned}$$

(30)

3.3 Higgs masses in the FDM

For the free parameters in the scalar sector of the FDM, we take $v_1=v_2,$ $\lambda _4'=\lambda _4''=\lambda _4/2,$ $\lambda _5'=\lambda _5''=\lambda _5/2,$ $\lambda _6'=\lambda _6''=\lambda _6/2$ and all parameters to be real for simplicity. In addition, $v_\chi$ is limited by the new $Z'$ boson mass as shown in Eq. (19), hence we take $v_\chi \ge 5~{\textrm{TeV}}$ in the following analysis. Considering the perturbative unitary bounds presented in Eq. (30), we scan the following parameter space

$$\begin{aligned}{} & {} v_1=(0,\;40)~{\textrm{GeV}},\;\lambda _i=(0,\;4)\ {\textrm{with}}\nonumber \\{} & {} \quad (i=1,\ldots ,9,\chi ),\;\lambda _{10}=(-4,\;0),\nonumber \\{} & {} v_\chi =(5,\;40)~{\textrm{TeV}},\;\kappa =(-3,\;-0.1)~{{\textrm{TeV}}}, \end{aligned}$$

(31)

to explore the Higgs mass spectrum in the FDM. In the scanning, we keep the next-to-lightest CP-even Higgs mass $M_{H_2}$ in the range $124~{{\textrm{GeV}}}<M_{H_2}<126~{{\textrm{GeV}}}$ and the scalar potential at the input $v_1,\;v_2,\;v_3,\;v_\chi$ are smaller than all the other stationary points to guarantee the stability of vacuum.

3.3.1 CP-even Higgs masses

Fig. 1

The results of CP-even Higgs masses $M_{H_1}$ (a), $M_{H_3}$ (b), $M_{H_4}$ (c) versus $v_1,$ $\kappa ,$ $v_{\chi }$ are plotted respectively by scanning the parameter space in Eq. (31)

The results of CP-even Higgs masses $M_{H_1}$ versus $v_1,$ $M_{H_3}$ versus $\kappa ,$ $M_{H_4}$ versus $v_{\chi }$ are plotted in Fig. 1a, b, c respectively. We do not present the results of the next-to-lightest CP-even Higgs mass $M_{H_2}$ in Fig. 1 because $M_{H_2}$ is limited in the range $124\;{\textrm{GeV}}<M_{H_2}<126\;{\textrm{GeV}}$ in the plotting. Figure 1a shows that the lightest Higgs mass $M_{H_1}$ in the FDM mainly depends on the chosen value of $v_1,$ and $M_{H_1}$ can reach $95\;{\textrm{GeV}}$ for $v_1\gtrsim 30\;{\textrm{GeV}}$ which will be explored in detail in our next work. As shown in Fig. 1b and c, $M_{H_3},$ $M_{H_4}$ are dominated by $\kappa ,$ $v_{\chi },$ where $M_{H_4}$ is about $110\;{\textrm{TeV}}$ for large $v_{\chi }$ while $M_{H_3}$ is about $13\;{\textrm{TeV}}$ for large $|\kappa |.$

Fig. 2

The results of $M_{H_2}$ versus $\lambda _3$ (a), $\lambda _9$ (b), where the solid, dashed, dotted curves denotes the results for $\lambda _\chi =2,\;3,\;4$ respectively, and the gray areas denote the range $124\;{\textrm{GeV}}<M_{H_2}<126\;{\textrm{GeV}}$

As mentioned above, $\Phi _3$ corresponds to the SM Higgs doublet, hence $\lambda _3$ may affect the $125\;{\textrm{GeV}}$ Higgs boson mass $M_{H_2}$ significantly. In addition, Eq. (6) shows that there are large mixing effects between $S_3$ and $S_\chi ,$ it indicates $\lambda _9,$ $\lambda _\chi$ can also affect $M_{H_2}.$ And to verify numerically that $M_{H_2}$ is mainly affected by $\lambda _3,$ $\lambda _9,$ $\lambda _\chi ,$ we take $v_1=20\;{\textrm{GeV}},\;\lambda _1=\lambda _2=\lambda _4=\lambda _5=\lambda _6=\lambda _7=\lambda _8=2,\;\lambda _{10}=-2,\;v_\chi =10\;{\textrm{TeV}},\;\kappa =-1\;{\textrm{TeV}}$ to explore the effects of $\lambda _3,$ $\lambda _9,$ $\lambda _\chi$ on $M_{H_2}.$ Then $M_{H_2}$ versus $\lambda _3,$ $\lambda _9$ are plotted in Fig. 2a and b respectively, where the solid, dashed, dotted curves denotes the results for $\lambda _\chi =2,\;3,\;4$ respectively, and the gray areas denote the range $124\;{\textrm{GeV}}<M_{H_2}<126\;{\textrm{GeV}}.$ The picture shows $M_{H_2}$ increases with increasing $\lambda _3,$ $\lambda _\chi$ and decreases with increasing $\lambda _9,$ and $\lambda _3,$ $\lambda _9,$ $\lambda _\chi$ affect the theoretical predictions on $M_{H_2}$ significantly.

3.3.2 CP-odd Higgs masses

Fig. 3

The results of CP-even Higgs masses $M_{A_1}$ (a), $M_{A_2}$ (b), $M_{A_2}$ (c) versus $\lambda _{10},$ $\kappa ,$ $v_\chi$ are plotted respectively by scanning the parameter space in Eq. (31)

There are two physical CP-odd Higgs in the FDM, and the results of CP-odd Higgs masses $M_{A_1}$ versus $\lambda _{10},$ $M_{A_2}$ versus $\kappa ,$ $M_{A_2}$ versus $v_\chi$ are plotted in Fig. 3a, b, c respectively. It is obvious in Fig. 3a that $M_{A_1}$ is dominated by the value of $\lambda _{10}$ completely, and $M_{A_1}$ increases with increasing $|\lambda _{10}|.$ In addition, $M_{A_2}$ is dominated by $\kappa ,$ $v_{\chi }$ as shown in Fig. 3b and c, where $M_{A_2}$ can be large when $|\kappa |$ and $v_{\chi }$ are large.

3.3.3 Charged Higgs masses

Fig. 4

The results of charged Higgs masses $M_{H^\pm _1}$ (a), $M_{H^\pm _2}$ (b), $M_{H^\pm _2}$ (c) versus $\lambda _{10},$ $\kappa ,$ $v_\chi$ are plotted respectively by scanning the parameter space in Eq. (31)

Similar to the case of CP-odd Higgs, there are also two physical charged Higgs in the FDM. The results of charged Higgs masses $M_{H^\pm _1}$ versus $\lambda _{10},$ $M_{H^\pm _2}$ versus $\kappa ,$ $M_{H^\pm _2}$ versus $v_\chi$ are plotted in Fig. 4a, b, c respectively. Figure 4a indicates that $M_{H^\pm _1}$ is mainly affected by $\lambda _{10},$ but the other scanning parameter can also influence the predicted $M_{H^\pm _1}$ especially for small $|\lambda _{10}|.$ Similar to the case of $M_{A_2},$ Fig. 4b and c show that $M_{H^\pm _2}$ is also dominated by $\kappa ,$ $v_{\chi }.$

4 The flavor changed neutral currents in the FDM

As shown in Eq. (11), the different generations of fermions couple to different Higgs bosons while $\Phi _3$ corresponding to the SM-like Higgs, which are quite different from the ones in the SM. In addition, the new defined Z and $Z'$ gauge bosons can also mediate the FCNCs. Hence, observing the FCNCs in the FDM may be effective to test the model. In this section, we focus on the B meson rare decay processes ${\bar{B}} \rightarrow X_s\gamma ,$ $B_s^0 \rightarrow \mu ^+\mu ^-,$ the top quark rare decay processes $t\rightarrow ch,$ $t\rightarrow uh$ and the charged lepton flavor violation processes $\tau \rightarrow 3e,$ $\tau \rightarrow 3\mu ,$ $\mu \rightarrow 3e$ predicted in the FDM. And for simplicity, we take the nonzero $U_F(1)$ charge $z=1$ in the following analysis.

4.1 B meson rare decay processes ${\bar{B}} \rightarrow X_s\gamma$ and $B_s^0 \rightarrow \mu ^+\mu ^-$ in the FDM

The B meson rare decay processes ${\bar{B}} \rightarrow X_s\gamma ,$ $B_s^0 \rightarrow \mu ^+\mu ^-$ are related closely to the NP contributions, and the average experimental data on the branching ratios of ${\bar{B}} \rightarrow X_s\gamma ,$ $B_s^0 \rightarrow \mu ^+\mu ^-$ are [3]

$$\begin{aligned}{} & {} {\textrm{Br}}({\bar{B}} \rightarrow X_s\gamma )=(3.49\pm 0.19)\times 10^{-4},\nonumber \\{} & {} {\textrm{Br}}(B_s^0 \rightarrow \mu ^+\mu ^-)=(3.01\pm 0.35)\times 10^{-9}. \end{aligned}$$

(32)

The newly introduced scalars in the FDM including CP-even Higgs, CP-odd Higgs and charged Higgs can make contributions to these two processes, the analytical calculations of the contributions are collected in the appendix [39].

Scanning the parameter spaces in Eqs. (22), (31) and the parameters $|m_{e,13}|,$ $\theta _{e,ij},\;(ij=12,\;13,\;23)$ in the following range

$$\begin{aligned}{} & {} |m_{e,13}|=(0.0\sim 0.3)\;{\textrm{GeV}},\;\theta _{e,ij}=(-\pi \sim \pi ), \end{aligned}$$

(33)

keeping $0.2243<|V_{us}|<0.2263,$ $0.003516<|V_{ub}|<0.003716,$ $0.4139<|V_{cb}|<0.4159$ and $M_{H_2}$ in the range $124\;{\textrm{GeV}}<M_{H_2}<126\;{\textrm{GeV}},$ we plot $M_{H^\pm _1}-M_{A_1},$ $v_1-\lambda _{10}$ in Fig. 5a, b respectively, where the black points, green points denote the results for ${\textrm{Br}}({\bar{B}} \rightarrow X_s\gamma )$ and ${\textrm{Br}}(B_s^0 \rightarrow \mu ^+\mu ^-)$ in the experimental $2\sigma ,$ $1\sigma$ intervals respectively, the ‘red star’ denotes the best fit with the B meson rare decay branching ratios in Eq. (32) corresponding to $\chi ^2=0.022.$ The results of this best fit are listed in Table 3.

Fig. 5

Scanning the parameter spaces in Eq. (22), Eq. (31), Eq. (33) and keeping $0.2243<|V_{us}|<0.2263,$ $0.003516<|V_{ub}|<0.003716,$ $0.4139<|V_{cb}|<0.4159,$ $M_{H_2}$ in the range $124\;{\textrm{GeV}}<M_{H_2}<126\;{\textrm{GeV}},$ the allowed ranges of $M_{H^\pm _1}-M_{A_1}$ (a) and $v_1-\lambda _{10}$ (b) are plotted, where the black points, green points denote the results for ${\textrm{Br}}({\bar{B}} \rightarrow X_s\gamma )$ and ${\textrm{Br}}(B_s^0 \rightarrow \mu ^+\mu ^-)$ in the experimental $2\sigma ,$ $1\sigma$ intervals respectively, the ‘red star’ denotes the best fit with the B meson rare decay branching ratios in Eq. (32) corresponding to $\chi ^2={\mathbf {0.022}}$

Table 3 Fit with the B meson rare decays: the results obtained for the best fit corresponding to $\chi ^2={\mathbf {0.022}}$

For the parameters not shown in Fig. 5 such as $\lambda _1,\;\lambda _2,\ldots ,$ they affect the predicted ${\textrm{Br}}({\bar{B}} \rightarrow X_s\gamma )$ and ${\textrm{Br}}(B_s^0 \rightarrow \mu ^+\mu ^-)$ mildly. The results presented in Fig. 5a indicate that $M_{H^\pm _1}$ is correlated strongly to $M_{A_1}$ because both of them mainly depend on $\lambda _{10}$ as shown in Figs. 3a and 4a. Equations (13) and (14) show that the Yukawa couplings increase with decreasing $v_1,$ i.e. the scalars in the FDM can make significant contributions to the B meson rare decay processes ${\bar{B}} \rightarrow X_s\gamma ,$ $B_s^0 \rightarrow \mu ^+\mu ^-$ for small $v_1,$ which leads to the experimental observations of ${\textrm{Br}}({\bar{B}} \rightarrow X_s\gamma )$ and ${\textrm{Br}}(B_s^0 \rightarrow \mu ^+\mu ^-)$ prefer large $v_1,$ and Fig. 5b shows that $v_1$ is limited in the range $v_1\gtrsim 15\;{\textrm{GeV}}.$

4.2 Top quark rare decay processes $t\rightarrow ch$ and $t\rightarrow uh$

The branching ratios of the top quark rare decay processes $t\rightarrow ch$ and $t\rightarrow uh$ can be written as [40]

$$\begin{aligned}{} & {} {{\textrm{Br}}}(t\rightarrow q_u h)\nonumber \\{} & {} \quad =\frac{|{\mathcal {M}}_{t q_u h}|^2\sqrt{((m_t+m_h)^2-m_{q_u}^2)((m_t-m_h)^2-m_{q_u}^2)}}{32\pi m_t^3\Gamma ^t_{\textrm{total}}},\nonumber \\ \end{aligned}$$

(34)

where $q_u=u,\;c,$ the amplitude ${\mathcal {M}}_{tq_uh}$ can be read directly from the Yukawa couplings in Eq. (11), and $\Gamma ^t_{\textrm{total}}=1.42$ GeV [3] is the total decay width of top quark. The measured quark masses, CKM matrix and B meson rare decay processes ${\bar{B}} \rightarrow X_s\gamma ,$ $B_s^0 \rightarrow \mu ^+\mu ^-$ should be considered in the calculations of top quark rare decay processes $t\rightarrow ch$ and $t\rightarrow uh,$ hence we take the points obtained in Fig. 5 as inputs.

Fig. 6

Taking the points obtained in Fig. 5 as inputs, the results of ${\textrm{Br}}(t\rightarrow ch)$ versus $|m_{u,13}|$ (a), $\theta _{u,12}$ (b) and the results of ${\textrm{Br}}(t\rightarrow uh)$ versus $|m_{u,13}|$ (c), $\theta _{u,12}$ (d) are plotted, where red and blue lines denote the upper bounds on ${\textrm{Br}}(t\rightarrow ch)$ and ${\textrm{Br}}(t\rightarrow uh)$ from Particle Data Group [3] respectively

Then we plot the results of ${\textrm{Br}}(t\rightarrow ch)$ versus $v_1$ in Fig. 6a, ${\textrm{Br}}(t\rightarrow uh)$ versus $v_1$ in Fig. 6b, and ${\textrm{Br}}(t\rightarrow ch)$ versus ${\textrm{Br}}(t\rightarrow uh)$ in Fig. 6c. The red and blue lines in Fig. 6 denote the upper bounds on ${\textrm{Br}}(t\rightarrow ch)$ and ${\textrm{Br}}(t\rightarrow uh)$ from Particle Data Group [3] respectively. The picture illustrates that the results of ${\textrm{Br}}(t\rightarrow ch),$ ${\textrm{Br}}(t\rightarrow uh)$ obtained in the FDM can be large, which indicates that the processes $t\rightarrow ch,$ $t\rightarrow uh$ have great opportunities to be observed experimentally. In addition, the parameter space of the model suffers constraints from the experimental upper bounds on ${\textrm{Br}}(t\rightarrow ch)$ and ${\textrm{Br}}(t\rightarrow uh).$

Fig. 7

Scanning the parameter space Eqs. (31), (33), (37) and keeping $M_{H_2}$ in the range $124\;{\textrm{GeV}}<M_{H_2}<126\;{\textrm{GeV}}$ and ${\textrm{Br}}(\tau \rightarrow 3e)<10^{-7},$ ${\textrm{Br}}(\tau \rightarrow 3\mu )<10^{-7},$ ${\textrm{Br}}(\mu \rightarrow 3e)<2\times 10^{-12},$ the results of ${\textrm{Br}}(\tau \rightarrow 3e)$ versus $|m_{e,13}|$ (a), ${\textrm{Br}}(\tau \rightarrow 3\mu )$ versus $\theta _{e,23}$ (b), ${\textrm{Br}}(\mu \rightarrow 3e)$ versus $\theta _{e,12}$ (c) and the allowed ranges of $v_\chi -v_1$ (d), $g_F-g_{YF}$ (e), $M_{Z'}-g_F$ (f) are plotted, where the gray points are excluded by the present limits, the green points denote the results which can reach future experimental sensitivities

4.3 Lepton flavor violation processes $\tau \rightarrow 3e,$ $\tau \rightarrow 3\mu$ and $\mu \rightarrow 3e$

Finally, we focus on the lepton flavor violation processes $\tau \rightarrow 3e,$ $\tau \rightarrow 3\mu ,$ $\mu \rightarrow 3e$ predicted in the FDM. The corresponding amplitude can be written as [41]

$$\begin{aligned}{} & {} {\mathcal {M}}(e_j\rightarrow e_i e_i{\bar{e}}_i)\nonumber \\{} & {} =C_1^L{\bar{u}}_{e_i}(p_2)\gamma _\mu P_L u_{e_j}(p_1) u_{e_i}(p_3)\gamma ^\mu P_L \nu _{e_i}(p_4)\nonumber \\{} & {} \quad +C_1^R{\bar{u}}_{e_i}(p_2)\gamma _\mu P_R u_{e_j}(p_1) u_{e_i}(p_3)\gamma ^\mu P_R \nu _{e_i}(p_4)\nonumber \\{} & {} \quad +[C_2^L{\bar{u}}_{e_i}(p_2)\gamma _\mu P_L u_{e_j}(p_1) u_{e_i}(p_3)\gamma ^\mu P_R \nu _{e_i}(p_4)\nonumber \\{} & {} \quad +C_2^R{\bar{u}}_{e_i}(p_2)\gamma _\mu P_R u_{e_j}(p_1) u_{e_i}(p_3)\gamma ^\mu P_L \nu _{e_i}(p_4)\nonumber \\ {}{} & {} \quad -(p_2\leftrightarrow p_3)]\nonumber \\{} & {} \quad +[C_3^L{\bar{u}}_{e_i}(p_2) P_L u_{e_j}(p_1) u_{e_i}(p_3) P_L \nu _{e_i}(p_4)\nonumber \\{} & {} \quad +C_3^R{\bar{u}}_{e_i}(p_2) P_R u_{e_j}(p_1) u_{e_i}(p_3) P_R \nu _{e_i}(p_4)\nonumber \\ {}{} & {} \quad -(p_2\leftrightarrow p_3)], \end{aligned}$$

(35)

where $i=1,\;2$ for $j=3,$ $i=1$ for $j=2,$ $u_{e_i}$ denotes the spinor of lepton, $\nu _{e_i}$ denotes the spinor of antilepton, $P_L=(1-\gamma _5)/2,$ $P_R=(1+\gamma _5)/2,$ and $p_k$ denotes the momentum of charged lepton with $k=1,2,3,4.$ The coefficients $C_{1,2,3}^{L,R}$ from the contributions of Higgs bosons and $Z,\;Z'$ gauge bosons, can be obtained through the Yukawa couplings in Eq. (11) and the definition of covariant derivative in Eq. (17). Then we can calculate the decay rate [41]

$$\begin{aligned}{} & {} \Gamma (e_j\rightarrow e_i e_i{\bar{e}}_i)=\frac{m_{e_j}^5}{1536\pi ^3}\Bigg [\frac{1}{2}(|C_1^L|^2+|C_1^R|^2)\nonumber \\{} & {} \quad +|C_2^L|^2+|C_2^R|^2+\frac{1}{8}(|C_3^L|^2+|C_3^R|^2)\Bigg ]. \end{aligned}$$

(36)

The total decay widthes of $\mu ,\;\tau$ are taken as $\Gamma ^\mu _{\textrm{total}}=2.996\times 10^{-19}$ GeV, $\Gamma ^\tau _{\textrm{total}}=2.265\times 10^{-12}$ GeV [3].

Scanning the free parameter space in Eqs. (31), (33) and

$$\begin{aligned}{} & {} g_{F}=(0,\;0.8),\;g_{F}=(-0.8,\;0.8), \end{aligned}$$

(37)

we plot the results of ${\textrm{Br}}(\tau \rightarrow 3e)$ versus $|m_{e,13}|,$ ${\textrm{Br}}(\tau \rightarrow 3\mu )$ versus $\theta _{e,23},$ ${\textrm{Br}}(\mu \rightarrow 3e)$ versus $\theta _{e,12}$ in Fig. 7a, b, c respectively by keeping $M_{H_2}$ in the range $124\;{\textrm{GeV}}<M_{H_2}<126\;{\textrm{GeV}}$ and ${\textrm{Br}}(\tau \rightarrow 3e)<10^{-7},$ ${\textrm{Br}}(\tau \rightarrow 3\mu )<10^{-7},$ ${\textrm{Br}}(\mu \rightarrow 3e)<2\times 10^{-12},$ then the allowed ranges of $v_\chi -v_1,$ $g_F-g_{YF},$ $M_{Z'}-g_F$ are plotted in Fig. 7d, e, f respectively. The gray points in Fig. 7 are excluded by the present limits, and the green points denote the results which can reach future experimental sensitivities, where the present limits and future sensitivities for the branching ratios of these LFV processes are listed in Table 4.

Table 4 Present limits and future sensitivities for the branching ratios for the LFV processes $\tau \rightarrow 3e,$ $\tau \rightarrow 3\mu$ and $\mu \rightarrow 3e$ [3, 42, 43]

Figure 7a, b, c show that the experimental upper bounds on ${\textrm{Br}}(\tau \rightarrow 3\mu ),$ ${\textrm{Br}}(\mu \rightarrow 3e)$ limit the parameter space strictly while the predicted ${\textrm{Br}}(\tau \rightarrow 3e)$ is less than about $10^{-12}$ which is hard to be observed in near future. In addition, the model predicts ${\textrm{Br}}(\tau \rightarrow 3\mu )\gtrsim 2\times 10^{-10},$ ${\textrm{Br}}(\mu \rightarrow 3e)\gtrsim 5\times 10^{-14},$ which indicates observing the LFV processes $\tau \rightarrow 3\mu$ and $\mu \rightarrow 3e$ is also effective to test the FDM. It is obvious in Fig. 7d that the experimental upper bounds on the branching ratios of these LFV processes limit $v_1\gtrsim 23\;{\textrm{GeV}},$ $v_\chi \gtrsim 20\;{\textrm{TeV}}.$ Figure 7e indicates experimental constraints prefer $-0.2\lesssim g_{YF} \lesssim 0.2$ and $g_{YF} \lesssim -0.2$ is excluded completely. From Fig. 7f, it can be seen explicitly that the allowed range of $M_{Z'}$ is related closely with the chosen value of $g_F$ and $M_{Z'}\gtrsim 5\;{\textrm{TeV}}.$

5 Summary

Motivated by the hierarchical structure of fermionic masses puzzle and fermionic flavor mixings puzzle, we propose a flavor-dependent model (FDM) to relate these two puzzles, i.e. the proposed FDM can explain the flavor mixings puzzle and mass hierarchy puzzle simultaneously. The model extends the SM by an extra $U(1)_F$ local gauge group, two scalar doublets, one scalar singlet and two right-handed neutrinos, where the new $U(1)_F$ charges are related to the particles’ flavor. In the FDM, only the third generation of quarks and charged leptons achieve the masses at the tree level, the first two generations achieve masses through the mixings with the third generation, and the neutrinos obtain tiny Majorana masses through the so-called Type I see-saw mechanism. In addition, the B meson rare decay processes ${\bar{B}} \rightarrow X_s\gamma ,$ $B_s^0 \rightarrow \mu ^+\mu ^-,$ the top quark rare decay processes $t\rightarrow ch,$ $t\rightarrow uh$ and the $\tau$ LFV processes $\tau \rightarrow 3e,$ $\tau \rightarrow 3\mu ,$ $\mu \rightarrow 3e$ predicted in the FDM are analyzed. It is found that observing the top quark rare decay processes $t\rightarrow ch,$ $t\rightarrow uh$ and the $\tau$ LFV decays $\tau \rightarrow 3\mu ,$ $\mu \rightarrow 3e$ is effective to test the FDM, while $\tau$ LFV decay $\tau \rightarrow 3e$ is hard to be observed experimentally. In addition, the model can fit the observed quark masses, CKM matrix, ${\textrm{Br}}({\bar{B}} \rightarrow X_s\gamma ),$ ${\textrm{Br}}(B_s^0 \rightarrow \mu ^+\mu ^-)$ well, and the VEVs of the two extra scalar doublets are limited to be larger than about $23\;{\textrm{GeV}},$ new $Z'$ gauge boson is heavier than about $5\;{\textrm{TeV}}$ and gauge kinetic mixing constant $g_{YF}$ is lager than $-0.2$ by considering the experimental upper bounds on the branching ratios of LFV decays $\tau \rightarrow 3\mu ,$ $\mu \rightarrow 3e.$

Appendix A: Contributions to \({\bar{B}} \rightarrow X_s\gamma \) and \(B_s^0 \rightarrow \mu ^+\mu ^-\) in the FDM

Generally, the effective Hamilton for the transition $b\rightarrow s$ at hadronic scale can be written as

$$\begin{aligned} H_{eff}= & {} -\frac{4G_F}{\sqrt{2}}V_{ts}^*V_{tb}\Bigg [C_1\mathcal {O}^c_1+C_2\mathcal {O}_2^c\nonumber \\{} & {} +\sum _{i=3}^6\mathcal {O}_i+\sum _{i=7}^{10}(C_i\mathcal {O}_i+C'_i\mathcal {O}'_i)\nonumber \\{} & {} +\sum _{i=S,P}(C_i\mathcal {O}_i+C'_i\mathcal {O}'_i)\Bigg ], \end{aligned}$$

(A1)

where [44,45,46,47,48,49]

$$\begin{aligned}{} & {} {\mathcal {O}}_{_1}^u=(\bar{s}_{_L}\gamma _\mu T^au_{_L})(\bar{u}_{_L}\gamma ^\mu T^ab_{_L}),\nonumber \\{} & {} {\mathcal {O}}_{_2}^u=(\bar{s}_{_L}\gamma _\mu u_{_L})(\bar{u}_{_L}\gamma ^\mu b_{_L}),\nonumber \\{} & {} {\mathcal {O}}_{_3}=(\bar{s}_{_L}\gamma _\mu b_{_L})\sum \limits _q(\bar{q}\gamma ^\mu q),\nonumber \\{} & {} {\mathcal {O}}_{_4}=(\bar{s}_{_L}\gamma _\mu T^ab_{_L})\sum \limits _q(\bar{q}\gamma ^\mu T^aq), \nonumber \\{} & {} {\mathcal {O}}_{_5}=(\bar{s}_{_L}\gamma _\mu \gamma _\nu \gamma _\rho b_{_L})\sum \limits _q(\bar{q}\gamma ^\mu \gamma ^\nu \gamma ^\rho q)\nonumber \\{} & {} {\mathcal {O}}_{_6}=(\bar{s}_{_L}\gamma _\mu \gamma _\nu \gamma _\rho T^ab_{_L})\sum \limits _q(\bar{q}\gamma ^\mu \gamma ^\nu \gamma ^\rho T^aq), \nonumber \\{} & {} {\mathcal {O}}_{_7}={e\over 16\pi ^2}m_{_b}(\bar{s}_{_L}\sigma _{_{\mu \nu }}b_{_R})F^{\mu \nu },\nonumber \\{} & {} {\mathcal {O}}_{_7}'={e\over 16\pi ^2}m_{_b}(\bar{s}_{_R}\sigma _{_{\mu \nu }}b_{_L})F^{\mu \nu },\;\; \nonumber \\{} & {} {\mathcal {O}}_{_8}={g_{_s}\over 16\pi ^2}m_{_b}(\bar{s}_{_L}\sigma _{_{\mu \nu }}T^ab_{_R})G^{a,\mu \nu },\nonumber \\{} & {} {\mathcal {O}}_{_8}'={g_{_s}\over 16\pi ^2}m_{_b}(\bar{s}_{_R}\sigma _{_{\mu \nu }}T^ab_{_L})G^{a,\mu \nu },\;\; \nonumber \\{} & {} {\mathcal {O}}_{_9}={e^2\over g_{_s}^2}(\bar{s}_{_L}\gamma _\mu b_{_L})\bar{l}\gamma ^\mu l,\;\; {\mathcal {O}}_{_9}'={e^2\over g_{_s}^2}(\bar{s}_{_R}\gamma _\mu b_{_R})\bar{l}\gamma ^\mu l,\;\; \nonumber \\{} & {} {\mathcal {O}}_{_{10}}={e^2\over g_{_s}^2}(\bar{s}_{_L}\gamma _\mu b_{_L})\bar{l}\gamma ^\mu \gamma _5 l,\;\; {\mathcal {O}}_{_{10}}'={e^2\over g_{_s}^2}(\bar{s}_{_R}\gamma _\mu b_{_R})\bar{l}\gamma ^\mu \gamma _5 l,\;\; \nonumber \\{} & {} {\mathcal {O}}_{_S}={e^2\over 16\pi ^2}m_{_b}(\bar{s}_{_L}b_{_R})\bar{l}l,\;\; {\mathcal {O}}_{_S}'={e^2\over 16\pi ^2}m_{_b}(\bar{s}_{_R}b_{_L})\bar{l}l,\;\;\nonumber \\{} & {} {\mathcal {O}}_{_P}={e^2\over 16\pi ^2}m_{_b}(\bar{s}_{_L}b_{_R})\bar{l}\gamma _5l,\;\; {\mathcal {O}}_{_P}'={e^2\over 16\pi ^2}m_{_b}(\bar{s}_{_R}b_{_L})\bar{l}\gamma _5l. \nonumber \\ \end{aligned}$$

(A2)

In the definitions above, $g_s$ is the strong coupling constant, $T^a\,(a=1,\ldots ,8)$ are SU(3) generators, $F^{\mu \nu }$ and $G^{\mu \nu }$ are the electromagnetic and gluon field strength tensors respectively.

Fig. 8

The one loop Feynman diagrams contributing to $\bar{B}\rightarrow X_s\gamma$ from charged Higgs in the FDM

Fig. 9

The Feynman diagrams contributing to the decay $B_s^0\rightarrow \mu ^+\mu ^-$ in the B-LSSM

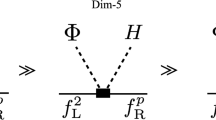
The dominant contributions to $b\rightarrow s\gamma$ come from the charged Higgs in the FDM, and the leading-order Feynman diagrams are plotted in Fig. 8. Then the branching ratio of $\bar{B}\rightarrow X_s\gamma$ can be written as

$$\begin{aligned} Br(\bar{B}\rightarrow X_s\gamma )=R\Big (|C_{7\gamma }(\mu _b)|^2+N(E_\gamma )\Big ), \end{aligned}$$

(A3)

where the overall factor $R=2.47\times 10^{-3},$ and the nonperturbative contribution $N(E_\gamma )=(3.6\pm 0.6)\times 10^{-3}$ [50]. $C_{7\gamma }(\mu _b)$ can be written as

$$\begin{aligned} C_{7\gamma }(\mu _b)=C_{7\gamma ,SM}(\mu _b)+C_{7,NP}(\mu _b), \end{aligned}$$

(A4)

where the hadron scale $\mu _b=2.5$ GeV and $C_{7\gamma ,SM}(\mu _b) = -0.3689$ for the SM contribution at NNLO level [50,51,52,53]. In new physics models, the corresponding Wilson coefficients at the bottom quark scale are [54, 55]

$$\begin{aligned} C_{7,NP}(\mu _b){\approx }0.5696 C_{7,NP}(\mu _{EW}){+}0.1107 C_{8,NP}(\mu _{EW}),\nonumber \\ \end{aligned}$$

(A5)

where

$$\begin{aligned} C_{7,NP}^{NP}(\mu _{EW})= & {} C_{7,NP}^{(1)}(\mu _{EW})+C_{7,NP}^{(2)}(\mu _{EW})\nonumber \\{} & {} +C_{7,NP}^{\prime (1)}(\mu _{EW})+C_{7,NP}^{\prime (2)}(\mu _{EW}),\nonumber \\ C_{8,NP}(\mu _{EW})= & {} C_{8g,NP}(\mu _{EW})+C_{8g,NP}^{\prime }(\mu _{EW}). \end{aligned}$$

(A6)

The coefficients $C_{7,NP}^{(1,2)}(\mu _{EW})$ are Wilson coefficients of the process $b\rightarrow s\gamma$ and can be calculated from the diagrams in Fig. 8(1), (2) respectively, the results read

$$\begin{aligned} C_{7,NP}^{(1)}(\mu _{EW})= & {} \sum _{H^-_i,u_j}\frac{s_W^2}{2e^2V^*_{ts}V_{tb}}\Bigg \{ \frac{1}{2}C_{H^-_i{\bar{s}} u_j}^R C_{H^-_i b {\bar{u}}_j}^{L}\nonumber \\{} & {} \times [-I_3(x_{u_j},x_{H^-_i})+I_4(x_{u_j},x_{H^-_i})]\nonumber \\{} & {} +\frac{m_{u_j}}{m_b}C_{H^-_i{\bar{s}} u_j}^L C_{H^-_i b {\bar{u}}_j}^{L}[-I_1(x_{u_j},x_{H^-_i})\nonumber \\{} & {} +I_3(x_{u_j},x_{H^-_i})]\Bigg \},\nonumber \\ C_{7,NP}^{(2)}(\mu _{EW})= & {} \sum _{H^-_j,u_i}\frac{s_W^2}{3e^2V^*_{ts}V_{tb}} \Bigg \{ \frac{1}{2}C_{H^-_j{\bar{s}} u_i}^R \nonumber \\{} & {} \times C_{H^-_j b {\bar{u}}_i}^{L}[-I_1(x_{u_i},x_{H^-_j})+2I_3(x_{u_i},x_{H^-_j})\nonumber \\{} & {} -I_4(x_{u_i},x_{H^-_j})]+\frac{m_{u_i}}{m_b}C_{H^-_j{\bar{s}} u_i}^L C_{H^-_j b {\bar{u}}_i}^{L}\nonumber \\{} & {} \times [I_1(x_{u_i},x_{H^-_j})-I_2(x_{u_i},x_{H^-_j})\nonumber \\{} & {} -I_3(x_{u_i},x_{H^-_j})]\Bigg \},\nonumber \\ C_{7}^{\prime NP(a)}(\mu _{EW})= & {} C_{7}^{\prime NP(a)}(\mu _{EW})(L\leftrightarrow R),\quad (a{=}1,2),\nonumber \\ \end{aligned}$$

(A7)

where $x_i=\frac{m_i^2}{m_W^2},$ $C_{abc}^{L,R}$ denotes the scalar parts of the interaction vertex about abc with a, b, c denoting the interactional particles, and the loop integral functions $I_{1,\ldots ,4}$ can be found in our previous work [39]. In addition, $C_{8g,NP}(\mu _{EW})$ and $C_{8g,NP}^{\prime }(\mu _{EW})$ at electroweak scale are

$$\begin{aligned}{} & {} C_{8g,NP}(\mu _{EW})=[C_{7,NP}^{(2)}(\mu _{EW})+C_{7,NP}^{(3)}(\mu _{EW})]/Q_u,\nonumber \\{} & {} C_{8g,NP}^{\prime }(\mu _{EW})=C_{8g,NP}(\mu _{EW})(L\leftrightarrow R), \end{aligned}$$

(A8)

where $Q_u=2/3.$

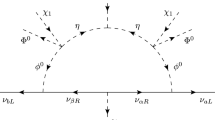
The main Feynman diagrams contributing to $B_s^0 \rightarrow \mu ^+\mu ^-$ are plotted in Fig. 9. At the electroweak energy scale $\mu _{EW},$ the corresponding Wilson coefficients can be written as

$$\begin{aligned}{} & {} C_{_{S,NP}}(\mu _{_\textrm{EW}})=\frac{\sqrt{2}s_{_W}c_{_W}}{4m_be^3V_{ts}^*V_{tb}}\Big [C_{_{S,NP}}^{(1)}(\mu _{_\textrm{EW}})+C_{_{S,NP}}^{(2)}(\mu _{_\textrm{EW}})\nonumber \\{} & {} \quad +C_{_{S,NP}}^{(3)}(\mu _{_\textrm{EW}})+C_{_{S,NP}}^{(4)}(\mu _{_\textrm{EW}}) +C_{_{S,NP}}^{(6)}(\mu _{_\textrm{EW}})\Big ],\nonumber \\{} & {} C_{_{S,NP}}^\prime (\mu _{_\textrm{EW}})=C_{_{S,NP}}(\mu _{_\textrm{EW}})(L\leftrightarrow R),\nonumber \\{} & {} C_{_{P,NP}}(\mu _{_\textrm{EW}})=\frac{\sqrt{2}s_{_W}c_{_W}}{4m_be^3V_{ts}^*V_{tb}}\Big [C_{_{P,NP}}^{(1)}(\mu _{_\textrm{EW}})+C_{_{P,NP}}^{(2)}(\mu _{_\textrm{EW}})\nonumber \\{} & {} \quad +C_{_{P,NP}}^{(3)}(\mu _{_\textrm{EW}})+C_{_{P,NP}}^{(4)}(\mu _{_\textrm{EW}}) +C_{_{P,NP}}^{(6)}(\mu _{_\textrm{EW}})\Big ],\nonumber \\{} & {} C_{_{P,NP}}^\prime (\mu _{_\textrm{EW}})=-C_{_{P,NP}}(\mu _{_\textrm{EW}})(L\leftrightarrow R),\nonumber \\{} & {} C_{_{9,NP}}(\mu _{_\textrm{EW}})=\frac{\sqrt{2}s_{_W}c_{_W}g_{_s}^2}{64\pi ^2e^3V_{ts}^*V_{tb}}\Big [C_{_{9,NP}}^{(5)}(\mu _{_\textrm{EW}})\nonumber \\{} & {} \quad +C_{_{9,NP}}^{(6)}(\mu _{_\textrm{EW}})+C_{_{9,NP}}^{(7)}(\mu _{_\textrm{EW}})+C_{_{9,NP}}^{(8)}(\mu _{_\textrm{EW}})\Big ],\nonumber \\{} & {} C_{_{9,NP}}^\prime (\mu _{_\textrm{EW}})=C_{_{9,NP}}(\mu _{_\textrm{EW}})(L\leftrightarrow R),\nonumber \\{} & {} C_{_{10,NP}}(\mu _{_\textrm{EW}})=\frac{\sqrt{2}s_{_W}c_{_W}g_{_s}^2}{64\pi ^2e^3V_{ts}^*V_{tb}} \Big [C_{_{10,NP}}^{(5)}(\mu _{_\textrm{EW}})+C_{_{10,NP}}^{(6)}(\mu _{_\textrm{EW}})\nonumber \\{} & {} \quad {+}C_{_{10,NP}}^{(7)}(\mu _{_\textrm{EW}}){+}C_{_{10,NP}}^{(8)}(\mu _{_\textrm{EW}})\Big ],\nonumber \\{} & {} C_{_{10,NP}}^\prime (\mu _{_\textrm{EW}}){=}{-}C_{_{10,NP}}(\mu _{_\textrm{EW}})(L\leftrightarrow R). \nonumber \\ \end{aligned}$$

(A9)

The superscripts $(1,\ldots ,8)$ corresponding to the contributions in Fig. 9$(1,\ldots ,8)$ respectively and the results can be written as

$$\begin{aligned}{} & {} C_{_{S,NP}}^{(1)}(\mu _{_\textrm{EW}})=\sum _{H^-_i,u_j,u_k}^{S=H_l,A_l}\frac{C_{{\bar{\mu }} S\mu }^L+C_{{\bar{\mu }} S\mu }^R}{2(m_b^2-m_S^2)}\nonumber \\{} & {} \quad \times \Big [C_{H^-_i{\bar{s}} u_j}^R C_{{\bar{u}}_j S u_k}^L C_{{\bar{u}}_k b H^-_i}^R G_2(x_{{\tilde{H}}^\pm _i},x_{u_j},x_{u_k})\nonumber \\{} & {} \quad +m_{u_j}m_{u_k}C_{H^-_i{\bar{s}} u_j}^R C_{{\bar{u}}_j S u_k}^R C_{{\bar{u}}_k b H^-_i}^R G_1(x_{{\tilde{H}}^\pm _i},x_{u_j},x_{u_k})\Big ],\nonumber \\{} & {} C_{_{P,NP}}^{(1)}(\mu _{_\textrm{EW}})=\sum _{H^-_i,u_j,u_k}^{S=H_l,A_l}\frac{-C_{{\bar{\mu }} S\mu }^L+C_{{\bar{\mu }} S\mu }^R}{2(m_b^2-m_S^2)}\nonumber \\{} & {} \quad \times \Big [C_{H^-_i{\bar{s}} u_j}^R C_{{\bar{u}}_j S u_k}^L C_{{\bar{u}}_k b H^-_i}^R G_2(x_{{\tilde{H}}^\pm _i},x_{u_j},x_{u_k})\nonumber \\{} & {} \quad +m_{u_j}m_{u_k}C_{H^-_i{\bar{s}} u_j}^R C_{{\bar{u}}_j S u_k}^R C_{{\bar{u}}_k b H^-_i}^R G_1(x_{{\tilde{H}}^\pm _i},x_{u_j},x_{u_k})\Big ], \nonumber \\ \end{aligned}$$

(A10)

$$\begin{aligned}{} & {} C_{_{S,NP}}^{(2)}(\mu _{_\textrm{EW}})=\sum _{u_i,H^\pm _j,H^\pm _k}^{S=H_l,A_l}\frac{1}{2(m_b^2-m_S^2)}\nonumber \\{} & {} \quad \times m_{u_i}C_{{\bar{s}} u_i H^\pm _j}^RC_{{\bar{u}}_i b H^\pm _k}^RC_{S H^\pm _j H^\pm _k}G_1(x_{u_i},x_{H^\pm _j},x_{H^\pm _k})\nonumber \\{} & {} \quad \times (C_{{\bar{\mu }} S\mu }^L+C_{{\bar{\mu }} S\mu }^R),\nonumber \\{} & {} C_{_{p,NP}}^{(2)}(\mu _{_\textrm{EW}})=\sum _{u_i,H^\pm _j,H^\pm _k}^{S=H_l,A_l}\frac{1}{2(m_b^2-m_S^2)}\nonumber \\{} & {} \quad \times m_{u_i}C_{{\bar{s}} u_i H^\pm _j}^RC_{{\bar{u}}_i b H^\pm _k}^RC_{S H^\pm _j H^\pm _k}G_1(x_{u_i},x_{H^\pm _j},x_{H^\pm _k})\nonumber \\{} & {} \quad \times (-C_{{\bar{\mu }} S\mu }^L+C_{{\bar{\mu }} S\mu }^R), \end{aligned}$$

(A11)

$$\begin{aligned}{} & {} C_{_{S,NP}}^{(3)}(\mu _{_\textrm{EW}})=\sum _{u_i,H^\pm _k}^{S=H_l,A_l}\frac{-C_{W^\pm S H^\pm _k}}{2(m_b^2-m_S^2)}\nonumber \\{} & {} \quad \times \Big [C_{{\bar{s}} W^\pm u_i}^LC_{{\bar{u}}_i H^\pm _k b}^RG_2(x_{u_i},1,x_{H^\pm _k}) -2m_bm_{u_i}C_{{\bar{s}} W^\pm u_i}^L\nonumber \\{} & {} \quad \times C_{{\bar{u}}_i H^\pm _k b}^LG_1(x_{u_i},1,x_{H^\pm _k})\Big ] (C_{{\bar{\mu }} S\mu }^L+C_{{\bar{\mu }} S\mu }^R),\nonumber \\{} & {} C_{_{P,NP}}^{(3)}(\mu _{_\textrm{EW}})=\sum _{u_i,H^\pm _k}^{S=H_l,A_l}\frac{-C_{W^\pm S H^\pm _k}}{2(m_b^2-m_S^2)}\nonumber \\{} & {} \quad \times \Big [C_{{\bar{s}} W^\pm u_i}^LC_{{\bar{u}}_i H^\pm _k b}^RG_2(x_{u_i},1,x_{H^\pm _k}) -2m_bm_{u_i}C_{{\bar{s}} W^\pm u_i}^L\nonumber \\{} & {} \quad \times C_{{\bar{u}}_i H^\pm _k b}^LG_1(x_{u_i},1,x_{H^\pm _k})\Big ](-C_{{\bar{\mu }} S\mu }^L+C_{{\bar{\mu }} S\mu }^R),\nonumber \\ \end{aligned}$$

(A12)

$$\begin{aligned}{} & {} C_{_{S,NP}}^{(4)}(\mu _{_\textrm{EW}})=\sum _{u_i,H^\pm _j}^{S=H_l,A_l}\frac{-C_{W^\pm S H^\pm _j}}{2(m_b^2-m_S^2)}C_{{\bar{s}} H^\pm _j u_i}^RC_{{\bar{u}}_i W^\pm b}^R\nonumber \\{} & {} \quad \times G_2(x_{u_i},x_{H^\pm _j},1)(C_{{\bar{\mu }} S\mu }^L+C_{{\bar{\mu }} S\mu }^R),\nonumber \\{} & {} C_{_{S,NP}}^{(4)}(\mu _{_\textrm{EW}})=\sum _{u_i,H^\pm _j}^{S=H_l,A_l}\frac{-C_{W^\pm S H^\pm _j}}{2(m_b^2-m_S^2)}\nonumber \\{} & {} \quad \times C_{{\bar{s}} H^\pm _j u_i}^RC_{{\bar{u}}_i W^\pm b}^RG_2(x_{u_i},x_{H^\pm _j},1) (-C_{{\bar{\mu }} S\mu }^L+C_{{\bar{\mu }} S\mu }^R), \nonumber \\ \end{aligned}$$

(A13)

$$\begin{aligned}{} & {} C_{_{9,NP}}^{(5)}(\mu _{_\textrm{EW}})=\sum _{{\tilde{H}}^\pm _i,u_j,u_k }^{V}\frac{C_{{\bar{\mu }} V\mu }^L+C_{{\bar{\mu }} V\mu }^R}{-2(m_b^2-m_V^2)}\nonumber \\{} & {} \quad \times \Big [-\frac{1}{2}C_{H^\pm _i{\bar{s}} u_j}^R C_{{\bar{u}}_j V u_k}^R C_{u_k s H^\pm _i}^L G_2(x_{H^\pm _i},x_{u_j},x_{u_k})\nonumber \\{} & {} \quad +m_{u_j}m_{u_k} C_{H^\pm _i{\bar{s}} u_j}^R C_{{\bar{u}}_j V u_k}^L C_{{\bar{u}}_k s H^\pm _i}^L G_1(x_{H^\pm _i},x_{u_j},x_{u_k})\Big ],\nonumber \\{} & {} C_{_{10,NP}}^{(5)}(\mu _{_\textrm{EW}})=\sum _{{\tilde{H}}^\pm _i,u_j,u_k }^{V}\frac{-C_{{\bar{\mu }} V\mu }^L+C_{{\bar{\mu }} V\mu }^R}{-2(m_b^2-m_V^2)}\nonumber \\{} & {} \quad \times \Big [-\frac{1}{2}C_{H^\pm _i{\bar{s}} u_j}^R C_{{\bar{u}}_j V u_k}^R C_{u_k s H^\pm _i}^L G_2(x_{H^\pm _i},x_{u_j},x_{u_k})\nonumber \\{} & {} \quad +m_{u_j}m_{u_k} C_{H^\pm _i{\bar{s}} u_j}^R C_{{\bar{u}}_j V u_k}^L C_{{\bar{u}}_k s H^\pm _i}^L G_1(x_{H^\pm _i},x_{u_j},x_{u_k})\Big ], \nonumber \\ \end{aligned}$$

(A14)

$$\begin{aligned}{} & {} C_{_{9,NP}}^{(6)}(\mu _{_\textrm{EW}})=\sum _{u_i,H^\pm _j,H^\pm _k}^V\frac{C_{{\bar{\mu }} V\mu }^L+C_{{\bar{\mu }} V\mu }^R}{4(m_b^2-m_V^2)}\nonumber \\{} & {} \quad \times C_{{\bar{s}} u_i H^\pm _j}^RC_{{\bar{u}}_i b H^\pm _k}^LC_{V H^\pm _j H^\pm _k}G_2(x_{u_i},x_{H^\pm _j},x_{H^\pm _k}),\nonumber \\{} & {} C_{_{10,NP}}^{(6)}(\mu _{_\textrm{EW}})=\sum _{u_i,H^\pm _j,H^\pm _k}^V\frac{-C_{{\bar{\mu }} V\mu }^L+C_{{\bar{\mu }} V\mu }^R}{4(m_b^2-m_V^2)}\nonumber \\{} & {} \quad \times C_{{\bar{s}} u_i H^\pm _j}^RC_{{\bar{u}}_i b H^\pm _k}^LC_{V H^\pm _j H^\pm _k}G_2(x_{u_i},x_{H^\pm _j},x_{H^\pm _k}),\nonumber \\{} & {} C_{_{S,NP}}^{(6)}(\mu _{_\textrm{EW}})=\sum _{u_i,H^\pm _j,H^\pm _k}^V\frac{C_{{\bar{\mu }} V\mu }^L+C_{{\bar{\mu }} V\mu }^R}{-2(m_b^2-m_V^2)}\nonumber \\{} & {} \quad \times m_bm_{u_i}C_{{\bar{s}} u_i H^\pm _j}^RC_{{\bar{u}}_i b H^\pm _k}^RC_{V H^\pm _j H^\pm _k} G_1(x_{u_i},x_{H^\pm _j},x_{H^\pm _k}),\nonumber \\{} & {} C_{_{P,NP}}^{(6)}(\mu _{_\textrm{EW}})=\sum _{u_i,H^\pm _j,H^\pm _k}^V\frac{C_{{\bar{\mu }} V\mu }^L-C_{{\bar{\mu }} V\mu }^R}{-2(m_b^2-m_V^2)}\nonumber \\{} & {} \quad \times m_bm_{u_i}C_{{\bar{s}} u_i H^\pm _j}^RC_{{\bar{u}}_i b H^\pm _k}^RC_{V H^\pm _j H^\pm _k} G_1(x_{u_i},x_{H^\pm _j},x_{H^\pm _k}), \nonumber \\ \end{aligned}$$

(A15)

$$\begin{aligned}{} & {} C_{_{9,NP}}^{(7)}(\mu _{_\textrm{EW}})=\sum _{u_i,H^\pm _k}^V\frac{C_{{\bar{\mu }} V\mu }^L+C_{{\bar{\mu }} V\mu }^R}{2(m_b^2-m_V^2)}\nonumber \\{} & {} \quad \times m_{u_i}C_{{\bar{s}} u_i W^\pm }^LC_{{\bar{u}}_i b H^\pm _k}^LC_{V W^\pm H^\pm _k} G_1(x_{u_i},x_W,x_{H^\pm _k}),\nonumber \\{} & {} C_{_{10,NP}}^{(7)}(\mu _{_\textrm{EW}})=\sum _{u_i,H^\pm _k}^V\frac{-C_{{\bar{\mu }} V\mu }^L+C_{{\bar{\mu }} V\mu }^R}{2(m_b^2-m_V^2)}\nonumber \\{} & {} \quad \times m_{u_i}C_{{\bar{s}} u_i W^\pm }^LC_{{\bar{u}}_i b H^\pm _k}^L C_{V W^\pm H^\pm _k}G_1(x_{u_i},x_W,x_{H^\pm _k}),\nonumber \\ \end{aligned}$$

(A16)

$$\begin{aligned}{} & {} C_{_{9,NP}}^{(8)}(\mu _{_\textrm{EW}})=\sum _{u_i,H^\pm _j}^V\frac{C_{{\bar{\mu }} V\mu }^L+C_{{\bar{\mu }} V\mu }^R}{2(m_b^2-m_V^2)}\nonumber \\{} & {} \quad \times m_{u_i}C_{{\bar{s}} u_i H^\pm _j}^RC_{{\bar{u}}_i b W^\pm }^L C_{V W^\pm H^\pm _k}G_1(x_{u_i},x_{H^\pm _j},x_W),\nonumber \\{} & {} C_{_{10,NP}}^{(8)}(\mu _{_\textrm{EW}})=\sum _{u_i,H^\pm _j}^V\frac{-C_{{\bar{\mu }} V\mu }^L+C_{{\bar{\mu }} V\mu }^R}{2(m_b^2-m_V^2)}\nonumber \\{} & {} \quad \times m_{u_i}C_{{\bar{s}} u_i H^\pm _j}^RC_{{\bar{u}}_i b W^\pm }^L C_{V W^\pm H^\pm _k}G_1(x_{u_i},x_{H^\pm _j},x_W),\nonumber \\ \end{aligned}$$

(A17)

where V denotes the vector bosons $\gamma ,$ Z,  $Z',$ and $C_{aVb}$ denote the scalar parts of the corresponding interaction vertex aVb. The concrete expressions for loop integral $G_k(k=1,\ldots ,4)$ can be found in the Appendix B of our previous work [39]. The Wilson coefficients at hadronic energy scale from the SM to next-to-next-to-logarithmic accuracy are shown in Table 5. In addition, the Wilson coefficients in Eq. (A9) should be evolved down to hadronic scale $\mu \sim m_b$ by the renormalization group equations (Table 5):

Table 5 At hadronic scale $\mu =m_{_b},$ SM Wilson coefficients to next-to-next-to-logarithmic accuracy

$$\begin{aligned}{} & {} \overrightarrow{C}_{_{NP}}(\mu )=\widehat{U}(\mu ,\mu _0)\overrightarrow{C}_{_{NP}}(\mu _0) ,\nonumber \\{} & {} \overrightarrow{C^\prime }_{_{NP}}(\mu )=\widehat{U^\prime }(\mu ,\mu _0) \overrightarrow{C^\prime }_{_{NP}}(\mu _0) \end{aligned}$$

(A18)

with

$$\begin{aligned}{} & {} \overrightarrow{C}_{_{NP}}^{T}=\Big (C_{_{1,NP}},\;\cdots ,\;C_{_{6,NP}}, C_{_{7,NP}}^{eff},\;C_{_{8,NP}}^{eff},\nonumber \\{} & {} \quad C_{_{9,NP}}^{eff}-Y(q^2),\; C_{_{10,NP}}^{eff}\Big ) ,\nonumber \\{} & {} \overrightarrow{C}_{_{NP}}^{\prime ,\;T}=\Big (C_{_{7,NP}}^{\prime ,\;eff},\; C_{_{8,NP}}^{\prime ,\;eff},\;C_{_{9,NP}}^{\prime ,\;eff},\; C_{_{10,NP}}^{\prime ,\;eff}\Big ). \end{aligned}$$

(A19)

Correspondingly, the evolving matrices $\widehat{U}(\mu ,\mu _0),\;\widehat{U^\prime }(\mu ,\mu _0)$ can be found in our previous work [39].

Then, the squared amplitude can be written as

$$\begin{aligned}{} & {} |{\mathcal {M}}_s|^2=16G_F^2|V_{tb}V_{ts}^*|^2M_{B_s^0}^2\Big [|F_S^s|^2+|F_P^s+2m_{\mu }F_A^s|^2\Big ],\nonumber \\ \end{aligned}$$

(A20)

and

$$\begin{aligned}{} & {} F_S^s=\frac{\alpha _{EW}(\mu _b)}{8\pi }\frac{m_b M_{B_s^0}^2}{m_b+m_s}f_{B_s^0}(C_S-C_S'), \end{aligned}$$

(A21)

$$\begin{aligned}{} & {} F_P^s=\frac{\alpha _{EW}(\mu _b)}{8\pi }\frac{m_b M_{B_s^0}^2}{m_b+m_s}f_{B_s^0}(C_P-C_P'), \end{aligned}$$

(A22)

$$\begin{aligned}{} & {} F_A^s=\frac{\alpha _{EW}(\mu _b)}{8\pi }f_{B_s^0}\Big [C_{10}^{eff}(\mu _b)-C_{10}^{\prime eff}(\mu _b)\Big ], \end{aligned}$$

(A23)

where $f_{B_s^0}=(227\pm 8)\;\textrm{MeV}$ denote the decay constants, $M_{B_s^0}=5.367\; {\textrm{GeV}}$ denote the masses of neutral meson $B_s^0.$ The branching ratio of $B_s^0\rightarrow \mu ^+\mu ^-$ can be written as

$$\begin{aligned} Br(B_s^0\rightarrow \mu ^+\mu ^-)=\frac{\tau _{B_s^0}}{16\pi }\frac{|{\mathcal {M}}_s|^2}{M_{B_s^0}}\sqrt{1-\frac{4m_{\mu }^2}{M_{B_s^0}^2}}, \end{aligned}$$

(A24)

with $\tau _{B_s^0}=1.466(31)\;\textrm{ps}$ denoting the life time of meson.