1 Introduction

The astronomical observations suggest that the observable universe is expanding with acceleration and it is homogeneous and isotropic at a great accuracy [1,2,3]. The fluid responsible for the observed accelerated expansion of the universe may have a negative pressure and it is dubbed as dark energy [4,5,6]. The origin and nature of the dark energy is still one of the fascinating and challenging component of the modern cosmology. The cosmological constant [7] may give rise to the negative pressure and thus, it may accelerate the universe expansion. However, it suffers with some serious theoretical shortcomings [8]. This issue motivates to search for the alternatives which may include scalar field models, modified gravity models and the unified dark energy models [4,5,6, 9].

The observed homogeneous and isotropic nature of the universe may be explained by the inflationary paradigm, which usually starts with the homogeneous and isotropic metric in the literature [10]. Planck probe results [3, 11] point toward the presence of anisotropic ‘anomalies’ in the cosmic background radiation spectrum. This creates a lot of interest towards the class of anisotropic geometries such as the Bianchi class of geometries [12] and the Kantowski–Sachs geometry [13]. Since, in these geometries the universe may evolve towards the homogeneity and isotropy from the anisotropic one, with some cosmological mechanism. Due to the richer dynamical structure yielded by the anisotropic models, one may also be able to analyze different issues such as the behavior of model near the spacetime singularities, issue of highly isotropic present day universe, the effects of anisotropy on different astronomical observables etc., as compared to the isotropic models. In the Bianchi classification [12], Bianchi I (BI) geometry is spatially flat but the Bianchi III (BIII) and Bianchi V geometries are the hyper-spherically curved geometries. Isotropic analogue of BI spacetime is the spatially flat Friedmann–Robertson–Walker (FRW) spacetime and the open FRW geometry may be obtained from the BIII and BV geometries under certain conditions of isotropization. On the other hand, the Kantowski–Sachs metric possess its isotropic analogue with the closed FRW metric. Different cosmological issues have been investigated with the Bianchi I [14,15,16,17,18,19,20,21,22,23,24,25], Bianchi III [26,27,28,29,30,31], Kantowski–Sachs [32,33,34,35,36,37,38] and Bianchi V geometries [39,40,41,42,43,44,45,46,47]. The Bianchi III geometry is a special case of Bianchi VI\({}_h\) (BVI\({}_h)\) geometry, in particular, BIII=BVI\({}_{-1}\) [46]. It is worthwhile to mention that the spatially homogeneous spacetimes may be classified into three broad classes, namely the Bianchi class A, Bianchi class B and Kantowski–Sachs geometries [12]. BI geometry belongs to class A and BIII, BV, BVI\({}_{h}\) belong to class B in the notations of Ellis and MacCallum [43]. In this paper, we proceed with the locally rotationally symmetric (LRS) spacetimes. A spatially homogeneous spacetime is said to be LRS if it admits an extra killing vector field, in addition to three killing vector fields needed for the spatial homogeneity. In class A, LRS cases are allowed by the Bianchi I, II, VII\({}_0,\) VIII and IX spacetimes. And, in class B, LRS cases are allowed for the Bianchi III, V and VII\({}_h\) spacetimes [12, 43, 48]. The Kantowski–Sachs spacetime automatically admits a fourth killing vector, in addition to the Killing vector fields for spatial homogeneity [13].

By considering an unified metric for the Bianchi I, Bianchi III and Kantowski–Sachs geometries and another LRS metric for Bianchi V geometry, we aim to perform a qualitative study of these geometries with affine equation of state using dynamical system technique. The dynamical system method and the corresponding phase space analysis allows to overcome the non-linear nature of the cosmological equations in an efficient way. This method allows to extract the qualitative description of the model and may also be used to identify the stability of solutions of cosmological interest, such as those with the phantom and/or quintessence evolution phases, stiff matter-, radiation-, matter- and/or de Sitter-like expansion phases. This method also offers for the study of universe evolution in a cosmological models, irrespective of the initial conditions. This method have been used extensively to study the cosmological models in different gravity theories and geometries [14,15,16,17, 20, 25,26,27,28, 32,33,41, 44, 46, 49,50,61], for a more technical detail on the theory of dynamical systems in cosmology, see [9, 12, 62, 63].

In the homogeneous and isotropic background, the barotropic fluid following an affine equation of state (EoS) yields either the de Sitter scenario at late-times or a bouncing universe evolution or a combination of both these scenarios [57]. The cyclic universe evolution may also be realized with this EoS in the alternative gravity framework [58, 59]. A bouncing universe evolution may be governed by the affine EoS in the close neighborhood of bounce in the non-conservative theories of gravity [19]. This fluid also offers accelerating universe evolution at late-times in the model-dependent investigations in the isotropic [60, 64] as well as anisotropic spacetime [65, 66]. A simple extension of the affine EoS may be the polytropic EoS [67,68,69,70,71,72]. Polytropic EoS may yield various interesting cosmological and astrophysical scenarios. In addition, barotropic fluids satisfying \(p=f(\rho )\) (where p and \(\rho \) are the pressure and energy density respectively and f denotes an arbitrary function) have also been incorporated in models to explain various cosmological issues, for more details see Bamba et al. [5]. However, we aim to explore the effects of inclusion of shear and three-curvature scalar in the class of anisotropic spacetime having the affine EoS in the matter sector of the Einstein’s field equations in the General Relativity framework. It would be interesting to see for the class of evolution scenarios of the universe in the model using dynamical system analysis, since the affine EoS is the simplest extension of EoS \(p=\alpha \rho .\) Broadly speaking, the compatibility of the evolution trajectories in the phase space with the observational features (such as the issue of accelerating universe transition from the decelerating evolution, present day observed isotropy etc.) may yield the validity for the application of the dynamical system method in the model.

The basic equations of the model have been written in the Sect. 2. In Sect. 3, we compose the autonomous system for the locally rotationally symmetric Bianchi I and Bianchi III geometries. We perform a detailed analysis of the system using qualitative tools such as the linear stability and statefinder diagnostic analysis. In Sect. 4, we study the autonomous system for the Kantowski–Sachs model in order to identify different evolutionary phases including for the possibility of a synchronous bouncing evolution of the universe. In Sect. 5, we study the locally rotationally symmetric Bianchi V geometry with affine EoS for its qualitative evolution. In Sect. 6, we summarize the obtained results with conclusions.

2 The model

We consider an anisotropic but homogeneous metric for the universe given by

$$\begin{aligned} ds^2=dt^2-{a_1}^2dr^2-{a_2}^2(d\theta ^2+f^2(\theta )d\phi ^2) \end{aligned}$$
(1)

where \(a_1,a_2\) are the directional scale factors. Due to the homogeneity property, \(a_1,a_2\) are the functions of cosmic time t only. Above metric may reduce into the Kantowski–Sachs (KS), locally rotationally symmetric Bianchi III (LRS BIII) and Bianchi I (LRS BI) metric for \(f(\theta )=\sin \theta , \sinh \theta , \theta \) respectively. We follow the units \(8\pi G=c=\hbar =k_b=1\) and define the directional Hubble parameters as \(H_i=\frac{\dot{a_i}}{a_i},i=1,2,\) where dot denotes the time derivative. The expansion/contraction of the volume is measured by the expansion scalar \((\Theta )\) and it is given by the divergence of 4-velocity field \(u^i.\) That is, \(\Theta ={u^i}_{;i}=3H\) and we take \(3H=H_1+2H_2,\) where H is the mean Hubble parameter. For the choice of tangent vector \(u^i,\) the propagation equations of \(\Theta ,\sigma ,{}^3R\) are

$$\begin{aligned}{} & {} \dot{\Theta }+\frac{1}{3}\Theta ^2+2\sigma ^2=-\frac{1}{2}(\rho +3p) \end{aligned}$$
(2)
$$\begin{aligned}{} & {} \dot{\sigma }+\Theta \sigma -\frac{1}{2\sqrt{3}}{}^3R=0 \end{aligned}$$
(3)
$$\begin{aligned}{} & {} {}^3\dot{R}+\frac{2}{3}\Theta \cdot {}^3R-\frac{2}{\sqrt{3}}{}^3R\sigma =0 \end{aligned}$$
(4)

where \({}^3R\) denotes the 3-curvature scalar and \(\sigma \) is the shear scalar (defined from the trace-free symmetric shear tensor \((\sigma _{ij})\) by \(\sigma ^2=\frac{1}{2}\sigma _{ij}\sigma ^{ij}).\) \(\rho \) and p denote the conventional matter density and pressure of the universe and it may be given from the perfect fluid energy-momentum tensor \(T_{ij}=(\rho +p)u_iu_j-pg_{ij}.\) The generalized Friedmann constraint relating the 3-space Ricci scalar with the matter energy density is

$$\begin{aligned} {}^3R=2\sigma ^2-\frac{2}{3}\Theta ^2+2\rho . \end{aligned}$$
(5)

Above equation is also known as the Gauss–Codazzi constraint. For LRS BI, LRS BIII and KS universe, \({}^3R=0,-\frac{2}{{a_2}^2},\frac{2}{{a_2}^2}\) respectively. The Bianchi identity \(({G_{ij}}^{;j}=0)\) would lead to the continuity equation given by

$$\begin{aligned} \dot{\rho }+\Theta (\rho +p)=0. \end{aligned}$$
(6)

The perfect fluid matter consisting of the radiation and matter (dark and baryonic) will decelerate the universe expansion due to the positive active gravitational mass of these components. Observations [1,2,3] suggest that the universe expansion is accelerating. In order to incorporate the cosmological mechanism for the accelerating universe evolution, we take the simplest modification of the equation of state \(p=\alpha \rho \) as [57, 73]

$$\begin{aligned} p=\alpha \rho -\rho _0 \end{aligned}$$
(7)

where \(\alpha ,\rho _0\) are some constants. This simple generalization provides a description of hydrodynamically unstable (stable) fluids for \(\alpha <0 \ (\alpha >0)\) respectively. On the basis of \(\rho _0\) value, for a very small \(\alpha \) with small magnitude of energy density, we may have a mechanism for the existence of negative pressure in the model. With the negative pressure component (dark energy), one may explain the accelerating expansion of the universe in the model. The null energy condition (NEC) may be satisfied for \(\rho +p=(1+\alpha )\rho -\rho _0>0.\) NEC will be violated during the phantom dominated evolution of the universe. The parameter \(\alpha \) may also be interpreted as the adiabatic sound speed squared of the linear perturbations and the model is said to be classically stable for \(0\le {c_s}^2\le 1,\) since \({c_s}^2=\frac{\partial p}{\partial \rho }.\) This EoS may yield different evolutionary aspects of the universe including the late-time accelerating universe, isotropic universe at late-times and the cyclic universe evolution etc. [19, 58,59,60, 64,65,66].

The point-wise energy conditions may be written by the use of energy momentum tensor \(T_{ij}=diag(\rho ,-p,-p,-p)\) as: Null energy condition (NEC) which is given by \(\rho +p\ge 0,\) Weak energy condition (WEC) which is given by \(\rho \ge 0, \ \rho +p\ge 0,\) Dominant energy condition (DEC) which is given by \(\rho \ge 0, \ \rho \pm p\ge 0\) and the Strong energy condition (SEC) which is given by \(\rho +p\ge 0, \ \rho +3p\ge 0\) respectively.

The brief outline for the identification of the stability nature of fixed points in the dynamical system analysis may be summed up as follows: The fixed point obtained from the autonomous system is used for the calculation of eigenvalues of the linearized matrix around the fixed points (Jacobian matrix). If all the eigenvalues are negative (positive), then the fixed point may be termed as stable (unstable) point respectively. The stable (unstable) point also act as a sink (source) of the system respectively. In other words, the stable (unstable) point act as attractor (repeller) of the cosmological dynamical system respectively. There may be a case where the eigenvalues at some particular fixed point are having positive as well as negative signs, this kind of point is termed as the saddle point. At saddle point, the trajectories in the phase plane are attracted towards the direction having negative sign and repels from the direction having positive sign. The saddle points are very useful to portray intermediate evolutionary phases such as the matter- and radiation dominated phases in the cosmological dynamical systems. And, the unstable and stable fixed points are useful to exhibit the origin and the ultimate fate the universe evolution respectively [9, 12, 62]. In the cosmological dynamical systems, the terminology of fixed point and critical point follows from the physical and mathematical view respectively.

3 LRS Bianchi I and Bianchi III cosmology

In order to explore the universe evolution in the LRS BI and BIII models with the affine EoS, we incorporate dynamical system technique. This will enable us to analyze different evolution trajectories, independent of the initial conditions. For these cases, we define the dynamical variables of the system in an unified way. For converting the propagation equations of the expansion scalar, shear scalar and spatial 3-curvature (given by Eqs. 2–4) into an autonomous system, we define

$$\begin{aligned} \Omega _m=\frac{\rho }{3H^2}, \ \Omega _k=\frac{{}^3R}{6H^2}, \ \Sigma =\frac{\sigma }{\sqrt{3}H}, \ \Omega _{\Lambda }=\frac{\rho _0}{3H^2}. \end{aligned}$$
(8)

The variables \(\Omega _m,\Omega _k\) and \(\Sigma \) measure, respectively, the dynamical importance of matter content of the universe, spatial geometry of the space-time and rate of shear in terms of volume expansion \(\Theta =3H.\) For LRS BI and BIII spacetime, \({}^3R\) will be 0 and \(-\frac{2}{{a_2}^2}\) respectively. The variable \(\Omega _m\) denotes the dimensionless energy density of the conventional matter in the universe composed of matter and radiation as a whole. We take the independent variable as logarithm of the scale factor given by \(N=\ln a\) and the ‘prime’ denotes the derivative with respect to it. This normalization variable is suitable for the study of expanding cosmological \((H>0)\) scenarios. For the LRS BI model, \({}^3R=0\) and thus \(\Omega _k=0\) in terms of the dynamical variables will correspond to the LRS BI case. In the LRS BIII cosmology, one may have the fixed points with \(\Omega _k=0,\) which in fact belong to the LRS BI boundary. However, the stability in the case of LRS BIII model may be different, since the system may evolve in the \(\Omega _k\) direction. It is also worthwhile to mention that the invariant sub-manifold of the dynamical system means that the system cannot go through the sub-manifold and it may only approach it in an asymptotic way.

The Gauss–Codazzi equation will yield a constraint (in terms of the dynamical variables) as

$$\begin{aligned} \Omega _m+\Sigma ^2-\Omega _k=1. \end{aligned}$$
(9)

The deceleration parameter (indicating the rate at which universe expansion is slowing down) is defined as \(q=-1-\frac{3\dot{\Theta }}{{\Theta }^2}.\) Equivalently, we may have \(q=-1-\frac{\dot{H}}{H^2}.\) We use deceleration parameter to define the effective equation of state (EoS) parameter as \(\omega =\frac{1}{3}(2q-1).\) From Eqs. (2), (7) and (8), we may write

$$\begin{aligned} \frac{\dot{H}}{H^2}=-1-2\Sigma ^2-\frac{1}{2}(1+3\alpha )\Omega _m+\frac{3}{2}\Omega _{\Lambda }. \end{aligned}$$
(10)

Due to one constraint equation, the resulting state space is 3-dimensional. The dynamical system governing the propagation of dimensionless variables are given by

$$\begin{aligned} {\Omega _m}'= & {} -\Omega _m \left( 1+3 \alpha +3 \Omega _{\Lambda }-4 \Sigma ^2\right) \nonumber \\{} & {} +3 \Omega _{\Lambda }+(1+3 \alpha ) {\Omega _m}^2 \end{aligned}$$
(11)
$$\begin{aligned} \Sigma '= & {} -1+\Omega _m+\Sigma ^2+2 \Sigma ^3\nonumber \\{} & {} +\,\frac{1}{2} \Sigma (-4+(1+3 \alpha ) \Omega _m-3 \Omega _{\Lambda }) \end{aligned}$$
(12)
$$\begin{aligned} {\Omega _{\Lambda }}'= & {} \Omega _{\Lambda } \left( 2+4 \Sigma ^2+(1+3 \alpha ) \Omega _m-3 \Omega _{\Lambda }\right) . \end{aligned}$$
(13)

In terms of variables (8), the deceleration and EoS parameters may be written as

$$\begin{aligned} q= & {} \frac{1}{2} \left( 4 \Sigma ^2-3 \Omega _{\Lambda } +(1+3 \alpha )\Omega _m\right) \end{aligned}$$
(14)
$$\begin{aligned} \omega= & {} \frac{1}{3} \left( -1+4 \Sigma ^2-3 \Omega _{\Lambda }+(1+3 \alpha ) \Omega _m\right) . \end{aligned}$$
(15)

The fixed points of the system (11–13) may be given from the equations \({\Omega _m}'=0,\Sigma '=0,{\Omega _{\Lambda }}'=0.\) Above system possess 7 fixed points. This system possesses one model parameter \(\alpha \) and we use different cosmologically viable criteria to constrain this parameter. The stability behaviors and cosmological implications at the fixed points are given below in a point-wise manner.

  • \(K_{-}(\Omega _m=0,\Sigma =-1,\Omega _{\Lambda }=0)\): This shear-dominated point will exist for all \(\alpha .\) The eigenvalues are given by \(\{6,2,-3 (\alpha -1)\}.\) The point is unstable for \(\alpha <1\) and thus, it may act as a source. It will be saddle otherwise.

  • \(K_{+}(\Omega _m=0,\Sigma =1,\Omega _{\Lambda }=0)\): This point will always exist in the model. The eigenvalues are \(\{6,6,-3 (\alpha -1)\}.\) For \(\alpha <1,\) this point will act as a source and saddle otherwise.

    The points \(K_{-}\) and \(K_{+}\) will belong to the spatially-flat \((\Omega _k=0)\) region of the spacetime. These points are corresponding to the vacuum Kasner models. The universe is decelerating with the effective stiff fluid-like domination. At these points, expansion scalar \((\Theta )\) scales with \(\frac{1}{t}\) and the directional scale factors may scale with either

    $$\begin{aligned} a_1\propto t, \ a_2\propto \text {constant},\text { or} \ a_1\propto t^{-\frac{1}{3}}, \ a_2 \propto t^{\frac{2}{3}}. \end{aligned}$$

  • \(R(\Omega _m=1,\Sigma =0,\Omega _{\Lambda }=0)\): The eigenvalues of the Jacobian matrix at this point are given by \(\left\{ \frac{3 (\alpha -1)}{2},3 (\alpha +1),3 \alpha +1\right\} .\) The point will be source (sink) for \(\alpha >1\) \((\alpha <-1)\) respectively and saddle otherwise.

    This point will exhibit solutions corresponding to the spatially flat, shear-free (isotropic) universe. The conventional matter dominating universe evolution will depend on the value of \(\alpha .\) For \(-1<\alpha <1,\) the point will be saddle in nature. For \(\alpha >-\frac{1}{3},\) the universe will be decelerating. However, the accelerating universe evolution may be realized at this point for \(\alpha <-\frac{1}{3}.\) For a classically stable universe \((0\le {c_s}^2\le 1),\) the universe evolution will be decelerating and the point will be exhibiting saddle behavior. In particular, for \(\alpha =\frac{1}{3},\) this point will represent a radiation-dominated universe. The expansion scalar will scale with \(\frac{3}{2t}\) and the directional scale factors will scale with either

    $$\begin{aligned}{} & {} a_1\propto \text {constant}, \ a_2 \propto t^{\frac{1}{4}}, \quad \text {or} \quad a_1\propto t, \ a_2 \propto t^{-\frac{1}{4}}, \quad \text {or} \\{} & {} a_1\propto t^{\frac{1}{2}}, \ a_2 \propto \text {constant}. \end{aligned}$$

  • \(M(\Omega _m=0,\Sigma =-\frac{1}{2},\Omega _{\Lambda }=0)\): The eigenvalues will be given by \(\left\{ 3,-\frac{3}{2},-3 \alpha \right\} .\) This point is always saddle in nature and the value of \(\alpha \) will not affect the stability nature of this point.

    The point belongs to the spatially-curved region \((\Omega _k<0)\) having LRS BIII geometry. This saddle point will lie on the vacuum boundary where shear is dominating. This point will represent matter-dominated decelerating universe in an effective sense for which \(q=\frac{1}{2}\) and \(\omega =0.\) The expansion scalar will scale with \(\frac{2}{t}\) and the directional scale factors will scale with either

    $$\begin{aligned}{} & {} a_1\propto \text {constant}, \ a_2\propto t^{\frac{1}{3}}, \quad \text {or} \quad a_1\propto t^{-\frac{2}{3}}, \ a_2\propto t^{\frac{2}{3}}, \quad \text {or} \\{} & {} a_1\propto t^{\frac{2}{3}}, \ a_2\propto \text {constant}. \end{aligned}$$

  • \(dS(\Omega _m=1,\Sigma =0,\Omega _{\Lambda }=1+\alpha )\): The eigenvalues are given by \(\{-3,-2,-3 (\alpha +1)\}.\) The point is sink for \(\alpha >-1\) and saddle otherwise.

    This point will represent spatially-flat, isotropic universe and it will act as an attractor for \(\alpha >-1.\) And, thus the dark energy-dominated accelerating universe expansion may be explained in the present anisotropic model. The dark energy component having negative pressure is due to the non-zero \(\Omega _{\Lambda }\) in the present case. \(\Omega _m=1\) signifies the presence of conventional matter in the model. The expansion scalar is constant and the directional scale factors may scale with

    $$\begin{aligned} a_1,a_2\propto e^{H_0t}. \end{aligned}$$

  • \(U_{-}(\Omega _m=-3\alpha ,\Sigma =-\frac{1}{2}(1+3\alpha ),\Omega _{\Lambda }=0)\): This point will reduce into point M for \(\alpha =0.\) In general, the eigenvalues are given by \(\lambda _1=3 (\alpha +1),\) \(\lambda _2=\frac{3}{4} \left( -1+\alpha -P\right) ,\) \(\lambda _3=\frac{3}{4} \left( -1+\alpha +P\right) ,\) where \(P=\sqrt{-24 \alpha ^3+17 \alpha ^2+6 \alpha +1}.\) The point is saddle in nature. \(\Omega _m>0\) for \(\alpha <0.\) For \(\alpha >-\frac{1}{3},\) the point will have \(\Omega _m<1.\) The cosmologically viable criterion \(0<\Omega _m<1\) will be satisfied for \(-\frac{1}{3}<\alpha <0.\) The point belongs to the spatially curved regions of the space-time having LRS BIII geometry. In particular, for \(\alpha =\frac{1}{3},\) one may have radiation-dominated decelerating expansion with \(\Omega _k=-1\) which is exhibiting the LRS BIII geometry for the universe. However, this radiation-like component may be the dark-radiation, since \(\Omega _m=-1.\) \(\Sigma =-1\) signifies the shear-dominated universe and the eigenvalues \(\{4,-2,1\}\) are exhibiting the saddle behavior.

  • \(U_{+}(\Omega _m=3,\Sigma =1,\Omega _{\Lambda }=3(1+\alpha ))\): The eigenvalues at this point are \(\{-6,3,-3 (\alpha +1)\}.\) The point is always saddle in nature.

    This point will represent exponentially accelerating expansion but the anisotropy will be increasing. The dark energy will drive the accelerating expansion. However, \(\Omega _m>1\) and \(\Omega _k>1\) scenarios will make this point un-physical and it has been given just for the sake of mathematical completeness. At this point, \(\rho \gg 3H^2\) and thus the universe may not be the ‘realistic’ one.

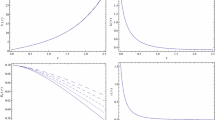
The 3-dimensional autonomous system and the stability character of fixed points have been depicted graphically in Fig. 1 and the corresponding projection on the \(\Sigma -\Omega _{\Lambda }\) plane. The point dS (exhibited by the red dot) acts as a stable attractor of the model which explain the late-time accelerated expansion of the universe. The specific evolution of the universe depicted by the evolution of cosmological quantities has been illustrated in Fig. 2. The deceleration parameter evolution (equivalently, the effective EoS parameter) shows the stiff matter-like evolution at early times, which transits into the radiation dominated phase and with the evolution of time (or scale factor), the accelerating universe expansion may be realized in the model. The corresponding fixed points to these phases are \(K_{+},\) R and dS respectively. The model consist of the fixed point corresponding to the matter-dominated phase but this point M (and the corresponding phase) is shear-dominated and it belongs to the spatially curved region having LRS BIII geometry. And, thus, one may have an evolution scenario having the stiff matter dominated phase at early-times, the matter dominated phase which is further transiting into the dark energy dominated phase corresponding to the points \(K_{-},\) M and dS respectively.

Fig. 1
figure 1

a Phase plane of the 3-D autonomous system of the LRS model where points are shown by blue \((K_{\mp }),\) green (R),  black (M) and red (dS) dots respectively, b projection on \(\Sigma -\Omega _{\Lambda }\) plane

Full size image

In the Fig. 2, the cosmological quantities are shown with the scale factor scale. According to the observational cosmology, in the scale factor scale, \(a=1\) is taken for the present day universe. In the Table 1, we list different criterion for the visualization of the past, present and the future universe according to the observational cosmology. It is worthwhile to mention that these scales are used interchangeably to illustrate the universe evolution in the cosmological dynamical systems. In the present model, we take \(N=\ln a\) and use the relation \(1+z=\frac{a_0}{a}\) for different illustrations in the Table 1. It is worthwhile to mention that \(\ln (1+z)\) and \(-\ln (1+z)\) will have vertical asymptote at \(z=-1\) and are not defined for \(z<-1.\) Here, we focus mainly on the cosmology concerned with the late-time universe.

3.1 Statefinder analysis

The statefinder diagnostic pair [74] enables to explore the dark energy properties in a model independent manner. These parameters are dimensionless. This geometrical diagnostic is algebraically related to the dark energy EoS and its derivative. In order to explore the characteristics of energy densities of different matter components in the model, we relate the dynamical variables of the autonomous system with the statefinder diagnostic pair. Since, this diagnostic pair uses the geometrical parameters (such as the scale factor, Hubble parameter and its derivatives), we apply this diagnostic to trace the cosmological behaviour of universe beyond the dark energy dominated phase having \(\omega <-\frac{1}{3}.\) We check the universe evolution for its whole history with this diagnostic. The statefinder diagnostic pair [74] \((\{r,s\})\) may also be converted into the form containing derivatives of \(N=\ln a\) as [75]

Fig. 2
figure 2

Evolution of the cosmological quantities in the LRS model for \(\alpha =\frac{1}{3}\)

Full size image
Table 1 Universe history in different scales
Full size table
$$\begin{aligned} r=q(1+2q)-\frac{dq}{dN}, \quad s=\frac{r-1}{3\left( q-\frac{1}{2} \right) }. \end{aligned}$$
(16)

For the variables defined in Eq. (8), these parameters may take the form

$$\begin{aligned} r= & {} \frac{1}{2} (-9 \alpha \Omega _{\Lambda } +(9 \alpha (\alpha +1)+2) \Omega _m\nonumber \\{} & {} +\,4 \Sigma (\Sigma (5-2 \Sigma )-2 \Omega _m+2)) \end{aligned}$$
(17)
$$\begin{aligned} s= & {} \frac{-9 \alpha \Omega _{\Lambda }{+}(9 \alpha (\alpha {+}1){+}2) \Omega _m{+}4 \Sigma (\Sigma (5{-}2 \Sigma ){-}2 \Omega _m{+}2){-}2}{3 \left( 3 \alpha \Omega _m{+}4 \Sigma ^2{-}3 \Omega _{\Lambda }{+}\Omega _m{-}1\right) }. \nonumber \\ \end{aligned}$$
(18)

On the basis of fixed points of the cosmological dynamical system, we may obtain the \(\{r,s\}\) parameters in different dynamical regimes of the cosmological history of model. For an evolving dark energy model, \(r\ne 1.\) In the \(r-s\) plane, \(r=1,s=0\) is a fixed point for the \(\Lambda \) cold dark matter \((\Lambda \)CDM) model. \(r=1,s=1\) is a fixed point for the standard cold dark matter (SCDM) model. And, the distance of trajectories from these points will illustrate the deviation of considered model from the \(\Lambda \)CDM and SCDM models. Also, in the \(r-s\) plane, \(r>1,s<0\) and \(r<1,s>0\) regions correspond to the models having Chaplygin gas- and quintessence-like properties [74] (Fig. 3).

Fig. 3
figure 3

Evolution of the statefinder diagnostic parameters with a in the LRS model

Full size image

The LRS model with affine EoS traces the cosmological history from the stiff matter-like evolution during early times to the radiation-, matter- and dark energy-dominated phases. The existence of fixed point signifying the dark energy dominated phase explains the accelerated expansion of the universe in the model. The statefinder diagnostic pair behavior highlights that the model approaches to the \(\Lambda \)CDM model-like characteristics at late-times from the quintessence era.

Various details about these points have been listed in Table 2.

Table 2 Cosmological quantities in the LRS BI and BIII model
Full size table

3.2 Energy conditions during the universe evolution

The universe evolution may be affected by the matter field behavior during the evolution. The energy conditions regulate the accelerating and decelerating behavior of the universe expansion. The Raychaudhuri equation [76,77,78,79] relates the active gravitational mass (equals \(\rho +3p\) for the perfect fluid matter) with the geometrical sector of the Einstein’s field equation and thus, the energy conditions, in particular, the strong energy condition may be related with the accelerating (or decelerating) universe evolution on the basis of \(\ddot{a}>0\) (or \(\ddot{a}<0)\) respectively. In the terms of dynamical variables of the model, the energy conditions may be satisfied if following criterion are true in the \(\Omega _m-\Omega _{\Lambda }\) plane:

  1. 1.

    NEC: \(\Omega _m\ge \frac{\Omega _{\Lambda }}{1+\alpha }.\)

  2. 2.

    WEC: \(\Omega _m\ge 0, \ \ \Omega _m\ge \frac{\Omega _{\Lambda }}{1+\alpha }.\)

  3. 3.

    DEC: \(\Omega _m\ge 0, \ \ \Omega _m\ge \frac{\Omega _{\Lambda }}{1+\alpha }, \ \ \Omega _m\ge \frac{\Omega _{\Lambda }}{\alpha -1}.\)

  4. 4.

    SEC: \(\Omega _m\ge \frac{\Omega _{\Lambda }}{1+\alpha }, \ \ \Omega _m\ge \frac{3\Omega _{\Lambda }}{1+3\alpha }.\)

We study the rate of change of \(\omega \) with N given by \(\omega '=\frac{d\omega }{dN}\) and plot its behavior in Fig. 2. From the figure, it may be observed that the curved spatial geometry plays a role during the transition from the shear dominated phase into the radiation dominated phase and in this duration \(\omega '\) also changes with the geometry.

4 Kantowski–Sachs cosmology

For the Kantowski–Sachs (KS) model, we define the dynamical variables as

$$\begin{aligned}{} & {} Q=\frac{\Theta }{3D}, \ \Sigma =\frac{\sigma }{3D}, \ \Omega _m=\frac{\rho }{3D^2}, \nonumber \\{} & {} \Omega _k=\frac{{}^3R}{3D^2}, \ \Omega _{\Lambda }=\frac{\rho _0}{3D^2} \end{aligned}$$
(19)

where \(D^2\equiv \frac{\Theta ^2}{9}+\frac{{}^3R}{6}.\) The variable D is real-valued, strictly positive quantity providing a monotonically increasing time variable. Since, from the Gauss–Codazzi constraint, we may have \(\frac{\Theta ^2}{3}+\frac{{}^3R}{2}=\rho +\sigma ^2.\) In the terms of dynamical variables, the constraints are given by \(Q^2+\Omega _k=1\) and \(\Omega _m+\Sigma ^2=1.\) Due to these constraints, the state space is 3-dimensional. From the Raychaudhuri equation, the deceleration parameter \(( q=-1-3\dot{\Theta }/{\Theta ^2}) \) may be written as

$$\begin{aligned} q=\frac{1}{2 Q^2}(1+3 \alpha +3 \Sigma ^2-3 \alpha \Sigma ^2-3 \Omega _{\Lambda }). \end{aligned}$$
(20)

The effective EoS parameter \((\omega )\) is given by

$$\begin{aligned} \omega =-\frac{1}{3 Q^2}(-1+3 \Omega _{\Lambda }+Q^2-3 \Sigma ^2+3 \alpha (\Sigma ^2-1)) \end{aligned}$$
(21)

where \(\omega =\frac{1}{3}(2q-1).\) The autonomous system in the KS model is given by

$$\begin{aligned} Q'= & {} \frac{1}{2} (Q^2-1)(1+2 Q \Sigma +3 \Sigma ^2-3 \Omega _{\Lambda } \nonumber \\{} & {} -\,3 \alpha (\Sigma ^2-1)) \end{aligned}$$
(22)
$$\begin{aligned} \Sigma '= & {} 1-\Sigma ^2+Q^2 (\Sigma ^2-1)\nonumber \\{} & {} -\,\frac{3}{2} Q \Sigma (1-\Sigma ^2+\Omega _{\Lambda }+\alpha (\Sigma ^2-1)) \end{aligned}$$
(23)
$$\begin{aligned} {\Omega _{\Lambda }}'= & {} \Omega _{\Lambda } (-2 \Sigma +2 \Sigma Q^2 -3 Q (-1-\Sigma ^2+\Omega _{\Lambda }\nonumber \\{} & {} +\,\alpha (\Sigma ^2-1))) \end{aligned}$$
(24)

along with the auxiliary variables evolution equations as

$$\begin{aligned} D'= & {} D(-(1+q)Q^3+\Omega _k(\Sigma -Q)) \end{aligned}$$
(25)
$$\begin{aligned} {\Omega _k}'= & {} -2QQ' \end{aligned}$$
(26)
$$\begin{aligned} {\Omega _m}'= & {} -2\Sigma \Sigma '. \end{aligned}$$
(27)

The fixed points of the system may be calculated by \(Q'=0,\Sigma '=0,{\Omega _{\Lambda }}'=0.\) The details about these fixed points have been given below:

  • \(dS_{-}(Q=-1,\Sigma = 0,\Omega _{\Lambda } = 0)\): The eigenvalues at this point are \(\left\{ \frac{-3 (\alpha -1)}{2},-3 (\alpha +1),-3 \alpha -1\right\} .\) This point is sink for \(\alpha >1\) and source for \(\alpha <-1.\)

  • \(dS_{+}(Q= 1,\Sigma = 0,\Omega _{\Lambda } = 0)\): The eigenvalues at \(dS_{+}\) are \(\left\{ \frac{3 (\alpha -1)}{2},3 (\alpha +1),3 \alpha +1\right\} .\) This point is source (sink) for \(\alpha >1 \ (\alpha <-1)\) respectively.

  • \(K_{{--}}(Q=-1,\Sigma =-1,\Omega _{\Lambda } =0)\): The eigenvalues are given by \(\{-6,-6,3 (\alpha -1)\}.\) This point will be stable for \(\alpha <1\) and saddle otherwise.

  • \(K_{++}(Q=1,\Sigma =1,\Omega _{\Lambda } =0)\): The eigenvalues are \(\{6,6,-3 (\alpha -1)\}.\) The point will act as source for \(\alpha <1\) and saddle otherwise.

  • \(K_{-+}(Q=-1,\Sigma =1,\Omega _{\Lambda } =0)\): The eigenvalues are \(\{-6,-2,3 (\alpha -1)\}.\) The point is stable for \(\alpha <1\) and saddle otherwise.

  • \(K_{+-}(Q=1,\Sigma =-1,\Omega _{\Lambda } =0)\): The eigenvalues are given by \(\{6,2,-3 (\alpha -1)\}.\) This point will act as source for \(\alpha <1\) and saddle otherwise.

  • \(P_{\alpha \mp }(Q=\mp 1,\Sigma =0,\Omega _{\Lambda } =\alpha +1)\): The eigenvalues are given by \(\{\pm 3,\pm 2,\pm 3 (\alpha +1)\}.\) For \(\alpha >-1,\) \(P_{-}\) and \(P_{+}\) are unstable and stable respectively. For \(\alpha <-1,\) these points are saddle in nature. For \(\alpha =-1,\) the points \(P_{\alpha \mp }\rightarrow dS_{\mp }\) respectively.

  • \(C_{c\mp }\left( Q=\mp \frac{1}{2};\Sigma =\mp \frac{1}{2};\Omega _{\Lambda } =\frac{3 (\alpha +1)}{4}\right) \): The eigenvalues at \(C_{c-}\) and \(C_{c+}\) are \(\left\{ 3,-\frac{3}{2},\frac{3 (\alpha +1)}{2}\right\} \) and \(\left\{ -3,\frac{3}{2},-\frac{3 (\alpha +1)}{2}\right\} \) respectively. These points are always saddle in nature. The value of \(\alpha \) will not convert these points into either source or sink. For \(\alpha =-1,\) these points belong to the \(Q-\Sigma \) sub-manifold and lie on the \(Q=\Sigma \) line.

  • \(U_{\alpha \mp }\left( Q=\mp \frac{2}{3 \alpha -1},\Sigma =\pm \frac{3 \alpha +1}{3 \alpha -1},\Omega _{\Lambda } =0\right) \): These points belong to the curved-spatial region of the spacetime. The eigenvalues of these points are having very long expressions, so we omit to write it here. These points are saddle in nature. For \(\alpha =-1,\) these points belong to the \(Q-\Sigma \) sub-manifold and lie on the \(Q=-\Sigma \) line.

  • \(U_{\mp }(Q=\mp 2;\Sigma =\pm 1;\Omega _{\Lambda } =0)\): The eigenvalues at \(U_{\mp }\) are given by \(\{\mp 6,\pm 3,\pm 6 \alpha \}\) respectively. These points are saddle in nature.

Fig. 4
figure 4

a Phase plane of the KS model for \(\alpha =-\frac{4}{3}\) where points are shown by blue \((dS_{\mp }),\) yellow \((K_{{--}},K_{++}),\) green \((K_{-+},K_{+-}),\) black \((P_{\alpha \mp }),\) red \((C_{c\mp })\) and magenta \((U_{\alpha \mp })\) dots respectively, b \(Q-\Sigma \) phase plane with Q and \(\Sigma \) on horizontal and vertical axis respectively for \(\alpha =-\frac{4}{3}\)

Full size image
Fig. 5
figure 5

a Phase plane of the KS model for \(\alpha =-\frac{1}{2}\) where points are shown by blue \((dS_{\mp }),\) yellow \((K_{{--}},K_{++}),\) green \((K_{-+},K_{+-}),\) black \((P_{\alpha \mp }),\) red \((C_{c\mp })\) and magenta \((U_{\alpha \mp })\) dots respectively, b \(Q-\Sigma \) phase plane with Q and \(\Sigma \) on horizontal and vertical axis respectively for \(\alpha =-\frac{1}{2}\)

Full size image
Fig. 6
figure 6

a Phase plane of the KS model for \(\alpha =\frac{1}{2}\) where points are shown by blue \((dS_{\mp }),\) yellow \((K_{{--}},K_{++}),\) green \((K_{-+},K_{+-}),\) black \((P_{\alpha \mp }),\) red \((C_{c\mp })\) and magenta \((U_{\alpha \mp })\) dots respectively, b \(Q-\Sigma \) phase plane with Q and \(\Sigma \) on horizontal and vertical axis respectively for \(\alpha =\frac{1}{2}\)

Full size image
Fig. 7
figure 7

a Phase plane of the KS model for \(\alpha =\frac{4}{3}\) where points are shown by blue \((dS_{\mp }),\) yellow \((K_{{--}},K_{++}),\) green \((K_{-+},K_{+-}),\) black \((P_{\alpha \mp }),\) red \((C_{c\mp })\) and magenta \((U_{\alpha \mp })\) dots respectively, b \(Q-\Sigma \) phase plane with Q and \(\Sigma \) on horizontal and vertical axis respectively for \(\alpha =\frac{4}{3}\)

Full size image

Various details about these points have been listed in Table 3 and the corresponding phase behavior in Figs. 4, 5, 6, 7.

Table 3 Cosmological quantities at the fixed points of the KS model
Full size table

4.1 Cosmological implications of the Kantowski–Sachs model

We list here the cosmological implications and behavior of the KS model at the fixed points.

  1. 1.

    The points \(dS_{\pm }\) correspond to \(Q^2=1\) space and the dimensionless matter density acts as the energy density of the cosmological constant in an effective sense. \(dS_{-}\) and \(dS_{+}\) represent contracting and expanding universe having shear-free (isotropic) evolution with flat-spatial geometry. The deceleration parameter q and the stability depend on the model parameter \(\alpha .\) In particular, for \(\alpha =-1,\) these points will realize de Sitter contraction and expansion respectively.

  2. 2.

    The points \(K_{{-}{-}}, K_{++}, K_{-+}\) and \(K_{+-}\) are characterized by \(Q^2=1\) and \(\Sigma ^2=1.\) These points are belonging to the \(Q-\Sigma \) phase space having \(\Omega _k=0,\Omega _m=0\) and \(\Omega _{\Lambda }=0.\) The boundaries \(\Sigma =\pm 1\) correspond to the vacuum Kasner models. The universe is decelerating with the effective stiff fluid-like domination. The expansion scalar and average scale factor may scale with \(\frac{1}{t}\) and \(t^{\frac{1}{3}}\) respectively. At these points, the directional scale factors may scale with either

    $$\begin{aligned} a_1\propto t, \ a_2\propto \text {constant, or} \ a_1\propto t^{-\frac{1}{3}}, \ a_2 \propto t^{\frac{2}{3}}. \end{aligned}$$
  3. 3.

    The points \(P_{\alpha \pm }\) belong to phase space region having \(\Omega _k=0\) and \(\Sigma =0.\) Therefore, the spacetime geometry corresponding to these points is isotropic and spatially flat. The value of parameter \(\alpha \) will determine the stability character of these points but the de Sitter-like expansion and contraction may be realized at \(P_{\alpha +}\) and \(P_{\alpha -}\) respectively. In particular, in \(\Omega _{\Lambda }>0\) plane (equivalently for \(\alpha >-1),\) these points will exhibit expanding de Sitter and contracting de Sitter solutions of the model which are stable and unstable respectively. Therefore, the accelerating expansion phase of the present universe may be realized in the model for the point \(P_{\alpha +}.\) The directional scale factors may scale with

    $$\begin{aligned} a_1,a_2\propto e^{H_0t}. \end{aligned}$$
  4. 4.

    The points \(C_{c\pm }\) belong to the spatially curved region of the spacetime having \(\Omega _k>0.\) At these saddle points, exponentially accelerated universe expansion may be realized with \(q=-1.\) The effective EoS exhibits cosmological constant-like behavior and the directional scale factors may scale with

    $$\begin{aligned} a_1,a_2\propto e^{H_0t}. \end{aligned}$$

    At these points, expansion scalar is proportional to the shear scalar. This model yields fixed points lying on the \(Q= \Sigma \) line for \(\alpha =-1.\) It simply means that there will exist a phase of universe evolution for which \(\Theta \propto \Sigma \) and it is exhibited by the trajectories parallel to \(Q=\Sigma \) in \(Q-\Sigma \) phase plane. In order to find the exact solutions [21, 22, 24, 66] and the qualitative behaviors [27, 28] of the LRS models in different gravity theories, the assumption of shear scalar proportional to the expansion scalar yields interesting implications. However, in the present case, this scenario is existing without any prior assumption.

  5. 5.

    The points \(U_{\alpha \pm }\) belong to the spatially curved region of the spacetime with \(\Omega _m>0\) for \(\alpha <0.\) At these saddle points, the expansion scalar and average scale factor may scale with \(\frac{2}{3(\alpha +1)t}\) and \(t^{\frac{2}{3(\alpha +1)t}}\) respectively. These points lie on the \(Q+\Sigma =0\) line in the \(Q-\Sigma \) phase space for \(\alpha =-1.\)

  6. 6.

    The fixed points \(U_{\pm }\) always lie outside the \(-1\le Q\le 1,-1\le \Sigma \le 1\) (physically accepted) region. These saddle points behaves as matter-dominated phase solutions representing decelerating universe. The directional scale factors may follow either

    $$\begin{aligned}{} & {} a_1\propto \text {constant}, \ a_2\propto t^{\frac{1}{3}}, \quad \text {or} \quad a_1\propto t^{-\frac{2}{3}}, \ a_2\propto t^{\frac{2}{3}}, \quad \text {or} \\{} & {} a_1\propto t^{\frac{2}{3}}, \ a_2\propto \text {constant}. \end{aligned}$$

    However, these points have \(\Omega _k=-3\) signifying spatially curved geometry. These points may not have physical significance in the KS model and it have been given for the mathematical completeness.

4.2 Bouncing behavior in the KS model

The Kantowski–Sachs model consist of two directional scale factors \(a_1\) and \(a_2.\) The bouncing universe subsequently expands from the contracting phase while attaining minima at the end of contacting era [80,81,82,83,84,85,86]. The active gravitational mass of the matter components affects the bouncing evolution of the universe in the model. This mass is related to the geometry of the universe by the Raychaudhuri equation. In the General relativity model, Null energy condition (NEC) may not be satisfied for flat and open spatial section models [81, 83]. However, closed spatial section models may satisfy NEC under certain conditions in their bouncing evolution [81, 83].

Due to the presence of more than one directional scale factors, the bouncing evolution of the universe may be visualized in the average scale factor \(V=a_1{a_2}^2=a^3,\) where a is the mean scale factor. The condition of bounce at \(t=t_b\) may be given by \(\Theta (t_b)=0\) and \(\dot{\Theta }>0\) in the small neighborhood of bounce instant [16, 19, 25, 29,30,31, 38]. In a more generic situation, one may consider a bouncing universe in any of the directional scale factor. There may also be a bounce in all of the directional scale factors, however, it may occur at different times.

We define the ‘synchronous bounce’ as the bouncing evolution occurring in different scale factors of the anisotropic spacetime at the same instant. It is worthwhile to mention that in a minimally coupled cosmological framework, the NEC is necessarily violated for the synchronous bounce [16, 31].

In the \(Q-\Sigma \) phase plane, the red and blue lines exhibit \(H_1=0\) and \(H_2=0\) respectively. The trajectories with \(Q'>0\) \((Q'<0)\) crossing the point \(Q=0,\Sigma =0\) are highlighting the synchronous bounce (turnaround) respectively. The Kantowski–Sachs model with affine equation of state yields the synchronous bouncing evolution for \(\alpha <0.\)

5 LRS Bianchi V cosmology

In this section, we investigate the qualitative dynamics of LRS Bianchi V (LRS BV) metric with affine EoS. For this, we write the propagation equations of the dynamical variables of the model and use the normalized variables (depending on expansion scalar) to convert these equations into an autonomous system. The LRS Bianchi V metric is given by [40]

$$\begin{aligned} ds^2=dt^2-{a_1}^2dx^2-{a_2}^2e^{2x}(dy^2+dz^2) \end{aligned}$$
(28)

where \(a_1,a_2\) are the directional scale factors and depend on cosmic time t only. This metric is a homogeneous axially symmetric metric, where axial symmetry with respect to x has been assumed. The expansion scalar \((\Theta ),\) shear scalar \((\sigma )\) and 3-curvature scalar for the metric (28) are respectively given by \(\Theta =H_1+2H_2,\) \(\sigma =\frac{1}{\sqrt{3}}(H_1-H_2)\) and \({}^3R=-\frac{6}{{a_1}^2},\) where \(H_i=\frac{\dot{a_i}}{a_i},i=1,2.\) We assume that the fluid \(4-\)velocity \(u^i\) is equal to the unit normal of the homogeneous spatial hyper-surfaces. And, thus, the propagation equations of these quantities are given by [87]

$$\begin{aligned}{} & {} \dot{\Theta }+\frac{1}{3}\Theta ^2+2\sigma ^2=-\frac{1}{2}(\rho +3p) \end{aligned}$$
(29)
$$\begin{aligned}{} & {} \dot{\sigma }+\Theta \sigma =0 \end{aligned}$$
(30)
$$\begin{aligned}{} & {} {}^3\dot{R}+\frac{2}{3}\Theta \cdot {}^3R=0 \end{aligned}$$
(31)

where \(\rho \) and p denote the conventional matter density and pressure of the universe. The Gauss–Codazzi constraint relating the 3-space Ricci scalar with the matter energy density is given by

$$\begin{aligned} {}^3R=2\sigma ^2-\frac{2}{3}\Theta ^2+2\rho . \end{aligned}$$
(32)

One may observe the difference between the 3-curvature scalar of LRS BV metric (28) and the LRS metric (1) along with the propagation equations of shear scalar and 3-curvature scalar. In order to explain the qualitative dynamics of the LRS Bianchi V model, we take the dynamical variables as

$$\begin{aligned} \Omega _m=\frac{\rho }{3H^2}, \ \Omega _k=\frac{{}^3R}{6H^2}, \ \Sigma =\frac{\sigma }{\sqrt{3}H}, \ \Omega _{\Lambda }=\frac{\rho _0}{3H^2}. \end{aligned}$$
(33)

We proceed with the independent variable \(N=\ln a\) and in this section, the ‘prime’ denotes the derivative with respect to N. The variable N is suitable for the study of expanding cosmological \((H>0)\) scenarios. The variable \(\Omega _m\) is used for the energy density of the conventional matter in the universe composed of matter and radiation as a whole. In the terms of above variables, the Gauss–Codazzi equation will yield a constraint equation given by

$$\begin{aligned} \Omega _m+\Sigma ^2-\Omega _k=1. \end{aligned}$$
(34)

The deceleration and effective equation of state (EoS) parameters may be written as

$$\begin{aligned} q= & {} \frac{1}{2} \left( 4 \Sigma ^2-3 \Omega _{\Lambda } +(1+3 \alpha )\Omega _m\right) \end{aligned}$$
(35)
$$\begin{aligned} \omega= & {} \frac{1}{3} \left( -1+4 \Sigma ^2-3 \Omega _{\Lambda }+(1+3 \alpha ) \Omega _m\right) \end{aligned}$$
(36)

where we use \(\frac{\dot{H}}{H^2}=-1-2\Sigma ^2-\frac{1}{2}(1+3\alpha )\Omega _m+\frac{3}{2}\Omega _{\Lambda }.\) The resulting state space is 3-dimensional due to the constraint equation (34). The dynamical system governing the propagation of dimensionless variables are given by

$$\begin{aligned} {\Omega _m}'= & {} 3 \Omega _{\Lambda }+\Omega _m \left( -3 \alpha -3 \Omega _{\Lambda }+(3 \alpha +1) \Omega _m+4 \Sigma ^2-1\right) \nonumber \\ \end{aligned}$$
(37)
$$\begin{aligned} \Sigma '= & {} \frac{1}{2} \Sigma \left( -3 \Omega _{\Lambda }+(3 \alpha +1) \Omega _m+4 \Sigma ^2-4\right) \end{aligned}$$
(38)
$$\begin{aligned} {\Omega _{\Lambda }}'= & {} \Omega _{\Lambda } \left( -3 \Omega _{\Lambda }+(3 \alpha +1) \Omega _m+4 \Sigma ^2+2\right) . \end{aligned}$$
(39)

The fixed points of the system (37–39) may be calculated by \({\Omega _m}'=0,\Sigma '=0,{\Omega _{\Lambda }}'=0.\) The system possess five fixed points which will always exist and thus may be used to determine different cosmological phases for the system. The details may be summarized as

Fig. 8
figure 8

a Phase plane of the 3-D autonomous system of the LRS Bianchi V model where points are shown by blue \((K_{v\mp }),\) green \((R_v),\) orange \((C_v)\) and red \((dS_v)\) dots respectively, b projection on \(\Sigma -\Omega _{\Lambda }\) plane

Full size image
Table 4 Cosmological quantities in the LRS BV model
Full size table

  • \(K_{v\pm }\ (\Omega _m= 0,\Sigma = \pm 1,\Omega _{\Lambda }= 0)\): These shear dominated points will lead to the decelerating universe evolution having \(q=2.\) These points will belong to the spatially flat region of the spacetime. The eigenvalues are given by \(\{6,4,-3 (\alpha -1)\}.\) These points will be unstable for \(\alpha <1\) and saddle otherwise. In the phase governed by these points, the universe will behave like universe governed by stiff fluid (having \(\omega =1).\) These points will correspond to the vacuum Kasner models. At these points, \(\Theta =\frac{1}{t}\) and the directional scale factors may scale with either

    $$\begin{aligned} a_1\propto t, \ a_2\propto \text {constant, or} \ a_1\propto t^{-\frac{1}{3}}, \ a_2 \propto t^{\frac{2}{3}}. \end{aligned}$$

    The cosmological behaviour of \(K_{v\pm }\) correspond to the cosmological behaviour of \(K_{\pm }\) of LRS BIII cosmology.

  • \(R_{v}\ (\Omega _m= 1,\Sigma = 0,\Omega _{\Lambda }= 0)\): This point will exhibit spatially flat, isotropic, decelerating or accelerating universe on the basis of parameter \(\alpha .\) For \(\alpha \ge 0,\) the point will correspond to the decelerating universe expansion, since \(\omega =\alpha .\) The deceleration parameter is given by \(q=\frac{1}{2} (3 \alpha +1).\) For \(\alpha =0,\) the point corresponds to the matter-dominated universe. For \(\alpha =\frac{1}{3},\) the point will correspond to the radiation dominated universe. The eigenvalues are given by \(\left\{ \frac{3 (\alpha -1)}{2},3 (\alpha +1),3 \alpha +1\right\} .\) The point will be stable (unstable) for \(\alpha <-1\) \((\alpha >1)\) respectively and saddle for \(-1<\alpha <1.\) The criteria for the classically stable universe will constrain \(\alpha \) as \(0\le \alpha \le 1\) and thus the matter dominated phase may correspond to \(\Theta =\frac{2}{t}\) and, \(a\propto t^{\frac{2}{3}}.\) The directional scale factors may follow either

    $$\begin{aligned}{} & {} a_1\propto \text {constant}, \ a_2\propto t^{\frac{1}{3}}, \ \text {or} \quad a_1\propto t^{-\frac{2}{3}}, \ a_2\propto t^{\frac{2}{3}}, \ \text {or}\\{} & {} a_1\propto t^{\frac{2}{3}}, \ a_2\propto \text {constant}. \end{aligned}$$

    For the radiation dominated phase, the mean scale factor will scale with \(t^{\frac{1}{2}}\) and the directional scale factors may follow either

    $$\begin{aligned}{} & {} a_1\propto \text {constant}, \ a_2\propto t^{\frac{1}{4}}, \ \text {or} \quad a_1\propto t, \ a_2\propto t^{-\frac{1}{4}}, \ \text {or} \\{} & {} a_1\propto t^{\frac{1}{2}}, \ a_2\propto \text {constant}. \end{aligned}$$

    The cosmological behaviour at this point correspond to the point R of LRS BIII cosmology.

  • \(C_{v}\ (\Omega _m= 0,\Sigma = 0,\Omega _{\Lambda }= 0)\): The spatially curved universe having \(\Omega _k=-1\) will neither accelerate nor decelerate corresponding to the phase governed by this point. And, thus the solution correspond to the Milne universe solution. The eigenvalues are given by \(\{-2,2,-3 \alpha -1\}.\) The point is saddle in nature and the values of \(\alpha \) will not affect the stability character of this point. The universe will have \(q=0\) and the corresponding equation of state parameter is given by \(\omega =-\frac{1}{3}.\) The mean scale factor will scale with \(a\propto t\) and the directional scale factors may scale with either

    $$\begin{aligned} a_1\propto \text {constant}, \ a_2\propto t^{\frac{1}{2}}, \ \text {or} \quad a_1\propto t, \ a_2\propto \text {constant}. \end{aligned}$$

    For \(\alpha >-\frac{1}{3},\) point is attractor in the shear-free \(\Omega _m-\Omega _{\Lambda }\) plane and trajectories emerging from \(K_{v-}\) evolve to \(C_v\) in \(\Sigma =0\) plane.

  • \(dS_{v}\ (\Omega _m= 1,\Sigma = 0,\Omega _{\Lambda }= \alpha +1)\): The point will correspond to the spatially flat, homogeneous and isotropic universe. The eigenvalues are given by \(\{-3,-2,-3 (\alpha +1)\}.\) The point is late-time attractor of the model for \(\alpha >-1\) and therefore it may explain the accelerating universe expansion in the model. The universe is dominated by the cosmological constant like fluid at this point given by \(\omega =-1\) with \(q=-1,\) \(\Omega _k=0.\) It simply means that the de Sitter dominated phase may be realized in the model. This is a consequence of non-zero \(\Omega _{\Lambda }\) in the present case. Since, the deceleration parameter is \(q=-1,\) the expansion scalar is constant and the directional scale factors will scale with \(a_1,a_2\propto e^{H_0t}.\) The cosmological behaviour of this point correspond to the point dS of LRS BIII cosmology.

The fixed points \(C_v,R_v\) and \(dS_v\) belong to the \(\Omega _m-\Omega _{\Lambda }\) sub-manifold having \(\Sigma =0\) and thus the universe is isotropic corresponding to the phases of these points. The fixed point \(C_v\) corresponding to the Milne universe solution existing in the dynamical system of LRS BV cosmology, which was not present in the dynamical system of LRS BIII cosmology. The fixed point M existing in the contracting shear region of the LRS BIII cosmology does not exist in the case of LRS BV cosmology. The LRS BIII and LRS BV cosmologies may explain the late-time accelerating universe expansion since the fixed points dS and \(dS_v\) exist in respective cosmologies. The three dimensional phase space behaviour of the dynamical system (37–39) and the corresponding projection on the \(\Sigma -\Omega _{\Lambda }\) plane has been given in Fig. 8. One may observe that there are two class of evolution scenarios possible in the model, namely \(K_{v+}\rightarrow R_v\rightarrow dS_v\) and \(K_{v-}\rightarrow C_v\rightarrow dS_v.\) The evolution law for the cosmological quantities at the fixed points have been listed in Table 4. The behaviour of deceleration parameter, EoS parameter and the statefinders are identical to the corresponding parameters of the LRS BIII cosmology, which may be visualized from Figs. 2 and 3 for \(K_{v+}\rightarrow R_v\rightarrow dS_v\) case.

6 Conclusions

We study the evolution scenarios for the universe with the affine equation of state in the anisotropic spacetimes using qualitative approach. In particular, we study the locally rotationally symmetric Bianchi I and B III metric in an unified way using the dynamical system approach. We also investigate the Kantowski–Sachs model with affine equation of state to explore the dynamical evolution on the basis of fixed points. Further, we study the locally rotationally symmetric Bianchi-V model with affine equation of state to explore the qualitative behaviour of the model and compare with LRS BIII cosmology, since both of these geometries are hyper-spherically curved geometries. These models may yield physically interesting cases such as the de Sitter evolution, existence of stable attractors which are also isotropic and the accelerating universe evolution from the decelerating phase etc, which are broadly consistent with the present day observations [1,2,3]. In the LRS BI and BIII models, the system possess seven fixed points. The points \(K_{\mp }\) belong to the BI boundary and correspond to the vacuum Kasner models. The matter distribution is stiff fluid-like in an effective sense and the universe expands with deceleration having \(q=2.\) These points are source for \(\alpha <1\) and saddle otherwise. The point R is dominated by the conventional matter and belongs to the Bianchi I boundary having \(\Omega _k=0.\) The expansion behavior may depend on the parameter \(\alpha .\) However, for \(\alpha =\frac{1}{3},\) the point may exhibit the radiation-dominated, decelerating universe evolution. Point M represents the matter-dominated phase in the effective sense but it is dominated by the shear with the LRS BIII geometry. And, the point dS acts as the stable attractor of the model corresponding the accelerating universe expansion of the present times, which is almost spatially flat and isotropic in nature. The radiation and matter-dominated phases represent decelerating universe expansion and the universe evolution in the model signifies that the universe has transited from the decelerated phase into the accelerated phase in the recent past. On the basis of fixed points, two important kind of evolution scenarios possible are as follows: \(K_{+}\rightarrow R\rightarrow dS\) and \(K_{-}\rightarrow M\rightarrow dS.\) Point \(U_{-}\) may have \(\Omega _m>0\) for \(\alpha <0\) but for \(\alpha =\frac{1}{3},\) the point represent the dark-radiation dominated universe evolution with \(\Omega _k=-1\) in the LRS BIII region of phase space. The Kantowski–Sachs model with affine equation of state possesses 14 fixed points. Out of these points, \(C_{c\mp }\) and \(P_{\alpha \pm }\) belong to the Kantowski–Sachs region of the phase space. Points \(dS_{\mp }\) and \(P_{\alpha \mp }\) will represent the isotropic universe evolution with \(\Omega _{\Lambda }=0\) and \(\Omega _{\Lambda } \ne 0\) respectively. The points corresponding to \(Q^2=1,\Sigma ^2=1\) will correspond to the vacuum Kasner solutions belonging to the Bianchi-I model boundary. The KS model yield fixed points corresponding to the stiff-matter dominated and the dark energy dominated phases of the universe evolution. For \(\alpha <0,\) the model may exhibit the synchronous bouncing universe evolution connecting \(dS_{-}\) to \(dS_{+}\) in the \(Q-\Sigma \) plane. It is worthwhile to mention that the Kantowski–Sachs universe yields \(Q\propto \Sigma \) scenario (that is, shear is proportional to the expansion scalar) during its intermediate phase of the evolution, without any prior assumption in the model. However, this scenario may not hold during the complete cosmological history of the universe.

The LRS BV spacetime possess hyper-spherically curved geometry but the 3-curvature scalar is different from the LRS BIII geometry. The qualitative analysis of LRS BV model with affine EoS shows that there will be five fixed points of the corresponding dynamical system. The points \(K_{v\pm }\) lies on the Kasner boundary and the universe will decelerate in the corresponding phases. The cosmological dynamics corresponding to the point \(R_v\) depends on model parameter \(\alpha .\) For a classically stable universe, this point is saddle in nature and may correspond either to a radiation- or matter-dominated phase of the universe evolution. The fixed point \(C_v\) is a point which was absent in the dynamics of LRS BIII model and corresponds to the Milne universe solution having \(\Omega _k=-1,\Sigma =0,\Omega _m=0\) and \(q=0\) with \(\omega =-\frac{1}{3}.\) The existence of the point \(dS_v\) having \(q=-1\) with \(\omega =-1\) highlights that the effective fluid corresponding to this phase in the universe will behave like the cosmological constant and may drive the universe acceleration during late-times. The affine EoS may be seen as the special case of polytropic EoS [67,68,69,70,71,72]. The polytropic EoS may affect the cosmological dynamics in a manner different from affine EoS at low and high energy limits. We leave the qualitative description of these issues for a future study.