Cosmological evolution in bimetric gravity: observational constraints and LSS signatures

Abstract

Bimetric gravity is an interesting alternative to standard GR given its potential to provide a concrete theoretical framework for a ghost-free massive gravity theory. Here we investigate a class of Bimetric gravity models for their cosmological implications. We study the background expansion as well as the growth of matter perturbations at linear and second order. We use low-redshift observations from SnIa (Pantheon+ and SH0ES), Baryon Acoustic Oscillations (BAO), the growth ($f\sigma _{8}$) measurements and the measurement from Megamaser Cosmology Project to constrain the Bimetric model. We find that the Bimetric models are consistent with the present data alongside the $\Lambda$CDM model. We reconstructed the “ effective dark energy equation of state”($\omega _{de}$) and “Skewness”($S_{3}$) parameters for the Bimetric model from the observational constraints and show that the current low-redshift data allow significant deviations in $\omega _{de}$ and $S_{3}$ parameters with respect to the $\Lambda$CDM behaviour. We also look at the ISW effect via galaxy-temperature correlations and find that the best fit Bimetric model behaves similarly to $\Lambda$CDM in this regard.

1 Introduction

Observed late time acceleration [1,2,3] of the average expansion of the Universe has been one of the central challenges of modern Cosmology for more than two decades. The two standard approaches to explain such late time acceleration have been: (1) assuming the presence of a new unobserved component, called dark energy in the energy budget of the universe [4] (similar to dark matter that it does not emit any light but with negative pressure instead of zero pressure) (2) modifying the standard theory of Gravitation (Einstein’s General Relativity) at large cosmological scales [5, 6]. The concordance $\Lambda CDM$ model [7] has been tremendously successful in explaining observations across time scales of Universe’s evolution [8, 9] (e.g Big Bang Nucleosynthesis era, matter-radiation decoupling era, structure formation era till the late time accelerated expansion era) despite a number of theoretical problems to construct such model [10]. But recently for the first time, $\Lambda$CDM model is facing some serious questions related to observational results. There is a discrepancy in values of Hubble constant ($H_0$) inferred from nearby cosmological observations [11], and those inferred from CMB observations [8, 9]. This tension, termed $H_0$ tension, has now reached at the level of $5\sigma$ and systematical errors as source for this tensions may not be enough to explain this tension [12, 13].

This has been the main driving force in the renewed exploration of the theoretical regime with dark energy models beyond $\Lambda CDM$ or modified theories of gravity. In relation to modified theories of gravity, massive gravity models are one of the most studied modified gravity models. In standard theory of gravity, the gravity is described by massless spin-2 field called gravitons which are still not observed. Fierz and Pauli [14] made the first attempt to make these spin-2 field massive with a linear theory. But it was later shown by Boulware and Deser [15] that the nonlinear extensions of such theories contain a ghost (Boulware–Deser (BW) Ghost). A ghost-free, nonlinear theory for massive spin-2 field in flat space time was first proposed by de Rham, Gabadadze and Trolley in 2011 [16], which is called the dRGT theory. Hassan and Rosen [17] later extended the dRGT theory for Bimetric gravity that describes a gravitating massive spin-2 field by introducing the dynamics in the second metric. Cosmological solutions in Bimetric gravity have been studied which can result in the late time acceleration of the Universe without any presence of explicit dark energy term. Different families of Bimetric gravity models have been studied [18,19,20,21,22,23] in light of CMB, BAO and Supernovae data. Gravitational waves in these theories with some constraints on parameter space are studied in [24, 25]. Big Bang Nucleosynthesis constraints were obtained in [26].

On the other hand, theories with phantom behaviour(i.e. equation of state w crossing below $-1$) [27, 28] have shown promise in reducing/overcoming the cosmological tensions, more specifically the Hubble tension although the theoretical underpinnings of phantom phenomenology are still under investigations as many of such theories may suffer from instabilities. The viable Bimetric gravity can also show phantom behaviour in some of their parameter space [29, 30]. Providing an effective $\Lambda$-like effect and the possibility of phantom behaviour can make Bimetric gravity suitable for investigation as a possible solution for the Hubble tension.

In the literature, there are studies related to the effect of Bimetric gravity on the large-scale structure formation in the universe [31,32,33]. In particular, the effects of modification of gravity at cosmological scales in higher-order clustering are still mostly unknown. One of the important parameters related to higher order clustering is the “skewness” parameter [34]. This is defined as the “normalized third order moment in count-in-cells statistics” which can describe the non-Gaussian feature in the probability distribution of the perturbed matter field. In a purely matter-dominated Einstein–de Sitter Universe, one gets $S_{3} \approx 34/7 \approx 4.857$. Any observed deviation from this value can be a signature for a modified gravity model [35].

Our aim in this work is to study the linear and second-order perturbations for a specific class of Bimetric gravity models and illustrate the effects of these modifications to gravity on observables related to perturbed Universe such as $f\sigma _8$, skewness parameter $S_{3}$ and Integrated Sachs-Wolfe(ISW) effect and compare the results with concordance $\Lambda$CDM models. This can be particularly interesting in the context of results from future surveys like Euclid which can provide an accurate measurement of the skewness parameter and can potentially distinguish $\Lambda$CDM model from different modified gravity models including the Bimetric gravity.

This paper is organized as follows: in Sect. 2, we briefly describe the theory of Bimetric gravity; in Sect. 3, we describe the perturbation theory formalism used for the Bimetric gravity and the discuss the effects of these perturbations on observables in respective Sect. 3.2. Data constraints are obtained in Sect. 4. In Sect. 5, we study ISW effect through galaxy-temperature cross-correlations. We conclude with a discussion in the last section.

2 Bimetric gravity and cosmology

Bimetric gravity is the theory of two interacting spin-2 fields, one massive and one massless. An interacting symmetric spin-2 field $f_{\mu \nu }$ is introduced together with the physical metric $g_{\mu \nu }$, which is a linear combination of massless and massive graviton states. The standard matter particles and fields are coupled to the physical metric $g_{\mu \nu }$ only. For ghost-free Bimetric gravity, where both metrics are dynamical, action can be written as [17, 19]

$$\begin{aligned} S= & {} -\int d^4x\sqrt{-g} \frac{R}{2m_g^2} - \int d^4x\sqrt{-f} \frac{\tilde{R}}{2m_f^2} \nonumber \\{} & {} +\int d^4x\sqrt{-g} m^4 V(g_{\mu \nu },f_{\mu \nu }) + \int d^4x\sqrt{-g} L_m, \end{aligned}$$

(1)

where R and $\tilde{R}$ are Ricci scalars for $g_{\mu \nu }$ and $f_{\mu \nu }$. $m_g$ and $m_f$ are the Planck’s mass for the metrics $g_{\mu \nu }$ and $f_{\mu \nu }$ respectively.. V is the interaction term which has the parametric form as

$$\begin{aligned} V = \sum _{n=0}^4\beta _{n}e_n(\chi ). \end{aligned}$$

(2)

Here $\chi$ is a matrix defined in such way that $\chi ^2=g_{\mu \nu }f^{\mu \nu }$. $e_n(\chi )$ is the elementary symmetry polynomials of eigenvalues of the matrix $\chi$ which can be written as follows

$$\begin{aligned} \begin{aligned} e_0(\chi )&=1,\quad e_1(\chi )=[\chi ],\quad e_2(\chi )=\frac{1}{2}\left( [\chi ]^2-[\chi ^2]\right) \\ e_0(\chi )&=\frac{1}{6}\left( [\chi ]^3-3[\chi ][\chi ^2]+2[\chi ^3]\right) , \quad e_4(\chi )=\text {det}(\chi ) \end{aligned} \end{aligned}$$

(3)

where, $[\chi ]$ is the trace of the matrix $\chi$ and $\text {det}(\chi )$ is the determinant of $\chi$. The Bimetric gravity is characterized by 5 constants $\beta _i$. Under the scaling transformation $f_{\mu \nu }\rightarrow \frac{m_g^2}{m_f^2}f_{\mu \nu }$ and $\beta _n\rightarrow \left( \frac{m_f}{m_g}\right) ^n \beta _n$, we can make $M_{*}^2=1$ where, $M_{*}=m_f/m_g$. Hence $M_{*}$ is not a free parameter. In what follows, we consider $M_{*}^2=1$ and $m_g=m_{f}$. With such rescaling [36], it is common to work in terms of dimensionless quantities which remain same under these scaling. Here we use the definitions and parameterisation of Dhawan et al. [19] to write the dimensionless parameters as

$$\begin{aligned} B_i\equiv \frac{m^2 \beta _i}{H_0}. \end{aligned}$$

(4)

There are various possible models depending on which Bs are non-zero. For simplicity, here we consider models with only $B_0$ and $B_1$ nonzero. Cosmological expansion for these models is given by [37]

$$\begin{aligned} \frac{H^2}{H_0^2} {=} \frac{\Omega _m(1{+}z)^3}{2} {+}\frac{B_0}{6} {+} \sqrt{\left( \frac{\Omega _m(1+z)^3}{2} {+}\frac{B_0}{6} \right) ^2 {+}\frac{B_1^2}{3}}, \end{aligned}$$

(5)

where due to spatial flatness condition, the parameter $B_{0}$ can be written in terms of other two parameters $\Omega _{m}$ and $B_{1}$ as

$$\begin{aligned} B_0 = 3\left( 1 - \Omega _m - \frac{B_1^2}{3} \right) , \end{aligned}$$

(6)

where $\Omega _{m}$ is the present day matter density parameter. As one can see in Eq. (5), the model naturally gives a cosmological constant term $\frac{B_0}{3}$ in the Universe which can be positive or negative depending on the values of $\Omega _{m}$ and $B_{1}$. This originates from the interacting potential itself. For early times $z\rightarrow \infty$,

$$\begin{aligned} \frac{H^2}{H_0^2} \approx {\Omega _m(1+z)^3} +\frac{B_0}{3}, \end{aligned}$$

(7)

which is $\Lambda CDM$ model. For future infinity $(z\rightarrow -1)$,

$$\begin{aligned} \frac{H^2}{H_0^2} \approx constant, \end{aligned}$$

(8)

and hence a de-Sitter or anti-de-Sitter model.

Writing $H^2/H_{0}^2 = \Omega _{m}(1+z)^3 + (1-\Omega _{m}) f(z)$, one can compare with Eq. (5) to find the effective dark energy density and subsequently can derive an expression for the effective dark energy equation of state ($w_{de}$). We plot $w_{de}(z)$ as a function of redshift(z) in Fig. 1 and observe that the Bimetric gravity can show phantom behavior. In the Fig. 2, where we show the dependence of $w_{de}(z=0)$ on $B_{1}$ and $\Omega _{m0}$, it is evident that Bimetric gravity shows phantom behavior at present for a range of parameter values and can provide a possible theoretical basis for parametric phantom models, which people have recently considered [27, 38] to alleviate the cosmological tensions.

Fig. 1

Equation of state $w_{de}$ for different values of parameter $B_1$. We set $\Omega _{m} =0.3$

Fig. 2

Present day w as a function of $B_1$ and $\Omega _{m}$.

3 Growth of perturbations and large scale structure

Next we study the effects of Bimetric gravity on the growth of matter perturbations. We study linear perturbations as well as second-order perturbations. Second-order perturbations affect the skewness ($S_3$) of the matter density field. We study the effects of modified theory parameters on skewness. We use the formalism of Multamaki et al. [39] to study the growth of matter perturbations but one can also use the formalism for modified gravity models by Lue et al. [40] and both of them give similar results.

Before describing the detail formalism and the results, we should discuss the issue of instability in the linear perturbations on the sub-horizon scales in the early time. It has been shown that linear perturbations around a background homogeneous and isotropic FLRW solutions are stable in the late times. But in order to define the initial conditions, these perturbations also need to be stable in the early time on sub horizon scales. However such perturbations are suffered from gradient instability on sub horizon scales in the early time as well as Higuchi Ghost as the Hubble scale exceeds that effective gradient mass $m_{eff}$ [32, 33, 41,42,43,44]. This is similar to the situation in Fierz-Pauli theory and the instability is precisely due to the fact that the massive spin-2 mass in linear theory does not possess a well defined massless limit in curved background. It was shown that the origin of these instabilities can be associated with the Stuckelberg fields arising due to the relation between the physical and fiducial sectors of the Bigravity theory and nonlinear interactions in these Stuckelberg fields may play role for these instabilities [45]. Subsequently it was shown that the nonlinear effects in the scalar graviton mass can solve this instability issue [45]. During the early time in cosmological evolution when $H \gg m_{eff}$, the Stuckelberg fields are nonlinear and due to these nonlinearity, the early growth of perturbations evolve as GR solutions, and as the $H~m_{efff}$, the bigravity modification to GR starts dominating and for $H\ll m_{eff}$, the linear perturbations are stable on sub-horizon scales [45]. In this regard, we want to stress that the transition from the GR to bigravity behaviour is still an unsettles issue and needs further exploration. There are also certain classes of bigravity models (related to certain choices of the parameters $\beta _{i}$), for which it was shown that the there is no gradient instability in the perturbed Universe in early phases of evolution while treating perturbations at full nonlinear level [46]. Moreover in numerical studies related to inhomogeneous evolution of the Universe, no exponential instabilities has been observed [47]. To settle the issue of linear stability, we may need to adapt more general prescription as described by Ijjas et al. [48]. Although this issue of solving the instability in the linear growth of perturbation at early stage using nonlinear effects, is still an open problem, in this work we rely on the assumption that nonlinear effect during the early phase when $H\gg m_{eff}$ can resolve this of instability and carry forward our subsequent calculations for linear perturbation in the matter sector.

3.1 Formalism and equations

We start with the formalism of Multamaki et al. [39], wherein Raychaudhuri’s equation is used to derive a general equation for the growth of perturbations at large scales. We should point out that Bimetric gravity is a modified theory of gravity containing only pressure-less matter in the energy budget of the Universe at late times (one can ignore the contribution from radiation at late times). The formalism developed by Multamaki et al. [39] to study the matter density perturbations for such modified theory of gravity is briefly discussed below.

The Raychaudhuri’s equation for a shearless and irrotational velocity field $v^\mu$ is given by

$$\begin{aligned} \dot{\Theta } + \frac{\Theta ^2}{3} = R_{\mu \nu }v^\mu v^\nu , \end{aligned}$$

(9)

where

$$\begin{aligned} \Theta = \nabla _\mu v^\mu , \qquad \theta = \nabla _i v^i. \end{aligned}$$

(10)

As shown in [39], this can be related to average Hubble expansion rate ($\bar{H}$) and locally perturbed expansion rate H as

$$\begin{aligned} \frac{\dot{\theta }}{a}+\frac{\theta }{a}\bar{H}+\frac{\theta ^2}{3a^2} = 3(\dot{H}+H^2-\dot{\bar{H}}-{\bar{H}}^2). \end{aligned}$$

(11)

Combining the above equation with the continuity equation for pressure-less matter

$$\begin{aligned} \frac{\partial \delta }{\partial t} + (1+\delta )\theta = 0, \end{aligned}$$

(12)

where $\delta$ is the matter overdensity. We get the evolution equation for $\delta$ [39] as

$$\begin{aligned}{} & {} \frac{d^2\delta }{d\eta ^2}+\left( 2 + \frac{\dot{\bar{H}}}{\bar{H}^2} \right) \frac{d\delta }{d\eta } - \frac{4}{3}\frac{1}{1+\delta }\left( \frac{d\delta }{d\eta } \right) ^2\nonumber \\{} & {} \quad = -3\frac{1+\delta }{\bar{H}^2}\left[ \left( \dot{H} + H^2 \right) -\left( \dot{\bar{H}} + \bar{H}^2 \right) \right] , \end{aligned}$$

(13)

where overdot represents derivative w.r.t. time and $\eta \equiv \ln (a)$. Quantities with overbar represent background quantities. Following [39], we can expand the r.h.s of Eq. (13) as

$$\begin{aligned} 3\frac{1+\delta }{\bar{H}^2}\left[ \left( \dot{H} + H^2 \right) -\left( \dot{\bar{H}} + \bar{H}^2 \right) \right] = 3(1+\delta )\sum _{n=1} c_n \delta ^n. \end{aligned}$$

(14)

We further expand $\delta$ as [39]

$$\begin{aligned} \delta = \sum _{i=1}^\infty \frac{D_i(\eta )}{i!}\delta _0^i, \end{aligned}$$

(15)

where $\delta _0$ is the small perturbation. We use Eq. (16) in (15) while expanding $\delta$ upto first and second order. Moreover, for background Hubble parameter, we put the expression given in Eq. (6) (we write it in terms of background matter density $\rho _{m}$) while for perturbed Hubble parameter, we use Eq. (6) with $\rho _{m}$ replaced by perturbed matter density $\rho _{m}(1+\delta )$ (For detail prescription in this regard, please see [39]).

With this we get the linear and second-order perturbation equations as

$$\begin{aligned} D_1^{\prime \prime } + \left( 2+\frac{\dot{\bar{H}}}{\bar{H}^2} \right) D_1^\prime +3c_1D_1 = 0, \end{aligned}$$

(16)

and

$$\begin{aligned} D_2^{\prime \prime } + \left( 2+\frac{\dot{\bar{H}}}{\bar{H}^2} \right) D_2^\prime -\frac{8}{3}{D_1^\prime }^2+ 3c_1D_2 + 6(c_1+c_2)D_1^2 = 0. \end{aligned}$$

(17)

For Bimetric gravity, which we are considering here, we get

$$\begin{aligned}{} & {} c_1 =\frac{\frac{-2\Omega _m}{a^3}\left( \frac{\Omega _m}{2a^3}+\frac{B_0}{6}\right) \left( \left( \frac{\Omega _m}{2a^3}+\frac{B_0}{6}\right) ^2+\frac{B_1^2}{3}\right) -\frac{2\Omega _m}{a^3}\left( \left( \frac{\Omega _m}{2a^3}+\frac{B_0}{6}\right) ^2+\frac{B_1^2}{3}\right) ^{3/2}-\frac{\Omega _m^2B_1^2}{a^6}}{8\left( \frac{\Omega _m}{2a^3}+\frac{B_0}{6}+\sqrt{\left( \frac{\Omega _m}{2a^3}+\frac{B_0}{6}\right) ^2+\frac{B_1^2}{3}}\right) \left( \left( \frac{\Omega _m}{2a^3}+\frac{B_0}{6}\right) ^2+\frac{B_1^2}{3}\right) ^{3/2}}, \end{aligned}$$

(18)

and

$$\begin{aligned}{} & {} c_2 =\nonumber \\{} & {} \quad \frac{\frac{-8\Omega _m^2 B_1^2}{a^6}\left( \left( \frac{\Omega _m}{2a^3}+\frac{B_0}{6}\right) ^2+\frac{B_1^2}{3}\right) +\frac{9\Omega _m^3 B_1^2}{a^9}\left( \frac{\Omega _m}{2a^3}+\frac{B_0}{6}\right) }{96\left( \frac{\Omega _m}{2a^3}+\frac{B_0}{6}+\sqrt{\left( \frac{\Omega _m}{2a^3}+\frac{B_0}{6}\right) ^2+\frac{B_1^2}{3}}\right) \left( \left( \frac{\Omega _m}{2a^3}+\frac{B_0}{6}\right) ^2+\frac{B_1^2}{3}\right) ^{5/2}},\nonumber \\ \end{aligned}$$

(19)

We solve for linear and second-order perturbations for values of $B_1$ and $\Omega _{m}$. We set the initial conditions at redshift $z = 1000$, assuming that model reproduces the Einstein–de Sitter Universe at that epoch (specifically we assume $D_{1}$ and $D_{2}$ and their first derivatives to be same as that for Einstein–de Stitter Universe with $\Omega _{m} = 1$ at $z=1000$) . Solving these equations, the linear growth rate is shown in Fig. 3 while the evolution of the second-order perturbations are shown in Fig. 4. As shown in Fig. 3, for smaller values of $B_{1}$, the linear growth is similar to $\Lambda$CDM model. But for higher values, in particular for values $B_{1} \ge 1.4$, there is an increase in growth around $z \sim 1$. This can be possibly due to some extra attractive gravitational pull provided by the Bimetric gravity for such values of $B_{1}$. The similar behaviour was also found by [46] for a bigravity model with non zero $B_{1}$ and $B_{2}$.

For the second order perturbation as shown in Fig. 4, we get the similar behaviour where the deviation from $\Lambda$CDM increases for larger values of $B_{1}$.

Fig. 3

Linear perturbations for different values of parameter $B_1$. For higher values of $B_1(>1.4)$, there is a very distinct feature of a brief epoch with growth faster than $\Lambda CDM$ as well as Einstein–diSitter

3.2 Observables

3.2.1 $f\sigma _8$

Linear theory calculations can be used to predict the growth and clustering of structures at appropriate length scales and times. Redshift surveys provide an estimate of a combination of linear growth $\delta$, its derivative given by growth factor f and its rms fluctuation at the length scale of $8h^{-1}~Mpc$ given by the parameter $\sigma _8$. The combination $f\sigma _8$ [49] is an important observable for perturbed Universe at linear scale. Here the growth factor f and the $\sigma _{8}$ parameters are given as

$$\begin{aligned} f(a) = \frac{d (log(\delta ))}{d (log (a))}, \end{aligned}$$

(20)

and

$$\begin{aligned} \sigma _8(a) = \sigma _8(a=1)\frac{\delta (a)}{\delta (1)}. \end{aligned}$$

(21)

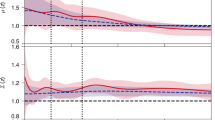
nt In Fig. 5, we show the $f\sigma _8$ for Bimetric gravity for the different values of the parameter $B_{1}$ along with the $\Lambda$CDM model. We observe that we always get larger $f\sigma _8$ for larger values of $B_{1}$ compared to $\Lambda$CDM ($B_{1}=0$). Moreover for larger values of $B_{1}$, the $f\sigma _{8}$ behaviour for Bimetric gravity models are not consistent in the redshift range $z \sim 0.25{-}0.5$. In this plot, we fix the value of $\sigma _{8}$ at $z=0$ by Planck-2018 observations [9] assuming a $\Lambda$CDM model. Hence for this figure, one expects that for higher values of $B_{1}$, a lower value for $\sigma _{8}$ may be necessary to make the $f\sigma _{8}$ for Bimetric theory more consistent with the observational data.

Fig. 4

Second order perturbations for different values of parameter $B_1$

Fig. 5

Combination $f\sigma _8$ as a function of redshift z for different theories. We also plot the data points from observations [50]

Fig. 6

Skewness $S_3$ as a function of scale factor for different values of $B_1$

Fig. 7

Deviation of $S_3$ from $\Lambda CDM$ model for different values of $B_1$. While the linear growth rate and second-order perturbations show huge differences, the percentage difference in the combination probed by $S_3$ is a few percent

3.2.2 Skewness (S3)

Second-order perturbations provide further connection with statistics of observed perturbations. Gaussian initial conditions evolve into non-gaussian distribution with time and the extent of non-gaussianity depends on dynamics of the individual fluid components of the universe or the theory of gravity which evolves the whole system. Mode coupling leads to an imbalance in the distribution of voids and overdense regions [51]. Second-order perturbations play a role in this and can be related to the skewness of the density field as [39, 51]

$$\begin{aligned} S_3 = \frac{\langle \delta ^3 \rangle }{\langle \delta ^2 \rangle ^2}, \end{aligned}$$

(22)

which can be written as

$$\begin{aligned} S_3 = 3\frac{D_2}{D_1^2}. \end{aligned}$$

(23)

$S_3$ can be sensitive to underlying dark energy characteristics [35] or modification of GR. Here we show that the growth of perturbations is sensitive to parameter $B_1$ as we illustrate in Figs. 3 and 4. In Fig. 6, we show the evolution of $S_3$ for different values of $B_1$. In Fig. 7 we show the present day percentage difference of $S_3$ from $\Lambda$CDM model as a function of $B_{1}$ and $\Omega _{m0}$. This can be used to distinguish the Bimetric models from the $\Lambda$CDM using the $S_{3}$ measurements in near future.

4 Observational constraints on bimetric model

Given the behaviour of Bimetric gravity in terms of different observables, we now study the observational constraints on Bimetric gravity using low redshift cosmological observations. In this regard, we do the Markov Chain Monte Carlo (MCMC) analysis using different latest cosmological observational data to put constraints on the model parameters for the Bimetric gravity. The analysis is performed using the EMCEE hammer [52], a PYTHON implementation of the MCMC sampler.

Table 1 The range of the uniform priors for the parameters used for the MCMC analysis.

Fig. 8

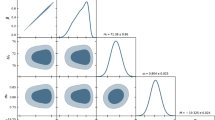
Marginalized posterior distribution of the set of parameters $\Omega _m$, h, $B_1$, $r_d$, $\sigma _8$ and M and their corresponding 2D confidence contours ($68\%$ and $95\%$), obtained from the MCMC analysis for the Bimetric gravity utilizing all the data sets mentioned in Sect. 4

We use the following data:

• Pantheon+ and SH0ES data [53] ;

• The Gold-2017 set for the $f\sigma _8$ data [50, 54];

• The Baryon acoustic oscillations (BAO) measurements by the completed Sloan Digital Sky Survey (SDSS) lineage of experiments on large scales [55];

• The angular diameter distances measured using water megamasers under the Megamaser Cosmology Project [56].

We use the uniform priors given in Table 1 for the model parameters for the Bimetric gravity. The posterior probability distributions and their corresponding confidence contours for different parameters are shown in Fig. 8. As one can see from this figure, a substantial deviation from $\Lambda$CDM model in terms of the parameter $B_{1}$ is allowed by the data although the $\Lambda$CDM behaviour ($B_{1}=0$) is still allowed. The reconstructed effective dark energy equation of state and the reconstructed $S_{3}$ parameters as a function of redshifts are shown in Figs. 9 and 10. The constrained Bimetric model gives a phantom-like effective dark energy equation of state. The data also allows substantial deviation in the parameter $S_{3}$ from $\Lambda$CDM model behaviour although the $\Lambda$CDM behaviours for $S_{3}$ is also allowed in the constrained behaviour of $S_{3}$.

5 Integrated Sachs Wolfe (ISW) effect

Given the observational constraints on the Bimetric gravity considered in this analysis, we study how far the ISW signal in this model deviates from the $\Lambda$CDM model within that constraints. CMB photons traveling through evolving spacetime, traverse potentials created by matter inhomogeneity and undergo changes in their wavelengths. This contributes to anisotropies of CMB spectrum and is dubbed ISW effect [57, 58]. The effect can be detected by cross-correlation of Large Scale Structure (LSS) tracers with CMB anisotropies [40, 58,59,60] which can be used as a probe for theories giving dark energy effects. Here we follow the formalism of Lue et al. [40] who gave a general prescription for studying the ISW effect in modified gravity theories. One of the criteria for applying this prescription for modified gravity models is the existence of static spacetime outside a spherically symmetric mass distribution. The important criteria for Birkhoff’s theorem is that the outside of a spherically symmetric mass distribution should be an empty space given by $R_{\mu \nu } = 0$ which can be extended to spacetime with constant curvature. In bimetric theory, this criteria does not hold true except the special choice of parameters for which the spacetime reduces to Schwarzschild A(dS). The question is whether one can get a static spacetime outside a spherically symmetric mass distribution for the choice of parameters used in this work. Kocic et al. [61] have obtained a non static spherically symmetric solution in Bimetric theory for a certain choice of the parameters $\beta _{i}$ which apparently violates the Birkhoff’s theorem. Our specific choice, where only $\beta _{0}$ and $\beta _{1}$ are non zero and rest of the $\beta _{i}$ are zero, is different from the constraints on $\beta _{i}$ for which Kocic et al. [61] have obtained the non static solution. With our choice of parameters, we have not found any non static spherically symmetric solution vacuum solution in Bimetric gravity theory in the literature (In [46], it was argued, although without details, that the Birkhoff’s theorem does not hold in bigravity theory for any combinations of $\beta _{i}$ parameters). On the other hand, Volkov has obtained a whole class of Black Hole solutions in Bimetric gravity which are static spacetimes outside a spherically symmetric mass distribution and they can be both asymptotically flat [62] or asymptotically non flat [63]. Just recently Rahman et al. [64] found a new static wormhole solution outside a spherically symmetric mass distribution in bimetric gravity with same choice of parameters used in this work. Keeping all these in mind, we assume a static spherically symmetric metric outside a spherical overdensity in order to apply the prescription given by Lue et al. [40].

We calculate the evolution of time derivatives of potentials for our Bimetric model and compare it with the standard $\Lambda$CDM model.

Following the prescription by Lue et al. [40], we characterize background expansion in Bimetric gravity theory by a function g(x) as

$$\begin{aligned} g(x) = \left( \frac{H}{H_0}\right) ^2, \end{aligned}$$

(24)

with x defined as

$$\begin{aligned} x \equiv \frac{8\pi G\rho _m}{3H_0^2}. \end{aligned}$$

(25)

For example, in $\Lambda CDM$, the function takes the form

$$\begin{aligned} g(x) = x + \Omega _{\Lambda }. \end{aligned}$$

(26)

For the Bimetric gravity, g(x) is given by

$$\begin{aligned} g(x) = \frac{1}{2}x + \frac{B_0}{6} + \sqrt{\left( \frac{1}{2}x + \frac{B_0}{6} \right) ^2 + \frac{B_1^2}{3} }. \end{aligned}$$

(27)

We start with the following convention for the perturbed metric [40]

$$\begin{aligned} ds^2 = -(1+2\Psi )dt^2 + a^2(1+2\Phi )(dr^2+r^2d\Omega ^2). \end{aligned}$$

(28)

Fig. 9

Reconstructed equation of state $\omega _{de}$ as a function of redshift z. Black line is the best fit value with shaded regions as $1\sigma$ and $2\sigma$ for the inner and the outer shaded region respectively

Fig. 10

Reconstructed skewness $S_3$ as a function of redshift z. Black line is the best fit value with shaded regions as $1\sigma$, $2\sigma$ and $3\sigma$ for the innermost to the outermost shaded region. Blue line is for the $\Lambda$CDM model

The ISW effect is proportional to a combination of temporal derivatives of potentials as

$$\begin{aligned}{} & {} A(\dot{\Psi }-\dot{\Phi }) \nonumber \\{} & {} \quad {=} \left[ (1-f^{MG})(g^\prime +(3/2) g^{\prime \prime }x) {+}\frac{3}{2}(5xg^{\prime \prime }+3x^2g^{\prime \prime \prime }) \right] D_{+} ,\nonumber \\ \end{aligned}$$

(29)

wherein $D_+$ is linear first order perturbation and f is growth rate defined as $\frac{d(lnD_+)}{d(ln a)}$. In Fig. 11, we compare this term for our constrained Bimetric gravity (for best fitted parameter values) with $\Lambda$CDM model as constrained by Planck-2018 . We see that the observationally constrained Bimetric model does not differ much from the $\Lambda$CDM model.

Finally, the cross-correlated ISW signal ($w_{gT}$) between LSS and CMB can be calculated as

$$\begin{aligned}{} & {} w_{gT} = 3T_0\Omega _{m0}b(2\pi )^2\frac{H_0}{c^3}\int dz\sqrt{(}g) D_+^2\nonumber \\{} & {} \quad \times \left[ (1-f)(g^\prime +(3/2) g^{\prime \prime }x) +\frac{3}{2}(5xg^{\prime \prime }+3x^2g^{\prime \prime \prime }) \right] \nonumber \\{} & {} \quad \times w_g(z) \int \frac{dk}{k}P(k)J_0(k\theta \chi ). \end{aligned}$$

(30)

Fig. 11

Comparison of the evolution of temporal derivatives of the potentials. Differences in linear growth rate are translated here as well

Fig. 12

Galaxy temperature correlation for the best fit Bimetric model along with $\Lambda CDM$. The two are very similar

Here $T_0$ is the present CMB temperature, b is the bias factor (assumed constant here), P(k) is present-day matter power spectrum, $\chi$ is comoving distance as a function of z, $J_0$ is zeroth Bessel function and $w_g(z)$ is the survey-dependent galaxy selection function. For $T_0$, we take the value $2.725 \mu K$, b is taken from Lue et al. [40] that is 5.47. We use the $w_g(z)$ of Takada and Jain [65] with mean redshift of 0.49.

This correlation function for best fitted Bimetric gravity as well as for $\Lambda$CDM model are plotted in Fig. 12 and it is evident that the cross-correlated ISW signal in Bimetric gravity is similar to $\Lambda$CDM model.

6 Conclusions

We study the cosmological evolution in a subclass of Bimetric gravity model, where only the parameters $B_{0}$ and $B_{1}$ are nonzero. We show that the effective dark energy behaviour in such a modified gravity theory can be phantom-like for a large range of parameter values. Moreover the model admits a cosmological constant that can be positive or negative depending on the values of the parameter $B_{1}$ and $\Omega _{m}$. This can naturally mimic a cosmological evolution where the Universe contains a phantom like dark energy plus a negative Cosmological Constant apart from the standard matter. As shown recently such set up can be useful to solve the Hubble Tension [27, 28, 38].

We also study the linear and second order growth of matter fluctuations in the Bimetric gravity. We find that the growth of both linear and second order perturbations are strongly dependent on the values of parameter $B_1$ that signifies the deviation from the corresponding $\Lambda CDM$ limit. This results in significant deviations of observables like“$f\sigma _{8}$”and“Skewness” parameter $S_{3}$ from the $\Lambda$CDM behaviour for higher values of the parameter $B_{1}$.

With these observations, we subsequently constrain the Bimetric model with low-redshift observational data from SnIa Observation (Pantheon+ and SH0ES), BAO observations as well as Growth measurements. It shows that the data allow significant deviation from $\Lambda$CDM behavior although $\Lambda$CDM limit of Bimetric theory ($B_{1} =0$) is also consistent with the data.

Finally we calculate the ISW signal by cross-correlating the CMB and LSS signals for our best fit Bimetric gravity model and show that it is mostly similar to the $\Lambda$CDM model as constrained by Planck-2018.

We want to stress that the issue of solving the instability in the linear perturbations on the sub-horizon scales in the early Universe with nonlinear effects is still an unresolved issue. Hence one should keep that in mind when considering observables in bimetric gravity that are related to the linear perturbations. This is also true for the validity of Birkhoff’s theorem in bimetric gravity which is still not properly resolved at present although there are hints that the Birkhoff’s theorem does not hold in bimetric gravity for any choice of parameters $\beta _{i}$. We need to keep in mind all these issues while studying perturbed Universe in bimetric gravity under the assumptions that the instability issue can be taken care of using nonlinear or other effects as well as assumption of validity of Birkhoff’s theorem, as done in the present work. Concrete validation of breaking down of any one of these assumptions in future, will need new approach for the present study.

To conclude, we show that the low-redshift observations allow Bimetric gravity that behaves differently than $\Lambda$CDM. This motivates us to study the behaviour of CMB fluctuations in such models and see whether they are consistent with the Planck-2018 measurements. We plan to study this in the near future.