Study the $B^{0}_{(s)}$ decays into $\phi$ and a scalar or vector meson

Abstract

In the present work, we investigate the decays of $B^{0}_{(s)} \rightarrow \phi \pi ^{+}\pi ^{-}$ with the final state interaction based on the chiral unitary approach. In the final state interaction of the $\pi ^+\pi ^-$ with its coupled channels, we study the effects of the $\eta \eta$ channel in the two-body interaction for the reproduction of the $f_{0}(980)$ state, where its contribution to the $f_{0}(980)$ state can be ignored. Our results for the $\pi ^+\pi ^-$ invariant mass distributions of the decay $B^{0}_{s} \rightarrow \phi \pi ^{+}\pi ^{-}$ describe the experimental data up to 1 GeV well, with the resonance contributions from the $f_{0}(980)$ and $\rho$. For the predicted invariant mass distributions of the $B^{0} \rightarrow \phi \pi ^{+}\pi ^{-}$ decay, we find that the contributions from the $f_{0}(500)$ are significant, but not from the $f_{0}(980)$ state. With some experimental branching ratios to determine the production vertex factors, we make predictions for the branching ratios of the other decay channels, including the vector mesons, in the $B^0_{(s)}$ decays, some of which are consistent with the experimental measurements within the uncertainties.

1 Introduction

The three body B meson decays have caught much attention of both theories and experiments to investigate the CP-violation phenomena or the physics beyond the Standard Model (SM). Due to the exceptional progress of the experiments, such as in Belle, BaBar, LHCb, many non-leptonic three body B meson decays have been measured (see the summarized results in Particle Data Group (PDG) [1]). On the other hand, to study the three body non-leptonic B meson decays in theories, some theoretical models are proposed, such as the SU(3) flavor symmetry framework [2,3,4,5,6,7,8,9], the heavy quark effective theory combined with the chiral perturbation theory and the final state interaction [10,11,12,13,14,15,16,17,18,19,20,21], QCD sum rules under the factorization approach [22,23,24,25,26,27,28,29,30], the perturbative QCD approach [31,32,33,34,35,36,37,38,39], the QCD factorization framework [40,41,42,43], the final state interaction formalism [44,45,46] based on the chiral unitary approach (ChUA) [47,48,49,50,51,52], and so on.

Aiming at searching for the physics beyond the SM, the LHCb collaboration has reported the first observation of the rare three body decays of $B^{0}_{(s)} \rightarrow \phi \pi ^{+}\pi ^{-}$ [53],¹ where the $B^{0}_{s} \rightarrow \phi \pi ^{+}\pi ^{-}$ decay was investigated for the $\pi ^{+}\pi ^{-}$ invariant mass in the range of $400 \textit{ MeV}< m(\pi \pi ) < 1600 \textit{ MeV}$, and the resonant contributions from the states of $\rho (770)$, $f_{0}(980)$, $f_{2}(1270)$, and $f_{0}(1500)$, were found in the $m(\pi \pi )$ invariant mass distributions. The decays of $B^0_{(s)} \rightarrow \phi \pi ^{+}\pi ^{-}$ are interesting because they are induced by the flavor changing neutral current [54] $b\rightarrow s\bar{s}s$ and $b\rightarrow d\bar{s}s$ processes at the quark level, which are forbidden at tree level diagram by the Cabibbo-Kobayashi-Maskawa (CKM) quark-mixing mechanism of the SM [55]. However, these decays are sensitive to the new physics beyond the SM because their amplitudes are described by the loop (penguin) diagrams [56]. After the experimental findings, the rare decay of $B^{0}_{s} \rightarrow \phi \pi ^{+}\pi ^{-}$ had been studied using the perturbative QCD approach in Ref. [55], where the nonperturbative contributions from the resonance $f_0(980)$ were introduced in the distribution amplitudes by the time-like scalar form factor, which were parameterized with the Flatté model. Applying the QCD factorization framework, the three-body decays of $B^0_{(s)} \rightarrow \phi \pi ^+\pi ^-$ were also investigated in Ref. [57], where the resonant contributions were taken into account for the three-body matrix element in terms of the Breit-Wigner formalism. Also using the perturbative QCD approach, the work of [58] looked into the direct CP violation in the decay of $B^{0}_{s} \rightarrow \rho (\omega ) \phi \rightarrow \phi \pi ^{+}\pi ^{-}$ via the $\rho -\omega$ mixing mechanism.

In the present work, in order to examine the resonant contributions and understanding the production of $f_{0}(500)$ and $f_{0}(980)$ in the final state interaction, we study the decays of $B^{0}_{(s)} \rightarrow \phi \pi ^{+}\pi ^{-}$ with the final state interaction taken from the ChUA as done in Refs. [44,45,46], where the $\bar{B}^{0}_{(s)}$ mesons decaying to $J/\psi$ with $\pi ^+ \pi ^-$ and the other final states were investigated. As found in Refs. [44, 46], the dominant resonance production in the $\bar{B}^{0}_{s}$ decay was the $f_{0}(980)$ with no significant evidence for the $f_{0}(500)$, which was in agreement with the experimental findings [59, 60], whereas, the production of $f_{0}(500)$ resonance was dominant in the $\bar{B}^{0}$ decay. In Refs. [47, 61], the states of $f_{0}(500)$ (or called as $\sigma$ state), $f_{0}(980)$, and $a_{0}(980)$ were dynamically reproduced in the coupled channel interaction via the potentials derived from the lowest order chiral Lagrangian [62, 63]. Recently, based on the ChUA (more applications about the ChUA can be found in recent reviews [64,65,66,67]), the work of [68] made a further investigation on the different properties of these states, $f_{0}(500)$, $f_{0}(980)$, and $a_{0}(980)$ in details, where the couplings, the compositeness, the wave functions, and the radii were calculated to reveal their nature.

Indeed, the mixing components for the states of $f_{0}(500)$ and $f_{0}(980)$, all of which mainly decay into the $\pi \pi$ channel, were studied in Ref. [69] with the QCD sum rule, where more experimental data were required to clarify the strange quark component in the $f_{0}(500)$ resonance as suggested in Ref. [70]. Thus, in the present work, we investigate the properties of the $f_{0}(500)$ and $f_{0}(980)$ states produced in the final state interaction of the decay processes of $B^{0}_{(s)} \rightarrow \phi \pi ^{+}\pi ^{-}$. In the next section, we will briefly introduce the formalism of the final state interaction with the ChUA for these decay processes of the $B^{0}_{(s)}$ mesons. In the following section, we discuss the vector meson production under the same weak decay mechanism. Then, we show the results of the $\pi ^+\pi ^-$ invariant mass distributions and the branching fractions of the other decay channels in the following section. At the end, we make a short conclusion.

2 The model for scalar meson production

Fig. 1

Feynman diagrams for the decays of $B^{0}_{(s)}$ into $\phi \, (s \bar{s})$ and a primary $q \bar{q}$ pair

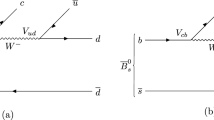
In the work of [44, 45], the decays of $B^0_{(s)} \rightarrow J/\psi \pi ^{+}\pi ^{-}$ are studied with the final state interaction approach. In the present work, we investigate the ones of $B^0_{(s)} \rightarrow \phi \pi ^{+}\pi ^{-}$ with the vector meson $J/\psi$ replaced by a $\phi$ in the hadron level. Nevertheless, at the weak decay level, the $B^0_{(s)}$ decays into $J/\psi$ and a $q \bar{q}$ pair through the tree level $b \rightarrow c$ transition. In our case, it should proceed via a gluonic $b \rightarrow s$ penguin transition for the $B^0_{(s)}$ decaying into $\phi$ and a $q \bar{q}$ pair, see Fig. 1. Thus, these decay processes are suppressed because they are forbidden at the tree level by the Cabibbo-Kobayashi-Maskawa (CKM) quark-mixing mechanism. Note that, the process of $B^0_{s} \rightarrow \phi \pi ^{+}\pi ^{-}$ in the penguin diagram of Fig. 1b is color allowed, whereas, the one of $B^0 \rightarrow \phi \pi ^{+}\pi ^{-}$ in Fig. 1a is color suppressed, see more discussions in Refs. [71,72,73]. We shall also discuss this suppression effect later. In fact, these parts of the weak decay mechanism are isolated with a dynamical factor in our formalism. For the present case of the decays $B^0_{(s)} \rightarrow \phi \pi ^{+}\pi ^{-}$, we focus on the process of the $q \bar{q}$ pair hadronized to the final states, which interact with each other, and can be obtained by the coupled channel interaction with the ChUA. Below we show the final state interaction framework in detail. The dominant weak decay mechanism for the $B^{0}_{(s)}$ decays is depicted in Fig. 1, which proceeds as,

$$\begin{aligned} B^{0} (\bar{b} d)&\Rightarrow (V_{ub} \bar{u} + V_{cb} \bar{c}) W^{+} d \Rightarrow (V_{ub} \bar{u} g + V_{cb} \bar{c} g) W^{+} d \nonumber \\&\Rightarrow (V_{ub} V_{ud} + V_{cb} V_{cd} ) (s\bar{s}) (d\bar{d}) \, , \end{aligned}$$

(1)

$$\begin{aligned} B^{0}_{s}(\bar{b} s)&\Rightarrow (V_{ub} \bar{u} + V_{cb} \bar{c}) W^{+} s \Rightarrow (V_{ub} \bar{u} g + V_{cb} \bar{c} g) W^{+} s \nonumber \\&\Rightarrow (V_{ub} V_{us} + V_{cb} V_{cs} ) (s\bar{s}) (s\bar{s}) \, , \end{aligned}$$

(2)

where $V_{q_1 q_2}$ is the element of the CKM matrix for the transition of the quark $q_1 \rightarrow q_2$ (see appendix A for the details of the CKM matrix), g the gluon and the one $W^+$ boson. As one can see, there are two pairs of $q\bar{q}$ generated at last, a pair of $s \bar{s}$ and the other ones of $d \bar{d}$ or $s \bar{s}$. Next, two $q\bar{q}$ pairs undergo the hadronization procedure. The ones of $s \bar{s}$ lead to a vector meson of the $\phi$ produced. The other primary $q\bar{q}$ pair creates a meson pair of $\pi ^{+}\pi ^{-}$ finally, which can be accomplished by extra $q \bar{q}$ pairs generated from the vacuum, written as $u\bar{u} +d\bar{d} + s\bar{s}$, as shown in Fig. 2. These hadronization processes are mathematically formulated as,

$$\begin{aligned} B^{0}&\Rightarrow (V_{ub} V_{ud} + V_{cb} V_{cd}) (s\bar{s}\rightarrow \phi ) [d\bar{d} \rightarrow d\bar{d}\nonumber \\&\cdot (u\bar{u}+d\bar{d}+s\bar{s}) ] \nonumber \\&\Rightarrow (V_{ub} V_{ud} + V_{cb} V_{cd}) (s\bar{s}\rightarrow \phi ) [ M_{22} \rightarrow (M \cdot M)_{22} ] \, , \end{aligned}$$

(3)

$$\begin{aligned} B^{0}_{s}&\Rightarrow (V_{ub} V_{us} + V_{cb} V_{cs} ) (s\bar{s} \rightarrow \phi ) [ s\bar{s} \rightarrow s\bar{s}\nonumber \\&\cdot (u\bar{u}+d\bar{d}+s\bar{s}) ] \nonumber \\&\Rightarrow (V_{ub} V_{us} + V_{cb} V_{cs} ) (s\bar{s}\rightarrow \phi ) [ M_{33} \rightarrow (M \cdot M)_{33} ] \, , \end{aligned}$$

(4)

with the $q\bar{q}$ matrix M defined as

$$\begin{aligned} M=\left( \begin{array}{lll} {u \bar{u}} &{} {u \bar{d}} &{} {u \bar{s}} \\ {d \bar{u}} &{} {d \bar{d}} &{} {d \bar{s}} \\ {s \bar{u}} &{} {s \bar{d}} &{} {s \bar{s}} \end{array}\right) . \end{aligned}$$

(5)

Fig. 2

Procedure for the hadronization $q\bar{q} \rightarrow q\bar{q}(u\bar{u}+d\bar{d}+s\bar{s})$

Fig. 3

Diagrammatic representation for the $\pi ^{+}\pi ^{-}$ production in the final state interaction of $B^{0}$ (a) and $B^{0}_{s}$ (b) decays

Furthermore, we can write the matrix elements of M in terms of the physical mesons, which corresponds to

$$\begin{aligned} \varPhi =\left( \begin{array}{ccc} {\frac{1}{\sqrt{2}} \pi ^{0}+\frac{1}{\sqrt{6}} \eta } &{} {\pi ^{+}} &{} {K^{+}} \\ {\pi ^{-}} &{} {-\frac{1}{\sqrt{2}} \pi ^{0}+\frac{1}{\sqrt{6}} \eta } &{} {K^{0}} \\ {K^{-}} &{} {\bar{K}^{0}} &{} {-\frac{2}{\sqrt{6}} \eta } \end{array}\right) , \end{aligned}$$

(6)

where we take $\eta \equiv \eta _{8}$. With the correspondence between the matrix M and $\varPhi$, the hadronization processes can be accomplished to the hadron level in terms of two pseudoscalar mesons,

$$\begin{aligned}&d \bar{d} \cdot (u \bar{u}+d \bar{d}+s \bar{s})\rightarrow (\varPhi \cdot \varPhi )_{22} \nonumber \\&\quad =\pi ^{+} \pi ^{-} +\frac{1}{2} \pi ^{0} \pi ^{0}-\frac{1}{\sqrt{3}} \pi ^{0} \eta \nonumber \\&\qquad +K^{0} \bar{K}^{0}+\frac{1}{6} \eta \eta , \nonumber \\&s \bar{s} \cdot (u \bar{u}+d \bar{d}+s \bar{s}) \rightarrow (\varPhi \cdot \varPhi )_{33}\nonumber \\&\quad =K^{-} K^{+} +K^{0} \bar{K}^{0}+\frac{4}{6} \eta \eta \, , \end{aligned}$$

(7)

where one can see that there are only $K\bar{K}$ and $\eta \eta$ produced in the $B^{0}_{s}$ decay, which is different from the one of $B^{0}$ decay having the other products ($\pi \pi$ for example) too. As we have known from the ChUA [47, 68], the $f_0(980)$ state is bound by the $K\bar{K}$ component, whereas, the $f_0(500)$ resonance is mainly contributed from the $\pi \pi$ channel. Thus, one can expect that these two states have different contributions for the $B^{0}$ and $B^{0}_{s}$ decays (see our results later). Once the final states are hadronized after the weak decay process, they can go to further interaction, as depicted in Fig. 3, where there are three processes taken into account, the $\phi$ emission in the weak decay, the meson pair creation in the primary $q\bar{q}$ hadronizations and the final state interaction of the hadronic pair, as discussed in details in Ref. [74]. Besides, for the color suppressed process of the $B^0 \rightarrow \phi \pi ^{+}\pi ^{-}$ decay as discussed before, we can roughly estimate its contribution as ${\mathcal {O}}(\frac{1}{N_{c}})$ [71, 72], due to the complicated evaluations of the penguin operators [40, 57, 75]. Then, the amplitudes for these final state productions and their interactions can be written as

$$\begin{aligned}&t \left( B^{0} \rightarrow \phi \pi ^{+} \pi ^{-}\right) \nonumber \\&\quad = \frac{V_{P}}{N_{c}} (V_{ub} V_{ud} + V_{cb} V_{cd} )\left( 1+G_{\pi ^{+} \pi ^{-}} T_{\pi ^{+} \pi ^{-} \rightarrow \pi ^{+} \pi ^{-}}\right. \nonumber \\&\qquad + \frac{1}{2} G_{\pi ^{0} \pi ^{0}} T_{\pi ^{0} \pi ^{0} \rightarrow \pi ^{+} \pi ^{-}} +G_{K^{0} \bar{K}^{0}} T_{K^{0} \bar{K}^{0} \rightarrow \pi ^{+} \pi ^{-}} \nonumber \\&\qquad \left. + \frac{1}{6} G_{\eta \eta } T_{\eta \eta \rightarrow \pi ^{+} \pi ^{-}}\right) \, , \end{aligned}$$

(8)

$$\begin{aligned}&t\left( B^{0}_{s} \rightarrow \phi \pi ^{+} \pi ^{-}\right) \nonumber \\&\quad = V_{P} (V_{ub} V_{us} +V_{cb} V_{cs} ) \left( G_{K^{+}K^{-}}T_{K^{+}K^{-} \rightarrow \pi ^{+} \pi ^{-}} \right. \nonumber \\&\qquad \left. +G_{K^{0} \bar{K}^{0}} T_{K^{0} \bar{K}^{0} \rightarrow \pi ^{+} \pi ^{-}} +\frac{4}{6} G_{\eta \eta } T_{\eta \eta \rightarrow \pi ^{+} \pi ^{-}}\right) , \end{aligned}$$

(9)

where $V_{P}$² is the production vertex factor, which contains all the dynamical factors and is assumed to be universal for these two reactions because of the similar production dynamics. Meanwhile, the differences for these two reactions are specified by the CKM matrix elements $V_{q_1 q_2}$. Besides, the factor $1/N_{c}$ in Eq. (8) accounts for the color suppression [71, 72], where we take $N_c=3$ for the color number.³ It is worth mentioning that, in Eqs. (8) and (9), there is a factor of 2 in the terms related with the identical particles (such as the $\pi ^{0}\pi ^{0}$ and $\eta \eta$) because of the two possibilities in the operators of Eq. (7) to create them, which has been cancelled with the factor of $\frac{1}{2}$ in their propagators within our normalization scheme, see more discussions in Ref. [45]. Besides, the scattering amplitude of $T_{ij}$ for the transition of $i \rightarrow j$ channel is evaluated by the coupled channel Bethe-Salpeter equation with the on-shell prescription,

$$\begin{aligned} T = [1-VG]^{-1}V , \end{aligned}$$

(10)

where the element of the diagonal matrix G is the loop function of two meson propagators, given by

$$\begin{aligned}&G_{ii} (s)\nonumber \\&\quad = i \int \frac{d^{ 4 } q}{( 2 \pi )^{ 4 }} \frac{1}{q^{2} - m_{1}^{2} + i \varepsilon } \frac{1}{\left( p_{1} + p_{2} -q \right) ^{2} - m_{2}^{2} + i \varepsilon } \, , \end{aligned}$$

(11)

with $p_{1}$ and $p_{2}$ the four-momenta of the two mesons in a certain channel, respectively, having $s=(p_1 + p_2)^2$, and $m_{1}$, $m_{2}$ the corresponding masses for them. Since Eq. (11) is logarithmically divergent, the regularization schemes should be utilized to solve this singular integral, either applying the three-momentum cutoff approach [47], where the analytic expression was given in Refs. [77, 78], or the dimensional regularization method [50]. In the present work, we take the cutoff method [47] for Eq. (11),

$$\begin{aligned} G_ {ii} (s) = \int _{0}^{q_{\max }} \frac{q^{2}dq}{(2\pi )^{2}} \frac{\omega _{1}+\omega _{2}}{\omega _{1} \omega _{2} \left[ s-\left( \omega _{1} +\omega _{2}\right) ^{2} +i\varepsilon \right] } \, ,\qquad \end{aligned}$$

(12)

with $q=|\mathbf{q} \,|$ and $\omega _{ i } = ( \mathbf{q} ^{ \,2 } +m_{ i }^{ 2 } )^{ 1 / 2 }$, where the free parameter of the cutoff $q_{max}$ is chosen as 600 MeV for the case of including $\eta \eta$ channel [44] and 931 MeV for the one of excluding $\eta \eta$ channel [79], see more discussions later. Furthermore, the matrix V is constructed by the scattering potentials of each coupled channel, where the elements for the $\pi \pi$ and $K\bar{K}$ channels are taken from Ref. [47] and the one for the $\eta \eta$ channel from Ref. [80]. Thus, after applying the S-wave projection, the elements of the potential $V_{ij}$ are given by

$$\begin{aligned}&V_{11}=-\frac{1}{2 f^{2}} s, \quad V_{12}=-\frac{1}{\sqrt{2} f^{2}} \left( s-m_{\pi }^{2}\right) , \nonumber \\&V_{13}=-\frac{1}{4 f^{2}} s ,\quad V_{14}=-\frac{1}{4 f^{2}} s,\nonumber \\&V_{15}=-\frac{1}{3 \sqrt{2} f^{2}} m_{\pi }^{2}, \quad V_{22}=-\frac{1}{2 f^{2}} m_{\pi }^{2} ,\nonumber \\&V_{23}=-\frac{1}{4 \sqrt{2} f^{2}} s, \quad V_{24}=-\frac{1}{4 \sqrt{2} f^{2}} s, \quad V_{25}=-\frac{1}{6 f^{2}} m_{\pi }^{2} ,\nonumber \\&V_{33}=-\frac{1}{2 f^{2}} s, \quad V_{34}=-\frac{1}{4 f^{2}} s ,\nonumber \\&V_{35}=-\frac{1}{12 \sqrt{2} f^{2}}\left( 9 s-6 m_{\eta }^{2}-2 m_{\pi }^{2}\right) , \quad V_{44}=-\frac{1}{2 f^{2}} s ,\nonumber \\&V_{45}=-\frac{1}{12 \sqrt{2} f^{2}}\left( 9 s-6 m_{\eta }^{2}-2 m_{\pi }^{2}\right) ,\nonumber \\&V_{55}=-\frac{1}{18 f^{2}}\left( 16 m_{K}^{2}-7 m_{\pi }^{2}\right) , \end{aligned}$$

(13)

where the indices 1 to 5 denote the five coupled channels of $\pi ^{+}\pi ^{-}$, $\pi ^{0}\pi ^{0}$, $K^{+}K^{-}$, $K^{0}\bar{K}^{0}$, and $\eta \eta$, respectively, and f is the pion decay constant, taken as $93\ \hbox {MeV}$ [47]. Note that, a normalization factor $\frac{1}{\sqrt{2}}$ has been taken into account in the corresponding channels with the identical particles, such as $\pi ^0\pi ^0$ and $\eta \eta$, and thus, there is no such a factor in the corresponding loop functions in the G matrix, see Eq. (10).

In order to analyze the $\pi \pi$ invariant mass distribution as given in the experiment [53], we need to evaluate the differential decay width $\frac{d\varGamma }{dM_{\mathrm{inv}}}$ in terms of the $\pi ^{+}\pi ^{-}$ invariant mass $M_{\mathrm{inv}}$. Before doing that, one needs to know the partial waves for the final states. If the hadronization parts of $q\bar{q} (\rightarrow \pi ^+\pi ^-)$ is in S-wave (see for P-wave in the next section), which lead to its $J^P =L^{(-1)^L} = 0^+$, then, the primary decay process is a $0^{-} \rightarrow 1^{-} \,+\, 0^{+}$ transition. Therefore, the angular momentum conservation requires a P-wave $L'=1$ for the outgoing vector meson $\phi$, and then, there will be a factor $p_\phi \cos \theta$ in the decay amplitude. Thus, we have finally

$$\begin{aligned} \frac{d \varGamma }{d M_{\mathrm{inv}}}=\frac{1}{(2 \pi )^{3}} \frac{1}{8 M_{B^0_{(s)}}^{2}} \frac{2}{3} p_{\phi }^{3} \tilde{p}_{\pi } \bar{\sum } \sum \left| t_{B_{(s)}^{0} \rightarrow \phi \pi ^{+} \pi ^{-}}\right| ^{2}, \end{aligned}$$

(14)

where the factor $\frac{2}{3}$ comes from the integral of $\cos ^{2}\theta$. Note that, when we fit the $\pi \pi$ invariant mass distributions, we take $\frac{d \varGamma }{d M_{\mathrm{inv}}} \rightarrow C \frac{d \varGamma }{d M_{\mathrm{inv}}}$ with an arbitrary constant C to match the events of the experimental data, see our results later. Besides, $p_{\phi }$ is the $\phi$ momentum in the rest frame of the decaying $B^0_{(s)}$ meson, and $\tilde{p}_{\pi }$ the pion momentum in the rest frame of the $\pi ^{+}\pi ^{-}$ system, which are given by

$$\begin{aligned}&p_{\phi }=\frac{\lambda ^{1 / 2}\left( M_{B^0_{(s)}}^{2}, M_{\phi }^{2}, M_{\mathrm{inv}}^{2}\right) }{2 M_{B_{(s)}}},\nonumber \\&\tilde{p}_{\pi }=\frac{\lambda ^{1 / 2}\left( M_{\mathrm{inv}}^{2}, m_{\pi }^{2}, m_{\pi }^{2}\right) }{2 M_{\text{ inv } }}, \end{aligned}$$

(15)

with the usual Källen triangle function $\lambda (a, b, c) = a^{2} + b^{2} + c^{2} - 2(ab + ac + bc)$.

3 The model for vector meson production

As discussed in last section, the hadronization parts $q\bar{q} (\rightarrow \pi ^+\pi ^-)$ can also be in P-wave, and thus, the quantum numbers of this part are $J^P =L^{(-1)^L} = 1^-$, which correspond to the vector meson production. Therefore, to preserve the angular momentum conservation in the transition $0^- \rightarrow 1^- \,+\, 1^-$, the produced vector mesons should be in the partial waves of $L=0,2$. As commented in Ref. [46], we only take $L=0$ for simplicity, and thus, there is no term of $p_{\phi } \cos \theta$ present in the amplitudes. We take the vector meson $\rho ^0$ production for example, as shown in Fig. 4, which can be generalized to the other vector meson production and discussed later. Then, the corresponding amplitude for the $B^{0}_{s} \rightarrow \phi \rho ^{0}$ decay is given by

$$\begin{aligned} t_{B^{0}_{s} \rightarrow \phi \rho ^{0}} = \frac{1}{\sqrt{2}} \tilde{V}_{P} V_{ub} V_{us}^{*} \, , \end{aligned}$$

(16)

where the prefactor $\frac{1}{\sqrt{2}}$ is the $u\bar{u}$ component in $\rho ^{0}$, and $\tilde{V}_{P}$ the production vertex factor which contains all the dynamical factors and is analogous to the one of $V_P$ discussed in last section. In general, for the decays $B^0_{(s)} \rightarrow \phi V$ with a final vector meson (V), the widths are given by

$$\begin{aligned} \varGamma _{B^{0}_{(s)} \rightarrow \phi V}=\frac{1}{8 \pi } \frac{1}{m_{B_{(s)}^{0}}^{2}}\left| t_{B^{0}_{(s)} \rightarrow \phi V}\right| ^{2} p_{\phi }. \end{aligned}$$

(17)

Next, since the produced vector meson $\rho ^0$ will decay into $\pi ^+\pi ^-$, its contributions to the $\pi ^+\pi ^-$ invariant mass distributions in the $B^{0}_{s}$ decay can be obtained by means of the spectral function [46, 81, 82],

$$\begin{aligned}&\frac{d \varGamma _{B^{0}_{s} \rightarrow \phi \rho ^{0}}}{d M_{\mathrm{inv}} \left( \pi ^{+} \pi ^{-}\right) }\nonumber \\&\quad =- \frac{1}{\pi } 2 m_{\rho } \hbox {Im} \frac{1}{M_{\mathrm{inv}}^{2}-m_{\rho }^{2}+i m_{\rho } \tilde{\varGamma }_{\rho } \left( M_{\mathrm{inv}}\right) } \varGamma _{B^{0}_{s} \rightarrow \phi \rho ^{0}}, \end{aligned}$$

(18)

where $\tilde{\varGamma }_{\rho }\left( M_{\mathrm{inv}}\right)$ is the energy dependent decay width of the $\rho ^{0}$ decaying into two pions, which is given by the parameterization,

$$\begin{aligned} \tilde{\varGamma }_{\rho }\left( M_{\mathrm{inv}}\right)&=\varGamma _{\rho } \, \left( \frac{p_{\pi }^{\text{ off } }}{p_{\pi }^{\text{ on } }}\right) ^{3},\nonumber \\ p_{\pi }^{\mathrm{off}}&=\frac{\lambda ^{1 / 2}\left( M_{\mathrm{inv}}^{2}, m_{\pi }^{2}, m_{\pi }^{2}\right) }{2 M_{\mathrm{inv}}} \theta \left( M_{\mathrm{inv}}-2 m_{\pi }\right) ,\nonumber \\ p_{\pi }^{\mathrm{on}}&=\frac{\lambda ^{1 / 2}\left( m_{\rho }^{2}, m_{\pi }^{2}, m_{\pi }^{2}\right) }{2 m_{\rho }}, \end{aligned}$$

(19)

with $p_{\pi }^{\mathrm{on}}(p_{\pi }^{\mathrm{off}})$ the pion on-shell (off-shell) three momentum in the rest frame of the $\rho ^0$ decay, $\varGamma _{\rho }$ the total $\rho ^0$ decay width, taking as $\varGamma _{\rho } = 149.1$ MeV [1], and the step function of $\theta \left( M_{\mathrm{inv}}-2 m_{\pi }\right)$.

Fig. 4

Diagram of $B^{0}_{s}$ decay into $\phi$ and $\rho ^{0}$ mesons

Fig. 5

Feynman diagrams for the $B^{0}_{(s)}$ decaying into $\phi$ and other vector mesons

Moreover, we can carry on the investigation of the other vector meson production, as shown in Fig. 5, where none of these decay processes is allowed at the tree level, see the suppression results later, and different from the one of Fig. 4. Once again, the case of the $B^0$ decay is color suppressed. The corresponding amplitudes of the decay diagrams in Fig 5 are written as,

$$\begin{aligned} t_{B^{0} \rightarrow \phi \rho ^{0}}&=-\frac{1}{\sqrt{2}N_{c}} \tilde{V}_{P}^{\prime } (V_{ub} V_{u d} +V_{c b} V_{c d} ), \nonumber \\ t_{B^{0} \rightarrow \phi \omega }&=\frac{1}{\sqrt{2}N_{c}} \tilde{V}_{P}^{\prime } (V_{ub} V_{u d} + V_{c b} V_{c d}), \nonumber \\ t_{B^{0}_{s} \rightarrow \phi \phi }&=2 \tilde{V}_{P}^{\prime } (V_{ub} V_{u s} +V_{c b} V_{c s} ), \nonumber \\ t_{B^{0}_{s} \rightarrow \phi \bar{K}^{* 0}}&=2 \tilde{V}_{P}^{\prime } (V_{ub} V_{u d} +V_{c b} V_{c d} ), \end{aligned}$$

(20)

where the factor $-\frac{1}{\sqrt{2}}$ is the $d\bar{d}$ component in $\rho ^{0}$, whereas, $\frac{1}{\sqrt{2}}$ in $\omega$, $\tilde{V}_{P}^{\prime }$ another vertex factor for these hadronization processes. Note that, one can see an extra factor of two in the two $B^{0}_{s}$ decay modes, $\phi \phi$ and $\phi \bar{K}^{* 0}$, because there are two possibilities to create the $\phi$, one by the internal gluon as shown in the lower parts of Fig. 5 and the other one by the external gluon analogous to the case of $B^0$ decay in the upper parts of Fig. 5. Note that, these two decay modes for the $B^{0}_{s}$ decay are different from the cases of $\varLambda _c$ decay with the internal or external W boson exchanges as discussed in Refs. [82,83,84]. The internal and external W emission mechanism is also discussed in the recent works for the reactions of $D^+\rightarrow \pi ^+\pi ^0\eta$ [85] and $D^0\rightarrow K^-\pi ^+\eta$ [86]. With the amplitudes given by Eq (20), one can calculate the decay widths for these decay modes with the vector production using Eq. (17), and thus, the decay ratios for them (see our results in the next section).

4 Results

As discussed in the introduction, the rare decays $B^{0}_{(s)} \rightarrow \phi \pi ^{+}\pi ^{-}$ had been reported by the LHCb collaboration [53], where the $\pi \pi$ invariant mass distributions and some related branching fractions were obtained. In the present work, considering the final state interaction, we look for the resonant contributions in these decays around the energy region lower than about 1 GeV. One should keep in mind that the only one free parameter $q_{max}$ (the cutoff in the loop functions) is taken as 600 MeV for including $\eta \eta$ channel [44] and 931 MeV for excluding $\eta \eta$ channel [79]. Especially, the one of 931 MeV was determined from the combined fit of several sets of experimental data in our former work of [79]. Therefore, the cutoff is fixed in our calculation, in order to investigate the properties of the resonances $f_{0}(500)$ and $f_{0}(980)$ reproduced in the final state interactions. Thus, our predictions later are obtained with a “general” parameter. We show the results of the $\pi \pi$ invariant mass distributions for the decay of $B^{0}_{s}\rightarrow \phi \pi ^{+} \pi ^{-}$ in Fig. 6, which is only plotted up to 1.1 GeV within the effective energy range of the ChUA for the meson-meson interaction [47]. From Fig. 6, one can see that the $f_0(980)$ resonance is the dominant contribution around the region 1 GeV, which is consistent with the one fitted with Flatté model in the experimental results of Ref. [53]. As discussed in the formalism, there are some theoretical uncertainties for the coupled channel interaction with [80] or without [47] $\eta \eta$ channel, see the results of the dashed (red, with $q_{max} = 600$ MeV) line and the dash-dot (black, with $q_{max} = 931$ MeV) line in Fig. 6, respectively, where the uncertainties of the cutoff are shown as the green and yellow bands by varying the cutoff within 10%. This uncertainties for the cutoff was taken from Ref. [79] and determined from the biggest error bar for the parameter to describe all the fitted data well, see the results in Ref. [79]. In Fig. 6, one can see that the line shape of the $f_0(980)$ state is narrower when the contribution of the $\eta \eta$ channel is taken into account. Since the threshold of the $\eta \eta$ channel is not far above the $f_0(980)$, it has nontrivial effects, which will give some uncertainties to the branching ratios, see our results later. Indeed, when the $\eta \eta$ channel is considered, the pole for the $f_0(980)$ state changes to lower energy region, see the dash-dot (blue) line and the dashed (green) line of Fig. 7. However, as found in Ref. [68], for the bound state of the $K\bar{K}$ channel, one should decrease the cutoff to move the pole of the $f_0(980)$ state to higher energy when the $\eta \eta$ channel is included, which will lead to the width of the pole decrease, see the solid (red) line of Fig. 7 and more discussions in Ref. [68]. This is why the peak of the $f_0(980)$ state become narrow when we add the coupled channel of $\eta \eta$, which is different from the interference effects in the case of narrow $\sigma$ state in the $J/\psi \rightarrow p \bar{p} \pi ^+\pi ^-$ decay [87] and the $J/\psi \rightarrow \omega \pi \pi$ decay [88]. Furthermore, the effect of $\eta \eta$ channel was also taken into account in a recent work of [89] to investigate $D^+\rightarrow K^-K^+K^+$ decay, where the dominant contributions were found from the $a_0(980)$ resonance near the $K\bar{K}$ threshold and the two-body scattering amplitudes were evaluated with the N/D method [90] to extend the applicability range of ChUA above 1 GeV. In our work, the considering of $\eta \eta$ channel is to check the uncertainties of its contribution to our results, since its influence is just come from the coupled channel effect due to its threshold a bit far above the mass of $f_0(980)$, see more discussions about the coupled channel effect in Ref. [91]. Thus, the results without its contribution are favoured from the physical point of view as done in Refs. [47, 68]. Note that, as one can see in Fig. 6, the peak of the $f_0(980)$ state, which was reproduced within our formalism, is a bit narrower than the experimental structure in the data. No matter what regularization schemes that we take, the width of the $f_0(980)$ state is not so large, see our results in Fig. 8, where the reproduced results are consistent with each other taking the dimensional regularization and the cutoff method for the loop functions. More discussions about the regularization schemes can be found in Refs. [92,93,94]. Indeed, as shown in the results of Ref. [68], the width of the $f_0(980)$ state increased not so much even though we varied the cutoff in a large range. In fact, our results with $q_{max} = 931$ are just a bit narrower and sharper than the line shape of Flatté model [53], leading to the lower part of the peak become narrow. On the other hand, the structure around 1 GeV in the data was also contributed by the higher resonances, such as the one of $f_2(1270)$, which will contribute to the fit around the region of 1.1 GeV through the interference effects as shown in the results of Ref. [53], more discussions therein. Since these higher resonances are out of the effective range of our formalism, they are not considered in our case.

Fig. 6

$\pi ^{+}\pi ^{-}$ invariant mass distributions of the $B^{0}_{s}\rightarrow \phi \pi ^{+}\pi ^{-}$ decay, where we plot $\frac{C \times 10^{-9}}{\varGamma _{B_{s}}} \frac{d \varGamma }{d M_{\mathrm{inv}}}$ with the reduced chi-square $\chi ^{2}/dof. = 79.84 / (18 - 2) = 4.99$. The dashed (red) line corresponds to the $f_{0}(980)$ resonance contributions with the coupled channel of $\eta \eta$ (normalization constant $C_1=1.13$), the dash-dot (black) line without the $\eta \eta$ channel ($C_1^\prime =4.46$), and the dot (magenta) line for the $\rho$ meson contributions ($C_2=6.64$), and the solid (blue) line represents the sum of the contributions of two states $f_{0}(980)$ and $\rho$. The green and yellow bands are the uncertainties with 10% changes to the cutoff. Data are taken from Ref. [53]

Fig. 7

Modulus square of the scattering amplitude of $t_{B^{0}_{s}\rightarrow \phi \pi ^{+}\pi ^{-}}$, see Eq. (9), where we only plot the last parts without the previous factors of the vertex $V_P$ and the CKM elements, for the case of including the $\eta \eta$ channel with the cutoff $q_{max}= 600$ MeV (the solid, red line), 931 MeV (the dash-dot, blue line) and excluding the $\eta \eta$ channel with the cutoff $q_{max}= 931$ MeV (the dashed, green line)

Fig. 8

Comparison of the $\pi ^{+}\pi ^{-}$ invariant mass distributions of the $B^{0}_{s}\rightarrow \phi \pi ^{+}\pi ^{-}$ decay using the cutoff and dimensional regularization methods

In the last section, we also take into account the contributions from the vector meson production when the final states of $\pi ^+\pi ^-$ are in P-wave, see the results of the dot (magenta) line in Fig. 6, which are the contribution of the $\rho$ meson, as indicated in the experiment [53]. From the results of the solid (blue) line in Fig. 6, our results for the contribution of the sum of two resonances, the $f_0(980)$ and $\rho$, describe the experimental data up to 1 GeV well. One thing should be mentioned that there are some uncertainties for the data around the region of $\rho$ meson. In fact, the contribution from $\rho$ meson is just a statistical significance of $4.5\,\sigma$ as discussed in Ref. [53]. As one can see that the results of Fig. 6 are just fitted with two free normalization factors (C) and describe the data well, which are meaningful. Furthermore, as found in the experiment [53], there is no clear signal for the $f_{0}(500)$ resonance. Indeed, in our formalism there is no such contributions, see Eq. (9), since the $f_{0}(500)$ state appears in the amplitude of $T_{\pi ^{+} \pi ^{-} \rightarrow \pi ^{+} \pi ^{-}}$, which is analogous to the case of $B^{0}_{s} \rightarrow J/\psi \pi ^{+} \pi ^{-}$ decay [44,45,46] (see our results in Appendix B). Conversely, this is not the case for the $B^{0}\rightarrow \phi \pi ^{+}\pi ^{-}$ decay, of which our predicted results for the S-wave $\pi ^{+}\pi ^{-}$ mass distribution are shown in Fig. 9 with the error bands for the cutoff. From the results of Fig. 9, one can see that the contributions from the broad peak of the $f_{0}(500)$ state above the $\pi \pi$ threshold are more significant than the ones of the $f_{0}(980)$ resonance, which shows up as a narrow and small peak near the $K\bar{K}$ threshold. There are some uncertainties for the effects of the $\eta \eta$ channel as shown in Fig. 9, where the contributions of the $f_{0}(500)$ state are stronger when the $\eta \eta$ channel is not considered, see the solid (red) line of Fig. 9. Note that, there are also some uncertainties from the values of the CKM matrix elements, taking the Wolfenstein parameterization or the absolute values, see Eqs. (34) and (37) in Appendix A, especially in the case of the $B^{0}\rightarrow \phi \pi ^{+}\pi ^{-}$ decay, see Eq. (8). However, our main results use the ones of the Wolfenstein parameterization.

Fig. 9

$\pi ^{+}\pi ^{-}$ invariant mass distributions of the $B^{0}\rightarrow \phi \pi ^{+}\pi ^{-}$ decay for the scattering amplitudes with (blue) and without (red) the $\eta \eta$ channel contribution. The error bands are also taken 10% changes to the cutoff

The only unknown parameter left in our formalism is the production vertex $V_{p}$, see the discussion after Eq. (9). In order to make the predictions for the $B^{0}\rightarrow \phi \pi ^{+}\pi ^{-}$ decay, we need to determine its value from the experimental branching ratios of the $B^{0}_{s}\rightarrow \phi f_{0}(980)$ decay. For the case of considering the $\eta \eta$ channel, using Eq. (14), we have

$$\begin{aligned} \text {Br}(B^{0}_{s} \rightarrow \phi f_{0}(980))&= \frac{\varGamma _{B^{0}_{s} \rightarrow \phi f_{0}(980)}}{\varGamma _{B_{s}}} \nonumber \\&= \frac{\int _{2m_{\pi }}^{1200}\frac{d\varGamma _{B^{0}_{s} \rightarrow \phi f_{0}(980)}}{dM_{inv}}dM_{inv}}{\varGamma _{B_{s}}} \nonumber \\&= \frac{V_{p}^{2}}{\varGamma _{B_{s}}} \times 32.95 \, , \end{aligned}$$

(21)

which turns out to be,

$$\begin{aligned} \text {Br}(B^{0}_{s} \rightarrow \phi f_{0}(980))&= \frac{\varGamma _{B^{0}_{s} \rightarrow \phi f_{0}(980)}}{\varGamma _{B_{s}}} \nonumber \\&= \frac{\int _{2m_{\pi }}^{1200}\frac{d\varGamma _{B^{0}_{s} \rightarrow \phi f_{0}(980)}}{dM_{inv}}dM_{inv}}{\varGamma _{B_{s}}} \nonumber \\&= \frac{V_{p}^{2}}{\varGamma _{B_{s}}} \times 51.18 \, , \end{aligned}$$

(22)

Table 1 Predicted branching ratios of $B^{0}\rightarrow \phi f_{0}(980)$ and $B^{0}\rightarrow \phi f_{0}(500)$

Table 2 Predictions for the other branching ratios

for the case without the $\eta \eta$ channel contribution. Thus, using the measured branching fraction of $\text {Br}(B^{0}_{s} \rightarrow \phi f_{0}(980))= (1.12 \pm 0.21) \times 10^{-6}$ [1], we obtain $\frac{V_{p}^{2}}{\varGamma _{B_{s}}}= (3.40 \pm 0.64) \times 10^{-8}$ and $\frac{V_{p}^{2}}{\varGamma _{B_{s}}}= (2.19 \pm 0.41) \times 10^{-8}$ for the two cases, respectively, where the uncertainties are estimated from the errors of the experimental branching ratio. Therefore, using the determined values of $\frac{V_{p}^{2}}{\varGamma _{B_{s}}}$ from Eqs. (21) and (22), we can evaluate the branching ratios of the decays $B^{0}\rightarrow \phi f_{0}(980)\rightarrow \phi \pi ^{+}\pi ^{-}$ and $B^{0}\rightarrow \phi f_{0}(500)\rightarrow \phi \pi ^{+}\pi ^{-}$ with

$$\begin{aligned}&\text {Br}(B^{0} \rightarrow \phi f_{0}(980))\nonumber \\&\quad =\frac{\varGamma _{B^{0} \rightarrow \phi f_{0}(980)}}{\varGamma _{B}} =\frac{\int _{900}^{1200} \frac{d\varGamma _{B^{0} \rightarrow \phi f_{0}(980)}}{dM_{inv}}dM_{inv}}{\varGamma _{B}}, \end{aligned}$$

(23)

$$\begin{aligned}&\text {Br}(B^{0} \rightarrow \phi f_{0}(500))\nonumber \\&\quad =\frac{\varGamma _{B^{0} \rightarrow \phi f_{0}(500)}}{\varGamma _{B}} =\frac{\int _{2m_{\pi }}^{900} \frac{d\varGamma _{B^{0} \rightarrow \phi f_{0}(500)}}{dM_{inv}}dM_{inv}}{\varGamma _{B}}, \end{aligned}$$

(24)

where the predicted results are shown in Table 1. From the results of Table 1, one can see that our predictions for the branching ratios of $\text {Br}(B^{0} \rightarrow \phi f_{0}(980))$ for two cases are within the upper limit of the experiment. Note that we have considered two uncertainties for the results in Table 1. The first one is estimated from the experimental error of the branching ratio used for determining the vertex factor. The second one comes from the integration limits of Eqs. (23) and (24), since there are uncertainties in the overlap region for the contributions of the $f_{0}(500)$ and $f_{0}(980)$ resonances, as shown in Fig. 9. For the central value, we have chosen 900 MeV for the cutting point of the contributions between two states of $f_{0}(500)$ and $f_{0}(980)$, see Eqs. (23) and (24). Thus, to estimate the uncertainties, we change the central value by $\pm 50$ MeV.

Analogously, we can also make some predictions for the ratios between different final states of the $B^{0}_{(s)}$ decays. In the present work, we study the suppressed decays of the $B^{0}_{(s)}\rightarrow \phi \pi ^{+} \pi ^{-}$ comparing to the Cabibbo allowed ones $B^{0}_{(s)} \rightarrow J/\psi \pi ^{+} \pi ^{-}$, see Refs. [44, 45], which are reproduced in detail in Appendix B. Thus, we can make the predictions of the ratios between all the other relevant channels, based on the experimental results to get the relation of the vertex factors, given by

$$\begin{aligned} \frac{\text {Br}(B^{0}_{s} \rightarrow \phi f_{0}(980))}{\text {Br}(B^{0}_{s} \rightarrow J/\psi f_{0}(980))}=(8.75 \pm 2.87) \times 10^{-3} \, , \end{aligned}$$

(25)

which indeed indicates that the decay of $B^{0}_{s}\rightarrow \phi \pi ^{+} \pi ^{-}$ is more suppressed than the one of $B^{0}_{s}\rightarrow J/\psi \pi ^{+} \pi ^{-}$. Within our theoretical model, we have

$$\begin{aligned} \frac{\text {Br}(B^{0}_{s} \rightarrow \phi f_{0}(980))}{\text {Br}(B^{0}_{s} \rightarrow J/\psi f_{0}(980))}=\left( \frac{V_{p}}{V_{p}^{\prime }}\right) ^{2} \times 3.78 \, . \end{aligned}$$

(26)

Therefore, we can obtain $(\frac{V_{p}}{V_{p}^{\prime }})^{2} = (2.31 \pm 0.76) \times 10^{-3}$. Moreover, this value is similar for both cases with or without the contributions of the $\eta \eta$ channel. Using the determined value of $\frac{V_{p}}{V_{p}^{\prime }}$, the predicted branching ratios are made, see the results in Table 2, where, again, the first uncertainty is relevant to the experimental results and the second one corresponds to the limits of the integration. Based on these results, using the experimental branching ratio of $\text {Br}(B^{0}\rightarrow J/\psi f_{0}(500))= 8 ^{+1.1}_{-0.9} \times 10^{-6}$, we can obtain the branching fraction of $B^{0}\rightarrow \phi f_{0}(500)$ for the case of without $\eta \eta$ channel,

$$\begin{aligned} \text {Br}(B^{0}\rightarrow \phi f_{0}(500)) =(6.29 ^{+2.93+0.03 }_{-2.77-0.02}) \times 10^{-9}, \end{aligned}$$

(27)

and for the one with $\eta \eta$ channel,

$$\begin{aligned} \text {Br}(B^{0}\rightarrow \phi f_{0}(500)) = (6.30^{+2.94+0.03 }_{-2.78-0.03})\times 10^{-9}, \end{aligned}$$

(28)

which are consistent with the results obtained in Table 1 within the uncertainties.

Furthermore, for the $B^{0}_{s} \rightarrow \phi \rho ^{0}$ decay, similarly we can determine the value of the vertex factor of $\tilde{V}_{P}$ by the experimental branching fraction of $B^{0}_{s} \rightarrow \phi \rho ^{0}$ in PDG [1], $\text {Br}(B^{0}_{s} \rightarrow \phi \rho ^{0})=(2.7\pm 0.8) \times 10^{-7}$. Using Eq. (17), we have

$$\begin{aligned} \text {Br}(B^{0}_{s} \rightarrow \phi \rho ^{0})= \frac{\varGamma _{B^{0}_{s} \rightarrow \phi \rho ^{0}}}{\varGamma _{B_{s}}}= \frac{\tilde{V}_{P}^{2}}{\varGamma _{B_{s}}} \times 1.14 \times 10^{-12}.\qquad \end{aligned}$$

(29)

Thus, using the experimental results, we can obtain $\frac{\tilde{V}_{P}^{2}}{\varGamma _{B_{s}}}= (2.36 \pm 0.70) \times 10^{5}$. On the other hand, also with Eq. (17), one can determine the branching ratios for the other vector decay channels $\phi V$. For example, the $\phi \phi$ decay channel, based on the measured branching fraction of $\text {Br}(B^{0}_{s} \rightarrow \phi \phi )= (1.87 \pm 0.15) \times 10^{-5}$ [1], we can obtain the value of the vertex factor as $\frac{(\tilde{V}_{P}^{\prime })^{2}}{\varGamma _{B_{s}}}= (8.05 \pm 0.65) \times 10^{2}$,⁴ where the uncertainty comes from the experimental value of the branching ratio. Analogous to the others, the results are related to the CKM matrix elements for the intermediate weak decay processes, and thus, one can easily get the ratios as below,

$$\begin{aligned} R_{1}^{th}&=\frac{\varGamma _{B^{0} \rightarrow \phi \rho ^{0}}}{\varGamma _{B^{0}_{s} \rightarrow \phi \phi }}\nonumber \\&=\frac{1}{N_{c}^{2}} \frac{1}{4} \frac{1}{2}\left| \frac{V_{ub} V_{u d} +V_{c b} V_{c d} }{V_{ub}V_{u s} +V_{c b} V_{c s} }\right| ^{2} \frac{m_{B^{0}_{s}}^{2}}{m_{B^{0}}^{2}} \frac{p_{\rho ^{0}}}{p_{\phi }}\nonumber \\&= 6.70 \times 10^{-4}, \nonumber \\ R_{2}^{th}&=\frac{\varGamma _{B^{0} \rightarrow \phi \omega }}{\varGamma _{B^{0}_{s} \rightarrow \phi \phi }}\nonumber \\&=\frac{1}{N_{c}^{2}} \frac{1}{4} \frac{1}{2} \left| \frac{V_{ub} V_{u d} +V_{c b} V_{c d} }{V_{ub} V_{u s} +V_{c b} V_{c s} }\right| ^{2} \frac{m_{B^{0}_{s}}^{2}}{m_{B^{0}}^{2}} \frac{p_{\omega }}{p_{\phi }}\nonumber \\&= 6.70 \times 10^{-4}, \nonumber \\ R_{3}^{th}&=\frac{\varGamma _{B^{0}_{s} \rightarrow \phi \bar{K}^{* 0}}}{\varGamma _{B^{0}_{s} \rightarrow \phi \phi }}\nonumber \\&= \left| \frac{V_{ub} V_{u d} +V_{c b} V_{c d} }{V_{ub} V_{u s} +V_{c b} V_{c s} }\right| ^{2} \frac{p_{\bar{K}^{* 0}}}{p_{\phi }}= 4.72 \times 10^{-2}. \end{aligned}$$

(30)

The only available experimental ratio in PDG [1] is

$$\begin{aligned} \qquad R_{3}^{exp}&= \frac{\text {Br}(B^{0}_{s} \rightarrow \phi \bar{K}^{* 0})}{\text {Br}(B^{0}_{s} \rightarrow \phi \phi )} \nonumber \\&= \frac{(1.14 \pm 0.30) \times 10^{-6} }{(1.87 \pm 0.15) \times 10^{-5}} \nonumber \\&= (6.09 \pm 2.09) \times 10^{-2} \, , \end{aligned}$$

(31)

where we can see that our predicted $R_{3}^{th}$ is consistent with the experimental results within the uncertainties. Besides, using the determined vertex factors above, we can also obtain the other three branching ratios,

$$\begin{aligned} \text {Br}(B^{0}&\rightarrow \phi \rho ^{0}) = \frac{\varGamma _{B^{0} \rightarrow \phi \rho ^{0}}}{\varGamma _{B}}= (1.25 \pm 0.10) \times 10^{-8},\nonumber \\ \text {Br}(B^{0}&\rightarrow \phi \omega )=\frac{\varGamma _{B^{0} \rightarrow \phi \omega }}{\varGamma _{B}}=(1.25 \pm 0.10) \times 10^{-8}, \nonumber \\ \text {Br}(B^{0}_{s}&\rightarrow \phi \bar{K}^{* 0})=\frac{\varGamma _{B^{0}_{s} \rightarrow \phi \bar{K}^{* 0}}}{\varGamma _{B_{s}}}= (8.83 \pm 0.71) \times 10^{-7}, \end{aligned}$$

(32)

which are consistent with the experimental results [1] within the upper limits,

$$\begin{aligned}&\text {Br}(B^{0} \rightarrow \phi \rho ^{0})< 3.3 \times 10^{-7},\nonumber \\&\text {Br}(B^{0} \rightarrow \phi \omega )< 7 \times 10^{-7}, \nonumber \\&\text {Br}(B^{0}_{s} \rightarrow \phi \bar{K}^{* 0})= (1.14 \pm 0.30) \times 10^{-6}. \end{aligned}$$

(33)

As one can see, for the case of $B^{0}_{s} \rightarrow \phi \bar{K}^{* 0}$, the predicted value for the branching ratio is in agreement with the experiment within the uncertainties.

5 Conclusions

The rare non-leptonic three body decays of $B^{0}_{s} \rightarrow \phi \pi ^{+}\pi ^{-}$ and $B^{0} \rightarrow \phi \pi ^{+}\pi ^{-}$, which are induced by the flavour changing neutral current $b\rightarrow s\bar{s}s$ and $b\rightarrow d\bar{s}s$, respectively, are studied by taking into account the final state interaction, based on the chiral unitary approach, where the contributions from the scalar resonances ($f_{0}(500)$ and $f_{0}(980)$) and vector mesons ($\rho$, $\omega$, $\phi$, and $\bar{K}^{* 0}$) are considered. Note that, in the coupled channel interaction, we find that the channel $\eta \eta$ can be ignored for the reproduction of the $f_{0}(980)$ state, since it is a bit far above the $K\bar{K}$ threshold. When we consider two resonances contributions of the $f_{0}(980)$ and $\rho$, our results of the $\pi ^+\pi ^-$ invariant mass distributions for the $B^{0}_{s}\rightarrow \phi \pi ^{+}\pi ^{-}$ decay describe the experimental data up to 1 GeV well, whereas, there are no clear contributions from the $f_{0}(500)$ state in our formalism as indicated in the experiments. Based on these results, we predict the invariant mass distributions of the $B^{0} \rightarrow \phi \pi ^{+}\pi ^{-}$ decay, where a broad resonance structure can be easily seen in the $\pi ^+\pi ^-$ invariant mass distributions and a small narrow peak corresponding to the $f_{0}(980)$ also can be found. These results reveal that the contributions from the $f_{0}(500)$ state are larger than the ones of the $f_{0}(980)$. From these results, one can conclude that the dominant components for the $f_{0}(500)$ resonance are the $\pi \pi$ parts, whereas, the $f_{0}(980)$ state is mainly contributed by the $K\bar{K}$ components. We also investigate the branching ratios for different decay processes with the scalar and vector meson produced in the final states, where some of our results are in agreement with the experiments. Besides, we study the ratios for the $B^0_{(s)}$ decaying into $\phi$ plus the other states and $J/\psi$ plus the same states. All the predicted results can be found in Tables 1, 2 and Eqs. (30), (32). Finally, we hope that our predicted $\pi ^+\pi ^-$ invariant mass distributions for the decay of $B^{0} \rightarrow \phi \pi ^{+}\pi ^{-}$ and some other branching ratios can be measured by future experiments.

Note added: When our work was ready, we found that the work of [95] also investigate the decays of $B^{0}_{(s)} \rightarrow \phi \pi ^{+}\pi ^{-}$ with the perturbative QCD approach, which focuses on the branching fractions, the CP asymmetries, and so on.

Appendices

Appendices

A CKM matrix

The CKM matrix elements are fundamental parameters of the SM. The elements of the CKM matrix have been determined from the experiments, which can be expressed according to the A, $\rho$, $\lambda$, and $\eta$ parameters, called the Wolfenstein parameterization [1, 96],

$$\begin{aligned} V_{\mathrm{CKM}}=&\left( \begin{array}{ccc} 1-\lambda ^{2} / 2 &{} \lambda &{} A \lambda ^{3}(\rho -i \eta ) \\ -\lambda &{} 1-\lambda ^{2} / 2 &{} A \lambda ^{2} \\ A \lambda ^{3}(1-\rho -i \eta ) &{} -A \lambda ^{2} &{} 1 \end{array}\right) \nonumber \\&+{\mathcal {O}}\left( \lambda ^{4}\right) , \end{aligned}$$

(34)

where the values of these parameters are given by [1]

$$\begin{aligned}&\lambda =0.22453 \pm 0.00044, \quad A=0.836 \pm 0.015, \nonumber \\&\bar{\rho }=0.122_{-0.017}^{+0.018}, \quad \bar{\eta }=0.355_{-0.011}^{+0.012}, \end{aligned}$$

(35)

with the definitions of

$$\begin{aligned} \bar{\rho }=\rho \left( 1-\frac{\lambda ^{2}}{2}\right) , \quad \bar{\eta } =\eta \left( 1-\frac{\lambda ^{2}}{2}\right) . \end{aligned}$$

(36)

Besides, the absolute value of the CKM matrix including the uncertainties can be given by

$$\begin{aligned} |V_{\mathrm{CKM}}|=\left( \begin{array}{ccc} 0.97446 (10) &{} 0.22452 (44) &{} 0.00365 (12) \\ 0.22438 (44) &{} 0.97359 (10) &{} 0.04214 (76) \\ 0.00896 (24) &{} 0.04133 (74) &{} 0.999105 (32) \\ \end{array}\right) . \end{aligned}$$

(37)

B Formalism for $B^{0}_{(s)}$ decaying to $J/\psi \pi ^{+}\pi ^{-}$

The details for the study of the $B^{0}_{(s)} \rightarrow J/\psi \pi ^{+} \pi ^{-}$ decays in the work of [44, 45] are summarized as follow,

$$\begin{aligned} B^{0}(\bar{b}d)&\Rightarrow [V_{cb}] \bar{c} W^{+} d \Rightarrow [V_{cb}][V_{cd}^{*} ]\, (c\bar{c})\, (d\bar{d})\nonumber \\&\Rightarrow [V_{cb}][V_{cd}^{*} ]\, (c\bar{c}\rightarrow J/\psi ) \,[d\bar{d}\rightarrow d\bar{d}\nonumber \\&\cdot (u\bar{u}+d\bar{d}+s\bar{s})] \nonumber \\&\Rightarrow [V_{cb}][V_{cd}^{*} ]\, (c\bar{c}\rightarrow J/\psi ) \, [M_{22}\rightarrow (M\cdot M)_{22}] \, , \end{aligned}$$

(38)

$$\begin{aligned} B^{0}_{s} (\bar{b}s)&\Rightarrow [V_{cb}] \bar{c} W^{+} s \Rightarrow [V_{cb}][V_{cs}^{*} ]\, (c\bar{c})\, (s\bar{s}) \nonumber \\&\Rightarrow [V_{cb}][V_{cs}^{*} ]\, (c\bar{c}\rightarrow J/\psi ) \, [s\bar{s} \rightarrow s\bar{s}\nonumber \\&\cdot (u\bar{u}+d\bar{d}+s\bar{s})] \nonumber \\&\Rightarrow [V_{cb}][V_{cs}^{*} ]\, (c\bar{c}\rightarrow J/\psi ) \, [M_{33}\rightarrow (M\cdot M)_{33}] \, , \end{aligned}$$

(39)

where the matrix M is defined in Eq. (5). Thus, we have for the hadronization procedures

$$\begin{aligned} d \bar{d} \cdot (u \bar{u}+d \bar{d}+s \bar{s})&\equiv (\varPhi \cdot \varPhi )_{22} =\pi ^{+} \pi ^{-}+\frac{1}{2} \pi ^{0} \pi ^{0}\nonumber \\&\quad -\frac{1}{\sqrt{3}} \pi ^{0} \eta +K^{0} \bar{K}^{0}+\frac{1}{6} \eta \eta ,\nonumber \\ s \bar{s} \cdot (u \bar{u}+d \bar{d}+s \bar{s})&\equiv (\varPhi \cdot \varPhi )_{33} =K^{-} K^{+}+K^{0} \bar{K}^{0}\nonumber \\&\quad +\frac{4}{6} \eta \eta , \end{aligned}$$

(40)

with the matrix $\varPhi$ given in Eq. (6).

Fig. 10

$\pi ^{+}\pi ^{-}$ invariant mass distributions of the $B^{0}_{s}\rightarrow J/\psi \pi ^{+}\pi ^{-}$ decay, where we plot $\frac{C^\prime \times 10^{-8}}{\varGamma _{B_{s}}} \frac{d \varGamma }{d M_{\mathrm{inv}}}$ and the data are taken from Ref. [60]. The dashed (red) and solid (green) lines correspond to the results with (the normalization constant $C^\prime =5.36$) and without ($C^\prime =19.71$) the $\eta \eta$ channel contributions in the two-body interaction, respectively

The amplitudes for the $\pi ^{+}\pi ^{-}$ production are given by

$$\begin{aligned}&t\left( B^{0} \rightarrow J/\psi \pi ^{+} \pi ^{-}\right) \nonumber \\&\quad = V^{\prime }_{P} (V_{cb}V_{cd}^{*} )\left( 1+G_{\pi ^{+} \pi ^{-}} t_{\pi ^{+} \pi ^{-} \rightarrow \pi ^{+} \pi ^{-}} \right. \nonumber \\&\qquad + \frac{1}{2} G_{\pi ^{0} \pi ^{0}} t_{\pi ^{0} \pi ^{0} \rightarrow \pi ^{+} \pi ^{-}}\nonumber \\&\qquad +G_{K^{0} \bar{K}^{0}} t_{K^{0} \bar{K}^{0} \rightarrow \pi ^{+} \pi ^{-}} \nonumber \\&\qquad \left. + \frac{1}{6} G_{\eta \eta } t_{\eta \eta \rightarrow \pi ^{+} \pi ^{-}}\right) , \nonumber \\&t\left( B^{0}_{s} \rightarrow J/\psi \pi ^{+} \pi ^{-}\right) \nonumber \\&\quad = V^{\prime }_{P} (V_{cb} V_{cs}^{*} )\left( G_{K^{+}K^{-}}t_{K^{+}K^{-} \rightarrow \pi ^{+} \pi ^{-}} \right. \nonumber \\&\qquad +G_{K^{0} \bar{K}^{0}} t_{K^{0} \bar{K}^{0} \rightarrow \pi ^{+} \pi ^{-}} \nonumber \\&\qquad \left. + \frac{4}{6} G_{\eta \eta } t_{\eta \eta \rightarrow \pi ^{+} \pi ^{-}}\right) , \end{aligned}$$

(41)

Finally, the partial decay widths can be written as

$$\begin{aligned} \frac{d \varGamma }{d M_{\mathrm{inv}}}=&\frac{1}{(2 \pi )^{3}} \frac{1}{8 M_{B_{(s)}}^{2}} \frac{2}{3} p_{J/\psi }^{2} p_{J/\psi } \tilde{p}_{\pi } \nonumber \\&\bar{\sum } \sum \left| t_{B_{(s)}^{0} \rightarrow J/\psi \pi ^{+} \pi ^{-}}\right| ^{2}. \end{aligned}$$

(42)

Thus, when the $\eta \eta$ channel is considered in the coupled channel interaction, we have

$$\begin{aligned} \text {Br}(B^{0}_{s} \rightarrow J/\psi f_{0}(980))&= \frac{\varGamma _{B^{0}_{s} \rightarrow J/\psi f_{0}(980)}}{\varGamma _{B_{s}}} \nonumber \\&= \frac{\int _{2m_{\pi }}^{1200}\frac{d\varGamma _{B^{0}_{s} \rightarrow J/\psi f_{0}(980)}}{dM_{inv}}dM_{inv}}{\varGamma _{B_{s}}} \nonumber \\&= \frac{V_{P}^{\prime 2}}{\varGamma _{B_{s}}} \times 8.66 \, , \end{aligned}$$

(43)

and ignored the $\eta \eta$ channel in the two-body interaction,

$$\begin{aligned} \text {Br}(B^{0}_{s} \rightarrow J/\psi f_{0}(980))&= \frac{\varGamma _{B^{0}_{s} \rightarrow J/\psi f_{0}(980)}}{\varGamma _{B_{s}}} \nonumber \\&= \frac{\int _{2m_{\pi }}^{1200}\frac{d\varGamma _{B^{0}_{s} \rightarrow J/\psi f_{0}(980)}}{dM_{inv}}dM_{inv}}{\varGamma _{B_{s}}} \nonumber \\&= \frac{V_{P}^{\prime 2}}{\varGamma _{B_{s}}} \times 13.54 \, . \end{aligned}$$

(44)

Using the measured branching fraction of $\text {Br}(B^{0}_{s} \rightarrow J/\psi f_{0} (980))= (1.28 \pm 0.18) \times 10^{-4}$ [1], we can obtain $\frac{V_{P}^{\prime 2}}{\varGamma _{B_{s}}}= (1.48 \pm 0.21) \times 10^{-5}$ and $\frac{V_{P}^{\prime 2}}{\varGamma _{B_{s}}}= (9.46 \pm 1.33) \times 10^{-6}$ for with and without the $\eta \eta$ channel contributions in the two-body interaction, respectively.

The $\pi ^{+}\pi ^{-}$ invariant mass distributions of $B^{0}_{s}\rightarrow J/\psi \pi ^{+} \pi ^{-}$ and $B^{0}\rightarrow J/\psi \pi ^{+} \pi ^{-}$ are shown in Figs. 10 and 11, respectively, which are consistent with the ones of Ref. [44].

Fig. 11

$\pi ^{+}\pi ^{-}$ invariant mass distributions for the $B^{0}\rightarrow J/\psi \pi ^{+}\pi ^{-}$ decay, where the solid (magenta) and dashed (black) lines represent the results with and without the coupled channel of $\eta \eta$, respectively