The production of singly charmed pentaquark ${\bar{c}} q qqq$ from bottom baryon

Abstract

In the paper, we study the production of pentaquark $\bar{c}q qqq$ from singly bottom baryon. The tensor representations of pentaquark $\bar{c}q qqq$ are completed at first. Under the light quark symmetry analysis, we decompose the singly charmed pentaquarks into 6, 15 and $15'$ multiple states, and deduce the representations of these states. Then we construct the production Hamiltonian of the multiple states in proper order. For completeness, we systematically study the production channels of pentaquark states, including the possible production amplitudes and decay relations between different channels, concurrently, the widths of selected channels are worked out with the effective Lagrangian approach. Ultimately, we expect that the chosen channels will be fairly valuable supports for future search experiments.

1 Introduction

Recently, a series of pentaquark state candidates were observed from the measurements of LHC experiment, the pentaquark states $P_c(4380)^+$ [1], $P_c(4440)^+$ [2], $P_c(4457)^+$ [2] and $P_c(4312)^+$ [2] from the analysis of $\Lambda _b^0\rightarrow J/\psi pK^-$, the probable strange pentaquark state $P_{cs}(4459)^0$ [3] in the decay of $\Xi _b^- \rightarrow J/\psi \Lambda K^-$ channel, and pentaquark candidate $P_{c}(4337)^+$ [4] in an amplitude analysis of $B_s^0 \rightarrow J/\psi p {\bar{p}}$. Proposed interpretation of the pentaquark states were anticipated in some theoretical models, including the compact pentaquark scenarios [5,6,7,8,9,10,11,12,13], the molecular models [14,15,16], the hadro-charmonium model [17], and kinematical effects [18]. The pentaquark states, consisting of four quarks and an anti-quark, have been predicted by the quark model. Theoretically, exactly as the discovered hidden-charmed pentaquark ${\bar{c}} c qqq$ $(q=u,d,s)$ above, open-charmed ones $c\bar{q}qqq/{\bar{c}} qqqq$ should be possible as well. However, no evidence of them has been found in the current experiments. This draw our interest and precipitate us to inquire about the story of singly charmed pentaquark. Under the “flavor antisymmetry principle”, Lipkin suggested that the states ${\bar{Q}} suud$ and ${\bar{Q}} sudd$ $(Q=c,b)$ are stable [19]. Then Jaffe and Wilczek estimated the masses of ${\bar{c}} ud ud$ and ${\bar{b}} ud ud$ [20]. Further more, Wise and collaborators predicted that the bound state ${\bar{b}} qq qq/{\bar{c}} qq qq$ are stable against strong decays [21]. In addition, the possible bound states were discussed respectively, by one pion exchange interaction [22], the modified chromo-magnetic interaction model [23], and the constituent model [24]. The authors analysis the mass spectrums and possible decay behaviors of the singly charmed pentaquark.

Although the theoretical studies devoted to the singly charmed pentaquark have achieved remarkable results, there is no conclusive consensus on the properties, e.g., the masses and stability are determined by differences [19, 22,23,24]. In the present work, we will not discuss the differences, instead, the production processes of the singly charmed pentaquark ${\bar{c}} qqqq$ with less controversy are the attentions. In principle, the light quark flavor SU(3) symmetry, a model independent method, has been successfully used to meson and baryon system [25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40], consequently to be a convincing tool dealing with ${\bar{c}} qqqq$. Though the SU(3) breaking effects might be sizable, the results can still behave well comparing with the experimental data in a global viewpoint [34, 41]. Referring to the LHC experiment, we consider the initial baryon with bqq components, which can form multiple states $\bar{3}$ and 6 in SU(3) symmetry. Therefore, the singly charmed pentaquark ${\bar{c}} qqqq$, which form multiple states 6, 15 and $15'$, can be produced by b-quark weak decay in initial baryon. Accordingly, we could make a systematical investigation on the pentaquark ${\bar{c}} qqqq$, constructing the possible Hamiltonian of production, and screening out several advantageous production channels. Since the pentaquark states, especially ground 6 states may near the thresholds of charm and light baryon $D{\mathcal {B}}$, the estimate of production width from b-baryon, by means of effective Lagrangian approach [42,43,44,45,46], will be beneficial for the examination in experiment.

The rest of the paper is organized as follows. In Sect. 2, we study the tensor representations, lifetimes and possible stability of multiple pentaquark states. Then we construct the possible production Hamiltonian of multiple pentaquark states, which including the production from singly bottom baryon in initial state, for definiteness, a collection of the golden channels are screen out. In addition, the production widths of selected channels from effective Lagrangian approach are worked out in Sect. 3. We make a short summary in the end.

2 Representations of pentaquark $\bar{c}q qqq$

Light quark SU(3) flavor symmetry is a good symmetry, especially at the level of hadrons. Aided by the language of group theory, the hadrons can be classified into different group representations, respectively matching with individual spin or orbital quantum number. The singly charmed pentaquark with four light quark ${\bar{c}} qqqq$ can then be transformed under the SU(3) symmetry.

$$\begin{aligned} 3 \otimes 3 \!\otimes \! 3 \otimes \!3=3\oplus \bar{3} \!\oplus \! \bar{3} \oplus \bar{6} \oplus \bar{6} \oplus 15 \oplus 15 \oplus 15 \oplus 15'.\nonumber \\ \end{aligned}$$

(1)

The irreducible representations of new combination states $\bar{6}$, 15 and $15'$, arising from group decomposition above, can be shown clearly with tensor reduction, expressing as different tensor forms. We deduce the tensor decomposition of pentaquark labeled with $T^{ijkl}$,

$$\begin{aligned} T^{ijkl}= & {} (\hat{T}_3)^{m} (A_1)^{ijkl}_m +(\hat{T}_{\bar{3}})^m (A_2)^{ijkl}_m +(\hat{T}_{\bar{3}})^m (A_3)^{ijkl}_m\nonumber \\{} & {} + (\overline{T}_{\bar{6}})_{\{\alpha \beta \}} (B_1)^{ijkl\alpha \beta } +(\overline{T}_{\bar{6}})_{\{\alpha \beta \}} (B_2)^{ijkl\alpha \beta }\nonumber \\{} & {} +(\widetilde{T}_{15})_{m}^{\{kl\}} (C_1)^{ijm}+(\widetilde{T}_{15})_{m}^{\{ij\}} (C_2)^{klm}\nonumber \\{} & {} +(\tilde{T}_{15})_m^{\{\alpha \beta \}} (C_3)^{ijklm}_{\alpha \beta }+(T_{15'})^{\{ijkl\}}, \end{aligned}$$

(2)

the coefficients of irreducible representations:

$$\begin{aligned} (A_1)^{ijkl}_m= & {} \frac{1}{8}(\varepsilon ^{kli}\delta ^j_m-\varepsilon ^{klj}\delta ^i_m),\\ (A_2)^{ijkl}_m= & {} \frac{1}{8}(\varepsilon ^{ijk}\delta ^l_m+\varepsilon ^{ijl}\delta _m^k),\\ (A_3)^{ijkl}_m= & {} \frac{1}{8}(\varepsilon ^{kli}\delta ^j_m+\varepsilon ^{klj}\delta _m^i),\\ (B_1)^{ijkl\alpha \beta }= & {} \frac{1}{4} \varepsilon ^{ij\alpha } \varepsilon ^{kl\beta },\\ (B_2)^{ijkl\alpha \beta }= & {} \frac{1}{12}\Big (\varepsilon ^{lk\alpha }\varepsilon ^{ij\beta }+\varepsilon ^{ij\alpha }\varepsilon ^{lk\beta }-4\varepsilon ^{lj\alpha }\varepsilon ^{ik\beta } \Big ),\\ (C_1)^{ijm}= & {} \frac{1}{2}\varepsilon ^{ijm},\\ (C_2)^{klm}= & {} \frac{1}{2}\varepsilon ^{klm},\\ (C_3)^{ijklm}_{\alpha \beta }= & {} \frac{1}{6}\Big ( 2\delta _{\alpha }^l \delta _{\beta }^j\varepsilon ^{ikm}+\delta _{\alpha }^i \delta _{\beta }^j \varepsilon ^{lkm}+\delta _{\alpha }^l\delta _{\beta }^k\varepsilon ^{ijm}\\{} & {} \qquad -4\delta _{\alpha }^i\delta _{\beta }^k\varepsilon ^{ljm}\Big ), \end{aligned}$$

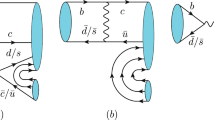
here, $\overline{T}_{\bar{6}}$, $\widetilde{T}_{15}$ and $T_{15'}$ are the irreducible representations of new combination states ${\bar{6}}$, 15 and $15\prime$, anti-symmetry index identified as [ij], and symmetry indexes signed with $\{ij\}$. All coefficients are expressed by antisymmetric tensor $\varepsilon$ and tensor $\delta$, both of which are SU(3) invariant symbols. More specifically, we deduce the possible representations of ${\bar{6}}$, 15 and $15'$ states, and list the nonzero components in Table 1. The quark components of the states in flavor space can be reached by expanding the tensor representations, see Appendix B. In addition, we draw the weight graphs of possible states ${\bar{6}}$, 15 and $15'$ in Fig. 1.

Table 1 The possible representations of pentaquark $T_{{\bar{c}} q qqq}$ with S-wave states ${\bar{6}}$, 15 and $15'$. Let S, F and T be the names of the states respectively. Meanwhile, we give the tensor representations $T_{{\bar{6}}}/T_{15}/T_{15'}$, isospin $I_3$ and hyper-charge Y of the corresponding states

Fig. 1

The weight graphs of singly bottom pentaquark ${\bar{c}} qqqq$, with S-wave sextet $P_{6}$ $(J^P=\frac{1}{2}^-)$ labeled as S in a, pentagonal states $P_{15}(J^P=\frac{1}{2}^-/\frac{3}{2}^-)$ and $P_{15'}(J^P=\frac{3}{2}^-/\frac{5}{2}^-)$ labeled as F and T in b and c. We recognize them with the electric charge in upper index and isospin $I_3$ in lower index

2.1 Lifetimes

We study the lifetimes of ground states pentaquark ${\bar{c}} qqqq$, signed as $S_6$(or $P_6$),under the parity $J^P=\frac{1}{2}^-$, with the framework of OPE. We proceed as follows, the decays width can be expressed as

$$\begin{aligned}{} & {} \Gamma (P_6({\bar{c}} qqqq)\rightarrow X)\nonumber \\{} & {} \quad =\frac{1}{2m_P} \sum _X \int \prod _i \Big [ \frac{d^3 \overrightarrow{p}_i}{(2\pi )^3 2E_i}\Big ] \left( 2\pi \right) ^4 \delta ^4\nonumber \\{} & {} \qquad \times \left( p_P-\sum _i p_i\right) N\sum _{\lambda }|\langle X|{\mathcal {H}}| P_6\rangle |^2, \end{aligned}$$

(3)

where, $m_P$, $\lambda$ and $p_P^{\mu }$ are the mass, spin and four-momentum of pentaquark $P_6$ respectively. The coefficient N takes $\frac{1}{2}$ for parity of pentaquark $J^P=\frac{1}{2}^-$. The matrix in full theory Hamiltonian ${\mathcal {H}}$ can match with that of electro-weak effective Hamiltonian ${\mathcal {H}}_{eff}^{ew}$,

$$\begin{aligned}{} & {} {\mathcal {H}}_{eff}^{ew}\nonumber \\{} & {} \quad =\frac{G_F}{\sqrt{2}} \left[ \sum _{q=u,c} V_c^q(C_1 Q_1^q+C_2 Q_2^q)-V_p \sum _{j=3} C_j O_j\right] ,\nonumber \\ \end{aligned}$$

(4)

the parameters $C_i$ and $O_i$ are Wilson coefficient and effective operator. Vs are the combinations of Cabibbo–Kobayashi–Maskawa (CKM) elements. Decay width of $\Gamma (P_6({\bar{c}} qqqq)\rightarrow X)$ can be deduced by optical theorem,

$$\begin{aligned} \Gamma (P_6\rightarrow X)= & {} \frac{1}{2m_P}\sum _{\lambda }\langle P_6|{\mathcal {T}}|P_6\rangle , \nonumber \\ {\mathcal {T}}= & {} Im\ i \int d^4x T\{ {\mathcal {H}}_{eff}(x) {\mathcal {H}}_{eff}(0)\}. \end{aligned}$$

(5)

The transition operator can be further expanded in the heavy quark expanding(HQE),

$$\begin{aligned} {\mathcal {T}}= & {} \frac{G_F^2m_c^5}{192\pi ^3} |V_{CKM}|^2 \Bigg [c_{3,c}({\bar{c}}c)+\frac{c_{5,c}}{m_c^2}({\bar{c}} g_s \sigma _{\mu \nu }G^{\mu \nu }c)\nonumber \\{} & {} +2\frac{c_{6,c}}{m_c^3}({\bar{c}}q)_{\Gamma }({\bar{q}} c)_{\Gamma } \Bigg ], \end{aligned}$$

(6)

$G_F$ is the Fermi constant, and the coefficients $c_{i,c}$ which coming from the heavy charmed quark decays are the perturbative coefficients. Therefore, the total decay width of the pentaquark $P_6({\bar{c}} qqqq)$ can be given in the leading dimension contribution,

$$\begin{aligned} \Gamma (P_6 \rightarrow X)= \frac{G_F^2m_c^5}{192\pi ^3} |V_{CKM}|^2 N \sum _{\lambda } \frac{\langle P_6|{\bar{c}} c|P_6\rangle }{2m_P}, \end{aligned}$$

(7)

where the heavy quark matrix elements are appear to be corresponding with charm number of pentaquark state.

$$\begin{aligned} \sum _{\lambda } \frac{\langle P_6|{\bar{c}} c|P_6\rangle }{2m_P}=1+{\mathcal {O}}(1/m_c). \end{aligned}$$

(8)

The short-distance coefficients have been determined as $c_{3,c}=6.29\pm 0.72$ at the leading order(LO) and $c_{3,c}=11.61\pm 1.55$ at the next-to-leading order(NLO) [47]. The heavy quark masses $m_c=1.4~{{\textrm{GeV}}}$. We expect the lifetimes of the pentaquark as

$$\begin{aligned}{} & {} \Gamma \left( P_6\left( \frac{1}{2}^-\right) \right) =\left\{ \begin{array}{l} (3.84^{+0.44}_{-0.44})\times 10^{-13}~{\textrm{GeV}} , \;\text {LO} \\ (7.09^{+0.95}_{-0.95})\times 10^{-13}~{\textrm{GeV}}, \; \text {NLO} \end{array}\right. ,\\{} & {} \quad \tau \left( P_6\left( \frac{1}{2}^-\right) \right) = \left\{ \begin{array}{l} (1.72^{+0.22}_{- 0.18})\times 10^{-12} s , \;\text {LO} \\ (9.30^{+1.43}_{-1.09})\times 10^{-13} s ,\; \text {NLO} \end{array}\right. . \end{aligned}$$

2.2 Stable states

The masses of ground sextet states $S_6$(as $P_6$) may be indistinguishable within a strictly SU(3) flavor symmetry. To identify them, the separation of s quark from u, d quarks should be considered, for instance, the loosely Lagrangian can be represented as $m_0 (\overline{P_6})^{\{ij\}}( {P_6})_{\{ij\}}+m_1 (\overline{P_6})^{\{i3\}}( {P_6})_{\{i3\}}+m_2 (\overline{P_6})^{\{33\}}( {P_6})_{\{33\}}(i,j=1,2)$, Once expanding the mass Lagrangian, the primitive results will be achieved, in particular,

$$\begin{aligned} \text {m}(S_{1/2}^0)= & {} \text {m}(S_{-1/2}^-)=m_0,\ \text {m}(S_{1}^0)=\text {m}(S_{-1}^{{-}{-}})\\= & {} \text {m}(S_{0}^-)=m_1,\text {m}(S_{0}^0)=m_3. \end{aligned}$$

Fortunately, there are several methods to study the masses of the pentaquark states, though inconsistent with each other seemingly. We list the typical results from quark model(QM) and chromomagnetic interaction model(CIM) in unit of GeV.

$$\begin{aligned} \text {QM}:\quad m(S^0_0)= & {} 2.71,\ m(S_{1/2}^0)=m(S_{-1/2}^-)=2.58,\\ m(S_0^-)= & {} 2.77,\\ \text {CIM}:\quad m(S^0_0)= & {} 2.87,\ m(S_{1/2}^0)=m(S_{-1/2}^-)=2.831,\\ m(S_0^-)= & {} 3.03,\ m(S_1^0)=m(S_{-1}^{{-}{-}})=3.22. \end{aligned}$$

It is apparently that $S^0_0, S_{1/2}^0, S_{-1/2}^-$ and $S_0^-$ can be the candidates of stable states within the frame of quark model (QM) [21], which decay against strong interaction. Nevertheless, the results from chromomagnetic interaction model (CIM) [23] show the inconsistent results, from which only $S_0^-$ can be stable. Although no agreement are reached for the stability, it is clearly that the ground states all are near the strong thresholds with charm meson and light baryon $D{\mathcal {B}}$.

To explore the stability of $S_6$, one may study the possible weak decay channels, those with different behaviors from strong interaction decays. We deduce the Hamiltonian of quark transition $H({\bar{c}}\rightarrow {\bar{s}} d{\bar{u}})$ by SU(3) symmetry, in which the final states are light baryon ${\mathcal {B}}$ and meson ${\mathcal {M}}$, A represents all independent possible Hamiltonian structures with different constructed indexes.

$$\begin{aligned} {\mathcal {H}}= {A}^{i'j'k'l'm'n'}_{ijklmn} (S_6)^{\{\alpha \beta \}} \varepsilon _{\alpha ij}\varepsilon _{\beta kl} (H)_{m}^{i'j'} {\mathcal {M}}^{k'}_{n} ({\mathcal {B}})^{l'm'n'}, \end{aligned}$$

when we consider the octet $n,p,\Lambda ,\Sigma$ in final state, it is not hard to find the suitable weak decay channels for experimental detection.

$$\begin{aligned}{} & {} S^0_0\rightarrow K^0 n,\ S_{1/2}^0\rightarrow \pi ^- p,\ S_{-1/2}^-\rightarrow \pi ^- n,\\{} & {} \quad S_1^0\rightarrow K^- p,\ S_0^-\rightarrow \pi ^-\Lambda ^0,\ S_{-1}^{{-}{-}}\rightarrow \pi ^- \Sigma ^-. \end{aligned}$$

The channels with largest branching ratio can be chosen as the golden ones to detect the stable pentaquark, of which the typical branching fractions might be a few percents for charm quark decay, furthermore, the construction of hadrons initial $S_6$ and final ${\mathcal {B}},{\mathcal {M}}$ should pay another order at least $10^{-5}$, then totally in order of $10^{-6}$ for the charm baryon decays.

3 The production of pentaquark ground state

In the section, we will discuss the production of lowest lying state pentaquark S from bottom baryon. Since the b-factory such as Belle, LHCb and superKEKB have been improved enough integrated luminosity, at the order of a few or even hundreds $fb^{-1}$, simultaneously the experiments have accumulated more and more b-baryon. Accordingly, these offer an opportunity to explore some previously undiscovered exotic particles, for instance the singly anti-charmed pentaquark ${\bar{c}} qqqq$. In the paper, we may concentrate on lowest lying state S of the pentaquark, whose masses may near the thresholds of charm meson and light baryon $D{\mathcal {B}}$. Generally, the transition in quark level of the production of pentaquark S from b-baryon could be weakly decays, Cabibbo allowed $b\rightarrow c{\bar{c}} d/s$ or Cabibbo suppressed $b\rightarrow u{\bar{c}} d/s$, leading the production ${\mathcal {B}}_b\rightarrow D+S_6$ or ${\mathcal {B}}_b\rightarrow M+S_6$ respectively in hadronic level, where ${\mathcal {B}}_b$, $S_6$ and M are initial b-baryon, final ground pentaquark 6 state and light meson. The strategy of our discussion is based on SU(3) symmetry analysis and effective Lagrangian approach, to study the suitable production channels for experimental detection, which leading to estimate of the production processes and widths.

3.1 SU(3) symmetry analysis

The strategy of SU(3) symmetry analysis needs the representations of hadrons and transition operators, which are pretty easy to achieve. For the singly bottom baryon in initial state, the representations can be decomposed into ${\bar{3}}$ and 6 [48, 49], in addition, light baryon can form 8 and 10 states. We show the representations of anti-triplet bottom baryons and octet light baryons.

$$\begin{aligned} (T_\mathbf{{b}{3}})^{[ij]}= & {} \left( \begin{array}{ccc} 0 &{} \Lambda _{b}^0 &{} \Xi _{b}^0 \\ -\Lambda _{b}^0 &{} 0 &{} \Xi _{b}^- \\ -\Xi _{b}^0 &{} -\Xi _{b}^- &{} 0 \end{array} \right) , \nonumber \\ F_8= & {} \! \left( \begin{array}{ccc} \frac{1}{\sqrt{2}}\Sigma ^0+\frac{1}{\sqrt{6}}\Lambda ^0 &{} \Sigma ^+ &{} p \\ \Sigma ^- &{} -\frac{1}{\sqrt{2}}\Sigma ^0+\frac{1}{\sqrt{6}}\Lambda ^0 &{} n \\ \Xi ^- &{} \Xi ^0 &{} -\sqrt{\frac{2}{3}}\Lambda ^0 \end{array} \!\right) .\nonumber \\ \end{aligned}$$

(9)

In the meson sector, singly charmed mesons form an SU(3) triplet or anti-triplet, light mesons form an octet plus singlet, all multiplets are collected as [39, 50]

$$\begin{aligned} M_{8}= & {} \begin{pmatrix} \frac{\pi ^0}{\sqrt{2}}+\frac{\eta }{\sqrt{6}} &{}\pi ^+ &{} K^+\\ \pi ^-&{}-\frac{\pi ^0}{\sqrt{2}}+\frac{\eta }{\sqrt{6}}&{}{K^0}\\ K^-&{}{\bar{K}}^0 &{}-2\frac{\eta }{\sqrt{6}} \end{pmatrix},\nonumber \\ D_i^T= & {} \left( \begin{array}{c} D^0 \\ D^+ \\ D^+_s \end{array}\right) ,\quad {\overline{D}}^i= \left( \begin{array}{c} {\overline{D}}^0 \\ D^- \\ D^-_s \end{array}\right) . \end{aligned}$$

(10)

The productions in quark level are the transition of $b\rightarrow c {\bar{c}} d/s$ and $b\rightarrow u {\bar{c}} d/s$, which can be decomposed into the operators $H_{\bar{3}}$ and $H_6$, as $(H_{\bar{3}})_2=V_{cs}^*, (H_6)^{\{13\}}=V_{cs}^*$ for the transition of $b\rightarrow u {\bar{c}} d/s$, $(H_3)^2=V_{cd}^*, (H_3)^3=V_{cs}^*$ for the transition of $b\rightarrow c {\bar{c}} d/s$ [35].

Fig. 2

The production Feynman diagrams of singly charmed pentaquark multiple states 6, 15 and $15'$, starting from singly bottom baryon bqq. Diagram a represents the process of producing one pentaquark multiple state and a charmed meson. Diagrams b–d show the transitions with a pentaquark multiple state and a light meson in final states

Since the representations of hadrons and transition operators have been determined, we can directly construct the possible Hamiltonian for the production of pentaquark $\bar{6}$, 15 and $15'$ states from the singly bottom baryon, on the hadronic level under the SU(3) symmetry frame. For clarity, the ones of 15 and $15'$ states will be shown in Appendix. The initial baryon which form multiple state ${\mathcal {B}}_{b\bar{3}}$(signed as ${T}_{b\bar{3}})$ can produce pentaquark sextet $\bar{S}_6(\bar{T}_6)$ and meson. Accordingly, we construct the possible Hamiltonian for the production of sextet $\bar{S}_6(\bar{T}_6)$, given as follows.

$$\begin{aligned} {\mathcal {H}}= & {} a_{1}(T_{b\bar{3}})_{i}(H_{3})^{j}(\bar{P}_{6})^{\{ik\}}\bar{D}_{[jk]}\\{} & {} +d_{1}(T_{b\bar{3}})_{i}(H_{\bar{3}})_{j}(\bar{P}_{6})^{\{ik\}}M_{k}^{j}\\{} & {} +d_{2}(T_{b\bar{3}})_{i}(H_{\bar{3}})_{j}(\bar{P}_{6})^{\{jk\}}M_{k}^{i}\\{} & {} +d_{3}(T_{b\bar{3}})_{i}(H_{6})^{\{ik\}}(\bar{P}_{6})^{\{jl\}}M_{j}^{m}\varepsilon _{klm}\\{} & {} +d_{4}(T_{b\bar{3}})_{i}(H_{6})^{\{jk\}}(\bar{P}_{6})^{\{il\}}M_{j}^{m}\varepsilon _{klm}. \end{aligned}$$

Here, the independent parameters, $a_1, \bar{a}_1, d_1, \ldots ,$ represent non-perturbative effect, $T_{b\bar{3}}$ is the multiple state of initial baryon. For completeness, we will arrange the production processes from $T_{b6}$ baryon in Appendix A. $T_{b6}$, $H_3$ or $H_6$ is the transition operator, $\bar{P}_6$ and ${\bar{D}}/M$ are respectively the pentaquark sextet and meson in final states. For completeness, the Feynman diagrams for hadronic level are shown in Fig. 2a–d. Particularly, the Hamiltonian with charmed meson in final states are corresponding with the Feynman diagram Fig. 2a, by comparison, the diagrams Fig. 2b–d are related to the Hamiltonian with light meson in final states.

We expand the Hamiltonian and harvest the possible amplitude results, aggregating into Table 2. The relations between different decay widths can be further deduced, when we approximately ignore the phase space differences. Our calculations show the relations given as follows.

$$\begin{aligned}{} & {} \Gamma ( \Lambda _b^0\rightarrow S_0^{0} D^0)=\Gamma (\Lambda _b^0\rightarrow S_{-1/2}^{-} D^+_s)\nonumber \\{} & {} \quad =\Gamma ( \Xi _b^0\rightarrow S_{1/2}^{0} D^0) \nonumber \\{} & {} \quad =\Gamma ( \Xi _b^0\rightarrow S_{0}^- D^+_s)=\Gamma ( \Xi _b^-\rightarrow S_{-1}^{{-}{-}} D^+_s)\nonumber \\{} & {} \quad =\Gamma ( \Xi _b^-\rightarrow S_{-1/2}^{-} D^0),\nonumber \\{} & {} \Gamma ( \Xi _b^-\rightarrow S_0^{0} K^-) =\Gamma ( \Xi _b^-\rightarrow S_{1/2}^{0} \pi ^-),\nonumber \\{} & {} \Gamma ( \Lambda _b^0\rightarrow S_{-1/2}^{-} D^+)=\Gamma ( \Lambda _b^0\rightarrow S_{1/2}^{0} D^0) \nonumber \\{} & {} \qquad \qquad \qquad \qquad \quad =\Gamma ( \Xi _b^0\rightarrow S_1^{0} D^0) \nonumber \\{} & {} \qquad \qquad \qquad \qquad \quad =\Gamma ( \Xi _b^0\rightarrow S_{0}^- D^+) \nonumber \\{} & {} \qquad \qquad \qquad \qquad \quad =\Gamma ( \Xi _b^-\rightarrow S_{-1}^{{-}{-}} D^+)\nonumber \\{} & {} \qquad \qquad \qquad \qquad \quad =\Gamma ( \Xi _b^-\rightarrow S_{0}^- D^0),\nonumber \\{} & {} \Gamma ( \Xi _b^-\rightarrow S_1^{0} \pi ^-) =\Gamma ( \Xi _b^-\rightarrow S_{1/2}^{0} K^-). \end{aligned}$$

(11)

Typically, the Cabibbo allowed production channels, may receive the largest contribution. Meanwhile, the charged final light meson possesses high detection efficiency. Consequently, we can extract these channels and suggest them as golden channels for the studying in the future experiment. We select the golden channels for the production from the Table 2, in which five states $S^-_{-1/2},S^0_{1/2},S_1^0,S_0^-,S^{{-}{-}}_{-1}$ of the sextet ground states are screened out in connection with suitable experimental detection channels, in particular, the remaining one $S^0_0$ is hard to probe currently. It is worth mentioning that many numbers have been accumulated for b-baryon $\Lambda _b$ in the experiments, which can be as the highest priority of production channels.

$$\begin{aligned}{} & {} \Lambda _b^0\rightarrow S_{-1/2}^{-} D^+,\ \Lambda _b^0\rightarrow S_{1/2}^{0} D^0,\ \Xi _b^0\rightarrow S_{1}^{0} D^0,\ \nonumber \\{} & {} \quad \Xi _b^0\rightarrow S_0^{-} D^+, \Xi _b^-\rightarrow S_{-1}^{{-}{-}} D^+,\nonumber \\{} & {} \quad \Lambda _b^0\rightarrow S_{0}^- K^+,\ \Lambda _b^0\rightarrow S_{-1/2}^{-} \pi ^+,\ \Xi _b^-\rightarrow S_{1/2}^{0} K^-,\nonumber \\{} & {} \quad \Xi _b^-\rightarrow S_{1}^{0} \pi ^-,\ \Xi _b^-\rightarrow S_{-1}^{{-}{-}} \pi ^+. \end{aligned}$$

(12)

Cabibbo allowed processes are the channels with charm meson in final state, but Cabibbo suppressed ones produce light mesons. Consequently, we will force on the Cabibbo allowed channels in the following.

Table 2 The productions of pentaquark sextet $P_{\bar{6}}$ from singly bottom baryons $T_{b\bar{3}}$, with charmed meson in the final state

3.2 The widths of ${\mathcal {B}}_b \rightarrow {\mathcal {S}}_6 {\mathcal {D}}$

The ground pentaquark $S_6$ can be produced by b-baryon, the transition in quark level have been shown in Fig. 2. To deal with the production widths of channels in Eq. (12), we would employ an effective Lagrangian approach. Since $S_6$ is near the threshold $D{\mathcal {B}}$, the production diagrams can be directly drawn as Fig. 3. More technically, the dominant contribution coming from diagram (a), which show the process with exchanged particles as light baryon N, $\Sigma$ or $\Lambda$. The exchanged particles in diagram (b) may be D meson, however, we would not study the diagram carefully, for the less important branching ratio of ${\mathcal {B}}_b \rightarrow {\mathcal {B}} J/\psi$. For example, the production $\Lambda _b^0\rightarrow S^-_{-1/2}D^+$, the exchanged baryons can be $n, \Sigma ^0, \Lambda ^0$ or $\Sigma ^-$.

Fig. 3

Diagrams contributing to ${\mathcal {B}}_b\rightarrow {\mathcal {S}} {\mathcal {D}}$. a Represents that b-baryon ${\mathcal {B}}_b$ start to weakly decay into ${\bar{D}} {\mathcal {B}}_c$, producing $S_6$ and D by exchanging $N/\Sigma /\Lambda$. b ${\mathcal {B}}_b$ turn into the color suppressed process $J/\psi {\mathcal {B}}$, for which we wound not consider the contribution carefully in the work

The effective Lagrangian related to the couplings between light baryon ${\mathcal {B}}$, charm baryon ${\mathcal {B}}_c$ and charm meson D, between ${\mathcal {B}}$, ground pentaquark $S_6$ and D meson, can be given respectively as,

$$\begin{aligned} {\mathcal {L}}= & {} g_{{\mathcal {B}} {\mathcal {B}}_c D}\ \overline{{\mathcal {B}}} {\mathcal {B}}_c D+H.c.,\end{aligned}$$

(13)

$$\begin{aligned} {\mathcal {L}}= & {} g_{{\mathcal {B}} S_6 {\bar{D}}}\ \overline{{\mathcal {B}}} S_6 {\bar{D}}+H.c.. \end{aligned}$$

(14)

From SU(3) symmetry [51], we can deduce the relations of different couplings. Obviously, the coupling Hamiltonian can only depend on a roughly coupling constant $g_1$ or $g_2$. We give the expressions,

$$\begin{aligned} {\mathcal {H}}_1=g_1 ({\mathcal {B}}_{c})_i D^j ({\mathcal {B}})^i_j,\quad {\mathcal {H}}_2=g_2 (S_6)_{\{\alpha i\}} {\bar{D}}_j ({\mathcal {B}})^i_k \varepsilon ^{\alpha j k}.\nonumber \\ \end{aligned}$$

(15)

We then conclude the coupling relations.

$$\begin{aligned} g_{\Lambda _c D N}= & {} -g_{\Xi _c^+ D^0 \Sigma ^+}=- \sqrt{6}g_{\Xi _c^+ D^+ \Lambda ^0}=\sqrt{2}g_{\Xi _c^+ D^+ \Sigma ^0}\\= & {} \sqrt{6}g_{\Xi _c^0 D^0 \Lambda ^0}=\sqrt{2}g_{\Xi _c^0 D^0 \Sigma ^0} =g_{\Xi _c^0 D^+ \Sigma ^-}.\\ g_{S_{-1/2}^{-} D^-_s n}= & {} \frac{\sqrt{6}}{3}g_{S_{-1/2}^{-} D^- \Lambda ^0}=\sqrt{2}g_{S_{-1/2}^{-} D^- \Sigma ^0 }\\= & {} -g_{S_{-1/2}^{-} {\overline{D}}^0 \Sigma ^-} =\frac{-\sqrt{6}}{3}g_{S_{1/2}^{0} {\overline{D}}^0 \Lambda ^0}=g_{S_{1/2}^{0} D^- \Sigma ^+}\\= & {} \sqrt{2}g_{S_{1/2}^{0} {\overline{D}}^0 \Sigma ^0} =-g_{S_{1/2}^{0} D^-_s p}=g_{S_1^{0} D^-_s \Sigma ^+}\\= & {} \frac{-\sqrt{2}}{2}g_{S_{0}^- D^-_s \Sigma ^0} =-g_{S_0^{0} {\overline{D}}^0 n }=g_{S_0^{0} D^- p}\\= & {} g_{S_{-1}^{{-}{-}} D^-_s \Sigma ^-}. \end{aligned}$$

In the consideration, we take $g_{\Lambda _c DN}=10.7$ GeV$^{-1}$ [52], and we take the pentaquark coupling constant $g_{S_6 {\bar{D}} {\mathcal {B}}}=2$ GeV$^{-1}$, which is similar with the value taken in pentaquark $P_c^+(4312)$ [42]. The propagators for the exchanged pseudoscalar D meson and baryons ${\mathcal {B}}$ are defined as,

$$\begin{aligned} P_D=\frac{i}{q^2-m_D^2},\quad P_{{\mathcal {B}}}= \frac{i(q\!\!\!/+m_{{\mathcal {B}}})}{q^2-m_{{\mathcal {B}}}^2}. \end{aligned}$$

(16)

The starting vertices of the production are the weakly decay ones, which in the form,

$$\begin{aligned} {\mathcal {L}}=i \overline{{\mathcal {B}}}_c (a+b\gamma _5) {\mathcal {B}}_b D, \end{aligned}$$

(17)

with the parameter a and b written as

$$\begin{aligned} a= & {} -\frac{G_F}{\sqrt{2}}V_{CKM}\ a_1 f_{D_{(s)}} \Big ((m_{{\mathcal {B}}_b}-m_{{\mathcal {B}}_c})F_1^V+ \frac{m_{D_{(s)}}^2}{m_{{\mathcal {B}}_b}}F_3^V\Big ),\nonumber \\ \end{aligned}$$

(18)

$$\begin{aligned} b= & {} -\frac{G_F}{\sqrt{2}}V_{CKM}\ a_1 f_{D_{(s)}} \Big ((m_{{\mathcal {B}}_b}+m_{{\mathcal {B}}_c})F_1^A+ \frac{m_{D_{(s)}}^2}{m_{{\mathcal {B}}_b}}F_3^A\Big ).\nonumber \\ \end{aligned}$$

(19)

Where Wilson coefficient $a_1=1.07$ [53], and decay constants $f_{D_{(s)}}=0.247$. In addition, $F_{1,3}^{V/A}$ are the transition form factors of ${\mathcal {B}}_b\rightarrow {\mathcal {B}}_c$, for instance $\Lambda _b\rightarrow \Lambda _c$, which can analytically continue to the timelike region, in which the form factors are relevant with physical process.

$$\begin{aligned} F_{1/3}^{V/A}=\frac{F(0)}{1-A (q^2/m_{{\mathcal {B}}_b}^2)+B (q^2/m_{{\mathcal {B}}_b}^2)^2}, \end{aligned}$$

(20)

The parameters A, B can be found in Ref. [54]. Accordingly, we can deduce amplitude of diagram (a),

$$\begin{aligned}{} & {} {\mathcal {M}}_{a}=i^3 \int \frac{d^4 q}{(2\pi )^4} (-i g_{{\mathcal {B}}{\mathcal {B}}_c D}{\bar{u}}_D) ({P\!\!\!\!/}_{{\mathcal {B}}_c}+m_{{\mathcal {B}}_c})\nonumber \\{} & {} \quad \times (q\!\!\!/+m_{{\mathcal {B}}}){\bar{u}}(S_6)(a+b\gamma _5) (-ig_{{\mathcal {B}}S_6 {\bar{D}}}u_{{\mathcal {B}}_b}) \end{aligned}$$

(21)

$$\begin{aligned}{} & {} \frac{1}{(P_{{\mathcal {B}}_c}^2-m_{{\mathcal {B}}_c}^2) (q^2-m_{{\mathcal {B}}}^2)(P_{D_{(s)}}^2-m_{D_{(s)}}^2)}K(q^2). \end{aligned}$$

(22)

The factor K is introduced to deal with the divergence of integration.

$$\begin{aligned} K(q^2)=\frac{m_{{\mathcal {B}}_b}^2-\Lambda _E^2}{q^2-{\Lambda _E}^2}. \end{aligned}$$

(23)

Here, $\Lambda =-m_E+\Lambda _E$ is a model parameter [55], $m_E$ is the mass of exchanged particle. In the work, we take naive value for $\Lambda =300$ MeV. Then the decay width can be reached in the CM frame,

$$\begin{aligned} \Gamma =\frac{1}{2}\frac{1}{8\pi }\frac{|{\textbf {p}}|}{m_{{\mathcal {B}}_b}^2} |{\mathcal {M}}|^2, \end{aligned}$$

(24)

the momentum ${\textbf {p}}=\sqrt{\lambda (m_{{\mathcal {B}}_b}^2,m_{S_6}^2,m_D^2)}/2m_{{\mathcal {B}}_b},\ \lambda (a,b,c)=a^2+b^2+c^2-2ab-2ac-2bc$. Adding the contribution from different exchanged particles, we obtain the production widths listed into Table 3. It seems that the results slightly break the prediction of SU(3) symmetry as Eq. (11). Loosely, the contribution from diagram (b) may be a effective source, besides, the sizable broken effect of charm hadron can play an important role on the issue. We plot the $\Lambda$ dependence of branching ratio $\mathfrak {B}({\mathcal {B}}_b \rightarrow S_6 D)$ of channels in Eq. (12), shown in Fig. 4, which is of order $10^{-6}$. Some comments are suitable, the branching ratios above can be improved as model parameter $\Lambda$, the contribution from diagram (b) and the increasing strong coupling $g_{S_6 D {\mathcal {B}}}$. Therefore, we expect that further efforts from both the theoretical and experimental sides to understand the nature of the states.

Fig. 4

Branching ratios of ${\mathcal {B}}_b\rightarrow D S_6$ in unit of $10^{-6}$ depending on parameter $\Lambda$

Table 3 The production widths of golden channels, which in order of $10^{-6}$

4 Summary

In conclusion, we discuss the production of singly charmed pentaquark ${\bar{c}} qqqq$, from the initial bottom baryon bqq, under the strategy of light quark SU(3) symmetry. The representation expressions of ${\bar{c}} qqqq$ are completed by the guidance of tensor reduction, formed by the projection of Eq. (2), in particular collected in Appendix B. Following the constructed possible Hamiltonian of the production, we obtain decays of golden production channels, as well as the relations between different channels. For definiteness, we discuss the production widths with the effective Lagrangian approach for the suggested several golden channels. Primitive results are at the order of $10^{-6}$, within the discoverable range of experiments. It is apparently that the model dependent parameter $\Lambda$ can improve the branching ratio commendably, Therefore, we suggest the possibility for searching the singly charmed pentaquark in future experiments. The establishment the existence of these states means a remarkable progress in hadron physics.

Appendices

Appendix A: States 15 and $15'$

Table 4 The productions of pentaquark sextet $S_6$ from singly bottom baryons ${\mathcal {B}}_{b6}$, with charmed meson in the final state

Similarly, we construct the possible Hamiltonian for the production of pentaquark 6 states from sextet ${\mathcal {B}}_6$ b-baryons, pentaquark 15 states from triplet ${\mathcal {B}}_3$ b-baryon, as well as pentaquark $15'$ states from triplet ${\mathcal {B}}_3$ b-baryon.

$$\begin{aligned} {\mathcal {H}}= & {} {H'}_6+H_{15}+H_{15'}\\= & {} \bar{a}_{1}(T_{b6})^{\{ij\}}(H_{3})_{[ik]}(\bar{P}_{6})^{\{kl\}}\bar{D}_{[jl]}\\{} & {} +b_{1}(T_{b\bar{3}})_{i}(H_{3})^{j}(\bar{P}_{15})_{\{jk\}}^{i}\bar{D}^{k}\\{} & {} +e_{1}(T_{b\bar{3}})_{i}(H_{\bar{3}})^{[ij]}(\bar{P}_{15})_{\{jk\}}^{l}M_{l}^{k}\\{} & {} +e_{2}(T_{b\bar{3}})_{i}(H_{\bar{3}})^{[jl]}(\bar{P}_{15})_{\{jk\}}^{i}M_{l}^{k}\\{} & {} +e_{3}(T_{b\bar{3}})_{i}(H_{6})^{\{ij\}}(\bar{P}_{15})_{\{jk\}}^{l}M_{l}^{k}\\{} & {} +e_{4}(T_{b\bar{3}})_{i}(H_{6})^{\{jl\}}(\bar{P}_{15})_{\{jk\}}^{i}M_{l}^{k}\\{} & {} +e_{5}(T_{b\bar{3}})_{i}(H_{6})^{\{jk\}}(\bar{P}_{15})_{\{jk\}}^{l}M_{l}^{i}\\{} & {} +f_{1}(T_{b\bar{3}})^{[im]}(H_{\bar{3}})^{[jl]}(\bar{P}_{15^{\prime }})_{\{ijkl\}}M_{m}^{k}\\{} & {} +f_{2}(T_{b\bar{3}})^{[im]}(H_{6})^{\{jk\}}(\bar{P}_{15^{\prime }})_{\{ijkl\}}M_{m}^{l}. \end{aligned}$$

The corresponding Feynman diagrams are shown in Fig. 2. It should be noted that one triplet baryon $T_{b3}$ can not produce the pentaquark $15'$ states, because the symmetry and anti-symmetry indexes in the only allowed Hamiltonian $(T_{b\bar{3}})^{[ij]}(H_{3})^{k}(\bar{P}_{15^{\prime }})_{\{ijkl\}}\bar{D}^{l}$ forbid the process. We collect the possible channels and amplitude results into Tables 4, 5 and 6. Several golden channels for producing pentaquark 15 state are arranged as,

$$\begin{aligned}{} & {} \Lambda _b^0\rightarrow F_{1/2}^{'0} D^0,\ \Xi _b^-\rightarrow F_{-1/2}^{{-}{-}} D^+_s,\ \Xi _b^-\rightarrow F_{0}^{-} D^0,\\{} & {} \quad \Xi _b^0\rightarrow F_{1}^{0} D^0,\ \Xi _b^0\rightarrow F_{1/2}^- D^+_s,\ \Xi _b^0\rightarrow {F'}_0^- D^+. \end{aligned}$$

For convenience, the decay relations between different channels with triplet or sextet baryon $T_{b\bar{3}}$ in initial state are reorganized in the following. The production relations of 6 state from sextet initial baryons are given as follows.

$$\begin{aligned} \Gamma ( \Sigma _{b}^{+}\rightarrow S_0^{0} D^+)= & {} 2\Gamma ( \Sigma _{b}^{0}\rightarrow S_0^{0} D^0) =2\Gamma ( \Xi _{b}^{\prime 0}\rightarrow S_{1/2}^{0} D^0) \\= & {} 2\Gamma ( \Xi _{b}^{\prime -}\rightarrow S_{-1/2}^{-} D^0) =2\Gamma ( \Xi _{b}^{\prime -}\rightarrow S_{-1}^{{-}{-}} D^+_s) \\= & {} \Gamma ( \Sigma _{b}^{+}\rightarrow S_{1/2}^{0} D^+_s)=\Gamma ( \Omega _{b}^{-}\rightarrow S_{-1}^{{-}{-}} D^+) \\= & {} \Gamma ( \Omega _{b}^{-}\rightarrow S_{0}^- D^0)=2\Gamma ( \Xi _{b}^{\prime 0}\rightarrow S_{0}^- D^+_s)\\= & {} \frac{1}{2}\Gamma ( \Xi _{b}^{\prime 0}\rightarrow S_{-1/2}^{-} D^+)\\= & {} 2\Gamma ( \Sigma _{b}^{0}\rightarrow S_{-1/2}^{-} D^+_s), \Gamma ( \Xi _b^-\rightarrow S_1^{0} \pi ^-) \\= & {} \Gamma ( \Xi _b^-\rightarrow S_{1/2}^{0} K^-),\\{} & {} \Gamma ( \Lambda _b^0\rightarrow S_{-1/2}^{-} \pi ^+) \\= & {} 2\Gamma ( \Lambda _b^0\rightarrow S_{1/2}^{0} \pi ^0),\\ 2\Gamma ( \Xi _{b}^{\prime -}\rightarrow S_{0}^- D^0)= & {} \Gamma ( \Sigma _{b}^{-}\rightarrow S_{-1/2}^{-} D^0) \\= & {} \Gamma ( \Sigma _{b}^{+}\rightarrow S_{1/2}^{0} D^+) \\= & {} 2\Gamma ( \Sigma _{b}^{0}\rightarrow S_{1/2}^{0} D^0) =\Gamma ( \Sigma _{b}^{-}\rightarrow S_{-1}^{{-}{-}} D^+_s) \\= & {} 2\Gamma ( \Sigma _{b}^{0}\rightarrow S_{-1/2}^{-} D^+)=\Gamma ( \Sigma _{b}^{+}\rightarrow S_1^{0} D^+_s) \\= & {} \frac{1}{2}\Gamma ( \Sigma _{b}^{0}\rightarrow S_{0}^- D^+_s) =2\Gamma ( \Xi _{b}^{\prime 0}\rightarrow S_1^{0} D^0) \\= & {} 2\Gamma ( \Xi _{b}^{\prime -}\rightarrow S_{-1}^{{-}{-}} D^+). \end{aligned}$$

The decay relations of 15 state are given as,

$$\begin{aligned} \Gamma ( \Lambda _b^0\rightarrow F_0^{0} D^0 )= & {} \Gamma ( \Lambda _b^0\rightarrow F_{-1}^- D^+ ) \\= & {} \Gamma ( \Lambda _b^0\rightarrow {F'}_{-1/2}^- D^+_s )=\Gamma ( \Xi _b^-\rightarrow F_{-1/2}^- D^0 )\\= & {} \Gamma ( \Xi _b^-\rightarrow F_{-1}^{{-}{-}} D^+_s )= \Gamma ( \Xi _b^0\rightarrow F_{1/2}^{0} D^0 ) \\= & {} \Gamma ( \Xi _b^0\rightarrow {F'}_0^- D^+_s )=\Gamma ( \Xi _b^-\rightarrow F_{-3/2}^{{-}{-}} D^+ ),\\ \Gamma ( \Lambda _b^0\rightarrow {F'}_{1/2}^{0} D^0 )= & {} \Gamma ( \Lambda _b^0\rightarrow {F'}_{-1/2}^- D^+ ) \\= & {} \Gamma ( \Xi _b^-\rightarrow F_0^- D^0 ) =\Gamma ( \Xi _b^-\rightarrow F_{-1}^{{-}{-}} D^+ )\\= & {} \Gamma ( \Xi _b^0\rightarrow F_1^{0} D^0 )= \Gamma ( \Xi _b^0\rightarrow {F'}_0^- D^+ ) \\= & {} \Gamma ( \Xi _b^0\rightarrow F_{1/2}^- D^+_s)\\= & {} \Gamma ( \Xi _b^-\rightarrow F_{-1/2}^{{-}{-}} D^+_s ),\\ \Gamma ( \Xi _b^-\rightarrow F_{1/2}^- K^0 )= & {} \Gamma ( \Xi _b^-\rightarrow {F'}_{-1/2}^- {\overline{K}}^0 ) = 6 \Gamma ( \Xi _b^-\rightarrow {F'}_0^- \eta _q ) \\= & {} 2 \Gamma ( \Xi _b^-\rightarrow {F'}_0^- \pi ^0 ),\\ \Gamma ( \Lambda _b^0\rightarrow F_{-1}^- \pi ^+)= & {} \Gamma ( \Lambda _b^0\rightarrow {F'}_{-1/2}^- K^+),\quad \Gamma ( \Lambda _b^0\rightarrow F_{1/2}^{0} K^0) \\= & {} \Gamma ( \Lambda _b^0\rightarrow F_{-1/2}^- K^+),\\ \Gamma ( \Xi _b^0\rightarrow F_1^{+} K^-)= & {} \Gamma ( \Xi _b^0\rightarrow F_0^- K^+),\quad \Gamma ( \Xi _b^-\rightarrow F_{-3/2}^{{-}{-}} \pi ^+ ) \\= & {} \Gamma ( \Xi _b^-\rightarrow F_{-1}^{{-}{-}} K^+ ),\\ \Gamma ( \Xi _b^0\rightarrow F_0^{0} {\overline{K}}^0)= & {} \Gamma ( \Xi _b^0\rightarrow F_{-1/2}^- \pi ^+),\quad \Gamma ( \Xi _b^0\rightarrow F_{3/2}^{+} \pi ^-) \\= & {} \Gamma ( \Xi _b^0\rightarrow F_1^{0} K^0),\\ \Gamma ( \Xi _b^-\rightarrow F_0^{0} K^-)= & {} \Gamma ( \Xi _b^-\rightarrow F_{1/2}^{0} \pi ^-),\quad \Gamma ( \Xi _b^-\rightarrow F_{-1}^{{-}{-}} \pi ^+ ) \\= & {} \Gamma ( \Xi _b^-\rightarrow F_{-1/2}^{{-}{-}} K^+ ), \\ \Gamma ( \Lambda _b^0\rightarrow {F'}_{-1/2}^- \pi ^+ )= & {} \Gamma ( \Lambda _b^0\rightarrow {F'}_{1/2}^{0} \pi ^0 ),\quad \Gamma ( \Lambda _b^0\rightarrow F_1^{+} K^- ) \\= & {} \Gamma ( \Lambda _b^0\rightarrow F_0^{0} {\overline{K}}^0 ),\\ \Gamma ( \Lambda _b^0\rightarrow F_1^{0} K^0 )= & {} \Gamma ( \Lambda _b^0\rightarrow F_0^- K^+ ),\quad \Gamma ( \Xi _b^0\rightarrow F_{1/2}^- K^+ ) \\= & {} \Gamma ( \Xi _b^0\rightarrow {F'}_0^- \pi ^+ ),\\ \Gamma ( \Xi _b^0\rightarrow F_0^- \pi ^+ )= & {} \Gamma ( \Xi _b^0\rightarrow {F'}_{1/2}^{0} {\overline{K}}^0 ),\quad \Gamma ( \Xi _b^-\rightarrow {F'}_{1/2}^{0} K^- ) \\= & {} \Gamma ( \Xi _b^-\rightarrow F_1^{0} \pi ^- ). \end{aligned}$$

The decay relations of $15'$ state are shown below.

$$\begin{aligned} \Gamma ( \Lambda _b^0\rightarrow T_{1}^{+} \pi ^- )= & {} \Gamma ( \Lambda _b^0\rightarrow T_{1/2}^{0} K^0 ) = \Gamma ( \Xi _b^0\rightarrow T_{1}^{+} K^- ) \\= & {} \Gamma ( \Xi _b^0\rightarrow T_{0}^{0} {\overline{K}}^0 ) =\Gamma ( \Xi _b^-\rightarrow T_{0}^{0} K^- ) \\= & {} \Gamma ( \Xi _b^-\rightarrow T_0^- K^0 ) =\Gamma ( \Xi _b^0\rightarrow T_{-1/2}^- \pi ^+ ) \\= & {} \Gamma ( \Xi _b^0\rightarrow T_0^- K^+ ) =\Gamma ( \Xi _b^-\rightarrow T_{1/2}^{0} \pi ^- ) \\= & {} \Gamma ( \Lambda _b^0\rightarrow T_{-1}^- \pi ^+ )\\= & {} \Gamma ( \Lambda _b^0\rightarrow T_{-1/2}^- K^+ ) =2 \Gamma ( \Xi _b^0\rightarrow T_{1/2}^{0} \pi ^0 ) \\= & {} 2 \Gamma ( \Xi _b^-\rightarrow T_{-1/2}^- \pi ^0 )\\= & {} \frac{1}{2} \Gamma ( \Lambda _b^0\rightarrow T_{0}^{0} \pi ^0 )\\= & {} \frac{2}{3} \Gamma ( \Xi _b^0\rightarrow T_{1/2}^{0} \eta _q ),\\ \Gamma ( \Lambda _b^0\rightarrow T_{3/2}^{+} \pi ^- )= & {} \Gamma ( \Xi _b^-\rightarrow T_{1/2}^{0} K^- ) \\= & {} \Gamma ( \Xi _b^-\rightarrow T_{-1/2}^- {\overline{K}}^0 )\\= & {} \Gamma ( \Lambda _b^0\rightarrow T_{1}^{0} K^0 ) =\Gamma ( \Xi _b^0\rightarrow T_{3/2}^{+} K^- ) \\= & {} \Gamma ( \Xi _b^0\rightarrow T_{1/2}^{0} {\overline{K}}^0 ) \\= & {} \Gamma ( \Xi _b^0\rightarrow T_0^- \pi ^+ ) =\Gamma ( \Xi _b^0\rightarrow T_{1/2}^- K^+ ) \\= & {} \Gamma ( \Xi _b^-\rightarrow T_{1}^{0} \pi ^- ) =\Gamma ( \Xi _b^-\rightarrow T_{1/2}^- K^0 ) \\= & {} \Gamma ( \Lambda _b^0\rightarrow T_{-1/2}^- \pi ^+ ) =\Gamma ( \Lambda _b^0\rightarrow T_0^- K^+ ) \\= & {} 2 \Gamma ( \Xi _b^0\rightarrow T_{1}^{0} \pi ^0 ) \\= & {} 2 \Gamma ( \Xi _b^-\rightarrow T_0^- \pi ^0 ) = \frac{1}{2} \Gamma ( \Lambda _b^0\rightarrow T_{1/2}^{0} \pi ^0 ). \end{aligned}$$

Table 5 The productions of pentaquark $P_{15}$ from singly bottom baryons ${\mathcal {B}}_{b\bar{3}}$, with one meson (charmed and light meson) in the final state

Table 6 The productions of pentaquark $P_{15'}$ from singly bottom baryons ${\mathcal {B}}_{b\bar{3}}$, with one meson (charmed and light meson) in the final state

Appendix B: Tensor forms

The pentaquark states ${\bar{c}} qqqq$($T^{ijkl}$) can be decomposed into different tensor representations upon the SU(3) flavor symmetry.

$$\begin{aligned}{} & {} T^{ijkl}:3 \otimes 3 \otimes 3 \otimes 3\nonumber \\{} & {} \quad = 6 \otimes 6 + 6 \otimes \bar{3} + \bar{3} \otimes 6 + \bar{3} \otimes \bar{3}\nonumber \\{} & {} \quad =3\oplus \bar{3} \oplus \bar{3} \oplus \bar{6} \oplus \bar{6} \oplus 15 \oplus 15 \oplus 15 \oplus 15'. \end{aligned}$$

(B1)

The tensor reduction Eq. (2) can tell the representations of irreducible tensors $\hat{T_3}$, $\bar{T}_{{\bar{6}}}$, $\widetilde{T}_{15}, \ldots$, with the way of projection. In addition, the traceless tensor 15 indicates the following equations.

$$\begin{aligned} T_1^{\{11\}}=-T_2^{\{12\}}-T_3^{\{13\}},\\ T_2^{\{22\}}=-T_1^{\{21\}}-T_3^{\{23\}},\\ T_3^{\{33\}}=-T_1^{\{31\}}-T_{2}^{\{32\}}. \end{aligned}$$

Therefore, filtering out redundant mathematical calculations, we directly list the tensor representations ${\bar{6}}$, 15 and $15'$ respectively. The 6 states can be obtained from $\bar{3}\otimes \bar{3}\rightarrow T_6$ or $6\otimes 6\rightarrow T'_6$,

$$\begin{aligned} (T_6)_{\{11\}}= & {} \bar{c}dsds-\bar{c}dssd-\bar{c}sdds+\bar{c}sdsd, \\ (T_6)_{\{12\}}= & {} \bar{c}dssu-\bar{c}dsus-\bar{c}sdsu+\bar{c}sdus, \\ (T_6)_{\{13\}}= & {} -\bar{c}dsdu+\bar{c}dsud+\bar{c}sddu-\bar{c}sdud, \\ (T_6)_{\{22\}}= & {} \bar{c}susu-\bar{c}suus-\bar{c}ussu+\bar{c}usus, \\ (T_6)_{\{23\}}= & {} -\bar{c}sudu+\bar{c}suud+\bar{c}usdu-\bar{c}usud, \\ (T_6)_{\{33\}}= & {} \bar{c}dudu-\bar{c}duud-\bar{c}uddu+\bar{c}udud,\\ (T'_6)_{\{11\}}= & {} \bar{c}ddss+\frac{1}{2} (-\bar{c}dsds-\bar{c}dssd\\{} & {} -\bar{c}sdds-\bar{c}sdsd)+\bar{c}ssdd, \\ (T'_6)_{\{12\}}= & {} \frac{1}{4} (\bar{c}dssu+\bar{c}dsus-2 \bar{c}duss\\{} & {} +\bar{c}sdsu+\bar{c}sdus-2 \bar{c}ssdu-2 \bar{c}ssud+\bar{c}suds\\{} & {} +\bar{c}susd-2 \bar{c}udss+\bar{c}usds+\bar{c}ussd), \\ (T'_6)_{\{13\}}= & {} \frac{1}{4} (-2 \bar{c}ddsu-2 \bar{c}ddus+\bar{c}dsdu\\{} & {} +\bar{c}dsud+\bar{c}duds+\bar{c}dusd+\bar{c}sddu+\bar{c}sdud\\{} & {} -2 \bar{c}sudd+\bar{c}udds+\bar{c}udsd-2 \bar{c}usdd), \\ (T'_6)_{\{22\}}= & {} \bar{c}ssuu+\frac{1}{2} (-\bar{c}susu-\bar{c}suus\\{} & {} -\bar{c}ussu-\bar{c}usus)+\bar{c}uuss,\\ (T'_6)_{\{23\}}= & {} \frac{1}{4} (-2 \bar{c}dsuu+\bar{c}dusu+\bar{c}duus-2 \bar{c}sduu\\{} & {} +\bar{c}sudu+\bar{c}suud+\bar{c}udsu+\bar{c}udus\\{} & {} +\bar{c}usdu+\bar{c}usud-2 \bar{c}uuds-2 \bar{c}uusd), \\ (T'_6)_{\{33\}}= & {} \bar{c}dduu+\frac{1}{2} (-\bar{c}dudu-\bar{c}duud\\{} & {} -\bar{c}uddu-\bar{c}udud)+\bar{c}uudd. \end{aligned}$$

The 15 states are decomposed from $\bar{3}\otimes 6\rightarrow T_{15}$, $6\otimes \bar{3}\rightarrow T'_{15}$ or $6\otimes 6\rightarrow T''_{15}$, the $T'_{15}$ can be obtained by exchanging two pair light quarks $[q_1 q_2]\leftrightarrow [q_3 q_4]$ in $T_{15} \ ({\bar{b}} [q_1 q_2][q_3 q_4])$, such as $(T'_{15})^{\{11\}}_2=\bar{c}uusu-\bar{c}uuus$.

$$\begin{aligned} (T_{15})^{\{11\}}_1= & {} \frac{1}{4} (2 \bar{c}dsuu+\bar{c}dusu+\bar{c}duus-2 \bar{c}sduu\\{} & {} -\bar{c}sudu-\bar{c}suud-\bar{c}udsu-\bar{c}udus+\bar{c}usdu+\bar{c}usud), \\ (T_{15})^{\{11\}}_2= & {} \bar{c}suuu-\bar{c}usuu, \\ (T_{15})^{\{11\}}_3= & {} \bar{c}uduu-\bar{c}duuu, \\ (T_{15})^{\{22\}}_1= & {} \bar{c}dsdd-\bar{c}sddd, \\ (T_{15})^{\{22\}}_3= & {} \bar{c}uddd-\bar{c}dudd, \\ (T_{15})^{\{33\}}_1= & {} \bar{c}dsss-\bar{c}sdss, \\ (T_{15})^{\{33\}}_2= & {} \bar{c}suss-\bar{c}usss, \\ (T_{15})^{\{12\}}_1= & {} \frac{3}{8}( \bar{c}dsdu+ \bar{c}dsud- \bar{c}sddu\\{} & {} - \bar{c}sdud)+\frac{1}{8}(\bar{c}duds+\bar{c}dusd-\bar{c}udds-\bar{c}udsd)\\{} & {} +\frac{2}{8}( \bar{c}usdd- \bar{c}sudd), \\ (T_{15})^{\{12\}}_2= & {} \frac{1}{8} (\bar{c}dusu-2 \bar{c}dsuu+\bar{c}duus\\{} & {} +2 \bar{c}sduu+3 \bar{c}sudu+3 \bar{c}suud-\bar{c}udsu-\bar{c}udus\\{} & {} -3 \bar{c}usdu-3 \bar{c}usud), \\ (T_{15})^{\{12\}}_3= & {} \frac{1}{2} (-\bar{c}dudu-\bar{c}duud+\bar{c}uddu+\bar{c}udud),\ (T_{15})^{\{13\}}_2\\{} & {} =\frac{1}{2} (\bar{c}susu+\bar{c}suus-\bar{c}ussu-\bar{c}usus), \\ (T_{15})^{\{13\}}_1= & {} \frac{1}{8} (3 \bar{c}dssu+3 \bar{c}dsus+2 \bar{c}duss-3 \bar{c}sdsu-3 \bar{c}sdus\\{} & {} -\bar{c}suds-\bar{c}susd-2 \bar{c}udss+\bar{c}usds+\bar{c}ussd), \\ (T_{15})^{\{13\}}_3= & {} \frac{1}{8} (3 \bar{c}udus-2 \bar{c}dsuu-3 \bar{c}dusu-3 \bar{c}duus+2 \bar{c}sduu\\{} & {} -\bar{c}sudu-\bar{c}suud+3 \bar{c}udsu+\bar{c}usdu+\bar{c}usud), \\ (T_{15})^{\{22\}}_2= & {} \frac{1}{4} (-\bar{c}dsdu-\bar{c}dsud+\bar{c}duds+\bar{c}dusd+\bar{c}sddu\\{} & {} +\bar{c}sdud+2 \bar{c}sudd-\bar{c}udds-\bar{c}udsd-2 \bar{c}usdd), \\ (T_{15})^{\{23\}}_2= & {} \frac{1}{8} (\bar{c}sdsu-\bar{c}dssu-\bar{c}dsus+2 \bar{c}duss+\bar{c}sdus\\{} & {} +3 \bar{c}suds+3 \bar{c}susd-2 \bar{c}udss-3 \bar{c}usds-3 \bar{c}ussd), \\ (T_{15})^{\{23\}}_3= & {} \frac{1}{8} (\bar{c}sddu-\bar{c}dsdu-\bar{c}dsud-3 \bar{c}duds-3 \bar{c}dusd\\{} & {} +\bar{c}sdud-2 \bar{c}sudd+3 \bar{c}udds+3 \bar{c}udsd+2 \bar{c}usdd), \\ (T_{15})^{\{33\}}_3= & {} \frac{1}{4} (\bar{c}sdsu-\bar{c}dssu-\bar{c}dsus-2 \bar{c}duss\\{} & {} +\bar{c}sdus-\bar{c}suds-\bar{c}susd+2 \bar{c}udss+\bar{c}usds+\bar{c}ussd),\\ (T_{15})^{\{23\}}_1= & {} \frac{1}{2} (\bar{c}dsds+\bar{c}dssd-\bar{c}sdds-\bar{c}sdsd), \\ (T''_{15})^{\{11\}}_1= & {} \frac{1}{4} (\bar{c}dusu+\bar{c}duus-\bar{c}sudu-\bar{c}suud\\{} & {} +\bar{c}udsu+\bar{c}udus-\bar{c}usdu-\bar{c}usud), \\ (T''_{15})^{\{11\}}_2= & {} \frac{1}{2} (\bar{c}suuu+\bar{c}usuu-\bar{c}uusu-\bar{c}uuus),\\ (T''_{15})^{\{11\}}_3= & {} \frac{1}{2} (-\bar{c}duuu-\bar{c}uduu+\bar{c}uudu+\bar{c}uuud), \\ (T''_{15})^{\{12\}}_1= & {} \frac{1}{12} (2 \bar{c}ddsu+2 \bar{c}ddus-\bar{c}dsdu-\bar{c}dsud\\{} & {} +2 \bar{c}duds+2 \bar{c}dusd-\bar{c}sddu-\bar{c}sdud-4 \bar{c}sudd\\{} & {} +2 \bar{c}udds+2 \bar{c}udsd-4 \bar{c}usdd), \\ (T''_{15})^{\{12\}}_2= & {} \frac{1}{12} (2 \bar{c}dsuu-\bar{c}dusu\\{} & {} -\bar{c}duus+2 \bar{c}sduu+2 \bar{c}sudu+2 \bar{c}suud-\bar{c}udsu\\{} & {} -\bar{c}udus+2 \bar{c}usdu+2 \bar{c}usud-4 \bar{c}uuds-4 \bar{c}uusd), \\ (T''_{15})^{\{12\}}_3= & {} \frac{1}{12} (-4 \bar{c}dduu-\bar{c}dudu-\bar{c}duud\\{} & {} -\bar{c}uddu-\bar{c}udud+8 \bar{c}uudd), \\ (T''_{15})^{\{13\}}_1= & {} \frac{1}{12} (\bar{c}dssu+\bar{c}dsus+4 \bar{c}duss\\{} & {} +\bar{c}sdsu+\bar{c}sdus-2 \bar{c}ssdu-2 \bar{c}ssud-2 \bar{c}suds\\{} & {} -2 \bar{c}susd+4 \bar{c}udss-2 \bar{c}usds-2 \bar{c}ussd), \\ (T''_{15})^{\{13\}}_2= & {} \frac{1}{12} (4 \bar{c}ssuu+\bar{c}susu\\{} & {} +\bar{c}suus+\bar{c}ussu+\bar{c}usus-8 \bar{c}uuss), \\ (T''_{15})^{\{13\}}_3= & {} \frac{1}{12} (-2 \bar{c}dsuu-2 \bar{c}dusu-2 \bar{c}duus\\{} & {} -2 \bar{c}sduu+\bar{c}sudu+\bar{c}suud-2 \bar{c}udsu-2 \bar{c}udus\\{} & {} +\bar{c}usdu+\bar{c}usud+4 \bar{c}uuds+4 \bar{c}uusd), \\ (T''_{15})^{\{22\}}_1= & {} \frac{1}{2} (\bar{c}ddds+\bar{c}ddsd-\bar{c}dsdd-\bar{c}sddd),\\ (T_{15})^{\{22\}}_3= & {} \frac{1}{2} (-\bar{c}dddu-\bar{c}ddud+\bar{c}dudd+\bar{c}uddd), \\ (T''_{15})^{\{22\}}_2= & {} \frac{1}{4} (\bar{c}dsdu+\bar{c}dsud-\bar{c}duds-\bar{c}dusd\\{} & {} +\bar{c}sddu+\bar{c}sdud-\bar{c}udds-\bar{c}udsd), \\ (T''_{15})^{\{23\}}_1= & {} \frac{1}{12} (8 \bar{c}ddss-\bar{c}dsds-\bar{c}dssd\\{} & {} -\bar{c}sdds-\bar{c}sdsd-4 \bar{c}ssdd), \\ (T''_{15})^{\{23\}}_2= & {} \frac{1}{12} (2 \bar{c}dssu+2 \bar{c}dsus-4 \bar{c}duss+2 \bar{c}sdsu\\{} & {} +2 \bar{c}sdus+2 \bar{c}ssdu+2 \bar{c}ssud-\bar{c}suds-\bar{c}susd\\{} & {} -4 \bar{c}udss-\bar{c}usds-\bar{c}ussd), \\ (T''_{15})^{\{23\}}_3= & {} \frac{1}{12} (-4 \bar{c}ddsu-4 \bar{c}ddus-\bar{c}dsdu-\bar{c}dsud\\{} & {} +2 \bar{c}duds+2 \bar{c}dusd-\bar{c}sddu-\bar{c}sdud+2 \bar{c}sudd\\{} & {} +2 \bar{c}udds+2 \bar{c}udsd+2 \bar{c}usdd), \\ (T''_{15})^{\{33\}}_1= & {} \frac{1}{2} (\bar{c}dsss+\bar{c}sdss-\bar{c}ssds-\bar{c}sssd),\\ (T''_{15})^{\{33\}}_2= & {} \frac{1}{2} (\bar{c}sssu+\bar{c}ssus-\bar{c}suss-\bar{c}usss), \\ (T''_{15})^{\{33\}}_3= & {} \frac{1}{4} (-\bar{c}dssu-\bar{c}dsus-\bar{c}sdsu-\bar{c}sdus\\{} & {} +\bar{c}suds+\bar{c}susd+\bar{c}usds+\bar{c}ussd). \end{aligned}$$

In addition, the tensor with fully symmetric index $15'$ can be derived from $6\otimes 6\rightarrow T_{15'}$.

$$\begin{aligned} (T_{15'})^{\{1123\}}= & {} \frac{1}{12} (\bar{c}dsuu+\bar{c}dusu+\bar{c}duus+\bar{c}sduu+\bar{c}sudu\\{} & {} +\bar{c}suud+\bar{c}udsu+\bar{c}udus+\bar{c}usdu+\bar{c}usud\\{} & {} +\bar{c}uuds+\bar{c}uusd) \\ (T_{15'})^{\{1223\}}= & {} \frac{1}{12} (\bar{c}ddsu+\bar{c}ddus+\bar{c}dsdu+\bar{c}dsud+\bar{c}duds\\{} & {} +\bar{c}dusd+\bar{c}sddu+\bar{c}sdud+\bar{c}sudd+\bar{c}udds\\{} & {} +\bar{c}udsd+\bar{c}usdd) \\ (T_{15'})^{\{1231\}}= & {} \frac{1}{12} (\bar{c}dsuu+\bar{c}dusu+\bar{c}duus+\bar{c}sduu+\bar{c}sudu\\{} & {} +\bar{c}suud+\bar{c}udsu+\bar{c}udus+\bar{c}usdu+\bar{c}usud\\{} & {} +\bar{c}uuds+\bar{c}uusd) \\ (T_{15'})^{\{1233\}}= & {} \frac{1}{12} (\bar{c}dssu+\bar{c}dsus+\bar{c}duss+\bar{c}sdsu+\bar{c}sdus\\{} & {} +\bar{c}ssdu+\bar{c}ssud+\bar{c}suds+\bar{c}susd+\bar{c}udss\\ {}{} & {} +\bar{c}usds+\bar{c}ussd) \\ (T_{15'})^{\{1112\}}= & {} \frac{1}{4} (\bar{c}duuu+\bar{c}uduu+\bar{c}uudu+\bar{c}uuud),\\ (T_{15'})^{\{1113\}}= & {} \frac{1}{4} (\bar{c}suuu+\bar{c}usuu+\bar{c}uusu+\bar{c}uuus) \\ (T_{15'})^{\{1222\}}= & {} \frac{1}{4} (\bar{c}dddu+\bar{c}ddud+\bar{c}dudd+\bar{c}uddd),\\ (T_{15'})^{\{1333\}}= & {} \frac{1}{4} (\bar{c}sssu+\bar{c}ssus+\bar{c}suss+\bar{c}usss) \\ (T_{15'})^{\{2223\}}= & {} \frac{1}{4} (\bar{c}ddds+\bar{c}ddsd+\bar{c}dsdd+\bar{c}sddd),\\ (T_{15'})^{\{2333\}}= & {} \frac{1}{4} (\bar{c}dsss+\bar{c}sdss+\bar{c}ssds+\bar{c}sssd) \\ (T_{15'})^{\{1122\}}= & {} \frac{1}{6} (\bar{c}dduu+\bar{c}dudu+\bar{c}duud\\{} & {} +\bar{c}uddu+\bar{c}udud+\bar{c}uudd) \\ (T_{15'})^{\{1133\}}= & {} \frac{1}{6} (\bar{c}ssuu+\bar{c}susu+\bar{c}suus\\{} & {} +\bar{c}ussu+\bar{c}usus+\bar{c}uuss) \\ (T_{15'})^{\{2233\}}= & {} \frac{1}{6} (\bar{c}ddss+\bar{c}dsds+\bar{c}dssd\\{} & {} +\bar{c}sdds+\bar{c}sdsd+\bar{c}ssdd) \\ (T_{15'})^{\{1111\}}= & {} \bar{c}uuuu,\\ (T_{15'})^{\{2222\}}= & {} \bar{c}dddd,\ (T_{15'})^{\{3333\}}=\bar{c}ssss. \end{aligned}$$