Possible pentaquark candidates: new excited $\Omega _c$ states

Abstract

In this article, we study the axialvector-diquark–scalar-diquark–antiquark type charmed pentaquark states with $J^P={\frac{3}{2}}^\pm$ with the QCD sum rules by carrying out the operator product expansion up to the vacuum condensates of dimension 13 in a consistent way. In calculations, we separate the contributions of the negative parity and positive parity pentaquark states unambiguously, and choose three sets input parameters to study the masses and pole residues of the charmed pentaquark states $uuuc\bar{u}$ and $sssc\bar{s}$ in details. Then we estimate the masses of the charmed pentaquark states $ssuc\bar{u}$, $susc\bar{u}$, $ssdc\bar{d}$ and $sdsc\bar{d}$ with $J^P={\frac{3}{2}}^-$ to be $3.15\pm 0.13\,\mathrm {GeV}$ according to the SU(3) breaking effects, which is compatible with the $\Omega _c(3050)$, $\Omega _c(3066)$, $\Omega _c(3090)$, $\Omega _c(3119)$.

1 Introduction

In 2017, the LHCb collaboration studied the $\Xi _c^+ K^-$ mass spectrum with a sample of pp collision data corresponding to an integrated luminosity of $3.3\mathrm {fb}^{-1}$ collected by the LHCb experiment and observed five new narrow excited $\Omega _c$ states, $\Omega _c(3000)$, $\Omega _c(3050)$, $\Omega _c(3066)$, $\Omega _c(3090)$, $\Omega _c(3119)$ [1]. The measured masses and widths are

$$\begin{aligned} \Omega _c(3000) : M&= 3000.4 \pm 0.2 \pm 0.1 \text{ MeV }, \nonumber \\ \Gamma&= 4.5\pm 0.6\pm 0.3 \text{ MeV } , \nonumber \\ \Omega _c(3050) : M&= 3050.2 \pm 0.1 \pm 0.1 \text{ MeV } , \nonumber \\ \Gamma&= 0.8\pm 0.2\pm 0.1 \text{ MeV } , \nonumber \\ \Omega _c(3066) : M&= 3065.6 \pm 0.1 \pm 0.3 \text{ MeV } , \nonumber \\ \Gamma&= 3.5\pm 0.4\pm 0.2 \text{ MeV } , \nonumber \\ \Omega _c(3090) : M&= 3090.2 \pm 0.3 \pm 0.5 \text{ MeV } , \nonumber \\ \Gamma&= 8.7\pm 1.0\pm 0.8 \text{ MeV } , \nonumber \\ \Omega _c(3119) : M&= 3119.1 \pm 0.3 \pm 0.9 \text{ MeV } , \nonumber \\ \Gamma&= 1.1\pm 0.8\pm 0.4 \text{ MeV }. \end{aligned}$$

(1)

Later, the Belle collaboration confirmed the excited $\Omega _c$ states $\Omega _c(3000)$, $\Omega _c(3050)$, $\Omega _c(3066)$ and $\Omega _c(3090)$ in the decay mode $\Xi _c^+K^-$ using the entire Belle data sample of $980\,\mathrm { fb}^{-1}$ of $e^+e^-$ collisions [2].

The largest mass gap between the newly observed excited $\Omega _c$ states and the ground $\Omega _c(2700)$ state is about $400\,\mathrm {MeV}$, which is large enough to excite a light quark–antiquark pair from the QCD vacuum. The observation of the excited $\Omega _c$ states have renewed the interest in the baryon spectroscopy, as the multiquark candidates of those excited states cannot be excluded. There have been several assignments for those new $\Omega _c$ states, such as the traditional $\Omega _c$ states [3,4,5,6,7,8,9,10,11,12,13,14,15], the compact pentaquark states [16,17,18,19], molecular pentaquark states [20,21,22,23], dynamically generated resonances [24,25,26].

In Refs. [16, 17], the authors assign the $\Omega _c(3050)$ and $\Omega _c(3119)$ to be the $J^P={\frac{1}{2}}^+$ and ${\frac{3}{2}}^+$ pentaquark states respectively in the exotic $\overline{15}$ in the chiral quark-soliton model, and take the experimental masses as input parameters to study other pentaquark states. In Ref. [18], An and Chen study the spectrum of several low-lying $sscq\bar{q}$ pentaquark configurations using the constituent quark model with the hyperfine interaction induced by the Goldstone boson exchange. In Ref. [19], Anisovich et al study the mass spectrum of the $sscq\bar{q}$ pentaquark states with the simple diquark–diquark-antiquark model.

In Refs. [27, 28], the authors studied the scalar-diquark–pseudoscalar-diquark–anti-charmed-quark type pentaquark states $udud\bar{c}$ with the QCD sum rules for the first time by taking into account the vacuum condensates of dimensions 0, 4, 6, 12 in the operator product expansion, and obtained a mass around $3.10\,\mathrm {GeV}$. In Ref. [29], Albuquerque, Lee and Nielsen construct both the scalar-diquark–scalar-diquark–antiquark type and scalar-diquark–pseudoscalar-diquark–antiquark type currents to study the charmed pentaquark states $udcd\bar{u}$ with $J^P={\frac{1}{2}}^+$ with the QCD sum rules by taking into account the vacuum condensates up to dimension 10 in the operator product expansion, and obtain the ground state masses $3.21 \pm 0.13$ and $4.15 \pm 0.11\,\mathrm {GeV}$, respectively.

In this article, we will focus on the scenario of pentaquark state interpretation, and study the masses of the $J^P={\frac{3}{2}}^\pm$ charmed pentaquark states based on the QCD sum rules by taking into account the vacuum condensates up to dimension 13 in a consistent way, and revisit the assignments of the new narrow excited $\Omega _c^0$ states.

The article is arranged as follows: we derive the QCD sum rules for the masses and pole residues of the $J^P={\frac{3}{2}}^\pm$ charmed pentaquark states in Sect. 2; in Sect. 3, we present the numerical results and discussions; and Sect. 4 is reserved for our conclusion.

2 QCD sum rules for the ${\frac{3}{2}}^\pm$ charmed pentaquark states

Firstly, let us write down the two-point correlation functions $\Pi _{\mu \nu }(p)$ in the QCD sum rules,

$$\begin{aligned} \Pi _{\mu \nu }(p)= & {} i\int d^4x e^{ip \cdot x} \langle 0|T\left\{ J_{\mu }(x)\bar{J}_{\nu }(0)\right\} |0\rangle , \end{aligned}$$

(2)

where $J_\mu (x)=J_{q^{\prime }q^{\prime \prime }q^{\prime \prime \prime }\bar{q},\mu }(x)$. We choose the axialvector-diquark–scalar-diquark–antiquark type currents to interpolate the $J^P={\frac{3}{2}}^{-}$ charmed pentaquark states,

$$\begin{aligned}&J_{q^{\prime }q^{\prime \prime }q^{\prime \prime \prime }\bar{q},\mu }(x)\nonumber \\&\quad =\varepsilon ^{ila} \varepsilon ^{ijk}\varepsilon ^{lmn} q^{\prime T}_j(x) C\gamma _\mu q^{\prime \prime }_k(x) q^{\prime \prime \prime T}_m(x) C\gamma _5 c_n(x) C\bar{q}^{T}_{a}(x) ,\nonumber \\ \end{aligned}$$

(3)

where $q^\prime$, $q^{\prime \prime }$, $q^{\prime \prime \prime }=u$, d, s, the i, j, k, l, m, n and a are color indices, the C is the charge conjugation matrix.

The constituents of the currents $J_{q^{\prime }q^{\prime \prime }q^{\prime \prime \prime }\bar{q},\mu }$ can be divided into two clusters, a diquark $q^{\prime T}_j C\gamma _\mu q^{\prime \prime }_k$ ($D_i$) plus a triquark $q^{\prime \prime \prime T}_m C\gamma _5 c_n C\bar{q}^{T}_{a}$ ($T_{mna}$). We take the isospin limit by assuming the u and d quarks have degenerate masses, and analyze the isospins of the two clusters,

$$\begin{aligned}&\hat{I}^2 \,\varepsilon _{ijk} q^T_j C\gamma _\mu q^\prime _j = 1(1+1)\,\varepsilon _{ijk} q^T_j C\gamma _\mu q^\prime _j , \nonumber \\&\hat{I}^2 \,\varepsilon _{ijk} q^T_j C\gamma _\mu s_j = \frac{1}{2}\left( \frac{1}{2}+1\right) \,\varepsilon _{ijk} q^T_j C\gamma _\mu s_j , \nonumber \\&\hat{I}^2 \,\varepsilon _{ijk} s^T_j C\gamma _\mu s^\prime _j = 0(0+1)\,\varepsilon _{ijk} s^T_j C\gamma _\mu s_j , \end{aligned}$$

(4)

$$\begin{aligned}&\hat{I}^2 \, u^T_m C\gamma _5 c_n C \bar{d}^T_a = 1\left( 1+1\right) \,u^T_m C\gamma _5 c_n C \bar{d}^T_a , \nonumber \\&\hat{I}^2 \, d^T_m C\gamma _5 c_n C \bar{u}^T_a = 1\left( 1+1\right) \,d^T_m C\gamma _5 c_n C \bar{u}^T_a , \nonumber \\&\hat{I}^2 \,\left[ u^T_m C\gamma _5 c_n C \bar{u}^T_a -d^T_m C\gamma _5 c_n C \bar{d}^T_a\right] \nonumber \\&\quad = 1\left( 1+1\right) \,\left[ u^T_m C\gamma _5 c_n C \bar{u}^T_a -d^T_m C\gamma _5 c_n C \bar{d}^T_a\right] , \nonumber \\&\hat{I}^2 \,\left[ u^T_m C\gamma _5 c_n C \bar{u}^T_a +d^T_m C\gamma _5 c_n C \bar{d}^T_a\right] \nonumber \\&\quad = 0\left( 0+1\right) \,\left[ u^T_m C\gamma _5 c_n C \bar{u}^T_a +d^T_m C\gamma _5 c_n C \bar{d}^T_a\right] , \nonumber \\&\hat{I}^2 \, q^T_m C\gamma _5 c_n C \bar{s}^T_a = \frac{1}{2}\left( \frac{1}{2}+1\right) \,q^T_m C\gamma _5 c_n C \bar{s}^T_a , \nonumber \\&\hat{I}^2 \, s^T_m C\gamma _5 c_n C \bar{q}^T_a = \frac{1}{2}\left( \frac{1}{2}+1\right) \,s^T_m C\gamma _5 c_n C \bar{q}^T_a , \nonumber \\&\hat{I}^2 \, s^T_m C\gamma _5 c_n C \bar{s}^T_a = 0\left( 0+1\right) \,s^T_m C\gamma _5 c_n C \bar{s}^T_a , \end{aligned}$$

(5)

where q, $q^\prime =u$, d, the $\hat{I}^2$ is the isospin operator. The diquark clusters $D_i$ and triquark clusters $T_{mna}$ have the isospins $I=1$, $\frac{1}{2}$ or 0. As the color interaction is flavor blinded, we can obtain some mass relations based on the SU(3) breaking effects of the u, d, s quarks, the mass relation among the diquark clusters $D_i$ is $m_{I=0}-m_{I=\frac{1}{2}}=m_{I=\frac{1}{2}}-m_{I=1}$, while the mass relation among the triquark clusters $T_{mna}$ is $m_{I=0}-m_{I=\frac{1}{2}}=m_{I=\frac{1}{2}}-m_{I=1}$, if the hidden-flavor (for u and d) isospin singlet $u^T_m C\gamma _5 c_n C \bar{u}^T_a +d^T_m C\gamma _5 c_n C \bar{d}^T_a$ is excluded. On the other hand, the isospin triplet $u^T_m C\gamma _5 c_n C \bar{u}^T_a -d^T_m C\gamma _5 c_n C \bar{d}^T_a$ and isospin singlet $u^T_m C\gamma _5 c_n C \bar{u}^T_a +d^T_m C\gamma _5 c_n C \bar{d}^T_a$ are expected to have degenerate masses, which can be inferred from the tiny mass difference between the vector mesons $\rho ^0(770)$ and $\omega (780)$. In fact, if we choose the currents $J_\mu (x)=\bar{u}(x)\gamma _\mu u(x)-\bar{d}(x)\gamma _\mu d(x)$ and $\bar{u}(x)\gamma _\mu u(x)+\bar{d}(x)\gamma _\mu d(x)$ to interpolate the $\rho ^0(770)$ and $\omega (780)$, respectively, we obtain the same QCD sum rules.

Now we can estimate the mass differences among the pentaquark states $P(D_i,T_{mna})$ according to the SU(3) breaking effects, or the numbers of the u, d, s (anti)quarks, i.e. $N_{q}$ and $N_{s}$. The current $J_{uuu\bar{u},\mu }(x)$ couples potentially to the lowest ground pentaquark state $uuuc\bar{u}$ with $N_{q}=4$ and $N_{s}=0$, while the current $J_{sss\bar{s},\mu }(x)$ couples potentially to the highest ground pentaquark state $sssc\bar{s}$ with $N_{q}=0$ and $N_{s}=4$. On the other hand, the currents $J_{ssu\bar{u},\mu }(x)$, $J_{sus\bar{u},\mu }(x)$, $J_{ssd\bar{d},\mu }(x)$, $J_{sds\bar{d},\mu }(x)$, $J_{uus\bar{s},\mu }(x)$, $J_{suu\bar{s},\mu }(x)$, $J_{dds\bar{s},\mu }(x)$ and $J_{sdd\bar{s},\mu }(x)$ couple potentially to the ground state doubly-strange pentaquark states $ssuc\bar{u}$, $susc\bar{u}$, $ssdc\bar{d}$, $sdsc\bar{d}$ or hidden-strange pentaquark states $uusc\bar{s}$, $suuc\bar{s}$, $ddsc\bar{s}$, $sddc\bar{s}$, respectively, which have the quantum numbers $N_{q}=2$ and $N_{s}=2$. We expect that the ground state pentaquark states with $N_{q}=2$ and $N_{s}=2$ have degenerated masses, and lie in between the lowest pentaquark state $uuuc\bar{u}$ and the highest pentaquark state $sssc\bar{s}$.

In this article, we choose the interpolating currents $J_{uuu\bar{u},\mu }(x)$ and $J_{sss\bar{s},\mu }(x)$ to study the lowest and the highest ground states. Compared to the hidden-charm pentaquark currents and triply-charmed pentaquark currents, it is very difficult to carry out the operator product expansion for the singly-charmed pentaquark currents. If the excited $\Omega _c$ states are pentaquark states, they may be couple potentially to the doubly-strange currents $J_{ssu\bar{u},\mu }(x)$, $J_{sus\bar{u},\mu }(x)$, $J_{ssd\bar{d},\mu }(x)$ or $J_{sds\bar{d},\mu }(x)$. It is even difficult to carry out the operator product expansion for the currents $J_{ssu\bar{u},\mu }(x)$, $J_{sus\bar{u},\mu }(x)$, $J_{ssd\bar{d},\mu }(x)$ or $J_{sds\bar{d},\mu }(x)$ due to the SU(3) breaking effects involving the masses and vacuum condensates, such as $m_q$, $m_s$, $\langle \bar{q}q\rangle$, $\langle \bar{s}s\rangle$, etc. We can estimate the masses of the doubly-strange pentaquark states $ssuc\bar{u}$, $susc\bar{u}$, $ssdc\bar{d}$ and $sdsc\bar{d}$ according to the SU(3) breaking effects of the pentaquark states $uuuc\bar{u}$ and $sssc\bar{s}$, and examine the possibility of assigning the new excited $\Omega _c^0$ states as the pentaquark states. If such possibility exists, we will study the mass spectrum of the $J^{P}={\frac{1}{2}}^\pm$, ${\frac{3}{2}}^\pm$ and ${\frac{5}{2}}^\pm$ charmed pentaquark states with the QCD sum rules directly in a systematic way in our next work, and examine the assignments of the new excited $\Omega _c^0$ states exactly.

At the phenomenological side, we insert a complete set of intermediate pentaquark states with the same quantum numbers as the current operators $J_{\mu }(x)$ and $i\gamma _5 J_{\mu }(x)$ into the correlation functions $\Pi _{\mu \nu }(p)$ to obtain the hadronic representation [30, 31]. We isolate the pole terms of the lowest charmed pentaquark states with $J^P={\frac{3}{2}}^\pm$, and obtain the results:

$$\begin{aligned} \Pi _{\mu \nu }(p)= & {} \left( \lambda _{-}^2 {\!\not \!{p}+ M_{-} \over M_{-}^{2}-p^{2} } +\lambda _{+}^2 {\!\not \!{p}- M_{+} \over M_{+}^{2}-p^{2} } \right) \nonumber \\&\times \left( - g_{\mu \nu }+\frac{\gamma _\mu \gamma _\nu }{3}+\frac{2p_\mu p_\nu }{3p^2}-\frac{p_\mu \gamma _\nu -p_\nu \gamma _\mu }{3\sqrt{p^2}} \right) +\cdots ,\nonumber \\= & {} \Pi (p^2)\,\left( - g_{\mu \nu }\right) +\cdots . \end{aligned}$$

(6)

The currents $J_{\mu }(0)$ couple potentially to the spin-parity ${\frac{3}{2}}^\pm$ charmed pentaquark states [32,33,34,35,36,37],

$$\begin{aligned} \langle 0| J_\mu (0)|P_{-}(p)\rangle= & {} \lambda _{-} U^{-}_{\mu }(p,s) ,\nonumber \\ \langle 0| J_\mu (0)|P_{+}(p)\rangle= & {} \lambda _{+} i\gamma _5 U^{+}_{\mu }(p,s) , \end{aligned}$$

(7)

where the $\lambda _{\pm }$ are the pole residues or the current–pentaquark couplings, the spinors $U^{\pm }_{\mu }(p,s)$ satisfy the relation,

$$\begin{aligned}&\sum _s U_\mu (p,s) \overline{U}_\nu (p,s)=\left( \!\not \!{p}+M_{\pm }\right) \nonumber \\&\quad \times \left( -\, g_{\mu \nu }+\frac{\gamma _\mu \gamma _\nu }{3}+\frac{2p_\mu p_\nu }{3p^2}-\frac{p_\mu \gamma _\nu -p_\nu \gamma _\mu }{3\sqrt{p^2}} \right) \, , \end{aligned}$$

(8)

and $p^2=M^{2}_{\pm }$ on mass-shell, the s are the polarizations or spin indexes of the spinors, and should be distinguished from the s quark or the energy s.

We can obtain the hadronic spectral densities at the phenomenological side through dispersion relation,

$$\begin{aligned} \frac{\mathrm{Im}\Pi (s)}{\pi }= & {} \!\not \!{p} \left[ \lambda _{-}^2 \delta \left( s-M_{-}^2\right) +\lambda _{+}^2 \delta \left( s-M_{+}^2\right) \right] \nonumber \\&+\left[ M_{-}\lambda _{-}^2 \delta \left( s-M_{-}^2\right) -M_{+}\lambda _{+}^2 \delta \left( s-M_{+}^2\right) \right] \nonumber \\= & {} \!\not \!{p}\, \rho ^1_{H}(s)+\rho ^0_{H}(s) , \end{aligned}$$

(9)

where the subscript H denotes the hadron (or phenomenological) side, then we introduce the weight function $\exp \left( -\frac{s}{T^2}\right)$ to obtain the QCD sum rules at the hadron side,

$$\begin{aligned}&\int _{m_c^2}^{s_0}ds \left[ \sqrt{s}\rho ^1_{H}(s)+\rho ^0_{H}(s)\right] \exp \left( -\frac{s}{T^2}\right) \nonumber \\&\quad =2M_{-}\lambda _{-}^2\exp \left( -\frac{M_{-}^2}{T^2}\right) , \end{aligned}$$

(10)

$$\begin{aligned}&\int _{m_c^2}^{s_0}ds \left[ \sqrt{s}\rho ^1_{H}(s)-\rho ^0_{H}(s)\right] \exp \left( -\frac{s}{T^2}\right) \nonumber \\&\quad =2M_{+}\lambda _{+}^2\exp \left( -\frac{M_{+}^2}{T^2}\right) , \end{aligned}$$

(11)

where the $s_0$ are the continuum threshold parameters and the $T^2$ are the Borel parameters [34,35,36,37]. We separate the contributions of the negative parity and positive parity charmed pentaquark states unambiguously according to Eqs. (9–11).

Now we briefly outline the operator product expansion for the correlation function $\Pi _{sss\bar{s},\mu \nu }(p)$, the correlation function $\Pi _{uuu\bar{u},\mu \nu }(p)$ can be obtained with a simple replacement. Firstly, we contract the s and c quark fields in the correlation function $\Pi _{sss\bar{s},\mu \nu }(p)$ with Wick theorem,

$$\begin{aligned} \Pi _{sss\bar{s},\mu \nu }(p)&=i\,\varepsilon ^{ila}\varepsilon ^{ijk} \varepsilon ^{lmn}\varepsilon ^{i^{\prime }l^{\prime }a^{\prime }} \varepsilon ^{i^{\prime }j^{\prime }k^{\prime }} \varepsilon ^{l^{\prime }m^{\prime }n^{\prime }}\nonumber \\&\quad \times \int d^4x e^{ip\cdot x}C S_{a^{\prime }a}^T(-x)C \nonumber \\&\quad \times \Big \{ 2 Tr\left[ \gamma _\mu S_{kk^\prime }(x) \gamma _\nu C S^{T}_{jj^\prime }(x)C\right] \,Tr\nonumber \\&\quad \times \left[ \gamma _5 C_{nn^\prime }(x) \gamma _5 C S^{T}_{mm^\prime }(x)C\right] \nonumber \\&\quad -\,4 Tr \left[ \gamma _\mu S_{kk^\prime }(x) \gamma _\nu C S^{T}_{mj^\prime }(x)C \gamma _5C_{nn^\prime }(x) \gamma _5 C S^{T}_{jm^\prime }(x)C\right] \Big \} ,\nonumber \\ \end{aligned}$$

(12)

where the $S_{ij}(x)$ and $C_{ij}(x)$ are the full s and c quark propagators, respectively [31, 38],

$$\begin{aligned} S_{ij}(x)= & {} \frac{i\delta _{ij}\!\not \!{x}}{ 2\pi ^2x^4}-\frac{\delta _{ij}m_s}{4\pi ^2x^2}-\frac{\delta _{ij}\langle \bar{s}s\rangle }{12} +\frac{i\delta _{ij}\!\not \!{x}m_s\langle \bar{s}s\rangle }{48}\nonumber \\&-\frac{\delta _{ij}x^2\langle \bar{s}g_s\sigma Gs\rangle }{192}+\frac{i\delta _{ij}x^2\!\not \!{x} m_s\langle \bar{s}g_s\sigma Gs\rangle }{1152} \nonumber \\&-\frac{ig_s G^{a}_{\alpha \beta }t^a_{ij}(\!\not \!{x} \sigma ^{\alpha \beta }+\sigma ^{\alpha \beta } \!\not \!{x})}{32\pi ^2x^2}\nonumber \\&-\frac{1}{8}\langle \bar{s}_j\sigma ^{\mu \nu }s_i \rangle \sigma _{\mu \nu } +\cdots , \nonumber \\ \end{aligned}$$

(13)

$$\begin{aligned} C_{ij}(x)= & {} \frac{i}{(2\pi )^4}\int d^4k e^{-ik \cdot x} \left\{ \frac{\delta _{ij}}{\!\not \!{k}-m_c}\right. \nonumber \\&\left. - \frac{g_sG^n_{\alpha \beta }t^n_{ij}}{4}\frac{\sigma ^{\alpha \beta } (\!\not \!{k}+m_c)+(\!\not \!{k}+m_c) \sigma ^{\alpha \beta }}{(k^2-m_c^2)^2}+\cdots \right\} , \nonumber \\ \end{aligned}$$

(14)

$t^n=\frac{\lambda ^n}{2}$, the $\lambda ^n$ is the Gell-Mann matrix. In Eq. (13), we add the term $\langle \bar{s}_j\sigma _{\mu \nu }s_i \rangle$ originates from the Fierz re-ordering of the $\langle s_i \bar{s}_j\rangle$ to absorb the gluons emitted from other quark lines to extract the mixed condensate $\langle \bar{s}g_s\sigma G s\rangle$. The term $-\frac{1}{8}\langle \bar{s}_j\sigma ^{\mu \nu }s_i \rangle \sigma _{\mu \nu }$ was introduced in Refs. [39,40,41,42]. We compute the integrals both in the coordinate space and momentum space to obtain the correlation function $\Pi (p^2)$ at the quark level, then obtain the QCD spectral densities through dispersion relation,

$$\begin{aligned} \frac{\mathrm{Im}\Pi (s)}{\pi }= & {} \!\not \!{p}\, \rho ^1_{QCD}(s)+\rho ^0_{QCD}(s) , \end{aligned}$$

(15)

the $\rho ^1_{QCD}(s)$ and $\rho ^0_{QCD}(s)$ are the QCD spectral densities.

We take the quark-hadron duality, introduce the continuum threshold parameters $s_0$ and the weight function $\exp \left( -\frac{s}{T^2}\right)$ to obtain the QCD sum rules:

$$\begin{aligned}&\int _{m_c^2}^{s_0}ds \left[ \sqrt{s}\rho ^1_{H}(s)+\rho ^0_{H}(s)\right] \exp \left( -\frac{s}{T^2}\right) \nonumber \\&\quad = \int _{m_c^2}^{s_0}ds \left[ \sqrt{s}\rho ^1_{QCD}(s)+\rho ^0_{QCD}(s)\right] \exp \left( -\frac{s}{T^2}\right) , \nonumber \\&\int _{m_c^2}^{s_0}ds \left[ \sqrt{s}\rho ^1_{H}(s)-\rho ^0_{H}(s)\right] \exp \left( -\frac{s}{T^2}\right) \nonumber \\&\quad = \int _{m_c^2}^{s_0}ds \left[ \sqrt{s}\rho ^1_{QCD}(s)-\rho ^0_{QCD}(s)\right] \exp \left( -\frac{s}{T^2}\right) \, ,\nonumber \\ \end{aligned}$$

(16)

where $\rho ^1_{QCD}(s)=\rho ^1(s)+\rho ^1_F(s)$ and $\rho ^0_{QCD}(s)=\rho ^0(s)+\rho ^0_F(s)$,

$$\begin{aligned} \rho ^{1}(s)= & {} \frac{1}{7372800\pi ^8}\int _{x_i}^1dx \,x\bar{x}^5(x+5)(s-\widetilde{m}_c^2)^5 \nonumber \\&+\frac{m_s m_c}{1474560\pi ^8}\int _{x_i}^1dx \,\bar{x}^5(x+5)(s-\widetilde{m}_c^2)^4 \nonumber \\&-\frac{m_c\langle \bar{s}s\rangle }{46080\pi ^6}\int _{x_i}^1dx \,\bar{x}^4(x+4)(s-\widetilde{m}_c^2)^3 \nonumber \\&-\frac{m_s\langle \bar{s}s\rangle }{4608\pi ^6}\int _{x_i}^1dx \,x\bar{x}^4(s-\widetilde{m}_c^2)^3 \nonumber \\&+\frac{m_c\langle \bar{s}g_s\sigma Gs\rangle }{12288\pi ^6}\int _{x_i}^1dx \,\bar{x}^3(x+3)(s-\widetilde{m}_c^2)^2 \nonumber \\&+\frac{m_s\langle \bar{s}g_s\sigma Gs\rangle }{4608\pi ^6}\int _{x_i}^1dx \,x\bar{x}^2(5-2x)(s-\widetilde{m}_c^2)^2 \nonumber \\&+\frac{\langle \bar{s} s\rangle ^2}{192\pi ^4}\int _{x_i}^1dx \,x\bar{x}^2(s-\widetilde{m}_c^2)^2 \nonumber \\&+\frac{m_s m_c\langle \bar{s} s\rangle ^2}{192\pi ^4}\int _{x_i}^1dx \,\bar{x}^2(4-x)(s-\widetilde{m}_c^2) \nonumber \\&-\frac{\langle \bar{s} s\rangle \langle \bar{s}g_s\sigma Gs\rangle }{96\pi ^4}\int _{x_i}^1dx \,x\bar{x} (s-\widetilde{m}_c^2)\nonumber \\&+\frac{m_s m_c\langle \bar{s} s\rangle \langle \bar{s}g_s\sigma Gs\rangle }{768\pi ^4}\int _{x_i}^1dx \,\bar{x}(5x-19) \nonumber \\&-\frac{m_c \langle \bar{s} s\rangle ^3 }{36\pi ^2}\int _{x_i}^1dx \,\bar{x} \nonumber \\&+\frac{m_s \langle \bar{s} s\rangle ^3 }{36\pi ^2}\int _{x_i}^1dx \,x +\frac{ \langle \bar{s}g_s\sigma Gs\rangle ^2 }{768\pi ^4}\int _{x_i}^1dx \, x \nonumber \\&+\frac{ m_s m_c \langle \bar{s}g_s\sigma Gs\rangle ^2 }{768\pi ^4}\int _{x_i}^1dx \, (3-x)\delta (s-\widetilde{m}_c^2)\nonumber \\&+\frac{m_c \langle \bar{s} s\rangle ^2 \langle \bar{s}g_s\sigma Gs\rangle }{48\pi ^2}\int _{x_i}^1dx \,\delta (s-\widetilde{m}_c^2) \nonumber \\&-\frac{m_s \langle \bar{s} s\rangle ^2 \langle \bar{s}g_s\sigma Gs\rangle }{54\pi ^2} \,\delta (s-m_c^2) \nonumber \\&-\frac{m_s m_c \langle \bar{s} s\rangle ^4 }{54T^2} \,\delta (s-m_c^2) \nonumber \\&-\frac{m_c \langle \bar{s} s\rangle \langle \bar{s}g_s\sigma Gs\rangle ^2 }{192\pi ^2 T^2} \,\delta (s-m_c^2)\nonumber \\&+\frac{7m_s \langle \bar{s} s\rangle \langle \bar{s}g_s\sigma Gs\rangle ^2 }{1728\pi ^2 T^2}\left( 1+\frac{s}{T^2} \right) \,\delta (s-m_c^2) , \end{aligned}$$

(17)

$$\begin{aligned} \rho ^{0}(s)= & {} \frac{m_s}{2457600\pi ^8}\int _{x_i}^1dx \,x\bar{x}^5(x+3)(s-\widetilde{m}_c^2)^5\nonumber \\&+\frac{m_s}{1474560\pi ^8}\int _{x_i}^1dx \,x\bar{x}^5(x+5)s(s-\widetilde{m}_c^2)^4 \nonumber \\&-\frac{\langle \bar{s}s\rangle }{184320\pi ^6}\int _{x_i}^1dx \,x\bar{x}^4(3x+7)(s-\widetilde{m}_c^2)^4\nonumber \\&-\frac{\langle \bar{s}s\rangle }{46080\pi ^6}\int _{x_i}^1dx \,x\bar{x}^4(x+4)s(s-\widetilde{m}_c^2)^3 \nonumber \\&-\frac{m_s m_c\langle \bar{s}s\rangle }{4608\pi ^6}\int _{x_i}^1dx \,\bar{x}^3(x+3)(s-\widetilde{m}_c^2)^3\nonumber \\&+\frac{\langle \bar{s}g_s\sigma Gs\rangle }{36864\pi ^6}\int _{x_i}^1dx \,x\bar{x}^3(3x+5)(s-\widetilde{m}_c^2)^3 \nonumber \\&+\frac{\langle \bar{s}g_s\sigma Gs\rangle }{12288\pi ^6}\int _{x_i}^1dx \,x\bar{x}^3(x+3)s(s-\widetilde{m}_c^2)^2 \nonumber \\&+\frac{m_s m_c \langle \bar{s}g_s\sigma Gs\rangle }{1536\pi ^6}\int _{x_i}^1dx \,\bar{x}^2(x+2) (s-\widetilde{m}_c^2)^2 \nonumber \\&+\frac{m_c \langle \bar{s} s\rangle ^2}{576\pi ^4}\int _{x_i}^1dx \,\bar{x}^2(x+2)(s-\widetilde{m}_c^2)^2\nonumber \\&+\frac{m_s \langle \bar{s} s\rangle ^2}{128\pi ^4}\int _{x_i}^1dx \,x\bar{x}^2(3-x)(s-\widetilde{m}_c^2)^2 \nonumber \\&+\frac{m_s \langle \bar{s} s\rangle ^2}{192\pi ^4}\int _{x_i}^1dx \,x\bar{x}^2(4-x)s(s-\widetilde{m}_c^2) \nonumber \\&-\frac{m_c \langle \bar{s} s\rangle \langle \bar{s}g_s\sigma Gs\rangle }{192\pi ^4}\int _{x_i}^1dx \,\bar{x}(x+1) (s-\widetilde{m}_c^2) \nonumber \\&+\frac{m_s \langle \bar{s} s\rangle \langle \bar{s}g_s\sigma Gs\rangle }{768\pi ^4}\int _{x_i}^1dx \,x\bar{x}(15x-43) (s-\widetilde{m}_c^2) \nonumber \\&+\frac{m_s \langle \bar{s} s\rangle \langle \bar{s}g_s\sigma Gs\rangle }{768\pi ^4}\int _{x_i}^1dx \,x\bar{x}(5x-19) s \nonumber \\&-\frac{ \langle \bar{s} s\rangle ^3 }{36\pi ^2}\int _{x_i}^1dx \,x\bar{x}(3s-2\widetilde{m}_c^2)\nonumber \\&+\frac{ m_s m_c \langle \bar{s} s\rangle ^3 }{36\pi ^2}\int _{x_i}^1dx \,(x-4) +\frac{ m_c \langle \bar{s}g_s\sigma Gs\rangle ^2 }{768\pi ^4}\int _{x_i}^1dx \, x \nonumber \\&+\frac{ m_s \langle \bar{s}g_s\sigma Gs\rangle ^2 }{768\pi ^4}\int _{x_i}^1dx \,x (7-3x) \nonumber \\&+\frac{ m_s \langle \bar{s}g_s\sigma Gs\rangle ^2 }{768\pi ^4}\int _{x_i}^1dx \,x (3-x) s \delta (s-\widetilde{m}_c^2) \nonumber \\&+\frac{ \langle \bar{s} s\rangle ^2 \langle \bar{s}g_s\sigma Gs\rangle }{24\pi ^2}\int _{x_i}^1dx \,x\left[ 1+\frac{s}{2} \delta (s-\widetilde{m}_c^2) \right] \nonumber \\&+\frac{m_s m_c \langle \bar{s} s\rangle ^2 \langle \bar{s}g_s\sigma Gs\rangle }{54\pi ^2}\int _{x_i}^1dx \, \delta (s-\widetilde{m}_c^2) \nonumber \\&+\frac{7m_s m_c \langle \bar{s} s\rangle ^2 \langle \bar{s}g_s\sigma Gs\rangle }{108\pi ^2} \, \delta (s-m_c^2) +\frac{ m_c \langle \bar{s} s\rangle ^4 }{27} \,\delta (s-m_c^2)\nonumber \\&-\frac{ m_s \langle \bar{s} s\rangle ^4 }{54} \left( 1+\frac{s}{T^2} \right) \,\delta (s-m_c^2) \nonumber \\&-\frac{ \langle \bar{s} s\rangle \langle \bar{s}g_s\sigma Gs\rangle ^2 }{192\pi ^2 }\left( 1+\frac{s}{T^2}\right) \,\delta (s-m_c^2) \nonumber \\&-\frac{ 29m_s m_c^3\langle \bar{s} s\rangle \langle \bar{s}g_s\sigma Gs\rangle ^2 }{1728\pi ^2T^4 } \,\delta (s-m_c^2) \nonumber \\&-\frac{ 7m_s m_c\langle \bar{s} s\rangle \langle \bar{s}g_s\sigma Gs\rangle ^2 }{1728\pi ^2T^2 } \,\delta (s-m_c^2) , \end{aligned}$$

(18)

$$\begin{aligned} \rho ^{1}_{F}(s)= & {} -\frac{m_c\langle \bar{s}g_s\sigma Gs\rangle }{61440\pi ^6}\int _{x_i}^1dx \frac{\bar{x}^4(x+4)}{x}(s-\widetilde{m}_c^2)^2 \nonumber \\&+\frac{m_c\langle \bar{s}g_s\sigma Gs\rangle }{491520\pi ^6}\int _{x_i}^1dx \frac{\bar{x}^4(2x+3)}{x}(s-\widetilde{m}_c^2)^2 \nonumber \\&+\frac{m_s\langle \bar{s}g_s\sigma Gs\rangle }{49152\pi ^6}\int _{x_i}^1dx\, \bar{x}^3(x+1)\,(s-\widetilde{m}_c^2)^2 \nonumber \\&+\frac{m_c\langle \bar{s}g_s\sigma Gs\rangle }{32768\pi ^6}\int _{x_i}^1dx\, \bar{x}^3(x+3)\,(s-\widetilde{m}_c^2)^2 \nonumber \\&+\frac{3m_s\langle \bar{s}g_s\sigma Gs\rangle }{8192\pi ^6}\int _{x_i}^1dx\, x\bar{x}^2\,(s-\widetilde{m}_c^2)^2 \nonumber \\&+\frac{m_s m_c \langle \bar{s} s\rangle \langle \bar{s}g_s\sigma Gs\rangle }{768\pi ^4}\int _{x_i}^1dx \frac{\bar{x}^2(2-x)}{x} \nonumber \\&-\frac{ \langle \bar{s} s\rangle \langle \bar{s}g_s\sigma Gs\rangle }{9216\pi ^4}\int _{x_i}^1dx \,\bar{x}^2(2x+1)\, (s-\widetilde{m}_c^2) \nonumber \\&+\frac{ m_s m_c \langle \bar{s} s\rangle \langle \bar{s}g_s\sigma Gs\rangle }{6144\pi ^4}\int _{x_i}^1dx \,\frac{\bar{x}^2(2x+1)}{x} \nonumber \\&-\frac{ \langle \bar{s} s\rangle \langle \bar{s}g_s\sigma Gs\rangle }{512\pi ^4}\int _{x_i}^1dx \,x\bar{x} \, (s-\widetilde{m}_c^2) \nonumber \\&+\frac{ m_s m_c \langle \bar{s} s\rangle \langle \bar{s}g_s\sigma Gs\rangle }{1024\pi ^4}\int _{x_i}^1dx \,\bar{x}(x+1)\nonumber \\&+\frac{m_s m_c \langle \bar{s}g_s\sigma Gs\rangle ^2}{1536\pi ^4}\int _{x_i}^1dx \frac{\bar{x}(x-3)}{x} \delta (s-\widetilde{m}_c^2) \nonumber \\&+\frac{ \langle \bar{s}g_s\sigma Gs\rangle ^2}{27648\pi ^4}\int _{x_i}^1dx \,x\bar{x} \nonumber \\&+\frac{ \langle \bar{s}g_s\sigma Gs\rangle ^2}{6144\pi ^4}\int _{x_i}^1dx \,x\bar{x} \nonumber \\&-\frac{ m_s m_c \langle \bar{s}g_s\sigma Gs\rangle ^2}{6144\pi ^4}\int _{x_i}^1dx \,\bar{x} \, \delta (s-\widetilde{m}_c^2) \nonumber \\&+\frac{ \langle \bar{s}g_s\sigma Gs\rangle ^2}{2048\pi ^4}\int _{x_i}^1dx \,x \nonumber \\&-\frac{ m_s m_c \langle \bar{s}g_s\sigma Gs\rangle ^2}{3072\pi ^4}\int _{x_i}^1dx \,x \, \delta (s-\widetilde{m}_c^2) \nonumber \\&-\frac{ m_c \langle \bar{s} s\rangle ^2 \langle \bar{s}g_s\sigma Gs\rangle }{144\pi ^2}\int _{x_i}^1dx \frac{\bar{x} }{x} \delta (s-\widetilde{m}_c^2) \nonumber \\&+\frac{ m_s \langle \bar{s} s\rangle ^2 \langle \bar{s}g_s\sigma Gs\rangle }{1152\pi ^2}\int _{x_i}^1dx \,(1-2x)\, \delta (s-\widetilde{m}_c^2) \nonumber \\&-\frac{ m_s \langle \bar{s} s\rangle ^2 \langle \bar{s}g_s\sigma Gs\rangle }{768\pi ^2}\, \delta (s-m_c^2) \nonumber \\&+\frac{ m_c \langle \bar{s} s\rangle \langle \bar{s}g_s\sigma Gs\rangle ^2 }{288\pi ^2 T^2}\int _{x_i}^1dx \frac{1 }{x} \delta (s-\widetilde{m}_c^2)\nonumber \\&-\frac{ m_s \langle \bar{s} s\rangle \langle \bar{s}g_s\sigma Gs\rangle ^2 }{20736\pi ^2 T^2}\int _{x_i}^1dx \, \delta (s-\widetilde{m}_c^2)\nonumber \\&+\frac{ m_s \langle \bar{s} s\rangle \langle \bar{s}g_s\sigma Gs\rangle ^2 }{41472\pi ^2 T^2} \, \delta (s-m_c^2)\nonumber \\&+\frac{5 m_s \langle \bar{s} s\rangle \langle \bar{s}g_s\sigma Gs\rangle ^2 }{13824\pi ^2 T^2} \, \delta (s-m_c^2) \nonumber \\&-\frac{5 m_s \langle \bar{s} s\rangle \langle \bar{s}g_s\sigma Gs\rangle ^2 }{6912\pi ^2 T^2} \int _{x_i}^1dx \, \delta (s-\widetilde{m}_c^2) \nonumber \\&+\frac{5 m_s \langle \bar{s} s\rangle \langle \bar{s}g_s\sigma Gs\rangle ^2 }{9216\pi ^2 T^2} \,\left( 1+\frac{s}{T^2} \right) \delta (s-m_c^2) , \end{aligned}$$

(19)

$$\begin{aligned} \rho ^{0}_{F}(s)= & {} -\frac{m_s m_c\langle \bar{s}g_s\sigma Gs\rangle }{12288\pi ^6}\int _{x_i}^1dx \frac{\bar{x}^3(x+3)}{x}(s-\widetilde{m}_c^2)^2 \nonumber \\&+\frac{m_s m_c\langle \bar{s}g_s\sigma Gs\rangle }{49152\pi ^6}\int _{x_i}^1dx \frac{\bar{x}^3(x+1)}{x}(s-\widetilde{m}_c^2)^2 \nonumber \\&+\frac{m_s m_c\langle \bar{s}g_s\sigma Gs\rangle }{8192\pi ^6}\int _{x_i}^1dx \, \bar{x}^2(x+2)\,(s-\widetilde{m}_c^2)^2 \nonumber \\&+\frac{ m_c\langle \bar{s} s\rangle \langle \bar{s}g_s\sigma Gs\rangle }{1152\pi ^4}\int _{x_i}^1dx \frac{\bar{x}^2(x+2)}{x}(s-\widetilde{m}_c^2) \nonumber \\&-\frac{ m_c\langle \bar{s} s\rangle \langle \bar{s}g_s\sigma Gs\rangle }{9216\pi ^4}\int _{x_i}^1dx \frac{\bar{x}^2(2x+1)}{x}(s-\widetilde{m}_c^2) \nonumber \\&-\frac{ m_s\langle \bar{s} s\rangle \langle \bar{s}g_s\sigma Gs\rangle }{1536\pi ^4}\int _{x_i}^1dx \,\bar{x}^2\,s \nonumber \\&-\frac{ m_c\langle \bar{s} s\rangle \langle \bar{s}g_s\sigma Gs\rangle }{1024\pi ^6}\int _{x_i}^1dx \,\bar{x} (x+1)\,(s-\widetilde{m}_c^2) \nonumber \\&-\frac{ m_s\langle \bar{s} s\rangle \langle \bar{s}g_s\sigma Gs\rangle }{256\pi ^6}\int _{x_i}^1dx \,x\bar{x} \,(3s-2\widetilde{m}_c^2) \nonumber \\&-\frac{ m_c \langle \bar{s}g_s\sigma Gs\rangle ^2}{1536\pi ^4}\int _{x_i}^1dx \frac{\bar{x}(x+1)}{x}\nonumber \\&+\frac{ m_s \langle \bar{s}g_s\sigma Gs\rangle ^2}{27648\pi ^4}\int _{x_i}^1dx \,\bar{x}\,s\, \delta (s-\widetilde{m}_c^2) \nonumber \\&+\frac{ m_c \langle \bar{s}g_s\sigma Gs\rangle ^2}{6144\pi ^4}\int _{x_i}^1dx\, \bar{x} \nonumber \\&+\frac{ m_s \langle \bar{s}g_s\sigma Gs\rangle ^2}{3072\pi ^4}\int _{x_i}^1dx\, \bar{x} \,s\, \delta (s-\widetilde{m}_c^2) \nonumber \\&+\frac{ m_c \langle \bar{s}g_s\sigma Gs\rangle ^2}{2048\pi ^4}\int _{x_i}^1dx\, x\nonumber \\&+\frac{ m_s \langle \bar{s}g_s\sigma Gs\rangle ^2}{512\pi ^4}\int _{x_i}^1dx\, x \,\left[ 1+\frac{s}{2}\, \delta (s-\widetilde{m}_c^2) \right] \nonumber \\&+\frac{ m_s m_c \langle \bar{s} s\rangle ^2\langle \bar{s}g_s\sigma Gs\rangle }{144\pi ^2}\int _{x_i}^1dx \frac{x-3}{x} \delta (s-\widetilde{m}_c^2) \nonumber \\&+\frac{ \langle \bar{s} s\rangle ^2\langle \bar{s}g_s\sigma Gs\rangle }{1152\pi ^2}\int _{x_i}^1dx \,\bar{x}\,s\, \delta (s-\widetilde{m}_c^2) \nonumber \\&+\frac{ m_s m_c \langle \bar{s} s\rangle ^2\langle \bar{s}g_s\sigma Gs\rangle }{1152\pi ^2}\int _{x_i}^1dx \frac{1-2x}{x} \delta (s-\widetilde{m}_c^2) \nonumber \\&+\frac{ \langle \bar{s} s\rangle ^2\langle \bar{s}g_s\sigma Gs\rangle }{192\pi ^2}\int _{x_i}^1dx\,x\, \left[ 1+\frac{s}{2} \delta (s-\widetilde{m}_c^2) \right] \nonumber \\&-\frac{ m_s m_c \langle \bar{s} s\rangle ^2\langle \bar{s}g_s\sigma Gs\rangle }{768\pi ^2} \delta (s-m_c^2)\nonumber \\&+\frac{ m_s m_c \langle \bar{s} s\rangle ^2\langle \bar{s}g_s\sigma Gs\rangle }{768\pi ^2} \int _{x_i}^1dx\, \delta (s-\widetilde{m}_c^2) \nonumber \\&+\frac{5 m_s m_c \langle \bar{s} s\rangle \langle \bar{s}g_s\sigma Gs\rangle ^2}{1728\pi ^2T^2}\int _{x_i}^1dx \frac{1}{x} \delta (s-\widetilde{m}_c^2)\nonumber \\&+\frac{13 m_s m_c \langle \bar{s} s\rangle \langle \bar{s}g_s\sigma Gs\rangle ^2}{1728\pi ^2T^2} \delta (s-m_c^2) \nonumber \\&+\frac{ \langle \bar{s} s\rangle \langle \bar{s}g_s\sigma Gs\rangle ^2}{20736\pi ^2 }\int _{x_i}^1dx \,\left( 1-\frac{s}{T^2} \right) \delta (s-\widetilde{m}_c^2) \nonumber \\&+\frac{ \langle \bar{s} s\rangle \langle \bar{s}g_s\sigma Gs\rangle ^2}{2304\pi ^2 }\int _{x_i}^1dx \,\left( 1-\frac{s}{T^2} \right) \delta (s-\widetilde{m}_c^2) \nonumber \\&+\frac{ 5m_s m_c\langle \bar{s} s\rangle \langle \bar{s}g_s\sigma Gs\rangle ^2}{13824\pi ^2 T^2} \delta (s-m_c^2) \nonumber \\&-\frac{ 5m_s m_c\langle \bar{s} s\rangle \langle \bar{s}g_s\sigma Gs\rangle ^2}{6912\pi ^2 T^2} \int _{x_i}^1dx \, \frac{1}{x}\delta (s-\widetilde{m}_c^2) \nonumber \\&-\frac{ \langle \bar{s} s\rangle \langle \bar{s}g_s\sigma Gs\rangle ^2}{768\pi ^2 }\int _{x_i}^1dx \,\left( 1+\frac{s}{T^2} \right) \delta (s-\widetilde{m}_c^2)\nonumber \\&+\frac{5m_s m_c^3 \langle \bar{s} s\rangle \langle \bar{s}g_s\sigma Gs\rangle ^2}{9216\pi ^2T^4 }\, \delta (s-m_c^2) \nonumber \\&-\frac{5m_s m_c \langle \bar{s} s\rangle \langle \bar{s}g_s\sigma Gs\rangle ^2}{9216\pi ^2T^2 }\, \delta (s-m_c^2) , \end{aligned}$$

(20)

$\widetilde{m}_c^2=\frac{m_c^2}{x}$, $x_i=\frac{m_c^2}{s}$, $\bar{x}=1-x$. With a simple replacement $m_s\rightarrow 0$, $\langle \bar{s}s\rangle \rightarrow \langle \bar{q}q\rangle$, $\langle \bar{s}g_s\sigma Gs\rangle \rightarrow \langle \bar{q}g_s\sigma Gq\rangle$, we can obtain the QCD spectral densities of the $uuu\bar{u}c$ pentaquark state. The components $\rho ^1_F(s)$ and $\rho ^0_F(s)$ denote the contributions involving the term,

$$\begin{aligned} -\frac{1}{8}\langle \bar{s}_j\sigma ^{\mu \nu }s_i \rangle \sigma _{\mu \nu } , \end{aligned}$$

(21)

in the full s-quark propagator. From the spectral densities $\rho ^1_F(s)$ and $\rho ^0_F(s)$, we can see that there are contributions of the vacuum condensates of dimensions 5, 8, 10, 11 and 13, which play an important role in determining the Borel windows therefore the predicted masses.

In this article, we carry out the operator product expansion to the vacuum condensates up to dimension-13 and assume vacuum saturation for the higher dimension vacuum condensates. We take the truncations $n\le 13$ and $k\le 1$ in a consistent way, the operators of the orders $\mathcal {O}( \alpha _s^{k})$ with $k> 1$ are discarded. For example, the vacuum condensates $\langle g_s^3 GGG\rangle$, $\langle \frac{\alpha _s GG}{\pi }\rangle ^2$, $\langle \frac{\alpha _s GG}{\pi }\rangle \langle \bar{s} g_s \sigma Gs\rangle$, $\langle \frac{\alpha _s GG}{\pi }\rangle ^2 \langle \bar{s}s\rangle$ have the dimensions 6, 8, 9, 11, respectively, but they are the vacuum expectations of the operators of the order $\mathcal {O}( \alpha _s^{3/2})$, $\mathcal {O}(\alpha _s^2)$, $\mathcal {O}( \alpha _s^{3/2})$, $\mathcal {O}(\alpha _s^2)$, respectively, and are discarded. The vacuum condensates $\langle \frac{\alpha _s}{\pi }GG\rangle$, $\langle \bar{s}s\rangle \langle \frac{\alpha _s}{\pi }GG\rangle$, $\langle \bar{s}s\rangle ^2\langle \frac{\alpha _s}{\pi }GG\rangle$ and $\langle \bar{s}s\rangle ^3\langle \frac{\alpha _s}{\pi }GG\rangle$ are the vacuum expectations of the operators of the order $\mathcal {O}(\alpha _s)$, and they are neglected due to the small contributions of the gluon condensates for the hidden-charm (hidden-bottom) tetraquark states and hidden-charm pentaquark states [34,35,36,37, 39,40,41,42].

The QCD sum rules can be written more explicitly,

$$\begin{aligned} 2M_{-}\lambda _{-}^2\exp \left( -\frac{M_{-}^2}{T^2}\right)= & {} \int _{m_c^2}^{s_0}ds \left[ \sqrt{s}\rho ^1_{QCD}(s)\right. \nonumber \\&\left. + \, \rho ^0_{QCD}(s)\right] \exp \left( -\frac{s}{T^2}\right) , \end{aligned}$$

(22)

$$\begin{aligned} 2M_{+}\lambda _{+}^2\exp \left( -\frac{M_{+}^2}{T^2}\right)= & {} \int _{m_c^2}^{s_0}ds \left[ \sqrt{s}\rho ^1_{QCD}(s)\right. \nonumber \\&\left. -\,\rho ^0_{QCD}(s)\right] \exp \left( -\frac{s}{T^2}\right) \, . \end{aligned}$$

(23)

The contributions of the negative parity and positive parity charmed pentaquark states are separated explicitly.

We derive Eqs. (22–23) with respect to $\tau =\frac{1}{T^2}$, then eliminate the pole residues $\lambda _{\pm }$ and obtain the QCD sum rules for the masses of the charmed pentaquark states,

$$\begin{aligned} M^2_{-}= & {} \frac{-\frac{d}{d\tau }\int _{m_c^2}^{s_0}ds \left[ \sqrt{s}\rho _{QCD}^1(s)+\rho _{QCD}^0(s)\right] \exp \left( -s\tau \right) }{\int _{m_c^2}^{s_0}ds \left[ \sqrt{s}\rho _{QCD}^1(s)+\rho _{QCD}^0(s)\right] \exp \left( -s\tau \right) } , \nonumber \\ \end{aligned}$$

(24)

$$\begin{aligned} M^2_{+}= & {} \frac{-\frac{d}{d\tau }\int _{m_c^2}^{s_0}ds \left[ \sqrt{s}\rho _{QCD}^1(s)-\rho _{QCD}^0(s)\right] \exp \left( -s\tau \right) }{\int _{m_c^2}^{s_0}ds \left[ \sqrt{s}\rho _{QCD}^1(s)-\rho _{QCD}^0(s)\right] \exp \left( -s\tau \right) }\, .\nonumber \\ \end{aligned}$$

(25)

Fig. 1

The absolute contributions of the vacuum condensates of dimension n for central values of the parameters A, where the (I) and (II) denote the pentaquark states $uuuc\bar{u}$ and $sssc\bar{s}$, respectively, the N and P denote the negative parity and positive parity pentaquark states, respectively

3 Numerical results and discussions

We take the standard values of the vacuum condensates $\langle \bar{q}q \rangle =-(0.24\pm 0.01\, \mathrm {GeV})^3$, $\langle \bar{q}g_s\sigma G q \rangle =m_0^2\langle \bar{q}q \rangle$, $\langle \bar{s}g_s\sigma G s \rangle =m_0^2\langle \bar{s}s \rangle$, $m_0^2=(0.8 \pm 0.1)\,\mathrm {GeV}^2$, $\langle \bar{s}s \rangle =(0.8\pm 0.1)\langle \bar{q}q \rangle$, $\langle \frac{\alpha _s GG}{\pi }\rangle =(0.33\,\mathrm {GeV})^4$ at the energy scale $\mu =1\, \mathrm {GeV}$ [30, 31, 43], and choose the $\overline{MS}$ masses $m_{c}(m_c)=(1.28\pm 0.03)\,\mathrm {GeV}$ and $m_s(\mu =2\,\mathrm {GeV})=0.096^{+0.008}_{-0.004}\,\mathrm {GeV}$ from the Particle Data Group [44]. Furthermore, we take into account the energy-scale dependence of the input parameters,

$$\begin{aligned}&\langle \bar{q}q \rangle (\mu )=\langle \bar{q}q \rangle (Q)\left[ \frac{\alpha _{s}(Q)}{\alpha _{s}(\mu )}\right] ^{\frac{12}{25}} , \nonumber \\&\langle \bar{s}s \rangle (\mu )=\langle \bar{s}s \rangle (Q)\left[ \frac{\alpha _{s}(Q)}{\alpha _{s}(\mu )}\right] ^{\frac{12}{25}} , \nonumber \\&\langle \bar{q}g_s \sigma Gq \rangle (\mu )=\langle \bar{q}g_s \sigma Gq \rangle (Q)\left[ \frac{\alpha _{s}(Q)}{\alpha _{s}(\mu )}\right] ^{\frac{2}{25}} , \nonumber \\&\langle \bar{s}g_s \sigma Gs \rangle (\mu )=\langle \bar{s}g_s \sigma Gs \rangle (Q)\left[ \frac{\alpha _{s}(Q)}{\alpha _{s}(\mu )}\right] ^{\frac{2}{25}} , \nonumber \\&m_c(\mu )=m_c(m_c)\left[ \frac{\alpha _{s}(\mu )}{\alpha _{s}(m_c)}\right] ^{\frac{12}{25}} ,\nonumber \\&m_s(\mu )=m_s(\mathrm{2GeV} )\left[ \frac{\alpha _{s}(\mu )}{\alpha _{s}(\mathrm{2GeV})}\right] ^{\frac{12}{25}} ,\nonumber \\&\alpha _s(\mu )=\frac{1}{b_0t}\left[ 1-\frac{b_1}{b_0^2}\frac{\log t}{t} \right. \nonumber \\&\left. \quad +\frac{b_1^2(\log ^2{t}-\log {t}-1)+b_0b_2}{b_0^4t^2}\right] , \end{aligned}$$

(26)

where $t=\log \frac{\mu ^2}{\Lambda ^2}$, $b_0=\frac{33-2n_f}{12\pi }$, $b_1=\frac{153-19n_f}{24\pi ^2}$, $b_2=\frac{2857-\frac{5033}{9}n_f+\frac{325}{27}n_f^2}{128\pi ^3}$, $\Lambda =210\,\mathrm {MeV}$, $292\,\mathrm {MeV}$ and $332\,\mathrm {MeV}$ for the flavors $n_f=5$, 4 and 3, respectively [44,45,46].

Table 1 The optimal energy scales $\mu$, Borel parameters $T^2$, continuum threshold parameters $s_0$ and pole contributions (pole) for the charmed pentaquark states

In this article, we choose three sets parameters,

A. We evolve the input parameters to the energy scale $\mu =\sqrt{M_{P}^2-{\mathbb {M}}_c^2}$ to extract the masses $M_{P}$;

B. We evolve the input parameters to the energy scale $\mu =1\,\mathrm {GeV}$ to extract the masses $M_{P}$;

C. We evolve the input parameters except for $m_c(m_c)$ to the energy scale $\mu =1\,\mathrm {GeV}$ to extract the masses $M_{P}$,

which is denoted by $\mu =\overline{1.0}\,\mathrm {GeV}$.

For example, the parameters A are chosen in Refs. [34,35,36,37, 39,40,41,42], the parameters B are chosen in Refs. [47,48,49], the parameters C are chosen in Refs. [27,28,29, 50, 51].

Fig. 2

The masses of the charmed pentaquark states with variations of the Borel parameters $T^2$ for the parameters A, where the (I), (II), (III) and (IV) correspond to the quantum numbers $(uuuc\bar{u},{\frac{3}{2}}^-)$, $(sssc\bar{s},{\frac{3}{2}}^-)$, $(uuuc\bar{u},{\frac{3}{2}}^+)$, and $(sssc\bar{s},{\frac{3}{2}}^+)$, respectively

Now we take a short digression to discuss the energy scale formula, $\mu =\sqrt{M_{P}^2-{\mathbb {M}}_Q^2}$. In the heavy quark limit, the Q-quark serves as a static well potential and can combine with a light quark q to form a heavy diquark in color antitriplet. The $\overline{Q}$-quark serves as another static well potential, and can combine with a light diquark $\varepsilon ^{ijk}q^i\,q^{\prime j}$ to form a heavy triquark in color triplet,

$$\begin{aligned}&q^j+Q^k \rightarrow \varepsilon ^{ijk}\, q^j\,Q^k , \nonumber \\&\varepsilon ^{ijl}q^i\,q^{\prime j} +\overline{Q}^k\rightarrow \varepsilon ^{lkm}\varepsilon ^{ijl}\,q^i \,q^{\prime j}\, \overline{Q}^k , \end{aligned}$$

(27)

where the i, j, k, l, m are color indexes. Then

$$\begin{aligned}&\varepsilon ^{ijk}\, q^j\,Q^k+\varepsilon ^{imn} \bar{q}^{\prime m}\,\overline{Q}^n \rightarrow \mathrm{compact \,\,\, tetraquark \,\,\, states} , \nonumber \\&\varepsilon ^{lkm}\varepsilon ^{ijl}\,q^i \,q^{\prime j}\, \overline{Q}^k\nonumber \\&\quad + \, \varepsilon ^{mnb} q^{\prime \prime n}\,Q^b \rightarrow \mathrm{compact \,\,\, pentaquark \,\,\, states}\, . \end{aligned}$$

(28)

The tetraquark states $q\bar{q}^\prime Q \overline{Q}$ ($X,\,Y,\,Z$) and pentaquark states $qq^\prime q^{\prime \prime } Q \overline{Q}$ (P) are characterized by the effective heavy quark masses ${\mathbb {M}}_Q$ and the virtuality $V=\sqrt{M^2_{X/Y/Z}-(2{\mathbb {M}}_Q)^2}$, $\sqrt{M^2_{P}-(2{\mathbb {M}}_Q)^2}$. It is natural to take the energy scales of the QCD spectral densities to be $\mu =V$.

Table 2 The predicted masses and pole residues of the charmed pentaquark states

The effective Q-quark masses ${\mathbb {M}}_Q$ have universal values, and embody the net effects of the complex dynamics [34,35,36,37, 39,40,41,42]. We fit the effective Q-quark masses ${\mathbb {M}}_{Q}$ to reproduce the experimental values $M_{Z_c(3900)}$ and $M_{Z_b(10610)}$ in the scenario of tetraquark states [39,40,41,42], then use the energy scale formula $\mu =\sqrt{M^2_{X/Y/Z}-(2{\mathbb {M}}_Q)^2}$ and $\sqrt{M^2_{P}-(2{\mathbb {M}}_c)^2}$ to study the hidden-charm (hidden-bottom) tetraquark states and hidden-charm pentaquark states, respectively, and obtain satisfactory results. In this article, we use the formula $\mu =\sqrt{M_{P}^2-{\mathbb {M}}_c^2}$ to determine the ideal energy scales of the QCD spectral densities, as there exists only one heavy quark, and take the updated value of the effective c-quark mass ${\mathbb {M}}_c=1.82\,\mathrm {GeV}$ [52].

Fig. 3

The masses of the charmed pentaquark states with variations of the Borel parameters $T^2$ for the parameters B, where the (I), (II), (III) and (IV) correspond to the quantum numbers $(uuuc\bar{u},{\frac{3}{2}}^-)$, $(sssc\bar{s},{\frac{3}{2}}^-)$, $(uuuc\bar{u},{\frac{3}{2}}^+)$, and $(sssc\bar{s},{\frac{3}{2}}^+)$, respectively

Fig. 4

The masses of the charmed pentaquark states with variations of the Borel parameters $T^2$ for the parameters C, where the (I), (II), (III) and (IV) correspond to the quantum numbers $(uuuc\bar{u},{\frac{3}{2}}^-)$, $(sssc\bar{s},{\frac{3}{2}}^-)$, $(uuuc\bar{u},{\frac{3}{2}}^+)$, and $(sssc\bar{s},{\frac{3}{2}}^+)$, respectively

Fig. 5

The pole residues of the charmed pentaquark states with variations of the Borel parameters $T^2$ for the parameters A, where the (I), (II), (III) and (IV) correspond to the quantum numbers $(uuuc\bar{u},{\frac{3}{2}}^-)$, $(sssc\bar{s},{\frac{3}{2}}^-)$, $(uuuc\bar{u},{\frac{3}{2}}^+)$, and $(sssc\bar{s},{\frac{3}{2}}^+)$, respectively

Fig. 6

The pole residues of the charmed pentaquark states with variations of the Borel parameters $T^2$ for the parameters B, where the (I), (II), (III) and (IV) correspond to the quantum numbers $(uuuc\bar{u},{\frac{3}{2}}^-)$, $(sssc\bar{s},{\frac{3}{2}}^-)$, $(uuuc\bar{u},{\frac{3}{2}}^+)$, and $(sssc\bar{s},{\frac{3}{2}}^+)$, respectively

We search for the ideal Borel parameters $T^2$ and continuum threshold parameters $s_0$ according to the four criteria:

• $\mathbf {1_\cdot }$ Pole dominance at the hadron side;

• $\mathbf {2_\cdot }$ Convergence of the operator product expansion;

• $\mathbf {3_\cdot }$ Appearance of the Borel platforms;

• $\mathbf {4_\cdot }$ Satisfying the energy scale formula $\mu =\sqrt{M_{P}^2-{\mathbb {M}}_c^2}$ for the parameters A, by try and error, and present the optimal energy scales $\mu$, ideal Borel parameters $T^2$, continuum threshold parameters $s_0$ and pole contributions in Table 1. From Table 1, we can see that the criterion $\mathbf {1}$ can be satisfied.

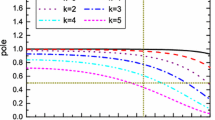
In Fig. 1, we plot the absolute contributions of the vacuum condensates |D(n)| in the operator product expansion for the central values of the parameters shown in Table 1 in the case of the parameters A,

$$\begin{aligned} D(n)= & {} \frac{ \int _{m_c^2}^{s_0} ds\,\rho _{n}(s)\,\exp \left( -\frac{s}{T^2}\right) }{\int _{m_c^2}^{s_0} ds \,\rho (s)\,\exp \left( -\frac{s}{T^2}\right) } , \end{aligned}$$

(29)

where the $\rho _{n}(s)$ are the QCD spectral densities for the vacuum condensates of dimension n, and the total spectral densities $\rho (s)=\sqrt{s}\rho ^1_{QCD}(s)\pm \rho ^0_{QCD}(s)$. From the figure, we can see that the dominant contributions come from the perturbative terms D(0) for the positive parity pentaquark states, the operator product expansion is well convergent, while for the negative parity pentaquark states, the contributions of the vacuum condensates of dimensions $n=10$, 12, 13 are tiny, the largest contributions come from the vacuum condensates of dimension $n=6$, but the contributions of the vacuum condensates of dimensions 6, 8, 9, 11 have the hierarchy $D(6)\gg |D(8)|\sim D(9)\gg |D(11)|$ or $D(6)\gg |D(8)|\gg D(9)\gg |D(11)|$, the operator product expansion is also convergent. On the other hand, from the figure, we can see that the contributions of the perturbative terms $D_0$ are tiny for the negative parity pentaquark states, so in this article we approximate the continuum contributions as $\rho (s)\Theta (s-s_0)$, and define the pole contributions $\mathrm {PC}$ as

$$\begin{aligned} \mathrm{PC}= & {} \frac{ \int _{m_c^2}^{s_0} ds\,\left[ \sqrt{s}\rho _{QCD}^1(s)\pm \rho _{QCD}^0(s)\right] \, \exp \left( -\frac{s}{T^2}\right) }{\int _{m_c^2}^{\infty } ds \,\left[ \sqrt{s}\rho _{QCD}^1(s)\pm \rho _{QCD}^0(s)\right] \,\exp \left( -\frac{s}{T^2}\right) }\, . \end{aligned}$$

(30)

In calculations, we observe that the dominant contributions come from the perturbative terms D(0) for the parameters shown in Table 1 in the case of the parameters B and C, the operator product expansion are well convergent. Now the criterion $\mathbf{1}$ and criterion $\mathbf{2}$ are satisfied, we expect to make reasonable predictions.

We take into account all uncertainties of the input parameters, and obtain the masses and pole residues of the charmed pentaquark states with $J^P={\frac{3}{2}}^\pm$, which are shown explicitly in Table 2. From Table 2, we can see that the criterion $\mathbf {4}$ can be satisfied for the parameters A. In Figs. 2, 3, 4, 5, 6 and 7, we plot the masses and pole residues of the charmed pentaquark states with variations of the Borel parameters $T^2$ at much larger intervals than the Borel windows shown in Table 1. In the Borel windows, the uncertainties of the masses and pole residues originate from the Borel parameters $T^2$ are very small, the Borel platforms exist, the criterion $\mathbf {3}$ can be satisfied. Now the four criteria are all satisfied, and we expect to make reliable predictions.

In the Borel windows, the uncertainties of the predicted masses are less than $5\%$, as we obtain the masses from a ratio, see Eqs. (24–25), the uncertainties originate from a special parameter in the numerator and denominator cancel out with each other, the net uncertainties are very small; while the uncertainties of the pole residues can be as large as $20\%$, as analogous cancelations do not exist.

If we choose analogous pole contributions, about (40–60)%, the predicted masses based on the three sets parameters have the relation, $M_\mathbf{A}<M_\mathbf{C}<M_\mathbf{B}$. From Table 2, we can see that for the negative parity charmed pentaquark states, the parameters A lead to much smaller predicted masses than the parameters B and C.

Fig. 7

The pole residues of the charmed pentaquark states with variations of the Borel parameters $T^2$ for the parameters C, where the (I), (II), (III) and (IV) correspond to the quantum numbers $(uuuc\bar{u},{\frac{3}{2}}^-)$, $(sssc\bar{s},{\frac{3}{2}}^-)$, $(uuuc\bar{u},{\frac{3}{2}}^+)$, and $(sssc\bar{s},{\frac{3}{2}}^+)$, respectively

In Ref. [29], Albuquerque et al. study the charmed pentaquark states $udcd\bar{u}$ with $J^P={\frac{1}{2}}^+$ with the QCD sum rules by taking into account the vacuum condensates up to dimension 10, and obtain the ground state masses $3.21 \pm 0.13$ and $4.15 \pm 0.11\,\mathrm {GeV}$ for the scalar-diquark–scalar-diquark–antiquark type and scalar-diquark–pseudoscalar-diquark–antiquark type pentaquark states, respectively. In Ref. [29], the parameters C are chosen, if we choose the parameters C, we obtain the prediction $M=4.53\pm 0.09\,\mathrm {GeV}$ for the axialvector-diquark–scalar-diquark–antiquark type pentaquark state $uuuc\bar{u}$ with $J^P={\frac{3}{2}}^+$. The calculations based on the QCD sum rules indicate that the axialvector light diquark states A have larger masses than the corresponding scalar light diquark states S, $M_{A}-M_{S}=0.15$–0.20 GeV [53]. We can estimate that the scalar-diquark–scalar-diquark–antiquark type pentaquark state $udcd\bar{u}$ with $J^P={\frac{1}{2}}^+$ has a mass about $4.36\pm 0.09\,\mathrm {GeV}$, which is much larger than the value $3.21 \pm 0.13\,\mathrm {GeV}$ obtained in Ref. [29] in a Borel window where the contributions of the vacuum condensates of dimension 10 are still very large, the convergent behavior of the operator product expansion is very bad. In this article, we carry out the operator product expansion up to the vacuum condensates of dimension 13 in a consistent way. We do not prefer the parameters C as they lead to two energy scales, $\mu =m_c$ and $\mu =1\,\mathrm {GeV}$, in the QCD spectral densities.

The predicated masses depend on the input parameters A, B and C, see Table 2. In Ref. [49], we obtain the mass $M_Z=4.44 \pm 0.19\,\mathrm {GeV}$ for the Z(4430) as the ground state diquark–antidiquark type axialvector tetraquark state based on the QCD sum rules for the parameters B. While in Ref. [54], we observe that the $Z_c(3900)$ and Z(4430) can be tentatively assigned to be the ground state and the first radial excited state of the diquark–antidiquark type axialvector tetraquark states respectively for the parameters A. In Ref. [55], we assign the $Z_c(3900)$ to be the diquark–antidiquark type axialvector tetraquark state, study its width with the QCD sum rules by taking into account all the Feynman diagrams for the parameters A, and reproduce the experimental value. From Refs. [49, 54] and present work, we can see that the parameters A lead to smaller or much smaller masses than the parameters B.

Fig. 8

The predicted masses with variations of the Borel parameters for central values of the parameters A, where the (I) and (II) denote the pentaquark states $uuuc\bar{u}$ and $sssc\bar{s}$, respectively, the N and P denote the negative parity and positive parity pentaquark states, respectively

In Fig. 8, we plot the predicted masses with variations of the Borel parameters for central values of the parameters A at very large intervals. From the figure, we can see that for small Borel parameters, the predicted masses of the negative parity pentaquark state $sssc\bar{s}$ and positive parity pentaquark states $uuuc\bar{u}$ and $sssc\bar{s}$ increase monotonously with the decrease of the Borel parameters, which warrant appearance of very flat Borel platforms, as the predicted masses always increase monotonously with the increase of the Borel parameters for large Borel parameters.

From Table 2, we can see that the predicted masses of the pentaquark states $uuuc\bar{u}$ and $sssc\bar{s}$ with $J^P={\frac{3}{2}}^-$ are $3.07^{+0.13}_{-0.14}\,\mathrm {GeV}$ and $3.22^{+0.12}_{-0.14}\,\mathrm {GeV}$ respectively based on the parameters A. The masses of the pentaquark states $ssuc\bar{u}$, $susc\bar{u}$, $ssdc\bar{d}$ and $sdsc\bar{d}$ can be estimated to be

$$\begin{aligned} M= & {} \frac{M_{uuuc\bar{u}}+M_{sssc\bar{s}}}{2}=3.15\pm 0.13\,\mathrm {GeV} , \end{aligned}$$

(31)

which lie in the same region of the masses of the $\Omega _c(3050)$, $\Omega _c(3066)$, $\Omega _c(3090)$, $\Omega _c(3119)$ from the LHCb collaboration [1]. In Ref. [19], Anisovich et al obtain the mass $M=3.2\pm 0.1\,\mathrm {GeV}$ for the pentaquark state $ussc\bar{u}$ with $J^P={\frac{3}{2}}^-$ based on the diquark–diquark-antiquark model, which is consistent with the present predictions. The new excited $\Omega _c$ states are possible candidates for the charmed pentaquark states, more experimental and theoretical works are still needed to make a solid assignment. In this article, we prefer the parameters A, because the parameters A can enhance the pole contributions remarkably and improve the convergent behaviors significantly in the operator product expansion in the QCD sum rules for the exotic hadrons, such as the tetraquark states, pentaquark states, molecular states, and lead to much smaller predicted masses than the parameters B and C. We can assign more exotic hadrons reasonably based on the QCD sum rules if the parameters A are chosen. However, the parameters B and C are not excluded, more experimental data are still needed to select the best parameters.

4 Conclusion

In this article, we focus on the scenario of pentaquark states interpretation of the new excited $\Omega _c$ states, and study the $J^P={\frac{3}{2}}^\pm$ charmed pentaquark states with the QCD sum rules by carrying out the operator product expansion up to the vacuum condensates of dimension 13 in a consistent way. In calculations, we separate the contributions of the negative parity and positive parity pentaquark states unambiguously, and choose three sets input parameters to study the masses and pole residues of the charmed pentaquark states $uuuc\bar{u}$ and $sssc\bar{s}$ with the QCD sum rules in details. Then we estimate the masses of the charmed pentaquark states $ssuc\bar{u}$, $susc\bar{u}$, $ssdc\bar{d}$ and $sdsc\bar{d}$ with $J^P={\frac{3}{2}}^-$ to be $3.15\pm 0.13\,\mathrm {GeV}$ according to the SU(3) breaking effects, which is compatible with the experimental values of the masses of the $\Omega _c(3050)$, $\Omega _c(3066)$, $\Omega _c(3090)$, $\Omega _c(3119)$. The new excited $\Omega _c$ states are possible candidates for the charmed pentaquark states, more experimental and theoretical works are still needed to make a solid assignment.