The production of charm pentaquark from B meson within SU(3) analysis

Abstract

We study the masses and production modes of pentaquark with the quark constituent $c\bar{q}qqq$, by the tridiquark-diquark model and systematical light flavor quark symmetry SU(3) analysis. The mass spectrums show that the S-wave singly charm pentaquark $c{\bar{n}}nnn,~c{\bar{s}}ssn,~c{\bar{n}}ssn$ and $c{\bar{n}}snn$ $(n=u,d)$ are above their strong decay thresholds, while $c{\bar{s}} nnn$ and $c\bar{s} snn$ with parity $\frac{1}{2}^-$ are below their strong decay thresholds, which imply the possibility of stable states. Furthermore, we discuss the production of the concerned 15 states from B meson, the analysis within SU(3) symmetry yields the golden channels of production process, ${\overline{B}}^0_s\rightarrow F_{\bar{s}udd}^{+} {\overline{p}},\ B^-\rightarrow F_{\bar{u}dds}^{-} {\overline{\Lambda }}^0$, which expected to be work worthily in b-factory.

1 Introduction

Recently, there is a renewed interest in the study of pentaquark with heavy quark constituents, especially, the LHCb observation in 2015 of hidden charm pentaquark $P_c$ states, $P_c(4380), P_c(4312), P_c(4440)$ and $P_c(4457)$, in the $\Lambda _b^0\rightarrow J/\Psi p K^-$ [1, 2], as well as $P_{cs}(4459)$ and $P_{c}(4337)$ in the $\Xi _b^-\rightarrow J/\Psi \Lambda K^-$ and $B_s\rightarrow J/\Psi p {\bar{p}}$ respectively [3, 4], which have triggered many theoretical studies [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19]. The existence of pentaquark are proposed by Gell-Mann and Zweig at the birth of quark model in 1964 [20, 21]. But until now, only a couple of hidden charm pentaquark come to light. The open heavy flavor ones, for instance open charm tetraquark state $T_{cc}^+$ [22] firstly observed by LHCb in the mass spectrum $D^0D^0\pi ^+$ in 2021, therefore are expected similarly. The discovered heavy narrow excited baryons, e.g. exotic $\Xi _c$ [23,24,25], $\Omega _c$ [26,27,28] states, have the potential to be the candidate for the open heavy flavor pentaquark states, see the review [29]. Theoretically, the open flavor pentaquarks with charm quark and $\bar{q}qqq$ have been discussed by the constituent quark model in Ref. [30], rough mass estimates are evaluated in the end of paper. The Chromomagnetic Interaction(CMI) model provides more accurate results in Ref. [31]. QCD sum rules and chiral effective field theory offer additional methods to investigate the singly heavy pentaquark, individually the mass around 3.21 GeV [32,33,34,35] and 2.7 GeV [36, 37] for ground $cudd{\bar{u}}$ state.

In the letter, we wound consider the charm pentaquark within the triquark-diquark model. The model is a suitable appropriate [38, 39] to deal with the many quarks system, in this framework, the colored diquarks and triquarks, with spin 0, color anti-triplet, known as good diquark $|(q'q'')^{spin:\textbf{0}}_{colour:\bar{\textbf{3}}}>$, and spin $\frac{1}{2}$, color triplet, builded as $|(cq\bar{q})_{colour:\textbf{3}}^{spin:\mathbf {\frac{1}{2}}}>$ triquark respectively, playing the key role. The lowest-lying pentaquark states $\{cq\bar{q}\}-\{q'q''\}$, whose orbital angular momentum $L=0$ and parity $J^P=\frac{1}{2}^-$, accordingly are divided into two non-singlet color clusters, which combining through the color-triplet binding mechanism [40]. To investigate the mass splitting of singly charm pentaquark, we adopt the effective Hamiltonian approach, which apart from the constituent quark and diquark masses, including dominant spin-spin and spin-orbit interactions [41].

Note that the light quark symmetry have been successfully adopted in generic hadronic system [42,43,44,45,46,47,48,49,50,51,52,53,54,55,56], which provides a general insight for the decays and productions of hadron, then to be an useful approach to discuss the pentaquark production from B meson. The study is based on the representations of pentaquark, final hadrons and weak transition operator. After constructing the corresponding production Hamiltonian, naturally expanding into transition matrix element, production channels can be attained. A large branching ratios and relatively clear final products wound be better for the choosing golden production channels. We prefer the production channels, which are expected to be observed in b-factory.

The paper is organized as follows. In Sect. 2, we present the discussion of the mass splitting of the charm pentaquark, including the discussion of S-wave and P-wave pentaquark. In Sect. 3, we analysis the production of the pentaquark states from B meson decays. Some further comments are proposed in Sect. 4.

2 The mass splitting of the charm pentaquark states

The dynamics of pentaquark depends upon how the five constituents are structured. It is believed that the pentaquark can be the loosely-bound hadronic-molecule [36, 37, 57,58,59,60,61,62,63,64] or the compact state [7,8,9, 41, 65]. For the compact one, color interaction receives more attention, and it is easily to form a stable bound state. The intuitive picture in which the heavier components form a color nucleus and the lighter color one is in the orbit around the nucleus, since it is energetically easier to excite the light degrees of freedom. We keep the lightest diquark $q'q''$ in the orbit for pentaquark, with the heavier color components $c\bar{q}q$, combined by the color-triplet binding mechanism [40], acting as the static color nucleus. Then the color and flavor structure of the pentaquark in the approach can be written as $[((cq)_{c\bar{\textbf{3}}}(\bar{q})_{c\bar{\textbf{3}}})_{c\textbf{3}}(q'q'')_{c\bar{\textbf{3}}}]$. Such a description is closer to the anti-charm baryons $[({\bar{c}} \bar{q})_{c\textbf{3}} \bar{q}_{c\bar{\textbf{3}}}]$, in which the charm quark is at the center. There is also the possibility to describe the internal structure of the pentaquark in which the light and heavy diquarks bind first into a tetraquark, then interacting with the light anti-quark, $[[(cq)_{c\bar{\textbf{3}}}(q'q'')_{c\bar{\textbf{3}}}]\bar{q}_{c\bar{\textbf{3}}}]$. The two internal structures provides a realistic template for the bound charm pentaquarks remains to be seen in further. In the work, we adopt the more intuitive former description with triquark-diquark system to study the mass spectrum of S-wave and P-wave pentaquark states ${c\bar{q}qqq}(q=u,d,s)$.

2.1 S-wave Pentaquark

In the triquark-diquark system, the singly charm pentaquark $[((cq)_{c\bar{\textbf{3}}}(\bar{q})_{c\bar{\textbf{3}}})_{c\textbf{3}}(q'q'')_{c\bar{\textbf{3}}}]$ include one color-triplet triquark with heavy diquark cq and light anti-quark $\bar{q}$, and one color anti-triplet diquark $q'q''$. The spin of triquark can be $S_t=1/2,3/2$, considering the spin of heavy diquark $S_{cq}=0,1$ and light anti-quark $S_{\bar{q}}=1/2$. More over, the spin of light diquark can be $S_{q'q''}=0$ (“good” diquark) and $S_{q'q''}=1$ (“bad” diquark) [66]. Generally, the structure of pentaquark can then be signed as $|S_{cq},S_t,L_t; S_{q'q''},L_{q'q''};S,L\rangle$. Following the effective Hamiltonian approach [41], the mass Hamiltonian of S-wave state ($L_t = 0,L_{q'q''}=L=0$), which based on the spin-spin interaction in diquark and different diquarks, can be written as

$$\begin{aligned} {H^{(L = 0)}}= & {} H_{t}+H_{ld},\nonumber \\ H_{t}= & {} m_{\bar{q}}+m_{hd}+2 (\mathcal {K}_{cq})_{{\bar{3}}} (S_c\cdot S_q)+2 (\mathcal {K}_{c\bar{q}})(S_c\cdot S_{\bar{q}})\nonumber \\{} & {} +2(\mathcal {K}_{q\bar{q}})(S_q\cdot S_{\bar{q}})),\nonumber \\ H_{ld}= & {} m_{ld}+2(\mathcal {K}_{qq'})_{{\bar{3}}} (S_{q}\cdot S_{q'})+2(\mathcal {K}_{cq'})_{{\bar{3}}}(S_c\cdot S_q')\nonumber \\{} & {} +2(\mathcal {K}_{qq''})_{{\bar{3}}}(S_q\cdot S_{q''})\nonumber \\{} & {} +2(\mathcal {K}_{cq''})_{{\bar{3}}}(S_c\cdot S_{q''})+2(\mathcal {K}_{qq'})_{{\bar{3}}}(S_q\cdot S_{q'})\nonumber \\{} & {} +2(\mathcal {K}_{q'\bar{q}})(S_q'\cdot S_{\bar{q}})+2(\mathcal {K}_{q''\bar{q}})(S_{q''}\cdot S_{\bar{q}}). \end{aligned}$$

(1)

Table 1 The values of the spin-spin couplings and the masses of quarks and diquarks [41, 67]. For the P-wave pentaquark, the strengths of the triquark spin-orbit $A_t$, light diquark spin-orbit $A_{ld}$ and orbital momentum couplings $B_L$ are extracted from $P_c(4457)^+$, $P_c(4440)^+$ and $P_c(4312)^+$ [41]

Here, $H_{t}$ describes the triquark picture, where $m_{\bar{q}}$ and $m_{hd}$ are the constituent masses of the anti-quark and singly charm diquark, respectively. In addition, $H_{t}$ reveals the spin-spin interactions of charm and light quarks in charm diquark, and the interactions between charm diquark and antiquark. The $H_{ld}$ Hamiltonian show the interaction in light diquark, the interaction between triquark and light diquark. In view of Ansatz on spin-spin couplings, the contribution to mass spectrum comes from spin-spin interaction of charm quark and one light quark cq, and two light quarks interaction $qq'$ for the diquark picture. It should be noted that we discuss the separation of light diquark by the good or bad spin case. Thus the contribution from light diquark are suppressed, then the cq interaction inside the diquark is assumed to be the dominant [41]. While the couplings between different diquarks, $c\bar{q}$ and $q\bar{q}$, the $q\bar{q}$ with more possible interaction terms, hence $\mathcal {K}_{q\bar{q}}$ turn out to be dominated for the coupling between different diquarks.

The S-wave pentaquark $|S_{cq},S_t,L_t=0; S_{q'q''}=0,L_{q'q''}=0;S,L=0\rangle$ with parity $J^P=\frac{1}{2}^-$ and $J^P=\frac{3}{2}^-$, under the good diquark scheme $S_{q'q''}=0$, sandwiching the effective mass Hamiltonian Eq. (1), then yield the mass spectrum matrix.

$$\begin{aligned}{} & {} \mathcal {M}^{S_{t}=1/2,S_{q'q''}=0}_{J=1/2} =m_{cq}+m_{\bar{q}}+m_{q'q''}+ \left( \begin{array}{cc} -\frac{3}{2}(\mathcal {K}_{cq})_{{\bar{3}}}-\frac{3}{2}(\mathcal {K}_{q'q''})_{{\bar{3}}}+\frac{3}{8} \mathcal {K}_{q\bar{q}}&{}\frac{1}{2}\sqrt{3}\mathcal {K}_{c\bar{q}}+\frac{1}{8}\sqrt{3}\mathcal {K}_{q\bar{q}}\\ \frac{1}{2}\sqrt{3}\mathcal {K}_{c\bar{q}}+\frac{1}{8}\sqrt{3}\mathcal {K}_{q\bar{q}}&{} \frac{1}{2}(\mathcal {K}_{cq})_{{\bar{3}}}-\frac{3}{2}(\mathcal {K}_{q'q''})_{{\bar{3}}}-\mathcal {K}_{c\bar{q}}+\frac{1}{8}\mathcal {K}_{q\bar{q}}\end{array}\right) ,\nonumber \\{} & {} \mathcal {M}^{S_{t}=3/2,S_{q'q''}=0}_{J=3/2}= m_{cq}+m_{\bar{q}}+m_{q'q''}+\frac{(\mathcal {K}_{cq})_{{\bar{3}}}}{2} -\frac{3(\mathcal {K}_{q'q''})_{{\bar{3}}}}{2}+\frac{\mathcal {K}_{c\bar{q}}}{2}+\frac{\mathcal {K}_{q\bar{q}}}{2}. \end{aligned}$$

(2)

In particular, we carefully count the spin-spin coupling or recoupling for the triquark-diquark picture, such as the spin-spin interaction inside the triquark, $S_c\cdot S_{\bar{q}}$ and $S_q\cdot S_{\bar{q}}$, can be recoupled from the wigner 6j-symbols. The interaction between triquark and light diquark, $S_{\bar{q}}\cdot S_{q'}$ and $S_{\bar{q}}\cdot S_{q''}$, can be described by the wigner 9j-symbols.

For the S-wave pentaquark with “bad” light diquark ($S_{q'q''} = 1$) scheme, the total spin is the sum of the triquark and the light diquark spins $S=S_t+S_{q'q''}$, the triquark spin $S_t$ can be 1/2 (heavy diquark $S_{cq}=0,1$, light anti-quark $S_{\bar{q}}=1/2$) and 3/2 ($S_{cq}=1$, $S_{\bar{q}}=1/2$), then it is possible to combine the pentaquark to form three states with spin 1/2, three states with spin 3/2 and one spin-5/2 state. The parity of the states depends on the orbital angular momentum as $P=(-1)^{L+1}$. It is negative for S-wave states and positive for the P-wave states. Thus the states can be different spin parities with $J^P = 1/2^-,3/2^-,5/2^-$, in which the $1/2^-$ states include three possibilities, mixed from $(3\times 3)$ mass matrix. Similarly, the three $3/2^-$ states are given by the recombined $(3\times 3)$ mass matrix. There in only one $5/2^-$ state without mixed matrix. The mass matrix forms can be found in Appendix B.

We diagonalize the mass matrices and obtain the mass splittings of the S-wave pentaquark ${c\bar{q}qqq}$ shown in Table 2. The spin-spin couplings and the masses of quark and diquark are listed in Table 1. We take $10\%$ as the error in this work, when considering the uncertainties from these couplings. The results from chromomagnetic interaction (CMI) [31] model, the Quark Delocalization Color Screening Model (QDCSM) [68, 69], QCD sum rules (QCDSR) [32,33,34,35], the Effective Lagrangian (EFL) method [36, 37, 60], the constituent quark model (CQM) [70, 71], the chiral quark model ($\chi$QM) [72,73,74] and the light-meson exchange (LME) [75] can be used as the comparative reference, shown in Table 8. Although there is no completely consistent result for each other, we can still find similar conclusions. Our study is similar with the calculation from QDCSM and EFL for $c{\bar{n}} nnn$, $c{\bar{n}} ssn$ $1/2^-$ states, but is different from the results of CMI. The values of $1/2^-$ $c{\bar{s}}snn$, $c{\bar{s}}ssn$ and $c{\bar{s}} nnn$ are near the results of LME, while the EFL and $\chi$QM are close to our considerations for all $c{\bar{n}} snn$ states.

• In our considering, both components $c{\bar{n}}nnn,~c\bar{s}ssn, c{\bar{n}}ssn$ and $c{\bar{n}}snn$ are sightly higher than their strong thresholds $\Lambda _c \pi ,~\Xi _{c}\eta ,~\Omega _{c}\pi$ and $\Xi _{c}\pi$ respectively. Further more, the masses of the components $c{\bar{s}} nnn$ and $c{\bar{s}} snn$ are close to the strong thresholds $\Lambda _c K$ and $~\Xi _{c}K$.

• It is interesting that the ground pentaquarks with constituents $c{\bar{s}} uud, c {\bar{s}} udd$ with parity $\frac{1}{2}^-$ are near their strong decay thresholds $\Lambda _c K$s, respectively below that about 53 MeV and 54 MeV. We notice the larger error with 57 MeV, it appears that the stability remains an open question.

• The component $c{\bar{n}}nnn$ in our work is higher than the strong threshold $\Lambda _c \pi$ about 236 MeV, while CMI show a different result, which is near that about several MeV, expected to be verified in future experiments (Tables 2, 3).

As a comparison, we calculate the mass spectrum of the pentaquark within tetraquark-antiquark picture shown in Appendix C. The results show that the masses in this case are larger than the triquark-diquark one for the S-wave states, the differences mainly come from the spin-spin interaction between different diquarks, of which center value between the two case are up to 200 MeV. We expect future experiments to verify the structure.

Table 2 The mass splitting of the S-wave singly charm pentaquark state $|S_{cq},S_t,L_t; S_{q'q''},L_{q'q''};S,L\rangle$ (with S-wave triquark spin $S_t=1/2,3/2$ and orbital momentum $L_{t} =0$, light diquark spin $S_{q'q''}=0,1$ and total orbital angular momentum $L_{ld}=L=0$) coming from the hyperfine structures of triquark $|((cq)_{colour:\bar{\textbf{3}}}^{spin:\textbf{0}}\bar{q}_{colour:\bar{\textbf{3}}}^{spin:\mathbf {1/2}})_{colour:\textbf{3}}^{spin:\mathbf {1/2}}\rangle$, $|((cq)_{colour:\bar{\textbf{3}}}^{spin:\textbf{1}}\bar{q}_{colour:\bar{\textbf{3}}}^{spin:\mathbf {1/2}})_{colour:\textbf{3}}^{spin:\mathbf {1/2}}\rangle$, $|((cq)_{colour:\bar{\textbf{3}}}^{spin\textbf{1}}\bar{q}_{colour:\bar{\textbf{3}}}^{spin:\mathbf {1/2}})_{colour:\textbf{3}}^{spin:\mathbf {3/2}}\rangle$ and the light diquark $|(q'q'')_{colour:\textbf{3}}^{spin:\textbf{0,1}}\rangle$, whose total parities are $J^P=\frac{1}{2}^-, \frac{3}{2}^-$ and $\frac{5}{2}^-$ respectively, where the superscript represents spin of diquark or triquark and subscript shows color multiplet. n represents the light quark u, d

Table 3 The mass spectrum comparisons of S-wave charm pentaquark with the chromomagnetic interaction (CMI) [31] model, the Quark Delocalization Color Screening Model (QDCSM), the Effective Lagrangian (EFL) method, the constituent quark model (CQM), the chiral quark model ($\chi$QM) and the light-meson exchange (LME) [75]

Fig. 1

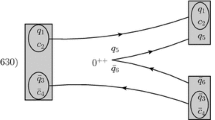
The typical topology diagrams for the production of charm pentaquark $P_{c\bar{q}qqq}$ from the bottom meson. The production depends on the weak decay of b quark, which leads to different topologies (a,b,c) including charm pentaquark, and light anti-baryon or anti-charm anti-baryon in final states

2.2 P-wave pentaquark

The effective Hamiltonian of mass spectrum for the orbitally-excited P-wave pentaquark can be written as,

$$\begin{aligned} H = H^{(L = 0)} + 2 A_t \left( \textbf{S}_t \cdot \textbf{L} \right) + 2 A_{ld} \left( \textbf{S}_{ld} \cdot \textbf{L} \right) + \frac{1}{2} \, B_L \, \textbf{L}^2 , \end{aligned}$$

(3)

the first term $H^{(L=0)}$ is the spin-spin interactions which is consistent with the description of S-wave one. $\textbf{S}_t\cdot \textbf{L}$ and $\textbf{S}_{q'q''}\cdot \textbf{L}$ mean the interactions between triquark, light diquark and orbital angular momentum, in addition, $\textbf{L}^2$ is the coupling of orbital angular momentum, the quantities $A_t$, $A_{ld}$ and $B_L$ respectively denote the strengths of the triquark spin-orbit, light diquark spin-orbit and orbital momentum couplings. It should be mentioned that the additional contribution from the interaction among the heavy triquark and light diquark is small, can thus be safely omitted [76] in the work.

The P-wave state $|S_{cq},S_t,L_t=0; S_{q'q''}=0,L_{q'q''}=1;S,L=1\rangle$ with good diquark $S_{q'q''}=0$ scheme can take the parity $J^P=\frac{1}{2}^+, \frac{3}{2}^+, \frac{5}{2}^+$. Particularly, the spin-orbit coupling from triquark $S_{t}=1/2$ and orbital momentum $L=1$ triggers two states with parity $1/2^+$ and two states with parity $3/2^+$. While the spin-orbit coupling from triquark $S_{t}=3/2$ and orbital momentum $L=1$ can lead to three unmixed states with $J^P=1/2^+$, $3/2^+$ and $5/2^+$,

$$\begin{aligned}{} & {} \mathcal {M}^{S_{t}=1/2,S_{q'q''}=0}_{J=1/2,3/2}= m_{cq}+m_{\bar{q}}+m_{q'q''} \nonumber \\{} & {} \quad + \left\{ \begin{array}{cc} \left( \begin{array}{cc} \frac{3(\mathcal {K}_{q\bar{q}})}{8}-\frac{3(\mathcal {K}_{cq})_{{\bar{3}}}}{2}-\frac{3(\mathcal {K}_{q'q''})_{{\bar{3}}}}{2}+B_L-2A_{t}&{}\frac{\sqrt{3}\mathcal {K}_{c\bar{q}}}{2}+\frac{\sqrt{3}\mathcal {K}_{q\bar{q}}}{8}\\ \frac{\sqrt{3}\mathcal {K}_{c\bar{q}}}{2}+\frac{\sqrt{3}\mathcal {K}_{q\bar{q}}}{8} &{}\quad \frac{(\mathcal {K}_{cq})_{{\bar{3}}}}{2}-\frac{3(\mathcal {K}_{q'q''})_{{\bar{3}}}}{2}-\mathcal {K}_{c\bar{q}}-\frac{\mathcal {K}_{q\bar{q}}}{8}+B_L-2A_{t}\end{array}\right) _{J=\frac{1}{2}}, \\ \left( \begin{array}{cc}\frac{3(\mathcal {K}_{q\bar{q}})}{8}-\frac{3(\mathcal {K}_{cq})_{{\bar{3}}}}{2}-\frac{3(\mathcal {K}_{q'q''})_{{\bar{3}}}}{2}+B_L+A_{t}&{}\frac{\sqrt{3}\mathcal {K}_{c\bar{q}}}{2}+\frac{\sqrt{3}\mathcal {K}_{q\bar{q}}}{8}\\ \frac{\sqrt{3}\mathcal {K}_{c\bar{q}}}{2}+\frac{\sqrt{3}\mathcal {K}_{q\bar{q}}}{8} &{}\quad \frac{(\mathcal {K}_{cq})_{{\bar{3}}}}{2}-\frac{3(\mathcal {K}_{q'q''})_{{\bar{3}}}}{2}-\mathcal {K}_{c\bar{q}}-\frac{\mathcal {K}_{q\bar{q}}}{8}+B_L+A_{t}\end{array}\right) _{J=\frac{3}{2}}. \end{array}\right. \nonumber \\{} & {} \mathcal {M}^{S_{t}=3/2,S_{q'q''}=0}_{J=1/2,3/2,5/2}= m_{cq}+m_{\bar{q}}+m_{q'q''} +\frac{(\mathcal {K}_{cq})_{{\bar{3}}}}{2}-\frac{3(\mathcal {K}_{q'q''})_{{\bar{3}}}}{2}+\frac{\mathcal {K}_{c\bar{q}}}{2}+\frac{\mathcal {K}_{q\bar{q}}}{2}+ \left\{ \begin{array}{cc} (-5A_{t}+B_L)_{J=\frac{1}{2}},\\ (-2A_{t}+B_L)_{J=\frac{3}{2}}, \\ (3A_{t}+B_L)_{J=\frac{5}{2}}.\\ \end{array} \right. \end{aligned}$$

(4)

The combining parameters $C=-2A_{t}+B_L,\ D=A_{t}+B_L$. The mass spectrums of P-wave states with the “bad” light diquark ($S_{ld} = 1$) scheme include six $1/2^+$ states mixed by one $(4 \times 4)$ mass matrix and a $(2 \times 2)$ mass matrix, seven $3/2^+$ states combined with one $(4 \times 4)$ mass matrix and a $(3\times 3)$ mass matrix, four $5/2^+$ states mixed by two $(2 \times 2)$ mass matrices and a $7/2^+$ state. We show the mass matrices forms in Appendix B. Finally, the mass spectrums of P-wave pentaquark are collected into Table 4.

Table 4 The mass splitting of the P-wave singly charm pentaquark $|S_{cq},S_t,L_t; S_{q'q''},L_{q'q''};S,L\rangle$ (with the orbital angular momentum $L_t=0$, $L_{ld}=L=1$) coming from triquark $|((cq)_{colour:\bar{\textbf{3}}}^{spin:\textbf{0}}\bar{q}_{colour:\bar{\textbf{3}}}^{spin:\mathbf {1/2}})_{colour:\textbf{3}}^{spin:\mathbf {1/2}}\rangle$, $|((cq)_{colour:\bar{\textbf{3}}}^{spin:\textbf{1}}\bar{q}_{colour:\bar{\textbf{3}}}^{spin:\mathbf {1/2}})_{colour:\textbf{3}}^{spin:\mathbf {1/2}}\rangle$, $|((cq)_{colour:\bar{\textbf{3}}}^{spin:\textbf{1}}\bar{q}_{colour:\bar{\textbf{3}}}^{spin:\mathbf {1/2}})_{colour:\textbf{3}}^{spin:\mathbf {3/2}}\rangle$ and the light diquark $|(q'q'')_{colour:\textbf{3}}^{spin:\textbf{0,1}}\rangle$, whose total parities are $J^P=\frac{1}{2}^+, \frac{3}{2}^+, \frac{5}{2}^+$ and $\frac{7}{2}^+$ respectively, the superscript represents spin of diquark or triquark and subscript is the color index. n represents the light quark u, d

3 Productions from B mesons

Table 5 The possible representations of pentaquark $c \bar{q} qqq(q=u,d,s)$ with states 6, 15 and 24. Let S, F and T be the names of the states respectively. Meanwhile, we give the tensor representations $S_{6}/F_{15}/T_{24}$, electric charge in superscript of the corresponding states. Some Symbols such as $S_{(\bar{q} q)ds}^0$, $F_{(\bar{q} q)us}^+$ are the abbreviation for $S_{({\bar{u}} u,{\bar{d}} d,{\bar{s}} s)ds}^0$, $F_{({\bar{u}} u,{\bar{d}} d,{\bar{s}} s)us}^+$, where q represents light flavor quark. The states marked by bold in 15 are likely to be stable ones

3.1 Representations of charm pentaquark

Light quarks satisfy the SU(3) flavor symmetry, and behave well at the level of hadrons. We can use group representations to describe the hadrons, in consideration of individual spin or orbital quantum number. We can transform the singly charm pentaquark $c \bar{q} qqq$ under the SU(3) symmetry,

$$\begin{aligned} 3 \otimes 3 \otimes 3 \otimes \bar{3}=\bar{3}\oplus \bar{3} \oplus 6 \oplus 15 \oplus {6} \oplus \bar{3} \oplus 6 \oplus 15 \oplus 24.\nonumber \\ \end{aligned}$$

(5)

After group decomposition above, we get the irreducible representations of new combination states 6, 15 and 24. By tensor reduction, the irreducible representations of singly heavy pentaquark can be expressed as different tensor forms that labeled with $T_i^{jkl}$,

$$\begin{aligned} T_i^{jkl}= & {} (\overline{F}_{15})_{\{i \alpha \}}^{l} (A_1)^{\alpha jk} +(\overline{F}_{15})_{\{i \alpha \}}^{\beta } (A_2)_{i \alpha \beta \gamma }^{i k \alpha \gamma l} \nonumber \\{} & {} +(\widetilde{S}_{6})^{\{l \beta \}} (B_1)_{i \alpha \beta }^{ \alpha jk} +(\widetilde{S}_{6})^{\{mn\}} (B_2)_{i \alpha \beta m n}^{ \alpha \beta ijk}\nonumber \\{} & {} +(\hat{T}_{ \bar{3}})_{m} (C_1)_{i \alpha \beta }^{ \alpha \beta jklm} +(\hat{T}_{ \bar{3}})_{\alpha } (C_2)_{i \gamma }^{ \alpha \gamma jkl} \nonumber \\{} & {} +(\hat{T}_{ \bar{3}})_{\alpha } (C_3)_{i }^{ \alpha jkl} +({T}_{24})_{i}^{\{ jkl \} } (D_1), \end{aligned}$$

(6)

and the coefficients of irreducible representations can be taken as follows,

$$\begin{aligned} (A_1)^{\alpha jk}= & {} \frac{1}{2}\varepsilon ^{\alpha jk},\ (A_2)_{i \alpha \beta \gamma }^{i k \alpha \gamma l}=\frac{1}{3}(\delta _{\beta }^i \delta _{\gamma }^k+\delta _{\beta }^k \delta _{\gamma }^i) \varepsilon ^{\alpha \gamma l},\\ (B_1)_{i \alpha \beta }^{ \alpha jk}= & {} \frac{1}{4} \varepsilon ^{\alpha jk} \varepsilon _{i \alpha \beta },\ (B_2)_{i \alpha \beta m n}^{ \alpha \beta ijk}=\frac{1}{6}\varepsilon _{i \alpha n}\varepsilon ^{\alpha \beta l (\delta _{\beta }^k \delta _{m}^i+\delta _{\beta }^j \delta _{m}^j)},\\ (C_1)_{i \alpha \beta }^{ \alpha \beta jklm}= & {} \frac{1}{8}\varepsilon ^{\alpha jk} \varepsilon _{i\alpha \beta } \varepsilon ^{ml \beta },\ (C_2)_{i \gamma }^{ \alpha \gamma jkl}\\= & {} -\frac{1}{18}(\delta _{i}^j \delta _{r}^k+\delta _i^k \delta _{\gamma }^j) \varepsilon ^{\alpha \gamma l},\\ (C_3)_{i }^{ \alpha jkl}= & {} \frac{1}{36}\Big ( 6\delta _i^{\alpha } \varepsilon ^{jkl}- \delta _{i}^j\varepsilon ^{\alpha kl}-\delta _{i}^k\varepsilon ^{\alpha jl} \Big ),\ (D_1)=\frac{1}{3}. \end{aligned}$$

The new combination states 6, 15 and 24 can be expressed as irreducible representations ${S}_{6}$, ${F}_{15}$ and $T_{24}$. Here the anti-symmetry index can be identified as [ij], and the symmetry indexes can be signed with $\{ij\}$. The coefficients consist of tensor $\delta$ and antisymmetric tensor $\varepsilon$. We can get the quark components of the states in flavor space by expanding the tensor representations which have been deduced above, and the nonzero components are listed in Table 5. We also give the weight graphs of states 6, 15 and 24 in Fig. 2, whose flavor structures given in Appendix A. The six states $F_{\bar{u}dds}^{-}$, $F_{\bar{u}dss}^-$, $F_{\bar{d}uus}^{++}$, $F_{\bar{d}uss}^+$, $F_{\bar{s}uud}^{++}$ and $F_{\bar{s}udd}^{+}$ in the 15 state, with charge Q in superscript, do not contain ${q\bar{q}}$ pair, so these six states are relatively stable [30] and wound be the concerned states in the work.

$$\begin{aligned} F_{\bar{u}dds}^{-}= & {} c\bar{u}\text {dsd}-c\bar{u}\text {sdd},\quad F_{\bar{u}dss}^- = c\bar{u}\text {dss}-c\bar{u}\text {sds},\quad \\ F_{\bar{d}uus}^{++}= & {} c\bar{d}\text {suu}-c\bar{d}\text {usu},\\ F_{\bar{d}uss}^+= & {} c\bar{d}\text {sus}-c\bar{d}\text {uss},\quad F_{\bar{s}uud}^{++} = c\bar{s}\text {udu}-c\bar{s}\text {duu},\quad \\ F_{\bar{s}udd}^{+}= & {} c\bar{s}\text {udd}-c\bar{s}\text {dud}. \end{aligned}$$

The masses of $F_{\bar{u}dds}^{-}$, $F_{\bar{d}uus}^{++}$, $F_{\bar{u}dss}^-$ and $F_{\bar{d}uss}^+$ are found respectively as 2.764 GeV, 2.764 GeV, 3.064 GeV and 3.064 GeV from Table 2. Obviously they are higher than their corresponding strong thresholds $\Xi _{c}^0\pi ^-$, $\Xi _{c}^+\pi ^+$, $\Omega _{c}^{0}\pi ^-$ and $\Omega _{c}^{0}\pi ^+$ with 157 MeV, 157 MeV, 229 MeV and 229 MeV. While the masses of $F_{\bar{s}uud}^{++}$ and $F_{\bar{s}udd}^{+}$ are both 2.833 GeV, nearing their strong thresholds $\Lambda _{c}^+K^+$ and $\Lambda _{c}^+K^0$ about 53 MeVs, indicating that they may be stable pentaquark states. However the sizeable value of the inaccurate coming from the spin-spin coupling $\mathcal {K}$ coefficients and the mass of diquark $m_{cq}$, are large enough to change the decay behaviour of the states. Accordingly the stability of the states $F_{\bar{s}uud}^{++}$ and $F_{\bar{s}udd}^{+}$ remains to be an open question. Nevertheless, the $F_{\bar{u}dds}^{-}$, $F_{\bar{d}uus}^{++}$, $F_{\bar{u}dss}^-$ and $F_{\bar{d}uss}^+$ with less controversial in our work, should be strongly decay, which expected to recognized in future experiments.

Fig. 2

The weight diagrams (a–c) show the 6, 15, 24 multiple states of singly charm pentaquark, signed as $S_6, F_{15}, T_{24}(q=u,d,s)$, with electric charge in superscript

3.2 The production by SU(3) analysis

According to the analysis of SU(3) light quark flavor symmetry, we will discuss the possible production of pentaquark states $c\bar{q}qqq$ in this subsection (Table 6). It can be realized by weak decay of B meson. The weak decay can be classified into two groups by the quantities of CKM matrix elements,

$$\begin{aligned} b\rightarrow c{\bar{c}}s/c{\bar{u}}d, \;\;\; b\rightarrow c {\bar{c}} d/c{\bar{u}} s, \end{aligned}$$

which are Cabibbo allowed, and singly Cabibbo suppressed transitions respectively. The transition $b \rightarrow c \bar{q} q$ can be decomposed as $\textbf{3}\otimes {\bar{\textbf{3}}}=\textbf{1}\oplus \textbf{8}$, while the operator of transition $b \rightarrow c {\bar{c}} q$ is flavor triplet $\textbf{3}$. Here we offer the nonzero SU(3) tensor components of Cabibbo allowed transition given as consistently. The operator of the transition $b\rightarrow c{\bar{c}}d/s$ form an triplet, with $(H_{3})^2=V_{cd}^*,~(H_{3})^3=V_{cs}^*$. And the operator of the transition $b\rightarrow c {\bar{u}} d/s$ can form an octet 8, whose nonzero composition followed as $(H_{8})_{1}^2=V_{ud}^*,~(H_{8})_{1}^3=V_{us}^*$.

The B meson, including one light quark, then form one triplet ${\overline{B}}^i=\big (\begin{array}{ccc}B^-,&{\overline{B}}^0,&{\overline{B}}^0_s \end{array} \big )$. Light anti-baryon $\mathcal {P}$ can be decomposed into an octet and an anti-decuplet in the SU(3) symmetry [50, 67], we show the octet written as

$$\begin{aligned} \mathcal {P}_8= \left( \begin{array}{ccc} \frac{1}{\sqrt{2}}{\overline{\Sigma }}^0+\frac{1}{\sqrt{6}} {\overline{\Lambda }}^0 &{} {\overline{\Sigma }}^- &{} {\overline{\Xi }}^- \\ {\overline{\Sigma }}^+ &{} -\frac{1}{\sqrt{2}} {\overline{\Sigma }}^0+\frac{1}{\sqrt{6}}{\overline{\Lambda }}^0 &{} {\overline{\Xi }}^0 \\ {\overline{p}} &{} {\overline{n}} &{} -\sqrt{\frac{2}{3}}{\overline{\Lambda }}^0 \end{array} \right) . \end{aligned}$$

(7)

The singly anti-charm anti-baryons $\mathcal {P}_c$ can be decomposed into triple and anti-sextet, respectively given as

$$\begin{aligned} \mathcal {P}_{c3}= & {} \left( \begin{array}{ccc} 0 &{} \overline{\Lambda }_{{\bar{c}}}^- &{} {\overline{\Xi }}_{{\bar{c}}}^- \\ -\overline{\Lambda }_{{\bar{c}}}^- &{} 0 &{} {\overline{\Xi }}_{{\bar{c}}}^0\\ \ -\overline{\Xi }_{{\bar{c}}}^- &{} -{\overline{\Xi }}_{{\bar{c}}}^0&{} 0 \end{array} \right) ,\quad \nonumber \\ \mathcal {P}_{c{\bar{6}}}= & {} \left( \begin{array}{ccc}{\overline{\Sigma }}_{\bar{c}}^{{-}{-}} &{} \frac{1}{\sqrt{2}}{\overline{\Sigma }}_{{\bar{c}}}^{-} &{} \frac{1}{\sqrt{2}} {\overline{\Xi }}_{{\bar{c}}}^{\prime -} \\ \frac{1}{\sqrt{2}}{\overline{\Sigma }}_{{\bar{c}}}^- &{} \overline{\Sigma }_{{\bar{c}}}^0 &{} \frac{1}{\sqrt{2}} {\overline{\Xi }}_{\bar{c}}^{\prime 0}\\ \ \ \frac{1}{\sqrt{2}}{\overline{\Xi }}_{\bar{c}}^{\prime -} &{} \frac{1}{\sqrt{2}}{\overline{\Xi }}_{{\bar{c}}}^{\prime 0}&{} {\overline{\Omega }}_{{\bar{c}}}^{0} \end{array} \right) . \end{aligned}$$

(8)

Table 6 The golden channels for the production of concerned ground pentaquark states from B mesons

Table 7 The productions of concerned pentaquark 15 state and light anti-baryons $({qqq})_{8/10}$ or anti-charm anti-baryon $(\bar{c}qq)_{3/{\bar{6}}}$ from B mesons

The possible Hamiltonian for the production of concerned pentaquark ground 15 states $F_{15}$ from one B meson, induced by the transition $b\rightarrow c \bar{c}d/s$ and $b\rightarrow c \bar{u}d/s$ in the quark level, can be written directly as,

$$\begin{aligned} {\mathcal {H}}_{15}= & {} a_{1}{B}_{i}(H_{3})^{j}({\overline{F}}_{15})_{j}^{\{ik\}}(\overline{\mathcal {P}}_{c3})_{k}\nonumber \\{} & {} +b_{1}{B}_{i}(H_{3})^{k}({\overline{F}}_{15})_{j}^{\{i\alpha \}}(\overline{\mathcal {P}}_{c\bar{6}})^{\{jl\}}\ \varepsilon _{\alpha kl}\nonumber \\{} & {} +c_{1}{B}_{i}(H_{8})_{j}^{i}(\overline{F}_{15})_{k}^{\{jl\}}(\overline{\mathcal {P}}_{8})_{l}^{k}\ \nonumber \\{} & {} + c_{2}{B}_{i}(H_{8})_{j}^{k}(\overline{F}_{15})_{k}^{\{il\}}(\overline{\mathcal {P}}_{8})_{l}^{j}\nonumber \\{} & {} +c_{3}{B}_{i}(H_{8})_{j}^{k}(\overline{F}_{15})_{k}^{\{jl\}}(\overline{\mathcal {P}}_{8})_{l}^{i}\nonumber \\{} & {} +c_{4}{B}_{i}(H_{8})_{j}^{l}(\overline{F}_{15})_{k}^{\{ij\}}(\overline{\mathcal {P}}_{8})_{l}^{k}\ \nonumber \\{} & {} + d_{1}{B}_{j}(H_{8})_{k}^{i}({\overline{F}}_{15})_{l}^{\{j\alpha \}}(\overline{\mathcal {P}}_{10})^{klm}\ \varepsilon _{\alpha im}\nonumber \\{} & {} +d_{2}{B}_{k}(H_{8})_{j}^{i}({\overline{F}}_{15})_{l}^{\{j\alpha \}}(\overline{\mathcal {P}}_{10})^{klm}\ \varepsilon _{\alpha im}. \end{aligned}$$

(9)

The parameters $a_{i}$ ($b_{i}$, $c_{i}$ or $d_i$ with $i=1,2,3,\ldots$) are the non-perturbative coefficients. ${\mathcal {P}}_{c3}$ and ${\mathcal {P}}_{c{\bar{6}}}$ are the triplet and anti-sextet anti-charm anti-baryon, while ${\mathcal {P}}_{8}$ and ${\mathcal {P}}_{\overline{10}}$ are octet and decuplet light anti-baryon. The concerned pentaquark ground states are noted with ${F}_{15}$, B represents the bottom meson. In the quark level, the productions of singly charm pentaquark from B meson can be described with topological diagrams, as shown with Fig. 1. We expand the Hamiltonian and collect the possible processes of concerned pentaquark 15 states, gathering into Table 7, as well as the fully results shown in Tables 9 and 10 of Appendix.D. Meanwhile, we can reduce the relations of decay widths between different channels by simply ignoring the effect of phase space, which given as follows.

$$\begin{aligned} \Gamma (B^-\rightarrow F_{{\bar{u}}dss}^- {\overline{\Xi }}_{\bar{c}}^0)&=\Gamma ({\overline{B}}^0\rightarrow F_{{\bar{d}}uss}^+ {\bar{\Xi }}_{\bar{c}}^- ),\qquad \\ \Gamma (B^-\rightarrow F_{{\bar{u}}dds}^- {\overline{\Xi }}_{\bar{c}}^0)&=\Gamma ({\overline{B}}^0_s\rightarrow F_{{\bar{s}}udd}^+ {\bar{\Lambda }}_{\bar{c}}^-),\\ \Gamma (B^-\rightarrow F_{\bar{u}dds}^{-} {\overline{\Sigma }}_{\bar{c}}^{0})&=2\Gamma (B^-\rightarrow F_{\bar{u}dss}^- \overline{\Xi }_{\bar{c}}^{\prime 0}) \\ =\Gamma ({\overline{B}}^0\rightarrow F_{\bar{d}uus}^{++} \bar{\Sigma }_{\bar{c}}^{{-}{-}})&=2\Gamma ({\overline{B}}^0\rightarrow F_{\bar{d}uss}^+ {\bar{\Xi }}_{\bar{c}}^{\prime -}),\\ \Gamma (B^-\rightarrow F_{\bar{u}dss}^- {\overline{\Omega }}_{\bar{c}}^{0})&=2\Gamma (B^-\rightarrow F_{\bar{u}dds}^{-} \overline{\Xi }_{\bar{c}}^{\prime 0}) \\ =\Gamma ({\overline{B}}^0_s\rightarrow F_{\bar{s}uud}^{++} \bar{\Sigma }_{\bar{c}}^{{-}{-}})&=2\Gamma ({\overline{B}}^0_s\rightarrow F_{\bar{s}udd}^{+} {\bar{\Sigma }}_{\bar{c}}^{-}),\\ \Gamma ({\overline{B}}^0_s\rightarrow F_{\bar{u}dds}^{-} \overline{\Xi }^{\prime +})&=\Gamma ({\overline{B}}^0\rightarrow F_{\bar{u}dss}^- {\overline{\Xi }}^{\prime +}) \\ =\Gamma ({\overline{B}}^0\rightarrow F_{\bar{u}dds}^{-} \overline{\Sigma }^{\prime +})&=\frac{1}{3}\Gamma ({\overline{B}}^0_s\rightarrow F_{\bar{u}dss}^- {\overline{\Omega }}^+),\\ \Gamma ({\overline{B}}^0_s\rightarrow F_{\bar{u}dss}^- \overline{\Xi }^{\prime +})&=\Gamma ({\overline{B}}^0\rightarrow F_{\bar{u}dss}^- {\overline{\Sigma }}^{\prime +})\\ =\frac{1}{3}\Gamma ({\overline{B}}^0\rightarrow F_{\bar{u}dds}^{-} \overline{\Delta }^{+})&=\Gamma ({\overline{B}}^0_s\rightarrow F_{\bar{u}dds}^{-} {\overline{\Sigma }}^{\prime +}),\\ \Gamma (B^-\rightarrow F_{\bar{u}dds}^{-} {\overline{\Sigma }}^{\prime 0})&=\Gamma (B^-\rightarrow F_{\bar{u}dss}^- {\overline{\Xi }}^{\prime 0}),\\ \Gamma ({\overline{B}}^0_s\rightarrow F_{\bar{s}uud}^{++} \overline{\Delta }^{{-}{-}})&=\frac{1}{3}\Gamma ({\overline{B}}^0_s\rightarrow F_{\bar{s}udd}^{+} {\overline{\Delta }}^{-}),\\ \Gamma ({\overline{B}}^0\rightarrow F_{\bar{d}uss}^+ \overline{\Sigma }^{\prime -})&=\Gamma ({\overline{B}}^0\rightarrow F_{\bar{d}uus}^{++} {\overline{\Delta }}^{{-}{-}}), \\ \Gamma (B^-\rightarrow F_{\bar{u}dss}^- \overline{\Sigma }^{\prime 0})&=\frac{1}{2}\Gamma (B^-\rightarrow F_{\bar{u}dds}^{-} {\overline{\Delta }}^{0}),\\ \frac{\Gamma (\overline{B}^0\rightarrow F_{{\bar{u}}dss}^- \overline{\Xi }^+)}{\Gamma (\overline{B}_s^0\rightarrow F_{{\bar{u}}dds}^- \overline{\Sigma }^+)}&=\frac{\Gamma (\overline{B}_s^0\rightarrow F_{\bar{u}dds}^- \overline{\Xi }^+)}{\Gamma (\overline{B}^0\rightarrow F_{{\bar{u}}dss} \overline{\Xi }^+)}\\ =\frac{\Gamma (\overline{B}_s^0\rightarrow F_{{\bar{s}}udd}^+ {\bar{p}})}{\Gamma (\overline{B}^0\rightarrow F_{{\bar{d}} uss}^+ \overline{\Sigma }^-)}&=\frac{\Gamma (B^-\rightarrow F_{{\bar{u}}dss}^- \overline{\Xi }^0)}{\Gamma (B^-\rightarrow F_{{\bar{u}}dds}^- {\bar{n}})}\\ =\frac{\Gamma (\overline{B}^0\rightarrow F_{{\bar{u}}dds}^- \overline{\Sigma }^+)}{\Gamma (\overline{B}_s^0\rightarrow F_{{\bar{u}}dss}^- \overline{\Xi }^+)}&= \frac{\Gamma ({\overline{B}}^0_s\rightarrow F_{\bar{u}dds}^{-} {\overline{\Xi }}^{\prime +})}{\Gamma (\overline{B}^0_s\rightarrow F_{\bar{u}dss}^- \overline{\Xi }^{\prime +})}\\ =\frac{\Gamma (B^-\rightarrow F_{\bar{u}dds}^{-} \overline{\Sigma }^{\prime 0})}{\Gamma ({\overline{B}}^0\rightarrow F_{\bar{d}uss}^+ {\overline{\Sigma }}^{\prime -})}&=\frac{V_{ud}^2}{V_{us}^2},\\ \frac{\Gamma (B^-\rightarrow F_{\bar{u}dss}^- \overline{\Xi }_{\bar{c}}^0)}{\Gamma (B^-\rightarrow F_{\bar{u}dds}^{-} \overline{\Xi }_{\bar{c}}^0)}&=\frac{\Gamma (B^-\rightarrow F_{\bar{u}dds}^{-} {\overline{\Sigma }}_{\bar{c}}^{0})}{\Gamma (B^-\rightarrow F_{\bar{u}dss}^- {\overline{\Omega }}_{\bar{c}}^{0})}=\frac{V_{cs}^2}{V_{cd}^2}. \end{aligned}$$

Considering the CKM and detection efficiency, one may exclude some channels with less important contribution. We remove all channels with the hadrons $\pi ^0, n, \Sigma ^+(\rightarrow p\pi ^0), \Sigma ^-(\rightarrow n\pi ^-)$, $\Xi ^0(\rightarrow \Lambda \pi ^0)$ in the final states, but keep the processes with $\pi ^{\pm }, \Sigma ^0(\rightarrow N\pi \gamma )$, $\Xi ^-(\rightarrow \Lambda \pi ^-)$ and $\Lambda ^0(\rightarrow p\pi ^-)$. Therefor, the golden channels producing the singly charm pentaquark ground states are selected in Table 6, from which, we screen out several finest processes for the concerned pentaquark $F_{15}$,

$$\begin{aligned} {\overline{B}}^0_s\rightarrow & {} F_{\bar{s}udd}^{+} {\overline{p}}, ~\overline{B}^0\rightarrow F_{\bar{d}uus}^{++} {\overline{\Sigma }}_{\bar{c}}^{{-}{-}}, {\overline{B}}^0\rightarrow F_{\bar{u}dss}^- {\overline{\Xi }}^+, \\ B^-\rightarrow & {} F_{\bar{u}dds}^{-} {\overline{\Lambda }}^0,{\overline{B}}^0\rightarrow F_{\bar{d}uss}^+ {\overline{\Xi }}_{\bar{c}}^{\prime -},~\overline{B}^0_s\rightarrow F_{\bar{s}uud}^{++} {\overline{\Delta }}^{{-}{-}}. \end{aligned}$$

One can make a rough estimate about the branching ratios of the processes, by assuming the weak coupling constants $G_{BF\mathcal {B}}$ for the B coupling with final pentaquark and baryon [56, 77].

$$\begin{aligned} \Gamma =\frac{G_{BF\mathcal {B}}^2}{8\pi }|V_{CKM}|^2\frac{|\textbf{q}|}{m_B^2}|F(\textbf{q}^2)|^2. \end{aligned}$$

(10)

The weak couplings constants are at the order of KeV, and one monopole function is introduced to describe the inner structure effect of the interaction vertices, $F(\textbf{q}^2)= { \Lambda ^2 \over \Lambda ^2 + \textbf{q}^2}$. The parameter $\Lambda =300$ MeV, and $\textbf{q}^2$ is the anti-baryon three-momentum in the rest frame of the B meson. We find that the branching ratios can reach to the order of $10^{-7}$.

4 Conclusions

In this work, we study the mass splitting of the S-wave singly charm pentaquark state ${c\bar{q}qqq}(q=u,d,s)$ in the framework of non-relativity triquark-diquark model, in which the hyperfine structure from spin-spin and spin-orbit interaction. We find that $c{\bar{s}} uud, \ c{\bar{s}} udd$ with parity $\frac{1}{2}^-$ are below their strong decay thresholds, which imply that they are the stable states. It should be checked in future experiments.

Within the SU(3) flavor symmetry, we discuss the production of the ground pentaquark state from B meson, several golden channels are selected, in particular, the estimation of branching ratios can reach to a sizeable order of $10^{-7}$. We further intend to consider the processes with more effective means, such as the effective Lagrangian method, expecting to acquire more convincing results for the experimental detection.

Appendices

Appendix A: Tensor decomposition

We list the tensor representations of pentaquark $c \bar{q} qqq$ with 6, 15 and 24 respectively. The 6 states $S_6$ can be obtained from the decomposition of $1\otimes 6$, $8\otimes 3$ or $8\otimes 6$.

$$\begin{aligned} (S_6)_{\{11\}}&= -c\bar{d}\text {duu}+c\bar{d}\text {udu}-c\bar{s}\text {suu}+c\bar{s}\text {usu},\\ (S_6)_{\{12\}}&= \frac{1}{2} (-c\bar{d}\text {dud}+c\bar{d}\text {udd}+c\bar{s}\text {dsu}\\&\quad -c\bar{s}\text {sdu}-c\bar{s}\text {sud}+c\bar{s}\text {usd}+c\bar{u}\text {duu}-c\bar{u}\text {udu}),\\ (S_6)_{\{13\}}&= \frac{1}{2} (-c\bar{d}\text {dsu}-c\bar{d}\text {dus}+c\bar{d}\text {sdu}\\&\quad +c\bar{d}\text {uds}-c\bar{s}\text {sus}+c\bar{s}\text {uss}+c\bar{u}\text {suu}-c\bar{u}\text {usu}),\\ (S_6)_{\{22\}}&= c\bar{s}\text {dsd}-c\bar{s}\text {sdd}+c\bar{u}\text {dud}-c\bar{u}\text {udd},\\ (S_6)_{\{23\}}&= \frac{1}{2} (-c\bar{d}\text {dsd}+c\bar{d}\text {sdd}+c\bar{s}\text {dss}\\&\quad -c\bar{s}\text {sds}+c\bar{u}\text {dus}+c\bar{u}\text {sud}-c\bar{u}\text {uds}-c\bar{u}\text {usd}),\\ (S_6)_{\{33\}}&= -c\bar{d}\text {dss}+c\bar{d}\text {sds}+c\bar{u}\text {sus}-c\bar{u}\text {uss}. \end{aligned}$$

And the 15 states $T_{15}$ are decomposed from $8\otimes 3$ or $8\otimes 6$,

$$\begin{aligned} (F_{15})^{\{11\}}_1&= \frac{1}{2} (c\bar{d}\text {dsd}-c\bar{d}\text {sdd}+c\bar{s}\text {dss}-c\bar{s}\text {sds}+2 c\bar{u}\text {dsu}\\&\quad +c\bar{u}\text {dus}-2c\bar{u}\text {sdu}-c\bar{u}\text {sud}-c\bar{u}\text {uds}+c\bar{u}\text {usd}),\\ (F_{15})^{\{11\}}_2&= c\bar{u}\text {dsd}-c\bar{u}\text {sdd}, (F_{15})^{\{11\}}_3 = c\bar{u}\text {dss}-c\bar{u}\text {sds} ,\\ (F_{15})^{\{12\}}_1&= \frac{1}{4} (c\bar{d}\text {dsu}+c\bar{d}\text {dus}-c\bar{d}\text {sdu}-c\bar{d}\text {uds}+c\bar{s}\text {sus}\\&\quad -c\bar{s}\text {uss}+3 c\bar{u}\text {suu}-3 c\bar{u}\text {usu}) ,\\ (F_{15})^{\{12\}}_2&= \frac{1}{4} (3 c\bar{d}\text {dsd}-3 c\bar{d}\text {sdd}+c\bar{s}\text {dss}\\&\quad -c\bar{s}\text {sds}+c\bar{u}\text {dus}+c\bar{u}\text {sud}-c\bar{u}\text {uds}-c\bar{u}\text {usd}) ,\\ (F_{15})^{\{12\}}_3&= \frac{1}{2} (c\bar{d}\text {dss}-c\bar{d}\text {sds}+c\bar{u}\text {sus}-c\bar{u}\text {uss}) ,\\ (F_{15})^{\{13\}}_1&= \frac{1}{4} (-c\bar{d}\text {dud}+c\bar{d}\text {udd}+c\bar{s}\text {dsu}-c\bar{s}\text {sdu}\\&\quad -c\bar{s}\text {sud}+c\bar{s}\text {usd}-3 c\bar{u}\text {duu}+3 c\bar{u}\text {udu}) ,\\ (F_{15})^{\{13\}}_2&= \frac{1}{2} (c\bar{s}\text {dsd}-c\bar{s}\text {sdd}-c\bar{u}\text {dud}+c\bar{u}\text {udd}) ,\\ (F_{15})^{\{13\}}_3&= \frac{1}{4} (c\bar{d}\text {dsd}-c\bar{d}\text {sdd}+3 c\bar{s}\text {dss}-3 c\bar{s}\text {sds}\\&\quad -c\bar{u}\text {dus}-c\bar{u}\text {sud}+c\bar{u}\text {uds}+c\bar{u}\text {usd}) ,\\ (F_{15})^{\{22\}}_1&= c\bar{d}\text {suu}-c\bar{d}\text {usu} ,\\ (F_{15})^{\{22\}}_2&= \frac{1}{2} (-c\bar{d}\text {dsu}{+}c\bar{d}\text {dus}{+}c\bar{d}\text {sdu}{+}2 c\bar{d}\text {sud}{-}c\bar{d}\text {uds}\\&\quad -2 c\bar{d}\text {usd}+c\bar{s}\text {sus}-c\bar{s}\text {uss}+c\bar{u}\text {suu}-c\bar{u}\text {usu}),\\ (F_{15})^{\{22\}}_3&= c\bar{d}\text {sus}-c\bar{d}\text {uss} , (F_{15})^{\{23\}}_1 = \frac{1}{2}(-c\bar{d}\text {duu}\\&\quad +c\bar{d}\text {udu}+c\bar{s}\text {suu}-c\bar{s}\text {usu}),\\ (F_{15})^{\{23\}}_2&= \frac{1}{4} (-3 c\bar{d}\text {dud}+3 c\bar{d}\text {udd}-c\bar{s}\text {dsu}+c\bar{s}\text {sdu}\\&\quad +c\bar{s}\text {sud}-c\bar{s}\text {usd}-c\bar{u}\text {duu}+c\bar{u}\text {udu}),\\ (F_{15})^{\{23\}}_3&= \frac{1}{4} (-c\bar{d}\text {dsu}-c\bar{d}\text {dus}+c\bar{d}\text {sdu}+c\bar{d}\text {uds}\\&\quad +3 c\bar{s}\text {sus}-3 c\bar{s}\text {uss}+c\bar{u}\text {suu}-c\bar{u}\text {usu}) ,\\ (F_{15})^{\{33\}}_1&= c\bar{s}\text {udu}-c\bar{s}\text {duu}\\ ,(F_{15})^{\{33\}}_2&= c\bar{s}\text {udd}-c\bar{s}\text {dud} ,\\ (F_{15})^{\{33\}}_3&= \frac{1}{2} (-c\bar{d}\text {dud}{+}c\bar{d}\text {udd}{-}c\bar{s}\text {dsu} {-}2 c\bar{s}\text {dus}+c\bar{s}\text {sdu}\\&\quad -c\bar{s}\text {sud}{+}2 c\bar{s}\text {uds}+c\bar{s}\text {usd}-c\bar{u}\text {duu}{+}c\bar{u}\text {udu}). \end{aligned}$$

In addition, the tensor $T_{24}$ is derived from $8\otimes 6$.

$$\begin{aligned} (T_{24})_{1}^{\{111\}}&= \frac{1}{5} (-c\bar{d}\text {duu}-c\bar{d}\text {udu}-c\bar{d}\text {uud}-c\bar{s}\text {suu}\\&\quad -c\bar{s}\text {usu}-c\bar{s}\text {uus}+2 c\bar{u}\text {uuu}) ,\\ (T_{24})_{1}^{\{112\}}&= \frac{1}{15} (-2 c\bar{d}\text {ddu}-2 c\bar{d}\text {dud}-2 c\bar{d}\text {udd}-c\bar{s}\text {dsu}\\&\quad -c\bar{s}\text {dus}-c\bar{s}\text {sdu}-c\bar{s}\text {sud}-c\bar{s}\text {uds}-c\bar{s}\text {usd}\\&\quad +3 c\bar{u}\text {duu}+3 c\bar{u}\text {udu}+3 c\bar{u}\text {uud}),\\ (T_{24})_{1}^{\{113\}}&= \frac{1}{15} (-c\bar{d}\text {dsu}-c\bar{d}\text {dus}-c\bar{d}\text {sdu}-c\bar{d}\text {sud}\\&\quad -c\bar{d}\text {uds}-c\bar{d}\text {usd}-2 c\bar{s}\text {ssu}-2 c\bar{s}\text {sus}\\&\quad -2 c\bar{s}\text {uss}+3 c\bar{u}\text {suu}+3 c\bar{u}\text {usu} +3 c\bar{u}\text {uus}) ,\\ (T_{24})_{1}^{\{122\}}&= \frac{1}{15} (-3 c\bar{d}\text {ddd}-c\bar{s}\text {dds}-c\bar{s}\text {dsd}-c\bar{s}\text {sdd}\\&\quad +4 c\bar{u}\text {ddu}+4 c\bar{u}\text {dud}+4 c\bar{u}\text {udd}) ,\\ (T_{24})_{1}^{\{123\}}&= \frac{1}{15} (-c\bar{d}\text {dds}-c\bar{d}\text {dsd}{-}c\bar{d}\text {sdd}{-}c\bar{s}\text {dss}-c\bar{s}\text {sds}\\&\quad -c\bar{s}\text {ssd}{+}2 c\bar{u}\text {dsu}{+}2 c\bar{u}\text {dus}+2 c\bar{u}\text {sdu}{+}2 c\bar{u}\text {sud}\\&\quad +2 c\bar{u}\text {uds}+2 c\bar{u}\text {usd}),\\ (T_{24})_{1}^{\{133\}}&= \frac{1}{15} (-c\bar{d}\text {dss}-c\bar{d}\text {sds}-c\bar{d}\text {ssd}-3 c\bar{s}\text {sss}\\&\quad +4 c\bar{u}\text {ssu}+4 c\bar{u}\text {sus}+4 c\bar{u}\text {uss}) ,\\ (T_{24})_{1}^{\{222\}}&= c\bar{u}\text {ddd} , (T_{24})_{1}^{\{223\}} {=} \frac{1}{3} (c\bar{u}\text {dds}{+}c\bar{u}\text {dsd}{+}c\bar{u}\text {sdd}) ,\\ (T_{24})_{1}^{\{233\}}&= \frac{1}{3} (c\bar{u}\text {dss}+c\bar{u}\text {sds}+c\bar{u}\text {ssd}) , \end{aligned}$$

$$\begin{aligned} (T_{24})_{1}^{\{332\}}&= \frac{1}{3} (c\bar{u}\text {dss}+c\bar{u}\text {sds}+c\bar{u}\text {ssd}) ,\\ (T_{24})_{1}^{\{333\}}&= c\bar{u}\text {sss} ,(T_{24})_{2}^{\{111\}} = c\bar{d}\text {uuu} ,\\ (T_{24})_{2}^{\{112\}}&= \frac{1}{15} (4 c\bar{d}\text {duu}+4 c\bar{d}\text {udu}+4 c\bar{d}\text {uud}\\&\quad -c\bar{s}\text {suu}-c\bar{s}\text {usu}-c\bar{s}\text {uus}-3 c\bar{u}\text {uuu}) ,\\ (T_{24})_{2}^{\{113\}}&= \frac{1}{3} (c\bar{d}\text {suu}+c\bar{d}\text {usu}+c\bar{d}\text {uus}) ,\\ (T_{24})_{2}^{\{122\}}&= \frac{1}{15} (3 c\bar{d}\text {ddu}+3 c\bar{d}\text {dud}+3 c\bar{d}\text {udd}-c\bar{s}\text {dsu}\\&\quad -c\bar{s}\text {dus}-c\bar{s}\text {sdu}-c\bar{s}\text {sud}-c\bar{s}\text {uds}-c\bar{s}\text {usd}\\&\quad -2 c\bar{u}\text {duu}-2 c\bar{u}\text {udu}-2 c\bar{u}\text {uud}),\\ (T_{24})_{2}^{\{123\}}&= \frac{1}{15} (2 c\bar{d}\text {dsu}+2 c\bar{d}\text {dus}+2 c\bar{d}\text {sdu}+2 c\bar{d}\text {sud}\\&\quad +2 c\bar{d}\text {uds}+2 c\bar{d}\text {usd}-c\bar{s}\text {ssu}-c\bar{s}\text {sus}-c\bar{s}\text {uss}\\&\quad -c\bar{u}\text {suu}-c\bar{u}\text {usu}-c\bar{u}\text {uus}),\\ (T_{24})_{2}^{\{133\}}&= \frac{1}{3} (c\bar{d}\text {ssu}+c\bar{d}\text {sus}+c\bar{d}\text {uss}) ,\\ (T_{24})_{2}^{\{222\}}&= \frac{1}{5} (2 c\bar{d}\text {ddd}-c\bar{s}\text {dds}-c\bar{s}\text {dsd}\\&\quad -c\bar{s}\text {sdd}-c\bar{u}\text {ddu}-c\bar{u}\text {dud}-c\bar{u}\text {udd}) ,\\ (T_{24})_{2}^{\{223\}}&= \frac{1}{15} (3 c\bar{d}\text {dds}+3 c\bar{d}\text {dsd}+3 c\bar{d}\text {sdd}-2 c\bar{s}\text {dss}\\&\quad -2 c\bar{s}\text {sds}-2 c\bar{s}\text {ssd}-c\bar{u}\text {dsu}-c\bar{u}\text {dus}-c\bar{u}\text {sdu}\\&\quad -c\bar{u}\text {sud}-c\bar{u}\text {uds}-c\bar{u}\text {usd}),\\ (T_{24})_{2}^{\{233\}}&= \frac{1}{15} (4 c\bar{d}\text {dss}+4 c\bar{d}\text {sds}+4 c\bar{d}\text {ssd}-3 c\bar{s}\text {sss}\\&\quad -c\bar{u}\text {ssu}-c\bar{u}\text {sus}-c\bar{u}\text {uss}),\\ (T_{24})_{2}^{\{333\}}&= c\bar{d}\text {sss} , (T_{24})_{3}^{\{111\}} = c\bar{s}\text {uuu} ,\\ (T_{24})_{3}^{\{112\}}&= \frac{1}{3} (c\bar{s}\text {duu}+c\bar{s}\text {udu}+c\bar{s}\text {uud}) ,\\ (T_{24})_{3}^{\{113\}}&= \frac{1}{15} (-c\bar{d}\text {duu}-c\bar{d}\text {udu}-c\bar{d}\text {uud}+4 c\bar{s}\text {suu}\\&\quad +4 c\bar{s}\text {usu}+4 c\bar{s}\text {uus}-3 c\bar{u}\text {uuu}) ,\\ (T_{24})_{3}^{\{122\}}&= \frac{1}{3} (c\bar{s}\text {ddu}+c\bar{s}\text {dud}+c\bar{s}\text {udd}) ,\\ (T_{24})_{3}^{\{123\}}&= \frac{1}{15} (-c\bar{d}\text {ddu}-c\bar{d}\text {dud}-c\bar{d}\text {udd}+2 c\bar{s}\text {dsu}\\&\quad +2 c\bar{s}\text {dus}+2 c\bar{s}\text {sdu}+2 c\bar{s}\text {sud}+2 c\bar{s}\text {uds}\\&\quad +2 c\bar{s}\text {usd}-c\bar{u}\text {duu}-c\bar{u}\text {udu}-c\bar{u}\text {uud}),\\ (T_{24})_{3}^{\{133\}}&= \frac{1}{15} (-c\bar{d}\text {dsu}-c\bar{d}\text {dus}-c\bar{d}\text {sdu}-c\bar{d}\text {sud}\\&\quad -c\bar{d}\text {uds}-c\bar{d}\text {usd}+3 c\bar{s}\text {ssu}+3 c\bar{s}\text {sus}+3 c\bar{s}\text {uss}\\&\quad -2 c\bar{u}\text {suu}-2 c\bar{u}\text {usu}-2 c\bar{u}\text {uus}),\\ (T_{24})_{3}^{\{222\}}&= c\bar{s}\text {ddd} , (T_{24})_{3}^{\{223\}} = \frac{1}{15} (-3 c\bar{d}\text {ddd}+4 c\bar{s}\text {dds}\\&\quad +4 c\bar{s}\text {dsd}{+}4 c\bar{s}\text {sdd}{-}c\bar{u}\text {ddu}{-}c\bar{u}\text {dud}{-}c\bar{u}\text {udd}),\\ (T_{24})_{3}^{\{233\}}&= \frac{1}{15} (-2 c\bar{d}\text {dds}-2 c\bar{d}\text {dsd}-2 c\bar{d}\text {sdd}+3 c\bar{s}\text {dss}\\&\quad +3 c\bar{s}\text {sds}+3 c\bar{s}\text {ssd}-c\bar{u}\text {dsu}-c\bar{u}\text {dus}-c\bar{u}\text {sdu}\\&\quad -c\bar{u}\text {sud}-c\bar{u}\text {uds}-c\bar{u}\text {usd}),\\ (T_{24})_{3}^{\{333\}}&= \frac{1}{5} (-c\bar{d}\text {dss}-c\bar{d}\text {sds}-c\bar{d}\text {ssd}\\&\quad +2 c\bar{s}\text {sss}-c\bar{u}\text {ssu}-c\bar{u}\text {sus}-c\bar{u}\text {uss}). \end{aligned}$$

Appendix B: Mass matrix with bad diquark scheme for S-wave and P-wave pentaquark

The mass matrices of S-wave singly charm pentaquark under the considering of “bad” light diquark $S_{q'q''}=1$, with the total quantum numbers $J=1/2,3/2,5/2$. For simplicity, we abbreviate the symbol, such as $(\mathcal {K}_{qq'})_{{\bar{3}}}$ as $\mathcal {K}_{qq'}^{{\bar{3}}}$ here.

$$\begin{aligned}{} & {} \mathcal {M}^{S_{t}=1/2,3/2,S_{q'q''}=1}_{J=1/2} =m_{cq}+m_{\bar{q}}+m_{q'q''}\nonumber \\{} & {} \quad +\left( \begin{array}{ccc} \frac{4\mathcal {K}_{q'q''}^{{\bar{3}}}-12\mathcal {K}_{cq}^{{\bar{3}}}+3\mathcal {K}_{q\bar{q}}+\mathcal {K}_{q'\bar{q}}+\mathcal {K}_{q''\bar{q}}}{8}&{}\frac{\sqrt{3}(4\mathcal {K}_{c\bar{q}}+\mathcal {K}_{q\bar{q}})}{8} &{}\frac{2(\mathcal {K}_{qq''}^{{\bar{3}}}+\mathcal {K}_{cq'}^{{\bar{3}}}+\mathcal {K}_{qq'}^{{\bar{3}}}+\mathcal {K}_{cq''}^{{\bar{3}}})}{-5}\\ \frac{\sqrt{3}(4\mathcal {K}_{c\bar{q}}+\mathcal {K}_{q\bar{q}})}{8} &{} \frac{4(\mathcal {K}_{cq}^{{\bar{3}}}+\mathcal {K}_{q'q''}^{{\bar{3}}})+\mathcal {K}_{q\bar{q}}-8\mathcal {K}_{c\bar{q}}}{8}&{}\frac{25(\mathcal {K}_{cq}^{{\bar{3}}}+\mathcal {K}_{q'q''}^{{\bar{3}}})-6(\mathcal {K}_{q'\bar{q}}+\mathcal {K}_{q''\bar{q}})}{50}\\ \frac{2(\mathcal {K}_{qq''}^{{\bar{3}}}+\mathcal {K}_{cq'}^{{\bar{3}}}+\mathcal {K}_{qq'}^{{\bar{3}}}+\mathcal {K}_{cq''}^{{\bar{3}}})}{-5} &{}\frac{25(\mathcal {K}_{cq}^{{\bar{3}}}-\mathcal {K}_{q'q''}^{{\bar{3}}})-6(\mathcal {K}_{q'\bar{q}}+\mathcal {K}_{q''\bar{q}})}{50} &{}\frac{3(\mathcal {K}_{cq}^{{\bar{3}}}+\mathcal {K}_{q'q''}^{{\bar{3}}}+\mathcal {K}_{cq}^{{\bar{3}}}+\mathcal {K}_{q\bar{q}})+\mathcal {K}_{q'\bar{q}}+\mathcal {K}_{q''\bar{q}}}{6}\\ \end{array}\right) \nonumber \\{} & {} \quad + \left( \begin{array}{ccc}0&{}\frac{\sqrt{3}(\mathcal {K}_{qq''}^{{\bar{3}}}+\mathcal {K}_{cq'}^{{\bar{3}}}+\mathcal {K}_{qq'}^{{\bar{3}}}+\mathcal {K}_{cq''}^{{\bar{3}}})}{-3}&{}0\\ \frac{\sqrt{3}(\mathcal {K}_{qq''}^{{\bar{3}}}+\mathcal {K}_{cq'}^{{\bar{3}}}+\mathcal {K}_{qq'}^{{\bar{3}}}+\mathcal {K}_{cq''}^{{\bar{3}}})}{-3}&{}\frac{2(\mathcal {K}_{q'\bar{q}}-\mathcal {K}_{q''\bar{q}})}{5}-\frac{17(\mathcal {K}_{qq''}^{{\bar{3}}}+\mathcal {K}_{cq'}^{{\bar{3}}}+\mathcal {K}_{qq'}^{{\bar{3}}}+\mathcal {K}_{cq''}^{{\bar{3}}})}{24}&{} \frac{9(\mathcal {K}_{qq''}^{{\bar{3}}}+\mathcal {K}_{cq'}^{{\bar{3}}}+\mathcal {K}_{qq'}^{{\bar{3}}}+\mathcal {K}_{cq''}^{{\bar{3}}})}{50}\\ 0&{}\frac{9(\mathcal {K}_{qq''}^{{\bar{3}}}+\mathcal {K}_{cq'}^{{\bar{3}}}+\mathcal {K}_{qq'}^{{\bar{3}}}+\mathcal {K}_{cq''}^{{\bar{3}}})}{50}&{} \frac{11(\mathcal {K}_{qq''}^{{\bar{3}}}+\mathcal {K}_{cq'}^{{\bar{3}}}+\mathcal {K}_{qq'}^{{\bar{3}}}+\mathcal {K}_{cq''}^{{\bar{3}}})}{-6} \end{array}\right) ,\end{aligned}$$

(B1)

$$\begin{aligned}{} & {} \mathcal {M}^{S_{t}=1/2,3/2,S_{q'q''}=1}_{J=3/2} =m_{cq}+m_{\bar{q}}+m_{q'q''}\nonumber \\{} & {} \quad + \left( \begin{array}{ccc}\frac{4(\mathcal {K}_{q'q''}^{{\bar{3}}}+\mathcal {K}_{q'\bar{q}}+\mathcal {K}_{q''\bar{q}})-12\mathcal {K}_{cq}^{{\bar{3}}}+3\mathcal {K}_{q\bar{q}}}{8}&{}\frac{\sqrt{3}(4\mathcal {K}_{c\bar{q}}+\mathcal {K}_{q\bar{q}})}{8}&{}\frac{2(\mathcal {K}_{qq''}^{{\bar{3}}}+\mathcal {K}_{cq'}^{{\bar{3}}}+\mathcal {K}_{qq'}^{{\bar{3}}}+\mathcal {K}_{cq''}^{{\bar{3}}})}{-5}\\ \frac{\sqrt{3}(4\mathcal {K}_{c\bar{q}}+\mathcal {K}_{q\bar{q}})}{8}&{}\frac{4(\mathcal {K}_{cq}^{{\bar{3}}}+\mathcal {K}_{q'q''}^{{\bar{3}}})+\mathcal {K}_{q\bar{q}}-8\mathcal {K}_{c\bar{q}}}{8}&{}\frac{8(\mathcal {K}_{cq}^{{\bar{3}}}+\mathcal {K}_{q'q''}^{{\bar{3}}})-3(\mathcal {K}_{q'\bar{q}}+\mathcal {K}_{q''\bar{q}})}{16}\\ \frac{2(\mathcal {K}_{qq''}^{{\bar{3}}}+\mathcal {K}_{cq'}^{{\bar{3}}}+\mathcal {K}_{qq'}^{{\bar{3}}}+\mathcal {K}_{cq''}^{{\bar{3}}})}{-5}&{}\frac{8(\mathcal {K}_{cq}^{{\bar{3}}}+\mathcal {K}_{q'q''}^{{\bar{3}}})-3(\mathcal {K}_{q'\bar{q}}+\mathcal {K}_{q''\bar{q}})}{16}&{}\frac{5(\mathcal {K}_{cq}^{{\bar{3}}}+\mathcal {K}_{q'q''}^{{\bar{3}}}+\mathcal {K}_{c\bar{q}}+\mathcal {K}_{q\bar{q}})+{2\sqrt{2}}(\mathcal {K}_{q'\bar{q}}+\mathcal {K}_{q''\bar{q}})}{10} \end{array}\right) \nonumber \\{} & {} \quad + \left( \begin{array}{ccc}0&{}\frac{\mathcal {K}_{qq''}^{{\bar{3}}}+\mathcal {K}_{cq'}^{{\bar{3}}}+\mathcal {K}_{qq'}^{{\bar{3}}}+\mathcal {K}_{cq''}^{{\bar{3}}}}{-5}&{}0\\ \frac{\mathcal {K}_{qq''}^{{\bar{3}}}+\mathcal {K}_{cq'}^{{\bar{3}}}+\mathcal {K}_{qq'}^{{\bar{3}}}+\mathcal {K}_{cq''}^{{\bar{3}}}}{-5}&{} \frac{6(\mathcal {K}_{q'\bar{q}}+\mathcal {K}_{q''\bar{q}})+7(\mathcal {K}_{qq''}^{{\bar{3}}}+\mathcal {K}_{cq'}^{{\bar{3}}}+\mathcal {K}_{qq'}^{{\bar{3}}}+\mathcal {K}_{cq''}^{{\bar{3}}})}{21}&{} 0\\ 0&{}0&{} \frac{\mathcal {K}_{qq''}^{{\bar{3}}}+\mathcal {K}_{cq'}^{{\bar{3}}}+\mathcal {K}_{qq'}^{{\bar{3}}}+\mathcal {K}_{cq''}^{{\bar{3}}}}{-10} \end{array}\right) ,\end{aligned}$$

(B2)

$$\begin{aligned}{} & {} \mathcal {M}^{S_{t}=3/2,S_{q'q''}=1}_{J=5/2} =m_{cq}+m_{\bar{q}}+m_{q'q''}+\frac{\mathcal {K}_{c\bar{q}}+\mathcal {K}_{q\bar{q}}+\mathcal {K}_{cq}^{{\bar{3}}}+\mathcal {K}_{q'q''}^{{\bar{3}}}+\mathcal {K}_{qq''}^{{\bar{3}}}+\mathcal {K}_{cq'}^{{\bar{3}}}+\mathcal {K}_{qq'}^{{\bar{3}}}+\mathcal {K}_{cq''}^{{\bar{3}}}}{2}. \end{aligned}$$

(B3)

The mass matrices of P-wave singly charm pentaquark under the considering of “bad” light diquark $S_{q'q''}=1$, with the total quantum numbers $J=1/2,3/2,5/2,7/2$.

$$\begin{aligned}{} & {} \mathcal {M}^{S_{t}=1/2,S_{q'q''}=1}_{J=1/2} =m_{cq}+m_{\bar{q}}+m_{q'q''}+ \left( \begin{array}{cccc} \frac{{6}A_{t}+{8}A_{ld}+3B_{L}}{3}&{}\frac{-2\sqrt{2}(A_{t}+A_{ld})+3B_{L}}{3}&{}0&{}0\\ \frac{-2\sqrt{2}(A_{t}+A_{ld})+3B_{L}}{3}&{}\frac{{5}A_{t}+{10}A_{ld}+3B_{L}}{3}&{}0&{}0\\ 0&{}0&{}\frac{{6}A_{t}+{8}A_{ld}+3B_{L}}{3}&{}\frac{-2\sqrt{2}(A_{t}+A_{ld})+3B_{L}}{3}\\ 0&{}0&{}\frac{-2\sqrt{2}(A_{t}+A_{ld})+3B_{L}}{3}&{}\frac{{5}A_{t}+{10}A_{ld}+3B_{L}}{3} \end{array}\right) \nonumber \\{} & {} \quad + \left( \begin{array}{cccc} \frac{4\mathcal {K}_{q'q''}^{{\bar{3}}}-12\mathcal {K}_{cq}^{{\bar{3}}}+3\mathcal {K}_{q\bar{q}}+\mathcal {K}_{q'\bar{q}}+\mathcal {K}_{q''\bar{q}}}{8}&{}0&{}\frac{\sqrt{3}(4\mathcal {K}_{c\bar{q}}+\mathcal {K}_{q\bar{q}})}{8}&{}0\\ 0&{}\frac{\mathcal {K}_{q'q''}^{{\bar{3}}}+\mathcal {K}_{q'\bar{q}}+\mathcal {K}_{q''\bar{q}}}{8}&{}0&{}\frac{\sqrt{3}(4\mathcal {K}_{c\bar{q}}+\mathcal {K}_{q\bar{q}})}{8}\\ \frac{\sqrt{3}(4\mathcal {K}_{c\bar{q}}+\mathcal {K}_{q\bar{q}})}{8}&{}0&{}\frac{20(\mathcal {K}_{cq}^{{\bar{3}}}+\mathcal {K}_{q'q''}^{{\bar{3}}})+5\mathcal {K}_{q\bar{q}}-40\mathcal {K}_{c\bar{q}}+16(\mathcal {K}_{q'\bar{q}}-\mathcal {K}_{q''\bar{q}})}{40}&{}0\\ 0&{}\frac{\sqrt{3}(4\mathcal {K}_{c\bar{q}}+\mathcal {K}_{q\bar{q}})}{8}&{}0&{}\frac{4(\mathcal {K}_{cq}^{{\bar{3}}}+\mathcal {K}_{q'q''}^{{\bar{3}}})+\mathcal {K}_{q\bar{q}}-8\mathcal {K}_{c\bar{q}}}{8} \end{array}\right) \end{aligned}$$

(B4)

$$\begin{aligned}{} & {} \quad + \left( \begin{array}{cccc} 0&{} 0&{}\frac{\sqrt{3}(\mathcal {K}_{qq''}^{{\bar{3}}}+\mathcal {K}_{cq'}^{{\bar{3}}}+\mathcal {K}_{qq'}^{{\bar{3}}}+\mathcal {K}_{cq''}^{{\bar{3}}})}{-3}&{}0\\ 0&{}\frac{3\mathcal {K}_{q\bar{q}}}{8} -\frac{{3}\mathcal {K}_{cq}^{{\bar{3}}}}{2}&{}0&{}\frac{\mathcal {K}_{qq''}^{{\bar{3}}}+\mathcal {K}_{cq'}^{{\bar{3}}}+\mathcal {K}_{qq'}^{{\bar{3}}}+\mathcal {K}_{cq''}^{{\bar{3}}}}{-5}\\ \frac{\sqrt{3}(\mathcal {K}_{qq''}^{{\bar{3}}}+\mathcal {K}_{cq'}^{{\bar{3}}}+\mathcal {K}_{qq'}^{{\bar{3}}}+\mathcal {K}_{cq''}^{{\bar{3}}})}{-3}&{}0&{}-\frac{17(\mathcal {K}_{qq''}^{{\bar{3}}}+\mathcal {K}_{cq'}^{{\bar{3}}}+\mathcal {K}_{qq'}^{{\bar{3}}}+\mathcal {K}_{cq''}^{{\bar{3}}})}{24}&{}0\\ 0&{}\frac{\mathcal {K}_{qq''}^{{\bar{3}}}+\mathcal {K}_{cq'}^{{\bar{3}}}+\mathcal {K}_{qq'}^{{\bar{3}}}+\mathcal {K}_{cq''}^{{\bar{3}}}}{-5}&{}0&{}\frac{6(\mathcal {K}_{q'\bar{q}}+\mathcal {K}_{q''\bar{q}})+7(\mathcal {K}_{qq''}^{{\bar{3}}}+\mathcal {K}_{cq'}^{{\bar{3}}}+\mathcal {K}_{qq'}^{{\bar{3}}}+\mathcal {K}_{cq''}^{{\bar{3}}})}{21} \end{array}\right) ,\nonumber \\ \end{aligned}$$

(B5)

$$\begin{aligned}{} & {} \mathcal {M}^{S_{t}=3/2,S_{q'q''}=1}_{J=1/2} =m_{cq}+m_{\bar{q}}+m_{q'q''}+ \left( \begin{array}{cc} \frac{3(\mathcal {K}_{cq}^{{\bar{3}}}+\mathcal {K}_{q'q''}^{{\bar{3}}}+\mathcal {K}_{c\bar{q}}+\mathcal {K}_{q\bar{q}})+\mathcal {K}_{q'\bar{q}}+\mathcal {K}_{q''\bar{q}}}{6}&{}0.527(A_{t}+A_{ld})+B_{L}\\ 0.527(A_{t}+A_{ld})+B_{L}&{}\frac{5(\mathcal {K}_{cq}^{{\bar{3}}}+\mathcal {K}_{q'q''}^{{\bar{3}}}+\mathcal {K}_{c\bar{q}}+\mathcal {K}_{q\bar{q}})+{2\sqrt{2}}(\mathcal {K}_{q'\bar{q}}+\mathcal {K}_{q''\bar{q}})}{10} \end{array}\right) \nonumber \\{} & {} \quad + \left( \begin{array}{cc} \frac{11(\mathcal {K}_{qq''}^{{\bar{3}}}+\mathcal {K}_{cq'}^{{\bar{3}}}+\mathcal {K}_{qq'}^{{\bar{3}}}+\mathcal {K}_{cq''}^{{\bar{3}}})}{-6}-3.3A_{t}+1.3A_{ld}+B_{L}&{}0\\ 0&{}\frac{\mathcal {K}_{qq''}^{{\bar{3}}}+\mathcal {K}_{cq'}^{{\bar{3}}}+\mathcal {K}_{qq'}^{{\bar{3}}}+\mathcal {K}_{cq''}^{{\bar{3}}}}{-10}-3.7A_{t}-1.3A_{ld}+B_{L} \end{array}\right) ,\end{aligned}$$

(B6)

$$\begin{aligned}{} & {} \mathcal {M}^{S_{t}=1/2,S_{q'q''}=1}_{J=3/2} =m_{cq}+m_{\bar{q}}+m_{q'q''}\nonumber \\{} & {} \quad + \left( \begin{array}{cccc} -0.333A_{t}+1.33A_{ld}+B_{L}&{}1.491(A_{t}+A_{ld})+B_{L}&{}0&{}0\\ 1.491(A_{t}+A_{ld})+B_{L}&{}-0.664A_{t}1.332A_{ld}+B_{L}&{}0&{}0\\ 0&{}0&{} -0.333A_{t}+1.33A_{ld}+B_{L}&{}1.491(A_{t}+A_{ld})+B_{L}\\ 0&{}0&{} 1.491(A_{t}+A_{ld})+B_{L}&{}-0.664A_{t}1.332A_{ld}+B_{L} \end{array}\right) \nonumber \\{} & {} \quad + \left( \begin{array}{cccc} \frac{4\mathcal {K}_{q'q''}^{{\bar{3}}}-12\mathcal {K}_{cq}^{{\bar{3}}}+3\mathcal {K}_{q\bar{q}}+\mathcal {K}_{q'\bar{q}}+\mathcal {K}_{q''\bar{q}}}{8}&{}0&{}\frac{\sqrt{3}(4\mathcal {K}_{c\bar{q}}+\mathcal {K}_{q\bar{q}})}{8}&{}0\\ 0&{}\frac{\mathcal {K}_{q'q''}^{{\bar{3}}}+\mathcal {K}_{q'\bar{q}}+\mathcal {K}_{q''\bar{q}}}{8}&{}0&{}\frac{\sqrt{3}(4\mathcal {K}_{c\bar{q}}+\mathcal {K}_{q\bar{q}})}{8}\\ \frac{\sqrt{3}(4\mathcal {K}_{c\bar{q}}+\mathcal {K}_{q\bar{q}})}{8}&{}0&{}\frac{20(\mathcal {K}_{cq}^{{\bar{3}}}+\mathcal {K}_{q'q''}^{{\bar{3}}})+5\mathcal {K}_{q\bar{q}}-40\mathcal {K}_{c\bar{q}}+16(\mathcal {K}_{q'\bar{q}}-\mathcal {K}_{q''\bar{q}})}{40}&{}0\\ 0&{}\frac{\sqrt{3}(4\mathcal {K}_{c\bar{q}}+\mathcal {K}_{q\bar{q}})}{8}&{}0&{}\frac{4(\mathcal {K}_{cq}^{{\bar{3}}}+\mathcal {K}_{q'q''}^{{\bar{3}}})+\mathcal {K}_{q\bar{q}}-8\mathcal {K}_{c\bar{q}}}{8} \end{array}\right) \nonumber \\{} & {} \quad + \left( \begin{array}{cccc} 0&{}0&{}\frac{\sqrt{3}(\mathcal {K}_{qq''}^{{\bar{3}}}+\mathcal {K}_{cq'}^{{\bar{3}}}+\mathcal {K}_{qq'}^{{\bar{3}}}+\mathcal {K}_{cq''}^{{\bar{3}}})}{-3}&{}0\\ 0&{}\frac{3\mathcal {K}_{q\bar{q}}}{8} -\frac{{3}\mathcal {K}_{cq}^{{\bar{3}}}}{2}&{}0&{}\frac{\mathcal {K}_{qq''}^{{\bar{3}}}+\mathcal {K}_{cq'}^{{\bar{3}}}+\mathcal {K}_{qq'}^{{\bar{3}}}+\mathcal {K}_{cq''}^{{\bar{3}}}}{-5}\\ \frac{\sqrt{3}(\mathcal {K}_{qq''}^{{\bar{3}}}+\mathcal {K}_{cq'}^{{\bar{3}}}+\mathcal {K}_{qq'}^{{\bar{3}}}+\mathcal {K}_{cq''}^{{\bar{3}}})}{-3}&{}0&{}-\frac{17(\mathcal {K}_{qq''}^{{\bar{3}}}+\mathcal {K}_{cq'}^{{\bar{3}}}+\mathcal {K}_{qq'}^{{\bar{3}}}+\mathcal {K}_{cq''}^{{\bar{3}}})}{24}&{}0\\ 0&{}\frac{\mathcal {K}_{qq''}^{{\bar{3}}}+\mathcal {K}_{cq'}^{{\bar{3}}}+\mathcal {K}_{qq'}^{{\bar{3}}}+\mathcal {K}_{cq''}^{{\bar{3}}}}{-5}&{}0&{}\frac{6(\mathcal {K}_{q'\bar{q}}+\mathcal {K}_{q''\bar{q}})+7(\mathcal {K}_{qq''}^{{\bar{3}}}+\mathcal {K}_{cq'}^{{\bar{3}}}+\mathcal {K}_{qq'}^{{\bar{3}}}+\mathcal {K}_{cq''}^{{\bar{3}}})}{21} \end{array}\right) ,\end{aligned}$$

(B7)

$$\begin{aligned}{} & {} \mathcal {M}^{S_{t}=3/2,S_{q'q''}=1}_{J=3/2} =m_{cq}+m_{\bar{q}}+m_{q'q''}\nonumber \\{} & {} \quad +\left( \begin{array}{ccc} -1.667A_{t}+0.666A_{ld}+B_{L}&{}-2.357(A_{t}+A_{ld})+B_{L}&{}B_{L}\\ -2.357(A_{t}+A_{ld})+B_{L}&{}0.366A_{t}+0.533A_{ld}+B_{L}&{}69.663A_{t}-1.467A_{ld}+B_{L}\\ B_{L}&{}69.663A_{t}-1.467A_{ld}+B_{L}&{}\frac{{21}A_{t}}{5}+\frac{{14}A_{ld}}{5}+B_{L} \end{array}\right) \nonumber \\{} & {} \quad + \left( \begin{array}{ccc} \frac{3(\mathcal {K}_{cq}^{{\bar{3}}}+\mathcal {K}_{q'q''}^{{\bar{3}}}+\mathcal {K}_{c\bar{q}}+\mathcal {K}_{q\bar{q}})+\mathcal {K}_{q'\bar{q}}+\mathcal {K}_{q''\bar{q}}}{6}&{}0&{}0\\ &{}\frac{5(\mathcal {K}_{cq}^{{\bar{3}}}+\mathcal {K}_{q'q''}^{{\bar{3}}}+\mathcal {K}_{c\bar{q}}+\mathcal {K}_{q\bar{q}})+{2\sqrt{2}}(\mathcal {K}_{q'\bar{q}}+\mathcal {K}_{q''\bar{q}})}{10}&{}0\\ 0&{}0&{}\frac{\mathcal {K}_{c\bar{q}}+\mathcal {K}_{q\bar{q}}+\mathcal {K}_{q'\bar{q}}+\mathcal {K}_{q''\bar{q}}+\mathcal {K}_{cq}^{{\bar{3}}}+\mathcal {K}_{q'q''}^{{\bar{3}}}}{2} \end{array}\right) \nonumber \\{} & {} \quad + \left( \begin{array}{ccc}\frac{11(\mathcal {K}_{qq''}^{{\bar{3}}}+\mathcal {K}_{cq'}^{{\bar{3}}}+\mathcal {K}_{qq'}^{{\bar{3}}}+\mathcal {K}_{cq''}^{{\bar{3}}})}{-6}&{}0&{}0\\ 0&{}\frac{\mathcal {K}_{qq''}^{{\bar{3}}}+\mathcal {K}_{cq'}^{{\bar{3}}}+\mathcal {K}_{qq'}^{{\bar{3}}}+\mathcal {K}_{cq''}^{{\bar{3}}}}{-10}&{}0\\ 0&{}0&{}\frac{\mathcal {K}_{qq''}^{{\bar{3}}}+\mathcal {K}_{cq'}^{{\bar{3}}}+\mathcal {K}_{qq'}^{{\bar{3}}}+\mathcal {K}_{cq''}^{{\bar{3}}}}{2} \end{array}\right) .\end{aligned}$$

(B8)

$$\begin{aligned}{} & {} \mathcal {M}^{S_{t}=1/2,S_{q'q''}=1}_{J=5/2} =m_{cq}+m_{\bar{q}}+m_{q'q''}\nonumber \\{} & {} \quad + \left( \begin{array}{cc} \frac{4(\mathcal {K}_{q'q''}^{{\bar{3}}}+\mathcal {K}_{q'\bar{q}}+\mathcal {K}_{q''\bar{q}})-12\mathcal {K}_{cq}^{{\bar{3}}}+3\mathcal {K}_{q\bar{q}}}{8}&{}\frac{\sqrt{3}(4\mathcal {K}_{c\bar{q}}+\mathcal {K}_{q\bar{q}})}{8}\\ \frac{\sqrt{3}(4\mathcal {K}_{c\bar{q}}+\mathcal {K}_{q\bar{q}})}{8}&{}\frac{4(\mathcal {K}_{cq}^{{\bar{3}}}+\mathcal {K}_{q'q''}^{{\bar{3}}})+\mathcal {K}_{q\bar{q}}-8\mathcal {K}_{c\bar{q}}}{8}-A_{t}-2A_{ld}+B_{L} \end{array}\right) \nonumber \\{} & {} \quad + \left( \begin{array}{cc} -A_{t}-{{2}{A_{ld}}}+B_{L}&{}\frac{\mathcal {K}_{qq''}^{{\bar{3}}}+\mathcal {K}_{cq'}^{{\bar{3}}}+\mathcal {K}_{qq'}^{{\bar{3}}}+\mathcal {K}_{cq''}^{{\bar{3}}}}{-5}\\ \frac{\mathcal {K}_{qq''}^{{\bar{3}}}+\mathcal {K}_{cq'}^{{\bar{3}}}+\mathcal {K}_{qq'}^{{\bar{3}}}+\mathcal {K}_{cq''}^{{\bar{3}}}}{-5}&{}\frac{6(\mathcal {K}_{q'\bar{q}}+\mathcal {K}_{q''\bar{q}})+7(\mathcal {K}_{qq''}^{{\bar{3}}}+\mathcal {K}_{cq'}^{{\bar{3}}}+\mathcal {K}_{qq'}^{{\bar{3}}}+\mathcal {K}_{cq''}^{{\bar{3}}})}{21} \end{array}\right) , \end{aligned}$$

(B9)

$$\begin{aligned}{} & {} \mathcal {M}^{S_{t}=3/2,S_{q'q''}=1}_{J=5/2} =m_{cq}+m_{\bar{q}}+m_{q'q''}\nonumber \\{} & {} \quad + \left( \begin{array}{cc} \frac{\mathcal {K}_{qq''}^{{\bar{3}}}+\mathcal {K}_{cq'}^{{\bar{3}}}+\mathcal {K}_{qq'}^{{\bar{3}}}+\mathcal {K}_{cq''}^{{\bar{3}}}}{-10}+\frac{{11}A_{t}}{5}+\frac{{4}A_{ld}}{5}+B_{L}&{}4.188A_{t}+1.496A_{ld}+B_{L}\\ 4.188A_{t}+1.496A_{ld}+B_{L}&{}\frac{(\mathcal {K}_{c\bar{q}}+\mathcal {K}_{q\bar{q}})+(\mathcal {K}_{q'\bar{q}}+\mathcal {K}_{q''\bar{q}})}{2}-0.794A_{t}-0.533A_{ld}+B_{L} \end{array}\right) \nonumber \\{} & {} \quad + \left( \begin{array}{cc} \frac{5(\mathcal {K}_{cq}^{{\bar{3}}}+\mathcal {K}_{q'q''}^{{\bar{3}}}+\mathcal {K}_{cq}^{{\bar{3}}}+\mathcal {K}_{q\bar{q}})+{2\sqrt{2}}(\mathcal {K}_{q'\bar{q}}+\mathcal {K}_{q''\bar{q}})}{10}&{}0\\ 0&{}\frac{\mathcal {K}_{cq}^{{\bar{3}}}+\mathcal {K}_{q'q''}^{{\bar{3}}}+\mathcal {K}_{qq''}^{{\bar{3}}}+\mathcal {K}_{cq'}^{{\bar{3}}}+\mathcal {K}_{qq'}^{{\bar{3}}}+\mathcal {K}_{cq''}^{{\bar{3}}}}{2} \end{array}\right) . \end{aligned}$$

(B10)

$$\begin{aligned}{} & {} \mathcal {M}^{S_{t}=3/2,S_{q'q''}=1}_{J=7/2} =m_{cq}+m_{\bar{q}}+m_{q'q''}-{3}A_{t}-{2}A_{ld}+B_{L}\nonumber \\{} & {} \quad +\frac{\mathcal {K}_{c\bar{q}}+\mathcal {K}_{q\bar{q}}+\mathcal {K}_{q'\bar{q}}+\mathcal {K}_{q''\bar{q}}+\mathcal {K}_{cq}^{{\bar{3}}}+\mathcal {K}_{q'q''}^{{\bar{3}}}+\mathcal {K}_{qq''}^{{\bar{3}}}+\mathcal {K}_{cq'}^{{\bar{3}}}+\mathcal {K}_{qq'}^{{\bar{3}}}+\mathcal {K}_{cq''}^{{\bar{3}}}}{2}. \end{aligned}$$

(B11)

Appendix C: Mass spectrum of S-wave pentaquark in tetraquark-antiquark picture

For the singly charm pentaquark with tetraquark-antiquark picture $(cq)(q'q'')(qbar)$, the spin-spin interactions between light antiquark and heavy diquark $2 \, \mathcal {K}_{{\bar{c}} q} ( \textbf{S}_{{\bar{c}}} \cdot \textbf{S}_q )$ and $2 \, \mathcal {K}_{{\bar{c}} c} ( \textbf{S}_{{\bar{c}}} \cdot \textbf{S}_c )$, can be reached by the decoupling of quasi-tetraquark by two Wigner 6-j coefficients,

$$\begin{aligned}{} & {} | S_{\bar{q}},\, (S_{hd}, \, S_{ld})_{S_{hd,ld}}; \, S \rangle \nonumber \\{} & {} \quad = \sum _{S_{\bar{q}, hd}} (-1)^{S_{\bar{q}} + S_{hd} + S_{ld} + S} \sqrt{(2 S_{\bar{q}, hd} + 1)\, (2 S_{{hd},{ld}} + 1)}\nonumber \\{} & {} \qquad \times \left\{ \begin{array}{rrr} S_{\bar{q}} &{} S_{hd} &{} S_{\bar{q}, hd} \\ S_{ld} &{} S &{} S_{hd,ld} \end{array} \right\} | (S_{\bar{q}},\, S_{hd})_{\bar{q}, hd}, \, S_{ld}; \, S \rangle , \nonumber \\ \end{aligned}$$

(C1)

$$\begin{aligned}{} & {} | S_{\bar{q}},\, (S_{c}, \, S_{q})_{hd}; \, S_{hd, \bar{q}} \rangle \nonumber \\{} & {} \quad = \sum _{S_{\bar{q} c}} (-1)^{S_{\bar{q}} + S_q + S_c + S_{hd, \bar{q}}} \sqrt{(2 S_{c \bar{q} } + 1)\, (2 S_{hd} + 1)} \nonumber \\{} & {} \qquad \times \left\{ \begin{array}{rrr} S_{\bar{q}} &{} S_c &{} S_{c \bar{q} } \\ S_q &{} S_{hd, \bar{q}} &{} S_{hd} \end{array} \right\} | (S_{\bar{q}},\, S_c)_{S_{c \bar{q} }}, \, S_q; \, S_{hd, \bar{q}} \rangle , \nonumber \\\end{aligned}$$

(C2)

$$\begin{aligned}{} & {} | S_{\bar{q}},\, (S_{q}, \, S_{c})_{hd}; \, S_{hd, \bar{q}} \rangle \nonumber \\{} & {} \quad = \sum _{S_{\bar{q} q}} (-1)^{S_{\bar{q}} + S_q + S_c + S_{hd, \bar{q}}} \sqrt{(2 S_{\bar{q} q} + 1)\, (2 S_{hd} + 1)} \nonumber \\{} & {} \qquad \times \left\{ \begin{array}{rrr} S_{\bar{q}} &{} S_q &{} S_{\bar{q} q} \\ S_c &{} S_{hd, \bar{q}} &{} S_{hd} \end{array} \right\} | (S_{\bar{q}},\, S_q)_{S_{\bar{q} q}}, \, S_c; \, S_{hd, \bar{q}} \rangle . \end{aligned}$$

(C3)

Where $S_{ld}$ and $S_{hd}$ are the spins of light diquark $[q'q'']$ and heavy diquark [cq] respectively, $S_{hd,\bar{q}}$ is the total spin of heavy diquark [cq] and anti-quark $\bar{q}$. Thus the contributions of the operators can be found as

(C4)

(C5)

After some tedious calculations, we obtain the mass spectrum of charm pentaquark under the tetraquark-antiquark picture. The results show that the masses in the case are larger than triquark-diquark one for the S-wave states, the differences mainly come from the spin-spin interaction between different diquarks. The mass spectrums given in Table 8.

Table 8 The mass splitting for the S-wave singly charm pentaquark state($S_{q'q''}=0$) within tetraquark-antiquark picture

Appendix D: States 6 and 15

Table 9 The productions of pentaquark $F_{15}$ and anti-charm anti-baryons $({cqq})_{3/{\bar{6}}}$ from B mesons

Table 10 The productions of pentaquark $F_{15}$ and light anti-baryons $({qqq})_{8/10}$ from B mesons

Table 11 The productions of pentaquark $S_6$, light anti-baryons $({qqq})_{8/10}$ or anti-charm anti-baryon $(\bar{c}qq)_{3/{\bar{6}}}$ from B mesons

The possible Hamiltonian for the production of pentaquark ground 6 states from one B meson, induced by the transition $b\rightarrow c \bar{c}d/s$ and $b\rightarrow c \bar{u}d/s$ in the quark level, can be written directly as,

$$\begin{aligned} {\mathcal {H}}_{6}= & {} a_{1}{B}_{i}(H_{3})^{j}({S}_{6})_{\{jk\}}({\mathcal {P}}_{c3})^{[ik]} +b_{1}{B}_{i}(H_{3})^{j}({S}_{6})_{\{jk\}}({\mathcal {P}}_{c{\bar{6}}})^{\{ik\}}\nonumber \\{} & {} +b_{2}{B}_{i}(H_{3})^{i}({S}_{6})_{\{jk\}}({\mathcal {P}}_{c{\bar{6}}})^{\{jk\}}+c_{1}{B}_{i}(H_{8})_{j}^{i}(S_{6})_{\{kl\}}({\mathcal {P}}_{8})_{\alpha }^{k}\ \varepsilon ^{\alpha jl}\nonumber \\{} & {} + c_{2}{B}_{i}(H_{8})_{j}^{k}(S_{6})_{\{kl\}}({\mathcal {P}}_{8})_{\alpha }^{i}\ \varepsilon ^{\alpha jl}+c_{3}{B}_{i}(H_{8})_{j}^{k}(S_{6})_{\{kl\}}({\mathcal {P}}_{8})_{\alpha }^{j}\ \varepsilon ^{\alpha il}\nonumber \\{} & {} +c_{4}{B}_{i}(H_{8})_{j}^{k}(S_{6})_{\{kl\}}({\mathcal {P}}_{8})_{\alpha }^{l}\ \varepsilon ^{\alpha ij}. \end{aligned}$$

(D1)

The production channels directly collected into Table 11, in addition, we show the fully production processes about all 15 states in the Tables 9 and 10. The relations between different production widths can then be deduced, the complete results for sextet given as (Table 11),

$$\begin{aligned} \Gamma (B^-\rightarrow S_{(\bar{u}u,\bar{s}s)dd}^{0} {\overline{\Lambda }}_{{\bar{c}}}^-)&= \Gamma (B^-\rightarrow S_{(\bar{q}q)ds}^{0} {\overline{\Xi }}_{{\bar{c}}}^-) \\ =\Gamma ({\overline{B}}^0\rightarrow S_{(\bar{q}q)ds}^{0} {\overline{\Xi }}_{{\bar{c}}}^0)&= \Gamma ({\overline{B}}^0_s\rightarrow S_{(\bar{u}u,\bar{s}s)dd}^{0} {\overline{\Xi }}_{{\bar{c}}}^0)\\ =\Gamma ({\overline{B}}^0\rightarrow S_{(\bar{q}q)ud}^{+} {\overline{\Lambda }}_{{\bar{c}}}^-)&=\Gamma ({\overline{B}}^0_s\rightarrow S_{(\bar{q}q)ud}^{+} {\overline{\Xi }}_{{\bar{c}}}^-),\\ \Gamma (B^-\rightarrow S_{(\bar{q}q)ds}^{0} {\overline{\Lambda }}_{{\bar{c}}}^-)&=\Gamma (B^-\rightarrow S_{(\bar{u}u,\bar{d}d)ss}^{0} {\overline{\Xi }}_{{\bar{c}}}^-)\\ =\Gamma ({\overline{B}}^0\rightarrow S_{(\bar{u}u,\bar{d}d)ss}^{0} {\overline{\Xi }}_{{\bar{c}}}^0)&=\Gamma ({\overline{B}}^0\rightarrow S_{(\bar{q}q)us}^{+} {\overline{\Lambda }}_{{\bar{c}}}^-)\\ = \Gamma ({\overline{B}}^0_s\rightarrow S_{(\bar{q}q)us}^{+} {\overline{\Xi }}_{{\bar{c}}}^-)&= \Gamma ({\overline{B}}^0_s\rightarrow S_{(\bar{q}q)ds}^{0} {\overline{\Xi }}_{{\bar{c}}}^0),\\ \Gamma (B^-\rightarrow S_{(\bar{q}q)ud}^{+} {\overline{\Sigma }}_{{\bar{c}}}^{{-}{-}})&= 2\Gamma (B^-\rightarrow S_{(\bar{u}u,\bar{s}s)dd}^{0} {\overline{\Sigma }}_{{\bar{c}}}^{-})\\&=2\Gamma (B^-\rightarrow S_{(\bar{q}q)ds}^{0}\\ {\overline{\Xi }}_{{\bar{c}}}^{\prime -}) =2\Gamma (B^-\rightarrow S_{(\bar{u}u,\bar{d}d)ss}^{0} {\overline{\Xi }}_{{\bar{c}}}^{\prime -})&=\Gamma ({\overline{B}}^0\rightarrow S_{(\bar{q}q)ds}^{0} {\overline{\Sigma }}_{{\bar{c}}}^{0})\\ =2\Gamma ({\overline{B}}^0\rightarrow S_{(\bar{q}q)us}^{+} {\overline{\Sigma }}_{{\bar{c}}}^{-})&=2\Gamma ({\overline{B}}^0\rightarrow S_{(\bar{u}u,\bar{d}d)ss}^{0}\\ {\overline{\Xi }}_{{\bar{c}}}^{\prime 0}&=2\Gamma ({\overline{B}}^0_s\rightarrow S_{(\bar{q}q)ud}^{+} {\overline{\Xi }}_{{\bar{c}}}^{\prime -})\\ =2\Gamma ({\overline{B}}^0_s\rightarrow S_{(\bar{u}u,\bar{s}s)dd}^{0} {\overline{\Xi }}_{{\bar{c}}}^{\prime 0})&=\Gamma ({\overline{B}}^0_s\rightarrow S_{(\bar{q}q)ds}^{0}\\ {\overline{\Omega }}_{{\bar{c}}}^{0})=\Gamma (B^-\rightarrow S_{(\bar{q}q)us}^{+} {\overline{\Sigma }}_{{\bar{c}}}^{{-}{-}})&= 2\Gamma ({\overline{B}}^0\rightarrow S_{(\bar{q}q)us}^{+} {\overline{\Sigma }}_{{\bar{c}}}^{-}),\\ {}&= \Gamma ({\overline{B}}^0\rightarrow S_{(\bar{q}q)ud}^{+} {\overline{\Sigma }}_{{\bar{c}}}^{-}) \\ {}&= \Gamma ({\overline{B}}^0\rightarrow S_{(\bar{q}q)ds}^{0} {\overline{\Xi }}_{{\bar{c}}}^{\prime 0}),\quad \\ \Gamma ({\overline{B}}^0\rightarrow S_{(\bar{q}q)ud}^{+} {\overline{\Sigma }}_{{\bar{c}}}^{-})&= \Gamma ({\overline{B}}^0\rightarrow S_{(\bar{q}q)ds}^{0} {\overline{\Xi }}_{{\bar{c}}}^{\prime 0}),\\ \Gamma ({\overline{B}}^0_s\rightarrow S_{(\bar{d}d,\bar{s}s)uu}^{++} {\overline{\Sigma }}_{{\bar{c}}}^{{-}{-}})&= \frac{1}{2}\Gamma ({\overline{B}}^0_s\rightarrow S_{(\bar{q}q)ud}^{+}\\ {\overline{\Sigma }}_{{\bar{c}}}^{-})&=\Gamma ({\overline{B}}^0_s\rightarrow S_{(\bar{u}u,\bar{s}s)dd}^{0} {\overline{\Sigma }}_{{\bar{c}}}^{0}),\\ 2\Gamma ({\overline{B}}^0\rightarrow S_{(\bar{d}d,\bar{s}s)uu}^{++} {\overline{\Sigma }}_{{\bar{c}}}^{{-}{-}})&= \Gamma ({\overline{B}}^0\rightarrow S_{(\bar{q}q)us}^{+}\\ {\overline{\Xi }}_{{\bar{c}}}^{\prime -})&=2\Gamma ({\overline{B}}^0\rightarrow S_{(\bar{u}u,\bar{d}d)ss}^{0} {\overline{\Omega }}_{{\bar{c}}}^{0}),\\ \Gamma (B^-\rightarrow S_{(\bar{q}q)ds}^{0} {\overline{p}})&= \Gamma (B^-\rightarrow S_{(\bar{u}u,\bar{d}d)ss}^{0} {\overline{\Sigma }}^-) \\ {}&= 2\Gamma ({\overline{B}}^0\rightarrow S_{(\bar{u}u,\bar{d}d)ss}^{0}\\ {\overline{\Sigma }}^0) =\Gamma (B^-\rightarrow S_{(\bar{u}u,\bar{d}d)ss}^{0} {\overline{\Sigma }}^-),\\ \Gamma (B^-\rightarrow S_{(\bar{u}u,\bar{s}s)dd}^{0} {\overline{p}})&= \Gamma (B^-\rightarrow S_{(\bar{q}q)ds}^{0} {\overline{\Sigma }}^-), \\ \Gamma ({\overline{B}}^0\rightarrow S_{(\bar{q}q)us}^{+} {\overline{\Sigma }}^-)&= \Gamma ({\overline{B}}^0\rightarrow S_{(\bar{u}u,\bar{d}d)ss}^{0} {\overline{\Xi }}^0),\\ \Gamma ({\overline{B}}^0_s\rightarrow S_{(\bar{q}q)ud}^{+} {\overline{\Sigma }}^-)&= 2\Gamma ({\overline{B}}^0_s\rightarrow S_{(\bar{u}u,\bar{s}s)dd}^{0} {\overline{\Sigma }}^0), \quad \\ \Gamma ({\overline{B}}^0_s\rightarrow S_{(\bar{q}q)ud}^{+} {\overline{p}})&= \Gamma ({\overline{B}}^0_s\rightarrow S_{(\bar{u}u,\bar{s}s)dd}^{0} {\overline{n}}),\\ \Gamma ({\overline{B}}^0_s\rightarrow S_{(\bar{q}q)us}^{+} {\overline{\Xi }}_{{\bar{c}}}^{\prime -})&=\Gamma ({\overline{B}}^0_s\rightarrow S_{(\bar{q}q)ds}^{0} {\overline{\Xi }}_{{\bar{c}}}^{\prime 0}),\\ \Gamma ({\overline{B}}^0_s\rightarrow S_{(\bar{q}q)us}^{+} {\overline{\Sigma }}^-)&= 2\Gamma ({\overline{B}}^0_s\rightarrow S_{(\bar{q}q)ds}^{0} {\overline{\Sigma }}^0). \end{aligned}$$

The production width relations of 15 states are gathered as,

$$\begin{aligned} \Gamma (B^-\rightarrow F_{(\bar{u}u,\bar{s}s)dd}^{0} {\bar{\Lambda }}_{\bar{c}}^-)&=\Gamma ({\overline{B}}^0\rightarrow F_{(\bar{q}q)us}^{+} {\bar{\Xi }}_{\bar{c}}^-) \\ =\Gamma ({\overline{B}}^0_s\rightarrow F_{(\bar{u}u,\bar{s}s)dd}^{0} {\overline{\Xi }}_{\bar{c}}^0)&= \Gamma ({\overline{B}}^0\rightarrow {F'}_{(\bar{q}q)ud}^{+} {\bar{\Lambda }}_{\bar{c}}^-)\\ =\Gamma ({\overline{B}}^0\rightarrow {F'}_{(\bar{q}q)us}^{+} {\bar{\Xi }}_{\bar{c}}^-)&=\Gamma ({\overline{B}}^0\rightarrow F_{(\bar{q}q)ds}^{0} {\overline{\Xi }}_{\bar{c}}^0)\\ =\Gamma ({\overline{B}}^0_s\rightarrow {F'}_{(\bar{q}q)ud}^{+} {\bar{\Xi }}_{\bar{c}}^-)&=\Gamma ({\overline{B}}^0_s\rightarrow F_{\bar{s}udd}^{+} {\bar{\Lambda }}_{\bar{c}}^-)\\ =\Gamma (B^-\rightarrow F_{\bar{u}dds}^{-} {\overline{\Xi }}_{\bar{c}}^0)&= \Gamma (B^-\rightarrow F_{(\bar{q}q)ds}^{0} {\bar{\Xi }}_{\bar{c}}^-),\\ \Gamma (B^-\rightarrow {F'}_{(\bar{q}q)ds}^{0} {\bar{\Lambda }}_{\bar{c}}^-)&=\Gamma (B^-\rightarrow F_{(\bar{u}u,\bar{d}d)ss}^{0} {\bar{\Xi }}_{\bar{c}}^-) \\ =\Gamma (B^-\rightarrow F_{\bar{u}dss}^- {\overline{\Xi }}_{\bar{c}}^0)&=\Gamma ({\overline{B}}^0\rightarrow F_{(\bar{u}u,\bar{d}d)ss}^{0} {\overline{\Xi }}_{\bar{c}}^0)\\ =\Gamma ({\overline{B}}^0\rightarrow {F'}_{(\bar{q}q)us}^{+} {\bar{\Lambda }}_{\bar{c}}^-)&=\Gamma ({\overline{B}}^0\rightarrow F_{\bar{d}uss}^+ {\bar{\Xi }}_{\bar{c}}^-)\\ =\Gamma ({\overline{B}}^0_s\rightarrow {F'}_{(\bar{q}q)us}^{+} {\bar{\Xi }}_{\bar{c}}^-)&=\Gamma ({\overline{B}}^0_s\rightarrow {F'}_{(\bar{q}q)ud}^{+} {\bar{\Lambda }}_{\bar{c}}^-)\\ =\Gamma ({\overline{B}}^0_s\rightarrow F_{(\bar{q}q)ud}^{+} {\bar{\Lambda }}_{\bar{c}}^-)&= \Gamma ({\overline{B}}^0_s\rightarrow {F'}_{(\bar{q}q)ds}^{0} {\overline{\Xi }}_{\bar{c}}^0),\\ \Gamma (B^-\rightarrow F_{(\bar{q}q)ud}^{+} {\bar{\Sigma }}_{\bar{c}}^{{-}{-}})&=2\Gamma (B^-\rightarrow F_{(\bar{u}u,\bar{s}s)dd}^{0} {\bar{\Sigma }}_{\bar{c}}^{-})\\ =2\Gamma (B^-\rightarrow F_{(\bar{q}q)ds}^{0} {\bar{\Xi }}_{\bar{c}}^{\prime -})&=\frac{1}{2}\Gamma (B^-\rightarrow {F'}_{(\bar{q}q)ds}^{0} {\bar{\Xi }}_{\bar{c}}^{\prime -})\\ =2\Gamma (B^-\rightarrow F_{\bar{u}dds}^{-} {\overline{\Xi }}_{\bar{c}}^{\prime 0})&=\Gamma (B^-\rightarrow F_{\bar{u}dss}^- {\overline{\Omega }}_{\bar{c}}^{0})\\ =\Gamma ({\overline{B}}^0\rightarrow F_{(\bar{d}d,\bar{s}s)uu}^{++} {\bar{\Sigma }}_{\bar{c}}^{{-}{-}})&=2\Gamma ({\overline{B}}^0\rightarrow {F'}_{(\bar{q}q)ud}^{+} {\bar{\Sigma }}_{\bar{c}}^{-})\\ =2\Gamma ({\overline{B}}^0\rightarrow F_{(\bar{q}q)us}^{+} {\bar{\Xi }}_{\bar{c}}^{\prime -})&=2\Gamma ({\overline{B}}^0\rightarrow {F'}_{(\bar{q}q)us}^{+} \\ {\bar{\Xi }}_{\bar{c}}^{\prime -}) =2\Gamma ({\overline{B}}^0\rightarrow F_{(\bar{q}q)ds}^{0} {\overline{\Xi }}_{\bar{c}}^{\prime 0})&=\Gamma ({\overline{B}}^0\rightarrow F_{(\bar{u}u,\bar{d}d)ss}^{0} {\overline{\Omega }}_{\bar{c}}^{0})\\ =\Gamma ({\overline{B}}^0_s\rightarrow F_{\bar{s}uud}^{++} {\bar{\Sigma }}_{\bar{c}}^{{-}{-}})&=2\Gamma ({\overline{B}}^0_s\rightarrow F_{\bar{s}udd}^{+} {\bar{\Sigma }}_{\bar{c}}^{-})\\ =2\Gamma ({\overline{B}}^0_s\rightarrow {F'}_{(\bar{q}q)ud}^{+} {\bar{\Xi }}_{\bar{c}}^{\prime -})&=\frac{1}{2}\Gamma ({\overline{B}}^0_s\rightarrow F_{(\bar{q}q)ud}^{+} {\bar{\Xi }}_{\bar{c}}^{\prime -})\\ =2\Gamma ({\overline{B}}^0_s\rightarrow F_{(\bar{u}u,\bar{s}s)dd}^{0} {\overline{\Xi }}_{\bar{c}}^{\prime 0})&=\Gamma ({\overline{B}}^0_s\rightarrow {F'}_{(\bar{q}q)ds}^{0} {\overline{\Omega }}_{\bar{c}}^{0}),\\ \Gamma (B^-\rightarrow F_{(\bar{q}q)us}^{+} {\bar{\Sigma }}_{\bar{c}}^{{-}{-}})&=\frac{1}{2}\Gamma (B^-\rightarrow F_{(\bar{q}q)ds}^{0} {\bar{\Sigma }}_{\bar{c}}^{-})\\ = 2\Gamma (B^-\rightarrow {F'}_{(\bar{q}q)ds}^{0}{\bar{\Sigma }}_{\bar{c}}^{-})&=\Gamma (B^-\rightarrow F_{\bar{u}dds}^{-} {\overline{\Sigma }}_{\bar{c}}^{0})\\ =2\Gamma (B^-\rightarrow F_{(\bar{u}u,\bar{d}d)ss}^{0} {\bar{\Xi }}_{\bar{c}}^{\prime -})&=2\Gamma (B^-\rightarrow F_{\bar{u}dss}^- {\overline{\Xi }}_{\bar{c}}^{\prime 0})\\ =\Gamma ({\overline{B}}^0\rightarrow F_{\bar{d}uus}^{++} {\bar{\Sigma }}_{\bar{c}}^{{-}{-}})&=\frac{1}{2}\Gamma ({\overline{B}}^0\rightarrow F_{(\bar{q}q)us}^{+} {\bar{\Sigma }}_{\bar{c}}^{-})\\ =2\Gamma ({\overline{B}}^0\rightarrow {F'}_{(\bar{q}q)us}^{+} {\bar{\Sigma }}_{\bar{c}}^{-})&=\Gamma ({\overline{B}}^0\rightarrow F_{(\bar{q}q)ds}^{0} \\ {\overline{\Sigma }}_{\bar{c}}^{0}) =2\Gamma ({\overline{B}}^0\rightarrow F_{\bar{d}uss}^+ {\bar{\Xi }}_{\bar{c}}^{\prime -})&=2\Gamma ({\overline{B}}^0\rightarrow F_{(\bar{u}u,\bar{d}d)ss}^{0} {\overline{\Xi }}_{\bar{c}}^{\prime 0})\\ =\Gamma ({\overline{B}}^0_s\rightarrow F_{(\bar{d}d,\bar{s}s)uu}^{++} {\bar{\Sigma }}_{\bar{c}}^{{-}{-}})&=2\Gamma ({\overline{B}}^0_s\rightarrow {F'}_{(\bar{q}q)ud}^{+} {\bar{\Sigma }}_{\bar{c}}^{-})\\ =2\Gamma ({\overline{B}}^0_s\rightarrow F_{(\bar{q}q)ud}^{+} {\bar{\Sigma }}_{\bar{c}}^{-})&=\Gamma ({\overline{B}}^0_s\rightarrow F_{(\bar{u}u,\bar{s}s)dd}^{0} {\overline{\Sigma }}_{\bar{c}}^{0})\\ \end{aligned}$$

$$\begin{aligned} =2\Gamma ({\overline{B}}^0_s\rightarrow {F'}_{(\bar{q}q)us}^{+} {\bar{\Xi }}_{\bar{c}}^{\prime -})&=2\Gamma ({\overline{B}}^0_s\rightarrow {F'}_{(\bar{q}q)ds}^{0} {\overline{\Xi }}_{\bar{c}}^{\prime 0}),\\ \Gamma (B^-\rightarrow F_{(\bar{q}q)ds}^{0} {\overline{p}})&=\Gamma (B^-\rightarrow F_{\bar{u}dds}^{-} {\overline{n}}) \\ =\Gamma ({\overline{B}}^0\rightarrow F_{(\bar{q}q)ds}^{0} {\overline{n}})&=\Gamma ({\overline{B}}^0\rightarrow F_{(\bar{q}q)us}^{+} {\overline{p}}),\\ \Gamma (B^-\rightarrow {F'}_{(\bar{q}q)ds}^{0} {\overline{\Sigma }}^-)&=\Gamma (B^-\rightarrow F_{\bar{u}dss}^- {\overline{\Xi }}^0)\\ =\Gamma ({\overline{B}}^0_s\rightarrow F_{(\bar{q}q)ud}^{+} {\overline{\Sigma }}^-)&=\Gamma ({\overline{B}}^0_s\rightarrow {F'}_{(\bar{q}q)ds}^{0} {\overline{\Xi }}^0),\\ \Gamma ({\overline{B}}^0\rightarrow {F'}_{(\bar{q}q)ud}^{+} {\overline{p}})&=\Gamma ({\overline{B}}^0\rightarrow {F'}_{(\bar{q}q)us}^{+} {\overline{\Sigma }}^-)\\ = \Gamma ({\overline{B}}^0_s\rightarrow {F'}_{(\bar{q}q)ud}^{+} {\overline{\Sigma }}^-)&=\Gamma ({\overline{B}}^0_s\rightarrow F_{\bar{s}udd}^{+} {\overline{p}}),\\ \Gamma ({\overline{B}}^0\rightarrow F_{(\bar{q}q)ud}^{+} {\overline{p}})&=\frac{2}{3}\Gamma ({\overline{B}}^0\rightarrow {F'}_{(\bar{q}q)ds}^{0} {\overline{\Lambda }}^0)\\ =2\Gamma ({\overline{B}}^0\rightarrow {F'}_{(\bar{q}q)ds}^{0} {\overline{\Sigma }}^0)&=\Gamma ({\overline{B}}^0\rightarrow F_{\bar{u}dss}^- {\overline{\Xi }}^+),\\&\Gamma ({\overline{B}}^0\rightarrow {F'}_{(\bar{q}q)us}^{+} {\overline{p}})\\ =\Gamma ({\overline{B}}^0\rightarrow F_{\bar{d}uss}^+ {\overline{\Sigma }}^-)&=\Gamma ({\overline{B}}^0_s\rightarrow {F'}_{(\bar{q}q)us}^{+} {\overline{\Sigma }}^-)\\&=\Gamma ({\overline{B}}^0_s\rightarrow {F'}_{(\bar{q}q)ud}^{+} {\overline{p}}),\\&\qquad \Gamma ({\overline{B}}^0_s\rightarrow F_{(\bar{q}q)us}^{+} {\overline{\Sigma }}^-)\\&= \Gamma ({\overline{B}}^0_s\rightarrow F_{\bar{u}dds}^{-} {\overline{\Sigma }}^+)\\&= \frac{1}{2}\Gamma ({\overline{B}}^0_s\rightarrow F_{(\bar{q}q)ds}^{0} {\overline{\Sigma }}^0),\\ \Gamma (B^-\rightarrow F_{(\bar{q}q)ud}^{+} {\overline{\Delta }}^{{-}{-}})&=3\Gamma (B^-\rightarrow F_{(\bar{u}u,\bar{s}s)dd}^{0} {\overline{\Delta }}^{-})\\ =\frac{3}{4}\Gamma (B^-\rightarrow F_{(\bar{q}q)ds}^{0} {\overline{\Sigma }}^{\prime -})&=3\Gamma (B^-\rightarrow {F'}_{(\bar{q}q)ds}^{0} {\overline{\Sigma }}^{\prime -})\\ =6\Gamma (B^-\rightarrow F_{\bar{u}dds}^{-} {\overline{\Sigma }}^{\prime 0})&=3\Gamma (B^-\rightarrow F_{\bar{u}dss}^- {\overline{\Xi }}^{\prime 0}),\\ \Gamma (B^-\rightarrow F_{(\bar{q}q)us}^{+} {\overline{\Delta }}^{{-}{-}})&=\frac{3}{4}\Gamma (B^-\rightarrow F_{(\bar{q}q)ds}^{0} {\overline{\Delta }}^{-})\\ =3\Gamma (B^-\rightarrow {F'}_{(\bar{q}q)ds}^{0} {\overline{\Delta }}^{-})&=3\Gamma (B^-\rightarrow F_{\bar{u}dds}^{-} {\overline{\Delta }}^{0})\\ =3\Gamma (B^-\rightarrow F_{(\bar{u}u,\bar{d}d)ss}^{0} {\overline{\Sigma }}^{\prime -})&=6\Gamma (B^-\rightarrow F_{\bar{u}dss}^- {\overline{\Sigma }}^{\prime 0}),\\ \Gamma ({\overline{B}}^0\rightarrow F_{(\bar{d}d,\bar{s}s)uu}^{++} {\overline{\Delta }}^{{-}{-}})&=3\Gamma ({\overline{B}}^0\rightarrow {F'}_{(\bar{q}q)ud}^{+} {\overline{\Delta }}^{-})\\ =3\Gamma ({\overline{B}}^0\rightarrow F_{(\bar{q}q)us}^{+} {\overline{\Sigma }}^{\prime -})&=4\Gamma ({\overline{B}}^0\rightarrow {F'}_{(\bar{q}q)us}^{+} {\overline{\Sigma }}^{\prime -})\\ =3\Gamma ({\overline{B}}^0\rightarrow F_{(\bar{u}u,\bar{d}d)ss}^{0} {\overline{\Xi }}^{\prime 0})&=\Gamma ({\overline{B}}^0_s\rightarrow F_{\bar{s}uud}^{++} {\overline{\Delta }}^{{-}{-}} )\\ =3\Gamma ({\overline{B}}^0_s\rightarrow F_{\bar{s}udd}^{+} {\overline{\Delta }}^{-})&=3\Gamma ({\overline{B}}^0_s\rightarrow {F'}_{(\bar{q}q)ud}^{+} {\overline{\Sigma }}^{\prime -}),\\ \Gamma ({\overline{B}}^0\rightarrow F_{(\bar{q}q)ud}^{+} {\overline{\Delta }}^{-})&=\Gamma ({\overline{B}}^0\rightarrow F_{(\bar{u}u,\bar{s}s)dd}^{0} {\overline{\Delta }}^{0})\\ =\frac{1}{2}\Gamma ({\overline{B}}^0\rightarrow {F'}_{(\bar{q}q)ds}^{0} {\overline{\Sigma }}^{\prime 0})&=\Gamma ({\overline{B}}^0\rightarrow F_{\bar{u}dds}^{-} {\overline{\Sigma }}^{\prime +})\\ =\Gamma ({\overline{B}}^0\rightarrow F_{\bar{u}dss}^- {\overline{\Xi }}^{\prime +})&=\Gamma ({\overline{B}}^0_s\rightarrow F_{(\bar{q}q)ds}^{0} {\overline{\Xi }}^{\prime 0} )\\ =\Gamma ({\overline{B}}^0_s\rightarrow F_{\bar{u}dds}^{-} {\overline{\Xi }}^{\prime +})&=\frac{1}{3}\Gamma ({\overline{B}}^0_s\rightarrow F_{\bar{u}dss}^- {\overline{\Omega }}^+),\\ \Gamma ({\overline{B}}^0\rightarrow F_{\bar{d}uus}^{++} {\overline{\Delta }}^{{-}{-}})&=3\Gamma ({\overline{B}}^0\rightarrow {F'}_{(\bar{q}q)us}^{+} {\overline{\Delta }}^{-})\\ =3\Gamma ({\overline{B}}^0\rightarrow F_{\bar{d}uss}^+ {\overline{\Sigma }}^{\prime -})&=\Gamma ({\overline{B}}^0_s\rightarrow F_{(\bar{d}d,\bar{s}s)uu}^{++} {\overline{\Delta }}^{{-}{-}}) \end{aligned}$$

$$\begin{aligned} =3\Gamma ({\overline{B}}^0_s\rightarrow {F'}_{(\bar{q}q)ud}^{+} {\overline{\Delta }}^{-} )&=3\Gamma ({\overline{B}}^0_s\rightarrow F_{(\bar{q}q)ud}^{+} {\overline{\Delta }}^{-})\\ =3\Gamma ({\overline{B}}^0_s\rightarrow F_{(\bar{u}u,\bar{s}s)dd}^{0} {\overline{\Delta }}^{0})&=3\Gamma ({\overline{B}}^0_s\rightarrow {F'}_{(\bar{q}q)us}^{+} {\overline{\Sigma }}^{\prime -}),\\ \Gamma ({\overline{B}}^0\rightarrow {F'}_{(\bar{q}q)ds}^{0} {\overline{\Delta }}^{0})&=\frac{1}{3}\Gamma ({\overline{B}}^0\rightarrow F_{\bar{u}dds}^{-} {\overline{\Delta }}^{+})\\ =\Gamma ({\overline{B}}^0\rightarrow F_{\bar{u}dss}^- {\overline{\Sigma }}^{\prime +})&=\Gamma ({\overline{B}}^0_s\rightarrow F_{(\bar{q}q)us}^{+} {\overline{\Sigma }}^{\prime -})\\ =\frac{1}{2}\Gamma ({\overline{B}}^0_s\rightarrow F_{(\bar{q}q)ds}^{0} {\overline{\Sigma }}^{\prime 0})&=\Gamma ({\overline{B}}^0_s\rightarrow F_{\bar{u}dds}^{-} {\overline{\Sigma }}^{\prime +})\\ =\Gamma ({\overline{B}}^0_s\rightarrow F_{(\bar{u}u,\bar{d}d)ss}^{0} {\overline{\Xi }}^{\prime 0})&=\Gamma ({\overline{B}}^0_s\rightarrow F_{\bar{u}dss}^- {\overline{\Xi }}^{\prime +}),\\ \Gamma ({\overline{B}}^0_s\rightarrow F_{(\bar{u}u,\bar{s}s)dd}^{0} {\overline{\Sigma }}^{\prime 0})&=\Gamma ({\overline{B}}^0\rightarrow F_{(\bar{q}q)ds}^{0} {\overline{\Sigma }}^{\prime 0}),\\ \Gamma ({\overline{B}}^0_s\rightarrow {F'}_{(\bar{q}q)ds}^{0} {\overline{\Sigma }}^{\prime 0})&=\Gamma ({\overline{B}}^0\rightarrow F_{(\bar{u}u,\bar{d}d)ss}^{0} {\overline{\Sigma }}^{\prime 0}),\\ \Gamma ({\overline{B}}^0\rightarrow F_{(\bar{u}u,\bar{s}s)dd}^{0} {\overline{n}})&= \Gamma ({\overline{B}}^0\rightarrow F_{\bar{u}dds}^{-} {\overline{\Sigma }}^+),\\ \Gamma ({\overline{B}}^0\rightarrow {F'}_{(\bar{q}q)ds}^{0} {\overline{n}})&=\Gamma ({\overline{B}}^0\rightarrow F_{\bar{u}dss}^- {\overline{\Sigma }}^+),\\ \Gamma ({\overline{B}}^0_s\rightarrow F_{(\bar{q}q)ds}^{0} {\overline{\Xi }}^0)&= \Gamma ({\overline{B}}^0_s\rightarrow F_{\bar{u}dds}^{-}{\overline{\Xi }}^+),\\ \Gamma ({\overline{B}}^0_s\rightarrow F_{(\bar{u}u,\bar{d}d)ss}^{0} {\overline{\Xi }}^0)&= \Gamma ({\overline{B}}^0_s\rightarrow F_{\bar{u}dss}^- {\overline{\Xi }}^+),\\ \Gamma (B^-\rightarrow F_{(\bar{q}q)ds}^{0} {\overline{\Sigma }}^-)&= 2\Gamma (B^-\rightarrow F_{\bar{u}dds}^{-} {\overline{\Sigma }}^0),\\ \Gamma (B^-\rightarrow F_{(\bar{u}u,\bar{d}d)ss}^{0} {\overline{\Sigma }}^-)&= 2\Gamma (B^-\rightarrow F_{\bar{u}dss}^- {\overline{\Sigma }}^0). \end{aligned}$$