1 Introduction

The searching for physics beyond the Standard Model (SM) has been one major part of particle physics research in high energy physics. In the flavor sector the lepton flavor universal is a key property of the SM gauge interactions. Evidence for violation of the property would be a clear sign of new physics (NP) beyond the SM. In the searching of NP, the second and third generation quarks and leptons are very important because they are comparatively heavier and are expected to be sensitive to NP. Exclusive \({B} \rightarrow D^{(*)} \ell \bar{\nu }_{\ell } \) decays have become precision probe of the semileptonic parton level transitions \( b\rightarrow c \ell \bar{\nu }_{\ell } \). The processes can provide excellent means for the determination of the corresponding Cabibbo–Kobayashi–Maskawa (CKM) matrix element \(V_{cb}\) of the SM. The combination of theoretical control and good experimental renders them to become very sensitive NP which potentially modifies both the angular distribution and normalization of these decay modes.

In recent years, the anomalous measurements on \({B} \rightarrow D^{(*)} \tau ^-\bar{\nu }_{\tau } \) decays indicate that the existence of NP that breaks the lepton flavour universality in \(b\rightarrow c \tau ^-\bar{\nu }_{\tau } \) transition [1,2,3,4,5,6,7,8,9,10]. The averaging results about \(R_{D^{(*)}}\) have been performed by the Heavy Flavor Averaging Group (HFLAV) [6], combining different experimental data by the BaBar [1, 2], Belle [4, 5, 7, 8] and LHCb [3, 9, 10] collaborations. The corresponding SM results shown in Ref. [6], \(R_{D}=0.299\pm 0.003\) and \(R_{D^*}=0.254\pm 0.005\), are obtained from the SM predictions in refs [11,12,13]. The \(R_{D^{(*)}}\) averaged experimental results exhibit a deviation with respect to the SM expectations by \(1.4\sigma \) and \(2.8\sigma \) level, respectively.

Apart from \(R_{D^{(*)}}\) measurements, the ratio \(R_{J/\psi }\) of the decay \(B_c\rightarrow J/\psi \ell \bar{\nu }_{\ell }\) has been measured by the LHCb collaboration [14] and it shows about \(1.8\sigma \) discrepancy with SM results, which are in the range \(R_{J/\psi }\approx [0.25,0.28]\) [15,16,17,18,19,20]. The \(B_c\rightarrow J/\psi \) transition form factors from the lattice QCD [21, 22] make the theoretical calculations more accurate, which makes it more interesting to revisit the NP effects in the \(B_c\rightarrow J/\psi \ell \bar{\nu }_{\ell }\) decays. At the same time, taking advantage of the results of Ref. [23], \(B_c\) decays induced by the \(c\rightarrow d/s \) transition at the quark level are also being investigated as a possible source of NP [24].

Motivated by above deviations, a lot of global fitting analyses have been carried out and find some different combinations of NP coupling parameters can well explain these anomalies [25,26,27,28,29]. The possibilities of extracting constraints on NP coupling parameters by using the current experimental results on the leptonic and semileptonic decays of pseudoscalar mesons have been studied in detail in many works. Furthermore, many works have been done based on the model independent framework [30,31,32,33,34,35] and some specific NP models by introducing new particles, such as charged Higgses model [36,37,38,39], R-parity violating supersymmetric models [40,41,42,43,44] and leptoquarks model [45,46,47,48,49]. And the NP effects can affect the corresponding \(b\rightarrow c(u) \ell \bar{\nu }_{\ell }\) processes, such as bottom meson decay processes \(B_c\rightarrow J/\psi (\eta _c) \ell \bar{\nu }_{\ell }\) [17,18,19,20, 50, 51], \(B^{(*)}\rightarrow P(V) \ell \bar{\nu }_{\ell }\) [32, 52,53,54,55] and bottom baryons decay processes \(\Lambda _b\rightarrow \Lambda _c (p)\ell \bar{\nu }_{\ell }\) [33, 56, 57], \(\Omega _b\rightarrow \Omega _c \ell \bar{\nu }_{\ell }\) [58], \(\Xi _b\rightarrow \Xi _c \ell \bar{\nu }_{\ell }\) [31], \(\Sigma _b\rightarrow \Sigma _c \ell \bar{\nu }_{\ell }\) [58,59,60].

The pseudoscalar heavy mesons, namely \(B_{u,d,c,s}\) have been studied extensively both in experiments and theories and they can only decay weakly. So these decays can provide an opportunity to do the precision investigation tests both in the SM and NP model. However, the vector mesons, \(B_{u,d,c,s}^*\) still lack enough experimental data (see [61]). The most important reason for this is that their production rates and detection efficiency are lower than the pseudoscalar partners. We hope the situation will become better because LHCb collecting more and more data and the experiments will make precise detection be possible. Besides, the future B factories, such as Belle II, will provide more information for these vector mesons. Another important property of these particles is that their masses are not large enough to decay to the corresponding pseudoscalar partner and light mesons via strong interaction. But they can decay weakly and electromagnetically. The partial widths of the electromagnetic decay channels, especially the photon decay process, are very dominant and can be used to estimate the total widths. And these channels can make the branching ratios of the weak decay processes to be within the detection ability of current experiments.

Recently, there are some interests of investigation about the \(B^*\) weak decays mediated by the quark level transition \(b\rightarrow s \ell ^+\ell ^-\) and \(b\rightarrow c(u)\ell ^-\bar{\nu }_{\ell }\) have been done both in the SM and the NP models [62,63,64,65,66]. So the theoretical study of these vector heavy mesons is also of interest and becomes more and more necessary. In this work, using the best fit solutions for the Wilson coefficients of the new operator and the relevant form factors resulted in the light-front quark model, we will provide numerical results and the contribution of NP effect on some observables which have not yet been measured, such as the differential decay rate \(d\Gamma /dq^2\), the ratio of the branching fraction \(R_V^*(q^2)\), the longitudinal polarization fraction of the daughter meson \(F_L^{*V}(q^2)\), the lepton forward-backward asymmetry \(A_{FB}^l(q^2)\), the lepton spin asymmetry \(P_{l}(q^2)\), the convexity parameter \(C_F^{l}(q^2)\) and other interesting observables.

The outline of this paper is as follows: The theory framework of our calculation is given in Sect. 2, which contain the corresponding low-energy effective Hamiltonian as well as the helicity amplitudes and some observables of the \(\bar{B}^* \rightarrow V \ell \bar{\nu }_{\ell }\) decays. The numerical results and discussions about the observables within the SM and in various NP scenarios are given in Sect. 3. Finally, Sect. 4 is devoted to our summary and conclusion.

2 Theory framework

2.1 Effective Hamiltonian

For \(\bar{B}^* \rightarrow V \ell ^- \bar{\nu }_{\ell }\) processes mediated by the quark level transition \(b\rightarrow c \ell ^- \bar{\nu }_{\ell }\), when we consider the NP contribution, the general effective Lagrangian is given by [19, 33, 67,68,69,70]

$$\begin{aligned} \mathcal L_\mathrm{eff}= & {} -\frac{4G_F}{\sqrt{2}}V_{c b}\,\Bigg \{(1 + V_L)\,\bar{l}_L\,\gamma _{\mu }\,\nu _L\,\bar{c}_L\,\gamma ^{\mu }\,b_L \nonumber \\&+V_R\,\bar{l}_L\,\gamma _{\mu }\,\nu _L\,\bar{c}_R\,\gamma ^{\mu }\,b_R \ +S_L\,\bar{l}_R\,\nu _L\,\bar{c}_R\,b_L \nonumber \\&+S_R\,\bar{l}_R\,\nu _L\,\bar{c}_L\,b_R \Bigg \} + \mathrm{h.c.}, \end{aligned}$$
(1)

where \(G_F\) is the Fermi constant and \(V_{cb}\) is the CKM matrix element. In Eq. (1), we do not consider the contributions of the right-handed neutrinos and the tensor operator. When we set the NP couplings \(V_L=V_R=S_L=S_R=0\), the SM contribution can be obtained.

We will consider the kinematics of the process \(\bar{B}^* \rightarrow V \ell ^- \bar{\nu }_{\ell }\) using the helicity amplitudes. In the formalism, \(\bar{B}^* \rightarrow V \ell ^- \bar{\nu }_{\ell }\) is considered to proceed through \(\bar{B}^* \rightarrow V W^{*-}\) and the off-shell \(W^{*-}\) decays to \(\ell ^-\bar{\nu }_{\ell }\). Using Eq. (1), the amplitudes of \(\bar{B}^* \rightarrow V \ell ^- \bar{\nu }_{\ell }\) can be written as

$$\begin{aligned} M(\bar{B}^*\rightarrow V l \bar{\nu }_l )=\frac{G_F}{\sqrt{2}}V_{cb}\sum _{k}C_k\langle V|\bar{c}\Gamma ^kb\rangle ~\bar{u}_{\ell }~\Gamma _k~\nu _{\nu } \end{aligned}$$
(2)

where \(\Gamma ^k\) is the product of gamma matrices that can give rise to different Lorentz structure of hadronic and leptonic currents shown in the Eq. (1), such as \(\Gamma ^k=\gamma ^{\mu }(1\pm \gamma _5)\) or \((1\pm \gamma _5)\). \(C_k\) is the NP coupling parameters with the following values

$$\begin{aligned} C_k=&\Bigg \{ \begin{array}{ll} 1 &{}\quad \mathrm{for~ SM} \\ V_{L,R},S_{L,R} &{}\quad \mathrm{for~ NP} \end{array} \Bigg . ~, \end{aligned}$$
(3)

and the square of the matrix element can be written as the product of leptonic (\(L_{\mu \nu }\)) and hadronic (\(H^{\mu \nu }\)) tensors. So the square amplitude can be written as

$$\begin{aligned} |M(\bar{B}^*\rightarrow V \ell \bar{\nu }_{\ell } )|^2 =\frac{G_F^2}{2}|V_{cb}|^2 \sum _{ij}C_{i,j}( L_{\mu \nu }^{ij}H^{\mu \nu ,ij} ) \end{aligned}$$
(4)

where the superscripts i, j represent the combination of the operators \(V\pm A\) and \(S\pm P\). One can refer to Refs. [32, 54, 55] for more details.

2.2 Form factors and helicity amplitude

For the \(\bar{B}^* \rightarrow V \ell ^- \bar{\nu }_{\ell }\) decay, the hadronic helicity amplitudes are defined as

$$\begin{aligned} H^{V_L,V_R}_{\lambda _{W^*}\lambda _{B^*}\lambda _{V}}(q^2)= & {} \langle V(p_V,\lambda _{V})|\bar{c}\gamma _{\mu }(1 \pm \gamma _5)b|\bar{B}^*(p_{B^*},\lambda _{B^*}) \rangle \bar{\epsilon }^{*\mu }(\lambda _{W^*}), \nonumber \\ H^{S_L,S_R}_{\lambda _{B^*}\lambda _{V}}(q^2)= & {} \langle V(p_V,\lambda _{V})|\bar{c}(1 \pm \gamma _5)b|\bar{B}^*(p_{B^*},\lambda _{B^*}) \rangle , \end{aligned}$$
(5)

this describe the decay of three helicity states of \(B^*\) meson into a vector meson V with three helicity states and the four helicity states of virtual W. The helicity states of both \(B^*\) and daughter meson V are \(\lambda _{B^*(V)}=0,\pm \), and \(\lambda _{W^*}=t,0,\pm \).

In order to calculate above hadronic helicity amplitudes, the following matrix elements for \(B^*\rightarrow V\) process can be used in this work [71, 72].

$$\begin{aligned}&\langle V(\epsilon _2, p_{V})|\bar{c}\gamma _{\mu } b|\bar{B}^*(\epsilon _1, p_{B^*})\rangle \\&\quad =(\epsilon _1 \!\cdot \epsilon _2^{*})\left[ -P_{\mu }\,V_1(q^2)+q_{\mu }\,V_2(q^2)\right] \\&\qquad +\frac{(\epsilon _1 \!\cdot \! q)(\epsilon _2^{*}\!\cdot q)}{m_{B^*}^2-m_{V}^2}\left[ P_{\mu }\!V_3(q^2)\!-q_{\mu }\!V_4(q^2)\right] \\&\qquad -(\epsilon _1\! \cdot q)\epsilon _{2\mu }^* \!V_5(q^2)+(\epsilon _2^*\! \cdot q)\epsilon _{1\mu }\!V_6(q^2)\!,\\&\langle V(\epsilon _2, p_V)|\bar{c} \gamma _{5} \gamma _{\mu } b|\bar{B}^*(\epsilon _1, p_{B^*})\rangle \\&\quad = -i\varepsilon _{\mu \nu \alpha \beta }\epsilon _1^{\alpha }\epsilon _2^{*\beta }\left[ P^{\nu }\!A_1(q^2)\!-\!q^{\nu }\!A_2(q^2)\right] \\&\qquad -\frac{i\epsilon _2^{*}\cdot q}{m_{B^*}^2-m_{V}^2}\varepsilon _{\mu \nu \alpha \beta }\epsilon _1^{\nu }P^{\alpha }q^{\beta }\,A_3(q^2)\\&\qquad +\frac{i\epsilon _1\cdot q}{m_{B^*}^2-m_{V}^2}\varepsilon _{\mu \nu \alpha \beta }\epsilon _2^{*\nu } P^{\alpha }q^{\beta }A_4(q^2) \end{aligned}$$

where \(V_{1,2,3,4,5,6}(q^2)\) and \(A_{1,2,3,4}(q^2)\) are the various form factors for \(B^* \rightarrow V \ell \bar{\nu }_{\ell }\). Furthermore, using the equation of motion,

$$\begin{aligned} i\partial _\mu (\bar{c}\gamma ^{\mu }b)= & {} (m_b-m_c)\bar{c}b, \nonumber \\ i\partial _\mu (\bar{c}\gamma ^{\mu }\gamma _5b)= & {} -(m_b+m_c)\bar{c}\gamma _5b, \end{aligned}$$
(6)

we can obtain the matrix elements for the scalar and pseudoscalar currents and they can be written as

$$\begin{aligned}&\langle V(\epsilon _2,p_V)|\bar{c}b|\bar{B}^*(\varepsilon _1,p_{B^*})\rangle = \frac{1}{m_b-m_c}\\&\quad \times \Bigg \{ (\epsilon _1 \cdot \epsilon _2^{*}) \left[ -P\cdot q\,V_1(q^2)+q^2~V_2(q^2)\right] \\&\quad +\frac{(\epsilon _1\! \cdot q)(\epsilon _2^{*}\cdot q)}{m_{B^*}^2-m_{V}^2}\left[ P\cdot q\,V_3(q^2)-q^2V_4(q^2)\right] \\&\quad -(\epsilon _1 \cdot q)\,(\epsilon _{2}^*\cdot q) \,V_5(q^2)\\&\quad +(\epsilon _2^* \cdot q)\,(\epsilon _{1}\cdot q)\,V_6(q^2)\Bigg \}, \\&\langle V(\epsilon _2,p_V)|\bar{c}\gamma _5b|\bar{B}^*(\varepsilon _1,p_{B^*})\rangle =\frac{-1}{m_b+m_c} \\&\quad \times \Bigg \{ i\varepsilon _{\mu \nu \alpha \beta }~q^{\mu }\epsilon _1^{\alpha }\epsilon _2^{*\beta }\left[ P^{\nu }\,A_1(q^2)-q^{\nu }\,A_2(q^2)\right] \\&\quad +\frac{i\epsilon _2^{*}\cdot q}{m_{B^*}^2-m_{V}^2}\varepsilon _{\mu \nu \alpha \beta }~q^{\mu }\epsilon _1^{\nu }P^{\alpha }q^{\beta }\,A_3(q^2) \\&\quad -\frac{i\epsilon _1\cdot q}{m_{B^*}^2-m_{V}^2}\varepsilon _{\mu \nu \alpha \beta }~q^{\mu }\epsilon _2^{*\nu } P^{\alpha }q^{\beta }A_4(q^2) \Bigg \}. \end{aligned}$$

where the \(m_{b,c}\) represent the current quark masses.

The detailed expressions about momenta of the meson \(B^*\), V and virtual \(W^*\), as well as the polarization vectors of them are given in Ref. [55]. Then, by contracting above hadronic matrix elements with the polarization vectors in the \(B^*\) meson rest frame, we obtain following non-vanishing helicity amplitudes for hadronic current \(V\pm A\) and \(S\pm P\)

$$\begin{aligned} H_{0++}(q^2)= & {} -\frac{m_{B^*}^2-m_{V}^2}{\sqrt{q^2}}A_1(q^2)+\sqrt{q^2}A_2(q^2)+\frac{2m_{B^*}|\mathbf {p}|}{\sqrt{q^2}}V_1(q^2),\\ H_{t++}(q^2)= & {} -\frac{2m_{B^*}|\mathbf {p}|}{\sqrt{q^2}}A_1(q^2)+\frac{m_{B^*}^2-m_{V}^2}{\sqrt{q^2}}V_1(q^2)-\sqrt{q^2}V_2(q^2),\\ H_{-+0}(q^2)= & {} -\frac{m_{B^*}^2+3m_{V}^2-q^2}{2m_{V}}A_1(q^2)+\frac{(m_{B^*}^2-m_{V}^2-q^2)}{2m_{V}}A_2(q^2)\\&-\frac{2m_{B^*}^2|\mathbf {p}|^2}{m_{V}(m_{B^*}^2-m_{V}^2)}A_3(q^2)-\frac{m_{B^*}|\mathbf {p}|}{m_{V}}V_6(q^2),\\ H_{0--}(q^2)= & {} \frac{m_{B^*}^2-m_{V}^2}{\sqrt{q^2}}A_1(q^2)-\sqrt{q^2}A_2(q^2)+\frac{2m_{B^*}|\mathbf {p}|}{\sqrt{q^2}}V_1(q^2),\\ H_{t--}(q^2)= & {} \frac{2m_{B^*}|\mathbf {p}|}{\sqrt{q^2}}A_1(q^2)+\frac{m_{B^*}^2-m_{V}^2}{\sqrt{q^2}}V_1(q^2)-\sqrt{q^2}V_2(q^2),\\ H_{+-0}(q^2)= & {} \frac{m_{B^*}^2+3m_{V}^2-q^2}{2m_{V}}A_1(q^2)-\frac{(m_{B^*}^2-m_{V}^2-q^2)}{2m_{V}}A_2(q^2)\\&+\frac{2m_{B^*}^2|\mathbf {p}|^2}{m_{V}(m_{B^*}^2-m_{V}^2)}A_3(q^2)-\frac{m_{B^*}|\mathbf {p}|}{m_{V}}V_6(q^2),\\ H_{+0+}(q^2)= & {} \frac{3m_{B^*}^2+m_{V}^2-q^2}{2m_{B^*}}A_1(q^2)-\frac{(m_{B^*}^2-m_{V}^2+q^2)}{2m_{B^*}}A_2(q^2)\\&+\frac{2m_{B^*}|\mathbf {p}|^2}{m_{B^*}^2-m_{V}^2}A_4(q^2)-|\mathbf {p}|V_5(q^2)\,,\\ H_{-0-}(q^2)= & {} -\frac{3m_{B^*}^2+m_{V}^2-q^2}{2m_{B^*}}A_1(q^2)+\frac{(m_{B^*}^2-m_{V}^2+q^2)}{2m_{B^*}}A_2(q^2)\\&-\frac{2m_{B^*}|\mathbf {p}|^2}{m_{B^*}^2-m_{V}^2}A_4(q^2)-|\mathbf {p}|V_5(q^2)\,,\\ H_{000}(q^2)= & {} \frac{|\mathbf {p}|(m_{B^*}^2+m_{V}^2-q^2)}{\sqrt{q^2}m_{V}}V_1(q^2)\\&+\frac{2m_{B^*}^2|\mathbf {p}|^3}{\sqrt{q^2}m_{V}(m_{B^*}^2-m_{V}^2)}V_3(q^2)\\&-\frac{|\mathbf {p}|(m_{B^*}^2-m_{V}^2-q^2)}{2\sqrt{q^2}m_{V}}V_5(q^2)\\&+\frac{|\mathbf {p}|(m_{B^*}^2-m_{V}^2+q^2)}{2\sqrt{q^2}m_{V}}V_6(q^2)\,,\\ H_{t00}(q^2)= & {} \frac{(m_{B^*}^2-m_{V}^2)(m_{B^*}^2+m_{V}^2-q^2)}{2\sqrt{q^2}m_{B^*}m_{V}}V_1(q^2)\\&-\frac{\sqrt{q^2}(m_{B^*}^2+m_{V}^2-q^2)}{2m_{B^*}m_{V}}V_2(q^2)\\&+\frac{m_{B^*}|\mathbf {p}|^2}{\sqrt{q^2}m_{V}}V_3(q^2)-\frac{m_{B^*}|\mathbf {p}|^2\sqrt{q^2}}{m_{V}(m_{B^*}^2-m_{V}^2)}V_4(q^2)\\&-\frac{m_{B^*}|\mathbf {p}|^2}{\sqrt{q^2}m_{V}}V_5(q^2)+\frac{m_{B^*}|\mathbf {p}|^2}{\sqrt{q^2}m_{V}}V_6(q^2)\,,\\ H_{++}(q^2) \!= & {} \!\frac{1}{m_b-m_c}\left[ (m_{B^*}^2\!-\!m_{V}^2) V_1(q^2)\!-\!q^2 V_2(q^2)\right] \!\\&+ \frac{2m_{B^*}|\mathbf {p}|}{m_b+m_c}A_1(q^2) , \\ H_{--}(q^2)\!= & {} \!\frac{1}{m_b-m_c}\left[ (m_{B^*}^2\!-\!m_{V}^2) V_1(q^2)\!-\!q^2 V_2(q^2)\right] \! \\&- \frac{2m_{B^*}|\mathbf {p}|}{m_b+m_c}A_1(q^2) , \\ H_{00}(q^2)= & {} \frac{1}{m_b-m_c}\{ \frac{m_{B^*}^2+m_{V}^2-q^2}{2m_{B^*}m_{V}}[ (m_{B^*}^2-m_{V}^2)V_2(q^2) \\&-q^2V_2(q^2) ] + \frac{|\mathbf {p}|^2 m_{B^*} }{m_{V}} [ \frac{-q^2}{m_{B^*}^2-m_{V}^2 }V_4(q^2)\\&+V_3(q^2)-V_5(q^2)+V_6(q^2) ] \}. \end{aligned}$$

where \(|\mathbf {p}|=\lambda ^{1/2}(m_{B^*}^2,m_V^2,q^2)\), \(\lambda (a,b,c)\equiv a^2+b^2+c^2- 2(ab+bc+ac)\) and \(m_l^2\le q^2 \le (m_{B^*}-m_V)^2\).

2.3 The decay distribution and other observables

We collect the formulae for the main observables entering our analysis, and from the effective Lagrangian of Eq. (1) we can obtain the differential decay rates as a function of the general set of Wilson coefficients and \(q^2\) with a given leptonic helicity state (\(\lambda _{\ell }=\pm \frac{1}{2}\))

$$\begin{aligned} \frac{d^2 \mathrm \Gamma ^{\lambda _{\ell }=1/2}}{dq^2d\cos \theta _l}= & {} \frac{G_F^2|V_{cb}|^2|\mathbf {p}|}{256\pi ^3m_{B^*}^2}\,\frac{1}{3}q^2\left( 1-\frac{m_\ell ^2}{q^2}\right) ^2\,\frac{m_{\ell }^2}{q^2} \Bigg \{ (|1+V_L|^2+|V_R|^2) \nonumber \\&\times \bigg [ \text {sin}^2\theta _l (H_{+0+}^2 +H_{+-0}^2+H_{-0-}^2+H_{-+0}^2)\nonumber \\&+2(H_{t++}-\text {cos}\,\theta _l\,H_{0++})^2+2(H_{t--}-\text {cos}\,\theta _l\,H_{0--})^2\nonumber \\&+2(H_{t00}-\text {cos}\,\theta _l\,H_{000})^2 \bigg ] +4Re[(1+V_L)V_R^*]\nonumber \\&\times \bigg [ \text {sin}^2\theta _l(H_{+0+}H_{-0-}+H_{+-0}H_{-+0})\nonumber \\&+ (H_{t00}-\text {cos}\,\theta _l\,H_{000})^2 +2(H_{t++}-\text {cos}\,\theta _l\,H_{0++})\nonumber \\&\times (H_{t--}-\text {cos}\,\theta _l\,H_{0--}) \bigg ]+ \frac{2q^2}{m_{\ell }^2} \bigg [ (|S_L|^2+|S_R|^2 )\nonumber \\&\times ( H_{00}^2+H_{++}^2+H_{--}^2 ) + 2Re[S_LS_R^*]( H_{00}^2+2H_{++}H_{--}) \bigg ]\nonumber \\&+ \frac{2\sqrt{q^2}}{m_{\ell }} 2Re[(1+V_L)S_L^* +V_RS_R^*]\bigg [ H_{00}(H_{t00}- H_{000} \text {cos}\theta _l)\nonumber \\&\! +H_{++}(H_{t++}\!-\! H_{0++} \text {cos}\theta _l)\!+\! H_{--}(H_{t--}\!- \!H_{0--} \text {cos}\theta _l) \bigg ]\nonumber \\&+ \frac{2\sqrt{q^2}}{m_{\ell }} 2Re[(1+V_L)S_R^* +V_RS_L^*]\bigg [ H_{00}(H_{t00}- H_{000} \text {cos}\theta _l)\nonumber \\&\!+H_{--}(H_{t++}\!-\! H_{0++} \text {cos}\theta _l)\!+\! H_{++}\!(H_{t--}\!-\! H_{0--}\! \text {cos}\theta _l) \bigg ]\Bigg \},\nonumber \\ \frac{d^2 \mathrm \Gamma ^{\lambda _{\ell }=-1/2}}{dq^2d\cos \theta _l}= & {} \frac{G_F^2|V_{cb}|^2|\mathbf {p}|}{256\pi ^3m_{B^*}^2}\,\frac{1}{3}q^2\left( 1-\frac{m_\ell ^2}{q^2}\right) ^2\, \Bigg \{ \Big [|1+V_L|^2 (1-\text {cos}\,\theta _l)^2\nonumber \\&+ |V_R|^2 (1+\text {cos}\,\theta _l)^2 \Big ](H_{+0+}^2+H_{+-0}^2)\nonumber \\&+\Big [|1+V_L|^2 (1+\text {cos}\,\theta _l)^2 + |V_R|^2 (1-\text {cos}\,\theta _l)^2 \Big ]\nonumber \\&\times (H_{-0-}^2+H_{-+0}^2)+ \big ( |1+V_L|^2+|V_R|^2 \big ) 2\sin \theta _{\ell }^2 \nonumber \\&\times \Big ( H_{000}^2+H_{0++}^2+H_{0--}^2 \Big ) +4Re[(1+V_L)V_R^*]\nonumber \\&\times \bigg [(1+\text {cos}\,\theta _l^2 ) \Big ( H_{+0+}H_{-0-}+H_{+-0}H_{-+0} \Big )\nonumber \\&+\text {sin}^2\,\theta _l( H_{000}^2 + 2H_{0++}H_{0--} )\bigg ] \Bigg \}, \end{aligned}$$
(7)

where the values of the helicity amplitudes are given in Sect. 2.2. Form Eq. (7), we note that the distributions for \(\lambda _{\ell }=-1/2\) do not contain the coupling parameter \(S_{L,R}\) which make them totally insensitive to the NP scalar operators. After integrating over \(\cos \theta _{\ell }\) we can get the \(q^2\) dependent differential decay rate \(d\Gamma ^{\lambda _{\ell }=\pm \frac{1}{2}}/dq^2\) and then can also get \(d\Gamma /dq^2\) after summing over \(d\Gamma ^{\lambda _{\ell }=+\frac{1}{2}}/dq^2\) and \(d\Gamma ^{\lambda _{\ell }=-\frac{1}{2}}/dq^2\)

$$\begin{aligned} \frac{d\mathrm \Gamma }{dq^2}= & {} \frac{G_F^2|V_{cb}|^2|\mathbf {p}|}{288\pi ^3m_{B^*}^2}\, q^2\,\left( 1-\frac{m_\ell ^2}{q^2}\right) ^2\,\Bigg \{ ( |1+V_L|^2+ |V_R|^2) \Big [\frac{3m_{\ell }^2}{2q^2}\nonumber \\&\times (H_{t++}^2+H_{t--}^2+H_{t00}^2)+(1+\frac{m_{\ell }^2}{2q^2})\big ( H_{+0+}^2+H_{+-0}^2+H_{-0-}^2 \nonumber \\&+H_{-+0}^2+H_{000}^2+H_{0--}^2+ H_{0++}^2 \big ) \Big ] + 2Re[(1+V_L)V_R^*]\Big [ \frac{3m_{\ell }^2}{2q^2}\nonumber \\&\times \big ( H_{t00}^2+2H_{t++}H_{t--}\big ) +\left( 1+\frac{m_{\ell }^2}{2q^2}\right) \Big ( H_{000}^2+ 2H_{+0+}H_{-0-}\nonumber \\&+2H_{+-0}H_{-+0}+2H_{0++}H_{0--} \Big )\Big ] + \frac{3}{2}(|S_L|^2+|S_R|^2)\nonumber \\&\times \Big ( H_{00}^2+H_{++}^2 + H_{--}^2 \Big ) +3Re[S_LS_R^*] \big ( H_{00}^2+2H_{++}H_{--} \big ) \nonumber \\&+ \frac{3m_{\ell }}{\sqrt{q^2}} \Big ( Re[(1+V_L)S_L^*]+Re[V_RS_R^*] \Big ) \Big ( H_{00}H_{t00}+H_{++}H_{t++} \nonumber \\&+H_{--}H_{t--} \Big )+ \frac{3m_{\ell }}{\sqrt{q^2}}\Big ( Re[(1+V_L)S_R^*]+Re[V_RS_L^*] \Big )\nonumber \\&\times \Big ( H_{00}H_{t00}+H_{++}H_{t--} +H_{--}H_{t++} \Big ) \Bigg \}\,. \end{aligned}$$
(8)

When we only consider the contribution from \(H_{t00}\), \(H_{+-0}\), \(H_{-+0}\) and \(H_{00}\) from Eq. (8), we can get the longitudinal decay rate of daughter meson V \(d\Gamma ^L/dq^2\). Apart from the differential decay rate, other NP sensitive \(q^2\)-dependent observables are also considered in this work and can be written as follow

(9)

We can also construct the following observables that are analogous to the ratios \( R_\mathrm{V}^{*(L)}(q^2)\) to probe the universality of lepton flavor

  • Lepton forward and backward fractions

    $$\begin{aligned} \chi _{1,2}(q^2)=\frac{1}{2}R^{*}_{V}(q^2)[ 1\pm A_\mathrm{FB}^l(q^2) ], \end{aligned}$$
    (10)

  • Lepton spin 1/2 and -1/2 fraction

    $$\begin{aligned} \chi _{3,4}(q^2)=\frac{1}{2}R^{*}_{V}(q^2)[ 1\pm P_l(q^2) ], \end{aligned}$$
    (11)

  • Ratios of the longitudinal (transverse) polarization asymmetries parameters of the daughter meson

    $$\begin{aligned} R_{F_\mathrm{L}^{V}}(q^2)= & {} \frac{F_\mathrm{L}^{*V}(\bar{B}^* \rightarrow V\tau ^-\bar{\nu }_{\tau })(q^2)}{F_\mathrm{L}^{*V}(\bar{B}^* \rightarrow V\mu ^-\bar{\nu }_{\mu })(q^2)} , \nonumber \\ R_{F_\mathrm{T}^{V}}(q^2)= & {} \frac{F_\mathrm{T}^{*V}(\bar{B}^* \rightarrow V\tau ^-\bar{\nu }_{\tau })(q^2)}{F_\mathrm{T}^{*V}(\bar{B}^* \rightarrow V\mu ^-\bar{\nu }_{\mu })(q^2)}. \end{aligned}$$
    (12)

The above observables are independent of the CKM matrix elements are canceled to a large extent. We also give predictions for the average values of these observables which are calculated by separately integrating over \(q^2\).

3 Numerical results and discussions

3.1 Input parameters

After collecting all the theoretical expressions of required observables, we now proceed towards numerical analysis and discussions. In this section, we give our prediction for the observables in \(\bar{B}^* \rightarrow V\tau ^-\bar{\nu }_{\tau }\) both within the SM as well as in various NP benchmark points. Firstly, the input parameters that are relevant for our numerical computation, such as the well known Fermi coupling constant \(G_F\) and the particles masses, we take the values of these input parameters from the Particle Data Group [61]. For the CKM element, \(|V_{cb}|=(41.0\pm 1.4)\times 10^{-3}\) are used in this work.

Besides the above input parameters, the transition form factors \(V_{1-6}(q^2)\) and \(A_{1-4}(q^2)\) listed in helicity amplitudes are also essential ingredients for evaluating observables, especially for the branching fraction of the semileptonic \(\bar{B}^*\) decays. The authors of Refs. [55, 73] have adopted the covariant light-front quark model (CLFQM) [74,75,76] to evaluate the values. The form factors in the dipole model have the following form

$$\begin{aligned} F(q^2)=\frac{F(0)}{1-a\,\frac{q^2}{m^2_{B^*}}+b\,(\frac{q^2}{m^2_{B^*}})^2}, \end{aligned}$$
(13)

the three parameters F(0), a and b are got from the Ref. [55] by using the best fit values of constituent quark masses and Gaussian parameter which are obtained in Refs. [77, 78]. And the theoretical prediction values of these three parameters are listed in Table 1.

Table 1 Input parameters of the form factors used in our numerical analysis [55]
Full size table

Many previous works about the model independent analyses to study the NP effects in \(b \rightarrow c \ell \bar{\nu }_{\ell }\) processes have been made [79,80,81,82,83]. A global fit to a general set of Wilson coefficients of an effective low energy Hamiltonian is presented and the solutions are also interpreted in terms of hypothetical NP mediators [28, 29, 82,83,84,85,86,87]. In order to investigate the effect of NP on the various observables of \(\bar{B}^* \rightarrow V\tau ^-\bar{\nu }_{\tau }\) decays, we choose a variety best-fit values of Wilson coefficients from Refs. [32, 85, 86] as our NP benchmark points (BMP). And these NP scenarios are classified as three kinds:

  • Case A: consider one real Wilson coefficient \(V_L\), \(V_R\), \(S_L\) and \(S_R\) at a time, \(V_L=-2.11\), \(V_R=-0.09\), \(S_L=-1.51\) and \(S_R=0.31\). We marked them as BMP1, BMP2, BMP3 and BMP4, respectively.

  • Case B: consider one complex Wilson coefficient \(V_L\), \(V_R\), \(S_L\) and \(S_R\) at a time, \((\mathrm Re[V_L],Im[V_L])=(-1.233,1.045)\), \((\mathrm Re[V_R],Im[V_R])=(-0.0034,-0.3783)\), \(\mathrm (Re[S_L],Im[S_L])\) \(=(0.097,0)\) and \(\mathrm (Re[S_R],Im[S_R])=(-0.695,-0.777)\). We marked them as BMP5, BMP6, BMP7 and BMP8, respectively.

  • Case C: consider various combinations of two real Wilson coefficients at a time, namely \((V_L,V_R)\)=(0.0694,-0.0026), \((V_L,S_L)\)=(0.0714,-0.0063), \((V_L,S_R)\)=(0.0724,-0.0086), \((V_R,S_L)\)=(-0.09,0.1726), \((V_R,S_R)\)=(-0.072,0.154), and \((S_L,S_R)\)=(-1.04,-0.449). We marked them as BMP9-BMP14.

The theoretical uncertainties of input parameters ( \(\bar{B}^* \rightarrow V\) form factors and \(V_{cb}\) ) are considered in our following numerical results. Until now, there is no available precise experimental measurement information on the \(\bar{B}^* \rightarrow V\ell ^-\bar{\nu }_{\ell }\) decays. Nevertheless, the same Wilson coefficients are appeared in the relevant semileptonic B meson decays, which have been well measured. The above best fit values of the Wilson coefficients are mainly from the experimental measurement of \(R_{D^{(*)}}\) and \(R_{J/\Psi }\). We adopt the same treatment as in many literatures [88,89,90,91,92], that is, only the central value of best-fit result of NP coupling parameters is considered as the benchmark point to qualitatively discuss the influence of the NP effect.

3.2 The effect of NP on \(\bar{B}^*\rightarrow V \tau ^-\bar{\nu }_{\tau }\) decays

After introducing theoretical formulas and the input parameters as well as the NP coupling parameters, and in order to discriminate among the different NP scenarios above, we proceed to investigate the effects of above NP coupling parameters on the above observables listed in Sect. 2.3 within the SM and in above various NP benchmark points in a model independent way. From our precious works [54, 55], it is noteworthy that the variation of different observables for the decay processes \(\bar{B}^*\rightarrow V \tau ^-\bar{\nu }_{\tau } (V=D^*_{u,d},D^*_s,J/\Psi )\) are similar to each other. In order to avoid repetition, we will take \(\bar{B}^{*-}\rightarrow D^{*0} \tau ^-\bar{\nu }_{\tau }\) as an example to illustrate in detail and display the \(q^2\) dependency of each observable for this decay, as well as the same goes in following text.

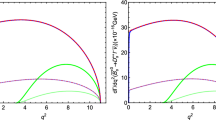
The \(q^2\) dependency of the observables \(d\Gamma /dq^2\), \(A_{FB}^{\tau }(q^2)\), \(C_{F}^{\tau }(q^2)\), \(A_{\tau }(q^2)\), \(F_{L}^{D^{*0}}(q^2)\) and \(R_{D^{*0}}^{*}(q^2)\) for \(\bar{B}^{*-}\rightarrow D^{*0} \tau ^-\bar{\nu }_{\tau }\) transition including the contribution of various types NP coupling parameters are reported in the Fig. 1. In the figure we incorporate both SM and various NP scenarios as well as they are distinguished by different colors, respectively. The width of each curve is derived from the theoretical uncertainties of input parameters (\(\bar{B}^{*-} \rightarrow D^{*0}\) form factors and \(V_{cb}\)). From the figure, we can see that

  • When we consider the effect of NP coupling parameters in the case A, the deviation from the SM prediction due to the \(V_L\) NP coupling is observed only in the ratio of branching ratio \(R_{D^{*0}}^*(q^2)\) and the total differential decay rate \(d\Gamma /dq^2\). Moreover, because the NP operators due to the \(V_L\) coupling parameter have the same Lorentz structure as the SM ones and the \(d\Gamma /dq^2\) are modified by the factor \((1+V_L)^2\). So the \(d\Gamma /dq^2\) is obviously decreased in the whole reasonable kinematic region when compared to the SM predictions. The effective coefficient \((1+V_L)^2\) appears in both the numerator and denominator of the expressions which describe \(A_{FB}^{\tau }(q^2)\), \(C_{F}^{\tau }(q^2)\), \(P_{\tau }(q^2)\) and \(F_{L}^{D^{*0}}(q^2)\). So there is no difference between the NP prediction including contributions of \(V_L\) coupling and the SM predictions of these observables. More interesting, the NP contribution of \(V_R\) to the observables \(d\Gamma /dq^2\), \(A_{FB}^{\tau }(q^2)\) and \(C_{F}^{\tau }(q^2)\) is similar to the NP contribution of \(S_L\). The \(P_{\tau }(q^2)\) including NP contribution of \(S_L\) is decreased but \(C_{F}^{\tau }(q^2)\), \(F_{L}^{D^{*0}}(q^2)\) and \(R_{D^{*0}}^*(q^2)\) are enhanced in the reasonable kinematic region. The \(P_{\tau }(q^2)\) including NP contribution due to \(V_R\) is enhanced but \(F_{L}^{D^{*0}}(q^2)\) is decreased in the reasonable kinematic region. After considering the presence of additional \(S_R\) coefficient, one can see that \(d\Gamma /dq^2\) depends on \(S_R\) and \(S_R^2\). So there is no cancellation in the numerator and denominator of the expressions in other observables simultaneously. From Fig. 1, it is clear to find that the deviation in all observables discussed in this work are comparatively large when consider the contribution of \(S_R\) coupling. Furthermore, the NP prediction curve due to the \(S_R\) coupling and the SM prediction curve show completely different behavior for some observables such as \(A_{FB}^{\tau }(q^2)\), \(P_{\tau }(q^2)\) and \(R_{D^{*0}}^*(q^2)\). The deviation from the SM prediction for \(d\Gamma /dq^2\) including NP contribution of \(S_R\) is most prominent at \(q^2\approx 9.0~\mathrm GeV^2\). And one can also notice that the zero crossing point of \(A_{FB}^{\tau }(q^2)\) including NP contribution of \(S_R\) deviates significantly towards left (low \(q^2\) region). In addition, there is no longer zero crossing point for \(P_{\tau }(q^2)\) considering NP contribution of \(S_R\), while there are zero crossing points in SM and after considering real \(V_L\), \(V_R\), \(S_L\) coupling parameters at \(q^2\in [4.5-5.5]~\mathrm GeV^2\), respectively. The deviations from their SM prediction for \(P_{\tau }(q^2)\) and \(R_{D^{*0}}^*(q^2)\) are most prominent at largest \(q^2\) region when consider the effect of four real NP coupling in the case A.

  • Though the NP coupling parameters are complex in case B, the NP effect of various observables in the case B is similar to the most results in the case A. The \(A_{FB}^{\tau }(q^2)\) including NP contribution due to one complex \(V_R\) coupling is enhanced comparing with the SM predictions. In the \(A_{FB}^{\tau }(q^2)\), the zero crossing point including effect from complex \(V_R\) coupling may shift slightly toward a large \(q^2\) value than in SM. Moreover, there is also a zero crossing in \(A_{FB}^{\tau }(q^2)\) including complex \(S_R\) coupling at \(q^2\approx 5.7~\mathrm GeV^2\) below which \(A_{FB}^{\tau }(q^2)\) takes positive values. Different from the results considering the real \(S_R\) coupling in case A, \(P_{\tau }(q^2)\) including the complex \(S_R\) coupling has a zero crossing around \(q^2\approx 3.7~\mathrm GeV^2\)

  • From last column in Fig. 1 in which two NP coupling parameters are considered one time in the case C, the change trend of each observable are similar to the case A and case B. Though the \(C_{F}^{\tau }(q^2)\) in both BMP12 and BMP13 scenarios are enhanced obviously comparing with the SM predictions, it is difficult to distinguish these two NP scenarios. The two endpoints of this observable are fixed at zero. For other observables, except BMP14 scenario, it is also difficult to distinguish different NP various from SM. The value of \(F_{L}^{D^{*0}}(q^2)\) in BMP14 scenarios at \(q^2_\mathrm{min}\) is about 0.2 and it is easy to distinguish this scenario from other NP scenarios and SM. Besides, \(F_{L}^{D^{*0}}\) in all NP scenarios and SM both great increasing with \(q^2\) over the all \(q^2\) region and get 0.335 at \(q^2_\mathrm{max}\).

Fig. 1
figure 1

The \(q^2\) dependence of various observables for the \(\bar{B}^{*-} \rightarrow D^{*0} \tau ^-\bar{\nu }_{\tau }\) decay mode in the SM, case A (left panel), case B (middle panel) and case C (right panel) NP scenarios, respectively. The width of each curve is derived from the theoretical uncertainties of input parameter (\(\bar{B}^{*-} \rightarrow D^{*0}\) form factors and \(V_{cb}\)). And the same in Fig. 2

Full size image

In order to further differentiate these different scenarios, analogy to the ratios \(R_{V}^{*}\), we also study some observables listed in Eqs. (10), (11) and (12). The predictions for the \(q^2\) dependency of these observables for \(\tau \) mode in the reasonable kinematic range are displayed in Fig. 2. Three observables \(\chi _{1,2,3}\) great increasing with \(q^2\) over the all \(q^2\) region The NP effects in the BMP4, BMP8 and BMP14 scenarios can significantly decrease the value of \(\chi _{1,2,3,4}(q^2)\) compared to the SM prediction. Furthermore, except above three NP scenarios including \(S_R\) coupling parameter, it is difficult to distinguish from each other in the observables \(\chi _{1,2,3}(q^2)\). And the NP effects of other NP scenarios have little impact on \(\chi _{1,2,3}(q^2)\). The \(q^2\) behavior of \(\chi _{4}(q^2)\) is quite different from \(\chi _{1,2,3}(q^2)\). And the deviations from their SM prediction for \(\chi _{4}(q^2)\) are most prominent at largest \(q^2\) region in various NP scenarios. Besides, \(\chi _{4}(q^2)\) show an almost positive slope over the whole \(q^2\) region in BMP4, BMP8 and BMP14 scenarios. The BMP14 scenario can decrease significant the predicted value of \(R_{F_\mathrm{L}^{D^{*0}}}(q^2)\), but BMP4 and BMP8 scenarios increase the value of the observable. Only the NP effect of BMP4 scenario makes the value of \(R_{F_\mathrm{L}^{D^{*0}}}(q^2)\) slightly greater than 1. Besides, the value of \(R_{F_\mathrm{L}^{D^{*0}}}(q^2)\) is about 0.69 at \(q^2_\mathrm{min}\) in BMP14 scenario. Furthermore, BMP3 and BMP12 make \(R_{F_\mathrm{L}^{D^{*0}}}(q^2)\) increase slightly. And BMP2, BMP7 and BMP13 make \(R_{F_\mathrm{L}^{D^{*0}}}(q^2)\) decrease slightly. For \(R_{F_\mathrm{T}^{D^{*0}}}(q^2)\), the \(q^2\) behavior of the observable presents a completely opposite change trend to \(R_{F_\mathrm{L}^{D^{*0}}}(q^2)\). But the variation trend of these two observables does not present an axial symmetric phenomenon between each other. One can see that the variation range of the values for \(R_{F_\mathrm{L}^{D^{*0}}}(q^2)\) is larger than that for \(R_{F_\mathrm{T}^{D^{*0}}}(q^2)\). At the same time, one can see that the predicted values of \(R_{F_\mathrm{L}^{D^{*0}}}(q^2)\) and \(R_{F_\mathrm{T}^{D^{*0}}}(q^2)\) both in the SM and all the NP scenarios approach to 1 at \(q^2_\mathrm{max}\).

Fig. 2
figure 2

The \(q^2\) dependence of the observables \(\chi _{1,2,3,4}(q^2)\) and \(R_{F_{L,T}^{D^{*0}}}\) for the \(\bar{B}^{*-} \rightarrow D^{*0} \tau ^-\bar{\nu }_{\tau }\) decay mode in the SM, case A, case B and case C NP scenarios, respectively

Full size image

4 Summary and conclusion

In various semileptonic B meson decays, the lepton flavor universality violation has been reported. The deviations between experimental measurements and the SM predictions in the semileptonic B meson decays mediated via \(b\rightarrow c(u) \) charged-current inactions and \(b \rightarrow s l l \) neutral-current interactions imply that NP may appear in the B meson decay processes. Inspired by the anomalies of \(R_{D^{(*)}(K^{(*)})}\) and \(R_{J/\Psi }\) in above decays, in this paper, we have performed phenomenology analysis of \(\bar{B}^*_{u,d,s,c} \rightarrow V \ell ^-\bar{\nu }_{\ell }\) decays which is induced by the \(b\rightarrow c \ell ^- \bar{\nu }_{\ell }\) quark level transitions in and beyond the Standard Model.

In this work, using the \(\bar{B}^* \rightarrow V\) form factors computed in the covariant light front quark model, we consider the NP effects of new vector and scalar type coupling separately and the combinations of vector and scalar couplings on the \(d\Gamma /dq^2\), \(A_{FB}^{\tau }(q^2)\), \(P_{\tau }(q^2)\), \(C_{F}^{\tau }(q^2)\), \(R_{D^{*0}}^*(q^2)\), \(F_{L}^{D^{*0}}(q^2)\), \(\chi _{1,2,3,4}(q^2)\) and \(R_{F_\mathrm{L(T)}^{D^{*0}}}(q^2)\) relative to \(\bar{B}^{*-}\rightarrow D^{*0} \tau ^-\bar{\nu }_{\tau }\) transition. The different NP scenarios are divided into three types NP benchmark points. The results show that the \(d\Gamma /dq^2\) and \(R_{D^{*0}}^*(q^2)\) including the some NP couplings are enhanced and have significant deviations comparing to their SM prediction. \(A_{FB}^{\tau }(q^2)\), \(P_{\tau }(q^2)\), \(C_{F}^{\tau }(q^2)\) and \(F_{L}^{D^{*0}}(q^2)\) are the same as their corresponding SM predictions in NP scenarios containing \(V_L\) only, since the numerator and the denominator of the expressions describing these observables both appear the common coefficient \(|1+V_L|^2\), simultaneously. The deviations from their SM prediction for \(P_{\tau }(q^2)\) , \(R_{D^{*0}}^*(q^2)\) and \(\chi _4(q^2)\) are most prominent at largest \(q^2\) region after considering the effect of various NP coupling parameters. Besides, we found that in three NP scenarios BMP4, BMP8 and BMP14 which mainly contain scalar NP coupling parameter \(S_R\), the NP effect of various observables are obvious. Furthermore, one can see that except BMP4, BMP8 and BMP14 scenarios including \(S_R\) coupling parameter, it is difficult to distinguish from each other in the observables \(\chi _{1,2,3}(q^2)\). The BMP14 can decrease significant result of \(R_{F_\mathrm{L}^{D^{*0}}}(q^2)\), but BMP3, BMP4, BMP8, BMP12 scenarios increase the value of the observable. At the same time, only the NP effect of BMP4 scenario makes the value of \(R_{F_\mathrm{L}^{D^{*0}}}(q^2)\) slightly greater than 1. Though the approximate opposite change trend situation occurs on the \(R_{F_\mathrm{T}^{D^{*0}}}(q^2)\), the variation trend of \(R_{F_\mathrm{L}^{D^{*0}}}(q^2)\) and \(R_{F_\mathrm{T}^{D^{*0}}}(q^2)\) does not present an axial symmetric phenomenon between each other.

Though there is no experimental measurement on these mesonic \(\bar{B}^*_{u,d,s,c} \rightarrow V \ell ^-\bar{\nu }_{\ell }\) decay processes, all of the results and finding in this paper is hopeful to be observed at running LHC and SuperKEKB/Belle-II experiments. And the study of these decays would be found to be very crucial in order to shed light on the nature of new physics and provide more definite answer concerning the anomalies got in \(b\rightarrow c \ell ^-\bar{\nu }_{\ell }\) process, restricting further or even deciphering the NP models.