Abstract
In this article, we predict the standard model (SM) values of the asymmetric and angular observables in \(B\rightarrow D^{(*)}\tau \nu _{\tau }\) decays, using the results of the new up-to-date analysis in \(B\rightarrow D^{(*)}\ell \nu _{\ell }\). We also revisit the SM prediction of the inclusive ratio \({\mathcal {R}}_{X_c}\), and we give its values in different schemes of the charm quark mass. This is the first analysis which includes all the known corrections in the SM. In addition, we analyze the \(b\rightarrow c\tau \nu _\tau \) decay modes in a model-independent framework of effective field theory beyond the standard model. Considering all the possible combinations of the effective operators in \(b \rightarrow c \tau \nu _{\tau }\) decays and using the Akaike information criterion, we find the scenarios which can best explain the available data on these channels. In the selected scenarios, best-fit values and correlations of the new parameters are extracted. Using these results, predictions are made on various observables in the exclusive and inclusive semitaunic \(b \rightarrow c \) decays. The graphical correlations between these observables are shown, which are found to be useful in discriminating various new physics scenarios.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The semileptonic \(B\rightarrow D^{(*)}\ell \nu _{\ell }\) (\(\ell = \mu \) or e) decays play an important role in the extraction of \(|V_{cb}|\) as well as in the extraction of the form factors associated with the \(b\rightarrow c\) decays. These form factors are the major input used in the predictions of \({\mathcal {R}}_{D^{(*)}} = {{{\mathcal {B}}}{(B\rightarrow D^{(*)}\tau \nu _{\tau })}}/{{{\mathcal {B}}}{(B\rightarrow D^{(*)}\ell \nu _{\ell })}}\), where \(\ell = \mu \) or e; for recent updates see [1,2,3,4,5,6,7]. There are additional form factors which cannot be extracted directly from the experimental data and one thus needs to rely on the heavy quark effective theory (HQET) input. On the other hand, the lattice simulations can predict these form factors at zero and non-zero recoils [8, 9]. The standard model (SM) predictions of \({\mathcal {R}}_{D^{(*)}}\) which are used in the literature are given by [1, 10]:
The prediction of \({\mathcal {R}}_{D}\) includes the up-to-date lattice input, whereas the prediction of \({\mathcal {R}}_{D^{*}}\) relies heavily on HQET input. Also, the current lattice results suggest that the HQET values of form factors at zero recoil are not in complete agreement with those from lattice [1, 3]. This discrepancy could be due to the missing higher order (\(\alpha ^2_s\) and \(\alpha _s{\varLambda }_{QCD}/m_b\)) corrections in the HQET relations of the form factors. The inclusion of lattice input increases the value of \({\mathcal {R}}_{D^{*}}\) [2, 5, 6]. Moreover, the data allow the unknown corrections in the ratios of the HQET form factors to be as large as 20% [6]. With all this input and using the Caprini–Lellouch–Neubert (CLN) [11] parametrization of the form factors, the SM prediction is given by \({\mathcal {R}}_{D^{*}} = 0.259 \pm 0.006\) [6]. On the experimental side, the current world averages are given by [12]
We note that the deviations in the two observables are a little less than 2.6\(\sigma \). Though these deviations can be explained by a variety of new physics models, we will follow a model-independent analysis, like the one in Ref. [13]. The other model-independent analyses, which are relatively new, can be seen in Refs. [14,15,16,17,18,19,20,21,22]. There are a few other observables, which could be constructed from the \(B\rightarrow D^{(*)}\tau \nu _{\tau }\) decays and which are potentially sensitive to the new physics (NP) beyond the SM. For an update, please see [23] and the references therein. Among these, the \(\tau \) polarization asymmetry has been measured by Belle [24], and it is consistent with the SM predictions (see Sect. 2 for details).
Recently, LHCb has published their result on another \(b\rightarrow c\tau \nu _{\tau }\) decay mode, where the observable and its measured value are given by [25]
\(\ell = \mu \) or e. Though the uncertainties are large, this measurement is 2\(\sigma \) above the corresponding SM prediction, which lies in between 0.25 and 0.29 [26,27,28,29]. We note that in both \({\mathcal {R}}_{D^{(*)}}\) and \({\mathcal {R}}_{J/\psi }\), the measured values are above the SM predictions and therefore, the NP should contribute constructively to the two decay modes, in order to explain the observed discrepancies. There are a few other \(b\rightarrow c\tau \nu _{\tau }\) decay modes like \(B_c\rightarrow \tau \nu _{\tau }\), \({\varLambda }_b \rightarrow {\varLambda }_c\tau \nu _{\tau }\) and the inclusive decay \(B\rightarrow X_c\tau \nu _{\tau }\), which are potentially sensitive to the new interactions and the NP affecting \({\mathcal {R}}_{D^{(*)}}\) and \({\mathcal {R}}_{J/\psi }\) should also have an impact on these decay modes.
Therefore, the correlation studies of the various observables associated with these decay modes will be an important probe for an indirect detection of NP. On the other hand, the precise measurements of some of these observables will be useful to constrain the new physics parameters associated with a model. This motivates one to predict the values of all the relevant observables for some specific model, which can then be further checked for consistency with the future measurements.
Two different approaches can be employed in the search of new physics: (1) physics-based modeling, (2) data driven approaches. In the first approach, one will look at the physics problem in hand and construct the model accordingly. One can then check the viability of that model once the experimental data are available. There are several models capable of describing the observed data and one is thus confronted with the problem of model selection. In the second approach, one could directly use the available experimental data to extract information as regards the probable new physics scenarios. In this approach, for low energy processes, one could use an effective field theory tool to dump the new physics information in various Wilson coefficients (WCs), which will appear as coefficients of different operators. This approach may not give us a direct access to the new particles, but it will provide information as regards the required new effective operators relevant for the processes under consideration, which will further help to construct the viable model(s).
In this article, we have done a model-independent analysis of the NP affecting the \(b\rightarrow c\tau \nu _{\tau }\) decay modes. The operator basis is exactly the same as that given in our earlier work [13, 23], which consists of scalar (S), vector (V), and tensor (T) type of operators. We did not consider the scenarios with right handed neutrinos. We have considered all possible combinations of these operators and categorized them as independent models.Footnote 1 We use the Akaike information criterion (AIC) to find the best possible model(s) for the existing data. A model-selection criterion is a formula that allows one to compare models; for details, see [30]. Alternative related approaches to the model selection are the bootstrap method and cross-validation. Cross-validation works poorly with small sample sizes, as in our case, and parametric bootstrap variants of AIC have recently been proposed [31], which we have not used in the present analysis. Using AIC, we have first selected the models best suited for explaining the existing data. Then, with the best-fit values of the model parameters, we have predicted the values of various observables associated with the above-mentioned decay modes. We have studied the correlations amongst the observables in detail as well. Here, we are basically adopting the second approach, where we have written the relevant effective operators for \(b\rightarrow c\tau \nu \) decays, and then tried to figure out which operator (or the set of operators) will give a plausible explanation of the available data. We want to emphasize here that the role of \({\text {AIC}}_c\) is to pinpoint those set of operators. The process of finding the most plausible effective operators will not decide the particle content of a model.
2 New physics and the observables
2.1 New operators
In this subsection, we will discuss the complete operator basis in \(b\rightarrow c\tau \nu _{\tau }\) decays. The most general effective Hamiltonian describing these transitions is given by
where \(C^\ell _W (W=V_1,V_2,S_1,S_2,T)\) are the Wilson coefficients corresponding to the following four-Fermi operators:
Here, we have considered only the left handed neutrinos.
2.2 Observables in \(b\rightarrow c\tau \nu _{\tau }\) decays
We will define various observables used in our analysis in this subsection.
2.2.1 \(B\rightarrow D^{(*)}\tau \nu _{\tau }\)
Following Ref. [13] and the references therein, we can write the differential decay rates for \(B\rightarrow D^{(*)} \tau \nu _\tau \) with the Hamiltonian in Eq. (4). The \(q^2\)-distribution of the decay rate of the decays \(B\rightarrow D^{(*)}\ell \nu _{\ell }\) are obtained by setting \(C_W = 0\) and \(m_{\tau } = m_{\ell }\). Here, we are assuming that new effects are present only in \(B\rightarrow D^{(*)}\tau \nu _{\tau }\) and the \(B\rightarrow D^{(*)}\ell \nu _{\ell }\) channels for \(\ell = \mu \) and e are free from any NP effects. \(H^s_{V, Y}(q^2)\) and \(H_{V, Y}(q^2)\) are the helicity amplitudes for \(\bar{B}\rightarrow D\) and \(\bar{B}\rightarrow D^*\) transitions, respectively (with \(Y = \pm , ~0\) and t). These amplitudes can be expressed in terms of form factors in \(B\rightarrow D^{(*)}\) transitions. The details of the form factors and their parametrizations can be looked up in [6] and the references in there.
In the present work, we have followed the CLN [11] parametrization of the \(B\rightarrow D^{(*)}\) form factors and have used both the fitted and the predicted values of these parameters obtained in [6]. In terms of the differential distributions, the ratios \({\mathcal {R}}_{D^{(*)}}\) are defined as
with \(q^2_{\max }= (m_B - m_{D^{(*)}})^2\), and \(\ell =e\) or \(\mu \).
Along with these ratios, there are a number of other observables, that can be constructed in these channels, which are sensitive to NP. Most of them are not yet measured experimentally. These are:
-
\(\tau \)-polarization is defined by studying further \(\tau \) decays:
$$\begin{aligned} P_{\tau }(D^{(*)}) = \frac{{\varGamma }^{(*)\lambda _{\tau }=1/2} - {\varGamma }^{(*)\lambda _{\tau }= -1/2}}{{\varGamma }^{(*)\lambda _{\tau }=1/2} + {\varGamma }^{(*)\lambda _{\tau }= -1/2}}, \end{aligned}$$(7)where \({\varGamma }^{(*)\lambda _{\tau }=\pm \frac{1}{2}} = \int _{m_{\tau }^2}^{q^2_{\max }}\frac{{\text {d}}{\varGamma }^{\lambda _{\tau }=\pm 1/2} (\bar{B}\rightarrow D^{(*)}\tau {\bar{\nu }})}{{\text {d}}q^2}\), \(\lambda _{\tau }\) is the \(\tau \) helicity, and \(q^2_{\max }= (m_B - m_{D^{(*)}})^2\).
-
\(D^*\) longitudinal polarization can be extracted from the angular distribution in \(D^* \rightarrow D \pi \) decays:
$$\begin{aligned} F_L^{D^*} = \frac{{\varGamma }^{\lambda _{D^*}=0}}{{\varGamma }^{\lambda _{D^*}=0} + {\varGamma }^{\lambda _{D^*}=1} + {\varGamma }^{\lambda _{D^*}=-1}}, \end{aligned}$$(8)where \({\varGamma }^{\lambda _{D^*}=0,\pm 1} = \int _{m_{\tau }^2}^{q^2_{\max }}\frac{d{\varGamma }^{\lambda _{D^*}=0,\pm 1}(\bar{B}\rightarrow D^{*}\tau {\bar{\nu }})}{{\text {d}}q^2}\).
-
If we write the double-differential decay distribution as
$$\begin{aligned} { {\text {d}}^2{\varGamma }\left( {\overline{B}} \rightarrow D^{(*)} \tau {\overline{\nu }}\right) \over {\text {d}}q^2 d\cos \theta }&= a^{(*)}_\theta (q^2) + b^{(*)}_\theta (q^2) \cos \theta \nonumber \\&\quad + c^{(*)}_\theta (q^2) \cos ^2\theta , \end{aligned}$$(9)where \(\theta \) is the angle between the three-momenta of \(\tau \) and \({\bar{B}}\) in the \(\tau {\bar{\nu }}\) rest frame, then \(b^{(*)}_\theta (q^2)\) determines the lepton forward–backward asymmetry in the following way:
$$\begin{aligned} {\mathcal {A}}^{(*)}_{\mathrm{FB}}&= { \int _0^1 {{\text {d}}{\varGamma }^{(*)} \over {\text {d}}\cos \theta }{\text {d}}\cos \theta -\int ^0_{-1}{{\text {d}}{\varGamma }^{(*)} \over {\text {d}}\cos \theta }{\text {d}}\cos \theta \over \int _{-1}^1 {{\text {d}}{\varGamma }^{(*)} \over {\text {d}}\cos \theta }{\text {d}}\cos \theta } \nonumber \\&= { \int b^{(*)}_\theta (q^2) {\text {d}}q^2 \over {\varGamma }^{(*)} } , \end{aligned}$$(10)
As mentioned earlier, in addition to these observables there are several other channels that will be affected by the same set of NP operators. We have used some of those most relevant observables in our analysis, either as fit input or as constraints and/or for prediction.
2.2.2 \(B_c \rightarrow {J/\psi }~\ell ~\nu _{\ell }\)
Ratios similar to those defined in Eq. (6) can be defined for the decay channel \(\bar{B_c}\rightarrow J/\psi \ell \bar{\nu _\ell }\) by replacing the respective mesons. For various form factors in \(B_c \rightarrow J/\psi \) decays, see [32].
Given the unavailability of a precise calculation of \(B_c\rightarrow J/\psi \) form factors till date, we have the option to choose from a collection of available parametrizations [27,28,29, 33,34,35,36]. Choosing different parametrizations results in varying the central value of \({\mathcal {R}}_{J/\psi }\) within the range 0.25–0.29, which is considered theoretical range in recent experimental analyses. Taking the uncertainties from different parametrizations into consideration, we see that the allowed theoretical range of \({\mathcal {R}}_{J/\psi }\) is actually larger than that. We consider two parametrizations residing at two far ends of this range, namely perturbative QCD (PQCD [29]), and the light-front covariant quark model (LFCQ [36]) in this work. A preliminary result on the form factor \(A_1(q^2_{\max })\) (this is the only form factor contributing to the decay at zero recoil) is available from the HPQCD collaboration [37]. This result is consistent with the parametrizations used in this draft (Table 1).
2.2.3 \({\varLambda }_b \rightarrow {\varLambda }_c \ell \nu _{\ell } \)
The \(q^2\) distribution for the decay process (\({\varLambda }_{b}\rightarrow {\varLambda }_{c} \tau ^{-} \nu _{\tau }\)) can be written as [47]
where \(A_1^{VA}\) and \(A_2^{VA}\) represent the contributions from the vector and axial vector currents, respectively. Their origin could be either the SM or any NP model. \(A_3^{SP}\) and \(A_4^{T}\) represent the contributions from the scalar–pseudoscalar and tensor currents, which will appear only in the NP models. \(A_5^{VA-SP}\) and \(A_6^{VA-T}\) are the interference terms which will have contributions from various operators in the SM, as well as in an NP model. These are functions of combinations of the helicity amplitudes \(H_{\lambda _{{\varLambda }_c},\lambda _{w}}\), which in turn can be expressed in terms of form factors and NP couplings. Several instances, where these form factors have been studied using sum rules and quark models, can be found in the literature [38, 48,49,50,51,52,53,54,55,56,57,58]. For our purpose, helicity form factors have been calculated using the formula from lattice QCD in the relativistic heavy quark limit [39].
Similar to the ratios defined earlier, two observables can be defined here, motivated by the lepton-flavor universality violation elsewhere:
Along with these ratios, we have also considered the forward–backward asymmetry in \({\varLambda }_{b}\rightarrow {\varLambda }_{c} \tau ^{-} \nu _{\tau }\), defined as
where \({\varGamma }^{(1)}={{\text {d}}{\varGamma }\over {\text {d}}\cos \theta _\tau }\) and \(\theta _\tau \) is the angle between the momenta of the \(\tau \) lepton and the \({\varLambda }_c\) baryon in the dilepton rest frame.
2.2.4 \( B \rightarrow X_c \tau {{\bar{\nu }}}_\tau \)
Similar to the ratios \({\mathcal {R}}_{D^{(*)}}\), we can define the following ratio for the inclusive decay \(B\rightarrow X_c\tau \nu _{\tau }\):
with \(\ell = \mu , e\). The decay \(B\rightarrow X_c\ell \nu _{\ell }\) is well studied in the literature; for a comprehensive update see [59] and the references therein. In the present work, the detailed mathematical expression of the decay width of \(B\rightarrow X_c \ell \nu _{\ell }\) and all other relevant input is taken from [40]. The simplified expression for the decay width of the inclusive semitaunic decay of B meson in SM are given in [60]:
Here, the terms involving \(C_0^{(0)}\), \(C_{0}^{(1)}\), and \(C_{0}^{(2)}\) represent the contributions from the leading order(LO), next-to-leading order (NLO) [61], and next-to-next-to-leading order (NNLO) [62] corrections in \(\alpha _s\), respectively, whereas \(C_{\mu _\pi ^2}\), \(C_{\mu _G^2}\), and \(C_{\rho _D^3}\), \(C_{\rho _{LS}^3}\) are the contributions at order \(1/{m_b}^2\) [63] and \(1/{m_b}^3\) [60], respectively. These coefficients depend on the quark and lepton masses and \({\varGamma }_0\), defined as
The parameters like \(\mu _{\pi }^2, \mu _G^2, \rho _D^3, \rho _{LS}^3\) are the matrix elements of the operators of dimension five and six, respectively, which are non-perturbative in nature. We have also included the well-known electroweak correction \(A_\mathrm{ew}(= 1.014)\). As mentioned earlier, the values of the various non-perturbative parameters and the masses (Eq. (16)) along with their correlations are taken from Tables II and III of Ref. [40]. In our analysis, the b quark mass is defined in the kinetic scheme, while the c quark mass has been defined in both the kinetic (\(m^{\text {Kin}}_c = 1.091 (20)\) GeV [64]) and the \({\overline{MS}}\) scheme (\(\overline{m_c}(3 \text {GeV}) = 0.9843 (56)\) GeV [65]). Relations of the pole masses (Eq. (16)) with the kinetic and \({\overline{MS}}\) masses are taken from [66] and [67], respectively. We have also considered \(\alpha _s = 0.22\pm 0.018\).
We have given the predictions for the ratio \({\mathcal {R}}_{X_c}\) instead of \(Br(B\rightarrow X_c\tau \nu _{\tau })\). As can be seen from the above expressions, this ratio is relatively clean, since the errors due to \(|V_{cb}|\) and the mass of the b-quark cancel in the ratio. Our predictions for \({\mathcal {R}}_{X_c}\) in the SM are given in Table 2. These predictions differ from each other due to the difference in the mass of the charm quark in two different schemes. We note that the central values of the two predictions change by \(\approx \) 2% due to scheme dependence, albeit being consistent within \(1\sigma \) uncertainties. Also, we have checked our prediction for the 1S scheme masses of the b and c quark, and we agree with that given in Ref. [41], which is also different from the predictions given in Table 2 (NLO and \(\frac{1}{m_b^2}\)). These results are clearly scheme-dependent.
In the case of \(m_c^{\text {kin}}\) (1 GeV), the correlation matrix for the non-perturbative parameters and the masses are given in Table 3, which are obtained from the analysis of [40]. This is the first analysis which includes all the known corrections in the prediction of \(R_{X_c}\). In Ref. [60], the analysis has been done with a similar set of input, without considering the NNLO corrections. We have checked that our result agrees with them, within the error bar, at the same level of accuracy. The input for the analysis with \(\overline{m_c}(3 \text {GeV})\) is taken from Table II of Ref. [40]. In this scheme, the predictions have larger uncertainties compared to those in the kinetic scheme. This is due to the difference in the correlation matrix of parameters given in Table 2.
To calculate the effects of new physics in the inclusive decay \( B \rightarrow X_c \tau {{\bar{\nu }}}_\tau \), we decompose the decay width as
Here, the first piece is arising solely from SM, while the second and third terms are the contributions from NP with different powers of the new couplings. The expressions of \({\varGamma }^{NP}_{(1)}\) and \({\varGamma }^{NP}_{(2)}\) are taken from [68]. Some other recent work, discussing NP effects in the inclusive mode, is in Refs. [69, 70].
2.2.5 \({\mathcal {B}}(B_c \rightarrow \tau \nu _\tau )\)
In terms of the general Hamiltonian defined in Eq. (4), the branching fraction of \(B_c \rightarrow \tau \nu _\tau \) can be expressed as [71],
where \(f_{B_c} = 0.434(15)\) GeV and \(\tau _{B_c} = 0.507(9)\) ps are the \(B_c\) decay constant and lifetime, respectively. Note that \(C_T\) does not enter in this decay.
The SM predictions of all these observables are listed in Table 1. The predictions of the \({\mathcal {R}}_{D^{(*)}}\) are based on the results of the analysis in [6]; here we have considered only the CLN parametrizations of the form factors. The predictions of \(P_{\tau }(D^{(*)})\), \(A_{FB}^{(*)}\), and \(P_{D^*}\) are new. They are presented along with the correlations amongst all the observables. All these predictions are based on the results of the analysis in [6].
2.3 Experimental status
All the experimental results used in the analysis of NP are tabulated in Table 4. There have been quite a few measurements of the ratios \({\mathcal {R}}_{D^{(*)}}\) in recent years. Apart from the most recent ones measuring \({\mathcal {R}}_{D^*}\), they are consistent with a sizable deviation from the SM. The experimental result most deviated from the SM predictions is still the first one reported by
 . Though it is apparent from the recent measurements that \({\mathcal {R}}_{D^*}\) values are coming down towards the SM, it is still too early to consider it as a trend for two reasons:
. Though it is apparent from the recent measurements that \({\mathcal {R}}_{D^*}\) values are coming down towards the SM, it is still too early to consider it as a trend for two reasons:
-
(a)
The experimental uncertainties are still quite large.
-
(b)
The actual deviation depends heavily on the correlation between \( {\mathcal {R}}_{D}~ \& ~ {\mathcal {R}}_{D^{*}}\), and any analysis bears the risk of being inconclusive without the simultaneous measurement of both of them. As an example, one can check the Belle result [43], where the \({\mathcal {R}}_{D^*}\) is consistent with the SM result within \(1\sigma \), but the combined result is in tension with the SM due to \({\mathcal {R}}_{D}\) and its correlation with \({\mathcal {R}}_{D^*}\).
The first, although quite imprecise, measurement of \(\tau \) polarization asymmetry has been done by Belle [43]. Though essentially it is an upper limit, we have included this measurement as a data point in our analysis. Table 4 also contains the recent measurement of \({\mathcal {R}}_{J/\psi }\) by LHCb [25]. Not only is this result in tension with the theoretical predictions, the central measured value is almost double of that predicted by SM. As the experimental uncertainty is large, they are still consistent with 90% C.L. range. LHCb has used a z-expansion parametrization [72] for the shared form factors for the signal and normalization modes and has determined them directly from the data. As is evident from the theoretical results for \({\mathcal {R}}_{J/\psi }\) (Table 1), the PQCD result is a little closer to the LHCb result. As has been pointed out in [73], and later also corroborated in [74], if the uncertainty decreases but the central value remains approximately the same in future experiments, NP effects which explain the increase in \({\mathcal {R}}_{D^{(*)}}\), will be unable to explain the measured value of \({\mathcal {R}}_{J/\psi }\). This should, in essence, result in a worse fit while this value is considered.
The decay \(B_c \rightarrow \tau \nu \), despite being out of the experimental reach for now [75, 76], can be used as an effective constraint on any NP effects that could potentially explain the \({\mathcal {R}}_{D^{(*)}}\) and \({\mathcal {R}}_{J/\psi }\) excesses. A conservative upper limit quoted for \({\mathcal {B}}(B_c \rightarrow \tau \nu )\), even after adding NP effects, is \(\lesssim 30\%\) [14]. A stronger upper bound of \(\lesssim 10\%\) is obtained from LEP data taken at Z-peak [18] with a prospect of an even tighter bound from the full L3 data [77]. In our analysis, we have used these two constraints.
3 Methodology
3.1 Numerical optimization
As mentioned earlier, the goal of this paper is to perform a model-independent multi-scenario analysis with the experimentally available results on the charged current anomalies, in conjunction with other relevant results, to obtain a data-based selection of a ‘best’ scenario and ranking and weighting of the remaining scenarios from a predefined set. If we consider the NP Wilson coefficients occurring in Eq. (4) to be complex, all possible combinations of the real and imaginary parts of the coefficients (10 parameters in total) should constitute such a predefined set, from which we can choose different scenarios. Scenarios containing only imaginary Wilson coefficients are neglected.
For each such scenario k, we define a \(\chi ^2\) statistic, which is a function of the real and/or imaginary parts of the Wilson coefficients (\(C^k_W\)) associated with the scenario in question, by
Here, \(O^{{\text {th}}}_p(C^k_W)\) are given by Eqs. (6), (7) and Sect. 2.2.2 as applicable, and \(O^{\mathrm{exp}}_p\) is the central value of the pth experimental result. Statistical (systematic) covariance matrices \(V^{{\text {stat }} {\text {(syst)}}}\), are constructed by taking separate correlations, wherever available. The nuisance parameters (Tables 5 and 6) occurring in the theoretical expressions are tuned to the fit using the term
where \(I_k^p\) and \(v_k^p\) are the kth input parameter and its respective value. For each scenario, we perform two sets of fits. First, we use different combinations of the experimental results of \({\mathcal {R}}_{D^{(*)}}\) (and \(P_{\tau }(D^*)\)). For the second set, we redo the fits including \({\mathcal {R}}_{J/\psi }\). As the form factor parametrization and the single experimental result for \({\mathcal {R}}_{J/\psi }\) are quite imprecise, instead of defining a \(\chi ^2_{{\text {nuis.}}}({\mathcal {R}}_{J/\psi })\), we add the SM uncertainty of \({\mathcal {R}}_{J/\psi }\) in quadrature to the experimental one. Following the discussion in Sect. 2.2.2, we do two sets of fits in this stage, with two different sets of form factor parametrization for \(B_c\rightarrow J/{\varPsi }\), namely LFCQ and PQCD.
After each fit, we determine the quality of it in terms of the p value obtained corresponding to the \(\chi ^2_{\min }\) values and the degrees of freedom (DoF) for that fit. We also double check the quality of the fit and existence of outliers in the fitted dataset by constructing a ‘Pull’ (\(= \left( O^{\mathrm{exp}}_i - O^{{\text {th}}}_i(C^k_W)\right) / ({\varDelta }O^{\mathrm{exp}}_i)\)) for each data point and check the normality (i.e. the probability that it is consistent with a Gaussian of \(\mu =0\) and \(\sigma =1\)) of their distribution. Due to the small number of data points in this analysis, no readily available normality test can perform with certainty and it is necessary to scrutinize each individual pull distribution. Still, we perform a variant of the “Shapiro–Wik” normality test as an extra criterion for elimination of scenarios. In other words, we drop the fits which have a pull distribution with probability to be a normal distribution \(\le 5\%\). Finally, we add the constraints according to Sects. 2.2.5 and 2.3 to our analysis and obtain the allowed parameter space. Next, we perform a model-selection procedure on the remaining set of viable scenarios for each data set. In the following subsection, we elaborate the method used to do the multi-model-selection procedure.
3.2 Model-selection criteria
One measure of the degree of structure in a model, inferred from the data, is its dimension, i.e. the number of parameters in it. In general, bias decreases and variance increases as the dimension of the model increases. The requirement of the optimum dimension of the model is called the ‘concept of parsimony’ [78], which is essentially a bias versus variance trade-off in statistical terms. All model-selection methods, to some extent, depend on the principle of parsimony [79].
The most generally applicable and reliable method for model comparison is ‘cross-validation’, which, in addition to testing the predictive power of the model, minimizes the bias and variance together by minimizing the mean-squared-error (MSE). The problem of applying cross-validation to the present analysis is that its applicability to very small sample sizes (as is the case here) is questionable [80, 81]. Thus, for model selection, we have used information-theoretic approaches, especially the second order variant of Akaike information criterion (\(\hbox {{{AIC}}}_c\)) [82] in the present work. This criterion and other competing criteria have previously been applied in one work of ours analyzing the charged current anomalies of b-decay [13]. In that analysis, we had worked with the binned data on the differential decay distribution of these channels.
Given that the notation for full reality or truth is f and an approximating model in terms of probability distribution is g, we can create a \(\chi ^2\) function in terms of the parameters of g and empirical results, following Sect. 3.1. For each model \(g_i\) in a set with R competing scenarios, we can define an \(\hbox {{{AIC}}}_c\) in terms of the \(\chi ^2_{\min }\) in the parameter space, which is equivalent to the maximum point of the empirical log-likelihood function:
where n is the number of data points and K is the number of estimable parametersFootnote 2 in \(g_i\). As a rule of thumb, use of \(\hbox {{{AIC}}}_c\) is preferred in the literature when \(n/K < 40\). In an application, the model with the smallest value of \(\hbox {{{AIC}}}_c\) is estimated to be the ‘closest’ to the unknown reality generating the data, among the considered models. Whereas all \(\hbox {{{AIC}}}^i_c\) are on a relative scale and are strongly dependent on sample size, simple differences of them (\({\varDelta }^{{\text {AIC}}}_i = \mathrm{AIC}^i_c - \mathrm{AIC}^{\min }_c\)) estimate the relative expected information loss between f and \(g_i\) allowing comparison and ranking of candidate models in increasing order of \({\varDelta }^{{\text {AIC}}}_i\). It is also possible to quantify the weight of evidence in favor of model i by defining a set of positive “Akaike weights”, \(w_i = (e^{(-{\varDelta }^{{\text {AIC}}}_i / 2)})/(\sum _{r = 1}^R e^{(-{\varDelta }^{{\text {AIC}}}_r / 2)})\), adding up to 1 [83]. As these depend on the entire set, adding or dropping a model during a post hoc analysis requires re-computation for all models in the new set.
The allowed parameter space of NP Wilson coefficients and their correlations considered in different scenarios for the dataset with all data, where \({\mathcal {R}}_{J/{\varPsi }}\) is calculated in PQCD (last dataset of Tables 5 and 7). Red (solid) and blue (dashed) contours enclose, respectively, \(1\sigma \) and \(3\sigma \) confidence levels(C.L.), as defined in Sect. 4.1. Shaded and diagonally hatched overlay regions represents parameter space disallowed by constraints \({\mathcal {B}}(B_c\rightarrow \tau \nu _\tau ) \le 30\%\) and \(10\%\), respectively. These plots are continued to Fig. 2
Plots for the remaining scenarios, continued from Fig. 1
4 Results
Following the methodology described in the previous subsection, we have taken several combinations of the available data and have performed the analysis in the following stages for each dataset.
4.1 Model selection
4.1.1 Analysis of present data
We have created the \(\chi ^2_k\) statistic for the kth scenario containing real and imaginary parts of the Wilson coefficients \(C^k_W\), and we repeated that for all k (let us reiterate here that scenarios containing all imaginary \(C_W\) are neglected). We have taken scenarios with as many as four individual components of \({\mathcal {R}}e(\text {or }{\mathcal {I}}m)(C_W)\). Then we have minimized each of those over the corresponding parameter space (with the form factor parameters as nuisance parameters). After checking normality for each fit and dropping scenarios with \(\le 5\%\) significance, we have arranged the remaining scenarios in ascending order of \(\hbox {{{AIC}}}_c\) and have kept only those with \({\varDelta }\hbox {{{AIC}}}_c \le 4\). These are, essentially, the best scenarios to explain the data in that specific dataset under the present experimental constraints. Tables 5, 13, 14 and 15 contain the listed scenarios of the data sets which are obtained from Table 4. Each table essentially contains three variations of similar datasets: the first one is data without \({\mathcal {R}}_{J/{\varPsi }}\) and the rest two, with it. The reason for treating \({\mathcal {R}}_{J/{\varPsi }}\) separately is the apparent tension of the measured central value with that of the SM one, as explained in Sect. 2.3. Moreover, the theoretical values of \({\mathcal {R}}_{J/{\varPsi }}\) are heavily dependent on the form factor parametrization and differ considerably over different choices of it, as explained in Sect. 2.2.2. Thus without showing bias to a particular type of parametrization, we treat LFCQ and PQCD separately in the second and third datasets of each table, respectively. As PQCD predicts relatively higher values for \({\mathcal {R}}_{J/{\varPsi }}\), the fits are generally better for these sets than those corresponding to the LFCQ ones, as can be checked from the p values listed in the second column of these datasets. The measured value of \(P_{\tau }(D^*)\) has a large error. Therefore, we have dropped the \(\tau \)-polarization asymmetry from the input listed in one of the fits (Table 13). The measured values of \({\mathcal {R}}_{D^{(*)}}\) by
 are relatively old, and they largely deviate from the respective SM predictions. Therefore, in order to check the impact of the
are relatively old, and they largely deviate from the respective SM predictions. Therefore, in order to check the impact of the
 data on our model selections, in one of the fit scenarios we have dropped the
data on our model selections, in one of the fit scenarios we have dropped the
 data (Table 14). We have also done the analysis with the measured \({\mathcal {R}}_{D^*}\) alone, which will help us to figure out the sensitivity of this observable towards a particular type of NP scenario.
data (Table 14). We have also done the analysis with the measured \({\mathcal {R}}_{D^*}\) alone, which will help us to figure out the sensitivity of this observable towards a particular type of NP scenario.
We notice that, for all datasets, the maximum number of independent fit parameters (for the listed scenarios) is two. As is explained in the previous sections, this is natural, because \(\hbox {{{AIC}}}_c\) penalizes the increased variance associated with increase in number of independent parameters. The fourth column in these tables, for each dataset, lists the \(w^{\text {{{AIC}}}_c}\) for each scenario, which estimates the relative likelihood for that scenario (among the given set of scenarios, the number of which is \(\approx 90 \sim 95\) for our analysis) to explain the data. As can be seen, the first few scenarios take up a large chunk of the total likelihood and it is evident that all unselected scenarios together constitute a very small fraction of it. This is another way of understanding why the listed scenarios are the best ones suited to describe the given dataset.
Once we have listed the best scenarios, we scrutinize the allowed parameter space for each of them. As all the finally selected models have at most two parameters (other than the nuisance parameters), we can plot the marginal confidence levels in the fit-parameter space with the help of the defined \(\chi ^2\) function. We have prepared plots for each of these scenarios either in terms of the goodness-of-fit contours (for two parameter scenarios), or by directly plotting the \(\chi ^2\) with respect to the parameter (for single parameter scenarios). The contour plots are prepared with constant \(\chi ^2\) contours equivalent to \(1\sigma \) and \(3\sigma \), which correspond to confidence levels of \(68.27\%\) and \(99.73\%\) respectively. For two parameters, the constant \(\chi ^2\) values are \(= \chi ^2_{\min } + {\varDelta }\chi ^2\), where \(\chi ^2_{\min }\) is the minimum value of \(\chi ^2\) obtained after minimization over the parameter space, and \({\varDelta }\chi ^2 = 2.296\) and 11.83 for \(1\sigma \) and \(3\sigma \), respectively. Similarly, for the single parameter case, \(1\sigma \) and \(3\sigma \) intervals are shown with \({\varDelta }\chi ^2 = 1\) and 9, respectively. As a representative case, we show the plots for all scenarios listed in the last dataset of Table 5 (‘All data’, where the theoretical value of \({\mathcal {R}}_{J/{\varPsi }}\) is calculated in PQCD) in Figs. 1 and 2.
We then use the limits on \({\mathcal {B}}(B_c\rightarrow \tau \nu )\) mentioned in Sect. 2.3 as our conservative constraint on each scenario. In Tables 5, 13, 14 and 15, the last column of each dataset indicates whether the corresponding scenario passes the constraint of \({\mathcal {B}}(B_c\rightarrow \tau \nu )\le 30\%\) (‘\(\checkmark \)’) or not (‘\(\pmb {\times }\)’). For many scenarios, there are multiple best-fit points (or at least, multiple 68% confidence regions). In some cases, some of these multiple minima are ruled out from the \({\mathcal {B}}(B_c\rightarrow \tau \nu ) \le 30\%\) constraints, while the rest are allowed. These scenarios are marked as ‘\(\checkmark \) !’ in the said column. By observing the nature of the confidence levels in the parameter space, we can pick out the minima which are allowed.
In the case of the plots depicting the parameter space, we show two limits: regions disallowed by \({\mathcal {B}}(B_c\rightarrow \tau \nu ) \le 30\%\) (gray shaded region) and \({\mathcal {B}}(B_c\rightarrow \tau \nu ) \le 10\%\) (diagonally hatched region), respectively. The first one is the conservative limit from \(B_c\) decay width and the second aggressive one is motivated from the studies quoted in Sect. 2.3 (though we call it aggressive, it is a perfectly reasonable upper bound, given the \(\sim 2\%\) SM prediction as shown in Table 1). We know that even if present, any NP effect is going to be small. Thus when multiple minima are allowed by these constraints, we quote the results for those which are closest to the origin (corresponding to SM) in the further analysis.Footnote 3 One more thing to note here is that scenarios with either real or imaginary part of \(C_T\) will not have any constraint on the corresponding axis in the parameter space, as \({\mathcal {B}}(B_c\rightarrow \tau \nu )\) is unaffected by tensor interactions.
Our results of the model selection with all the available data are shown in Table 5. We note that the best possible scenarios are the models with either of the operator \({\mathcal {O}}^{\ell }_T\) or \({{{\mathcal {O}}}}^{\ell }_{V_1}\) with real \(C_W\). The explanations with the operator \({{{\mathcal {O}}}}^{\ell }_{S_1}\) are disfavored by the bound from \({\mathcal {B}}(B_c \rightarrow \tau \nu _{\tau })\). These one-operator scenarios are allowed even if we choose \({\varDelta }{{\text {AIC}}}_c \le 2\). The same criterion does not allow the two-operator scenarios. However, the constraint \({\varDelta }\hbox {{{AIC}}}_c \le 4\) allows a few of the two-operator scenarios. In all these less preferred two-operator scenarios, the operators like \({\mathcal {O}}^{\ell }_{V_2}\), \({{{\mathcal {O}}}}^{\ell }_{S_1}\), \({{{\mathcal {O}}}}^{\ell }_{S_2}\) appear in combination with either of \({{{\mathcal {O}}}}^{\ell }_T\) and \({\mathcal {O}}^{\ell }_{V_1}\). Also, we note that the operator \({\mathcal {O}}^{\ell }_{V_2}\) with complex \(C_W\) is favored by the data.
As can be seen in Table 13, our conclusions on the selected models will not change if we drop the experimental input on \(P_{\tau }(D^*)\) from our fit. Also, if we drop the
 data on \({\mathcal {R}}_{D^{(*)}}\) from the the input list for the fit, the best preferred scenarios are still the one with the operator \({\mathcal {O}}^{\ell }_T\) or \({{{\mathcal {O}}}}^{\ell }_{V_1}\) with real \(C_W\)s. However, there are other one-operator scenarios with \({{{\mathcal {O}}}}^{\ell }_{V_2}\) or \({{{\mathcal {O}}}}^{\ell }_{S_1}\) with real \(C_W\), which are then allowed by the criterion \({\varDelta }\hbox {{{AIC}}}_c \le 4\); see Table 14 for details. Here too, there are a few two-operator scenarios which successfully pass the above-mentioned criterion. Finally, in order to understand the impact of the \({\mathcal {R}}_{D^{*}}\), we have also done an analysis considering only the data on \({\mathcal {R}}_{D^{*}}\) (Table 15). It shows that all of \({\mathcal {O}}^{\ell }_{V_1}\), \({{{\mathcal {O}}}}^{\ell }_T\), \({{{\mathcal {O}}}}^{\ell }_{V_2}\), \({{{\mathcal {O}}}}^{\ell }_{S_1}\) and \({{{\mathcal {O}}}}^{\ell }_{S_2}\) are allowed by the criterion \({\varDelta }\hbox {{{AIC}}}_c \le 4\). However, the constraints from \({\mathcal {B}}(B_c\rightarrow \tau \nu _{\tau })\) disfavors the scenarios with scalar operators. As can be seen across all the tables, our conclusions will not change much if we incorporate \({\mathcal {R}}_{J/\psi }\) as input in our fit. This could be due to the large uncertainties present both in the predictions and in the measured values of \({\mathcal {R}}_{J/\psi }\).
data on \({\mathcal {R}}_{D^{(*)}}\) from the the input list for the fit, the best preferred scenarios are still the one with the operator \({\mathcal {O}}^{\ell }_T\) or \({{{\mathcal {O}}}}^{\ell }_{V_1}\) with real \(C_W\)s. However, there are other one-operator scenarios with \({{{\mathcal {O}}}}^{\ell }_{V_2}\) or \({{{\mathcal {O}}}}^{\ell }_{S_1}\) with real \(C_W\), which are then allowed by the criterion \({\varDelta }\hbox {{{AIC}}}_c \le 4\); see Table 14 for details. Here too, there are a few two-operator scenarios which successfully pass the above-mentioned criterion. Finally, in order to understand the impact of the \({\mathcal {R}}_{D^{*}}\), we have also done an analysis considering only the data on \({\mathcal {R}}_{D^{*}}\) (Table 15). It shows that all of \({\mathcal {O}}^{\ell }_{V_1}\), \({{{\mathcal {O}}}}^{\ell }_T\), \({{{\mathcal {O}}}}^{\ell }_{V_2}\), \({{{\mathcal {O}}}}^{\ell }_{S_1}\) and \({{{\mathcal {O}}}}^{\ell }_{S_2}\) are allowed by the criterion \({\varDelta }\hbox {{{AIC}}}_c \le 4\). However, the constraints from \({\mathcal {B}}(B_c\rightarrow \tau \nu _{\tau })\) disfavors the scenarios with scalar operators. As can be seen across all the tables, our conclusions will not change much if we incorporate \({\mathcal {R}}_{J/\psi }\) as input in our fit. This could be due to the large uncertainties present both in the predictions and in the measured values of \({\mathcal {R}}_{J/\psi }\).
Our goal in this analysis is to see what type new operators can best explain the existing data. Our operator basis consists of all the linearly independent operators that are relevant for the \(b\rightarrow c \tau \nu _{\tau }\) decays. Therefore, we did not extend our analysis to look for new physics models whose effects in \(b\rightarrow c\tau \nu _{\tau }\) can be parametrized by one or more of the operators of our operator basis. Our priority is the analysis of the data, and the data can guide us to build models (Table 8).
After ensuring that we are dealing only with the scenarios allowed by \({\varDelta }\hbox {{{AIC}}}_c\), as well as constraints, we estimate the values of the parameters along with their uncertainties. Ideally, these would be obtained from the projections of the \({\varDelta }\chi ^2 = 1\) regions on the parameter line.Footnote 4 For simplicity, and to avoid asymmetric uncertainties, we consider a parabolic approximation around the chosen minimum and not only obtain the uncertainties of all parameters for each case, but also the correlation between them in the two parameter cases. These results are tabulated in Tables 7, 16, 17 and 18. For some scenarios, instead of the results, the reader is asked to check the corresponding plots. In these scenarios, the best fit, instead of being an isolated point, is actually a contour in the parameter space. Figure 1c is such an example. We note that we do not need large values of the \(C_W\)s (\(< 1\)) to explain the observed discrepancies in general. Among the best possible scenarios, the data is more sensitive to the model with operator \({{{\mathcal {O}}}}^{\ell }_{V_1}\) (with real \(C_W\)) or \({{{\mathcal {O}}}}^{\ell }_{V_2}\) (with complex \(C_W\)) than the one with operator \({{{\mathcal {O}}}}^{\ell }_T\). From the best-fit values we note that \({\mathcal {R}}e(C_{V_2})< {\mathcal {R}}e(C_{V_1})<< {\mathcal {R}}e(C_T) < 1\).
These results could be used by model builders to effectively put bounds on the parameter space of their lepton-flavor universality violating model, satisfying \(b\rightarrow c\ell \nu \) transitions.
4.1.2 Possible effects of future results
At the moment, the one-operator scenarios with real Wilson coefficients provide the best possible solutions, when the number of data points is not large. It is expected that with the increase in number of data points, the value of \({{AIC}}_c\) will decrease in all the scenarios. However, whether the analysis will pick up one or more parameter scenarios depends more on the likelihood function than the number of parameters. To check this, we have performed an analysis with the addition of a pseudo-dataset. The pseudo-dataset contains three synthetic data points, one from each of \({\mathcal {R}}_{D}\), \({\mathcal {R}}_{D^*}\) and \(P_{\tau }(D^*)\). The central values of these data points are taken from Table 8 (values corresponding to Scenario 7, i.e., with \(\{{\mathcal {R}}e(C_{S_2})\) and \({\mathcal {R}}e(C_{V_1})\}\)). With increase in statistics, future measurements are expected to be more precise. Thus the uncertainties of these synthetic data points are considered to be one order of magnitude less than that of the corresponding present experimental world average. As these new data are taken from the prediction table for a specific scenario (i.e. 7), we expect to get this scenario as the best one from the fit results, with increased goodness-of-fit. We find exactly this result, as can be checked from Table 10. Not only the best case selected is that with \(\{{\mathcal {R}}e(C_{S_2})\) and \({\mathcal {R}}e(C_{V_1})\}\), but the quality of fit is also improved as expected (p values are around 90–95\(\%\)). Interestingly, only 2 parameter scenarios are selected by the condition \( {\varDelta }{\text {AIC}}_c\le 2\). This gives us one example where the changes in the likelihood function (due to change in uncertainties; other parameters are fixed) the \({\text {AIC}}_c\) values of the two parameter scenarios become less compared to the one parameter scenarios.
In a second variation of a similar analysis, we take the new data points with the same central value as the present world average, and the uncertainties one order of magnitude less. Table 11 showcases the results. Here too, we find that only the change in the likelihood changes the results and two-parameter scenarios are selected over the one-parameter ones.
4.2 Prediction of observables and correlations amongst them
Using these NP results, we have predicted the values of the observables listed in Table 1. Our predictions for all pertinent scenarios for the dataset without \({\mathcal {R}}_{J/{\varPsi }}\) are listed in Tables 8 and 9. Predictions for the inclusive ratio \({\mathcal {R}}_{X_c}\) are given in a separate table (Table 12).
All of the predicted values for NP show deviations from their respective SM predictions. Moreover, neither all observables are equally deviated for a particular type of NP scenario, nor a single observable has similar deviations for different types of NP scenarios. Therefore, in trying to explain the deviations in \({\mathcal {R}}_{D^{(*)}}\) for a specific type of NP, we get information as regards the expected deviations in other associated observables. The obtained patterns then can be compared with the future measurements of these observables for a consistency check of the SM and to look for the types of NP. Any result inconsistent with SM but consistent with a future prediction of some observable could be indirect evidence in support for that specific scenario. In this regard, the correlations between the observables will play an important role. We need to mention here that the correlation plots contain features both due to the nature of the NP operators and the structure of experimental data, but fortunately for us, there is a way to distinguish between them in the present analysis. The present set of data, with a couple of exceptions, is mainly uncorrelated, while their SM predictions are correlated (with negligible uncertainties). Hence, any non-normal structure in the correlation plots is mainly due to the theoretical structure of the NP operators, but their central values and uncertainties are entirely due to present data. In Figs. 3, 4, 5, and 6 we show the correlations between the various observables in different NP scenarios which are allowed by our model-selection criteria. The following points illuminate our findings after scrutinizing these plots:
Correlation plots among different observables for one-operator scenarios listed in the first column of Table 7. Blue (solid), orange(dashed), and red (dotted) contours correspond to the scenarios with \({\mathcal {R}}e(C_{T})\), \({\mathcal {R}}e(C_{V_1})\), and complex \(C_{V_2}\), respectively. For each of these scenarios, \(1\sigma \) (filled region) and \(3\sigma \) contours are given
Correlation plots among different observables for all one-operator scenarios listed in the first column of Table 17. Blue (solid), orange (dashed), red (dotted), and green (dot-dashed) contours correspond to the scenarios with \({\mathcal {R}}e(C_{T})\), \({\mathcal {R}}e(C_{V_1})\), \({\mathcal {R}}e(C_{V_2})\), and \({\mathcal {R}}e(C_{S_1})\) respectively. For each of these scenarios, \(1\sigma \) (filled region) and \(3\sigma \) contours are given
Correlation plots among different observables for some of the two-operator scenarios listed in the first column of Table 7. Green (dot-dashed), magenta (dashed) and brown (non-uniform dot-dashed) contours correspond to the scenarios with \(\left[ {\mathcal {R}}e(C_{T}),{\mathcal {R}}e(C_{V_2})\right] \), \(\left[ {\mathcal {R}}e(C_{V_1}),{\mathcal {R}}e(C_{V_2})\right] \) and \(\left[ {\mathcal {R}}e(C_{T}),{\mathcal {R}}e(C_{V_1})\right] \) respectively. For each of these scenarios, \(1\sigma \) (filled region) and \(3\sigma \) contours are given
Correlation plots among different observables for two-operator scenarios listed in the first column of Table 17. Blue (solid), orange (dashed), red (dotted) and green (dot-dashed) contours correspond to the scenarios with \(\left[ {\mathcal {R}}e(C_{S_2}),{\mathcal {R}}e(C_{V_1})\right] \), \(\left[ {\mathcal {R}}e(C_{S_2}),{\mathcal {R}}e(C_{T})\right] \), \(\left[ {\mathcal {R}}e(C_{S_2}),{\mathcal {R}}e(C_{V_2})\right] \) and \(\left[ {\mathcal {R}}e(C_{T}),{\mathcal {R}}e(C_{V_2})\right] \) respectively. For each of these scenarios, \(1\sigma \) (filled region) and \(3\sigma \) contours are given
Correlation plot of \({\mathcal {R}}_{D^*}\) vs. \(F^{D^*}_L\) for two-operator scenarios previously showed in Figs. 3, 4, 5, and 6. We overlap these plots with the experimental results of \({\mathcal {R}}_{D^*}\) (Eq. (1)) and \(F^{D^*}_L\) (Eq. (22)), up to \(1\sigma \) (solid black) and \(2\sigma \) (dashed black) ranges. The scenario with \({\mathcal {R}}e(C_T)\) is discarded in the presence of the new result
-
1.
Let us first note the very important correlations between \({\mathcal {R}}_{D}\) and \({\mathcal {R}}_{D^*}\) in the scenarios which are allowed by our model-selection criteria. In Figs. 3a and 4a, we plot these correlations for the scenarios with one operator at a time, such as \({{{\mathcal {O}}}}^{\ell }_T\), \({{{\mathcal {O}}}}^{\ell }_{V_1}\), \({\mathcal {O}}^{\ell }_{V_2}\), and \({{{\mathcal {O}}}}^{\ell }_{S_1}\). We note that in all the scenarios, except the one with \({{{\mathcal {O}}}}^{\ell }_{V_2}\), the above two observables are positively correlated but the slopes are very different. By looking at the correlations, one can distinguish between the contributions from different NP operators. In the presence of either \({\mathcal {R}}e(C_{V_1})\), \({\mathcal {R}}e(C_{V_2})\), or \({\mathcal {R}}e(C_{S_1})\), if one of the observables is consistent with the SM, then so must be the other. However, in the case of \({\mathcal {R}}e(C_T)\), there are regions in which \({\mathcal {R}}_{D^*}\) is consistent with the SM, whereas \({\mathcal {R}}_{D}\) is largely deviated from its SM prediction. Therefore, if future data shows that \({\mathcal {R}}_{D^*}\) is within the SM ballpark but \({\mathcal {R}}_{D}\) has a large value above its SM prediction, then any scenario with either \({\mathcal {R}}e(C_{V_1})\), \({\mathcal {R}}e(C_{V_2})\) or \({\mathcal {R}}e(C_{S_1})\) has less chance to explain the data, but one with the operator \({{{\mathcal {O}}}}^{\ell }_T\) will still be able to explain it. The situation is completely opposite in the case of \({\mathcal {R}}e(C_{V_2})\), where the enhancement in \({\mathcal {R}}_{D^*}\) over its SM prediction is associated with a decrease in \({\mathcal {R}}_{D}\) from its SM value. On the other hand, the contributions from \({{{\mathcal {O}}}}^{\ell }_{V_2}\) with complex \(C_{V_2}\) will show deviations in the two observables.
-
2.
All the asymmetric and angular observables are insensitive to the operator \({{{\mathcal {O}}}}_{V_1}\), as its effect gets canceled in the ratios. Thus, if future measurements show deviations only in \({\mathcal {R}}_{D}\) and \({\mathcal {R}}_{D^*}\), and all the other asymmetric and angular observables in \(B\rightarrow D^{(*)}\tau \nu _{\tau }\) decays are consistent with their SM values, then the presence of \({{{\mathcal {O}}}}_{V_1}\) can be singled out.
-
3.
On top of this, \(P_{\tau }(D)\) is insensitive to the operator \({{{\mathcal {O}}}}_{V_2}\); detailed correlations can be seen in Figs. 3b and 4b. Therefore, large deviations in \(P_{\tau }(D)\) in future experiments could point to either tensor or scalar operators. Also, a measured value, well above its SM prediction, can only be explained by the scalar operator. On the other hand, if the value is below its SM prediction, then, depending on whether or not there are deviations in \({\mathcal {R}}_{D^*}\), tensor or scalar operators are favored. Hence, if future measurements do not see large deviations in \({\mathcal {R}}_{D}\) and \(P_{\tau }(D)\), then the presence of a scalar or tensor operator can be ruled out.
-
4.
As explained earlier, the effects of \({{{\mathcal {O}}}}_{V_2}\) can be distinguished from those of the other operators in the \({\mathcal {R}}_{D}-{\mathcal {R}}_{D^*}\) correlations. Further observations about \({{{\mathcal {O}}}}_{V_2}\), which can be seen in Figs. 3 and 4, are as follows:
-
Large deviations in both \({\mathcal {R}}_{D}\) and \({\mathcal {R}}_{D^*}\).
-
\(P_{\tau }(D)\) will be consistent with its SM value.
-
Measured values of \(P_{\tau }(D^*)\) and \(F_L(D^*)\) are consistent with their respective SM predictions.
-
The measured value of \({{{\mathcal {A}}}}_{FB}^*\) will be above its SM prediction.
-
-
5.
Let us accentuate a few other important points here. In Fig. 3b, c, we have shown the correlations between \(P_{\tau }(D^{(*)})\) and \({\mathcal {R}}_{D^*}\). In the presence of a tensor operator \({\mathcal {O}}_T\), the \({\mathcal {R}}_{D^*}\) is negatively and positively correlated with \(P_{\tau }(D)\) and \(P_{\tau }(D^*)\), respectively. However, when \({\mathcal {R}}_{D^*}\) is consistent with the SM, the \(\tau \) polarization asymmetries will not be consistent with their respective SM predictions. In the presence of \(C_T\), the values of \(P_{\tau }(D)\) and \(P_{\tau }(D^*)\) will be below and above their respective SM predictions, respectively. Also, \(P_{\tau }(D^*)\) can be positive, whereas the SM predicted value is negative. In the same scenario, the correlations of \({\mathcal {R}}_{D^*}\) with \({\mathcal {A}}_{FB}^*\) and \(F_L(D^*)\) are similar to those obtained for \(P_{\tau }(D^*)\) and \(P_{\tau }(D)\), respectively; for instance, see Fig. 3d, e. Also, here the forward–backward and the \(D^*\) polarization asymmetries largely deviate from their respective SM predictions even when \({\mathcal {R}}_{D^*}\) is consistent with the SM. On the other hand, we do not see such a behavior in the presence of \({{{\mathcal {O}}}}_{S_1}\). In this case, the \(P_{\tau }(D^{(*)})\), \({{{\mathcal {A}}}}_{FB}^*\) and \(F_L(D^*)\) are consistent with their SM predictions depending on whether or not \({\mathcal {R}}_{D^*}\) is consistent with its SM prediction (see Fig. 4b–e).
-
6.
In the case of the dataset with only \({\mathcal {R}}_{J/\psi }\) dropped from the fit, the correlations of \({\mathcal {R}}_{D^*}\) with other observables like \({\mathcal {R}}_{J/\psi }\), \({\mathcal {R}}_{{\varLambda }}^{\mu }\), and \(A_{FB}^{{\varLambda }}\) are shown in Fig. 3f–h, respectively. Similar plots, which are obtained by dropping the
 data, are given in Fig. 4f–h, respectively. In all the one-operator scenarios, the correlations are positive. Due to the large uncertainty in the SM prediction of \({\mathcal {R}}_{J/\psi }\), the predicted values of these observables are consistent with its SM prediction in all these cases. It is difficult to distinguish between the cases with either \({\mathcal {R}}e(C_{V_1})\), \({\mathcal {R}}e(C_{V_2})\) or \({\mathcal {R}}e(C_{S_1})\). A very large deviation in \({\mathcal {R}}_{D^*}\) may allow us to see a small deviation in \({\mathcal {R}}_{J/\psi }\). Also, the contribution from \({\mathcal {R}}e(C_T)\) can be distinguished from other new operators. In a high precision experiment, contributions of various of the above-mentioned operators are separable from each other by observing the correlation between \({\mathcal {R}}_{{\varLambda }}^\mu \) and \({\mathcal {R}}_{D^*}\). The contribution from \({\mathcal {R}}e(C_T)\) may allow for a large deviation in \({\mathcal {R}}_{{\varLambda }}^\mu \), with a sizable effect in \({\mathcal {R}}_{D^*}\). Similar patterns are observed in the correlations of \(A_{FB}^{{\varLambda }}\).
data, are given in Fig. 4f–h, respectively. In all the one-operator scenarios, the correlations are positive. Due to the large uncertainty in the SM prediction of \({\mathcal {R}}_{J/\psi }\), the predicted values of these observables are consistent with its SM prediction in all these cases. It is difficult to distinguish between the cases with either \({\mathcal {R}}e(C_{V_1})\), \({\mathcal {R}}e(C_{V_2})\) or \({\mathcal {R}}e(C_{S_1})\). A very large deviation in \({\mathcal {R}}_{D^*}\) may allow us to see a small deviation in \({\mathcal {R}}_{J/\psi }\). Also, the contribution from \({\mathcal {R}}e(C_T)\) can be distinguished from other new operators. In a high precision experiment, contributions of various of the above-mentioned operators are separable from each other by observing the correlation between \({\mathcal {R}}_{{\varLambda }}^\mu \) and \({\mathcal {R}}_{D^*}\). The contribution from \({\mathcal {R}}e(C_T)\) may allow for a large deviation in \({\mathcal {R}}_{{\varLambda }}^\mu \), with a sizable effect in \({\mathcal {R}}_{D^*}\). Similar patterns are observed in the correlations of \(A_{FB}^{{\varLambda }}\). -
7.
Similar correlations in the allowed two-operator scenarios are shown in Figs. 5 and 6. We note that it will be hard to distinguish the allowed two-operator scenarios from each other just from the correlations of \({\mathcal {R}}_{D^*}\) with \({\mathcal {R}}_{D}\), \({\mathcal {R}}_{J/\psi }\), and \({\mathcal {R}}_{{\varLambda }}^{\mu }\), as all the scenarios have similar correlations. However, the shape of the confidence regions of the two-operator scenarios are different from those of the one-operator ones.
For the two-operator scenarios containing \({{{\mathcal {O}}}}_{V_1}\), the NP-predicted values of the angular and asymmetric observables are consistent with their SM values in general. Here too \(P_{\tau }(D)\) is insensitive to the operator-combination [\({\mathcal {O}}_{V_1}, {{\mathcal {O}}}_{V_2}\)]. We note that the contributions from [\({\mathcal {R}}e(C_T)\), \({\mathcal {R}}e(C_{V_2})\)] in \(P_{\tau }(D^*)\), \({{{\mathcal {A}}}}_{FB}^*\) and \(F_L(D^*)\) can be identified. It is hard to distinguish the contributions of the rest of the operators with \({{\mathcal {O}}}_{S_2}\) and all the asymmetric and angular observables are consistent with their respective SM values for them. The correlation of \(A_{FB}^{{\varLambda }}\) shows that except the contribution from [\(\mathcal {R}e(C_T)\), \({\mathcal {R}}e(C_{V_2})\)], all other allowed two-operator scenarios are consistent with the SM even if there is a large deviation in \({\mathcal {R}}_{D^*}\). By looking at these correlations, one will be able to distinguish a two-operator scenario from the one-operator ones.
4.3 Recent measurement of \(F^{D^*}_L\)
Recently, after the publication of the first preprint of this work, a preliminary measurement of \(F^{D^*}_L\) was announced [84]. According to that talk, the recently measured value is
One immediate conclusion is that the operator \({{\mathcal {O}}}_{V_1}\) alone cannot explain such a large value in \(F_L(D^*)\), since its effect is canceled in the ratio. In the hope that this result may help us discriminate between our selected models, we recreate the \(F^{D^*}_L\) vs. \({\mathcal {R}}_{D^*}\) correlation plots of Figs. 3, 4, 5, and 6 in Fig. 7. Keeping in mind the preliminary nature of this result, we show the corresponding experimental results up to \(2 \sigma \). We note that the new tensor type operator with the Wilson coefficient \(C_T\) cannot explain the observed result of \(D^*\) polarization asymmetry, though it is one of the best possible solutions for the explanations of the observed discrepancy in \(R(D^*)\). However, the other operators like \( {{\mathcal {O}}}_{V_2}\) alone, and the combinations of operators like \({{\mathcal {O}}}_{V_1}\), \({{\mathcal {O}}}_{S_{1/2}}\) are amongst the most probable scenarios that can accommodate the present data.
5 Summary
In this paper, we have predicted the SM values of the angular observables associated with the \(B\rightarrow D^{(*)}\tau \nu _{\tau }\) decays, following the results of an earlier up-to-date analysis on \(B\rightarrow D^{(*)}\ell \nu _{\ell }\). Also, we have updated the SM prediction of \({\mathcal {R}}_{X_c}\) using the results of [40] along with the proper correlations between the various non-perturbative parameters and masses. These predictions are based on two different schemes of the charm quark mass (\({\overline{MS}}\) and kinetic). These include the NNLO perturbative corrections, and power-corrections up to order \(1/{m_b}^3\). We have separately mentioned results with power-corrections up to \(1/{m_b}^2\) order too. Our best results are \({\mathcal {R}}_{X_c} = \text {0.214(4)}\) for \(\overline{m_c} (3 \,{GeV}) = 0.987(13)\) GeV, and \({\mathcal {R}}_{X_c} = \text {0.209(4)}\) when \(m_c^{{\text {kin}}} = 1.091 (20)\) GeV where in both cases we have taken \(m_b^{{\text {kin}}} = 4.56(21)\) GeV.
In the next part of our analysis, we have analyzed the semitaunic \(b\rightarrow c\tau \nu _{\tau }\) decays in a model-independent framework with the \({\varDelta }B = {\varDelta }C = 1\) semileptonic operators. We have included the complete set of vector, scalar and tensor operators, while assuming the neutrinos to be left handed. Different possible combinations of all the effective operators have been considered, and following \(\hbox {{{AIC}}}_c\), the combinations, which are best suited for the available data, are considered for further studies. We have performed the analysis on several different prepared data sets. We note that, for all of the data sets, the one-operator scenarios, with a real \(C_W\), can best explain the available data. However, in most of them, the scalar operators are not allowed by the constraint \(Br(B_c \rightarrow \tau \nu _{\tau }) \le 30\%\). The most favored scenarios are the ones with tensor (\({{\mathcal {O}}}_T\)) or \((V-A)\) (\({\mathcal {O}}_{V_1}\)) type of operators. Also, the \((V+A)\) type of interactions, with a complex \(C_W\), though less favored, are allowed. In the absence of the
 data on \({\mathcal {R}}_{D^{(*)}}\) from our analysis, one-operator scenarios like \((V \pm A)\), \(S - P\), and tensor operators with real \(C_W\) are the most favored ones. These one-operator scenarios are easily distinguishable from each other by studying the correlations of \({\mathcal {R}}_{D^*}\) with \({\mathcal {R}}_{D}\) and all the other asymmetric and angular observables. Also, the patterns of the future measurements of all such observables can easily discriminate the types of NP. Among all the possible combinations of \((V \pm A)\), tensor and \(( S - P)\) operators, there are quite a few two-operator scenarios which pass all the selection criteria. In these cases, one cannot differentiate between the contributions from NP scenarios by looking at the correlations of \({\mathcal {R}}_{D^*}\) with \({\mathcal {R}}_{D}\), \({\mathcal {R}}_{J/\psi }\), and \({\mathcal {R}}_{{\varLambda }}^{\mu }\). However, the correlations of \({\mathcal {R}}_{D^*}\) with the various angular and asymmetric observables could be useful for such a discrimination. We have also predicted the numerical values of all the observables along with their errors, for the allowed scenarios.
data on \({\mathcal {R}}_{D^{(*)}}\) from our analysis, one-operator scenarios like \((V \pm A)\), \(S - P\), and tensor operators with real \(C_W\) are the most favored ones. These one-operator scenarios are easily distinguishable from each other by studying the correlations of \({\mathcal {R}}_{D^*}\) with \({\mathcal {R}}_{D}\) and all the other asymmetric and angular observables. Also, the patterns of the future measurements of all such observables can easily discriminate the types of NP. Among all the possible combinations of \((V \pm A)\), tensor and \(( S - P)\) operators, there are quite a few two-operator scenarios which pass all the selection criteria. In these cases, one cannot differentiate between the contributions from NP scenarios by looking at the correlations of \({\mathcal {R}}_{D^*}\) with \({\mathcal {R}}_{D}\), \({\mathcal {R}}_{J/\psi }\), and \({\mathcal {R}}_{{\varLambda }}^{\mu }\). However, the correlations of \({\mathcal {R}}_{D^*}\) with the various angular and asymmetric observables could be useful for such a discrimination. We have also predicted the numerical values of all the observables along with their errors, for the allowed scenarios.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Author’s comment: All data in this manuscript are available upon request by contacting with the corresponding author.]
Notes
Here, models are indicating different scenarios with one or more operators, and real or complex WC(s).
There is a subtle point here concerned with the number of ‘estimable parameters’. As an example, there are two competing scenarios in the present analysis: (a) with non-zero \({\mathcal {R}}e(C_{V_1})\) and (b) with non-zero \({\mathcal {R}}e(C_{V_1})\) and \({\mathcal {I}}m(C_{V_1})\). Now, the two parameters of case (b) always appear together in an identical manner in the expressions of our observables, essentially making the number of ‘estimable parameters’ = 1. Thus, in the first column of Table 5, cases 1–4 have the same number of DOF = 8. We follow this throughout the analysis.
Another way of finding the ‘number of estimable parameters’ is to calculate the p value of the fit from toy Monte Carlo (MC) method. This value, in conjunction to the approximation that the fit-statistic follows a \(\chi ^2\) distribution, can give us the number of degrees of freedom, and thus the number of estimable parameters (as we have also checked). As we need \({\varDelta }\hbox {{{AIC}}}_c\) instead of the absolute value of the \(\hbox {{{AIC}}}_c\) in our analysis, the naive way of estimation of the number of parameters (except the case \(C_{V_1}\), as explained above and which we treat as a special case) works just fine.
As an example, for scenario 4 given in the last dataset of Table 5 (with \({\mathcal {R}}e(C_{S_2})\) and \({\mathcal {R}}e(C_{V_1})\)), the symbol for the constraint column is ‘\(\checkmark \) !’. The corresponding plot in Fig. 1e shows that out of the four possible minima, only two are outside the shaded regions. Interestingly, the global minima of the \(\chi ^2\) in this case lies within the shaded region (thus being disallowed), but there are two more allowed local \(1\sigma \) C.L. regions. In Table 7 (last dataset), the corresponding result is quoted for the one closest to zero.
For an illustration with the one parameter case, check Fig. 1d, where there are two minima. Only one of them is the global minimum and the end points of the red projection region on the parameter line give the \(1\sigma \) uncertainty. There is another region allowed by \(3\sigma \) around the other local minimum, colored in blue.
References
D. Bigi, P. Gambino, Revisiting \(B\rightarrow D \ell \nu \). Phys. Rev. D 94(9), 094008 (2016)
F.U. Bernlochner, Z. Ligeti, M. Papucci, D.J. Robinson, Combined analysis of semileptonic \(B\) decays to \(D\) and \(D^*\): \(R(D^{(*)})\), \(|V_{cb}|\), and new physics. Phys. Rev. D 95(11), 115008 (2017)
D. Bigi, P. Gambino, S. Schacht, A fresh look at the determination of \(|V_{cb}|\) from \(B\rightarrow D^{*} \ell \nu \). Phys. Lett. B 769, 441–445 (2017)
B. Grinstein, A. Kobach, Model-Independent Extraction of \(|V_{cb}|\) from \(\bar{B}\rightarrow D^* \ell {\overline{\nu }}\). Phys. Lett. B 771, 359–364 (2017)
D. Bigi, P. Gambino, S. Schacht, \(R(D^*)\), \(|V_{cb}|\), and the Heavy Quark Symmetry relations between form factors. JHEP 11, 061 (2017)
S. Jaiswal, S. Nandi, S.K. Patra, Extraction of \(|V_{cb}|\) from \(B\rightarrow D^{(*)}\ell \nu _\ell \) and the Standard Model predictions of \(R(D^{(*)})\). JHEP 12, 060 (2017)
F.U. Bernlochner, Z. Ligeti, M. Papucci, D.J. Robinson, Tensions and correlations in \(|V_{cb}|\) determinations. Phys. Rev. D 96(9), 091503 (2017)
J.A. Bailey et al., BD form factors at nonzero recoil and |\(\text{ V }_{{cb}}\)| from 2+1-flavor lattice QCD. Phys. Rev. D 92(3), 034506 (2015)
H. Na, C.M. Bouchard, G.P. Lepage, C. Monahan, J. Shigemitsu, \(B \rightarrow D l \nu \) form factors at nonzero recoil and extraction of \(|V_{cb}|\). Phys. Rev. D 92(5), 054510 (2015). [Erratum: Phys. Rev.D93,no.11,119906(2016)]
S. Fajfer, J.F. Kamenik, I. Nisandzic, On the \(B \rightarrow D^* \tau {\bar{\nu }}_{\tau }\) Sensitivity to New Physics. Phys. Rev. D 85, 094025 (2012)
I. Caprini, L. Lellouch, M. Neubert, Dispersive bounds on the shape of anti-B –> D(*) lepton anti-neutrino form-factors. Nucl. Phys. B 530, 153–181 (1998)
HFAG, “Average of \({\cal{R}}(D)\) and \({\cal{R}}(D^*)\) for FPCP 2017.” http://www.slac.stanford.edu/xorg/hflav/semi/fpcp17/RDRDs.html. Accessed 30 Sep 2010
S. Bhattacharya, S. Nandi, S.K. Patra, Looking for possible new physics in \(B\rightarrow D^{(\ast )}\tau \nu _{\tau }\) in light of recent data. Phys. Rev. D 95(7), 075012 (2017)
R. Alonso, B. Grinstein, J. Martin Camalich, Lifetime of \(B_c^-\) constrains explanations for anomalies in \(B\rightarrow D^{(*)}\tau \nu \). Phys. Rev. Lett. 118(8), 081802 (2017)
D. Choudhury, A. Kundu, S. Nandi, S.K. Patra, Unified resolution of the \(R(D)\) and \(R(D^*)\) anomalies and the lepton flavor violating decay \(h\rightarrow \mu \tau \). Phys. Rev. D 95(3), 035021 (2017)
A. Celis, M. Jung, X.-Q. Li, A. Pich, Scalar contributions to \(b\rightarrow c (u) \tau \nu \) transitions. Phys. Lett. B 771, 168–179 (2017)
M.A. Ivanov, J.G. Krner, C.-T. Tran, Probing new physics in \(\bar{B}^0 \rightarrow D^{(\ast )} \tau ^- {\bar{\nu }}_{\tau }\) using the longitudinal, transverse, and normal polarization components of the tau lepton. Phys. Rev. D 95(3), 036021 (2017)
A.G. Akeroyd, C.-H. Chen, Constraint on the branching ratio of \(B_c \rightarrow \tau \bar{\nu }\) from LEP1 and consequences for \(R(D^{(*)})\) anomaly. Phys. Rev. D 96(7), 075011 (2017)
D. Buttazzo, A. Greljo, G. Isidori, D. Marzocca, B-physics anomalies: a guide to combined explanations. JHEP 11, 044 (2017)
M. Gonzlez-Alonso, J. Martin Camalich, K. Mimouni, Renormalization-group evolution of new physics contributions to (semi)leptonic meson decays. Phys. Lett. B 772, 777–785 (2017)
A. Azatov, D. Bardhan, D. Ghosh, F. Sgarlata, E. Venturini, Anatomy of \(b \rightarrow c \tau \nu \) anomalies (2018)
W. Altmannshofer, P. Bhupal Dev, A. Soni, \(R_{D^{(*)}}\) anomaly: a possible hint for natural supersymmetry with \(R\)-parity violation. Phys. Rev. D 96(9), 095010 (2017)
S. Bhattacharya, S. Nandi, S.K. Patra, Optimal-observable analysis of possible new physics in \(B\rightarrow D^{(\ast )}\tau \nu _{\tau }\). Phys. Rev. D 93(3), 034011 (2016)
S. Hirose et al., Measurement of the \(\tau \) lepton polarization and \(R(D^*)\) in the decay \(\bar{B} \rightarrow D^* \tau ^- {\bar{\nu }}_\tau \). Phys. Rev. Lett. 118(21), 211801 (2017)
R. Aaij et al., Measurement of the ratio of branching fractions \({\cal{B}}(B_c^+\,\rightarrow \,J/\psi \tau ^+\nu _\tau )\)/\({\cal{B}}(B_c^+\,\rightarrow \,J/\psi \mu ^+\nu _\mu )\) (2017)
M.A. Ivanov, J.G. Korner, P. Santorelli, Semileptonic decays of \(B_c\) mesons into charmonium states in a relativistic quark model. Phys. Rev. D 71, 094006 (2005). [Erratum: Phys. Rev.D75,019901(2007)]
E. Hernandez, J. Nieves, J.M. Verde-Velasco, Study of exclusive semileptonic and non-leptonic decays of \(B_c\)—in a nonrelativistic quark model. Phys. Rev. D 74, 074008 (2006)
M.A. Ivanov, J.G. Korner, P. Santorelli, Exclusive semileptonic and nonleptonic decays of the \(B_c\) meson. Phys. Rev. D 73, 054024 (2006)
W.-F. Wang, Y.-Y. Fan, Z.-J. Xiao, Semileptonic decays \(B_c\rightarrow (\eta _c, J/\Psi )l\nu \) in the perturbative QCD approach. Chin. Phys. C 37, 093102 (2013)
H. Akaike, Selected Papers of Hirotugu Akaike (Springer, New York, NY, 1998)
J. Shang, J.E. Cavanaugh, Bootstrap variants of the akaike information criterion for mixed model selection. Comput. Stat. Data Anal. 52(4), 2004–2021 (2008)
R. Watanabe, New Physics effect on \(B_c \rightarrow J/\psi \tau {{\bar{\nu }}}\) in relation to the \(R_{D^{(*)}}\) anomaly. Phys. Lett. B 776, 5–9 (2018)
AYu. Anisimov, I.M. Narodetsky, C. Semay, B. Silvestre-Brac, The \(B_c\) meson lifetime in the light front constituent quark model. Phys. Lett. B 452, 129–136 (1999)
D. Ebert, R.N. Faustov, V.O. Galkin, Weak decays of the \(B_c\) meson to charmonium and \(D\) mesons in the relativistic quark model. Phys. Rev. D 68, 094020 (2003)
V.V. Kiselev, Exclusive decays and lifetime of \(B_c\) meson in QCD sum rules (2002)
W. Wang, Y.-L. Shen, C.-D. Lu, Covariant light-front approach for B(c) transition form factors. Phys. Rev. D 79, 054012 (2009)
A. Lytle, B. Colquhoun, C. Davies, J. Koponen, C. McNeile, Semileptonic \(B_c\) decays from full lattice QCD. PoS BEAUTY2016, 069 (2016)
M.-Q. Huang, D.-W. Wang, Light cone QCD sum rules for the semileptonic decay Lambda(b) -> p l anti-nu. Phys. Rev. D 69, 094003 (2004)
W. Detmold, C. Lehner, S. Meinel, \(\varLambda _b \rightarrow p \ell ^- {\bar{\nu }}_\ell \) and \(\varLambda _b \rightarrow \varLambda _c \ell ^- {\bar{\nu }}_\ell \) form factors from lattice QCD with relativistic heavy quarks. Phys. Rev. D 92(3), 034503 (2015)
A. Alberti, P. Gambino, K.J. Healey, S. Nandi, Precision determination of the Cabibbo–Kobayashi–Maskawa element \(V_{cb}\). Phys. Rev. Lett. 114(6), 061802 (2015)
M. Freytsis, Z. Ligeti, J.T. Ruderman, Flavor models for \(\bar{B} \rightarrow D^{(*)} \tau \bar{\nu }\). Phys. Rev. D 92(5), 054018 (2015). https://doi.org/10.1103/PhysRevD.92.054018. arXiv:1506.08896
J.P. Lees et al., Measurement of an Excess of \(\bar{B} \rightarrow D^{(*)}\tau ^- {\bar{\nu }}_\tau \) Decays and Implications for Charged Higgs Bosons. Phys. Rev. D 88(7), 072012 (2013)
M. Huschle et al., Measurement of the branching ratio of \(\bar{B} \rightarrow D^{(\ast )} \tau ^- {\bar{\nu }}_\tau \) relative to \(\bar{B} \rightarrow D^{(\ast )} \ell ^- {\bar{\nu }}_\ell \) decays with hadronic tagging at Belle. Phys. Rev. D 92(7), 072014 (2015)
A. Abdesselam et al., Measurement of the branching ratio of \(\bar{B}^0 \rightarrow D^{*+} \tau ^- {\bar{\nu }}_{\tau }\) relative to \(\bar{B}^0 \rightarrow D^{*+} \ell ^- {\bar{\nu }}_{\ell }\) decays with a semileptonic tagging method. In: Proceedings, 51st Rencontres de Moriond on Electroweak Interactions and Unified Theories: La Thuile, Italy, March 12–19, 2016 (2016)
R. Aaij et al., Measurement of the ratio of branching fractions \({\cal{B}}(\bar{B}^0 \rightarrow D^{*+}\tau ^{-}{\bar{\nu }}_{\tau })/{\cal{B}}(\bar{B}^0 \rightarrow D^{*+}\mu ^{-}{\bar{\nu }}_{\mu })\). Phys. Rev. Lett. 115(11), 111803 (2015). [Erratum: Phys. Rev. Lett.115,no.15,159901(2015)]
R. Aaij et al., Measurement of the \(B^0 \rightarrow D^{*-} \tau ^+ \nu _{\tau }\) branching fraction using three-prong \(\tau \) decays (2017)
A. Datta, S. Kamali, S. Meinel, A. Rashed, Phenomenology of \( {\varLambda }_b\rightarrow {\varLambda }_c\tau {{\overline{\nu }}}_{\tau } \) using lattice QCD calculations. JHEP 08, 131 (2017)
F. Cardarelli, S. Simula, Isgur-Wise form-factors of heavy baryons within a light front constituent quark model. Phys. Lett. B 421, 295–302 (1998)
H.G. Dosch, E. Ferreira, M. Nielsen, R. Rosenfeld, Evidence from QCD sum rules for large violation of heavy quark symmetry in Lambda(b) semileptonic decay. Phys. Lett. B 431, 173–178 (1998)
C.-S. Huang, C.-F. Qiao, H.-G. Yan, Decay Lambda(b) –> p lepton anti-neutrino in QCD sum rules. Phys. Lett. B 437, 403–407 (1998)
R.S. Marques de Carvalho, F.S. Navarra, M. Nielsen, E. Ferreira, H.G. Dosch, Form-factors and decay rates for heavy Lambda semileptonic decays from QCD sum rules. Phys. Rev. D 60, 034009 (1999)
M. Pervin, W. Roberts, S. Capstick, Semileptonic decays of heavy lambda baryons in a quark model. Phys. Rev. C 72, 035201 (2005)
H.-W. Ke, X.-Q. Li, Z.-T. Wei, Diquarks and Lambda(b) –> Lambda(c) weak decays. Phys. Rev. D 77, 014020 (2008)
Y.-M. Wang, Y.-L. Shen, C.-D. Lu, Lambda(b) –> p, Lambda transition form factors from QCD light-cone sum rules. Phys. Rev. D 80, 074012 (2009)
K. Azizi, M. Bayar, Y. Sarac, H. Sundu, Semileptonic Lambda(b, c) to Nucleon Transitions in Full QCD at Light Cone. Phys. Rev. D 80, 096007 (2009)
A. Khodjamirian, C. Klein, T. Mannel, Y.M. Wang, Form factors and strong couplings of heavy baryons from QCD light-cone sum rules. JHEP 09, 106 (2011)
T. Gutsche, M.A. Ivanov, J.G. Krner, V.E. Lyubovitskij, P. Santorelli, Heavy-to-light semileptonic decays of \(\varLambda _b\) and \(\varLambda _c\) baryons in the covariant confined quark model. Phys. Rev. D 90(11), 114033 (2014). [Erratum: Phys. Rev.D94,no.5,059902(2016)]
T. Gutsche, M.A. Ivanov, J.G. Krner, V.E. Lyubovitskij, P. Santorelli, N. Habyl, Semileptonic decay \(\rightarrow + \tau ^- + \bar{\nu _\tau }\) in the covariant confined quark model. Phys. Rev. D 91(7), 074001 (2015). [Erratum: Phys. Rev. D91, no. 11, 119907 (2015)]
S. Nandi, Theory update on the inlcusive determination of \(|V_{cb}|\). PoS CKM2016, 048 (2017)
T. Mannel, A.V. Rusov, F. Shahriaran, Inclusive semitauonic \(B\) decays to order \({{{\cal{O}}}} (\varLambda _{QCD}^3/m_b^3)\). Nucl. Phys. B 921, 211–224 (2017)
A. Czarnecki, M. Jezabek, J.H. Kuhn, Radiative corrections to b –> c tau anti-tau-neutrino. Phys. Lett. B 346, 335–341 (1995)
S. Biswas, K. Melnikov, Second order QCD corrections to inclusive semileptonic b –> X(c) l anti-nu(l) decays with massless and massive lepton. JHEP 02, 089 (2010)
A.F. Falk, Z. Ligeti, M. Neubert, Y. Nir, Heavy quark expansion for the inclusive decay anti-B –> tau anti-neutrino X. Phys. Lett. B 326, 145–153 (1994)
K.G. Chetyrkin, J.H. Kuhn, A. Maier, P. Maierhofer, P. Marquard, M. Steinhauser, C. Sturm, Charm and bottom quark masses: an update. Phys. Rev. D 80, 074010 (2009)
A. Bazavov et al., Up-, down-, strange-, charm-, and bottom-quark masses from four-flavor lattice QCD, ArXiv e-prints, Feb. 2018
D. Benson, I.I. Bigi, T. Mannel, N. Uraltsev, Imprecated, yet impeccable: On the theoretical evaluation of Gamma(B –> X(c) l nu). Nucl. Phys. B 665, 367–401 (2003)
K. Melnikov, Tv Ritbergen, The Three loop relation between the MS-bar and the pole quark masses. Phys. Lett. B 482, 99–108 (2000)
W.D. Goldberger, Semileptonic B decays as a probe of new physics (1999)
S. Kamali, A. Rashed, A. Datta, New physics in inclusive \(B \rightarrow X_c\ell {\bar{\nu }}\) decay in light of \(R(D^{(*)})\) measurements. Phys. Rev. D 97(9), 095034 (2018)
P. Colangelo, F. De Fazio, Scrutinizing \( {\overline{B}}\rightarrow {D}^{\ast }\left(D\pi \right){\ell }^{-}{{\overline{\nu }}}_{\ell } \) and \( {\overline{B}}\rightarrow {D}^{\ast }\left(D\gamma \right){\ell }^{-}{{\overline{\nu }}}_{\ell } \) in search of new physics footprints. JHEP 06, 082 (2018)
M. Gonzlez-Alonso, J. Martin Camalich, Global effective-field-theory analysis of new-physics effects in (semi)leptonic kaon decays. JHEP 12, 052 (2016)
C. Bourrely, I. Caprini, L. Lellouch, Model-independent description of B –> pi l nu decays and a determination of |V(ub)|. Phys. Rev. D 79, 013008 (2009). [Erratum: Phys. Rev. D82, 099902 (2010)]
A.K. Alok, D. Kumar, J. Kumar, S. Kumbhakar, S.U. Sankar, \(R_{J/\psi }\) confronts \(R_D\) and \(R_{D^*}\) (2017)
A. Biswas, D.K. Ghosh, A. Shaw, S.K. Patra, \(b \rightarrow c \ell \nu \) anomalies in light of extended scalar sectors (2018)
I.P. Gouz, V.V. Kiselev, A.K. Likhoded, V.I. Romanovsky, O.P. Yushchenko, Prospects for the \(B_c\) studies at LHCb. Phys. Atom. Nucl. 67, 1559–1570 (2004)
I.P. Gouz, V.V. Kiselev, A.K. Likhoded, V.I. Romanovsky, O.P. Yushchenko, Prospects for the \(B_c\) studies at LHCb. Yad. Fiz. 67, 1581 (2004)
M. Acciarri et al., Measurement of D(s)- –> tau- anti-tau-neutrino and a new limit for B- –> tau- anti-tau-neutrino. Phys. Lett. B 396, 327–337 (1997)
G. Box, G. Jenkins, Time series analysis: forecasting and control (Holden-Day, London, 1970)
L. Breiman, The little bootstrap and other methods for dimensionality selection in regression: X-fixed prediction error. J. Am. Stat. Assoc. 87(419), 738–754 (1992)
C. Beleites, U. Neugebauer, T. Bocklitz, C. Krafft, J. Popp, Sample size planning for classification models. Anal. Chim. Acta 760, 25–33 (2013)
G. Varoquaux, Cross-validation failure: small sample sizes lead to large error bars (2017)
N. Sugiura, Further analysts of the data by akaike’s information criterion and the finite corrections. Commun. Stat. Theory Methods 7(1), 13–26 (1978)
K.P. Burnham, D.R. Anderson, Model selection and multimodel inference: a practical information-theoretic approach (Springer, New York, NY, 2002)
K. Adamczyk, B to semitauonic decays at Belle / Belle II. CKM 2018 (2018)
Acknowledgements
We would like to thank Paolo Gambino for valuable input in the analysis and Zoltan Ligeti for his valuable comments. S.K.P. is supported by the grants IFA12-PH-34 and SERB/PHY/2016348.
Author information
Authors and Affiliations
Corresponding author
Appendix: Extra tables
Appendix: Extra tables
See Tables 13, 14, 15, 16, 17 and 18.
 dropped (i.e., only with Belle and LHCb data; with or without \({\mathcal {R}}_{J/{\varPsi }}\))
dropped (i.e., only with Belle and LHCb data; with or without \({\mathcal {R}}_{J/{\varPsi }}\))Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3.
About this article
Cite this article
Bhattacharya, S., Nandi, S. & Patra, S.K. \(b \rightarrow c \tau \nu _{\tau }\) Decays: a catalogue to compare, constrain, and correlate new physics effects. Eur. Phys. J. C 79, 268 (2019). https://doi.org/10.1140/epjc/s10052-019-6767-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-019-6767-7


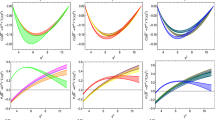
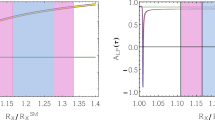








 data, are given in Fig.
data, are given in Fig.