1 Introduction

The problem of generating quantum matter in gravitational fields is considered mainly in the semi-classical approach of quantum field theory (QFT) in the presence of classical external gravity, which determines either the form of the solutions or directly the two-point functions of the quantum free fields. The principal backgrounds considered in these investigations are the \((1+3)\)-dimensional spatially flat Friedmann–Lemaître–Robertson–Walker (FLRW) manifolds, where the momentum is conserved and the free fields implicitly allow plane-wave modes that can be written in the conformal local chart just as in special relativity. However, on these manifolds, the energy is no longer conserved, such that the frequency separation must be solved by a supplemental condition fixing the vacuum. This relative flexibility in setting the vacua inspired the method of cosmological particle creation [1,2,3,4,5,6,7,8,9,10,11,12,13,14] based on Bogolyubov transformations between states of free fields prepared in different vacua.

On the de Sitter expanding universe, which has been intensively studied [15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42], the most popular vacuum is the adiabatic one of the Bunch–Davies type [21] that can be applied to the massive Klein–Gordon and Dirac fields [15]. This vacuum has been used successfully in cosmological particle creation or other models, but leads to some difficulties when one tries to apply perturbative methods. This is because the rest frame limit (for vanishing momentum, \(\mathbf{p}=0\)) of the Dirac plane waves is undefined in the adiabatic vacuum [43] such that the flat limit is also affected, remaining undefined for \(\mathbf{p}=0\). For this reason, it is difficult to apply the methods of QFT to individual particles in an adiabatic vacuum whose states in rest frames are undefined [44].

An alternative, proposed many years ago, is to consider states in which the Hamiltonian is diagonal in any momentum frame including the rest frame where the frequencies have to be separated [45,46,47,48,49,50,51,52,53]. Unfortunately, in this manner, one obtains momentum-dependent vacua that cannot be used properly in QFT.

Under such circumstances, we proposed a new vacuum called the rest frame vacuum (r.f.v.), which diagonalizes the Hamiltonian exclusively in rest frames. This vacuum can be fixed in any spatially flat FLRW manifold separating the frequencies just as in special relativity, at least for the massive Klein–Gordon [54], Dirac [55], and Proca [56] fields. We thus obtain plane waves in de Sitter QFT having well-defined rest and flat limits, suitable for calculating in any frame transition amplitudes between pure quantum states. For the massless particles with spin, we can exploit the conformal invariance of Maxwell’s equation or the covariance of Dirac’s one, taking over in conformal local charts the quantum modes of special relativity defined in Minkowskian vacua. Note that for massive fields with spin, the Minkowskian vacua simultaneously satisfy the conditions defining both the adiabatic and rest frame vacua. In our opinion, the de Sitter r.f.v. is closer to the Minkowskian one, as in both cases the frequencies are separated in rest frames. However, the aforementioned vacua do not exclude each other, these depending on the conditions in which the quantum states are prepared or measured. Our results obtained so far indicate that the r.f.v. seems to be useful mainly in analysing processes in perturbative QFT, while the adiabatic vacuum has its commonly accepted role in cosmological models.

Another consequence of missing energy conservation in spatially flat FLRW manifolds is that the processes in the first order of perturbations are no longer forbidden as in the flat Minkowski spacetime. A special case is the de Sitter expanding universe, where the energy is still conserved but the energy operator does not commute with the momentum one such that the energy and momentum cannot be conserved simultaneously, their measurement being affected by uncertainty [57, 58]. This was an opportunity for many authors who, turning back to the perturbative QFT, successfully studied various processes in the first order of perturbations [45,46,47,48,49, 59,60,61,62,63] that could explain how classical gravity may give rise to the quantum matter in these manifolds.

Inspired by these results, we built the quantum electrodynamics (QED) in Coulomb gauge on the de Sitter expanding universe [44], rigorously applying the Lehmann–Symanzik–Zdoiermann (LSZ) reduction formalism [64,65,66] and setting the adiabatic vacuum for the Dirac field [15, 67]. In this framework, we studied the processes in the first order of perturbations, focusing on the particle creation from vacuum [44, 68, 69]. Moreover, we applied our approach to a spatially flat FLRW spacetime with a Milne-type scale factor, where we studied the first-order processes but setting the r.f.v. instead of the adiabatic one, as this does not make sense in this spacetime having a finite Big Bang time [70]. Surprisingly, this new vacuum changes the entire physical picture, imposing more restrictive selection rules, and inhibiting all the first-order transitions between charged states, while those between neutral states become dominant. Therefore, we may ask what happens in the de Sitter QED if we set the r.f.v. instead of the adiabatic one.

In this paper, we would like to find an answer by studying the first-order processes of de Sitter QED in which we set the r.f.v. for quantizing the Dirac field. We specify that our approach respects ad litteram the quantum principles assuming that the quantum states are prepared or measured by a global apparatus represented by an algebra of operators; among them, the conserved ones (herein called observables) are just the Killing vector fields defined globally. We can thus prepare global quantum modes, regardless of the coordinates we choose, as eigenvectors of a system of commuting observables whose eigenvalues are conserved quantities labelling the quantum modes. The problem of setting the vacuum arises only because of the operator algebras of these manifolds from which one cannot extract complete systems of commuting observables in any momentum frame. From this point of view, we may say that in the r.f.v., we complete this system with the Hamiltonian operator that can be diagonalized only in rest frames [55, 58].

On the other hand, in our new QED, in any vacuum, we had to re-define the transition rates as in Ref. [70], since the Dirac \(\delta \) function of the energy conservation is replaced here by a usual time integral. With such a definition, we obtained in the Milne-type universe plausible transition rates and probabilities [70] but which lay out the well-known old sickness of the perturbation theory, namely the infrared catastrophe, and divergences on some particular directions. As the first one cannot be removed without suitable infrared regulators, the angular divergences can be removed at any time, extracting physical results according to the method of reduced amplitudes proposed by Yennie et al. [74] and commonly used in other investigations. We thus succeeded in pointing out the angular dependence of the transition probabilities of the first-order processes in the Milne-type universe [70]. This encourages us to adopt herein a similar method looking for a more refined definition of transition rates and associated reduction procedures.

Technically speaking, we perform the calculations in conformal local charts, where we can take over some results obtained in the flat case. However, for interpreting the final results, we use the physical local chart with Painlevé–Gullstrand coordinates [75, 76] where one performs the physical measurements. The principal new results we obtain here are the transition amplitudes, rates and probabilities per unit of volume and unit of time of neutral and charged transitions, i.e. transitions in which both the in and out states are either neutral or charged. The neutral transitions are the pairs created from the photon, \(\gamma \rightarrow e^+ + e^-\), and leptons created from vacuum, \(vac\rightarrow \gamma + e^+ + e^-\), while the charged ones are the photon emission, \(e^{\pm }\rightarrow e^{\pm }+\gamma \), or adsorption, \(e^{\pm }+\gamma \rightarrow e^{\pm }\). Using a more refined definition of the transition rates, we find that the rates of charged transitions are decreasing in time, while those of neutral ones remain constant. This suggests us to adopt the point of view of an observer, performing measurement at a very late time when the charged transitions can be neglected. Therefore, we focus on the neutral transitions, calculating their rates and probabilities, finding that these are singular in critical positions in which the fermion momenta are either parallel or anti-parallel and the helicity is conserved. What is new here is that, apart from the usual simple pole, a new logarithmic singularity affects these amplitudes. For this reason, we must first apply a regularization to remove the logarithmic singularity before using the reduction procedure for removing the pole. In this manner, we obtain reduced probabilities which reach their maxima only in the critical positions, thus favouring the helicity conservation. Moreover, we show that in the physical local chart, the probabilities per unit of volume and unit of time are rapidly decreasing in time, as \(a(t)^{-4}\) where a(t) is the de Sitter scale factor. With these probabilities, we construct a simple model of lepton creation from vacuum, \(vac\rightarrow \gamma +e^++e^-\rightarrow (e^++e^-)+e^++e^-\), which rapidly reaches saturation because of the probability of pair creation from a photon which is dominant. Hereby, we conclude that a late observer will measure only a relic photon density after the charged leptons are combined with the hadronic matter.

We start in Sect. 2 presenting the Dirac fundamental spinors of the momentum-helicity basis in r.f.v. and the polarized plane-wave solutions of the Maxwell field in Coulomb gauge. We derive in the next section amplitudes of the processes in the first order of perturbations and define the rates and probabilities per unit of volume and unit of time, pointing out their asymptotic behaviour. As all these quantities are singular for the parallel or anti-parallel fermion momenta, we devote Sect. 4 to procedures for removing the singularities by regularization of the logarithmic singularity before the pole reduction. The principal properties of the reduced probabilities, including their angular behaviour, are briefly discussed with the help of a graphical analysis. In Sect. 5, we study the above-mentioned model of lepton creation from vacuum governed by the reduced probabilities derived previously. We show that this model is working properly, reaching saturation rapidly and giving rise to time-independent photon and fermion densities that can be measured at a late time. Finally, we present our concluding remarks. In three appendices, we present the polarization of fermions and photons, the integrals we use for deriving the probabilities, and the principal function determining the amplitudes.

We use natural Planck units with \(c=\hslash =G=1\).

2 Free fields in de Sitter expanding universe

The de Sitter expanding universe \(M_+\) is defined as the expanding portion of the \((1+3)\)-dimensional de Sitter spacetime whose de Sitter–Hubble constant (frequency) we denote here by \(\omega \) such that the scale factor depends on the cosmic time \(t\in \mathbb {R}\) as \(a(t)=e^{\omega t}\) [71]. In this manifold, the covariant fields with spin may be defined in frames \(\{x;e\}\) formed by local charts of coordinates \(x^{\mu }\) (\(\mu ,\nu ,\ldots =0,1,2,3\)) and orthogonal (non-holonomic) local frames determined by tetrads of components \(e_{\hat{\mu }}^{\alpha }\) and \(\hat{e}^{\hat{\mu }}_{\alpha }\). These are labelled by local indices (\(\hat{\alpha },\hat{\beta },\ldots \) \(=0,1,2,3\)) raised or lowered by the Minkowski metric \(\eta =\mathrm{diag}(1,-1,-1,-1)\), while for the natural indices, we have to use the metric tensor

$$\begin{aligned} g_{\mu \nu }=\eta _{\hat{\alpha }\hat{\beta }}\hat{e}^{\hat{\alpha }}_{\mu }\hat{e}^{\hat{\beta }}_{\nu }, \quad g^{\mu \nu }=\eta ^{\hat{\alpha }\hat{\beta }} e_{\hat{\alpha }}^{\mu } e_{\hat{\beta }}^{\nu }, \end{aligned}$$
(1)

of the manifold \(M_+\) for which we denote \(\sqrt{g}=\sqrt{|\mathrm{det}(g)|}\) .

The simplest local coordinates are the conformal time \(t_\mathrm{c}\) and the co-moving Cartesian coordinates, \(\mathbf{x}_\mathrm{c}\in \mathbb {R}^3\). The conformal chart \(\{t_\mathrm{c},\mathbf{x}_\mathrm{c}\}\) has the line element

$$\begin{aligned} \mathrm{d}s^{2} =\frac{1}{(\omega t_\mathrm{c})^2}\,\left( \mathrm{d}t_\mathrm{c}^{2}- \mathrm{d}{} \mathbf{x}_\mathrm{c}\cdot \mathrm{d}{} \mathbf{x}_\mathrm{c}\right) ,\quad \sqrt{g}=(\omega t_\mathrm{c})^{-4}, \end{aligned}$$
(2)

covering the expanding portion of the de Sitter manifold for \(t_\mathrm{c}\in (-\infty ,0]\). The notation we use here prevents the confusion with the physical coordinates of Painlevé–Gullstrand type [75, 76], \(\{t,\mathbf{x}\}\), formed by the cosmic time, t, and the physical space coordinates, \(\mathbf{x}\), largely used now in investigating dynamical particles in various FLRW manifolds (see for instance [77]). These coordinates can be introduced by substituting

$$\begin{aligned} t_\mathrm{c}=-\frac{1}{\omega }e^{-\omega t}, \quad \mathbf{x}_\mathrm{c}=\mathbf{x}e^{-\omega t}, \end{aligned}$$
(3)

such that for \(t\rightarrow \infty \) we have \(t_\mathrm{c}\rightarrow 0\). The line element in the physical local chart,

$$\begin{aligned} \mathrm{d}s^2=\left( 1-\omega ^2 \mathbf{x}^2\right) \mathrm{d}t^2+2\omega \, \mathbf{x}\cdot \mathrm{d}{} \mathbf{x}\,\mathrm{d}t-\mathrm{d}{} \mathbf{x}\cdot \mathrm{d}{} \mathbf{x}, \end{aligned}$$
(4)

lays out the event horizon at \(|\mathbf{x}|=\omega ^{-1}\). Thus, we avoid the FLRW local chart \(\{t,\mathbf{x}_\mathrm{c}\}\) with its well-known line element \(\mathrm{d}s^2=\mathrm{d}t^2-a(t)^2\,\mathrm{d}{} \mathbf{x}_\mathrm{c}\cdot \mathrm{d}{} \mathbf{x}_\mathrm{c}\) in which we may have some difficulties in interpreting the transition rates and probabilities we define here.

2.1 Dirac field in the rest frame vacuum

The free Dirac field \(\psi \) of mass m, minimally coupled to gravity, has the action

$$\begin{aligned} {\mathscr {S}}[\psi ]=\int \mathrm{d}^4 x\sqrt{g}\, {\mathscr {L}}_\mathrm{D}(\psi ), \end{aligned}$$
(5)

depending on the Lagrangian density [67],

$$\begin{aligned} {\mathscr {L}}_\mathrm{D}(\psi )=\frac{i}{2}\,[\overline{\psi }\gamma ^{\hat{\alpha }}D_{\hat{\alpha }}\psi - (\overline{D_{\hat{\alpha }}\psi })\gamma ^{\hat{\alpha }}\psi ] - m\overline{\psi }\psi , \end{aligned}$$
(6)

where \(\overline{\psi }=\psi ^+\gamma ^0\) is the Dirac adjoint, while \(D_{\hat{\alpha }}\) denote the covariant derivatives in local frames that guarantee the tetrad-gauge invariance of the Lagrangian theory [67]. The point-independent Dirac matrices \(\gamma ^{\hat{\mu }}\) satisfy \(\{ \gamma ^{\hat{\alpha }},\, \gamma ^{\hat{\beta }} \}= 2\eta ^{\hat{\alpha }\hat{\beta }}\), giving rise to the basis generators \(S^{\hat{\alpha }\hat{\beta }}=\frac{i}{4} [\gamma ^{\hat{\alpha }}, \gamma ^{\hat{\beta }} ]\) of the spinor representation \((\frac{1}{2},0)\otimes (0,\frac{1}{2})\) of the \(SL(2,{\mathbb {C}})\) group that induces the spinor covariant representation [57, 58, 67]. The Lagrangian density remains invariant under the transformations \(\psi \rightarrow e^{-i\alpha }\psi \) of the internal gauge group \(U(1)_{em}\), while the whole action (5) is invariant under isometries as long the Dirac field transforms according to the spinor covariant representation [58, 67].

For the Dirac theory on \(M_+\), we set the diagonal tetrad-gauge defined by the vector fields

$$\begin{aligned} e_{0}= & {} e_0^{\mu }\partial _{\mu }=-\omega t_\mathrm{c}\partial _{t_\mathrm{c}}=\partial _t+\omega x^i\partial _{x^i},\nonumber \\ e_{i}= & {} e_i^{\mu }\partial _{\mu }=-\omega t_\mathrm{c}\,\partial _{x^i_\mathrm{c}}=\partial _{x^i}, \end{aligned}$$
(7)

and the corresponding dual 1 forms

$$\begin{aligned} \omega ^{0}= & {} \hat{e}^0_{\mu }\mathrm{d}x^{\mu }=-\frac{1}{\omega t_\mathrm{c}}\mathrm{d}t_\mathrm{c}=\mathrm{d}t,\nonumber \\ \omega ^{i}= & {} \hat{e}^i_{\mu }\mathrm{d}x^{\mu }=-\frac{1}{\omega t_\mathrm{c}}\mathrm{d}x^i_\mathrm{c}=\mathrm{d}{x}^i-\omega {x}^i \mathrm{d}t, \end{aligned}$$
(8)

which preserve the global SO(3) symmetry, allowing us to systematically use the SO(3) vectors. In conformal frame \(\{t_\mathrm{c},\mathbf{x}_\mathrm{c};e\}\), the free Dirac equation [67]

$$\begin{aligned} \left[ -i\omega t\left( \gamma ^0\partial _{t}+\gamma ^i\partial _i\right) +\frac{3i\omega }{2}\gamma ^{0}-m\right] \psi (x)=0, \end{aligned}$$
(9)

can be solved analytically in momentum representation, allowing general solutions of the form

$$\begin{aligned} \psi ( x_\mathrm{c})= & {} \psi ^{(+)}( x_\mathrm{c})+\psi ^{(-)}( x_\mathrm{c})\nonumber \\= & {} \int \mathrm{d}^3 p \sum _{\sigma }\left[ U_{\mathbf{p},\sigma }(x_\mathrm{c}) {\mathfrak {a}}(\mathbf{p},\sigma )+V_{\mathbf{p}, \sigma }(x_\mathrm{c}){\mathfrak {b}}^{\dagger }(\mathbf{p}, \sigma ) \right] . \nonumber \\ \end{aligned}$$
(10)

These are expressed in terms of field operators, \({\mathfrak {a}}\) and \({\mathfrak {b}}\), and the corresponding fundamental spinors of this basis, \(U_{\mathbf{p},\sigma }\) and \(V_{\mathbf{p},\sigma }\), respectively, which depend on the momentum \(\mathbf{p}\) and polarization \(\sigma =\pm 1/2\). We assume that these spinors form an orthonormal basis, being related through the charge conjugation,

$$\begin{aligned} V_{\mathbf{p},\sigma }( x_\mathrm{c})=U^\mathrm{c}_{\mathbf{p},\sigma }( x_\mathrm{c}) =C\left[ {U}_{\mathbf{p},\sigma }( x_\mathrm{c})\right] ^* , \quad C=i\gamma ^2, \end{aligned}$$
(11)

and satisfying the orthogonality relations

$$\begin{aligned} \langle U_{\mathbf{p},\sigma }, U_{{\mathbf{p}\,}',\sigma '}\rangle _\mathrm{D}= & {} \langle V_{\mathbf{p},\sigma }, V_{{\mathbf{p}\,}',\sigma '}\rangle _\mathrm{D}= \delta _{\sigma \sigma ^{\prime }}\delta ^{3}(\mathbf{p}-\mathbf{p}\,^{\prime }) \end{aligned}$$
(12)
$$\begin{aligned} \langle U_{\mathbf{p},\sigma }, V_{{\mathbf{p}\,}',\sigma '}\rangle _\mathrm{D}= & {} \langle V_{\mathbf{p},\sigma }, U_{{\mathbf{p}\,}',\sigma '}\rangle _\mathrm{D} =0, \end{aligned}$$
(13)

with respect to the relativistic scalar product [67]

$$\begin{aligned} \langle \psi , \psi '\rangle _\mathrm{D}= & {} \int \mathrm{d}^{3}x \sqrt{g}\,e^0_0\,\overline{\psi }(x)\gamma ^{0}\psi (x) \nonumber \\= & {} \int \frac{ \mathrm{d}^3 x_\mathrm{c}}{(-\omega t_\mathrm{c})^3}\overline{\psi }(x_\mathrm{c})\gamma ^{0}\psi (x_\mathrm{c}) \end{aligned}$$
(14)

of the Dirac theory on \(M_+\). Moreover, this basis is supposed to be complete, accomplishing the condition [67]

$$\begin{aligned}&\int \mathrm{d}^{3}p \sum _{\sigma }\left[ U_{\mathbf{p},\,\sigma }(x_\mathrm{c})U^{+}_{\mathbf{p},\sigma }(x_\mathrm{c}^{\prime })+V_{\mathbf{p},\sigma }(x_\mathrm{c})V^{+}_{\mathbf{p},\sigma }( x_\mathrm{c}^{\prime })\right] \nonumber \\&\quad =(-\omega t_\mathrm{c})^{3}\delta ^{3}(\mathbf{x}_\mathrm{c}-\mathbf{x}_\mathrm{c}^{\prime }). \end{aligned}$$
(15)

We thus obtain the orthonormal basis of the momentum representation in which the particle (\({\mathfrak {a}},{\mathfrak {a}}^{\dagger })\) and antiparticle (\({\mathfrak {b}},{\mathfrak {b}}^{\dagger }\)) operators satisfy canonical anti-commutation relations, [67]

$$\begin{aligned} \{{\mathfrak {a}}(\mathbf{p},\sigma ), {\mathfrak {a}}^{\dagger }({\mathbf{p}}^{\,\prime },\sigma ^{\prime })\}= & {} \{{\mathfrak {b}}(\mathbf{p},\sigma ), {\mathfrak {b}}^{\dagger }({\mathbf{p}}^{\,\prime },\sigma ^{\prime })\}\nonumber \\= & {} \delta _{\sigma \sigma ^{\prime }}\delta ^3 (\mathbf{p}-{\mathbf{p}}^{\,\prime }), \end{aligned}$$
(16)

just as in the flat case.

For describing the polarization in a simple manner, we chose the fundamental spinors of the momentum-helicity basis that can be written in the standard representation of the Dirac matrices (with diagonal \(\gamma ^0\)) as [55]

$$\begin{aligned} U_{\mathbf{p},\sigma }(x_\mathrm{c})= & {} (-\omega t_\mathrm{c})^{\frac{3}{2}}\left( \begin{array}{c} u^+_p(t_\mathrm{c}) \, \xi _{\sigma }(\mathbf{p})\\ 2\sigma \,u^-_p(t_\mathrm{c})\,\xi _{\sigma }(\mathbf{p}) \end{array}\right) \frac{ e^{i\mathbf{p}\cdot \mathbf{x}_\mathrm{c}}}{(2\pi )^{\frac{3}{2}}}, \end{aligned}$$
(17)
$$\begin{aligned} V_\mathbf{{p},\sigma }(x_\mathrm{c})= & {} (-\omega t_\mathrm{c})^{\frac{3}{2}} \left( \begin{array}{c} 2\sigma \,v^+_p(t_\mathrm{c}) \,\eta _{\sigma }(\mathbf{p})\\ -v^-_p(t_\mathrm{c}) \,\eta _{\sigma }(\mathbf{p}) \end{array}\right) \frac{ e^{-i\mathbf{p}\cdot \mathbf{x}_\mathrm{c}}}{(2\pi )^{\frac{3}{2}}}, \end{aligned}$$
(18)

in terms of time modulation functions, \(u^{\pm }_p(t_\mathrm{c})\) and \(v^{\pm }_p(t_\mathrm{c})\), depending on the conformal time and \(p=|\mathbf{p}|\). The spin degrees of freedom are now given by the Pauli spinors of the helicity basis presented briefly in Appendix A.

The principal pieces of our approach are the time modulation functions which satisfy the equations

$$\begin{aligned} \left[ i\partial _{t_\mathrm{c}}\pm \frac{m}{\omega t_\mathrm{c}}\right] u_p^{\pm }(t_\mathrm{c})= & {} {p}\,u_p^{\mp }(t_\mathrm{c}), \end{aligned}$$
(19)
$$\begin{aligned} \left[ i\partial _{t_\mathrm{c}} \pm \frac{m}{\omega t_\mathrm{c}}\right] v_p^{\pm }(t_\mathrm{c})= & {} -{p}\,v_p^{\mp }(t_\mathrm{c}), \end{aligned}$$
(20)

resulting from Eq. (9) after substituting Eqs. (17) and (18). This system can be solved analytically by selecting the integration constants according to the charge conjugation (11), which requires

$$\begin{aligned} v_p^{\pm }=\left[ u_p^{\mp }\right] ^* \end{aligned}$$
(21)

and imposing the normalization

$$\begin{aligned} |u_p^+|^2+|u_p^-|^2=|v_p^+|^2+|v_p^-|^2 =1, \end{aligned}$$
(22)

which guarantees that Eqs. (12) and (13) are accomplished. However, these conditions are not sufficient for completely determining the integration constants, remaining with one constant that has to be fixed according to a supplemental physical assumption defining the vacuum.

In spite of the fact that the adiabatic vacuum of the Bunch–Davies type has long been used on \(M_+\) for quantizing the Dirac field, here we consider only the r.f.v., imposing the condition [43, 55]

$$\begin{aligned} \lim _{p\rightarrow 0}u^-_p=0 ~~\rightarrow ~~ \lim _{p\rightarrow 0}|u^+_p|=1, \end{aligned}$$
(23)

to eliminate the terms depending on helicity that do not make sense in the rest frame. In this vacuum, the time modulation functions

$$\begin{aligned} u^+_p(t_\mathrm{c})= & {} e^{i\alpha (p)}\frac{e^{\frac{1}{2}\pi \mu }}{ \sqrt{1+e^{2\pi \mu }}}\sqrt{-\pi p t_\mathrm{c} }\,J_{-\nu _-}(-p t_\mathrm{c}), \end{aligned}$$
(24)
$$\begin{aligned} u^-_p(t_\mathrm{c})= & {} ie^{i\alpha (p)} \frac{e^{\frac{1}{2}\pi \mu }}{ \sqrt{1+e^{2\pi \mu }}}\sqrt{-\pi p t_\mathrm{c}}\,J_{\nu _+}(-p t_\mathrm{c}), \end{aligned}$$
(25)

are expressed in terms of Bessel functions, \(J_{\nu }\), of indices

$$\begin{aligned} \nu _{\pm }=\frac{1}{2}\pm i\mu , \quad \mu =\frac{m}{\omega }=\left[ \frac{mc^2}{\hslash \omega }\right] _\mathrm{SI\, units}. \end{aligned}$$
(26)

The time modulation functions \(v_p^{\pm }\) have to be derived according to Eq. (21). The general phase [43],

$$\begin{aligned} \alpha (p)=\mu \left[ \ln \left( \frac{\sqrt{m^2+p^2}+m}{p}\right) -\frac{\sqrt{m^2+p^2}}{m}\right] , \end{aligned}$$
(27)

ensures the correct flat limit for \(\omega \rightarrow 0\) and \(\mu \rightarrow \infty \), which are the Minkowskian time modulation functions,

$$\begin{aligned} \lim _{\mu \rightarrow \infty }u_p^{\pm }(t) =\sqrt{\frac{E(p)\pm m}{2 E(p)}}\, e^{-iE(p)t}, \end{aligned}$$
(28)

where \(E(p)=\sqrt{m^2+p^2}\) is the special relativistic energy. Thus, we see that the well-known vacuum of special relativity is nothing other than a r.f.v. in the sense of our definition (23). Moreover, in the rest frame we have \(u^+_0(t)=e^{-m t}\), which means that the rest frame spinors in Minkowski and de Sitter spacetimes are proportional.

Note that in our actual expanding universe where \(\omega \sim 2\, 10^{-17} s^{-1}\), and \(\mu \sim 3.5\, 10^{38}\), we are so close to the flat limit that the gravitational field does not produce measurable quantum effects. Therefore, the theory we present here mainly addresses the strong gravitational fields of the early universe in inflationary and eventually electroweak epochs for which \(\mu \ll 10^8\).

2.2 Maxwell field in Coulomb gauge

The theory of the free Maxwell field minimally coupled to gravity is governed by the action

$$\begin{aligned} {\mathscr {S}}[A]=\int \mathrm{d}^{4}x \sqrt{g}\,{\mathscr {L}}_{\mathrm{M}}(A)=-\frac{1}{4}\int \mathrm{d}^{4}x \sqrt{g}\,F_{\mu \nu }F^{\mu \nu } , \end{aligned}$$
(29)

where A is the (electromagnetic) potential and \(F_{\mu \nu }=\partial _{\mu } A_{\nu }-\partial _{\nu } A_{\mu }\) is the field strength. Now, the canonical variables are the covariant components \(A_{\mu }\) carrying natural indices and transforming usually under isometries.

In the conformal frame \(\{t_\mathrm{c}, \mathbf{x}_\mathrm{c};e\}\), we may exploit the conformal invariance of the free Maxwell equation derived from this action for taking over the solutions we know in the flat case. As the Lorentz condition is invariant only in Coulomb gauge [72, 73] we must fix this gauge taking

$$\begin{aligned} A_0=0, \quad \partial _{x_\mathrm{c}^i} A_i=0. \end{aligned}$$
(30)

In this gauge, the free Maxwell equation on \(M_{+}\),

$$\begin{aligned} (\partial _{t_\mathrm{c}}^2-\varDelta _\mathrm{c})A_i(x_\mathrm{c})=0, \end{aligned}$$
(31)

can be solved in a momentum-helicity basis [72, 73] where the potential

$$\begin{aligned} \mathbf{A}(x_\mathrm{c})= & {} \mathbf{A}^{(+)}(x_\mathrm{c})+\mathbf{A}^{(-)}(x_\mathrm{c})\nonumber \\= & {} \int \mathrm{d}^3k \sum _{\lambda }\left[ \mathbf{w}_{\mathbf{k},\lambda }(x_\mathrm{c}) \alpha (\mathbf{k},\lambda )+\mathbf{w}_{\mathbf{k},\lambda }(x_\mathrm{c})^* \alpha ^{\dagger }(\mathbf{k},\lambda )\right] , \nonumber \\ \end{aligned}$$
(32)

is expressed in terms of the modes vectors [72],

$$\begin{aligned} \mathbf{w}_{\mathbf{k},\lambda }(x_\mathrm{c})= \frac{1}{(2\pi )^{\frac{3}{2}}}\frac{1}{\sqrt{2k}}\,e^{-ikt_\mathrm{c}+i\mathbf{k}\cdot \mathbf{x}_\mathrm{c}}\,\mathbf{e}_{\lambda }(\mathbf{k}), \end{aligned}$$
(33)

depending on momentum, \(\mathbf{k}\) (\(k=|\mathbf{k}|\)), and helicity, \(\lambda =\pm 1\). The polarization vectors \(\mathbf{e}_{\lambda }(\mathbf{k})\) in Coulomb gauge are given in Appendix A. According to our prescription, the particle mode vectors are progressive plane waves, as in the flat case.

The modes vectors (33) we consider here are orthonormal [72],

$$\begin{aligned} \left\langle w_{\mathbf{k},\lambda },w_{\mathbf{k}\,'\lambda '}\right\rangle _\mathrm{M}= & {} -\left\langle w^*_{\mathbf{k},\lambda },w^*_{\mathbf{k}\,',\lambda '}\right\rangle _\mathrm{M}\nonumber \\= & {} \delta _{\lambda \lambda '}\delta ^3(\mathbf{k}-\mathbf{k}\,'), \end{aligned}$$
(34)
$$\begin{aligned} \left\langle w_{\mathbf{k},\lambda },w^*_{\mathbf{k}\,',\lambda '}\right\rangle _\mathrm{M}= & {} \left\langle w^*_{\mathbf{k},\lambda },w_{\mathbf{k}\,',\lambda '}\right\rangle _\mathrm{M}=0, \end{aligned}$$
(35)

with respect to the relativistic scalar product of Maxwell’s theory [72]

$$\begin{aligned} \left\langle w,w'\right\rangle _\mathrm{M}=i \int \mathrm{d}^3 x_\mathrm{c}\, w^*_i( x_\mathrm{c}){\mathop {\partial _{t_\mathrm{c}}}\limits ^{\leftrightarrow }}w_i'( x_\mathrm{c}), \end{aligned}$$
(36)

where we denote \(f{\mathop {\partial }\limits ^{\leftrightarrow }} g=f\partial g-g\partial f\).

The conformal invariance of the Maxwell theory on \(M_{+}\) allows us to perform the second quantization in Coulomb gauge as in special relativity, assuming that the photon field operators satisfy [72, 73]

$$\begin{aligned}{}[\alpha (\mathbf{k},\lambda ), \alpha ^{\dagger }(\mathbf{k}^{\,\prime },\lambda ')] =\delta _{\lambda \lambda '} \delta ^3 (\mathbf{k}-\mathbf{k}^{\,\prime }). \end{aligned}$$
(37)

Then the Hermitian field \(A=A^{\dagger }\) and its momentum density \(\pi ^j=\partial _{t}A_j\) satisfy the well-known canonical rule [66, 72, 73].

3 First-order processes in the rest frame vacuum

In what follows, we would like to study the first-order processes in r.f.v. of the de Sitter QED in Coulomb gauge we constructed some time ago according to the LSZ reduction formalism [44], but by using the traditional adiabatic vacuum of the Bunch–Davies type [21]. The Dirac field \(\varPsi \) and electromagnetic potential \({\mathscr {A}}_{\mu }\) are minimally coupled to the gravity of \(M_+\) interacting between them according to the QED action

$$\begin{aligned} {\mathscr {S}}=\int \mathrm{d}^4 x\sqrt{g}\, \left[ {\mathscr {L}}_\mathrm{D}(\varPsi )+{\mathscr {L}}_{\mathrm{M}}({\mathscr {A}})+{\mathscr {L}}_\mathrm{int}(\psi ,{\mathscr {A}})\right] , \end{aligned}$$
(38)

where the Lagrangians of the Dirac (D) and Maxwell (M) free fields have the standard form as in Ref. [44], while the interacting part,

$$\begin{aligned} {\mathscr {L}}_\mathrm{int}(\psi ,{A})=-e_0 \bar{\varPsi }(x)\gamma ^{\hat{\mu }}e^{\nu }_{\hat{\mu }}(x){\mathscr {A}}_{\nu }(x)\varPsi (x), \end{aligned}$$
(39)

corresponds to the minimal electromagnetic coupling given by the electrical charge \(e_0\).

The quantization of the entire theory and the perturbation procedure based on the LSZ formalism was performed exploiting the usual in–out initial/final asymptotic conditions in the conformal frame [44]. In this manner, we obtained a perturbation procedure allowing us to calculate the transition amplitudes between two free states, \(\alpha \rightarrow \beta \), as \(\langle out, \beta |in, \alpha \rangle =\langle \beta |S |\alpha \rangle \), by using the operator [44]

$$\begin{aligned} {S}=T\,\exp \left[ -ie_0\int \frac{\mathrm{d}^4x_\mathrm{c}}{(-\omega t_\mathrm{c})^3}\, :\overline{\psi }(x_\mathrm{c})\,\mathbf {\gamma }\cdot \mathbf{A}(x_\mathrm{c})\,\psi (x_\mathrm{c}):\right] , \end{aligned}$$
(40)

expressed in terms of free fields, \(\psi \) and A, in Coulomb gauge (30), multiplied in chronological order [66]. Note that in this formalism, the free fields involved in the perturbation procedure are arbitrary, different from the in or out ones which were used as auxiliary tools in constructing the LSZ formalism of the de Sitter QED [44].

3.1 First-order amplitudes

We now focus on the effects in the first order of the perturbation theory which are allowed because the energy is no longer conserved on \(M_+\), in contrast to the Minkowski spacetime where the energy-momentum conservation forbids similar effects. There are two types of processes involving electrons \(e^-(\mathbf{p},\sigma )\), positrons \(e^+(\mathbf{p}',\sigma ')\) and photons \(\gamma (\mathbf{k},\lambda )\), namely transitions between charged or neutral states.

1. The neutral transitions involve only neutral in and out states as in the cases of pair creation, \(\gamma \rightarrow e^- + e^+\), and lepton creation from vacuum, \(vac\rightarrow \gamma + e^- + e^+\), and the corresponding annihilation processes, \(e^- + e^+ \rightarrow \gamma \) and \( \gamma + e^- + e^+\rightarrow vac\) with similar amplitudes. In what follows, we focus on the creation processes starting with the amplitude of pair creation

$$\begin{aligned}&A^{+}_{\lambda ,\sigma ,\sigma '}(\mathbf{k};\mathbf{p},\mathbf{p}')=\langle e^-(\mathbf{p},\sigma ),e^+(\mathbf{p}',\sigma ') |\mathbf{S}_1|\gamma (\mathbf{k},\lambda ) \rangle \nonumber \\&\quad =-ie_0\int \frac{\mathrm{d}^4x_\mathrm{c}}{(-\omega t_\mathrm{c})^3}\,\overline{U}_{\mathbf{p},\sigma }(x_\mathrm{c})\, \mathbf {\gamma }\cdot \mathbf{w}_{\mathbf{k},\lambda }(x_\mathrm{c})\, V_{{\mathbf{p}\,}',\sigma '}(x_\mathrm{c}).\nonumber \\ \end{aligned}$$
(41)

By replacing \(\mathbf{w}\rightarrow \mathbf{w}^{*}\) in the above integral, we obtain the amplitudes of creating leptons from vacuum we denote as \(A^{-}_{\lambda ,\sigma ,\sigma '}(\mathbf{k},\mathbf{p},\mathbf{p}')\). Note that the inverse processes of pair annihilation, \(e^-+e^+\rightarrow \gamma \), or lepton annihilation to vacuum, \(\gamma +e^-+e^+\rightarrow vac\), are less probable, requiring the particles to meet each other spontaneously in the same point.

2. The charged transitions, between charged in and out states, are processes in which a photon is adsorbed or emitted. The amplitude of a photon adsorbed by an electron, \(e^-+\gamma \rightarrow e^-\), reads

$$\begin{aligned}&A_{\sigma '}^{\sigma ,\lambda }(\mathbf{p},\mathbf{k};\mathbf{p}')=\langle e^-(\mathbf{p}',\sigma ') |\mathbf{S}_1|e^-(\mathbf{p},\sigma ),\gamma (\mathbf{k},\lambda )\rangle \nonumber \\&\quad =-ie_0\int \frac{\mathrm{d}^4x_\mathrm{c}}{(-\omega t_\mathrm{c})^3}\,\overline{U}_{{\mathbf{p}\,}',\sigma '}(x_\mathrm{c})\, \mathbf {\gamma }\cdot \mathbf{w}_{\mathbf{k},\lambda }(x_\mathrm{c})\, U_{\mathbf{p},\sigma }(x_\mathrm{c}).\nonumber \\ \end{aligned}$$
(42)

When the photon is adsorbed by a positron, we have to replace \({U}_{{\mathbf{p}\,}',\sigma '}\rightarrow {V}_{\mathbf{p},\sigma }\) and \({U}_{\mathbf{p},\sigma }\rightarrow {V}_{{\mathbf{p}\,}',\sigma '}\). Whether we replace \(\mathbf{w}\rightarrow \mathbf{w}^*\), we then obtain the amplitudes of the transitions \(e^-\rightarrow e^- +\gamma \) and \(e^{+}\rightarrow e^{+}+\gamma \), respectively, in which a photon is emitted.

In what follows, we focus on the above amplitudes that can be put in the form

$$\begin{aligned}&A^+_{\lambda ,\sigma ,\sigma '}(\mathbf{k};\mathbf{p},\mathbf{p}')=i \frac{e_0}{\sqrt{2 k}\,(2\pi )^{\frac{3}{2}}}\nonumber \\&~~~\times \delta ^3(\mathbf{p}+\mathbf{p}'-\mathbf{k}) \, \varPi _{\sigma ,\sigma '}^{\lambda }(\mathbf{k};\mathbf{p},\mathbf{p}')\,I^\mathrm{n}({p},{p}',{k}), \end{aligned}$$
(43)
$$\begin{aligned}&A^-_{\lambda ,\sigma ,\sigma '}(\mathbf{k},\mathbf{p},\mathbf{p}')=i \frac{e_0}{\sqrt{2 k}\,(2\pi )^{\frac{3}{2}}}\nonumber \\&~~~\times \delta ^3(\mathbf{p}+\mathbf{p}'+\mathbf{k}) \, \varPi _{\sigma ,\sigma '}^{-\lambda }(\mathbf{k};\mathbf{p},\mathbf{p}')\,I^\mathrm{n}({p},{p}',-{k}), \end{aligned}$$
(44)
$$\begin{aligned}&A^{\sigma ,\lambda }_{\sigma '}(\mathbf{p},\mathbf{k};\mathbf{p}')=i \frac{e_0}{\sqrt{2 k}\,(2\pi )^{\frac{3}{2}}}\nonumber \\&~~~\times \delta ^3(\mathbf{p}-\mathbf{k}-\mathbf{p}') \,\varPi _{\sigma '}^{\sigma ,\lambda }(\mathbf{p},\mathbf{k};\mathbf{p}')\,I^\mathrm{c}({p'},{p},{k}), \end{aligned}$$
(45)

after separating the polarization terms,

$$\begin{aligned} \varPi _{\sigma '}^{\sigma ,\lambda }(\mathbf{p},\mathbf{k};\mathbf{p}')= & {} \xi _{\sigma '}^+(\mathbf{p}')\,\mathbf {\sigma }\cdot \mathbf{e}_{\lambda }(\mathbf{k})\,\xi _{\sigma }(\mathbf{p}), \end{aligned}$$
(46)
$$\begin{aligned} \varPi _{\sigma ,\sigma '}^{\lambda }(\mathbf{k};\mathbf{p},\mathbf{p}')= & {} \xi _{\sigma }^+(\mathbf{p})\,\mathbf {\sigma }\cdot \mathbf{e}_{\lambda }(\mathbf{k})\,\eta _{\sigma '}(\mathbf{p}'), \end{aligned}$$
(47)

from the time integrals

$$\begin{aligned} I^{\mathrm{n/c}}({p},{p}',{k})=\int ^{0}_{-\infty } \mathrm{d}t_\mathrm{c}\,K_{\sigma ,\sigma '} ^{\mathrm{n/c}}({p},{p}',{k};t_\mathrm{c}), \end{aligned}$$
(48)

whose time-dependent functions,

$$\begin{aligned} K ^{\mathrm{n}}({p},{p}',{k};t_\mathrm{c})= & {} e^{- i k t_\mathrm{c}}\left[ u^+_p(t_\mathrm{c})^*u^+_{p'}(t_\mathrm{c})^*\right. \nonumber \\&\left. -\frac{\sigma }{\sigma '}\,u^-_p(t_\mathrm{c})^*u^-_{p'}(t_\mathrm{c})^* \right] , \end{aligned}$$
(49)
$$\begin{aligned} K_{\sigma ,\sigma '} ^{\mathrm{c}}({p},{p}',{k};t_\mathrm{c})= & {} -e^{- i k t_\mathrm{c}}\left[ 2\sigma \,u^+_p(t_\mathrm{c})^*u^-_{p'}(t_\mathrm{c})\right. \nonumber \\&\left. +2\sigma ' \,u^-_p(t_\mathrm{c})^*u^+_{p'}(t_\mathrm{c}) \right] , \end{aligned}$$
(50)

are expressed in terms of time modulation functions, (24) and (25). Thanks to the correct flat limit (28) of our time modulation functions, we deduce that in this limit, the functions (49) and (50) behave as

$$\begin{aligned} \lim _{\mu \rightarrow \infty }K ^{\mathrm{n}}({p},{p}',{k};t_\mathrm{c})\propto & {} e^{ i (E(p)+E(p')-k )t_\mathrm{c}}, \end{aligned}$$
(51)
$$\begin{aligned} \lim _{\mu \rightarrow \infty }K ^{\mathrm{c}}({p},{p}',{k};t_\mathrm{c})\propto & {} e^{ i (E(p)-E(p')-k )t_\mathrm{c}}, \end{aligned}$$
(52)

generating the Dirac \(\delta \) functions of energy conservation which forbid these processes in Minkowski’s flat spacetime.

3.2 Rates and probabilities

The previous results lead to the conclusion that the amplitudes of the transitions \(\alpha \rightarrow \beta \) we study here have the general form

$$\begin{aligned} A_{\alpha \beta } =\langle out\, \beta |in\, \alpha \rangle =\delta ^3(\mathbf{p}_{\alpha }-\mathbf{p}_{\beta }) M_{\alpha \beta }I_{\alpha \beta }, \end{aligned}$$
(53)

laying out the Dirac \(\delta \) function of momentum conservation but without conserving the energy. Therefore, in the conformal frame \(\{t_\mathrm{c},\mathbf{x}_\mathrm{c};e\}\), the time integration gives the quantity

$$\begin{aligned} I_{\alpha \beta }=\int ^0_{-\infty }\mathrm{d}t_\mathrm{c}\, K _{\alpha \beta }(t_\mathrm{c}), \end{aligned}$$
(54)

instead of the familiar \(\delta (E_{\alpha }-E_{\beta })\) we encounter in the flat case when the energy is conserved. We remind the reader that the limit \(t_\mathrm{c}\rightarrow 0\) corresponds to the limit \(t\rightarrow \infty \) of the proper time.

We have recently shown that for passing over this impediment, we must redefine the rates and probabilities [70]. We first introduce the time-dependent amplitudes

$$\begin{aligned} A_{\alpha \beta }(t_\mathrm{c})= & {} \delta ^3(\mathbf{p}_{\alpha }-\mathbf{p}_{\beta }) M_{\alpha \beta }I_{\alpha \beta }(t_\mathrm{c})\nonumber \\= & {} \delta ^3(\mathbf{p}_{\alpha }-\mathbf{p}_{\beta }) M_{\alpha \beta }\int _{-\infty }^{t_\mathrm{c}} \mathrm{d}t_\mathrm{c}'K _{\alpha \beta }(t_\mathrm{c}'), \end{aligned}$$
(55)

then defining the transition rate in a conformal frame at the instant \(t_\mathrm{c}\),

$$\begin{aligned} { R}_{\alpha \beta }(t_\mathrm{c})= \frac{1}{2V_\mathrm{c}}\frac{\mathrm{d}}{\mathrm{d}t_\mathrm{c}}\left| A_{\alpha \beta }(t_\mathrm{c})\right| ^2. \end{aligned}$$
(56)

In this frame, we may use the trick of total volume, \(V_\mathrm{c}\sim (2\pi )^3 \delta ^3(0)\), which works as in special relativity where we use the same three-dimensional Fourier integrals. We thus obtain the final result

$$\begin{aligned} { R}_{\alpha \beta }(t_\mathrm{c})=\delta ^3(\mathbf{p}_{\alpha }-\mathbf{p}_{\beta })\frac{|M_{\alpha \beta }|^2}{(2\pi )^3}|I_{\alpha \beta }|\,| K_{\alpha \beta }(t_\mathrm{c})|, \end{aligned}$$
(57)

after substituting \(A_{\alpha \beta }(t_\mathrm{c})\rightarrow \lim _{t_\mathrm{c}\rightarrow 0}A_{\alpha \beta }(t_\mathrm{c})\) for technical reasons, as the integral (53) cannot be evaluated at arbitrary \(t_\mathrm{c}<0\). Fortunately, this approximation gives convenient rates which match perfectly to the Minkowski ones whose functions K depend on time only through phase factors. Keeping the same definition in the physical frame, \(\{t,\mathbf{x};e\}\), using Eqs. (3) and observing that \(V=V_\mathrm{c}\, e^{3\omega t}\), we obtain the rates in this frame,

$$\begin{aligned} {\hat{R}}_{\alpha \beta }(t)=\lim _{t\rightarrow \infty } \frac{1}{2V}\frac{\mathrm{d}}{\mathrm{d}t}\left| A_{\alpha \beta }(t)\right| ^2={R}_{\alpha \beta }(t_\mathrm{c}(t))\,e^{-4\omega t}, \end{aligned}$$
(58)

for which \({\hat{R}}_{\alpha \beta }(0)={R}_{\alpha \beta }(t_{\mathrm{c}\,0})\) play the role of initial conditions at the time \(t_0=0\) (when \(t_{\mathrm{c}\,0}=-\omega ^{-1}\)).

Applying the above definitions to the transition rates of the processes under consideration, we start analysing the time behaviour of the functions (49) and (50) for increasing \(t\rightarrow \infty \) or \(t_\mathrm{c}\rightarrow 0\). As the time modulation functions (24) and (25) depend in fact only on the product \(p\,t_\mathrm{c}\), we understand that

$$\begin{aligned} \lim _{t_\mathrm{c}\rightarrow 0} u^-_p(t_\mathrm{c})= & {} \lim _{p\rightarrow 0} u^-_p(t_\mathrm{c})=0, \end{aligned}$$
(59)
$$\begin{aligned} \lim _{t_\mathrm{c}\rightarrow 0}| u^+_p(t_\mathrm{c})|= & {} \lim _{p\rightarrow 0}| u^+_p(t_\mathrm{c})|=1, \end{aligned}$$
(60)

according to the condition (23) which sets the r.f.v. Hereby, we obtain for \(t_\mathrm{c}\sim 0\) the interesting behaviour,

$$\begin{aligned} \left| K_{\sigma ,\sigma '}^{\mathrm{n}}({p},{p}',{k};t_\mathrm{c}) \right|\sim & {} 1, \end{aligned}$$
(61)
$$\begin{aligned} \left| K_{\sigma ,\sigma '}^{\mathrm{c}}({p},{p}',{k};t_\mathrm{c}) \right|\sim & {} -\omega t_\mathrm{c}, \end{aligned}$$
(62)

showing that the rates of all the processes involving charged states are decreasing in time, while the transitions between neutral states remain asymptotically constant.

This gives us the opportunity to study a simple model in which an observer performing measurements at a very late time, when the transitions between charged states can be neglected, measures how the leptons are created from vacuum and the pairs created from photons. In other words, the late observer measures the late effects of the lepton creation from vacuum due to the de Sitter gravity, which are less influenced by the transitions between charged states, which may be of interest mainly in local scattering effects. In what follows we devote our attention to this model, for which we first have to calculate the probabilities.

3.3 Probabilities of neutral transitions

Focusing on the neutral transitions, we substitute the functions (24) and (25) in amplitudes (43) and (44), respectively, and apply the general rule (57), obtaining the rates,

$$\begin{aligned}&{ R}^{\pm }_{\lambda ,\sigma ,\sigma '}(\mathbf{k};\mathbf{p},\mathbf{p}')= \frac{\kappa \,(2\pi )^3}{\cosh \pi \mu }\,\delta ^3(\mathbf{p}+\mathbf{p}'\mp \mathbf{k})\nonumber \\&~~~~\times |\varPi _{\sigma ,\sigma '}^{\pm \lambda }(\pm \mathbf{p}\pm \mathbf{p}';\mathbf{p},\mathbf{p}')|^2\,\frac{\sqrt{pp'}}{k}\,| J_{\sigma ,\sigma '}'({p},{p}',\pm {k})|,\nonumber \\ \end{aligned}$$
(63)

where

$$\begin{aligned} \kappa =\frac{e_0^2}{8(2\pi )^5}, \end{aligned}$$
(64)

while the notation

$$\begin{aligned} J_{\sigma ,\sigma '}'({p},{p}',{k})=\lim _{\varepsilon \rightarrow 0}\left[ -i\partial _kJ_{\sigma ,\sigma '}^{\varepsilon }({p},{p}',{k})\right] , \end{aligned}$$
(65)

stands for the derivative with respect to k of the integral

$$\begin{aligned} J_{\sigma ,\sigma '}^{\varepsilon }({p},{p}',{k})= & {} \int _0^{\infty }\mathrm{d}\tau \, e^{-\varepsilon \tau +i k\tau }\left[ J_{-\nu _+}(p\tau )J_{-\nu _+}(p'\tau )\right. \nonumber \\&\left. + \frac{\sigma }{\sigma '}J_{\nu _-}(p\tau )J_{\nu _-}(p'\tau )\right] , \end{aligned}$$
(66)

in the new variable \(\tau =-t_\mathrm{c}\in \mathbb {R}^+\). As the original integral is divergent, we introduced the small \(\varepsilon >0\) for ensuring its convergence, bearing in mind that the final physical results have to be obtained in the limit of \(\varepsilon \rightarrow 0\).

On the other hand, the identities (A.6) allow us to introduce the self-explanatory simpler notation of the polarization factors,

$$\begin{aligned} \varPi ^{\lambda }_{\sigma ,\sigma '}(\mathbf{n},\mathbf{n}')= & {} \varPi _{\sigma ,\sigma '}^{\lambda }(\mathbf{p}+\mathbf{p}';\mathbf{p},\mathbf{p}')\nonumber \\= & {} \varPi _{\sigma ,\sigma '}^{-\lambda }(-\mathbf{p}-\mathbf{p}';\mathbf{p},\mathbf{p}'), \end{aligned}$$
(67)

which depend only on the unit vectors of the momenta \(\mathbf{p}=\mathbf{n}p\) and \(\mathbf{p}'=\mathbf{n}'p'\). Note that when \(\mathbf{n}\) and \(\mathbf{n}'\) are parallel or anti-parallel, the helicity is conserved as spin projections along the same direction, either \(\mathbf{n}\) or \(\mathbf{n}'\). Therefore, the following selection rules,

$$\begin{aligned} \varPi _{\sigma , \sigma }^{\lambda =2\sigma }(\mathbf{n},\mathbf{n})=\sqrt{2},&\quad&\varPi _{\sigma ,- \sigma }^{\lambda }(\mathbf{n},\mathbf{n})=0, \end{aligned}$$
(68)
$$\begin{aligned} \varPi _{\sigma , -\sigma }^{\lambda =2\sigma }(\mathbf{n},-\mathbf{n})=\sqrt{2},&\quad&\varPi _{\sigma , \sigma }^{\lambda }(\mathbf{n},-\mathbf{n})=0, \end{aligned}$$
(69)

can be derived easily by using the form of helicity spinors given in Appendix A.

Under such circumstances, we may define the probabilities per unit of volume and unit of time (p.v.t.s) in conformal frame as

$$\begin{aligned}&{ P}^{\pm }_{\lambda ,\sigma ,\sigma '}(\mathbf{p},\mathbf{p}')=\int \frac{\mathrm{d}^3k}{(2\pi )^3}\, { R}^{\pm }_{\lambda ,\sigma ,\sigma '}(\mathbf{k};\mathbf{p},\mathbf{p}')=\frac{\kappa }{\cosh \pi \mu }\nonumber \\&~~~\times |\varPi _{\sigma ,\sigma '}^{\lambda }(\mathbf{n},\mathbf{n}')|^2\,\frac{\sqrt{pp'}}{k(\theta )}\,|J_{\sigma ,\sigma '}'({p},{p}',\pm {k}(\theta ))|, \end{aligned}$$
(70)

where the quantity

$$\begin{aligned} k(\theta )=\left| \mathbf{p}+\mathbf{p}'\right| =\sqrt{p^2 +2p p'\cos \theta +{p'}^2} \end{aligned}$$
(71)

depends on the angle \(\theta \) between \(\mathbf{n}\) and \(\mathbf{n}'\). \({ P}^{+}_{\lambda ,\sigma ,\sigma '}(\mathbf{p},\mathbf{p}')\) is the p.v.t. of creating the pair \(\{{ e}^- (\mathbf{p},\sigma ),{e}^+ (\mathbf{p}',\sigma ')\}\) from a photon of polarization \(\lambda \), while \({ P}^{-}_{\lambda ,\sigma ,\sigma '}(\mathbf{p},\mathbf{p}')\) is the p.v.t. of finding the same pair and a photon of polarization \(\lambda \) in the final state created from vacuum. The corresponding time-dependent p.v.t.s in the physical frame may be obtained by multiplying these p.v.t.s by the general factor \(e^{-4\omega t}\). In what follows these processes will be referred simply as the pair creation \((+)\) and lepton creation \((-)\).

It remains for us to evaluate the integral (66) and the function (65) we need to obtain the closed expressions of rates and p.v.t.s. According to the arguments of Appendix B, after a few manipulations, we may write

$$\begin{aligned} \frac{\sqrt{pp'}}{k(\theta )}\left| J_{\sigma ,\sigma '}'(p,p',\pm k(\theta ))\right| =\frac{1}{pp'}\, \varDelta _{\sigma ,\sigma '}^{\pm }(\mu ,\theta ), \end{aligned}$$
(72)

where we introduced the new functions

$$\begin{aligned} \varDelta _{\sigma ,\sigma }^{\pm }(\mu ,\theta )= & {} \left( e^{\pm 2\pi \mu } [\Re f(\mu ,\theta )]^2+[\Im g(\mu ,\theta )]^2\right) ^{\frac{1}{2}}, \end{aligned}$$
(73)
$$\begin{aligned} \varDelta _{\sigma ,-\sigma }^{\mu ,\pm }(\mu ,\theta )= & {} \left( e^{\pm 2\pi \mu } [\Im f(\mu ,\theta )]^2+[\Re g(\mu ,\theta )]^2\right) ^{\frac{1}{2}}, \end{aligned}$$
(74)

defined in terms of the auxiliary functions

$$\begin{aligned} f(\mu ,\theta )= & {} {\mathscr {F}}(\mu , \cos \theta ), \end{aligned}$$
(75)
$$\begin{aligned} g(\mu ,\theta )= & {} {\mathscr {F}}(\mu ,-\cos \theta ), \end{aligned}$$
(76)

depending on the function

$$\begin{aligned} {\mathscr {F}}(\mu ,x)=\frac{i\mu (i\mu +1)}{\sinh 2\pi \mu } F\left( 2+i\mu ,1-i\mu ;2;\frac{1+x}{2}\right) , \end{aligned}$$
(77)

resulting after solving the integrals (B.3) and (B.4). Thus, we arrive at the final result putting both the p.v.t.s (70) in closed form,

$$\begin{aligned} { P}^{\pm }_{\lambda ,\sigma ,\sigma '}(\mathbf{p},\mathbf{p}')= & {} \frac{\kappa }{pp'} |\varPi _{\sigma ,\sigma '}^{\lambda }(\mathbf{n},\mathbf{n}')|^2 \varDelta _{\sigma ,\sigma '}^{\pm }(\mu ,\theta ). \end{aligned}$$
(78)

All these quantities depend on the angle \(\theta \) (between \(\mathbf{n}\) and \(\mathbf{n}'\)) and parameter \(\mu =\frac{m}{\omega }\) measuring the strength of de Sitter gravity, from the very strong fields with \(\mu \sim 0\) up to the very weak fields with very small \(\omega \) and \(\mu \) increasing to infinity.

As usually happens in perturbations, the functions (75) and (76) are divergent in critical positions, having the limits

$$\begin{aligned} \lim _{\theta \rightarrow 0}\sin ^2\frac{\theta }{2}\, f(\mu ,\theta )= & {} \lim _{\theta \rightarrow \pi } \cos ^2\frac{\theta }{2}\, g(\mu ,\theta )\nonumber \\= & {} \frac{i}{2\pi \cosh \pi \mu },\quad \forall \mu \in \mathbb {R}^+, \end{aligned}$$
(79)

resulting from Eq. (B.8). In other respects, bearing in mind that \(F(1,2;2;x)=(1-x)^{-1}\), we find the limits

$$\begin{aligned} \lim _{\mu \rightarrow 0}f(\mu ,\theta )= & {} \frac{i}{2\pi }\frac{1}{\sin ^2\frac{\theta }{2}}, \end{aligned}$$
(80)
$$\begin{aligned} \lim _{\mu \rightarrow 0}g(\mu ,\theta )= & {} \frac{i}{2\pi }\frac{1}{\cos ^2\frac{\theta }{2}}, \end{aligned}$$
(81)

in extremely strong gravitational fields, which is in accordance with the limits (79), having singularities in \(\theta =0\) and \(\theta =\pi \), respectively. These singularities are simple poles given by terms of the form \((1\pm \cos \theta )^{-1}\) that can be removed by applying the usual reduction method [74]. However, the surprise is that there exists, in addition, the logarithmic singularity presented in Appendix C that cannot be removed by reduction. Therefore, we must combine the reduction with a regularization for eliminating the logarithmic singularity.

4 Regularization and reduction

The reduction and regularization problems are sensitive since the angular divergences arise for parallel (\(\theta =0\)) or anti-parallel (\(\theta =\pi \)) momenta, which are just the positions in which the helicity is conserved, complying with precise selection rules. For this reason, after removing the singularities, we must recover these rules with accuracy. This will be the criterion in selecting the reduction and regularization procedures.

The reduction procedure of Ref. [74] consists in putting by hand suitable factors of the form \((1\pm \cos \theta )^\mathrm{n}\) in the divergent parts of the transition amplitudes for removing the poles in \(\cos \theta \) of the order n, called the reduction order. The particularity here is of having two divergent auxiliary functions that have, in addition, logarithmic singularities for which there are many possible prescriptions of regularization and reduction.

4.1 Reduced probabilities

The limits (79) show that here we have simple poles that can be reduced in the first order (\(n=1\)). Therefore, we first consider the simplest prescription reducing the function (77) as

$$\begin{aligned} {\mathscr {F}}(\mu ,x)~~\rightarrow ~~\mathrm{red}{\mathscr {F}}(\mu ,x)=\frac{1-x}{2}\,{\mathscr {F}}(\mu ,x), \end{aligned}$$
(82)

since this removes all the singularities, including the logarithmic one. After substituting these functions in Eqs. (73) and (74), we obtain the reduced functions \(\hbox {red}\varDelta ^{\pm }_{\sigma ,\sigma '}\) and the corresponding reduced p.v.t.s. A rapid test shows that for the pair production (\(+\)) and parallel momenta (\(\theta =0\)), we have red\(\varDelta ^+_{\sigma ,\sigma }(\mu ,0)< \mathrm{red}\varDelta ^+_{\sigma ,-\sigma }(\mu ,0)\) which violates the helicity conservation that favours the processes with \(\sigma '=\sigma \) in this position. Similarly, for the lepton production \((-)\) and anti-parallel momenta (\(\theta =\pi \)), we encounter the same inversion. This unwanted behaviour comes from this reduction which is brutal removing the singularities but cancelling simultaneously the non-singular contributions of physical interest. Therefore, we must give up this prescription as affecting severely the physical meaning.

A more refined reduction must protect the non-singular terms of the real part of the function (77) but only after extracting its logarithmic singularity. This can be done by defining the regularized function

$$\begin{aligned} {\mathscr {F}}_\mathrm{reg}(\mu ,x)={\mathscr {F}}(\mu ,x)-\frac{\mu }{2\pi \cosh \pi \mu }\ln \left( \frac{1-x}{2}\right) , \end{aligned}$$
(83)

which now has a regular real part, and applying then the reduction to its imaginary part for removing simultaneously the effects of the pole and logarithmic singularity. We thus obtain the reduced function

$$\begin{aligned} \mathrm{Red}{\mathscr {F}}(\mu ,x)=\Re \,{\mathscr {F}}_\mathrm{reg}(\mu ,x)+i\, \frac{1-x}{2}\Im \,{\mathscr {F}}(\mu ,x), \end{aligned}$$
(84)

and the new reduced auxiliary functions

$$\begin{aligned} \mathrm{Red}f(\mu , \theta )= & {} \mathrm{Red}{\mathscr {F}}(\mu ,\cos \theta ), \end{aligned}$$
(85)
$$\begin{aligned} \mathrm{Red}\,g(\mu ,\theta )= & {} \mathrm{Red}{\mathscr {F}}(\mu ,-\cos \theta ), \end{aligned}$$
(86)

which are regular in both their variables. In the critical positions, these have the limits

$$\begin{aligned} \mathrm{Red}\,f(\mu , 0)= & {} \mathrm{Red}\,g(\mu ,\pi )=h(\mu )+\frac{i}{2\pi \cos \pi \mu }, \end{aligned}$$
(87)
$$\begin{aligned} \mathrm{Red}\,f(\mu , \pi )= & {} \mathrm{Red}\,g(\mu ,0)=\frac{i\mu }{\sin 2\pi \mu }, \end{aligned}$$
(88)

where

$$\begin{aligned} h(\mu )=\lim _{x\rightarrow 1_-}\Re \,\mathrm{Red}{\mathscr {F}}(\mu ,x)=\lim _{x\rightarrow 1_-}\Re \,{\mathscr {F}}_\mathrm{reg}(\mu ,x) \end{aligned}$$
(89)

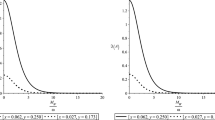
is a function whose values have to be obtained numerically (see Fig. 1), as we do not know its analytic form. By substituting then the functions (85) and (82) in Eqs. (73) and (74), we obtain the reduced functions \(\mathrm{Red}\,\varDelta _{\sigma ,\sigma }^{\pm }(\mu ,\theta )\) and \(\mathrm{Red}\,\varDelta _{\sigma ,-\sigma }^{\pm }(\mu ,\theta )\) and the corresponding reduced p.v.t.s

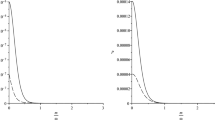
$$\begin{aligned}&\mathrm{Red}\,{P}^{\pm }_{\lambda ,\sigma ,\sigma '}(\mathbf{p},\mathbf{p}')\nonumber \\&\quad =\frac{\kappa }{pp'} |\varPi _{\sigma ,\sigma '}^{\lambda }(\mathbf{n},\mathbf{n}')|^2 \mathrm{Red}\,\varDelta _{\sigma ,\sigma '}^{\pm }(\mu , \theta ), \end{aligned}$$
(90)

with a correct physical meaning as we shall see in the next section. Note that the regularization by subtraction of the term containing a logarithmic singularity is in accordance with the general reduction method of eliminating poles by multiplication with suitable binomials. In Fig. 2, we show the effect of removing the logarithmic singularity plotting p.v.t.s before and after reduction.

Fig. 1
figure 1

Functions \(h(\mu )\) (left panel) and \(e^{\pi \mu }h(\mu )\) (right panel)

Full size image

On the other hand, the reduction modifies the dependence on \(\mu \) of the functions \(\mathrm{Red}\,\varDelta _{\sigma ,\sigma '}^{\pm }(\mu ,\theta )\) and implicitly of the reduced p.v.t.s. After reduction, the limits (80) and (81) become regular and independent of \(\theta \),

$$\begin{aligned} \lim _{\mu \rightarrow 0}\mathrm{Red}\,f(\mu ,\theta )=\lim _{\mu \rightarrow 0}\mathrm{Red}\,g(\mu ,\theta )=\frac{i}{2\pi }, \end{aligned}$$
(91)

and consequently, we obtain the common limit

$$\begin{aligned} \lim _{\mu \rightarrow 0}\mathrm{Red}\,\varDelta ^{\pm }_{\sigma ,\sigma '}(\mu ,\theta )=\frac{1}{2\pi },~~~ \forall \, \theta \in [0,\pi ]\,;\sigma ,\sigma '=\pm \frac{1}{2}. \end{aligned}$$
(92)

Therefore, both the reduced p.v.t.s have the same limit

$$\begin{aligned} \lim _{\mu \rightarrow 0}\mathrm{Red}\,{ P}^{\pm }_{\lambda ,\sigma ,\sigma '}(\mathbf{p},\mathbf{p}')= \frac{\kappa }{2 \pi pp'} |\varPi _{\sigma ,\sigma '}^{\lambda }(\mathbf{n},\mathbf{n}')|^2, \end{aligned}$$
(93)

depending on polarizations only through the polarization factors (67).

For larger values of \(\mu \), we may study the limit for \(\mu \rightarrow \infty \) thanks to the asymptotic representation of the hypergeometric functions (15.12.5) of Ref. [78]. Our preliminary calculations indicate that

$$\begin{aligned} \lim _{\mu \rightarrow \infty }\mathrm{Red}\,{ P}^{\pm }_{\lambda ,\sigma ,\sigma '}(\mathbf{p},\mathbf{p}')=0 \end{aligned}$$
(94)

for any relative positions of the momenta \(\mathbf{p}\) and \(\mathbf{p}'\) except the case of creating a pair of fermions with parallel momenta when the limit

$$\begin{aligned} \lim _{\mu \rightarrow \infty }\mathrm{Red}\,{ P}^{+}_{\lambda =2\sigma ,\sigma ,\sigma }(p\,\mathbf{n},p'\mathbf{n})\propto \lim _{\mu \rightarrow \infty } e^{\pi \mu } h(\mu ) \end{aligned}$$
(95)

cannot be specified neither by applying Eq. (15.12.5) nor by using numerical methods. However, this behaviour is mainly of academic interest as this approach addresses the early universe where \(\mu \ll 10^8\). In Fig. 1, we see that for \(\mu <10^4\), the function (89) can be approximated satisfactorily as \(h(\mu )\sim \mu e^{-\pi \mu }\).

Fig. 2
figure 2

The effect of removing the logarithmic singularities from p.v.t.s of the pair creation (+) and \(\sigma '=\sigma \) (left panel) and lepton creation \((-)\) and \(\sigma '=-\sigma \) (right panel)

Full size image

4.2 Angular behaviour

Turning now to the angular behaviour of reduced p.v.t.s (90), it is convenient to consider a particular frame \(\{e\}=\{\mathbf{e}_1,\mathbf{e}_2,\mathbf{e}_3\}\) in which the photon momentum is oriented along the third axis while the vectors \(\mathbf{p}\) and \(\mathbf{p}'\) are in the plane \(\{\mathbf{e}_1,\mathbf{e}_3\}\) having the spherical coordinates \(\mathbf{p}=(p,\alpha ,0)\) and \({\mathbf{p}\,}'=(p',\beta ,\pi )\), such that

$$\begin{aligned} \theta= & {} \alpha +\beta , \end{aligned}$$
(96)
$$\begin{aligned} p\sin \alpha= & {} p'\sin \beta . \end{aligned}$$
(97)

In the case of pair creation, we have \(\mathbf{k}=k(\theta )\mathbf{e}_3\) as in Fig. 3 where we present the momenta for \(p>p'\). For the lepton creation, we imagine similar momenta \(\mathbf{p}\) and \(\mathbf{p}'\) but with \(\mathbf{k}=-k(\theta )\mathbf{e}_3\) oriented in the opposite direction.

In this geometry, the polarization vectors take the simple form \(\mathbf{e}_{\lambda =\pm 1}(\mathbf{e}_3)=\frac{1}{\sqrt{2}}(\mathbf{e}_1\pm i \mathbf{e}_2)\) allowing us to derive the polarization factors \(|{\varPi }^{\lambda }_{\sigma ,\sigma '}(\mathbf{p},\mathbf{p}')|\) forming the matrices

$$\begin{aligned} \varPi ^{\lambda =1}= & {} \sqrt{2}\,\left( \begin{array}{cc} \cos \frac{\alpha }{2}\cos \frac{\beta }{2}&{}\quad \cos \frac{\alpha }{2}\sin \frac{\beta }{2}\\ \sin \frac{\alpha }{2}\cos \frac{\beta }{2}&{}\quad \sin \frac{\alpha }{2}\sin \frac{\beta }{2} \end{array}\right) , \end{aligned}$$
(98)
$$\begin{aligned} \varPi ^{\lambda =-1}= & {} \sqrt{2}\,\left( \begin{array}{cc} \sin \frac{\alpha }{2}\sin \frac{\beta }{2}&{}\quad \sin \frac{\alpha }{2}\cos \frac{\beta }{2}\\ \cos \frac{\alpha }{2}\sin \frac{\beta }{2}&{}\quad \cos \frac{\alpha }{2}\cos \frac{\beta }{2} \end{array}\right) . \end{aligned}$$
(99)

In this frame, we remain with the parameters \(p,\,p'\) and \(\theta \) only, as the angles we need for calculating the polarization matrices can be derived as

$$\begin{aligned} \alpha= & {} \mathrm{arctan}\left( \frac{\sin \theta }{r+\cos \theta }\right) ,\quad r=\frac{p}{p'}, \end{aligned}$$
(100)
$$\begin{aligned} \beta= & {} \theta -\alpha =\mathrm{arctan}\left( \frac{r\sin \theta }{1+r\cos \theta }\right) . \end{aligned}$$
(101)

Note that these relations are invariant when we change \(\alpha \leftrightarrow \beta \) and \(p \leftrightarrow p'\). Obviously, for \(p=p'\), we have \(\alpha =\beta =\frac{\theta }{2}\).

Fig. 3
figure 3

Kinematics of the pair production showing the critical positions for \(p>p'\): A \(\theta =0\), \(k=p+p',\,\sigma '=\sigma ,\,\lambda =2\sigma \) and B \(\theta =\pi \), \(k=p-p',\,\sigma '=-\sigma ,\,\lambda =2\sigma \)

Full size image

In this parametrization, the reduced p.v.t.s can be rewritten as

$$\begin{aligned} \mathrm{Red}\,{ P}^{\pm }_{\lambda ,\sigma ,\sigma '}(p, p', \theta )=\frac{\kappa }{pp'}( \varPi _{\sigma ,\sigma '}^{\lambda })^2 \mathrm{Red}\,\varDelta _{\sigma ,\sigma '}^{\pm }(\mu , \theta ),\nonumber \\ \end{aligned}$$
(102)

in a suitable form for a brief graphical analysis. In order to obtain intuitive profiles, avoiding very large or small numbers, we chose an extremely strong gravitational field with \(\mu =3\), plotting the reduced p.v.t.s in units of \(\kappa (pp')^{-1}\) and a logarithmic scale. As mentioned before, the principal objective is to verify if the angular behaviour of the reduced p.v.t.s complies with the helicity conservation in the critical positions, \(\theta =0\) and \(\theta =\pi \).

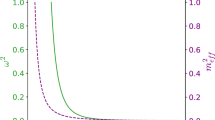
The reduced p.v.t. of pair creation (+) reaches its maximum as in Fig. 4a for \(\theta =0\) when all the momenta are oriented along the third axis with \(k=p+p'\), and the helicity is conserved as the spin projections with respect to this axis such that \(\sigma '=\sigma \) and \(\lambda =2\sigma \). In Fig. 4b, we see that for \(\sigma '=-\sigma \), there exists a very small p.v.t. for anti-parallel fermion momenta, \(k=p-p'\) \((p>p')\), and the conserved \(\lambda =2\sigma \). In contrast, for the fermion creation from vacuum \((-)\), the p.v.t., plotted in Fig. 4d, reaches its maximum when the fermion momenta are anti-parallel, one fermion being emitted is the same direction as the photon such that \(k+p-p'=0\) \((p<p')\), and the helicity is conserved with \(\sigma '=-\sigma \) and \(\lambda =2\sigma \). In Fig. 4c, we see a small p.v.t. of creating parallel fermions and a photon in the opposite direction with \(\sigma '=\sigma \) and \(\lambda =2\sigma \).

We conclude that the reduction procedure adopted here leads to reduced p.v.t.s, with an obvious and correct physical meaning, complying with the selection rules of the conserved helicity on the critical directions. Remarkably, the maxima of reduced p.v.t.s arise just in the critical positions where the original ones were singular, convincing us that the regularization and reduction procedures preserve the entire physical meaning.

Fig. 4
figure 4

The reduced p.v.t.s versus \(\theta \) for the pair creation (+) in the upper panels and for the lepton creation \((-)\) in the lower panels

Full size image

5 Creating leptons from vacuum

We now have all the elements we need for studying how an observer measures at a very late time the lepton creation in two steps,

$$\begin{aligned} vac\xrightarrow {(-)}\gamma +e^++e^-\xrightarrow {(+)} (e^++e^-)+e^++e^-, \end{aligned}$$
(103)

for determining the photon density n(t) and the electron density e(t), assuming the positron and electron densities as being equal for ensuring the neutrality. Moreover, we suppose that these densities are very low such that the annihilations become improbable and can be neglected. We thus obtain the dynamical equations

$$\begin{aligned} \frac{\mathrm{d} n(t)}{\mathrm{d}t}= & {} \hat{P}^-(t)-\hat{P}^+(t)\, n(t), \end{aligned}$$
(104)
$$\begin{aligned} \frac{\mathrm{d} e(t)}{\mathrm{d}t}= & {} \hat{P}^-(t)+\hat{P}^+(t)\, n(t), \end{aligned}$$
(105)

which depend only on the total reduced p.v.t.s

$$\begin{aligned} \hat{P}^{\pm }(t)=P_{\pm }(\mu )\,e^{-4\omega t}, \end{aligned}$$
(106)

in the physical frame \(\{t,\mathbf{x};e\}\) where the observer performs measurements.

The factors \(P_{\pm }(\mu )\) might result after integrating the reduced p.v.t.s (90) over momenta, but this is less relevant and somewhat arbitrary because of the cut-off needed for eliminating the ultraviolet catastrophe. For this reason, we introduce a new constant, \(P_0\), as a free parameter encapsulating all these contributions. Furthermore, bearing in mind that the reduced p.v.t.s reach their maxima just in the critical positions where the auxiliary functions have the forms (87) and (88), we may write

$$\begin{aligned} P_+(\mu )= & {} P_0\,\varDelta ^+_{\sigma ,\sigma }(\mu ,0) \sim P_0\,e^{\pi \mu }h(\mu ), \end{aligned}$$
(107)
$$\begin{aligned} P_-(\mu )= & {} P_0\,\varDelta ^-_{\sigma ,-\sigma }(\mu ,\pi ) \sim P_0\,h(\mu ), \end{aligned}$$
(108)

as for \(\mu >1\) we may neglect the term \(e^{-\pi \mu }\) with respect to 1. Note that the ratio

$$\begin{aligned} r(\mu )=\frac{\hat{P}^+(t)}{\hat{P}^-(t)}=\frac{P_+(\mu )}{P_-(\mu )}=e^{\pi \mu }, \end{aligned}$$
(109)

which is independent on time, shows that the p.v.t. of pair creation is dominant.

We thus obtained a simplified model that may be solved easily with the initial conditions \(n(t)|_{t=0}=n_0\) and \(e(t)|_{t=0}=e_0\), obtaining the solutions

$$\begin{aligned} n(t)= & {} r(\mu ) -e^{-\chi (t)}\left( r(\mu )-n_0\right) , \end{aligned}$$
(110)
$$\begin{aligned} e(t)= & {} n_0+e_0+e^{-\chi (t)}\left( r(\mu )-n_0\right) \nonumber \\&-r(\mu )\left[ 1-2\chi (t)\right] , \end{aligned}$$
(111)

which depend on time only through the function

$$\begin{aligned} \chi (t)=\frac{P_-(\mu )}{4\omega }\left( 1-e^{-4\omega t}\right) , \end{aligned}$$
(112)

that is increasing strictly from \(\chi (0)=0\) up to the asymptotic value

$$\begin{aligned} \chi _\mathrm{a}= \lim _{t\rightarrow \infty }\chi (t)=\frac{P_-(\mu )}{4\omega }=\frac{P_0}{4m}\mu h(\mu ). \end{aligned}$$
(113)

Remarkably, this model reaches the saturation rapidly thanks to the pair creation which is favoured as in Eq. (109). This mechanisms creates leptons from an initial vacuum with \(n_0=e_0=0\), giving rise to the asymptotic densities,

$$\begin{aligned} e_\mathrm{a}= & {} \lim _{t\rightarrow \infty }e(t)=r(\mu )(2\chi _\mathrm{a}-1+e^{-\chi _\mathrm{a}}), \end{aligned}$$
(114)
$$\begin{aligned} n_\mathrm{a}= & {} \lim _{t\rightarrow \infty }n(t)=r(\mu )(1-e^{-\chi _\mathrm{a}}), \end{aligned}$$
(115)

such that the total asymptotic lepton density takes the simple form

$$\begin{aligned} l_\mathrm{a}=e_\mathrm{a}+n_\mathrm{a}=2\chi _\mathrm{a} r(\mu )=\frac{P_0}{2m}\mu e^{\pi \mu }h(\mu ), \end{aligned}$$
(116)

depending only on \(\mu \) and \(P_0\). Thus, the principal physical result depends on the function \(h(\mu )\) which is accessible numerically in the domain of physical interest. The late observer has to measure the asymptotic densities, but if the leptons are created simultaneously with other particles able to capture them, then the observer will measure only the photons perceived as a relic radiation of density \(n_\mathrm{a}\sim \frac{1}{2}l_\mathrm{a}\).

6 Concluding remarks

We presented the complete theory of creating leptons from vacuum in the first order of perturbations of the de Sitter QED in Coulomb gauge [44] where the Dirac field is quantized in the r.f.v. This new vacuum could be a suitable partner for the adiabatic one in a process of cosmological particle creation during inflation. We can imagine that initially the leptons are prepared in adiabatic vacuum arriving in the electroweak epoch in r.f.v., thus having similar properties as the actual leptons. As the off-diagonal Bogolyubov coefficient of this transition is proportional to \((1+e^{2\pi \mu })^{-\frac{1}{2}}\), we see that the probability of this process decreases rapidly with \(\mu \) such that for \(\mu =4\), this is less than \(10^{-10}\). Therefore, for \(\mu >1\), the lepton creation could continue mainly thanks to the first-order transitions studied here, involving leptons prepared in r.f.v. as in the above-presented simplified model. However, in a realistic cosmological scenario, this model must be improved, considering momentum-dependent densities and the probabilities (90) instead of the rough approximation used here.

In this paper, we tried to address some technical problems of our approach, proposing appropriate definitions of transition rates and probabilities and looking for suitable reduction methods selected and controlled by the physical criterion of helicity conservation on critical directions. This was the first step to a complete de Sitter QED whose important results are expected in higher orders of perturbations. For this purpose, we recently proposed a new integral representation of the Dirac [79] and Klein–Gordon [80] propagators in the de Sitter expanding universe and for all the Dirac propagators in spatially flat FLRW spacetimes [81]. We thus have the opportunity to calculate Feynman diagrams in any order of perturbations as in special relativity, without resorting to the laborious Schwinger–Keldysh method [82,83,84] used so far. With these integral representations in r.f.v., we hope to calculate the second-order diagrams including the electron and photon self-energies for which we must find an appropriate regularization procedure before renormalization. The vertex diagram will contribute to all the processes discussed here which will be affected by the charge renormalization. A crucial task is to obtain closed forms of renormalized self-energies for writing down the corresponding Dyson equations which could help us to understand more subtle mechanisms of generating quantum matter in strong gravitational fields [40, 41].