Production of massive $W^{\pm }$ bosons and fermion–antifermion pairs from vacuum in the de Sitter Universe

Abstract

In this paper we study the charged electro-weak interactions in the de Sitter geometry. We develop the reduction formalism for the Proca field with the help of the solutions for the interacting fields. Perturbation theory is used for obtaining the definition of the transition amplitudes in the first order. We apply our formalism to the study of spontaneous vacuum emission of fermions, anti-fermions and $W^{\pm }$ bosons in the expanding de Sitter universe. Our results are generalizations of the Weinberg–Salam electro-weak theory to curved space-time, in the case of $W^{\pm }$ boson interaction with leptons. The probability and transition amplitude are found to be a quantities which depend on the Hubble parameter. Our analytical and graphical results prove that such perturbative processes are possible only for the large expansion conditions of the early Universe. The total probability and rate of transition are obtained for the case of large expansion and we use dimensional regularization for the momenta integrals. In the end we recover the Minkowski limit, where our probabilities vanish, thus confirming the well known fact that spontaneous vacuum emission of $W^{\pm }$ bosons and fermions is forbidden in flat space-time due to energy–momentum conservation.

1 Introduction

The theory of weak interactions allows us to understand fundamental quantum processes between quarks, leptons and massive bosons. One example of this is the process where a “down” quark transforms into an “up” quark by emitting a $W^-$ boson (or absorbing a $W^+$ boson). The massive boson is unstable and decays into an electron and an antineutrino, which enables neutrons to turn into protons [1]. This process is known as $\beta ^-$ decay and increases the atomic number of an atomic nucleus by one, while emitting an electron and an antineutrino. The inverse transformation turns an “up” quark into a “down” quark. There is also large number of observed $\beta$-decays in nuclei and all these involve the transformations of neutrons into protons and vice versa [1]. These processes are possible due to the existence and properties of the charged $W^{\pm }$ bosons. The charged massive bosons $W^{\pm }$ could exist as stable particles only in the early universe, as long as the background energy was greater than or equal to their rest energy. Subsequently these bosons have decayed long ago into more light and stable particles, such as electrons and neutrinos. It is also well established that, in the very early stages of universe, the temperatures and densities were high enough to allow these bosons to exist in large numbers at thermal equilibrium [2, 3]. In this paper we want to understand how the creation and decay rates for standard model particles were modified in the conditions of the early Universe, when the expansion rate was large. This is important for our understanding of the state of the Universe at the end of inflation, as well as for how the Universe thermalizes after inflation (preheating).

Space-time expansion could also be a mechanism of massive boson production. This effect can be revealed by using the perturbative methods of quantum field theory from flat space-time. The perturbative approach allows one to obtain the dependence of the transition rates on the Hubble parameter and explore the Minkowski limit, where processes which involve the spontaneous emission of particles from vacuum are forbidden. In this paper we explore the vacuum generation of massive $W^{\pm }$ bosons due to space-time expansion in the de Sitter geometry.

The electro-weak theory in Minkowski space-time was developed in order to understand the interactions between massive bosons and fermions. As far as free fields are concerned, the massive vector fields are described by the Proca equation, which was first proposed in [4,5,6,7]. There are a few results that consider the study of the Proca field in curved space-times [8, 9], where the problem of fundamental solutions and propagators was approached. It is a well established fact that the massive charged $W^{\pm }$ bosons were generated in the early universe [2], but the mechanisms that were involved deserve further studies. This is because the conditions of the early universe, where a large space-time expansion is present, are suitable for a perturbative treatment of the problems which involve particle production. The perturbative approach could help one study particle generation from field interactions [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25]. The problem related to quantum fields in the presence of the large expansion conditions of the early universe was also studied in [10,11,12,13,14,15,16,17,18,19, 22,23,24,25,26, 26,27,28], where perturbative methods were used. The theory of the free Dirac and Proca fields in the de Sitter geometry was studied in [8,9,10, 29], and a model which investigates neutral current interactions in the de Sitter geometry was proposed in [10, 20]. The perturbative photon mass was calculated in scalar electrodynamics on de Sitter for the first time in [30, 31]. We also mention the results obtained in [32] where the photon and scalar masses in scalar electrodynamics were computed, as well as the energy–momentum tensor and effective potential, using a non-perturbative methods.

The Weinberg–Salam theory [1, 2, 4,5,6,7, 33,34,35,36,37,38,39,40,41,42] of electro-weak interactions in Minkowski space-time can be extended to the de Sitter geometry by using perturbations for defining the transition amplitudes, with the specification that the Feynman rules will be written down in the coordinate representation. This allows us to extend the definitions of the transition amplitudes from the Minkowski theory to curved space-time. In order for this to work we use the minimal coupling of the Dirac and Proca fields to gravity. In our study we will also consider, for the first time, the problem of spontaneous vacuum emission of the triplet $W^-$ boson, positron and neutrino, $vac \rightarrow W^-+e^++\nu$, as well as the process involving the positively charged boson $vac \rightarrow W^++e^-+{\widetilde{\nu }}$. The theory of electro-weak interactions between the charged $W^{\pm }$ bosons and fermions can be constructed by considering the Lagrangian densities for the free Dirac and Proca fields, as well as the interaction Lagrangian density, constructed as the electrodynamic coupling $-J^\mu A_\mu$, where the current represents the charged currents. The non-perturbative approach to the problem of massive boson generation is less studied in literature, and we mention here the results obtained in [43]. Our approach is based on the fundamental results obtained in [22,23,24,25], where the ideas that space-time expansion could generate particles were first proposed. In our study we use a perturbative approach for defining the first order transition amplitudes corresponding to the de Sitter electro-weak theory with charged currents. This approach could be one of the mechanisms that explain the generation of massive $W^{\pm }$ bosons in the early universe. The perturbative approach to the problem of particle production in expanding geometries was also examined in [44, 45], without taking into account the problem of massive boson generation.

Our methods are based on [21], where the problem of massive Z boson generation from vacuum in the de Sitter universe was discussed. In [21] the formalism necessary for the study of interactions intermediated by neutral currents was developed and the transition probabilities and rates were computed. These results prove that the Z bosons could be generated only in the very early epoch of the universe when the expansion parameter was larger than the Z boson mass. We want to extend these results to the interactions intermediated by charged currents which allow us to study the generation of massive $W^{\pm }$ bosons in the early universe.

The paper is organized as follows: in the second section we present the equations of interaction intermediated by charged currents in de Sitter space-time. The third and forth sections are dedicated to computing the amplitude and probability corresponding to the process of spontaneous generation from vacuum of $W^{\pm }$ bosons, fermions and anti-fermions in the case of transverse polarizations. In section five we present the amplitude and probability for the case of longitudinal polarization. In the sixth section we compute the total probability by using dimensional regularization and the substraction method for the integrals over the final momenta. The rate of transition is obtained in the seventh section, where we also discuss the limit of a large expansion factor, relative to the particle masses. Our conclusions are summarized in section eight. The Appendix contains sections nine to eleven: in Appendix A we present the reduction formalism for the Proca field in terms of transverse and longitudinal modes and define the transition amplitudes of electro-weak theory with charged $W^{\pm }$ bosons on de Sitter in both cases. The main steps needed for computing the transition amplitudes for transversal and longitudinal Proca modes are presented in Appendix B. Appendix C contains formulas which help us establish the final form of the probabilities and transition rates.

2 Equations for interacting fields

Let us begin with the de Sitter line element written in conformal form [46]:

$$\begin{aligned} ds^2=dt^2-e^{2\omega t}d\vec {x}^2=\frac{1}{(\omega t_{c})^2}(dt_{c}^2-d\vec {x}^2) \end{aligned}$$

(1)

The conformal time is related to the proper time by $t_{c}=\frac{-e^{-\omega t}}{\omega }$, where $\omega$ is the Hubble parameter ($\omega >0$).

In our present study we propose for the first time a perturbative approach to the problem of massive charged $W^{\pm }$ boson production in the early universe. Our computations are done in the de Sitter geometry, defined by a conformal chart with conformal time $t_{c}\in (-\infty ,0)$, which covers the expanding portion of de Sitter space-time [46]. For the line element (1) in the Cartesian gauge we have the non-vanishing tetrad components:

$$\begin{aligned} e^{0}_{{\widehat{0}}}=-\omega t_c;\,\,\,e^{i}_{{\widehat{j}}}=-\delta ^{i}_{{\widehat{j}}}\,\omega t_c. \end{aligned}$$

(2)

The perturbative QED in de Sitter space-time was developed in [10], where it was shown that the generators of the covariant representation are the differential operators produced by the Killing vectors, which are associated with isometries, according to the generalized Carter and McLenaghan formula [47]. These generators come from an algebra of conserved observables that commute with the operators of the field equations. With this method the quantum states can be defined on the entire manifold and be independent of local coordinates, so the vacuum state is unique and stable [10]. This approach allows one to consider that the quantum states are prepared and measured by the same global apparatus which consists of the largest freely generated algebra which includes the conserved operators [10]. For developing the theory of electro-weak interactions between charged $W^{\pm }$ bosons and fermions we assume that the electro-weak transitions are measured by the same global apparatus which prepares all the quantum states, and this includes the IN and OUT asymptotic free fields which are minimally coupled to gravity. This apparatus complies with an asymptotic prescription of frequency separation which assures the uniqueness and stability of the vacuum state of the free fields [8, 48].

There are some concerns about the definition of the asymptotic IN/OUT states in the de Sitter geometry [30, 31, 49, 50]. In [30, 31], scalar electrodynamics in de Sitter was studied and it was proven that the continued growth of infrared logarithms will finally overwhelm even the smallest loop-counting parameter. This means that perturbative methods could become problematic when $\omega t=\ln (a)\ll \frac{1}{\alpha _e}$, where t is the physical time, and $\alpha _e$ is the fine structure constant of scalar electrodynamics [30, 31]. In addition, in [49, 50] it was proven that a rigorous derivation of the IN-OUT formalism requires a definition of the asymptotic past and future, which is also problematic in de Sitter space-time. In [49, 50] the problems of defining amplitudes corresponding to particle production in scalar QED in de Sitter space-time were discussed. The asymptotic scenario explored in [49, 50] considers a geometry with Minkowski space-time at $t\rightarrow -\infty$, which then becomes an expanding de Sitter space-time for a long while, and in the end returns to flat space-time again. Moreover a situation when quantum field theory on this background can be treated semiclassically is considered. A possible solution to the mentioned issues related to the IN-OUT formalism in de Sitter geometry [30, 31, 49, 50] could be stated as follows: it is known that a field equation can have many Green’s functions and for this reason one could choose not to use the retarded/advanced Green’s functions when defining the IN/OUT fields. In this setup one can construct the theory of interactions by choosing Green’s functions such that they vanish at two finite times before and after the interaction and construct the IN/OUT fields at these times. We hope to approach this topic in a future research.

In our study we assume that the IN/OUT fields can be defined, and we give clarifications in what follows. We cannot solve all the problems related to the definitions of the IN/OUT fields in the de Sitter geometry in the present paper, but, as we previously mentioned, we want to propose a better justification of our approach in a future paper. Nonetheless we must point out that the IN/OUT fields we use are the exact Dirac free field and Maxwell free field on the de Sitter space-time. They represent the asymptotic limit of interacting fields in the de Sitter expanding universe. Thus this situation is different from the case when one deals with Minkowskian asymptotic fields on asymptotically flat manifolds, in which case the IN/OUT amplitudes deal only with gravitational effects. We consider in our study electromagnetic asymptotic free fields instead of gravitational fields.

This is very different from cosmological particle production, where the particles are created during space-time expansion and the IN/OUT states differ between local charts [44]. Our apparatus can record particle creation only in the presence of electromagnetic interactions, and the difference between our apparatus and the local detectors which record cosmological particle production [51,52,53,54,55] is that the latter can record particle production without electromagnetic interaction. We are dealing with a relativistic quantum scattering, where we have a quantum interaction between quantum fields that is facilitated by the background energy provided by space-time curvature and by the violation of energy–momentum conservation. Due to their minimal coupling to gravity and the tetrad gauge, the IN/OUT states can be regarded as asymptotically free with respect to the interaction time of the quantum transition which happens in the local chart in the same manner as in Minkowski space-time.

In this section we present the main steps for developing the interaction theory between massive charged bosons and fermions. We start with the action integral, which contains the Lagrangian densities for the free Dirac field, the free charged Proca field and the interaction term from the electro-weak theory corresponding to charged currents. We also assume that the Dirac and Proca fields are minimally coupled to gravity.

$$\begin{aligned} S = \int d^{4}x \sqrt{-g(x)} \left( \mathcal {L}_{Proca} + \mathcal {L}_{Dirac} + \mathcal {L}_{int} \right) \end{aligned}$$

The explicit form of the action can be found below, where the action is expressed in terms of the tetrad-gauge invariant Lagrangian density, which determines the coupling between $W^{\pm }$ bosons and leptons, written in turn with regard to the point independent Dirac matrices $\gamma ^{{\hat{\mu }}}$ and tetrad fields $e_{\hat{\alpha }}^{\mu }$:

$$\begin{aligned} S{} & {} = \int d^{4}x \sqrt{{-}g(x)}\Bigg \{\frac{i}{2}\left[ \bar{\psi }_{(e)}\gamma ^{\hat{\alpha }}(D_{\hat{\alpha }}\psi _{(e)}){-}(D_{\hat{\alpha }}\bar{\psi }_{(e)})\gamma ^{\hat{\alpha }}\psi _{(e)}\right] \nonumber \\{} & {} \quad -m\bar{\psi }_{(e)}\psi _{(e)}\nonumber \\{} & {} \quad +\frac{i}{2}\left[ \bar{\psi }_{(\nu )}\gamma ^{\hat{\alpha }}(D_{\hat{\alpha }}\psi _{(\nu )})-(D_{\hat{\alpha }}\bar{\psi }_{(\nu )})\gamma ^{\hat{\alpha }}\psi _{(\nu )}\right] \nonumber \\{} & {} \quad -\frac{1}{2}F_{\mu \nu }^+ F^{\mu \nu } + M_W^{2}A_{\mu }^+A^{\mu }\nonumber \\{} & {} \quad -\frac{g}{2\sqrt{2}}\bar{\psi }_{(e)}\gamma ^{\hat{\alpha }}e_{\hat{\alpha }}^{\mu }\left( 1-\gamma ^{5}\right) \psi _{(\nu )} A_{\mu }\nonumber \\{} & {} \quad -\frac{g}{2\sqrt{2}}\bar{\psi }_{(\nu )}\gamma ^{\hat{\alpha }}e_{\hat{\alpha }}^{\mu }\left( 1-\gamma ^{5}\right) \psi _{(e)} A_{\mu }^+\Bigg \}, \end{aligned}$$

(3)

where $\psi _{(e)}$ describes the electron-positron field and $\psi _{(\nu )}$ is the neutrino-antineutrino field. The vector potentials $A_\mu$ and $A_\mu ^+$ describe the massive boson fields $W^{-}$ and $W^{+}$, with field strength $F_{\mu \nu }=\partial _\mu A_{\nu }-\partial _\nu A_{\mu }$. The coupling constant g is expressed in terms of Fermi constant as $\frac{G_F}{\sqrt{2}}=\frac{g^2}{8M_W^2}$.

Term $D_{\hat{\alpha }}=\partial _{\hat{\alpha }}+\Gamma _{\hat{\alpha }}$ denotes the covariant derivatives in local frames. The covariant derivative depends on the spin connections $\Gamma _{\hat{\alpha }}=\Gamma _{\hat{\alpha }\hat{\mu }\hat{\nu }}S^{\hat{\mu }\hat{\nu }}$, which are given in terms of the basis generators $S^{\hat{\mu }\hat{\nu }}=i/4 [ \gamma ^{\hat{\mu }},\gamma ^{\hat{\nu }}]$ of the spinorial representation of the $SL(2,{{\textbf {C}}})$ group.

By using Euler–Lagrange equations we obtain a set of four interaction equations for the fields $\psi _{(e)},\psi _{(\nu )},A_\mu ,A_\mu ^+$:

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}(i\gamma ^{\hat{\alpha }}D_{\hat{\alpha }}-m)\psi _{(e)}(x)\\ &{}\quad =\frac{g}{2\sqrt{2}}\sqrt{-g(x)}\left[ \gamma ^{\hat{\alpha }}e_{\hat{\alpha }}^{\mu }(1-\gamma ^{5})\psi _{(\nu )}(x)A_{\mu }(x)\right] , \\ &{}i\gamma ^{\hat{\alpha }}D_{\hat{\alpha }}\psi _{(\nu )}(x)\\ &{}\quad =\frac{g}{2\sqrt{2}}\sqrt{-g(x)}\left[ \gamma ^{\hat{\alpha }}e_{\hat{\alpha }}^{\mu }(1-\gamma ^{5})\psi _{(e)}(x)A_{\mu }(x)\right] ,\\ &{}\partial _\rho \big ( g^{\rho \alpha } g^{\mu \beta } \sqrt{-g(x)}F_{\alpha \beta }(x) \big ) + \sqrt{-g} \, M_W^2 A^\mu (x)\\ &{}\quad =\frac{g}{2\sqrt{2}}\sqrt{-g(x)}\left[ \bar{\psi }_{(\nu )}(x)\gamma ^{\hat{\alpha }}e_{\hat{\alpha }}^{\mu }(1-\gamma ^{5})\psi _{(e)}(x)\right] ,\\ &{}\partial _\rho \big ( g^{\rho \alpha } g^{\mu \beta } \sqrt{-g(x)}F_{\alpha \beta }^+(x) \big ) + \sqrt{-g} \, M_W^2 A^{\mu +}(x)\\ &{}\quad =\frac{g}{2\sqrt{2}}\sqrt{-g(x)}\left[ \bar{\psi }_{(e)}(x)\gamma ^{\hat{\alpha }}e_{\hat{\alpha }}^{\mu }(1-\gamma ^{5})\psi _{(\nu )}(x)\right] \end{array}\right. }\nonumber \\ \end{aligned}$$

(4)

The Dirac operator in the de Sitter metric has the expression [48]:

$$\begin{aligned} i\gamma ^{\hat{\alpha }}D_{\hat{\alpha }}-m=E_{D} = -i\omega t_{c} (\gamma ^{0}\partial _{t_{c}} + \gamma ^{i}\partial _{i})+\frac{3i\omega }{2}\gamma ^{0}-m\nonumber \\ \end{aligned}$$

(5)

In the case of the free Proca field, the equations for the temporal and spatial components of the vector potential in the de Sitter metric and chart $\{t_c,\vec x\}$ can be found by using the Lorenz condition [8]:

$$\begin{aligned} \partial _{\mu }(\sqrt{-g}A^{\mu })=0 \end{aligned}$$

(6)

The equations for the components of the vector potential are [8]:

$$\begin{aligned} {\left\{ \begin{array}{ll} -\Delta A_{0} + \frac{\mu ^{2}}{t_{c}^{2}}A_{0} + \partial _{t_{c}}(\partial _{i}A_{i}) = 0,\\ \left( \partial _{t_{c}}^{2}-\Delta + \frac{\mu ^{2}}{t_{c}^{2}}\right) A_{i} - \partial _{t_{c}}\left( \partial _{i}A_{0}\right) - \partial _{i}\left( \partial _{k}A_{k}\right) = 0, \end{array}\right. } \end{aligned}$$

(7)

where $\mu =\frac{M_W}{\omega }$.

The above equations for the vector potential can be derived from the following equation:

$$\begin{aligned} \sqrt{-g(x)}\left[ \delta _{\mu }^{\rho }\left( g^{\alpha \beta }\partial _{\alpha }\partial _{\beta } + m^{2}\right) - g^{\alpha \rho }\partial _{\alpha }\partial _{\mu } \right] A_{\rho } = 0, \end{aligned}$$

(8)

where we introduce the Proca operator:

$$\begin{aligned} {(E_{P})}^{\rho }\,_{\mu }= \delta _{\mu }^{\rho }\left( g^{\alpha \beta }(x)\partial _{\alpha }\partial _{\beta } + m^{2}\right) - g^{\alpha \rho }(x)\partial _{\alpha }\partial _{\mu } \end{aligned}$$

(9)

With the help of (9), the last two equations from (4) can be rewritten in the form:

$$\begin{aligned} {(E_{P})}_{\mu }\,^{\beta }A^\mu= & {} \frac{g}{2\sqrt{2}}\sqrt{-g(x)}\nonumber \\{} & {} \times \left[ \bar{\psi }_{(\nu )}(x)\gamma ^{\hat{\alpha }}e_{\hat{\alpha }}^{\beta }(1-\gamma ^{5})\psi _{(e)}(x)\right] ,\nonumber \\ {(E_{P})}_{\mu }\,^{\beta }A^{\mu +}= & {} \frac{g}{2\sqrt{2}}\sqrt{-g(x)}\nonumber \\{} & {} \times \left[ \bar{\psi }_{(e)}(x)\gamma ^{\hat{\alpha }}e_{\hat{\alpha }}^{\beta }(1-\gamma ^{5})\psi _{(\nu )}(x)\right] . \end{aligned}$$

(10)

The problem of the propagator for the Proca field in curved space-time was first discussed by Allen and Jacobson in [56]. The propagator in the Lorenz gauge was constructed by Tsamis and Woodard [9] and also discussed by Cotăescu in [8].

The transverse Green’s functions of the Proca equation that obey the Lorenz condition [8, 9]

$$\begin{aligned}{} & {} \partial _\mu [\sqrt{-g(x)}g^{\mu \nu }(x) G_{\nu \sigma }^{tr}(x,x')]\nonumber \\{} & {} \quad =\partial \,'_\mu [\sqrt{-g(x')}g^{\mu \nu }(x') G_{\sigma \nu }^{tr}(x,x')]=0 \end{aligned}$$

(11)

are defined [8, 9]:

$$\begin{aligned} G_{\mu \nu }^{tr}(x,x')=G_{\mu \nu }(x,x')+\frac{1}{m^2}\partial _\mu \partial \,'_\nu \Delta (x,x') \end{aligned}$$

(12)

where $\Delta (x,x')$ is the massless scalar Green’s function.

The equation for the transverse Green’s function is [8, 9]:

$$\begin{aligned}{} & {} \sqrt{-g(x)}g^{\alpha \beta }(x)\partial _{\alpha }\left[ \partial _{\beta }G_{\mu \nu }^{tr}(x,x')-\partial _{\mu }G_{\beta \nu }^{tr}(x,x')\right] \nonumber \\{} & {} \qquad + m^2\sqrt{-g(x)}G_{\mu \nu }^{tr}(x,x') \nonumber \\{} & {} \quad =g_{\mu \nu }(x)\delta ^{4}(x-y)+\sqrt{-g(x)}\partial _\mu \partial \,'_\nu \Delta (x,x') \end{aligned}$$

(13)

This can be written in terms of the Proca operator as:

$$\begin{aligned}{} & {} \left[ \delta _{\mu }^{\rho }\left( g^{\alpha \beta }(x)\partial _{\alpha }\partial _{\beta } + m^{2}\right) - g^{\alpha \rho }(x)\partial _{\alpha }\partial _{\mu } \right] G_{\rho \nu }^{tr}(x,x')\nonumber \\{} & {} \quad =\frac{g_{\mu \nu }(x)}{\sqrt{-g(x)}}\delta ^{4}(x-y)+\partial _\mu \partial \,'_\nu \Delta (x,x') \end{aligned}$$

(14)

The propagator of the Dirac field on the de Sitter space-time in the configuration representation was constructed by Candelas and Reine [57], where for the first time the one- loop effective action for fermions on de Sitter space was computed. The propagator for the Dirac field was also obtained as a mode sum by Koskma and Prokopec in general Friedmann–Lemaître–Robertson–Walker space-times of arbitrary dimensions [29]. A recent result obtained by Cotăescu [58] proves that the massive Dirac propagator in de Sitter space-time can be written in integral representation on momentum space.

Green’s functions for the Dirac field will satisfy the following equations [29, 48, 58]:

$$\begin{aligned} E_{D}S(x-y)= & {} -\frac{1}{\sqrt{-g}}\delta ^{4}(x-y). \end{aligned}$$

(15)

In order to develop the reduction formalism for the Proca field we will use the method of Green’s functions [1, 59, 60] to write the solutions for the interacting field equations (10), and we specify that we use the transverse Green’s functions that obey the exact Lorenz condition:

$$\begin{aligned} A_{\beta }(x)= & {} {\hat{A}}_{\beta }(x) + \int d^{4}y \sqrt{-g(y)}G^{tr}_{\beta \nu }(x,y)J^{\nu }(y)\nonumber \\= & {} {\hat{A}}_{\beta }(x) + \frac{g}{2\sqrt{2}}\int d^{4}y \sqrt{-g(y)}G^{tr}_{\beta \nu }(x,y)\bar{\psi }_{(\nu )}(y)\nonumber \\{} & {} \times \gamma ^{\hat{\alpha }}e_{\hat{\alpha }}^{\nu }(1-\gamma ^{5})\psi _e(y) \end{aligned}$$

(16)

The validity of the above solution can be verified if one applies the Proca operator ${(E_{P})}_{\mu }^{\beta }$ to it. Finally the solution for the interacting fields (16) can be expressed as:

$$\begin{aligned} A_{\beta }(x) = {\hat{A}}_{\beta }(x) + \int d^{4}y G^{tr}_{\beta \nu }(x,y) (E_{P})_{\rho }^{\nu }(y)A^{\rho }(y),\nonumber \\ \end{aligned}$$

(17)

where ${\hat{A}}_{\beta }(x)$ represents the free field.

We proceed further by defining the IN and OUT fields with the help of the retarded and advanced Green’s functions, while specifying that these fields are defined up to a normalization constant denoted by $\sqrt{z_3}$:

$$\begin{aligned}{} & {} \sqrt{z_3}A_{\beta }^{IN/OUT}(x) \nonumber \\{} & {} \quad = {\hat{A}}_{\beta }(x) - \int d^{4}y G^{tr\,R/A}_{\beta \nu }(x,y) E_{\rho }^{\nu }(y)A^{\rho }(y) \end{aligned}$$

(18)

The above fields are asymptotically equal to free fields for $t\rightarrow \pm \infty$, where the advanced and retarded Green’s functions vanish. The IN/OUT fields defined above represent the basis for the reduction formalism which is presented in Appendix A. Also in Appendix A we obtain the definition for the first order transition amplitudes for the electro-weak theory with charged currents in de Sitter space-time. These results will be used in the next section where we compute the amplitude corresponding to the spontaneous particle production from vacuum in de Sitter universe.

3 The amplitude for $\lambda = \pm 1$

For the process $vac\rightarrow W^-+e^++\nu$ we will split the amplitude in terms of the polarization $\lambda$ of $W^{-}$, which can take the values 0 and $\pm 1$. Firstly we are going to compute for $\lambda =\pm 1$, using the results from Appendix A where we define the transition amplitudes as:

$$\begin{aligned} A_{i\rightarrow f}= & {} \frac{ig}{2\sqrt{2}} \int d^{4}x \sqrt{-g(x)} \, {\bar{u}}_{\vec {p}\sigma }(x) \gamma ^{{\hat{i}}}\nonumber \\{} & {} \times e_{{\hat{i}}}^{j}(1-\gamma ^5) v_{\vec {p^{\prime }}\sigma ^{\prime }}(x){{f^{*}}_{\vec {P}\lambda }}_{j} (x). \end{aligned}$$

(19)

Fig. 1

The real and imaginary parts of A with respect to $\frac{M_{W}}{\omega }$ for $k=0.1$ and momenta values $p' = 0.2, p = 0.1, P = 0.4$ for the straight line and $p' = 0.25, p = 0.1, P = 0.6$ for the dotted line

Fig. 2

The real and imaginary parts of B with respect to $\frac{M_{W}}{\omega }$ for $k=0.1$ and momenta values $p' = 0.2, p = 0.1, P = 0.4$ for the straight line and $p' = 0.25, p = 0.1, P = 0.6$ for the dotted line

Fig. 3

The real and imaginary parts of C with respect to $\frac{M_{W}}{\omega }$ for $k=0.1$ and momenta values $p' = 0.2, p = 0.1, P = 0.4$ for the straight line and $p' = 0.25, p = 0.1, P = 0.6$ for the dotted line

The solutions of the Proca equation in de Sitter space-time for $\lambda =\pm 1$ contain only the spatial part, while the temporal component of the Proca solution is 0, [8]:

$$\begin{aligned} {{f^{*}}_{\vec {P}\lambda =\pm 1,}}_{0} (x)= & {} 0 \nonumber \\ {{f^{*}}_{\vec {P}\lambda =\pm 1,}}_{j} (x)= & {} \frac{\sqrt{\pi } e^{-\pi K/2}}{2(2\pi )^{3/2}}\sqrt{-t_{c}} \mathcal {H}_{-iK}^{(1)} (-P t_{c}) \nonumber \\{} & {} \times e^{-i\vec {P}\vec {x}} {\epsilon }^{*}_{j}(\vec {P},\lambda =\pm 1), \end{aligned}$$

(20)

where $\mathcal {H}_{-iK}^{(2)}(-P t_{c})$ are Hankel functions of first kind, $K=\sqrt{\left( \frac{M_W}{\omega }\right) ^{2}-\frac{1}{4}}$ and $\vec {\epsilon }\,(\vec {P},\lambda )$ are the polarization vectors. For $\lambda =\pm 1$ these vectors are orthogonal with the momentum $\vec {P}\cdot \vec {\epsilon }\,({P},\lambda =\pm 1)=0$.

The solutions with well determined momentum and helicity for the Dirac equation in de Sitter geometry were obtained in [48]. In the case of zero mass fermions, the solution for the neutrino was also obtained in [48]:

$$\begin{aligned} u_{\vec {p}\sigma }^{\dag }(x) = \left( \frac{-\omega t_c}{2\pi }\right) ^{3/2} \left( \left( \frac{1}{2}-\sigma \right) \xi _{\sigma }^{\dag }(x),0 \right) e^{-i\vec {p}\vec {x} + ipt_c},\nonumber \\ \end{aligned}$$

(21)

considering that ${\bar{u}}=u^{\dag }\gamma ^{0}$. We also mention that problem of Majorana neutrinos on de Sitter space-time is addressed in a recent paper [61].

For the positron we have the solution with respect to the helicity basis [48]:

$$\begin{aligned} v_{\vec {p^{\prime }}\sigma ^{\prime }}(x)= & {} i\sqrt{\frac{\pi p^{\prime }}{\omega }}\left( \frac{1}{2\pi }\right) ^{3/2}\nonumber \\{} & {} \times \left( \begin{array}{c} {-}\sigma ^{\prime } e^{-\pi k/2} \mathcal {H}_{\nu _{-}}^{(2)}\left( \frac{p^{\prime }}{\omega }e^{-\omega t}\right) \eta _{\sigma ^{\prime }}(\vec {p^{\prime }}) \\ \frac{1}{2} e^{\pi k/2}\mathcal {H}_{\nu _{+}}^{(2)}\left( \frac{p^{\prime }}{\omega }e^{-\omega t}\right) \eta _{\sigma ^{\prime }}(\vec {p^{\prime }}) \\ \end{array} \right) \nonumber \\{} & {} \times e^{-i\vec {p^{\prime }}\vec {x}-2\omega t},\nonumber \\ \end{aligned}$$

(22)

where $\mathcal {H}^{(1)}_{\nu }(z), \mathcal {H}^{(2)}_{\nu }(z)$ are Hankel functions of the first and second kind and $k=\frac{m_{e}}{\omega },\nu _{\pm }=\frac{1}{2}\pm ik$.

The helicity spinors satisfy the relation:

$$\begin{aligned} \vec {\sigma }\vec {p}\,\xi _{\sigma }(\vec {p}\,)=2p\sigma \xi _{\sigma }(\vec {p}\,) \end{aligned}$$

(23)

with $\sigma =\pm 1/2$, where $\vec {\sigma }$ are the Pauli matrices, and $p=\mid \vec {p}\mid$ is the modulus of the momentum vector, while $\eta _{\sigma }(\vec {p}\,)= i\sigma _2 [\xi _{\sigma }(\vec {p}\,)]^{*}$.

The spatial integral has the same form as in the Minkowski theory (see Eq. (169) from Appendix B), and gives the momentum conservation in this process. The temporal integral is analysed in Apendix B in Eqs. (167), (168), (170), (171), (176) and we mention that the integration variable is changed from t to $z=-t_c=\frac{1}{\omega }e^{-\omega t}$.

The amplitude in terms of the new variable z is:

$$\begin{aligned} A_{i\rightarrow f}= & {} -\frac{g}{2\sqrt{2}}\frac{\pi \sqrt{p^{\prime }} e^{-\pi K/2}e^{-\pi k/2}}{(2\pi )^{3/2}}\delta ^{3}(\vec {p}+\vec {p^{\prime }}+\vec {P})\nonumber \\{} & {} \times \left( \frac{1}{2}-\sigma \right) \sigma ^{\prime } \nonumber \\{} & {} \times \int _{0}^{+\infty } dz \cdot z e^{-ipz}\mathcal {H}_{\nu _{-}}^{(2)}(p^{\prime }z)\mathcal {H}_{-iK}^{(2)}(P z)\nonumber \\{} & {} \times \xi _{\sigma }^{\dag }(\vec {p})\sigma ^{i}\eta _{\sigma ^{\prime }}(\vec {p^{\prime }}){\epsilon }^{*}_{i}(\vec {P},\lambda =\pm 1). \end{aligned}$$

(24)

Fig. 4

The real and imaginary parts of D with respect to $\frac{M_{W}}{\omega }$ for $k=0.1$ and momenta values $p' = 0.2, p = 0.1, P = 0.4$ for the straight line and $p' = 0.25, p = 0.1, P = 0.6$ for the dotted line

The next step is to solve the integral with respect to z. For that we will use the connection between $\mathcal {J}$ Bessel functions and Hankel functions as explained in Eqs. (176), (177), (178) from Appendix B.

We can then rewrite the amplitude:

$$\begin{aligned} A_{i\rightarrow f}= & {} -\frac{g}{2}\frac{\sqrt{\pi } \sqrt{pp^{\prime }}\sqrt{i} e^{-\pi k/2}}{(2\pi )^{3/2}}\delta ^{3}(\vec {p}+\vec {p^{\prime }}+\vec {P})\nonumber \\{} & {} \times \left( \frac{1}{2}-\sigma \right) \sigma ^{\prime } \frac{e^{-i\frac{\pi }{4}}}{i\,\cosh (\pi k)}\nonumber \\{} & {} \times [T_{1}-T_{2}-T_{3}+T_{4}] \xi _{\sigma }^{\dag }(\vec {p})\sigma ^{i}\nonumber \\{} & {} \times \eta _{\sigma ^{\prime }}(\vec {p^{\prime }}){\epsilon }^{*}_{i}(\vec {P},\lambda =\pm 1), \end{aligned}$$

(25)

where the terms $T_{1},T_{2},T_{3}$ and $T_{4}$ are defined in Eq. (181) from Appendix B. Each of these terms may now be integrated using formula (193) from Appendix B, taking note of the fact that in this case $Q=\frac{5}{2}$.

After integration the results are:

$$\begin{aligned} T_{1}= & {} \frac{ie^{\pi k}\sqrt{2}p^{\frac{1}{2}}{p^{\prime }}^{\frac{1}{2}-ik}(iP)^{-\frac{7}{2}+ik}}{\Gamma \left( \frac{3}{2}\right) \Gamma \left( \frac{3}{2}-ik\right) } \Gamma \left( \frac{\frac{7}{2}-i(k-K)}{2}\right) \nonumber \\{} & {} \times \Gamma \left( \frac{\frac{7}{2}-i(k+K)}{2}\right) \nonumber \\{} & {} \times \mathcal {F}_{4}\left( \frac{\frac{7}{2}-i(k-K)}{2},\frac{\frac{7}{2}-i(k+K)}{2},\frac{3}{2},\frac{3}{2}\right. \nonumber \\{} & {} \left. -ik,\frac{p^{2}}{P^{2}},\frac{{p^{\prime }}^{2}}{P^{2}}\right) ; \end{aligned}$$

(26)

$$\begin{aligned} T_{2}= & {} \frac{\sqrt{2}p^{\frac{1}{2}}{p^{\prime }}^{-\frac{1}{2}+ik}(iP)^{-\frac{5}{2}-ik}}{\Gamma \left( \frac{3}{2}\right) \Gamma \left( \frac{1}{2}+ik\right) } \Gamma \left( \frac{\frac{5}{2}+i(k+K)}{2}\right) \nonumber \\{} & {} \times \Gamma \left( \frac{\frac{5}{2}+i(k-K)}{2}\right) \nonumber \\{} & {} \times \mathcal {F}_{4}\left( \frac{\frac{5}{2}+i(k+K)}{2},\frac{\frac{5}{2}+i(k-K)}{2},\frac{3}{2},\frac{1}{2}\right. \nonumber \\{} & {} \left. +ik,\frac{p^{2}}{P^{2}},\frac{{p^{\prime }}^{2}}{P^{2}}\right) ; \end{aligned}$$

(27)

$$\begin{aligned} T_{3}= & {} \frac{e^{\pi k}\sqrt{2}p^{-\frac{1}{2}}{p^{\prime }}^{\frac{1}{2}-ik}(iP)^{-\frac{5}{2}+ik}}{\Gamma \left( \frac{1}{2}\right) \Gamma \left( \frac{3}{2}-ik\right) } \Gamma \left( \frac{\frac{5}{2}-i(k-K)}{2}\right) \nonumber \\{} & {} \times \Gamma \left( \frac{\frac{5}{2}-i(k+K)}{2}\right) \nonumber \\{} & {} \times \mathcal {F}_{4}\left( \frac{\frac{5}{2}-i(k-K)}{2},\frac{\frac{5}{2}-i(k+K)}{2},\frac{1}{2},\frac{3}{2}\right. \nonumber \\{} & {} \left. -ik,\frac{p^{2}}{P^{2}},\frac{{p^{\prime }}^{2}}{P^{2}}\right) ; \end{aligned}$$

(28)

$$\begin{aligned} T_{4}= & {} \frac{\frac{1}{i}\sqrt{2}p^{-\frac{1}{2}}{p^{\prime }}^{-\frac{1}{2}+ik}(iP)^{-\frac{3}{2}-ik}}{\Gamma \left( \frac{1}{2}\right) \Gamma \left( \frac{1}{2}+ik\right) } \Gamma \left( \frac{\frac{3}{2}+i(k+K)}{2}\right) \nonumber \\{} & {} \times \Gamma \left( \frac{\frac{3}{2}+i(k-K)}{2}\right) \nonumber \\{} & {} \times \mathcal {F}_{4}\left( \frac{\frac{3}{2}+i(k+K)}{2},\frac{\frac{3}{2}+i(k-K)}{2},\frac{1}{2},\frac{1}{2}\right. \nonumber \\{} & {} \left. +ik,\frac{p^{2}}{P^{2}},\frac{{p^{\prime }}^{2}}{P^{2}}\right) , \end{aligned}$$

(29)

Fig. 5

The real and imaginary parts of A with respect to $\frac{m_{e}}{\omega }$ for $\frac{M_{W}}{\omega }=0.6$ and momenta values $p' = 0.2, p = 0.1, P = 0.4$ for the straight line and $p' = 0.25, p = 0.1, P = 0.6$ for the dotted line

Fig. 6

The real and imaginary parts of B with respect to $\frac{m_{e}}{\omega }$ for $\frac{M_{W}}{\omega }=0.6$ and momenta values $p' = 0.2, p = 0.1, P = 0.4$ for the straight line and $p' = 0.25, p = 0.1, P = 0.6$ for the dotted line

Fig. 7

The real and imaginary parts of C with respect to $\frac{m_{e}}{\omega }$ for $\frac{M_{W}}{\omega }=0.6$ and momenta values $p' = 0.2, p = 0.1, P = 0.4$ for the straight line and $p' = 0.25, p = 0.1, P = 0.6$ for the dotted line

Fig. 8

The real and imaginary parts of D with respect to $\frac{m_{e}}{\omega }$ for $\frac{M_{W}}{\omega }=0.6$ and momenta values $p' = 0.2, p = 0.1, P = 0.4$ for the straight line and $p' = 0.25, p = 0.1, P = 0.6$ for the dotted line

Each of the four terms is expressed in terms of Gamma Euler functions $\Gamma$ and the $\mathcal {F}_{4}$ Appell’s function, which is defined by the double series [62, 63]:

$$\begin{aligned}{} & {} \mathcal {F}_{4}(\alpha ,\beta ,\gamma ,\gamma ';x,y)\nonumber \\{} & {} \quad =\sum _{m=0}^{\infty } \sum _{n=0}^{\infty } \frac{\Gamma (\alpha +m+n)\Gamma (\beta +m+n)\Gamma (\gamma )\Gamma (\gamma ')}{\Gamma (\alpha )\Gamma (\beta )\Gamma (\gamma +m)\Gamma (\gamma ' +n)} \nonumber \\{} & {} \qquad \cdot \frac{x^{m}y^{n}}{m!n!}. \end{aligned}$$

(30)

There is little research on Appell’s functions $\mathcal {F}_{4}$ and there are just a few known cases where they can be converted into other kinds of hypergeometric functions, with the mention that this does not apply to our case. For this reason we will use in our further analysis the double series definition without any approximation.

The behaviour of the amplitude will be determined by the behaviour of the four terms which depend on Appell’s function. The parameters of interest are $K=\sqrt{\left( \frac{M_{W}}{\omega }\right) ^{2}-\frac{1}{4}}$ and $k=\frac{m_{e}}{\omega }$, where $M_{W}$ is the mass of the W boson, $m_{e}$ is the mass of the positron and $\omega$ is the expansion parameter.

We want to see the behaviour of the amplitude as it relates to the ratios of the particle masses and the expansion parameter, and so we want to graphically represent each of the four terms $T_{1},T_{2},T_{3}$ and $T_{4}$ in some way. We must also choose values for momenta $p', p, P$, which are present explicitly in the amplitude, as well as present in Appell’s functions as arguments $x=p^{2}/P^{2}$ and $y={p^{\prime }}^{2}/P^{2}$.

In order to add up all relevant factors we denote:

$$\begin{aligned} A = \frac{\sqrt{i}\sqrt{pp^{\prime }}e^{-\frac{\pi i}{4}}{e^{-\pi \frac{k}{2}}}}{i\,\cosh (\pi k)} \, T_{1};\,\,\,B=\frac{\sqrt{i}\sqrt{pp^{\prime }}e^{-\frac{\pi i}{4}}{e^{-\pi \frac{k}{2}}}}{i\,\cosh (\pi k)}\,T_2;\nonumber \\ C = \frac{\sqrt{i}\sqrt{pp^{\prime }}e^{-\frac{\pi i}{4}}{e^{-\pi \frac{k}{2}}}}{i\,\cosh (\pi k)} \, T_{3};\,\,\,D=\frac{\sqrt{i}\sqrt{pp^{\prime }}e^{-\frac{\pi i}{4}}{e^{-\pi \frac{k}{2}}}}{i\,\cosh (\pi k)}\,T_4.\nonumber \\ \end{aligned}$$

(31)

The amplitude in terms of the new notation is:

$$\begin{aligned}{} & {} A_{i\rightarrow f}= -\frac{g}{2}\frac{\sqrt{\pi }}{(2\pi )^{3/2}}\delta ^{3}(\vec {p}+\vec {p'}+\vec {P}) \left( \frac{1}{2}-\sigma \right) \sigma ' \nonumber \\ {}{} & {} \quad \times [A-B-C+D] \xi _{\sigma '}^{\dag }(\vec {p'})\sigma ^{i}\eta _{\sigma }(\vec {p}\,){\epsilon }^{*}_{i}(\vec {P},\lambda =\pm 1).\nonumber \\ \end{aligned}$$

(32)

We will plot the real and imaginary parts of the functions that define the amplitude for a clear picture of their behaviour, in terms of parameters $\frac{m_{e}}{\omega },\,\frac{M_{W}}{\omega }$, for fixed values of momenta.

Figures 1, 2, 3 and 4 show terms A, B, C, D of the amplitude with respect to $\frac{M_{W}}{\omega }$, while Figs. 5, 6, 7 and 8 show terms A, B, C, D with respect to $\frac{m_{e}}{\omega }$.

Fig. 9

The absolute value of $F_{1}$ for $\frac{m_{e}}{\omega }=0.1$ on the left and $\frac{M_{W}}{\omega }=0.6$ on the right, and momenta values $p' = 0.2, p = 0.1, P = 0.4$ for the straight line and $p' = 0.25, p = 0.1, P = 0.6$ for the dotted line

The amplitude of the particle production process is significantly higher when $\frac{M_{W}}{\omega }\rightarrow 0$, and wanes as the rest energy of the boson becomes much larger than the energy of the expanding background. This shows that this kind of process could have only taken place in the most early period of the universe, when space-time expansion was exceptionally high. The same observations are valid for the amplitude as it relates to $\frac{m_{e}}{\omega }$. The graphical analysis also proves that as $\frac{M_{W}}{\omega }\rightarrow \infty$ and $\frac{m_{e}}{\omega }\rightarrow \infty$, the transition amplitude vanishes and we recover the Minkowski limit, where this process is forbidden by energy and momentum conservation laws.

4 The probability for $\lambda = \pm 1$

We can obtain the probability of this process by taking the absolute square value of the amplitude and by summing over all possible helicities, with the observation that in the case of neutrino the helicity is fixed:

$$\begin{aligned} P_{i\rightarrow f} = \frac{1}{4} \sum _{\sigma '\lambda }|A_{i\rightarrow f}A_{i\rightarrow f}^{*}|. \end{aligned}$$

(33)

This results in:

$$\begin{aligned} P_{i\rightarrow f}= & {} \frac{1}{4} \sum _{\sigma '\lambda } \frac{g^{2}}{4}\frac{\pi }{(2\pi )^{3}}\delta ^{3}(\vec {p}+\vec {p'}+\vec {P}) \left( \frac{1}{2}-\sigma \right) ^{2}\sigma '^{2} \nonumber \\{} & {} \times \left| F_{1} F_{1}^{*} \right| \left| \xi _{\sigma }^{\dag }(\vec {p}\,)\sigma ^{i}\eta _{\sigma '}(\vec {p'}\,){\epsilon }^{*}_{i}(\vec {P},\lambda =\pm 1)\right| ^{2},\nonumber \\ \end{aligned}$$

(34)

where we have denoted $F_{1} = (A-B-C+D)$.

We can assess the behaviour of the probability by looking at the absolute value of the product $F_{1}F_{1}^{*}$, which again contains all relevant terms to the evolution of the probability (Fig. 9).

From the graphical analysis of the probability it is clear that the phenomenon of spontaneous generation from vacuum of the massive W bosons and fermions has nonvanishing probability only when the expansion factor exceeds the particle masses, which in our notations refers to small values of parameters $\frac{m_{e}}{\omega },\,\frac{M_{W}}{\omega }$. In the limit of small values of ratios $\frac{m_{e}}{\omega },\,\frac{M_W}{\omega }$ it is, in principle, possible to compute the total probability and total transition rate, which are the important physical quantities that are proportional with the density number of produced particles. For large values of $\frac{m_{e}}{\omega },\,\frac{M_{W}}{\omega }$, the probabilities vanish as expected in the Minkowski limit.

The computation of total probability is related to the dependence of the Appell hypergeometric functions on the momenta, which does not allow us to extract an analytical result when integrating over the final momenta. A solution may be to work with the functions A, B, C, D where we neglect the Appell hypergeometric functions. The numerical and graphical analysis reveals that we can neglect Appell’s functions since graphs of the probability in terms of parameters $\frac{m_{e}}{\omega },\,\frac{M_W}{\omega }$ are approximatively the same without them. We intend to approach this subject in a future study. In this way one may obtain the total probability dependence on the parameters $\frac{m_e}{\omega },\,\frac{M_W}{\omega }$.

4.1 The Minkowski limit

Let us analyse the Minkowski limit of our results. First our graphical analysis proves that the amplitudes and probability is vanishing for $\frac{m_{e}}{\omega }, \frac{M_W}{\omega } \rightarrow \infty$, which represents the Minkowski limit in our computations.

We start by considering one of the terms:

$$\begin{aligned} A&= \frac{\sqrt{i}e^{-\frac{\pi i}{4}}{e^{\pi \frac{k}{2}}}}{\cosh (\pi k)}\frac{\sqrt{2}{pp^{\prime }}^{1-ik}(iP)^{-\frac{7}{2}+ik}}{\Gamma \left( \frac{3}{2}\right) \Gamma \left( \frac{3}{2}-ik\right) }\,\nonumber \\&\quad \times \Gamma \left( \frac{\frac{7}{2}-i(k-\frac{M_W}{\omega })}{2}\right) \Gamma \left( \frac{\frac{7}{2}-i(k+\frac{M_W}{\omega })}{2}\right) \nonumber \\&\quad \times \mathcal {F}_{4}\left( \frac{\frac{7}{2}-i(k-\frac{M_W}{\omega })}{2},\frac{\frac{7}{2}-i(k+\frac{M_W}{\omega })}{2},\right. \nonumber \\&\quad \left. \frac{3}{2},\frac{3}{2}-ik,\frac{p^{2}}{P^{2}},\frac{{p^{\prime }}^{2}}{P^{2}}\right) . \end{aligned}$$

(35)

Its behaviour is determined mainly by $\cosh ^{-1}(\pi k)$ and the Gamma functions. Although the $\mathcal {F}_{4}$ functions diverge to infinity as the expansion parameter approaches zero, the Gamma functions and $cosh^{-1}(\pi k)$ factors decrease much more rapidly to zero, and make it so that term A (and by extension B, C and D) converges to zero as $\omega \rightarrow 0$, as seen below and also in Figs. 1, 2, 3, 4, 5, 6, 7 and 8.

Fig. 10

The real and imaginary parts of A with respect to $\frac{M_{W}}{\omega }$ for $k=0.1$ and momenta values $p' = 0.2, p = 0.1, P = 0.4$

Fig. 11

The real and imaginary parts of A with respect to $\frac{m_{e}}{\omega }$ for $\frac{M_{W}}{\omega }=0.6$ and momenta values $p' = 0.2, p = 0.1, P = 0.4$

The A, B, C, D functions that define the amplitude will be analysed for large values of parameters $\frac{m_{e}}{\omega }, \frac{M_{W}}{\omega }$. The parameter K can be approximated as $K=\sqrt{\frac{M_W^2}{\omega ^2}-\frac{1}{4}}\simeq \frac{M_W}{\omega }$ for $M_W\gg \omega$ (Figs. 10, 11).

The Gamma functions can be further approximated by using the Stirling formula for $z \rightarrow \infty$ [62, 63]:

$$\begin{aligned} \Gamma (z) \simeq e^{-z}z^{z}\left( \frac{2\pi }{z}\right) ^{1/2}. \end{aligned}$$

(36)

We will transform the following functions for large arguments:

$$\begin{aligned} \Gamma \left( \frac{3}{2} - ik\right) = e^{-\frac{3}{2}+ik}\left( \frac{3}{2}-ik\right) ^{1-ik}\sqrt{2\pi }, \end{aligned}$$

(37)

and use

$$\begin{aligned} i^{-\frac{7}{2}+ik} = e^{-\frac{7i\pi }{4}}e^{-\frac{\pi k }{2}}. \end{aligned}$$

(38)

This will allow us to write down the Gamma Euler functions as:

$$\begin{aligned}{} & {} \Gamma \left( \frac{7}{4}-\frac{i(k+\frac{M_W}{\omega })}{2}\right) \Gamma \left( \frac{7}{4}-\frac{i(k-\frac{M_W}{\omega })}{2}\right) \nonumber \\{} & {} \quad =\frac{8\pi e^{-\frac{7}{2}+ik}}{\sqrt{49-4k^2-28ik+4\frac{M_W^2}{\omega ^2}}}\nonumber \\{} & {} \qquad \times \left( \frac{7}{4} - \frac{i(k+\frac{M_W}{\omega })}{2}\right) ^{\frac{7}{4}-\frac{i(k+\frac{M_W}{\omega })}{2}}\nonumber \\{} & {} \qquad \times \left( \frac{7}{4} - \frac{i(k-\frac{M_W}{\omega })}{2}\right) ^{\frac{7}{4}-\frac{i(k-\frac{M_W}{\omega })}{2}}. \end{aligned}$$

(39)

Then for $M_{W}/\omega \gg 1$ and $m_{e}/\omega \gg 1$ we have:

$$\begin{aligned}&A \simeq \frac{8\sqrt{i\pi } e^{-2-2\pi i}p (p^{\prime })^{1-ik} (P)^{-\frac{7}{2}+ik}}{e^{\pi k}\Gamma \left( \frac{3}{2}\right) \left( \frac{3}{2}-ik\right) ^{1-ik}}\nonumber \\&\quad \times \frac{\left( \frac{7}{4} - \frac{i(k+\frac{M_W}{\omega })}{2}\right) ^{\frac{7}{4}-\frac{i(k+\frac{M_W}{\omega })}{2}}\left( \frac{7}{4} - \frac{i(k-\frac{M_W}{\omega })}{2}\right) ^{\frac{7}{4}-\frac{i(k-\frac{M_W}{\omega })}{2}}}{\sqrt{49{-}4k^2{-}28ik+4\frac{M_W^2}{\omega ^2}}}\nonumber \\&\quad \times \mathcal {F}_{4}\left( \frac{\frac{7}{2}{-}i(k{-}\frac{M_W}{\omega })}{2},\frac{\frac{7}{2}{-}i(k{+}\frac{M_W}{\omega })}{2},\frac{3}{2},\frac{3}{2}{-}ik,\frac{p^{2}}{P^{2}},\frac{{p^{\prime }}^{2}}{P^{2}}\right) . \end{aligned}$$

(40)

The rest of the functions B, C, D have similar expressions:

$$\begin{aligned} B&\simeq \frac{8\sqrt{i\pi } e^{-2-3\pi i/2}p (p^{\prime })^{ik} (P)^{-\frac{5}{2}-ik}}{ie^{\pi k}\Gamma \left( \frac{3}{2}\right) \left( \frac{1}{2}+ik\right) ^{ik}}\nonumber \\&\quad \times \frac{\left( \frac{5}{4} + \frac{i(k+\frac{M_W}{\omega })}{2}\right) ^{\frac{5}{4}+\frac{i(k+\frac{M_W}{\omega })}{2}}\left( \frac{5}{4} + \frac{i(k-\frac{M_W}{\omega })}{2}\right) ^{\frac{5}{4}+\frac{i(k-\frac{M_W}{\omega })}{2}}}{\sqrt{25-4k^2+20ik+4\frac{M_W^2}{\omega ^2}}}\nonumber \\&\quad \times \mathcal {F}_{4}\left( \frac{\frac{5}{2}{+}i(k{+}\frac{M_W}{\omega })}{2},\frac{\frac{5}{2}{+}i(k{-}\frac{M_W}{\omega })}{2},\frac{3}{2},\frac{1}{2}{+}ik,\frac{p^{2}}{P^{2}},\frac{{p^{\prime }}^{2}}{P^{2}}\right) ; \end{aligned}$$

(41)

$$\begin{aligned} C&\simeq \frac{8\sqrt{i\pi }e^{-1-3\pi i/2}(p^{\prime })^{1-ik} (P)^{-\frac{5}{2}+ik}}{ie^{\pi k}\Gamma \left( \frac{1}{2}\right) \left( \frac{3}{2}-ik\right) ^{1-ik}}\nonumber \\&\quad \times \frac{\left( \frac{5}{4} - \frac{i(k-\frac{M_W}{\omega })}{2}\right) ^{\frac{5}{4}-\frac{i(k-\frac{M_W}{\omega })}{2}}\left( \frac{5}{4} - \frac{i(k+\frac{M_W}{\omega })}{2}\right) ^{\frac{5}{4}-\frac{i(k+\frac{M_W}{\omega })}{2}}}{\sqrt{25-4k^2-20ik+4\frac{M_W^2}{\omega ^2}}}\nonumber \\&\quad \times \mathcal {F}_{4}\left( \frac{\frac{5}{2}{-}i(k{-}\frac{M_W}{\omega })}{2},\frac{\frac{5}{2}{-}i(k{+}\frac{M_W}{\omega })}{2},\frac{1}{2},\frac{3}{2}{-}ik,\frac{p^{2}}{P^{2}},\frac{{p^{\prime }}^{2}}{P^{2}}\right) ; \end{aligned}$$

(42)

$$\begin{aligned} D&\simeq -\frac{8\sqrt{i\pi } e^{-1-i\pi }(p^{\prime })^{ik} (P)^{-\frac{3}{2}-ik}}{e^{\pi k}\Gamma \left( \frac{1}{2}\right) \left( \frac{1}{2}+ik\right) ^{ik}}\nonumber \\&\quad \times \frac{\left( \frac{3}{4} + \frac{i(k+\frac{M_W}{\omega })}{2}\right) ^{\frac{3}{4}+\frac{i(k+\frac{M_W}{\omega })}{2}}\left( \frac{3}{4} + \frac{i(k-\frac{M_W}{\omega })}{2}\right) ^{\frac{3}{4}+\frac{i(k-\frac{M_W}{\omega })}{2}}}{\sqrt{9-4k^2+12ik+4\frac{M_W^2}{\omega ^2}}}\nonumber \\&\quad \times \mathcal {F}_{4}\left( \frac{\frac{3}{2}{+}i(k{+}\frac{M_W}{\omega })}{2},\frac{\frac{3}{2}{+}i(k{-}\frac{M_W}{\omega })}{2},\frac{1}{2},\frac{1}{2}{+}ik,\frac{p^{2}}{P^{2}},\frac{{p^{\prime }}^{2}}{P^{2}}\right) . \end{aligned}$$

(43)

We obtain that in the limit $\frac{M_{W}}{\omega } \gg 1,\, \frac{m_{e}}{\omega } \gg 1$, terms A, B, C, D decrease to zero like the functions $e^{-\pi m_{e}/\omega }$ and $\frac{1}{M_W/\omega }$ multiplied by factors at imaginary powers. It is also important to mention that the behaviour of these functions in terms of $m_{e}/\omega , M_W/\omega$ is mainly determined by the factors which multiply the Appell hypergeometric functions. These factors cancel any divergent behaviour of Appell’s functions in the considered limit. The transition probabilitiy behaves like $e^{-2\pi m_{e}/\omega }$ and $\frac{1}{(M_{W}/\omega )^2}$, assuring the Minkowski limit when the ratios between particle masses and expansion factor become infinite. In the Minkowski theory, the amplitude and probability vanish due to the simultaneous conservation of momentum and energy [1, 59, 60].

5 Transition amplitude and probability for $\lambda = 0$

The amplitude defined in Eq. (165) from Appendix B, contains both spatial and temporal contributions in the case of longitudinal polarization, because the solution of the Proca equation has a nonvanishing temporal component in this case [8]:

$$\begin{aligned} {f_{\vec {p}\lambda }}_{0}(\vec {x}) = \frac{\sqrt{\pi }e^{-K\pi /2}\omega P}{2(2\pi )^{3/2}M_W}(-t_c)^{3/2}\mathcal {H}_{iK}^{(1)}(-Pt_c)e^{i\vec {P}\vec {x}}. \end{aligned}$$

(44)

Moreover, for $\lambda =0$ the spatial component of the solution also has two terms [8]:

$$\begin{aligned}{} & {} {f_{\vec {p}\lambda }}_{i} (\vec {x}) \nonumber \\{} & {} \quad = \frac{i\sqrt{\pi }e^{-k\pi /2}\omega P}{2(2\pi )^{3/2}M_W}\left[ \left( \frac{1}{2}+iK\right) \frac{\sqrt{-t_c}}{P}\mathcal {H}_{iK}^{(1)}(-Pt_c)\right. \nonumber \\{} & {} \qquad \left. - (-t_{c})^{3/2}\mathcal {H}_{1+iK}^{(1)}(-Pt_c)\right] \epsilon _{i}(\vec {K},\lambda )e^{i\vec {P}\vec {x}}. \end{aligned}$$

(45)

In this case the amplitude reads:

$$\begin{aligned} A_{i\rightarrow f}= & {} \frac{ig}{2\sqrt{2}} \int d^{4}x \sqrt{-g(x)} {\bar{u}}_{\vec {p}\sigma }(x) \gamma ^{\hat{\alpha }} e_{\hat{\alpha }}^{\mu }\nonumber \\{} & {} \times (1-\gamma ^5) v_{\vec {p^{\prime }}\sigma ^{\prime }}(x){f^{*}_{\vec {P}\lambda }}_{\mu } (x)\nonumber \\= & {} \frac{ig}{2\sqrt{2}} \int d^{4}x \sqrt{-g(x)} {\bar{u}}_{\vec {p}\sigma }(x) \gamma ^{{\hat{0}}} e_{{\hat{0}}}^{0}\nonumber \\{} & {} \times (1-\gamma ^5) v_{\vec {p^{\prime }}\sigma ^{\prime }}(x){f^{*}_{\vec {P}\lambda }}_{0} (x)\nonumber \\{} & {} +\frac{ig}{2\sqrt{2}} \int d^{4}x \sqrt{-g(x)} {\bar{u}}_{\vec {p}\sigma }(x) \gamma ^{{\hat{i}}} e_{{\hat{i}}}^j\nonumber \\{} & {} \times (1-\gamma ^5) v_{\vec {p^{\prime }}\sigma ^{\prime }}(x){f^{*}_{\vec {P}\lambda }}_{j} (x). \end{aligned}$$

(46)

Because of the nature of the Proca solutions [8], we are going to split the amplitude into three terms, for convenience:

$$\begin{aligned}{} & {} A_{i\rightarrow f}(\lambda =0) \nonumber \\{} & {} \quad = A_{i\rightarrow f}^{(1)} (\lambda = 0)+ A_{i\rightarrow f}^{(2)} (\lambda = 0) + A_{i\rightarrow f}^{(3)} (\lambda = 0). \end{aligned}$$

(47)

The first term will contain the temporal component and we obtain something very similar to the case of $\lambda =\pm 1$:

$$\begin{aligned} A_{i\rightarrow f}^{(1)} (\lambda = 0)= & {} -\frac{g}{2\sqrt{2}}\frac{\omega P}{M_{W}}\frac{ \pi \sqrt{p^{\prime }} e^{-\pi K/2}e^{-\pi k/2}}{(2\pi )^{3/2}}\nonumber \\{} & {} \times \delta ^{3}(\vec {p}+\vec {p^{\prime }}+\vec {P}) \left( \frac{1}{2}-\sigma \right) \nonumber \\{} & {} \times \sigma ^{\prime }\int _{0}^{+\infty } dz \cdot z^{2} e^{-ipz}\mathcal {H}_{\nu _{-}}^{(2)}(p^{\prime }z)\mathcal {H}_{-iK}^{(2)}(P z)\nonumber \\{} & {} \times \xi _{\sigma }^{\dag }(\vec {p}\,)\eta _{\sigma ^{\prime }}(\vec {p^{\prime }}). \end{aligned}$$

(48)

This term can also be rewritten after transforming the Hankel functions into Bessel functions [62]:

$$\begin{aligned} A_{i\rightarrow f}^{(1)} (\lambda = 0)= & {} -\frac{g}{2}\frac{\sqrt{\pi } P\sqrt{pp^{\prime }}\sqrt{i} e^{-\pi k/2}}{(2\pi )^{3/2}}\frac{\omega }{M_{W}}\nonumber \\{} & {} \times \delta ^{3}(\vec {p}+\vec {p^{\prime }}+\vec {P}) \left( \frac{1}{2}-\sigma \right) \sigma ^{\prime } \frac{e^{-i\frac{\pi }{4}}}{i\, \cosh (\pi k)}\nonumber \\ {}{} & {} \times [T_{5}-T_{6}-T_{7}+T_{8}] \xi _{\sigma }^{\dag }(\vec {p}\,)\eta _{\sigma ^{\prime }}(\vec {p^{\prime }}),\nonumber \\ \end{aligned}$$

(49)

where the terms $T_{5},T_{6},T_{7},T_{8}$ denote the temporal integrals defined in Eq. (185) from Appendix B.

The following expressions are obtained for $T_{5},T_{6},T_{7},T_{8}$ after solving the temporal integrals using formula (193) from the Appendix B:

$$\begin{aligned} T_{5}= & {} \frac{ie^{\pi k}{2}^{3/2}p^{\frac{1}{2}}{p^{\prime }}^{\frac{1}{2}-ik}(iP)^{-\frac{9}{2}+ik}}{\Gamma \left( \frac{3}{2}\right) \Gamma \left( \frac{3}{2}-ik\right) } \Gamma \left( \frac{\frac{9}{2}-i(k-K)}{2}\right) \nonumber \\{} & {} \times \Gamma \left( \frac{\frac{9}{2}-i(k+K)}{2}\right) \nonumber \\{} & {} \times \mathcal {F}_{4}\left( \frac{\frac{9}{2}-i(k-K)}{2},\frac{\frac{9}{2}-i(k+K)}{2},\frac{3}{2},\frac{3}{2}\right. \nonumber \\{} & {} \left. -ik,\frac{p^{2}}{P^{2}},\frac{{p^{\prime }}^{2}}{P^{2}}\right) ; \end{aligned}$$

(50)

$$\begin{aligned} T_{6}= & {} \frac{{2}^{3/2}p^{\frac{1}{2}}{p^{\prime }}^{-\frac{1}{2}+ik}(iP)^{-\frac{7}{2}-ik}}{\Gamma \left( \frac{3}{2}\right) \Gamma \left( \frac{1}{2}+ik\right) } \Gamma \left( \frac{\frac{7}{2}+i(k+K)}{2}\right) \nonumber \\{} & {} \Gamma \left( \frac{\frac{7}{2}+i(k-K)}{2}\right) \nonumber \\{} & {} \times \mathcal {F}_{4}\left( \frac{\frac{7}{2}+i(k-K)}{2},\frac{\frac{7}{2}+i(k-K)}{2},\frac{3}{2},\frac{1}{2}\right. \nonumber \\{} & {} \left. +ik,\frac{p^{2}}{P^{2}},\frac{{p^{\prime }}^{2}}{P^{2}}\right) ;\end{aligned}$$

(51)

$$\begin{aligned} T_{7}= & {} \frac{e^{\pi k}{2}^{3/2}p^{-\frac{1}{2}}{p^{\prime }}^{\frac{1}{2}-ik}(iP)^{-\frac{7}{2}+ik}}{\Gamma \left( \frac{1}{2}\right) \Gamma \left( \frac{3}{2}-ik\right) } \Gamma \left( \frac{\frac{7}{2}-i(k-K)}{2}\right) \nonumber \\{} & {} \times \Gamma \left( \frac{\frac{7}{2}-i(k+K)}{2}\right) \nonumber \\{} & {} \times \mathcal {F}_{4}\left( \frac{\frac{7}{2}-i(k-K)}{2},\frac{\frac{7}{2}-i(k+K)}{2},\frac{1}{2},\frac{3}{2}\right. \nonumber \\{} & {} \left. -ik,\frac{p^{2}}{P^{2}},\frac{{p^{\prime }}^{2}}{P^{2}}\right) ;\end{aligned}$$

(52)

$$\begin{aligned} T_{8}= & {} \frac{\frac{1}{i}2^{3/2}p^{-\frac{1}{2}}{p^{\prime }}^{-\frac{1}{2}+ik}(iP)^{-\frac{5}{2}-ik}}{\Gamma \left( \frac{1}{2}\right) \Gamma \left( \frac{1}{2}+ik\right) } \Gamma \left( \frac{\frac{5}{2}+i(k+K)}{2}\right) \nonumber \\{} & {} \times \Gamma \left( \frac{\frac{5}{2}+i(k-K)}{2}\right) \nonumber \\{} & {} \times \mathcal {F}_{4}\left( \frac{\frac{5}{2}+i(k+K)}{2},\frac{\frac{5}{2}+i(k-K)}{2},\frac{1}{2},\frac{1}{2}\right. \nonumber \\{} & {} \left. +ik,\frac{p^{2}}{P^{2}},\frac{{p^{\prime }}^{2}}{P^{2}}\right) . \end{aligned}$$

(53)

The second term and third terms of the amplitude sum over the spatial components of the Proca solution:

$$\begin{aligned} A_{i\rightarrow f}^{(2)} (\lambda = 0)= & {} -\frac{g}{2\sqrt{2}}\frac{\omega P}{M_{W}}\frac{ i\pi \sqrt{p^{\prime }} e^{-\pi K/2}e^{-\pi k/2}}{(2\pi )^{3/2}}\nonumber \\{} & {} \times \delta ^{3}(\vec {p}+\vec {p^{\prime }}+\vec {P}) \left( \frac{1}{2}-\sigma \right) \sigma ^{\prime }\frac{\left( \frac{1}{2}-iK\right) }{P} \nonumber \\ {}{} & {} \times \int _{0}^{+\infty } dz \,z\, e^{-ipz}\mathcal {H}_{\nu _{-}}^{(2)}(p^{\prime }z)\mathcal {H}_{-iK}^{(2)} (P z)\nonumber \\{} & {} \times \xi _{\sigma }^{\dag }(\vec {p}\,)\sigma ^{i}\eta _{\sigma ^{\prime }}(\vec {p^{\prime }}){\epsilon }^{*}_{i}(\vec {P},\lambda = 0).\nonumber \\ \end{aligned}$$

(54)

This second term is actually the amplitude for $\lambda =\pm 1$ up to a an imaginary factor and the ratio of the expansion parameter to the boson mass:

$$\begin{aligned} A_{i\rightarrow f}^{(2)}= & {} -i\left( \frac{1}{2} - iK\right) \frac{g}{2}\frac{\omega }{M_{W}}\frac{\sqrt{\pi } \sqrt{pp^{\prime }}\sqrt{i} e^{-\pi k/2}}{(2\pi )^{3/2}}\nonumber \\{} & {} \times \delta ^{3}(\vec {p}+\vec {p^{\prime }}+\vec {P}) \left( \frac{1}{2}-\sigma \right) \sigma ^{\prime } \frac{e^{-i\frac{\pi }{4}}}{i\,\cosh (\pi k)}\nonumber \\ {}{} & {} \times [T_{1}-T_{2}-T_{3}+T_{4}] \nonumber \\{} & {} \times \xi _{\sigma }^{\dag }(\vec {p}\,)\sigma ^{i}\eta _{\sigma ^{\prime }}(\vec {p^{\prime }}){\epsilon }^{*}_{i}(\vec {P},\lambda =\pm 0), \end{aligned}$$

(55)

where $T_1,T_2,T_3,T_4$ are defined in Eq. (26).

The third term is very close to the first term of $A_{i\rightarrow f}(\lambda =0)$, with the exception of the Hankel function dependent on P:

$$\begin{aligned} A_{i\rightarrow f}^{(3)} (\lambda = 0)= & {} \frac{g}{2\sqrt{2}}\frac{\omega P}{M_{W}}\frac{i \pi \sqrt{p^{\prime }} e^{-\pi K/2}e^{-\pi k/2}}{(2\pi )^{3/2}}\\{} & {} \times \delta ^{3}(\vec {p}+\vec {p^{\prime }}+\vec {P}) \left( \frac{1}{2}-\sigma \right) \sigma ^{\prime } \\{} & {} \times \int _{0}^{+\infty } dz \cdot z^{2} e^{-ipz}\mathcal {H}_{\nu _{-}}^{(2)}(p^{\prime }z)\mathcal {H}_{1-iK}^{(2)}(P z)\\{} & {} \times \xi _{\sigma }^{\dag } (\vec {p}\,)\sigma ^{i}\eta _{\sigma ^{\prime }}(\vec {p^{\prime }}){\epsilon }^{*}_{i}(\vec {P},\lambda = 0). \end{aligned}$$

Fig. 12

The absolute value of $F_{2}$ for $k=0.1$ on the left and $\frac{M_{W}}{\omega }=0.6$ on the right, and momenta values $p' = 0.2, p = 0.1, P = 0.4$ for the straight line and $p' = 0.25, p = 0.1, P = 0.6$ for the dotted line

Written with respect to Bessel functions [62], $A_{i\rightarrow f}^{(3)} (\lambda = 0)$ becomes:

$$\begin{aligned} A_{i\rightarrow f}^{(3)} (\lambda = 0)= & {} \frac{g}{2}\frac{\sqrt{\pi } P\sqrt{pp^{\prime }}i\sqrt{i} e^{-\pi k/2}}{(2\pi )^{3/2}}\frac{\omega }{M_{W}}\nonumber \\{} & {} \times \delta ^{3}(\vec {p}+\vec {p^{\prime }}+\vec {P}) \left( \frac{1}{2}-\sigma \right) \sigma ^{\prime } \frac{e^{i\frac{\pi }{4}}}{i\, \cosh (\pi k)}\nonumber \\ {}{} & {} \times [T_{9}-T_{10}-T_{11}+T_{12}]\nonumber \\{} & {} \times \xi _{\sigma }^{\dag }(\vec {p}\,)\sigma ^{i}\eta _{\sigma ^{\prime }}(\vec {p^{\prime }}){\epsilon }^{*}_{i}(\vec {P},\lambda = 0), \end{aligned}$$

(56)

where the integrals that define the terms $T_{9},T_{10},T_{11},T_{12}$ are given in Eq. (189) from Appendix B.

The explicit form of these terms can be found below and was obtained by using formula (193) from Appendix B:

$$\begin{aligned} T_{9}= & {} \frac{ie^{\pi k}{2}^{3/2}p^{\frac{1}{2}}{p^{\prime }}^{\frac{1}{2}-ik}(iP)^{-\frac{9}{2}+ik}}{\Gamma \left( \frac{3}{2}\right) \Gamma \left( \frac{3}{2}-ik\right) } \Gamma \left( \frac{\frac{7}{2}-i(k-K)}{2}\right) \nonumber \\{} & {} \times \Gamma \left( \frac{\frac{11}{2}-i(k+K)}{2}\right) \nonumber \\{} & {} \times \mathcal {F}_{4}\left( \frac{\frac{7}{2}-i(k-K)}{2},\frac{\frac{11}{2}-i(k+K)}{2},\frac{3}{2},\frac{3}{2}\right. \nonumber \\{} & {} \left. -ik,\frac{p^{2}}{P^{2}},\frac{{p^{\prime }}^{2}}{P^{2}}\right) ; \end{aligned}$$

(57)

$$\begin{aligned} T_{10}= & {} \frac{{2}^{3/2}p^{\frac{1}{2}}{p^{\prime }}^{-\frac{1}{2}+ik}(iP)^{-\frac{7}{2}-ik}}{\Gamma \left( \frac{3}{2}\right) \Gamma \left( \frac{1}{2}+ik\right) } \Gamma \left( \frac{\frac{5}{2}+i(k+K)}{2}\right) \nonumber \\{} & {} \times \Gamma \left( \frac{\frac{9}{2}+i(k-K)}{2}\right) \nonumber \\{} & {} \times \mathcal {F}_{4}\left( \frac{\frac{5}{2}+i(k-K)}{2},\frac{\frac{9}{2}+i(k-K)}{2},\frac{3}{2},\frac{1}{2}\right. \nonumber \\{} & {} \left. +ik,\frac{p^{2}}{P^{2}},\frac{{p^{\prime }}^{2}}{P^{2}}\right) ; \end{aligned}$$

(58)

$$\begin{aligned} T_{11}= & {} \frac{e^{\pi k}{2}^{3/2}p^{-\frac{1}{2}}{p^{\prime }}^{\frac{1}{2}-ik}(iP)^{-\frac{7}{2}+ik}}{\Gamma \left( \frac{1}{2}\right) \Gamma \left( \frac{3}{2}-ik\right) } \Gamma \left( \frac{\frac{5}{2}-i(k-K)}{2}\right) \nonumber \\{} & {} \times \Gamma \left( \frac{\frac{9}{2}-i(k+K)}{2}\right) \nonumber \\{} & {} \times \mathcal {F}_{4}\left( \frac{\frac{5}{2}-i(k-K)}{2},\frac{\frac{9}{2}-i(k+K)}{2},\frac{1}{2},\frac{3}{2}\right. \nonumber \\{} & {} \left. -ik,\frac{p^{2}}{P^{2}},\frac{{p^{\prime }}^{2}}{P^{2}}\right) ; \end{aligned}$$

(59)

$$\begin{aligned} T_{12}= & {} \frac{\frac{1}{i}2^{3/2}p^{-\frac{1}{2}}{p^{\prime }}^{-\frac{1}{2}+ik}(iP)^{-\frac{5}{2}-ik}}{\Gamma \left( \frac{1}{2}\right) \Gamma \left( \frac{1}{2}+ik\right) } \Gamma \left( \frac{\frac{3}{2}+i(k+K)}{2}\right) \nonumber \\{} & {} \times \Gamma \left( \frac{\frac{7}{2}+i(k-K)}{2}\right) \nonumber \\{} & {} \times \mathcal {F}_{4}\left( \frac{\frac{3}{2}+i(k+K)}{2},\frac{\frac{7}{2}+i(k-K)}{2},\frac{1}{2},\frac{1}{2}\right. \nonumber \\{} & {} \left. +ik,\frac{p^{2}}{P^{2}},\frac{{p^{\prime }}^{2}}{P^{2}}\right) . \end{aligned}$$

(60)

We can see that for $\lambda = 0$ there is a much stronger dependence on the expansion factor as a consequence of all terms being multiplied by the ratio between $\omega$ and $M_{W}$.

The probability for this process, when computed with the longitudinal modes for the $W^-$ boson, is defined as the square modulus of the amplitude summed over $\sigma '$, since $\lambda , \sigma$ are fixed:

$$\begin{aligned} P(\lambda =0)= & {} \frac{1}{2}\sum _{\sigma '}|A_{i\rightarrow f} (\lambda = 0)|^2\nonumber \\= & {} \frac{1}{2}\sum _{\sigma '}|(A_{i\rightarrow f}^{(1)} + A_{i\rightarrow f}^{(2)} \nonumber \\{} & {} + A_{i\rightarrow f}^{(3)} )(A_{i\rightarrow f}^{(1)} + A_{i\rightarrow f}^{(2)} + A_{i\rightarrow f}^{(3)} )^*|. \end{aligned}$$

(61)

To assess this probability we again have to take into account all terms which depend on the expansion parameter. In this case they are:

$$\begin{aligned} F_{2}= & {} -\frac{\omega }{M_{W}}\frac{P\sqrt{p p^{\prime }}\sqrt{i}e^{-\pi k/2}e^{-i \pi /4}}{i\, \cosh (\pi k)}[T_{5}-T_{6}-T_{7}+T_{8}] \nonumber \\{} & {} -i\left( \frac{1}{2}-iK\right) \frac{\omega }{M_{W}}\frac{\sqrt{pp^{\prime }}\sqrt{i}e^{-\pi k/2}e^{-i\pi /4}}{i\, \cosh (\pi k)}\nonumber \\{} & {} \times [T_{1}-T_{2}-T_{3}+T_{4}] \nonumber \\{} & {} +\frac{\omega }{M_{W}}\frac{P\sqrt{pp^{\prime }}i\sqrt{i}e^{-\pi k/2}e^{i\pi /4}}{i\, \cosh (\pi k)}[T_{9}-T_{10}-T_{11}+T_{12}].\nonumber \\ \end{aligned}$$

(62)

As before, the relevant term for the probability is the absolute value of the product $F_{2}F_{2}^{*}$.

For the graph in Fig. 12 with respect to the W boson mass, the starting value is $M_{W}/\omega =0.52$ in order to avoid the divergence which emerges at $M_{W}/\omega =0$ due to a factor of $\omega / M_{W}$ which multiplies all terms in $F_{2}$. Figure 12 proves that the probability of boson production for modes with $\lambda =0$ was high in the early universe, when the expansion factor was much bigger than the mass of the W bosons. In the Minkowski limit, where $\omega \rightarrow 0$, the probability vanishes as expected.

6 Total probability for $\lambda =\pm 1$ in the case of large expansion

In the limiting case of large expansion, the ratios between particle masses and expansion factor become very small and it is possible to write $m_e/\omega =M_W/\omega = 0$. In this limit, the amplitude given in Eq. (165) reduces to a more simple form:

$$\begin{aligned}{} & {} A_{i\rightarrow f}= -\frac{g}{\sqrt{2}}\frac{\pi \sqrt{p\,^{\prime }} }{(2\pi )^{3/2}}\delta ^{3}(\vec {p}+\vec {p^{\prime }}+\vec {P}) \left( \frac{1}{2}-\sigma \right) \sigma ^{\prime } \nonumber \\{} & {} \quad \times \int _{0}^{+\infty } dz z e^{-ipz}\mathcal {H}_{\frac{1}{2}}^{(2)}(p^{\prime }z)\mathcal {H}_{\frac{1}{2}}^{(2)}(P z)\,\xi _{\sigma }^{\dag }(\vec {p}\,)\nonumber \\{} & {} \quad \times \sigma ^{i}\eta _{\sigma ^{\prime }}(\vec {p^{\prime }}){\epsilon }^{*}_{i}(\vec {P},\lambda =\pm 1). \end{aligned}$$

(63)

Taking into account that the neutrino polarization can take only the value $\sigma =-\frac{1}{2}$, the final result for the amplitude reads as:

$$\begin{aligned} A_{i\rightarrow f}= & {} \frac{ig}{2\sqrt{2P}}\frac{ 1}{(2\pi )^{3/2}}\frac{\delta ^{3}(\vec {p}+\vec {p^{\prime }}+\vec {P})}{(p+p'+P)}\nonumber \\{} & {} \times sgn(\sigma ^{\prime })\,\xi _{-\frac{1}{2}}^{\dag }(\vec {p}\,)\sigma ^{i}\eta _{\sigma ^{\prime }}(\vec {p^{\prime }}){\epsilon }^{*}_{i}(\vec {P},\lambda =\pm 1). \end{aligned}$$

(64)

The probability per unit volume takes the form:

$$\begin{aligned} P(\lambda =\pm 1)= & {} \frac{1}{4}\sum _{\lambda \sigma '}\frac{g^2}{8(2\pi )^{3}}\frac{\delta ^{3}(\vec {p}+\vec {p^{\prime }}+\vec {P})}{P(p+p'+P)^2}\nonumber \\{} & {} \times |\xi _{-\frac{1}{2}}^{\dag }(\vec {p}\,)\sigma ^{i}\eta _{\sigma ^{\prime }}(\vec {p^{\prime }}){\epsilon }^{*}_{i}(\vec {P},\lambda =\pm 1)|^2. \end{aligned}$$

(65)

We set up both the neutrino and the positron to be emitted in the direction of the third axis, such that the angle between the momenta vectors is 0, i.e $\vec p=p\,\vec e_3,\,\vec p\,'=p'\,\vec e_3$. In this case the bispinor summation is reduced to a number since the helicity bispinors are reduced to a column matrix with elements $0,\,\pm 1$. The momentum of the $W^-$ boson is considered to also be on the third axis such that $\vec P=-P\,\vec e_3$. Since the momenta are on fixed directions, the helicity bispinors are very simple and no longer depend on the momenta. This will facilitate our computations of the momenta integrals:

$$\begin{aligned} \xi _{-\frac{1}{2}} (\vec {p}\,) = \begin{pmatrix} 0 \\ 1 \end{pmatrix}; \quad \eta _{\frac{1}{2}} (\vec {p}\,) = \begin{pmatrix} 0 \\ -1 \end{pmatrix}; \quad \eta _{-\frac{1}{2}} (\vec {p}\,) = \begin{pmatrix} 1 \\ 0 \end{pmatrix}.\nonumber \\ \end{aligned}$$

(66)

In this particular case the bispinor and polarization vector summation gives:

$$\begin{aligned}{} & {} \sum _{\lambda \sigma '}|\xi _{-\frac{1}{2}}^{\dag }(\vec {p}\,)\sigma ^{i}\eta _{\sigma ^{\prime }}(\vec {p^{\prime }}){\epsilon }^{*}_{i}(\vec {P},\lambda =\pm 1)|^2\nonumber \\{} & {} \quad =\sum _{\lambda \sigma '}\xi _{-\frac{1}{2}}^{\dag }(\vec {p}\,)\sigma ^{i} {\epsilon }^{*}_{i}(\vec {P},\lambda =\pm 1){\epsilon }^{*}_{j}(\vec {P},\lambda =\pm 1)\nonumber \\{} & {} \qquad \times \eta _{\sigma ^{\prime }}(\vec {p^{\prime }})\eta _{\sigma '}^{\dag }(\vec {p^{\prime }})\sigma ^{j}\xi _{-\frac{1}{2}}(\vec {p}\,), \end{aligned}$$

(67)

which reduces to unity if we use the above equations for spinors and the following relations:

$$\begin{aligned}{} & {} \sum _{\lambda }\epsilon _i^*(\vec {n}_{\mathcal {P}},\,\lambda )\epsilon _j(\vec {n}_{\mathcal {P}},\,\lambda )=\delta _{ij},\nonumber \\{} & {} \sum _{\sigma '}\eta _{\sigma ^{\prime }}(\vec {p^{\prime }})\eta _{\sigma '}^{\dag }(\vec {p^{\prime }})=I_{2\times 2}. \end{aligned}$$

(68)

The total probability for the process is obtained by computing the integral with respect to the momenta of the final particles:

$$\begin{aligned} P_{tot}=\int d^{3}p \int d^{3}P \int d^{3}p^{\prime }\,P(\lambda =\pm 1)D(p,p',P).\nonumber \\ \end{aligned}$$

(69)

where the function $D(p,p',P)=\frac{1}{p_0p'_0P_0}$ represents the density of states and helps one define the integration measure $\frac{d^3p}{p_0}$ for electrons, neutrinos and W bosons. In the Minkowski theory, the density of states for a system has units of $Volume^{-1}Energy^{-1}$. In the de Sitter case we come upon an entirely different situation, since the energy is no longer determined. In our case we assume that the density of states will contribute with a factor of $1/p_0,1/P_0$ for the positron and boson in the final state and a factor of $1/p'_0$ for the neutrino in the final state. We will consider the case when $P_0=\sqrt{M_W^2+P^2}$, while for the electron and neutrino $p_0=p,p'_0=p'$.

We denote the momenta integrals by I and solve the integral with regards to $p'$ by using the properties of the delta Dirac function:

$$\begin{aligned} I= & {} \int \frac{d^{3}p}{p} \int \frac{d^{3}P}{\sqrt{M_W^2+P^2}} \int \frac{d^{3}p^{\prime }}{p'}\, \frac{\delta ^{3}(\vec {p}+\vec {p^{\prime }}+\vec {P})}{(2\pi )^3P(p^{\prime } + p + P)^{2}}\nonumber \\= & {} \frac{1}{4(2\pi )^3}\int \frac{d^{3}P}{P\sqrt{M_W^2+P^2}} \int d^{3}p \frac{1}{p(p+P)^{3}}, \end{aligned}$$

(70)

keeping in mind that $|\vec p\,'+\vec p|=p'+p$, because the particles move in the same direction and the momenta are aligned with $\vec e_3$.

Next we use $\int _0^\infty dp\frac{p}{(p+P)^{3}}=\frac{1}{2P}$ and obtain:

$$\begin{aligned} I=\frac{\pi }{2(2\pi )^3}\int \frac{d^{3}P}{P^2\sqrt{M_W^2+P^2}} \end{aligned}$$

(71)

Because our remaining P integrals are divergent, we make use of dimensional regularization, a method used for studying the properties of propagators in the de Sitter geometry [29, 32]. We mention that the problem of Dirac and Proca propagators in the momentum and coordinate representations in the de Sitter geometry was analysed in [9, 29, 57, 58].

The P integral will be solved using dimensional regularization [64,65,66,67,68] such that the integral in D dimensions becomes:

$$\begin{aligned}{} & {} \int \frac{d^{3}P}{(2\pi )^3P^2\sqrt{M_W^2+P^2}} \rightarrow I(D)\nonumber \\{} & {} \quad =\int \frac{d^{D}P}{(2\pi )^{D}P^2\sqrt{M_W^2+P^2}}\nonumber \\{} & {} \quad =\frac{2\pi ^{D/2}}{(2\pi )^D\Gamma (D/2)}\int _0^\infty \frac{dP P^{D-1}}{P^2\sqrt{M_W^2+P^2}}, \end{aligned}$$

(72)

If we make the variable change $P=M_W\sqrt{y}$ the above integral changes into:

$$\begin{aligned} I(D) = \frac{\pi ^{D/2}M_W^{D-3}}{(2\pi )^{D}\Gamma (D/2)}\int _0^\infty \frac{dy \,y^{D/2-2}}{(1+y)^{1/2}}. \end{aligned}$$

(73)

This is just the integral of the Beta Euler function $B(\alpha ,\gamma )$, defined in Eq. (198) from Appendix C. Then for $\alpha =D/2-1,\,\beta =(3-D)/2$ the result of the integral is:

$$\begin{aligned} I(D) = \frac{2M_W^{D-3}}{(4\pi )^{D/2}}\frac{\Gamma \left( \frac{D}{2}-1\right) \Gamma \left( \frac{3-D}{2}\right) }{\Gamma \left( \frac{1}{2}\right) \Gamma \left( \frac{D}{2}\right) }. \end{aligned}$$

(74)

The above result contains ultraviolet divergences for $D\ge 3$ and infrared divergences for $D\le 0$. These divergences are contained in the poles of the Gamma Euler functions. For canceling the divergence in the total probability we will use the method of minimal substraction proposed in [68, 69]. We are interested in the divergence in $D=3$ contained in the Gamma function and we use $z\Gamma (z)=\Gamma (1+z)$ for rewriting the divergent function:

$$\begin{aligned} \Gamma \bigg ( \frac{3-D}{2} \bigg ) = \frac{2 \Gamma \big ( \frac{5-D}{2} \big )}{(3-D)}. \end{aligned}$$

(75)

The result for I(D) can be written in the form:

$$\begin{aligned} I(D) = \frac{2 M_W^{D-3} \Gamma \big (\frac{D}{2} -1\big ) \Gamma \big (\frac{5-D}{2} \big )}{\sqrt{\pi }\Gamma \big (\frac{D}{2} \big ) (4\pi )^{D/2} (3-D)}. \end{aligned}$$

(76)

The above I(D) has a pole in $D=3$ with residue:

$$\begin{aligned} R=\lim _{D\rightarrow 3}(D-3)I(D)=\frac{1}{2\pi ^{2}}. \end{aligned}$$

(77)

Then we choose a counter-term with a mass parameter $\mu$ of the form $\frac{\mu ^{s}R}{3-D}$, where s is taken such that this term has the same dimension as I(D).

Thus one can define the renormalized integral:

$$\begin{aligned} I(D)_{ren}= & {} I(D) - \frac{ \mu ^{D-3}}{2\pi ^2 (3-D) }\nonumber \\= & {} - \frac{1}{ (D-3)} \Bigg [\frac{2M_W^{D-3}\Gamma \big ( \frac{5-D}{2} \big )\Gamma \big ( \frac{D}{2}-1 \big ) }{\sqrt{\pi }(4\pi )^{\frac{D}{2}}\Gamma \big ( \frac{D}{2} \big )} {-} \frac{\mu ^{D{-}3}}{2\pi ^2} \Bigg ].\nonumber \\ \end{aligned}$$

(78)

The parenthesis from the above equation can be expanded around $D=3$

$$\begin{aligned}{} & {} \frac{2M_W^{D-3}\Gamma \big ( \frac{5-D}{2} \big )\Gamma \big ( \frac{D}{2}-1 \big ) }{\sqrt{\pi }(4\pi )^{\frac{D}{2}}\Gamma \big ( \frac{D}{2}\big )} - \frac{\mu ^{D-3}}{2\pi ^2}\nonumber \\{} & {} \quad =\frac{D-3}{4\pi ^2}\left[ -\ln \left( \frac{4\pi \mu ^2}{M_W^2}\right) -\psi (3/2)+\psi (1/2)\right] \nonumber \\{} & {} \quad \quad +\mathcal {O}((D-3)^2)\nonumber \\{} & {} \quad =\frac{D-3}{4\pi ^2}\left[ -2+\gamma -\ln \left( \frac{4\pi \mu ^2}{M_W^2}\right) \right] +\mathcal {O}((D-3)^2)\nonumber \\ \end{aligned}$$

(79)

The divergent term $D-3$ is canceled by the expansion around $D=3$.

The final result for the renormalized integral will be finite and we obtain:

$$\begin{aligned} I(D)_{ren} = \frac{1}{4\pi ^2}\left[ 2-\gamma +\ln \left( \frac{4\pi \mu ^2}{M_W^2}\right) \right] , \end{aligned}$$

(80)

Collecting our prior results, we can write down the total probability in the case of large expansion:

$$\begin{aligned} P_{tot}= & {} \frac{g^2}{4\cdot 64\pi }\left[ 2-\gamma +\ln \left( \frac{4\pi \mu ^2}{M_W^2}\right) \right] \nonumber \\= & {} \frac{G_F\,M_W^2}{32\sqrt{2}\pi }\left[ 2-\gamma +\ln \left( \frac{4\pi \mu ^2}{M_W^2}\right) \right] , \end{aligned}$$

(81)

where the second equality is obtained by expressing g in terms of Fermi constant $G_F$.

In this section we have shown that the total probabilities can be renormalized to obtain a finite result, by applying dimensional regularization and the substraction method where we add a counter-term that cancels all the divergences. We also must point out that the result obtained in Eq. (81) for the total probability represents the limit of large expansion that corresponds to the conditions of the early universe, where the W bosons could be produced in such perturbative processes.

7 The transition rate for $\lambda =\pm 1$

The probability of the particle production process suggests that this type of boson emission was highly likely for $\omega \gg M_{W}$, however one must find measurable quantities to validate such a process. This leads to the problem of computing the transition rate, i.e. the probability per unit time.

In flat space-time, energy–momentum conservation allows us to find a transition rate which depends on the volume V and interaction time T. But energy and momentum are not simultaneously conserved in de Sitter space-time, and the amplitude is also time-dependant.

We can see this better when writing the amplitude as such:

$$\begin{aligned}{} & {} A_{i\rightarrow f}= -\frac{ig}{2\sqrt{2}}\frac{ \sqrt{p^{\prime }} e^{-\pi k/2}}{(2\pi )^{3/2}}\delta ^{3}(\vec {p}+\vec {p^{\prime }}+\vec {P}) \left( \frac{1}{2}-\sigma \right) \sigma ^{\prime } \nonumber \\{} & {} \quad \times \int _{0}^{+\infty } dz z e^{-ipz}\mathcal {H}_{\nu _{-}}^{(2)}(p^{\prime }z)\mathcal {K}_{-iK}(iP z)\nonumber \\{} & {} \quad \times \xi _{\sigma }^{\dag } (\vec {p})\sigma ^{i}\eta _{\sigma ^{\prime }}(\vec {p^{\prime }}){\epsilon }^{*}_{i}(\vec {P},\lambda =\pm 1). \end{aligned}$$

(82)

The previous expression for amplitude can be rewritten as

$$\begin{aligned} A_{i\rightarrow f} = M_{i\rightarrow f}I_{i\rightarrow f}\delta ^{3}(\vec {p_{f}}-\vec {p_{i}}), \end{aligned}$$

(83)

where $I_{i\rightarrow f}$ represents the time-dependent integral:

$$\begin{aligned} I_{i\rightarrow f} = e^{-\pi k/2}\int _{0}^{\infty } K_{i\rightarrow f} dz, \end{aligned}$$

(84)

The integrand in (84) is given by:

$$\begin{aligned} K_{i\rightarrow f} = z\,e^{-ipz} \mathcal {H}_{\nu _{-}}^{(2)}(p^{\prime }z)\mathcal {K}_{-iK}(P z), \end{aligned}$$

(85)

while

$$\begin{aligned} M_{i\rightarrow f}= & {} -\frac{ig}{2\sqrt{2}}\frac{\pi \sqrt{p^{\prime }}}{(2\pi )^{3/2}} \left( \frac{1}{2} -\sigma \right) \sigma ^{\prime }\nonumber \\{} & {} \times \xi _{\sigma }^{\dag }(\vec {p})\sigma ^{i}\eta _{\sigma ^{\prime }}(\vec {p^{\prime }}){\epsilon }^{*}_{i}(\vec {P},\lambda = \pm 1). \end{aligned}$$

(86)

The transition rate with respect to the conformal time is defined by [70]:

$$\begin{aligned} R_{i\rightarrow f}=\lim _{t_c\rightarrow 0}\frac{1}{2V}\frac{d}{dt_c}|A_{if}|^2=\lim _{t\rightarrow \infty }\frac{e^{\omega t}}{2V}\frac{d}{dt}| A_{if}|^2. \end{aligned}$$

(87)

This expression can be brought to the form:

$$\begin{aligned} R_{i\rightarrow f}= & {} \frac{1}{(2\pi )^{3}}\delta ^{3}(\vec {p_{f}}-\vec {p_{i}})|M_{i\rightarrow f}|^{2}|I_{i\rightarrow f}|\nonumber \\{} & {} \times \lim _{t\rightarrow \infty }| e^{\omega t}K_{i\rightarrow f}|. \end{aligned}$$

(88)

In our case we must take into account the summations after $\sigma ',\lambda$ since $\sigma =-1/2$. We also specify that the limit in Eq. (88) will be taken up to a sufficiently large time after the interaction, denoted by $t_{\infty }$.

With these things in mind, the formula of the transition rate in our case is:

$$\begin{aligned} R_{i\rightarrow f}= & {} \frac{1}{4}\sum _{\sigma '\lambda }\frac{1}{(2\pi )^{3}}\delta ^{3}(\vec {p_{f}}-\vec {p_{i}})|M_{i\rightarrow f}|^{2}|I_{i\rightarrow f} | \nonumber \\{} & {} \times \lim _{t\rightarrow t_{\infty }}|e^{\omega t}K_{i\rightarrow f}|. \end{aligned}$$

(89)

Fig. 13

The absolute value of $R_{1}$ for $\frac{m_e}{\omega }=0.1$ on the left and $\frac{M_{W}}{\omega }=0.6$ on the right, and momenta values $p' = 0.2, p = 0.1, P = 0.4$ for the straight line and $p' = 0.25, p = 0.1, P = 0.6$ for the dotted line

Because we are working in the limit $t\rightarrow t_{\infty }$, the Hankel functions may be approximated using the formula for small arguments [62]:

$$\begin{aligned} \mathcal {H}_{\nu }^{(2)}(z) \approx i\left( \frac{2}{z}\right) ^{\nu }\frac{\Gamma (\nu )}{\pi }, \end{aligned}$$

(90)

which works for $z\rightarrow 0$.

Thus the first Hankel function becomes:

$$\begin{aligned} \mathcal {H}_{\frac{1}{2}-ik}^{(2)}\left( \frac{p^{\prime }}{\omega }e^{-\omega t}\right) \simeq i \left( \frac{2}{\frac{p^{\prime }}{\omega }e^{-\omega t}}\right) ^{\frac{1}{2}-ik}\frac{\Gamma (\frac{1}{2}-ik)}{\pi }. \end{aligned}$$

(91)

The transition rate is relevant when $\omega \gg M_{W}$ and $\omega \gg m_{e}$, meaning that we can further approximate the index of the modified Bessel function $\mathcal {K}_{-iK}$:

$$\begin{aligned} -iK = -i\sqrt{\left( \frac{M_{W}}{\omega }\right) ^{2}-\frac{1}{4}} = \frac{1}{2}\sqrt{1 - 4\left( \frac{M_{W}}{\omega }\right) ^{2}}\approx \frac{1}{2}.\nonumber \\ \end{aligned}$$

(92)

Consequently, the behaviour of the modified Bessel function for small arguments is:

$$\begin{aligned} \mathcal {K}_{-iK} \left( \frac{P}{\omega }e^{-\omega t}\right) \simeq \frac{\Gamma (1/2)}{\sqrt{2i\frac{P}{\omega }e^{-\omega t}}}. \end{aligned}$$

(93)

This leads to the limit:

$$\begin{aligned} \lim _{t\rightarrow t_{\infty } } |e^{\omega t}K_{i\rightarrow f}|= & {} \lim _{t\rightarrow t_{\infty } }\bigg |i\frac{e^{-\omega t}}{\omega }e^{-ip\frac{e^{-\omega t}}{\omega }} \left( \frac{2}{\frac{p^{\prime }}{\omega }e^{-\omega t}}\right) ^{\frac{1}{2}-ik}\nonumber \\{} & {} \times \frac{\Gamma (\frac{1}{2}-ik)}{\pi }\frac{\Gamma (1/2)}{\sqrt{2i\frac{P}{\omega }e^{-\omega t}}}\bigg |\nonumber \\= & {} \frac{1}{\sqrt{Pp^{\prime }\cosh (\pi k)}}, \end{aligned}$$

(94)

where we have used [62]:

$$\begin{aligned} \Gamma \left( \frac{1}{2}-ik\right) \Gamma \left( \frac{1}{2}+ik\right) = \frac{\pi }{\cosh (\pi k)}. \end{aligned}$$

(95)

By substituting the limit of the temporal integral in the transition rate formula (88) we get:

$$\begin{aligned} R_{i\rightarrow f}= & {} \sum _{\sigma '\lambda } \frac{g^2\pi ^2pp'}{32(2\pi )^{3}}\delta ^{3}(\vec {p}+\vec {p^{\prime }} + \vec {P})\nonumber \\{} & {} \times |\xi _{-1/2}^{\dag }(\vec {p})\sigma ^{i}\eta _{\sigma ^{\prime }}(\vec {p^{\prime }}){\epsilon }^{*}_{i}(\vec {P},\lambda = \pm 1)|^{2}\nonumber \\{} & {} \times \frac{|I_{i\rightarrow f}| }{\sqrt{Pp^{\prime }\cosh (\pi k)}}, \end{aligned}$$

(96)

where $|I_{i\rightarrow f}| = \sqrt{I_{i\rightarrow f}I_{i\rightarrow f}^{*}}$.

The explicit form of $I_{i\rightarrow f}$ is:

$$\begin{aligned} I_{i\rightarrow f}=\frac{e^{-i\pi /4}e^{-\pi k/2}}{i\sqrt{p}\cosh (\pi k)}(T_1-T_2-T_3+T_4), \end{aligned}$$

(97)

where $T_1,T_2,T_3,T_4$ are defined in equations (26).

The final result for the transition rate in the general case is:

$$\begin{aligned} R_{i\rightarrow f}= & {} \frac{g^2\pi ^2\sqrt{pp'}}{32(2\pi )^{3}}\delta ^{3}(\vec {p}+\vec {p^{\prime }} + \vec {P})\frac{e^{-\pi k/2}}{\cosh (\pi k)}\nonumber \\{} & {} \times \sqrt{\frac{(T_1-T_2-T_3+T_4)(T_1-T_2-T_3+T_4)^* }{P\cosh (\pi k)}}.\nonumber \\ \end{aligned}$$

(98)

For the sake of examining the behaviour of the transition rate it is useful to perform a graphical analysis of the terms that depend on $\frac{m}{\omega }$ and $\frac{M_{W}}{\omega }$:

$$\begin{aligned} R_{1}= & {} \frac{\sqrt{pp'}e^{-\pi k/2}}{\cosh (\pi k)}\nonumber \\{} & {} \times \sqrt{\frac{(T_1-T_2-T_3+T_4)(T_1-T_2-T_3+T_4)^* }{P\cosh (\pi k)}}.\nonumber \\ \end{aligned}$$

(99)

The transition rate variation with respect to $\frac{m_e}{\omega },\frac{M_{W}}{\omega }$, presented in the above figures, shows that the spontaneous vacuum generation of W bosons and fermions is a process possible only when the expansion parameter is far larger than the particle masses, which corresponds to the early universe period. In the Minkowski limit, which corresponds to infinite values of parameters k, K, the rate vanishes. It is also worth mentioning that massive bosons can exist as stable particles only as long as the background energy is larger than their rest energy. When this condition is no longer valid, the massive bosons decay into more stable particles with smaller masses (Fig. 13).

7.1 Total rate in the limit of large expansion

In this section we will discuss the problem of the total transition rate in the limit of large expansion, where the functions that define the amplitude and transition rate from the previous section become simpler and depend only on the momenta of the emitted particles.

The first task is to establish the expression of the transition rate in the limit $\frac{m_e}{\omega }=\frac{M_W}{\omega }=0$. In order to do this we first need to write the amplitude in this limit:

$$\begin{aligned} A_{i\rightarrow f}= & {} -\frac{ig}{2\sqrt{2}}\frac{ \sqrt{p^{\prime }} }{(2\pi )^{3/2}}\delta ^{3}(\vec {p}+\vec {p^{\prime }}+\vec {P}) \left( \frac{1}{2}-\sigma \right) \sigma ^{\prime } \nonumber \\{} & {} \times \int _{0}^{+\infty } dz z e^{-ipz}\mathcal {H}_{1/2}^{(2)}(p^{\prime }z)\mathcal {K}_{1/2}(iP z)\nonumber \\{} & {} \times \xi _{\sigma }^{\dag }(\vec {p}\,)\sigma ^{i}\eta _{\sigma ^{\prime }}(\vec {p^{\prime }}){\epsilon }^{*}_{i}(\vec {P},\lambda =\pm 1)\nonumber \\= & {} M_{i\rightarrow f}I_{i\rightarrow f}\delta ^{3}(\vec {p_{f}}-\vec {p_{i}}), \end{aligned}$$

(100)

where $M_{i\rightarrow f}$ is defined in Eq. (86).

The temporal integral is solvable for the Bessel and Hankel functions of index 1/2:

$$\begin{aligned} I_{i\rightarrow f}= & {} \lim _{\varepsilon \rightarrow 0}\frac{i}{\sqrt{ip'P}}\int _{0}^{+\infty } dz\,e^{-i(p+p'+P)z-\varepsilon z}\nonumber \\= & {} \frac{1}{\sqrt{ip'P}(p+p'+P)}. \end{aligned}$$

(101)

The integrand is of the form $K_{i\rightarrow f}=e^{-i(p+p'+P)z}$, while the limit that needs to be done for computing the rate reads:

$$\begin{aligned} \lim _{t\rightarrow t_{\infty } } |e^{\omega t}K_{i\rightarrow f}|= & {} \lim _{t\rightarrow t_{\infty } }\bigg |\frac{1}{\sqrt{ip'P}}e^{-i(p+p'+P)\frac{e^{-\omega t}}{\omega }}\bigg |\nonumber \\= & {} \frac{1}{\sqrt{p'P}}, \end{aligned}$$

(102)

which is precisely the limit obtained directly from Eq. (94) for $k=0$.

Then the rate in the limit $\frac{m_e}{\omega }=\frac{M_W}{\omega }=0$ can be written in final form as:

$$\begin{aligned} R=\frac{g^2}{8(2\pi )^{6}}\delta ^{3}(\vec {p}+\vec {p^{\prime }}+\vec {P})\frac{1}{P(p+p'+P)}, \end{aligned}$$

(103)

where the results of the $\sigma ',\lambda$ summations were included.

The total rate of transition can be obtained by integrating over all possible values of the momenta:

$$\begin{aligned} R_{vac\rightarrow W^-\nu e^+}=\int d^{3}p\,d^{3}p^{\prime }\,d^{3}P\, D(p,p',P)R_{i\rightarrow f},\nonumber \\ \end{aligned}$$

(104)

where $D(p,p',P)=\frac{1}{p_0p'_0P_0}$ was defined as the density of states for electrons, neutrinos and W bosons.

We assume that the particles are emitted in the same direction as in the case of the total probability, with the momenta of the neutrino and positron being oriented in the direction of the positive third axis, while the boson momentum is oriented in the direction of the negative third axis.

First we present the situation when the momenta of the W boson is large i.e. $p'_0=\sqrt{p'^2+m^2},\, p_0=p,\, P_0=P$ and solve the integrals:

$$\begin{aligned} I= & {} \int \frac{d^{3}p}{p} \int \frac{d^{3}P}{P} \int \frac{d^{3}p^{\prime }}{\sqrt{p'^2+m^2}}\nonumber \\{} & {} \times \frac{\delta ^{3}(\vec {p}+\vec {p^{\prime }} +\vec {P})}{(2\pi )^3P(p+p^{\prime }+P)}\nonumber \\= & {} 2\pi \int \frac{d^{3}p^{\prime }}{\sqrt{p'^2+m^2}} \int _0^\infty \frac{dP}{(2\pi )^3(P+p')^2}\nonumber \\= & {} \frac{1}{(2\pi )^2}\int \frac{d^{3}p^{\prime }}{p'\sqrt{p'^2+m^2}}. \end{aligned}$$

(105)

The above result is obtained if we solve first the integral over P first and afterwards solve the integral over p.

The $p'$ integral is divergent, therefore we have to make use of dimensional regularization [64,65,66,67,68] in order to solve it. The integral in D dimensions becomes:

$$\begin{aligned}{} & {} \int \frac{d^{3}p^{\prime }}{(2\pi )^3p'\sqrt{p'^2+m^2}} \rightarrow I(D)=\int \frac{d^{D}p'}{(2\pi )^{D}p'\sqrt{p'^2+m^2}}\nonumber \\{} & {} \quad =\frac{2\pi ^{D/2}}{(2\pi )^{D}\Gamma (D/2)}\int _0^\infty \frac{d^{D}p'\,p'^{D-1}}{(2\pi )^{D}p'\sqrt{p'^2+m^2}}. \end{aligned}$$

(106)

By performing the change of variables $p'=m\sqrt{y}$, one obtains:

$$\begin{aligned} I(D) = \frac{2\pi ^{D/2}m^{D-2}}{2(2\pi )^{D}\Gamma (D/2)}\int _0^\infty \frac{dy \,y^{D/2-3/2}}{(1+y)^{1/2}}. \end{aligned}$$

(107)

This is just the integral of the Beta Euler function defined for $\alpha =\frac{D-1}{2},\,\beta =1-\frac{D}{2}$:

$$\begin{aligned} I(D) = \frac{\pi ^{D/2}m^{D-2}}{(2\pi )^{D}}\frac{\Gamma \left( 1-\frac{D}{2}\right) \Gamma \left( \frac{D-1}{2}\right) }{\Gamma \left( \frac{1}{2}\right) \Gamma \left( \frac{D}{2}\right) }. \end{aligned}$$

(108)

The above result contains ultraviolet divergences for $D\ge 2$ and infrared divergences for $D\le 0$. These divergences are contained in the poles of the Gamma Euler functions. The poles of the Gamma functions can be removed by introducing an arbitrary mass parameter denoted by $\mu$ and an arbitrary coupling dimensionless constant denoted by $\rho =\lambda \mu ^{D-3}=\lambda \mu ^{-\varepsilon }$, such that the regularized result is $I(D)_r =-\lambda I(D)$. Then the final result for integral (107) as a function of $\gamma$ and $\varepsilon$ for $D=3-\varepsilon$ is:

$$\begin{aligned} I(D)_r =\frac{-\rho m}{\sqrt{\pi }(4\pi )^{3/2}}\left( \frac{4\pi \mu ^{2}}{m^{2}}\right) ^{\epsilon /2}\frac{\Gamma \left( 1-\frac{\epsilon }{2}\right) \Gamma \left( \frac{\epsilon -1}{2}\right) }{\Gamma \left( \frac{3-\epsilon }{2}\right) }.\nonumber \\ \end{aligned}$$

(109)

The series expansions of the Gamma Euler functions and power function in terms of $\epsilon$ are:

$$\begin{aligned}{} & {} \frac{\Gamma (1-\frac{\epsilon }{2})\Gamma (\frac{\epsilon -1}{2})}{\Gamma \left( \frac{3-\epsilon }{2}\right) }\nonumber \\{} & {} \quad =-4-2\epsilon [\gamma +\psi (3/2)+\psi (-1/2)]+\mathcal {O}(\epsilon ^2),\nonumber \\{} & {} \quad \left( \frac{4\pi \mu ^{2}}{m^{2}}\right) ^{\epsilon /2}=1+\frac{\epsilon }{2}\ln \left( \frac{4\pi \mu ^{2}}{m^{2}}\right) +\mathcal {O}(\epsilon ^2). \end{aligned}$$

(110)

where $\psi (a)$ are the Digamma Euler functions defined in Appendix.

Finally we obtain for the regularized integral:

$$\begin{aligned} I(D)_r= & {} \frac{-\rho m}{(8\pi ^2)}\biggl \{ -4-2\epsilon \left[ \gamma +\psi (3/2)+\psi (-1/2)\right. \nonumber \\{} & {} \left. + \ln \left( \frac{4\pi \mu ^{2}}{m^{2}}\right) \right] + \mathcal {O}(\epsilon ^{2}) \bigg \}. \end{aligned}$$

(111)

In the limit where $\epsilon =0$, the regularized integral is convergent:

$$\begin{aligned}{} & {} \lim _{\epsilon \rightarrow 0}I(D)_r = \frac{\rho m}{2\pi ^2}. \end{aligned}$$

(112)

The final result for rate in the ultra-relativistic case (when $P\gg M_W$) is:

$$\begin{aligned}{} & {} R_{vac\rightarrow W^-\nu e^+}=\frac{g^2\rho m}{8\pi (2\pi )^3}=\frac{\rho G_F mM_W^2}{8\pi ^4 \sqrt{2} }. \end{aligned}$$

(113)

Let us now consider the case when $P_0=\sqrt{P^2+M_W^2},\, p_0=p$ for computing the transition rate. This is a more realistic case since the W bosons have a mass much larger than the electron.

We consider the situation when the particles are on the same direction i.e. the third axis, $\vec p=p \vec e_3,\,\,\vec p\,'=p' \vec e_3$ and $\vec P=-P\vec e_3$. We perform the integral over $p'$:

$$\begin{aligned} I= & {} \int \frac{d^{3}p}{p} \int \frac{d^{3}P}{\sqrt{P^2+M_W^2}} \int \frac{d^{3}p^{\prime }}{p'} \frac{\delta ^{3}(\vec {p}+\vec {p^{\prime }} +\vec {P})}{(2\pi )^3P(p+p^{\prime }+P)}\nonumber \\= & {} \int \frac{d^{3}p}{p} \int \frac{d^{3}P }{2(2\pi )^3P\sqrt{P^2+M_W^2}(p+P)^2} \end{aligned}$$

(114)

We choose the situation where the momenta of the W boson and neutrino are close in value, such that we can approximate $(p+P)^2\simeq 2(p^2+P^2)$ and then expand the radical to $\sqrt{P^2+M_W^2}\simeq P+\frac{M_W^2}{2P}$.

With this supposition the P integrals can be solved by using dimensional regularization and become:

$$\begin{aligned}{} & {} \int d^{3}P\frac{1}{ P\left( P+\frac{M_W^2}{2P}\right) \left( p^2+P^2\right) }\nonumber \\{} & {} \quad =4\pi \int _0^\infty \frac{dP\, P}{ \left( P+\frac{M_W^2}{2P}\right) \left( p^2+P^2\right) }=\frac{2\sqrt{2}\pi ^2}{M_W+\sqrt{2}p}\nonumber \\ \end{aligned}$$

(115)

We arrive at the final p integral, where we use the dimensional regularization and write the integral in D dimensions:

$$\begin{aligned}{} & {} \int \frac{d^{3}p}{(2\pi )^3p(M_W+\sqrt{2}p)}\rightarrow \int \frac{d^{D}p}{(2\pi )^Dp(M_W+\sqrt{2}p)}\nonumber \\{} & {} \quad =\frac{2\pi ^{D/2}}{(2\pi )^D\Gamma (D/2)}\int _0^{\infty } \frac{dp\,p^{D-1}}{p(M_W+\sqrt{2}p)}. \end{aligned}$$

(116)

The substitution $p=\frac{M_W\,y}{\sqrt{2}}$ allows one to bring the integral in the form of a Beta Euler function

$$\begin{aligned} I(D)= & {} \frac{2\pi ^{D/2}(M_W)^{D-2}\sqrt{2}}{(\sqrt{2})^D(2\pi )^D\Gamma (D/2)}\int _0^{\infty }dy \frac{y^{D-2}}{1+y}\nonumber \\= & {} \frac{2\pi ^{D/2}(M_W)^{D-2}\sqrt{2}}{(\sqrt{2})^D(2\pi )^D\Gamma (D/2)}\Gamma (2-D)\Gamma (D-1).\nonumber \\ \end{aligned}$$

(117)

The result is divergent for $D=3$ and we use the method of minimal substraction for obtaining a finite result. From the recurrence realtion of Gamma functions $z\Gamma (z)=\Gamma (1+z)$ we obtain:

$$\begin{aligned} \Gamma (2-D)=\frac{\Gamma (4-D)}{(2-D)(3-D)}, \end{aligned}$$

(118)

such that our result for I(D) becomes:

$$\begin{aligned} I(D)=\frac{2\pi ^{D/2}(M_W)^{D-2}\sqrt{2}}{(\sqrt{2})^D(2\pi )^D\Gamma (D/2)}\frac{\Gamma (D-1)\Gamma (4-D)}{(2-D)(3-D)}.\nonumber \\ \end{aligned}$$

(119)

Further one can compute the residue of I(D) in $D=3$

$$\begin{aligned} R=\lim _{D\rightarrow 3}(3-D)I(D)=\frac{M_W}{4\pi ^2}, \end{aligned}$$

(120)

and choose a counter-term with a mass parameter $\mu$ of the form $\frac{\mu ^{s}R}{3-D}$, where s is taken such that this term has the same dimension as I(D).

The renormalized integral reads:

$$\begin{aligned} I(D)_{ren}= & {} I(D) - \frac{ \mu ^{D-3}}{4\pi ^2 (3-D) }\nonumber \\= & {} - \frac{1}{ (D-3)} \Bigg [\frac{2\pi ^{D/2}(M_W)^{D-2}\sqrt{2}}{(\sqrt{2})^D(2\pi )^D\Gamma (D/2)}\nonumber \\{} & {} \times \frac{\Gamma (D-1)\Gamma (4-D)}{(2-D)(3-D)} + \frac{\mu ^{D-3}M_W}{4\pi ^2} \Bigg ]. \end{aligned}$$

(121)

The parenthesis can be expanded around $D=3$:

$$\begin{aligned} I(D)_{ren}= & {} \frac{M_W(D-3)}{8\pi ^2}\left[ \psi (3/2)+\ln \left( \frac{4\pi \mu ^2}{M_W^2}\right) \right] \nonumber \\{} & {} +\mathcal {O}((D-3)^2) \end{aligned}$$

(122)

The final result for the renormalized integral is:

$$\begin{aligned} I(D)_r=\frac{M_W}{8\pi ^2}\left[ \psi (3/2)+\ln \left( \frac{4\pi \mu ^2}{M_W^2}\right) \right] . \end{aligned}$$

(123)

The result for the transition rate is then finite:

$$\begin{aligned} R_{vac\rightarrow W^-\nu e^+}= & {} \frac{g^2 M_W}{128\sqrt{2}(2\pi )^3 }\left[ \psi (3/2)+\ln \left( \frac{4\pi \mu ^2}{M_W^2}\right) \right] \nonumber \\= & {} \frac{ G_F\,M_W^3}{16\sqrt{2}(2\pi )^3 }\left[ \psi (3/2)+\ln \left( \frac{4\pi \mu ^2}{M_W^2}\right) \right] ,\nonumber \\ \end{aligned}$$

(124)

where the last equality is obtained when we introduce the Fermi constant $G_F$.

The density number of W bosons must be proportional with the ratio between the rate of production from vacuum $R_{vac\rightarrow W^-\nu e^+}$ and the decay rate of the W boson $R_{des}$, multiplied by a factor of 1/3 since we have three particles in the final state. For these reasons an estimation of the density number of W bosons per cubic meter using Eq. (124) for the total rate gives:

$$\begin{aligned} n_{W}\sim \frac{R_{vac\rightarrow W^-\nu e^+}}{3R_{des}}. \end{aligned}$$

(125)

The above quantity represents the density number of W bosons produced in a pure gravitational field by the large space-time expansion and must be completed with the density number obtained via other processes that generate massive W bosons. For an accurate estimation of this number one needs to also compute the total rate of W boson decay in de Sitter geometry, since the influence of space-time expansion should also affect the well known rate of W boson decay from the Minkowski theory $R_{des}=2.085 GeV$.

For a complete picture of boson densities due to perturbative production it will be necessary to analyse all first order processes which give contribution to the density number of W bosons, including those processes in which massive bosons are emitted by fermions.

We must also mention results obtained by other ways [43], where the authors consider non-perturbative methods for studying the production of massive bosons in gravitational fields. In our opinion, both perturbative and non-perturbative methods should be taken into account when the problem of particle production in the early universe is approached. An analysis of the both perturbative and non-perturbative methods for particle production in gravitational fields can be found in [44, 45].

Our analysis presents a microscopic process which is produced by a large scale event, namely space-time expansion, which could play a similar role to the thermal bath. The two effects must be taken into account when we analyse the mechanisms that generate matter and anti-matter in the early universe.

At the end of this section we discuss the results obtained in the present paper in relation with the results obtained in [21]. First one can observe that the massive $Z, W^{\pm }$ bosons could be generated in perturbative processes due to the large expansion of the early universe in processes that are forbidden in flat electro-weak field theory. However, differences related to the densities number of massive neutral and massive charged bosons could appear. To analyse the differences one would need to compute the decay rates for both types of bosons in the de Sitter geometry and then obtain density numbers. This means computing all the decay rates for massive bosons into fermions-antifermions in de Sitter space-time, and then exploring the limit of large expansion. Both studies are also important for understanding the standard model dynamics in the early universe, and could represent a theoretical model which explains the generation of massive bosons from vacuum due to the strong gravitational fields of the early universe. Another important result is related to the fact that the total rates are obtained by using dimensional regularization together with the minimal substraction method in both cases. A result obtained in the present study, which was not obtained in [21], is related to the total rate when the momenta of the W boson is not ultra-relativistic, that is when $P_0=\sqrt{P^2+M_W^2}$. This can be found in Eq. (124).

8 Concluding remarks

The present paper focuses on the study of the interaction between charged $W^{\pm }$ bosons and fermions in the de Sitter geometry by using perturbative methods. The equations of interaction between massive charged vector fields and fermions are established and their solutions are written with the help of the usual method of the Green’s functions. With this approach one can introduce the IN/OUT fields and develop the formalism of reduction for the Proca field in the de Sitter geometry. The definition of the transition amplitudes in the first order of perturbation theory is also established. This is a powerful tool for the study of the phenomenon of particle production in the early stages of the universe.

As an application of our formalism, we have studied the problem of generating the triplet $W^{-}$ boson, positron and neutrino from the de Sitter vacuum. We established the transition amplitudes for both the transversal and longitudinal modes and defined the transition probabilities per unit volume. From our analytical and graphical results we prove that that the phenomenon of massive boson production is present during the inflation period. From our general results one recovers the Minkowski limit, where the amplitude and probability of this process vanish. We also study the interesting limiting case where $m_{e}/\omega =M_{W}/\omega =0$, which corresponds to large values of the expansion parameter $\omega$. Under these limiting conditions we obtain the total probability and rate of transition by using dimensional regularization and the substraction method for computing the momenta integrals. We conclude that the process of spontaneous particle emission from vacuum is possible only for a large expansion factor, which corresponds to the early universe period.

For further analysis, the study of all possible processes which generate charged $W^{\pm }$ bosons would be of interest, since all possible transitions in the first order of perturbation theory have non-vanishing amplitudes for the large expansion conditions of the early universe. Our results aim to open the way for the study of electro-weak interactions in curved backgrounds and for applying perturbative methods to the understanding of mechanisms which generate massive bosons in the early universe.

Appendices

Appendix A: Reduction formalism for the Proca field: Definition of transition amplitudes

We apply the same method of reduction as in the flat space-time field theory [59]. The reduction of the Proca field from the OUT state can be constructed by starting with the amplitude that corresponds to a transition of a Proca particle between IN/OUT states. We also denote the other particles by $\alpha ,\beta$ in the matrix element:

$$\begin{aligned}{} & {} \langle \,out \,\beta \, 1 (\vec {p^{\prime }},\lambda ^{\prime }) \,|\, in\,\alpha \, 1 (\vec {p},\lambda )\,\rangle \nonumber \\{} & {} \quad = \langle \, out \, \beta \,|\,a_{out}(\vec {p^{\prime }},\lambda ^{\prime })\,|\,in\, \alpha \,1(\vec {p},\lambda )\, \rangle \end{aligned}$$

(126)

By using the properties of the creation and annihilation operators $a^{\dag }$ and a:

$$\begin{aligned} \left[ a(\vec {p},\lambda ),a^{\dag }(\vec {p^{\prime }},\lambda ^{\prime })\right] = \delta _{\lambda \lambda ^{\prime }}\delta ^{3}(\vec {p}-\vec {p^{\prime }}), \end{aligned}$$

(127)

we can rewrite the amplitude in the following way:

$$\begin{aligned}{} & {} \langle \, out \, \beta \,|\, (a_{out}(\vec {p^{\prime }},\lambda ^{\prime }) \,|\, in \, \alpha \,1 (\vec {p},\lambda )\, \rangle \nonumber \\ {}{} & {} \quad =\langle \, out \, \beta \,|\, [a_{out}(\vec {p^{\prime }},\lambda ^{\prime })- a_{in}(\vec {p^{\prime }},\lambda ^{\prime })] \,|\, in \,\alpha \,1(\vec {p},\lambda )\,\rangle \nonumber \\ {}{} & {} \qquad + \langle \, out \, \beta \,|\, a_{in}(\vec {p^{\prime }},\lambda ^{\prime })a_{in}^{\dag }(\vec {p},\lambda )\,|\, in \, \alpha \, \rangle . \end{aligned}$$

(128)

The field operator for the Proca field can be expanded in terms of the fundamental solutions for the Proca equation in the momentum-helicity basis [8]:

$$\begin{aligned} A_{\beta } (x) = \sum _{\lambda } \int d^{3}p \,[ a(\vec {p},\lambda )f_{{\vec {p}\lambda }_{\beta }}(x) + b^{\dag }(\vec {p},\lambda )f_{{\vec {p}\lambda }_{\beta }}^{*}(x)],\nonumber \\ \end{aligned}$$

(129)

where $a(\vec {p},\lambda )$ are the operators for the particle while $b^{\dag }(\vec {p},\lambda )$ are the operators for the antiparticle.

The definitions for the creation and annihilation operators for the Proca particle are:

$$\begin{aligned}{} & {} {a^{\dag }}^{IN/OUT} = i \int f_{\vec {p}\lambda }^{\mu }(x) {\mathop {\partial _{t_c}}\limits ^{\leftrightarrow }} A_{\mu }^{IN/OUT\dag } (x) d^{3}x \end{aligned}$$

(130)

$$\begin{aligned}{} & {} a^{IN/OUT} = -i \int {f^{*}}_{\vec {p}\lambda }^{\mu }(x) {\mathop {\partial _{t_c}}\limits ^{\leftrightarrow }} A_{\mu }^{IN/OUT} (x) d^{3}x. \end{aligned}$$

(131)

1.1 A. Transverse modes

Then IN/OUT fields for transverse modes, when $\lambda =\pm 1$ and we have only the spatial part in solution of the Proca equation (20), are:

$$\begin{aligned}{} & {} \sqrt{z_3}A_{i}^{IN/OUT}(x) \nonumber \\{} & {} \quad = {\hat{A}}_{i}(x) - \int d^{4}y \sqrt{-g(y)} {G_{ik}^{tr}}^{A/R}(x,y) E_{l}^{k}(y)A^{l}(y)\nonumber \\ \end{aligned}$$

(132)

The reduction formula in terms of transverse Green’s functions:

$$\begin{aligned}{} & {} a_{out} (\vec {p^{\prime }},\lambda ^{\prime }) - a_{in} (\vec {p^{\prime }},\lambda ^{\prime })\nonumber \\{} & {} \quad = i\int d^3x f_{\vec {p'}\lambda '}^{i*}(x){\mathop {\partial _{t_c}}\limits ^{\leftrightarrow }} \left[ A_{i}^{OUT}(x) - A_{i}^{IN}(x)\right] \nonumber \\{} & {} \quad = \frac{i}{\sqrt{z_3}} \int d^{4}y \sqrt{-g(y)} \int d^{3}x {f}_{\vec {p^{\prime }}\lambda ^{\prime }}^{i*} (x) {\mathop {\partial _{t_c}}\limits ^{\leftrightarrow }}\nonumber \\{} & {} \qquad \times \left[ G_{ik}(x,y) {+}\frac{1}{m^2}\partial _i(x)\partial _k(y)\Delta (x,y)\right] \nonumber \\ {}{} & {} \qquad \times ({E_{P}})_{l}^{k}(y)A^{l}(y),\nonumber \\ \end{aligned}$$

(133)

where we have replaced Green’s function for spatial components with:

$$\begin{aligned} G_{ik}^{tr}=G_{ik}(x,y) +\frac{1}{m^2}\partial _i(x)\partial _k(y)\Delta (x,y). \end{aligned}$$

(134)

Green’s function $\Delta (x,y)$ for the massless scalar field:

$$\begin{aligned} \Delta (x,y)=i \int d^{3}p\left[ f_{\vec {p}}(x)f^{*}_{\vec {p}}(y)-f^{*}_{\vec {p}}(x)f_{\vec {p}}(y)\right] , \end{aligned}$$

(135)

is defined in terms of the solution for the masless scalar field [44]:

$$\begin{aligned} f_{\vec {p}}\,(x)=\frac{i e^{\frac{3i\pi }{4}}e^{\frac{3\omega t}{2}}}{(2\pi )^{3/2}\sqrt{2\omega }}\frac{\left( 1+\frac{i}{(-p t_{c})}\right) }{\sqrt{(-p t_{c})}} e^{i\vec {p}\vec {x}-ipt_{c}}, \end{aligned}$$

(136)

while the total commutator function with transverse modes is defined as:

$$\begin{aligned} G_{ik}(x,y)= & {} i\sum _{\lambda } \int d^{3}p \left[ {f_{\vec {p}\lambda }}_{i}(x){{f^{*}}_{\vec {p}\lambda }}_{k}(y) \right. \nonumber \\{} & {} \left. - {{f^{*}}_{\vec {p}\lambda }}_{i}(x){f_{\vec {p}\lambda }}_{k}(y)\right] , \end{aligned}$$

(137)

where ${f_{\vec {p}\lambda }}(x)$ are the solutions for the Proca field in de Sitter space-time.

The first term from the second equality of Eq. (133) gives:

$$\begin{aligned} i\int d^{3}x {f^{*}}_{\vec {p^{\prime }}\lambda ^{\prime }}^{i}(x) {\mathop {\partial _{t_c}}\limits ^{\leftrightarrow }} G_{ik}(x,y) = i {{f^{*}}_{\vec {p^{\prime }}\lambda ^{\prime }}}_{{k}}(y). \end{aligned}$$

(138)

By using the divergence theorem in the second term of equation (133), we can split the spatial integral of the massless propagator:

$$\begin{aligned}{} & {} i \int d^{3}x {f^{*}}_{\vec {p^{\prime }}\lambda ^{\prime }}^{i} (x) {\mathop {\partial _{t_c}}\limits ^{\leftrightarrow }}\left( \frac{1}{m^{2}}\partial _{i}(x)\partial _{j}(y)\Delta (x,y)\right) \nonumber \\{} & {} \quad = -i\int \partial _{i}(x) {f^{*}}_{\vec {p^{\prime }}\lambda ^{\prime }}^{i} (x) {\mathop {\partial _{t_c}}\limits ^{\leftrightarrow }}\left( \frac{1}{m^{2}}\partial _{j}(y)\Delta (x,y)\right) \nonumber \\{} & {} \qquad + \oint _{i} d\Sigma _{i} {f^{*}}_{\vec {p^{\prime }}\lambda ^{\prime }}^{i} (x) {\mathop {\partial _{t_c}}\limits ^{\leftrightarrow }}\left( \frac{1}{m^{2}}\partial _{j}(y)\Delta (x,y)\right) \end{aligned}$$

(139)

The surface integral vanishes. The term that is left contains the spatial derivative of the Proca solution $\partial _{i}{f^{*}}_{\vec {p^{\prime }}\lambda ^{\prime }}^{i} (x)$, and giving that the Proca solution is proportional to the polarisation vector $\epsilon _{i}\left( \vec {p^{\prime }}\lambda ^{\prime }\right)$, the aforementioned derivative is equivalent to the transversality condition $p_{i}{\epsilon ^{*}}^{i}=0$:

$$\begin{aligned} \partial _{i}{f^{*}}_{\vec {p^{\prime }}\lambda ^{\prime }}^{i} (x)=-i p^{\prime }_{i}{f^{*}}_{\vec {p^{\prime }}\lambda ^{\prime }}^{i} (x)=0, \end{aligned}$$

(140)

Therefore the integral with the scalar Green’s function from Eq. (133) vanishes.

The final result for the reduction of the transverse modes from the OUT state is:

$$\begin{aligned}{} & {} \langle \, out \, \beta \,|\, (a_{out}(\vec {p^{\prime }},\lambda ^{\prime }) \,|\, in \, \alpha \,1 (\vec {p},\lambda )\, \rangle \nonumber \\{} & {} \quad = \delta _{\lambda \lambda ^{\prime }}\delta ^{3}(\vec {p}-\vec {p^{\prime }}) \langle \, out \, \beta \,|\, in \, \alpha \rangle \nonumber \\{} & {} \qquad +\frac{i}{\sqrt{z_3}}\int d^4y \sqrt{-g(y)}{{f^{*}}_{\vec {p'}\lambda '}}_{k}(x)({E_{P}})_{l}^{k}\nonumber \\{} & {} \qquad \times \langle \, out \, \beta \,|A^l(y)|\, in \, \alpha \,1 (\vec {p},\lambda )\, \rangle . \end{aligned}$$

(141)

When all particles from the IN and OUT states are reduced we obtain the vacuum expectation value of a time-ordered product of field operators. This allows us to use perturbative methods for defining the amplitudes by making T-contractions between the kinetic part obtained from the reduction formalism and the dynamical part given by the different orders in the S operator.

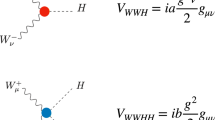
In order to study the vacuum emission of charged bosons and fermion–antifermion pairs, we are going to consider the process $vac\rightarrow W^-+e^++\nu$. The first step in finding out the amplitude is to compute the S-matrix elements using the reduction method. The IN state is empty, whereas in the OUT state there are one negatively charged boson, a positron and a neutrino. We denote the momenta and polarizations of $W^{-}$, $e^{+}$ and $\nu$ by $(P,\lambda )$, (p’$,\sigma$’) and $(p,\sigma )$, respectively. The reduction formalism for fermions in the de Sitter space-time can be found in [10, 71].

The Lagrangian of interaction between leptons and charged bosons $W^{\pm }$ from the flat space-time theory [1], will be adapted to our de Sitter geometry and will be written in terms of the point independent Dirac matrices $\gamma ^{{\hat{k}}}$ and the tetrad fields $e_{{\hat{k}}}^{l}$,:

$$\begin{aligned} \mathcal {L}_{int}= & {} -\frac{g}{2\sqrt{2}}\left[ \bar{\psi }_{(\nu )} \gamma ^{{\hat{k}}} e_{{\hat{k}}}^{l} (1-\gamma ^{5}) \psi _{(e)} A_{l}^+ \right. \nonumber \\{} & {} \left. + \bar{\psi }_{(e)} \gamma ^{{\hat{k}}} e_{{\hat{k}}}^{l} (1-\gamma ^5) \psi _{(\nu )} A_l\right] , \end{aligned}$$

(142)

where g is the coupling constant and we have used only spatial components.

Let us now define the transition amplitude for the process $vac\rightarrow W^-+e^++\nu$ with the transverse solutions of the Proca equation:

$$\begin{aligned}{} & {} \!\!\!\langle out\, | 1(P,\lambda ), 1(p,\sigma ),{\tilde{1}}(p^{\prime },\sigma ^{\prime })| \, in 0 \rangle \nonumber \\{} & {} \quad {=} \bigg ( \frac{i}{\sqrt{z_3}} \bigg ) \bigg ( \frac{i}{\sqrt{z_2}}\bigg )^2 \int d^{4}y_1 \sqrt{-g(y_1)} {f^{*}}_{\vec {P}\lambda }^i(y_1)(E_{P})_{i}^{j}(y_1)\nonumber \\{} & {} \qquad \times \int d^{4}y_2 \sqrt{-g(y_2)} {\bar{u}}_{\vec {p}\sigma }(y_2) E_{D}(y_2) \nonumber \\{} & {} \qquad \times \int d^{4}y_3 \sqrt{-g(y_3)} v_{\vec {p^{\prime }}\sigma ^{\prime }}(y_3)E_{D}(y_3)\nonumber \\{} & {} \qquad \times \langle 0|T(A_{j}(y_1)\psi (y_2)\bar{\psi }(y_3))|0 \, \rangle . \end{aligned}$$

(143)

To compute the time-ordered product of interacting fields we make use of the scattering operator [1, 10, 59]:

$$\begin{aligned} S=T(exp(-i\int d^{4}x \sqrt{-g}\mathcal {L}_{int})). \end{aligned}$$

(144)

The first order term in the series expansion of the S operator is:

$$\begin{aligned} S^{(1)}= & {} -\frac{ig}{2\sqrt{2}}\int d^{4}x \sqrt{-g(x)}\left[ \bar{\psi }_{(\nu )} \gamma ^{{\hat{k}}} e_{{\hat{k}}}^{l} (1-\gamma ^{5}) \psi _{(e)} A_{l}^+ \right. \nonumber \\{} & {} \left. + \bar{\psi }_{(e)} \gamma ^{{\hat{k}}} e_{{\hat{k}}}^{l} (1-\gamma ^5) \psi _{(\nu )} A_l \right] . \end{aligned}$$

(145)

For the process we are considering we are only going to use the second part of the first order term of the scattering operator, which corresponds to the transition involving the $W^-$ boson.

In this case the T-contractions give the transverse Green’s function defined only with spatial modes:

$$\begin{aligned}{} & {} \langle 0|T(A_{j}(y_1)\psi (y_2)\bar{\psi }(y_3)[\bar{\psi }_{(e)} \gamma ^{{\hat{k}}} e_{{\hat{k}}}^{l} (1-\gamma ^5) \nonumber \\{} & {} \quad \times \psi _{(\nu )} A_l](x))|0 \rangle = \frac{1}{i}D^{tr}_{jl}(y_1-x)\frac{1}{i}S(y_2-x)\gamma ^{{\hat{k}}}\nonumber \\{} & {} \quad e_{{\hat{k}}}^{l} (1-\gamma ^5)\left( \frac{-1}{i}\right) S(y_3-x), \end{aligned}$$

(146)

where $D^{tr}_{\beta \mu }(y-x)$ and $S(y-x)$ are the Feynman propagators for the Proca and Dirac fields, respectively.

For the Proca propagator we use relation (14) for spatial components:

$$\begin{aligned}{} & {} E_{i}^{j}(y_{1}) D^{tr}_{jl} (y_{1}-x) \nonumber \\{} & {} \quad = \frac{g_{il}(y_{1})}{\sqrt{-g(y_{1})}} \delta ^{4}(y_{1} - x) + \partial _{i}(y_{1})\partial _{l}(x)\Delta (y_{1},x),\nonumber \\ \end{aligned}$$

(147)

to obtain an matrix element of the form:

$$\begin{aligned}{} & {} \int d^{4}x \sqrt{-g(x)} \int d^{4}y_{1} \int d^{4}y_{2} \int d^{4}y_{3}\quad {\bar{u}}_{\vec {p}\sigma }(y_{2})\nonumber \\{} & {} \quad \times \delta ^{4}(y_{2}-x)\left[ {f^{*}}_{\vec {P}\lambda }^{i}(y_1)g_{il}(y_{1})\delta ^{4}(y_{1}-x)\right. \nonumber \\{} & {} \quad \left. + {f^{*}}_{\vec {P}\lambda }^{i}(y_1) \sqrt{-g(y_{1})}\partial _{i}(y_{1})\partial _{l}(x)\Delta (y_{1},x)\right] \nonumber \\ {}{} & {} \quad \times \gamma ^{{\hat{k}}}e_{{\hat{k}}}^l\left( 1-\gamma ^{5}\right) v_{p^{\prime }\sigma ^{\prime }}(y_{3})\delta ^{4}(y_{3}-x) \end{aligned}$$

(148)

If we integrate the second term of the above equation after $y_1$ we get:

$$\begin{aligned}{} & {} \int d^{3}y_{1}\sqrt{-g(y_{1})}{f^{*}}_{\vec {P}\lambda }^{i}(y_1)\partial _{i}(y_{1})\partial _{l}(x)\Delta (y_{1},x)\nonumber \\{} & {} \quad = - \int d^{3}y_{1} \partial _{i}(y_{1}) \left( \sqrt{-g(y_{1})} {f^{*}}_{\vec {P}\lambda }^{i}(y_1)\right) \partial _{l}(x)\Delta (y_{1},x) \nonumber \\{} & {} \qquad + \int d\Sigma _{i}\sqrt{-g(y_{1})} {f^{*}}_{\vec {P}\lambda }^{i}(y_1) \partial _{l}(x)\Delta (y_{1},x)=0,\nonumber \\ \end{aligned}$$

(149)

because the surface integral vanishes and from the first term we get exactly the Lorenz condition for spatial modes:

$$\begin{aligned} \partial _{i}\left( \sqrt{-g} {f^{*}}_{\vec {P}\lambda }^{i}\right) =0. \end{aligned}$$

(150)

We mention that $\sqrt{-g} = e^{3\omega t}$ and so its spatial derivative vanishes.

The final form of the transition amplitude of the process $vac\rightarrow W^-+e^++\nu$ for transverse modes is:

$$\begin{aligned} A_{i\rightarrow f}= & {} \frac{ig}{2\sqrt{2}} \int d^{4}x \sqrt{-g(x)} \, {\bar{u}}_{\vec {p}\sigma }(x) \gamma ^{{\hat{k}}} e_{{\hat{k}}}^{i}(1-\gamma ^5)\nonumber \\{} & {} \times v_{\vec {p^{\prime }}\sigma ^{\prime }}(x){{f^{*}}_{\vec {P}\lambda \,}}_{i} (x), \end{aligned}$$

(151)

where ${{f^{*}}_{\vec {P}\lambda \,}}_{\mu } (x), {\bar{u}}_{\vec {p}\sigma }(x)$ and $v_{\vec {p^{\prime }}\sigma ^{\prime }}(x)$ are the field equation solutions in the de Sitter geometry, written in the momentum-helicity basis. For the neutrino we have ${\bar{u}}_{\vec {p}\sigma }(x)$ and for the positron we have $v_{\vec {p^{\prime }}\sigma ^{\prime }}(x)$.

Finally it is important to specify that from our final formulas for the transition amplitudes we recover the well known formula for the scattering amplitude defined in Minkowski electro-weak theory if $\omega =0$ and $\sqrt{-g}\rightarrow 1;\,e_{{\hat{j}}}^{i}=\delta ^{i}_{{\hat{j}}}$.

1.2 B. Longitudinal modes

In the case of longitudinal modes with $\lambda =0$ we have a non-vanishing temporal component in the Proca solution.

The same as before, to find the amplitude for longitudinal modes one can evaluate the difference from Eq. (128):

$$\begin{aligned}{} & {} a_{out} (\vec {p^{\prime }},\lambda ^{\prime }) - a_{in} (\vec {p^{\prime }},\lambda ^{\prime }) = i \int d^{3}x {f^{*}}_{\vec {p^{\prime }}\lambda ^{\prime }}^{\beta } (x) {\mathop {\partial _{t_c}}\limits ^{\leftrightarrow }}\nonumber \\{} & {} \qquad \times \left[ A_{\beta }^{OUT}(x) - A_{\beta }^{IN}(x)\right] \nonumber \\{} & {} \quad = \frac{i}{\sqrt{z_3}} \int d^{4}y \sqrt{-g(y)} \int d^{3}x {f^{*}}_{\vec {p^{\prime }}\lambda ^{\prime }}^{\beta } (x) {\mathop {\partial _{t_c}}\limits ^{\leftrightarrow }}\nonumber \\{} & {} \qquad \times \left[ G_{\beta \nu }(x,y)+\frac{1}{m^2}\partial _\beta \partial \,'_\nu \Delta (x,x')\right] ({E_{P}})_{\alpha }^{\nu }(y)A^{\alpha }(y),\nonumber \\ \end{aligned}$$

(152)

where we have used Eq. (12) in the second equality.

The total commutator function is now defined with temporal components as well:

$$\begin{aligned}{} & {} G_{\beta \nu }(x,y) = G_{\beta \nu }^{A}(x,y) - G_{\beta \nu }^{R}(x,y)\nonumber \\{} & {} \quad = i\sum _{\lambda } \int d^{3}p \left[ {f_{\vec {p}\lambda }}_{\beta }(x){{f^{*}}_{\vec {p}\lambda }}_{\nu }(y) {-} {{f^{*}}_{\vec {p}\lambda }}_{\beta }(x){f_{\vec {p}\lambda }}_{\nu }(y)\right] .\nonumber \\ \end{aligned}$$

(153)

Then we solve the x integrals

$$\begin{aligned} i\int d^{3}x {f^{*}}_{\vec {p^{\prime }}\lambda ^{\prime }}^{\beta }(x) {\mathop {\partial _{t_c}}\limits ^{\leftrightarrow }} G_{\beta \nu }(x,y) = i {{f^{*}}_{\vec {p^{\prime }}\lambda ^{\prime }}}_{\nu }(y), \end{aligned}$$

(154)

and one obtains the final result for the operator difference:

$$\begin{aligned}{} & {} a_{out} (\vec {p^{\prime }},\lambda ^{\prime }) - a_{in} (\vec {p^{\prime }},\lambda ^{\prime }) \nonumber \\{} & {} \quad = i \int d^{4}y \sqrt{-g(y)} {{f^{*}}_{\vec {p^{\prime }}\lambda ^{\prime }}}_{\nu }(y) ({E_{P}})_{\alpha }^{\nu }(y)A^{\alpha }(y). \end{aligned}$$

(155)

The final reduction formula for the Proca field in the OUT state is:

$$\begin{aligned}{} & {} \langle \, out\, \beta \, 1(\vec {p^{\prime }},\lambda ^{\prime }) \,|\, in\,\alpha \, 1(\vec {p},\lambda )\, \rangle \nonumber \\{} & {} \quad =\delta _{\lambda \lambda ^{\prime }}\delta ^{3}(\vec {p}-\vec {p^{\prime }}) \langle \,out \,\beta \,|\,in \,\alpha \, \rangle \nonumber \\{} & {} \qquad + \frac{i}{\sqrt{z_3}} \int d^{4}y \sqrt{-g(y))} {{f^{*}}_{\vec {p^{\prime }}\lambda ^{\prime }}}_{\nu }(y)\nonumber \\{} & {} \qquad \times (E_{P})_{\alpha }^{\nu }(y) \langle \, out\, \beta \, |\, A^{\alpha }(y)\,|\,in \, \alpha \,1 (\vec {p},\lambda )\,\rangle , \end{aligned}$$

(156)

where the first term represents the process when the Proca particle does not interact with other particles and the IN/OUT transition and will be neglected when we compute the amplitude.

In the case of reduction from the IN state the final reduction formula for the Proca field is:

$$\begin{aligned}{} & {} \langle \, out\, \beta \, 1(\vec {p^{\prime }},\lambda ^{\prime }) \,|\, in\,\alpha \, 1(\vec {p},\lambda )\, \rangle \nonumber \\{} & {} \quad =\delta _{\lambda \lambda ^{\prime }}\delta ^{3}(\vec {p}-\vec {p^{\prime }}) \langle \,out \,\beta \,|\,in \,\alpha \, \rangle \nonumber \\{} & {} \qquad + \frac{i}{\sqrt{z_3}} \int d^{4}y \sqrt{-g(y)} {f_{\vec {p}\lambda }}_{\nu }(y) (E_{P})_{\alpha }^{\nu }(y) \nonumber \\{} & {} \qquad \times \langle \,out\, \beta \, 1(\vec {p^{\prime }},\lambda ^{\prime })\, |\, A^{\alpha }(y)\,|\,in \, \alpha \,\rangle . \end{aligned}$$

(157)

Considering our process $vac\rightarrow W^-+e^++\nu$ we can use the electro-weak interaction Lagrangian like we did in (142), but taking into account the temporal components as well:

$$\begin{aligned} \mathcal {L}_{int}= & {} -\frac{g}{2\sqrt{2}}\left[ \bar{\psi }_{(\nu )} \gamma ^{\hat{\alpha }} e_{\hat{\alpha }}^{\mu } (1-\gamma ^{5}) \psi _{(e)} A_{\mu }^+ \right. \nonumber \\{} & {} \left. + \bar{\psi }_{(e)} \gamma ^{\hat{\alpha }} e_{\hat{\alpha }}^{\mu } (1-\gamma ^5) \psi _{(\nu )} A_\mu \right] , \end{aligned}$$

(158)

where g is the coupling constant.

The reduction formula for the OUT particles is:

$$\begin{aligned}{} & {} \!\!\!\langle \, out \, 1\, |\, (P,\lambda ), 1(p,\sigma ),{\tilde{1}}(p^{\prime },\sigma ^{\prime })| \, in \,0 \, \rangle \nonumber \\{} & {} \quad = \bigg ( \frac{i}{\sqrt{z_3}} \bigg ) \bigg ( \frac{i}{\sqrt{z_2}}\bigg )^2 \int d^{4}y_1 \sqrt{-g(y_1)} {f^{*}}_{\vec {P}\lambda }^\nu (y_1)(E_{P})_{\nu }^{\beta }(y_1)\nonumber \\{} & {} \quad \times \int d^{4}y_2 \sqrt{-g(y_2)} {\bar{u}}_{\vec {p}\sigma }(y_2) E_{D}(y_2)\nonumber \\{} & {} \quad \times \int d^{4}y_3 \sqrt{-g(y_3)} v_{\vec {p^{\prime }}\sigma ^{\prime }}(y_3)E_{D}(y_3) \nonumber \\{} & {} \quad \times \langle 0|T(A_{\beta }(y_1)\psi (y_2)\bar{\psi }(y_3))|0 \rangle . \end{aligned}$$

(159)

In this case the first order term in the series expansion of the S is:

$$\begin{aligned} S^{(1)}= & {} -\frac{ig}{2\sqrt{2}}\int d^{4}x \sqrt{-g(x)}\left[ \bar{\psi }_{(\nu )} \gamma ^{\hat{\alpha }} e_{\hat{\alpha }}^{\mu } (1-\gamma ^{5}) \psi _{(e)} A_{\mu }^+ \right. \nonumber \\{} & {} \left. + \bar{\psi }_{(e)} \gamma ^{\hat{\alpha }} e_{\hat{\alpha }}^{\mu } (1-\gamma ^5) \psi _{(\nu )} A_\mu \right] . \end{aligned}$$

(160)

If we use only the term corresponding to the $W^-$ boson transition from (145) all possible T-contractions give:

$$\begin{aligned}{} & {} \langle 0|T(A_{\beta }(y_1)\psi (y_2)\bar{\psi }(y_3)[\bar{\psi }_{(e)} \gamma ^{\hat{\alpha }} e_{\hat{\alpha }}^{\mu } (1-\gamma ^5) \psi _{(\nu )} A_\mu ](x))|0 \rangle = \nonumber \\{} & {} \quad \frac{1}{i}D^{tr}_{\beta \mu }(y_1-x)\frac{1}{i}S(y_2-x)\gamma ^{\hat{\alpha }} e_{\hat{\alpha }}^{\mu } (1-\gamma ^5)\left( \frac{-1}{i}\right) S(y_3-x),\nonumber \\ \end{aligned}$$

(161)

where $D^{tr}_{\beta \mu }(y-x)$ and $S(y-x)$ are the Feynman propagators.

We use relation:

$$\begin{aligned}{} & {} E_{\nu }^{\beta }(y_{1}) D^{tr}_{\beta \mu } (y_{1}-x) \nonumber \\{} & {} \quad = \frac{g_{\mu \nu }(y_{1})}{\sqrt{-g(y_{1})}} \delta ^{4}(y_{1} - x) + \partial _{\nu }(y_{1})\partial _{\mu }(x)\Delta (y_{1},x), \end{aligned}$$

(162)

to obtain the matrix element in the form:

$$\begin{aligned}{} & {} \int d^{4}x \sqrt{-g(x)} \int d^{4}y_{1} \int d^{4}y_{2} \int d^{4}y_{3} {\bar{u}}_{\vec {p}\sigma }(y_{2})\delta ^{4}(y_{2}-x)\nonumber \\{} & {} \quad \times \left[ {f^{*}}_{\vec {P}\lambda }^{\nu }(y_1)g_{\mu \nu }(y_{1})\delta ^{4}(y_{1}-x) + {f^{*}}_{\vec {P}\lambda }^{\nu }(y_1)\right. \nonumber \\{} & {} \quad \times \left. \sqrt{-g(y_{1})}\partial _{\nu }(y_{1})\partial _{\mu }(x)\Delta (y_{1},x)\right] \nonumber \\{} & {} \quad \times \gamma ^{\hat{\alpha }}e_{\hat{\alpha }}\left( 1-\gamma ^{5}\right) v_{p^{\prime }\sigma ^{\prime }}(y_{3})\delta ^{4}(y_{3}-x) \end{aligned}$$

(163)

The term proportional with the scalar Green’s function from Eq. (163) will be:

$$\begin{aligned}{} & {} \int d^{4}y_{1}\sqrt{-g(y_{1})}{f^{*}}_{\vec {P}\lambda }^{\nu }(y_1)\partial _{\nu }(y_{1})\partial _{\mu }(x)\Delta (y_{1},x)\\{} & {} \quad = - \int d^{4}y_{1} \partial _{\nu }(y_{1}) \left( \sqrt{-g(y_{1})} {f^{*}}_{\vec {P}\lambda }^{\nu }(y_1)\right) \partial _{\mu }(x)\Delta (y_{1},x) \\{} & {} \qquad + \int d\Sigma _{\nu }\sqrt{-g(y_{1})} {f^{*}}_{\vec {P}\lambda }^{\nu }(y_1) \partial _{\mu }(x)\Delta (y_{1},x)=0 \end{aligned}$$

The surface integral vanishes, while from the first term we get exactly the Lorenz condition:

$$\begin{aligned} \partial _{\nu }\left( \sqrt{-g} {f^{*}}_{\vec {P}\lambda }^{\nu }\right) =0. \end{aligned}$$

(164)

Finally we can define the amplitude for the process of spontaneous vacuum emission of a $W^{-}$ boson, a positron and a neutrino in the case of longitudinal modes:

$$\begin{aligned} A_{i\rightarrow f}= & {} \frac{ig}{2\sqrt{2}} \int d^{4}x \sqrt{-g(x)} \, {\bar{u}}_{\vec {p}\sigma }(x) \gamma ^{\hat{\alpha }}\nonumber \\{} & {} \times e_{\hat{\alpha }}^{\mu }(1-\gamma ^5) v_{\vec {p^{\prime }}\sigma ^{\prime }}(x){{f^{*}}_{\vec {P}\lambda }}_{\mu } (x), \end{aligned}$$

(165)

where ${{f^{*}}_{\vec {P}\lambda }}_{\mu } (x)$, ${\bar{u}}_{\vec {p}\sigma }(x)$ and $v_{\vec {p^{\prime }}\sigma ^{\prime }}(x)$ are the field equation solutions in the de Sitter geometry, written in the momentum-helicity basis.

The amplitude corresponding to the vacuum emission of a $W^{+}$ boson, an electron and an anti-neutrino is:

$$\begin{aligned} A_{i\rightarrow f}'= & {} \frac{ig}{2\sqrt{2}} \int d^{4}x \sqrt{-g(x)} \, {\bar{u}}_{\vec {p\,'}\sigma '}(x) \gamma ^{\hat{\alpha }}\nonumber \\{} & {} \times e_{\hat{\alpha }}^{\mu }(1-\gamma ^5) v_{\vec {p}\sigma }(x){{f}_{\vec {P}\lambda }}_{\mu } (x), \end{aligned}$$

(166)

where in this case ${\bar{u}}_{\vec {p\,'}\sigma '}(x)$ describes the electron while $v_{\vec {p}\sigma }(x)$ describes the anti-neutrino. We mention that the probabilities corresponding to the above mentioned processes are equal.

Appendix B: Computing the transition amplitudes

Here we present the main steps for computing the transition amplitudes for the process $vac \rightarrow W^-+e^++\nu$. In the case $\lambda =\pm 1$, by substituting the solutions into the amplitude we get:

$$\begin{aligned}{} & {} A_{i\rightarrow f} = \frac{-g}{2\sqrt{2}} \int d^{4}x \sqrt{-g(x)} \left( \frac{-\omega t_c}{2\pi }\right) ^{3/2}\nonumber \\{} & {} \quad \times \left( -2\sigma ^i\left( \frac{1}{2}-\sigma \right) \xi _{\sigma }^{\dag }(\vec {p}),0 \right) e^{-i\vec {p}\vec {x} + ipt_c} \times \sqrt{\frac{\pi p^{\prime }}{\omega }}\left( \frac{1}{2\pi }\right) ^{3/2}\nonumber \\{} & {} \quad \times \left( \begin{array}{c} -\sigma ^{\prime } e^{-\pi k/2} \mathcal {H}_{\nu _{-}}^{(2)}\left( \frac{p^{\prime }}{\omega }e^{-\omega t}\right) \eta _{\sigma ^{\prime }}(\vec {p^{\prime }}) \\ \frac{1}{2} e^{\pi k/2}\mathcal {H}_{\nu _{+}}^{(2)}\left( \frac{p^{\prime }}{\omega }e^{-\omega t}\right) \eta _{\sigma ^{\prime }}(\vec {p^{\prime }}) \\ \end{array} \right) e^{-i\vec {p^{\prime }}\vec {x}-2\omega t} \nonumber \\{} & {} \quad \times e_{{\hat{i}}}^{j}\frac{\sqrt{\pi } e^{-\pi K/2}}{2(2\pi )^{3/2}} \sqrt{-t_{c}} \mathcal {H}_{-iK}^{(2)}(-P t_{c}) e^{-i\vec {P}\vec {x}}\nonumber \\{} & {} \quad \times {\epsilon }^{*}_{j}(\vec {P},\lambda =\pm 1), \end{aligned}$$

(167)

where we have used the chiral basis for representing the Dirac matrices and have replaced term $\gamma ^0\gamma ^{{\hat{i}}}e_{{\hat{i}}}^{j}(1-\gamma ^5)$.

The conformal map we are working in is defined by $t_c=-\frac{1}{\omega }e^{-\omega t}$. The metric in this map is $\sqrt{-g} = e^{3\omega t}$ and the tetrad coefficients are $e_{{\hat{i}}}^{j} = -e^{-\omega t}\delta _{ij}$.

We can group some of the time-dependent terms:

$$\begin{aligned} \sqrt{-g}(-\omega t_c)^{3/2}e_{{\hat{i}}}^{j} \frac{1}{\sqrt{\omega }}e^{-2\omega t}\sqrt{t_{c}}= -\frac{1}{\omega }e^{-2\omega t}\delta _{ij}. \end{aligned}$$

(168)

We can also directly compute the spatial integral:

$$\begin{aligned} \int d^{3}x e^{-i(\vec {p}+\vec {p^{\prime }}+\vec {P})\vec {x}} = (2\pi )^{3}\delta ^{3}(\vec {p}+\vec {p^{\prime }}+\vec {P}), \end{aligned}$$

(169)

which takes care of momentum conservation in this process.

By substituting all of the above results and multiplying the matrices and vectors the transition amplitude becomes:

$$\begin{aligned} A_{i\rightarrow f}= & {} -\frac{g}{2\sqrt{2}}\frac{\pi \sqrt{p^{\prime }} e^{-\pi K/2}e^{-\pi k/2}}{(2\pi )^{3/2}}\delta ^{3}(\vec {p}+\vec {p^{\prime }}+\vec {P})\nonumber \\{} & {} \times \int _{-\infty }^{+\infty } d t \frac{e^{-2\omega t}}{\omega }e^{ip^{\prime }t_{c}}\left( \frac{1}{2}-\sigma \right) \sigma ^{\prime } \nonumber \\{} & {} \times \mathcal {H}_{\nu _{-}}^{(2)}\left( \frac{p^{\prime }}{\omega }e^{-\omega t}\right) \mathcal {H}_{-iK}^{(2)}(-P t_{c})\nonumber \\{} & {} \times \xi _{\sigma }^{\dag }(\vec {p}\,)\sigma ^{i}\eta _{\sigma ^{\prime }}(\vec {p^{\prime }}){\epsilon }^{*}_{i}(\vec {P},\lambda =\pm 1). \end{aligned}$$

(170)

To use relation (193), we need to transform the Hankel functions and the exponential from (24) into Bessel functions. The following relations and properties allow us to do so [62, 63]:

$$\begin{aligned}{} & {} e^{-z} = \sqrt{\frac{2z}{\pi }}\mathcal {K}_{\frac{1}{2}}(z); \end{aligned}$$

(171)

$$\begin{aligned}{} & {} \mathcal {K}_{\nu }(iz) = \mathcal {H}_{\nu }^{(2)}(z)\frac{\pi }{2i}e^{-i\nu _\frac{\pi }{2}}; \end{aligned}$$

(172)

$$\begin{aligned}{} & {} \mathcal {H}_{\nu }^{(2)}(z) = \frac{2i}{\pi }e^{i\nu _\frac{\pi }{2}}\mathcal {K}_{\nu }(iz); \end{aligned}$$

(173)

$$\begin{aligned}{} & {} \mathcal {H}_{\nu }^{(2)}(z) = \frac{e^{i\pi \nu }\mathcal {J}_{\nu }(z)-\mathcal {J}_{-\nu }(z)}{i \sin ({\pi \nu })}. \end{aligned}$$

(174)

From the exponential factor in the amplitude integral (24) we want to obtain a Hankel function by firstly using (171) and then (172), meaning we get:

$$\begin{aligned} e^{-ipz}=\sqrt{\frac{2ipz}{\pi }}\frac{\pi }{2i}e^{-i\frac{\pi }{4}}\mathcal {H}_{\frac{1}{2}}^{(2)}(pz). \end{aligned}$$

(175)

We further transform the Hankel function in the above relation into Bessel functions using (174) [62, 63]:

$$\begin{aligned}{} & {} \sqrt{\frac{2ipz}{\pi }}\frac{\pi }{2i}e^{-i\frac{\pi }{4}}\mathcal {H}_{\frac{1}{2}}^{(2)}(pz) \nonumber \\{} & {} \quad = \sqrt{\frac{2ipz}{\pi }}\frac{\pi }{2i}e^{-i\frac{\pi }{4}}\left[ \mathcal {J}_{\frac{1}{2}}(pz)-\frac{1}{i}\mathcal {J}_{-\frac{1}{2}}(pz)\right] , \end{aligned}$$

(176)

The Hankel function from the $v_{\vec {p^{\prime }}\sigma ^{\prime }}(x)$ solution also becomes, by virtue of (174) [62, 63]:

$$\begin{aligned} \mathcal {H}_{\frac{1}{2}-ik}^{(2)}(p^{\prime }z)=\frac{ie^{\pi k}\mathcal {J}_{\frac{1}{2}-ik}(p^{\prime }z)-\mathcal {J}_{-\frac{1}{2}+ik}(p^{\prime }z)}{i\, \cosh (\pi k)}. \end{aligned}$$

(177)

The Hankel function which depends on the momentum of the $W^{-}$ boson becomes a modified Bessel $\mathcal {K}$ function [62, 63]:

$$\begin{aligned} \mathcal {H}_{-iK}^{(2)}(Pz)=\frac{2i}{\pi }e^{\frac{K\pi }{2}} \mathcal {K}_{-iK}(iPz). \end{aligned}$$

(178)

Now we may substitute (176), (177) and (178) into the temporal integral and we obtain:

$$\begin{aligned}{} & {} \!\!\!\int _{0}^{\infty } dz\quad z e^{-ipz}\mathcal {H}_{\nu _{-}}^{(2)}(p^{\prime }z)\mathcal {H}_{-i {K}}^{(2)}(P z) \nonumber \\{} & {} \quad {=} \sqrt{\frac{2ip^{\prime }}{\pi }}e^{-i\frac{\pi }{4}}e^{\mathcal {K}\frac{\pi }{2}}\int _{0}^{\infty }dz\quad z\sqrt{z}\left[ \mathcal {J}_{\frac{1}{2}}(pz){-}\frac{1}{i}\mathcal {J}_{-\frac{1}{2}}(pz)\right] \nonumber \\{} & {} \qquad \times \left[ \frac{ie^{\pi k}\mathcal {J}_{\frac{1}{2}-ik}(p^{\prime }z)-\mathcal {J}_{-\frac{1}{2}+ik}(p^{\prime }z)}{i\,\cosh (\pi k)}\right] \mathcal {K}_{-iK}(iPz).\nonumber \\ \end{aligned}$$

(179)

The final form of the temporal integral is:

$$\begin{aligned}{} & {} \int _{0}^{\infty } dz\cdot z e^{-ipz}\mathcal {H}_{\nu _{-}}^{(2)}(p^{\prime }z)\mathcal {H}_{-i {K}}^{(2)}(P z) \nonumber \\{} & {} \quad =\frac{\sqrt{\frac{2ip^{\prime }}{\pi }}e^{-i\frac{\pi }{4}}e^{K\frac{\pi }{2}}}{i\, cosh(\pi k)}[T_{1}-T_{2}-T_{3}+T_{4}], \end{aligned}$$

(180)

where the terms $T_{1},T_{2},T_{3}$ and $T_{4}$ denote the following integrals:

$$\begin{aligned} T_{1}= & {} \int _{0}^{\infty } dz\, z\sqrt{z}\,\mathcal {J}_{\frac{1}{2}}(pz)ie^{\pi k}\mathcal {J}_{\frac{1}{2}-ik}(p^{\prime }z)\mathcal {K}_{-iK}(iPz); \nonumber \\ \end{aligned}$$

(181)

$$\begin{aligned} T_{2}= & {} \int _{0}^{\infty } dz\, z\sqrt{z}\,\mathcal {J}_{\frac{1}{2}}(pz)\mathcal {J}_{-\frac{1}{2}+ik}(p^{\prime }z)\mathcal {K}_{-iK}(iPz); \nonumber \\ \end{aligned}$$

(182)

$$\begin{aligned} T_{3}= & {} \int _{0}^{\infty } dz\, z\sqrt{z}\,e^{\pi k}\mathcal {J}_{-\frac{1}{2}}(pz)\mathcal {J}_{\frac{1}{2}-ik}(p^{\prime }z)\mathcal {K}_{-iK}(iPz); \nonumber \\ \end{aligned}$$

(183)

$$\begin{aligned} T_{4}= & {} \int _{0}^{\infty } dz\, z\sqrt{z}\,\frac{1}{i}\mathcal {J}_{-\frac{1}{2}}(pz)\mathcal {J}_{-\frac{1}{2}+ik}(p^{\prime }z)\mathcal {K}_{-iK}(iPz).\nonumber \\ \end{aligned}$$

(184)

For obtaining the final result for the transition amplitude in the case of $\lambda =0$, we can follow the same steps presented above for the amplitude calculations with transversal Proca modes.

The temporal integral in $A_{i\rightarrow f}^{(1)}$ is made up of the following terms $T_{5},T_{6},T_{7},T_{8}$:

$$\begin{aligned} T_{5}= & {} \int _{0}^{\infty } dz\, z^2\,\sqrt{z}\,\mathcal {J}_{\frac{1}{2}}(pz)ie^{\pi k}\mathcal {J}_{\frac{1}{2}-ik}(p^{\prime }z)\mathcal {K}_{-iK}(iPz); \nonumber \\ \end{aligned}$$

(185)

$$\begin{aligned} T_{6}= & {} \int _{0}^{\infty } dz\, z^2\,\sqrt{z}\,\mathcal {J}_{\frac{1}{2}}(pz)\mathcal {J}_{-\frac{1}{2}+ik}(p^{\prime }z)\mathcal {K}_{-iK}(iPz); \nonumber \\ \end{aligned}$$

(186)

$$\begin{aligned} T_{7}= & {} \int _{0}^{\infty } dz\, z^2\,\sqrt{z}\,e^{\pi k}\mathcal {J}_{-\frac{1}{2}}(pz)\mathcal {J}_{\frac{1}{2}-ik}(p^{\prime }z)\mathcal {K}_{-iK}(iPz); \nonumber \\ \end{aligned}$$

(187)

$$\begin{aligned} T_{8}= & {} \int _{0}^{\infty } dz\, z^2\,\sqrt{z}\,\frac{1}{i}\mathcal {J}_{-\frac{1}{2}}(pz)\mathcal {J}_{-\frac{1}{2}+ik}(p^{\prime }z)\mathcal {K}_{-iK}(iPz).\nonumber \\ \end{aligned}$$

(188)

The temporal integrals that define the third term $A_{i\rightarrow f}^{(3)}$ in the amplitude, denoted by $T_{9},T_{10},T_{11},T_{12}$, are:

$$\begin{aligned} T_{9}= & {} \int _{0}^{\infty } dz\, z^2\,\sqrt{z}\,\mathcal {J}_{\frac{1}{2}}(pz)ie^{\pi k}\mathcal {J}_{\frac{1}{2}-ik}(p^{\prime }z)\mathcal {K}_{1-iK}(iPz);\nonumber \\ \end{aligned}$$

(189)

$$\begin{aligned} T_{10}= & {} \int _{0}^{\infty } dz\, z^2\,\sqrt{z}\,\mathcal {J}_{\frac{1}{2}}(pz)\mathcal {J}_{-\frac{1}{2}+ik}(p^{\prime }z)\mathcal {K}_{1-iK}(iPz);\nonumber \\ \end{aligned}$$

(190)

$$\begin{aligned} T_{11}= & {} \int _{0}^{\infty } dz\, z^2\,\sqrt{z}\,e^{\pi k}\mathcal {J}_{-\frac{1}{2}}(pz)\mathcal {J}_{\frac{1}{2}-ik}(p^{\prime }z)\mathcal {K}_{1-iK}(iPz);\nonumber \\ \end{aligned}$$

(191)

$$\begin{aligned} T_{12}= & {} \int _{0}^{\infty } dz\, z^2\,\sqrt{z}\,\frac{1}{i}\mathcal {J}_{-\frac{1}{2}}(pz)\mathcal {J}_{-\frac{1}{2}+ik}(p^{\prime }z)\mathcal {K}_{1-iK}(iPz).\nonumber \\ \end{aligned}$$

(192)

We make use of the following formula for solving the temporal integrals in our amplitudes [62, 63]:

$$\begin{aligned}{} & {} \int _{0}^{\infty } x^{Q-1} \mathcal {J}_{\lambda }(ax)\mathcal {J}_{\mu }(bx)\mathcal {K}_{\nu }(cx) dx {=}\frac{2^{Q-2}a^{\lambda }b^{\mu }c^{-Q-\lambda -\mu }}{\Gamma (\lambda {+}1)\Gamma (\mu {+}1)}\nonumber \\{} & {} \quad \times \Gamma \left( \frac{Q+\lambda +\mu -\nu }{2}\right) \Gamma \left( \frac{Q+\lambda +\mu +\nu }{2}\right) \nonumber \\{} & {} \quad \times F_{4} \left( \frac{Q+\lambda +\mu -\nu }{2},\frac{Q+\lambda +\mu +\nu }{2},\right. \nonumber \\{} & {} \quad \left. \lambda +1,\mu +1,-\frac{a^{2}}{c^{2}},-\frac{b^{2}}{c^{2}}\right) , \end{aligned}$$

(193)

where $\mathcal {J}$ is the Bessel function of the first kind, $\mathcal {K}$ is the modified Bessel function and $\mathcal {F}_{4}$ is Appell$^{\prime }$s function.

Appendix C: Relations with Euler functions

The Gamma Euler function can be expanded as [72]

$$\begin{aligned} \Gamma (\epsilon - n)= & {} \frac{(-1)^{n}}{n!}\left\{ \frac{1}{\epsilon } + \psi (n+1) + \frac{\epsilon }{2} \left[ \frac{\pi ^{2}}{3} + \psi ^{2}(n+1)\right. \right. \nonumber \\{} & {} \left. \left. -\psi ^{\prime }(n+1)\right] +\mathcal {O}(\epsilon ^{2})\right\} \end{aligned}$$

(194)

where $\psi$ are the Digamma Euler functions defined below [62]

$$\begin{aligned} \psi (n)= & {} -\gamma + \sum _{l=1}^{n-1}\frac{1}{2}; \end{aligned}$$

(195)

$$\begin{aligned} \psi ^{\prime }(n)= & {} \frac{\pi ^{2}}{6} - \sum _{l=1}^{n-1}\frac{1}{l^{2}}, \end{aligned}$$

(196)

while the Euler constant is

$$\begin{aligned} \gamma =-0,5772. \end{aligned}$$

(197)

The Beta Euler function is defined with the following integral:

$$\begin{aligned} B(\alpha ,\gamma ) = \frac{\Gamma (\alpha )\Gamma (\gamma )}{\Gamma (\alpha + \gamma )} = \int _{0}^{\infty } dy \frac{y^{\alpha -1}}{(1+y)^{\alpha + \gamma }}. \end{aligned}$$

(198)