Abstract
EOS is an open-source software for a variety of computational tasks in flavor physics. Its use cases include theory predictions within and beyond the Standard Model of particle physics, Bayesian inference of theory parameters from experimental and theoretical likelihoods, and simulation of pseudo events for a number of signal processes. EOS ensures high-performance computations through a C++ back-end and ease of usability through a Python front-end. To achieve this flexibility, EOS enables the user to select from a variety of implementations of the relevant decay processes and hadronic matrix elements at run time. In this article, we describe the general structure of the software framework and provide basic examples. Further details and in-depth interactive examples are provided as part of the EOS online documentation.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction and physics case
Flavor physics phenomenology has a long history of substantial impact on the development of the Standard Model (SM) of particle physics. Over the last decades, two developments are particularly noteworthy:
First, the determination of the Cabibbo–Kobayashi–Maskawa (CKM) matrix elements has developed into a precision enterprise, thanks in large parts to the efforts at the B-factory experiments BaBar and Belle [1] and more recently the LHCb experiment [2], the technological progress in lattice gauge theory predictions [3], and the development of precision phenomenology with continuum methods.
Second, the emergence of the so-called “b anomalies” has led to cautious excitement in the community. These anomalies are substantial tensions between theory predictions of b-quark decay observables and their measurements by the ATLAS, BaBar, Belle, CMS, and LHCb experiments, which present a coherent pattern that might be due to Beyond the Standard Model (BSM) effects, but do not yet reach individually the required significance of \(5\,\sigma \); see e.g. Refs. [4, 5] for recent reviews.
Both developments have led to increasingly sophisticated phenomenological analyses.
Such analyses involve researchers regularly carrying out structurally similar and recurring tasks. These typical use cases include
-
1.
predicting flavor observables and assessing their theory uncertainties both within the SM and for general BSM scenarios in the Weak Effective Theory (WET);
-
2.
inferring hadronic, SM, and/or WET parameters from an extendable database of experimental and theoretical likelihoods;
-
3.
simulating flavor processes and producing high-quality pseudo events for use in sensitivity studies and for the preparation of experimental analyses.
The EOS software [6] has been continuously developed since 2011 [7, 8] to achieve these tasks. EOS is a free software published under the GNU General Public License 2 [9]. It has produced publication-quality results for approximately 30 peer-reviewed and published phenomenological studies [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38].
Besides applications in phenomenology, EOS also has been used in a number of published experimental studies by the CDF [39], the CMS [40, 41] and the LHCb [42,43,44,45,46,47] experiments. The Belle II experiment has included EOS as part of the external software [48] within the Belle II software analysis framework [49].
In this article, we describe the EOS user interface. Although the software is developed mainly in C++, it is designed to be used in Python [50]. As such, EOS relies heavily on the numpy [51] and pypmc [52] packages. We highly recommend new users to use EOS within a Jupyter notebook environment [53].
EOS can be installed in binary form on Linux-based systemsFootnote 1 with a single command:

To avoid conflicts with the system packages, we strongly recommend to install EOS in a virtual Python environment, as described in the frequently-asked questions [55, FAQ].
Afterwards, the EOS Python module can be accessed, e.g. within a Jupyter notebook, using

We note that this means of installation also works for the “Windows Subsystem for Linux v2 (WSL2)”. For the purpose of installing EOS, WSL2 can be treated like any Linux system. Although EOS can also be built and installed from source on macOS systems, we do not currently support these. For macOS users we recommend to install on a remote-accessible Linux system and access a Jupyter notebook via SSH; our recommendation is described in detail as part of the frequently-asked questions [55]. Prospective EOS developers find detailed instructions on how to build EOS from source in the installation section of the documentation [55].
Presently, EOS provides a total of 844 (pseudo-)observablesFootnote 2 pertaining to a large variety of flavor processes. Obtaining and browsing the full list of observables is discussed in Sect. 2.4. The processes implemented include
-
(semi)leptonic charged-current \({\bar{B}}\) meson decays (e.g., \({\bar{B}}\rightarrow D^*\tau {\bar{\nu }}\));
-
semileptonic charged-current \(\varLambda _b\) baryon decays (e.g., \(\varLambda _b\rightarrow \varLambda _c(\rightarrow \varLambda \pi )\mu {\bar{\nu }}\));
-
rare (semi)leptonic and radiative neutral-current \({\bar{B}}\) meson decays (e.g., \({\bar{B}}\rightarrow {\bar{K}}^*\mu ^+\mu ^-\));
-
rare semileptonic and radiative neutral-current \(\varLambda _b\) baryon decays (e.g., \(\varLambda _b\rightarrow \varLambda (\rightarrow p \pi ) \mu ^+\mu ^-\)); and
-
B-meson mixing observables (e.g., \(\varDelta m_s\)).
EOS is designed to be self documenting: a complete list of processes and their respective observables is automatically generated as part of documentation, which is accessible both through the software itself and online [55]. The theoretical descriptions of most observables use the WET to account for both SM and BSM predictions. Details of the EOS bases of WET operators are described in Appendix A.2.
Although EOS is – to our knowledge – the first publicly available open-source flavor physics software [7, 8], it is by far not the only one. EOS competes with the flavio [56], SuperIso [57], HEPfit [58] and FlavBit [59] software. Major distinctions between EOS and these competitors are:
-
EOS focuses on the simultaneous inference of hadronic and BSM parameters;
-
EOS ensures modularity of hadronic matrix elements, i.e., the possibility to select from various hadronic models and parametrizations at run time;
-
EOS provides means to produce pseudo events for use in sensitivity studies and in preparation for experimental measurements; and
-
EOS provides means to predict hadronic matrix elements from QCD sum rules.
These distinctions make analyses possible that cannot currently be carried out with the competing software [13, 15, 26, 29, 60], e.g., due to multi-modal or otherwise complicated posteriors that cannot be captured by Markov chain Monte Carlo methods alone. However, this benefit comes with an increased level of complexity, which we address in the EOS documentation [55] and – to some extent – in this article.
1.1 How to read this document
Although this paper will give you a first impression of EOS and basic examples to try in a Jupyter notebook, it is not meant to be a stand-alone document. To obtain a deeper understanding, additional documentation, and further examples, the user is referred to Refs. [55, 61, 62]. Wherever we list Python code, we assume that the reader evaluates it within a Jupyter notebook environment, to make full use of its rich display capabilities.
In Sect. 2, we illustrate the basic usage of EOS, beginning with an overview of the various classes and concepts available through the Python interface. In Sect. 3 we continue with a discussion of and examples for the main use cases. In a series of appendices we provide further details.
-
We describe the three physics models available in EOS in Appendix A.
-
We relegate lengthy Python code examples that would otherwise interrupt reading Sect. 3 to Appendix B.
-
We document the EOS internal data format for storing experimental and theoretical likelihoods in Appendix C.
-
We include a glossary of the main EOS objects and associated methods in Appendix D.
This article is accompanied by a number of auxiliary files, containing example Jupyter notebooks for the basic usage and each of the use cases. These notebooks correspond to the examples contained in the public source code repository [62] as of EOS version 1.0.
2 Basic classes and concepts
EOS provides a number of Python classes that make it possible to fulfill the physics use cases discussed in Sect. 3. Three of the most relevant classes are used as follows:
-
hadronic and BSM parameters are represented by objects of the eos.Parameter class;
-
physical observables and pseudo-observables (such as hadronic form factors) are represented by objects of the eos.Observable class;
-
likelihood functions, stemming from either experimental measurements or theoretical calculations, are represented by objects of the eos.Constraint class.
To facilitate their handling, EOS has databases for all known objects of these classes. The user can interactively inspect these databases within a Jupyter notebook in the following way:

EOS provides a rich display for most classes, including the above, which is not shown here for brevity. Note that the information displayed by the above commands can also be obtained form the list of parameters, observables, and constraints that are part of the EOS documentation [55].
All three databases can be searched by name of the target object. EOS uses the same naming scheme for all three databases, which is enforced through use of the eos.QualifiedName class. The naming scheme is

where parts shown in square brackets are optional. The individual parts have the following meaning:
-
 The prefix part is used to separate objects with (otherwise) identical names into different namespaces, to avoid conflicts. Examples of prefixes include parameter categories (e.g., mass or decay-constant), physical processes (e.g., B->Kll), or sectors of the WET (e.g., sbsb).
The prefix part is used to separate objects with (otherwise) identical names into different namespaces, to avoid conflicts. Examples of prefixes include parameter categories (e.g., mass or decay-constant), physical processes (e.g., B->Kll), or sectors of the WET (e.g., sbsb). -
 The name part is used to identify objects within its PREFIX namespace. Examples include observable names (e.g., BR for a branching ratio) or names of WET Wilson coefficients (e.g., cVL for a coefficient of a left-handed vector operator).
The name part is used to identify objects within its PREFIX namespace. Examples include observable names (e.g., BR for a branching ratio) or names of WET Wilson coefficients (e.g., cVL for a coefficient of a left-handed vector operator). -
 The (optional) suffix part is used to distinguish between objects of otherwise identical names based on context. One example is the parameter describing the \(\varLambda _b\) baryon polarization, which takes different values based on the experimental environment. Generally, the \(\varLambda _b\) polarization would be represented by Lambda_b::polarization. The use of @LHCb and @unpolarized as a suffix distinguishes between the average polarization encountered within the LHCb experiment and an unpolarized setting (e.g. when using the whole phase space of the ATLAS and CMS experiments).
The (optional) suffix part is used to distinguish between objects of otherwise identical names based on context. One example is the parameter describing the \(\varLambda _b\) baryon polarization, which takes different values based on the experimental environment. Generally, the \(\varLambda _b\) polarization would be represented by Lambda_b::polarization. The use of @LHCb and @unpolarized as a suffix distinguishes between the average polarization encountered within the LHCb experiment and an unpolarized setting (e.g. when using the whole phase space of the ATLAS and CMS experiments). -
 The option list is an optional comma-separated list of key/value pairs, which allows to modify the named object in an unambiguous way. One example is model=SM,l=mu,q=s, which instructs an observable to use the Standard Model, \(\mu \) lepton flavor, and strange-flavored spectator quarks. Details on possible options are discussed in Sect. 2.4.
The option list is an optional comma-separated list of key/value pairs, which allows to modify the named object in an unambiguous way. One example is model=SM,l=mu,q=s, which instructs an observable to use the Standard Model, \(\mu \) lepton flavor, and strange-flavored spectator quarks. Details on possible options are discussed in Sect. 2.4.
In the remainder of this section we discuss how to use the six representation classes and their corresponding database classes
-
eos.Parameter within eos.Parameters,
-
eos.KinematicVariable within eos.Kinematics,
-
eos.Option within eos.Options,
-
eos.Observable within eos.Observables,
-
eos.Constraint within eos.Constraints, and
-
eos.SignalPDF within eos.SignalPDFs,
and the utility classes eos.Analysis and eos.Plotter. The relationship between the first four sets of classes are illustrated in Fig. 1. We provide a few examples here. However, for more exhaustive and interactive examples we refer to the notebook named basics.ipynb, which is part of the collection of EOS example notebooks [62].
2.1 Classes eos.Parameters and eos.Parameter
EOS makes extensive use of the eos.Parameter class, which provides access to a single real-valued scalar parameter. Any such eos.Parameter object is part of a large set of built-in parameters. Users cannot directly create new objects of the eos.Parameter class. However, new named sets of parameters can be created from which the parameter of interest can be extracted, inspected, and altered.
We begin by creating and displaying a new set of parameters:

The new variable parameters now contains a representation of all parameters known to EOS. The Jupyter display command has been augmented to provide a sectioned list of the known parameters, which is rather lengthy and not shown here. It is equivalent to the section “List of Parameters“ in the EOS documentation [55]. The display provides the user with an overview of all parameter names, their canonical physical notation, and their value and unit. A single parameter, here the muon mass as an example, can be isolated:

Again, the user is provided with an overview of the parameter, including its qualified name, unit, default value, and current value. The value of an eos.Parameter object can be altered with the set method:

In this example, the muon mass parameter within parameters has been set to the measured value for the tauon mass, and the m_mu object, which represents this parameter, has transparently changed its value. Put differently: any eos.Parameter object “remembers“ the set of parameters (i.e., the eos.Parameters object) that it belongs to and forwards all changes to that set. To obtain an independent set of parameters, the user can use

A parameter’s properties can be readily accessed through the methods name, latex, and evaluate

A parameter object can be used like any other Python object, e.g., as an element of a list, a dict, or a tuple:

These properties allow to bind a function (e.g., the functional expression of an observable or a likelihood function) to an arbitrary number of parameters, let the function evaluate these parameters in a computationally efficient way, and let the user change these parameters at a whim. Parameter sets are meant to be shared, i.e., a single set of parameters is meant to be used by any number of functions. The sharing of parameters across observables makes it possible for EOS to consistently and efficiently evaluate a large number of functions.
The default set of parameters is stored in YAML files that are installed together with the binary EOS library and the Python modules and scripts. The default parameter set can be replaced. To do this, the user must set the environment variable EOS_HOME to point to an accessible directory. The YAML files found within EOS_HOME/parameters will be used instead of the default set of parameters contained in the EOS package. The class eos.Parameters facilitates creating such files, through the dump method, which writes the current set of parameters to a YAML file. Alternatively, to use mostly the default parameter set, but override a subset of parameters in a persistent way, the user can use the override_from_file method to load only a subset of parameters from a given file.
2.2 Classes eos.Kinematics and eos.KinematicVariable
EOS uses the eos.Kinematics class to store a set of real-valued scalar kinematic variables by name. Contrary to the class eos.Parameters, there are neither default variables nor default values. Instead, eos.Kinematics objects are empty by default. Moreover, their variables are only defined within the scope of a single eos.Observable object: two observables that do not share an eos.Kinematics object can use identically-named, independent kinematic variables. Therefore, the names of kinematic variables do not require any prefix, and are simply (short) strings.
An empty set of kinematic variables can be created by

A new kinematic variable can be declared with the existing (empty) set by providing a key/value pair to the kinematics object, e.g.

In this example, we have also captured the newly created kinematic variables as objects k1, k2, and k3 of class eos.KinematicVariable for latter use. EOS uses the following guidelines for names and units of kinematic variables:
-
using ’q2’, ’p2’, and so on for the squares of four momenta \(q^\mu \), \(p^\mu \);
-
using ’E_pi’, ’E_gamma’, and so on for the energies of states \(\pi \), \(\gamma \) in the rest frame of a decaying particle;
-
using ’cos(theta_pi)’ and similar for the cosine of a helicity angle \(\theta _\pi \);
-
using natural units, i.e., expressing all momenta and energies as powers of \(\mathrm {GeV}\).
The new eos.KinematicVariable objects are now collected within the kinematics object. They can be collectively inspected using

In addition, the individual objects k1, k2, etc. can also be inspected

To directly obtain an eos.Kinematics object pre-populated with the variables one needs, a Python dict can be provided to the constructor:

To extract a previously declared kinematic variable from the kinematics object, the eos.Kinematics provides access via the subscript operator [...]

In the above, the set method is used to change the value of k1.
Kinematic variables and their naming usually pertain to only one observable, which will be discussed below in Sect. 2.4. Therefore, when creating observables, the user should create only a single independent set of kinematic variables per observable. Nevertheless, it is possible to create observables that have a common set of kinematic variables. This makes it possible to investigate correlations among observables that share a kinematic variable (e.g., LFU ratios such as \(R_K\) as a function of the lower dilepton momentum cut-off).
2.3 Class eos.Options
EOS uses objects of the eos.Options class to modify the behavior of observables at runtime. A new and empty set of options is created as follows

This object is usually populated with individual options, which are key/value pairs of str objects. Typical keys and their respective values include:
-
 is used to change the behavior of the low-energy observables. As of EOS version 1.0, it can take the values SM, CKM, WET.
is used to change the behavior of the low-energy observables. As of EOS version 1.0, it can take the values SM, CKM, WET.When choosing SM, the observables are computed within the SM, and the values of the WET Wilson coefficients are computed from SM parameters. CKM matrix elements are computed within the Wolfenstein parametrization. Details, such as the relevant parameter names, are discussed in Appendix A.1.
When choosing CKM, the observables are computed with SM values for the WET Wilson coefficients. However, the CKM matrix elements are not computed from the Wolfenstein parameters. Instead, each CKM matrix elements is parametrized in terms of two parameters for its absolute value and complex argument. This choice makes fitting CKM matrix elements possible. Details, such as the relevant parameter names, are discussed in Appendix A.1.
When choosing WET, the observables are computed with generic values for the WET Wilson coefficients. The CKM matrix elements are treated as in the CKM case. This choice makes fitting WET Wilson coefficients possible. Details, such as the EOS convention for the basis of WET operators and the relevant parameter names, are discussed in Appendix A.2.
-
 is used to select from one of the available parametrizations of hadronic form factors that are pertinent to the process. Its values are process-specific. For true observables (e.g., a semileptonic branching ratio) a sensible default choice is always provided. For pseudo-observables (e.g., the hadronic form factors \(f_+(q^2)\) in \(B\rightarrow \pi \) transitions) the choice must be made by the user.
is used to select from one of the available parametrizations of hadronic form factors that are pertinent to the process. Its values are process-specific. For true observables (e.g., a semileptonic branching ratio) a sensible default choice is always provided. For pseudo-observables (e.g., the hadronic form factors \(f_+(q^2)\) in \(B\rightarrow \pi \) transitions) the choice must be made by the user. -
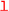 is used to select the charged lepton flavor in processes with at least one charged lepton. Allowed values are generally e, mu and tau. Individual processes might restrict the set of allowed values further, e.g., when hadronic matrix elements relevant to semitauonic decays are either unknown or unimplemented.
is used to select the charged lepton flavor in processes with at least one charged lepton. Allowed values are generally e, mu and tau. Individual processes might restrict the set of allowed values further, e.g., when hadronic matrix elements relevant to semitauonic decays are either unknown or unimplemented. -
 is used to select the spectator quark flavor. Allowed values are typically u, d, s, and c. Individual processes might restrict the set of allowed values further. Processes with s and c spectator quarks are typically accessible through explicit specification of the spectator quark flavor in the process name, e.g., B_s->K^*lnu.
is used to select the spectator quark flavor. Allowed values are typically u, d, s, and c. Individual processes might restrict the set of allowed values further. Processes with s and c spectator quarks are typically accessible through explicit specification of the spectator quark flavor in the process name, e.g., B_s->K^*lnu.
Obtaining the full list of option keys pertaining to a specific observable and their allowed keys is discussed in Sect. 2.4.
Adding new options to an existing options object is achieved as follows

Analogously to the kinematic variables, an eos.Options object can be created pre-populated with the values one needs using a Python dict

2.4 Classes eos.Observables and eos.Observable
EOS uses the eos.Observable class to provide theory predictions for a variety of flavor physics processes and their associated (pseudo-)observables. The complete list of observables known to EOS is available as part of the online documentation [55, List of Observables] and interactively in a Jupyter notebook via

Within this list, all observables are uniquely identified by an eos.QualifiedName object; see the beginning of Sect. 2 for information on how such a name is structured. To ease recognition, the typically used mathematical symbol for each observable is shown next to its name. To search within this list, keyword arguments for the prefix part, name part, or suffix part of a qualified name will filter the output. For example, the following code displays only branching ratios (BR) in processes involving a \(B^\mp \) meson (B_u)

Amongst others, this command lists the observable B_u->lnu::BR, representing the branching ratio of \(B^\mp \rightarrow \ell ^\mp {\bar{\nu }}\) decays. As part of the output the user is notified that this particular observable requires no kinematic variables. The user is also notified about the eos.Options keys recognized by this observable, which include model and l.
To create a new eos.Observable object the user needs to
-
identify it by name;
-
provide a set of parameters that can optionally be shared with other observables;
-
provide a set of kinematic variables that can optionally be shared with other observables; and
-
specify the relevant options.
Again, the branching ratio of \(B^\mp \rightarrow \ell ^\mp {\bar{\nu }}\) is used as an example, specifically for a \(\tau \) in the final state. The observable is created as an eos.Observable object as follows

Here B_u->lnu::BR is the eos.QualifiedName for this particular observable, and default parameters are provided when using eos.Parameters(). This observable does not require any kinematic variables, and therefore an empty eos.Kinematics object is provided. Setting the l option to tau selects a \(\tau \) final state. Setting the model option to WET enables the user to evaluate the observable in the WET for arbitrary values of the Wilson coefficients; see Appendix A.2 for details. The eos.Observable class provides access to the name, parameters, kinematics, options, and current value of an observable by means of the following methods

Note that each observable is associated with one object of the class eos.Parameters. To illustrate this feature, the above code is repeated to create a second observable observable2

Even though the two objects observable1 and observable2 share the same name and options, their respective parameter sets are independent, as can be checked as follows:

To correlate any number of observables, it is necessary to create all of them using the same eos.Parameters object; this will be further discussed in Sect. 3.2. In the above, this is not the case, since for the creation of each observable the call to eos.Parameters() created a new, independent set of parameters as explained in Sect. 2.1.
In many cases, observables have a default set of options, e.g., the default choice of hadronic form factors or the default choice of a BSM model. In some cases, it does not make sense to have a default choice. In such cases, an error will be shown through a Python exception if the user does not provide a valid option value. An example for this behavior are the form factor pseudo-observables, e.g., B->K^*::V(q2), which always require providing a valid value for the option form-factors. This is achieved by including the option as part of the eos.QualifiedName. In this case, B->K^*::V(q2); form-factors=BSZ2015 selects the form factor parametrization as used by Bharucha, Straub, and Zwicky [63] in 2015. A full list of all option keys and their respective valid values is available as part of the online documentation [55] and by displaying eos.Observables() in an interactive Jupyter notebook.
Contrary to parameters and kinematic variables, modifying the eos.Options object of any observable after its creation has no effect

This design decision ensures high-performance evaluations of all observables.
Objects of type eos.Observable are regular Python objects. For example, they can be collected in a list, which is useful for evaluating a number of identical observables at different points in their phase space. This can be achieved as follows

Here the instantiation of all observables with the same eos.Parameters object parameters ensures that they share the same numerical values for all parameters. As a consequence, changes of numerical values within parameters are broadcasted to all these instances and are taken into account in their subsequent evaluations.
2.5 Classes eos.Constraints and eos.Constraint
EOS uses the class eos.Constraint to manage and create individual likelihood functions at run time. To this end, objects of type eos.Constraint contain both information on the concrete likelihood (e.g., mean values and standard deviation of a Gaussian measurement) and meta-information about the constrained observables (e.g., the EOS internal names for an observable, relevant kinematic variables, and required options).
Besides (multivariate) Gaussian likelihood functions, EOS also supports LogGamma and Amoroso functions [64], and Gaussian mixture densities. The database of constraints makes it possible to construct a likelihood function for any experimental measurement and/or theory input in terms of eos.Observable objects. Hence, eos.Constraint objects are the building blocks for parameter inference studies that use the EOS software.
EOS provides a database of constraints, which is available as part of the online documentation [55, List of Constraints] as well as interactively accessible in a Jupyter notebook via

This database is stored within EOS in a series of YAML files. Most EOS users will not require knowledge about the file format. However, advanced users may need to provide constraints that are not part of the built-in database. In such a case, the user can specify a manual constraint; see Sect. 2.7 and Ref. [61] for details. Alternatively, similar to the eos.Parameters database, the user can set the EOS_HOME environment variable to point to an accessible directory. All YAML files within EOS_HOME/constraints will be loaded and used instead of the default eos.Constraints database. We document the format in Appendix C and an example entry is shown in Listing C.1.
Examples of built-in constraints that are used later on in this document include:
-
The constraint B->D::f_++f_0@FNAL+MILC:2015B describes a lattice QCD result for the \({\bar{B}}\rightarrow D\) form factors \(f_+\) and \(f_0\). Here the suffix indicates that this constraint has been extracted from Ref. [65], which is included in the EOS list of references as FNAL+MILC:2015B. The constraint can be used to create a likelihood function for the model parameters for the form factors \(f_+\) and \(f_0\), e.g., when using the BSZ2015 parametrization as the form factor model. Using B->D::f_++f_0@FNAL/MILC:2015B;form-factors=BSZ2015 (i.e., the constraint name including an option list that specificies the form factor model) ensures that the correct form factor model (here: BSZ2015) is used when creating a likelihood from this constraint.
-
The constraint B^0->D^+e^-nu::BRs@Belle:2015A describes the correlated measurement of the \({\bar{B}}^0\rightarrow D^+e^-{\bar{\nu }}\) branching ratio in 10 bins of the kinematic variable \(q^2\). Here the suffix indicates that the results have been extracted from Ref. [66], which is included in the EOS list of references as Belle:2015A.
2.6 Classes eos.SignalPDFs and eos.SignalPDF
EOS uses the eos.SignalPDF class to provide a theoretical prediction for the Probability Density Function (PDF) that describes a physical process, be it a decay or a scattering process. The dependence on an arbitrary number of kinematic variables are modeled through a shared object of class eos.Kinematics, and its eos.KinematicVariable objects. Parameters can be modified or inferred through a shared eos.Parameters object. Hence, each eos.SignalPDF object works very similar to an eos.Observable object. The list of PDFs can be accessed using the eos.SignalPDFs class. Searching for a specific PDF in the EOS database of signal PDFs is possible by filtering by the prefix part, name part, or suffix part of the signal PDF qualified name, very similar to how the database of observables is searchable

The signal PDF B->Dlnu::dGamma/dq2 features one kinematic variable, q2. Its boundaries are also passed by means of eos.KinematicVariable objects, which are conventionally named q2_min and q2_max.

The PDF’s parameters, kinematics, and options can be accessed with eponymous methods. This design permits the user some flexibility. It makes it possible to produce pseudo-events within the SM and in the generic WET; see Sect. 3.3 for this use case. In addition, it enables unbinned likelihood fits; their description goes beyond the scope of this document.
2.7 Class eos.Analysis
EOS uses the eos.Analysis as an interface for the user to describe a Bayesian analysis to infer one or more parameters. When creating an eos.Analysis object, the following arguments are used:
-
 is a mandatory list describing the univariate priors. This argument must describe at least one prior. Each prior is described through a dict object, the structure of which is documented as part of the Python API documentation [61, eos.Analysis].
is a mandatory list describing the univariate priors. This argument must describe at least one prior. Each prior is described through a dict object, the structure of which is documented as part of the Python API documentation [61, eos.Analysis]. -
 is a mandatory list describing all the constraints that enter the likelihood. Each element is a str or eos.QualifiedName, specifying a single constraint. Although it is a mandatory parameter, this list can be left empty.
is a mandatory list describing all the constraints that enter the likelihood. Each element is a str or eos.QualifiedName, specifying a single constraint. Although it is a mandatory parameter, this list can be left empty. -
 is an optional dict describing the options that will be applied to all the observables that enter the likelihood. Note that these global options override those specified via the qualified name scheme. For example, in a BSM analysis, it is useful to include ’model’: ’WET’ as a global option, to ensure that all observables will be evaluated using a selectable point in the WET parameter space.
is an optional dict describing the options that will be applied to all the observables that enter the likelihood. Note that these global options override those specified via the qualified name scheme. For example, in a BSM analysis, it is useful to include ’model’: ’WET’ as a global option, to ensure that all observables will be evaluated using a selectable point in the WET parameter space. -
 is an optional dict describing parameters that shall be fixed to non-default values as part of the analysis. For example, to carry out a BSM analysis of \(b\rightarrow c\tau \nu \) processes for a non-default renormalization scale, the user can set the scale parameter to a fixed value of \(3\,\mathrm {GeV}\) using ’cbtaunutau::mu’: ’3.0’.
is an optional dict describing parameters that shall be fixed to non-default values as part of the analysis. For example, to carry out a BSM analysis of \(b\rightarrow c\tau \nu \) processes for a non-default renormalization scale, the user can set the scale parameter to a fixed value of \(3\,\mathrm {GeV}\) using ’cbtaunutau::mu’: ’3.0’. -
 is an optional dict describing constraints that are not yet included in the EOS database of constraints. The constraint format is described in Appendix C. Note that to use any of the manual constraints as part of the likelihood, their qualified names must still be added to the likelihood argument.
is an optional dict describing constraints that are not yet included in the EOS database of constraints. The constraint format is described in Appendix C. Note that to use any of the manual constraints as part of the likelihood, their qualified names must still be added to the likelihood argument.

In Listing 1 we define a statistical analysis for the inference of \(|V_{cb}|\) from measurements of the \({\bar{B}}\rightarrow D\ell ^-{\bar{\nu }}\) branching ratios by the Belle experiment. This example will be further discussed in Sect. 3.2.1. First, we define all the arguments used in our analysis.
-
Using the global_options, we choose the BSZ2015 parametrization [63] to model the hadronic form factors that enter semileptonic \({\bar{B}}\rightarrow D\) transitions. We also choose the CKM model to ensure that \(|V_{cb}|\) is represented by a single parameter.
-
Priors for both the \(|V_{cb}|\) parameter and the BSZ2015 parameters are described in priors. Here, each parameter is assigned a uniform prior, which is chosen to contain at least \(98\%\) (\(\sim 3\,\sigma \)) of the ideal posterior probability, i.e., the priors have been chosen to be wide enough to “contain“ the posterior defined by this analysis.
-
The likelihood is defined through a list of constraints, which in the above includes both theoretical lattice QCD results as well as experimental measurements by the Belle collaboration. For the first part we combine the correlated lattice QCD results published by the Fermilab/MILC and HPQCD collaborations in 2015 [67, 68]. For the second part, we combine binned measurements of the branching ratio for \({\bar{B}}^0\rightarrow D^+e^-{\bar{\nu }}\) and \({\bar{B}}^0\rightarrow D^+\mu ^-{\bar{\nu }}\) decay. We reiterate that EOS treats genuine physical observables and pseudo-observables identically.
The class eos.Analysis further provides convenience methods to carry out the statistical analysis:
-
 uses the scipy.optimize module to find the best fit point of the posterior. Optional parameters determine the abort condition for the optimization and the starting point.
uses the scipy.optimize module to find the best fit point of the posterior. Optional parameters determine the abort condition for the optimization and the starting point. -
 uses the pypmc module to produce random variates of the posterior using an adaptive version of the Metropolis-Hastings algorithm [69,70,71] with a single Markov chain. This method can be run several times to repeatedly explore the posterior density and accurately sample from it.
uses the pypmc module to produce random variates of the posterior using an adaptive version of the Metropolis-Hastings algorithm [69,70,71] with a single Markov chain. This method can be run several times to repeatedly explore the posterior density and accurately sample from it. -
 uses the pypmc module to produce random variates of the posterior using the Population Monte Carlo algorithm [72]. To this end, an initial guess of the posterior in form of a Gaussian mixture density is created [73] from Markov chain Monte Carlo samples obtained using sample.
uses the pypmc module to produce random variates of the posterior using the Population Monte Carlo algorithm [72]. To this end, an initial guess of the posterior in form of a Gaussian mixture density is created [73] from Markov chain Monte Carlo samples obtained using sample.
At any point, the attribute parameters can be used to access the analysis’ parameter set, e.g., to save the set to a file via the dump method. We refer to the documentation of the EOS Python API [61] for further information.
Note that the C++ backend used by eos.Analysis parallelizes the evaluation of the likelihood function. By default, the number of concurrent threads will match the number of available processors. Users who need to limit this number (e.g., due to using EOS on a multi-user system in parallel to other users’ jobs) can do so by setting the EOS_MAX_THREADS environment variable to the limit.
2.8 Class eos.Plotter
EOS implements a versatile plotting framework based on the class eos.Plotter, which relies on matplotlib [74] for the actual plotting. Its input must be formatted as a dictionary containing two keys: plot contains metadata and contents describes the plot items. The value associated to the plot key is a dictionary; it describes the layout of the plot, including axis labels, positioning of the legend, and similar settings that affect the entire plot. The value associated to the contents key is a list; it describes the contents of the plot, expressed in terms of independent plot items. Possible types of plot items include points, bands, contours, histograms.

Each of the items is represented by a dictionary that contains a type key and an optional name key. A full description of all item types and their parameters is available as part of the EOS Python API documentation [61]. Here, we provide a brief summary for the most common types, which are used within examples in the course of this document:
-
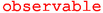 plots a single EOS observable without uncertainties as a function of one kinematic variable or one parameter. See Listing 3 for an example.
plots a single EOS observable without uncertainties as a function of one kinematic variable or one parameter. See Listing 3 for an example. -

-
 plots either a 1D or a 2D histogram of pre-existing random samples. These samples can be contained in Python objects within the notebook’s memory or contained in a datafile on disk. See listing 5 and listing 14 for examples.
plots either a 1D or a 2D histogram of pre-existing random samples. These samples can be contained in Python objects within the notebook’s memory or contained in a datafile on disk. See listing 5 and listing 14 for examples. -
 plots the uncertainty band of an observables as a function of one kinematic variable or one parameter. The random samples for the observables can be contained in Python objects within the notebook’s memory or contained in a datafile on disk. See Listing 7 for an example.
plots the uncertainty band of an observables as a function of one kinematic variable or one parameter. The random samples for the observables can be contained in Python objects within the notebook’s memory or contained in a datafile on disk. See Listing 7 for an example. -
 displays a constraint either from the EOS library or a manually added constraint. See listing 11 for an example.
displays a constraint either from the EOS library or a manually added constraint. See listing 11 for an example.
Beyond type and name keys, all item types also recognise the following optional keys:
 :
:-
A float, between 0.0 and 1.0, which describes the opacity of the plot item expressed as an alpha value. A value of 0.0 means completely transparent, 1.0 means completely opaque.
 :
:-
A str, containing any valid matplotlib color specification, which describes the color of the plot item. Defaults to one of the colors in the matplotlib default color cycler.
 :
:-
A str, containing LaTeX commands, which describes the label that appears in the plot’s legend for this plot item.
In Listing 2, FILENAME is an optional argument naming the file into which the plot shall be placed. The file format is automatically determined based on the file name extension.
2.9 Classes eos.References, eos.Reference, and eos.ReferenceName
EOS strives to give complete credit to the various works that underpin the theory predictions and the experimental and phenomenological analyses that provide likelihoods. To this end, EOS keeps a database of bibliographical metadata, which is accessible via the eos.References class. Each entry is a tuple of an eos.ReferenceName object that uniquely identifies the reference and the metadata data of the reference as an eos.Reference object. For a complete list of works used within EOS, we refer to the documentation [55, List of References].
Each observable provides a list of reference names, corresponding to the pertinent pieces of literature that were used in their implementations. This list is obtained via the references method, which returns a generator of eos.ReferenceName objects:

Further information on this reference can be obtained from its eos.Reference object:

In a similar way, by convention the suffix part of each eos.Constraint is a valid reference name. Therefore, to look up the reference that provides a constraint (e.g., B->D::f_++f_0@FNAL+MILC:2015B) the user can look up the associated bibliographical metadata based on the name’s suffix part:

If you feel that your work should be listed as part of a reference for any of the EOS observables, please contact the authors to include it.
3 Use cases
Each of the three major use cases introduced in Sect. 1 is discussed in details in Sects. 3.1 to 3.3.
3.1 Theory predictions
[The example developed in this section can be run interactively from the example notebook for theory predictions available from Ref. [8], file examples/predictions.ipynb]
EOS is equipped to produce theory predictions including their parametric uncertainties for any of its built-in observables using Bayesian statistics. This requires knowledge of the probability density function (PDF) of the pertinent parameters. Here and throughout we will denote the set of parameters as \(\mathbf {\vartheta }\), with
where \(\mathbf {x}\) represents the parameters of interest, and \(\mathbf {\nu }\) represents the nuisance parameters. This distinction is entirely a semantic one, and no technical differences arise from treating a parameter either way. Production of theory predictions then falls into one of the following cases:
-
1.
theory predictions for fixed values of all parameters \(\mathbf {\vartheta }= \mathbf {\vartheta }^*\);
-
2.
a priori predictions with propagation of uncertainties due to the prior PDF \(P_0(\mathbf {\vartheta })\);
-
3.
a posteriori predictions with propagation of uncertainties due to the posterior PDF \(P(\mathbf {\vartheta }|D)\), where D represents some data D.
Case 1 has been already mentioned with the concluding example of Sect. 2.4. In Sect. 3.1.1 we provide an example showcasing how to efficiently obtain these predictions. Cases 2 and 3 can be handled identically in a Monte-Carlo framework and are discussed collectively in Sect. 3.1.2.
3.1.1 Direct evaluation for fixed parameters
In Sect. 2 we have explained how to evaluate an observable for a single configuration of the kinematic variables, e.g., an integrated branching ratio with fixed integration boundaries, or a differential branching ratio at one point in the kinematic phase space. Commonly, users need to plot such differential observables as a function of the kinematic variable but for fixed values of its parameters. To illustrate how this can be achieved with EOS, we use the differential branching ratios for \({\bar{B}} \rightarrow D\lbrace \mu ^-,\tau ^-\rbrace {\bar{\nu }}\) as an example. The eos.Plotter class (see Sect. 2.8), provides means to plot any EOS observable as a function of a single kinematic variable (here: \(q^2\)).

The output is a plot containing the branching ratios for \(\ell =\mu , \tau \), where x axis shows the kinematic variable \(q^2\), and the y axis shows the value of the differential branching ratio. The output corresponds to the central curves shown in the right plot of Output 1. In the listing above, the statement ’variable’: ’q2’ specifies that the kinematic variable q2 is varied in the available range.
Similarly, we can plot an observable as a function of a single parameter, with all other parameters kept fixed and for a given kinematic configuration. To this end, the ’xrange’ requires adjustment compared to the previous example, and the contents should be replaced by

Here the dependence of the differential branching fraction at \(q^2 = 2\,\mathrm {GeV}^2\) on the real part of the WET Wilson coefficient \(C_{S_L}\) in the \({\bar{c}}b\mu \nu _\mu \) sector of the WET is plotted. Note that the kinematics key is used to provide the fixed set of kinematic variables and the parameters key is used to modify parameter values. As before, variable selects the entity that is plotted on the x axis, which is now recognized to be an eos.Parameter object rather than an eos.KinematicVariable object.
3.1.2 Predictions from Monte Carlo sampling
EOS provides the means for a more sophisticated estimation of theory uncertainties using Monte Carlo techniques, including importance sampling techniques. For the sampling of a probability density function, EOS relies on the pypmc package that provides methods for adaptive Metropolis-Hastings [69,70,71] and Population Monte Carlo [72, 73] sampling. The uncertainty of an observable O is estimated from its random variates. We recall that \(O \sim P(O)\) with [75]
Here the Dirac \(\delta \)-function was used and \(f_O(\mathbf {\vartheta })\) is the theoretical expression that predicts O for a given set of parameters \(\mathbf {\vartheta }\). With this knowledge at hand, we approach the two cases 2 and 3 as discussed in 3.1 in a basically identical way:
For case 2, we use \(P(\mathbf {\vartheta }) = P_0(\mathbf {\vartheta })\), i.e., the prior PDF. We note that EOS treats all priors \(P_0\) as univariate PDFs and therefore as uncorrelated. Mathematically, a multivariate prior is equivalent to a multivariate likelihood with flat, univariate priors. By design, EOS implements multivariate correlated priors in terms of a multivariate correlated likelihood. For example, the parameters in the parameterizations of hadronic form factors are constrained by various theoretical methods like lattice QCD calculations, light-cone sum rule calculations, unitarity bounds and constraints that arise in the limit of a heavy-quark mass. Under these circumstances one might still use the terminology prior prediction whenever the included constraints are only of theoretical nature, i.e. no experimental information was used.
For case 3, we use \(P(\mathbf {\vartheta }) = P(\mathbf {\vartheta }| D)\), i.e., the posterior PDF as obtained from a previous fit given some data D. Although based on case 3, the examples below also illustrate case 2, since this distinction is entirely a semantic one.
We continue using the integrated branching ratios of \(B^-\rightarrow D^0 \lbrace \mu ^-, \tau ^-\rbrace {\bar{\nu }}\) decays as examples. The largest source of theoretical uncertainty in these decays arises from the hadronic matrix elements, i.e., from the form factors \(f^{{\bar{B}}\rightarrow D}_+(q^2)\) and \(f^{{\bar{B}}\rightarrow D}_0(q^2)\). Both form factors have been obtained independently using lattice QCD simulations by the HPQCD [67] and FNAL/MILC [65] collaborations. In the following this information is used as part of the data D in the form of a joint likelihood. The form factors at different \(q^2\) values of each calculation are available in EOS as eos.Constraint objects under the names B->D::f_++f_0@HPQCD:2015A and B->D::f_++f_0@FNAL+MILC:2015B. Here, we use these two constraints to construct a multivariate Gaussian prior as follows:

Next we create two observables: the semimuonic branching ratio and the semitauonic branching ratio. By using prior.parameters in the construction of these observables, we ensure that our observables and the prior share the same parameter set. This means that changes to prior.parameters will affect the evaluation of both observables.

In the above, we provide the option ’form-factors’: ’BSZ2015’ to ensure that the form factor plugin corresponds to the set of parameters that are described by prior. Sampling from the natural logarithm of the prior PDF and – at the same time – producing prior-predictive samples of both observables is achieved using the sample method. This method runs one Markov chain using the pypmc package, and it is discussed in more detail in Sect. 3.2. Here N=5000 samples of both the parameter set and the observable set are produced, and we discard the values of the log prior for each parameter sample by assigning the return value to _. Note that the production of posterior-predictive samples is achieved in the same way. The distinction between a prior PDF and a posterior PDF is entirely a semantic one.
To illustrate the prior-predictive samples we use EOS ’ plotting framework:

The arithmetic mean and the variance of the samples can be determined with standard techniques, e.g., using the NumPy routines numpy.average and numpy.var.
A further recurring task is to produce and plot uncertainty bands for differential observables. Here, we use the differential branching ratios for the previously discussed semimuonic and semitauonic decays. Using EOS we approach this task by creating two lists of observables. The first list includes only the \({\bar{B}}\rightarrow D\mu ^-{\bar{\nu }}\) at various points in its phase space. Due to the strong dependence of the branching ratio on \(q^2\), we do not distribute the points equally across the full phase space. Instead, we equally distribute half of the points in the interval \([0.02\,\mathrm {GeV}^2, 1.00\,\mathrm {GeV}^2]\) and the other half in the remainder of the phase space. The second list is constructed similarly for \({\bar{B}}\rightarrow D\tau ^-{\bar{\nu }}\). We then pass these lists to sample, to obtain prior-predictive samples of the observables:

We plot the so-obtained prior-predictive samples with EOS ’s plotting framework:

Plot of the branching ratios of \({\bar{B}}\rightarrow D\lbrace \mu ^-,\tau ^-\rbrace {\bar{\nu }}\). Left: prior-predictive samples for the integrated branching ratios obtained from the code in Listing 4. Right: differential branching ratios as functions of \(q^2\). The central curves are obtained from Listing 3. The uncertainty bands are obtained from the samples obtained in Listing 6 using the plotting code in Listing 7
3.2 Parameter inference
[The example developed in this section can be ran interactively from the example notebook for parameter inference available from Ref. [8], file examples/inference.ipynb]
EOS infers parameters from a database of experimental or theoretical constraints in combination with its built-in observables. This section illustrates how to construct an eos.Analysis object that represents the statistical analysis and to infer the best-fit point and uncertainties of a list of parameters through optimization and Monte Carlo methods. We pick up the example introduced in Sect. 2.7 to illustrate the above-mentioned features of EOS. In particular, we use the two experimental constraints B^0->D^+e^-nu::BRs@Belle:2015A and B^0->D^+mu^-nu::BRs@Belle:2015A, to infer the value of the CKM matrix element \(|V_{cb}|\).
3.2.1 Defining the statistical analysis
To define our statistical analysis for the inference of \(|V_{cb}|\) from measurements of the \({\bar{B}}\rightarrow D\ell ^-{\bar{\nu }}\) branching ratios, some decisions are needed. First, we must decide how to parametrize the hadronic form factors that describe semileptonic \({\bar{B}}\rightarrow D\) transitions. For what follows we will use the parametrization of Ref. [63], referred to as [BSZ:2015A]. Next, we must decide the theory input for the form factors. For this, we will combine the correlated lattice QCD results published by the Fermilab/MILC and HPQCD collaborations in 2015 [67, 68].
The corresponding eos.Analysis object is shown in Listing 1; it has been used previously as an example in Sect. 2.7. The global options ensure that our choice of form factor parametrization is used throughout, and that for CKM matrix elements the CKM model is used. The latter provides parametric access to the \(V_{cb}\) matrix element through two objects of type eos.Parameter: the absolute value CKM::abs(V_cb) and the complex phase CKM::arg(V_cb). The latter is not accessible from \(b\rightarrow c\ell {\bar{\nu }}\).
We also set the starting value of CKM::abs(V_cb) to a sensible value of  via
via

To maximize the (logarithm of the) posterior density we can call the optimize method, as shown in Listing 8. In a Jupyter notebook, it is useful to display the return value of this method, which illustrates the best-fit point. Further useful information is contained in the goodness-of-fit summary. The latter lists each constraint, its degrees of freedom, and its \(\chi ^2\) value (if applicableFootnote 3), alongside the p-value for the entire likelihood.

Instead of setting individual parameters to sensible values as we did for CKM::abs(V_cb) earlier, a starting point can alternatively be provided to optimize using the start_point keyword argument.
The maximization of the posterior by means of optimize uses SciPy ’s optimize module [76]. The default optimization algorithm is the Sequential Least SQuares Programming (SLSQP). Other algorithms can be selected and configured through keyword arguments that optimize forwards to scipy.optimize.
To interface with optimizers other than available within SciPy, EOS provides the log_pdf method. As its first argument, it expects the list of the parameter values. The parameters’ ordering must correspond to the ordering of analysis.varied_parameters, and each parameter’s values must be rescaled to the interval \([-1, +1]\), where the boundaries correspond to the minimal/maximal value in the prior specification.
3.2.2 Importance sampling of the posterior
To sample from the posterior, EOS provides the sample method. Optionally, this can also produce posterior-predictive samples for a list of observables. We can use these samples to illustrate the results of our fit in relation to the experimental constraints.
For this example, we produce such posterior-predictive samples for the differential \({\bar{B}}\rightarrow D^+\mu ^-{\bar{\nu }}\) branching ratio in the 40 points of the kinematic variable \(q^2\) used in the previous examples (redefined in the following listing for completeness).

In the above we start sampling at the best-fit point as obtained earlier through optimization, which is optional. We carry out 5 burn-in runs/preruns of 1000 samples each. The samples obtained in each of these preruns are used to adapt the Markov chain but are then discarded. The main run produces a total of N * stride = 100000 random Markov Chain samples. The latter are thinned down by a factor of stride = 5 to obtain N = 20000 samples, which are stored in parameter_samples. The thinning reduces the autocorrelation of the samples. The values of the log(posterior) are stored in log_posterior. The posterior-predictive samples for the observables are only returned if the observables keyword argument is provided; in the above example, they are stored in mu_samples.
We can now illustrate the posterior samples either as a histogram or as a kernel density estimate (KDE) using the built-in plotting functions, see Output 3 and listing B.1. Contours at given levels of posterior probability, as shown in Output 3, can be obtained for any pair of parameters using listing B.2.
Distribution of samples (left) of the 1D-marginal posterior of \(|V_{cb}|\) as a regular histogram and as a kernel density estimate (blue line); and (right) of the 2D-marginal joint posterior of \(|V_{cb}|\) and \(f^{{\bar{B}}\rightarrow D}_+(0)\) as contours at \(68\%\) and \(95\%\) probability (orange lines and filled areas). The plots are produced by listing B.1 and listing B.2, respectively
Sampling with the Metropolis-Hastings algorithm is known to work well for unimodal densities. However, in cases of multimodal densities or blind directions, problems regularly arise. EOS provides the means to follow the approach of Ref. [73], which proposes to use (potentially unadapted) Markov chains to explore the parameter space to initialize a Gaussian mixture density. The latter is then adapted using the Population Monte Carlo algorithm [72], for which EOS uses the pypmc package [52]. Within EOS, we use schematically the following approach:

Plot of the posterior-predictive importance samples for the differential \({\bar{B}}\rightarrow D^+\mu ^-{\bar{\nu }}\) branching ratio vs. \(q^2\), juxtaposed with bin-averaged measurements of the \({\bar{B}}\rightarrow D^+\lbrace e^-,\mu ^-\rbrace {\bar{\nu }}\) branching ratio by the Belle experiment
We can visualize the posterior-predictive samples using:

Note that the use of ’rescale-by-width’: True converts the database’s existing entry for the bin-integrated branching ratio into the bin-averaged branching ratio. Only that latter can be meaningfully compared with the differential branching ratio’s curve.
3.3 Event simulation
[The example developed in this section can be run interactively from the example notebook for event simulation available from Ref. [8], file examples/simulation.ipynb]
EOS contains built-in probability density functions (PDFs) from which pseudo events can be simulated using Markov chain Monte Carlo techniques.
3.3.1 Constructing a 1D PDF and simulating pseudo events
The simulation of events is performed using the sample_mcmc method. For example, the construction of the one-dimensional PDF describing the \(B\rightarrow D\ell \nu _\ell \) decay distribution in the variable \(q^2\) and for \(\ell =\mu \) leptons requires:
-
the q2 kinematic variable that can be set to an arbitrary starting value.
-
the boundaries, q2_min and q2_max, for the phase space from which we want to sample. If needed, the phase space can be shrunk to a volume smaller than physically allowed; the normalization of the PDF will automatically adapt.
For \(B\rightarrow D\ell \nu _\ell \), the Markov chains can self adapt to the PDF in 3 preruns with 1000 pseudo events/samples each.
The simulation of stride*N=250000 pseudo events/samples from the PDF, which are thinned down to N=50000, is performed with the following code:

Samples for other lepton flavors, e.g., \(\ell =\tau \), require only a change of the eos.Options object to use ’l’: ’tau’ instead and adjustment of the phase space. Similar to observables, eos.SignalPDF objects can be plotted as a function of a single kinematic variable, while keeping all other kinematic variables fixed. The fixed kinematic variables are provided as a dict via the kinematics key. We show two such plots in combination with histograms of the PDF samples in Output 5 (left). The Output shows excellent agreement between the simulations and the respective analytic expressions for the 1D PDFs.
3.3.2 Constructing a 4D PDF and simulating pseudo events
Samples can also be drawn for PDFs with more than one kinematic variable. As an example, we use the full four-dimensional PDF for \({\bar{B}}\rightarrow D^*\ell \bar{\nu }\) decays. Declaration and initialization of all four kinematic variables (q2, cos(theta_l), cos(theta_d), and phi) is similar to the 1D case.

We then produce the samples in a similar way as for the 1D PDF:

The samples of the individual kinematic variables can be accessed as the columns of the dstarlnu_samples object. We can now show correlations of the kinematic variables by plotting 2D histograms, e.g. \(q^2\) vs \(\cos \theta _\ell \):

Left: Distribution of \(B\rightarrow D\ell \nu _\ell \) events for \(\ell =\mu , \tau \), as implemented in EOS (solid lines) and as obtained from Markov Chain Monte Carlo importance sampling (histograms). The samples are produced from listing 12, and the plot is produced by listing B.3. Right: 2D histogram of the \({\bar{B}}\rightarrow D^*(\rightarrow D\pi )\mu ^-{\bar{\nu }}\) PDF in the variables \(q^2\) and \(\cos (\theta _\ell )\). This output is produced by the code shown in listing 14
4 Conclusion and outlook
We have presented the EOS software in version 1.0 and explained its three main use cases at the hand of concrete examples in the field of flavor physics phenomenology. Beyond these examples, EOS has been used extensively for numerical evaluations, statistical analyses and plots in a number of peer-reviewed publications. We plan to extend EOS with further processes and observables, while keeping the Python interface unchanged.
To keep this document concise, some advanced aspects of EOS have not been discussed. These aspects, documented in the online documentation [55], include
-
the possibility to combine existing observables in arithmetic expressions at run time;
-
the command line interface intended to use as part of massively parallelized batch jobs in grid or cluster environments; and
-
the addition of C++ code for new observables and processes.
Despite ongoing unit testing and development of the software, we are conscious that EOS is neither free of bugs nor providing all the features the user could possibly need. We therefore encourage the users to report any and all bugs found and to request additional features. We ask that any such reports or requests are communicated as issues within the EOS Github repository [8]. We are very happy to discuss the addition of further observables and processes with interested parties from the phenomenological and experimental communities.
Data Availability
This manuscript has data included as electronic supplementary material. The online version of this article contains supplementary material, which is available to authorized users.
Notes
This is limited to systems with Python version 3.6 or later that also fulfill the “manylinux_2_17_x86_64” platform requirement as defined in PEP 600 [54].
EOS does not distinguish between true observables, which can be unambiguously measured in an experimental setting, and pseudo-observables, which can not be unambiguously inferred from experimental or theoretical data. Pseudo-observables in EOS include hadronic form factors and other auxiliary hadronic quantities.
Note that EOS supports likelihood functions that do not have a \(\chi ^2\) test statistic or any test statistic at all.
The choice of \(\mu _0\) should, in general, not be changed, and for some sectors there is more than one high scale involved.
References
A.J. Bevan et al., The physics of the B factories. Eur. Phys. J. C 74, 3026 (2014). https://doi.org/10.1140/epjc/s10052-014-3026-9
R. Aaij et al., Implications of LHCb measurements and future prospects. Eur. Phys. J. C 73(4), 2373 (2013). https://doi.org/10.1140/epjc/s10052-013-2373-2
S. Aoki et al., FLAG Review 2019: Flavour Lattice Averaging Group (FLAG). Eur. Phys. J. C 80(2), 113 (2020). https://doi.org/10.1140/epjc/s10052-019-7354-7
J. Albrecht, D. van Dyk, C. Langenbruch, Flavour anomalies in heavy quark decays. Prog. Part. Nucl. Phys. 120, 103885 (2021). https://doi.org/10.1016/j.ppnp.2021.103885
F.U. Bernlochner, M.F. Sevilla, D.J. Robinson, G. Wormser, Semitauonic \(b\)-hadron decays: a lepton flavor universality laboratory (2021)
D. van Dyk, F. Beaujean, T. Blake, C. Bobeth, M. Bordone, E. Eberhard, E. Graverini, N. Gubernari, A. Kokulu, S. Kürten, D. Leljak, P. Lüghausen, M. Reboud, M. Ritter, E. Romero, I. Toijala, K.K. Vos, EOS v1.0—a software for flavor physics phenomenology (2021). https://doi.org/10.5281/zenodo.5730384
D. van Dyk, The decays \(\bar{B} \rightarrow \bar{K}^{(*)} \ell ^+ \ell ^-\) at low recoil and their constraints on new physics. Ph.D. thesis, Dortmund University (2012)
D. van Dyk et al., EOS source code repository (2021). https://github.com/eos/eos
Gnu general public license. https://www.gnu.org/licenses/old-licenses/gpl-2.0.html
C. Bobeth, G. Hiller, D. van Dyk, The benefits of \(\bar{B} \rightarrow \bar{K}^* \ell ^+ \ell ^-\) decays at low recoil. JHEP 07, 098 (2010). https://doi.org/10.1007/JHEP07(2010)098
C. Bobeth, G. Hiller, D. van Dyk, More benefits of semileptonic rare B decays at low recoil: CP violation. JHEP 07, 067 (2011). https://doi.org/10.1007/JHEP07(2011)067
C. Bobeth, G. Hiller, D. van Dyk, C. Wacker, The decay \(B \rightarrow K \ell ^+ \ell ^-\) at low hadronic recoil and model-independent \(\Delta B = 1\) constraints. JHEP 01, 107 (2012). https://doi.org/10.1007/JHEP01(2012)107
F. Beaujean, C. Bobeth, D. van Dyk, C. Wacker, Bayesian fit of exclusive \(b \rightarrow s \bar{\ell }\ell \) decays: the standard model operator basis. JHEP 08, 030 (2012). https://doi.org/10.1007/JHEP08(2012)030
C. Bobeth, G. Hiller, D. van Dyk, General analysis of \(\bar{B} \rightarrow \bar{K}^{(*)}\ell ^+ \ell ^-\) decays at low recoil. Phys. Rev. D 87(3), 034016 (2013). https://doi.org/10.1103/PhysRevD.87.034016
F. Beaujean, C. Bobeth, D. van Dyk, Comprehensive Bayesian analysis of rare (semi)leptonic and radiative \(B\) decays. Eur. Phys. J. C 74, 2897 (2014). https://doi.org/10.1140/epjc/s10052-014-2897-0 [Erratum: Eur. Phys. J. C 74, 3179 (2014)]
S. Faller, T. Feldmann, A. Khodjamirian, T. Mannel, D. van Dyk, Disentangling the decay observables in \(B^- \rightarrow \pi ^+\pi ^-\ell ^-\bar{\nu }_\ell \). Phys. Rev. D 89(1), 014015 (2014). https://doi.org/10.1103/PhysRevD.89.014015
I. Sentitemsu Imsong, A. Khodjamirian, T. Mannel, D. van Dyk, Extrapolation and unitarity bounds for the B \(\rightarrow {\pi }\) form factor. JHEP 02, 126 (2015). https://doi.org/10.1007/JHEP02(2015)126
P. Böer, T. Feldmann, D. van Dyk, Angular analysis of the decay \(\Lambda _b \rightarrow \Lambda (\rightarrow N \pi ) \ell ^+\ell ^-\). JHEP 01, 155 (2015). https://doi.org/10.1007/JHEP01(2015)155
F. Beaujean, C. Bobeth, S. Jahn, Constraints on tensor and scalar couplings from \(B\rightarrow K\bar{\mu }\mu \) and \(B_s\rightarrow \bar{\mu }\mu \). Eur. Phys. J. C 75(9), 456 (2015). https://doi.org/10.1140/epjc/s10052-015-3676-2
T. Feldmann, B. Müller, D. van Dyk, Analyzing \(b\rightarrow u\) transitions in semileptonic \(\bar{B}_s \rightarrow K^{*+}(\rightarrow K \pi )\ell ^-\bar{\nu }_\ell \) decays. Phys. Rev. D 92(3), 034013 (2015). https://doi.org/10.1103/PhysRevD.92.034013
T. Mannel, D. van Dyk, Zero-recoil sum rules for \(\Lambda _b \rightarrow \Lambda _c\) form factors. Phys. Lett. B 751, 48 (2015). https://doi.org/10.1016/j.physletb.2015.10.016
M. Bordone, G. Isidori, D. van Dyk, Impact of leptonic \(\tau \) decays on the distribution of \(B\rightarrow P\mu \bar{\nu }\) decays. Eur. Phys. J. C 76(7), 360 (2016). https://doi.org/10.1140/epjc/s10052-016-4202-x
S. Meinel, D. van Dyk, Using \(\Lambda _b\rightarrow \Lambda \mu ^+\mu ^-\) data within a Bayesian analysis of \(|\Delta B| = |\Delta S| = 1\) decays. Phys. Rev. D 94(1), 013007 (2016). https://doi.org/10.1103/PhysRevD.94.013007
P. Böer, T. Feldmann, D. van Dyk, QCD factorization theorem for \(B \rightarrow \pi \pi \ell \nu \) decays at large dipion masses. JHEP 02, 133 (2017). https://doi.org/10.1007/JHEP02(2017)133
N. Serra, R. Silva Coutinho, D. van Dyk, Measuring the breaking of lepton flavor universality in \(B\rightarrow K^*\ell ^+\ell ^-\). Phys. Rev. D 95(3), 035029 (2017). https://doi.org/10.1103/PhysRevD.95.035029
C. Bobeth, M. Chrzaszcz, D. van Dyk, J. Virto, Long-distance effects in \(B\rightarrow K^*\ell \ell \) from analyticity. Eur. Phys. J. C 78(6), 451 (2018). https://doi.org/10.1140/epjc/s10052-018-5918-6
T. Blake, M. Kreps, Angular distribution of polarised \(\Lambda _b\) baryons decaying to \(\Lambda \ell ^+\ell ^-\). JHEP 11, 138 (2017). https://doi.org/10.1007/JHEP11(2017)138
P. Böer, M. Bordone, E. Graverini, P. Owen, M. Rotondo, D. van Dyk, Testing lepton flavour universality in semileptonic \(\Lambda _b \rightarrow \Lambda _c^*\) decays. JHEP 06, 155 (2018). https://doi.org/10.1007/JHEP06(2018)155
T. Feldmann, D. van Dyk, K.K. Vos, Revisiting \(B \rightarrow \pi \pi \ell \nu \) at large dipion masses. JHEP 10, 030 (2018). https://doi.org/10.1007/JHEP10(2018)030
N. Gubernari, A. Kokulu, D. van Dyk, \(B\rightarrow P\) and \(B\rightarrow V\) form factors from \(B\)-meson light-cone sum rules beyond leading twist. JHEP 01, 150 (2019). https://doi.org/10.1007/JHEP01(2019)150
P. Böer, A. Kokulu, J.N. Toelstede, D. van Dyk, Angular analysis of \(\Lambda _b\rightarrow \Lambda _c (\rightarrow \Lambda \pi )\ell \bar{\nu }\). JHEP 12, 082 (2019). https://doi.org/10.1007/JHEP12(2019)082
M. Bordone, M. Jung, D. van Dyk, Theory determination of \(\bar{B}\rightarrow D^{(*)}\ell ^-\bar{\nu }\) form factors at \(\cal{O}(1/m_c^2)\). Eur. Phys. J. C 80(2), 74 (2020). https://doi.org/10.1140/epjc/s10052-020-7616-4
T. Blake, S. Meinel, D. van Dyk, Bayesian analysis of \(b\rightarrow s\mu ^+\mu ^-\) Wilson coefficients using the full angular distribution of \(\Lambda _b\rightarrow \Lambda (\rightarrow p\, \pi ^-)\mu ^+\mu ^-\) decays. Phys. Rev. D 101(3), 035023 (2020). https://doi.org/10.1103/PhysRevD.101.035023
M. Bordone, N. Gubernari, D. van Dyk, M. Jung, Heavy-quark expansion for \({{\bar{B}}_s\rightarrow D^{(*)}_s}\) form factors and unitarity bounds beyond the \({SU(3)_F}\) limit. Eur. Phys. J. C 80(4), 347 (2020). https://doi.org/10.1140/epjc/s10052-020-7850-9
N. Gubernari, D. van Dyk, J. Virto, Non-local matrix elements in \(B_{(s)}\rightarrow \{K^{(*)},\phi \}\ell ^+\ell ^-\). JHEP 02, 088 (2021). https://doi.org/10.1007/JHEP02(2021)088
S. Bruggisser, R. Schäfer, D. van Dyk, S. Westhoff, The flavor of UV physics. JHEP 05, 257 (2021). https://doi.org/10.1007/JHEP05(2021)257
D. Leljak, B. Melić, D. van Dyk, The \(\bar{B} \rightarrow \pi \) form factors from QCD and their impact on \(|V_{ub}|\). JHEP 07, 036 (2021). https://doi.org/10.1007/JHEP07(2021)036
C. Bobeth, M. Bordone, N. Gubernari, M. Jung, D. van Dyk, Lepton-flavour non-universality of \({\bar{B}}\rightarrow D^*\ell {{\bar{\nu }}}\) angular distributions in and beyond the Standard Model. Eur. Phys. J. C 81(11), 984 (2021). https://doi.org/10.1140/epjc/s10052-021-09724-2
T. Aaltonen et al., Measurements of the angular distributions in the decays \(B \rightarrow K^{(*)} \mu ^+ \mu ^-\) at CDF. Phys. Rev. Lett. 108, 081807 (2012). https://doi.org/10.1103/PhysRevLett.108.081807
S. Chatrchyan et al., Angular analysis and branching fraction measurement of the decay \(B^0 \rightarrow K^{*0} \mu ^+\mu ^-\). Phys. Lett. B 727, 77 (2013). https://doi.org/10.1016/j.physletb.2013.10.017
V. Khachatryan et al., Angular analysis of the decay \(B^0 \rightarrow K^{*0} \mu ^+ \mu ^-\) from pp collisions at \(\sqrt{s} = 8\) TeV. Phys. Lett. B 753, 424 (2016). https://doi.org/10.1016/j.physletb.2015.12.020
R. Aaij et al., Measurement of the isospin asymmetry in \(B \rightarrow K^{(*)}\mu ^+\mu ^-\) decays. JHEP 07, 133 (2012). https://doi.org/10.1007/JHEP07(2012)133
R. Aaij et al., Differential branching fraction and angular analysis of the decay \(B^{0} \rightarrow K^{*0} \mu ^{+}\mu ^{-}\). JHEP 08, 131 (2013). https://doi.org/10.1007/JHEP08(2013)131
R. Aaij et al., Angular analysis of charged and neutral \(B \rightarrow K \mu ^+\mu ^-\) decays. JHEP 05, 082 (2014). https://doi.org/10.1007/JHEP05(2014)082
R. Aaij et al., Angular analysis of the \(B^{0} \rightarrow K^{*0} \mu ^{+} \mu ^{-}\) decay using 3 fb\(^{-1}\) of integrated luminosity. JHEP 02, 104 (2016). https://doi.org/10.1007/JHEP02(2016)104
R. Aaij et al., Angular moments of the decay \(\Lambda _b^0 \rightarrow \Lambda \mu ^{+} \mu ^{-}\) at low hadronic recoil. JHEP 09, 146 (2018). https://doi.org/10.1007/JHEP09(2018)146
R. Aaij et al., Measurement of \(CP\)-averaged observables in the \(B^{0}\rightarrow K^{*0}\mu ^{+}\mu ^{-}\) decay. Phys. Rev. Lett. 125(1), 011802 (2020). https://doi.org/10.1103/PhysRevLett.125.011802
Belle-II Framework Software Group. https://github.com/belle2/externals
T. Kuhr, C. Pulvermacher, M. Ritter, T. Hauth, N. Braun, The Belle II Core Software. Comput. Softw. Big Sci. 3(1), 1 (2019). https://doi.org/10.1007/s41781-018-0017-9
G. Van Rossum, F.L. Drake Jr., Python tutorial (Centrum voor Wiskunde en Informatica, Amsterdam, 1995)
C.R. Harris et al., Array programming with NumPy. Nature 585(7825), 357 (2020). https://doi.org/10.1038/s41586-020-2649-2
F. Beaujean, S. Jahn, pypmc online documentation (2021). https://pypmc.github.io
T. Kluyver, B. Ragan-Kelley, F. Pérez, B. Granger, M. Bussonnier, J. Frederic, K. Kelley, J. Hamrick, J. Grout, S. Corlay, P. Ivanov, D. Avila, S. Abdalla, C. Willing, Jupyter development team, in Positioning and Power in Academic Publishing: Players, Agents and Agendas, ed. by F. Loizides, B. Schmidt (IOS Press, Netherlands, 2016), pp. 87–90. https://eprints.soton.ac.uk/403913/
N.J. Smith, T. Kluyver, Future ’manylinux’ Platform Tags for Portable Linux Built Distributions (2019). https://www.python.org/dev/peps/pep-0600/
D. van Dyk et al., EOS v1.0 online documentation (2021). https://eos.github.io/doc/v1.0/
D.M. Straub, flavio: a Python package for flavour and precision phenomenology in the Standard Model and beyond (2018)
S. Neshatpour, F. Mahmoudi, Flavour Physics with SuperIso. PoS TOOLS2020, 036 (2021). https://doi.org/10.22323/1.392.0036
J. De Blas et al., HEPfit: a code for the combination of indirect and direct constraints on high energy physics models. Eur. Phys. J. C 80(5), 456 (2020). https://doi.org/10.1140/epjc/s10052-020-7904-z
F.U. Bernlochner et al., FlavBit: a GAMBIT module for computing flavour observables and likelihoods. Eur. Phys. J. C 77(11), 786 (2017). https://doi.org/10.1140/epjc/s10052-017-5157-2
N. Gubernari, M. Reboud, D. van Dyk, J. Virto, (2021). To appear
D. van Dyk et al., EOS v1.0 Python API (2021). https://eos.github.io/doc/v1.0/api/python.html
D. van Dyk et al., EOS example notebooks (2021). https://github.com/eos/eos/tree/v1.0/examples/
A. Bharucha, D.M. Straub, R. Zwicky, \(B\rightarrow V\ell ^+\ell ^-\) in the Standard Model from light-cone sum rules. JHEP 08, 098 (2016). https://doi.org/10.1007/JHEP08(2016)098
G.E. Crooks, The amoroso distribution (2015)
J.A. Bailey et al., \(B\rightarrow D \ell \nu \) form factors at nonzero recoil and \(|V_{cb}|\) from 2+1-flavor lattice QCD. Phys. Rev. D 92(3), 034506 (2015). https://doi.org/10.1103/PhysRevD.92.034506
R. Glattauer et al., Measurement of the decay \(B\rightarrow D\ell \nu _\ell \) in fully reconstructed events and determination of the Cabibbo-Kobayashi-Maskawa matrix element \(|V_{cb}|\). Phys. Rev. D 93(3), 032006 (2016). https://doi.org/10.1103/PhysRevD.93.032006
H. Na, C.M. Bouchard, G.P. Lepage, C. Monahan, J. Shigemitsu, \(B \rightarrow D \ell \nu \) form factors at nonzero recoil and extraction of \(|V_{cb}|\). Phys. Rev. D 92(5), 054510 (2015). https://doi.org/10.1103/PhysRevD.93.119906 [Erratum: Phys. Rev. D 93, 119906 (2016)]
J.A. Bailey et al., \(B\rightarrow D\ell \nu \) form factors at nonzero recoil and \(|V_{cb}|\) from 2+1-flavor lattice QCD. Phys. Rev. D 92(3), 034506 (2015). https://doi.org/10.1103/PhysRevD.92.034506
N. Metropolis, A.W. Rosenbluth, M.N. Rosenbluth, A.H. Teller, E. Teller, Equation of state calculations by fast computing machines. J. Chem. Phys. 21(6), 1087 (1953). https://doi.org/10.1063/1.1699114
W.K. Hastings, Monte Carlo sampling methods using Markov chains and their applications. Biometrika 57(1), 97 (1970). https://doi.org/10.1093/biomet/57.1.97
H. Haario, E. Saksman, J. Tamminen, An adaptive metropolis algorithm. Bernoulli 7(2), 223 (2001). http://www.jstor.org/stable/3318737
M. Kilbinger, D. Wraith, C.P. Robert, K. Benabed, O. Cappé, J.F. Cardoso, G. Fort, S. Prunet, F.R. Bouchet, Bayesian model comparison in cosmology with Population Monte Carlo. MNRAS 405(4), 2381 (2010). https://doi.org/10.1111/j.1365-2966.2010.16605.x
F. Beaujean, A. Caldwell, Initializing adaptive importance sampling with Markov chains. arXiv:1304.7808 (2013)
J.D. Hunter, Matplotlib: a 2d graphics environment. Comput. Sci. Eng. 9(3), 90 (2007). https://doi.org/10.1109/MCSE.2007.55
A. Gelman, J.B. Carlin, H.S. Stern, D.B. Rubin, Bayesian Data Analysis, 2nd edn. (Chapman and Hall/CRC, 2004)
P. Virtanen, R. Gommers, T.E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, J. Bright, S.J. van der Walt, M. Brett, J. Wilson, K.J. Millman, N. Mayorov, A.R.J. Nelson, E. Jones, R. Kern, E. Larson, C.J. Carey, İ Polat, Y. Feng, E.W. Moore, J. VanderPlas, D. Laxalde, J. Perktold, R. Cimrman, I. Henriksen, E.A. Quintero, C.R. Harris, A.M. Archibald, A.H. Ribeiro, F. Pedregosa, P. van Mulbregt, SciPy 1.0 Contributors, SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 17, 261 (2020). https://doi.org/10.1038/s41592-019-0686-2
L. Wolfenstein, Parametrization of the Kobayashi–Maskawa matrix. Phys. Rev. Lett. 51, 1945 (1983). https://doi.org/10.1103/PhysRevLett.51.1945
J. Charles, A. Hocker, H. Lacker, S. Laplace, F.R. Le Diberder, J. Malcles, J. Ocariz, M. Pivk, L. Roos, CP violation and the CKM matrix: assessing the impact of the asymmetric \(B\) factories. Eur. Phys. J. C 41(1), 1 (2005). https://doi.org/10.1140/epjc/s2005-02169-1
G. Buchalla, A.J. Buras, M.E. Lautenbacher, Weak decays beyond leading logarithms. Rev. Mod. Phys. 68, 1125 (1996). https://doi.org/10.1103/RevModPhys.68.1125
A.J. Buras, In Les Houches Summer School in Theoretical Physics, Session 68: Probing the Standard Model of Particle Interactions (1998)
A.J. Buras, Climbing NLO and NNLO Summits of Weak Decays (2011)
J. Aebischer, M. Fael, C. Greub, J. Virto, B physics beyond the Standard Model at one loop: complete renormalization group evolution below the electroweak scale. JHEP 09, 158 (2017). https://doi.org/10.1007/JHEP09(2017)158
E.E. Jenkins, A.V. Manohar, P. Stoffer, Low-energy effective field theory below the electroweak scale: operators and matching. JHEP 03, 016 (2018). https://doi.org/10.1007/JHEP03(2018)016
J. Aebischer et al., WCxf: an exchange format for Wilson coefficients beyond the Standard Model. Comput. Phys. Commun. 232, 71 (2018). https://doi.org/10.1016/j.cpc.2018.05.022
The WCxf Authors. EOS WET basis (2021). https://wcxf.github.io/assets/pdf/WET.EOS.pdf
J. Aebischer, J. Kumar, D.M. Straub, Wilson: a Python package for the running and matching of Wilson coefficients above and below the electroweak scale. Eur. Phys. J. C 78(12), 1026 (2018). https://doi.org/10.1140/epjc/s10052-018-6492-7
W. Buchmuller, D. Wyler, Effective Lagrangian analysis of new interactions and flavor conservation. Nucl. Phys. B 268, 621 (1986). https://doi.org/10.1016/0550-3213(86)90262-2
B. Grzadkowski, M. Iskrzynski, M. Misiak, J. Rosiek, Dimension-six terms in the standard model Lagrangian. JHEP 10, 085 (2010). https://doi.org/10.1007/JHEP10(2010)085
K. Adel, Y.P. Yao, \(O(\alpha _s)\) calculation of the decays \(b \rightarrow s \gamma \) and \(b \rightarrow s g\). Phys. Rev. D 49, 4945 (1994). https://doi.org/10.1103/PhysRevD.49.4945
C. Greub, T. Hurth, Two loop matching of the dipole operators for \(b \rightarrow s \gamma \) and \(b \rightarrow s g\). Phys. Rev. D 56, 2934 (1997). https://doi.org/10.1103/PhysRevD.56.2934
C. Bobeth, M. Misiak, J. Urban, Photonic penguins at two loops and \(m_t\) dependence of \(BR[B \rightarrow X_s \ell ^+ \ell ^-]\). Nucl. Phys. B 574, 291 (2000). https://doi.org/10.1016/S0550-3213(00)00007-9
K.G. Chetyrkin, M. Misiak, M. Münz, Weak radiative \(B\) meson decay beyond leading logarithms. Phys. Lett. B 400, 206 (1997) [Erratum: Phys. Lett. B 425, 414 (1998)]. https://doi.org/10.1016/S0370-2693(97)00324-9
C. Bobeth, P. Gambino, M. Gorbahn, U. Haisch, Complete NNLO QCD analysis of \(B \rightarrow X_s \ell ^+ \ell ^-\) and higher order electroweak effects. JHEP 04, 071 (2004). https://doi.org/10.1088/1126-6708/2004/04/071
M. Gorbahn, U. Haisch, Effective Hamiltonian for non-leptonic \(|\Delta F| = 1\) decays at NNLO in QCD. Nucl. Phys. B 713, 291 (2005). https://doi.org/10.1016/j.nuclphysb.2005.01.047
M. Gorbahn, U. Haisch, M. Misiak, Three-loop mixing of dipole operators. Phys. Rev. Lett. 95, 102004 (2005). https://doi.org/10.1103/PhysRevLett.95.102004
T. Huber, E. Lunghi, M. Misiak, D. Wyler, Electromagnetic logarithms in \(B \rightarrow X_s \ell ^+ \ell ^-\). Nucl. Phys. B 740, 105 (2006). https://doi.org/10.1016/j.nuclphysb.2006.01.037
M. Misiak, J. Urban, QCD corrections to FCNC decays mediated by Z penguins and W boxes. Phys. Lett. B 451, 161 (1999). https://doi.org/10.1016/S0370-2693(99)00150-1
G. Buchalla, A.J. Buras, The rare decays \(K\rightarrow \pi \nu \bar{\nu }\), \(B \rightarrow X \nu \bar{\nu }\) and \(B \rightarrow l^+ l^-\): An Update. Nucl. Phys. B 548, 309 (1999). https://doi.org/10.1016/S0550-3213(99)00149-2
A. Sirlin, Large \(m_W, m_Z\) behavior of the \(O(\alpha )\) corrections to semileptonic processes mediated by W. Nucl. Phys. B 196, 83 (1982). https://doi.org/10.1016/0550-3213(82)90303-0
A.J. Buras, M. Jamin, P.H. Weisz, Leading and next-to-leading QCD corrections to \(\epsilon \) parameter and \(B^0 - \bar{B}^0\) mixing in the presence of a heavy top quark. Nucl. Phys. B 347, 491 (1990). https://doi.org/10.1016/0550-3213(90)90373-L
P. Gambino, A. Kwiatkowski, N. Pott, Electroweak effects in the \(B^0 - \bar{B}^0\) mixing. Nucl. Phys. B 544, 532 (1999). https://doi.org/10.1016/S0550-3213(98)00860-8
A.J. Buras, M. Misiak, J. Urban, Two loop QCD anomalous dimensions of flavor changing four quark operators within and beyond the standard model. Nucl. Phys. B 586, 397 (2000). https://doi.org/10.1016/S0550-3213(00)00437-5
O. Ben-Kiki, C. Evans, I. döt Net. YAML Ain’t Markup Language (YAML™) version 1.2 (2021). https://yaml.org/spec/1.2.2/
Acknowledgements
DvD is grateful to Gudrun Hiller, Thomas Mannel, Gino Isidori, and Nico Serra, whose support made the development of EOS possible in the first place. We thank all EOS contributors who are not authors of this paper, including Bastian Müller, Romy O’Connor, Stefanie Reichert, Martin Ritter, Eduardo Romero, Ismo Toijala, and Christian Wacker. The work of DvD, EE, NG, SK, and MR and the development of EOS is supported by the German Research Foundation (DFG) within the Emmy Noether Programme under grant DY 130/1-1 and by the National Natural Science Foundation of China (NSFC) and the DFG through the funds provided to the Sino-German Collaborative Research Center TRR110 “Symmetries and the Emergence of Structure in QCD” (NSFC Grant No. 12070131001, DFG Project-ID 196253076 – TRR 110). The work of TB is supported by the Royal Society (United Kingdom). The work of CB was supported by the DFG under grant BO-4535/1-1. The work of MB and MJ is supported by the Italian Ministry of Research (MIUR) under grant PRIN 20172LNEEZ. The work of NG is also supported by the DFG under grant 396021762 – TRR 257 “Particle Physics Phenomenology after the Higgs Discovery”. The work of RSC and EG was supported by the Swiss National Science Foundation (SNSF) under contracts 159948, 172637 and 174182. The work of PL is supported by the Cluster of Excellence “ORIGINS” funded by the DFG under Germany’s Excellence Strategy – EXC-2094 – 390783311. The work of JV is supported by funding from the Spanish MICINN through the “Ramón y Cajal” program RYC-2017-21870, the “Unit of Excellence María de Maeztu 2020-2023” award to the Institute of Cosmos Sciences (CEX2019-000918-M) and from PID2019-105614GB-C21 and 2017-SGR-929 grants.
Author information
Authors and Affiliations
Consortia
Corresponding author
Additional information
EOS-2021-04, TUM-HEP 1371/21, P3H-21-094, SI-HEP-2021-32.
In the original article a change history entry shall be added: ”The original online version of this article was revised: The monospace words were rendered as images in the HTML version. They have been rendered as text in the revised version. The code blocks were rendered as small images and have been enlarged in the revised version.
Appendices
Details on the models
1.1 The CKM model and parameters
When evaluating low-energy observables within the SM, the CKM matrix elements are evaluated using the Wolfenstein parametrization [77] expanded to order \(\lambda ^8\) [78]. The Wolfenstein parameters \(\lambda \) and A are used without modifications. The \(\rho \) and \(\eta \) parameters are traded for \(\bar{\rho }\) and \(\bar{\eta }\) [78], the coordinates of the apex of the standard unitarity triangle. The two parameters are defined to all orders in \(\lambda \) as [78]
These four parameter can be accessed via CKM::lambda, CKM::A, CKM::rhobar, and CKM::etabar, respectively.
A frequent physics use case involves inferring the absolute value or complex argument of a CKM matrix element from data. Choosing the CKM model using ’model’: ’CKM’ ensures that each complex-valued CKM matrix element is parametrized in terms of its absolute value and complex argument. For example, the parametrization of the CKM matrix element \(V_{ub}\) involves the parameters CKM::abs(V_ub) and CKM::arg(V_ub). The names for the remaining CKM parameter follow the same naming scheme.
1.2 The WET model, operator bases, and parameters
The observables for low-energy processes below the electroweak scale rely on a description in the WET, both within the SM [79,80,81] and in BSM scenarios [82, 83]. Observables can be evaluated within the WET by setting the model option to WET. Within this model, WET Wilson coefficients are parametrized by individual EOS parameters, and CKM matrix elements are treated as in the CKM model; see appendix A.1.
Within EOS, the WET is parametrized as
where \({\mathcal {S}}\) denotes a sector of the WET, i.e., a set of operators with definite quantum numbers under global symmetries preserved by the renormalization group evolution [84]. For each sector, EOS follows the WCxf convention [84]:
Here \({\mathcal {O}}\) denotes the dimension-six operators, and \({\mathcal {C}}\) is a dimensionless Wilson coefficient renormalized at an appropriate low-energy scale \(\mu \). This scale is accessible as an eos.Parameter. The prefix part of its qualified name corresponds to the sector and the name part of its qualified name is mu, i.e., for the sector sbsb this parameter is named sbsb::mu.
As of version 1.0, EOS supports the following sectors:
-
sb
-
sbee, sbmumu, sbtautau
-
sbnunu
-
sbsb
-
cbenue, cbmunumu, cbtaunutau
-
ubenue, ubmunumu, ubtaunutau
Changes to the parameters representing the Wilson coefficients only affect observables that are constructed with the model option set to ’WET’. By convention the Wilson coefficients comprise both their SM value and potential BSM shifts, i.e.:
A complete list of the sectors and their operators supported by EOS is part of the WCxf basis file [85]. The parameters describing the Wilson coefficients are listed as part of the EOS documentation [55, List of Parameters]. Using WCxf and the wilson package [86], constraints on the WET can be readily interpreted as constraints at a different scale in the WET or as constraints on Wilson coefficients in the Standard Model Effective Field Theory [87, 88].
The SM values of the WET Wilson Coefficients up to mass dimension six are known to high precision in the SM. By default, EOS evaluates observables with the model option set to ’SM’. This choice of option leads EOS to compute the WET Wilson Coefficients at the electroweak scale \(\mu _0\) and evolve them to the appropriate low-energy scale \(\mu \) Footnote 4.
-
For the sectors sb, sbee, sbmumu, and sbtautau, the SM values are computed to NNLO in QCD [89,90,91]. The RG evolution to the low-energy scale \(\sim m_b\) crucially requires the resummation of radiative QCD and partially also QED corrections [92,93,94,95,96].
-
For the sector sbnunu, the SM values are computed to NLO in QCD [97, 98].
-
For the sectors cbenue through ubtaunutau, the SM values are computed to next-to-leading order in QED [99].
-
For the sector sbsb, the SM values are computed to NLO in QCD [100] and NLO in EW [101]. The RG evolution to the low scale \(\sim m_b\) crucially requires the resummation of radiative QCD corrections [102].
Collection of examples
Here we collect a number of code examples that are used in the main text to produce a variety of plots. They have been moved to this appendix to ease legibility of the main text.



Constraints data format
Constraints are stored as YAML [103] files within the EOS source repository in the directory eos/constraints/. Each constraint file is an associative array, with the top-level keys corresponding to the constraint’s qualified name, and the value describing the constraint data. The constraint data itself is also an associative array. The type key determines the type of the likelihood, and therefore which other keys must be present. EOS supports the following types of likelihood:
-
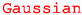 The likelihood is a univariate Gaussian density. It requires the following keys:
The likelihood is a univariate Gaussian density. It requires the following keys:-
 The name of the observable that appears in this likelihood, as an eos.QualifiedName.
The name of the observable that appears in this likelihood, as an eos.QualifiedName. -
 The kinematic variables and their values that underlay the likelihood’s observable, as an associative array.
The kinematic variables and their values that underlay the likelihood’s observable, as an associative array. -
 The option keys and values that underlay the likelihood’s observable, as an associative array.
The option keys and values that underlay the likelihood’s observable, as an associative array. -
 The mean of the likelihood, as a floating point value.
The mean of the likelihood, as a floating point value. -
 The statistical uncertainty of the likelihood, as an associative array with keys hi and lo. For a completely symmetric uncertainty, set both keys to the same value.
The statistical uncertainty of the likelihood, as an associative array with keys hi and lo. For a completely symmetric uncertainty, set both keys to the same value. -
 The systematic uncertainty of the likelihood, as an associative array with keys hi and lo. For a completely symmetric uncertainty, set both keys to the same value.
The systematic uncertainty of the likelihood, as an associative array with keys hi and lo. For a completely symmetric uncertainty, set both keys to the same value. -
 The degrees of freedom, as a floating point value. Must be set to 1 to be backward compatible.
The degrees of freedom, as a floating point value. Must be set to 1 to be backward compatible.
-
-
 The likelihood is a multivariate Gaussian density, and correlations and total uncertainties are specified through the covariance matrix. It requires the following keys:
The likelihood is a multivariate Gaussian density, and correlations and total uncertainties are specified through the covariance matrix. It requires the following keys:-
 The dimension of the covariance matrix, as an integer. Denoted below as D.
The dimension of the covariance matrix, as an integer. Denoted below as D. -
 The degrees of freedom, as an integer.
The degrees of freedom, as an integer. -
 The names of the observables that appear in this likelihood, as an ordered list of eos.QualifiedName of length P. Denoted below as \(\mathbf {o}\).
The names of the observables that appear in this likelihood, as an ordered list of eos.QualifiedName of length P. Denoted below as \(\mathbf {o}\). -
 The kinematic configuration for each of the observables, as an ordered list of length P of associative arrays.
The kinematic configuration for each of the observables, as an ordered list of length P of associative arrays. -
 The options for each of the observables, as an ordered list of length P of associative arrays.
The options for each of the observables, as an ordered list of length P of associative arrays. -
 The mean values of the likelihood, as an ordered list of floating point values. Denoted below as \(\mu \).
The mean values of the likelihood, as an ordered list of floating point values. Denoted below as \(\mu \). -
 The \(D\times D\)-dimensional covariance matrix of the likelihood, as an ordered list of ordered lists of floating point values (row-first ordering). Denoted below as \(\varSigma \).
The \(D\times D\)-dimensional covariance matrix of the likelihood, as an ordered list of ordered lists of floating point values (row-first ordering). Denoted below as \(\varSigma \). -
 The optional \(D\times P\)-dimensional response matrix that converts a P dimensional theory prediction into a D dimension measurement. If not specified, EOS assumes that \(P=D\) and that the response matrix is the identity matrix. Specified as an ordered list of ordered lists of floating point values (row-first ordering). The response matrix is used to fold the theory predictions. This enables fits involving experimental results that have not or cannot be unfolded. Denoted below as R.
The optional \(D\times P\)-dimensional response matrix that converts a P dimensional theory prediction into a D dimension measurement. If not specified, EOS assumes that \(P=D\) and that the response matrix is the identity matrix. Specified as an ordered list of ordered lists of floating point values (row-first ordering). The response matrix is used to fold the theory predictions. This enables fits involving experimental results that have not or cannot be unfolded. Denoted below as R.
The logarithm of the likelihood L reads
$$\begin{aligned} -2 \ln L = -2 \ln {\mathcal {N}}_D(R \mathbf {o}\,|\,\mathbf {\mu }, \varSigma ) \sim \left( \mathbf {\mu }- R \mathbf {o}\right) ^T \varSigma ^{-1} \left( \mathbf {\mu }- R \mathbf {o}\right) . \end{aligned}$$(C.5)In the above, \({\mathcal {N}}_D(\cdot \,|\,\mathbf {\mu },\varSigma )\) denotes a D-variate Gaussian PDF centered at \(\mu \) with covariance \(\varSigma \).
-
-
 The likelihood is a mixture density, with all mixture components being multivariate Gaussian densities. Their correlations and total uncertainties are specified through their respective covariance matrices. It requires the following keys:
The likelihood is a mixture density, with all mixture components being multivariate Gaussian densities. Their correlations and total uncertainties are specified through their respective covariance matrices. It requires the following keys:-
 The dimension of each covariance matrix, as an integer. Denoted below as D.
The dimension of each covariance matrix, as an integer. Denoted below as D. -
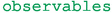 The names of the observables that appear in this likelihood, as an ordered list of eos.QualifiedName of length D. Denoted below as \(\mathbf {o}\).
The names of the observables that appear in this likelihood, as an ordered list of eos.QualifiedName of length D. Denoted below as \(\mathbf {o}\). -
 The kinematic configuration for each of the observables, as an ordered list of length D of associative arrays.
The kinematic configuration for each of the observables, as an ordered list of length D of associative arrays. -
 The options for each of the observables, as an ordered list of length D of associative arrays.
The options for each of the observables, as an ordered list of length D of associative arrays. -
 The description of the mixture components as a list of length N. Each list element is an associative array that requires the following keys:
The description of the mixture components as a list of length N. Each list element is an associative array that requires the following keys:-
 The mean values of this component, as a list of floats of length D. Denoted below as \(\mathbf {\mu }_n\).
The mean values of this component, as a list of floats of length D. Denoted below as \(\mathbf {\mu }_n\). -
 The covariance of this component, as a list of lists of floats. Denoted below as \(\varSigma _n\).
The covariance of this component, as a list of lists of floats. Denoted below as \(\varSigma _n\).
-
-
 The weights of the mixture components as a list of length N. Denoted below as \(\alpha _n\).
The weights of the mixture components as a list of length N. Denoted below as \(\alpha _n\).
The likelihood L reads
$$\begin{aligned} L = \sum _{n=1}^N \alpha _n\, {\mathcal {N}}_D(\mathbf {o}\,|\,\mathbf {\mu }_n, \varSigma _n) \qquad \text {with} \qquad \sum _{n=1}^N \alpha _n = 1. \end{aligned}$$(C.6) -

Glossary of EOS classes
-
eos.Analysis.....5, 10, 11, 16
-
log_pdf....................17
-
optimize..............11, 17
-
parameters...............11
-
sample.............11, 15-17
-
sample_pmc..........11, 18
-
eos.Constraint 4, 5, 9, 13, 15
-
eos.Constraints......5, 9, 10
-
eos.Kinematics........5-8, 10
-
declare.....................6
-
eos.KinematicVariable 5-7, 10, 14
-
set............................7
-
eos.Observable.....4-6, 8-10
-
evaluate....................9
-
kinematics................9
-
make........................8, 9
-
name...........................9
-
options.....................9
-
parameters................9
-
references...............13
-
eos.Observables..........5, 8
-
eos.Option......................5
-
eos.Options..........5, 7-9, 20
-
declare.....................8
-
eos.Parameter.....4-6, 14, 23
-
evaluate....................6
-
latex.........................6
-
name...........................6
-
set........................6, 11
-
eos.Parameters.....5, 6, 9, 10
-
dump......................6, 11
-
override_from_file..6
-
eos.Plotter ...........5, 12, 14
-
alpha.......................12
-
color.......................12
-
constraint...............12
-
histogram................12
-
histogram2D.............12
-
label.......................12
-
observable...............12
-
plot............14-16, 19, 21
-
uncertainty.............12
-
eos.QualifiedName..4, 8-10, 25, 26
-
eos.Reference...........12, 13
-
eos.ReferenceName....12, 13
-
eos.References .............12
-
eos.SignalPDF........5, 10, 20
-
sample_mcmc.............20
-
eos.SignalPDFs..........5, 10
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3. SCOAP3 supports the goals of the International Year of Basic Sciences for Sustainable Development.
About this article
Cite this article
van Dyk, D., Beaujean, F., Blake, T. et al. EOS: a software for flavor physics phenomenology. Eur. Phys. J. C 82, 569 (2022). https://doi.org/10.1140/epjc/s10052-022-10177-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-022-10177-4



 The prefix part is used to separate objects with (otherwise) identical names into different namespaces, to avoid conflicts. Examples of prefixes include parameter categories (e.g.,
The prefix part is used to separate objects with (otherwise) identical names into different namespaces, to avoid conflicts. Examples of prefixes include parameter categories (e.g.,  The name part is used to identify objects within its
The name part is used to identify objects within its  The (optional) suffix part is used to distinguish between objects of otherwise identical names based on context. One example is the parameter describing the
The (optional) suffix part is used to distinguish between objects of otherwise identical names based on context. One example is the parameter describing the  The option list is an optional comma-separated list of key/value pairs, which allows to modify the named object in an unambiguous way. One example is
The option list is an optional comma-separated list of key/value pairs, which allows to modify the named object in an unambiguous way. One example is 
 is used to change the behavior of the low-energy observables. As of
is used to change the behavior of the low-energy observables. As of  is used to select from one of the available parametrizations of hadronic form factors that are pertinent to the process. Its values are process-specific. For true observables (e.g., a semileptonic branching ratio) a sensible default choice is always provided. For pseudo-observables (e.g., the hadronic form factors
is used to select from one of the available parametrizations of hadronic form factors that are pertinent to the process. Its values are process-specific. For true observables (e.g., a semileptonic branching ratio) a sensible default choice is always provided. For pseudo-observables (e.g., the hadronic form factors  is used to select the charged lepton flavor in processes with at least one charged lepton. Allowed values are generally
is used to select the charged lepton flavor in processes with at least one charged lepton. Allowed values are generally  is used to select the spectator quark flavor. Allowed values are typically
is used to select the spectator quark flavor. Allowed values are typically  is a mandatory
is a mandatory  is a mandatory
is a mandatory  is an optional
is an optional  is an optional
is an optional  is an optional
is an optional  uses the
uses the  uses the
uses the  uses the
uses the 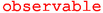 plots a single
plots a single 
 plots either a 1D or a 2D histogram of pre-existing random samples. These samples can be contained in
plots either a 1D or a 2D histogram of pre-existing random samples. These samples can be contained in  plots the uncertainty band of an observables as a function of one kinematic variable or one parameter. The random samples for the observables can be contained in
plots the uncertainty band of an observables as a function of one kinematic variable or one parameter. The random samples for the observables can be contained in  displays a constraint either from the
displays a constraint either from the  :
: :
: :
:




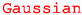 The likelihood is a univariate Gaussian density. It requires the following keys:
The likelihood is a univariate Gaussian density. It requires the following keys: The name of the observable that appears in this likelihood, as an
The name of the observable that appears in this likelihood, as an  The kinematic variables and their values that underlay the likelihood’s observable, as an associative array.
The kinematic variables and their values that underlay the likelihood’s observable, as an associative array. The option keys and values that underlay the likelihood’s observable, as an associative array.
The option keys and values that underlay the likelihood’s observable, as an associative array. The mean of the likelihood, as a floating point value.
The mean of the likelihood, as a floating point value. The statistical uncertainty of the likelihood, as an associative array with keys
The statistical uncertainty of the likelihood, as an associative array with keys  The systematic uncertainty of the likelihood, as an associative array with keys
The systematic uncertainty of the likelihood, as an associative array with keys  The degrees of freedom, as a floating point value. Must be set to
The degrees of freedom, as a floating point value. Must be set to  The likelihood is a multivariate Gaussian density, and correlations and total uncertainties are specified through the covariance matrix. It requires the following keys:
The likelihood is a multivariate Gaussian density, and correlations and total uncertainties are specified through the covariance matrix. It requires the following keys: The dimension of the covariance matrix, as an integer. Denoted below as D.
The dimension of the covariance matrix, as an integer. Denoted below as D. The degrees of freedom, as an integer.
The degrees of freedom, as an integer. The names of the observables that appear in this likelihood, as an ordered list of
The names of the observables that appear in this likelihood, as an ordered list of  The kinematic configuration for each of the observables, as an ordered list of length P of associative arrays.
The kinematic configuration for each of the observables, as an ordered list of length P of associative arrays. The options for each of the observables, as an ordered list of length P of associative arrays.
The options for each of the observables, as an ordered list of length P of associative arrays. The mean values of the likelihood, as an ordered list of floating point values. Denoted below as
The mean values of the likelihood, as an ordered list of floating point values. Denoted below as  The
The  The optional
The optional  The likelihood is a mixture density, with all mixture components being multivariate Gaussian densities. Their correlations and total uncertainties are specified through their respective covariance matrices. It requires the following keys:
The likelihood is a mixture density, with all mixture components being multivariate Gaussian densities. Their correlations and total uncertainties are specified through their respective covariance matrices. It requires the following keys: The dimension of each covariance matrix, as an integer. Denoted below as D.
The dimension of each covariance matrix, as an integer. Denoted below as D.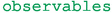 The names of the observables that appear in this likelihood, as an ordered list of
The names of the observables that appear in this likelihood, as an ordered list of  The kinematic configuration for each of the observables, as an ordered list of length D of associative arrays.
The kinematic configuration for each of the observables, as an ordered list of length D of associative arrays. The options for each of the observables, as an ordered list of length D of associative arrays.
The options for each of the observables, as an ordered list of length D of associative arrays. The description of the mixture components as a list of length N. Each list element is an associative array that requires the following keys:
The description of the mixture components as a list of length N. Each list element is an associative array that requires the following keys: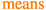 The mean values of this component, as a list of floats of length D. Denoted below as
The mean values of this component, as a list of floats of length D. Denoted below as  The covariance of this component, as a list of lists of floats. Denoted below as
The covariance of this component, as a list of lists of floats. Denoted below as  The weights of the mixture components as a list of length N. Denoted below as
The weights of the mixture components as a list of length N. Denoted below as