$D_s \rightarrow f_0(980)$ form factors and the $D_s^+ \rightarrow (f_0(980) \rightarrow )\left[ \pi \pi \right] _{S}^{\textrm{I} = 0} e^+ \nu _e$ decay from light-cone sum rules

Abstract

In this paper we revisit $D_s \rightarrow f_0(980)$ form factors from the light-cone sum rules based on the ${\bar{q}}q$ picture of $f_0(980)$. The main motivation of this study is the decay width of $D_s^+ \rightarrow \left[ \pi \pi \right] _{S}^{\textrm{I} = 0} e^+ \nu _e$ measured recently by BESIII collaboration and the $D_s \rightarrow f_0(980)$ form factor extracted under the resonant model, here the subscript S and superscript $\textrm{I}=0$ indicate the S-wave isoscalar dipion system. Our result of the differential width of $D_s^+ \rightarrow f_0(980) (\rightarrow \left[ \pi \pi \right] _{S}^{\textrm{I} = 0}) e^+ \nu _e$ decay obtained under the narrow width approximation is lower than the data, the result obtained under the resonant Flatté model is consistent with the data, indicating a sizable mixing $\sim 20^{\circ }$ between ${\bar{s}}s$ and ${\bar{u}}u+{\bar{d}}d$ of $f_0$. In order to get a model independent prediction, we suggest to calculate $D_s \rightarrow \left[ \pi \pi \right] ^{\textrm{I} = 0}$ form factors with the isoscalar dipion light-cone distribution amplitudes. Our calculation of $D_s \rightarrow \left[ \pi \pi \right] ^{\textrm{I} = 0}$ form factors is carried out at leading twist level due to the finite knowledge of dipion system, the differential width shows a moderate evolution in contrast to that obtained from the narrow width approximation and the Flatté model. Since the $D_s \rightarrow f_0(980)$ form factors is dominated by the twist three contribution, further measurements on four-body semileptonic charm decays would help us to study the dimeson light-cone distribution amplitudes, especially for the subleading twist one.

1 Introduction

Weak decays of hadrons containing at least a valence bottom or charm quarks play an important role in the precise examination of standard model (SM) and offer one of the best chance for the discovery of new physics (NP), in which the semileptonic $D_s$ weak decays provide the clear environment to study the structure of light hadrons [1]. For examples, the semileptonic decay with $D_s \rightarrow \eta ^{(\prime )}$ transition provides an opportunity to study the $\eta$-$\eta ^\prime$ mixing [2,3,4], the decay deduced by $D_s \rightarrow f_0(980)$ and $D_s \rightarrow a_0(980)$ transitions could help us to understand the composition figure of scalar mesons [5,6,7] and the isospin-violated $f_0$-$a_0$ mixing [8, 9]. In this work, we focus on the $D_s^+ \rightarrow f_0(980) e^+ \nu _e$ decay by considering the width effect in the differential width.

From the quark model and the spectral analysis of low-energy scattering experiments, the underlying assignments of scalar mesons like $f_0(980)$ is still not clear. Pictures like the tetraquark [10, 11], the glueball [12], the hybrid state [13] and the molecule state [14] are discussed, in which the tetraquark assignment is more favorite nowadays. The case is different in the B meson decay where $f_0(980)$ is energetic and the process happens with large recoiling, then the conventional $q{\bar{q}}$ assignment is the favorite one since the possibility to form a tetra-quark state is power suppressed with comparing to the state of quark pair [15]. In the $D_s \rightarrow f_0(980)$ decay, one may doubt the $q{\bar{q}}$ assignment since $f_0(980)$ is not fast moving enough, but the light-cone sum rules calculations of $D_s \rightarrow a_0(980)$ and $D_s \rightarrow f_0(980)$ form factors, under the ${\bar{q} q}$ assignment with possible mixing between ${\bar{s}}s$ and ${\bar{u}}u + {\bar{d}}d$, explain the measurements well [7, 16]. So a revisiting on this channel with considering the width effect is highly anticipated to check the energetic picture of $f_0(980)$ in charm decay. From the experimental perspective, CLEO collaboration published the first absolute branching fraction measurement of $D_s$ semileptinic decay including a scalar meson in the final state one decade ago. The result is $\mathcal{B}(D_s^+ \rightarrow f_0(980) e^+ \nu _e) \times \mathcal{B}(f_0 \rightarrow \pi ^+\pi ^-) = \left( 2.0 \pm 0.3 \pm 0.1 \right) \times 10^{-3}$ [17,18,19]. Recently, BESIII collaboration has updated the measurements with much better accuracy, the result are $\mathcal{B}(D_s^+ \rightarrow f_0(980) e^+ \nu _e) \times \mathcal{B}(f_0(980) \rightarrow \pi ^0\pi ^0) = \left( 0.79 \pm 0.14 \pm 0.03 \right) \times 10^{-3}$ for the neutral channel [20] and $\mathcal{B}(D_s^+ \rightarrow f_0(980) e^+ \nu _e) \times \mathcal{B}(f_0 \rightarrow \pi ^+\pi ^-) = \left( 1.72 \pm 0.13 \pm 0.10 \right) \times 10^{-3}$ for the charged one [21]. More important result is that BESIII extracted the $D_s \rightarrow f_0(980)$ form factor under the Flatté resonant model with the data corresponding to an integrated luminosity of 7.33 fb$^{-1}$, the result at the full recoiled point is $f_+(q^2=0) = 0.518 \pm 0.018 \pm 0.036$ [21] with the statistical and systematic uncertainties.

In this paper, we revisit the $D_s \rightarrow f_0(980)$ form factor under the ${\bar{q}}q$ assignment to check the reliability of energetic picture of $f_0(980)$ in charm decays. With considering the mixing angle $\theta = 20^{\circ } \pm 10^{\circ }$ between ${\bar{s}}s$ and ${\bar{u}}u + {\bar{d}}d$, the updated LCSRs calculation of $D_s \rightarrow f_0(980)$ form factor is basically in line with the one extracted from the $D_s^+ \rightarrow f_0(980)(\rightarrow \pi \pi ) e^+ \nu _e$ decay under the Flatté model by BESIII. Our calculation is carried out at leading order of strong coupling constant. In order to estimate the next-to-leading-order (NLO) correction, we vary the charm quark mass ${{\bar{m}}}_c(m_c) = 1.3$ GeV by $\pm 0.3$ GeV which deduces $20\%-30\%$ additional uncertainty. We adopt the Flatté formula to discuss the width effect in semileptonic decay $D_s^+ \rightarrow f_0(980)( \rightarrow \pi ^+\pi ^- ) e^+ \nu _e$ and compare the differential width to the recent BESIII measurement [21]. In order to obtain a model independent prediction, we suggest to calculate $D_s \rightarrow \left[ \pi \pi \right] ^{\textrm{I}=0}$ form factors with dipion distribution amplitudes ($2\pi$DAs) and compare directly to the measurement without involving resonants. The $q^2$ dependence of $D_s^+ \rightarrow \left[ \pi ^+\pi ^- \right] _S^{\textrm{I}=0} e^+ \nu _e$ decay width with the direct calculation of $D_s \rightarrow \left[ \pi \pi \right] ^{\textrm{I}=0}$ form factors indeed shows a different behavior comparing to that obtained with a resonant model. Here the subscript S and superscript $\textrm{I}=0$ indicate the S-wave isoscalar dipion system. Our calculation of $D_s \rightarrow \left[ \pi \pi \right] ^{\textrm{I}=0}$ form factors is carried out at leading twist level due to the finite knowledge of $2\pi$DAs. The subleading twist $2\pi$DAs is urgent to help us to complete the model independent calculation, more precise measurement is highly anticipated to help us determine the subleading twist $2\pi$DAs.

The rest of this paper is organized as follows. In the next section, the $D_s \rightarrow f_0(980)$ transition form factors are calculated from the light-cone sum rules under the single particle approximation. In Sect. 3, the chiral even generalized $\pi \pi$ distribution amplitudes are introduced and the $D_s \rightarrow \left[ \pi \pi \right] ^{\textrm{I}=0}$ form factors are obtained at leading twist level. The phenomena related to the recent BESIII measurement is presented in Sect. 4, where the differential width is discussed under the narrow width approximation, Flatté resonant model and the direct $D_s \rightarrow \left[ \pi \pi \right] _S^{\textrm{I}=0}$ transition. The summary is given in Sect. 5. In Appendix A, we revisit the QCD sum rules for the decay constant and LCDAs of scalar meson.

Table 1 Scenarios of the currents to evaluate the $D_s \rightarrow f_0$ form factors

2 $D_s \rightarrow f_0(980)$ form factors

$D_s \rightarrow f_0(980)$ form factors with the momentum transfer $q = p - p_1$ are defined by

$$\begin{aligned}{} & {} \langle f_0(p_1) \vert {\bar{s}} \gamma _\mu \gamma _5 c \vert D_s^+(p) \rangle \nonumber \\{} & {} \quad = -i f_1(q^2) \left[ (p + p_1)_\mu - \frac{m_{D_s}^2 - m_{f_0}^2}{q^2} q_\mu \right] \nonumber \\{} & {} \qquad - i f_0(q^2) \frac{m_{D_s}^2 - m_{f_0}^2}{q^2} q_\mu \nonumber \\{} & {} \quad = -i \left[ f_+(q^2) \left( p + p_1 \right) _\mu + f_-(q^2) q_\mu \right] . \nonumber \\{} & {} \qquad \langle f_0(p_1) \vert {\bar{s}} \sigma _{\mu \nu } \gamma _5 q^\mu c \vert D_s^+(p) \rangle \nonumber \\{} & {} \quad = - \frac{f_T(q^2)}{m_{D_s} + m_{f_0}} \left[ q^2 \left( p + p_1 \right) _\nu - \left( m_{D_s}^2 - m_{f_0}^2 \right) q_\nu \right] .\nonumber \\ \end{aligned}$$

(1)

For the transition deduced by the axial-vector current, the two definitions are related by

$$\begin{aligned}{} & {} f_+(q^2) = f_1(q^2) , \nonumber \\{} & {} f_-(q^2) = \frac{m_{D_s}^2 - m_{f_0}^2}{q^2} f_0(q^2) - \frac{m_{D_s}^2 - m_{f_0}^2}{q^2} f_1(q^2) . \end{aligned}$$

(2)

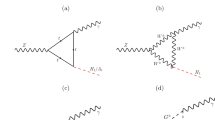
To evaluate the form factors, we start with the correlation functions

$$\begin{aligned}{} & {} \varPi _\mu ^{\mathrm{S_i}}(p_1,q) = i \int d^4x e^{iqx} \langle f_0(p_1) \vert \textrm{T} \{j_{1,\mu }^{\mathrm{S_i}}(x), j_{2}^{\mathrm{S_i}} \} \vert 0 \rangle , \end{aligned}$$

(3)

$$\begin{aligned}{} & {} \tilde{\varPi }_\mu ^{\mathrm{S_i}}(p_1,q) = i \int d^4x e^{iqx} \langle f_0(p_1) \vert T\{\tilde{j}_{1,\mu }^{\mathrm{S_i}}(x), j_{2}^{\mathrm{S_i}} \} \vert 0 \rangle , \end{aligned}$$

(4)

where $j_{1,\mu }$ and $\tilde{j}_{1,\mu }$ are the weak transition currents, $j_2$ is the hadron interpolating current. $\phi$ and $\phi ^{s/\sigma }$ are the leading and subleading twist light-cone distribution amplitudes (LCDAs) of $f_0$ meson under the single particle approximation, respectively. As shown in Table 1, the Roman alphabets $\mathrm{S_i}$ denote different scenarios of the currents. We highlight that both the leading and subleading twist LCDAs of scalar meson contribute to $D_s \rightarrow f_0(980)$ form factors if we take the conventional currents $\mathrm{S_1}$, while only the leading or subleading twist LCDAs contribute to the form factors if we take the chiral currents $\mathrm{S_{2,3}}$.

In the physical region, the long-distance quark–gluon interaction between the two currents in Eqs. (3, 4) begins to form hadrons. In this respect, the correlation function can be understood by the sum of contributions from all possible intermediate states with appropriate subtractions. We take the (axial)-vector current in the weak vertex for example to show the dispersion relation of invariant amplitudes on the variable $(p_1+q)^2 > 0$, which is written as

$$\begin{aligned} \varPi _\mu ^{\mathrm{S_1, had}}(p_1,q)= & {} \frac{\langle f_0(p_1) \vert j_{1,\mu }^{\mathrm{S_1}}(x) \vert D_s(p_1+q) \rangle \langle D_s \vert j_2^{\mathrm{S_1}}(0) \vert 0 \rangle }{m_{D_s}^2 - (p_1+q)^2} \nonumber \\{} & {} + \frac{1}{\pi } \int _{s^i_0}^\infty ds \frac{\rho _\mu ^h(s,q^2)}{s-(p_1+q)^2}. \end{aligned}$$

(5)

The contribution from the ground state $D_s$ is isolated from the excited states and continuum spectra by introducing a threshold value $s_0$. With the form factors defined in Eq. (1) and the decay constant defined by $\langle D_s(p_1+q) \vert j_s^{\mathrm{S_1}}(0) \vert 0 \rangle = m_{D_s}^2 f_{D_s}/(m_c+m_s)$, we replace Eq. (5) by

$$\begin{aligned}{} & {} \varPi _\mu ^{\mathrm{S_1, had}}(p_1,q) \nonumber \\{} & {} \quad = \frac{-i m_{D_s}^2 f_{D_s} \left[ 2 f_+(q^2) p_{1 \nu } + \left( f_+(q^2) + f_-(q^2) \right) q_\mu \right] }{ (m_c+m_s) \left[ m_{D_s}^2 - (p_1+q)^2 \right] } \nonumber \\{} & {} \qquad + \frac{1}{\pi } \int _{s^1_0}^\infty ds \frac{\rho _+^h(s,q^2) p_{1 \mu } + \rho _-^h(s,q^2) q_{\mu } }{s-(p_1+q)^2}. \end{aligned}$$

(6)

At the hadron level, the correlation functions under different scenarios $\mathrm{S_i}$ of the weak currents have the relations

$$\begin{aligned} \varPi _\mu ^{\mathrm{S_1, had}}(p_1,q) = \varPi _\mu ^{\mathrm{S_2, had}}(p_1,q) = - \varPi _\mu ^{\mathrm{S_3}}(p_1,q). \end{aligned}$$

(7)

In the Euclidean momenta space with negative $q^2$, the correlation functions can be evaluated directly by QCD at the quark–gluon level. Since the operator product expansion (OPE) is valid for large energies of the final state mesons, the momentum transfer squared is restricted to be not too large $0 \leqslant \vert q^2 \vert \leqslant q^2_{\textrm{max}}$, in this way the operator product of the c-quark fields in the correlation function can be expanded near the light cone $x^2 \sim 0$ with the large virtuality

(8)

The first and second term in the propagator expression correspond to the free charm quark propagator and the quark–gluon interaction at leading power, respectively, the ellipsis denotes the high power corrections from the quark–gluon interaction. We note that u and ${\bar{u}} = 1 - u$ are the momentum fractions carried by antiquark and quark respectively in the meson. At the parton level, the correlation function defined in Eq. (3) is formulated in a general convolution of hard functions with various LCDAs at different twists

$$\begin{aligned}{} & {} \varPi _\mu ^{\mathrm{S_i, OPE}}(p_1,q) \nonumber \\{} & {} \quad = \sum _{t} \int _0^1 du \, T^{(t)}_\mu (u, q^2, (p_1+q)^2) \otimes \phi ^{(t)}(u) \nonumber \\{} & {} \qquad + \int _0^1 du \int _0^u \mathcal{D} \alpha _i \, T^\prime _\mu (u, \alpha _i, q^2, (p_1+q)^2) \otimes \phi _{3f_0}(\alpha _i),\nonumber \\ \end{aligned}$$

(9)

where the first term comes from two-particle LCDAs, and the second term comes from three-particle LCDAs started at twist three. We can also write the OPE amplitudes in a dispersion integral on the invariant mass of the interpolating heavy meson,

$$\begin{aligned}{} & {} \varPi _\mu ^{\mathrm{S_i, OPE}}(p_1,q) \nonumber \\{} & {} \quad = \frac{1}{\pi } \int _0^1 du \, \sum _{n =1, 2}\nonumber \\{} & {} \qquad \times \left[ \frac{\textrm{Im} \varPi _{+,n}^{\mathrm{S_i, OPE}}(q^2, u) \, p_{1 \mu }+ \textrm{Im} \varPi _{-,n}^{\mathrm{S_i, OPE}}(q^2, u) q_\mu }{u^n \left[ s_2(u) - \left( p_1+q\right) ^2\right] ^n} \right. \nonumber \\{} & {} \qquad + \left. \int _0^u \mathcal{D}\alpha _i \frac{\textrm{Im} \varPi _{+,n}^\mathrm{S_i, OPE}(q^2, u,\alpha _i) \, p_{1 \mu } + \textrm{Im} \varPi _{-,n}^{\mathrm{S_i, OPE}}(q^2, u,\alpha _i) \, q_\mu }{\left[ \alpha _2 + v \left( 1-\alpha _1-\alpha _2 \right) \right] ^n \left[ s_3(u,\alpha _i) - \left( p_1+q\right) ^2\right] ^n} \right] . \nonumber \\ \end{aligned}$$

(10)

The kinematical variables read as $s_2(u) = {\bar{u}} m_{f_0}^2 + (m_c^2 - {\bar{u}} q^2)/u$ and $s_3(u,\alpha _i) = (1 - \alpha _2 - v \alpha _3) m_{f_0}^2 + [m_c^2 - (1 - \alpha _2 - v \alpha _3) q^2 ]/(\alpha _2 + v \alpha _3)$. We then implement the quark-hadron duality to eliminate the contribution from the excited and continuum spectra with introducing the threshold invariant mass $s_0^{i}$. In order to improve the reliability of quark-hadron duality, we Borel transfer both the hadronic representation and the OPE evaluation of the correlation functions. This operation, from one hand, sticks out the ground scalar meson by suppressing the contribution from the excited and continuum spectra in the hadron representation, and from the other hand, guarantees the convergent power expansion in the OPE evaluation. With considering different weak decay currents, the $D_s \rightarrow f_0(980)$ form factors are obtained from LCSRs approach as (${\bar{u}}_0 \equiv 1 - u_0$)

$$\begin{aligned}{} & {} f_+^{\textrm{S1}}(q^2) = \frac{m_c + m_s}{2m_{D_s}^2 f_{D_s}} \left\{ \int _{u_0}^1 \frac{du}{u} \Big [ -m_c \phi (u) + u m_{f_0} \phi ^s(u) \right. \nonumber \\{} & {} \quad + \frac{m_{f_0} \phi ^\sigma (u)}{3} + \frac{m_{f_0} \phi ^\sigma (u)}{6} \frac{m_c^2 + q^2 - u^2m_{f_0}^2}{uM^2} \Big ] e^{\frac{-s_2(u) + m_{D_s}^2}{M^2}} \nonumber \\{} & {} \quad + \int _{u_0}^1 du \int _0^u d \alpha _1 \int _0^{{\bar{u}}} \frac{d \alpha _2}{\alpha _3} \frac{8 m_{f_0}^2 f_{3f_0}^s \phi _{3f_0}^s(\alpha _i)}{\left[ \alpha _2 + v \alpha _3 \right] M^2} \, e^{\frac{-s_3(u,\alpha _i) + m_{D_s}^2}{M^2}} \nonumber \\{} & {} \quad + \frac{m_{f_0} \phi ^\sigma (u_0)}{6} \frac{m_c^2 + q^2 - u_0^2m_{f_0}^2}{m_c^2 - q^2 + u_0^2m_{f_0}^2} \, e^{\frac{-s_0^1 + m_{D_s}^2}{M^2}} + \int _0^{u_0} d \alpha _1 \int _0^{{\bar{u}}_0} \frac{d \alpha _2}{\alpha _3} \nonumber \\{} & {} \quad \left. \cdot \frac{8 m_{f_0}^2 f_{3f_0}^s \phi _{3f_0}^s(\alpha _i) \, \left( \alpha _2 + v_0 \alpha _3 \right) }{\left[ m_c^2 - q^2 + \left( \alpha _2 + v_0 \alpha _3 \right) ^2 m_{f_0}^2\right] } \, e^{\frac{-s_0^1 + m_{D_s}^2}{M^2}} \right\} , \end{aligned}$$

(11)

$$\begin{aligned}{} & {} f_+^{\textrm{S1}}(q^2) + f_-^{\textrm{S1}}(q^2) = \frac{m_c + m_s}{m_{D_s}^2 f_{D_s}} \left\{ \int _{u_0}^1 \frac{du}{u} \Big [ m_{f_0} \phi ^s(u) \right. \nonumber \\{} & {} \quad + \frac{m_{f_0} \phi ^\sigma (u)}{6u} - \frac{m_{f_0} \phi ^\sigma (u)}{6} \frac{m_c^2 - q^2 + u^2m_{f_0}^2}{u^2M^2} \Big ] e^{\frac{-s_2(u) + m_{D_s}^2}{M^2}} \nonumber \\{} & {} \quad + \int _{u_0}^1 du \int _0^u d \alpha _1 \int _0^{{\bar{u}}} \frac{d \alpha _2}{\alpha _3} \frac{8 m_{f_0}^2 f_{3f_0}^s \phi _{3f_0}^s(\alpha _i)}{\left[ \alpha _2 + v \alpha _3 \right] ^2 M^2} \, e^{\frac{-s_3(u,\alpha _i) + m_{D_s}^2}{M^2}} \nonumber \\{} & {} \quad - \frac{m_{f_0} \phi ^\sigma (u_0)}{6 u_0} \, e^{\frac{-s_0^1 + m_{D_s}^2}{M^2}} + \int _0^{u_0} d \alpha _1 \int _0^{{\bar{u}}_0} \frac{d \alpha _2}{\alpha _3} \nonumber \\{} & {} \quad \left. \cdot \frac{8 m_{f_0}^2 f_{3f_0}^s \phi _{3f_0}^s(\alpha _i)}{\left[ m_c^2 - q^2 + \left( \alpha _2 + v_0 \alpha _3 \right) ^2 m_{f_0}^2 \right] } \, e^{\frac{-s_0^1 + m_{D_s}^2}{M^2}} \right\} , \end{aligned}$$

(12)

$$\begin{aligned}{} & {} f_T^{\textrm{S1}}(q^2) = \frac{\left( m_c + m_s\right) \left( m_{D_s}+m_{f_0}\right) }{m_{D_s}^2 f_{D_s}} \nonumber \\{} & {} \quad \times \left\{ \int _{u_0}^1 \frac{du}{u} \Big [ - \frac{\phi (u)}{2} + \frac{m_{f_0} \phi ^\sigma (u)}{6}\frac{m_c}{u M^2} \Big ] e^{\frac{-s_2(u)+m_{D_s}^2}{M^2}} \right. \nonumber \\{} & {} \quad \left. + \frac{m_{f_0} \phi ^\sigma (u_0)}{6} \frac{m_c}{\left[ m_c^2 - q^2 + u_0^2m_{f_0}^2 \right] } \, e^{\frac{-s_0^1+m_{D_s}^2}{M^2}} \right\} , \end{aligned}$$

(13)

$$\begin{aligned}{} & {} f_+^{\textrm{S2}}(q^2) = - \frac{m_c \left( m_c + m_s\right) }{m_{D_s}^2 f_{D_s}} \int _{u_0}^1 \frac{du}{u} \phi (u) e^{\frac{-s_2(u) + m_{D_s}^2}{M^2}}, \end{aligned}$$

(14)

$$\begin{aligned}{} & {} f_+^{\textrm{S2}}(q^2) + f_-^{\textrm{S2}}(q^2) = 0, \end{aligned}$$

(15)

$$\begin{aligned}{} & {} f_T^{\textrm{S2}}(q^2) = - \frac{\left( m_c + m_s\right) \left( m_{D_s}+m_{f_0}\right) }{m_{D_s}^2 f_{D_s}} \nonumber \\{} & {} \quad \cdot \int _{u_0}^1 \frac{du}{u} \phi (u) e^{\frac{-s_2(u)+m_{D_s}^2}{M^2}}, \end{aligned}$$

(16)

$$\begin{aligned}{} & {} f_+^{\textrm{S3}}(q^2) = \frac{\left( m_c + m_s\right) m_{f_0}}{2 m_{D_s}^2 f_{D_s}} \left\{ \int _{u_0}^1 \frac{du}{u} \Big [ 2 u \phi ^s(u) + \frac{2 \phi ^\sigma (u)}{3} \right. \nonumber \\{} & {} \quad + \frac{\phi ^\sigma (u)}{3} \frac{m_c^2 + q^2 - u^2m_{f_0}^2}{uM^2} \Big ] e^{\frac{-s_2(u) + m_{D_s}^2}{M^2}} \nonumber \\{} & {} \quad + \int _{u_0}^1 du \int _0^u d \alpha _1 \int _0^{{\bar{u}}} \frac{d \alpha _2}{\alpha _3} \frac{16 m_{f_0} f_{3f_0}^s \phi _{3f_0}^s(\alpha _i)}{\left[ \alpha _2 + v \alpha _3 \right] M^2} \, e^{\frac{-s_3(u,\alpha _i) + m_{D_s}^2}{M^2}} \nonumber \\{} & {} \quad +\frac{\phi ^\sigma (u_0)}{3} \frac{m_c^2 + q^2 - u_0^2m_{f_0}^2}{m_c^2 - q^2 + u_0^2m_{f_0}^2} \, e^{\frac{-s_0^1 + m_{D_s}^2}{M^2}} + \int _0^{u_0} d \alpha _1 \int _0^{{\bar{u}}_0} \frac{d \alpha _2}{\alpha _3} \nonumber \\{} & {} \quad \left. \cdot \frac{16 m_{f_0} f_{3f_0}^s \phi _{3f_0}^s(\alpha _i) \left( \alpha _2 + v_0 \alpha _3 \right) }{\left[ m_c^2 - q^2 + \left( \alpha _2 + v_0 \alpha _3 \right) ^2 m_{f_0}^2\right] } \, e^{\frac{-s_0^1 + m_{D_s}^2}{M^2}} \right\} , \end{aligned}$$

(17)

$$\begin{aligned}{} & {} f_+^{\textrm{S3}}(q^2) + f_-^{\textrm{S3}}(q^2) = \frac{\left( m_c + m_s\right) m_{f_0}}{m_{D_s}^2 f_{D_s}} \left\{ \int _{u_0}^1 \frac{du}{u} \Big [ 2 \phi ^s(u) \right. \nonumber \\{} & {} \quad + \frac{\phi ^\sigma (u)}{3u} - \frac{\phi ^\sigma (u)}{3} \frac{m_c^2 - q^2 + u^2m_{f_0}^2}{u^2M^2} \Big ] e^{\frac{-s_2(u) + m_{D_s}^2}{M^2}}\nonumber \\{} & {} \quad + \int _{u_0}^1 du \int _0^u d \alpha _1 \int _0^{{\bar{u}}} \frac{d \alpha _2}{\alpha _3} \frac{16 m_{f_0} f_{3f_0}^s \phi _{3f_0}^s(\alpha _i)}{\left[ \alpha _2 + v \alpha _3 \right] ^2 M^2} \, e^{\frac{-s_3(u,\alpha _i) + m_{D_s}^2}{M^2}} \nonumber \\{} & {} \quad - \frac{\phi ^\sigma (u_0)}{3 u_0} \, e^{\frac{-s_0^1 + m_{D_s}^2}{M^2}} + \int _0^{u_0} d \alpha _1 \int _0^{{\bar{u}}} \frac{d \alpha _2}{\alpha _3} \nonumber \\{} & {} \quad \left. \cdot \frac{16 m_{f_0} f_{3f_0}^s \phi _{3f_0}^s(\alpha _i)}{\left[ m_c^2 - q^2 + \left( \alpha _2 + v_0 \alpha _3 \right) ^2 m_{f_0}^2 \right] } \, e^{\frac{-s_0^1 + m_{D_s}^2}{M^2}} \right\} , \end{aligned}$$

(18)

$$\begin{aligned}{} & {} f_T^{\textrm{S3}}(q^2) = \frac{\left( m_c + m_s\right) \left( m_{D_s}+m_{f_0}\right) m_c m_{f_0}}{m_{D_s}^2 f_{D_s}} \nonumber \\{} & {} \quad \cdot \left\{ \int _{u_0}^1 \frac{du}{u} \frac{\phi ^\sigma (u)}{3 M^2} \, e^{\frac{-s_2(u)+m_{D_s}^2}{M^2}}\right. \nonumber \\{} & {} \quad \left. + \frac{\phi ^\sigma (u_0)}{3 \left[ m_c^2 - q^2 + u_0^2m_{f_0}^2 \right] } \, e^{\frac{-s_0^1+m_{D_s}^2}{M^2}} \right\} . \end{aligned}$$

(19)

We take the same thresholds for the contributions from two-particle and three-particle LCDAs $s_0 \equiv s_0^1 = s_0^2$, $u_0$ is the threshold momentum fraction taken the solution of $s_i(u_0) = s_0$

$$\begin{aligned} u_0^{i=2,3}= & {} \frac{- (s_0^i - q^2 - m_{f_0}^2) }{2 m_{f_0}^2} \nonumber \\{} & {} + \frac{\sqrt{(s_0^i - q^2 - m_{f_0}^2)^2 + 4 m_{f_0}^2 (m_c^2 - q^2)}}{2 m_{f_0}^2}. \end{aligned}$$

(20)

Table 2 $D_s \rightarrow f_0(980)$ form factors obtained from various theoretical work under the ${\bar{s}}s$ description of $f_0(980)$

Our result shown in Eqs. (11–13), Eqs. (14–16) and Eqs. (17–19) are consistent with that obtained in Ref. [22], Ref. [23] and Ref. [24], respectively. All the calculations are carried out under the ideal ${\bar{q}}q$ configuration that $f_0(980)$ is purely an $s{\bar{s}}$ state. In fact, there are several experiment measurements indicate the mixing between $f_0(980)$ and $f_0(500)$,

$$\begin{aligned}{} & {} f_0(500) = \vert {\bar{n}}n \rangle \cos \theta + \vert {\bar{s}}s \rangle \sin \theta , \nonumber \\{} & {} f_0(980) = - \vert {\bar{n}}n \rangle \sin \theta + \vert {\bar{s}}s \rangle \cos \theta . \end{aligned}$$

(21)

Here ${\bar{n}}n = ({\bar{u}}u + {\bar{d}}d)/\sqrt{2}$. The $D_s \rightarrow f_0(980)$ form factors are then obtained by multiplying Eqs. (12–19) by an angle dependence $\cos \theta$. The mixing angle extracted from the data is not larger than $40^{\circ }$ [25,26,27], and a recent LHCb measurement of the upper limit on the branching fraction $\mathcal{B}({{\bar{B}}}^0 \rightarrow J/\varPsi f_0) \times \mathcal{B}(f_0 \rightarrow \pi ^+\pi ^-)$ indicates $\vert \theta \vert < 30^{\circ }$ [28]. In the numerics, we would take $\theta = 20^{\circ } \pm 10^{\circ }$.

The value of Borel mass squared is implied by the internal virtuality of propagator which is smaller than the cutoff threshold value, saying $M^2 \sim \mathcal {O}(u m_{D_s}^2 + {\bar{u}} q^2 - u {\bar{u}} m_{f_0}^2) < s_0$, this value is a litter bit larger than the factorisation scale we chosen at $\mu _f^2 = m^2_{D_s} - m_c^2 = 1.48^2 \, \textrm{GeV}^2$ with the quark mass ${{\overline{m}}_c}(m_c) = 1.30 \, \textrm{GeV}$. In practice the selection of Borel mass is actually a compromise between the overwhelming chosen of ground state in hadron spectral which demands a small value and the convergence of OPE evaluation which prefers a larger one, this competition results in a region where $H_{ij}(q^2)$ shows an extremum in $M^2$

$$\begin{aligned} \frac{d}{d(1/M^2)} \textrm{ln} H_{ij}(q^2) = 0 . \end{aligned}$$

(22)

The continuum threshold is usually set to close to the outset of the first excited state with the same quantum number as $D_s$ and characterized by $s_0 \approx (m_{D_s} + \chi )^2$, which is finally determined by considering the maximal stable evolution of physical quantities on the Borel mass squared. The chose of these two parameters should guarantee the convergence of twist expansion in the truncated OPE calculation (high twists contributions are no more than thirty percents) and simultaneously the high energy cutoff in the hadron interpolating (the contributions from high excited state and continuum spectral is smaller than thirty percents). We finally set them at $M^2 = 5.0 \pm 0.5$ GeV$^2$ and $s_0 = 6.0 \pm 0.5$ GeV$^2$. The value of Borel mass is a litter bit larger than it chosen in the $D_s \rightarrow \pi , K$ transition [29], close to it chosen in the $D_s \rightarrow \phi$ [22], $D_s \rightarrow \eta ^{\prime }$ [2] and $D_s \rightarrow f_0(980)$ transition [3].

Fig. 1

The Borel mass dependence of $D_s \rightarrow f_0(980)$ form factors from the LCSRs

Fig. 2

The $q^2$ dependence of $D_s \rightarrow f_0(980)$ form factors from the LCSRs

With the LCDAs of $f_0(980)$ depicted in Appendix A, we show the LCSRs result of $D_s \rightarrow f_0(980)$ form factors in Table 2, the results obtained from other approaches are also presented for parallel comparison. We see that the result obtained by adopting different currents ($\mathrm{S_1,S_2,S_3}$) are different, especially for the form factors $f_+$ which contributes in semileptonic $D_s^+ \rightarrow f_0(980) e^+ \nu$ decays. The difference can be traced back to the ill-defined sum rules with the chiral currents under scenario $\mathrm{S_2}$ and $\mathrm{S_3}$, in which only the axial-vector current ${\bar{s}} \gamma _\mu \gamma _5 c$ is considered in the $D_s \rightarrow f_0(980)$ decay while the vector current ${\bar{s}} \gamma _\mu c$ with the $D_{s0}^*\rightarrow f_0(980)$ transition is overlooked at the hadron level. Hereafter we would pay attention on the sum rules under scenario $\mathrm{S_1}$. Our result $f_+(0) = 0.58 \pm 0.07$ is much larger than the previous LCSRs calculation $f_+(0)=0.30 \pm 0.03$ [22], but more consistent with $0.52 \pm 0.05$ extracted by BESIII collaboration [21]. The main reason of the difference is the input of decay constant ${{\tilde{f}}}_{f_0}$, whose value is taken at 180 MeV in the previous work [22], while the updated QCDSR evaluation presented in Appendix A.1 shows a much larger result 335 MeV. Besides it, we have also considered the mixing between ${\bar{s}}s$ and ${\bar{u}}u + {\bar{d}}d$ components in $f_0(980)$ and added the first Gegenbauer expansion terms in the LCDAs whose contributions are ignored in the previous work.

We show the dependence of form factors on the Borel mass squared in Fig. 1, where the gray and magenta curves correspond to the result obtained up to leading twist and subleading twist LCDAs, the uncertainties come from the threshold value $s_0$. We see that the subleading twist contribution is dominate in the form factors $f_+$, while the leading twist contribution become more important for the form factor $f_-$ and $f_T$. The large twist three contribution in $f_+$ does not indicate a breakdown of the twist expansion. Strictly speaking, the twist is defined by the conformal dimension minus collinear spin $j - s$ [30]. In the practice of exclusive processes, different twists LCDAs correspond to different power contributions $\mathcal{O}(1/m_Q)$, so one usually expect the leading twist LCDA give the dominate contribution. Actually, this is truly for many processes, but not for all. For example, in $B \rightarrow \pi$ transitions the twist three LCDAs from pion give the dominate contribution due to the chiral enhancement $m^\pi _0 = m_\pi ^2/(m_u+m_d)$ [31, 32], and in the $D_s \rightarrow f_0$ transition we are interesting now, the asymptotic term in the leading twist LCDAs is zero ($a_{0} = 0$) due to the charge conjugate invariance, and the leading twist LCDAs only have the QCD correction terms with odd Gegenbauer coefficients ($a_{n=odd} \ne 0$) as we can read from Eqs. (78, 84), so the twist three LCDAs give the dominate contribution in $f_+$. The form factors combination $f_+ + f_-$ only have twist three LCDA contributions since the leading twist parts are cancelled between them. For the tenor form factor $f_T$, two twist three terms are largely cancelled with each other, as we can see in Eq. (13), so the dominate contribution comes from leading twist LCDA.

We plot the $q^2$ dependence of the form factors in Fig. 2 with the maximal momentum transfer $q^2_{\textrm{max}} = 0.4 \, \textrm{GeV}^2$ allowed in the LCSRs evaluation [33], where the uncertainties associated to single $M^2$ and to both $M^2$ and $s_0$ are shown in the gray and magenta bands, respectively. We find that the uncertaintes of LCSRs prediction to $D_s \rightarrow f_0$ form factors is full dominated by $M^2$. To estimate the uncertainties associated to scale $\mu _f$, we vary the charm quark mass in ${{\bar{m}}_c}(m_c) = 1.30 \pm 0.30 \, \textrm{GeV}$ followed with $\mu _f = 1.48 \pm 0.30 \, \textrm{GeV}$, this variation brings another $20\%$ uncertainty to $f_+(q^2)$ and $f_T(q^2)$, and bring much significant corrections to $f_-(q^2)$ (large than $50\%$).

Fig. 3

Left: leading twist $D_s \rightarrow f_0(980)$ form factor obtained from LCSRs with comparing to the BESIII extraction. Right: the LCSRs prediction (gray) and the SSE extrapolation (lightblue) of $D_s \rightarrow f_0(980)$ form factor $f_+(q^2)$

In the left panel of Fig. 3, we show the LCSRs result of $D_s \rightarrow f_0(980)$ form factor $f_+(q^2)$ at leading twist. For the sake of comparison, we plot the form factor extracted by the BESIII collaboration under the Flatté model. We find that the leading twist result is much smaller than the measurement, indicating that the contributions from subleading twist LCDAs are dominate in $D_s \rightarrow f_0(980)$ transition. We then depict the LCSRs prediction up to subleading twist level in the right panel (gray band), and extrapolate it to the small recoiled region (lightblue band) by the simple z-series expansion parameterization (SSE) [34]. We truncate the SSE after the linear term for the form factors $f_+(q^2)$,

$$\begin{aligned} f_+(q^2) = \frac{a}{1-q^2/m_{D_{s0}^*}^2} \Big \{1 + b \, [ z(q^2) - z(0) ] \Big \}, \end{aligned}$$

(23)

the quadratic term is checked could be negligible here. In the expansion, $1/(1-q^2/m_{D_{s0}^*}^2)$ denotes the simple pole corresponding to the lowest-lying resonance in the $D_s f_0$ spectrum with $m_{D_{s0}^*} = 2.3177$ GeV [35], $a \equiv f_+(0)$ indicates the normalization conditions. The SSE formula bases on a rapidly converging series

$$\begin{aligned} z(q^2) = \frac{\sqrt{t_+ - q^2} - \sqrt{t_+ - t_0}}{\sqrt{t_+ - q^2} + \sqrt{t_+ - t_0}} \end{aligned}$$

(24)

with $t_\pm \equiv (m_{D_s} \pm m_{f_0})^2$ and $t_0 \equiv t_+ (1- \sqrt{1-t_-/t_+})$. Our fit result for the parameters are $a = 0.58 \pm 0.07$ and $b = 7.38 \pm 0.05$. Under the ${\bar{q}}q$ assignment of $f_0$, the LCSRs prediction of $D_s \rightarrow f_0$ form factor $f_+$ up to twist three level is marginally consistent with the data extraction with showing a litter bit larger.

3 $D_s \rightarrow \left[ \pi \pi \right] ^{\textrm{I}=0}$ form factors

$f_0(980)$ is measured via $\pi \pi$ invariant mass spectral, a natural key issue is to look close at the role of $f_0(980)$ in the $\pi \pi$ state, that is to say, how to consider the width effect of the intermediated resonants? A model independent study is to follow closely the stable $\pi \pi$ state on-shell rather than the intermediate $f_0$. In the process $D_s(p) \rightarrow \left[ \pi (k_1)\pi (k_2) \right] ^{\textrm{I}=0} l(p_2) \nu (p_3)$ we are interest, the decay amplitude is written as

$$\begin{aligned}{} & {} \mathcal{M}(D_s^+ \rightarrow \left[ \pi \pi \right] ^{\textrm{I}=0} e^+ \nu ) \nonumber \\{} & {} \quad = - \frac{i G_F}{\sqrt{2}} V_{cs}^*{\bar{u}}_e(p_2) \gamma ^\mu (1 - \gamma _5) v_{\nu _4}(p_3) \nonumber \\{} & {} \qquad \cdot \langle \left[ \pi (k_1)\pi (k_2) \right] ^{\textrm{I}=0} \vert {\bar{s}} \gamma _\mu (1 - \gamma _5) c \vert D_s^+(p) \rangle . \end{aligned}$$

(25)

The remaining hadron transition matrix element is furtherlly decomposed in terms of the orthogonal form factors

$$\begin{aligned}{} & {} \langle \left[ \pi (k_1)\pi (k_2) \right] ^{\textrm{I}=0} \vert {\bar{s}} \gamma _\mu (1 - \gamma _5) c \vert D_s^+(p) \rangle \nonumber \\{} & {} \quad = - i F_t(q^2, s, \zeta ) k_\mu ^t - i F_0(q^2, s, \zeta ) k_\mu ^0 - i F_\parallel (q^2, s, \zeta ) k_\mu ^\parallel \nonumber \\ \end{aligned}$$

(26)

with the kinematical variables

$$\begin{aligned}{} & {} k_\mu ^t = \frac{q_\mu }{\sqrt{q^2}} , \nonumber \\{} & {} k_\mu ^0 = \frac{2\sqrt{q^2}}{\sqrt{\lambda _{D_s}}} \left( k_\mu - \frac{k \cdot q}{q^2} q_\mu \right) , \nonumber \\{} & {} k_\mu ^\parallel = \frac{1}{\sqrt{k^2}} \left( {{\bar{k}}}_\mu - \frac{4 (q \cdot k)(q \cdot {{\bar{k}}})}{\lambda _{D_s} } k_\mu + \frac{4 k^2 (q \cdot {{\bar{k}}})}{\lambda _{D_s}} q_\mu \right) .\nonumber \\ \end{aligned}$$

(27)

Besides the momentum transfer squared $q^2$ in the weak decay and the invariant mass squared $k^2 \equiv (k_1 + k_2)^2$ of dipion system, $D_s \rightarrow \left[ \pi \pi \right] ^{\textrm{I}=0}$ form factors have an additional independent variable

$$\begin{aligned} 2 q \cdot {{\bar{k}}}\equiv & {} 2 q \cdot (k_1 - k_2) = \sqrt{\lambda _{D_s}} (2 \zeta -1)\nonumber \\= & {} \sqrt{\lambda _{D_s}} \beta _{\pi \pi }(k^2) \cos \theta _\pi . \end{aligned}$$

(28)

Here $\theta _\pi$ is the angle between the 3-momenta of $\pi (k_2)$ meson and the $D_s(p)$ meson in the dipion rest frame, the Kallën function is $\lambda (a,b,c) = a^2 + b^2 +c^2 - 2ab - 2ac - 2bc$ and $\lambda _{D_s} = \lambda (m_{D_s}^2, k^2, q^2)$, $\beta _{\pi \pi }(k^2) = \sqrt{1-4m_\pi ^2/s}$ is the $\pi \pi$ phase factor. Multiplying both sides of Eq. (26) by the polarization vector of weal current (lepton-neutrino pair), we can define the helicity form factors

$$\begin{aligned}{} & {} {\bar{\epsilon }}^\mu (i) \langle \left[ \pi (k_1)\pi (k_2) \right] ^{\textrm{I}=0} \vert {\bar{s}} \gamma _{\mu } (1 - \gamma _5) c \vert D_s^+(p) \rangle \nonumber \\{} & {} \quad = H_{i}^{D_s \rightarrow \left[ \pi \pi \right] ^{\textrm{I}=0}}(q^2, k^2, \zeta ). \end{aligned}$$

(29)

The subscript $i = 0, t$ denotes the polarization direction, hereafter we would not show explicitly the superscript for the sake of simplicity. The helicity form factors relate to the orthogonal Lorentz form factors as

$$\begin{aligned}{} & {} H_{0}(q^2, k^2, \zeta ) = - i F_0(q^2, k^2, \zeta ), \nonumber \\{} & {} H_{t}(q^2, k^2, \zeta ) = -i F_t(q^2, k^2, \zeta ). \end{aligned}$$

(30)

Three-order differential width of $D_s^+(p) \rightarrow \big [ \pi (k_1)\pi (k_2) \big ]^{\textrm{I}=0}$ $e^+(p_2) \nu _e(p_3)$ decay is written in terms of the helicity form factor.

$$\begin{aligned}{} & {} \frac{d^3\varGamma (D_s^+ \rightarrow \left[ \pi \pi \right] ^{\textrm{I}=0} l^+ \nu )}{dk^2 dq^2 d(\cos \theta _\pi )} \nonumber \\{} & {} \quad = \frac{G_F^2 \vert V_{cs}\vert ^2}{192 \pi ^3 m_{D_s}^3} \frac{\beta _{\pi \pi }(k^2) \sqrt{\lambda _{D_s}} q^2 }{16 \pi } \left[ -i F_0(q^2, k^2, \zeta ) \right] ^2.\nonumber \\ \end{aligned}$$

(31)

The key issue in the phenomenology is then turns to the calculation of the $D_s \rightarrow \left[ \pi \pi \right] ^{\textrm{I}=0}$ form factors $F_0(q^2, k^2, \zeta )$. Noticeability, $D_s \rightarrow \left[ \pi \pi \right] ^{\textrm{I}=0} l \nu$ decay is the kinematically simplest channel since the invariant amplitude depends only on the invariant mass of dipion system and not rely on its angular orientation with respecting the the remaining particles, meanwhile, it is the most important channel due to the $\left[ \pi \pi \right] ^{\textrm{I}=0}$ phase shift shows a very board rise.

3.1 The chiral even generalized $2\pi$ distribution amplitudes

In order to calculate $D_s \rightarrow \left[ \pi \pi \right] ^{\textrm{I}=0}$ form factors, we need the LCDAs of isoscalar $\pi \pi$ system ($2\pi$DAs). As similar as in the $f_0(500)-f_0(980)$ mixing, we introduce an angle to describe the mixing between ${\bar{n}}n$ and ${\bar{s}}s$ in the isoscalar $\pi \pi$ and KK states

$$\begin{aligned}{} & {} \left[ \pi \pi \right] ^{\textrm{I}=0} = \vert {\bar{n}}n \rangle \cos \theta + \vert {\bar{s}}s \rangle \sin \theta , \nonumber \\{} & {} \left[ KK \right] ^{\textrm{I}=0} = - \vert {\bar{n}}n \rangle \sin \theta + \vert {\bar{s}}s \rangle \cos \theta . \end{aligned}$$

(32)

The chiral even two quark $2\pi$DAs [36, 37] involved in our calculation is then defined by

$$\begin{aligned}{} & {} \bigg \langle \left[ \pi ^a(k_1) \pi ^b(k_2)\right] ^{\textrm{I}=0} \vert {\bar{s}}(xn) \gamma _\mu s(0) \vert 0 \bigg \rangle \nonumber \\{} & {} \quad = 2 \delta ^{ab} k_\mu \sin \theta \int du e^{iu x(k \cdot n)} \varPhi _{\parallel , \pi \pi }^{\textrm{I}=0, s{\bar{s}}} (u, \zeta , k^2) . \end{aligned}$$

(33)

Hereafter we will omit the superscript $s{\bar{s}}$ excepting special descriptions. It is easy to check the C-parity symmetry properties

$$\begin{aligned}{} & {} \varPhi _{\parallel , \pi \pi }^{\textrm{I}=0}(u, \zeta , k^2) = - \varPhi _{\parallel , \pi \pi }^{\textrm{I}=0}(1- u, \zeta , k^2) \nonumber \\{} & {} \quad = \varPhi _{\parallel , \pi \pi }^{\textrm{I}=0}(u, 1-\zeta , k^2) . \end{aligned}$$

(34)

There are three independent kinematical variables in the $2\pi$DAs, they are the momentum fraction u carried by the quark with respect to the total momentum k, the longitudinal momentum fraction $\zeta = k^{+}_1/k^{+}$ carried by a pion in the system, and the invariant mass squared $k^2$.

The generalized $2\pi$DAs is written by means of the detached Gegenbauer and Legendre polynomials,

$$\begin{aligned}{} & {} \varPhi _{\parallel , \pi \pi }^{\textrm{I}=0}(u, \zeta , k^{2}, \mu ) = 6 u (1-u) \sum _{n=1, \textrm{odd}}^{\infty } \sum _{l=0, \textrm{even}}^{n+1} \nonumber \\{} & {} B^{\textrm{I}=0}_{\parallel , nl}(k^{2}, \mu ) C_n^{3/2}(2u-1)C_l^{1/2}(2 \zeta -1) . \end{aligned}$$

(35)

It is normalized by the quark part of energy momentum tensor form factor

$$\begin{aligned}{} & {} \int du (2u - 1) \varPhi _{\parallel , \pi \pi }^{\textrm{I}=0}(u, \zeta , k^{2}) \nonumber \\{} & {} \quad =- 2 M_2^{(\pi )} \zeta (1-\zeta ) F_\pi ^{ \mathrm EMT}(k^{2}), \end{aligned}$$

(36)

in which $M_2^{(\pi )}$ is the second moment of quark distributions in the pion $M_2^{(\pi )} = 2 \int _0^1 du u \left[ q_\pi (u) + {\bar{q}}_\pi (x) \right]$, and $F_\pi ^{ \mathrm EMT}(0) = 1$. The double expansion coefficient $B_{nl}$ has the similar scale evolution as the Gegenbauer coefficients in the LCDAs of $f_0$ meson [38], and the $k^2$-dependence could be expressed in terms of the phase shift $\delta _l^{\textrm{I}=0}(s)$ of $\pi \pi$ scattering amplitude based on the Watson theorem.

$$\begin{aligned} B^{\textrm{I}=0}_{\parallel , nl}(\mu , k^{2})= & {} B^{\textrm{I}=0}_{\parallel , nl}(0) \left[ \frac{\alpha _s(\mu )}{\alpha _s(\mu _0)}\right] ^{\frac{\gamma _n^{(0)} - \gamma _0^{(0)}}{2\beta _0}} \nonumber \\{} & {} \cdot \textrm{Exp} \Big [ \sum _{m=1}^{N-1} \frac{k^{2m}}{m!} \frac{d^m \ln B^{\textrm{I}=0}_{\parallel , nl}(k^2)}{dk^{2m}} \Big \vert _{k^2 \rightarrow 0} \nonumber \\{} & {} + \frac{k^{2N}}{\pi } \int _{4m_\pi ^2}^\infty ds \frac{\delta _l^{\textrm{I}=0}(s)}{s^N (s-k^{2}-i0)} \Big ]. \end{aligned}$$

(37)

The exponential function in Eq. (37) is the Omn$\grave{\textrm{e}}$s solution of the N-subtracted dispersion relation for the coefficient $B_{nl}$ [39], whose evolution could touch up to $\sim 2.5$ GeV$^2$ [40]. The expansion coefficient $B^{\textrm{I}=0}_{\parallel , nl}(0)$ corresponds to the renormalization condition in Eq. (36) at zero energy point. At one-loop level, $\beta _0 = 11 - 2 N_f/3$, the anomalous dimension reads as

$$\begin{aligned} \gamma _n^{\parallel ,(0)} = 8 C_F \left( \sum _{k=1}^{n+1} \frac{1}{k} - \frac{3}{4} - \frac{1}{2(n+1)(n+2)} \right) . \end{aligned}$$

(38)

Table 3 The parameters [43] taken to fit the phase shift $\delta _{0}^{\mathrm{I=0}}(s)$ in the K matrix Eq. (42)

Fig. 4

The phase shifts $\delta ^{I=0}_l(s)$ (left) and the expansion coefficients $B_{1l}^{I=0}(s)$ (right) of isoscalar $\pi \pi$ system in the S and D-waves

Concerning the coefficients at the zero energy point, the soft pion theorem relates it with the Gegenbauer moments $a_n$, the crossing symmetry relates it to the moments of quark distribution $M_N$ in pion.

$$\begin{aligned}{} & {} \sum _{l=0}^{n+1} B^{\textrm{I}=0}_{\parallel , nl}(0) = 0, \nonumber \\{} & {} B^{\textrm{I}=0}_{\parallel , N-1N}(0) = \frac{1}{3} \frac{2N+1}{N+1} M^{(\pi )}_{N = \textrm{even}}. \end{aligned}$$

(39)

The derivation of theses relations can be found in the sections 2 and 3 in the Ref. [37]. For the first power of expansion and subtraction, we use the result obtained from the effective low-energy quark-pion theory [41, 42]

$$\begin{aligned}{} & {} B^{\textrm{I}=0}_{\parallel , 10}(0) = -B^{\textrm{I}=0}_{\parallel , 12}(0) = - 0.556, \nonumber \\{} & {} \frac{d \ln B^{\textrm{I}=0}_{\parallel , 10}(k^2)}{d k^2}\Big \vert _{k^2 \rightarrow 0} = \frac{d \ln B^{\textrm{I}=0}_{\parallel , 12}(k^2)}{d k^2}\Big \vert _{k^2 \rightarrow 0} \nonumber \\{} & {} \qquad \qquad \qquad \qquad \qquad = \frac{N_c}{48 \pi ^2 f_\pi ^2} = 0.375 \, \textrm{GeV}^{-2}. \end{aligned}$$

(40)

The phase shift $\delta _{l}^{\textrm{l}=0}(s)$ is obtained from the amplitude analysis of $\pi \pi$ scattering with a combination of dispersion relations and unitarity [43], where the coupled-channel K-matrix parametrization [44] is used.

$$\begin{aligned} T(s) = K(s) \left[ 1- C(s) K(s) \right] ^{-1}. \end{aligned}$$

(41)

Here $\sqrt{s}$ is the energy in the center of mass frame, K(s) is a real matrix which is parameterized by

$$\begin{aligned} K_{ij}(s) = \sum _{m=1} \frac{f^m_i f^m_j}{(s_l - s)(s_l-s_0)} + \sum _{n=0} c^n_{ij} \left( \frac{s}{4m_K^2} - 1\right) ^n.\nonumber \\ \end{aligned}$$

(42)

$f_i$, $s_l$ and $c^n_{ij}$ are free parameters, and in practice $s_l$ and $c^n_{ij}$ are constrained by $s_{l \geqslant 2} =0$, $c^{n \geqslant 2 }_{ij}=0$ and $c^{n}_{12}=c^{n}_{21}$ to reduce the model dependence. The diagonal matrix C(s), in the once subtracted dispersion relation, is written as

$$\begin{aligned} C_i(s) = \frac{s}{\pi } \int _{s_{\textrm{th} i}}^\infty ds' \frac{\rho _i(s')}{s' (s' - s - i 0)}, \end{aligned}$$

(43)

where the subscript $i =1$ and 2 denote the $\pi \pi \rightarrow \pi \pi$ and $K{{\bar{K}}} \rightarrow \pi \pi$ channels with the thresholds $s_{\textrm{th} 1} = 4m_\pi ^2$ and $s_{\textrm{th} 2} = 4m_K^2$, and the phase factors $\rho _1(s) = \sqrt{1- 4m_\pi ^2/s}$ and $\rho _2(s) = \sqrt{1- 4m_K^2/s}$, respectively. The scattering amplitude in Eq. (41) can be rewritten in an intuitive way in terms of phase shift an inelasticity

$$\begin{aligned} T^{\textrm{I}}_{J} = \frac{1}{2i\rho _\pi (s)}\left[ \eta ^{\textrm{I}}_J e^{2i \delta ^{\textrm{I}}_J} -1 \right] = \vert T^{\textrm{I}}_J \vert e^{i \phi _J^{\textrm{I}}}. \end{aligned}$$

(44)

The phase shift and inelasticity are fit to the hadronic data of reaction $\pi ^- p \rightarrow \pi ^- \pi ^+ n$, including the $\pi \pi$ phase shift from $\sqrt{s} = 600$ MeV to 900 MeV [45, 46] and from 1.0 GeV to 1.8 GeV [47], and also the BABAR Dalitz plot analysis of $D_s ^+ \rightarrow \pi ^+\pi ^- \pi ^+$ [48] and $D_s^+ \rightarrow K^+K^-\pi ^+$ [49]. In the fit, the Constrained Fit to Data IV (CFDIV) parametrization of T-matrix from Madrid-Krakow collaboration with imposing the $\pi \pi$ scattering amplitudes of Peláez et al. is taken as a data set up to $\sqrt{s} = 1.42$ GeV [50,51,52,53,54]. In the near threshold region, the dispersive results of Buttiker et al. [55] on the $\pi \pi \rightarrow KK$ amplitude are included as important constraints, the effects of isospin breaking are also took into account by the 8 MeV mass difference between the $K^+K^-$ and ${{\bar{K}}}^0K^0$ thresholds. Above that energy, the Regge form of the full $\gamma \gamma \rightarrow \pi \pi$ amplitude are adopted [50,51,52,53,54] The details of the fit could be found in Ref. [43], we would like to thank Ling-yun Dai for sharing us with the original result of their global fit analysis in Eq. (42). The fitted parameters of S-wave phase shift $\delta _{0}^{\mathrm{I=0}}(s)$ is quoted in Table 3, and the result of D-wave $\delta _{2}^{\mathrm{I=0}}(s)$ could be found directly in [50,51,52,53,54]. In Fig. 4, we depict the phase shift $\delta _{l}^{\textrm{I}=0}(s)$ on the left panel and the expansion coefficient $B_{1l}^{\textrm{I}=0}(s)$ obtained from Eq. (37) on the right panel. We can clearly see a sharp dip around the $f_0$ region in the S-wave phase shift and hence the first-order expansion coefficient, additionally, a quick rising around $f_0(1370)$ region in the D-wave.

3.2 $D_s \rightarrow \left[ \pi \pi \right] ^{\textrm{I}=0}$ form factor $F_0^{(l)}(q^2, s)$ at leading twist

To calculate the $D_s \rightarrow \left[ \pi \pi \right] ^{\textrm{I}=0}$ form factors, we consider the nonlocal correlation function

$$\begin{aligned}{} & {} \varPi _\mu ^{ab}(q, k_1, k_2) \nonumber \\{} & {} \quad = i \int d^4x e^{iq \cdot x} \langle \pi ^a(k_1) \pi ^b(k_2) \vert T \{j_{1, \mu }^{\textrm{S1}}(x), j_{2}^{\textrm{S1}}(0) \} \vert 0 \rangle ,\nonumber \\ \end{aligned}$$

(45)

take the $D_s$ interpolating current and the weak decay currents as the same as in the scenario I ($\textrm{S1}$) in the calculation of $D_s \rightarrow f_0$ form factors. Furthermore, we consider an auxiliary correlation function

$$\begin{aligned}{} & {} \varPi ^{ab}(q, k_1, k_2) \nonumber \\{} & {} \quad = i \int d^4x e^{iq \cdot x} \langle \pi ^a(k_1) \pi ^b(k_2) \vert T \{j_5(x), j_{2}^{\textrm{S1}}(0) \} \vert 0 \rangle \nonumber \\ \end{aligned}$$

(46)

to calculate the timelike helicity form factor $F_t$ with the current $j_5 = - i m_c {\bar{s}} \gamma _5 c$. The auxiliary correlation function is obtained by multiplying Eq. (45) with $q_\mu$.

For the sake of simplicity, we take the neutral dipion system with electric charge $a=b=0$ for example to show the LCSRs evaluation. The correction functions in Eqs. (45, 46), in the hadron representation, are written down by isolating the ground state contributions.

$$\begin{aligned}{} & {} \varPi _\mu ^{\textrm{had}}(q, k_1, k_2) \nonumber \\{} & {} \quad = \frac{im_{D_s}^2 f_{D_s}}{\left[ m_{D_s}^2 - (k+q)^2 \right] (m_c + m_s)} \nonumber \\{} & {} \quad \cdot \left[ F_t(q^2,k^2,\zeta ) k_\mu ^t + F_0(q^2,k^2,\zeta ) k_\mu ^0 + F_\parallel (q^2,k^2,\zeta ) k_\mu ^\parallel \right] \nonumber \\{} & {} \quad + \frac{1}{\pi } \int _{s_0}^\infty ds \frac{\rho _t^h(q^2,s) k_\mu ^t + \rho _0^h(q^2,s) k_\mu ^0 + \rho _\parallel ^h(q^2,s) k_\mu ^\parallel }{s - (k+q)^2} , \end{aligned}$$

(47)

$$\begin{aligned}{} & {} \varPi ^{\textrm{had}}(q, k_1, k_2) \nonumber \\{} & {} \quad = \frac{m_{D_s}^2 f_{D_s}}{\left[ m_{D_s}^2 - (k+q)^2 \right] (m_c + m_s)} \left[ \sqrt{q^2} F_t(q^2,k^2,\zeta ) \right] \nonumber \\{} & {} \quad + \frac{1}{\pi } \int _{s_0}^\infty ds \frac{\rho ^h(q^2,s)}{s - (k+q)^2} . \end{aligned}$$

(48)

Meanwhile, the OPE calculation of these correlation functions result in

$$\begin{aligned} \varPi _\mu ^{\textrm{OPE}}(q, k_1, k_2)= & {} 2 i \sin \theta m_c k_\mu \int _0^1 \frac{du}{u} \frac{\varPhi _{\parallel , \pi \pi }^{\textrm{I}=0}(u, \zeta , k^2)}{s^\prime _2(u) - (k+q)^2} , \end{aligned}$$

(49)

$$\begin{aligned} \varPi ^{\textrm{OPE}}(q, k_1, k_2)= & {} \frac{m_c \sin \theta }{2} \int _0^1 \frac{du}{u} \varPhi _{\parallel , \pi \pi }^{\textrm{I}=0}(u, \zeta , k^2)\nonumber \\{} & {} \cdot \frac{ \left[ m_{D_s}^2 - q^2 - (1-2u) k^2 \right] }{s^\prime _2(u) - (k+q)^2} . \end{aligned}$$

(50)

After applying the quark-hadron duality and Borel transformation, we have the relations

$$\begin{aligned}{} & {} \frac{2 \sqrt{q^2}}{\lambda _{D_s}} F_0(q^2, k^2, \zeta ) - \frac{4(q \cdot k)(q \cdot {{\bar{k}}})}{\lambda _{D_s} \sqrt{k^2}} F_\parallel (q^2, k^2, \zeta ) \nonumber \\{} & {} \quad = \frac{2 m_c (m_c + m_s) \sin \theta }{m_{D_s}^2 f_{D_s}} \int _{u_0}^1 \frac{du}{u} \, \varPhi _{\parallel , \pi \pi }^{\textrm{I}=0}(u, \zeta , k^2) \, e^{- \frac{s^\prime _2(u) - m_{D_s}^2}{M^2}}, \end{aligned}$$

(51)

$$\begin{aligned}{} & {} \frac{F_t(q^2, k^2, \zeta )}{\sqrt{q^2}} - \frac{2 (q \cdot k) F_0(q^2, k^2, \zeta )}{\sqrt{\lambda _{D_s} q^2} } \nonumber \\{} & {} \quad + \frac{4 \sqrt{ k^2} (q \cdot {{\bar{k}}}) F_\parallel (q^2, k^2, \zeta )}{\lambda _{D_s}} = 0, \end{aligned}$$

(52)

here $s^\prime _2(u) = {\bar{u}} k^2 + (m_c^2 - {\bar{u}}q^2)/u$. The sum rules are ultimately obtained as

$$\begin{aligned}{} & {} \cos \theta _\pi F_\parallel (q^2, k^2, \zeta ) = \frac{m_c(m_c+m_s) \sin \theta }{m_{D_s}^2 f_{D_s} \sqrt{\lambda _{D_s}} \beta _{\pi \pi }(k^2) } \int _{u_0}^1 \frac{du}{u} \nonumber \\{} & {} \quad \cdot \varPhi _{\parallel , \pi \pi }^{\textrm{I}=0}(u, \zeta , k^2) 4 u \left( k^2 \right) ^{3/2} \, e^{- \frac{s^\prime _2(u) - m_{D_s}^2}{M^2}}, \end{aligned}$$

(53)

$$\begin{aligned}{} & {} F_0(q^2, k^2, \zeta ) = \frac{m_c(m_c+m_s) \sin \theta }{m_{D_s}^2 f_{D_s} \sqrt{\lambda _{D_s}} \sqrt{q^2} } \int _{u_0}^1 \frac{du}{u} \varPhi _{\parallel , \pi \pi }^{\textrm{I}=0}(u, \zeta , k^2)\nonumber \\{} & {} \quad \cdot \left[ \lambda _{D_s} + 2u k^2 \left( m_{D_s}^2 + q^2 - k^2 \right) \right] e^{- \frac{s^\prime _2(u) - m_{D_s}^2}{M^2}}, \end{aligned}$$

(54)

$$\begin{aligned}{} & {} \sqrt{q^2} F_t(q^2, k^2, \zeta ) = \frac{m_c (m_c + m_s) \sin \theta }{m_{D_s}^2 f_{D_s}} \int _{u_0}^1 \frac{du}{u} \varPhi _{\parallel , \pi \pi }^{\textrm{I}=0}(u, \zeta , k^2)\nonumber \\{} & {} \quad \cdot \left[ m_{D_s}^2 - q^2 - (1-2u)k^2 \right] \, e^{- \frac{s^\prime _2(u) - m_{D_s}^2}{M^2}}. \end{aligned}$$

(55)

We can check that $F_0(q^2, k^2, \zeta ) = F_t(q^2, k^2, \zeta )$ at the full recoiled point $q^2 = 0$.

Fig. 5

Upper: Evolution of the S-wave orthogonal form factor on the momentum transfers $\sqrt{q^2}F_{0}^{(l=0)}(q^2, s = 8 m_\pi ^2)$ (left) and on the invariant mass $\sqrt{q^2}F_{0}^{(l=0)}(q^2 = 0, s)$ (right). Lower: the same as the upper panel, but for the D-wave form factor

From the view of partial-wave analysis [57], $D_s \rightarrow \left[ \pi \pi \right] ^{\textrm{I} = 0}$ form factors are expanded by

$$\begin{aligned}{} & {} F_{0,t}(q^2, k^2, \zeta ) = \sum _{\ell =0}^\infty \sqrt{2\ell +1} \, F_{0,t}^{(\ell )}(q^2, k^2) P_\ell ^{(0)}(\cos \theta _\pi ), \end{aligned}$$

(56)

$$\begin{aligned}{} & {} F_{\parallel ,\perp }(q^2, k^2, \zeta ) = \sum _{\ell = 0} \sqrt{2\ell +1} \, F_{\parallel ,\perp }^{(\ell )}(q^2,k^2) \frac{P_\ell ^{(1)}(\cos \theta _\pi )}{\sin \theta _\pi }.\nonumber \\ \end{aligned}$$

(57)

The associated Legendre polynomials have the orthogonality relations

$$\begin{aligned}{} & {} \int _{-1}^1 P_\ell ^n(x) P_k^n(x) dx = \frac{2}{2 \ell +1} \frac{(\ell +n)!}{(\ell - n)!} \delta _{k \ell }, \nonumber \\{} & {} \int _{-1}^1 \frac{P_\ell ^m(x) P_\ell ^n(x)}{1-x^2} dx = \frac{(\ell + m)!}{m (\ell - m)!} \delta _{mn}\, \quad \textrm{with} \, m,n \ne 0. \nonumber \\ \end{aligned}$$

(58)

Multiplying $P_\ell ^{(0)}(\cos \theta _\pi )$ to both sides of Eqs. (53, 54) and integrating over $\cos \theta _\pi$, we obtain the sum rules of $D_s \rightarrow \left[ \pi \pi \right] ^{\textrm{I} = 0}$ form factors at $\ell ^\prime$-wave ($\ell ^\prime = \textrm{even}$ and $\ell ^\prime \leqslant n+1$)

$$\begin{aligned}{} & {} \sum _{\ell =1}^\infty I_{\ell ^\prime \ell }^{\textrm{I}=0} \, F_\parallel ^{(\ell )}(q^2, k^2) = \frac{m_c(m_c+m_s) \sin \theta }{m_{D_s}^2f_{D_s}\sqrt{\lambda _{Ds}}} \sum _{n=1,\textrm{odd}}^\infty \nonumber \\{} & {} \quad \frac{1}{2 \ell ^\prime + 1} \, J_n^\parallel (q^2,k^2,M^2,s_0) \, B_{n \ell ^\prime , \parallel }^{\textrm{I}=0}(k^2), \end{aligned}$$

(59)

$$\begin{aligned}{} & {} F_0^{(\ell ^\prime )}(q^2,k^2) = \frac{m_c(m_c+m_s) \sin \theta }{m_{D_s}^2f_{D_s}\sqrt{\lambda _{Ds}}\sqrt{q^2}} \sum _{n=1,\textrm{odd}}^\infty \nonumber \\{} & {} \quad \frac{\beta _{\pi \pi }(k^2) }{\sqrt{2 \ell ^\prime + 1}} \, J_n^0(q^2,k^2,M^2,s_0) \, B_{n \ell ^\prime , \parallel }^{\textrm{I}=0}(k^2), \end{aligned}$$

(60)

$$\begin{aligned}{} & {} F_t^{(\ell ^\prime )}(q^2,k^2) = \frac{m_c(m_c+m_s) \sin \theta }{m_{D_s}^2f_{D_s}\sqrt{q^2}} \sum _{n=1,\textrm{odd}}^\infty \nonumber \\{} & {} \quad \frac{\beta _{\pi \pi }(k^2)}{\sqrt{2 \ell ^\prime + 1}} \, J_n^t(q^2,k^2,M^2,s_0) \, B_{n \ell ^\prime , \parallel }^{\textrm{I}=0}(k^2). \end{aligned}$$

(61)

The conformal expansion functions $J_n$ read as

$$\begin{aligned} J_n^\parallel (q^2,k^2,M^2,s_0)= & {} 6 \int _{u_0}^1 du \, {\bar{u}} \, C_n^{3/2}(2u-1) \nonumber \\{} & {} \cdot 4 \left( k^2 \right) ^{3/2} \, e^{- \frac{s^\prime _2(u) - m_{D_s}^2}{M^2}}, \end{aligned}$$

(62)

$$\begin{aligned}{} & {} J_n^0(q^2,k^2,M^2,s_0) = 6 \int _{u_0}^1 du \, {\bar{u}} \, C_n^{3/2}(2u-1) \nonumber \\{} & {} \quad \cdot \left[ \lambda _{D_s} + 2u k^2 \left( m_{D_s}^2 + q^2 - k^2 \right) \right] e^{- \frac{s^\prime _2(u) - m_{D_s}^2}{M^2}}, \end{aligned}$$

(63)

$$\begin{aligned}{} & {} J_n^t(q^2,k^2,M^2,s_0) = 6 \int _{u_0}^1 du \, {\bar{u}} \, C_n^{3/2}(2u-1) \nonumber \\{} & {} \quad \cdot \left[ m_{D_s}^2 - q^2 - (1-2u) k^2 \right] e^{- \frac{s^\prime _2(u) - m_{D_s}^2}{M^2}}, \end{aligned}$$

(64)

and the additional partial-wave expansion function $I_{\ell ^\prime \ell }$ read as

$$\begin{aligned}{} & {} I_{\ell ^\prime \ell }^{\textrm{I}=0} = \sqrt{2l+1} \, \int _{-1}^1 d (\cos \theta _\pi ) \frac{\cos \theta _\pi }{\sin \theta _\pi } \, \nonumber \\{} & {} \hspace{1cm} \cdot P_{\ell ^{\prime \prime }}^{(0)}(\cos \theta _\pi ) P_{\ell }^{(1)}(\cos \theta _\pi ) . \end{aligned}$$

(65)

We mark that $I_{\ell \ell ^\prime }^{\textrm{I}=0}$ is zero when $\ell$ goes over odd number, $I_{02}^{\textrm{I}=0} = -2 \sqrt{5}, I_{22}^{\textrm{I}=0} = -4/\sqrt{5}$ and $I_{\ell ^\prime 2}^{\textrm{I}=0} = 0$ when $\ell ^\prime > 2$.

Fig. 6

The dependence of the form factor $\sqrt{q^2} F^{(l=0,2)}_{0}(q^2)$ on the momentum transfers

In Fig. 5 we depict the evolutions of S-wave (up) and D-wave (down) orthogonal form factor $\sqrt{q^2}F_{0}^{(l=0,2)}$ of $D_s \rightarrow \left[ \pi \pi \right] _\textrm{S}$ transition on the momentum transfer squared (left) and the invariant mass squared (right). The sum rules parameters $M^2$ and $s_0$ are chosen as the same ones in the $D_s \rightarrow f_0$ form factors, saying $M^2 = 5.0 \pm 0.5$ GeV$^2$ and $s_0 = 6.0 \pm 0.5$ GeV$^2$. We obtain the errors by taking the squared average of the parameters. As we can see in Eq. (60), form factors $F_{0}$ and $F_{t}$ are highly suppressed by the phase space when s approaching $4m_\pi ^2$, so we plot the $q^2$ evolution at the invariant mass squared $k^2 = 8 m_\pi ^2$ on the left panel. We take the mixing angle between the isoscalar $\pi \pi$ and KK states at $\theta = 20^{\circ } \pm 10^{\circ }$ which is similar as the angle in the $\sigma$-$f_0$ mixing [25]. The uncertainty arose from the mixing angle is added up to the LCSRs parameters uncertainty and shown in the magnate bands. We find that the D-wave form factor $\sqrt{q^2}F_{0}^{(l=2)}(q^2)$ is much smaller than the S-wave $\sqrt{q^2}F_{0}^{(l=0)}(q^2)$ when the invariant mass is small, while in the resonant regions D-wave contribution is comparable or even larger than the S-wave. Integrating out the invariant mass dependence, we obtain the dependence of the form factor on the momentum transfer squared $q^2$

$$\begin{aligned} \sqrt{q^2} F^{(l)}_{0}(q^2) = \int _{4m_\pi ^2}^{s_{\textrm{max}}(q^2)} ds \sqrt{q^2} F^{(l)}_{0}(q^2, s), \end{aligned}$$

(66)

which is depicted in Fig. 6. Again, in the small recoiling regions where the LCSRs calculation is invalid, the form factors are extrapolated by the SSE parameterization.

Fig. 7

Left: The differential width (in unit of ${\textrm{ns}^{-1}/{\textrm{GeV}}^{2}/{\textrm{c}}^{4}}$) of $D_s^+ \rightarrow (f_0(980) \rightarrow ) \left[ \pi \pi \right] ^{I=0}_{S} e^+ \nu _e$ obtained from the narrow width approximation (blue) and the Flatt${\acute{\textrm{e}}}$ resonant formula (black). Right: The leading twist differential width under the narrow width approximation (lightblue), Flatté resonant model (gray) and model-independent $D_s \rightarrow [\pi \pi ]_{S}^{\textrm{I} = 0}$ form factor calculation

4 $D_s^+ \rightarrow (f_0(980) \rightarrow ) \left[ \pi \pi \right] _{S}^{\textrm{I}=0} e^+ \nu _e$ decay and $D_s^+ \rightarrow \left[ \pi \pi \right] _S^{\textrm{I} = 0} e^+ \nu _e$ decay at leading twist

Ignoring the masses of lepton and neutrino, the differential width of $D_s^+(p) \rightarrow f_0(p_1) e^+ (p_2) \nu _e(p_3)$ decay is proportional to the transition form factor $f_+$

$$\begin{aligned}{} & {} \frac{d^2\varGamma (D_s^+ \rightarrow f_0(980) e^+ \nu _e)}{dE_2 dq^2} \nonumber \\{} & {} \quad = \frac{G_F^2 m_{D_s}^2 \vert V_{cs}\vert ^2}{16 \pi ^3} \vert f_+(q^2) \vert ^2 \left[ 2x(1+y-z) - 4x^2 -y \right] .\nonumber \\ \end{aligned}$$

(67)

The dimensionless quantities are

$$\begin{aligned} x \equiv \frac{E_2}{m_{D_s}} \, \quad y \equiv \frac{q^2}{m_{D_s^*}^2} , \quad z \equiv \frac{m_{f_0}^2}{m_{D_s}^2} \end{aligned}$$

(68)

with $E_2$ being the energy of lepton and $q^2 \equiv m_{23}^2 = (p_2 + p_3)^2 = (p - p_1)^2$ being the invariant mass of lepton-neutrino pair. Integrating over the lepton energy, we obtain the one-dimension differential decay width on the momentum transfers

$$\begin{aligned}{} & {} \frac{d\varGamma (D_s^+ \rightarrow f_0(980) e^+ \nu _e)}{dq^2} \nonumber \\{} & {} \quad = \frac{G_F^2 \vert V_{cs}\vert ^2 \lambda ^{3/2}(m_{D_s}^2, m_{f_0}^2, q^2)}{192 \pi ^3 m_{D_s}^3} \vert f_+(q^2) \vert ^2. \end{aligned}$$

(69)

In order to take into account the width effect of the intermediate resonant, we firstly take the Flatté model to describe the $D_s^+ \rightarrow (f_0(980) \rightarrow ) \left[ \pi \pi \right] _{S}^{\textrm{I}=0} e^+ \nu _e$ decay as BESIII collaboration did in the analysis [21]. The differential width in Eq. (67) is modified to

$$\begin{aligned}{} & {} \frac{d^2\varGamma (D_s^+ \rightarrow (f_0(980) \rightarrow ) \left[ \pi \pi \right] ^{\textrm{I}=0}_{S} e^+ \nu _e)}{dE_2 dq^2} \nonumber \\{} & {} \quad = \frac{1}{\pi } \int _{4m_\pi ^2}^{s_{\textrm{max}}(q^2)} ds \frac{g_1^2 \beta _{\pi \pi }}{ \vert s - m_{f_0}^2 + i (g_1^2 \beta _{\pi \pi } +g_2^2 \beta _{KK}) \vert ^2} \nonumber \\{} & {} \qquad \cdot \frac{d^2\varGamma (D_s^+ \rightarrow f_0(980) l^+ \nu )}{dE_2 dq^2}. \end{aligned}$$

(70)

Here $s_{\textrm{max}}(q^2)$ is the solution of $\lambda (m_{D_s}^2, q^2, s) = 0$, $\beta _{\pi \pi }(s)$ and $\beta _{KK}(s) = \sqrt{1-4m_K^2/s}$ are the phase factors, $g_1^2 = 0.165$ GeV$^2$ and $g_2^2 = 0.695$ GeV$^2$ are the weighted parameters [56]. Integrating over the invariant mass one arrives at the differential width on the momentum transfers

$$\begin{aligned}{} & {} \frac{d\varGamma (D_s^+ \rightarrow (f_0(980) \rightarrow ) \left[ \pi \pi \right] ^{\textrm{I}=0}_{S} e^+ \nu _e)}{dq^2} \nonumber \\{} & {} \quad = \frac{1}{\pi } \frac{G_F^2 \vert V_{cs}\vert ^2}{192 \pi ^3 m_{D_s}^3} \vert f_+(q^2) \vert ^2 \int _{4m_\pi ^2}^{s_{\textrm{max}}(q^2)} ds \nonumber \\{} & {} \qquad \cdot \frac{\lambda ^{3/2}(m_{D_s}^2, s, q^2) \, g_1^2 \beta _{\pi \pi }(s)}{ \vert s - m_{f_0}^2 + i (g_1^2 \beta _{\pi \pi }(s) +g_2^2 \beta _{KK}(s)) \vert ^2}. \end{aligned}$$

(71)

In the left panel of Fig. 7, we depict the differential width (in unit of $\mathrm{ns^{-1}/GeV^{2}/c^4}$) of $D_s^+ \rightarrow (f_0(980) \rightarrow ) \left[ \pi \pi \right] ^{\textrm{I}=0}_{S}$ $e^+ \nu _e$ on the momentum transfers, where the result obtained from the narrow width approximation in Eq. (69) and the Flatté resonant model in Eq. (71) are plotted in blue and black curves, respectively. The curve of decay width obtained from the narrow width approximation is a litter bit lower than the data, the result with considering the width effect by resonant model is consistent with the data. We would like to comment the model dependence in the extraction of $D_s \rightarrow f_0(980)$ form factor from the differential decay width by the BESIII collaboration, and a model independent analysis is highly anticipated to directly explain the differential decay width.

The $D_s^+ \rightarrow \left[ \pi \pi \right] _S^{\textrm{I} = 0}$ form factor provides a possibility. Taking in to account the partial-wave expansion in Eq. (57) and the orthogonal conditions in Eq. (58), we obtain the differential decay width of $D_s^+ \rightarrow \left[ \pi \pi \right] _S^{\textrm{I} = 0} e^+ \nu _e$ decay after integrating over the angle $\theta _\pi$,

$$\begin{aligned}{} & {} \frac{d^2\varGamma (D_s^+ \rightarrow \left[ \pi \pi \right] _{S}^{\textrm{I} = 0} l^+ \nu )}{dk^2 dq^2} \nonumber \\{} & {} \quad = \frac{G_F^2 \vert V_{cs}\vert ^2}{192 \pi ^3 m_{D_s}^3} \frac{\beta _{\pi \pi }(k^2) \sqrt{\lambda _{D_s}}}{16 \pi } 2 \vert \sqrt{q^2} F_0^{(\ell =0)}(q^2, k^2) \vert ^2.\nonumber \\ \end{aligned}$$

(72)

In the right panel of Fig. 7, we plot the $q^2$ dependence of the decay width with the form factor defined in Eq. (66) and shown in Fig. 6 (left). We mark that the result is obtained at leading twist level of the the dipion LCDAs, so we compare it with the result obtained from the narrow width approximation and Flatté resonant model with the leading twist $D_s \rightarrow f_0(980)$ form factor. We find that the direct calculation from $D_s \rightarrow \left[ \pi \pi \right] _{S}^{\textrm{I} = 0}$ form factor shows a relatively gentle evolution with much broader region of momentum transfers. Keep in mind that the twist three LCDAs of $f_0$ give the dominate contribution to $D_s \rightarrow f_0(980)$ form factors, as shown in Fig. 3, so the twist three LCDAs of isoscalar scalar $\pi \pi$ system is the key ingredient to explain the BESIII measurement of the differential decay width. We would postpone this study somewhere together with other decays channels like $B_{(s)} \rightarrow \left[ \pi \pi \right] _S^{\textrm{I} = 0} e^+ \nu _e$.

5 Summary

In this work we calculate the $D_s \rightarrow f_0(980)$ transition form factors and the differential decay width of $D_s^+ \rightarrow (f_0(980) \rightarrow ) \left[ \pi \pi \right] _S^{\textrm{I} = 0} e^+ \nu _e$ decay from the LCSRs approach under the conventional ${\bar{q}}q$ picture of $f_0(980)$. To this end, we firstly revisit the QCD sum rules of the scalar decay constant and the LCDAs of $f_0(980)$ in the appendix. The updated scalar decay constant is $\tilde{f}_{f_0(980)} = 335^{+9}_{-12}$ MeV, the lowest nonzero Gegenbauer coefficients are $a_1(f_0(980)) = -0.891^{+0.040}_{-0.034}$ and $a_2^s(f_0(980)) = 0.296 \pm 0.044, a_2^\sigma (f_0(980)) = 0.169 \pm 0.026$ respectively in the leading twist and subleading twist LCDAs. With considering the mixing between ${\bar{s}}s$ and ${\bar{u}}u+{\bar{d}}d$ compositions, we then obtain the $D_s \rightarrow f_0(980)$ form factor $f_+(q^2)$ which is comparable with the value extracted by the BESIII collaboration, indicating that the energetic picture of $f_0(980)$ is still reliable in the charm meson decay. We find that the width effect of $f_0$ is sizable in the $D_s \rightarrow (f_0(980) \rightarrow ) \left[ \pi \pi \right] _S^{\textrm{I} = 0} e^+ \nu _e$ decay, the result obtained under the narrow width approximation shows a litter bit lower than the measurement, and the result obtained under the intermediate resonant model with Flatté formula shows a consistence with the data. We introduce the dipion LCDAs to describe the unstable scalar meson and calculate the $D_s \rightarrow [\pi \pi ]^{\textrm{I}=0}_{S}$ form factors with the leading twist $\pi \pi$ LCDAs. The obtained differential width of $D_s^+ \rightarrow [\pi \pi ]_{S}^{\textrm{I} = 0} e^+\nu _e$ decay exhibits a gentle evolution on the momentum transfers, comparing to the result obtained under the single meson assumption and the resonant model.

Our calculation of $D_s \rightarrow [\pi \pi ]^{\textrm{I}=0}$ form factors is carried out at leading twist due to the finite knowledge of dipion LCDAs, so an important issue of further development in this project is to construct the twist three dipion LCDAs and take in to account their contributions. Of course, the next-to-leading-order QCD radiation corrections of the correlation function is also imperative to improve the prediction accuracy. This work reveals a bright prospect to study the four-body semileptonic decays of heavy mesons with the dimeson light-cone distribution amplitudes [57], the future experiment with larger integrated luminosity [58, 59] would help us to understand the LCDAs of dipion system much better.

Appendix A: Light-cone distribution amplitudes of scalar meson

LCDAs is defined by a nonlocal matrix element sandwiched between vacuum and the onshell hadron state. Up to twist three level, the light-cone expansion of scalar meson (S) is

(73)

$$\begin{aligned}{} & {} \langle S(p_1) \vert {\bar{q}}_{2\beta }(z) g_s G_{\mu \nu }(vz) \sigma _{\rho \delta } q_{1\alpha }(-z) \vert 0 \rangle \nonumber \\{} & {} \quad = \left[ p_{1\mu } \left( p_{1\rho } g_{\nu \delta }^\perp - p_{1\delta } g_{\nu \rho }^\perp \right) - \mu \leftrightarrow \nu \right] \nonumber \\{} & {} \qquad \cdot \int \mathcal{D} \alpha _i \, \phi _{3S}(\alpha _i) \, e^{ipz(-\alpha _1+\alpha _2+v \alpha _3)}. \end{aligned}$$

(74)

In the definitions $\phi$ and $\phi ^{s,\sigma }$ are the twist two and twist three LCDAs of the ${\bar{q}}q$ composition, respectively, $\phi _{3S}$ is the twist three LCDA in the ${\bar{q}}gq$ composition. Here $v = (u - \alpha _1)/\alpha _3$ and $\alpha _3 = 1- \alpha _1 - \alpha _2$, the measure of three particle integral reads as

$$\begin{aligned} \int _0^u \, \mathcal{D} \alpha _i = \int _0^u d \alpha _1 \int _0^{1-u} \frac{d \alpha _2 }{1-\alpha _1-\alpha _2}. \end{aligned}$$

(75)

The leading twist and two particle twist three LCDAs are normalized to the vector and scale-dependent scalar decay constants, which are defined by the local matrix elements deduced by the vector and scalar currents, respectively,

$$\begin{aligned}{} & {} \int _0^1 du \, \phi (u) = f_S, \qquad \langle f_0(p_1) \vert {\bar{q}}_{2} \gamma _\mu q_1 \vert 0 \rangle = f_S p_{1 \mu }, \end{aligned}$$

(76)

$$\begin{aligned}{} & {} \int _0^1 du \, \phi ^{(s/\sigma )}(u) = {{\bar{f}}}_S, \qquad \langle f_0(p_1) \vert {\bar{q}}_2 q_1 \vert 0 \rangle = {{\bar{f}}}_S m_S.\nonumber \\ \quad \end{aligned}$$

(77)

For the neutral scalar meson like $f_0$ and $a_0$ which could not be produced via the vector current, $f_S = 0$ due to the charge conjugate invariance or the conservation of vector current. This is also implied in the relation

$$\begin{aligned} {{\bar{f}}}_S = \mu _S f_S, \qquad \mu _S \equiv \frac{m_S}{m_{q_2}(\mu ) - m_{q_1}(\mu )}, \end{aligned}$$

(78)

from which we can see that $f_S$ vanishes in the $\mathrm{SU(3)}$ or isospin limit.

Table 4 The scalar decay constant of $f_0$ obtained from QCD sum rules

1.1 A.1 The scalar decay constant

To calculate the scalar coupling, we consider the following correlation function

$$\begin{aligned} \varPi (q) = i \int d^4x e^{i q \cdot x} \langle 0 \vert \textrm{T} \{ {\bar{q}}_2(x)q_1(x), {\bar{q}}_1(0)q_2(0) \} \vert 0 \rangle .\nonumber \\ \end{aligned}$$

(79)

The QCD sum rule (QCDSR) of the neutral scalar coupling is quoted as

$$\begin{aligned}{} & {} m_S^2 {{\bar{f}}}_S^2(\mu ) e^{- m_S^2/M^2} = I_0^{\textrm{pert}}(s_0,M^2) + \langle {\bar{q}}q \rangle I_0^{\langle {\bar{q}}q \rangle }(M^2) \nonumber \\{} & {} \quad + \langle \alpha _s G^2 \rangle I_0^{\langle \alpha _s G^2 \rangle }(M^2, \mu ) + \langle g_s {\bar{q}} \sigma T G q \rangle I_0^{\langle g_s {\bar{q}} \sigma T G q \rangle }(M^2) \nonumber \\{} & {} \quad + \langle g_s{\bar{q}}q \rangle ^2 I_0^{\langle g_s{\bar{q}}q \rangle ^2}(M^2) + \langle g_s^2{\bar{q}}q \rangle ^2 I_0^{\langle g_s^2{\bar{q}}q \rangle ^2}(M^2,\mu ), \nonumber \\ \end{aligned}$$

(80)

where the expressions of weighted functions $I_0$ and the renormalization group equations of vacuum condensations can be found in Refs. [60,61,62]. In the numerics, we take $\alpha _s (1 \, \textrm{GeV}) = 0.47$ corresponding to the world average $\alpha _s(m_Z) = 0.118$ and the follow vacuum condensates [63] where the default scale is 1 GeV.

$$\begin{aligned}{} & {} \langle {\bar{q}}q \rangle = - 0.0156 \, \textrm{GeV}^3, \qquad \langle {\bar{s}}s \rangle = 0.8 \langle {\bar{q}}q \rangle , \qquad m_0^2 = 0.8, \nonumber \\{} & {} \langle \alpha _s G^2 \rangle = 0.038 \, \textrm{GeV}^4, \qquad \langle g_s {\bar{q}} \sigma T G q \rangle = m_0^2 \langle {\bar{q}}q \rangle , \nonumber \\{} & {} \langle g_s{\bar{q}}q \rangle ^2 = \frac{-16}{9} \langle {\bar{q}}q \rangle ^2, \qquad \langle g_s^2{\bar{q}}q \rangle ^2 = \frac{-16}{3} \langle {\bar{q}}q \rangle ^2. \end{aligned}$$

(81)

The quark condensate density is obtained from the Gell–Mann–Oakes–Renner relation: $\langle {\bar{q}}q \rangle = - f_\pi ^2m_\pi ^2/2/(m_u+m_d)$. In Ref. [63], one may use the values of quark masses $m_u = 4.2$ MeV and $m_d = 7.5$ MeV suggested by Weinberg [64].

Fig. 8

The Borel mass dependence of $m^2_{f_0} \tilde{f}^2_{f_0} e^{-m^2_{f_0}/M^2}$ obtained from QCDSR (left) and BFTSR (right)

The scalar coupling is also studied by the sum rules within the back ground field (BFTSR) [65, 66]. In this approach the perturbative term, the quark condensate, dimension-4 gluon condensate and dimension-6 quark–gluon condensate are the same as in the traditional one, while the dimension-6 four quark condensates are different. We mark that this difference results from the different treatments for the color factorization when adopting the vacuum saturation hypothesis [67,68,69,70]. The non-perturbative vacuum condensates appearing in the BFTSR are

$$\begin{aligned}{} & {} \langle {\bar{q}}q \rangle = - 0.0197 \, \textrm{GeV}^3, \qquad \langle {\bar{s}}s \rangle = 0.8 \langle {\bar{q}}q \rangle , \nonumber \\{} & {} \langle \alpha _s G^2 \rangle = 0.038 \, \textrm{GeV}^4, \qquad \langle g_s {\bar{q}} \sigma T G q \rangle = 0.8 \langle {\bar{q}}q \rangle , \nonumber \\{} & {} \langle g_s{\bar{q}}q \rangle ^2 = 2.229 \times 10^{-3} \, \textrm{GeV}^6, \nonumber \\{} & {} \langle g_s^2{\bar{q}}q \rangle ^2 = 7.960 \times 10^{-3 } \, \textrm{GeV}^6, \nonumber \\{} & {} \langle g_s^3 f G^3 \rangle = 0.045 \, \textrm{GeV}^6. \end{aligned}$$

(82)

Here the quark condensate density is obtained by taken $m_u + m_d = 6.9$ MeV at the scale 2 GeV [71] in the Gell–Mann–Oakes–Renner relation, and then evolutes to the default scale 1 GeV. The scale-independent gluon condensate density is the same as in the QCDSR. The dimension-six condensate densities are taken from the phenomenological analysis [65].

The Borel mass $M^2$ is usually chosen by a priori criterion that the contribution from high dimension condensates is no more than twenty percents, and simultaneously the contribution from high excited states and continuum spectral is smaller than thirty percents. The threshold value $s_0$ is close to the outset of the first excited state with the same quantum number and determined by the maximal stability of physical quantities once the Borel mass has been set down. Under the statement of ${{\bar{f}}}^s_{\sigma } = 0$ [15], we consider the $f_0$ as the ground state with ${\bar{s}}s$ component in the sum rules Eq. (79) with $q_1=q_2=s$. Taking $M^4 \partial /\partial M^2 \ln$ to both sides of Eq. (80), we obtain the sum rules of $m_{f_0}$. In this work we fix $m_{f_0}$ at $990 \pm 50 \, \textrm{MeV}$ [71], which is different from the previous work whose value is obtained by tunning the sum rules parameters. Here we fix $m_{f_0}$ to find the optimal Borel mass and threshold value, and then to calculate the scalar decay constant. We find that the sum rules parameter as well as the scalar decay constant are obtained as the same in the two types sum rules. This agreement is not a coincidence but a rational result since the dimension-6 four-quark condensate giving different contributions in the QCDSR and BFTSR is highly suppressed.

In Table 4, we show the sum rules result of scalar decay constant at the default scale 1 GeV. For the sake of comparison, we also present the previous sum rules result [5] where both the ground state $f_0$ and the first excited state $f_0(1500)$ are taken in to account. The QCDSR is is also studied under the statement that $f_0(1500)$ is the ground state with conventional ${\bar{s}}s$ component [62], and the similar BFTSRs study is carried out in Ref. [24]. In Fig. 8, we show the Borel mass dependence of the sum rules of scalar decay constant as shown in Eq. (80), in which the uncertainty band corresponds to different values of $s_0$.

1.2 A.2 Leading twist light-cone distribution amplitudes

The leading twist LCDA is usually expanded in terms of the Gegenbauer polynomials

$$\begin{aligned} \phi (u, \mu ) = {{\bar{f}}}_S 6 u {\bar{u}} \sum _{n=0}^\infty a_n(\mu ) C_n^{3/2}(2u-1), \end{aligned}$$

(83)

from which the multiplicatively renormalization coefficients can be written by

$$\begin{aligned} a_n(\mu ) = \frac{1}{{{\bar{f}}}_S} \frac{2(2n+3)}{3(n+1)(n+2)} \int _0^1 C_n^{3/2}(2u-1) \phi (u, \mu ) du.\nonumber \\ \end{aligned}$$

(84)

Substituting Eq. (83) into the normalization condition in Eq. (76), we obtain $a_{n = \textrm{even}} \propto 1/\mu _S$ and hence the even coefficients are zero for the neutral scalar mesons. Taking in to account the expansion of Gegenbauer polynomials, the renormalization coefficients is rewritten by means of the moments $\langle \zeta _n \rangle$

$$\begin{aligned} \langle \zeta ^{q}_{n} \rangle = \frac{1}{{{\bar{f}}}_S} \int _0^1 (2u-1)^n \phi (u, \mu ) du. \end{aligned}$$

(85)

The first two renormalization coefficients are related to the moments by

$$\begin{aligned} a_1(\mu ) = \frac{5}{3} \langle \zeta ^{q}_1(\mu ) \rangle , \qquad a_3(\mu ) = \frac{21}{4} \langle \zeta ^{q}_3(\mu ) \rangle - \frac{9}{4} \langle \zeta ^{q}_1(\mu ) \rangle . \nonumber \\ \end{aligned}$$

(86)

Here $q=u,d,s$ is the quark component of scalar meson. The renormalization group equation of the Gegenbauer coefficients read as

$$\begin{aligned} a_n(\mu ) = a_n(\mu _0) \left[ \frac{\alpha _s(\mu _0)}{\alpha _s(\mu )} \right] ^{-\left( \gamma _n^{(0)} \right) /b} L^{-1}(\mu ,\mu _0) \end{aligned}$$

(87)

with the one-loop anomalous dimension

$$\begin{aligned} \gamma _n^{(0)} = C_F \left[ 3 + \frac{2}{(n+1)(n+2)} - 4 \psi (n+2) - 4 \gamma _E \right] ,\nonumber \\ \end{aligned}$$

(88)

in which $b = (11 N_c - 2 n_f)/3, C_F = (N_c^2-1)/(2N_c)$.

We consider the correlation function

(89)

In the deep Euclidean region $q^2 \ll 0$, it can be evaluated directly by applying the OPE technique

(90)

Here $S_0^{q_2}$ denotes the free propagator of $q_2$ quark. When $q^2$ shifts from deeply negative to positive, the ${\bar{q}}q$ state begins to form hadrons and the correlation function can be expressed by the sum of contributions from all possible intermediate states with appropriate subtractions. Writing the hadron representation in the dispersion relation and isolating the ground state contribution, for $q^2 > 0$ we have

$$\begin{aligned}{} & {} \varPi _n(z,q) = \frac{1}{\pi } \int _0^\infty ds \frac{\textrm{Im} \varPi ^{\textrm{had}}_n(s,q^2)}{s - q^2} \nonumber \\{} & {} \quad = {{\bar{f}}}_S^2 m_S \langle \zeta _n \rangle + \frac{1}{4\pi ^3} \int _{s_0}^\infty ds \frac{3m_q}{(n+2) (s - q^2)}, \end{aligned}$$

(91)

in which the relationships and $\langle 0 \vert {\bar{q}}_{1} q_2 \vert S \rangle = m_S {{\bar{f}}}_S \langle \zeta ^s_0 \rangle$ are implied. We take the convention $\langle \zeta ^s_0 \rangle = 1$ in the following. After implement the quark-hadron duality and the Borel transformation, the QCDSRs of leading twist LCDA moments ($n = \textrm{odd}$) is

Fig. 9

The Borel mass dependence of the first moment obtained from the QCDSR (left) and BFTSR (right)

Table 5 The first Gegenbauer coefficients obtained from QCD sum rules

$$\begin{aligned} \langle \zeta _n(\mu ) \rangle= & {} I_n^{\textrm{pert}}(s_0,M^2) + \langle {\bar{q}}q \rangle I_n^{\langle {\bar{q}}q \rangle }(M^2) \nonumber \\{} & {} + \langle g_s {\bar{q}} \sigma T G q \rangle I_n^{\langle g_s {\bar{q}} \sigma T G q \rangle }(M^2) \nonumber \\{} & {} + \langle \alpha _s G^2 \rangle \langle {\bar{q}}q \rangle I_n^{\langle \alpha _s G^2 \rangle \langle {\bar{q}}q \rangle }(M^2, \mu ), \end{aligned}$$

(92)

the weighted functions $I_n$ up to dimension six can be found in Ref. [5].

The leading twist LCDA moments are also studied under the BFTSR [66] and the result is

$$\begin{aligned} \langle \zeta _{n=\textrm{odd}}(\mu ) \rangle= & {} I_n^{\textrm{pert}}(s_0,M^2) + \langle {\bar{q}}q \rangle I_n^{\langle {\bar{q}}q \rangle }(M^2) \nonumber \\{} & {} + \langle g_s {\bar{q}} \sigma T G q \rangle I_n^{\langle g_s {\bar{q}} \sigma T G q \rangle }(M^2) \nonumber \\{} & {} + \langle \alpha _s G^2 \rangle I_n^{\langle \alpha _s G^2 \rangle }(M^2, \mu ) \nonumber \\{} & {} + \langle \alpha _s G^2 \rangle \langle {\bar{q}}q \rangle I_n^{\langle \alpha _s G^2 \rangle \langle {\bar{q}}q \rangle }(M^2) \nonumber \\{} & {} + \langle g_s{\bar{q}}q \rangle ^2 I_n^{\langle g_s{\bar{q}}q \rangle ^2}(M^2)\nonumber \\{} & {} + \langle g_s^2{\bar{q}}q \rangle ^2 I_n^{\langle g_s^2{\bar{q}}q \rangle ^2}(M^2,\mu ) \nonumber \\{} & {} + \langle g_s^3 f G^3 \rangle I_n^{\langle g_s^3 f G^3 \rangle }(M^2,\mu ). \end{aligned}$$

(93)

The weighted functions associated to the perturbative and quark condensate terms are the same as in the QCDSR, while the other terms are different.

In Fig. 9 we show the Borel mass dependence of the first moment obtained from sum rules. Because the moments are dominated by the nonperturbative contributions, we see that $\langle \zeta _1 \rangle$ is not sensitive to the threshold value $s_0$. In Table 5 we show the result of the first Gegenbauer coefficient, where the first and second errors arise from $M^2$ and $s_0$, respectively. For the sake of comparison, we also present the result obtained from previous sum rules.¹ Our result of the first Gegenbauer coefficient $a_1$ obtained from the QCDSR is consist with the previous sum rules determination [5], the result is almost the same as that obtained from the BFTSR with the same sum rules parameters.

1.3 A.3 Subleading twist light-cone distribution amplitudes

Twist three light-cone distribution amplitudes associated with two particle composition are expanded also in terms of Gegenbauer polynomials [72]

$$\begin{aligned}{} & {} \phi ^s(u,\mu ) = {{\bar{f}}}_S \left[ 1 + \sum _{n=1}^\infty a_n^{s}(\mu ) C_n^{1/2}(2u-1) \right] , \nonumber \\{} & {} \phi ^\sigma (u,\mu ) = {{\bar{f}}}_S 6u {\bar{u}} \left[ 1 + \sum _{n=1}^\infty a_n^{\sigma }(\mu ) C_n^{3/2}(2u-1) \right] . \end{aligned}$$

(94)

The scalar and tensor moments defined in

$$\begin{aligned} \langle \zeta _n^{s/\sigma } \rangle = \int _0^1 du (2u-1)^n \phi ^{s/\sigma }(u,\mu ) \end{aligned}$$

(95)

relate to the Gegenbauer coefficients $a_n^{s/\sigma }$ by

$$\begin{aligned}{} & {} a_1^s = 3 \langle \zeta _1^s \rangle , \quad a_2^s = \frac{5}{2} \left[ 3 \langle \zeta _2^s \rangle - 1 \right] , \nonumber \\{} & {} a_4^s = \frac{9}{8} \left[ 35 \langle \zeta _4^s \rangle - 30 \langle \zeta _2^s \rangle + 3 \right] , \nonumber \\{} & {} a_1^\sigma = \frac{5}{3} \langle \zeta _1^\sigma \rangle , \quad a_2^\sigma = \frac{7}{12} \left[ 5 \langle \zeta _2^\sigma \rangle - 1 \right] , \nonumber \\{} & {} a_4^\sigma = \frac{11}{24} \left[ 21 \langle \zeta _4^\sigma \rangle - 14 \langle \zeta _2^\sigma \rangle + 1 \right] . \end{aligned}$$

(96)

We consider two correlation functions

$$\begin{aligned}{} & {} \varPi _n^s(z,q) \nonumber \\{} & {} \quad = i \int d^4x \, e^{iq \cdot x} \langle 0 \vert \textrm{T} \left\{ {\bar{q}}_2(x) \left( i z \cdot \overleftrightarrow {D} \right) ^n q_1(x), {\bar{q}}_1(0) q_2(0) \right\} \vert 0 \rangle \nonumber \\{} & {} \quad = - \left( z \cdot q \right) ^n I_n(q^2), \end{aligned}$$

(97)

$$\begin{aligned}{} & {} \varPi _n^\sigma (z,q) \nonumber \\{} & {} \quad = i \int d^4x \, e^{iq \cdot x} \langle 0 \vert \textrm{T} \left\{ {\bar{q}}_2(x) \sigma _{\mu \nu } \left( i z \cdot \overleftrightarrow {D} \right) ^n q_1(x), {\bar{q}}_1(0) q_2(0) \right\} \vert 0 \rangle \nonumber \\{} & {} \quad = i \left( q_\mu z_\nu - q_\nu z_\mu \right) \left( z \cdot q \right) ^n I_n^\sigma (q^2). \end{aligned}$$

(98)

The dispersion relation representation of the correlation functions in the physical regions reads as

$$\begin{aligned} \varPi _n^{s/\sigma }(z,q) = \frac{1}{\pi } \int ds \frac{\textrm{Im} \varPi _n^{s/\sigma , \textrm{had}}(s,q^2)}{s-q^2}. \end{aligned}$$

(99)

With the definitions of local matrix elements in terms of moments

$$\begin{aligned}{} & {} \langle 0 \vert {\bar{q}}_2(x) \left( i z \cdot \overleftrightarrow {D} \right) ^n q_1(x) \vert S(q) \rangle \nonumber \\{} & {} \quad = m_S {{\bar{f}}}_S \left( q \cdot z \right) ^n \langle \zeta _n^s \rangle , \nonumber \\{} & {} \quad \langle 0 \vert {\bar{q}}_2(x) \sigma _{\mu \nu } \left( i z \cdot \overleftrightarrow {D} \right) ^{n+1} q_1(x) \vert S(q) \rangle \nonumber \\{} & {} \quad = - i \frac{n+1}{3} m_S {{\bar{f}}}_S \left( q_{\mu }z_\nu - q_{\nu }z_\mu \right) \left( q \cdot z \right) ^n \langle \zeta _n^\sigma \rangle , \end{aligned}$$

(100)

we obtain the imaginary parts for the neutral scalar mesons.

$$\begin{aligned} \frac{1}{\pi } \textrm{Im} I^{s, \textrm{had}}_{n = \textrm{even}}= & {} - \delta (q^2 - m_S^2) m_S^2 {{\bar{f}}}_S^2 \langle \zeta _{n= \textrm{even}}^s \rangle \nonumber \\{} & {} + \varTheta (q^2 - s_0^s) \frac{3 \left( -q^2 + 4m_q^2 \right) }{8 \pi ^2} \frac{1}{n+1}, \nonumber \\ \frac{1}{\pi } \textrm{Im} I^{\sigma , \textrm{had}}_{n = \textrm{even}}= & {} - \delta (q^2 - m_S^2) m_S^2 {{\bar{f}}}_S^2 \langle \zeta _{n= \textrm{even}}^\sigma \rangle \frac{n+1}{3} \nonumber \\{} & {} + \varTheta (q^2 - s_0^s) \frac{3 \left( -q^2 + 2 m_q^2 \right) }{8 \pi ^2} \frac{1}{n+3}.\nonumber \\ \end{aligned}$$

(101)

We here concentrate on the correlation functions with even n since the odd ones result to zero moments for the neutral meson due to the C-parity conservation. In the deep Euclidean region, the correlation functions can be evaluated using operator product expansion at quark level. After applying the quark-hadron duality to math the result of $I_n^{s/\sigma }(q^2)$ obtained from the hadron interpolating and OPE calculation, for the neutral scalar mesons, the Borelization result of the second moments are [62]

$$\begin{aligned}{} & {} -m_S^2 {{\bar{f}}}_S^2 e^{-m_S^2/M^2} \langle \zeta _{n = \textrm{even}}^s \rangle \nonumber \\{} & {} \quad = - \frac{3}{8 \pi ^2} \frac{1}{n+1} \int _0^{s_0^s} s e^{-s/M^2} ds - \langle \alpha _s G^2 \rangle \frac{1}{8\pi } \nonumber \\{} & {} \qquad - \langle {\bar{q}} q \rangle (n+3) m_q + \langle g_s {\bar{q}} \sigma T G q \rangle \frac{(4 n^2 + 23n + 12) m_{q}}{12} \frac{1}{M^2} \nonumber \\{} & {} \qquad + 4\pi \alpha _s \langle {\bar{q}} q \rangle ^2 \frac{(-8n^2 + 16n + 150)}{81} \frac{1}{M^2}, \end{aligned}$$

(102)

$$\begin{aligned}{} & {} -\frac{1}{3} m_S^2 {{\bar{f}}}_S^2 e^{-m_S^2/M^2} \langle \zeta _{n = \textrm{even}}^\sigma \rangle \nonumber \\{} & {} \quad = - \frac{3}{8 \pi ^2} \frac{1}{(n+1)(n+3)} \int _0^{s_0^\sigma } s e^{-s/M^2} ds \nonumber \\{} & {} \qquad - \langle \alpha _s G^2 \rangle \frac{1}{24 \pi } \frac{1}{n+1} - \langle {\bar{q}} q \rangle m_q \nonumber \\{} & {} \qquad + \frac{1}{n+1} \frac{1}{M^2} \Big \{ \langle g_s {\bar{q}} \sigma T G q \rangle \frac{(4n^2+7n+5) m_q}{12} \nonumber \\{} & {} \qquad - 4\pi \alpha _s \langle {\bar{q}} q \rangle ^2 \left[ \frac{8n^2+9n-35)}{162} + \frac{2 \delta _{n0}}{9} \right] \Big \}. \end{aligned}$$

(103)

Besides the QCDSR result, the BFTSR also applied to calculate the scalar and tensor moments with the accuracy up to the linear terms of quark mass contributions [24].

$$\begin{aligned}{} & {} -m_S^2 {{\bar{f}}}_S^2 e^{-m_S^2/M^2} \langle \zeta _{n = \textrm{even}}^s \rangle \nonumber \\{} & {} \quad = - \frac{3}{8 \pi ^2} \frac{1}{n+1} M^4 \nonumber \\{} & {} \qquad + \frac{3}{8 \pi ^2} \frac{e^{-s_0^s/M^2}}{n+1} \left[ M^4 + s_0^s M^2 - 2 (n+2) m_q^2 M^2 \right] \nonumber \\{} & {} \qquad - \langle \alpha _s G^2 \rangle \frac{1}{8\pi } - \langle {\bar{q}} q \rangle (n+3) m_q + \langle g_s^3 f G^3 \rangle \frac{n}{96 \pi ^2} \frac{1}{M^2} \nonumber \\{} & {} \qquad + \langle g_s {\bar{q}} \sigma T G q \rangle \frac{(8 n^2 +13n - 18) m_{q}}{18} \frac{1}{M^2} \nonumber \\{} & {} \qquad + 4\pi \alpha _s \langle {\bar{q}} q \rangle ^2 \frac{(-4n^2 - 14n +168 )}{81} \frac{1}{M^2}, \end{aligned}$$

(104)

$$\begin{aligned}{} & {} -\frac{1}{3} m_S^2 {{\bar{f}}}_S^2 e^{-m_S^2/M^2} \langle \zeta _{n = \textrm{even}}^\sigma \rangle \nonumber \\{} & {} \quad = -\frac{3}{8 \pi ^2} \frac{1}{(n+1)(n+3)} M^4 \nonumber \\{} & {} \qquad + \frac{3}{8 \pi ^2} \frac{e^{-s_0^\sigma /M^2}}{(n+1)(n+3)} \left[ M^4 + s_0^s M^2 - 2 (n+3) m_q^2 M^2 \right] \nonumber \\{} & {} \qquad - \langle \alpha _s G^2 \rangle \frac{1}{24 \pi } \frac{1}{n+1} - \langle {\bar{q}} q \rangle m_q \nonumber \\{} & {} \qquad + \langle g_s {\bar{q}} \sigma T G q \rangle \frac{(8n+7) m_q}{18} \frac{1}{M^2} \nonumber \\{} & {} \qquad + 4\pi \alpha _s \langle {\bar{q}} q \rangle ^2 \frac{(-4n+10)}{81} \frac{1}{M^2}. \end{aligned}$$

(105)

Fig. 10

Upper: The Borel mass dependence of the second scalar moment $\langle \zeta _2^{s} \rangle$ obtained from the QCDSR (left) and BFTSR (right). Lower: The Borel mass dependence of the second tensor moment $\langle \zeta _2^{\sigma } \rangle$ obtained from the QCDSR (left) and BFTSR (right)

Table 6 The second Gegenbauer coefficients $a_2^{s,\sigma }$ obtained from sum rules

Figure 10 shows the Borel mass dependence of the second scalar and tensor moments. Its easy to find the apparent difference between the result obtained from QCDSR and BFTSR, and hence the different predictions for the Gegenbauer coefficients as shown in Table 6. We found the correction from strange quark in BFTSR, in comparison to QCDSR, is negligible. The significant different result obtained from two sum rules, as shown in the left and right panels, is mainly due to the different input value of vacuum condensates, especially the quark condensate density.

Twist three LCDAs also contributed from three particle composition [30, 73, 74]

$$\begin{aligned}{} & {} \phi _{3S}^{q}(p_1, \alpha _i) \nonumber \\{} & {} \quad = 360 f_{3S} \alpha _1 \alpha _2 \alpha _3^2 \left[ 1 + \lambda _{3S} \left( \alpha _1 - \alpha _2 \right) + \omega _{3S} \left( 7 \alpha _3 - 3 \right) \right] . \qquad \nonumber \\ \end{aligned}$$

(106)

where the nonperturbative parameters is defined by the local matrix elements

$$\begin{aligned}{} & {} \langle S(p_1) \vert {\bar{q}}_2(z) g_s G \cdot \sigma q_1(z) \vert 0 \rangle = 2 f_{3S} \left( p_1 \cdot z \right) ^2, \nonumber \\{} & {} \qquad \langle S(p_1) \vert {\bar{q}}_2(z) \overleftarrow{D} g_s G \cdot \sigma q_1(z) - {\bar{q}}_2(z) g_s G \cdot \sigma \overrightarrow{D} q_1(z)\vert 0 \rangle \nonumber \\{} & {} \quad = - 2 f_{3S} \lambda _{3S} \left( p_1 \cdot z \right) ^3/14, \nonumber \\{} & {} \qquad \langle S(p_1) \vert {\bar{q}}_2(z) \sigma ^{\mu \nu } \left[ i D, g_s G_{\mu \nu } \right] q_1(z) \vert 0 \rangle \nonumber \\{} & {} \qquad - \langle S(p_1) \vert \frac{3}{7} \partial {\bar{q}}_2(z) g_s G \cdot \sigma \overrightarrow{D} q_1(z) \vert 0 \rangle \nonumber \\{} & {} \quad = - f_{3S} \omega _{3S} \left( p_1 \cdot z \right) ^3/14. \end{aligned}$$

(107)

The renormalization group equations of them are

$$\begin{aligned}{} & {} f_{3S}(\mu )= f_{3S}(\mu _0) L(\mu , \mu _0)^{-\gamma _{f_{3S}}/8}, \nonumber \\{} & {} \left[ f_{3S}\lambda _{3S}\right] (\mu )= \left[ f_{3S}\lambda _{3S}\right] (\mu _0) L(\mu , \mu _0)^{-\gamma _{\lambda _{3S}}/8}, \nonumber \\{} & {} \left[ f_{3S}\omega _{3S}\right] (\mu )= \left[ f_{3S}\lambda _{3S}\right] (\mu _0) L(\mu , \mu _0)^{-\gamma _{\omega _{3S}}/8}, \end{aligned}$$

(108)

at one loop accuracy, the anomalous dimensions are

$$\begin{aligned} \gamma _{f_{3S}}^{(0)} = \frac{110}{9}, \quad \gamma _{\lambda _{3S}}^{(0)} = \frac{139}{9}, \quad \gamma _{\omega _{3S}}^{(0)} = \frac{208}{9}. \end{aligned}$$

(109)

In the numerics we take $\lambda _{3f_0} =0$ due to the G-odd definition, and $\omega _{3f_0}(\textrm{1GeV}) = -1.5 \pm 0.7$ as the same as $\omega _{3\pi }$. The additional scalar coupling is related to the gegengauer moments $\langle \zeta _{n=0,2}^{s/\sigma } \rangle$ and ${{\bar{f}}}_{f_0}$ by by the equation of motion

$$\begin{aligned}{} & {} \langle \zeta _{2}^{s} \rangle = \frac{1}{3} \langle \zeta _{0}^{s} \rangle + \frac{4}{m_{f_0}} \frac{{{\bar{f}}}_{3f_0}}{{{\bar{f}}}_{f_0}}, \nonumber \\{} & {} \langle \zeta _{2}^{\sigma } \rangle = \frac{1}{5} \langle \zeta _{0}^{\sigma } \rangle + \frac{12}{5m_{f_0}} \frac{{\bar{f}}_{3f_0}}{{{\bar{f}}}_{f_0}} - \frac{8}{5m_{f_0}} \frac{{\bar{f}}_{3f_0}}{{{\bar{f}}}_{f_0}} \langle \langle \alpha _3 \rangle \rangle _{f_0}. \end{aligned}$$

(110)

The moments of three particle distribution amplitudes are defined

$$\begin{aligned}{} & {} \langle \langle \left( \alpha _2 - \alpha _1 + v \alpha _3 \right) ^n \rangle \rangle \nonumber \\{} & {} \quad = \int \mathcal{D} \alpha _i \phi _{3S}(\alpha _i) \left( \alpha _2 - \alpha _1 + v \alpha _3 \right) ^n. \end{aligned}$$

(111)