Chiral dynamics and S-wave contributions in ${\bar{B}}^0/D^0 \rightarrow \pi ^{\pm }\eta \ l^{\mp } \nu$ decays

Abstract

In this work, we analyze the semi-leptonic decays $\bar{B}^0/D^0 \rightarrow (a_0(980)^{\pm }\rightarrow \pi ^{\pm }\eta ) l^{\mp } \nu$ within light-cone sum rules. The two and three-body light-cone distribution amplitudes (LCDAs) of the B meson and the only available two-body LCDA of the D meson are used. To include the finite-width effect of the $a_0(980)$, we use a scalar form factor to describe the final-state interaction between the $\pi \eta$ mesons, which was previously calculated within unitarized Chiral Perturbation Theory. The result for the decay branching fraction of the $D^0$ decay is in good agreement with that measured by the BESIII Collaboration, while the branching fraction of the ${\bar{B}}^0$ decay can be tested in future experiments.

1 Introduction

The study of scalar mesons is an interesting topic in the hadron physics, partly due to the fact that the scalar mesons have the same quantum numbers as the QCD vacuum. Furthermore, the highly non-perturbative nature of the strong interactions at low energies makes it difficult to understand the internal structure and dynamics of these particles. There are a number of scenarios to understand the structure of the isovector scalar meson $a_0(980)$, like a ${\bar{q}} q$ state, a four-quark state, a molecular state, the glueball picture, or a hybrid states [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18]. However, until now there is no definite conclusion on which scenario is correct, however, there are some indications in favor of the molecular picture.

The semi-leptonic heavy meson decays are ideal platforms for the study of scalar mesons such as the $a_0(980)$. Experimentally, such processes have a much cleaner background than e.g. hadronic decays, and theoretically, all the strong dynamics is encapsulated in the hadronic transition matrix elements, which are the objects to be dealt with. Nowadays there are a number of theoretical investigations for the $B\rightarrow a_0(980)$ [19,20,21,22,23,24] and the $D\rightarrow a_0(980)$ transitions [25,26,27,28,29]. In the narrow-width limit, where the $a_0(980)$ is considered as a quasi-stable particle, calculating these single-body transitions is enough for predicting the decay branching fractions. However, in real physical processes the $a_0(980)$ is an intermediate resonance which can further decay into light mesons. Recently, the BESIII Collaboration has announced a measurement of the branching fraction [30]:

$$\begin{aligned}&\mathcal{{B}}\left( D^0 \rightarrow \left( a_0(980)\rightarrow \pi ^{-}\eta \right) \ e^{+} \nu \right) \nonumber \\&\quad =(1.33\pm 0.09)\times 10^{-4}. \end{aligned}$$

(1)

Note that the actual measured final-state is $\pi \eta$. Thus to analyze the full decay process one must consider the finite-width effect and should also deal with the final-state interaction between the $\pi$ and the $\eta$.

As shown in the previous works, see e.g. [31,32,33], the S-wave two-meson final-state interaction can be described by a two-meson scalar form factor. This is justified by the Watson–Migdal theorem [34, 35], which ensures that the phase of the $B/D\rightarrow \pi \eta$ transition matrix element in the semi-leptonic decay must be equal to the phase of the $\pi \eta$ elastic scattering amplitude. The two-meson scalar form factor was calculated using unitarized Chiral Perturbation Theory (uChPT) assisted by a numerical iteration based on a dispersion relation [36]. Such a scalar form factor satisfies the unitary constraint and is free from unphysical singularities (which often appear in the framework of uCHPT, see e.g. the discussion in Ref. [37]). In those previous works the transition matrix element was calculated from Light-Cone Sum Rules (LCSRs), where the light-cone distribution amplitudes (LCDAs) of the scalar meson or the generalized LCDAs for the final two mesons are used. In this work, instead of assuming the structure of the $a_0(980)$ and test it with the corresponding decay width calculation, we aim to theoretically reproduce the measured branching fraction of $D^0 \rightarrow (a_0(980)\rightarrow \pi ^{-}\eta ) e^{+} \nu$. Therefore, we choose to use the LCDAs of the initial heavy meson and create the $\pi \eta$ state by interpolating a scalar current with the same quantum numbers on the vacuum. For the detailed calculation procedure we follow Refs. [38, 39], where the transitions form factors for $B\rightarrow (\rho \rightarrow \pi \pi )$ and $B_s\rightarrow (f_0(980)\rightarrow KK)$ were calculated.

This article is organized as follows: Sect. 2 is an illustration on the framework of the LCSR, where we derive the sum rule equation for the ${\bar{B}}^0/D^0\rightarrow \pi \eta$ form factors by considering the finite-width effect. Section 3 gives the numerical results including the form factors and the decay branching fractions. Section 4 contains a brief summary. Some technicalities are relegated to the appendices.

2 ${\bar{B}}^0/D^0 \rightarrow \pi ^{\pm }\eta$ form factors in a LCSR

In the spirit of LCSRs, to study the transition ${\bar{B}}^0/D^0 \rightarrow \pi ^{\pm }\eta$, one should start with a correlation function. In the case of a $B^0$ decay with the $b\rightarrow u$ transition it reads

$$\begin{aligned}&\Pi _{\mu }(p,q) \nonumber \\&\quad =i\int d^{4}x\ e^{ip\cdot x}\langle 0|T\left\{ J^{\bar{d}u}(x)J_{\mu }^{V-A}(0)\right\} |B^{0}(p+q)\rangle ~, \end{aligned}$$

(2)

where $J^{\bar{d}u}$ is the scalar current with the same quantum number as the final S-wave $\pi ^+\eta$ state, and $J_{\mu }^{V-A}$ is the standard $V-A$ current. Their explicit forms are

$$\begin{aligned} J^{\bar{d}u}(x)=\bar{d}(x)u(x),\ \ \ \ J_{\mu }^{V-A}(0)=\bar{u}(0)\gamma _{\mu }(1-\gamma _{5})b(0).\nonumber \\ \end{aligned}$$

(3)

For the case of a $D^0$ decay with the $c\rightarrow d$ transition, the correlation function is similar except that $J^{\bar{d}u}$ and $J_{\mu }^{V-A}$ should be changed to $J^{\bar{u}d}={\bar{u}} d$ and $J_{\mu }^{V-A}={\bar{d}} \gamma _{\mu }(1-\gamma _5)c$, respectively. The correlation function in Eq. (2) will be calculated both at the hadron as well as the quark–gluon level, and the results from these two distinct approaches are related by quark–hadron duality.

2.1 Hadron level

In terms of a dispersion relation, the correlation function in Eq. (2) can be expressed as:

$$\begin{aligned} \Pi _{\mu }^H (p,q)=\frac{1}{\pi }\int _{0}^{\infty }ds\ \frac{{\mathrm{Im}}\ \Pi _{\mu }^H (s,q^{2})}{s-p^{2}-i\epsilon }~. \end{aligned}$$

(4)

If the narrow-width approximation is applied, the imaginary part above is just a single meson pole of the $a_0(980)$ plus a continuous spectrum including higher excited states. However, if the finite-width effect is considered, the single meson pole should be replaced by a multi-meson state, which has a finite distribution width. The lowest two-meson state created by $J^{\bar{d}u}$ is $\pi ^{\pm }\eta$, while the heavier two-meson state of $K{\bar{K}}$ can be absorbed into the continuous spectrum. The imaginary part of the correlation function thus reads

$$\begin{aligned}&2i\ {\mathrm{Im}}\ \Pi _{\mu }^H(s,q^{2}) ={\mathrm{Disc}}\ \Pi _{\mu }^H(s,q^{2})\nonumber \\&\quad = \ i\int d\tau _{2}(2\pi )^{4}\delta ^{4}(p-k)\langle 0|J^{\bar{d}u}(0)|\pi (k_{1})\eta (k_{2})\rangle \nonumber \\&\quad \quad \times \langle \pi (k_{1})\eta (k_{2})|J_{\mu }^{V-A}(0)|{\bar{B}}^{0}(p+q)\rangle +\cdots , \end{aligned}$$

(5)

where the ellipsis denotes the higher continuous spectrum contribution, which will be omitted later for convenience. Further, $d\tau _2$ is the two-body integral measure:

$$\begin{aligned} d\tau _{2}=\frac{d^{3}{\vec {k}}_{1}}{(2\pi )^{3}}\frac{1}{2E_{k_{1}}}\frac{d^{3}{\vec {k}}_{2}}{(2\pi )^{3}}\frac{1}{2E_{k_{2}}}~, \end{aligned}$$

(6)

with $s=p^2$ and $k=k_1+k_2$. The first matrix element in Eq. (5) is parameterized by the two-meson scalar form factor:

$$\begin{aligned} \langle \pi (k_{1})\eta (k_{2})|J^{\bar{d}u}(0)|0\rangle =B_0 F_{\pi \eta }(k^2). \end{aligned}$$

(7)

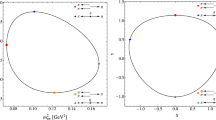
Here, $B_0$ is proportional to the QCD quark condensate: $3 F^2 B_0 =-\langle {{\bar{u}}} u+{\bar{d}} d+{\bar{s}} s \rangle$, with F the pion decay constant in the SU(3) chiral limit. $F_{\pi \eta }(k^2)$ has been calculated in the Ref. [36] using uChPT associated with a dispersion relation iteration to ensure the unitary constraint and remove the unphysical singularities. The obtained form factor is applicable up to a relatively high energy of around 1.2 GeV, and its real and imaginary parts are shown in Fig. 1. The three lines correspond to the form factors derived by three sets of low-energy constants (LECs) of ChPT. The one labeled “old” is taken from earlier works [40, 41]. The other two sets are fitted in Ref. [36] using the latest data, where the authors used two fit approaches denoted as Fit 1 and Fit 2. In this work, all the three results shown in Fig. 1 will be used, and the difference between them will be taken as the uncertainty of the numerical results.

Fig. 1

Left panel: real (red solid lines) and imaginary (blue dashed lines) parts of $F_{\pi \eta }(k^2)$. Right panel: the norm of $F_{\pi \eta }(k^2)$. For further details, see Ref. [36]

On the other hand, the second matrix element in Eq. (5) is parameterized by the $B^0\rightarrow \pi ^+\eta$ form factors [42]. For the S-wave component, only the axial-vector current contributes. Its matrix element is parameterized as:

$$\begin{aligned}&-i\left\langle \pi (k_{1}) \eta (k_{2})|\bar{u} \gamma _{\mu } \gamma _{5} b | \bar{B}^{0}(q+k)\right\rangle \nonumber \\&\quad = F_{t} \frac{q_{\mu }}{\sqrt{q^{2}}}+F_{0} \frac{2 \sqrt{q^{2}}}{\sqrt{\lambda _{B}}}\left( k_{\mu }-\frac{k \cdot q}{q^{2}} q_{\mu }\right) \nonumber \\&\qquad + \frac{F_{\Vert }}{\sqrt{k^{2}}}\left( \bar{k}_{\mu }-\frac{4(q \cdot k)(q \cdot \bar{k})}{\lambda _{B}} k_{\mu }+\frac{4 k^{2}(q \cdot \bar{k})}{\lambda _{B}} q_{\mu }\right) , \end{aligned}$$

(8)

where ${\bar{k}}=k_1-k_2$, $q\cdot k=(1/2)(m_B^2-k^2-q^2)$ and $\lambda _B=m_{B}^{4}+k^{4}+q^{4}-2\left( m_{B}^{2} k^{2}+m_{B}^{2} q^{2}+k^{2} q^{2}\right)$. Each form factor $F_i$ ($i=0,t,{\Vert }$) is a function of $q^2$, $k^2$ and

$$\begin{aligned} q\cdot \bar{k}=\left( m_{\pi }^{2}-m_{\eta }^{2}\right) \sqrt{\frac{\lambda _{B}}{4k^{2}}+\frac{q^{2}}{k^{2}}}+\frac{\sqrt{\lambda _{B}\lambda _{\pi \eta }(k^2)}}{2k^{2}}{\mathrm{cos}}\ \theta _{\pi },\nonumber \\ \end{aligned}$$

(9)

where $\theta _{\pi }$ is the angle between the pion momenta ${\vec {k}}_1$ and ${\vec {q}}$ in the rest-frame of the $\pi -\eta$ system and $\lambda _{\pi \eta }(k^2)=m_{\pi }^{4}+m_{\eta }^{4}+k^{4}-2\left( m_{\pi }^{2}m_{\eta }^{2} +m_{\eta }^{2} k^{2}+m_{\pi }^{2}k^{2}\right)$. As illustrated in Ref. [42], one can apply a partial wave expansion on the form factors $F_i$ using the associated Legendre polynomials:

$$\begin{aligned}&F_{0, t}(q^{2}, k^{2}, q \cdot \bar{k})=\sum _{l=0}^{\infty } \sqrt{2 l+1} F_{0, t}^{(l)}(q^{2}, k^{2}) P_{l}^{(0)}(\cos \theta _{\pi }), \nonumber \\&F_{\Vert }(q^{2}, k^{2}, q \cdot \bar{k})=\sum _{l=1}^{\infty } \sqrt{2 l+1} F_{\Vert }^{(l)}(q^{2}, k^{2}) \frac{P_{l}^{(1)}(\cos \theta _{\pi })}{\sin \theta _{\pi }}. \end{aligned}$$

(10)

When this expansion is inserted into Eq. (5), the two-body phase space integration $\int d\tau _2$ will act as an S-wave projector so that the contribution of $F_{\Vert }$ vanishes. Applying Eqs. (7), (8) and (10) to Eq. (5), and performing the phase space integration, one arrives at

$$\begin{aligned}&{\mathrm{Im}}\Pi _{\mu }^{\mathrm{H}}(s,q^{2})=\frac{i}{16\pi }\frac{\sqrt{\lambda _{\pi \eta }(s)}}{s}B_0 F^{*}_{\pi \eta }(s)\nonumber \\&\quad \times \left[ F_{t}^{(0)}(s,q^{2})\frac{q_{\mu }}{\sqrt{q^{2}}}+F_{0}^{(0)}\left( s,q^{2}\right) \frac{2\sqrt{q^{2}}}{\sqrt{\lambda _{B}}}\left( p_{\mu }-\frac{p\cdot q}{q^{2}}q_{\mu }\right) \right] . \end{aligned}$$

(11)

Using the dispersion relation, Eq. (4), we can obtain the correlation function at the hadron level.

2.2 Quark–gluon level

At quark–gluon level, the correlation function in Eq. (2) should be calculated in the deep Euclidean region with $p^2, q^2\ll 0$ utilizing the operator-product-expansion (OPE). For the ${\bar{B}}^0$ decay the OPE is performed in the heavy quark limit with the bottom quark field being translated to an effective field in the heavy quark effective theory (HQET), $b(x)=\mathrm{exp}(-im_b v\cdot x)b_v(x)$, where v is the four-velocity of the ${\bar{B}}^0$. The correlation function is expressed as a convolution of a perturbative kernel and the B meson light-cone distribution amplitudes (LCDAs).

Since the internal light quark propagates in the background field of soft gluons, in the calculation of the perturbative kernel, one should use a light quark propagator of the form [43, 44]:

(12)

where i, j are the color indices, u is a dimensionless parameter, $G_{\mu \nu }=G_{\mu \nu }^a t^a$ is the gluon field strength tensor. Here, the fixed-point gauge $x\cdot A(x)=0$ is used.

Fig. 2

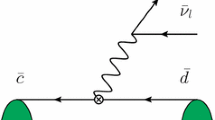
Diagrams for the calculation of the quark–gluon contribution to the two and three-body B meson LCDAs. The circle cross denotes the $V-A$ current while the black dot denotes the interpolating current for the $\pi \eta$ state. The gray bubbles represent two- or three-particle LCDAs of the B meson

The corresponding diagrams are shown in Fig. 2. In the diagram (a) the u quark line is a free propagator and the gray bubble denotes two-particle B meson LCDAs. In the diagram (b) the u quark absorbs a soft gluon emitted from the B meson state, and the gray bubble denotes the three-particle B meson LCDAs. The two and three-particle B meson LCDAs are defined as [45,46,47,48]:

(13)

where $\alpha ,\beta$ are spinor indexes, $\omega$ and $\xi$ are the plus components of the light-quark and gluon momentum, respectively, in the B meson. [x, 0] is the Wilson line along the light-cone direction. As illustrated in Ref. [49], in the deep Euclidean region $p^2, q^2\ll 0$, the space-time interval x of the correlation function in Eq. (2) is almost on the light-cone: $x^2\sim -1/q^2\rightarrow 0$. Therefore, the fixed-point gauge $x\cdot A=0$ used for the light quark propagator in Eq. (12) is equivalent to the light-cone gauge $n\cdot A=0$, so that the Wilson line [x, 0] can be set to 1. The explicit form of the B meson LCDAs can be found in Appendix A.

In Eq. (13), the $v\cdot x$ in the denominator is difficult to be dealt with directly. To overcome this difficulty, we define a new set of LCDAs as

$$\begin{aligned} {\psi }^{(1)}(\omega )=\int _{0}^{\omega }d\tau \ \psi (\tau ),&{\psi }^{(2)}(\omega )=\int _{0}^{\omega }d\tau \ \psi ^{(1)}(\tau ),\nonumber \\&\psi (\omega )=\frac{d^n}{d\omega ^n}\psi ^{(n)}(\omega )~ \end{aligned}$$

(14)

where $\psi$ can be any LCDA appears in Eq. (13). The advantage of this definition is that, with the help of integration by part, one can eliminate the $v\cdot x$ denominator:

$$\begin{aligned}&\int d^{4}x\ e^{ip\cdot x}\int _{0}^{\infty }d\omega \ e^{-i\omega v\cdot x}\frac{\psi (\omega )}{(v\cdot x)^{n}}\cdots \nonumber \\&\quad =i^n\int d^{4}x\ e^{ip\cdot x}\int _{0}^{\infty }d\omega \ e^{-i\omega v\cdot x}{\psi }^{(n)}(\omega )\cdots . \end{aligned}$$

(15)

The ellipsis denotes the terms independent of $\omega$. Note that during the integration by part, since ${\psi }(0)=0$, the boundary term at $\omega =0$ vanishes trivially. On the other hand, it seems that the boundary term at $\omega =\infty$ is nonzero since ${\psi }^{(n)}(\infty )$ is finite. However, when $\omega \rightarrow \infty$, the exponential $\mathrm{exp}(-i\omega v\cdot x)$ fluctuates heavily during the integration of x. Thus the boundary term at $\omega =\infty$ is also zero. A detailed explanation is given in Appendix B.

Unlike for the B meson, there is no systematic development of the D meson LCDAs in the literature. The only available one is the two-particle LCDA defined in Refs. [50, 51]:

(16)

where i, j are the color indices, and $f_D$ is the D meson decay constant. $\varphi _D(u)$ is the two-particle LCDA of D meson, which has the form

$$\begin{aligned} \varphi _D(u)=6u(1-u)\left[ 1-C_d(1-2u)\right] ~. \end{aligned}$$

(17)

$C_d$ is a parameter ranging from 0 to 1, which can be fixed from experiments, $C_d=0.7$ [50].

In the case of the ${\bar{B}}^0$ decay, the OPE calculation for the correlation function with contributions from the two-particle LCDAs are

$$\begin{aligned}&\Pi _{\mu }^{\mathrm{OPE}}(p,q)^{(2)} \nonumber \\&\quad =\ if_{B}m_{B}\int _{0}^{\infty }d\omega \frac{1}{\Delta _2}\Bigg \{ \phi _{+}(\omega )\Bigg [(m+\omega )v_{\mu }-p_{\mu } \Bigg ]\nonumber \\&\qquad -4{\Phi ^{(1)}}(\omega )v_{\mu }\Bigg \} \nonumber \\&\qquad -2if_{B}m_{B}\int _{0}^{\infty }d\omega \frac{1}{\Delta _2^{2}}\Bigg (1-\frac{\omega }{m_{B}}\Bigg ){\Phi ^{(1)}}(\omega )\nonumber \\&\qquad \times \Bigg [(m-\omega )p_{\mu }+\Bigg (\frac{\omega }{m_B} \Bigg (m_B^2+p^2-q^2\Bigg )-p^{2}\Bigg )v_{\mu }\Bigg ], \end{aligned}$$

(18)

where m is the u quark mass $m_u$ in the ${\overline{MS}}$ scheme at the scale $\mu =2$ GeV, which is given by the Particle Data Group (PDG) [52]. For the $D^0$ decay m denotes the d quark mass $m_d$. The discontinuity of the correlation function across the complex plane of $p^2$ comes from the denominators $1/\Delta _2^n$. On the other hand, the correlation function contributed by the three-particle LCDAs contains the similar denominators $1/\Delta _3^n$. However, it is much more involved so we do not show it here explicitly. These denominators read

$$\begin{aligned}&\Delta _3 =\left[ p-(\omega +u\xi ) v\right] ^{2}-m^{2}\nonumber \\&\quad =\left( 1-\frac{\omega +u\xi }{m_{B}}\right) \left[ p^{2}-\Sigma (\omega ,\xi , q^{2},m^2)\right] ,\nonumber \\&\Delta _2=\Delta _3(\xi =0),\nonumber \\&\qquad \Sigma \left( \omega ,\xi , q^{2},m^2\right) =\frac{\omega +u\xi }{m_{B}-\omega -u\xi }\left( m_{B}^{2}-q^{2}\right) \nonumber \\&\qquad -\frac{m_{B}[(\omega +u\xi )^2-m^{2}]}{m_{B}-\omega -u\xi }~. \end{aligned}$$

(19)

Extracting the discontinuity across the complex plane of $p^2$ for the correlation function is equivalent to extracting the discontinuity of $1/\Delta _{2,3}^n$. For the single power terms $1/\Delta _{2,3}$, their discontinuity can be obtained by the replacement

$$\begin{aligned} \frac{1}{\Delta _3}\rightarrow (-2\pi i)\frac{m_B}{m_B-\omega -u\xi }\delta \left( p^{2}-\Sigma \left( \omega ,\xi ,q^{2},m^2\right) \right) , \end{aligned}$$

(20)

and for $1/\Delta _{2}$ the replacement is the same but with $\xi =0$. To extract the discontinuity of the higher power terms $1/\Delta _{2,3}^n$, we can firstly transform it into the form of a derivative on the $1/\Delta _{2,3}$, which reads

$$\begin{aligned}&\mathrm{Disc}\left[ \int \frac{1}{\Delta _{3}^{n}}(\cdots )\right] =\frac{(-2{\pi }i)}{(n-1)!} \left( \frac{\partial }{\partial \Omega }\right) ^{n-1}\nonumber \\&\quad \times \int { {\delta }}\left( \left[ p-(\omega +u\xi )v\right] ^{2}-\Omega \right) (\cdots )\Big |_{\Omega =m^{2}}~, \end{aligned}$$

(21)

where $(\cdots )$ denotes all the terms except $1/\Delta _{2,3}^n$ in the integrand of Eq. (18). Finally, we obtain the correlation function at the quark–gluon level by the dispersion relation

$$\begin{aligned} \Pi _{\mu }^{\mathrm{OPE}} (p,q)=\frac{1}{\pi }\int _{0}^{\infty }ds\ \frac{\mathrm{Im}\Pi _{\mu }^{\mathrm{OPE}} (s,q^{2})}{s-p^{2}-i\epsilon }~, \end{aligned}$$

(22)

which should be equal to that given in Eq. (4): $\Pi _{\mu }^{\mathrm{H}}=\Pi _{\mu }^{\mathrm{OPE}}$. According to the quark–hadron duality, the dispersion integral in the region $s_0^{\pi \eta }<s<\infty$ on the two sides are canceled, where $s_0^{\pi \eta }=4 m_K^2$ is the threshold of $K{\bar{K}}$, which is the lowest two-meson state above the $\pi \eta$ state. After Borel transformation, one arrives at the sum rules equation. For $F_{0}^{(0)}(s,q^{2})$ it reads as

$$\begin{aligned}&\frac{1}{16\pi ^{2}}\int _{(m_{\pi }+m_{\eta })^{2}}^{s_{0}^{\pi \eta }}ds\ e^{-s/M^{2}}\frac{\sqrt{\lambda _{\pi \eta }(s)}}{s}\times B_{0}F_{\pi \eta }^{*}(s)F_{0}^{(0)}\left( s,q^{2}\right) \frac{2\sqrt{q^{2}}}{\sqrt{\lambda _{B}}}\nonumber \\&\quad = \ f_{B}\sum _{n=0}^{1}\left( m_B^{2}\frac{\partial }{\partial \Omega }\right) ^n\nonumber \\&\qquad \times \int _{0}^{\infty }d\omega \ \Theta \left( \omega ,0,s_{0}^{\pi \eta },M^2,q^2,m^2\right) I_{2}^{(n)}\left( \omega ,q^{2}\right) \Big |_{\Omega =m^{2}}\nonumber \\&\qquad +f_{B}\sum _{n=1}^{3}\frac{1}{n!}\left( m_B^{2}\frac{\partial }{\partial \Omega }\right) ^n\nonumber \\&\qquad \times \int _{0}^{\infty }d\omega d\xi \ \Theta \left( \omega ,\xi ,s_{0}^{\pi \eta },M^2,q^2,\Omega \right) I_{3}^{(n)}\left( \omega ,\xi ,q^{2},\Omega \right) \Big |_{\Omega {=}m^{2}}~, \end{aligned}$$

(23)

where

$$\begin{aligned} \Theta \left( \omega ,\xi ,s_{0}^{\pi \eta },M^2,q^2,\Omega \right)&=e^{\Sigma (\omega ,\xi ,q^{2},\Omega )/M^{2}}\theta \left( \Sigma (\omega ,\xi ,q^{2},\Omega )\right) \nonumber \\&\quad \times \theta \left( s_{0}^{\pi \eta }-\Sigma (\omega ,\xi ,q^{2},\Omega )\right) . \end{aligned}$$

(24)

For $F_{t}^{(0)}(s,q^{2})$, the sum rules equation is similar, it reads

$$\begin{aligned}&\frac{1}{16\pi ^{2}}\int _{(m_{\pi }+m_{\eta })^{2}}^{s_{0}^{\pi \eta }}ds\ e^{-s/M^{2}}\frac{\sqrt{\lambda _{\pi \eta }(s)}}{s}B_{0}F_{\pi \eta }^{*}(s)\nonumber \\&\qquad \times \left( F_{t}^{(0)}(s,q^{2})\frac{1}{\sqrt{q^{2}}}-F_{0}^{(0)}(s,q^{2})\frac{2p\cdot q}{\sqrt{\lambda _{B}q^{2}}}\right) \nonumber \\&\quad = \ f_{B}\sum _{n=0}^{1}\left( m_B^{2}\frac{\partial }{\partial \Omega }\right) ^n\nonumber \\&\qquad \int _{0}^{\infty }d\omega \ \Theta \left( \omega ,0,s_{0}^{\pi \eta },M^2,q^2,m^2\right) J_{2}^{(n)}(\omega ,q^{2})\Big |_{\Omega =m^{2}}\nonumber \\&\qquad +f_{B}\sum _{n=1}^{3}\frac{1}{n!}\left( m_B^{2}\frac{\partial }{\partial \Omega }\right) ^n\nonumber \\&\qquad \times \int _{0}^{\infty }d\omega d\xi \ \Theta \left( \omega ,\xi ,s_{0}^{\pi \eta },M^2,q^2,\Omega \right) J_{3}^{(n)}\left( \omega ,\xi ,q^{2},\Omega \right) \Big |_{\Omega =m^{2}}. \end{aligned}$$

(25)

The explicit expression for the $I_{2,3}^{(n)}$ and $J_{2,3}^{(n)}$ functions are given in Appendix C.

On the other hand, for the $D^0$ decay the treatment is more simple because there is only one two-particle LCDA $\varphi _D$ and no $v\cdot x$ terms appear in the denominator. The sum rule equations for the $D^0$ decay are

$$\begin{aligned}&\frac{1}{16\pi ^{2}}\int _{(m_{\pi }+m_{\eta })^{2}}^{s_{0}^{\pi \eta }}ds\ e^{-s/M^{2}}\frac{\sqrt{\lambda _{\pi \eta }(s)}}{s}\nonumber \\&\qquad \times B_{0}F_{\pi \eta }^{*}(s)F_{0}^{(0)}\left( s,q^{2}\right) \frac{2\sqrt{q^{2}}}{\sqrt{\lambda _{B}}}\nonumber \\&\quad =\ f_{D}\int _{0}^{1}\frac{du}{{\bar{u}}}\ \Theta ^{\prime }\left( u,s_{0}^{\pi \eta },M^2,q^2,m^2\right) (m-{\bar{u}} m_D)\varphi _D(u)~,\nonumber \\&\frac{1}{16\pi ^{2}}\int _{(m_{\pi }+m_{\eta })^{2}}^{s_{0}^{\pi \eta }}ds\ e^{-s/M^{2}}\frac{\sqrt{\lambda _{\pi \eta }(s)}}{s}B_{0}F_{\pi \eta }^{*}(s)\nonumber \\&\qquad \times \left( F_{t}^{(0)}(s,q^{2})\frac{1}{\sqrt{q^{2}}}-F_{0}^{(0)}\left( s,q^{2}\right) \frac{2p\cdot q}{\sqrt{\lambda _{B}q^{2}}}\right) \nonumber \\&\quad = \ f_{D}\int _{0}^{1}\frac{du}{{\bar{u}}}\ \Theta ^{\prime }\left( u,s_{0}^{\pi \eta },M^2,q^2,m^2\right) (m+u m_D)\varphi _D(u)~. \end{aligned}$$

(26)

where ${\bar{u}}=1-u$ and

$$\begin{aligned}&\Theta ^{\prime }\left( u,s_{0}^{\pi \eta },M^{2},q^{2},m^{2}\right) \nonumber \\&\quad =\ e^{-\left( um_{D}^{2}+\frac{m^{2}-uq^{2}}{\bar{u}}\right) \Big /M^{2}}\theta \left( um_{D}^{2}+\frac{m^{2}-uq^{2}}{\bar{u}}\right) \nonumber \\&\qquad \times \theta \left( s_{0}^{\pi \eta }-um_{D}^2-\frac{m^{2}-uq^{2}}{\bar{u}}\right) . \end{aligned}$$

(27)

From the sum rules Eqs. (23) and (26), it can be concluded that the convolution on the left hand side must be real. This means that the strong phase of the transition form factor and the $\pi \eta$ scalar form factor must cancel each other:

$$\begin{aligned} \mathrm{Im}\left[ F_{\pi \eta }^{*}(s)F_{0,t}^{(0)}(s,q^{2})\right] =0~. \end{aligned}$$

(28)

This result is exactly the one deduced from the Watson–Migdal theorem [34, 35]. We thus can conclude that since the $\pi \eta$ system is decoupled from the leptons, the phase measured in $\pi \eta$ elastic scattering and the transition matrix element $B^0\rightarrow \pi \eta$ must be equal.

2.3 Comparison with the LCSR in the narrow-width limit

In the narrow-width limit, instead of the $1\rightarrow 2$ process as given in Eq. (8), one only considers the $1\rightarrow 1$ process ${\bar{B}}^0\rightarrow a_0(980)$ which is parameterized as

$$\begin{aligned} -i\left\langle a_0(p)|\bar{u} \gamma _{\mu } \gamma _{5} b | \bar{B}^{0}(q+p)\right\rangle = F_{+}(q^2) p_{\mu }+F_{-}(q^2) q_{\mu }. \end{aligned}$$

(29)

Using this parameterization, one obtains the sum rules equations. For example, the sum rule for $F_{+}(q^2)$ is

$$\begin{aligned}&m_{a_{0}}f_{a_{0}}e^{-m_{a_{0}}^{2}/M^{2}}F_{+}(q^{2})\nonumber \\&\quad =\frac{1}{\pi }\int _{0}^{s_{0}^{\pi \eta }}ds\ e^{-s/M^2} \mathrm{Im}\Pi _{\mu }^{\mathrm{OPE}}(s,q^{2})~. \end{aligned}$$

(30)

The sum rule Eq. (25) must be consistent with the above one in the narrow-width limit. To realize this matching, one should find a suitable parameterization for $F_{0,t}^{(0)}(s,q^{2})$, which must have an explicit dependence on the $a_0$ decay width $\Gamma _{a_0}^{\mathrm{tot}}$ so that it has a definite limit when $\Gamma _{a_0}^{tot}\rightarrow 0$. Following the method from Refs. [38, 39] and with the constraint of Eq. (28), instead of directly using the numerical result in Fig. 1 one can temporarily assume the form of $F_{\pi \eta }^{\bar{d}u}(s)^{*}$ as

$$\begin{aligned} F_{\pi \eta }^{*}(s)=\frac{g_{a_{0}\pi \eta }m_{a_{0}}f_{a_{0}}}{m_{a_{0}}^{2}-s+i\sqrt{s}\Gamma _{a_{0}}(s)}e^{-i\phi _{a_{0}}(s)}, \end{aligned}$$

(31)

where $g_{a_{0}\pi \eta }$ is the strong coupling of the $a_0$ to $\pi \eta$, and $f_{a_{0}}$ is the decay constant of the $a_0$:

$$\begin{aligned} \langle 0|\bar{d}u|a_{0}\rangle =m_{a_{0}}f_{a_{0}}, \end{aligned}$$

(32)

and

$$\begin{aligned} \Gamma _{a_{0}}(s)= & {} \frac{g_{a_{0}\pi \eta }^{2}\sqrt{\lambda _{\pi \eta }(s)}}{16\pi s^{3/2}}\theta \left( s-(m_{\pi }+m_{\eta })^{2}\right) \nonumber \\\equiv & {} \Gamma _{a_{0}}^{tot}\frac{m_{a_0}^3}{s^{3/2}}\sqrt{\frac{\lambda _{\pi \eta }(s)}{\lambda _{\pi \eta }(m_{a_0}^2)}}\theta \left( s-(m_{\pi }+m_{\eta })^{2}\right) \end{aligned}$$

(33)

is the decay width of the $a_0\rightarrow \pi \eta$ with the mass squared of the $a_0$ being a variable s. Accordingly, to satisfy Eq. (28), $F_0^{(0)}(s,q^2)$ must have an inverse complex phase, which reads

$$\begin{aligned} F_{0}^{(0)}(s,q^{2})\frac{2\sqrt{q^{2}}}{\sqrt{\lambda _{B}}}=\frac{g_{a_{0}\pi \eta }F_{+}(q^{2})}{m_{a_{0}}^{2}-s-i\sqrt{s}\Gamma _{a_{0}}(s)}e^{i\phi _{a_{0}}(s)}~. \end{aligned}$$

(34)

Thus using Eq. (28) we can obtain the phase of $F_{0,t}^{(0)}(s,q^{2})$ as

$$\begin{aligned} \phi _{a_0}(s)=\delta _{\pi \eta }(s)-\mathrm{arctan}\left[ \frac{{\sqrt{s}}\ \Gamma _{a_0}(s)}{m_{a_0}^2-s}\right] ~, \end{aligned}$$

(35)

where $\delta _{\pi \eta }(s)$ is the phase of $F_{\pi \eta }(s)$, which is taken from Fig. 1. After inserting Eqs. (31) and (34) into Eq. (23), and taking the narrow-width limit of $\Gamma _{a_0}^{\mathrm{tot}}\rightarrow 0$, one arrives at exactly the same sum rule as Eq. (30). It should be mentioned that for Eq. (31) one should in principle multiply it by an additional factor on the right-hand-side to make the normalization consistent with that given in Fig. 1. However, this factor can be absorbed by $F_{\pm }(q^2)$ in Eq. (34) so we neglect it here. Similarly, the $F_t^{(0)}(s,q^2)$ can be parameterized by $F_-(q^2)$ as

$$\begin{aligned}&F_{t}^{(0)}\left( s,q^{2}\right) \frac{1}{\sqrt{q^{2}}}-F_{0}^{(0)}\left( s,q^{2}\right) \frac{2p\cdot q}{\sqrt{\lambda _{B}q^{2}}}\nonumber \\&\quad =\frac{g_{a_{0}\pi \eta }F_{-}(q^{2})}{m_{a_{0}}^{2}-s-i\sqrt{s}\Gamma _{a_{0}}(s)}e^{i\phi _{a_{0}}(s)}~. \end{aligned}$$

(36)

Finally, inserting Eqs. (34) and (36) into the sum rules equations: Eqs. (25) and the one for three-body LCDA contribution, one can extract the $F_{\pm }(q^{2})$.

Note that since the form factors obtained here are only applicable to the small $q^2$ region due to the light-cone OPE, one should extent their applicability to the physical region with larger $q^2$. In Eq. (34) the dependence on s and $q^2$ are factorized, which enables us to find an appropriate parameterization for $F_{\pm }(q^{2})$ to realize the extension of $q^2$. This factorization approach can also be used for the $D^0$ decay.

3 Numerical results

The parameters used are: $m_{\pi }=0.139$ GeV, $m_K=0.496$ GeV, $m_{a_0}=0.98$ GeV, $m_B=5.28$ GeV, $m_D=1.87$ GeV, $m_u=2.2$ MeV, $m_d=4.7$ MeV [52]; $f_B=0.207$ GeV [53], $f_D=0.207$ GeV [50]; $g_{{a_0}\pi \eta } =m_{a_0}{\sqrt{8\pi {{\bar{g}}_{\eta }}}}=3.307$ GeV [54] with ${\bar{g}}_{\eta }=0.453$ [55]; $B_0=1.7$ GeV [49]. According to Eq. (35), we can obtain the phase of the form factors. The numerical result for $\phi _{a_0}(s)$ is shown in Fig. 3, which is nonzero above the $\pi \eta$ threshold. The blue band shows the uncertainty from the Borel parameter and the LECs of ChPT.

Fig. 3

The phase of the $B^0/D^0\rightarrow \pi \eta$ form factors, with the blue band showing the uncertainty from the Borel parameter and the LECs of ChPT

In the calculation of $F_{\pm }(q^2)$, instead of infinity the upper limits of the $\omega$ and $\xi$ integrations are chosen as $\omega +\xi <2\omega _0$ with $\omega _0=(2/3){\bar{\Lambda }}$ [56], where ${\bar{\Lambda }}=m_B-m_b=0.45$ GeV in the heavy quark limit [57]. It can be found that numerically the different integration upper limits $2\omega _0$ and $\infty$ lead to almost the same result. The reason is that at large energies, the original LCDAs: $\phi _+$, $\psi _{V,A}$ are highly suppressed by their exponential behavior, while the contributions from the newly defined LCDAs such as $\Phi ^{(1)}$, $X_A^{(1)}$, $Y_A^{(1)}$... are cut off by the theta functions of Eq. (24). The Borel parameter M is taken so that the fraction of the pole contribution is around 40$\%$:

$$\begin{aligned}&\int _{0}^{s_{th}^{\pi \eta }}ds\ e^{-s/M^{2}}\mathrm{Im}\Pi _{\mu }^{\mathrm{OPE}}\left( s,q^{2}\right) \Big /\nonumber \\&\int _{0}^{\infty }ds\ e^{-s/M^{2}}\mathrm{Im}\Pi _{\mu }^{\mathrm{OPE}}(s,q^{2})\approx 40\%~. \end{aligned}$$

(37)

Note that this fraction is an empirical value, practically one should allow a finite region for the choice of the Borel parameter. Accordingly, we choose the region of the Borel parameters as $1.0~\mathrm{GeV}<M<1.2~\mathrm{GeV}$ for the ${\bar{B}}^0$ decay and $1.2~\mathrm{GeV}<M<1.4~\mathrm{GeV}$ for the $D^0$ decay, where the center value of each region corresponds to the empirical fraction. The numerical result will depend on the Borel parameter, and the regions for the Borel parameters are used to estimate the error of the numerical results.

To extend the applicability of $F_{\pm }(q^2)$ to the whole physical region for $q^2$, one should use a suitable parameterization for $F_{\pm }(q^2)$ to realize the extension. One of the popular parameterization is the z-series expansion [58]:

$$\begin{aligned} F_{\pm }(q^{2})= & {} \frac{F_{\pm }(0)}{1-\frac{q^{2}}{m_{\mathrm{fit}}^{2}}}\left[ 1+b_{\pm } \zeta \left( q^{2}\right) +c_{\pm } \zeta ^{2}\left( q^{2}\right) \right] , \end{aligned}$$

(38)

where

$$\begin{aligned}&\zeta \left( q^{2}\right) =z\left( q^{2}\right) -z(0),~~~ z\left( q^{2}\right) \nonumber \\&\quad =\frac{\sqrt{t_{+}-q^{2}}-\sqrt{t_{+}-t_{0}}}{\sqrt{t_{+}-q^{2}}+\sqrt{t_{+}-t_{0}}} \end{aligned}$$

(39)

with $t_{\pm } \equiv (m_{B_{s}} \pm m_{f_{0}})^{2}$ and $t_0=t_+(1-\sqrt{1-t_-/t_+})$. The fitting regions are chosen as $0~\mathrm{GeV^2}<q^2<2~\mathrm{GeV^2}$ for $F_{\pm }^{{\bar{B}}^0\rightarrow a_0}$, $0~\mathrm{GeV^2}<q^2<0.7~\mathrm{GeV^2}$ for $F_{+}^{D^0\rightarrow a_0}$ and $0\ \mathrm{GeV^2}<q^2<0.3\ \mathrm{GeV^2}$ for $F_{-}^{D^0\rightarrow a_0}$. The fit results are listed in Table 1, and the corresponding curves are shown in Figs. 4 and 5.

Table 1 Fit results for the $F_{\pm }(q^2)$

Fig. 4

$F_+(q^2)$ (left) and $F_-(q^2)$ (right) for the ${\bar{B}}^0$ decay. The blue bands reflect the uncertainty from the Borel parameter and the LECs of ChPT

Fig. 5

$F_+(q^2)$ (left) and $F_-(q^2)$ (right) for the $D^0$ decay. The red bands reflect the uncertainty from the Borel parameter and the LECs of ChPT

Note that in Ref. [58] $m_{\mathrm{fit}}$ is fixed as the pole mass, which is equal to $m_B$ or $m_D$ for the B or D decays, respectively. Here, we try to choose it as a free parameter for the fit to improve the fit result. However, since the phase space of $q^2$ for the B decay is very large, the fitted mass pole $m_{\mathrm{fit}}^2$ may be smaller than the upper limit of $q^2$, so that it will cause a singularity during the phase space integration. Thus we just fix it as $m_B$ in the fitting. On the other hand, we find that for the $D^0$ form factors, the fitted $b_-$ and $c_{\pm }$ are extremely large. A possible reason is that the $D^0$ form factors are insensitive to the terms proportional to $b_-\zeta \left( q^{2}\right)$ and $c_{\pm }\zeta ^2\left( q^{2}\right)$ in Eq. (38). Therefore, for the fit of $F_{+}^{D^0\rightarrow a_0}$, we fix $c_{\pm }=0$, while for the fit of $F_{-}^{D^0\rightarrow a_0}$, we fix $b_{\pm }=c_{\pm }=0$ and $m_{\mathrm{fit}}=m_D$.

Finally, we calculate the decay branching fraction of ${\bar{B}}^0/D^0 \rightarrow (a_0(980)\rightarrow \pi ^{\pm }\eta )l{\bar{\nu }}$. The expression of the differential decay width reads:

$$\begin{aligned}&\frac{d^{3}\Gamma \left( {\bar{B}}^0/D^0 \rightarrow \pi ^{\pm }\eta \ l^{\mp } \nu \right) }{dq^{2}dk^{2}d\mathrm{cos}\theta _{\pi }}\nonumber \\&\quad =\frac{2G_{F}^{2}|V_{bu/cd}|^{2}(q^{2}-m_{l}^{2})^{2}\sqrt{\lambda _{B/D}\lambda _{\pi \eta }}}{32(2\pi )^{5}m_{B/D}^{3}k^{2}q^{2}}\nonumber \\&\qquad \times \left[ F_{0}^{0}\left( k^2,q^{2}\right) ^{2}\mathrm{sin^{2}}\theta _{\pi }+\frac{m_{l}^{2}}{q^{2}}\left( F_{t}^{0}\left( k^2,q^{2}\right) \nonumber \right. \right. \\&\left. \left. \qquad -F_{0}^{0}\left( k^2,q^{2}\right) \mathrm{cos}\theta _{\pi }\right) ^2\right] ~, \end{aligned}$$

(40)

where $m_l$ is the lepton mass and it is chosen as zero for e and $\mu$. The numerical result of the total decay widths are

$$\begin{aligned} \mathcal{{B}}(D^0 \rightarrow \pi ^{-}\eta \ l^{+} \nu )&=(1.36\pm 0.21)\times 10^{-4},\nonumber \\ \mathcal{{B}}({\bar{B}}^0 \rightarrow \pi ^{+}\eta \ l^{-} \nu )&=(0.60\pm 0.07)\times 10^{-4}. \end{aligned}$$

(41)

We note that the branching fraction obtained above for the $D^0$ decay is consistent with that measured by the BESIII Collaboration [30]:

$$\begin{aligned} \mathcal{{B}}\left( D^0 \rightarrow \pi ^{-}\eta \ e^{+} \nu \right) =(1.33\pm 0.09)\times 10^{-4}. \end{aligned}$$

(42)

This agreement is quite amazing. It is known that the D meson LCDA are not developed as well as those of the B meson. One may expect that the result of $D^0$ decay contains larger uncertainties. However, although the error of the $D^0$ decay branching fraction is one order larger than that of the ${\bar{B}}^0$ decay, it is still small enough to give consistency with the experimental result. Furthermore, we find that in the numerical calculation for the B decay, the contribution from the 3-particle LCDA is two orders of magnitude smaller than the one from the 2-particle LCDA. Therefore we also do not expect a sizeable contribution from such corrections in the D meson case. On the other hand, up to now there is no experimental measurement on the branching fraction for ${\bar{B}}^0 \rightarrow (a_0(980)\rightarrow \pi ^{+}\eta ) e^{-} \nu$, so our result can be tested by future experiments.

4 Conclusions

In this work, we have analyzed the semi-leptonic decays ${\bar{B}}^0/D^0 \rightarrow (a_0(980)^{\pm }\rightarrow \pi ^{\pm }\eta ) l^{\mp } \nu$ within light-cone sum rules. In the calculation at the quark–gluon level, we used the two- and three-body LCDAs of the B meson for the ${\bar{B}}^0$ decay and the only available two-body LCDA of the D meson for the $D^0$ decay. In the calculation at the hadron level, to include the finite-width effect of the $a_0(980)$, we use a scalar form factor to describe the final-state interaction between in the $\pi \eta$ system, which was previously calculated in the framework of unitarized Chiral Perturbation Theory. The resulting value of the decay branching fraction of the $D^0$ decay shows an amazing agreement with the one measured by the BESIII Collaboration, while the branching fraction of the ${\bar{B}}^0$ decay can be tested in future experiments.

Appendices

Appendix A: LCDAs of B and D mesons

In this appendix we list the explicit expressions for the LCDAs of the B meson [48]. The two-particle LCDAs are

$$\begin{aligned} \phi _B^{+}(\omega )&= {\omega \over \omega _0^2} \, e^{-\omega /\omega _0}, \nonumber \\ \phi _B^{-}(\omega )&= {1 \over \omega _0} \, e^{-\omega /\omega _0}\nonumber \\&\quad - {\lambda _E^2 - \lambda _H^2 \over 9 \, \omega _0^3} \, \left[ 1 - 2 \, \left( {\omega \over \omega _0} \right) + {1 \over 2} \, \left( {\omega \over \omega _0} \right) ^2 \right] \, e^{-\omega /\omega _0}~, \end{aligned}$$

(A1)

where $2 \, {\bar{\Lambda }}^2 = 2 \, \lambda _E^2 + \lambda _H^2$ and $\lambda _H^2=2 \lambda _E^2$. The three-particle LCDAs are classified by different twists:

$$\begin{aligned} \Phi _3(\omega , \xi )= & {} \Psi _A(\omega , \xi ) - \Psi _V(\omega , \xi ), \nonumber \\ \Phi _4(\omega , \xi )= & {} \Psi _A(\omega , \xi ) + \Psi _V(\omega , \xi ), \nonumber \\ \Psi _4(\omega , \xi )= & {} \Psi _A(\omega , \xi ) + X_A(\omega , \xi ), \nonumber \\ \bar{\Psi }_4(\omega , \xi )= & {} \Psi _V(\omega , \xi ) - \bar{X}_A(\omega , \xi ), \nonumber \\ \Phi _5(\omega , \xi )= & {} \Psi _A(\omega , \xi ) + \Psi _V(\omega , \xi )\nonumber \\&+ 2 \, \left[ Y_A - \bar{Y}_A + W \right] (\omega , \xi ), \nonumber \\ \Psi _5(\omega , \xi )= & {} - \Psi _A(\omega , \xi ) + X_A(\omega , \xi ) - 2 \, Y_A(\omega , \xi ) , \nonumber \\ \bar{\Psi }_5(\omega , \xi )= & {} - \Psi _V(\omega , \xi ) - \bar{X}_A(\omega , \xi ) + 2 \, \bar{Y}_A(\omega , \xi ) , \nonumber \\ \Phi _6(\omega , \xi )= & {} \Psi _A(\omega , \xi ) - \Psi _V(\omega , \xi )\nonumber \\&+ 2 \, \left[ Y_A + \bar{Y}_A + W - 2 \, Z \right] (\omega , \xi ) . \end{aligned}$$

(A2)

Each LCDA with definite twist has the explicit form of:

$$\begin{aligned} \Phi _3(\omega , \xi )= & {} {\lambda _E^2 - \lambda _H^2 \over 6 \, \omega _0^5} \, \omega \, \xi ^2 \, e^{-(\omega + \xi )/\omega _0} , \nonumber \\ \Phi _4(\omega , \xi )= & {} {\lambda _E^2 + \lambda _H^2 \over 6 \, \omega _0^4} \, \xi ^2 \, e^{-(\omega + \xi )/\omega _0} , \nonumber \\ \Psi _4(\omega , \xi )= & {} {\lambda _E^2 \over 3 \, \omega _0^4} \, \omega \, \xi \, e^{-(\omega + \xi )/\omega _0} , \nonumber \\ \bar{\Psi }_4(\omega , \xi )= & {} {\lambda _H^2 \over 3 \, \omega _0^4} \, \omega \, \xi \, e^{-(\omega + \xi )/\omega _0} , \nonumber \\ \Phi _5(\omega , \xi )= & {} {\lambda _E^2 + \lambda _H^2 \over 3 \, \omega _0^3} \, \omega \, e^{-(\omega + \xi )/\omega _0} , \nonumber \\ \Psi _5(\omega , \xi )= & {} - {\lambda _E^2 \over 3 \, \omega _0^3} \, \xi \, e^{-(\omega + \xi )/\omega _0} , \nonumber \\ \bar{\Psi }_5(\omega , \xi )= & {} - {\lambda _H^2 \over 3 \, \omega _0^3} \, \xi \, e^{-(\omega + \xi )/\omega _0} , \nonumber \\ \Phi _6(\omega , \xi )= & {} {\lambda _E^2 - \lambda _H^2 \over 3 \, \omega _0^2} \, e^{-(\omega + \xi )/\omega _0} . \end{aligned}$$

(A3)

Appendix B: Vanishing of the boundary terms at $\omega =\infty$

Here we give a detailed explanation for the vanishing of the boundary terms at $\omega =\infty$ when deriving Eq. (15). For example, consider the integration

$$\begin{aligned} \int d^{4}x\ e^{ip\cdot x}\int _{0}^{\infty }d\omega \ e^{-i\omega v\cdot x}\frac{\psi (\omega )}{(v\cdot x)^{2}}F(x), \end{aligned}$$

(B1)

where F(x) is a certain function depending on $x^{\mu }$ and independent of $\omega$. Since $\psi (\omega )=(d/d\omega )\psi ^{(1)}(\omega )$, after integration by part, the above equation becomes

$$\begin{aligned}&\int d^{4}x\ e^{ip\cdot x}\ e^{-i\omega v\cdot x}\frac{\psi ^{(1)}(\omega )}{(v\cdot x)^{2}}F(x)\Big |_{\omega =0}^{\omega =\infty }\nonumber \\&\quad +i\int d^{4}x\ e^{ip\cdot x}\int _{0}^{\infty }d\omega \ e^{-i\omega v\cdot x}\frac{\psi ^{(1)}(\omega )}{v\cdot x}F(x). \end{aligned}$$

(B2)

Using $\psi ^{(1)}(\omega )=(d/d\omega )\psi ^{(2)}(\omega )$ and integration by part for the second term, we have

$$\begin{aligned}&\int d^{4}x\ e^{ip\cdot x}\ e^{-i\omega v\cdot x}\frac{\psi ^{(1)}(\omega )}{(v\cdot x)^{2}}F(x)\Big |_{\omega =0}^{\omega =\infty }\nonumber \\&\quad +i\int d^{4}x\ e^{ip\cdot x}\ e^{-i\omega v\cdot x}\frac{\psi ^{(2)}(\omega )}{v\cdot x}F(x)\Big |_{\omega =0}^{\omega =\infty }\nonumber \\&\quad +\ i^2\int d^{4}x\ e^{ip\cdot x}\int _{0}^{\infty }d\omega \ e^{-i\omega v\cdot x}\psi ^{(2)}(\omega )F(x). \end{aligned}$$

(B3)

According to the definition of $\psi ^{(1)}(\omega )$ and $\psi ^{(2)}(\omega )$, the boundary terms at $\omega =0$ vanish trivially. The only non-trivial problem is whether the boundary terms at $\omega =\infty$ also vanish. Since the first two terms of the above equation are similar, we take the first term as an example. We define $p_{\perp }^{\mu }=p^{\mu }-(p\cdot v)v^{\mu }$, $x_{\parallel }=v\cdot x$ and $x_{\perp }^{\mu }=x^{\mu }-x_{\parallel }v^{\mu }$, then this term becomes

$$\begin{aligned} \int d^{3}\vec {x}_{\perp }e^{ip_{\perp }\cdot x_{\perp }}\int dx_{\parallel }e^{-i\omega x_{\parallel }}e^{i p\cdot vx_{\parallel }}\frac{\psi ^{(1)}(\omega )}{x_{\parallel }^{2}}F(x_{\parallel },x_{\perp })\Big |_{\omega =\infty }. \end{aligned}$$

(B4)

Note that $\psi ^{(1)}(\infty )=\int _0^{\infty }d\tau \psi (\tau )$ is finite. For the integration of $dx_{\parallel }$, consider two very nearby values of $x_{\parallel }$: $x_{\parallel }=\tau _0$ and $x_{\parallel }=\tau _0+\delta$ with $\delta =\pi /\omega \ll 1$, the corresponding integrands are

$$\begin{aligned}&e^{-i\omega \tau _0}\frac{\psi ^{(1)}(\infty )}{\tau _0^{2}}e^{i p\cdot v\tau _0}F(\tau _0,x_{\perp }),~~\text { and }~~\nonumber \\&\quad (-1)e^{-i\omega \tau _0}\frac{\psi ^{(1)}(\infty )}{(\tau _0+\delta )^{2}}e^{i p\cdot v(\tau _0+\delta )}F(\tau _0+\delta ,x_{\perp }). \end{aligned}$$

(B5)

Since $\delta$ is extremely small when $\omega$ approaches infinity, the value of the above two integrands are almost the same except the difference of sign. Thus during the integration of $x_{\parallel }$ the contributions from each pairs of the integrands like the two above will cancel with each other, and the boundary term at $\omega =\infty$ is also zero.

Appendix C: I, J functions in the OPE calculation

The explicit expressions for the I, J functions in the OPE calculation are

$$\begin{aligned}&I_{2}^{(0)}(\omega )\nonumber \\&\quad =4{\Phi }^{(1)}(\omega )-\phi _{+}(\omega )(m-m_{B}+\omega ),\nonumber \\&J_{2}^{(0)}(\omega )\nonumber \\&\quad =4{\Phi }^{(1)}(\omega )-\phi _{+}(\omega )(m+\omega ),\nonumber \\&I_{2}^{(1)}(\omega ,q^{2},\Omega )\nonumber \\&\quad =2{\Phi }^{(1)}(\omega )\left( 1-\frac{\omega }{m_{B}}\right) \left[ \frac{m}{m_{B}}-\frac{\Sigma _0}{m_{B}^{2}}+\frac{\omega (\Sigma _0-q^{2})}{m_{B}^{3}}\right] ,\nonumber \\&J_{2}^{(1)}(\omega ,q^{2},\Omega )\nonumber \\&\quad =2{\Phi }^{(1)}(\omega )\left( 1-\frac{\omega }{m_{B}}\right) \left[ \frac{\omega }{m_{B}}-\frac{\Sigma _0}{m_{B}^{2}}+\frac{\omega (\Sigma _0-q^{2})}{m_{B}^{3}}\right] ,\nonumber \\&I_{3}^{(1)}(\omega ,\xi ,q^{2},\Omega )\nonumber \\&\quad =\frac{1}{m_B^4}\left[ m_B^2\left( 3\left( m(\Psi _A+\Psi _V)-{{\bar{X}}}_A^{(1)}\nonumber \right. \right. \right. \\&\left. \qquad -X_A^{(1)}+4{{\bar{Y}}}_A^{(1)}+4Y_A^{(1)}\right) \nonumber \\&\qquad +12(1-2u)W^{(1)}+(4u-3)\omega (\Psi _A-\Psi _V)\nonumber \\&\left. \qquad +u(4u-3)\xi (\Psi _A-\Psi _V)+6u X_A^{(1)}-24u Y_A^{(1)}\right) \nonumber \\&\qquad +m_B^3\left( (1-4u)\Psi _A-(1+2u)\Psi _V\right) )\nonumber \\&\qquad +2m_B\left( (u-1)\left( q^2-\Sigma _{\xi }\right) (\Psi _A-\Psi _V)\nonumber \right. \\&\left. \qquad +3u(u\xi +\omega )\xi \left( 4W^{(1)}-X_A^{(1)}+4Y_A^{(1)}\right) \right) \nonumber \\&\left. \qquad -2u(\omega +u\xi )(q^2-\Sigma _{\xi })(\Psi _A-\Psi _V)\right] ,\nonumber \\&J_{3}^{(1)}(\omega ,\xi ,q^{2},\Omega )\nonumber \\&\quad = \frac{1}{m_B^4}\left[ m_B^2\left( 3\left( m(\Psi _A+\Psi _V)-{{\bar{X}}}_A^{(1)}\nonumber \right. \right. \right. \\&\left. \qquad -X_A^{(1)}+4{{\bar{Y}}}_A^{(1)}+4Y_A^{(1)}\right) \nonumber \\&\qquad +12(1-2u)W^{(1)}+(2u-3)\omega (\Psi _A-\Psi _V)\nonumber \\&\left. \qquad +u(2u-3)\xi (\Psi _A-\Psi _V)+6u X_A^{(1)}-24u Y_A^{(1)}\right) \nonumber \\&\qquad -2m_B^3(u-1)(\Psi _A-\Psi _V)\nonumber \\&\qquad +2m_B\left( (u-1)\left( q^2-\Sigma _{\xi }\right) (\Psi _A-\Psi _V)\nonumber \right. \\&\left. \qquad +3u(u\xi +\omega )\xi \left( 4W^{(1)}-X_A^{(1)}+4Y_A^{(1)}\right) \right) \nonumber \\&\left. \qquad -2u(\omega +u\xi )\left( q^2-\Sigma _{\xi }\right) (\Psi _A-\Psi _V)\right] ,\nonumber \\&I_{3}^{(2)}\left( \omega ,\xi ,q^{2},\Omega \right) \nonumber \\&\quad = \frac{1}{m_B^6}({m_B}-\xi u-\omega ) \left[ m \left( {m_B}^2 \left( -6 W^{(1)}-2 {{\bar{X}}}_A^{(1)}\nonumber \right. \right. \right. \\ \end{aligned}$$

$$\begin{aligned}&\left. \qquad +{X}_A^{(1)}+12 {{\bar{Y}}}_A^{(1)}-6 {Y}_A^{(1)}\right) \nonumber \\&\left. \qquad -12 {m_B}\left( W^{(2)}-4 Z^{(2)}\right) +\left( \Sigma _{\xi }-{q^2}\right) \left( 2 {{\bar{X}}}_A^{(1)}-{X}_A^{(1)}\right) \right) \nonumber \\&\qquad +{m_B}^3 \left( 4 u {X}_A^{(1)}-2 {{\bar{X}}}_A^{(1)}-{X}_A^{(1)}\right) \nonumber \\&\qquad +2 {m_B}^2 \left( (\xi u+\omega ) \left( -2 u {X}_A^{(1)}+2 W^{(1)}+{{\bar{X}}}_A^{(1)}\nonumber \right. \right. \\&\left. \left. \qquad +{X}_A^{(1)}+4 {{\bar{Y}}}_A^{(1)}+2 {Y}_A^{(1)}\right) -6 W^{(2)}+36 Z^{(2)}\right) \nonumber \\&\qquad +{m_B} \left( {q^2} \left( -4 u{X}_A^{(1)}+2 {{\bar{X}}}_A^{(1)}+{X}_A^{(1)}\right) \nonumber \right. \\&\qquad +\Sigma _{\xi } \left( 6 (4 u-1) W^{(1)}-4 u {X}_A^{(1)}+24 u {Y}_A^{(1)}+2 {{\bar{X}}}_A^{(1)}\nonumber \right. \\&\left. \left. \qquad +{X}_A^{(1)}-6 \left( 2 {{\bar{Y}}}_A^{(1)}+{Y}_A^{(1)}\right) \right) +12 W^{(2)} (\xi u+\omega )\right) \nonumber \\&\qquad +2 \left( \Sigma _{\xi } \left( 6 W^{(2)}-(\xi u+\omega ) \left( (12 u-1) W^{(1)}\nonumber \right. \right. \right. \\&\left. \left. \qquad -2 \left( u{X}_A^{(1)}+{{\bar{Y}}}_A^{(1)}\right) +(12 u-1) {Y}_A^{(1)}+{{\bar{X}}}_A^{(1)}\right) \right) -{q^2}\nonumber \\&\qquad \times \left( (\xi u+\omega ) \left( -2 u {X}_A^{(1)}+W^{(1)}-{{\bar{X}}}_A^{(1)}\nonumber \right. \right. \\&\left. \left. \left. \left. \qquad +2 {{\bar{Y}}}_A^{(1)}+{Y}_A^{(1)}\right) +6 W^{(2)}\right) \right) \right] ,\nonumber \\&J_{3}^{(2)}(\omega ,\xi ,q^{2},\Omega )\nonumber \\&\quad = \frac{1}{m_B^6}({m_B}-\xi u-\omega ) \left[ {m_B}^2\left( m(2 {{\bar{X}}}_A^{(1)}-{X}_A^{(1)})\nonumber \right. \right. \\&\qquad +2(\omega +u\xi )\left( W^{(1)}-{{\bar{X}}}_A^{(1)}\nonumber \right. \\&\left. \left. \qquad +2{{\bar{Y}}}_A^{(1)}\right) +12 W^{(2)}\right) \nonumber \\&\qquad +2m_B\left( 6\left( 4mZ^{(2)}-mW^{(2)}+u\xi W^{(2)}+\omega W^{(2)}\right) \nonumber \right. \\&\qquad +\Sigma _{\xi }\left( (12u-3) \left( W^{(1)}+Y_A^{(1)}\right) +(1-4u) X_A^{(1)}-6 {{\bar{Y}}}_A^{(1)}\nonumber \right. \\&\left. \left. \qquad +2{{\bar{X}}}_A^{(1)}\right) \right) \nonumber \\&\qquad -q^2\left( m\left( 2{{\bar{X}}}_A^{(1)}-X_A^{(1)}\right) +2(\omega +u\xi )\left( W^{(1)}-{{\bar{X}}}_A^{(1)}\nonumber \right. \right. \\&\left. \left. \qquad +2{{\bar{Y}}}_A^{(1)}+Y_A^{(1)}\right) +12 W^{(2)}\right) \nonumber \\&\qquad +\Sigma _{\xi }\left( m\left( 2{{\bar{X}}}_A^{(1)}-X_A^{(1)}\right) \nonumber \right. \\&\qquad -2(\omega +u\xi )\left( (12u-1)\left( W^{(1)} +Y_A^{(1)}\right) -4u X_A^{(1)}+{{\bar{X}}}_A^{(1)}\nonumber \right. \\&\left. \left. \left. \qquad -2{{\bar{Y}}}_A^{(1)}\right) +12 W^{(2)}\right) \right] ~,\nonumber \\&I_{3}^{(3)}(\omega ,\xi ,q^{2},\Omega )\nonumber \\&\quad = \frac{12}{m_B^{10}}(\omega +u\xi -m_B)^2\left[ m_B\left( q^2-\Sigma _{\xi }\right) \Sigma _{\xi } W^{(2)}\nonumber \right. \\&\qquad +m_B^3 \Sigma _{\xi } \left( W^{(2)}-6 Z^{(2)}\right) \nonumber \\&\qquad +m m_B^2\left( \left( \Sigma _{\xi }+q^2-m_B^2\right) W^{(2)}-6\Sigma _{\xi }Z^{(2)}\right) \nonumber \\&\qquad +\left( q^2-\Sigma _{\xi }\right) ^2(\omega +u\xi )W^{(2)}\nonumber \\&\qquad +4m_B^4(\omega +u\xi )Z^{(2)}-m_B^2(\omega +u\xi )\left( \left( q^2+\Sigma _{\xi }\right) W^{(2)}\nonumber \right. \\&\left. \left. \qquad +2\left( 2q^2-\Sigma _{\xi }\right) Z^{(2)}\right) \right] ~,\nonumber \\&J_{3}^{(3)}(\omega ,\xi ,q^{2},\Omega )\nonumber \\&\quad = \frac{12}{m_B^{10}}(\omega +u\xi -m_B)^2\left[ (m_B \Sigma _{\xi } \left( q^2-\Sigma _{\xi }-m_B^2\right) W^{(2)}\nonumber \right. \\&\qquad +2 m m_B^2 \left( W^{(2)}-3 Z^{(2)}\right) \nonumber \\&\qquad +m_B^4 (\omega +u\xi )W^{(2)}+ (\omega +u\xi )(q^2-\Sigma _{\xi })^2 W^{(2)}\nonumber \\&\left. \qquad -2m_B^2(\omega +u\xi )\left( q^2 W^{(2)}+\Sigma _{\xi } Z^{(2)}\right) \right] ~, \end{aligned}$$

(C1)

where $\Sigma _0=\Sigma (\omega ,0,q^{2},\Omega )$ and $\Sigma _{\xi }=\Sigma (\omega ,\xi ,q^{2},\Omega )$.