Chiral dynamics, S-wave contributions and angular analysis in $D\rightarrow \pi \pi \ell \bar{\nu }$

Abstract

We present a theoretical analysis of the $D^-\rightarrow \pi ^+\pi ^- \ell \bar{\nu }$ and $\bar{D}^0\rightarrow \pi ^+\pi ^0 \ell \bar{\nu }$ decays. We construct a general angular distribution which can include arbitrary partial waves of $\pi \pi$. Retaining the S-wave and P-wave contributions we study the branching ratios, forward–backward asymmetries and a few other observables. The P-wave contribution is dominated by $\rho ^0$ resonance, and the S-wave contribution is analyzed using the unitarized chiral perturbation theory. The obtained branching fraction for $D\rightarrow \rho \ell \nu$, at the order $10^{-3}$, is consistent with the available experimental data. The S-wave contribution has a branching ratio at the order of $10^{-4}$, and this prediction can be tested by experiments like BESIII and LHCb. Future measurements can also be used to examine the $\pi$–$\pi$ scattering phase shift.

1 Introduction

The Cabbibo–Kobayashi–Maskawa (CKM) matrix elements are key parameters in the Standard Model (SM). They are essential to understand CP violation within the SM and search for new physics (NP). Among these matrix elements, $|V_{cd}|$ can be determined from either exclusive or inclusive weak D decays, which are governed by $c\rightarrow d$ transition, for example, $c\rightarrow d\ell \nu$ transitions. However, for a general D decay process it is difficult to extract CKM matrix elements, because strong and weak interactions may be entangled.

The semi-leptonic D decays are ideal channels to determine $|V_{cd}|$, not only because the weak and strong dynamics can be separated in these process, but also the clean experimental signals. Moreover, one can study the dynamics in the heavy-to-light transition from semi-leptonic D decays. For leptons do not participate in the strong interaction, all the strong dynamics is included in the form factors; thus it provides a good platform to measure the form factors. The $D\rightarrow \rho$ form factors have been measured from $D^0\rightarrow \rho ^- e^+ \nu _e$ and $D^+\rightarrow \rho ^0 e^+ \nu _e$ at the CLEO-c experiment for both charged and neutral channels [1]. Because of the large width of the $\rho$ meson, $D\rightarrow \rho \ell \bar{\nu }_{\ell }$ is in fact a quasi-four body process $D\rightarrow \pi \pi \ell \bar{\nu }_{\ell }$. The $\rho$ can be reconstructed from the P-wave $\pi \pi$ mode. However, other $\pi \pi$ resonant or non-resonant states may interfere with the P-wave $\pi \pi$ pair, and thus it is necessary to analyze the S-wave contribution to $D\rightarrow \pi \pi \ell \bar{\nu }_{\ell }$.

In addition, the internal structure of light mesons is an important issue in hadron physics. It is difficult to study light mesons by QCD perturbation theory due to the large strong coupling in the low-energy region. On the other hand, because of the large mass scale, one can establish factorization for many heavy meson decay processes, thus heavy mesons like B and D can be used to probe the internal structure of light mesons [2, 3]. As mentioned above, $D\rightarrow \pi \pi \ell \bar{\nu }_{\ell }$ can receive contributions from various partial waves of $\pi \pi$. $\rho$(770) dominant for D to P-wave $\pi \pi$ decay, at the same time, D meson can decay into S-wave $\pi \pi$ through $f_0(980)$. The structure of $f_0$(980) is not fully understood yet. Analysis of $D\rightarrow \pi \pi \ell \bar{\nu }_{\ell }$ may shed more light on understanding the nature of $f_0$(980). The BESIII collaboration has collected 2.93 $\mathrm {fb}^{-1}$ data in $e^+e^-$ collisions at the energy around 3.773 GeV [4], which can be used to study the semi-leptonic D decays. Thus it presently is mandatory to make reliable theoretical predictions. Some analyses of multi-body heavy meson decays can be found in Refs. [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19], where the final state interactions between the light pseudoscalar mesons are taken into account.

In this paper we present a theoretical analysis of $D^-\rightarrow \pi ^+\pi ^-\ell \bar{\nu }_{\ell }$ and $D^0\rightarrow \pi ^+\pi ^0\ell \bar{\nu }_{\ell }$ decays. In Sect. 2, we will present the results of $D\rightarrow f_0$ (980) and $D\rightarrow \rho$ form factors. We also calculate D to S-wave $\pi \pi$ pair form factors in non-resonance region, the $\pi \pi$ form factor will be calculated by using unitarized chiral perturbation theory. Based on these results, we present a full analysis on the angular distribution of $D\rightarrow \pi \pi \ell \bar{\nu }_{\ell }$. We explore various distribution observables, including the differential decay width, the S-wave fraction, forward–backward asymmetry, and so on. These results will be collected in Sect. 3. The conclusion of this paper will be given in Sect. 4. The details of the coefficients in angular distributions are relegated to the appendix.

2 Heavy-to-light transition form factors

Fig. 1

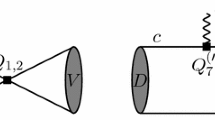
Feynman diagram for the $D\rightarrow \pi \pi \ell ^-\bar{\nu }_{\ell }$ decays. The lepton could be an electron or a muon, $\ell =e,\mu$. Depending on the D meson, the spectator could be a u or a d quark, corresponding to $D^0\rightarrow \pi ^+\pi ^0 \ell ^-\bar{\nu }_{\ell }$ and $D^-\rightarrow \pi ^+\pi ^- \ell ^-\bar{\nu }_{\ell }$

Feynman diagram for the $D\rightarrow \pi \pi \ell ^-\bar{\nu }_{\ell }$ decay is shown in Fig. 1. The lepton can be an electron or a muon, $\ell =e,\mu$. The spectator quark could be the u or d quark, corresponding to $D^0\rightarrow \pi ^+\pi ^0 \ell ^-\bar{\nu }_{\ell }$ and $D^-\rightarrow \pi ^+\pi ^- \ell ^-\bar{\nu }_{\ell }$. Integrating out the virtual W-boson, we obtain the effective Hamiltonian describing the $c\rightarrow d$ transition

$$\begin{aligned} \mathcal{H}_{\mathrm{eff}} = \frac{G_\mathrm{F}}{\sqrt{2}} V_{cd} \left[ \bar{d} \gamma _\mu (1-\gamma _5) c\right] \left[ \bar{\nu }\gamma ^\mu (1-\gamma _5) \ell \right] +h.c., \end{aligned}$$

(1)

where $G_\mathrm{F}$ is the Fermi constant and $V_{cd}$ is the CKM matrix element. The leptonic part is calculable using the perturbation theory, while the hadronic effects are encoded into the transition form factors.

2.1 $D \rightarrow \rho$ form factors

For the P-wave $\pi \pi$ state, the dominant contribution is from the $\rho (770)$ resonance. The $D\rightarrow \rho$ form factors are parametrized by [20]

$$\begin{aligned}&\left\langle \rho (p_2,\epsilon )|\bar{d}\gamma ^{\mu }c|D(p_D)\right\rangle =-\frac{2V(q^2)}{m_{D}+m_{\rho }}\epsilon ^{\mu \nu \rho \sigma } \epsilon ^*_{\nu } p_{D\rho }p_{2\sigma }, \nonumber \\&\left\langle \rho (p_2,\epsilon )|\bar{d}\gamma ^{\mu }\gamma _5 c| D(p_D)\right\rangle =2im_{{\rho }} A_0(q^2)\frac{\epsilon ^*\cdot q }{ q^2}q^{\mu } \nonumber \\&\quad +i(m_{D}+m_{{\rho }})A_1(q^2)\left[ \epsilon ^{*\mu } -\frac{\epsilon ^*\cdot q }{q^2}q^{\mu } \right] \nonumber \\&\quad -iA_2(q^2)\frac{\epsilon ^* \cdot q }{ m_{D}+m_{{\rho }} } \left[ P^{\mu }-\frac{m_{D}^2-m_{{\rho }}^2}{q^2}q^{\mu } \right] , \end{aligned}$$

(2)

with $q=p_D-p_2$, and $P=p_D+p_2$. The $V(q^2)$, and $A_{i}(q^2) (i=0,1,2)$ are nonperturbative form factors.

These form factors have been computed in many different approaches [21,22,23,24,25], and here we quote the results from the light-front quark model (LFQM) [23, 24] and light-cone sum rules (LCSR) [25]. To access the momentum distribution in the full kinematics region, the following parametrization has been used:

$$\begin{aligned} F_{i}(q^{2})=\frac{F_{i}(0)}{1-a_{i}\frac{q^{2}}{m_{D}^{2}}+b_{i}\left( \frac{q^{2}}{m_{D}^{2}}\right) ^{2}}. \end{aligned}$$

(3)

Their results are collected in Table 1. We note that a different parametrization is adopted in Ref. [25], where $A_3$ appears instead of $A_0$. The relation between $A_0$ and $A_3$ is given by

$$\begin{aligned} A_{0}(q^{2})= & {} \frac{1}{2m_{\rho }(m_{D}+m_{\rho })}\left[ A_{1}(q^{2}) (m_{D}+m_{\rho })^{2}\right. \nonumber \\&\left. +A_{2}(q^{2})(m_{\rho }^{2}-m_{D}^{2})-A_{3}(q^{2})q^{2}\right] . \end{aligned}$$

(4)

Table 1 $D \rightarrow \rho$ form factors derived by LFQM (left) [23, 24] and LCSR (right) [25], respectively

2.2 Scalar $\pi \pi$ form factor and D to S-wave $\pi \pi$

We first give the $D\rightarrow f_0(980)$ form factor parametrized as

$$\begin{aligned}&\langle f_0(p_2) |\bar{d} \gamma _\mu \gamma _5 c| {D^-}(p_{D})\rangle =-i\left\{ F_+^{D\rightarrow f_0} (q^2)\right. \nonumber \\&\quad \left. \times \left[ P_\mu - \frac{m_{D}^2-m_{f_0}^2}{q^2}q_\mu \right] +F_0^{D\rightarrow f_0} (q^2)\frac{m_{D}^2-m_{f_0}^2}{q^2}q_\mu \right\} ,\nonumber \\ \end{aligned}$$

(5)

where $F^{D\rightarrow f_0}_+$ and $F^{D\rightarrow f_0}_0$ are $D\rightarrow f_0$ form factors. We will use LCSR to compute the $D \rightarrow f_0(980)$ transition form factors with some inputs, and we refer the reader to Ref. [26] for a detailed derivation in LCSR. The meson masses are fixed to the PDG values $m_D=1.870$ GeV and $m_{f_0}=0.99$ GeV [27]. For quark masses we use $m_c=1.27$ GeV [27] and $m_d=5$ MeV. As for decay constants, we use $f_D=0.21$ GeV [27] and $f_{f_0}=0.18$ GeV [28]. The threshold $s_0$ is fixed at $s_0=4.1$ GeV$^2$, which should correspond to the squared mass of the first radial excitation of D. The parameters $F_i(0)$, $a_i$ and $b_i$ are fitted in the region $-0.5~\mathrm {GeV^2}<q^2<0.5~\mathrm {GeV^2}$, and the Borel parameter $M^2$ is taken to be $(6\pm 1)~\mathrm {GeV}^{-2}$. With these parametrizations, we give the numerical results in Table 2.

Table 2 Fitted parameters of the $D \rightarrow f_0$ form factors derived by LCSR, which are fitted using Eq. (3)

In the region where the two pseudo-scalar mesons strongly interacts, the resonance approximation fails and thus has to be abandoned. One of the such examples is the S-wave partial wave under 1 GeV, for which we can use the form factors as defined in Ref. [29]:

$$\begin{aligned}&\langle (\pi \pi )_S(p_{\pi \pi })|\bar{u} \gamma _\mu \gamma _5 c| D (p_D) \rangle \nonumber \\&\quad = -i \frac{1}{m_{\pi \pi }} \bigg \{ \bigg [P_{\mu } -\frac{m_{D}^2-m_{\pi \pi }^2}{q^2} q_\mu \bigg ] \mathcal{F}_{1}^{D\rightarrow \pi \pi }(m_{\pi \pi }^2, q^2) \nonumber \\&\qquad +\frac{m_{D}^2-m_{\pi \pi }^2}{q^2} q_\mu \mathcal{F}_{0}^{D\rightarrow \pi \pi }(m_{\pi \pi }^2, q^2) \bigg \}. \end{aligned}$$

(6)

The Watson theorem implies that phases measured in $\pi \pi$ elastic scattering and in a decay channel in which the $\pi \pi$ system has no strong interaction with other hadrons are equal modulo $\pi$ radians. In the process we consider here, the lepton pair $\ell \bar{\nu }$ indeed decouples from the $\pi \pi$ final state, and thus the phases of D to scalar $\pi \pi$ decay amplitudes are equal to $\pi \pi$ scattering with the same isospin. It is plausible that

$$\begin{aligned} \langle (\pi \pi )_S|\bar{d} \Gamma c|D\rangle \propto F_{\pi \pi }(m_{\pi \pi }^2), \end{aligned}$$

(7)

where the scalar form factor is defined as

$$\begin{aligned} \langle 0| \bar{d}d |\pi ^+\pi ^-\rangle = B_0 F_{\pi \pi }(m_{\pi \pi }^2), \end{aligned}$$

(8)

where $B_0=(1.7\pm 0.2)$ GeV [10] is the QCD condensate parameter.

An explicit calculation of these quantities requires knowledge of generalized light-cone distribution amplitudes (LCDAs) [30]. The twist-3 one has the same asymptotic form with the LCDAs for a scalar resonance [31]. Inspired by this similarity, we may plausibly introduce an intuitive matching between the $D\rightarrow f_0$ and $D\rightarrow (\pi \pi )_{S}$ form factors [7]:

$$\begin{aligned} \mathcal{F}_i^{D\rightarrow \pi \pi }(m_{\pi \pi }^2, q^2) \simeq B_0\frac{1}{ f_{f_0}} F_{\pi \pi }(m_{\pi \pi }^2) F_{i}^{D\rightarrow f_0} (q^2). \end{aligned}$$

(9)

It is necessary to stress at this stage that the Watson theorem does not strictly guarantee that one may use Eq. (9). Instead it indicates that, below the opening of inelastic channels the strong phases in the $D\rightarrow \pi \pi$ form factor and $\pi \pi$ scattering are the same. First above the $4\pi$ or $K\bar{K}$ threshold, additional inelastic channels will also contribute. The $K\bar{K}$ contribution can be incorporated in a coupled-channel analysis. As a process-dependent study, it has been demonstrated that states with two additional pions may not give sizable contributions to the physical observables [32]. Secondly, some polynomials with nontrivial dependence on $m_{\pi \pi }$ have been neglected in Eq. (9). In principle, once the generalized LCDAs for the $(\pi \pi )_S$ system are known, the $D\rightarrow \pi \pi$ form factor can be straightforwardly calculated in LCSR and thus this approximation in the matching equation can be avoided. On the one side, the space-like generalized parton distributions for the pion have been calculated at one-loop level in the chiral perturbation theory ($\chi$PT) [33]. The analysis of time-like generalized LCDAs in $\chi$PT and the unitarized framework is in progress. On the other side, the $\gamma \gamma ^*\rightarrow \pi ^+\pi ^-$ reaction is helpful to extract the generalized LCDAs for the $(\pi \pi )_S$ system [34, 35]. The experimental prospects at BEPC-II and BELLE-II in the near future are very promising.

In the kinematic region where the $\pi$ is soft, the crossed channel from $D+\pi \rightarrow \pi$ will contribute as well and this crossed channel would modify Eq. (9) by an inhomogeneous part. For the analogous decay of K or B mesons, it has been taken into account either dynamically in terms of phase shifts (in the case of the kaon decay) [36] or approximately in terms of a pole contribution (in the case of the B meson decay) [15]. However, if both pions move fast, the D–$\pi$ invariant mass is far from the $D^*$ pole and this contribution is negligible. In this case, the transition amplitude for the D to 2-pion form factor can be calculated in light-cone sum rules [7]. This will lead to the conjectured formula in Eq. (9).

The scalar $\pi \pi$ form factor can be handled using the unitarized chiral perturbation theory. In the following, we will give a brief description of this approach. In terms of the isoscalar S-wave states

$$\begin{aligned} |\pi \pi \rangle _{\mathrm {I=0}}^{}= & {} \frac{1}{\sqrt{3}} \left| \pi ^+\pi ^-\right\rangle + \frac{1}{\sqrt{6}} \left| \pi ^0\pi ^0\right\rangle , \end{aligned}$$

(10)

$$\begin{aligned} |K\bar{K}\rangle _{\mathrm {I=0}}^{}= & {} \frac{1}{\sqrt{2}}\left| K^+K^-\right\rangle + \frac{1}{\sqrt{2}}\left| K^0\bar{K}^0\right\rangle , \end{aligned}$$

(11)

the scalar form factors for the $\pi$ and K mesons are defined as

$$\begin{aligned} \sqrt{2}B_0\, F^{n/s}_1(s)= & {} \langle 0|\bar{n}n /\bar{s}s|\pi \pi \rangle _{\mathrm {I=0}}^{}, \\ \sqrt{2}B_0\,F^{n/s}_2(s)= & {} \langle 0|\bar{n}n/\bar{s}s|K\bar{K} \rangle _{\mathrm {I=0}}^{}, \nonumber \end{aligned}$$

(12)

where $s=m_{\pi \pi }^2$. The $\bar{n}n = (\bar{u}u+\bar{d}d)/\sqrt{2}$ denotes the non-strange scalar current, and the notation ($\pi$ = 1, K = 2) has been introduced for simplicity. With the above notation, we have

$$\begin{aligned} F_{\pi \pi }(m_{\pi \pi }^2) = \sqrt{\frac{2}{3}} F_1^n(m_{\pi \pi }^2). \end{aligned}$$

(13)

Expressions have already been derived in $\chi$PT up to next-to-leading order [37,38,39,40]:

$$\begin{aligned} F_1^n(s)= & {} \sqrt{\frac{3}{2}} \left[ 1 + \mu _\pi - \frac{\mu _\eta }{3} + \frac{16 m_\pi ^2}{f^2}\left( 2L_8^r-L_5^r\right) \right. \nonumber \\&\left. + 8\left( 2L_6^r-L_4^r\right) \frac{2m_K^2 + 3m_\pi ^2}{f^2} + \frac{8s}{f^2} L_4^r + \frac{4s}{f^2} L_5^r \right. \nonumber \\&+ \left. \left( \frac{2s - m_\pi ^2}{2f^2}\right) J^r_{\pi \pi }(s) + \frac{s}{4f^2} J^r_{KK}(s) + \frac{m_\pi ^2}{18f^2} J^r_{\eta \eta }(s) \right] , \end{aligned}$$

(14)

$$\begin{aligned} F_1^s(s)= & {} \frac{\sqrt{3}}{\,2}\left[ \frac{16 m_\pi ^2}{f^2}\left( 2L_6^r-L_4^r\right) + \frac{8s}{f^2} L_4^r\right. \nonumber \\&\left. +\frac{s}{2f^2} J^r_{KK}(s) + \frac{2}{9}\frac{m_\pi ^2}{f^2} J^r_{\eta \eta }(s) \right] ,\end{aligned}$$

(15)

$$\begin{aligned} F_2^n(s)= & {} \frac{1}{\sqrt{2}} \left[ 1 + \frac{8 L_4^r}{f^2} \left( 2s - m_\pi ^2 - 6 m_K^2\right) + \frac{4 L_5^r}{f^2} \left( s - 4 m_K^2\right) \right. \nonumber \\&\left. + \frac{16 L_6^r}{f^2} \left( 6 m_K^2 + m_\pi ^2\right) + \frac{32 L_8^r}{f^2}\,m_K^2 + \frac{2}{3} \mu _\eta \right. \nonumber \\&+ \left. \left( \frac{9s - 8 m_K^2}{36f^2}\right) J^r_{\eta \eta }(s) + \frac{3s}{4f^2} J^r_{KK}(s) + \frac{3s}{4f^2} J^r_{\pi \pi }(s) \right] , \end{aligned}$$

(16)

$$\begin{aligned} F_2^s(s)= & {} 1 + \frac{8 L_4^r}{f^2} \left( s - m_\pi ^2 - 4 m_K^2\right) + \frac{4 L_5^r}{f^2} \left( s - 4 m_K^2\right) \nonumber \\&+ \frac{16 L_6^r}{f^2} \left( 4 m_K^2 + m_\pi ^2\right) + \frac{32 L_8^r}{f^2}\,m_K^2 + \frac{2}{3} \mu _\eta \nonumber \\&+ \left( \frac{9s - 8 m_K^2}{18f^2}\right) J^r_{\eta \eta }(s) + \frac{3s}{4f^2} J^r_{KK}(s). \end{aligned}$$

(17)

Here the $L_i^r$ are the renormalized low-energy constants, and f is the pion decay constant at tree level. The $\mu _i$ and $J_{ii}^r$ are defined as follows:

$$\begin{aligned} \mu _i= & {} \frac{m_i^2}{32\pi ^2 f^2} \ln \frac{m_i^2}{\mu ^2},\end{aligned}$$

(18)

$$\begin{aligned} J_{ii}^r(s)= & {} \frac{1}{16\pi ^2}\left[ 1 - \log \left( \frac{m_i^2}{\mu ^2}\right) - \sigma _i(s)\log \left( \frac{\sigma _i(s)+1}{\sigma _i(s)-1}\right) \right] ,\nonumber \\ \end{aligned}$$

(19)

with $\sigma _i(s) = \sqrt{1- {4m_i^2}/{s}}$. It is interesting to note that the next-to-next-to-leading order results can also be found in Refs. [41, 42]. Imposing the unitarity constraints, the scalar form factor can be expressed in terms of the algebraic coupled-channel equation

$$\begin{aligned} F(s)= & {} [I+K(s)\,g(s)]^{-1} R(s) \\= & {} [I-K(s)\,g(s)]\,R(s) \,+\, \mathcal {O}(p^6), \nonumber \end{aligned}$$

(20)

where R(s) has no right-hand cut and in the second line, the equation has been expanded up to NLO in the chiral expansion. K(s) is the S-wave projected kernel of meson-meson scattering amplitudes that can be derived from the leading-order chiral Lagrangian:

$$\begin{aligned} K_{11} = \frac{2s - m_\pi ^2}{2f^2}, \quad K_{12} = K_{21} = \frac{\sqrt{3}s}{4f^2}, \quad K_{22} = \frac{3s}{4f^2}. \end{aligned}$$

The loop integral can be calculated either in the cutoff-regularization scheme with $q_\mathrm{max}\sim 1~$GeV being the cutoff (cf. Erratum of Ref. [43] for an explicit expression) or in dimensional regularization with the $\overline{\mathrm{MS}}$ subtraction scheme. In the latter scheme, the meson loop function $g_i(s)$ is given by

$$\begin{aligned} J_{ii}^r(s)\equiv & {} \frac{1}{16\pi ^2}\left[ 1 - \log \left( \frac{m_i^2}{\mu ^2}\right) - \sigma _i(s)\log \left( \frac{\sigma _i(s)+1}{\sigma _i(s)-1}\right) \right] \nonumber \\= & {} -g_i(s). \end{aligned}$$

(21)

The expressions for the $R_i$ are obtained by matching the unitarization and chiral perturbation theory [44, 45]:

$$\begin{aligned} R_1^n(s)= & {} \sqrt{\frac{3}{2}} \bigg \{ 1 + \mu _\pi - \frac{\mu _\eta }{3} + \frac{16 m_\pi ^2}{f^2}\left( 2L_8^r-L_5^r\right) \nonumber \\&+ 8\left( 2L_6^r-L_4^r\right) \frac{2m_K^2 + 3m_\pi ^2}{f^2} + \frac{8s}{f^2} L_4^r + \frac{4s}{f^2} L_5^r \nonumber \\&- \frac{m_\pi ^2}{288\pi ^2 f^2} \bigg [1 + \log \left( \frac{m_\eta ^2}{\mu ^2}\right) \bigg ] \bigg \}, \end{aligned}$$

(22)

$$\begin{aligned} R_1^s(s)= & {} \frac{\sqrt{3}}{\,2} \left\{ \frac{16 m_\pi ^2}{f^2}\left( 2L_6^r-L_4^r\right) + \frac{8s}{f^2} L_4^r \right. \nonumber \\&\left. - \frac{m_\pi ^2}{72\pi ^2 f^2} \left[ 1 + \log \left( \frac{m_\eta ^2}{\mu ^2}\right) \right] \right\} ,\end{aligned}$$

(23)

$$\begin{aligned} R_2^n(s)= & {} \frac{1}{\sqrt{2}} \left\{ 1 + \frac{8 L_4^r}{f^2} \left( 2s - 6m_K^2 - m_\pi ^2\right) + \frac{4 L_5^r}{f^2} \left( s - 4m_K^2\right) \right. \nonumber \\&\left. + \frac{16 L_6^r}{f^2} \left( 6m_K^2 + m_\pi ^2\right) + \frac{32 L_8^r}{f^2} m_K^2 + \frac{2}{3} \mu _\eta \right. \nonumber \\&+ \left. \frac{m_K^2}{72\pi ^2 f^2} \left[ 1 + \log \left( \frac{m_\eta ^2}{\mu ^2}\right) \right] \right\} , \end{aligned}$$

(24)

$$\begin{aligned} R_2^s(s)= & {} 1 + \frac{8 L_4^r}{f^2} \left( s - 4m_K^2 - m_\pi ^2\right) + \frac{4 L_5^r}{f^2} \left( s - 4m_K^2\right) \nonumber \\&+ \frac{16 L_6^r}{f^2} \left( 4m_K^2 + m_\pi ^2\right) + \frac{32 L_8^r}{f^2} m_K^2 + \frac{2}{3} \mu _\eta \nonumber \\&+ \frac{m_K^2}{36\pi ^2 f^2} \left[ 1 + \log \left( \frac{m_\eta ^2}{\mu ^2}\right) \right] . \end{aligned}$$

(25)

With the above formulas and the fitted results for the low-energy constants $L_i^r$ in Ref. [45] (evolved from $M_\rho$ to the scale $\mu = 2q_\mathrm{max}/\sqrt{e}$), we show the non-strange $\pi \pi$ form factor in Fig. 2. The modulus, real part and imaginary part are shown as solid, dashed and dotted curves. As the figure shows, the chiral unitary ansatz predicts a form factor $F^n_{1}$ with a zero close to the $\bar{K}K$ threshold. This feature has been extensively discussed in Ref. [46].

Fig. 2

The non-strange $\pi \pi$ scalar form factor obtained in the unitarized chiral perturbation theory. The modulus, real part and imaginary part are shown in solid, dashed and dotted curves

Fig. 3

Kinematics in the $D\rightarrow \pi \pi \ell \bar{\nu }$. The $\pi \pi$ moves along the z axis in the $\overline{D}$ rest frame. $\theta _\pi (\theta _{\ell })$ is defined in the $\pi \pi$ (lepton pair) rest frame as the angle between z-axis and the flight direction of $\pi ^+$ ($\ell ^-$), respectively. The azimuth angle $\phi$ is the angle between the $\pi \pi$ decay and lepton pair planes

3 Full angular distribution of $D\rightarrow \pi \pi \ell \bar{\nu }$

In this section, we will derive a full angular distribution of $D\rightarrow \pi \pi \ell \bar{\nu }$. For the literature, one may consult Refs. [47, 48]. We set up the kinematics for the $D^-\rightarrow \pi ^+\pi ^- \ell \bar{\nu }$ as shown in Fig. 3, which can also be used for $\overline{D}^0\rightarrow \pi ^+\pi ^0 \ell \bar{\nu }$. The $\pi \pi$ moves along the z axis in the $D^-$ rest frame. $\theta _{\pi ^+}(\theta _{\ell })$ is defined in the $\pi \pi$ (lepton pair) rest frame as the angle between z-axis and the flight direction of ${\pi }^+$ ($\ell ^-$), respectively. The azimuth angle $\phi$ is the angle between the $\pi \pi$ decay and lepton pair planes.

Decay amplitudes for $D\rightarrow \pi \pi \ell \bar{\nu }_{\ell }$ can be divided into several individual pieces and each of them can be expressed in terms of the Lorentz invariant helicity amplitudes. The amplitude for the hadronic part can be obtained by the evaluation of the matrix element:

$$\begin{aligned} A_{\lambda } = \sqrt{ N_{f_0/\rho }} \frac{iG_{\mathrm{F}}}{\sqrt{2}} V_{cd}^* \epsilon _{\mu }^*(h) \left\langle \pi \pi |\bar{c} \gamma ^\mu (1-\gamma _5) d |\overline{D}\right\rangle , \end{aligned}$$

(26)

where $\epsilon _\mu (h)$ is an auxiliary polarization vector for the lepton pair system and $h= 0, \pm , t$, $N_{f_0/\rho }= \sqrt{\lambda } q^2\beta _l /(96 \pi ^3m_{D}^3)$, $\beta _l=1-\hat{m}_l^2$ and $\hat{m}_l= m_{l}/\sqrt{q^2}$. $|V_{cd}|$ is taken to be 0.22 [27]. The functions $A_{i}$ can be decomposed into different partial waves,

$$\begin{aligned} A_{0/t }(q^2, m_{\pi \pi }^2,\theta _{\pi ^+})= & {} \sum _{J=0,1,2\ldots } A^J_{0/t }(q^2, m_{\pi \pi }^2)Y_{J}^0(\theta _{\pi ^+},0),\nonumber \\ A_{||/\perp }(q^2, m_{\pi \pi }^2,\theta _{\pi ^+})= & {} \sum _{J= 1,2\ldots } A^J_{||/ \perp }(q^2, m_{\pi \pi }^2)Y_{J}^{-1}(\theta _{\pi ^+},0),\nonumber \\ A^J_{0/t }(q^2, m_{\pi \pi }^2)= & {} \sqrt{ N_{f_0/{\rho }}} \mathcal{M}_D(f_0/{\rho }, 0/t )(q^2) L_{f_0/{\rho }}(m_{\pi \pi }^2)\nonumber \\\equiv & {} | A^J_{ 0/t }| e^{i\delta ^J_{{ 0/t }}},\nonumber \\ A^J_{ ||/\perp }(q^2, m_{\pi \pi }^2)= & {} \sqrt{ N_{f_0/{\rho }}} \mathcal{M}_D(f_0/{\rho }, ||/\perp )(q^2) L_{f_0/{\rho }}(m_{\pi \pi }^2)\nonumber \\\equiv & {} | A^J_{||/\perp }| e^{i\delta ^J_{{ ||/ \perp }}}. \end{aligned}$$

(27)

Here J denotes the partial wave of the $\pi \pi$ system and the script t denotes the time-like component of a virtual vector/axial-vector meson decays into a lepton pair. The $L_{f_0/\rho }(m_{\pi \pi })$ is the lineshape and for the P-wave $\rho$ we use the Breit–Wigner distribution:

$$\begin{aligned} L_{{\rho }}(m_{\pi \pi }^2)= \sqrt{ \frac{ m_{{\rho }} \Gamma _{{\rho }\rightarrow \pi \pi } }{\pi } } \frac{1}{m_{\pi \pi }^2 -m_{{\rho }}^2+ i m_{{\rho }}\Gamma _{{\rho }}}. \end{aligned}$$

(28)

Considering the momentum dependence of the $\rho$ decay, we have the running width as

$$\begin{aligned} \Gamma _{ \rho } (m_{\pi \pi }^2) = \Gamma _{{\rho }}^0 \left( \frac{ |\vec q\,|}{ | \vec q_0|}\right) ^3 \frac{m_{{\rho }}}{m_{\pi \pi }} \frac{1+ (R|\vec q_0|)^2}{1+ (R|\vec q\,|)^2}, \end{aligned}$$

(29)

and the Blatt–Weisskopf parameter $R=(2.1\pm 0.5\pm 0.5)~ \mathrm{GeV}^{-1}$ [49].

The spin-0 final state has only one polarization state and the amplitudes are

$$\begin{aligned} i\mathcal{M}_D(f_0,0)= & {} N_1 i\Bigg [ \frac{\sqrt{\lambda }}{\sqrt{ q^2}} F_1(q^2) \Bigg ],\nonumber \\ i\mathcal{M}_D(f_0,t)= & {} N_1 i\Bigg [ \frac{m_{D}^2-m_{f_0}^2}{\sqrt{q^2}} F_0(q^2) \Bigg ], \end{aligned}$$

(30)

with $N_1= {iG_\mathrm{F}}V_{cd}^*/{\sqrt{2}}$. For mesons with spin $J\ge 1$, the $\pi ^+\pi ^-$ system can be either longitudinally or transversely polarized and thus we have the following form:

$$\begin{aligned} i\mathcal{M}_D(\rho ,0)= & {} -\frac{ \alpha _L^J N_1 i}{2m_{\rho }\sqrt{q^2}}\nonumber \\&\times \left[ (m_{D}^2-m_{\rho }^2-q^2)(m_{D}+m_{\rho })A_1\right. \nonumber \\&\left. -\frac{\lambda }{m_{D}+m_{\rho }}A_2\right] ,\nonumber \\ i\mathcal{M}_D({\rho },\pm )= & {} -\beta _T^J N_1 i \left[ (m_{D}+m_{\rho })A_1\pm \frac{\sqrt{\lambda }}{m_{D}+m_{\rho }}V \right] ,\end{aligned}$$

(31)

$$\begin{aligned} i\mathcal{M}_D({\rho }, t)= & {} -\alpha _L^J i N_{1} \frac{\sqrt{\lambda }}{\sqrt{q^2}}A_0. \end{aligned}$$

(32)

The $\alpha _L^J$ and $\beta _T^J$ are products of the Clebsch–Gordan coefficients

$$\begin{aligned} \alpha _L^J= & {} C^{J,0}_{1,0;J-1,0} C^{J-1,0}_{1,0; J-2,0} \cdots C^{2,0}_{1,0;1,0},\nonumber \\ \beta _T^J= & {} C^{J,1}_{1,1;J-1,0} C^{J-1,0}_{1,0; J-2,0} \cdots C^{2,0}_{1,0;1,0}. \end{aligned}$$

(33)

For the sake of convenience, we define

$$\begin{aligned} i\mathcal{M}_{D}(\rho , \perp /||)= & {} \frac{1}{\sqrt{2}}[i\mathcal{M}_D(\rho , +) \mp i\mathcal{M}_D(\rho , -)],\nonumber \\ i\mathcal{M}_D(\rho , \perp )= & {} -i\beta _T^J \sqrt{2} N_1\left[ \frac{\sqrt{\lambda }V}{m_{D}+m_{\rho }} \right] , \nonumber \\ i\mathcal{M}_D(\rho ,||)= & {} -i\beta _T^J\sqrt{2} N_{1} \left[ (m_{D}+m_{\rho })A_1 \right] . \end{aligned}$$

(34)

Using the generalized form factor, the matrix elements for D decays into the spin-0 non-resonating $\pi \pi$ final state are given as

$$\begin{aligned} A_0^0= & {} \sqrt{ N_2} i\frac{1}{m_{\pi \pi }} \Bigg [ \frac{\sqrt{\lambda }}{\sqrt{ q^2}}\mathcal{F}_1^{\pi \pi }(m_{\pi \pi }^2, q^2) \Bigg ] ,\nonumber \\ A_t^0= & {} \sqrt{ N_2} i \frac{1}{m_{\pi \pi }}\Bigg [ \frac{m_{D}^2-m_{\pi \pi }^2}{\sqrt{q^2}} \mathcal{F}_0^{\pi \pi }(m_{\pi \pi }^2, q^2)\Bigg ], \end{aligned}$$

(35)

$N_2=N_1 N_{\rho } \rho _{\pi }/(16\pi ^2)$, with $\rho _{\pi }= \sqrt{1-4m_{\pi }^2/m^2_{\pi \pi }}$.

The above quantities can lead to the full angular distributions

$$\begin{aligned}&\frac{\mathrm{d}^5\Gamma }{\mathrm{d}m_{\pi \pi }^2\mathrm{d}q^2\mathrm{d}\cos \theta _{\pi ^+} \mathrm{d}\cos \theta _l \mathrm{d}\phi }\nonumber \\&\quad = \frac{3}{8}\Big [I_1(q^2, m_{\pi \pi }^2, \theta _{\pi ^+}) \nonumber \\&\qquad +I_2 (q^2, m_{\pi \pi }^2, \theta _{\pi ^+}) \cos (2\theta _{\ell }) \nonumber \\&\qquad + I_3(q^2, m_{\pi \pi }^2, \theta _{\pi ^+}) \sin ^2\theta _{\ell } \cos (2\phi ) \nonumber \\&\qquad +I_4(q^2, m_{\pi \pi }^2, \theta _{\pi ^+}) \sin (2\theta _{\ell })\cos \phi \nonumber \\&\qquad +I_5 (q^2, m_{\pi \pi }^2, \theta _{\pi ^+}) \sin (\theta _{\ell }) \cos \phi \nonumber \\&\qquad +I_6 (q^2, m_{\pi \pi }^2, \theta _{\pi ^+}) \cos \theta _{\ell } \nonumber \\&\qquad +I_7 (q^2, m_{\pi \pi }^2, \theta _{\pi ^+}) \sin (\theta _{\ell }) \sin \phi \nonumber \\&\qquad +I_8(q^2, m_{\pi \pi }^2, \theta _{\pi ^+}) \sin (2\theta _{\ell })\sin \phi \nonumber \\&\qquad +I_9(q^2, m_{\pi \pi }^2, \theta _{\pi ^+}) \sin ^2\theta _{\ell } \sin (2\phi )\Big ]. \end{aligned}$$

(36)

For the general expressions of $I_i$, we refer the reader to the appendix and to Refs. [48, 50] for the formulas with the S-, P- and D-waves. In the following, we shall only consider the S-wave and P-wave contributions and thus the above general expressions are reduced to:

$$\begin{aligned} I_1= & {} \frac{1}{4\pi } \left[ (1+\hat{m}_l^2) |A^0_{0}|^2 +2 \hat{m}_l^2 |A_t^0|^2\right] \nonumber \\&+ \frac{3}{4\pi } \cos ^2\theta _{\pi ^{+}} \left[ (1+\hat{m}_l^2) |A^1_{0}|^2 +2 \hat{m}_l^2 |A_t^1|^2\right] \nonumber \\&+ \frac{2\sqrt{3} \cos \theta _{\pi ^{+}}}{4\pi } \left[ (1+\hat{m}_l^2) \mathrm{Re}[A^0_{0} A^{1*}_{0}] + 2\hat{m}_l^2 \mathrm{Re}[A^0_{t} A^{1*}_{t}] \right] \nonumber \\&+ \frac{3+\hat{m}_l^2}{2} \frac{3}{8\pi } \sin ^2\theta _{\pi ^{+}} \left[ |A^1_{\perp }|^2+|A^1_{||}|^2 \right] ,\nonumber \\ I_2= & {} -\beta _l \bigg \{ \frac{1}{4\pi } |A^0_{0}|^2 + \frac{3}{4\pi }\cos ^2\theta _{\pi ^{+}} |A^1_{0}|^2 \nonumber \\&+ \frac{2\sqrt{3} \cos \theta _{\pi ^{+}}}{4\pi } \mathrm{Re}[A^0_{0} A^{1*}_{0}] \bigg \}\nonumber \\&+ \frac{1}{2}\beta _l \frac{3}{8\pi } \sin ^2\theta _{\pi ^{+}} \left( |A^1_{\perp }|^2+|A^1_{||}|^2\right) , \nonumber \\ I_3= & {} \beta _l \frac{3}{8\pi } \sin ^2\theta _{\pi ^{+}} \left( |A^1_{\perp }|^2-|A^1_{||}|^2\right) , \nonumber \\ I_4= & {} 2 \beta _l \left[ \frac{\sqrt{3} \sin \theta _{\pi ^{+}}}{4\sqrt{2}\pi } \mathrm{Re}\left[ A^0_{0}A^{1*}_{||} \right] \right. \nonumber \\&\left. + \frac{3\sin \theta _{\pi ^{+}}\cos \theta _{\pi ^{+}} }{4\sqrt{2}\pi } \mathrm{Re}\left[ A^1_{0}A^{1*}_{||} \right] \right] , \nonumber \\ I_5= & {} 4\Bigg \{\frac{\sqrt{3} \sin \theta _{\pi ^{+}}}{4\sqrt{2}\pi } \bigg (\mathrm{Re}[A^0_{0}A^{1*}_{\perp } ] -\hat{m}_l^2 \mathrm{Re}[A^0_{t}A^{1*}_{||} ] \bigg ) \nonumber \\&+ \frac{ 3 \sin \theta _{\pi ^{+}}\cos \theta _{\pi ^{+}} }{4\sqrt{2}\pi } \bigg ( \mathrm{Re}[A^1_{0}A^{1*}_{\perp } ] -\hat{m}_l^2 \mathrm{Re}[A^1_{t}A^{1*}_{||} ]\bigg ) \Bigg \} , \nonumber \\ I_6= & {} 4\bigg \{ \frac{3}{8\pi } \sin ^2\theta _{\pi ^{+}} \mathrm{Re}[ A^1_{||}A^{1*}_{\perp } ] + \hat{m}_l^2 \frac{1}{4\pi } \mathrm{Re}[A_t^0 A_{0}^{0*}] \nonumber \\&+ \hat{m}_l^2 \frac{3}{4\pi } \cos ^2\theta _{\pi ^{+}} \mathrm{Re}[A_t^1 A_{0}^{1*}] \bigg \} \nonumber \\ I_7= & {} 4\Bigg \{\frac{\sqrt{3}}{4\sqrt{2}\pi } \sin \theta _{\pi ^{+}} \bigg (\mathrm{Im}[A^0_{0}A^{1*}_{||}] - \hat{m}_l^2 \mathrm{Im}[ A_t^0 A_\perp ^{1*}] \bigg ) \nonumber \\&+ \frac{3}{4\sqrt{2}\pi } \sin \theta _{\pi ^{+}} \cos \theta _{\pi ^{+}} \bigg (\mathrm{Im}[A^1_{0}A^{1*}_{||}] - \hat{m}_l^2 \mathrm{Im}[ A_t^1 A_\perp ^{1*}] \bigg )\Bigg \} \nonumber \\ I_8= & {} 2 \beta _l \Bigg \{\frac{\sqrt{3}}{4\sqrt{2}\pi } \sin \theta _{\pi ^{+}} \mathrm{Im} \bigg [A_0^0 A_\perp ^{1*}\bigg ]\nonumber \\&+ \frac{ 3}{4\sqrt{2}\pi } \sin \theta _{\pi ^{+}} \cos \theta _{\pi ^{+}} \mathrm{Im} \bigg [A_0^1 A_\perp ^{1*}\bigg ]\Bigg \}, \nonumber \\ I_9= & {} 2 \beta _l \frac{3}{8\pi } \sin ^2\theta _{\pi ^{+}} \mathrm{Im}\left[ A_\perp ^1 A_{||}^{1*} \right] . \end{aligned}$$

(37)

Since the phase in P-wave contributions arise from the lineshape which is the same for different polarizations, the $I_9$ term and the second line in the $I_7$ are zero.

3.1 Differential and integrated decay widths

Using the narrow width approximation, we obtain the integrated branching fraction:

$$\begin{aligned}&\mathcal{B}(D^-\rightarrow \rho ^0 e^-\bar{\nu })= (2.24\pm 0.09)\times 10^{-3}/(2.16\pm 0.36) \nonumber \\&\quad \times 10^{-3} \mathrm {(LFQM/LCSR)},\end{aligned}$$

(38)

$$\begin{aligned}&\mathcal{B}(D^-\rightarrow \rho ^0 \mu ^-\bar{\nu })\nonumber \\&\quad = (2.15\pm 0.08)\times 10^{-3}/(2.06\pm 0.35)\times 10^{-3} \mathrm {(LFQM/LCSR)}, \end{aligned}$$

(39)

$$\begin{aligned}&\mathcal{B}(\bar{D}^0\rightarrow \rho ^+ e^-\bar{\nu }) \nonumber \\&\quad = (1.73\pm 0.07)\times 10^{-3}/(1.67\pm 0.27)\times 10^{-3}\mathrm {(LFQM/LCSR)},\nonumber \\ \end{aligned}$$

(40)

where theoretical errors are from the heavy-to-light transition form factors. These theoretical results are in good agreement with the data [27]:

$$\begin{aligned} \mathcal{B}(D^-\rightarrow \rho ^0 e^-\bar{\nu })= & {} (2.18^{+0.17}_{-0.25})\times 10^{-3},\end{aligned}$$

(41)

$$\begin{aligned} \mathcal{B}(D^-\rightarrow \rho ^0 \mu ^-\bar{\nu })= & {} (2.4\pm 0.4)\times 10^{-3},\end{aligned}$$

(42)

$$\begin{aligned} \mathcal{B}(\bar{D}^0\rightarrow \rho ^+ e^-\bar{\nu })= & {} (1.77\pm 0.16)\times 10^{-3}. \end{aligned}$$

(43)

The starting point for detailed analysis of $D\rightarrow \pi \pi \ell \bar{\nu }$ is to obtain the double-differential distribution $\mathrm{d}^2\Gamma /\mathrm{d}q^2 \mathrm{d}m_{\pi \pi }^2$ after performing integration over all the angles

$$\begin{aligned} \frac{\mathrm{d}^2\Gamma }{\mathrm{d}q^2 \mathrm{d}m_{\pi \pi }^2}= & {} \left( 1+\frac{\hat{m}_l^2}{2}\right) \left( |A_{0}^0|^2 + |A_{0}^1|^2 + |A_{||}^1|^2 + |A_{\perp }^1|^2\right) \nonumber \\&+ \frac{3}{2} \hat{m}_l^2 \left( |A_{t}^1|^2 + |A_{t}^0|^2 \right) , \end{aligned}$$

(44)

where apparently in the massless limit for the involved lepton, the total normalization for angular distributions changes to the sum of the S-wave and P-wave amplitudes

$$\begin{aligned} \frac{\mathrm{d}^2\Gamma }{\mathrm{d}q^2 \mathrm{d}m_{\pi \pi }^2} = |A_{0}^0|^2 + |A_{0}^1|^2 + |A_{||}^1|^2 + |A_{\perp }^1|^2. \end{aligned}$$

(45)

In Fig. 4, we give the dependence of branching fraction on $m_{\pi \pi }$ in the $D^-\rightarrow \pi ^+\pi ^-e^-\bar{\nu }_e$ process. The solid, dashed, and dotted curves correspond to the total, S-wave and P-wave contributions. For the S-wave contribution, there is no resonance around 0.98 GeV, and theoretically, this should be a dip.

Due to the quantum number constraint, the process $\bar{D}^0\rightarrow \pi ^+\pi ^0 \ell \bar{\nu }$ receives only a P-wave contribution and $D^-\rightarrow \pi ^0\pi ^0 \ell \bar{\nu }$ is generated by the S-wave term.

Fig. 4

The dependence of branching fraction on $m_{\pi \pi }$ in the $D^-\rightarrow \pi ^+\pi ^-e^-\bar{\nu }_e$ process. The heavy-to-light form factors are evaluated by using LCSR

Fig. 5

Differential decay widths for the $D^-\rightarrow \pi ^+\pi ^-\ell \bar{\nu }_{\ell }$ with $\ell =e$ in (a) and $\ell = \mu$ in (b). The $q^2$-dependent ratio $R_{\pi \pi }^{\mu /e}$ as defined in Eq. (55) is given in (c). The dashed and dotted curves are produced using the LFQM and LCSR results for $D\rightarrow \rho$ form factors. Errors from the form factors are shown as shadowed bands, and most errors cancel in the ratio $R_{\pi \pi }^{\mu /e}$ given in (c)

To match the kinematics constraints implemented in experimental measurements, one may explore the generic observable with $m_{\pi \pi }^2$ integrated out:

$$\begin{aligned} \langle O\rangle = \int _{(m_{\rho }-\delta _m)^2}^{(m_{\rho }+\delta _m)^2} \mathrm{d}m^2_{\pi \pi } \frac{\mathrm{d}O}{\mathrm{d}m_{\pi \pi }^2}. \end{aligned}$$

(46)

We use the following choice in our study of $D\rightarrow \pi \pi \ell \bar{\nu }$:

$$\begin{aligned} \delta _m = \Gamma _\rho . \end{aligned}$$

(47)

In the narrow width-limit, the integration of the lineshape is conducted as

$$\begin{aligned} \int \mathrm{d}m^2_{\pi \pi }|L_{\rho }(m^2_{\pi \pi })|^2 = \mathcal{B}(\rho ^0\rightarrow \pi ^-\pi ^+)=1. \end{aligned}$$

(48)

However, with the explicit form given in Eq. (29), we find that the integration

$$\begin{aligned} \int _{(m_{\rho }-\delta _m)^2}^{(m_{\rho }+\delta _m)^2} \mathrm{d}m^2_{\pi \pi }|L_{\rho }(m^2_{\pi \pi })|^2 =0.70 \end{aligned}$$

(49)

is below the expected value. On the other hand, the integrated S-wave lineshape in this region is

$$\begin{aligned} \int _{(m_{\rho }-\delta _m)^2}^{(m_{\rho }+\delta _m)^2} \mathrm{d}m^2_{\pi \pi }|L_{S}(m^2_{\pi \pi })|^2 ={ 0.37}, \end{aligned}$$

(50)

which is smaller but at the same order. Integrated from $m_{\rho }-\Gamma _{\rho }$ to $m_{\rho }+\Gamma _{\rho }$, we have

$$\begin{aligned}&\mathcal{B}(D^-\rightarrow \rho ^0 (\rightarrow \pi ^+\pi ^-) e^-\bar{\nu }) \nonumber \\&\quad = (1.57\pm 0.07)\times 10^{-3}/(1.51\pm 0.26)\times 10^{-3}\ (\mathrm {LFQM/LCSR}), \end{aligned}$$

(51)

$$\begin{aligned}&\mathcal{B}(D^-\rightarrow \rho ^0 (\rightarrow \pi ^+\pi ^-) \mu ^-\bar{\nu }) \nonumber \\&\quad = (1.57\pm 0.07)\times 10^{-3}/(1.51\pm 0.26)\times 10^{-3}\ (\mathrm {LFQM/LCSR}).\nonumber \\ \end{aligned}$$

(52)

The S-wave branching fractions for $2m_{\pi }<m_{\pi \pi }< 1.0~\mathrm {GeV}$ are given as

$$\begin{aligned} \mathcal{B}(D^-\rightarrow (\pi ^+\pi ^-)_S e^-\bar{\nu })= & {} (6.99\pm 2.46)\times 10^{-4},\end{aligned}$$

(53)

$$\begin{aligned} \mathcal{B}(D^-\rightarrow ( \pi ^+\pi ^-)_S \mu ^-\bar{\nu })= & {} (7.20\pm 2.52)\times 10^{-4}. \end{aligned}$$

(54)

Above 1 GeV, the unitarized $\chi$PT will fail and thus we lack any reliable prediction.

Furthermore, one may explore the $q^2$-dependent ratio

$$\begin{aligned} R_{\pi \pi }^{\mu /e}(q^2)= & {} \frac{\left\langle d\Gamma (D\rightarrow \pi \pi \mu \bar{\nu }_{\mu })/\mathrm{d}q^2 \right\rangle }{\left\langle d\Gamma ( D\rightarrow \pi \pi e\bar{\nu }_e)/\mathrm{d}q^2\right\rangle }. \end{aligned}$$

(55)

Differential decay widths for $D\rightarrow \pi \pi \ell \bar{\nu }_{\ell }$ are given in Fig. 5, with $\ell = e$ in panel (a) and $\ell =\mu$ in panel (b). The $q^2$-dependent ratio $R_{\pi \pi }^{\mu /e}$ is given in panel (c). Errors from the form factors and QCD condensate parameter $B_0$ are shown as shadowed bands, and most errors cancel in the ratio $R_{\pi \pi }^{\mu /e}$ given in panel (c).

3.2 Distribution in $\theta _{\pi ^{+}}$

Fig. 6

Same as Fig. 5 but for the S-wave contributions (a) and the longitudinal polarizations in P-wave contributions (b) to the $D\rightarrow \pi \pi \ell \bar{\nu }_{\ell }$, and the forward–backward asymmetry $\overline{A_{FB}^{\pi }}$ (c). Notice that, for the $\overline{A_{FB}^{\pi }}$, there is a sign ambiguity arising from the use of Watson theorem. These diagrams are for the light lepton e, while the results for the $\mu$ lepton are similar

We explore the distribution in $\theta _{\pi ^{+}}$:

$$\begin{aligned} \frac{\mathrm{d}^3\Gamma }{ \mathrm{d}q^2 \mathrm{d}m_{\pi \pi }^2 \mathrm{d}\cos \theta _{\pi ^{+}}}= & {} \frac{\pi }{2} (3I_1-I_2) \nonumber \\= & {} \frac{1}{8} \bigg \{ (4+2\hat{m}_l^2) |A_0^0|^2 + 6\hat{m}_l^2 |A_t^0|^2 \nonumber \\&+ \sqrt{3} (8+4\hat{m}_l^2) \cos \theta _{\pi ^{+}} \mathrm{Re}[A_0^0 A_{0}^{1*}] \nonumber \\&+ 12\sqrt{3} \hat{m}_l^2 \cos \theta _{\pi ^{+}} \mathrm{Re}[A_t^0 A_{t}^{1*}] \nonumber \\&+ (12+ 6\hat{m}_l^2) |A_0^1|^2 \cos ^2\theta _{\pi ^{+}}\nonumber \\&+ 18\hat{m}_l^2 \cos ^2\theta _{\pi ^{+}} |A_t^1|^2 \nonumber \\&+ (6+3\hat{m}_l^2) \sin ^2\theta _{\pi ^{+}} (|A_\perp ^1|^2 + |A_{||}^1|^2) \bigg \}.\nonumber \\ \end{aligned}$$

(56)

Compared to the distribution with only P-wave contribution, namely $D\rightarrow \rho (\rightarrow \pi \pi )\ell \bar{\nu }$, the first two lines of Eq. (56) are new: the first one is the S-wave $\pi \pi$ contribution, while the second line arises from the interference of S-wave and P-wave. Based on this interference, one can define a forward–backward asymmetry for the involved pion,

$$\begin{aligned} A_{\mathrm{FB}}^{\pi }\equiv & {} \bigg [\int _{0}^1 - \int _{-1}^0\bigg ] \mathrm{d}\cos \theta _{\pi ^{+}} \frac{\mathrm{d}^3\Gamma }{ \mathrm{d}q^2 \mathrm{d}m_{\pi \pi }^2 \mathrm{d}\cos \theta _{\pi ^{+}}} \nonumber \\= & {} \frac{\sqrt{3}}{2} (2+ \hat{m}_l^2) \mathrm{Re}[A_0^0 A_{0}^{1*}] + \frac{3\sqrt{3}}{2} \hat{m}_l^2 \mathrm{Re}[A_t^0 A_{t}^{1*}]. \end{aligned}$$

(57)

We define the polarization fraction at a given value of $q^2$ and $m_{\pi \pi }^2$:

$$\begin{aligned} \mathcal{F}_{S} (q^2, m_{\pi \pi }^2)= & {} \frac{ (1+\hat{m}_l^2/2) |A_0^0|^2 + 3/2 \hat{m}_l^2 |A_t^0|^2 }{ {\mathrm{d}^2\Gamma }/({\mathrm{d}q^2 \mathrm{d}m_{\pi \pi }^2})} ,\nonumber \\ \mathcal{F}_{P } (q^2, m_{\pi \pi }^2)= & {} \frac{ (1+\hat{m}_l^2/2)(|A_{0}^1|^2 + |A_{||}^1|^2 + |A_{\perp }^1|^2 ) + 3/2\hat{m}_l^2 |A^1_t|^2 }{ {\mathrm{d}^2\Gamma }/({\mathrm{d}q^2 \mathrm{d}m_{\pi \pi }^2})},\nonumber \\ \end{aligned}$$

(58)

and also

$$\begin{aligned}&F_L (q^2, m_{\pi \pi }^2) \nonumber \\&\quad = \frac{ (1+\hat{m}_l^2/2)|A_{0}^1(q^2, m_{\pi \pi }^2)|^2 + 3/2\hat{m}_l^2 |A^1_t|^2 }{ (1+\hat{m}_l^2/2)(|A_{0}^1|^2 + |A_{||}^1|^2 + |A_{\perp }^1|^2 ) + 3/2\hat{m}_l^2 |A^1_t|^2 },\nonumber \\&\overline{A_{\mathrm{FB}}^{\pi }}(q^2, m_{\pi \pi }^2)\nonumber \\&\quad = \frac{ {\sqrt{3}}/{2} (2+\hat{m}_l^2) \mathrm{Re}[A_0^0 A_{0}^{1*}] + {3\sqrt{3}}/{2} \hat{m}_l^2 \mathrm{Re}[A_t^0 A_{t}^{1*}] }{ {\mathrm{d}^2\Gamma }/({\mathrm{d}q^2 \mathrm{d}m_{\pi \pi }^2})} . \end{aligned}$$

(59)

By definition, $\mathcal{F}_S+\mathcal{F}_P=1$.

In Fig. 6, we give our results for the S-wave fraction $\langle F_S\rangle$ (panel (a)), longitudinal polarization fraction $\langle F_L\rangle$ in P-wave contributions (panel (b)) and the asymmetry $\langle \overline{A_{FB}^{\pi }} \rangle$ (panel (c)). Only the curves for the light lepton e are shown since the results for the $\mu$ lepton are similar. These observables and the following ones are defined by the integration over $m_{\pi \pi }^2$; for instance,

$$\begin{aligned} \langle F_{S} (q^2) \rangle = \frac{\int \mathrm{d}m_{\pi \pi }^2 [ (1+\hat{m}_l^2/2) |A_0^0|^2 + 3/2 \hat{m}_l^2 |A_t^0|^2] }{\int \mathrm{d}m_{\pi \pi }^2 {\mathrm{d}^2\Gamma }/({\mathrm{d}q^2 \mathrm{d}m_{\pi \pi }^2})} ,\nonumber \\ \end{aligned}$$

(60)

and likewise for the others.

3.3 Distribution in $\theta _l$ and forward–backward asymmetry

Fig. 7

Same as Fig. 5 but for the asymmetry $\overline{\mathcal{A}_{FB}^l}$ in the $D\rightarrow \pi \pi \ell \bar{\nu }_{\ell }$

Integrating over $\theta _{\pi ^{+}}$ and $\phi$, we have the distribution:

$$\begin{aligned} \frac{\mathrm{d}^3\Gamma }{ \mathrm{d}q^2 \mathrm{d}m_{\pi \pi }^2 \mathrm{d}\cos \theta _l}= & {} \frac{3\pi }{4}\int \mathrm{d}\cos \theta _{\pi ^{+}} \nonumber \\&\times \left( I_1 +I_2\cos (2\theta _l) +I_6 \cos \theta _l \right) \nonumber \\= & {} \frac{3}{4} \hat{m}_l^2 \left( \left( |A_{t}^0|^2 +|A_{t}^1|^2 \right) \right) + \frac{3}{2} \cos \theta _l\nonumber \\&\times \left( \mathrm{Re}[A_{||}^1 A_{\perp }^{1*}] + \hat{m}_l^2 \mathrm{Re}[A_{t}^0 A_{0}^{0*}+A_{t}^1 A_{0}^{1*}]\right) \nonumber \\&+\frac{3}{4} \left[ 1 -(1-\hat{m}_l^2)\cos ^2\theta _l\right] \left( |A_{0}^0|^2 +|A_{0}^1|^2 \right) \nonumber \\&+ \frac{3}{8} \left[ (1+\hat{m}_l^2) + (1-\hat{m}_l^2) \cos ^2\theta _l \right] \nonumber \\&\times (|A_{||}^1|^2 +|A_{\perp }^1|^2 ). \end{aligned}$$

(61)

The forward–backward asymmetry is defined as

$$\begin{aligned} \mathcal{A}_{\mathrm{FB}}^{l}\equiv & {} \bigg [\int _{0}^1 - \int _{-1}^0\bigg ] \mathrm{d}\cos \theta _l \frac{\mathrm{d}^3\Gamma }{ \mathrm{d}q^2 \mathrm{d}m_{\pi \pi }^2 \mathrm{d}\cos \theta _l }\nonumber \\= & {} \frac{3}{2} \left( \mathrm{Re}[A_{||}^1 A_{\perp }^{1*}] + \hat{m}_l^2 \mathrm{Re}\left[ A_{t}^0 A_{0}^{0*}+A_{t}^1 A_{0}^{1*}\right] \right) , \end{aligned}$$

(62)

and the results for $\overline{\mathcal{A}_{FB}^l}$ are given in Fig. 7.

3.4 Distribution in the azimuth angle $\phi$

Fig. 8

Same as Fig. 5 but for the normalized coefficients in the $\phi$ distributions of the $D^-\rightarrow \pi ^+ \pi ^- \ell \bar{\nu }_{\ell }$. The left panels (a, c, e) are for the light lepton e, while the right panels (b, d, f) are for the $\mu$ lepton

The angular distribution in $\phi$ is derived as

$$\begin{aligned} \frac{\mathrm{d}^3\Gamma }{ \mathrm{d}q^2 \mathrm{d}m_{\pi \pi }^2 \mathrm{d}\phi }= & {} a_\phi +b_\phi ^c \cos \phi + b_\phi ^s \sin \phi \nonumber \\&+ c_\phi ^c \cos (2\phi ) + c_\phi ^s \sin (2\phi ) \end{aligned}$$

(63)

with

$$\begin{aligned} a_\phi= & {} \frac{1}{2\pi } \frac{\mathrm{d}^2\Gamma }{ \mathrm{d}q^2 \mathrm{d}m_{\pi \pi }^2} ,\nonumber \\ b_\phi ^c= & {} \frac{3}{16}\pi \int I_5 \mathrm{d}\cos \theta _{\pi ^{+}}\nonumber \\= & {} \frac{3\sqrt{3}}{32\sqrt{2}\pi } \bigg (\mathrm{Re}[A_0^0 A_{\perp }^{1*}]-\hat{m}_l^2 \mathrm{Re}[A_t^0 A_{\perp }^{1*}]\bigg ),\nonumber \\ b_\phi ^s= & {} \frac{3}{16}\pi \int I_7 \mathrm{d}\cos \theta _{\pi ^{+}}\nonumber \\ {}= & {} \frac{3\sqrt{3}}{32\sqrt{2}\pi } \bigg (\mathrm{Im}[A_0^0 A_{\perp }^{1*}]-\hat{m}_l^2 \mathrm{Im}[A_t^0 A_{\perp }^{1*}]\bigg ),\nonumber \\ c_\phi ^c= & {} \frac{1}{2} \int I_3 \mathrm{d}\cos \theta _{\pi ^{+}}\nonumber \\= & {} \frac{1}{4\pi } \beta _l (|A_{\perp }^1|^2-|A_{||}^1|^2), \nonumber \\ c_\phi ^s= & {} \frac{1}{2} \int I_9 \mathrm{d}\cos \theta _{\pi ^{+}}\nonumber \\ {}= & {} \frac{1}{ 2 \pi } \beta _l \mathrm{Im}[A_{\perp }^1 A_{||}^{1*}]. \end{aligned}$$

(64)

Since the complex phase in the P-wave amplitudes comes from the Breit–Wigner lineshape, the coefficient $c_\phi ^s$ vanishes.

Numerical results for the normalized coefficients using the two sets of form factors are shown in Fig. 8. The coefficients $b_\phi ^c$ and $b_\phi ^s$ contain a very small prefactor, ${3\sqrt{3}}/({32\sqrt{2}\pi } )\sim 0.037$, and thus are numerically tiny, as shown in this figure. The $c_\phi ^c$ is also small due to the cancellation between the $|A_{\perp }|^2$ and $|A_{||}|^2$.

3.5 Polarization of $\mu$ lepton

Fig. 9

Same as Fig. 5 but for the polarization distribution of $D\rightarrow \pi \pi \mu \bar{\nu }_{\mu }$. Theoretical errors are negligible

In this work, we also give the polarized angular distributions as

$$\begin{aligned}&\frac{\mathrm{d}^5\Gamma (\lambda _\mu )}{\mathrm{d}m_{\pi \pi }^2\mathrm{d}q^2\mathrm{d}\cos \theta _{\pi ^{+}} \mathrm{d}\cos \theta _l \mathrm{d}\phi } \nonumber \\&\quad = \frac{3}{8}\Big [I_1^{(\lambda _\mu )} +I_2 ^{(\lambda _\mu )} \cos (2\theta _l) + I_3^{(\lambda _\mu )} \sin ^2\theta _l \cos (2\phi ) \nonumber \\&\qquad +I_4^{(\lambda _\mu )} \sin (2\theta _l)\cos \phi +I_5^{(\lambda _\mu )} \sin (\theta _l) \cos \phi +I_6 ^{(\lambda _\mu )} \cos \theta _l \nonumber \\&\qquad +I_7^{(\lambda _\mu )} \sin (\theta _l) \sin \phi +I_8^{(\lambda _\mu )} \sin (2\theta _l)\sin \phi \nonumber \\&\qquad +I_9^{(\lambda _\mu )} \sin ^2\theta _l \sin (2\phi )\Big ], \end{aligned}$$

(65)

with the coefficients

$$\begin{aligned}&I_1^{(-1/2)} = |A_{0}|^2 +\frac{3}{2} (|A_{\perp }|^2 +|A_{||}|^2), \nonumber \\&I_2^{(-1/2)} = - |A_{0}|^2+ \frac{1}{2} (|A_{\perp }|^2 +|A_{||}|^2), \nonumber \\&I_3^{(-1/2)} = |A_{\perp }|^2-|A_{||}|^2 ,\quad I_4^{(-1/2)} = 2\mathrm{Re}(A_{0}A_{||}^*),\nonumber \\&I_5^{(-1/2)} =4 \mathrm{Re}(A_{0}A_{\perp }^*), \nonumber \\&I_6^{(-1/2)} = 4 \mathrm{Re}(A_{||}A^*_{\perp }),\quad I_7^{(-1/2)} = 4 \mathrm{Im}(A_{0}A^*_{||}) , \nonumber \\&I_8^{(-1/2)} = 2 \mathrm{Im}(A_{0}A^*_{\perp }),\quad I_9^{(-1/2)} =2 \mathrm{Im}(A_{\perp }A^*_{||}). \end{aligned}$$

(66)

The coefficients for the $\lambda _\mu =1/2$ are easily obtained by comparing Eqs. (66) and (37). For instance, the lepton polarization fraction is defined as

$$\begin{aligned}&\overline{A^{\lambda _\mu }}(q^2, m_{\pi \pi }^2 ) = \frac{ {\mathrm{d}^2\Gamma ^{(1/2)}}/{\mathrm{d}q^2\mathrm{d}m_{\pi \pi }^2 }- {\mathrm{d}^2\Gamma ^{(-1/2)}}/{\mathrm{d}q^2\mathrm{d}m_{\pi \pi }^2 }}{ {\mathrm{d}^2\Gamma }/{\mathrm{d}q^2\mathrm{d}m_{\pi \pi }^2 }} \nonumber \\&\quad = \frac{ \big (-1+ {\hat{m}_l^2}/{2}\big )( |A_{0}^0|^2 + |A_{0}^1|^2 + |A_{||}^1|^2 + |A_{\perp }^1|^2 ) + \frac{3}{2} \hat{m}_l^2 (|A_{t}^1|^2 + |A_{t}^0|^2 )}{ {\mathrm{d}^2\Gamma }/{\mathrm{d}q^2\mathrm{d}m_{\pi \pi }^2 }},\nonumber \\ \end{aligned}$$

(67)

and we show the numerical results in Fig. 9.

3.6 Theoretical uncertainties

Before closing this section, we will briefly discuss the theoretical uncertainties in this analysis. The parametric errors in heavy-to-light transition form factors and QCD condensate parameter $B_0$ have been included in the above. As one can see, these uncertainties are sizable to branching fractions and other related observables, but are negligible in the ratios like $R_{\pi \pi }^{\mu /e}$. This is understandable, since most uncertainties will cancel in the ratio.

For the heavy-to-light form factors, we have used the LCSR and LFQM results. In LCSR, the theoretical accuracy for most form factors is at leading order in $\alpha _s$. An analysis of $B_s\rightarrow f_0$ [26] has indicated the NLO radiative corrections to form factors may reach $20\%$. The radiative corrections are, in general, channel-dependent but should be calculated in a high precision study. It should be pointed out that radiative corrections in the light-front quark model is not controllable.

A third type of uncertainties resides in the scalar $\pi \pi$ form factor. In this work, we have used the unitarized results from Refs. [44, 45], where the low-energy constants ($L_i$s) are obtained by fitting the $J/\psi$ decay data. A Muskhelishvili–Omnès formalism has been developed for the scalar $\pi \pi$ form factor in Ref. [18]. Compared to the results in Ref. [18], we find an overall agreement in the shape of the non-strange $\pi \pi$ form factor, but the modulus from Ref. [18] is about $20\%$ larger. This would induce about $40\%$ uncertainties to the branching ratios of the $D\rightarrow \pi \pi \ell \bar{\nu }_\ell$, while the results for the ratio observables are not affected.

Finally, the Watson theorem does not always guarantee the use of Eq. (9), the matching of $D\rightarrow \pi \pi$ form factor and $D\rightarrow f_0$ form factors. As we have discussed in Sect. 2, such an approximation might be improved in the future.

4 Conclusions

In summary, we have presented a theoretical analysis of the $D^-\rightarrow \pi ^+\pi ^- \ell \bar{\nu }$ and $\bar{D}^0\rightarrow \pi ^+\pi ^0 \ell \bar{\nu }$ decays. We have constructed a general angular distribution which can include arbitrary partial waves of $\pi \pi$. Retaining the S-wave and P-wave contributions we have studied the branching ratios, forward–backward asymmetries and a few other observables. The P-wave contribution is dominated by $\rho ^0$ resonance, and the S-wave contribution is analyzed using the unitarized chiral perturbation theory. The obtained branching fraction for $D\rightarrow \rho \ell \nu$, at the order $10^{-3}$, is consistent with the available experimental data, while the S-wave contribution is found to have a branching ratio at the order of $10^{-4}$, and this prediction can be tested by experiments like BESIII and LHCb. The BESIII collaboration has accumulated about $10^7$ events of the $D^0$ and will collect about 3 fb$^{-1}$ data at the center-of-mass $\sqrt{s}= 4.17$ GeV to produce the $D_s^+D_s^-$ [51, 52]. All these data can be used to study the charm decays into the $f_0$ mesons. In addition, sizable branching fractions also indicate a promising prospect at the ongoing LHC experiment [53], the forthcoming Super-KEKB factory [54] and the under-design Super Tau-Charm factory. Future measurements can be used to study the $\pi$–$\pi$ scattering phase shift.

Angular coefficients

In the angular distribution, the coefficients have the form

$$\begin{aligned}&I_1 = (1+\hat{m}_l^2) |A_{0}|^2 +2 \hat{m}_l^2 |A_t|^2 + (3+\hat{m}_l^2)/2(|A_{\perp }|^2 +|A_{||}|^2) \nonumber \\&I_2 = -\beta _l |A_{0}|^2+ \beta _l /2 (|A_{\perp }|^2 +|A_{||}|^2), \nonumber \\&I_3 = \beta _l (|A_{\perp }|^2-|A_{||}|^2),\quad I_4 = 2 \beta _l [\mathrm{Re}(A_{0}A_{||}^*)],\nonumber \\&I_5 =4 [\mathrm{Re}(A_{0}A_{\perp }^*) -\hat{m}_l^2 \mathrm{Re}(A_{t}A_{||}^*) ],\nonumber \\&I_6 = 4 \left[ \mathrm{Re}(A_{||}A^*_{\perp })+ \hat{m}_l^2 \mathrm{Re}(A_{t}A^*_{0})\right] ,\nonumber \\&I_7 = 4\left[ \mathrm{Im}(A_{0}A^*_{||})-\hat{m}_l^2 \mathrm{Im}(A_{t}A^*_{\perp })\right] ,\nonumber \\&I_8 = 2 \beta _l [\mathrm{Im}(A_{0}A^*_{\perp })],\quad I_9 = 2\beta _l [\mathrm{Im}(A_{\perp }A^*_{||})]. \end{aligned}$$

(A1)

Substituting the expressions for $A_i$ into the above equation, we obtain the general expressions

$$\begin{aligned}&I_1(q^2, m_{\pi \pi }^2, \theta _{\pi ^{+}})\sum _{J=0,\ldots } \bigg \{ |Y_J^0(\theta _{\pi ^{+}}, 0)|^2 \nonumber \\&\quad = \left[ (1+\hat{m}_l^2) |A^J_{0}|^2 +2 \hat{m}_l^2 |A_t^J|^2\right] \nonumber \\&\qquad + 2\sum _{ J'=J+1, \ldots } Y_J^0(\theta _{\pi ^{+}}, 0)Y_{J'}^0(\theta _{\pi ^{+}}, 0) \nonumber \\&\qquad \times \left[ \cos (\delta _{0}^J - \delta ^{J'}_{0})|A^J_{0}||A^{J'*}_{0}| \right. \nonumber \\&\qquad \left. + 2\hat{m}_l^2 \cos (\delta _{t}^J -\delta _{t}^{J'} )|A^J_t||A^{J'}_t|\right] \bigg \} \nonumber \\&\qquad + \frac{3+\hat{m}_l^2}{2} \sum _{J=1,\ldots } \bigg \{ |Y_J^{-1}(\theta _{\pi ^{+}}, 0)|^2 \left[ [|A^J_{\perp }|^2+|A^J_{||}|^2 ] \right] \nonumber \\&\qquad + \sum _{ J'=J+1, \ldots } Y_J^{-1}(\theta _{\pi ^{+}}, 0)Y_{J'}^{-1}(\theta _{\pi ^{+}}, 0)\nonumber \\&\qquad \times \left[ 2\cos (\delta _{\perp }^{J} - \delta _{\perp }^{J'})|A_{\perp }^J||A_{\perp }^{J'}| \right] \bigg \}, \end{aligned}$$

(A2)

$$\begin{aligned}&I_2(q^2, m_{\pi \pi }^2, \theta _{\pi ^{+}}) = -\beta _l \sum _{J=0,\ldots } \bigg \{ |Y_J^0|^2 |A^J_{0}(\theta _{\pi ^{+}}, 0)|^2\nonumber \\&\quad + 2 \sum _{ J'=J+1, \ldots } Y_J^0(\theta _{\pi ^{+}}, 0)Y_{J'}^0(\theta _{\pi ^{+}}, 0) \cos (\delta _{0}^J - \delta ^{J'}_{0})|A^J_{0} A^{J'}_{0}| \bigg \} \nonumber \\&\quad + \frac{1}{2}\beta _l \sum _{J=1,\ldots } \bigg \{ |Y_J^{-1}(\theta _{\pi ^{+}}, 0)|^2 (|A^J_{\perp }|^2+|A^J_{||}|^2) \nonumber \\&\quad +2\sum _{ J'=J+1} Y_J^{-1}(\theta _{\pi ^{+}}, 0)Y_{J'}^{-1}(\theta _{\pi ^{+}}, 0)\nonumber \\&\quad \times \left[ \cos (\delta _{\perp }^J - \delta ^{J'}_{\perp })|A^J_{\perp } A^{J'}_{\perp }| + \cos (\delta _{||}^J - \delta ^{J'}_{||})|A^J_{||}A^{J'}_{||}| \right] \bigg \}, \end{aligned}$$

(A3)

$$\begin{aligned}&I_3(q^2, m_{\pi \pi }^2, \theta _{\pi ^{+}}) = \beta _l \sum _{J=1,\ldots } \bigg \{ \left| Y_J^{-1}(\theta _{\pi ^{+}}, 0)\right| ^2 \nonumber \\&\quad \times \left( |A^J_{\perp }|^2-|A^J_{||}|^2\right) +2\sum _{ J'=J+1,\ldots } Y_J^{-1}(\theta _{\pi ^{+}}, 0)Y_{J'}^{-1}(\theta _{\pi ^{+}}, 0)\nonumber \\&\quad \times \left[ \cos (\delta _{\perp }^J - \delta ^{J'}_{\perp })|A^J_{\perp } A^{J'}_{\perp }| - \cos (\delta _{||}^J - \delta ^{J'}_{||})|A^J_{||}A^{J'}_{||}| \right] \bigg \}, \end{aligned}$$

(A4)

$$\begin{aligned}&I_4(q^2, m_{\pi \pi }^2, \theta _{\pi ^{+}}) =2 \beta _l \sum _{J=0, \ldots } \sum _{J'=1,\ldots } \nonumber \\&\quad \times \left[ Y_J^0(\theta _{\pi ^{+}}, 0) Y_{J'}^{-1}(\theta _{\pi ^{+}}, 0) | A^J_{0}A^{J'*}_{||} | \cos (\delta _{0}^J -\delta _{||}^{J'}) \right] , \end{aligned}$$

(A5)

$$\begin{aligned}&I_5(q^2, m_{\pi \pi }^2, \theta _{\pi ^{+}}) =4 \sum _{J=0, \ldots } \sum _{J'=1, \ldots }Y_J^0(\theta _{\pi ^{+}}, 0) Y_{J'}^{-1} (\theta _{\pi ^{+}}, 0) \nonumber \\&\quad \left[ | A^J_{0}A^{J'*}_{\perp } | \cos (\delta _{0}^J -\delta _{\perp }^{J'}) -\hat{m}_l^2 | A^J_{t}A^{J'*}_{||} | \cos (\delta _{t}^J -\delta _{||}^{J'})\right] , \end{aligned}$$

(A6)

$$\begin{aligned}&I_6(q^2, m_{\pi \pi }^2, \theta _{\pi ^{+}})= 4 \sum _{J,J'=1,\ldots } \nonumber \\&\quad \times \bigg \{ Y_J^{-1} (\theta _{\pi ^{+}}, 0)Y_{J'}^{-1} (\theta _{\pi ^{+}}, 0)| A^J_{||}A^{J'*}_{\perp } | \cos (\delta _{||}^J -\delta _{\perp }^{J'}) \bigg \} + \hat{m}_l^2 \nonumber \\&\quad \times \sum _{J,J'=0,\ldots } \bigg \{ Y_J^{0}(\theta _{\pi ^{+}}, 0) Y_{J'}^{0}(\theta _{\pi ^{+}}, 0) | A^J_{t}A^{J'*}_{0} | \cos (\delta _{t}^J -\delta _{0}^{J'}) \bigg \},\nonumber \\ \end{aligned}$$

(A7)

$$\begin{aligned}&I_7(q^2, m_{\pi \pi }^2, \theta _{\pi ^{+}}) =4 \sum _{J=0, \ldots } \sum _{J'=1, \ldots } Y_J^0(\theta _{\pi ^{+}}, 0) Y_{J'}^{-1}(\theta _{\pi ^{+}}, 0) \nonumber \\&\qquad \times \left[ | A^J_{0}A^{J'*}_{||} | \sin (\delta _{0}^J -\delta _{||}^{J'}) -\hat{m}_l^2 | A^J_{t}A^{J'*}_{\perp } | \sin (\delta _{t}^J -\delta _{\perp }^{J'})\right] , \end{aligned}$$

(A8)

$$\begin{aligned}&I_8 (q^2, m_{\pi \pi }^2, \theta _{\pi ^{+}})= 2 \beta _l \sum _{J=0, \ldots } \sum _{J'=1,\ldots } \nonumber \\&\quad \times \left[ Y_J^0 (\theta _{\pi ^{+}}, 0)Y_{J'}^{-1}(\theta _{\pi ^{+}}, 0) | A^J_{0}A^{J'*}_{\perp } | \sin (\delta _{0}^J -\delta _{\perp }^{J'}) \right] , \end{aligned}$$

(A9)

$$\begin{aligned}&I_9(q^2, m_{\pi \pi }^2, \theta _{\pi ^{+}}) = 2\beta _l \sum _{J=1, \ldots } \sum _{J'=1, \ldots } \nonumber \\&\quad \times \left[ Y_J^{-1}(\theta _{\pi ^{+}}, 0) Y_{J'}^{-1}(\theta _{\pi ^{+}}, 0) | A^J_{\perp }A^{J'*}_{||} | \sin (\delta _{\perp }^J -\delta _{||}^{J'}) \right] . \end{aligned}$$

(A10)