1 Introduction

Since the detection of invisible matter known as “Dark Matter (DM)” from the rotational curve of spiral galaxies [1,2,3], many researchers are attracted towards the nature of DM theoretically and experimentally. Bertone et al. [4] presented a piece of promising evidence that the dominating matter in the Universe is also DM. Many suggestions have been made by several authors that the constituent particles of DM and WIMPs may be the beyond-the-standard model of particles such as supersymmetric particle neutralinos [5, 6]. It is always possible that DM from galactic halo can be accreted onto compact stars like neutron stars (NS) [7, 8] and white dwarfs [9, 10]. The accretion of DM influence the late cooling rate of NS longer than 10\(^{7}\) years [7, 12]. The structure of NS was first discussed by Oppenheimer and Volkoff [11] by assuming an equation of state of the cold degenerate neutrons and determined the maximum mass of about 0.75 \(M_\odot \), however, the exact composition is yet to determine. Although, a variety of composition in NS have been made by Lattimer and Prakash [13]. Nowadays, it is well known in the literature that there are several compositions of NS like super-fluid neutrons, super-conducting protons, condensation of pions and kaons, skermions, hyperons, quark-gluon plasma etc. Witten [14] proposed that strange quark matter (SQM) such as u,  d and s quarks is the ground state of hadronic matters. The mechanism of transformation from NS to SQM is possible via leptonic weak interaction [15,16,17]. Another mechanism was also suggested by Perez-Garcia et al. [18] where WIMPs may trigger a conversion of hadronic NS matter to SQM through an external seeding mechanism. Narain et al. [19] construct a compact star model composed of fermionic DM (FDM). They have shown that the maximum mass of compact star made of FDM strongly depends on the interaction parameter. On the other hand, Bertolami and Paramos [20] considered a generalized Chaplygin gas (GCG) equation of state and predicted the condition for formation to Chaplygin dark star. It is found that the formation is possible if the sound velocity doesn’t exceed the expansion velocity.

Lopes et al. [21] have enumerated the profiles of mass-to-radius for dark matter admixed strange quark stars in the Starobinsky model of modified gravity. The structures of NSs, which are influenced by the spin polarized self-interacting DM have investigated by using the polytropic equation of state, the equation of state of spin polarized self-interacting DM and the equation of state from the rotational curves of galaxies [22, 23]. The gravitational effects of condensed DM on compact stellar objects have studied in [24, 25]. Ciarcelluti et al. [26] have focused on the existence of DM core within the NSs and very recent it is shown that the DM core of NS effects on its maximum mass, mass-radius relation and tidal deformability parameter [27]. A general class of exact interior solutions describing mixed relativistic stars containing both ordinary and dark energy (DE) in different proportions are derived by using the phantom scalar description of DE [28]. The equilibrium structure of the stellar compact objects with DM cores and formed by the admixture of generated DM and the normal nuclear matter has studied in [29, 30], respectively. Hadjimichef et al. [31] have studied a DM compact star in the framework of the pseudo-complex general relativity.

In relativistic astrophysics, the presence of a mixture of fluids, rotational motion, superfluid, superconductor, magnetic field, phase transition are the causes of anisotropic nature of the fluid configuration. Herrera and Santos [32] studied the physical consequences in celestial configuration due to anisotropy in details. Itoh [33] suggested the possible existence of stable quarks stars due to the high density of compact stars. Moreover, Bodmer [34] shown that the quarks matter with u,  d and s quarks is more stable than the nuclear matter. In the literature, there is a renowned MIT Bag Model, where quarks can be considered as free particles trapped inside the impenetrable hadronic sphere according to the quantum chromodynamics. The MIT Bag Model commands a simple linear equation of state \(p_r(r) = \frac{1}{3} \{ \rho (r)-4B_g\}\), where \(B_g\) is known as the bag constant. The physical properties of compact stars have been studied by using the MIT Bag model equation of state in [35,36,37,38].

In this article, we have considered a generalized form of the pseudo-isothermal density profile of DM and MIT-bag model type linear equation of state (EoS) to study the structural characteristics of anisotropic fluid configurations, the anisotropy nature is widely accepted in the research community because of its more realistic nature. We are presenting theoretical investigations about astrophysical stellar systems namely, neutron stars or quark stars. The presented solution is compatible with the observed masses and radii of actual compact stars such as EXO 1785-248, Vela X-1, Cen X-3, LMC X-4 and 4U 1538-52. Very recently, after the observation of the event horizon, black hole / singularity is also one of the hot spots for researchers. As a part of our paper, the solution can also represent regular singularity for the certain value of \(\gamma \). This is, in fact, a very interesting solution because solutions representing both singularity and non-singular compact star solution are very rare / few.

The content of the article has been designed as follows: we have set up the Einstein field equations for the spherically symmetric matter distribution in Sect. 2. In Sect. 3, we have determined the exact expressions of mass m(r), compactness parameter u(r), redial pressure \(p_r(r)\), transverse pressure \( p_t(r)\), anisotropic factor \(\Delta (r)\) and surface red-shift \(z_s\) with the help of a generalized form of the pseudo-isothermal density profile and linear equation of state(EoS). The Sect. 4 contains the central values of the physical parameters and restriction of an assumed constant \(\beta \). We have estimated the values of assumed constants and bag constant using boundary conditions in Sect. 5. The energy and equilibrium conditions are analyzed in Sects. 6 and 7, respectively. The stability analysis is made in Sect. 8 via three subsections: (8.1) Velocity of sound along with Causality and Stability conditions, (8.2) Stability condition with respect to the adiabatic index and (8.3) Static stability condition with the help of Harrison–Zeldovich–Novikov criterion. The Sect. 9 is about the moment of inertia and equation of state. Finally, the discussion and conclusion of our work have been made in Sect. 10 into two subsections: (10.1) Graphical aspect and (10.2) Numerical aspect.

2 Einstein’s field equations

We consider the line element to describe the interior of a static and spherically symmetric stellar configuration in Schwarzschild coordinate system as:

$$\begin{aligned} ds^{2}=-e^{\nu (r)}dt^{2}+e^{\lambda (r)}dr^{2}+r^{2}\left( d\theta ^{2}+\sin ^{2}\theta d\phi ^{2} \right) , \end{aligned}$$
(1)

where \(e^{\nu (r)},~e^{\lambda (r)} \) are called metric coefficients, functions of the radial coordinate r only.

In gravitational unit (\(G = c = 1\)), the Einstein field equations can be written as:

$$\begin{aligned} \mathcal {T}_{\mu \nu } =\frac{1}{8\pi } \left\{ \mathcal {R}_{\mu \nu }-{1\over 2}\mathcal {R}~g_{\mu \nu }\right\} , \end{aligned}$$
(2)

where \( \mathcal {R}_{\mu \nu }, ~ g_{\mu \nu }, ~ \mathcal {T}_{\mu \nu }\) and \(\mathcal {R}\) are the Ricci tensor, metric tensor, stress energy tensor and Ricci scalar, respectively.

For an anisotropic DM matter distribution the energy momentum tensor can be written as:

$$\begin{aligned} \mathcal {T}_{\mu \nu } = (\rho +p_t)U_\mu U_\nu -p_t g_{\mu \nu }+(p_r-p_t)\chi _\mu \chi _\nu , \end{aligned}$$
(3)

where \(\rho = \rho (r)\), \(p_r = p_r(r)\) and \( p_t = p_t(r)\) are stand for the energy density, radial pressure and transverse pressure of fluid sphere, respectively and \(U^\mu U_\mu = -\chi ^\mu \chi _\mu = 1,~U^\mu \chi _\mu =0\).

For the metric (1) and energy momentum tensor (3), the Einstein field Eq. (2) takes the following form:

$$\begin{aligned} \rho (r)= & {} \frac{1}{8\pi }\left\{ \frac{1-e^{-\lambda }}{r^{2}}+\frac{e^{-\lambda }\lambda '}{r} \right\} , \end{aligned}$$
(4)
$$\begin{aligned} p_{r}(r)= & {} \frac{1}{8\pi }\left\{ \frac{e^{-\lambda }-1}{r^{2}} +\frac{e^{-\lambda }\nu '}{r}\right\} , \end{aligned}$$
(5)
$$\begin{aligned} p_t(r)= & {} \frac{e^{-\lambda }}{8\pi }\left\{ \frac{\nu ''}{2}+\frac{\nu '^{2}}{4} -\frac{\nu '\lambda '}{4}+\frac{\nu '-\lambda '}{2r} \right\} . \end{aligned}$$
(6)

The anisotropic factor is defined as \(\Delta (r) = p_t(r) - p_r(r)\). The radial and transverse equation of parameters are defined as \(\omega _r(r) = p_r(r)/\rho (r)\) and \(\omega _t(r) = p_t(r)/\rho (r)\), these two are most important tools in the study of anisotropic matter configuration and they satisfy the condition \( 0<\omega _r(r),~\omega _t(r)<1\) for physical matter distribution [39].

The scalar curvature (or the Ricci scalar) for the line element(1) is given by

$$\begin{aligned} \mathcal {R}= & {} \frac{2}{r^2}-\frac{e^{-\lambda (r)}}{2r^2}\bigg [4+4r\nu ^{\prime }(r) +r^2(\nu ^{\prime }(r))^2+2r^2\nu ^{\prime \prime }(r)\nonumber \\&-r\lambda ^{\prime }(r)(4+r\nu ^{'}(r))\bigg ]. \end{aligned}$$
(7)

3 Anisotropic solutions with pseudo-isothermal density profile

We consider a couple of generalized form of the pseudo-isothermal density profile of dark matter (DM) and linear equation of state (EoS) to study the physical properties of anisotropic compact stars formed by physical DM:

$$\begin{aligned} \rho (r)= & {} a\left[ 1+\left( {r\over b}\right) ^2\right] ^{-\gamma }, \end{aligned}$$
(8)
$$\begin{aligned} p_r(r)= & {} \alpha \rho (r)-\beta , \end{aligned}$$
(9)

where a (km\(^{-2})\), b (km), \(\alpha ,~\beta \) (km\(^{-2})\) and \(\gamma \) are non-zero positive constants.

In the year 1986, Kent [40] proposed the density profile (8) for \(\gamma = 1\) and later Spano et al. [41] used this density profile for \(\gamma = 1.5\). In our study, we shall consider \(\gamma \) as a generalized parameter along with the values corresponding to the Kent density profiles. The similar form of Eq. (9) to the MIT bag model equation of state (EoS) yields the bag constant for our model is \(B_g = \frac{3}{4}\beta \).

Motivation The anisotropic compact stars are highly dense objects, which have huge curiosity to know the exact details of its internal compositions including its density profile. Therefore, we were motivated to investigate the properties of compact stars with the density profile of pseudo-isothermal DM and seek for new results. The density profile (8) is finite and monotonically decreasing in nature for positive values of \(\gamma \) within the stellar interior.

Now, the mass of stellar configuration can be obtained as:

$$\begin{aligned} m(r)=4\pi \int _0^r r'^2 \rho (r') dr'= \frac{4}{3}\pi a r^3H(r), \end{aligned}$$
(10)

where \(H(r)= {_2F_1}\left[ \frac{3}{2},\gamma ,\frac{5}{2},-\left( \frac{r}{b}\right) ^2\right] \) and \(_2F_1\) is the usual hypergeometric function, defined as

$$\begin{aligned} _2F_1 (j,~k;~l;~w) = \sum _{i=0}^\infty {(j)_i (k)_i \over (l)_i} {w^i \over i!}, \end{aligned}$$
(11)

Here \((x)_n\) is the Pochhammer symbol, which is defined as

$$\begin{aligned} (x)_i = \left\{ \begin{array}{lcl} 1 &{}\quad \text{ for } &{} i=0 \\ x(x+1)\ldots (x+i-1) &{}\quad \text{ for } &{} i>0. \end{array}\right. \end{aligned}$$
(12)

Therefore, the compactness parameter is obtained as

$$\begin{aligned} u(r)=\frac{2m(r)}{r}= \frac{8}{3}\pi a r^2H(r). \end{aligned}$$
(13)

In the Schwarzschild coordinate, we can define a metric coefficient function

$$\begin{aligned} e^{-\lambda (r)} = 1-\frac{2m(r)}{r}= 1-\frac{8}{3}\pi a r^2 H(r), \end{aligned}$$
(14)

On using Eqs. (8)–(9), we get the expression of radial pressure

$$\begin{aligned} p_r(r)= & {} a\alpha \left[ 1+\left( {r\over b}\right) ^2\right] ^{-\gamma }-\beta . \end{aligned}$$
(15)

On imposing Eqs. (14)–(15) in Eq. (5) we get

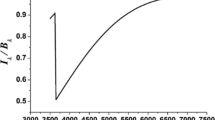
$$\begin{aligned} \nu '(r)= & {} \frac{8\pi r \left[ 3a\alpha \left( 1+\frac{r^2}{b^2}\right) ^{-\gamma }-3\beta +aH(r)\right] }{3-8a\pi r^2 H(r)}. \end{aligned}$$
(16)

One can see that the above expression for \(\nu '(r)\) is very complicated due to the presence of a hypergeometric function H(r) and therefore, finding the exact solution is impractical. For this reason, we have solved Eq. (16) numerically and provide a graphical representation for \(e^{\nu (r)}\) in Fig. 1. From Fig. 1, we can see that \(e^{\nu }\) and \(e^{-\lambda }\) meet at the surface showing the boundary is matched.

Fig. 1
figure 1

\(e^{\nu (r)}\) and \(e^{-\lambda (r)}\) are plotted with respect to the radial coordinate r for the compact star EXO 1785-248 corresponding to values of constants given in Table 2

Full size image
Fig. 2
figure 2

The energy density is plotted with respect to the radial coordinate r for the compact star EXO 1785-248 corresponding to values of constants given in Table 2

Full size image
Fig. 3
figure 3

The radial and transverse pressures are plotted with respect to the radial coordinate r for the compact star EXO 1785-248 corresponding to values of constants given in Table 2

Full size image

The expressions for transverse pressure and anisotropic factor are obtained in the following forms:

$$\begin{aligned} p_t(r)= & {} \left( 1+\frac{r^2}{b^2}\right) ^{-2\gamma }\bigg [3a\chi _{1}-3 \beta (r^2+b^2)\nonumber \\&\times \,(2\pi \beta r^2-1)-2a\pi r^2H(r)\chi _{2}-6\pi \chi _{3}\bigg ]\nonumber \\&\times \,\bigg [(r^2+b^2)(8\pi ar^2 H(r)-3)\bigg ]^{-1}, \end{aligned}$$
(17)
$$\begin{aligned} \Delta (r)= & {} \left( 1+\frac{r^2}{b^2}\right) ^{-2\gamma }\bigg [3a\chi _{1} -3\beta (r^2+b^2)\nonumber \\&\times \,(2\pi \beta r^2-1)-2a\pi r^2H(r)\chi _{2}-6\pi \chi _{3}\bigg ]\nonumber \\&\times \,\bigg [(r^2+b^2)(8\pi ar^2 H(r)-3)\bigg ]^{-1}+\beta \nonumber \\&-\,a\alpha \left[ 1+\left( {r\over b}\right) ^2\right] ^{-\gamma }, \end{aligned}$$
(18)

whereas

$$\begin{aligned} \chi _{1}= & {} \left( 1+\frac{r^2}{b^2}\right) ^{\gamma }[(r^2+b^2)\{2\pi \beta r^2(1+2\alpha )-\alpha \}\nonumber \\&+\alpha \gamma r^2],\nonumber \\ \chi _{2}= & {} \left( 1+\frac{r^2}{b^2}\right) ^{\gamma }\bigg [4a\alpha \gamma r^2+a(1-3\alpha )(r^2+b^2)\nonumber \\&+3\beta (r^2+b^2)\left( 1+\frac{r^2}{b^2}\right) ^{\gamma }\bigg ],\nonumber \\ \chi _{3}= & {} \alpha (1+\alpha )a^2r^2(r^2+b^2). \end{aligned}$$
(19)

The exact behaviors of density, radial and transverse pressures, equation of state parameters and anisotropy are shown in Figs. 2, 3, 4, 5, 6 corresponding to \(\gamma =\)1, 1.1, 1.2, 1.3, 1.4 respectively. We have used these values of \(\gamma \) for all graphical representations of our solutions. The density is positive, maximum at the centre and decreasing towards the surface of the fluid sphere (see Fig. 2). The radial pressure and transverse pressure both are positive and maximum at the center. Moreover, the radial pressure is decreasing towards the surface of compact star and vanishes at the surface, clear from Fig. 3. Figure 5 indicates that the anisotropic factor is positive for our solutions. Both the equations of state parameters are within the required region \(0< \omega _r(r), \omega _t{r} < 1\), Fig. 4. Also, the behaviors of mass function and compactness parameter are shown in Fig. 6. The parameter \(\eta (r) = \frac{p_r(r)}{p_t(r)}\) is an important parameter and with respect to \(\eta (r)\) we can analyzed the effects of the presence of anisotropy in equilibrium configurations as similar of Newtonian treatment. we have shown the variation of \(\eta (r)\) in Fig. 7, which represents that the anisotropic force is positive throughout the fluid sphere i.e. outward directed as similar to the result in Fig. 5. The graphical representation of scalar curvature for our solution is shown in Fig. 8 and it shows that the scalar curvature as required is positive and monotonically decreasing in nature against the radial coordinate r. We, therefore, can say that all the physical parameters involved in our solutions are physically well-behaved.

Fig. 4
figure 4

The equation of state parameters are plotted with respect to the radial coordinate r for the compact star EXO 1785-248 corresponding to values of constants given in Table 2

Full size image
Fig. 5
figure 5

The anisotropic factor is plotted with respect to the radial coordinate r for the compact star EXO 1785-248 corresponding to values of constants given in Table 2

Full size image

The expression for surface red-shift is given as

$$\begin{aligned} z_s= e^\frac{\lambda (R)}{2}-1=\left\{ 1-\frac{8}{3}\pi a R^2H(R)\right\} ^{-\frac{1}{2}}-1. \end{aligned}$$
(20)

The numerical value of surface red-shift is given in Table 3, which is constant for each considered compact star i.e. independent of \(\gamma \).

Fig. 6
figure 6

The mass and compactness parameter are plotted with respect to the radial coordinate r for the compact star EXO 1785-248 corresponding to values of constants given in Table 2

Full size image
Fig. 7
figure 7

The parameter \(\eta (r)\) is plotted with respect to the radial coordinate r for the compact star EXO 1785-248 corresponding to values of constants given in Table 2

Full size image
Fig. 8
figure 8

The scalar curvature is plotted with respect to the radial coordinate r for the compact star EXO 1785-248 corresponding to values of constants given in Table 2

Full size image

4 Values of physical parameters at the center

The central values of energy density and pressures must be positively finite for ensuring the physical acceptability of the solutions. For our solutions, the central values of density and pressures are obtained as:

$$\begin{aligned} \rho _c= & {} a >0, \end{aligned}$$
(21)
$$\begin{aligned} p_{rc}= & {} p_{tc} = a\alpha -\beta > 0. \end{aligned}$$
(22)

For satisfying the Zeldovich’s criterion by any physical fluid [42], we can get \(p_{rc}/ \rho _c \le 1\), which implies

$$\begin{aligned} \beta \ge {a(\alpha -1)}, \end{aligned}$$
(23)

Therefore, Eqs. (22) and (23) simultaneously yield a boundary representing constraint on \(\beta \) in the following form:

$$\begin{aligned} {a(\alpha -1)} \le \beta < {a\alpha }. \end{aligned}$$
(24)

5 Determination of constants using boundary conditions

For obtain the values of important assumed constants, we match our interior solutions with the exterior Schwarzschild solutions at the surface \(r = R\) of the fluid sphere. The exterior Schwarzschild solutions given by

$$\begin{aligned} ds^{2}= & {} -\left( 1-\frac{2M}{r}\right) dt^{2}+\left( 1-\frac{2M}{r}\right) ^{-1}dr^{2} \nonumber \\&+r^{2}\big (d\theta ^{2}+\sin ^{2}\theta d\phi ^{2} \big ), \end{aligned}$$
(25)

where the surface radius R must be greater than 2M to avoiding the singularity.

Therefore, the continuous behavior of metric coefficient at the surface \(r = R\) of fluid sphere yields the following equation:

$$\begin{aligned} e^{-\lambda (R)} = \left( 1-\frac{2M}{R}\right) , \end{aligned}$$
(26)

Further, the radial pressure vanishes at the surface, which implies

$$\begin{aligned} a\alpha \left[ 1+\left( {R\over b}\right) ^2\right] ^{-\gamma }-\beta = 0, \end{aligned}$$
(27)

On using the boundary conditions (26)–(27), we get the values of a and \(\alpha \) in terms of \(\beta \), b, \(\gamma \) and the radius R and mass M of compact star as:

$$\begin{aligned} a= & {} \frac{3M}{4\pi R^3 H(R)}, \end{aligned}$$
(28)
$$\begin{aligned} \alpha= & {} {\beta \over a} \left( 1+\frac{R^2}{b^2}\right) ^{\gamma } \end{aligned}$$
(29)

and we know that \(\beta =4B_g/3\). To design a realistic EoS, we chose the widely acceptable value of \(B_g\) as 60  MeV/fm\(^3\) and b as per physical validity.

6 Energy conditions

The physical mass distribution must satisfy all the energy conditions within its interior accordingly. The energy conditions are (i) Null energy condition (NEC), (ii) Weak energy condition (WEC) and (iii) Strong energy condition (SEC). All these energy conditions can be presented by following inequalities [43, 44]:

$$\begin{aligned} \text {NEC}_r&{:} \rho (r)-p_r(r) \ge 0,\nonumber \\ \text {NEC}_t&{:} \rho (r)-p_t(r) \ge 0,\nonumber \\ \text {WEC}_r&{:} \rho (r) \ge 0,~\rho (r)-p_r(r) \ge 0,\nonumber \\ \text {WEC}_t&{:} \rho (r) \ge 0,~\rho (r)-p_t(r) \ge 0,\nonumber \\ \text {SEC}&{:} \rho (r)-p_r(r)-2p_t(r) \ge 0. \end{aligned}$$
(30)

The graphical representations of L.H.Ss of all the above inequalities are shown in Fig. 9. From Fig. 9 along with Fig. 2 we can see that our solutions satisfy all the mentioned energy conditions within the stellar interior. Consequently, our solutions represent the DM configuration, which is also physical in nature.

7 Equilibrium analysis

Here, we are going to verify the equilibrium condition of the matter configuration represented by our solutions. Any anisotropic celestial fluid distribution is in equilibrium position under the action of three different forces, which are gravitational force, hydrostatics force and anisotropic force. The equilibrium position of any fluid configuration can be analyzed by satisfying the generalized Tolman–Oppenheimer–Volkoff (TOV) equation. The generalized TOV equation is of the following form:

$$\begin{aligned} -\frac{M_g(r)(\rho +p_r)}{r}e^{\{\nu (r)-\lambda (r)\}/ 2}-\frac{dp_r}{dr}+\frac{2}{r}(p_t-p_r)=0, \end{aligned}$$
(31)

where \(M_g(r) \) stands for the gravitational mass of the fluid sphere of radius r. The exact form of \(M_g(r) \) can be derived with the help of the Tolman-Whittaker formula and the Einstein field equations and it is defined as

$$\begin{aligned} M_g(r)= & {} 4 \pi \int _0^r r^2 e^{\nu +\lambda \over 2}\big (T^t_t-T^r_r-T^\theta _\theta -T^\phi _\phi \big ) dr, \end{aligned}$$
(32)

On using Eqs. (4)–(6), the expression for gravitational mass \(M_g(r) \) becomes in the following form:

$$\begin{aligned} M_g(r)=\frac{1}{2}re^{(\lambda -\nu )/2}~\nu '. \end{aligned}$$
(33)
Fig. 9
figure 9

The energy conditions are plotted with respect to the radial coordinate r for the compact star EXO 1785-248 corresponding to values of constants given in Table 2

Full size image

Plugging the value of \(M_g(r)\) in Eq. (31), the TOV equation reduces as

$$\begin{aligned} -\frac{\nu '}{2}(\rho +p_r)-\frac{dp_r}{dr}+\frac{2}{r}(p_t-p_r)=0. \end{aligned}$$
(34)

The above equation can be written as

$$\begin{aligned} F_g(r)+F_h(r)+F_a(r)=0, \end{aligned}$$
(35)

where

$$\begin{aligned} F_g(r)= & {} -\frac{\nu '}{2}(\rho +p_r),~\text {is called gravitational force,}\\ F_h(r)= & {} -\frac{dp_r}{dr},~\text {is called hydrostatics force,}\\ F_a(r)= & {} {2\Delta \over r},~\text {is called anisotropic force.} \end{aligned}$$

For our solutions, the closed forms of these three forces are obtained as:

$$\begin{aligned} F_g(r)= & {} 4\pi r \left( 1+\frac{r^2}{b^2}\right) ^{-2\gamma }(a+a\alpha -\beta )\bigg [3a\alpha \nonumber \\&+\left( 1+\frac{r^2}{b^2}\right) ^{\gamma }(aH(r)-3\beta )\bigg ]\nonumber \\&\times \, \big [8\pi ar^2 H(r)-3\big ]^{-1},\nonumber \\ F_h(r)= & {} \frac{2a\alpha \gamma r}{b^2}\left( 1+\frac{r^2}{b^2}\right) ^{-1-\gamma }, \end{aligned}$$
(36)
$$\begin{aligned} F_a(r)= & {} 2r\left( 1+\frac{r^2}{b^2}\right) ^{-2\gamma } \Big [6\pi a^2\alpha (1+\alpha )(r^2+b^2) \nonumber \\&+6\pi F_1-3aF_2+2 H(r)F_3 \Big ] \end{aligned}$$
(37)
$$\begin{aligned}&\times \Big [(r^2+b^2)(3-8\pi ar^2H(r))\Big ]^{-1}. \end{aligned}$$
(38)

whereas

$$\begin{aligned} F_1= & {} \beta ^2(r^2+b^2)\left( 1+\frac{r^2}{b^2}\right) ^{2\gamma },\nonumber \\ F_2= & {} \left( 1+\frac{r^2}{b^2}\right) ^{\gamma }\{2\pi (1+2\alpha )\beta (r^2+b^2)+\alpha \gamma \},\nonumber \\ F_3= & {} a\pi \left( 1+\frac{r^2}{b^2}\right) ^{\gamma }\bigg [a(1+\alpha )(r^2+b^2)+4a\alpha \gamma r^2\nonumber \\&-\beta (r^2+b^2)\left( 1+\frac{r^2}{b^2}\right) \bigg ]. \end{aligned}$$
(39)

Figure 10 shows that the mass distribution represented by our solutions is in equilibrium state by satisfying the TOV equation.

Fig. 10
figure 10

The acting forces are plotted with respect to the radial coordinate r for the compact star EXO 1785-248 corresponding to values of constants given in Table 2

Full size image

8 Stability analysis

Here we shall focus on the stability analysis for our model via stability factor, adiabatic index and Harrison–Zeldovich–Novikov’s static stability condition.

8.1 Velocity of sound

\(\bullet \) The causality condition: The causality condition states that whenever sound passes through within a physical compact star then its radial and transverse velocities must be less than the velocity of light, the maximum velocity in GTR. Otherwise, matter configuration will not be physical. The square of radial velocity \(\{v_{r}(r)\}^{2}\) and transverse velocity \(\{v_{t}(r)\}^{2}\) of sound can be determined by using the following formulae:

$$\begin{aligned} v_{r}^{2} = {dp_r(r) \over d\rho (r)}=\alpha ,~~v_{t}^{2} = {dp_t(r) \over d\rho (r)}. \end{aligned}$$
(40)

Therefore, the causality condition can be describe as \(0 \le v_r(r) = \sqrt{{dp_r(r)\over d\rho (r)}} < 1\) and \(0 \le v_t(r) = \sqrt{{dp_t(r) \over d\rho (r)}} < 1\) for physical matter distribution.

Our solutions satisfy the causality condition (see Fig. 11) i.e. our model is of physical matter distribution.

\(\bullet \) The stability condition: To study the stability of an anisotropic stellar fluid L. Herrera [45] proposed proposed the cracking method under the radial perturbations and using the cracking concept Abreu et al. [46] provided the conditions with respect to the stability factor \([\{v_t(r)\}^2 - \{v_r(r)\}^2]\) for an anisotropic fluid model. The stability condition described in the following manner:

The region is potentially stable if \(-1<\{v_t(r)\}^2 - \{v_r(r)\}^2< 0\) and the region is potentially unstable if \(0< \{v_t(r)\}^2 - \{v_r(r)\}^2 < 1\). The bounded region of mass distribution represented by our solutions is potentially stable, clear from Fig. 12.

Fig. 11
figure 11

The sound speeds are plotted with respect to the radial coordinate r for the compact star EXO 1785-248 corresponding to values of constants given in Table 2

Full size image
Fig. 12
figure 12

The stability factor is plotted with respect to the radial coordinate r for the compact star EXO 1785-248 corresponding to values of constants given in Table 2

Full size image

8.2 Adiabatic index

The relativistic adiabatic indices are defined as the ratio of two specific heats. The adiabatic indices are also important parameters that affect the stability of any stellar object. The relativistic adiabatic indices are defined as [47]:

$$\begin{aligned} \Gamma _r(r)= & {} \frac{\rho (r)+p_r(r)}{p_r(r)} ~ \frac{dp_r(r)}{d\rho (r)}, \end{aligned}$$
(41)
$$\begin{aligned} \Gamma _t(r)= & {} \frac{\rho (r)+p_t(r)}{p_t(r)} ~\frac{dp_t(r)}{d\rho (r)}. \end{aligned}$$
(42)

For a stable Newtonian sphere \(\Gamma _r(r)>4/3\) and \(\Gamma _r(r) =4/3\) is the condition for a neutral equilibrium proposed by Bondi [48]. This condition changes for a relativistic isotropic sphere due to the regenerative effect of pressure, which renders the sphere more unstable.

The value of adiabatic index \(\Gamma _r(r)\) is more than 4/3 for our solutions, shown in Fig. 13 and hence stable.

Fig. 13
figure 13

The adiabatic indexes are plotted with respect to the radial coordinate r for the compact star EXO 1785-248 corresponding to values of constants given in Table 2

Full size image

8.3 Harrison–Zeldovich–Novikov’s static stability condition

Harrison et al. [49] and Zeldovich–Novikov [42] proposed that any fluid configuration is stable if the mass and surface radius of star are increasing with respect to the central density i.e. \(\frac{\partial M(\rho _c)}{\partial \rho _c} > 0\) and \(\frac{\partial R(\rho _c)}{\partial \rho _c} > 0\), whereas the mass and surface radius of star are decreasing with respect to the central density i.e. \(\frac{\partial M(\rho _c)}{\partial \rho _c} < 0\) and \(\frac{\partial R(\rho _c)}{\partial \rho _c} < 0\) for unstable fluid configuration.

For our model, the mass and surface radius are obtained as the function of central density in following forms

$$\begin{aligned} M(\rho _c)= & {} \frac{4}{3}\pi \rho _c R^3H(R), \end{aligned}$$
(43)
$$\begin{aligned} R(\rho _c)= & {} b\left[ \left( \frac{\alpha \rho _c}{\beta }\right) ^\frac{1}{\gamma }-1\right] ^\frac{1}{2}, \end{aligned}$$
(44)

Therefore

$$\begin{aligned} {\partial M (\rho _c) \over \partial \rho _c}= & {} \frac{4}{3}\pi R^3H(R) >0, \end{aligned}$$
(45)
$$\begin{aligned} {\partial R (\rho _c) \over \partial \rho _c}= & {} \frac{b}{2\gamma \rho _c}\left( \frac{\alpha \rho _c}{\beta }\right) ^\frac{1}{\gamma }\left[ \left( \frac{\alpha \rho _c}{\beta }\right) ^\frac{1}{\gamma }-1\right] ^{-\frac{1}{2}} \nonumber \\> & {} 0. \end{aligned}$$
(46)

The mass \(M(\rho _c)\) and radius \(R(\rho _c)\) are increasing with respect to the central density \(\rho _c\) (see Figs. 14, 15) i.e. \(\frac{\partial M(\rho _c)}{\partial \rho _c} > 0\) and \(\frac{\partial R(\rho _c)}{\partial \rho _c} > 0\), which ensure that our presented stellar configuration is stable under the static stability criterion.

Fig. 14
figure 14

The mass function is plotted with respect to the central density \(\rho _c\) for the compact star EXO 1785-248 corresponding to values of constants given in Table 2

Full size image
Fig. 15
figure 15

The surface radius is plotted with respect to the central density \(\rho _c\) for the compact star EXO 1785-248 corresponding to values of constants given in Table 2

Full size image
Fig. 16
figure 16

The moment of inertia is plotted with respect to the mass M for \(b=12.55\) km and \(B_g=60\) MeV/fm\(^3\). The red dot represents \(\big (M,I_{max}\big )\) and black dot \(\big (M_{max},I\big )\)

Full size image

9 Moment of inertia and equation of state

For a uniformly rotating star with angular velocity \(\Omega \), the moment of inertia is given by Lattimer and Prakash [13]

$$\begin{aligned} I = {8\pi \over 3} \int _0^R r^4 (\rho +p_r) e^{(\lambda -\nu )/2} ~{\bar{\omega } \over \Omega }~dr \end{aligned}$$
(47)

where, the rotational drag \(\bar{\omega }\) satisfy the Hartle’s equation [50]

$$\begin{aligned} {d \over dr} \left( r^4 j ~{d\bar{\omega } \over dr} \right) =-4r^3\bar{\omega }~ {dj \over dr} . \end{aligned}$$
(48)

with \(j=e^{-(\lambda +\nu )/2}\) which has boundary value \(j(R)=1\). The approximate solution of moment of inertia I up to the maximum mass \(M_{max}\) was given by Bejger and Haensel [51] as

$$\begin{aligned} I = {2 \over 5} \Big (1+x\Big ) {MR^2}, \end{aligned}$$
(49)

where parameter \(x = (M/R)\cdot \mathrm{km}/M_\odot \). For the solutions we have plotted mass vs I in Fig. 16, that shows as \(\gamma \) increases, the mass also increase and the moment of inertia increases till up to certain value of mass and then decreases. Comparing Figs. 16 and 17, the mass corresponding to \(I_{max}\) is not equal to \(M_{max}\) from M–R diagram. In fact the mass corresponding to \(I_{max}\) is lower by few percent from the \(M_{max}\). This happens to the EoSs without any strong high-density softening due to hyperonization or phase transition to an exotic state [52]. Using this graph we can estimate the maximum moment of inertia for a particular compact star or by matching the observed I with the \(I_{\max }\) we can determine the validity of a model.

Fig. 17
figure 17

The mass is potted with respect to the surface radius R for the compact star EXO 1785-248 corresponding to values of constants given in Table 2

Full size image
Fig. 18
figure 18

The static mass and rotating mass are plotted with respect to the surface radius R for the compact star EXO 1785-248 corresponding to \(b=12.55\) km and \(B_g=60\) MeV/fm\(^3\)

Full size image

A rotating compact star can hold higher \(M_{max}\) than non-rotating one. The mass relationship between static and rotating is given by (in the unit \(G=C=1\)) [53]

$$\begin{aligned} M_{rot} = M_{stat}+{1 \over 2}I\Omega ^2. \end{aligned}$$
(50)

Due to centrifugal force, the radius at the equator increases as some factor as compare to the static one. Cheng and Harko [54] find out the approximate radius formulas for static and rotating stars as \(R_{rot}/R_{stat} \approx 1.626\). Assuming the compact star is rotating in Kepler frequency \(\Omega _K=(GM_{stat}/R^3_{stat})^{1/2}\) and on using the Cheng-Harko formula we have plotted the M–R for rotating and non-rotating (Fig. 18).

10 Discussions and conclusion

In this article, we have presented a unique anisotropic dark matter (DM) compact stars model. The interior solutions are determined by solving Einstein’s field equations using the general form of the pseudo-isothermal density profile of DM and linear equation of state (EoS). To analyze our obtained solutions with respect to graphical representations we have considered the compact star EXO 1785-248 and throughout the paper, all the plots are drawn for that compact star. Moreover, we have demonstrated the numerical values of constants and all the physical parameters for the compact star EXO 1785-248 as well as other four well-know compact stars, namely Vela X-1, Cen X-3, LMC X-4 and 4U 1538-52 in tabular forms to compact our solutions.

Some of the key features of our solutions regarding the anisotropic stellar configuration formed by DM are as follows:

Table 1 Numerical values of masses M, radii R and average density \(\rho _{av}\) for five well-known compact stars
Full size table
Table 2 Numerical values of arbitrary assumed constants corresponding to the masses and radii of five well-known compact stars given in Table 1 with \(B_g=60\) MeV/fm\(^3\) and \(\gamma \) = 1, 1.1, 1.2, 1.3, 1.4 respectively
Full size table
Table 3 Numerical values of central density \(\rho _c\), surface density \(\rho _s\), cental pressure \(p_c\), surface redshift \(z_s\) and surface compactness parameter \(u_s\) for five well-known compact stars corresponding to \(B_g=60\) MeV/fm\(^3\) and \(\gamma = 1, 1.1, 1.2, 1.3\) and 1.4, respectively (From above to below)
Full size table

10.1 Graphical aspect

  • The energy density is positively finite within the star, monotonically decreasing in nature and free from the singularity, shown in Fig. 2. The value of scalar curvature is finite i.e. the solution is non-singular and as expected it is monotonic decreasing in nature (Fig. 8).

  • From the profiles of radial and transverse pressures in Fig. 3 we have found that the pressures are positive, finite within the star. The radial pressure is decreasing in nature against the radial coordinate r and vanishes at the surface. Moreover, \(p_r(r) = p_t(r)\) at the centre of the stellar object whereas \(p_t(r) - p_r(r) > 0\) i.e. the anisotropic factor is positive and increasing in \(0 < r \le R \) (see Fig. 5) and hence the force \(\frac{2\Delta (r)}{r}\) due to anisotropy is pointing outward (see Fig. 10) i.e. able to construct more compact object. Also, the Fig. 4 indicates that the equation of state parameters are in \(0 \le \omega _r(r), \omega _t(r)\le 1\), which suggests that our solutions representing matter distribution is physical.

  • The profiles of mass function (Fig. 6) suggest that it is regular, positive and monotonically increasing in nature. The compactness parameter is positive and increasing in nature (see Fig. 6). Also, the compactness parameter for our presented solutions satisfied the Buchdahl condition, (See Table 2).

  • All the energy conditions are satisfied by our solutions (see Fig. 9) i.e. our solutions represent the physically possible matter configuration.

  • The final state of any anisotropic compact star always is in equilibrium state by satisfying the general Tolman–Oppenheimer–Volkoff (TOV) equation. The obtained solutions satisfied the TOV equation, clear from Fig. 10 where hydrostatic, anisotropic forces act in outward direction and gravitational force acts in inward direction. Therefore, our solutions represent equilibrium matter distribution.

  • We have analyzed the stability situation through the stability factor, adiabatic index and Harrison–Zeldovich–Novikov’s static stability condition : (a) For our model, we have \(-1< \{v_t(r)\}^2 - \{v_r(r)\}^2 < 0\) (see Fig. 12) i.e. the model is potentially stable also the causality condition hold good(see Fig. 11) (b) The obtained adiabatic index \(\Gamma _r(r)>\) \(\frac{4}{3}\) (see Fig. 13), which indicates the stable configuration. (c) The mass and surface radius of the stellar object increases with increase of the central density and hence the static stability condition hold good and also the mass of stelar configuration is proportional to its central density, obvious from Figs. 14 and 15.

  • The maximum masses resulting from the solutions with respect to the parameter \(\gamma \) are also demonstrated in Fig. 17 showing that the maximum mass increases with decrease in the value of \(\gamma \). For \(\gamma =1\), one can’t determine the maximum mass and maximum moment of inertia as there is no saturation in mass.

  • The comparative M–R graph for static and rotating configuration (see Fig. 18) signifies that the \(M_{rot}\) is slightly higher than \(M_{stat}\), however, both the maximum mass lie within \(3.2 M_{\odot }\) i.e. Rhoades–Ruffini limit [55].

10.2 Numerical aspect

We have also calculated the numerical values of central density, surface density, central pressure, compactness parameter and surface redshift in Table 3 corresponding to the numerical values of constants in Table 2 for the five well-known compact stars given in Table 1. Table 3 shows that the central and surface densities both are of order \(10^{14}\) g/cm\(^3\) for all five compact stars. Also, these values are well-fitted with the average density given in Table 1. The numerical values of central pressure are of order \(10^{34}\) dyne/cm\(^2\) for all five compact stars corresponding to \(\gamma =\)1, 1.1, 1.2, 1.4 and 1.4 (see Table 3). The values of surface redshift \(z_s=z(r=R)\) is independent of \(\gamma =\) as it depends only on M and R. Further, all the values of \(z_s\) are within the range suggested by the Ref. [56]. The surface values of compactness parameter \(u_s = u(r=R)=\frac{2M}{R}\) are also not dependent on \(\gamma \) for each fluid configuration. Moreover, all the values of \(u_s < \frac{8}{9}\), the Buchdahl limit [57], follows from Table 3. For \(\gamma =1\) the M–I behavior has no saturation points and therefore can’t determine the \(I_{max}\).

Finally, all these results prevail that our proposed model can be used to describe the interior of anisotropic stellar fluid sphere.