1 Introduction

In 1975 Hawking [1] predicted that semi classically black holes can also radiate particles, which is known as the Hawking effect. The Hawking effect is one of the most remarkable results of quantum field theory in curved spacetime, considered to be the cornerstone in understanding the black hole thermodynamics [2,3,4]. Usually Hawking effect is understood using Bogoliubov transformation between ingoing and outgoing field modes, which are described in terms of the null coordinates. Therefore, to provide a Hamiltonian based derivation of the Hawking effect one faces the basic hurdle that these null coordinates do not account for the dynamics of the spacetime and the construction of a non trivial field Hamiltonian is not possible using these coordinates. To overcome this difficulty in our previous work [5] we have introduced a set of near-null coordinates which possess spacelike and timelike properties, and enables one to formulate the Hamiltonians for the study of the Hawking effect.

It is believed that inclusion of extra spatial dimensions in a spacetime have the potential of solving the hierarchy problem [6,7,8,9,10,11], which is related to the issue concerning the huge difference between the gravitational scale and Electro-Weak scale. Although experimental observation of the higher dimensional microscopic black holes are not yet verified in the latest state of the art particle colliders (LHC), these black holes remain interesting arenas to venture in for their enthralling properties coming from the extra dimensions.

In this work we are going to consider a n-dimensional spherically symmetric static black hole spacetime, which is a higher dimensional generalization for the usual Schwarzschild black hole, better known as the Schwarzschild–Tangherlini [12] spacetime. Then we have considered scalar field both in the Bulk and in 3-brane. The introduction of extra spatial dimensions changes the linear relation between the radius of the event horizon and the mass of the black hole, and it also has a signature in the surface gravity of the event horizon. Then the temperature corresponding to the Hawking effect gets modified. In this work we are going to provide a Hamiltonian based derivation of the Hawking effect in this n-dimensional Schwarzschild–Tangherlini black hole spacetime using the near-null coordinates [5, 13, 14].

Furthermore, the spectrum of the Hawking radiation as seen by an asymptotic observer is not a complete black body distribution and it is properly described by a greybody distribution. The greybody factor is obtained from the transmission amplitude as the field modes pass from near horizon region to an asymptotic observer through the effective potential, created due to the spacetime geometry. Estimation of this greybody factor is a very difficult job and often utilises various approximations like evaluating the greybody factors particularly in asymptotically low or high frequency regimes [15,16,17,18,19,20,21,22,23]. Sometimes, one is forced to take the extremal limit to evaluate these quantities [24,25,26]. Otherwise, one can take numerical approaches to estimate these greybody factors [18, 27,28,29,30,31,32,33]. On the other hand one can also evaluate the bounds on these greybody factors [34,35,36], which have the advantages of providing analytical results even for intermediate frequency regimes and for all angular momentums [37,38,39,40,41,42,43]. We are going to estimate this bound on the greybody factor for scalar fields both in the bulk and in 3-brane of the Schwarzschild–Tangherlini black hole spacetime. It is generally believed that for large number of extra dimensions, most of the energy corresponding to the Hawking effect is radiated in the brane [27, 44, 45]. We intend to verify this phenomena from the bound on the greybody factors and also understand the dependence of this bound on the spacetime dimensionality n [46].

In Sect. 2 we start with an introduction to the Schwarzschild–Tangherlini black hole spacetime. Then we consider a massless minimally coupled free scalar field both in the bulk and also in the 3-brane of the higher dimensional spacetime. It is observed that the field equation in the bulk is separable in terms of the radial and angular coordinates using the higher dimensional spherical harmonics on \((n-2)\)-dimensional sphere. We also notice that both the bulk and brane scalar field action can be transformed to a \((1+1)\) dimensional reduced form. In the subsequent Sect. 3 we first define the near-null coordinates and then using these coordinates provide the formulation for the canonical derivation of the Hawking effect. In Sect. 4 we give a Hamiltonian based derivation of the Hawking effect in the Schwarzschild–Tangherlini black hole spacetime. In the subsequent Sect. 5 we evaluate the bounds on the greybody factor, and discuss the results in Sect. 6.

2 Schwarzschild–Tangherlini black hole spacetime

Higher dimensional black holes have their own relevance in brane world models and string theory where large extra spatial dimensions can exist, [24, 47,48,49,50]. The statistical counting of entropy was first provided in string theory for a 5-dimensional black hole [51]. In this section we are going to discuss the Schwarzschild–Tangherlini (ST) black hole spacetime [12], which is a higher dimensional generalization of the \((3+1)\)-dimensional Schwarzschild black holes.

2.1 Metric and horizon of the ST black hole

The generalization of the four dimensional Schwarzschild black holes to higher dimensions, say n-dimensions, is described by the Schwarzschild–Tangherlini line-element [9, 27, 38, 52,53,54,55,56], given by

$$\begin{aligned} ds^2 = -f(r)dt^2 + \frac{1}{f(r)}dr^2 + r^2 d\varOmega ^2_{n-2}, \end{aligned}$$
(1)

which satisfies the n-dimensional vacuum Einstein’s equations. Here \(d\varOmega ^2_{n-2}\) denotes the metric on a \((n-2)\)-dimensional unit sphere. The function f(r) is given by

$$\begin{aligned} f(r) = 1-\left( \frac{r_H}{r}\right) ^{n-3}, \end{aligned}$$
(2)

where

$$\begin{aligned} r_H= \left[ \frac{16GM}{(n-2){\tilde{\eta }}_{n-2}}\right] ^{\frac{1}{n-3}};\quad {\tilde{\eta }}_{n-2} = \frac{2\pi ^{\frac{n-1}{2}}}{\varGamma \left( \frac{n-1}{2}\right) }, \end{aligned}$$
(3)

and \(G=1/M_{Pl}^{n-2}\) is the \((n-2)\) dimensional Newton constant. Here \({\tilde{\eta }}_{n-2}\) denotes the volume of the unit \((n-2)\) dimensional sphere. We note that \(r=r_H\) describes the position of the event horizon. From Eqs. (1) and (2) we also observe that when \(n=4\) the metric reduces to the \(4-\)dimensional Schwarzschild metric. On the other hand from Eq.(3) we notice that the radius of the event horizon is not linearly related to the mass of the black hole for \(n>4\).

The metric on the 3-brane is obtained by fixing the angular coordinates, which represent the excess dimensions in addition to the \((3+1)\)-dimensional spacetime. In our case we have fixed the coordinates \(\theta _{i}=\pi /2\) with i from 1 to \((n-4)\). The line element on the brane is expressed as

$$\begin{aligned} ds^2 = -f(r)dt^2 + \frac{1}{f(r)}dr^2 + r^2 d\varOmega ^2_{2}, \end{aligned}$$
(4)

where \(d\varOmega ^2_{2}\) denotes the line element on a unit two sphere, with f(r) and \(r_H\) given by the same previous expressions. In ST black hole spacetime the tortoise coordinate \(r_{\star }\) is obtained from

$$\begin{aligned} \frac{dr_{\star }}{dr}= & {} \frac{1}{f(r)}\nonumber \\ ~= & {} \frac{n-2}{2(n-3)} + \frac{r_H}{(n-3)(r-r_H)} + g'(r-r_H), \end{aligned}$$
(5)

where \(g'(r-r_H)\) is a polynomial function of \((r-r_H)\) such that \(g'(0)=0\) and it is assumed to represent the derivative of \(g(r-r_H)\) with respect to r. Then with suitable choice of integration constant the tortoise coordinate becomes

$$\begin{aligned} r_{\star }= \frac{n-2}{2(n-3)}r + \frac{r_H}{(n-3)}\ln {\left( \frac{r}{r_H}-1\right) } + g(r-r_H). \end{aligned}$$
(6)

The expression of the tortoise coordinate from Eq. (6) is crucial to get a relation between the spatial near-null coordinates for the two observers corresponding to the Hawking effect. Furthermore, this relation in the limit \(r\rightarrow r_H\) determines the spectrum of the Hawking effect.

2.2 Reduced scalar field action

We consider a massless minimally coupled free scalar field \(\varPhi (x)\) in n-dimensional ST black hole spacetime with the action given by

$$\begin{aligned} S_{\varPhi } = \int d^{n}x \left[ -\frac{1}{2} \sqrt{-g} g^{\mu \nu } \nabla _{\mu }\varPhi (x) \nabla _{\nu }\varPhi (x) \right] . \end{aligned}$$
(7)

We first consider the scalar field in the bulk and the corresponding line element is taken from Eq. (1). In n- dimensional spacetime the coordinates \(x^{\mu }\) are \(\left( t, r, \theta _{1},\ldots ,\theta _{n-2}\right) \) where \(0\le \theta _{n-2}\le 2\pi \) and \(0\le \theta _{i}\le \pi \), for \(i=1,\ldots ,n-3\). In ST black hole spacetime the determinant of the metric tensor g provides

$$\begin{aligned} \sqrt{-g} = r^{n-2} \sin ^{n-3}{\theta _{1}}\sin ^{n-4}{\theta _{2}}\ldots \sin {\theta _{n-3}}. \end{aligned}$$
(8)

The components of the inverse metric are \(g^{00}=-1/f(r)\), \(g^{11}=f(r)\), \(g^{22}=1/r^2\), \(g^{33}=1/\left( r^2\sin ^2{\theta _{1}}\right) \),..., \(g^{n-1,n-1}=1/\left( r^2\sin ^2{\theta _{1}}\cdots \sin ^2{\theta _{n-3}}\right) \). We assume the field decomposition \(\varPhi (x) = \sum _{l,m}{\tilde{\varphi }}_{lm}(t,r) ~ Y^{n}_{lm}(\varOmega )\), where \(Y^{n}_{lm}(\varOmega )\) is the spherical harmonics on the \((n-2)\)-dimensional sphere. Then the action from Eq. (7) becomes

$$\begin{aligned}&S_{\varPhi } = \frac{1}{2}\int dtdrd\theta _{1}\cdots d\theta _{n-2}~\sqrt{-g}\left[ \frac{1}{f}(\partial _{t}\varPhi )^2 - f(\partial _{r}\varPhi )^2\right. \nonumber \\&\qquad -\left. \frac{1}{r^2}\left\{ (\partial _{\theta _{1}}\varPhi )^2 + \frac{(\partial _{\theta _{2}}\varPhi )^2}{\sin ^2{\theta _{1}}}+\cdots +\frac{ (\partial _ { \theta _{n-2}}\varPhi )^2}{\sin ^2{ \theta _{1}} \ldots \sin ^2{ \theta _{n-3}}} \right\} \right] \nonumber \\&\qquad = \sum _{l,m}\int dtdr_{\star }~\frac{r^{n-2}}{2}\left[ (\partial _{t}{\tilde{\varphi }}_{lm})^2 - (\partial _{r_{\star }}{\tilde{\varphi }}_{lm})^2 \right. \nonumber \\&\qquad \left. +\frac{{\mathcal {A}}^{n}_{lm}}{r^2}~\tilde{ \varphi } _ { lm } ^2 \right] , \end{aligned}$$
(9)

where the angular integrals are carried out and \({\mathcal {A}}^{n}_{lm}\) is the eigen-value of the n-dimensional spherical harmonics equation [57]. We further assume \({\tilde{\varphi }}_{lm}=\varphi _{lm}(t,r)/r^{\frac{n-2}{2}}\) then the action reduces to \(S_{\varPhi } = \sum _{lm} S_{lm}\), where

$$\begin{aligned} S_{lm}= & {} \frac{1}{2}\int dtdr_{\star }\left[ (\partial _{t}\varphi _{lm})^2 - (\partial _{r_{\star }}\varphi _{lm})^2 \right. \nonumber \\ ~+ & {} \left. \frac{(n-2)f}{r}\varphi _{lm} \partial _{r_{\star }}\varphi _{lm} -\frac{f\varphi _{lm}^2}{r^2}\left\{ f\left( \tfrac{n-2}{2} \right) ^2 - {\mathcal {A}}^{n}_{lm}\right\} \right] .\nonumber \\ \end{aligned}$$
(10)

For a brane localized scalar field the line element is taken from Eq. (4) and action for the scalar field is defined by the same Eq. (7) with \(n=4\). Then performing a similar field decomposition, however this time with respect to the spherical harmonics on two sphere and \({\tilde{\varphi }}_{lm}=\varphi _{lm}(t,r)/r\), we shall obtain the action after the angular integrals are carried out, as

$$\begin{aligned} S_{lm}= & {} \frac{1}{2}\int dtdr_{\star }\left[ (\partial _{t}\varphi _{lm})^2 - (\partial _{r_{\star }}\varphi _{lm})^2 \right. \nonumber \\ ~+ & {} \left. \frac{2f}{r}\varphi _{lm} \partial _{r_{\star }}\varphi _{lm} -\frac{f\varphi _{lm}^2}{r^2}\left\{ f - {\mathcal {A}}^{4}_{lm}\right\} \right] . \end{aligned}$$
(11)

Now in the asymptotic regions, i.e. near scriminus \({\mathscr {I}}^{-}\) and scriplus \({\mathscr {I}}^{+}\) we have \(r\rightarrow \infty \), on the other hand at the event horizon \(f(r_H)=0\). Then in asymptotic regions and in regions near the horizon the above actions from Eqs. (10) and (11) simplifies to

$$\begin{aligned} S_{lm} \simeq \frac{1}{2}\int dtdr_{\star }\left[ (\partial _{t}\varphi _{lm})^2 - (\partial _{r_{\star }}\varphi _{lm})^2 \right] , \end{aligned}$$
(12)

which represents the action corresponding to a \((1+1)\) dimensional flat Minkowski spacetime. This reduction enables one to utilize the techniques of field theory from standard flat spacetime to these specific regions of the ST black hole spacetime. The ST metric is independent of time, thus the spacetime is time translation invariant and one may express the field mode \(\varphi _{lm}(t,r_{\star }) = e^{i\omega t}\psi _{lm}(r_{\star })\). Then from Eqs. (10) and (11) one can find out the corresponding equation of motions as

$$\begin{aligned} \partial ^{2}_{r_{\star }}\psi _{lm} + \left[ \omega ^2 - {\mathbb {V}}(r) \right] \psi _{lm} = 0, \end{aligned}$$
(13)

with the potential for the field in the bulk, given by

$$\begin{aligned} {\mathbb {V}}(r) = f(r)\left[ \frac{(n-2)(n-4)f(r)}{4r^2}+ \frac{(n-2)f'(r)}{2r} - \frac{{\mathcal {A}}^{n}_{lm}}{r^2} \right] ,\nonumber \\ \end{aligned}$$
(14)

and the potential for the brane localized scalar field

$$\begin{aligned} {\mathbb {V}}(r) = f(r)\left[ \frac{f'(r)}{r} - \frac{{\mathcal {A}}^{4}_{lm}}{r^2} \right] , \end{aligned}$$
(15)

where \(f'(r)\) denotes differentiation of f(r) with respect to r. We also mention that the eigen-value of the n-dimensional spherical harmonics [57, 58] is given by \({\mathcal {A}}^{n}_{lm}=-l(l+n-3)\).

2.3 Number density of Hawking quanta at \({\mathscr {I}}^{+}\)

The field equation corresponding to the action (12) has solutions given by

$$\begin{aligned} \varphi _{lm}\sim \frac{1}{\sqrt{2\pi \omega }}e^{-i\omega (t\pm r_{\star })}. \end{aligned}$$
(16)

Therefore the field modes near past null infinity, near future null infinity and near the horizon have characteristics of plane waves. In this work and as also discussed in the original work by Hawking the black hole is assumed to be formed through the collapse of matters, where the initial spacetime in the past is described by a Minkowski metric. On the other hand the final metric is denoted by respective black hole spacetime. It is generally accepted that this dynamical nature of the spacetime metric generates the notion of particle creation. However, for a derivation of the Hawking radiation it is not necessary to understand the details of the collapse. In particular, according to Hawking the Bogoliubov transformation between the modes at past null infinity \({\mathscr {I}}^{-}\) and the outgoing modes which have just escaped the creation of the black hole provide the Planckian distribution of the Hawking effect. For a massless minimally coupled free scalar field described by the action (7) the corresponding number density of Hawking quanta is

$$\begin{aligned} N_{\omega } = \frac{1}{e^{2\pi \omega /\mathrm {\varkappa }_{H}}-1}, \end{aligned}$$
(17)

where \(\mathrm {\varkappa }_{H}\) is the surface gravity at the event horizon and \(\omega \) corresponds to the frequency of the wave mode. The field modes then pass through the black hole spacetime to be observed by an asymptotic observer near future null infinity \({\mathscr {I}}^{+}\). We have seen from Eq. (13) that there is a potential barrier between the horizon and the spatial infinity at \({\mathscr {I}}^{+}\). Then because of this potential barrier, spectrum of the Hawking radiation observed at \({\mathscr {I}}^{+}\) would also get modified and the above mentioned black body distribution transforms to a Greybody distribution. The transmission probability through the potential barrier denotes the greybody factor and the number density corresponding to the Hawking quanta at \({\mathscr {I}}^{+}\) becomes

$$\begin{aligned} N_{\omega } = \frac{\varGamma \left( \omega \right) }{e^{2\pi \omega /\mathrm {\varkappa }_{H}}-1}, \end{aligned}$$
(18)

where \(\varGamma \left( \omega \right) \) denotes the greybody factor, which generally depends on the frequency \(\omega \) of the outgoing modes and on the black hole parameters.

3 Canonical formulation

Usually, the Bogoliubov transformation between ingoing and outgoing field modes, expressed in terms of the null coordinates v and u, generates the Hawking effect. However, these null coordinates do not describe the dynamics of the system, and one cannot construct true matter field Hamiltonian out of them. To overcome this difficulty we consider the recently introduced near-null coordinates [5]. Using these near-null coordinates the Hamiltonians for the two observers \({\mathbb {O}}^{-}\) and \({\mathbb {O}}^{+}\), which are located respectively near the past null infinity \({\mathscr {I}}^{-}\) and near the horizon, are formed. We mention that two different time-independent metrics correspond to the spacetimes for these two observers, with the one near the event horizon developed through the collapse of a matter shell. This dynamical nature of the spacetime, which evolves from being n-dimensional Minkowski to n-dimensional Schwarzschild, directly governs particle creation in curved spacetime. We note that in [5], the observer \({\mathbb {O}}^{+}\) was assumed to be stationed near \({\mathscr {I}}^{+}\), which was reasonable as there we did not consider the greybody factors and the spectrum of the Hawking effect near the horizon was regarded to be the spectrum seen by an asymptotic observer.

3.1 The observers \({\mathbb {O}}^{-}\) and \({\mathbb {O}}^{+}\)

3.1.1 Near-null coordinates

Here we define a set of near-null coordinates by slightly deforming the null coordinates [5, 13, 14]. In particular for observer \({\mathbb {O}}^{-}\) we define the near-null coordinates as

$$\begin{aligned} \tau _{-} = t - (1-\varepsilon )r_{\star };~~ \xi _{-} = -t - (1+\varepsilon )r_{\star }, \end{aligned}$$
(19)

where \(\varepsilon \gg \varepsilon ^2\) is considered to be a small parameter. Similarly, we define the near-null coordinates for observer \({\mathbb {O}}^{+}\), as

$$\begin{aligned} \tau _{+} = t + (1-\varepsilon )r_{\star };~~ \xi _{+} = -t + (1+\varepsilon )r_{\star }. \end{aligned}$$
(20)

We note that timelike characteristics of coordinates \(\tau _{-}\) and \(\tau _{+}\) are preserved in the whole range \(0<\varepsilon <2\) of the parameter \(\varepsilon \), though for convenience this parameter is considered to be small in our case.

3.1.2 Field hamiltonian

We are considering the black hole to be formed by the collapse of matters with the spacetime for the observer \({\mathbb {O}}^{-}\) near \({\mathscr {I}}^{-}\) being flat Minkowskian. Then for the past observer \({\mathbb {O}}^{-}\), the \((1+1)\) dimensional reduced spacetime is described by the Minkowski metric \( ds^2 = -dt^2 + dr_{\star }^2 = -dt^2 + dr^2\). On the other hand, for the future observer \({\mathbb {O}}^{+}\) near the horizon, the black hole is already formed, and the \((1+1)\) dimensional reduced spacetime can be expressed by the metric \( ds^2 = -dt^2 + dr_{\star }^2\). Using the near-null coordinates (20) and (19), the invariant line-elements for observers \({\mathbb {O}}^{+}\) and \({\mathbb {O}}^{-}\) become

$$\begin{aligned} ds^2_{\pm } = \tfrac{\varepsilon }{2} [ - d\tau _{\pm }^2 + d\xi _{\pm }^2 +\tfrac{2}{\varepsilon } d\tau _{\pm } d\xi _{\pm } ] \equiv \tfrac{\varepsilon }{2}~ g^{0}_{\mu \nu }dx_{\pm }^{\mu } dx_{\pm }^{\nu } ~ ,\nonumber \\ \end{aligned}$$
(21)

where flat metric \(g^{0}_{\mu \nu }\) is conformally transformed. Then for both of the observers the reduced scalar field action (12) can be expressed as

$$\begin{aligned} S_{\varphi } = \int d\tau _{\pm } d\xi _{\pm } \left[ -\tfrac{1}{2} \sqrt{-g^{0}} g^{0\mu \nu } \partial _{\mu }\varphi \partial _{\nu } \varphi \right] . \end{aligned}$$
(22)

From Eq. (21) we observe that the lapse function \(N = 1/\varepsilon \), shift vector \(N^1 = 1/\varepsilon \) and determinant of the spatial metric \(q = 1\). Then the scalar field Hamiltonians for observers \({\mathbb {O}}^{+}\) and \({\mathbb {O}}^{-}\) can be written as

$$\begin{aligned} H_{\varphi }^{\pm } = \int d\xi _{\pm }\; \tfrac{1}{\varepsilon }\left[ \left\{ \tfrac{1}{2} \varPi ^2 + \tfrac{1}{2} (\partial _{\xi _{\pm }}\varphi )^2 \right\} + \varPi ~ \partial _{\xi _{\pm }} \varphi \right] . \end{aligned}$$
(23)

From this Eq. (23) we observe that when \(\varepsilon =0\), the Hamiltonians become ill-defined, which signifies the necessity of having near-null coordinates to construct the Hamiltonians. Using Hamilton’s equation, the field momentum \(\varPi \) can be expressed as

$$\begin{aligned} \varPi (\tau _{\pm },\xi _{\pm }) = \varepsilon \;\partial _{\tau _{\pm }}\varphi - \partial _{\xi _{\pm }}\varphi , \end{aligned}$$
(24)

which satisfies a Poisson bracket with the field \(\varphi \), as

$$\begin{aligned} \{\varphi (\tau _{\pm },\xi _{\pm }), \varPi (\tau _{\pm },\xi _{\pm }')\} = \delta (\xi _{\pm } - \xi _{\pm }'). \end{aligned}$$
(25)

3.1.3 Fourier modes

We consider finite fiducial boxes in the intermediate steps of calculations for both of the observers to avoid dealing with formally divergent spatial volumes \(\int d\xi _{\pm }\sqrt{q}\), where \(\sqrt{q}=1\). The finite volumes are given by

$$\begin{aligned} V_{\pm } = \int _{\xi _{\pm }^L}^{\xi _{\pm }^R} d\xi _{\pm }\sqrt{q} = {\xi _{\pm }^R} - {\xi _{\pm }^L}. \end{aligned}$$
(26)

Subsequently, we define the respective Fourier modes of the scalar field and the conjugate momentum for the observers \({\mathbb {O}}^{+}\) and \({\mathbb {O}}^{-}\) as

$$\begin{aligned} \varphi (\tau _{\pm },\xi _{\pm })= & {} \tfrac{1}{\sqrt{V_{\pm }}}\sum _{k} {\tilde{\phi }}^{\pm }_{k} e^{i k \xi _{\pm }}, \nonumber \\ \varPi (\tau _{\pm },\xi _{\pm })= & {} \tfrac{1}{\sqrt{V_{\pm }}} \sum _{k} \sqrt{q}~ {\tilde{\pi }}^{\pm }_{k} e^{i k \xi _{\pm }}, \end{aligned}$$
(27)

where \({\tilde{\phi }}^{\pm }_{k} = {\tilde{\phi }}^{\pm }_{k} (\tau _{\pm })\), \({\tilde{\pi }}^{\pm }_{k} = {\tilde{\pi }}^{\pm }_{k} (\tau _{\pm })\) are the complex-valued mode functions. The finite volumes of the fiducial boxes lead to the definition of Kronecker delta and Dirac delta as \(\int d\xi _{\pm }\sqrt{q} e^{i(k-k')\xi _{\pm }} = V_{\pm } \delta _{k,k'}\) and \(\sum _k e^{ik(\xi _{\pm }-\xi _{\pm }')} = V_{\pm } \delta (\xi _{\pm }-\xi _{\pm }')/\sqrt{q}\) . The definition of these two deltas together imply \(k\in \{k_s\}\) where \(k_s=2\pi s/V_{\pm }\) with s being a nonzero integer. These definitions help us to express the scalar field Hamiltonians (23) in terms of the Fourier modes as \(H_{\varphi }^{\pm } = \sum _{k} \tfrac{1}{\varepsilon } \left( {\mathcal {H}}_{k}^{\pm } + {\mathcal {D}}_{k}^{\pm }\right) \) where the Hamiltonian densities and diffeomorphism generators are

$$\begin{aligned} {\mathcal {H}}_{k}^{\pm } = \tfrac{1}{2} {\tilde{\pi }}^{\pm }_{k} {\tilde{\pi }}^{\pm }_{-k} + \tfrac{1}{2} k^2 {\tilde{\phi }}^{\pm }_{k} {\tilde{\phi }}^{\pm }_{-k}, \end{aligned}$$
(28)

and

$$\begin{aligned} {\mathcal {D}}_{k}^{\pm } = -\tfrac{i k}{2} ( {\tilde{\pi }}^{\pm }_{k} {\tilde{\phi }}^{\pm }_{-k} - {\tilde{\pi }}^{\pm }_{-k} {\tilde{\phi }}^{\pm }_{k} ), \end{aligned}$$
(29)

respectively. The corresponding Poisson brackets are

$$\begin{aligned} \{{\tilde{\phi }}^{\pm }_{k}, {\tilde{\pi }}^{\pm }_{-k'}\} = \delta _{k,k'}. \end{aligned}$$
(30)

The number density corresponding to Hawking quanta will be obtained from the expectation value of the Hamiltonian density operator for the field modes of the observer \({\mathbb {O}}^{+}\) in the vacuum state of observer \({\mathbb {O}}^{-}\).

3.2 Relation between Fourier modes

It can be shown that the Fourier components of the scalar field and its conjugate momentum for the two observers maintain relations among themselves, analogous to the Bogoliubov transformation, given by

$$\begin{aligned} {\tilde{\phi }}^{+}_{\kappa } = \sum _{k} {\tilde{\phi }}^{-}_{k} F_{0}(k,-\kappa );~ {\tilde{\pi }}^{+}_{\kappa } = \sum _{k} {\tilde{\pi }}^{-}_{k} F_{1}(k,-\kappa ), \end{aligned}$$
(31)

where the Fourier modes are considered on fixed spatial hyper-surfaces. The coefficient functions \(F_{n}(k,\kappa )\), where \(n=0,1\), are obtained from the relation \(\varphi (\tau _{-},\xi _{-}) = \varphi (\tau _{+},\xi _{+})\), as the field is scalar, and the relation \(\varPi (\tau _{+},\xi _{+}) = (\partial \xi _{-}/\partial \xi _{+})~\varPi (\tau _{-},\xi _{-})\) [5] between the field momentums. We note that for \(k,\kappa >0\) the coefficient functions \(F_{n}(-k,-\kappa )\) are analogous to the Bogoliubov mixing coefficients \(\beta _{\omega \omega '}\) whereas \(F_{n}(k,-\kappa )\) are analogous to the Bogoliubov coefficients \(\alpha _{\omega \omega '}\) of [1]. The expression of these coefficient functions \(F_{n}(k,\kappa )\) are given by

$$\begin{aligned} F_{n}(k,\kappa ) = \frac{1}{\sqrt{V_{-} V_{+}}} \int d\xi _{+} \left( \tfrac{\partial \xi _{-}}{\partial \xi _{+}}\right) ^n ~e^{i k \xi _{-} + i \kappa \xi _{+}}. \end{aligned}$$
(32)

Using this mathematical expression of the coefficient functions one can obtain a relation

$$\begin{aligned} F_{1}(\pm k,\kappa ) = \mp \left( \tfrac{\kappa }{k}\right) F_{0}(\pm k,\kappa ), \end{aligned}$$
(33)

which indicates evaluating only \(F_{0}(\pm k,\kappa )\) is sufficient for the subsequent analysis.

3.3 Consistency condition and relation between Hamiltonian densities and diffeomorphism generators

The coefficient functions \(F_0(\pm k,\kappa )\) satisfy a relation among themselves, which results from the simultaneous satisfaction of the two different Poisson brackets \(\{{\tilde{\phi }}^{-}_{k},{\tilde{\pi }}^{-}_{-k'}\} = \delta _{k,k'}\) and \(\{{\tilde{\phi }}^{+}_{\kappa },{\tilde{\pi }}^{+}_{-\kappa '}\} = \delta _{\kappa ,\kappa '}\). Using the Eq. (33) this relation can be expressed as

$$\begin{aligned} {\mathbb {S}}_{-}(\kappa ) - {\mathbb {S}}_{+}(\kappa ) =\sum _{k>0} \frac{\kappa }{k} \left[ |F_{0}(-k,\kappa )|^2-|F_{0}(k,\kappa )|^2\right] = 1.\nonumber \\ \end{aligned}$$
(34)

This relation is analogous to the consistency condition between Bogoliubov coefficients [59]. Using relations (31) and (33) one can express the Hamiltonian density \({\mathcal {H}}_{\kappa }^{+}\) for the observer \({\mathbb {O}}^{+}\) in terms of the Hamiltonian density \({\mathcal {H}}_{k}^{-}\) of the observer \({\mathbb {O}}^{-}\) as

$$\begin{aligned} {\mathcal {H}}_{\kappa }^{+} = h_{\kappa }^1 + \sum _{k>0} \left( \frac{\kappa }{k}\right) ^2 \left[ \right| F_{0}(-k,\kappa )|^2 + |F_{0}(k,\kappa )|^2] ~{\mathcal {H}}_k^{-},\nonumber \\ \end{aligned}$$
(35)

where \(h_{\kappa }^1 = \sum _{k\ne k'} (\kappa ^2/2 k k') F_{0}(k,-\kappa ) F_{0}(-k',\kappa ) \{{\tilde{\pi }}^{-}_{k} {\tilde{\pi }}^{-}_{-k'} + kk' {\tilde{\phi }}^{-}_{k} {\tilde{\phi }}^{-}_{-k'} \}\). \(h_{\kappa }^1\) being linear in \(\phi ^{-}_{k}\) and its conjugate momentum, the vacuum expectation value of its quantum counterpart vanishes. Similarly, the diffeomorphism generators of the two observers can be related as

$$\begin{aligned} {\mathcal {D}}_{\kappa }^{+} = d_{\kappa }^1 + \sum _{k>0} \left( \frac{\kappa }{k}\right) ^2 \left[ \right| F_{0}(-k,\kappa )|^2 + |F_{0}(k,\kappa )|^2] ~{\mathcal {D}}_k^{-},\nonumber \\ \end{aligned}$$
(36)

where \( d_{\kappa }^1 = \sum _{k\ne k'} (i\kappa ^2/2k)~ \{F_{0}(-k,\kappa ) F_{0}(k',-\kappa )~ {\tilde{\pi }}^{-}_{-k} {\tilde{\phi }}^{-}_{k'} - F_{0}(k,-\kappa ) F_{0}(-k',\kappa )~ {\tilde{\pi }}^{-}_{k} {\tilde{\phi }}^{-}_{-k'} \}\) which is also linear in field mode and its conjugate momentum.

3.4 Fock quantization and the vacuum state

We define real-valued field modes out of the complex valued Fourier modes \({\tilde{\phi }}_{k}={\tilde{\phi }}^{*}_{-k}\) by suitably choosing the real-valued parts [5, 60], such that this newly defined filed modes are all independent. Then the Hamiltonian density represent simple harmonic oscillators as

$$\begin{aligned} {\mathcal {H}}_{k}^{\pm } = \frac{1}{2} \pi ^{2}_{k} + \frac{1}{2} k^2 \phi ^{2}_{k},~~\{\phi ^{2}_{k},\pi ^{2}_{k'}\}=\delta _{k,k'}, \end{aligned}$$
(37)

and the diffeomorphism generator vanish \({\mathcal {D}}_k^{-} = 0\), where \(\phi _{k}\) and \(\pi _{k}\) are the redefined real-valued field modes. Now we restrict ourselves with the modes where \(k,\kappa > 0\) and for the considered massless scalar field the mode frequency can be identified as \(\omega = k\). For \(k^{th}\) oscillator mode the energy spectrum is given by \(\hat{{\mathcal {H}}}_{k}^{-}|n_k\rangle = ({\hat{N}}_{k}^{-}+\tfrac{1}{2}) k |n_k\rangle = (n+\tfrac{1}{2}) k |n_k\rangle \) where \({\hat{N}}_{k}^{-}\) is the number operator, \(|n_k\rangle \) represent eigen-states with integer eigenvalues. We realize the Hawking effect by computing the expectation value of the Hamiltonian density operator \(\hat{{\mathcal {H}}}_{\kappa }^{+} \equiv ({\hat{N}}_{\kappa }^{+}+\tfrac{1}{2})\kappa \) corresponding to the observer \({\mathbb {O}}^{+}\) in the vacuum state \(|0_{-}\rangle = \varPi _{k} |0_k\rangle \) corresponding to the observer \({\mathbb {O}}^{-}\). Therefore, the expectation value of the number density operator corresponding to the Hawking quanta of frequency \(\omega = \kappa \), using the Eqs. (34) and (35), can be expressed as

$$\begin{aligned} N_{\omega } = N_{\kappa } \equiv \langle 0_{-}|{\hat{N}}_{\kappa }^{+}|0_{-}\rangle = {\mathbb {S}}_{+}(\kappa ), \end{aligned}$$
(38)

where we have used \(\langle 0_k|{\hat{\phi }}_{k} |0_k\rangle = 0\) and \(\langle 0_k|{\hat{\pi }}_{k} |0_k\rangle = 0\).

4 The Hawking effect for Schwarzschild–Tangherlini black holes

In actual derivation of the Hawking effect it was shown that there is a logarithmic relation between the ingoing and outgoing null coordinates in a black hole spacetime, which is crucial to get the thermal distribution of the Hawking effect. In canonical formulation we are going to obtain a similar relation between the spatial near-null coordinates of the two observers, which produces the number density for Hawking quanta in an analogous manner.

4.1 Relation between spatial coordinates \(\xi _{-}\) and \(\xi _{+}\)

In order to establish the relation between the coordinates \(\xi _{-}\) and \(\xi _{+}\), following [5], we consider a pivotal point \(\xi _{-}^0\) on a \(\tau _{-} = constant\) hyper-surface. A spacelike interval on this hyper-surface can be written as

$$\begin{aligned} (\xi _{-} - \xi _{-}^0)_{|\tau _{-}} = 2(r_{\star }^0-r_{\star })_{|\tau _{-}} = 2(r^0-r)_{|\tau _{-}} \equiv \varDelta , \end{aligned}$$
(39)

where \(r^0\) is a pivotal value corresponding to \(\xi _{-}^0\). In deriving Eq. (39) we have used fact that for the observer \({\mathbb {O}}^{-}\) the spacetime was Minkowskian. In a similar manner using the expression of the tortoise coordinate from Eq. (6) we can express a spacelike interval on a \(\tau _{+} = constant\) hyper-surface as

$$\begin{aligned} (\xi _{+} - \xi _{+}^0)_{|\tau _{+}}= & {} \frac{n-2}{2(n-3)}\varDelta + \frac{1}{\mathrm {\varkappa }_{H}} \ln \left( 1 + \frac{\varDelta }{\varDelta _{0}}\right) \nonumber \\ ~&+2~g\left( \frac{\varDelta +\varDelta _{0}}{2}\right) - 2~g\left( \frac{\varDelta _{0}}{2}\right) , \end{aligned}$$
(40)

where \(\varDelta _{0} \equiv 2(r^0 - r_{H})_{|\tau _{+}}\) and \(\mathrm {\varkappa }_{H}\) is the surface gravity at the event horizon. Further, we have identified the interval \(2(r - r^0)_{|\tau _{+}}\) as \(\varDelta \) using geometric optics approximation. We choose the pivotal values \(\xi _{-}^0 = \varDelta _{0}\) and \(\xi _{+}^0 = \frac{n-2}{2(n-3)}\xi _{-}^0 + \frac{1}{\mathrm {\varkappa }_{H}} \ln (\mathrm {\varkappa }_{H} \xi _{-}^0)+ 2~g(\xi _{-}^0/2)\). These choices lead to the relation

$$\begin{aligned} \xi _{+} = \frac{n-2}{2(n-3)}\xi _{-} + \frac{1}{\mathrm {\varkappa }_{H}} \ln (\mathrm {\varkappa }_{H} \xi _{-})+ 2~g\left( \frac{\xi _{-}}{2}\right) . \end{aligned}$$
(41)

The modes that give rise to the Hawking radiation, travel out from the region very close to the horizon and for them \(\mathrm {\varkappa }_{H}\xi _{-} \ll 1\). Consequently for these modes, the relation (41) can be approximated as

$$\begin{aligned} \xi _{+} \approx \frac{1}{\mathrm {\varkappa }_{H}} \ln (\mathrm {\varkappa }_{H}\xi _{-}). \end{aligned}$$
(42)

We note from the Eq. (42) that the full domain of the coordinate \(\xi _{+}\) is \((-\infty ,\infty )\) whereas it is \((0,\infty )\) for \(\xi _{-}\) i.e. the domains are the same as implied by the Eq. (41). However, as mentioned earlier, we shall restrict ourselves within a finite fiducial box during the intermediate steps in our analysis.

4.2 Evaluation of coefficient functions \(F_{0}(\pm k,\kappa )\)

From the Eqs. (34) and (38) we observe that the consistency condition and the number density of the Hawking quanta both require the expression of \(F_{0}(\pm k,\kappa )\), which can be written as

$$\begin{aligned} F_{0}(\pm k,\kappa ) = \int \frac{d\xi _{-}}{\sqrt{V_{-} V_{+}}} \frac{e^{\pm i k \xi _{-} + i (\kappa /\mathrm {\varkappa }_{H})\ln (\mathrm {\varkappa }_{H}\xi _{-})}}{\mathrm {\varkappa }_{H}\xi _{-}}. \end{aligned}$$
(43)

The integrand being oscillatory in nature, the coefficient function \(F_{0}(k,\kappa )\) (43) is formally divergent. In order to regulate this integral we introduce the standard ‘\(i\delta \)’ regulator, with small \(\delta >0\), as follows

$$\begin{aligned} F_{0}^{\delta }(\pm k,\kappa )= & {} \int \frac{d\xi _{-}}{\sqrt{V_{-} V_{+}}} (\mathrm {\varkappa }_{H}\xi _{-})^{-1} ~ e^{\pm i k \xi _{-}} \nonumber \\&~ \times ~ e^{(\delta + i\kappa /\mathrm {\varkappa }_{H} )\ln (\mathrm {\varkappa }_{H}\xi _{-})}. \end{aligned}$$
(44)

In the limit \(\delta \rightarrow 0\), the regulated expression \(F_{0}^{\delta }(\pm k,\kappa )\) reduces to \(F_{0}(\pm k,\kappa )\). By introducing variables \(b_0 = (\delta + i\kappa /\mathrm {\varkappa }_{H})\) and \(\xi = k ~\xi _{-}\), we can express regulated coefficient function as

$$\begin{aligned} F_{0}^{\delta }(\pm k,\kappa )= & {} \frac{(\mathrm {\varkappa }_{H}/k)^{b_0}}{\mathrm {\varkappa }_{H} \sqrt{V_{-} V_{+}}} \int d\xi ~e^{\pm i\xi } ~\xi ^{b_0-1}\nonumber \\ ~= & {} \frac{(\mathrm {\varkappa }_{H}/k)^{b_0} ~\varGamma (b_0)}{\mathrm {\varkappa }_{H} \sqrt{V_{-} V_{+}}} e^{\pm i{b_0} \pi /2}, \end{aligned}$$
(45)

where \(\varGamma (b_0)\) is the Gamma function. Given the fiducial box has a finite volume, we have added two boundary terms \(\varDelta I^{L} = \int _0^{\xi ^L} d\xi e^{\pm i\xi } \xi ^{b_0-1}\) and \(\varDelta I^{R} = \int _{\xi ^R}^{\infty } d\xi e^{\pm i\xi } \xi ^{b_0-1}\) to make the Gamma function complete. Both of these terms vanish when one removes the volume regulators by taking the limit \(\xi ^L \equiv (k~\xi _{-}^L)\rightarrow 0\) and \(\xi ^R \equiv (k~\xi _{-}^R)\rightarrow \infty \). We note an useful property

$$\begin{aligned} F_{0}^{\delta }(-k,\kappa ) = e^{\pi (\kappa /\mathrm {\varkappa }_{H} - i\delta )}~F_{0}^{\delta }(k,\kappa ). \end{aligned}$$
(46)

Equation (46) shows that these coefficient functions satisfy a relation analogous to the relation between Bogoliubov coefficients from [1].

4.3 Consistency condition

The Eq. (45) together with the relation \(k := k_s = (2\pi s/V_{-})\) leads to

$$\begin{aligned} {\mathbb {S}}^{\delta }_{+}(\kappa ) = \frac{\kappa ~|\varGamma (b_0)|^2 e^{-\pi \kappa /\mathrm {\varkappa }_{H}}}{\mathrm {\varkappa }_{H}^{2-2\delta } (2\pi )^{1+2\delta }} ~ \left( \frac{\zeta (1+2\delta )}{V_{-}^{-2\delta } V_{+}} \right) , \end{aligned}$$
(47)

where \(\zeta (1+2\delta ) = \sum _{s=1}^{\infty } s^{-(1+2\delta )}\) is the Riemann zeta function. Furthermore, \({\mathbb {S}}^{\delta }_{-}(\kappa ) = e^{2\pi \kappa /\mathrm {\varkappa }_{H}} ~ {\mathbb {S}}^{\delta }_{+}(\kappa )\) is implied from Eq. (46). Given \(\zeta (1)\) is divergent, it is clear that in order to keep the term \({\mathbb {S}}^{\delta }_{\pm }\) finite one needs to remove volume regulators \(\xi _{-}^L\) and \(\xi _{-}^R\) along with the integral regulator \(\delta \). To find the required dependency among the regulators, we use the regulated expression (45) such that the consistency condition (34) becomes

$$\begin{aligned} \frac{\sinh (\pi \kappa /\mathrm {\varkappa }_{H})}{\pi ~(\kappa /\mathrm {\varkappa }_{H})^{-1} |\varGamma (b_0)|^{-2}} = \frac{(\mathrm {\varkappa }_{H}V_{+}) (2\pi /\mathrm {\varkappa }_{H}V_{-})^{2\delta } }{\zeta (1+2\delta )}. \end{aligned}$$
(48)

Using Gamma function identity \(\varGamma (z)\varGamma (1-z) = \pi /\sin \pi z\), zeta function identity \(\lim _{\delta \rightarrow 0}[\delta ~ \zeta (1+\delta )] = 1\) and the Eq. (42) one can show that the consistency condition demands \(\mathrm {\varkappa }_{H} \xi _{-}^L \sim e^{-1/2\delta }\), i.e. the volume regulator \(\xi _{-}^L\) and integral regulator \(\delta \) should be varied together. Once this limit is taken other volume regulator \(\xi _{-}^R\) drops off from the expression of \({\mathbb {S}}^{\delta }_{+}(\kappa )\).

4.4 Number density of Hawking quanta

We observe from Eq. (38), that the expectation value of the number density operator corresponding to the Hawking quanta as seen by an observer \({\mathbb {O}}^{+}\) is \(N_{\kappa } = {\mathbb {S}}_{+}(\kappa )\). Then from Eq. (47), with the help of the consistency relation from Eq. (48), we get this number density for a Schwarzschild–Tangherlini black hole as

$$\begin{aligned} N_{\kappa } = \langle {\hat{N}}_{\kappa =\omega }\rangle = \frac{1}{e^{2\pi \omega /\mathrm {\varkappa }_{H}} - 1}, \end{aligned}$$
(49)

which represents a blackbody distribution at the Hawking temperature \(T_H \equiv \mathrm {\varkappa }_{H}/(2\pi k_B) = (n-3)/(4\pi k_B r_H)\) [61,62,63]. Clearly, the Hawking temperature for ST black hole depends both on its mass M, represented by \(r_H\) and the dimensionality of the spacetime n. We also want to mention that this number density as observed by an asymptotic observer will be represented by a greybody distribution, given by

$$\begin{aligned} N_{\omega } = \frac{\varGamma (\omega )}{e^{2\pi \omega /\mathrm {\varkappa }_{H}} - 1}. \end{aligned}$$
(50)

In the next section we center our attention on this greybody factor.

5 Bounds on the greybody factor

As discussed in our previous section the spectrum of Hawking quanta as seen by an asymptotic future observer is described by a greybody distribution, which is modified from the blackbody distribution as the wave modes pass through the black hole spacetime. Any physical observer that intends to detect the Hawking radiation is expected to be stationed at a far away distance from the black hole event horizon. Then the estimation of the greybody factor becomes important to obtain a general form of the Hawking spectrum to these observers. In literature researchers have introduced diverse technicalities [15, 55, 56, 64,65,66,67,68,69,70] to estimate these greybody factors. In this work we are going to provide the bounds on these greybody factors for ST black holes. Unlike other approximate methods, these bounds can be estimated for all frequencies, field angular momentums and spacetime dimensions.

5.1 Bounds

We mention that in [34], very general bounds on the transmission and reflection coefficients corresponding to an one-dimensional potential scattering are provided. These bounds can be analytically studied for the whole range of the frequency \(\omega \). Now from Eq. (13) we observe that the scalar field equation in a Schwarzschild–Tangherlini black hole spacetime also acts as a one-dimensional potential problem. As it is understood, the transmission coefficient through this potential provides the greybody factor corresponding to the Hawking effect. Then it becomes plausible enough to study the previously mentioned bound for Eq. (13) to provide an understanding of the greybody factors corresponding to the Hawking effect in an ST black hole spacetime. To obtain these bounds on the greybody factor, the equation of motion (13) with the potentials from Eqs. (14) and (15) are considered. Eigen-values of the n-dimensional spherical harmonics are given by \({\mathcal {A}}^{n}_{lm} = -l(l+n-3)\). In Fig. 1, we have depicted the potentials as varying functions of the radial distance r for different spacetime dimensionality n corresponding to scalar field in bulk and in brane. We further use these potentials to get the general bounds on the greybody factor [34, 35, 37], as

$$\begin{aligned} \varGamma (\omega ) \ge {{\,\mathrm{sech}\,}}^2{\left\{ \int _{-\infty }^{\infty }\varrho ~~ dr_{\star }\right\} }, \end{aligned}$$
(51)

where

$$\begin{aligned} \varrho = \frac{\sqrt{(h')^2+(\omega ^2-{\mathbb {V}}-h^2)^2}}{2h}. \end{aligned}$$
(52)

Here \({\mathbb {V}}\) represents the potential, \(h\equiv h(r_{\star })\) and \(h(r_{\star })>0\), which is an arbitrary function satisfying \(h(-\infty ) = h(\infty ) = \omega \). We consider two particular functional forms of h [37] and obtain the resulting bound on the greybody factor in ST black hole spacetime.

Fig. 1
figure 1

a Plot of the potential \({\mathbb {V}}(r)\) corresponding to a scalar field in the bulk with respect to the radial coordinate r for \(l=0\), \(r_{H}=1\) and different dimensionality n. b Plot of the potential \({\mathbb {V}}(r)\) corresponding to a brane-localized scalar field with respect to the radial coordinate r for \(l=0\), \(r_{H}=1\) and different dimensionality n

Full size image

Case I: Here we consider the situation when \(h=\omega \). For this case \(\varrho = {\mathbb {V}}/2\omega \) and the bound is given by

$$\begin{aligned} \varGamma (\omega ) \ge {{\,\mathrm{sech}\,}}^2{\left\{ \frac{1}{2\omega }\int _{r_H}^{\infty } \frac{{\mathbb {V}}(r)}{f(r)}dr \right\} }. \end{aligned}$$
(53)
Fig. 2
figure 2

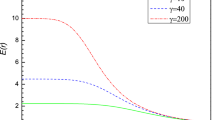
a Here we plot the bound on the greybody factor with respect to the frequency \(\omega \) for \(l=1\), \(r_H=1\) and different values of spacetime dimensionality n. b Here we provide the plot of the bound on the greybody factor with respect to varying spacetime dimension n for \(l=1\), \(r_H=1\). The frequency \(\omega =8\) is chosen conveniently. In both of these cases the considered potential corresponds to a scalar field in the bulk and the particular assumption on h is \(h=\omega \)

Full size image
Fig. 3
figure 3

a Here we plot the bound on the greybody factor, corresponding to a brane-localized scalar field, with respect to different spacetime dimension n for \(l=1\), \(r_H=1\). b The plot of the ratio of the bounds on the greybody factor, corresponding to the brane to bulk scalar field, with respect to varying dimension n for \(l=1\), \(r_H=1\). For both of the cases the frequency \(\omega =8\) is chosen conveniently and the particular assumption on h is \(h=\omega \)

Full size image

First, we consider the scalar field in the bulk. Using the functional form of potential from Eq. (14) one can get this bound evaluated to be

$$\begin{aligned} \varGamma (\omega ) \ge {{\,\mathrm{sech}\,}}^2{\left\{ \frac{6+4l^2+4l(n-3)+n^2-5n}{8\omega r_H} \right\} }, \end{aligned}$$
(54)

which is finite for any infinitesimally small \(\omega \), and vanishes [71, 72] in the limit of \(\omega \rightarrow 0\). When \(\omega \) is large one can series expand the above quantity and the bound becomes

$$\begin{aligned} \varGamma (\omega ) \ge 1- \frac{\left[ 6+4l^2+4l(n-3)+n^2-5n\right] ^2}{64r_H^2\omega ^2}+ {\mathcal {O}}\left( \frac{1}{\omega ^4}\right) .\nonumber \\ \end{aligned}$$
(55)

This result signifies that for very high frequency outgoing waves the potential barrier becomes almost transparent. We observe that for \(n=4\) the above expression from Eq. (54) reproduces the bound obtained for \((3+1)\) dimensional Schwarzschild black hole [37]. In Fig. 2 we have depicted the variation of this bound on the greybody factor with respect to the frequency \(\omega \) for different values of the spacetime dimensionality n. We also observe that the bound decreases as n increases, see Fig. 2. This feature, also mentioned in [37], is a consequence of the fact that as n increases the height of the potential barrier increases and thus the transmission probability should decrease.

On the other hand one can also consider the brane-localized scalar field and take the potential from Eq. (15) to obtain the bound as

$$\begin{aligned} \varGamma (\omega ) \ge {{\,\mathrm{sech}\,}}^2{\left\{ \frac{n+l(l+1)(n-2)-3}{2\omega r_H(n-2)} \right\} }. \end{aligned}$$
(56)

One can observe that when \(n=4\) this expression gives the bound obtained for \((3+1)\) dimensional Schwarzschild black hole. For large \(\omega \) this bound can be series expanded to give

$$\begin{aligned} \varGamma (\omega ) \ge 1- \left[ \frac{n+l(l+1)(n-2)-3}{2r_H\omega (n-2)}\right] ^2+ {\mathcal {O}}\left( \frac{1}{\omega ^4}\right) ,\nonumber \\ \end{aligned}$$
(57)

and similarly for large n one gets,

$$\begin{aligned} \varGamma (\omega ) \ge {{\,\mathrm{sech}\,}}^2\left[ \frac{1+l+l^2}{2r_H\omega }\right] + {\mathcal {O}}\left( \frac{1}{n}\right) . \end{aligned}$$
(58)

From Eq. (57) one can notice that with the rise of frequency the transmission probability grows also for a brane-localized scalar field. On the other hand from Eqs. (54) and (58) we observe that unlike the bulk case the lower bound on the greybody factor never goes to zero even for infinitely large n for a scalar field in 3-brane. From Fig. 3 we observe that this bound slowly decreases as n increases for a brane localized scalar field compared to the field in bulk. Besides, in this particular figure we observe that the ratio of these bounds for brane to bulk is always greater than one and increases as the spacetime dimensionality increases. This suggests that for a ST black hole with large extra spatial dimensions most of the Hawking emission arrives to an asymptotic observer in 3-brane.

Case II:In this part we consider the ansatz \(h=\sqrt{\omega ^2-{\mathbb {V}}}\) [37]. With this form of h the expression of \(\varrho \) from Eq. (52) gets simplified and the bound on the greybody factor can be represented by the integral

$$\begin{aligned} \varGamma (\omega ) \ge {{\,\mathrm{sech}\,}}^2{\left\{ \frac{1}{2}\int _{-\infty }^{\infty } \frac{|h'|}{h}dr_{\star }\right\} }. \end{aligned}$$
(59)

After carrying out the integration we get

$$\begin{aligned} \varGamma (\omega ) \ge {{\,\mathrm{sech}\,}}^2{\left\{ -\ln {\left( \frac{\sqrt{\omega ^2-{\mathbb {V}}_{peak}}}{\omega } \right) } \right\} }, \end{aligned}$$
(60)

where \({\mathbb {V}}_{peak}\) represents the maximum value or the peak value of the potential \({\mathbb {V}}\). One can observe from this bound that it has meaning only when \(\omega ^2>{\mathbb {V}}_{peak}\). The region \(\omega ^2<{\mathbb {V}}_{peak}\) is classically forbidden and do not contribute to this particular calculation. The expression of the bound from Eq. (60) can be further simplified to

$$\begin{aligned} \varGamma (\omega ) \ge 1 - \frac{{\mathbb {V}}_{peak}^2}{(2\omega ^2-{\mathbb {V}}_{peak})^2}. \end{aligned}$$
(61)
Fig. 4
figure 4

a Here we plot the bound on the greybody factor with respect to the frequency \(\omega \) for \(l=0\), \(r_H=1\) and different values of spacetime dimension n. b The plot of the bound on the greybody factor with respect to varying spacetime dimensionality n for \(l=0\), \(r_H=1\) and a conveniently chosen frequency \(\omega =8\). Both of the plots correspond to a scalar field in the Bulk and the considered case is \(h=\sqrt{\omega ^2-{\mathbb {V}}}\)

Full size image
Fig. 5
figure 5

a Here we plot the bound on the greybody factor, corresponding to a brane-localized scalar field, with respect to different spacetime dimension n for \(l=1\), \(r_H=1\). b The plot of the ratio of the bounds on the greybody factor, corresponding to the brane to bulk scalar field, with respect to varying dimension n for \(l=1\), \(r_H=1\). For both of the cases the frequency \(\omega =8\) is chosen conveniently and the particular assumption on h is \(h=\sqrt{\omega ^2-{\mathbb {V}}}\)

Full size image

To estimate this bound explicitly for certain frequency \(\omega \), angular momentum l and spacetime dimensionality n, one needs to evaluate the value of \(r_{peak}\) which corresponds to the \({\mathbb {V}}_{peak}\) in each case. We have numerically done this particular computation for \(l=0\) and also for varying l for a scalar field in both bulk and in the brane.

We have observed that when \(l=0\) the plot given in Fig. 4 shows similar characteristics as was obtained from the previous case for a scalar field in the bulk. We have seen that as \(\omega \) increases the bound increases and potential barrier becomes more transparent Fig. 4, i.e. high frequency wave modes travel much smoothly than the low frequency modes through the potential barrier. Here also as the spacetime dimensionality n increases the bound decreases, see Fig. 4. However in this particular case one can not expect to get the bound for arbitrarily small frequency w, as \(\omega ^2<{\mathbb {V}}_{peak}\) was excluded from the calculation. One can also analytically obtain the value of \(r_{peak}\) corresponding to a scalar field in the bulk, when \(l=0\), and it is given by

$$\begin{aligned} r_{peak} = r_H~ \left[ \frac{n-1+(n-3)\sqrt{4n-7}}{2~(n-2)^2}\right] ^{-\frac{1}{n-3}}, \end{aligned}$$
(62)

where for few values of the spacetime dimension n we have tabulated the corresponding \(r_{peak}\) and \({\mathbb {V}}_{peak}\) as

\(n=4\)

\(r_{peak}=4r_H/3\)

\({\mathbb {V}}_{peak}=0.105/r_H^2\)

\(n=5\)

\(r_{peak}=1.267r_H\)

\({\mathbb {V}}_{peak}=0.505/r_H^2\)

\(n=6\)

\(r_{peak}=1.226r_H\)

\({\mathbb {V}}_{peak}=1.269/r_H^2\)

\(n=7\)

\(r_{peak}=1.197r_H\)

\({\mathbb {V}}_{peak}=2.432/r_H^2\)

\(n=8\)

\(r_{peak}=1.176r_H\)

\({\mathbb {V}}_{peak}=4.017/r_H^2\)

where we explicitly observe that as n increases \(r_{peak}\) gets nearer to the horizon and the value of \({\mathbb {V}}_{peak}\) increases for a given horizon radius \(r_H\). For a brane localized scalar field we have, when \(l=0\), the expression of \(r_{peak}\) as

$$\begin{aligned} r_{peak} = r_H\left[ \frac{n-1}{2~(n-2)}\right] ^{-\frac{1}{n-3}}. \end{aligned}$$
(63)

Some of the values of this \(r_{peak}\) and corresponding \({\mathbb {V}}_{peak}\) for different spacetime dimensionality n are tabulated below

Fig. 6
figure 6

a Here we plot the bound on the greybody factor for a scalar field in Bulk with respect to varying spacetime dimensionality n for \(r_H=1\), different values of l and a conveniently chosen frequency \(\omega =8\). b Here we plot the bound on the greybody factor for a scalar field in 3-Brane with respect to varying spacetime dimensionality n for \(r_H=1\), different values of l and a conveniently chosen frequency \(\omega =8\). Both of the plots correspond to the second case \(h=\sqrt{\omega ^2-{\mathbb {V}}}\)

Full size image

\(n=4\)

\(r_{peak}=4r_H/3\)

\({\mathbb {V}}_{peak}=0.105/r_H^2\)

\(n=5\)

\(r_{peak}=1.225r_H\)

\({\mathbb {V}}_{peak}=0.296/r_H^2\)

\(n=6\)

\(r_{peak}=1.170r_H\)

\({\mathbb {V}}_{peak}=0.514/r_H^2\)

\(n=7\)

\(r_{peak}=1.136r_H\)

\({\mathbb {V}}_{peak}=0.744/r_H^2\)

\(n=8\)

\(r_{peak}=1.114r_H\)

\({\mathbb {V}}_{peak}=0.980/r_H^2\)

where \(r_{peak}\) and \({\mathbb {V}}_{peak}\) shows the behavior similar to the scalar field in the bulk. However the increment in \({\mathbb {V}}_{peak}\) with respect to the dimension n is lesser compared to the bulk. From Eq. (61) it is observed that as the value of \({\mathbb {V}}_{peak}\) increases the bound on the greybody factor decreases. Then the above tables imply that the greybody factor decreases with increasing spacetime dimensionality. In Fig. 5 one can observe that for a brane-localized scalar field the bound on the greybody factor decreases as the spacetime dimensionality n increases. In the second part of the same figure we have also plotted the ratio of the brane to bulk bound on the greybody factor. We observed that this quantity is always greater than one and increases as n increases to large values, suggesting that for large extra dimensions the black hole emit Hawking radiation mainly in the brane. When \(l>0\) the analytical expression of \(r_{peak}\) for a scalar field in the bulk can be given by

$$\begin{aligned} r_{peak} = r_H~ \left[ \frac{-\gamma _{1}+\sqrt{\gamma _{1}^2+4\gamma _{2}}}{2~(n-2)^3}\right] ^{ -\frac{1}{ n-3}}, \end{aligned}$$
(64)

where \(\gamma _{1} = (n-1)\left[ 2+2l^2+2l(n-3)-n\right] \) and \(\gamma _{2} = (n-2)^3\left[ (n-2)^2+2\gamma _{1}/(n-1)\right] \), which also asserts that for a fixed l the value of \(r_{peak}\) gets nearer to the event horizon as higher dimensions are considered. On the other hand for a brane localized scalar field, when \(l>0\), we have

Fig. 7
figure 7

Here we plot the ratio of the bounds for brane to bulk localized scalar fields with respect to varying spacetime dimensionality n for \(r_H=1\), different values of l and a conveniently chosen frequency \(\omega =8\). This plot corresponds to the second case \(h=\sqrt{\omega ^2-{\mathbb {V}}}\)

Full size image
$$\begin{aligned} r_{peak} = r_H~ \left[ \frac{\gamma _3+\sqrt{\gamma _3^2+16l(l+1)\gamma _4}}{4~\gamma _4}\right] ^{ -\frac{1}{n-3}}, \end{aligned}$$
(65)

where \(\gamma _3 = -(3+l+l^2-n)(n-1)\) and \(\gamma _4 = (n-3)(n-2)\). We have provided a plot in Fig. 6 depicting the bound on the greybody factor with respect to the spacetime dimension n for \(l>0\) corresponding to bulk and brane-localized scalar fields. It is observed that as n increases the bound decreases even for different \(l(\ne 0)\). On the other hand from Fig. 7 it is observed that the brane to bulk ratio of the bound increases as the spacetime dimensionality n increases. This further reaffirms that the quanta of the Hawking effect, with large number of extra dimensions, is mostly radiated in the brane.

6 Discussion

Higher dimensional black holes provide some very interesting black hole spacetimes. In this work we have considered a n-dimensional Schwarzschild–Tangherlini black hole spacetime and shown that the action corresponding to massless minimally coupled free scalar fields both in the bulk and in 3-brane can be simplified to express a \((1+1)\) dimensional flat spacetime in the near horizon and asymptotic regions. This particular characteristic allows one to express the field modes in terms of plane wave solutions in these regions, a feature necessary for the formulation of the Hawking effect. Then with the help of the near-null coordinates [5, 13, 14] we provided a Hamiltonian based derivation of the Hawking effect in the Schwarzschild–Tangherlini black hole spacetime. We observed that the temperature corresponding to the Hawking effect is dependent on the spacetime dimensionality and same for both the bulk and brane-localized scalar field. The second feature is obvious as the temperature corresponding to the Hawking effect only depends on the black hole horizon and for both of the cases the horizon structure is the same. However, the geometries outside the horizon are different, which results in different form of the greybody factors in bulk and in the brane. We reconfirmed [46] that the bounds on the greybody factors for both bulk and brane-localized scalar field decrease as the spacetime dimensionality n increases. We noticed that this decrease is slower for the case of a brane-localized scalar field. We have also reaffirmed for both the bulk and brane-localized scalar field that as the frequency increases the bound on the greybody factor increases signifying that the potential barrier becomes more transparent corresponding to the field modes of higher frequency. These bounds from Eqs. (54) and (56), also predict that as the angular momentum quantum number l increases the transmission of the field modes through the potential barrier gets depleted. We have further observed that as the spacetime dimensionality n increases the ratio of the bounds on the greybody factor for brane to bulk increases and this quantity is always greater than one. This signifies that for a higher dimensional black hole with large extra spatial dimensions the Hawking emission gets specifically restricted to the brane, which is widely predicted in the literature [27, 44, 73]. However, in this work we have inferred this entirely from the consideration of the bounds on the greybody factor. We should mention that from [27], it is evident the brane to bulk energy emission ratio for higher dimensional static black holes remains greater than one for spacetime dimensionality to be larger than four. However, this ratio is not strictly increasing and varies a lot with increasing dimensionality n. On the other hand, the ratio of the bounds for brane to bulk greybody factors, as observed from Figs. 3, 5 and 7, shows a increasing nature with increasing dimensionality n. Most of the calculations related to these bounds can be analytically performed and they are valid in the entire frequency regime of the Hawking spectra for all values of the angular momentum quantum number l. We want to mention that one can also calculate these bounds on the greybody factor explicitly for the higher dimensional rotating black holes [42, 73, 74] and study the corresponding dependence on the spacetime dimensionality.