1 Introduction

The current scenario of the accelerated expansion of the Universe confirmed through various observational schemes by Riess et al. [1, 2]. Cosmological observations and Cosmic Microwave Background (CMB) data suggest [3, 4] that the Universe is spatially flat and is dominated by an exotic component with huge negative pressure dubbed as Dark Energy (DE). It is also believed that DE occupies 73% of the energy of our Universe, Dark Matter (DM) occupies 23% and the 6% energy is baryonic matter [5, 6]. In order to convey this late time acceleration, two main various approaches have been advocated: one is to construct different DE candidates and the second one is the modifications of Einstein’s theory of gravitation. Among the many modifications, Brans–Dicke [7] and Saez–Ballester [8] scalar–tensor theories played a significant role.

Saez and Ballester [8] introduced a scalar–tensor theory in which metric is combined with a dimensionless scalar-field was developed. This coupling is used to describe the weak fields satisfactorily. This scalar–tensor theory plays an important part in solving the issue of missing matter problem and in removing the graceful issue of exit in non-flat FRW cosmologies and the inflation era. In SB theory, the field equations are given by

$$\begin{aligned} R_{ij}-\frac{1}{2}Rg_{ij}-w \phi ^{n}\Big (\phi _{,i}\phi _{,j}- \frac{1}{2}g_{ij}\phi _{,k}\phi ^{,k}\Big )~=~-\frac{8\pi G}{c^4}T_{ij}, \end{aligned}$$
(1)

and the scalar field (\(\phi \)) satisfies the following equation

$$\begin{aligned} 2\phi ^n \phi _{,i}^{,i}+n\phi ^{n-1}\phi _{,k}\phi ^{,k}~=~0, \end{aligned}$$
(2)

here \(T_{ij}\) is the energy momentum tensor of the matter, the gravitational constant G, w is a dimensionless constant and, comma (,) and semicolon (;) represents partial and covariant differentiation respectively. The energy-conservation equation is given by

$$\begin{aligned} T_{;~j}^{ij}~=~0. \end{aligned}$$
(3)

In past years, the holographic principle had attracted considerable attention due to its importance in quantum gravity [9,10,11], which is defined as the entropy of a given system which does not depend upon the volume, but rather on the surface area surrounding it. In the cosmological context, the holographic principle establishes an upper limit for the entropy of the Universe and there is a theoretical relation between IR and Ultraviolet (UV) cutoffs. If there is an energy density (\(\rho _{de}\)) in a region associated to the UV, then the total energy in a phase of size L cannot be greater than the mass of a black hole with the same size, so that [12], \(L^3\rho _{de}>LM_p^2\). In this case, the largest value of L can be obtained by considering the equality in equation such that the holographic energy density is given by \(\rho _{de}=3c^2M_p^2 L^{-2}\), where c is a numerical constant and \(M_p^2=8\pi G\) is the reduced Planck mass. Li [13] has shown that Hubble horizons and particle horizons are not in good agreement with the Universe while the future event horizon is the best model for non-interacting holographic DE with suitable constant c. Gao et al. [14] have pointed out that holographic DE with future event horizon is plagued with causality problem. Inspired by this, several authors have modified the IR cutoff as a function of the Ricci scalar [15, 16]. Since the energy density of the holographic DE is based on the area law of entropy, any modification of the area law leads to a modified holographic DE. The entropy expression is associated with the apparent horizon of FRW Universe in DGP braneworld motivated Sheykhi et al. [17] to introduce a new model for the holographic DE known as New Holographic DE (NHDE). They have investigated the cosmological consequences of this NHDE model by choosing the Hubble radius \(L=H^{-1}\) as the system’s IR cutoff and have proved that it can explain the current cosmic acceleration of the Universe.

Nojiri and Odintsov [18] have proposed a unifying approach to early-time and late-time Universe based on phantom cosmology is proposed. Also, they have discussed the bound for holographic entropy which decreases in phantom era. Medved [19] has given a comment on holographic DE and mentioned that their interpretation of the DE turns out to be suggestive of a natural resolution to the cosmic coincidence problem. Bisabr [20] has studied the holographic DE model in a generalized scalar–tensor theory. He has shown that various types of potentials, the equation of state parameter is negative and transition from deceleration to acceleration expansion of the Universe is possible. Many researchers [21,22,23,24,25,26,27,28,29,30] have studied HDE models in various theories of gravitation. In particular, Mazumder and Chakraborty [31] have investigated the validity of the generalized second law of thermodynamics of the universe bounded by the event horizon in the holographic DE model. Setare and Jamil [32] have presented a detailed discussion on statefinder diagnostic and stability of modified gravity consistent with holographic and agegraphic DE. Sharif and Khanum [33] have investigated the Kaluza–Klein (KK) cosmology in which modified holographic DE is interacting with DM. Further, they have shown that the generalized second law of thermodynamics holds without any constraint. Mohammadi and Malekjani [34] have discussed the entropy-corrected version of interacting holographic DE, in the non-flat Universe enclosed by apparent horizon. Two corrections of entropy so-called logarithmic and power law in this model with apparent horizon as an IR-cutoff is studied. Sharif and Jawad [35] have discussed cosmological evolution of interacting NHDE in non-flat Universe. Li et al. [36] have performed a detailed investigation on the cosmological constraints on the Holographic Dark Energy (HDE) model by using the Plank data. Praseetha and Mathew [37] have studied the cosmology and thermodynamics of HDE, and also, they have analyzed the generalized second law of thermodynamics in a flat Universe consisting of interacting DE and DM. Jawad et al. [38] have discussed the modified holographic Ricci DE model in Chameleon Brans–Dicke gravity with its energy density in interaction with energy density of Cold Dark Matter (CDM) and explored its thermodynamic consequence. Aditya and Reddy [39] have investigated anisotropic new holographic dark energy model in the framework of Saez–Ballester theory of gravitation. Very recently, Prasanthi and Aditya [40] have investigated anisotropic Renyi HDE models in the framework of general relativity. In recent years, various entropy formalisms have been used to investigate the gravitational and cosmological setups. Among them Tsallis HDE (THDE) model based on the Tsallis generalized entropy, which is never stable at the classical level [41, 42]. Hence, with this motivation, in this paper, we assume the HDE with new entropy formalism i.e., Tsallis HDE.

Here, we would like to study the difference between our work and the other THDE models studied in literature [43,44,45,46,47,48,49,50,51,52,53]. Zadeh et al. [43] have explored the effects of various IR cutoffs on the properties of THDE model. Sharma and Pradhan [44] have investigated diagnosing THDE models with statefinder and \({\omega _t-\omega _t^{'}}\) plane analysis. Sadri [45] and Aditya et al. [46] have studied observational constraints on interacting THDE models in Brans–Dicke scalar–tensor theory. Sharif and Saba [47], Maity and Debnath [48] and Ayman [48] have investigated different THDE models in various theories of gravitation. It is observed that all these studies are in the isotropic background of the universe, i.e., with FRW space-time. But in view of the importance of anisotropic space-times, many authors have investigated THDE models in the anisotropic background. These anisotropic models will help for a better understanding of the early stages of evolution of the Universe. Korunur [50] has studied THDE model in Bianchi type-III Universe with scalar fields. Zadeh et al. [51] explained the cosmic evolution of Bianchi type-I THDE model with sign-changeable interaction between DM and DE with various IR cutoffs. Dubey et al. [52] have discussed THDE models with Hubble horizon as IR cutoff in axially symmetric Biachi type-I space-time whereas, Dubey et al. [53] have studied THDE in Bianchi type-I Universe using hybrid expansion law with k-essence. THDE model with anisotropic background and in the framework of Saez–Ballester scalar–tensor theory of gravitation has not been, so far, studied in literature. Hence, in our work, we studied the behavior of THDE with Hubble horizon as the IR cutoff in the background of Biachi type-III space-time within the framework of Saez–Ballester scalar–tensor theory of gravitation. We obtained an exact and viable solution by solving the field equations of our proposed THDE model without considering any spacial expansion law for average scale factor of the model.

The plan of this work as follows: in Sect. 2 we have derived SB field equations with the help of Bianchi type-III metric in the presence of two minimally interacting fields: DM and THDE components. Section 3 devoted to the cosmological solution of the field equations. Also, we have constructed non-interacting and interacting THDE models along with their physical discussions. In Sect. 4, we presented a comparative analysis of our work with the recent works on THDE and with the modern observational data. In the last section, we have summarized our results.

2 Metric and SB field equations

We consider the spatially homogeneous and anisotropic Bianchi type-III space-time described by the following metric

$$\begin{aligned} ds^2=dt^2-A^2(t)dx^2-B^2(t)e^{-2x}dy^2-C^2(t)dz^2, \end{aligned}$$
(4)

where A(t), B(t), and C(t) represent the metric potentials of the Universe.

The Saez–Ballester field equations for combined matter and DE are given by

$$\begin{aligned} R_{ij}-\frac{1}{2}Rg_{ij}-w \phi ^{n}\Big (\phi _{,i}\phi _{,j}-\frac{1}{2} g_{ij}\phi _{,k}\phi ^{,k}\Big )~=~-(T_{ij}+\bar{T_{ij}}), \end{aligned}$$
(5)

and the scalar fields (\(\phi \)) satisfies the Eq. (2). We have energy conservation equation as

$$\begin{aligned} (T_{ij}+\bar{T_{ij}})_{;j}=0. \end{aligned}$$
(6)

Here the energy–momentum tensor for matter (\(T_{ij}\)) and THDE (\(\bar{T_{ij}}\)) are given as follows:

$$\begin{aligned} T_{ij}= & {} \rho _m u_i u_j\nonumber \\= & {} diag [1,0,0,0] \rho _m, \end{aligned}$$
(7)
$$\begin{aligned} \bar{T_{ij}}= & {} (p_t+\rho _t)u_iu_j-p_t~g_{ij}\nonumber \\= & {} diag[1,-\omega _t,-\omega _t,-\omega _t] \rho _t, \end{aligned}$$
(8)

it can be parameterized as

$$\begin{aligned} \bar{T_{ij}}=diag[1,-\omega _t,-\omega _t,-(\omega _t+\gamma )] \rho _t, \end{aligned}$$
(9)

where \(\rho _t\), \(\rho _m\) are energy densities of THDE and matter, respectively and \(p_t\) is the pressure of THDE. \(\omega _t=\frac{p_t}{\rho _t}\) is an equation of state (EoS) parameter. Here \(\gamma \) is the deviation from EoS parameter in z direction, known as skewness parameter.

The SB field equations for Bianchi type-III universe (4) with the help of Eq. (5) can be written as

$$\begin{aligned}&\frac{\ddot{B}}{B}+\frac{\ddot{C}}{C}+\frac{\dot{B}\dot{C}}{BC}-\frac{w}{2}\phi ^{n}\dot{\phi }^{2}~=~-\omega _t~ \rho _t, \end{aligned}$$
(10)
$$\begin{aligned}&\frac{\ddot{A}}{A}+\frac{\ddot{C}}{C}+\frac{\dot{A}\dot{C}}{AC}-\frac{w}{2}\phi ^{n}\dot{\phi }^{2}~=~-\omega _t~ \rho _t, \end{aligned}$$
(11)
$$\begin{aligned}&\frac{\ddot{A}}{A}+\frac{\ddot{B}}{B}+\frac{\dot{A}\dot{B}}{AB}-\frac{1}{A^{2}}-\frac{w}{2}\phi ^{n}\dot{\phi }^{2}~=~-(\omega _t+\gamma )~ \rho _t, \end{aligned}$$
(12)
$$\begin{aligned}&\frac{\dot{A}\dot{B}}{AB}+\frac{\dot{B}\dot{C}}{BC}+\frac{\dot{A}\dot{C}}{AC}-\frac{1}{A^{2}}+\frac{w}{2}\phi ^{n}\dot{\phi }^{2}~=~\rho _m+\rho _t, \end{aligned}$$
(13)
$$\begin{aligned}&\frac{\dot{A}}{A}-\frac{\dot{B}}{B}=0, \end{aligned}$$
(14)
$$\begin{aligned}&\ddot{\phi }+\left( \frac{\dot{A}}{A}+\frac{\dot{B}}{B}+\frac{\dot{C}}{C}\right) \dot{\phi }+\frac{n}{2}\frac{\dot{\phi ^{2}}}{\phi }=0. \end{aligned}$$
(15)

We can write the continuity equation (6) of the matter and THDE as

$$\begin{aligned} \dot{\rho _m}+\dot{\rho _t}+\left( \frac{\dot{A}}{A}+ \frac{\dot{B}}{B}+\frac{\dot{C}}{C}\right) (\rho _m+(1+\omega _t)\rho _t)+\gamma \frac{\dot{C}}{C} \rho _t=0, \end{aligned}$$
(16)

where overhead dot (.) denotes for ordinary differentiation with respect to t.

3 Solution of field equations and cosmological models

From Eq. (14), we have

$$\begin{aligned} A=B. \end{aligned}$$
(17)

In view of Eq. (17), the field equations (10)–(15) constitute a system of four independent equations with six unknowns: A, C, \(\rho _m\), \(\omega _t\), \(\phi \) and \(\gamma \). Hence, in order to find the determinate solution of the non-linear field equations we use the following plausible physical condition:

The shear scalar (\(\sigma ^2)\) is proportional to the scalar expansion (\(\theta \)) which leads to a relationship between metric potentials [54]

$$\begin{aligned} A=C^k \end{aligned}$$
(18)

where \(k \ne 1\) is a positive constant which preserves the non-isotropic behavior of the space-time.

Now from Eqs. (10), (11), (17) and (18), we get

$$\begin{aligned} \frac{\ddot{C}}{C}+2k\frac{\dot{C}}{C}=\frac{1-\gamma \rho _{t}C}{(k-1)\dot{C}} \end{aligned}$$
(19)

in order to solve this Eq. (19), we use the physically viable assumption as given below

$$\begin{aligned} \gamma =\frac{1-(k-1)\gamma _0\dot{C}}{C\rho _t}. \end{aligned}$$
(20)

where \(\gamma _0\) is an arbitrary constant.

Now from Eqs. (19) and (20), we get the metric potentials

$$\begin{aligned} A= & {} B=\Big (\frac{(2k+1)c_1 e^{\gamma _0 t}}{\gamma _0}+c_2(2k+1)\Big )^{\frac{k}{2k+1}}, \end{aligned}$$
(21)
$$ \begin{aligned}{} \& C= & {} \Big (\frac{(2k+1)c_1 e^{\gamma _0 t}}{\gamma _0}+c_2(2k+1)\Big )^{\frac{1}{2k+1}}, \end{aligned}$$
(22)

where \(c_1\) and \(c_2\) are integration constants. Using the metric potentials (21) and (22) in metric (4), we can write

$$\begin{aligned} ds^2= & {} dt^2-\Big [\frac{(2k+1)c_1 e^{\gamma _0 t}}{\gamma _0}+c_2(2k+1)\Big ]^{\frac{2k}{2k+1}}\nonumber \\&\times (dx^2+e^{-2x}dy^2)\nonumber \\&-\Big [\frac{(2k+1)c_1 e^{\gamma _0 t}}{\gamma _0}+c_2(2k+1)\Big ]^{\frac{2}{2k+1}}dz^2. \end{aligned}$$
(23)

Equation (23) describes Bianchi type-III Tsallis holographic dark energy cosmological model in Saez–Ballester scalar–tensor theory of gravitation along with the following properties:

The energy density of the Tsallis holographic DE is given by the following relation [42]

$$\begin{aligned} \rho _t=\alpha L^{2\delta -4} \end{aligned}$$
(24)

where \(\alpha \) is a constant, L can be considered as the size of the current Universe such as the Hubble scale and the future event horizon, and \(\delta \) is a free parameter. It can be seen that \(\rho _t\) reduces to the energy density of HDE model at \(\delta = 1\).

We consider the Hubble horizon as the IR cutoff of the system \(L = H^{-1}\), where H is the Hubble parameter of the model. Hence, in SB theory the energy density (24) takes the form

$$\begin{aligned} \rho _t=\alpha H^{4-2\delta }. \end{aligned}$$
(25)

For our model, the Hubble parameter (H) can be obtained as

$$\begin{aligned} H=\frac{1}{3}\Big (2\frac{\dot{A}}{A}+\frac{\dot{C}}{C}\Big ) =\frac{c_1(2k+1)e^{\gamma _0t}}{3\Big (\big (\frac{2k+1}{\gamma _0}\big )c_1e^{\gamma _0 t}+c_2(2k+1)\Big )}. \end{aligned}$$
(26)

From Eqs. (25) and (26), we get the energy density of the THDE as

$$\begin{aligned} \rho _t= & {} \alpha \left[ \frac{c_1(2k+1)e^{\gamma _0t}}{3\Big (\big (\frac{2k+1}{\gamma _0}\big )c_1e^{\gamma _0 t}+c_2(2k+1)\Big )}\right] ^{4-2\delta }. \end{aligned}$$
(27)

Using Eqs. (21), (22), (26), (27) in (1213), we get the energy density of the matter in terms of Hubble parameter as

$$\begin{aligned} \rho _m= & {} \frac{9k(k+2)}{(2k+1)^2}H^2-\Big (\frac{c_1(2k+1)e^{\gamma _0 t}}{3H}\Big )^{\frac{-2k}{2k+1}} \nonumber \\&+\frac{w{\phi }_0^{2}}{2}\frac{9H^{2} e^{-2 {\gamma _0} t}}{c_1^2(2k+1)^{2}}-\alpha H^{4-2\delta }. \end{aligned}$$
(28)

Using Eqs. (21) and (22) in (15) and (20) we get the SB scalar field \(\phi \) as

$$\begin{aligned} \phi ^{\frac{n+2}{2}}=\frac{n+2}{2} \int \phi _0\Big (\big (\frac{2k+1}{\gamma _0}\big )c_1e^{\gamma _0 t}+c_2(2k+1)\Big )^{-1}dt+c_4, \end{aligned}$$
(29)

where \(\phi _0\) and \(c_4\) are integration constants.

$$\begin{aligned} \gamma =\frac{1-(k-1)c_1\gamma _0 e^{\gamma _0 t}\Big ( \big (\frac{2k+1}{\gamma _0}\big )c_1e^{\gamma _0 t}+c_2(2k+1)\Big )^{\frac{-1}{2k+1}}}{\rho _t \Big (\big (\frac{2k+1}{\gamma _0}\big )c_1e^{\gamma _0 t}+c_2(2k+1)\Big )^{\frac{2k}{2k+1}}} \end{aligned}$$
(30)
Fig. 1
figure 1

Plot of skewness parameter (\(\gamma \)) versus redshift (z) for \(c_{1}=0.01\), \(c_{2}=0.115\), \(k=0.325\) and \(\alpha =0.06\)

Full size image
Fig. 2
figure 2

Plot of energy density (\(\rho _m\)) of matter versus redshift (z) for \(c_{1}=0.01\), \(c_{2}=0.115\), \(k=0.325\), \(\gamma _0=2.13\), \(w=100\), and \(\phi _0=1\)

Full size image
Fig. 3
figure 3

Plot of energy density (\(\rho _t\)) of THDE versus redshift (z) for \(c_{1}=0.01\), \(c_{2}=0.115\), \(k=0.325\), \(\gamma _0=2.13\), \(\delta =2.5\) and \(\alpha =1.5\)

Full size image

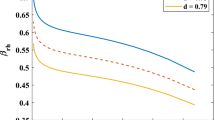
In Fig. 1, we have plotted the behavior of skewness parameter (\(\gamma \)) versus redshift (z) for the different values of \(\gamma _0=2.13,2.23,2.33\). We observe that skewness parameter is positive throughout evolution of the Universe. It can be seen that at initial epoch it increases, reaches a maximum value at present epoch and vanishes at late times. Also, as \(\gamma _0\) increases the skewness parameter value increases. The Figs. 2 and 3 represent the plots of energy density (\(\rho _m\)) of matter and THDE with the Hubble horizon cutoff against redshift (z) for the values, respectively. It is observed that both \(\rho _m\) and \(\rho _t \) are positive and decrease as universe evolves.

In the coming sections, we consider the two cases: Non-interacting model and interacting model. We determine in both the cases, energy density of THDE \(\rho _t\), EoS parameter \({\omega }_t\), squared sound speed \({v_s^{2}}\) and \({\omega }_t-{\omega }_t^{'}\) plane by solving the SB field equations. We also discussed their physical behavior.

Fig. 4
figure 4

Plot of EoS parameter (\(\omega _t\)) versus redshift (z) for \(c_{1}=0.01\), \(c_{2}=0.115\), \(k=0.925\), \(\gamma _0=2.13, 2.23, 2.33\)

Full size image

3.1 Non-interacting model

Firstly, we consider that there is no energy exchange between the two components (dark sectors), and hence, the energy conservation equation (16) leads us to the following separate conservation equations:

$$\begin{aligned}&\dot{\rho _m}+3H\rho _m=0, \end{aligned}$$
(31)
$$\begin{aligned}&\dot{\rho _t}+3H(1+\omega _t)\rho _t+\gamma \frac{\dot{C}}{C} \rho _t=0. \end{aligned}$$
(32)

Using Eqs. (26), (27) and (30) in Eq. (32), we get the EoS parameter of THDE as

$$\begin{aligned} \omega _t= & {} -1+\frac{3(k^2-1)H^{2(\delta -1)}}{(2k+1)^2 \gamma _0\alpha }\nonumber \\&-\frac{(k+1)(\frac{3}{2k+1})^{\frac{4k+1}{2k+1}}}{(c_1 e^{\gamma _0 t})^{\frac{2k}{2k+1}}}H^{\frac{2k\delta +2\delta -4k-3}{2k+1}} \nonumber \\&-\frac{(4-2\delta )}{3}\dot{H}H\nonumber \\&+\frac{(c_1(2k+1)e^{\gamma _0 t})^\frac{1}{2k+1}(3H)^\frac{2k}{2k+1}-3(k-1)c_1\gamma _0 e^{\gamma _0 t}H}{c_1(2k+1)^2e^{\gamma _0 t}},\nonumber \\ \end{aligned}$$
(33)

where \(\dot{H}=\frac{c_1c_2(2k+1)^2\gamma _0t}{3\Big [(\frac{2k+1}{\gamma _0})c_1e^{\gamma _0t}+c_2(2k+2)\Big ]^2}\).

Fig. 5
figure 5

Plot of \(\omega _t\) versus \(\omega _t^{'}\) for \(c_{1}=0.01\), \(c_{2}=0.115\), \(k=0.325\), \(\gamma _0=2.13\), and \(\alpha =1.5\)

Full size image
Fig. 6
figure 6

Plot of energy density of THDE versus redshift (z) for \(c_{1}=0.01\), \(c_{2}=0.115\), \(k=0.325\), \(\gamma _0=2.13, 2.23, 2.33\), and \(\alpha =1.5\)

Full size image

Caldwell and Linder [55] have pointed out that the quintessence phase of DE can be separated into two distinct regions, i.e., thawing (\(\omega _t^{'}>0\), \(\omega _t<0\)) and freezing \((\omega _t^{'}<0\), \(\omega _t<0)\) regions through \(\omega _t- \omega _t^{'}\) plane. Taking the derivative of Eq. (33) with respect to ln a, we get

$$\begin{aligned} \omega _t^{'}= & {} \frac{6(k^2-1)}{\gamma _0\alpha (2k+1)^2} H^{2\delta -4}\dot{H}-\Big (\frac{4-2\delta }{3}\Big )\Big (\ddot{H}+ \frac{\dot{H}^2}{H}\Big )\nonumber \\&-\Big (\Big (\frac{k+1}{{c_1}^{\frac{2k}{2k+1}}}\Big ) \Big (\frac{3}{2k+1}\Big )^{\frac{4k+1}{2k+1}}\Big )\nonumber \\&\times \Big (\frac{2k\delta +2\delta -4k-3}{2k+1}\frac{\dot{H}}{H} -2k\delta \Big )\frac{e^{\frac{-2k\gamma _0t}{2k+1}}}{2k+1} H^{\frac{2k\delta +2\delta -6k-4}{2k+1}}\nonumber \\&+\frac{e^{-\gamma _0 t}}{c_1(2k+1)^2}\Big [(c_1(2k+1)e^{\gamma _0 t})^{\frac{1}{2k+1}}(3)^{\frac{2k}{2k+1}}\big ((1-\gamma _0) H^{\frac{2k}{2k+1}}\nonumber \\&+\frac{2k}{2k+1}H^{\frac{-1}{2k+1}} \dot{H}\big )\nonumber \\&-3c_1(k-1)\gamma _0 e^{\gamma _0 t}\big (\gamma _0 H+\dot{H}\big )+3c_1\gamma _0^2(k-1)e^{\gamma _0 t}H\Big ],\nonumber \\ \end{aligned}$$
(34)

where \(\ddot{H}=\frac{\gamma _0 c_1c_2(2k+1)^3(c_2\gamma _0-c_1e^{\gamma _0 t})e^{\gamma _0 t}}{3\Big ((\frac{2k+1}{\gamma _0})c_1e^{\gamma _0 t}+c_2(2k+2)\Big )^3}\).

The squared sound speed (\(v_s^2\)) is used for studying the stability of the DE models. If \(v_s^2<0\), we obtain a unstable model and if \(v_s^2>0\), we obtain stable model. For our non-interacting THDE model \(v_s^2\) takes the following form

$$\begin{aligned} \left. \begin{aligned} v_s^2&=-1+\frac{3(k^2-1)H^{2(\delta -1)}}{(2k+1)^2 \gamma _0\alpha }-\frac{(k+1)(\frac{3}{2k+1})^{\frac{4k+1}{2k+1}}}{(c_1 e^{\gamma _0 t})^{\frac{2k}{2k+1}}}H^{\frac{2k\delta +2\delta -4k-3}{2k+1}}\\&\quad -\Big (\frac{4-2\delta }{3}\Big )\dot{H}H \\&\quad +\frac{(c_1(2k+1)e^{\gamma _0 t})^\frac{1}{2k+1}(3H)^\frac{2k}{2k+1} -3(k-1)c_1\gamma _0 e^{\gamma _0 t}H}{c_1(2k+1)^2e^{\gamma _0 t}} \\&\quad +\frac{1}{4-2\delta }\Bigg [\frac{6(k^2-1)}{\gamma _0\alpha (2k+1)^2} H^{2\delta -3}\dot{H} -\Big (\frac{4-2\delta }{3}\Big )\Big (H\ddot{H} +\dot{H}^2\Big )\\&\quad -\Bigg (\Big (\frac{k+1}{{c_1}^{\frac{2k}{2k+1}}}\Big ) \Big (\frac{3}{2k+1}\Big )^{\frac{4k+1}{2k+1}}\Bigg )\\&\quad \times \Bigg (\Big (\frac{2k\delta +2\delta -4k-3}{2k+1}\Big ) \frac{\dot{H}}{H}-2k\gamma _0\Bigg )\frac{e^{\frac{-2k\gamma _0t}{2k+1}}}{2k+1}H^{\frac{2k\delta +2\delta -6k-1}{2k+1}} \\&\quad +\frac{e^{-\gamma _0 t}}{c_1(2k+1)^2}\Big [(c_1(2k+1) e^{\gamma _0 t})^{\frac{1}{2k+1}}(3)^{\frac{2k}{2k+1}} \big ((1-\gamma _0)H^{\frac{2k}{2k+1}}\\&\quad +\frac{2k}{2k+1}H^{\frac{-1}{2k+1}}\dot{H}\big )\\&\quad -3c_1(k-1)\gamma _0 e^{\gamma _0 t}\big (\gamma _0 H+\dot{H}\big )+3c_1\gamma _0^2(k-1)e^{\gamma _0 t}H\Big ]\Bigg ]\frac{H}{\dot{H}} \end{aligned}\right\} \end{aligned}$$
(35)

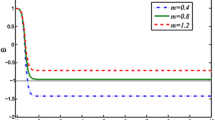
The behaviour of the EoS parameter (\(\omega _t\)) versus redshift (z) for non-interacting THDE model is depicted in the Fig. 4 for different values of \(\gamma _0\). It can be observed that the model starts from matter dominated era, crosses quintessence and vacuum DE (CDM) model (\(\omega _t=-1\)) and finally approached to phantom region (\(\omega _t<-1\)). Also, we observe that as the skewness parameter increases the EoS parameter attains high phantom values.

The \(\omega _t-\omega _t^{'}\) plane for non-interacting THDE model for different values of \(\gamma _0=2.13,2.23,2.33\) is plotted in Fig. 5. It can be observed that the \(\omega _t-\omega _t^{'}\) plane corresponds to both thawing and freezing regions for all values of \(\gamma _0\). This shows that the plane analysis is consistent with the accelerated expansion of the Universe.

We plot squared sound speed \((v_s^2)\) in terms of redshift (z) as represented in Fig. 6. The squared speed of sound bears a decreasing behavior but with negative signature which exhibits unstable behavior of our non-interacting THDE model.

Fig. 7
figure 7

Plot of EoS parameter of THDE versus redshift (z) for \(c_{1}=0.01\), \(c_{2}=0.115\), \(k=0.325\), \(\gamma _0=2.13\), \(\alpha =1.5\), and \(\beta =-0.10,-0.12,-0.14\)

Full size image
Fig. 8
figure 8

Plot of EoS parameter of THDE versus redshift (z) for \(c_{1}=0.01\), \(c_{2}=0.115\), \(k=0.325\), \(\gamma _0=2.23\), and \(\alpha =1.5\), \(\beta =-0.10,-0.12,-0.14\)

Full size image

3.2 Interacting model

In this case, we consider the interaction between two dark components. Since the nature of both DE and DM is still unknown, there is no physical argument to exclude the possible interaction between them. Recently, some observational data shows that there is an interaction between dark sectors [56, 57]. Abdalla et al.  [58, 59] have investigated the signature of interaction between DE and DM by using optical, X-ray and weak lensing data from the relaxed galaxy clusters. So, it is reasonable to assume the interaction between DE and DM in cosmology. For this purpose, we can write the energy conservation equations as

$$\begin{aligned}&\dot{\rho _m}+3H\rho _m=Q \end{aligned}$$
(36)
$$\begin{aligned}&\dot{\rho _t}+3H(1+\omega _t)\rho _t+\gamma \frac{\dot{C}}{C} \rho _t=-Q, \end{aligned}$$
(37)

where the quantity Q denotes interaction between DE components. From the Eqs. (36) and (36), we can say that the total energy is conserved. Since there is no natural information from fundamental physics on the interaction term Q, one can only study it to a phenomenological level. Various forms of interaction term extensively considered in literature include \(Q =3cH\rho _m\), \(Q=3cH\rho _{de}\) and \(Q=3cH(\rho _m+\rho _{de})\). Here, c is a coupling constant and positive c means that DE decays into DM, while negative c means DM decays into DE. Here we consider \(Q=3\beta H\rho _t\) as the interaction term with the coupling parameter \(\beta \).

Using Eqs. (26), (27), (30) in (3637), we find that the EoS parameter

$$\begin{aligned} \omega _t= & {} -1-3\beta +\frac{3(k^2-1)H^{2(\delta -1)}}{(2k+1)^2 \gamma _0\alpha } \nonumber \\&-\frac{(k+1)(\frac{3}{2k+1})^{\frac{4k+1}{2k+1}}}{(c_1 e^{\gamma _0 t})^{\frac{2k}{2k+1}}}H^{\frac{2k\delta +2\delta -4k-3}{2k+1}} -\frac{(4-2\delta )}{3}\dot{H}H\nonumber \\&+\frac{(c_1(2k+1)e^{\gamma _0 t})^\frac{1}{2k+1}(3H)^\frac{2k}{2k+1}-3(k-1)c_1\gamma _0 e^{\gamma _0 t}H}{c_1(2k+1)^2e^{\gamma _0 t}}.\nonumber \\ \end{aligned}$$
(38)
Fig. 9
figure 9

Plot of EoS parameter of THDE versus redshift (z) for \(c_{1}=0.01\), \(c_{2}=0.115\), \(k=0.325\), \(\gamma _0=2.33\), \(\beta =-0.10,-0.12,-0.14\), and \(\alpha =1.5\)

Full size image
Fig. 10
figure 10

Plot of for \(c_{1}=0.01\), \(c_{2}=0.115\), \(k=0.325\), \(\beta =-0.10,-0.12,-0.14\), \(\alpha =1.5\), and \(\gamma _0=2.13\)

Full size image
Fig. 11
figure 11

Plot of for \(c_{1}=0.01\), \(c_{2}=0.115\), \(k=0.325\), \(\beta =-0.10,-0.12,-0.14\), \(\alpha =1.5\), and \(\gamma _0=2.23\)

Full size image

Three Figs. 7, 8 and 9 show that the behavior of EoS parameter for interacting THDE model versus redshift (z) for different values of \(\gamma _0\) and \(\beta \). It is observed that for all the considered values of \(\gamma _0\) and \(\beta \), the model starts from matter dominated era, crosses the quintessence phase \(-1<\omega _t<-0.33\) and finally approaches to \(\Lambda \)CDM model \(\omega _t=-1\). Also, we observe that as \(\beta \) increases the EoS parameter of our model approaches high phantom values.

Taking the derivative of Eq. (38) with respect to lna, we get

$$\begin{aligned} \omega _t^{'}= & {} \frac{6(k^2-1)}{\gamma _0\alpha (2k+1)^2} H^{2\delta -4}\dot{H}- \Bigg (\frac{4-2\delta }{3}\Bigg ) \Bigg (\ddot{H}+\frac{\dot{H}^2}{H}\Bigg ) \nonumber \\&-\Bigg (\Bigg (\frac{k+1}{{c_1}^{\frac{2k}{2k+1}}}\Bigg ) \Bigg (\frac{3}{2k+1}\Bigg )^{\frac{4k+1}{2k+1}}\Bigg ) \frac{e^{\frac{-2k\gamma _0t}{2k+1}}}{2k+1}\nonumber \\&\times \Bigg (\frac{(2k\delta +2\delta -4k-3)}{2k+1} \frac{\dot{H}}{H}-2k\delta \Bigg )H^{\frac{2k\delta +2\delta -6k-4}{2k+1}}\nonumber \\&+\frac{e^{-\gamma _0 t}}{c_1(2k+1)^2} \Bigg [(c_1(2k+1)e^{\gamma _0 t})^{\frac{1}{2k+1}}(3)^{\frac{2k}{2k+1}}\nonumber \\&\times \bigg ((1-\gamma _0)H^{\frac{2k}{2k+1}}+\frac{2k}{2k+1} H^{\frac{-1}{2k+1}}\dot{H}\bigg )\nonumber \\&-3c_1(k-1)\gamma _0 e^{\gamma _0 t} (\gamma _0 H+\dot{H})+3c_1\gamma _0^2(k-1)e^{\gamma _0 t}H\Bigg ],\nonumber \\ \end{aligned}$$
(39)
Fig. 12
figure 12

Plot of energy density of THDE versus redshift (z) for \(c_{1}=0.01\), \(c_{2}=0.115\), \(k=0.325\), \(\beta =-0.10,-0.12,-0.14\), \(\alpha =1.5\), and \(\gamma _0=2.33\)

Full size image
Fig. 13
figure 13

Plot of squared sound speed (\(v_s^2\) ) versus redshift (z) for \(c_{1}=0.01\), \(c_{2}=0.115\), \(k=0.325\), \(\gamma _0=2.13,2.23,2.33\), \(\alpha =1.5\), and \(\beta =-0.10\)

Full size image
Fig. 14
figure 14

Plot of squared sound speed (\(v_s^2\) ) versus redshift (z) for \(c_{1}=0.01\), \(c_{2}=0.115\), \(k=0.325\), \(\gamma _0=2.13,2.23,2.33\), \(\alpha =1.5\), and \(\beta =-0.12\)

Full size image

The \(\omega _t-\omega _t^{'}\) plane for interacting THDE model for different values of \(\gamma _0\) and \(\beta \) shown in the Figs. 10, 11 and 12. It can be observed that the plane corresponds to the thawing phase \(\omega _t^{'}>0\) and \(\omega _t<0\) for all considered values of \(\gamma _0\) and \(\beta \).

The squared sound speed \(v_s^2\) in this case is obtained as

$$\begin{aligned} \left. \begin{aligned} v_s^2=&-1-3\beta +\frac{3(k^2-1)H^{2(\delta -1)}}{(2k+1)^2 \gamma _0\alpha }\\&-\frac{(k+1)\bigg (\frac{3}{2k+1}\bigg )^{\frac{4k+1}{2k+1}}}{(c_1 e^{\gamma _0 t})^{\frac{2k}{2k+1}}}H^{\frac{2k\delta +2\delta -4k-3}{2k+1}} -\Bigg (\frac{4-2\delta }{3}\Bigg )\dot{H}H \\&\times \frac{(c_1(2k+1)e^{\gamma _0 t})^\frac{1}{2k+1}(3H)^\frac{2k}{2k+1}-3(k-1)c_1\gamma _0 e^{\gamma _0 t}H}{c_1(2k+1)^2e^{\gamma _0 t}}\\&+\frac{1}{(4-2\delta )}\frac{H}{\dot{H}}\Bigg [\frac{6(k^2-1)}{\gamma _0\alpha (2k+1)^2}H^{2\delta -3}\dot{H} \\&-\Bigg (\frac{4-2\delta }{3}\Bigg )\Bigg (H\ddot{H}+\dot{H}^2\Bigg )\\&-\Bigg (\Bigg (\frac{k+1}{{c_1}^{\frac{2k}{2k+1}}}\Bigg ) \Bigg (\frac{3}{2k+1}\Bigg )^{\frac{4k+1}{2k+1}}\Bigg )\frac{e^{\frac{-2k\gamma _0t}{2k+1}}}{2k+1}H^{\frac{2k\delta +2\delta -6k-1}{2k+1}}\\&\times \Bigg (\Bigg (\frac{2k\delta +2\delta -4k-3}{2k+1}\Bigg )\frac{\dot{H}}{H}-2k\gamma _0\Bigg )\\&+\frac{e^{-\gamma _0 t}}{c_1(2k+1)^2}\Bigg [(c_1(2k+1)e^{\gamma _0 t})^{\frac{1}{2k+1}}(3)^{\frac{2k}{2k+1}}\\&\times \bigg ((1-\gamma _0)H^{\frac{2k}{2k+1}}+\frac{2k}{2k+1}H^{\frac{-1}{2k+1}}\dot{H}\bigg )\\&-3c_1(k-1)\gamma _0 e^{\gamma _0 t}\big (\gamma _0 H+\dot{H}\big )+3c_1\gamma _0^2(k-1)e^{\gamma _0 t}H\Big ]\Bigg ] \end{aligned}\right\} \end{aligned}$$
(40)
Fig. 15
figure 15

Plot of squared sound speed (\(v_s^2\) ) versus redshift (z) for \(c_{1}=0.01\), \(c_{2}=0.115\), \(k=0.325\), \(\gamma _0=2.13,2.23,2.33\), \(\alpha =1.5\), and \(\beta =-0.14\)

Full size image

We plot the squared sound speed in terms of redshift (z) as represented in Figs. 13, 14, and 15. The squared speed of sound is negative and decreasing function as Universe evolves. This shows that our model is unstable.

Fig. 16
figure 16

Plot of Deceleration parameter (q) versus redshift (z) for \(c_{1}=0.01\), \(c_{2}=0.115\), \(k=0.325\), \(\gamma _0=2.13\)

Full size image

3.3 Deceleration parameter (DP)

The sign of DP (q) shows whether the model either accelerates or decelerates. If \(q>0\), the model exhibits decelerating expansion, if \(q=0\) a constant rate of expansion and an accelerating expansion if \(-1<q<0\). The Universe exhibits exponential expansion or de Sitter expansion for \(q=-1\) and super exponential expansion for \(q<-1\). The DP for our model, in both (non-interacting and interacting) cases, is given by

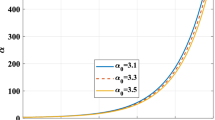
$$\begin{aligned} q=\frac{-a\ddot{a}}{\dot{a}^2}=-1-\frac{3c_2\gamma _0t}{c_1e^{\gamma _0t}} \end{aligned}$$
(41)

The plot of deceleration parameter versus redshift (z) is shown in the Fig. 16. It indicates that q exhibits negative behavior throughout evolution and finally approaches to \(-1\), which shows accelerating behavior. Also, it can be observed that initially our models exhibit super exponential expansion \((q<-1)\) and late times it approaches to exponential expansion \((q=-1)\).

Fig. 17
figure 17

Plot of statefinder parameter (r, s) for \(c_{1}=0.01\), \(c_{2}=0.115\), \(k=0.325\), \(\gamma _0=2.13\)

Full size image

3.4 Statefinder parameters (r, s)

Sahni et al. [60] and Alam et al. [61] proposed a new geometrical diagnostic pair named the statefinder pair (r, s), where r is generated from the average scale factor (a) and its derivatives with respect to the cosmic time t up to the third order and s is a simple combination of r and this (r, s) is defined as follows:

$$\begin{aligned} r= & {} \frac{\dddot{a}}{aH^3}; s=\frac{r-1}{3(q-\frac{1}{2})} \end{aligned}$$
(42)
$$\begin{aligned} r= & {} \frac{9}{c_1^{2}(2k+1)^{2}}\Bigg [\gamma _0^{2}e^{-2\gamma _0t} \Bigg (\bigg (\frac{2k+1}{\gamma _0}\bigg )c_1e^{\gamma _0 t}+c_2(2k+1)\Bigg )^{2}\nonumber \\&-\frac{2(2k+3)\gamma _0}{3}\nonumber \\&e^{\gamma _0t}\Bigg (\bigg (\frac{2k+1}{\gamma _0}\bigg )c_1e^{\gamma _0 t}+c_2(2k+1)\Bigg )-\frac{2c_1^{2}(2k+1)}{3}\Bigg ]\nonumber \\ \end{aligned}$$
(43)

and

$$\begin{aligned} s= & {} \Bigg \{\gamma _0^{2}e^{-2\gamma _0t}\Bigg (\bigg (\frac{2k+1}{\gamma _0}\bigg )c_1e^{\gamma _0 t}+c_2(2k+1)\Bigg )^{2}\nonumber \\&-\frac{2(2k+3)\gamma _0}{3}e^{\gamma _0t} \Bigg (\bigg (\frac{2k+1}{\gamma _0}\bigg )c_1e^{\gamma _0 t}+c_2(2k+1)\Bigg )\nonumber \\&-\frac{2c_1^2(2k+1)}{3}-\frac{c_1^{2}(2k+1)}{9}\Bigg \} \Bigg \{\Bigg [\frac{1}{2}\nonumber \\&-\frac{\gamma _0}{c_1(2k+1)} e^{-\gamma _0t}\Bigg (\bigg (\frac{2k+1}{\gamma _0}\bigg ) c_1e^{\gamma _0}+c_2(2k+1)\Bigg )\nonumber \\&-c_2(2k+1)e^{\gamma _0t}\Bigg ]c_1^2(2k+1)^2\Bigg \}^{-1} \end{aligned}$$
(44)

In Fig. 17, we have plotted the trajectories of the \(r-s\) plane. It can be observed that the region belongs to \(s>0\) and \(r<1\). Hence our model corresponds to the DE regions such as quintessence and phantom.

3.5 Om diagnostic:

Sahni et al. [62] has been proposed Om-diagnostic parameter as a complementary to the statefinder parameter, which helps to distinguish the present matter density contrast Om in different models more effectively. This is also a geometrical diagnostic that explicitly depends on redshift (z) and the Hubble parameter (H). It is defined as follows:

$$\begin{aligned} Om(z)=\frac{\frac{H^{2}(z)}{H_{0}^{2}}-1}{(1+z)^{3}-1}, \end{aligned}$$
(45)

here \(H_0\) is the present value of the Hubble parameter.

Fig. 18
figure 18

Plot of Om versus redshift (z) for \(c_{1}=0.01\), \(c_{2}=0.115\), \(k=0.325\), \(\gamma _0=2.13\), and \(H_0=1\)

Full size image

We have plotted the evolution of Om(z) in the Fig. 18. It can be observed that initially the slope of Om(z) is negative and finally it approaches to positive value. Hence, our models initially behave like quintessence model and finally approaches to phantom region. We can conclude that the behavior of Om-diagnostic parameter coincides with the behavior of EoS parameter.

4 Discussion and comparison

In this section, we present a comparative analysis of our work with the recent works on THDE and with the modern observational data.

Ghaffari et al. [63] have studied FRW THDE model in Brans–Dicke cosmology. They found that in both interacting and non-interacting THDE models, the EoS parameter approaches to the cosmological constant in future. The models are not stable. Zadeh et al. [43] have studied FRW THDE by assuming various infrared cutoffs. It is observed that the EoS parameter of interacting and non-interacting THDE models exhibit phantom DE behavior for all the IR cutoffs. Also, they are unstable. Aditya et al. [46] have discussed observational constraints on THDE in Brans–Dicke scalar–tensor theory with logarithmic scalar field. They have investigated an EoS parameter starts from matter dominated era, then goes towards quintessence region, and finally, approaches to vacuum DE era in non-interacting case, while in interacting case, the EoS parameter starts from quintessence region and turns towards phantom region by crossing phantom divide line. Ghaffari et al. [64] have investigated THDE in fractal Universe. They have discussed an EoS parameter in non-interacting case, THDE model in the fractal universe emulates the cosmological constant while in interacting case, THDE model can cross the phantom divide line at the late time. Sharif and Saba [47] have discussed THDE models in f(G, T) gravity. They have concluded that the EoS parameter indicates phantom phase while the deceleration parameter demonstrates accelerated cosmic epoch for both conserved as well as non-conserved energy–momentum tensor. Dubey et al. [53, 65] have studied Bianchi type-I and III THDE models. In both the models, the EoS parameter approaches to \(\Lambda \)CDM model in future. Dubey et al. [52] have discussed THDE models with Hubble horizon as IR cutoff in axially symmetric space-time. They have obtained an EoS parameter which varies quintessence region, crosses the phantom divide line.

In our Bianchi type-III THDE models, the study of EoS parameter reveals that the model starts from matter dominated era, varies in quintessence phase and finally approaches phantom region in non-interacting case. In interacting case, the model starts from matter dominated era and finally approaches to \(\Lambda \)CDM model at late times. It can be observed that the behavior of EoS parameter in our models is coincide with the models given in the literature mentioned above. The stability analysis also coincides with the existing THDE models. The behavior of deceleration parameter coincides with the THDE model obtained by Sharif and Saba [47].

Also, it is worthwhile to mention here that the present values of EoS parameter of our DE models are in agreement with the modern Plank observational data given by Aghanim et al. [66]. It gives the constraints on EoS parameter of dark energy as follows:

$$\begin{aligned} \omega _t= & {} -1.56^{+0.60}_{-0.48}(Planck+TT+lowE)\\ \omega _t= & {} -1.58^{+0.52}_{-0.41}(Planck+TT, EE+lowE)\\ \omega _t= & {} -1.57^{+0.50}_{-0.40}\\&(Planck+TT, TE, EE+lowE+lensing)\\ \omega _t= & {} -1.04^{+0.10}_{-0.10}\\&(Planck+TT, TE, EE+lowE+lensing+BAO) \end{aligned}$$

It can be observed from the Figs. 4, and (7, 8, 9) that the EoS parameter of our models in both non-interacting and interacting cases lie within the above observational limits which shows the consistency of our results with the above cosmological data.

5 Conclusions

The current scenario of accelerated expansion of the universe has become an important subject of investigation. In order to explain this cosmic acceleration, two approaches have been suggested. One way is to study various dynamical DE models and the other is to consider alternative theories of gravity. Here, we have studied the accelerated expansion by assuming the THDE in Bianchi type-III universe within the framework of SB scalar–tensor theory of gravity. Using the relation between the metric potentials, we have obtained the solution of SB field equations which leads to a varying DP. We have considered interacting and non-interacting models of matter and THDE. We have also constructed different cosmological parameters to analyze the viability of these models and our conclusions are the following:

  • For models, we observe that skewness parameter is positive throughout evolution of the Universe. It can be seen (Fig. 1) that at initial epoch it increases, reaches a maximum value at present epoch and vanishes at late times. Also, as \(\gamma _0\) increases the skewness parameter value increases. Skewness parameter increases with increase in the parameter \(\phi \). It is observed from Figs. 2 and 3 both \(\rho _m\) and \(\rho _t \) are positive and decrease as universe evolves.

  • It can be observed that the EoS parameter of non-interacting THDE model starts from matter dominated era, varies in quintessence era and finally approaches to phantom region(\(\omega _t<-1\)) by crossing vacuum DE (\(\omega _t=-1\)) for \(\gamma _0=2.13\), \(\gamma _0=2.23\), \(\gamma _0=2.33\). Also, we observe that as the skewness parameter increases the EoS parameter of our model attains maximum phantom value. The EoS parameter of interacting THDE model starts from matter dominated era, varies in quintessence phase and finally approaches to \(\Lambda \)CDM model (ref. Figs. 7, 8, 9) for all the the values of \(\gamma _0=2.13,2.23,2.33\) and \(\beta =-0.10, -0.12,-0.14\). Finally, we observed that the EoS parameter of our models coincide with the existing THDE literature and the present values of EoS parameter lie within the modern Planck observational data.

  • It can be observed that the \(\omega _t-\omega _t^{'}\) plane corresponds to both thawing and freezing regions for all values of \(\gamma _0\) in non-interacting case, whereas in interacting case the model varies in thawing region only. However, the trajectories of \(\omega _t-\omega _t^{'}\) plane shows consistent results with the observational data and can be considered as viable THDE models. It is observed that our both non-interacting and interacting THDE models are unstable (ref. Figs. 6, 13, 14, 15).

  • The deceleration parameter, statefinder and Om-diagnostic parameters are same for both non-interacting and interacting models. It can be observed that deceleration parameter exhibits negative behavior throughout evolution and finally approaches to \(-1\), which shows accelerating behavior (ref. Fig. 16). Also, we observed that initially our models exhibit super exponential expansion \((q<-1)\) and at late times it approaches to exponential expansion. This behavior coincides with the THDE model obtained by Sharif and Saba [47]. Statefinder analysis gives that our THDE model corresponds to the DE regions such as quintessence and phantom (ref. Fig. 17). We observe that the slope of Om(z) is negative, hence our models behave like quintessence model (ref. Fig. 18).