1 Introduction

One the most important milestones for research in modern Cosmology as well as gravitational physics is observed late time acceleration of the Universe, Which is indicated by observational data from the Cosmic microwave background [1], observations of Type Ia Supernovae [2, 3] and large scale structure [4]. In Ref. [5, 6] believed that dark energy (DE) occupies 73% of the Universe, dark matter (DM) occupies 23%, and rest of the energy 4% is baryonic matter. In order to the details of this late time acceleration, two different approaches have been advocated: (i) to construct various DE candidate and (ii) the modification of Einstein theory of gravitation. Among the several modifications of the theories Brans–Dicke (BD) [7] and Saez–Ballester (SB)[8] scalar-tensor theories play vital role. In literatures [9,10,11,12,13,14,15], there are very interesting reviews on both dynamical DE models and modified theories. Several dynamical DE models include a family of scalar field such as quintessence [16,17,18,19], Phantom [20,21,22,23], Quintom [24, 25], Tachon [26, 27], K-Essence [28], Chaplygin gas and modified Chaplygin gas [29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44] models have been developed.

Amongst various DE candidates, the holographic DE (HDE) and new agegraphic DE, Tsallis holographic DE (THDE), which contain some significant properties of the quantum gravity have drawn considerable attention to solve the DE puzzle. HDE is depends on principle of holographic [45, 46] that states that the no. of degrees of freedom of a physical system scales with its bounding are rather than with its volume. HDE model was conjectured with Benkenstein entropy and Hubble horizon as IR cut-off which fails to produce suitable explanation for the history of a flat FRW Universe [47,48,49]. Li et al. [50] have performed a detailed investigation on the cosmological constraints on the holographic dark energy (HDE) model by using the Plank data. Tavayef et al. [51] have discussed about THDE model and found that the identification of IR-cutoff with the Hubble radius provides the late time accelerated Universe in the absence of interaction between two dark sectors of the Universe. Sharif et al. [52] have reconstruction paradigm for THDE model with dust fluid has been studied using generalized Tsallis entropy conjecture with Hubble horizon in the background of f(G, T) gravity and the cosmological evolution through cosmic diagnostic parameters and phase planes discussed. According to Ref. [53], Tsallis HDE in BD cosmology have been studied by considering the Hubble horizon as the IR cutoff and studied the the stability analysis which shows that both the interacting and non-interacting models are classically unstable. Abdollahi Zadeh et al. [54] has explained a short note on THDE model. Gunjan et al. [55] has discussed Statefinder diagnosis for interacting THDE models with \(\omega _t\)-\(\omega _t^{'}\) pair. Ghaffari et al. [53] have explained Tsallis holographic dark energy in Fractal Universe. Sadri [56] has discussed observational constraints on interacting THDE model. Aditya et al. [57] have studied observational constraint on interacting THDE in logarithmic BD theory. Sharif and Saba [58] have established a reconstruction scenario for THDE model in the background of modified theory of gravity with the Hubble horizon as well as the generalised Tsallis entropy conjecture using the powerlaw solution of the scale factor.

The Bianchi type (BT) models are the nice and simplest anisotropic models, which completely explain the anisotropic effects. Mishra et al. [59] have investigated BT-V string cosmological model with anisotropic distribution of DE. Aditya and Reddy [60] have studied BT-I string models in modified theory of gravity. Sharif et al. [61] have investigated BT-I new HDE model in the background of BD theory of gravity. Aditya and Reddy [62] have investigated anisotropic new HDE model in the framework of SB theory of gravitation.

Chandra et al. [63] have studied THDE in BT-I Universe using hybrid expansion law with k-essence. Korunur [64] has studied THDE model in Bianchi type-III Universe with scalar fields. Zadeh et al. [65] explained the cosmic evolution of THDE in BT-I model filled by DE and DM interacting with each other throughout a sign-changeable interaction with various IR cut-offs. Recently, Prasanthi and Aditya [66] have investigated BT-VI\(_0\) Renyi HDE models in the frame-work of general relativity. Very recently, Santhi and Sobhanbabu [67, 68] have studied BT-III and BT-VI\(_0\) THDE models in Scalar tensor theories of gravitation.

In this work, inspired by the above investigations, we have considered the Kantowski–Sachs Universe THDE model with SB theory of gravitation. The organization of this work is as follows: In the next section, we have derived SB field equations with the help of kantowski–Sachs in the presence of two interacting fields: DM and THDE components. Also, devoted to the cosmological solution of the field equations. In Sect. 3, we study the evolution of the Universe by considering an non-interaction and sign-changeable interaction between DM and THDE whose IR cut-offs are the apparent horizon. Finally, in last section, we presented the conclusions of this work.

2 Metric and SB field equations

We consider a homogeneous and anisotropic Kantowski–Sachs (KK) Universe described by the line-element

$$\begin{aligned} ds^{2}=dt^{2}-A^{2}(t)dr^{2}-B^{2}(t)(d\theta ^{2} +sin^{2}\theta d\phi ^{2}), \end{aligned}$$
(1)

where A(t) and B(t) are functions of cosmic time t only. For the Universe filled by a DM without pressure with energy density \((\rho _M)\), and DE candidate with energy density (\(\rho _{T}\)), The SB field equations are

$$\begin{aligned} G_{ij}-w \phi ^{n}\Big (\phi _{,i}\phi _{,j}-\frac{1}{2}g_{ij}\phi _{,k}\phi ^{,k}\Big ) =~-(T_{ij} +\bar{T_{ij}}), \end{aligned}$$
(2)

where \(T_{ij}\) and \(\bar{T_{ij}}\) are energy momentum tensors (EMT) for DM and DE respectively. Scalar field \(\phi \) equation

$$\begin{aligned} 2\phi ^n \phi _{,i}^{,i}+n\phi ^{n-1}\phi _{,k}\phi ^{,k}~=~0, \end{aligned}$$
(3)

and energy conservation equations are

$$\begin{aligned} T_{ij}+\bar{T_{ij}}~=~0. \end{aligned}$$
(4)

The EMT for DM (\(T_{ij}\)) and anisotropic DE are given by

$$\begin{aligned}&T_{ij}=diag [1,0,0,0] \rho _M,~~and~~\nonumber \\&\bar{T_{ij}}=diag[1,-\omega _T,-(\omega _T+\gamma ),-(\omega _T+\gamma )] \rho _T, \end{aligned}$$
(5)

where \(\omega _T=\frac{p_T}{\rho _T}\) is equation of state (EoS) parameter, \(p_t\) represents pressure of THDE and \(\alpha \) is skewness parameter is in deviation from EoS parameter \(\omega _T\) on y and z axes respectively.

The SB field Eq. (2), for KK line-element Eq. (1) with the help of Eq. (5), can be written as

$$\begin{aligned}&2\frac{{\ddot{B}}}{B}+\frac{\dot{B^2}}{B^2}+\frac{1}{B^2} -\frac{w}{2}\phi ^{n}{\dot{\phi }}^{2}~=~-\omega _T~ \rho _T, \end{aligned}$$
(6)
$$\begin{aligned}&\frac{{\ddot{A}}}{A}+\frac{{\ddot{B}}}{B}+\frac{{\dot{A}}{\dot{B}}}{AB} -\frac{w}{2}\phi ^{n}{\dot{\phi }}^{2}~=~-(\omega _T+\alpha )~ \rho _T, \end{aligned}$$
(7)
$$\begin{aligned}&2\frac{{\dot{A}}{\dot{B}}}{AB}+\frac{\dot{B^{2}}}{B^2}+\frac{1}{B^{2}} +\frac{w}{2}\phi ^{n}{\dot{\phi }}^{2}~=~\rho _M+\rho _T, \end{aligned}$$
(8)
$$\begin{aligned}&\ddot{\phi }+\left( \frac{{\dot{A}}}{A}+2\frac{{\dot{B}}}{B}\right) {\dot{\phi }} +\frac{n}{2}\frac{\dot{\phi ^{2}}}{\phi }=0. \end{aligned}$$
(9)

We can write the continuity Eq. (4) of the DM and DE as

$$\begin{aligned}&\dot{\rho _M}+\left( \frac{{\dot{A}}}{A}+2\frac{{\dot{B}}}{B}\right) {\rho _m}+\dot{\rho _T}+\left( \frac{{\dot{A}}}{A}+2\frac{{\dot{B}}}{B}\right) (1+\omega _T)\rho _T\nonumber \\&\quad +2\frac{{\dot{B}}}{B}\alpha \rho _T=0, \end{aligned}$$
(10)

where overhead dot (.) represents ordinary differentiation with respect to cosmic time t.

The SB field equations Eqs. (6)–(8) form a system of four non-linear equations with seven (7) unknowns: A, B, \(\rho _M\), \(\rho _{T}\), \(\omega _T\), \(\alpha \), and \(\phi \). Hence to find a deterministic solution of the non linear equations we use the condition that the shear scalar \(\sigma ^2\) is directly proportional to scalar expansion \(\theta \) which leads to a relation between the metric potentials so that in Ref. [69] we have

$$\begin{aligned} A=B^k, \end{aligned}$$
(11)

where \(k\ne 1\) is positive constant. From Eqs. (6), (7), and (11), we get

$$\begin{aligned}&\frac{{\ddot{B}}}{B}+(1+k)\frac{{\dot{B}}}{B}=\frac{1}{k-1}\left( \alpha \rho _{T} +\frac{1}{B^2}\right) \frac{B}{{\dot{B}}}. \end{aligned}$$
(12)

To get the solution of the models we consider the ref [70, 71]

$$\begin{aligned} \alpha =\frac{\alpha _0(k-1){\dot{B}}B-1}{B^2\rho _{T}}, \end{aligned}$$
(13)

where \(\alpha _0\) is an arbitrary constant. Now from equations (12) and (13), we obtain the metric potentials as

$$\begin{aligned} A&=\Big [\frac{\alpha _1(k+2)}{\alpha _0}e^{\alpha _0 t}+\alpha _2(k+2)\Big ]^{\frac{k}{k+2}},\nonumber \\ B&=\Big [\frac{\alpha _1(k+2)}{\alpha _0}e^{\alpha _0 t}+\alpha _2(k+2)\Big ]^{\frac{1}{k+2}}, \end{aligned}$$
(14)

where \(\alpha _1\) and \(\alpha _2\) is an constants of integrations. The line-element Eq (1) can, be written as

$$\begin{aligned} ds^{2}= & {} dt^{2}-\Big [\frac{\alpha _1(k+2)}{\alpha _0}e^{\alpha _0 t}+\alpha _2(k+2)\Big ]^{\frac{2k}{k+2}}dr^{2}\nonumber \\&-\Big [\frac{\alpha _1(k+2)}{\alpha _0}e^{\alpha _0 t}+\alpha _2(k+2)\Big ]^{\frac{2}{k+2}}(d\theta ^{2} +sin^{2}\theta d\phi ^{2}).\nonumber \\ \end{aligned}$$
(15)

Equation (15) describes KK THDE cosmological model in SB scalar tensor theory of gravitation.

The Hubble parameter H for our model can be obtain as

$$\begin{aligned} H=\frac{1}{3}\left( \frac{{\dot{A}}}{A}+2\frac{{\dot{B}}}{B}\right) =\frac{\alpha _1}{\left( \frac{\alpha _1}{\alpha _0}+\alpha _2 e^{-\alpha _0 t}\right) } \end{aligned}$$
(16)

The THDE has been proposed by Tavayef et al., [72]. The energy density of THDE is can be written as

$$\begin{aligned} \rho _{T}=\gamma _1 H^{4-2\delta }=\Big [\frac{\alpha _1}{\big (\frac{\alpha _1}{\alpha _0}+\alpha _2 e^{-\alpha _0 t}\big )}\Big ]^{4-2\delta }, \end{aligned}$$
(17)

where \(\gamma _1\) and \(\delta \) are constants.

Fig. 1
figure 1

Plot of skewness parameter (\(\alpha \)) versus time (t) for \(k=1.9\), \(\alpha _1=1.2\), \(\alpha _2=0.52\), \(w=1000\), \(\phi _0=1\), and \(\gamma _1=101\)

Full size image

3 Non-interacting THDE in the SB cosmology

In this case, we consider that there is no energy exchange between the cosmos sectors (DM, THDE), and hence, the energy conservation equations can be written in separately, so that we have from Eq. (10),

$$\begin{aligned} \dot{\rho _M}+3H\rho _M=0, \end{aligned}$$
(18)

and

$$\begin{aligned} \dot{\rho _T}+3H(1+\omega _T)\rho _{T}+2\alpha \rho _{T}\frac{{\dot{B}}}{B}=0 \end{aligned}$$
(19)

From Eq. (9), we get

$$\begin{aligned}&\phi ^{\frac{n+2}{2}}=\left( \frac{n+2}{2}\right) \phi _0\nonumber \\&\quad \times \int \left[ \frac{\alpha _1(k+2)}{\alpha _0}e^{\alpha _0 t}+\alpha _2(k+2)\right] ^{-3}dt+\phi _1, \end{aligned}$$
(20)

where \(\phi _0\) and \(\phi _1\) are constants of integration. Taking the cosmic time derivative of Eq. (17), we have

$$\begin{aligned} \dot{\rho _{T}}=\gamma _1 (4-2\delta )H^{3-2\delta }{\dot{H}}. \end{aligned}$$
(21)

Now using Eqs. (14), (17), and (20) in Eq. (8), we get

$$\begin{aligned} \left. \begin{aligned} \rho _M&=\frac{(2k+1)\alpha _1^2 e^{2\alpha _0 t}}{\Big [\frac{\alpha _1(k+2)}{\alpha _0}e^{\alpha _0 t}+\alpha _2(k+2)\Big ]^{2}}+\frac{1}{\Big [\frac{\alpha _1(k+2)}{\alpha _0}e^{\alpha _0 t}+\alpha _2(k+2)\Big ]^{\frac{2}{2+k}}}\\&\quad +\frac{w}{2}\phi _0^{2}\Big [\frac{\alpha _1(k+2)}{\alpha _0}e^{\alpha _0 t}+\alpha _2(k+2)\Big ]^{-6}-\gamma _1\Big [\frac{\alpha _1}{\frac{\alpha _1}{\alpha _0}+\alpha _2 e^{-\alpha _0 t}}\Big ]^{4-2\delta } \end{aligned}\right\} \end{aligned}$$
(22)
Fig. 2
figure 2

Plot of energy density (\(\rho _T\)) of THDE versus time (t) for \(k=1.9\), \(\alpha _1=1.2\), \(\alpha _2=0.52\), and \(\gamma _1=101\)

Full size image

Using Eqs. (14), (17) in Eq. (13), we get skewness parameter \(\alpha \) is

$$\begin{aligned} \alpha =\frac{\alpha _0 \alpha _1(k-1)e^{\alpha _0 t}\Big [\frac{\alpha _1(k+2)}{\alpha _0}e^{\alpha _0 t}+\alpha _2(k+2)\Big ]^{\frac{-k}{2+k}}-1}{\gamma _1 \Big [\frac{\alpha _1(k+2)}{\alpha _0}e^{\alpha _0 t}+\alpha _2(k+2)\Big ]^{2}\Big [\frac{\alpha _1}{\frac{\alpha _1}{\alpha _0}+\alpha _2 e^{-\alpha _0 t}}\Big ]^{4-2\delta }}\nonumber \\ \end{aligned}$$
(23)

From Eqs. (14), (16), (17) and (19), we get the EoS parameter \(\omega _T\) of THDE is

$$\begin{aligned} \left. \begin{aligned} \omega _T&=-1+2\alpha _0\alpha _1\alpha _2\gamma _1(\delta -2)e^{\alpha _0 t}H^{3-2\delta }+ \frac{2\alpha _1^{4\delta -9}}{3\gamma _1}\\&\quad \times \Big [1-\alpha _0 \alpha _1(k-1)e^{\alpha _0t}\Big [\frac{\alpha _1(k+2)}{\alpha _0}e^{\alpha _0 t}+\alpha _2(k+2)\Big ]^{\frac{-k}{2+k}}\Big ]\\&\quad \times \Big [\frac{\alpha _1(k+2)}{\alpha _0}e^{\alpha _0 t}+\alpha _2(k+2)\Big ]^{-(\frac{4+k}{2+k})}H^{5-2\delta } \end{aligned}\right\} \nonumber \\ \end{aligned}$$
(24)

Taking the derivative of Eq. (24) with respect to \(x=lna\), we get

$$\begin{aligned} \left. \begin{aligned}&\omega _t^{'}{=}2\alpha _0\alpha _1\alpha _2\gamma _1(\delta {-}2)e^{\alpha _0 t}H^{1{-}2\delta }\Big ((3{-}2\delta ){\dot{H}}{+}\alpha _0H\Big )H^{2{-}2\delta }\\&+\frac{2\alpha _1^{4\delta -9}}{3\gamma _1}\Big [\frac{\alpha _1(k+2)}{\alpha _0}e^{\alpha _0 t}+\alpha _2(k+2)\Big ]^{-(\frac{4+k}{2+k})}H^{4-2\delta }\\&\times \Big [\Big (1{-}\alpha _0\alpha _1(k-1)e^{\alpha _0t} \Big [\frac{\alpha _1(k{+}2)}{\alpha _0}e^{\alpha _0 t}{+}\alpha _2(k{+}2)\Big ]^{{-}(\frac{k}{2+k})}\Big )\\&\times \Big ((5{-}2\delta )\frac{{\dot{H}}}{H}{-}(\frac{4{+}k}{2{+}k}) \Big [\frac{\alpha _1(k{+}2)}{\alpha _0}e^{\alpha _0 t}{+}\alpha _2(k{+}2)\Big ]^{{-}1}\Big )\Big ]\\&+\alpha _0^2\alpha _1(1-k)e^{\alpha _0t}\Big [\Big [\frac{\alpha _1(k+2)}{\alpha _0}e^{\alpha _0 t}+\alpha _2(k+2)\Big ]^{-\frac{k}{2+k}}\\&-\frac{\alpha _1k}{\alpha _0}e^{\alpha _0t}\Big [\frac{\alpha _1(k+2)}{\alpha _0}e^{\alpha _0 t}+\alpha _2(k+2)\Big ]^{-(\frac{k+1}{2+k})}\Big ], \end{aligned}\right\} \nonumber \\ \end{aligned}$$
(25)

where \({\dot{H}}=\frac{\alpha _0\alpha _1\alpha _2 e^{-\alpha _0t}}{(\frac{\alpha _0}{\alpha _0}+\alpha _2e^{-\alpha _0t})^2}\)

Fig. 3
figure 3

Plot of energy density (\(\rho _M\)) of DM versus time (t) for \(k=1.9\), \(\alpha _1=1.2\), \(\alpha _2=0.52\), and \(\gamma _1=101\)

Full size image

The squared of sound speed \(v_s^2\) is useful to study the stability of the model. If \(v_s^2\) is positive, we obtain stable model and \(v_s^2\) is negative, we obtain unstable model. In this case \(v_s^2\) takes the form

$$\begin{aligned} \left. \begin{aligned} v_s^2&=-1+2\alpha _0\alpha _1\alpha _2\gamma _1(\delta -2)e^{\alpha _0 t}H^{3-2\delta }+\frac{2\alpha _1^{4\delta -9}}{3\gamma _1}\Big [1-\alpha _0 \alpha _1(k-1)e^{\alpha _0t}\Big [\frac{\alpha _1(k+2)}{\alpha _0}e^{\alpha _0 t}\\&\quad +\alpha _2(k+2)\Big ]^{\frac{-k}{2+k}}\Big ] \Big [\frac{\alpha _1(k+2)}{\alpha _0}e^{\alpha _0 t}+\alpha _2(k+2)\Big ]^{-(\frac{4+k}{2+k})}H^{5-2\delta } +2\alpha _0\alpha _1\alpha _2\gamma _1(\delta -2)e^{\alpha _0 t}H^{1-2\delta }\\&\quad \times \Big ((3-2\delta ){\dot{H}}+\alpha _0H\Big ) \frac{H^{3-2\delta }}{(4-2\delta ){\dot{H}}} +\frac{2\alpha _1^{4\delta -9}H^{6-2\delta }}{3\gamma _1(4-2\delta ) {\dot{H}}}\Big [\frac{\alpha _1(k+2)}{\alpha _0}e^{\alpha _0 t}+\alpha _2(k+2)\Big ]^{-(\frac{4+k}{2+k})}\\&\quad \times \Big [\Big (1-\alpha _0\alpha _1(k-1)e^{\alpha _0t} \Big [\frac{\alpha _1(k+2)}{\alpha _0}e^{\alpha _0 t}+\alpha _2(k+2)\Big ]^{-(\frac{k}{2+k})}\Big )\Big ((5-2\delta )\frac{{\dot{H}}}{H}\\&\quad -\Big (\frac{4+k}{2+k}\Big )\Big [\frac{\alpha _1(k+2)}{\alpha _0}e^{\alpha _0 t}+\alpha _2(k+2)\Big ]^{-1}\Big )+\alpha _0^2\alpha _1(1-k)e^{\alpha _0t} \Big [\Big [\frac{\alpha _1(k+2)}{\alpha _0}e^{\alpha _0 t}+\alpha _2(k+2)\Big ]^{-\frac{k}{2+k}}\\&\quad -\frac{\alpha _1k}{\alpha _0}e^{\alpha _0t} \Big [\frac{\alpha _1(k+2)}{\alpha _0}e^{\alpha _0 t}+\alpha _2(k+2)\Big ]^{-(\frac{k+1}{2+k})}\Big ]\Big ]. \end{aligned}\right\} \end{aligned}$$
(26)

In order to understand the role of skewness parameter \(\alpha \) and in the evolution of cosmos, we analyze the dynamical parameters through graphical representation for various values of \(\alpha _0=3.1, 3.3, 3.5\). The graphical nature of skewness parameter \(\alpha \) versus cosmic time t for THDE model with Hubble horizon cut-off is shown in Fig. 1. It is observed that skewness parameter \(\alpha \) varies in the positive region and do not vanish throughout its evolution for chosen values of \(\alpha _0\).

Figure 2 represents the plot of energy density of THDE with Hubble horizon cut-off against cosmic time t for different values of \(\alpha _0\). The trajectories of \(\rho _{T}\) indicates that the positive behavior for the values of \(\alpha _0=3.1,3.3,3.5\). It can be seen that \(\rho _{T}\) decreases with increases of \(\alpha _0\). And also, we observed that in the beginning suggest that the energy density \(\rho _{T}\) dominates the early Universe but for large cosmic time t \(\rho _{T}\) vanish (negligible).

According to Fig. 5, we have drawn \(\omega _T-\omega _T^{'}\) plane. we can see \(\omega _T<0\) and \(\omega _T^{'}>0\) for different values \(\alpha _0=3.1,3.3,3.5\). Hence, our model completely lies in the thawing region.

The plot of energy density of DM versus cosmic time t for different values of \(\alpha _0\) is shown in Fig. 3. It can be seen that \(\rho _M\) is positive and increasing function of time t for the values of \(\alpha _0=3.1,3.3,3.5\). We can also, observed that the energy density of DM \(\rho _M\) increases with decreases of \(\alpha _0\). This behavior is opposite to the behavior energy density of THDE \(\rho _{T}\).

The behavior of EoS parameter versus cosmic time t for the non-interacting THDE model is depicted in Fig. 4 for different values of \(\alpha _0\). It may be observe that the model starts in matter dominated region and varies in quintessence region and finally, its reached to LCDM model for the values of \(\alpha _0=3.1,3.3,3.5\).

Fig. 4
figure 4

Plot of EoS parameter (\(\omega _T\)) versus time (t) for \(k=1.9\), \(\alpha _1=1.2\), \(\alpha _2=0.52\), and \(\gamma _1=101\)

Full size image
Fig. 5
figure 5

Plot of \(\omega _T\) versus \(\omega _T^{'}\) for \(k=1.9\), \(\alpha _1=1.2\), \(\alpha _2=0.52\), and \(\gamma _1=101\)

Full size image
Fig. 6
figure 6

Plot of \(v_s^2\) versus time (t) for \(k=1.9\), \(\alpha _1=1.2\), \(\alpha _2=0.52\), and \(\gamma _1=101\)

Full size image
Fig. 7
figure 7

Plot of EoS parameter (\(\omega _T\)) versus time (t) for \(k=1.9\), \(\alpha _1=1.2\), \(\alpha _2=0.52\), \(\gamma _1=101\), and \(\beta =-0.1\)

Full size image
Fig. 8
figure 8

Plot of EoS parameter (\(\omega _T\)) versus time (t) for \(k=1.9\), \(\alpha _1=1.2\), \(\alpha _2=0.52\), \(\gamma _1=101\), and \(\beta =-0.3\)

Full size image
Fig. 9
figure 9

Plot of EoS parameter (\(\omega _T\)) versus time (t) for \(k=1.9\), \(\alpha _1=1.2\), \(\alpha _2=0.52\), \(\gamma _1=101\), and \(\beta =-0.5\)

Full size image
Fig. 10
figure 10

Plot of \(\omega _T\) versus \(\omega _T^{'}\) for \(k=1.9\), \(\alpha _1=1.2\), \(\alpha _2=0.52\), \(\gamma _1=101\), and \(\beta =-0.1\)

Full size image
Fig. 11
figure 11

Plot of \(\omega _T\) versus \(\omega _T^{'}\) for \(k=1.9\), \(\alpha _1=1.2\), \(\alpha _2=0.52\), \(\gamma _1=101\), and \(\beta =-0.3\)

Full size image
Fig. 12
figure 12

Plot of \(\omega _T\) versus \(\omega _T^{'}\) for \(k=1.9\), \(\alpha _1=1.2\), \(\alpha _2=0.52\), \(\gamma _1=101\), and \(\beta =-0.5\)

Full size image

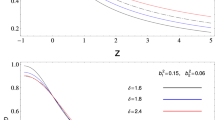
According to Figs. 10, 11 and 12, we can observe that \(\omega _T\) is negative and \(\omega _T^{'}\) is positive for different values of \(\alpha _0\) and \(\beta \). Hence, our model completely in the thawing region.

According to Fig. 6, we shown that \(v_s^2\) versus cosmic time t we can observed that \(v_s^2\) is negative, which shows that our model is unstable.

3.1 Sign-changeable interaction

In the KK anisotropic background, filled with DM and THDE interacting with each other, The EM conservation law Eq. (10) is separated into

$$\begin{aligned} \dot{\rho _M}+3H\rho _M=Q, \end{aligned}$$
(27)

and

$$\begin{aligned} \dot{\rho _T}+3H(1+\omega _T)\rho _{T}+2\alpha \rho _{T}\frac{{\dot{B}}}{B}=-Q, \end{aligned}$$
(28)

where Q represents the interaction term, and assume that it has the \(Q=3\beta H q\rho _{T}\) from the ref. [73,74,75]. Here \(\beta \) is a coupling constant and this \(\beta \) should assumed to be negative because if \(\beta \) is positive then the result in \(\rho _{T}\) is negative. Definitely, as the expansion of the Universe changes from deceleration \(q>0\) to acceleration \(q<0\). Q can be changing from negative to positive.

$$\begin{aligned} \left. \begin{aligned} \omega _T&=-1+2\alpha _0\alpha _1\alpha _2\gamma _1(\delta -2)e^{\alpha _0 t}H^{3-2\delta } +\frac{2\alpha _1^{4\delta -9}}{3\gamma _1}\\&\quad \times \Big [1-\alpha _0 \alpha _1(k-1)e^{\alpha _0t}\Big [\frac{\alpha _1(k+2)}{\alpha _0}e^{\alpha _0 t}+\alpha _2(k+2)\Big ]^{\frac{-k}{2+k}}\Big ]\\&\quad \times \Big [\frac{\alpha _1(k+2)}{\alpha _0}e^{\alpha _0 t}+\alpha _2(k+2)\Big ]^{-(\frac{4+k}{2+k})}H^{5-2\delta }-\beta q \end{aligned}\right\} \nonumber \\ \end{aligned}$$
(29)

Taking the derivative of Eq. (29) with respect to \(x=lna\), we get

$$\begin{aligned} \left. \begin{aligned} \omega _t^{'}&=2\alpha _0\alpha _1\alpha _2\gamma _1(\delta -2)e^{\alpha _0 t}H^{1-2\delta }\Big ((3-2\delta ){\dot{H}}+\alpha _0H\Big )H^{2-2\delta }\\&\quad +\frac{2\alpha _1^{4\delta -9}}{3\gamma _1}\Big [\frac{\alpha _1(k+2)}{\alpha _0}e^{\alpha _0 t}+\alpha _2(k+2)\Big ]^{-(\frac{4+k}{2+k})}H^{4-2\delta }\\&\quad \times \Big [\Big (1-\alpha _0\alpha _1(k-1)e^{\alpha _0t} \Big [\frac{\alpha _1(k+2)}{\alpha _0}e^{\alpha _0 t}+\alpha _2(k+2)\Big ]^{-(\frac{k}{2+k})}\Big )\\&\quad \times \Big ((5-2\delta )\frac{{\dot{H}}}{H} -(\frac{4+k}{2+k})\Big [\frac{\alpha _1(k+2)}{\alpha _0}e^{\alpha _0 t}+\alpha _2(k+2)\Big ]^{-1}\Big )\Big ]\\&\quad +\alpha _0^2\alpha _1(1-k)e^{\alpha _0t}\Big [\Big [\frac{\alpha _1(k+2)}{\alpha _0}e^{\alpha _0 t}+\alpha _2(k+2)\Big ]^{-\frac{k}{2+k}}\\&\quad -\frac{\alpha _1k}{\alpha _0}e^{\alpha _0t} \Big [\frac{\alpha _1(k+2)}{\alpha _0}e^{\alpha _0 t}+\alpha _2(k+2)\Big ]^{-(\frac{k+1}{2+k})}\Big ]-\beta {\dot{q}}, \end{aligned}\right\} \nonumber \\ \end{aligned}$$
(30)

where \({\dot{q}}=-\frac{\alpha _0^2\alpha _2e^{-\alpha _0t}}{\alpha _1}\).

The squared sound speed \(v_s^2\) is obtained as

$$\begin{aligned} \left. \begin{aligned} v_s^2&=-1+2\alpha _0\alpha _1\alpha _2\gamma _1(\delta -2)e^{\alpha _0 t}H^{3-2\delta }+\frac{2\alpha _1^{4\delta -9}}{3\gamma _1}\Big [1-\alpha _0 \alpha _1(k-1)e^{\alpha _0t}\Big [\frac{\alpha _1(k+2)}{\alpha _0}e^{\alpha _0 t}\\&\quad +\alpha _2(k+2)\Big ]^{\frac{-k}{2+k}}\Big ] \Big [\frac{\alpha _1(k+2)}{\alpha _0}e^{\alpha _0 t}+\alpha _2(k+2)\Big ]^{-(\frac{4+k}{2+k})} H^{5-2\delta }+2\alpha _0\alpha _1\alpha _2\gamma _1(\delta -2)e^{\alpha _0 t}H^{1-2\delta }\\&\quad \times \Big ((3-2\delta ){\dot{H}}+\alpha _0H\Big )\frac{H^{3-2\delta }}{(4-2\delta ){\dot{H}}}+\frac{2\alpha _1^{4\delta -9}H^{6-2\delta }}{3\gamma _1(4-2\delta ){\dot{H}}}\Big [\frac{\alpha _1(k+2)}{\alpha _0}e^{\alpha _0 t}+\alpha _2(k+2)\Big ]^{-(\frac{4+k}{2+k})}\\ {}&\times \Big [\Big (1-\alpha _0\alpha _1(k-1)e^{\alpha _0t} \Big [\frac{\alpha _1(k+2)}{\alpha _0}e^{\alpha _0 t}+\alpha _2(k+2)\Big ]^{-(\frac{k}{2+k})}\Big )\Big ((5-2\delta )\frac{{\dot{H}}}{H}\\&\quad -\Big (\frac{4+k}{2+k}\Big )\Big [\frac{\alpha _1(k+2)}{\alpha _0}e^{\alpha _0 t}+\alpha _2(k+2)\Big ]^{-1}\Big ) +\alpha _0^2\alpha _1(1-k)e^{\alpha _0t}\Big [\Big [\frac{\alpha _1(k+2)}{\alpha _0}e^{\alpha _0 t}\\&\quad +\alpha _2(k+2)\Big ]^{-\frac{k}{2+k}}-\frac{\alpha _1k}{\alpha _0}e^{\alpha _0t}\Big [\frac{\alpha _1(k+2)}{\alpha _0}e^{\alpha _0 t}+\alpha _2(k+2)\Big ]^{-(\frac{k+1}{2+k})}\Big ]\Big ]-\frac{\beta {\dot{q}}}{H}. \end{aligned}\right\} \nonumber \\ \end{aligned}$$
(31)

The behavior of EoS parameter \(\omega _T\) versus cosmic time t for interacting THDE model is depicted in Figs. 7, 8 and 9 for the different values of \(\alpha _0\) and \(\beta \). It can be that our model starts in radiation region and passes through matter dominated region and enters into the quintessence phase while the model crosses the phantom divide line and finally, its reached to the constant value in phantom region.

According to Fig. 13, we can say that \(v_s^2\) is negative, which shows that our model unstable. The rate of acceleration or deceleration of the Universe can be described by a single parameter (q) is \(q=-1-\frac{{\dot{H}}}{H^2}\) a more sensitive discriminator of the expansion rate and hence THDE can be constructed by considering the general form for the expansion factor of the Universe. for our model DP is

$$\begin{aligned} q=-1+\frac{\alpha _0\alpha _2}{\alpha _1}e^{-\alpha _0t} \end{aligned}$$
(32)

According to Fig. 14, we can observed that our model exhibits a smooth transition from decelerating to accelerating region of the Universe.

The statefinder indicative (r, s) pair is taken for the geometric idea of the models. We can find the difference in different THDE models by state-finder analysis.

$$\begin{aligned} r&=-\frac{\alpha _0^2 \alpha _2 e^{-\alpha _0 t}}{\alpha _1^2}\Big [\frac{\alpha _1}{\alpha _0}+\alpha _2(1+2e^{-\alpha _0 t})\alpha _2\Big ] +\frac{3\alpha _0\alpha _2e^{-\alpha _0 t}}{\alpha _1}-6, \end{aligned}$$
(33)
$$\begin{aligned} s&=2\Big [\frac{-\alpha _0^2 \alpha _2e^{-\alpha _0 t}\Big [\frac{\alpha _1}{\alpha _0}+\alpha _2(1+2e^{-\alpha _0 t})\alpha _2\Big ]+3\alpha _0\alpha _1\alpha _2e^{-\alpha _0 t}{\alpha _1}-6\alpha _1^2}{3\alpha _1(2\alpha _0\alpha _2e^{-\alpha _0 t}-3\alpha _1)}\Big ] \end{aligned}$$
(34)

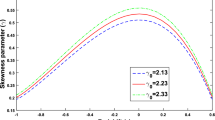
According to Fig. 15, we can observe that the trajectories of (r, s) plane gives a correspondence with Chaplygin gas model for \(r>1\) and \(s<0\).

Fig. 13
figure 13

Plot of \(v_s^2\) versus time (t) for \(k=1.9\), \(\alpha _1=1.2\), \(\alpha _2=0.52\), \(\gamma _1=101\), and \(\beta =-0.1, -0.3, -0.5\)

Full size image
Fig. 14
figure 14

Plot of \(v_s^2\) versus time (t) for \(k=1.9\), \(\alpha _1=1.2\), \(\alpha _2=0.52\), and \(\gamma _1=101\)

Full size image
Fig. 15
figure 15

Plot of \(v_s^2\) versus time (t) for \(k=1.9\), \(\alpha _1=1.2\), \(\alpha _2=0.52\), and \(\gamma _1=101\)

Full size image

4 Conclusions

We have investigated the THDE in the spatially homogeneous anisotropic KK Universe within the frame-work of SB scalar-tensor theory of gravity filled with DM and THDE. To obtainthe deterministic solution of the model of the Universe, we consider some physically plausible conditions, these conditions lead to a varying deceleration parameter which represents decelerating to accelerating expansion of the Universe. We have summarized the conclusions as follows:

  • For our models, we have observed that skewness parameter \(\alpha \) varies in the positive region and do not vanish throughout its evolution for chosen values of \(\alpha _0=3.1, 3.3, 3.5\). From the trajectories of \(\rho _{T}\) indicates that the positive behavior for the values of \(\alpha _0=3.1,3.3,3.5\). And energy density of THDE (\(\rho _{T}\)) decreases with increases of \(\alpha _0\). And also, we observed that in the begining suggest that the energy density \(\rho _{T}\) dominates the early Universe but for large cosmic time (t) \(\rho _{T}\) is negligible.

  • The energy density of DM \(\rho _M\) is positive and increasing function of time t for the various values of \(\alpha _0\). We can also, observed that the energy density of DM \(\rho _M\) increases with decreases of \(\alpha _0\). This behavior is opposite to the behavior energy density of THDE \(\rho _{T}\).

  • For our non-interacting THDE model, the behavior of EoS parameter for different values of \(\alpha _0\). It may be observe that the model starts in matter dominated region and varies in quintessence region and finally, its reached to LCDM model.

  • We have drawn \(\omega _T-\omega _T^{'}\) plane (From the Fig. 5). We can observed \(\omega _T<0\) and \(\omega _T^{'}>0\) for different values \(\alpha _0\). Our model completely lies in the thawing region. And the squared sound speed \(v_s^2\) versus cosmic time t, we can observed that \(v_s^2\) is negative, which shows that our model is unstable.

  • For our sign-changeable THDE model, the behavior of EoS parameter \(\omega _T\) for the different values of \(\alpha _0\) and \(\beta \). It can be that our model starts in radiation region and passes through matter dominated region and enters into the quintessence phase while the model crosses the phantom divide line and finally, its reached to the constant value in phantom region.

  • According to Figs. 10, 11 and 12, we can observe that \(\omega _T\) is negative and \(\omega _T^{'}\) is positive for different values of \(\alpha _0\) and \(\beta \). Hence, our model completely in the thawing region. In both cases, our models completely in the thawing region. And Fig. 13, we can say that \(v_s^2\) is negative, which shows that our model unstable and also, we observed that in both cases, our models unstable.

  • For both the models, DP parameter exhibits a smooth transition from decelerating to accelerating region of the Universe. The trajectories of (r, s) plane gives a correspondence with Chaplygin gas model for \(r>1\) and \(s<0\).

We expect the above analysis will definitely help to have a better understanding of THDE in SB scalar-tensor theory.