The photon polarization in radiative D decays, phenomenologically

Abstract

We work out the phenomenology of untagged time-dependent analysis with radiative $D^0$-decays into CP eigenstates, which allows to probe the photon polarization by means of the charm mesons’ finite width difference. We show that $D^0 \rightarrow \phi \gamma$ or $D^0 \rightarrow \bar{K}^{0 *} \gamma$ decays, which are SM-dominated, or SM-like, respectively, together with U-spin allow to obtain chirality-predictions for radiative decay amplitudes. The order of magnitude of wrong-chirality contributions in the SM can be cross-checked with an up–down asymmetry in $D^0 \rightarrow \bar{K}_1^0 (\rightarrow \bar{K} \pi \pi ) \gamma$. We explore the sensitivity to new physics in $|\Delta c|=|\Delta u|=1$ dipole couplings in the decays $D^0 \rightarrow \rho ^0 \gamma$. We point out the possibility to test the SM with $D_s \rightarrow K_1^+( \rightarrow K \pi \pi ) \gamma$ decays.

1 Introduction

Rare charm decays provide a unique view to flavor in the up sector, which, however, is mostly blurred by hadronic uncertainties. These are particularly difficult to control in charm, as unlike in K- or B-physics, effective theory methods are not expected to work well. Observables related to approximate symmetries of the standard model (SM), CP, lepton flavor conservation and universality are examples where nevertheless useful tests of the SM can be performed. Here we investigate the photon polarization in $|\Delta c|=|\Delta u|=1$ processes. Short-distance contributions from the weak scale are expected to inherit the V-A-structure of the SM, a feature that is generically not shared by SM extensions. We propose to test the SM with the photon polarization in $c \rightarrow u \gamma$ transitions.

Methods to extract the photon polarization can be inferred from B-physics [1,2,3,4,5]. These include the study of polarized $\Lambda _c$ hadrons in $\Lambda _c \rightarrow p \gamma$ decays [6], following the proposal for $\Lambda _b$’s [5]. Another possibility is to probe the photon dipole contribution in semileptonic decays at very low dilepton invariant mass with angular observables [2, 7,8,9].

In this work we study time-dependence in $D \rightarrow V \gamma$ decays, where V denotes a vector meson, following a proposal for $B_s$-mesons [10],¹ and briefly discussed in [11] for charm. As first-principle theory predictions have large uncertainties, we propose to use data and U-spin to obtain a data-driven SM prediction for the photon polarization in $D^0 \rightarrow V \gamma , V=\bar{K}^{*0}, \phi , \rho ^0,\omega$. We work out the phenomenology, and provide predictions in models beyond the SM (BSM). We further suggest to study an up–down asymmetry in $D \rightarrow \bar{K}_1 ( \rightarrow \bar{K} \pi \pi ) \gamma$ along the lines the one known to B-decays [4, 12,13,14], as a consistency check of the SM prediction for the photon polarization. An analogous asymmetry allows to test the SM with $D_s \rightarrow K_1^+ ( \rightarrow K \pi \pi ) \gamma$ decays.

The paper is organized as follows: In Sect. 2 we review time-dependence in decays into CP-eigenstates and show how the photon polarization in $D \rightarrow V \gamma$ decays can be probed. Features of different charm decay observables and their relations are discussed in Sect. 3. In Sect. 4 we show how the SM can be tested and give BSM expectations. In Sect. 5 we summarize. In the appendix we give the angular distribution of $D_{(s)} \rightarrow K_1 \gamma \rightarrow K \pi \pi \gamma$ decays.

2 Time-dependence in $D \rightarrow V \gamma$

The $D \rightarrow V \gamma$ decay amplitudes can be written as

$$\begin{aligned} {\mathcal {A}}_{L,R}={\mathcal {A}}(D\rightarrow V\gamma _{L,R})=\sum _j A_{L,R}^{(j)}e^{i\delta _{L,R}^{(j)}}e^{i\phi _{L,R}^{(j)}} , \end{aligned}$$

(1)

where L, R denote the chirality, j labels different amplitudes, $A_{L,R}^{(j)} \ge 0$, $\delta _{L,R}^{(j)}$ are strong phases and $\phi _{L,R}^{(j)}$ are weak phases. The corresponding CP-conjugated amplitudes are

$$\begin{aligned} \bar{{\mathcal {A}}}_R&=\text {CP}({\mathcal {A}}_L)=\xi \sum _j A_L^{(j)}e^{i\delta _L^{(j)}}e^{-i\phi _L^{(j)}} ,\nonumber \\ \bar{{\mathcal {A}}}_L&=\text {CP}({\mathcal {A}}_R)=\xi \sum _j A_R^{(j)}e^{i\delta _R^{(j)}}e^{-i\phi _R^{(j)}} , \end{aligned}$$

(2)

where $\xi$ denotes the CP eigenvalue of the self-conjugate vector meson V, i.e. $\xi =+1$ for $V=\rho ^0,\phi ,\bar{K}^{*0}(K_S^0\pi ^0)$ and $\xi =-1$ for $V=\bar{K}^{*0}(K_L^0\pi ^0)$.

We define the normalized CP asymmetry as usual

$$\begin{aligned} {\mathcal {A}}_{\text {CP}}(D\rightarrow V\gamma )=\frac{\Gamma (D\rightarrow V\gamma )-\bar{\Gamma }(D\rightarrow V\gamma )}{\Gamma (D\rightarrow V\gamma )+\bar{\Gamma }(D\rightarrow V\gamma )} , \end{aligned}$$

(3)

where $\Gamma (D\rightarrow V\gamma )=\Gamma (D\rightarrow V\gamma _L)+\Gamma (D\rightarrow V\gamma _R)$. The time-dependent decay rate is given as

$$\begin{aligned} \Gamma (t)&={\mathcal {N}}e^{-\Gamma t}\left( \cosh [\Delta \Gamma t/2]+A^\Delta \sinh [\Delta \Gamma t/2]\right. \nonumber \\&\quad \left. +\,\zeta C\cos [\Delta mt]-\zeta S\sin [\Delta mt]\right) , \end{aligned}$$

(4)

where $\zeta =+1$ for a D meson, $\zeta =-1$ for a $\bar{D}$ meson and the normalization ${\mathcal {N}}$ can be found in, e.g., [15]. Here, $\Delta \Gamma =\Gamma _H-\Gamma _L>0$ and $\Delta m=m_H-m_L$ are the differences between the heavy and light D mass eigenstates and $\Gamma$ is the mean width. Note that different sign conventions and notations are used in the literature. The direct CP asymmetry $A_{CP}^\mathrm{dir}=C$ and the observable S [10] can be measured only when the initial flavor is tagged. On the other hand, $A^\Delta$ can be observed in untagged time-dependent measurements by means of a finite width difference $\Delta \Gamma$, as has been shown already for the decays $B_s^0\rightarrow \phi \gamma$ [16].

The observable $A^\Delta$ is given in terms of the decay amplitudes as

$$\begin{aligned} A^\Delta =&\, \frac{2\,\mathrm {Re}\left[ \frac{q}{p}\left( \bar{{\mathcal {A}}}_L{\mathcal {A}}_L^*+\bar{{\mathcal {A}}}_R{\mathcal {A}}_R^*\right) \right] }{\left| {\mathcal {A}}_L\right| ^2+\left| {\mathcal {A}}_R\right| ^2+\left| \frac{q}{p}\right| ^2\left( \left| \bar{{\mathcal {A}}}_L\right| ^2+\left| \bar{{\mathcal {A}}}_R\right| ^2\right) } \nonumber \\ =&\, \frac{1}{N}4\,\xi \left| \frac{q}{p}\right| \sum _{j,k}A_R^{(j)}A_L^{(k)}\cos \left[ \delta _R^{(j)}-\delta _L^{(k)}\right] \nonumber \\&\times \cos \left[ \phi -\phi _R^{(j)}-\phi _L^{(k)}\right] , \end{aligned}$$

(5)

where

$$\begin{aligned} N =&\sum _{j,k}A_L^{(j)}A_L^{(k)}\left( \left( 1+\left| \frac{q}{p}\right| ^2\right) \cos \left[ \delta _L^{(j)}-\delta _L^{(k)}\right] \cos \left[ \phi _L^{(j)}-\phi _L^{(k)}\right] \right. \nonumber \\&\left. -\left( 1-\left| \frac{q}{p}\right| ^2\right) \sin \left[ \delta _L^{(j)}-\delta _L^{(k)}\right] \sin \left[ \phi _L^{(j)}-\phi _L^{(k)}\right] \right) +\left[ L\leftrightarrow R\right] . \end{aligned}$$

(6)

The 95% C.L. intervals of the $D^0-\bar{D}^0$ mixing parameters read [15]

$$\begin{aligned}&\left| \frac{q}{p}\right| \in [0.77,1.12] ,\nonumber \\&\phi =\text {Arg}(q/p)\in [-30.2,10.6]^{\circ } ,\nonumber \\&\Delta \Gamma /(2\Gamma )\in [0.50,0.80]\% . \end{aligned}$$

(7)

It is instructive to consider $A^\Delta$ in the limit $q/p\simeq 1$ and assuming that the decays can be described by only one amplitude per chirality. One obtains in this limit

$$\begin{aligned} A^\Delta&\simeq 2 \xi \frac{ A_L A_R }{ |A_L|^2 + |A_R|^2} \cos ( \delta _L-\delta _R) \cos ( \phi _L -\phi _R) , \end{aligned}$$

(8)

where $A_a, \delta _a$ and $\phi _a$ denote the modulus, strong and weak phase, respectively of the chirality amplitude $\mathcal{{A}}_a=A_a e^{ i \delta _a} e^{ i \phi _a}, a=L,R$. Equation (8) holds if there is no CP violation in the decay, or if strong phases are negligible. As CKM-induced CP violation in charm is small due to the GIM-mechanism this is a useful approximation within the SM and in models with no BSM sources of CP-violation. Defining the photon polarization fraction r as

$$\begin{aligned} r = \frac{A_R}{A_L} , \end{aligned}$$

(9)

it follows

$$\begin{aligned} A^\Delta&\simeq 2 \xi \frac{ r }{ 1+r^2} \cos ( \delta _L-\delta _R) \cos ( \phi _L -\phi _R) . \end{aligned}$$

(10)

The polarization fraction in $D \rightarrow V \gamma$ decays can be extracted via $A^\Delta$ obtained from the time-dependent distribution (4) with an $\mathcal{{O}}(1 \%)$ coefficient (7). As direct CP violation requires the presence of both strong and weak phase, a measurement of $A_\mathrm{CP}$ is complementary to $A^\Delta$. In this work we consider only BSM models with negligible CP-violation. The expression for $A^\Delta$ valid for this type of models including the full dependence on the mixing parameters reads

$$\begin{aligned} A^\Delta&= \frac{4\,\xi \left| \frac{q}{p}\right| \cos \phi }{\left( 1+\left| \frac{q}{p}\right| ^2\right) } \, \frac{ r }{ 1+r^2} \, \cos ( \delta _L-\delta _R) . \end{aligned}$$

(11)

We discuss expectations for the strong phases $\delta _{L,R}$ and relations between $D^0 \rightarrow V \gamma$ modes in Sect. 3.

3 Decay anatomies

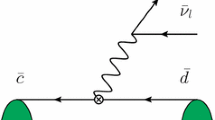
The decays $D \rightarrow V \gamma , V=\bar{K}^{*0}, \phi , \rho ^0,\omega$ are dominated in the SM by weak annihilation (WA) [6, 11, 17], see Fig. 1, plot to the left.

Fig. 1

Weak annihilation (left) and short-distance (right) diagrams for $D\rightarrow V\gamma$ decays. There are additional diagrams (not shown) induced by $Q_{1,2}$ where the photon is emitted from other quark lines

While this holds model-independently for $V=\bar{K}^{*0}$, the final state mesons $\rho ^0,\omega$ and, to a lesser degree, the $\phi$ allow for additional contributions in and beyond the SM. Here we consider BSM effects in dipole operators,

$$\begin{aligned} Q_7&=\frac{e\,m_c}{16\pi ^2}(\bar{u}_L\sigma ^{\mu _1\mu _2}c_R)F_{\mu _1\mu _2},\nonumber \\ Q_7'&=\frac{e\,m_c}{16\pi ^2}(\bar{u}_R\sigma ^{\mu _1\mu _2}c_L)F_{\mu _1\mu _2},\nonumber \\ Q_8&=\frac{g_s\,m_c}{16\pi ^2}(\bar{u}_L\sigma ^{\mu _1\mu _2}T^ac_R)G^a_{\mu _1\mu _2},\nonumber \\ Q_8'&=\frac{g_s\,m_c}{16\pi ^2}(\bar{u}_R\sigma ^{\mu _1\mu _2}T^ac_L)G^a_{\mu _1\mu _2}, \end{aligned}$$

(12)

in the effective Lagrangian

$$\begin{aligned} {\mathcal {L}}_\text {eff}^\text {weak}=\frac{4G_F}{\sqrt{2}}\left( \sum _{q=d,s}V_{cq}^*V_{uq}\sum _{i=1}^2C_iQ_i^{(q)} +\sum _{i=7}^8\left( C_iQ_i+C_i'Q_i'\right) \right) , \end{aligned}$$

(13)

where $G_F$ is the Fermi constant and $V_{ij}$ are CKM matrix elements. The left- and right-handed Wilson coefficients $C_{7,8}$ and $C_{7,8}^\prime$, respectively, are purely BSM as their SM contributions vanish by GIM-cancellations. The chromomagnetic operators $Q_8^{(\prime )}$ enter radiative decay amplitudes at higher order [6, 11, 18], but there is a contribution from mixing onto $Q_7^{(\prime )}$. It can be absorbed effectively into the coefficient $C_7^{(\prime )}$, see, e.g., [6] for explicit formulae. Corresponding contributions to $D \rightarrow V \gamma$ are illustrated in Fig. 1, plot to the right. The four-fermion operators $Q_{1,2}^{(q)} \sim \bar{u}_L \gamma _\mu q_L \bar{q}_L \gamma ^\mu c_L$ are SM-like and induce WA amplitudes. It is possible that chirality-flipped versions of $Q_{1,2}^{(q)}$ are present in BSM scenarios. As we neglect CP-violation such contributions are not distinguishable from the V-A ones, and effectively accounted for in our framework.

To test the SM using $A^\Delta$ requires sufficient understanding of its SM value – it is the main point of this paper to obtain such a prediction experimentally by relating $A^\Delta$ from SM-dominated modes $V=\bar{K}^{*0}, \phi$ to $A^\Delta$ from $V= \rho ^0,\omega$ using U-spin. We show in Sect. 4 that this framework describes available data in a consistent way.

In the following we give details on $D^0 \rightarrow V \gamma$ decays for $V= \bar{K}^{*0}, \rho ^0$ and $\phi$ in Sects. 3.1, 3.2 and 3.3, respectively. These decays enter the SM tests described in Sect. 4. In Sects. 3.4 and 3.5 we discuss $D^0 \rightarrow \bar{K}_1^0( \rightarrow \bar{K} \pi \pi ) \gamma$ and $D_s \rightarrow K_1^+( \rightarrow K \pi \pi ) \gamma$ decays, respectively. The former mode assists the extraction of the SM’s photon polarization from $A^\Delta$ as argued in Sect. 3.1 as well as serves as a standard candle for BSM searches with the latter, the $D_s$-decays.

3.1 $D^0\rightarrow \bar{K}^{*0}\gamma$ decays

The decay $D^0\rightarrow \bar{K}^{*0}\gamma$ is purely induced by WA and SM-like. Strong phases are small [6, 11, 17], however, beyond leading order effects could induce non-vanishing phases.² Note that predictions for the $D^0\rightarrow \bar{K}^{*0}\gamma$ branching ratio obtained in other, hybrid chiral frameworks [19,20,21] are in line with experimental data given in Table 1 only if interfering amplitudes add coherently [6], i.e., for small relative strong phases. Therefore, Eq. (11) simplifies

$$\begin{aligned} A^\Delta (D^0\rightarrow \bar{K}^{*0}\gamma ) \simeq \frac{4\,\xi _{\bar{K}^{*0}} \left| \frac{q}{p}\right| \cos \phi }{\left( 1+\left| \frac{q}{p}\right| ^2\right) } \frac{r_0}{1+r_0^2} , \end{aligned}$$

(14)

where $r_0$ denotes the corresponding $D^0\rightarrow \bar{K}^{*0}\gamma$ photon polarization fraction. Theoretical predictions for $r_0$ are rather uncertain as $A_R$ is presently not known, except for being power suppressed with respect to $A_L$ [6],

$$\begin{aligned} r_0=O\left( \frac{\Lambda _{\text {QCD}}}{m_c}\right) . \end{aligned}$$

(15)

Due to the low charm mass corrections can be considerable and $r_0$ unsuppressed [11]. As $r_0<1$ for a convergent power series a measurement of $r_0$ allows to probe the performance of the expansion.

In view of the sizeable uncertainties we refrain from using theory input on $r_0$ and propose to use the value that can be determined experimentally via $A^\Delta$. To do so we assume that the strong phase difference $\delta _L-\delta _R$ and $r_0$ are not both large, because in this case a suppressed $A^\Delta$ could not unambiguously point to a suppressed $r_0$, see Eq. (11). This possibility, although being not the plain-vanilla theory expectation, can only be cross-checked with other measurements:

We propose to study an up–down asymmetry in $D^0 \rightarrow \bar{K}_1 \gamma$ with $\bar{K}_1 \rightarrow \bar{K} \pi \pi$, constructed from the photon with respect to the plane formed by the pions in the $\bar{K}_1$’s rest frame, discussed further in Sect. 3.4, and defined in the appendix. The advantage of measuring the up–down asymmetry in $D^0 \rightarrow \bar{K}_1 \gamma$ decays is that it probes the photon polarization parameter

$$\begin{aligned} \lambda _\gamma =- \frac{1-r_0^2(\bar{K}_1)}{1+r_0^2(\bar{K}_1)} , \end{aligned}$$

(16)

which is independent of the relative phase between $A_L$ and $A_R$. On the flip-side, $D^0$-tagging is required, because $\lambda _\gamma$ changes sign between $D^0$ and $\bar{D}^0$. Note, $K^- \pi ^+ \pi ^0$ final states are self-tagging, unlike $\bar{K}^0 \pi ^+ \pi ^-$ ones. This method returns predominantly the polarization fraction of the $\bar{K}_1(1270)$-resonance, $r_0(\bar{K}_1)$, rather than of the one of the vector $\bar{K}^{*0}(892), r_0$. As spin, flavor and color counting are identical and masses not too much apart we expect the dynamics to be sufficiently related. There is a doubly-Cabibbo suppressed contamination from $D^0 \rightarrow K_1^0 \gamma , K_1 \rightarrow K \pi \pi$ decays affecting $\lambda _\gamma$ at order $V_{cd}^* V_{us}$, that is, a few percent. One may also use the doubly-Cabibbo suppressed but color-enhanced modes $D^+ \rightarrow K_1^+ \gamma$ to estimate the size of the SM polarization.

Another way is to look for large relative (strong) phases with CP-asymmetries in the $D^0\rightarrow \rho ^0\gamma$ time-dependent distribution (4), which are sensitive to phases in a complementary way. The last method requires to establish a finite CP-asymmetry in $D^0 \rightarrow \rho ^0 \gamma$. The current measurement $A_\mathrm{CP}(D^0 \rightarrow \rho ^0 \gamma )=0.056\pm 0.152\pm 0.006$ [24] is consistent with zero. We note that the phase differences probed in CP-asymmetries are those corresponding to same chirality amplitudes, so the relation to $\delta _L-\delta _R$ is not immediate.

3.2 $D^0\rightarrow \rho ^0\gamma$ decays

The WA-contributions of $D^0\rightarrow \rho ^0\gamma$ and $D^0\rightarrow \bar{K}^{*0}\gamma$ are related by U-spin. Therefore, in the SM,

$$\begin{aligned} A_{L,R}^{\text {SM}} (\rho ^0)=A_{L,R} (\bar{K}^{*0}) \times \text {[U-spin corrections]} . \end{aligned}$$

(17)

Here we neglected contributions from the soft gluon operator $c \rightarrow u \gamma g$ [25], see also [26], to $D \rightarrow \rho ^0 \gamma$, where it is GIM-suppressed [6]. The perturbative and hard spectator interaction induced SM-amplitudes for $c\rightarrow u$ transitions are negligible with respect to the WA-amplitude [6].

While the U-spin breaking from differences in masses and CKM elements can be accounted for trivially, the residual one on the left and right-chiral amplitude, denoted by $f_L, f_R$, respectively, depends on hadronic physics. Note, $f_{L,R}$ are in general complex-valued. Estimations based on factorization identify the largest WA-contributions as the ones with the photon being radiated off the initial state [6, 17, 27]. In this case, the breaking in the matrix element is given by the final vector meson’s matrix element, $\langle V |\bar{q} \gamma _\mu q^\prime |0 \rangle \propto m_V f_V$. For the modes at hand, $f_{L,R}=m_\rho f_\rho /(m_{K^{*0}} f_{K^*}) \simeq 0.9$, an effect within the nominal size of U-spin breaking in charm, $\mathcal{{O}}(0.2-0.3)$, e.g., [28,29,30]. We find that in the hybrid model [20, 21], also [31], using the expressions compiled in [6], the U-spin breaking is of similar size, $f_{L,R}\simeq 0.9 \pm 0.1$, where we varied input parameters.

From (17) follows

$$\begin{aligned} r^\mathrm{SM}=r_0 , \end{aligned}$$

(18)

subject to corrections of the order $f_R/f_L$. Eq. (18) provides, once $r_0$ is known from $D^0\rightarrow \bar{K}^{*0}\gamma$ data, a SM-prediction for $D^0 \rightarrow \rho ^0 \gamma$. Hence, up to U-spin breaking,

$$\begin{aligned} A_{\text {SM}}^\Delta (D^0\rightarrow \rho ^0\gamma ) \simeq \xi _{\bar{K}^{*0}} \xi _{\rho ^0} A^\Delta (D^0\rightarrow \bar{K}^{*0}\gamma ) . \end{aligned}$$

(19)

Any sizeable deviation from Eq. (19) would signal BSM physics in the $c\rightarrow u$ transition which contributes to $D^0\rightarrow \rho ^0\gamma$, but not to $D^0\rightarrow \bar{K}^{*0}\gamma$.  On the other hand, experimental confirmation of Eq. (19) would establish $c\rightarrow u\gamma$ amplitudes other than WA ones to be subleading.

3.3 $D^0\rightarrow \phi \gamma$ decays

The decay $D^0\rightarrow \phi \gamma$ is not a pure WA-induced decay due to the $d \bar{d} +u\bar{u}$ admixture, or rescattering [32]. We parameterize such effects by a complex-valued parameter y, and $y \lesssim O(0.1)$ as follows [6]

$$\begin{aligned} A_{L,R} (\phi ) \simeq A_{L,R}^\mathrm{WA} (\phi ) + y \left( A_{L,R}^\mathrm{WA} (\rho ^0) - A_{L,R}^\mathrm{7,8} (\rho ^0) \right) , \end{aligned}$$

(20)

where $A_{L,R}(\rho ^0) = A_{L,R}^\mathrm{SM}{(\rho ^0)} + A_{L,R}^\mathrm{7,8} (\rho ^0)$. Here $A_{L,R}^\mathrm{7,8}$ denote contributions from dipole operators $Q^{(\prime )}_{7,8}$. The different sign between the $\phi$ and the $\rho ^0$ arises from the SU(3)-decomposition. Up to U-spin breaking between the $\phi$ and the $\bar{K}^{*0}$ of the order $f_R/f_L$ holds

$$\begin{aligned} r_\phi =r_0 (1+\mathcal{{O}}(y)) , \end{aligned}$$

(21)

where $r_\phi$ denotes the polarization fraction of the photon in $D \rightarrow \phi \gamma$ decays. Therefore,

$$\begin{aligned} A^\Delta (D^0\rightarrow \phi \gamma )\simeq \xi _{\bar{K}^{*0}} \xi _\phi A^\Delta (D^0\rightarrow \bar{K}^{*0}\gamma ) \, (1 +\mathcal{{O}}(y) ) \, . \end{aligned}$$

(22)

As already discussed in Sect. 3.2 for the $\rho ^0$, the leading U-spin breaking based on dominance of initial state radiation is given by $f_{L,R} =m_\phi f_\phi /(m_{K^{*0}} f_{K^*}) \simeq 1.3$. Similarly, the numerical agreement with the hybrid model is good. We find $f_{L,R}\simeq 1.2 \pm 0.1$, where the amplitudes have been added coherently. For destructive interference, which is in conflict with data on the $D^0 \rightarrow \phi \gamma$ branching ratio, $f_{L,R}\simeq 1.5$.

When y can be neglected with respect to other uncertainties or contributions, $D^0\rightarrow \phi \gamma$ becomes a standard candle very much like $D^0\rightarrow \bar{K}^{*0} \gamma$. At higher precision, at $\mathcal{{O}}(y)$, the decay $D^0\rightarrow \phi \gamma$ becomes sensitive to BSM physics similar to $D^0\rightarrow \rho ^0\gamma$.

3.4 $D^0 \rightarrow \bar{K}_1^0 \gamma$ decays

The up–down asymmetry in $D^0 \rightarrow \bar{K}_1^0 \gamma$ with $\bar{K}_1^0 \rightarrow \bar{K} \pi \pi$ probes the photon polarization by measuring the polarization of the kaon resonance $\bar{K}_1^0$. The asymmetry is the D-decay version of the one in $B \rightarrow K_1 \gamma$ decays [12]. It is proportional to the photon polarization parameter $\lambda _\gamma$ (16), see the appendix for details. The proportionality factor depends on the details of hadronic decays of the $\bar{K}_1$. As such, it is independent of the resonance’s production, hence, is the same for B- and D-decays. The rate of $\bar{K} \pi \pi$ events, of course, differs as well as the relative importance of resonances and their interference effects.

The contribution from the K(1400)-family and higher, which includes resonances which dilute the asymmetry, is phase space suppressed in charm relative to the $\bar{K}_1(1270)$ one by about a factor of two. This reduces the impact of interference effects and suggests a single-resonance analysis in terms of the $\bar{K}_1(1270)$. As stressed in the more recent B-physics literature [13, 14, 22, 23], insufficient understanding of the hadronic structure of the $\bar{K}_1$-decay prohibits a precision extraction of the photon polarization. While this can be overcome [14, 23], here, we merely need to check whether the wrong-chirality amplitudes satisfy $A_R \sim A_L$ or not in a SM-like decay.

The proportionality factor between the integrated up–down asymmetry (A2) and $\lambda _\gamma$ has been estimated for the $\bar{K}_1(1270) \rightarrow \bar{K}^0 \pi ^+ \pi ^-$ to be within $-13\%$ to $+24 \%$, and for $\bar{K}_1(1270) \rightarrow K^- \pi ^+ \pi ^0$ to be around $-(7-10) \%$ [14]. Measurement of a near maximal asymmetry would imply a small $r_0(\bar{K}_1)$. A detailed analysis of $\bar{K}_1$-distributions is beyond the scope of this work.

3.5 $D_s \rightarrow K_1^+ \gamma$ decays

The decay $D_s \rightarrow K_1^+ ( \rightarrow K \pi \pi ) \gamma$ is color-allowed, hence the sensitivity to BSM physics is suppressed by $1/N_C$, where $N_C$ denotes the number of colors, relative to the one in $D^0 \rightarrow ( \rho ^0, \omega ) \gamma$ decays. A similar up–down asymmetry as in $D^0 \rightarrow \bar{K}_1^0 ( \rightarrow \bar{K} \pi \pi ) \gamma$ can be constructed, see appendix. Predictions for the polarization fraction of $D_s \rightarrow K_1^+ \gamma$ decays, $r_s( K_1)$, are

$$\begin{aligned}&r_s( K_1) =r_0(\bar{K}_1) (1 +\mathcal{{O}}(1/(V_{us} N_C)) ~~~~\text{ or }~~ \nonumber \\&r_s( K_1)\sim \mathcal{{O}}(1/N_C) r ~~~~\text{ if } ~~ r_0 \simeq 0 . \end{aligned}$$

(23)

In the latter case, for negligible SM-contribution to $A_R$, $\lambda _{\gamma s} +1$ becomes a null test of the SM, where $\lambda _{\gamma s}$ denotes the corresponding photon polarization parameter (16) in $D_s \rightarrow K_1^+ \gamma$ decays

$$\begin{aligned} \lambda _{\gamma s}=- \frac{1-r_s^2( K_1)}{1+r_s^2( K_1)} . \end{aligned}$$

(24)

In the SM it has to be equal to $\lambda _\gamma$, Eq. (16), up to U-spin corrections. Significant deviations can signal BSM physics.

Table 1 Experimental data on $D^0\rightarrow V\gamma$ branching ratios. The corresponding numerical values for the reduced branching ratios $\mathcal {B}$, see Eqs. (26, 29) and analogously for $\phi \gamma$, are given in the last row. $^\dagger$Statistical and systematic uncertainties are added in quadrature

4 Testing the SM

We provide explicit expressions on how to probe BSM-sensitive contributions in the photon polarization fraction in $D^0 \rightarrow \rho ^0 \gamma$ decays using $D^0 \rightarrow \bar{K}^{*0} \gamma$ in Sect. 4.1, and using $D^0 \rightarrow \phi \gamma$ in Sect. 4.2. We also show consistency of the framework – WA dominance in SM-dominated modes consistent with leading U-spin breaking – with current data on branching ratios, and give expectations for the photon polarization in $D \rightarrow \rho ^0 \gamma$ decays in BSM models.

4.1 $D^0 \rightarrow \bar{K}^{*0} \gamma$

The $D^0 \rightarrow \bar{K}^{*0} \gamma$ is a WA-induced mode. Its branching ratio can be written as

$$\begin{aligned}&\mathcal{{B}}(D^0 \rightarrow \bar{K}^{*0} \gamma ) = \tau _{D^0} \frac{m_{D_0}^3}{32 \pi } \left( 1-\frac{m_{K^*}^2}{m_{D_0}^2} \right) ^3 \frac{ \alpha _e (G_F m_c )^2}{\pi ^3} \cdot \mathcal{{B}}_0 , \end{aligned}$$

(25)

$$\begin{aligned}&\mathcal{{B}}_0 = |a_0|^2 +|a_0^{\prime }|^2 , \end{aligned}$$

(26)

where, in the notation of the previous sections, $a_0,a_0^\prime$ correspond to $A_L,A_R$, respectively. Then, the ratio of right- to left-handed photons is given as

$$\begin{aligned} r_0 = \left| \frac{a_0^{\prime }}{a_0}\right| . \end{aligned}$$

(27)

A measurement of $\mathcal{{B}}_0, r_0$ returns the magnitude of both amplitudes

$$\begin{aligned}&|a_0| =\sqrt{ \frac{ \mathcal{{B}}_0 }{1+r_0^2}} , \qquad |a_0^{\prime }| =r_0 \sqrt{ \frac{ \mathcal{{B}}_0 }{1+r_0^2}} . \end{aligned}$$

(28)

The BSM-sensitive mode $D^0 \rightarrow \rho ^0 \gamma$ can be affected by contributions from left- and right-handed Wilson coefficients $C_7$ and $C_7^\prime$, respectively. We write the branching ratio as (note, factor 1 / 2 for isospin)

$$\begin{aligned}&\mathcal{{B}}(D^0 \rightarrow \rho ^0 \gamma ) = 1/2 \, \tau _{D^0} \frac{m_{D_0}^3}{32 \pi } \left( 1-\frac{m_{\rho }^2}{m_{D_0}^2} \right) ^3 \frac{ \alpha _e (G_F m_c )^2}{\pi ^3} \cdot \mathcal{{B}} , \nonumber \\&\mathcal{{B}} = |a + T C_7|^2 + |a^{\prime } + T C_7^\prime |^2 , \end{aligned}$$

(29)

$$\begin{aligned}&a^{ (\prime )} = - \frac{V^*_{cd}}{V^*_{cs}} a_0^{ (\prime )} \times f_{L (R)} , \end{aligned}$$

(30)

where T denotes the $D^0 \rightarrow \rho ^0$ dipole form factor at maximum momentum transfer, and $f_{L,R} \ne 1$ accounts for U-spin breaking effects beyond phase space and CKM already discussed in Sect. 3. The polarization fraction of $D^0 \rightarrow \rho ^0 \gamma$ is given as

$$\begin{aligned} r = \left| \frac{a^{\prime }+T C_7^\prime }{a+T C_7}\right| . \end{aligned}$$

(31)

Experimental findings for the reduced branching ratios $\mathcal{{ B}}_0$, $\mathcal{{ B}}$ and $\mathcal{{ B}}_\phi$, the latter corresponding to $D \rightarrow \phi \gamma$ decays, are given in Table 1.

Measurement of 4 observables, $\mathcal{{B}}, \mathcal{{B}}_0,r,r_0$ determines 4 coefficients, the SM contributions $a, a^{ \prime }$ and the BSM ones $C_7, C_7^\prime$. By definition, $r,r_0 \ge 0$. Presently, only branching ratios are measured, see Table 1. It would be desirable to have more precise data available, in particular, the discrepancy in $D^0\rightarrow \bar{K}^{*0}\gamma$ between Belle and BaBar should be settled.

Fig. 2

The polarization fraction r, Eq. (32) and $2 r/(1+r^2)$, which drives $A^\Delta$, Eq. (11), as a function of $| TC_7'|$ (blue shaded band) for the current data on $\mathcal{{B}}$ assuming $r_0\simeq 0$. The range accessible by leptoquark models is indicated by the green box. Model-independently, and in generic SUSY models, there is no upper limit on r

In absence and anticipation of future polarization data we discuss the following limiting cases:

• (a) $C_7, C_7^\prime \simeq 0$. This corresponds to the SM, $r \simeq r_0$, discussed around Eq. (18).

• (b) $r_0 \simeq 0$. It follows

  $$\begin{aligned} r=\frac{|T C_7^\prime |}{ \sqrt{ \mathcal{{B}}-|T C_7^\prime |^2}} . \end{aligned}$$

  (32)

  The polarization fraction r is a null test of the SM for negligible $r_0$. We can already now make a data-based prediction for r given $C_7^\prime$ irrespective of $C_7$. Possible values of r from Eq. (32) are illustrated in Fig. 2, where the blue band displays the one sigma range of $\mathcal{{B}}$. Within leptoquark models holds $|C_7'|\lesssim 0.02$, which, using $T=0.7$ [6], implies $r\lesssim 0.09$, indicated by the green box. On the other hand, SUSY models can provide significantly higher values $|C_7'|\lesssim 0.3$, while model-independently holds $|C_7'|\lesssim 0.5$. As r diverges towards $C_7^\prime \simeq 0.15$, in both latter cases there is no upper limit on r. Upper limits on the Wilson coefficients are taken from [6].

• (c) $C_7 \simeq 0$

  $$\begin{aligned} r=\frac{ \sqrt{\mathcal{{B}} -|a|^2}}{ |a| } . \end{aligned}$$

  (33)

  This allows to predict r if one calculates a. Using the results for the WA-amplitude in the heavy quark limit obtained in [6] we find (for $\lambda _D\ge 0.1\,\text {GeV}$) $r\ge 2$. Such large values of r are consistent with the fact that the corresponding SM prediction for the $D^0 \rightarrow \rho ^0 \gamma$ branching ratio $\mathcal{{B}}=0.005 \cdot (0.1 \, \text{ GeV }/\lambda _D)^2$ is significantly below the measured one given in Table 1. Note that for the SM-dominated modes the agreement is much better, $\mathcal{{B}}_{\phi }=0.016 \cdot (0.1 \, \text{ GeV }/\lambda _D)^2$ and $\mathcal{{B}}_{0}=0.16 \cdot (0.1 \, \text{ GeV }/\lambda _D)^2$. Here, $\lambda _D$ denotes a non-perturbative parameter expected to be of the order $\Lambda _\mathrm{QCD}$.

• (d) $C_7^\prime \simeq 0$

  $$\begin{aligned} r= \frac{ r_0 |a|}{ \sqrt{ \mathcal{{B}}-r_0^2 |a|^2 } } . \end{aligned}$$

  (34)

  This will be useful once $r_0$ in addition to $\mathcal{{B}}_0$ is measured and, using Eq. (30), allows to illustrate viable ranges for r in BSM scenarios.

Note, Eq. (32) and Fig. 2, and Eq. (33) are independent of U-spin breaking.

In the present situation where only branching fraction measurements are available, it is useful to define the ratio

$$\begin{aligned} R(\rho ^0/\bar{K}^{*0})&=\bigg | \frac{V_{cs}}{V_{cd}} \bigg |^2\frac{\mathcal {B}}{{\mathcal {B}}_{0}}=\frac{1+r^2}{1+r_0^2}\frac{{r'}^2}{r^2}\nonumber \\&= \frac{1+r^2}{1+r_0^2} |1+T C_7/a|^2, \end{aligned}$$

(35)

where $r'=|(a^{\prime }+T C_7')/a|$, and we used Eq. (30). The ratio R equals one if only WA contributes, that is, $r=r_0$ and $C_7=C_7^\prime =0$, irrespective of the size of the SM contributions. With BSM physics, the ratio can be larger or smaller than one. Similar ratios have been mentioned in [36] as a test of the SM.

In R only trivial U-spin breaking from phase space and CKM-elements has been accounted for. We define in addition the ratio $\bar{R}$, in which also the leading dynamical one $\propto m_V f_V$ is covered.

$$\begin{aligned} \bar{R}(\rho ^0/\bar{K}^{*0})= \frac{1}{f^2} \bigg | \frac{V_{cs}}{V_{cd}} \bigg |^2\frac{\mathcal {B}}{{\mathcal {B}}_{0}} , \end{aligned}$$

(36)

where, here, we use $f=m_\rho f_\rho /(m_{K^{*0}} f_{K^*}) \simeq 0.9$.

Using the data compiled in Table 1 and adding uncertainties in quadrature, we find

$$\begin{aligned}&R(\rho ^0/\bar{K}^{*0})^\text {Belle}=1.14\pm 0.21,\nonumber \\&R(\rho ^0/\bar{K}^{*0})^\text {BaBar}=1.61\pm 0.33 , \end{aligned}$$

(37)

$$\begin{aligned}&\bar{R}(\rho ^0/\bar{K}^{*0})^\text {Belle}=1.40\pm 0.26,\nonumber \\&\bar{R}(\rho ^0/\bar{K}^{*0})^\text {BaBar}=1.97 \pm 0.40 . \end{aligned}$$

(38)

Here, Belle and BaBar refers to the respective measurement of the $D \rightarrow \bar{K}^{*0} \gamma$ branching ratio, which unfortunately, exhibit presently a significant experimental spread. Inflating errors a la PDG [35] due to the Belle/BaBar discrepancy, which exceeds one $\sigma$, we obtain for the average $\bar{R}(\rho ^0/\bar{K}^{*0})^\text {ave}=1.57\pm 0.26$.

Fig. 3

The polarization fraction r as a function of $r_0$ (plots to the left) and $2r/(1+r^2)$ as a function of $2r_0/(1+r_0^2)$ (plots to the right), in the cases a (SM case) $C_7,C_7'\simeq 0$ (black, dashed curve), c $C_7\simeq 0$ (green, upper band) and d $C_7^\prime \simeq 0$ (red, lower band). The upper (lower) plots correspond to $\bar{R}=1.6\pm 0.3$ ($\bar{R}=1.6\pm 0.45$ from $50 \%$ inflated uncertainty)

In Fig. 3 we show r (plots to the left) for the cases (a), (c) and (d) for $\bar{R}=1.6\pm 0.3$ (upper row) and $\bar{R}=1.6\pm 0.45$ (lower row), illustrating the data’s discriminative power. Case (b) has already been considered in Fig. 2. We learn that r can be order one, and that it can be close to $r_0$, in which case discrimination from the SM is not possible. In the plots to the right we show $2r/(1+r^2)$ as a function of $2r_0/(1+r_0^2)$, which enter the observables $A^\Delta (D^0 \rightarrow \bar{K}^{*0} \gamma )$ and $A^\Delta (D^0 \rightarrow \rho ^0\gamma )$, respectively, for (a), (c) and (d). Within present data on $\bar{R}$, scenario (d) with no right-handed BSM physics (red band) cannot be sufficiently separated from the SM (black dashed curve), while scenario (c) with only $C_7^\prime$ present (green band), exhibits a significant SM-deviation. For $\bar{R} <1$ the green band corresponding to scenario (c) would be below the SM curve while the band corresponding to scenario (d) would be above it. The lower plots in Fig. 3 correspond to a value of $\bar{R}$ with $50 \%$ larger uncertainty, mimicking larger U-spin corrections. As the upper and lower plots are similar we learn that such effects do not change the picture qualitatively.

We can apply this strategy to probe for new physics in the decay $D \rightarrow \omega \gamma$, once its branching ratio and its polarization fraction become available.

4.2 $D^0 \rightarrow \phi \gamma$

Due to the hybrid nature of the $\phi$, one may ask whether the $D \rightarrow \phi \gamma$ branching ratio is consistent with the assumption of a predominantly WA-induced decay amplitude. Corresponding ratios,

$$\begin{aligned}&R(\phi /\bar{K}^{*0})=\bigg | \frac{V_{ud}}{V_{us}} \bigg |^2\frac{{\mathcal {B}}_\phi }{{\mathcal {B}}_{0}} , \quad \bar{R}(\phi /\bar{K}^{*0})= \frac{1}{f^2} \bigg | \frac{V_{ud}}{V_{us}} \bigg |^2\frac{{\mathcal {B}}_\phi }{\mathcal{{B}}_{0}} , \end{aligned}$$

(39)

where $\mathcal{{B}}_\phi$ is the reduced branching ratio analogous to $\mathcal{{B}}$ for $D \rightarrow \rho ^0 \gamma$, Eq. (29), and using $f =m_\phi f_\phi /(m_{K^{*0}} f_{K^*}) \simeq 1.3$, are obtained as

$$\begin{aligned}&R(\phi /\bar{K}^{*0})^\text {Belle}=1.46 \pm 0.15,\nonumber \\&R(\phi /\bar{K}^{*0})^\text {BaBar}=2.10 \pm 0.37 , \end{aligned}$$

(40)

$$\begin{aligned}&\bar{R}(\phi /\bar{K}^{*0})^\text {Belle}=0.87 \pm 0.09 ,\nonumber \\&\bar{R}(\phi /\bar{K}^{*0})^\text {BaBar}=1.24 \pm 0.22 . \end{aligned}$$

(41)

Leading U-spin breaking makes both branching ratios of similar size. This is consistent with

$$\begin{aligned} \bar{R} (\phi /\bar{K}^{*0}) =1+O(y) , \end{aligned}$$

(42)

which, together with Eq. (21), holds in the SM and beyond. While this numerical agreement could be accidental, it does give a consistent picture between the predominantly SM-like modes and the size of U-spin breaking in the range obtained within the lowest order heavy quark expansion [6], sum rules [17] and hybrid models [20, 21]. This is beneficial as time-dependent analysis with $\bar{K}^{*0} \rightarrow K_{S,L} \pi ^0$ is more difficult than with $\phi \rightarrow K^+ K^-$. We therefore suggest to use $r_\phi$, the polarization fraction of the photon in $D \rightarrow \phi \gamma$ decays, as a SM prediction for r.

We repeat the analysis previously performed with $\rho ^0$ and $\bar{K}^{*0}$, Eqs. (37), (38), for the $\rho ^0$ and the $\phi$. We obtain

$$\begin{aligned}&R(\rho ^0/\phi )^\text {Belle}=0.78\pm 0.17,\nonumber \\&R(\rho ^0/\phi )^\text {BaBar}=0.77\pm 0.21 , \end{aligned}$$

(43)

$$\begin{aligned}&\bar{R}(\rho ^0/\phi )^\text {Belle}=1.62\pm 0.34,\nonumber \\&\bar{R}(\rho ^0/\phi )^\text {BaBar}=1.59\pm 0.43 , \end{aligned}$$

(44)

and for the average $\bar{R}(\rho ^0/\phi )^\text {ave}=1.61\pm 0.27$. The good agreement seen in the data, between Eqs. (38) and (44), supports that the $\phi$ indeed can be used as a standard candle as long as effects of O(y) can be neglected, and that the working assumption of the leading U-spin breaking is consistent with data.

5 Summary

Untagged, time-dependent analysis into CP eigenstates allows to extract the photon polarization in radiative charm decays. Given a measurement of the photon’s polarization fraction, its interpretation requires control of SM contributions to $D \rightarrow V \gamma$ decays. We explore the possibility to obtain the size of the SM background to wrong-chirality contributions from data and U-spin. While there are sizeable uncertainties related to this procedure, there is presently no measurement available and large room for BSM physics.

Specifically, we propose measurement of $A^\Delta$ in $D^0 \rightarrow \phi (\rightarrow K^+ K^-) \gamma$ decays to obtain the SM fraction, $r_\phi$. While the $\phi$ is not purely $s\bar{s}$ and therefore not purely WA-induced, the final state is advantageous over the one from the pure SM-mode, $D^0 \rightarrow \bar{K}^{0*} (\rightarrow K_{S,L} \pi ^0) \gamma$. If feasible, the latter should be studied experimentally as well.

If $r_\phi$, or $r_0$, the polarization fraction of $D^0 \rightarrow \bar{K}^{0*} \gamma$ decays, is negligible, the photon polarization and therefore $A^\Delta$ in $D^0 \rightarrow \rho ^0 (\rightarrow \pi ^+ \pi ^-) \gamma$ becomes a null test of the SM. Possible ranges depending on the BSM model are illustrated in Fig. 2. $A^\Delta$ in $D^0 \rightarrow \rho ^0 \gamma$ decays can be $\mathcal{{O}}(1)$ in SUSY models, while leptoquark models give SM-like values. The method works as well for $D^0 \rightarrow \omega \gamma$ decays, however, the branching ratios of the $\omega$ into suitable final states such as $\pi ^+ \pi ^-$ are small [35].

We further explored the correlation between the SM and BSM polarization fraction based on ratios of branching fraction measurements, shown in Fig. 3. Our study shows that U-spin breaking effects of nominal size are not qualitatively changing the picture. In particular, we find that available branching ratios, Table 1, are consistent with U-spin hierarchies predicted by the heavy quark expansion, and other theory frameworks [17, 20, 21]. However, uncertainties are large, and more study is needed to achieve a completer picture. This includes the clarification of the discrepancy in the $\mathcal{{B}}(D^0 \rightarrow \bar{K}^{*0} \gamma )$ data. A cleaner BSM interpretation would require better knowledge of the dipole form factor T(0).

We point out that another way to probe the photon polarization in radiative charm decays is provided by an up–down asymmetry (A2). As in the time-dependent analysis the SM value can be extracted from a SM-like decay, here $D^0 \rightarrow \bar{K}_1^0 \gamma$, and then used together with U-spin for a SM test in a BSM-sensitive mode, $D_s \rightarrow K_1^+ \gamma$ decays. Due to limited phase space the $K_1(1270)$ is more pronounced in charm relative to higher resonances than in B-decays.

The study of the photon polarization complements BSM searches with CP asymmetries in $c \rightarrow u \gamma$ transitions.

Appendix A: Up–down asymmetry

The differential distribution of $D\rightarrow R\gamma \rightarrow P_1P_2P_3\gamma$ decays via a $J^P=1^+$ resonance R can be written as [4, 12,13,14]

$$\begin{aligned}&\frac{{\mathrm {d}}\Gamma }{{\mathrm {ds}}_{13}\,{\mathrm {ds}}_{23}\,{\mathrm {d}}\cos \theta }\propto |\vec J|^2(1+\cos ^2\theta )\nonumber \\&\quad +\lambda _\gamma 2\,\mathrm {Im}[\vec n\cdot (\vec J\times \vec J^*)]\cos \theta , \end{aligned}$$

(A1)

where $\lambda _\gamma =(|{\mathcal {A}}_R|^2-|{\mathcal {A}}_L|^2)/(|{\mathcal {A}}_R|^2+|{\mathcal {A}}_L|^2)$ denotes the photon polarization parameter, $s_{ij}=(p_i+p_j)^2$ with the four momenta $p_i$ of the mesons $P_i$ and $\theta$ is the angle between the normal $\hat{n}=((\vec p_1\times \vec p_2)/|(\vec p_1\times \vec p_2)|)$ and the direction opposite to the photon in the rest frame of R. The integrated up–down asymmetry reads

$$\begin{aligned} A_{up-down}&=\left( \int _0^1\frac{{\mathrm {d}}\Gamma }{{\mathrm {d}}\cos \tilde{\theta }}{\mathrm {d}}\cos \tilde{\theta }\right. \nonumber \\&\quad \left. -\int _{-1}^0\frac{{\mathrm {d}}\Gamma }{{\mathrm {d}}\cos \tilde{\theta }}{\mathrm {d}}\cos \tilde{\theta }\right) \bigg /\int _{-1}^1\frac{{\mathrm {d}}\Gamma }{{\mathrm {d}}\cos \tilde{\theta }}{\mathrm {d}}\cos \tilde{\theta }\nonumber \\&=\frac{3}{4}\frac{\left<\mathrm {Im}[\hat{n}\cdot (\vec J\times \vec J^*)]\,\mathrm {sgn}[s_{13}-s_{23}]\right>}{\langle |\vec J|^2\rangle }\lambda _\gamma , \end{aligned}$$

(A2)

where $\cos \theta =\mathrm {sgn}[s_{12}-s_{23}]\cos \tilde{\theta }$ and the $\langle \cdots \rangle$-brackets denote integration over $s_{13}$ and $s_{23}$. Here, $\vec J$ is defined by the decay amplitude ${\mathcal {A}}(R\rightarrow P_1P_2P_3)=\epsilon ^\mu J_\mu$ with the polarization vector $\epsilon$ of R. Formulas for J including contributions from resonances with different spin and parity, e.g., the K(1400)-family and their interference effects can be extracted from [4, 12,13,14]. Decay chains involving a kaon resonance are collected in Table 2. Decays of $D^+$ and $D_s$ are self-tagging.

Table 2 Decay chains involving a kaon resonance decaying via $K_1^+\rightarrow (K^{*+}\pi ^0,K^{*0}\pi ^+,\rho ^+K^0)\rightarrow K^0\pi ^+\pi ^0, K_1^+\rightarrow (K^{*0}\pi ^+,\rho ^0K^+)\rightarrow K^+\pi ^+\pi ^-, K_1^0\rightarrow (K^{*+}\pi ^-,K^{*0}\pi ^0,\rho ^-K^+)\rightarrow K^+\pi ^-\pi ^0$ and $K_1^0\rightarrow (K^{*+}\pi ^-,\rho ^0K^0)\rightarrow K^0\pi ^+\pi ^-$. Here, CF, SCS and DCS denote Cabibbo-favored, singly Cabibbo-suppressed and doubly Cabibbo-suppressed WA-amplitudes, respectively. While ‘SM’ indicates a WA-induced decay, ‘FCNC’ indicates the presence of $c \rightarrow u$ contributions