Analysis of the $QQ\bar{Q}\bar{Q}$ tetraquark states with QCD sum rules

Abstract

In this article, we study the $J^{PC}=0^{++}$ and $2^{++}$ $QQ\bar{Q}\bar{Q}$ tetraquark states with the QCD sum rules, and we obtain the predictions $M_{X(cc\bar{c}\bar{c},0^{++})} =5.99\pm 0.08\,\mathrm {GeV}$, $M_{X(cc\bar{c}\bar{c},2^{++})} =6.09\pm 0.08\,\mathrm {GeV}$, $M_{X(bb\bar{b}\bar{b},0^{++})} =18.84\pm 0.09\,\mathrm {GeV}$ and $M_{X(bb\bar{b}\bar{b},2^{++})} =18.85\pm 0.09\,\mathrm {GeV}$, which can be confronted to the experimental data in the future. Furthermore, we illustrate that the diquark–antidiquark type tetraquark state can be taken as a special superposition of a series of meson–meson pairs and that it embodies the net effects.

1 Introduction

The observations of the charmonium-like and bottomonium-like states have provided us with a good opportunity to study the exotic states and understand the strong interactions, especially those charged states $Z_c(3885)$, $Z_c(3900)$, $Z_c(4020)$, $Z_c(4025)$, $Z_c(4200)$, Z(4430), $Z_b(10610)$, $Z_b(10650)$, they are excellent candidates for the multiquark states [1, 2]. If they are tetraquark states, they consist two heavy quarks and two light quarks, we have to deal with both the heavy and the light degrees of freedom of the dynamics. On the other hand, if there exist tetraquark configurations that consist of four heavy quarks, the dynamics is very simple. There has been a variety of work on the mass spectrum of the $QQ\bar{Q}\bar{Q}$ tetraquark states, such as the non-relativistic potential models [3,4,5,6,7], the Bethe–Salpeter equation [8], the constituent diquark model with spin–spin interaction [9, 10], the constituent quark model with color–magnetic interaction [11], the moment QCD sum rules [12], etc. In this article, we study the tetraquark states consist of four heavy quarks with the Borel QCD sum rules.

The QCD sum rules method is a powerful theoretical tool in studying the ground state tetraquark states and molecular states, and it has given many successful descriptions of the masses and hadronic coupling constants [13,14,15,16,17,18,19,20,21,22,23,24]. In this article, we study the $J^{PC}=0^{++}$ and $2^{++}$ $QQ\bar{Q}\bar{Q}$ tetraquark states, which may be observed in the $e^+e^-$ and pp collisions, for example, $e^+e^- \rightarrow J/\psi \bar{c}c$, $pp\rightarrow \bar{c}c\bar{c}c$. The ATLAS, CMS and LHCb collaborations have measured the cross section for double charmonium production [25,26,27], the CMS collaboration has observed $\Upsilon$ pair production [28].

The quarks have color SU(3) symmetry, we can construct the tetraquark states according to the routine $\mathrm{quark}\rightarrow \mathrm{diquark}\rightarrow \mathrm{tetraquark}$,

$$\begin{aligned}&(\mathbf{3}_c\otimes \mathbf{3}_c)\otimes (\overline{\mathbf{3}}_c\otimes \overline{\mathbf{3}}_c) \rightarrow (\overline{\mathbf{3}}_c\oplus \mathbf{6}_c)\otimes (\mathbf{3}_c\oplus \overline{\mathbf{6}}_c)\nonumber \\&\quad \rightarrow (\overline{\mathbf{3}}_c\otimes \mathbf{3}_c)\oplus (\mathbf{6}_c\otimes \overline{\mathbf{6}}_c) \rightarrow (\mathbf{1}_c\oplus \mathbf{8}_c) \oplus \cdots , \end{aligned}$$

(1)

where $\mathbf{1}_c$, $\mathbf{3}_c$ ($\overline{\mathbf{3}}_c$), $\mathbf{6}_c$ and $\mathbf{8}_c$ denote the color singlet, triplet (antitriplet), sextet and octet, respectively. The one-gluon exchange leads to attractive (repulsive) interaction in the color antitriplet (sextet) channel, which favors (disfavors) the formation of diquark states in the color antitriplet (sextet) [29, 30]. The diquarks $\varepsilon ^{ijk} q^{T}_j C\Gamma q^{\prime }_k$ in color antitriplet have five structures in Dirac-spinor space, where i, j and k are color indices, $C\Gamma =C\gamma _5$, C, $C\gamma _\mu \gamma _5$, $C\gamma _\mu$ and $C\sigma _{\mu \nu }$ for the scalar, pseudoscalar, vector, axial-vector and tensor diquarks, respectively. The stable diquark configurations are the scalar ($C\gamma _5$) and axial-vector ($C\gamma _\mu$) diquark states from the QCD sum rules [31,32,33]. The double-heavy diquark states $\varepsilon ^{ijk} Q^{T}_j C\gamma _5 Q_k$ cannot exist due to the Pauli principle. In this article, we take the double-heavy diquark states $\varepsilon ^{ijk} Q^{T}_j C\gamma _\mu Q_k$ as basic constituents to construct the tetraquark states.

The article is arranged as follows: we derive the QCD sum rules for the masses and pole residues of the $QQ\bar{Q}\bar{Q}$ tetraquark states in Sect. 2; in Sect. 3, we present the numerical results and discussions; Sect. 4 is reserved for our conclusion.

2 QCD sum rules for the $QQ\bar{Q}\bar{Q}$ tetraquark states

We write down the two-point correlation functions $\Pi _{\mu \nu \alpha \beta }(p)$ and $\Pi (p)$ in the QCD sum rules,

$$\begin{aligned}&\Pi _{\mu \nu \alpha \beta }(p)=i\int \mathrm{d}^4x \mathrm{e}^{ip \cdot x} \langle 0|T \{J_{\mu \nu }(x)J_{\alpha \beta }^{\dagger }(0) \}|0\rangle , \nonumber \\&\Pi (p)=i\int \mathrm{d}^4x \mathrm{e}^{ip \cdot x} \langle 0|T \{J(x)J^{\dagger }(0) \}|0\rangle , \end{aligned}$$

(2)

where

$$\begin{aligned}&J_{\mu \nu }(x)=\frac{\varepsilon ^{ijk}\varepsilon ^{imn}}{\sqrt{2}} \{Q^j(x)C\gamma _\mu Q^k(x) \bar{Q}^m(x) \gamma _\nu C \bar{Q}^n(x) \nonumber \\&~~~~~~~~~~~~~~~ + Q^j(x)C\gamma _\nu Q^k(x) \bar{Q}^m(x)\gamma _\mu C \bar{Q}^n(x) \} , \nonumber \\&J(x)=\varepsilon ^{ijk}\varepsilon ^{imn}Q^j(x)C\gamma _\mu Q^k(x) \bar{Q}^m(x)\gamma ^\mu C \bar{Q}^n(x) , \end{aligned}$$

(3)

$Q=c,b$, i, j, k, m, n are color indices, C is the charge conjunction matrix. We choose the currents J(x) and $J_{\mu \nu }(x)$ to interpolate the $J^{PC}=0^{++}$ and $2^{++}$ diquark–antidiquark type $QQ\bar{Q}\bar{Q}$ tetraquark states, respectively. In Ref. [12], Chen et al. choose the currents $\eta ^i(x)$ and $\eta ^j_{\mu \nu }(x)$ with $i=1,2,3,4,5$ and $j=1,2$ to interpolate the $0^{++}$ and $2^{++}$ $QQ\bar{Q}\bar{Q}$ tetraquark states, respectively,

$$\begin{aligned}&\eta ^i(x)=Q^a(x)C\Gamma ^i Q^b(x) \bar{Q}^a(x)\Gamma ^i C \bar{Q}^b(x) , \nonumber \\&\eta ^j_{\mu \nu }(x)=Q^a(x)C\Gamma ^j_\mu Q^b(x) \bar{Q}^a(x)\Gamma ^j_\nu C \bar{Q}^b(x)\nonumber \\&~~~~~~~~~~~~~~+Q^a(x)C\Gamma ^j_\nu Q^b(x) \bar{Q}^a(x)\Gamma ^j_\mu C \bar{Q}^b(x) , \end{aligned}$$

(4)

where $\Gamma ^1=\gamma _5$, $\Gamma ^2=\gamma _\mu \gamma _5$, $\Gamma ^3=\sigma _{\mu \nu }$, $\Gamma ^4=\gamma _\mu$, $\Gamma ^5=1$, $\Gamma ^1_\mu =\gamma _\mu$, $\Gamma ^2_\mu =\gamma _\mu \gamma _5$, the a and b are color indices. The $C\gamma _5$, C, $C\gamma _\mu \gamma _5$ are antisymmetric, while $C\gamma _\mu$, $C\sigma _{\mu \nu }$ are symmetric. So the currents $\eta ^{1/2/5}(x)$ and $\eta ^2_{\mu \nu }(x)$ are in color $\mathbf{6}_c\otimes {\bar{\mathbf{6}}}_c$ representation, while the currents $\eta ^{3/4}(x)$ and $\eta ^1_{\mu \nu }(x)$ have both color $\mathbf{6}_c\otimes {\bar{\mathbf{6}}}_c$ and ${\bar{\mathbf{3}}}_c\otimes \mathbf{3}_c$ components. The currents J(x) and $J_{\mu \nu }(x)$ chosen in this article are in the color ${\bar{\mathbf{3}}}_c\otimes \mathbf{3}_c$ representation, and significantly differ from the currents $\eta ^{4}(x)$ and $\eta ^1_{\mu \nu }(x)$ chosen in Ref. [12], respectively. The one-gluon exchange leads to attractive (repulsive) interaction in the color ${\bar{\mathbf{3}}}_c$ ($\mathbf{6}_c$) channel [29, 30], the currents or quark structures chosen in the present work and in Ref. [12] couple potentially to the tetraquark states with different masses.

At the phenomenological side, we can insert a complete set of intermediate hadronic states with the same quantum numbers as the current operators $J_{\mu \nu }(x)$ and J(x) into the correlation functions $\Pi _{\mu \nu \alpha \beta }(p)$ and $\Pi (p)$ to obtain the hadronic representation [34,35,36]. After isolating the ground state contributions of the scalar and tensor $QQ\bar{Q}\bar{Q}$ tetraquark states (denoted by X), we get the following results:

$$\begin{aligned}&\Pi _{\mu \nu \alpha \beta } (p) =\frac{\lambda _X^2}{M_X^2-p^2}\left( \frac{\widetilde{g}_{\mu \alpha }\widetilde{g}_{\nu \beta }+\widetilde{g}_{\mu \beta }\widetilde{g}_{\nu \alpha }}{2}-\frac{\widetilde{g}_{\mu \nu }\widetilde{g}_{\alpha \beta }}{3}\right) \nonumber \\&~~~~~~~~~~~~~~~~~~~~+\cdots , \end{aligned}$$

(5)

$$\begin{aligned}&\Pi (p) =\frac{\lambda _X^2}{M^2_X-p^2} +\cdots , \end{aligned}$$

(6)

where $\widetilde{g}_{\mu \nu }=g_{\mu \nu }-\frac{p_{\mu }p_{\nu }}{p^2}$, the pole residues $\lambda _{X}$ are defined by

$$\begin{aligned}&\langle 0|J_{\mu \nu }(0)|X (p)\rangle = \lambda _{X} \varepsilon _{\mu \nu }(\lambda ,p) , \nonumber \\&\langle 0|J (0)|X (p)\rangle = \lambda _{X} , \end{aligned}$$

(7)

$\varepsilon _{\mu \nu }(\lambda ,p)$ is the polarization vector of the tensor tetraquark states,

$$\begin{aligned} \sum _{\lambda }\varepsilon ^*_{\alpha \beta }(\lambda ,p)\varepsilon _{\mu \nu }(\lambda ,p)= & {} \frac{\widetilde{g}_{\alpha \mu }\widetilde{g}_{\beta \nu }+\widetilde{g}_{\alpha \nu }\widetilde{g}_{\beta \mu }}{2}-\frac{\widetilde{g}_{\alpha \beta }\widetilde{g}_{\mu \nu }}{3} .\nonumber \\ \end{aligned}$$

(8)

Now we briefly outline the operator product expansion for the correlation functions $\Pi _{\mu \nu \alpha \beta }(p)$ and $\Pi (p)$ in perturbative QCD. We contract the heavy quark fields in the correlation functions $\Pi _{\mu \nu \alpha \beta }(p)$ and $\Pi (p)$ with the Wick theorem, and obtain the results

$$\begin{aligned} \Pi _{\mu \nu \alpha \beta }(p)= & {} \frac{i\varepsilon ^{ijk}\varepsilon ^{imn}\varepsilon ^{i^{\prime }j^{\prime }k^{\prime }}\varepsilon ^{i^{\prime }m^{\prime }n^{\prime }}}{2}\int \mathrm{d}^4x e^{ip \cdot x} \nonumber \\&\times \{\mathrm{Tr} [ \gamma _{\mu }S^{kk^{\prime }}(x)\gamma _{\alpha } CS^{jj^{\prime }T}(x)C ] \nonumber \\&\times \mathrm{Tr} [ \gamma _{\beta } S^{n^{\prime }n}(-x)\gamma _{\nu } C S^{m^{\prime }mT}(-x)C] \nonumber \\&+\mathrm{Tr} [ \gamma _{\nu } S^{kk^{\prime }}(x)\gamma _{\beta } CS^{jj^{\prime }T}(x)C ] \nonumber \\&\times \mathrm{Tr} [ \gamma _{\alpha } S^{n^{\prime }n}(-x)\gamma _{\mu } C S^{m^{\prime }mT}(-x)C ] \nonumber \\&+\mathrm{Tr} [ \gamma _{\mu } S^{kk^{\prime }}(x) \gamma _{\beta } CS^{jj^{\prime }T}(x)C ]\nonumber \\&\times \mathrm{Tr} [ \gamma _{\alpha } S^{n^{\prime }n}(-x) \gamma _{\nu }C S^{m^{\prime }mT}(-x)C ] \nonumber \\&+\mathrm{Tr} [ \gamma _{\nu } S^{kk^{\prime }}(x)\gamma _{\alpha } CS^{jj^{\prime }T}(x)C ] \nonumber \\&\times \mathrm{Tr} [ \gamma _{\beta } S^{n^{\prime }n}(-x)\gamma _{\mu } C S^{m^{\prime }mT}(-x)C ] \} , \nonumber \\ \Pi (p)= & {} i\varepsilon ^{ijk}\varepsilon ^{imn}\varepsilon ^{i^{\prime }j^{\prime }k^{\prime }}\varepsilon ^{i^{\prime }m^{\prime }n^{\prime }}\int \mathrm{d}^4x \mathrm{e}^{ip \cdot x} \nonumber \\&\times \mathrm{Tr} [ \gamma _{\mu }S^{kk^{\prime }}(x)\gamma _{\alpha } CS^{jj^{\prime }T}(x)C ]\nonumber \\&\times \mathrm{Tr} [ \gamma ^{\alpha } S^{n^{\prime }n}(-x)\gamma ^{\mu } C S^{m^{\prime }mT}(-x)C ] , \end{aligned}$$

(9)

where $S_{ij}(x)$ is the full Q quark propagator,

(10)

and $t^n=\frac{\lambda ^n}{2}$, the $\lambda ^n$ are the Gell-Mann matrices [36]. Then we compute the integrals both in the coordinate and momentum spaces to obtain the correlation functions $\Pi _{\mu \nu \alpha \beta }(p)$ and $\Pi (p)$, therefore the QCD spectral densities using the dispersion relation. The calculations are straightforward but tedious.

We take the quark–hadron duality below the continuum thresholds $s_0$ and perform the Borel transform with respect to the variable $P^2=-p^2$ to obtain the QCD sum rules:

$$\begin{aligned}&\lambda ^2_{X} \exp \left( -\frac{M^2_{X}}{T^2}\right) \nonumber \\&\quad = \int _{16m_Q^2}^{s_0} \mathrm{d}s \int _{z_i}^{z_f}\mathrm{d}z \int _{t_i}^{t_f}\mathrm{d}t \int _{r_i}^{r_f}\mathrm{d}r \rho (s,z,t,r) \nonumber \\&\qquad \times \exp \left( -\frac{s}{T^2}\right) , \end{aligned}$$

(11)

where $\rho (s,z,t,r) =\rho _S(s,z,t,r)$ and $\rho _T(s,z,t,r)$ for the scalar and tensor tetraquark states, respectively, the explicit expressions are given in the appendix,

$$\begin{aligned} r_{f/i}= & {} \frac{1}{2}\left\{ 1-z-t \pm \sqrt{(1-z-t)^2-4\frac{1-z-t}{\hat{s}-\frac{1}{z}-\frac{1}{t}}}\right\} ,\nonumber \\ t_{f/i}= & {} \frac{1}{2\left( \hat{s}-\frac{1}{z}\right) }\left\{ (1-z)\left( \hat{s}-\frac{1}{z}\right) \right. \nonumber \\&\left. -3 \pm \sqrt{ \left[ (1-z)\left( \hat{s}-\frac{1}{z}\right) -3\right] ^2-4 (1-z)\left( \hat{s}-\frac{1}{z}\right) }\right\} ,\nonumber \\ z_{f/i}= & {} \frac{1}{2\hat{s}}\left\{ \hat{s}-8 \pm \sqrt{\left( \hat{s}-8\right) ^2-4\hat{s} }\right\} , \end{aligned}$$

(12)

and $\hat{s}=\frac{s}{m_Q^2}$.

We derive Eq. (11) with respect to $\tau =\frac{1}{T^2}$, then eliminate the pole residues $\lambda _{X}$, and obtain the QCD sum rules for the masses of the scalar and tensor $QQ\bar{Q}\bar{Q}$ tetraquark states,

$$\begin{aligned} M^2_{X}= & {} - \frac{\frac{\mathrm{d}}{\mathrm{d} \tau }\int _{16m_Q^2}^{s_0} \mathrm{d}s \int _{z_i}^{z_f}\mathrm{d}z \int _{t_i}^{t_f}\mathrm{d}t \int _{r_i}^{r_f}\mathrm{d}r \rho (s,z,t,r) \exp \left( -\tau s\right) }{\int _{16m_Q^2}^{s_0} \mathrm{d}s \int _{z_i}^{z_f}\mathrm{d}z \int _{t_i}^{t_f}\mathrm{d}t \int _{r_i}^{r_f}\mathrm{d}r \rho (s,z,t,r) \exp \left( -\tau s\right) } .\nonumber \\ \end{aligned}$$

(13)

In the moment QCD sum rules, the moments $\overline{M}_n(P_0^2)$ at the phenomenological side are defined by

$$\begin{aligned} \overline{M}_n(P_0^2)= & {} \frac{\lambda _X^2}{(M_X^2+P_0^2)^{n+1}}+\frac{\lambda _{X^\prime }^2}{(M_X^{\prime 2}+P_0^2)^{n+1}}+\cdots , \nonumber \\= & {} \frac{\lambda _X^2}{(M_X^2+P_0^2)^{n+1}}\left[ 1+ \frac{\lambda _{X^\prime }^2}{\lambda _X^2}\frac{(M_X^2+P_0^2)^{n+1}}{(M_X^{\prime 2}+P_0^2)^{n+1}}+\cdots \right] , \nonumber \\= & {} \frac{\lambda _X^2}{(M_X^2+P_0^2)^{n+1}} [1+\delta _n(P_0^2)] , \end{aligned}$$

(14)

where $X^\prime$ denotes the first radial excited state of the X, $P_0^2$ is a particular value for the parameter $P^2=-p^2$. We can extract the mass $M_X$ according to the ratio $r(n,P_0^2)$ at large values of n,

$$\begin{aligned} r(n,P_0^2)= & {} \frac{\overline{M}_n(P_0^2)}{\overline{M}_{n+1}(P_0^2)}=(M_X^2+P_0^2)\frac{1+\delta _n(P_0^2)}{1+\delta _{n+1}(P_0^2)} , \end{aligned}$$

(15)

where the small values $\delta _{n}(P_0^2)\approx \delta _{n+1}(P_0^2)$. In Refs. [37, 38], we observe that $\frac{\lambda _{X^\prime }^2}{\lambda _X^2}=6.6$ (or 9.6) for the central values of the pole residues for $X=Z_c(3900)$, $X^\prime =Z(4430)$ (or $X=X(3915)$, $X^\prime =X(4500)$) in the scenario of tetraquark states. So n has to be postponed to very large values [12]. In the present work, the contributions of the high resonances and continuum states are depressed by the weight function $\exp \left( -\frac{s}{T^2}\right)$. The differences between the predicted masses in the present work and in Ref. [12] originate from the different currents or quark structures.

3 Numerical results and discussions

We take the gluon condensate to be the standard value [34,35,36, 39], and take the $\overline{MS}$ masses $m_{c}(m_c)=(1.275\pm 0.025)\,\mathrm {GeV}$ and $m_{b}(m_b)=(4.18\pm 0.03)\,\mathrm {GeV}$ from the Particle Data Group [40]. We take into account the energy-scale dependence of the $\overline{MS}$ masses from the renormalization group equation,

$$\begin{aligned} m_c(\mu )= & {} m_c(m_c)\left[ \frac{\alpha _{s}(\mu )}{\alpha _{s}(m_c)}\right] ^{\frac{12}{25}} ,\nonumber \\ m_b(\mu )= & {} m_b(m_b)\left[ \frac{\alpha _{s}(\mu )}{\alpha _{s}(m_b)}\right] ^{\frac{12}{23}} ,\nonumber \\ \alpha _s(\mu )= & {} \frac{1}{b_0t}\left[ 1-\frac{b_1}{b_0^2}\frac{\log t}{t} +\frac{b_1^2(\log ^2{t}-\log {t}-1)+b_0b_2}{b_0^4t^2}\right] ,\nonumber \\ \end{aligned}$$

(16)

where $t=\log \frac{\mu ^2}{\Lambda ^2}$, $b_0=\frac{33-2n_f}{12\pi }$, $b_1=\frac{153-19n_f}{24\pi ^2}$, $b_2=\frac{2857-\frac{5033}{9}n_f+\frac{325}{27}n_f^2}{128\pi ^3}$, $\Lambda =213$, 296 and $339\,\mathrm {MeV}$ for the flavors $n_f=5$, 4 and 3, respectively [40].

The values of the thresholds are $2M_{\eta _c}=5966.8\,\mathrm {MeV}$, $2M_{J/\psi }=6193.8\,\mathrm {MeV}$, $2M_{\eta _b}=18{,}798.0\,\mathrm {MeV}$, $2M_{\Upsilon }=18{,}920.6\,\mathrm {MeV}$ from the Particle Data Group [40]. The masses of the $0^{++}$ and $2^{++}$ $QQ\bar{Q}\bar{Q}$ tetraquark states from the phenomenological quark models lie above or below those thresholds [3,4,5,6,7,8,9,10,11,12]. In Ref. [41], we study the vector and axial-vector $B_c$ mesons with the QCD sum rules and obtain the masses $M_{B_{c}^*}=6.337\pm 0.052\,\mathrm {GeV}$ and $M_{B_{c1}}=6.730\pm 0.061\,\mathrm {GeV}$ at the typical energy scale $\mu =2\,\mathrm {GeV}$. The $B_c$ mesons have two heavy quarks, and the mass $M_{B_{c}^*}=6.337\pm 0.052\,\mathrm {GeV}$ lies slightly above the threshold $2M_{J/\psi }=6193.8\,\mathrm {MeV}$, so we expect that the ideal energy scale to extract masses of the $cc\bar{c}\bar{c}$ tetraquark states from the QCD sum rules is about $\mu =2\,\mathrm {GeV}$. This is indeed the case.

Fig. 1

The masses of the $cc\bar{c}\bar{c}$ tetraquark states with variations of the energy scales and Borel parameters, where the A and B denote the $cc\bar{c}\bar{c}(0^{++})$ and $cc\bar{c}\bar{c}(2^{++})$, respectively

Fig. 2

The masses of the $bb\bar{b}\bar{b}$ tetraquark states with variations of the energy scales and Borel parameters, where the C and D denote the $bb\bar{b}\bar{b}(0^{++})$ and $bb\bar{b}\bar{b}(2^{++})$, respectively

In Fig. 1, we plot the masses of the $cc\bar{c}\bar{c}$ tetraquark states with variations of the energy scales and Borel parameters for the threshold parameters $s_S^0=42\,\mathrm {GeV}^2$ and $S_T^0=44\,\mathrm {GeV}^2$. From the figure, we can see that the predicted masses decrease monotonously and slowly with increase of the energy scales, the QCD sum rules are stable with variations of the Borel parameters at the energy scales $1.2\,\mathrm{{GeV}}<\mu <2.2\,\mathrm{GeV}$. At the energy scale $\mu =2.0\,\mathrm {GeV}$, the relation $S_{S/T}^0= (M_{S/T}+0.5\,\mathrm {GeV} )^2$ is satisfied, naively, we expect that the energy gap between the ground states and the first radial excited states ia about $0.5\,\mathrm {GeV}$. In the QCD sum rules, we usually take the continuum threshold parameters as $\sqrt{s_0}=M_{gr}+(0.4-0.6)\,\mathrm {GeV}$ for the conventional mesons, where gr denotes the ground states. Experimentally, the energy gaps $M_{\psi ^\prime }-M_{J/\psi }=589\,\mathrm {MeV}$ and $M_{\eta _c^\prime }-M_{\eta _c}=656\,\mathrm {MeV}$ from the Particle Data Group [40]. Now we revisit the mass gaps of the tetraquark states. In Ref. [37], we tentatively assign the $Z_c(3900)$ and Z(4430) to be the ground state and the first radial excited state of the axial-vector tetraquark states with $J^{PC}=1^{+-}$, respectively, and reproduce the experimental values of the masses with the QCD sum rules. In Ref. [38], we tentatively assign X(3915) and X(4500) to the ground state and the first radial excited state of the scalar $cs\bar{c}\bar{s}$ tetraquark states with $J^{PC}=0^{++}$, respectively, and reproduce the experimental values of the masses with the QCD sum rules. The mass gaps are $M_{Z(4430)}-M_{Z_c(3900)}=576\,\mathrm {MeV}$ and $M_{X(4500)}-M_{X(3915)}=588\,\mathrm {MeV}$, which also satisfy the relation $\sqrt{s_0}=M_{gr}+(0.4{-}0.6)\,\mathrm {GeV}$, if only the ground states are taken into account in the QCD sum rules. In this article, we take the relation $\sqrt{s_0}=M_{gr}+(0.4{-} 0.6)\,\mathrm {GeV}$ as a constraint, and search for the optimal values of the $s_0$ to reproduce $M_{gr}$. At the regions $S_{S/T}^0\le (M_{S/T}+0.6\,\mathrm {GeV} )^2$, the contributions of the excited states are expected not to be included.

Table 1 The Borel parameters, continuum threshold parameters, energy scales, pole contributions, masses and pole residues of the tetraquark states

Fig. 3

The masses of the tetraquark states with variations of the Borel parameters $T^2$, where A, B, C and D denote $cc\bar{c}\bar{c}(0^{++})$, $cc\bar{c}\bar{c}(2^{++})$, $bb\bar{b}\bar{b}(0^{++})$ and $bb\bar{b}\bar{b}(2^{++})$, respectively

In Fig. 2, we plot the masses of the $bb\bar{b}\bar{b}$ tetraquark states with variations of the energy scales and Borel parameters for the threshold parameters $s_S^0=374\,\mathrm {GeV}^2$ and $S_T^0=375\,\mathrm {GeV}^2$. From the figure, we can see that the predicted masses also decrease monotonously and slowly with increase of the energy scales, the QCD sum rules are stable with variations of the Borel parameters at the energy scales $2.5\,\mathrm{{GeV}}<\mu <3.3\,\mathrm{GeV}$. At the energy scale $\mu =3.1\,\mathrm {GeV}$, the relation $S_{S/T}^0=\left( M_{S/T}+0.5\,\mathrm {GeV}\right) ^2$ is satisfied. For the conventional mesons, the energy gaps $M_{\Upsilon ^\prime }-M_{\Upsilon }=563\,\mathrm {MeV}$ and $M_{\eta _b^\prime }-M_{\eta _b}=600\,\mathrm {MeV}$ from the Particle Data Group [40]. It is also reasonable to choose the relation $S_{S/T}^0\le \left( M_{S/T}+0.6\,\mathrm {GeV}\right) ^2$.

Fig. 4

The pole residues of the tetraquark states with variations of the Borel parameters $T^2$, where A, B, C and D denote $cc\bar{c}\bar{c}(0^{++})$, $cc\bar{c}\bar{c}(2^{++})$, $bb\bar{b}\bar{b}(0^{++})$ and $bb\bar{b}\bar{b}(2^{++})$, respectively

We search for the Borel parameters $T^2$ and continuum threshold parameters $s_0$ to satisfy the two criteria of the QCD sum rules: pole dominance at the phenomenological side and convergence of the operator product expansion at the QCD side. Furthermore, we take the relation $\sqrt{S_{S/T}^0}= M_{S/T}+(0.4{-}0.6)\,\mathrm {GeV}$ as an additional constraint to obey. The resulting Borel parameters, continuum threshold parameters, energy scales, pole contributions are shown explicitly in Table 1. From the table, we can see that the pole dominance at the phenomenological side is well satisfied. In the Borel windows, the dominant contributions come from the perturbative terms, the contributions of the gluon condensate are about $-10\%$, the operator product expansion is well convergent. Now the two criteria of the QCD sum rules are all satisfied, we expect to make reasonable predictions.

In Ref. [42], we tentatively assign $D_{s3}^*(2860)$ to be a D-wave $c\bar{s}$ meson, and we study the mass and decay constant of $D_{s3}^*(2860)$ with the QCD sum rules by calculating the contributions of the vacuum condensates up to dimension-6 in the operator product expansion. In calculations, we observe that only the perturbative term, gluon condensate and three-gluon condensate have contributions. At the Borel window, the contributions are about (107–109) %, −(7–9) % and $\ll$1%, respectively; see the first diagram in Fig. 3 [42]. The three-gluon condensate can be neglected safely. In the present case, the contributions of the gluon condensate are about $-10\%$, just like in the case of the QCD sum rules for $D_{s3}^*(2860)$, so neglecting the three-gluon condensate cannot impair the predictive ability. As the dominant contributions come from the perturbative terms, perturbative $\mathcal {O}(\alpha _s)$ corrections amount to multiplying the perturbative terms by a factor $\kappa$, which can be absorbed into the pole residues and cannot impair the predicted masses remarkably.

We take into account all uncertainties of the input parameters, and we obtain the values of the ground state masses and pole residues, which are also shown explicitly in Table 1 and Figs. 3 and 4. From Table 1, we can see that the additional constraint is also satisfied. In Figs. 3 and 4, we plot the masses and pole residues with variations of the Borel parameters at much larger intervals than the Borel windows shown in Table 1. From Figs. 3 and 4, we can see that the predicted masses and pole residues are rather stable with variations of the Borel parameters, the uncertainties originate from the Borel parameters in the Borel windows are very small.

From Table 1, we can see that the mass splitting between the $0^{++}$ and $2^{++}$ $bb\bar{b}\bar{b}$ tetraquark states is much smaller than that for the $cc\bar{c}\bar{c}$ tetraquark states. The heavy quark effective Lagrangian can be written as

$$\begin{aligned} \mathcal{L}= & {} \bar{h}_viv\cdot Dh_v+{1\over 2m_Q} \left[ \bar{h}_v(iD_\perp )^2h_v +{g_s\over 2}\,\bar{h}_v\sigma ^{\alpha \beta } G_{\alpha \beta }h_v\right] \nonumber \\&+\cdots , \end{aligned}$$

(17)

where $D^\mu _\perp =D^\mu -v^\mu v\cdot D$, $D_\mu$ is the covariant derivative, and $h_v$ is the effective heavy quark field. The heavy quark spin symmetry breaking terms appear at the order $\mathcal {O}(1/m_Q)$ [43]. The $\overline{MS}$ masses are $m_{c}(m_c)=(1.275\pm 0.025)\,\mathrm {GeV}$ and $m_{b}(m_b)=(4.18\pm 0.03)\,\mathrm {GeV}$ from the Particle Data Group [40], the heavy quark spin symmetry breaking effects in the c-quark systems are much larger than that in the b-quark systems.

In 2002, the SELEX collaboration reported the first observation of a signal for the double-charm baryon state $\Xi _{cc}^+$ in the decay mode $\Xi _{cc}^+\rightarrow \Lambda _c^+K^-\pi ^+$ [44], and confirmed later by the same collaboration in the decay mode $\Xi _{cc}^+\rightarrow pD^+K^-$ with the measured mass $M_{\Xi }=(3518.9 \pm 0.9) \,\mathrm { MeV }$ [45]. In Ref. [46], we study the ${1\over 2}^+$ doubly heavy baryon states $\Omega _{QQ}$ and $\Xi _{QQ}$ by subtracting the contributions from the corresponding ${1\over 2}^-$ doubly heavy baryon states with the QCD sum rules, and obtain the value $M_{\Xi _{cc}}=3.57\pm 0.14\,\mathrm {GeV}$. If exciting additional quark–antiquark pair $q\bar{q}$ with $J^{PC}=0^{++}$ costs energy about $1\,\mathrm {GeV}$, then $M_{X(cc\bar{c}\bar{c},0^{++}/2^{++})}\approx 2M_{\Xi _{cc}}-1\,\mathrm {GeV}=6.14\pm 0.14\,\mathrm {GeV}$, which is consistent with the present prediction.

The predicted masses are

$$\begin{aligned} \begin{aligned} M_{X(cc\bar{c}\bar{c},0^{++})}&=5.91{-}6.07\,\mathrm {GeV} , \\ M_{X(cc\bar{c}\bar{c},2^{++})}&=6.01{-}6.17\,\mathrm {GeV} , \\ M_{X(bb\bar{b}\bar{b},0^{++})}&=18.75{-}18.93\,\mathrm {GeV} , \\ M_{X(bb\bar{b}\bar{b},2^{++})}&=18.76{-}18.94\,\mathrm {GeV} . \end{aligned} \end{aligned}$$

(18)

The decays

$$\begin{aligned} \begin{aligned}&X(cc\bar{c}\bar{c},0^{++}/2^{++}) \rightarrow \eta _c \eta _c \rightarrow \gamma \gamma \gamma \gamma ,\\&X(bb\bar{b}\bar{b},0^{++}/2^{++}) \rightarrow \eta _b \eta _b \rightarrow \gamma \gamma \gamma \gamma , \end{aligned} \end{aligned}$$

(19)

are kinematically allowed, but the available spaces are small. The decays

$$\begin{aligned} \begin{aligned} X(cc\bar{c}\bar{c},0^{++}/2^{++})&\rightarrow J/\psi J/\psi ,\\ X(bb\bar{b}\bar{b},0^{++}/2^{++})&\rightarrow \Upsilon \Upsilon , \end{aligned} \end{aligned}$$

(20)

are kinematically forbidden, but the decays

$$\begin{aligned} \begin{aligned}&X(cc\bar{c}\bar{c},0^{++}/2^{++}) \rightarrow J/\psi {J/\psi }^* \rightarrow \mu ^+\mu ^- \mu ^+\mu ^- ,\\&X(bb\bar{b}\bar{b},0^{++}/2^{++}) \rightarrow \Upsilon \Upsilon ^* \rightarrow \mu ^+\mu ^- \mu ^+\mu ^- , \end{aligned} \end{aligned}$$

(21)

can take place. We can search for the $X(cc\bar{c}\bar{c},0^{++}/2^{++})$ and $X(bb\bar{b}\bar{b},0^{++}/2^{++})$ in the mass spectrum of the $\mu ^+\mu ^- \mu ^+\mu ^-$ in the future.

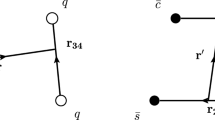
In the following, we perform a Fierz re-arrangement to the tensor current $J_{\mu \nu }$ and scalar current J both in the color and Dirac-spinor spaces to obtain the results,

$$\begin{aligned} J_{\mu \nu }= & {} \frac{1}{\sqrt{2}} \{ \bar{Q}\gamma _\mu \gamma _5Q \bar{Q}\gamma _\nu \gamma _5Q+\bar{Q}\gamma _\nu \gamma _5Q \bar{Q}\gamma _\mu \gamma _5Q \nonumber \\&-\bar{Q}\gamma _\mu Q \bar{Q}\gamma _\nu Q-\bar{Q}\gamma _\nu Q \bar{Q}\gamma _\mu Q \nonumber \\&+g^{\alpha \beta } (\bar{Q}\sigma _{\mu \alpha }Q \bar{Q}\sigma _{\nu \beta }Q+\bar{Q}\sigma _{\nu \alpha }Q \bar{Q}\sigma _{\mu \beta }Q ) \nonumber \\&+g_{\mu \nu } ( \bar{Q}Q \bar{Q}Q+\bar{Q}i\gamma _5Q \bar{Q}i\gamma _5Q\nonumber \\&+\bar{Q}\gamma _{\alpha } Q \bar{Q}\gamma ^{\alpha }Q-\bar{Q}\gamma _{\alpha }\gamma _5 Q \bar{Q}\gamma ^{\alpha }\gamma _5Q\nonumber \\&-\frac{1}{2}\bar{Q}\sigma _{\alpha \beta } Q \bar{Q}\sigma ^{\alpha \beta }Q ) \} , \end{aligned}$$

(22)

$$\begin{aligned} J= & {} 2\bar{Q}Q \bar{Q}Q+2\bar{Q}i\gamma _5Q \bar{Q}i\gamma _5Q\nonumber \\&+\bar{Q}\gamma _{\alpha } Q \bar{Q}\gamma ^{\alpha }Q-\bar{Q}\gamma _{\alpha }\gamma _5 Q \bar{Q}\gamma ^{\alpha }\gamma _5Q . \end{aligned}$$

(23)

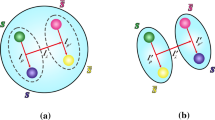
Now we can see that the diquark–antidiquark type current can be changed to a current as a special superposition of color singlet-singlet type currents, which couple potentially to the meson–meson pairs. The diquark–antidiquark type tetraquark state can be taken as a special superposition of a series of meson–meson pairs, and embodies the net effects. The decays to its components (meson–meson pairs) are Okubo–Zweig–Iizuka super-allowed, but the re-arrangements in the color-space are highly non-trivial.

We take the current J as an example to illustrate that the scalar tetraquark state can embody the net effects of all the meson–meson pairs. At the phenomenological side, we can insert a complete set of intermediate hadronic states with the same quantum numbers as the current operator J(x) into the correlation function $\Pi (p)$ to obtain the hadronic representation [34,35,36]. After isolating the lowest meson–meson pairs, we get the following result:

$$\begin{aligned}&\Pi (p) =\frac{i}{(2\pi )^4}\int \mathrm{d}^4q \frac{i}{q^2-M_{\eta _c}^2}\frac{i}{(q+p)^2-M_{\eta _c}^2}\nonumber \\&\quad \times \left\{ \frac{f_{\eta _c}^4q^4(q+p)^4}{4m_c^4} +f_{\eta _c}^4 [q \cdot (q+p) ]^2 \right. \nonumber \\&\quad \left. +\frac{f_{\eta _c}^4q^2(q+p)^2 q \cdot (q+p)}{m_c^2}\right\} \nonumber \\&\quad +\frac{i}{(2\pi )^4}\int \mathrm{d}^4q \frac{i}{q^2-M_{J/\psi }^2}\frac{i}{(q+p)^2-M_{J/\psi }^2}\nonumber \\&\quad \times f_{J/\psi }^4 q^2(q+p)^2 \left[ g_{\mu \nu }-\frac{q_\mu q_\nu }{q^2} \right] \nonumber \\&\quad \times \left[ g^{\mu \nu }-\frac{(q+p)^\mu (q+p)^\nu }{(q+p)^2} \right] \nonumber \\&\quad +\frac{i}{(2\pi )^4}\int \mathrm{d}^4q \frac{i}{q^2-M_{\chi _{c0}}^2}\frac{i}{(q+p)^2-M_{\chi _{c0}}^2}\nonumber \\&\quad \times \{4f_{\chi _{c0}}^4 q^2(q+p)^2 + f_{\chi _{c0}}^4 [q \cdot (q+p) ]^2 \nonumber \\&\quad +4f_{\chi _{c0}}^4 \sqrt{q^2(q+p)^2} q \cdot (q+p) \} \nonumber \\&\quad +\frac{i}{(2\pi )^4}\int \mathrm{d}^4q \frac{i}{q^2-M_{\chi _{c1}}^2}\nonumber \\&\quad \times \frac{i}{(q+p)^2-M_{\chi _{c1}}^2} f_{\chi _{c1}}^4 q^2(q+p)^2 \left[ g_{\mu \nu }-\frac{q_\mu q_\nu }{q^2} \right] \nonumber \\&\quad \times \left[ g^{\mu \nu }-\frac{(q+p)^\mu (q+p)^\nu }{(q+p)^2} \right] +\cdots , \end{aligned}$$

(24)

where the decay constants $f_{\eta _c}$, $f_{J/\psi }$, $f_{\chi _{c0}}$ and $f_{\chi _{c1}}$ are defined by

$$\begin{aligned}&\langle 0|J(0)|\eta _c(q)\eta _c(q+p)\rangle \nonumber \\&\quad =2\frac{f_{\eta _c}q^2}{2m_c} \frac{f_{\eta _c}(q+p)^2}{2m_c}+f_{\eta _c}^2 q \cdot (q+p) , \nonumber \\&\langle 0|J(0)|J/\psi (q)J/\psi (q+p)\rangle =f_{J/\psi }^2 \sqrt{q^2(q+p)^2} \varepsilon _\alpha \varepsilon ^\alpha , \nonumber \\&\langle 0|J(0)|\chi _{c0}(q)\chi _{c0}(q+p)\rangle \nonumber \\&\quad =2f_{\chi _{c0}}^2 \sqrt{q^2(q+p)^2}+ f_{\chi _{c0}}^2 q \cdot (q+p) , \nonumber \\&\langle 0|J(0)|\chi _{c1}(q)\chi _{c1}(q+p)\rangle =f_{\chi _{c1}}^2 \sqrt{q^2(q+p)^2} \varepsilon _\alpha \varepsilon ^\alpha , \end{aligned}$$

(25)

the $\varepsilon _{\mu }$ are the polarization vectors of the $J/\psi$ and $\chi _{c1}$.

We can rewrite the correlation function $\Pi (p)$ in the following form using the dispersion relation:

$$\begin{aligned} \Pi (p)= & {} \frac{f_{\eta _c}^4}{16\pi ^2}\int _{4M_{\eta _c}^2}^{s_0} \mathrm{d}s \frac{1}{s-p^2} \left\{ \frac{M_{\eta _c}^8}{4m_c^4} + \left( \frac{s}{2}-M_{\eta _c}^2\right) ^2 \right. \nonumber \\&\left. -\frac{M_{\eta _c}^4}{m_c^2} \left( \frac{s}{2}-M_{\eta _c}^2\right) \right\} \sqrt{1-\frac{4M_{\eta _c}^2}{s}} \nonumber \\&+\frac{f_{J/\psi }^4}{16\pi ^2}\int _{4M_{J/\psi }^2}^{s_0}\mathrm{d}s \frac{1}{s-p^2} M_{J/\psi }^4 \nonumber \\&\times \left\{ 2 +\frac{ \Big (\frac{s}{2}-M_{J/\psi }^2\Big )^2}{M_{J/\psi }^4} \right\} \sqrt{1-\frac{4M_{J/\psi }^2}{s}} \nonumber \\&+\frac{f_{\chi _{c0}}^4}{16\pi ^2}\int _{4M_{\chi _{c0}}^2}^{s_0}\mathrm{d}s \frac{1}{s-p^2} \left\{ 4M_{\chi _{c0}}^4 + \Big (\frac{s}{2}-M_{\chi _{c0}}^2\Big )^2 \right. \nonumber \\&\left. -4M_{\chi _{c0}}^2 \Big (\frac{s}{2}-M_{\chi _{c0}}^2\Big ) \right\} \sqrt{1-\frac{4M_{\chi _{c0}}^2}{s}} \nonumber \\&+\frac{f_{\chi _{c1}}^4}{16\pi ^2}\int _{4M_{\chi _{c1}}^2}^{s_0}\mathrm{d}s \frac{1}{s-p^2} M_{\chi _{c1}}^4\nonumber \\&\times \left\{ 2 +\frac{ \Big (\frac{s}{2}-M_{\chi _{c1}}^2\Big )^2}{M_{\chi _{c1}}^4} \right\} \sqrt{1-\frac{4M_{\chi _{c1}}^2}{s}} +\cdots .\nonumber \\ \end{aligned}$$

(26)

In this article, we choose the value $s_0<4M_{\chi _{c0}}^2, 4M_{\chi _{c1}}^2$, the meson pairs $\chi _{c0}\chi _{c0}$ and $\chi _{c1}\chi _{c1}$ have no contributions, the QCD sum rules can be written as

$$\begin{aligned}&\frac{f_{\eta _c}^4}{16\pi ^2}\int _{4M_{\eta _c}^2}^{s_0} \mathrm{d}s \left\{ \frac{M_{\eta _c}^8}{4m_c^4} + \left( \frac{s}{2}-M_{\eta _c}^2\right) ^2 \right. \nonumber \\&\qquad \left. -\frac{M_{\eta _c}^4}{m_c^2} \left( \frac{s}{2}-M_{\eta _c}^2\right) \right\} \sqrt{1-\frac{4M_{\eta _c}^2}{s}} s\, \exp \Big (-\frac{s}{T^2}\Big )\nonumber \\&\qquad +\frac{f_{J/\psi }^4}{16\pi ^2}\int _{4M_{J/\psi }^2}^{s_0}\mathrm{d}s M_{J/\psi }^4 \nonumber \\&\qquad \times \left\{ 2 +\frac{ \Big (\frac{s}{2}-M_{J/\psi }^2\Big )^2}{M_{J/\psi }^4} \right\} \sqrt{1-\frac{4M_{J/\psi }^2}{s}} s\, \exp \left( -\frac{s}{T^2}\right) \nonumber \\&\quad = \kappa ^2 \int _{16m_c^2}^{s_0} \mathrm{d}s \int _{z_i}^{z_f}\mathrm{d}z \int _{t_i}^{t_f}\mathrm{d}t \int _{r_i}^{r_f}\mathrm{d}r \nonumber \\&\qquad \times \rho _S(s,z,t,r) s \exp \left( -\frac{s}{T^2}\right) , \end{aligned}$$

(27)

$$\begin{aligned}&\frac{f_{\eta _c}^4}{16\pi ^2}\int _{4M_{\eta _c}^2}^{s_0}\mathrm{d}s \left\{ \frac{M_{\eta _c}^8}{4m_c^4} + \left( \frac{s}{2}-M_{\eta _c}^2\right) ^2 \right. \nonumber \\&\qquad \left. -\frac{M_{\eta _c}^4}{m_c^2} \left( \frac{s}{2}-M_{\eta _c}^2\right) \right\} \sqrt{1-\frac{4M_{\eta _c}^2}{s}} \exp \left( -\frac{s}{T^2}\right) \nonumber \\&\qquad +\frac{f_{J/\psi }^4}{16\pi ^2}\int _{4M_{J/\psi }^2}^{s_0}\mathrm{d}s M_{J/\psi }^4 \nonumber \\&\qquad \times \left\{ 2 +\frac{ \Big (\frac{s}{2}-M_{J/\psi }^2\Big )^2}{M_{J/\psi }^4} \right\} \sqrt{1-\frac{4M_{J/\psi }^2}{s}} \exp \left( -\frac{s}{T^2}\right) \nonumber \\&\quad =\kappa ^2 \int _{16m_c^2}^{s_0} \mathrm{d}s \int _{z_i}^{z_f}\mathrm{d}z \int _{t_i}^{t_f}\mathrm{d}t \int _{r_i}^{r_f}\mathrm{d}r \nonumber \\&\qquad \times \rho _S(s,z,t,r) \exp \left( -\frac{s}{T^2}\right) , \end{aligned}$$

(28)

where we introduce a coefficient $\kappa$, if $\kappa =1$, the QCD sum rules can be saturated by the meson pairs $\eta _c\eta _c$ and $J/\psi J/\psi$.

We choose the input parameters as $M_{\eta _c}=2.9834\,\mathrm {GeV}$, $M_{J/\psi }=3.0969\,\mathrm {GeV}$ [40], $f_{\eta _c}=0.387\,\mathrm {GeV}$, $f_{J/\psi }=0.418\,\mathrm {GeV}$ [47], $s_0=42\,\mathrm {GeV}^2$. In Fig. 5, we plot the coefficient $\kappa$ coming from Eq. (28) with variation of the Borel parameter $T^2$. From the figure, we can see that the values of $\kappa$ are rather stable with variation of the Borel parameter. Now we choose the special value $T^2=4.4\,\mathrm {GeV}^2$, and plot the coefficient $\kappa$ with variation of the energy scale $\mu$ in Fig. 6. From the figure, we can see that the coefficient $\kappa$ decreases monotonously and quickly with increase of the energy scale $\mu$ at the region $\mu \le 1.6\,\mathrm {GeV}$. In the vicinity of the energy scale $\mu =1.5\,\mathrm {GeV}$, $\kappa \approx 1$, however, the reliable QCD sum rules do not depend heavily on the energy scale $\mu$. So the QCD sum rules cannot be saturated by the meson pairs $\eta _c\eta _c$ and $J/\psi J/\psi$.

Fig. 5

The coefficient $\kappa$ with variation of the Borel parameter $T^2$

Fig. 6

The coefficient $\kappa$ with variation of the energy scale $\mu$, where A and B denote the values come from Eqs. (27) and (28), respectively

Now we saturate the QCD sum rules by the meson pairs $\eta _c\eta _c$, $J/\psi J/\psi$ plus a scalar tetraquark state $X(cc\bar{c}\bar{c},0^{++})$ at the phenomenological side,

$$\begin{aligned}&\lambda ^2_{X} M^2_{X} \exp \left( -\frac{M^2_{X}}{T^2}\right) \nonumber \\&\qquad +\frac{f_{\eta _c}^4}{16\pi ^2}\int _{4M_{\eta _c}^2}^{s_0}\mathrm{d}s \left\{ \frac{M_{\eta _c}^8}{4m_c^4} + \left( \frac{s}{2}-M_{\eta _c}^2\right) ^2 \right. \nonumber \\&\qquad \left. -\frac{M_{\eta _c}^4}{m_c^2} \left( \frac{s}{2}-M_{\eta _c}^2\right) \right\} \sqrt{1-\frac{4M_{\eta _c}^2}{s}} s\, \exp \left( -\frac{s}{T^2}\right) \nonumber \\&\qquad +\frac{f_{J/\psi }^4}{16\pi ^2}\int _{4M_{J/\psi }^2}^{s_0}\mathrm{d}s M_{J/\psi }^4 \nonumber \\&\qquad \times \left\{ 2 +\frac{ \Big (\frac{s}{2}-M_{J/\psi }^2\Big )^2}{M_{J/\psi }^4} \right\} \sqrt{1-\frac{4M_{J/\psi }^2}{s}} s\, \exp \left( -\frac{s}{T^2}\right) \nonumber \\&\quad = \int _{16m_c^2}^{s_0} \mathrm{d}s \int _{z_i}^{z_f}\mathrm{d}z \int _{t_i}^{t_f}\mathrm{d}t \int _{r_i}^{r_f}\mathrm{d}r \nonumber \\&\qquad \times \rho _S(s,z,t,r) s\, \exp \left( -\frac{s}{T^2}\right) , \end{aligned}$$

(29)

$$\begin{aligned}&\lambda ^2_{X} \exp \left( -\frac{M^2_{X}}{T^2}\right) \nonumber \\&\qquad +\frac{f_{\eta _c}^4}{16\pi ^2}\int _{4M_{\eta _c}^2}^{s_0}\mathrm{d}s \left\{ \frac{M_{\eta _c}^8}{4m_c^4} + \left( \frac{s}{2}-M_{\eta _c}^2\right) ^2 \right. \nonumber \\&\qquad \left. -\frac{M_{\eta _c}^4}{m_c^2} \left( \frac{s}{2}-M_{\eta _c}^2\right) \right\} \sqrt{1-\frac{4M_{\eta _c}^2}{s}} \exp \left( -\frac{s}{T^2}\right) \nonumber \\&\qquad +\frac{f_{J/\psi }^4}{16\pi ^2}\int _{4M_{J/\psi }^2}^{s_0}\mathrm{d}s M_{J/\psi }^4\nonumber \\&\qquad \times \left\{ 2 +\frac{ \Big (\frac{s}{2}-M_{J/\psi }^2\Big )^2}{M_{J/\psi }^4} \right\} \sqrt{1-\frac{4M_{J/\psi }^2}{s}} \exp \left( -\frac{s}{T^2}\right) \nonumber \\&\quad = \int _{16m_c^2}^{s_0} \mathrm{d}s \int _{z_i}^{z_f}\mathrm{d}z \int _{t_i}^{t_f}\mathrm{d}t \int _{r_i}^{r_f} \mathrm{d}r \nonumber \\&\qquad \times \rho _S(s,z,t,r) \exp \left( -\frac{s}{T^2}\right) . \end{aligned}$$

(30)

Fig. 7

The mass $M_{X(cc\bar{c}\bar{c},0^{++})}$ with variation of the Borel parameter $T^2$ from Eqs. (29, 30)

Fig. 8

The mass $M_{X(cc\bar{c}\bar{c},0^{++})}$ with variation of the energy scale $\mu$ from Eqs. (29, 30)

In Fig. 7, we plot the mass $M_{X(cc\bar{c}\bar{c},0^{++})}$ comes from Eqs. (29, 30) with variation of the Borel parameter $T^2$, from the figure, we can see that the values of the $M_{X(cc\bar{c}\bar{c},0^{++})}$ are rather stable with variation of the Borel parameter at the energy scale $\mu \ge 1.8\,\mathrm {GeV}$. Now we choose the special value $T^2=4.4\,\mathrm {GeV}^2$, and plot the mass $M_{X(cc\bar{c}\bar{c},0^{++})}$ with variation of the energy scale $\mu$ in Fig. 8. From the figure, we can see that the mass $M_{X(cc\bar{c}\bar{c},0^{++})}$ increases monotonously and quickly with increase of the energy scale $\mu$ at the region $\mu \le 1.8\,\mathrm {GeV}$, and decreases monotonously and slowly at the region $\mu \ge 2.0\,\mathrm {GeV}$. In the range $\mu =$ (1.8–2.0) GeV, the predicted mass $M_{X(cc\bar{c}\bar{c},0^{++})}$ is rather stable, $M_{X(cc\bar{c}\bar{c},0^{++})}=5.76\,\mathrm {GeV}$, which is below the threshold $2M_{\eta _c}=5966.8\,\mathrm {MeV}$. On the other hand, the pole residue $\lambda _{X(cc\bar{c}\bar{c},0^{++})}$ increases monotonously and quickly with increase of the energy scale $\mu$ at the region $\mu \ge 1.6\,\mathrm {GeV}$, no stable QCD sum rules can be obtained; see Fig. 9. So the QCD sum rules cannot be saturated by the meson pairs $\eta _c\eta _c$, $J/\psi J/\psi$ plus a scalar tetraquark state $X(cc\bar{c}\bar{c},0^{++})$.

In this article, the diquark–antidiquark type tetraquark state is taken as a special superposition of a series of meson–meson pairs, and embodies the net effects. The decays to its components (meson–meson pairs) are Okubo–Zweig–Iizuka super-allowed, but the re-arrangements in the color-space are highly non-trivial. In other words, the lowest states $X(QQ\bar{Q}\bar{Q},0^{++}/2^{++})$ can saturate the QCD sum rules satisfactorily.

Fig. 9

The residue $\lambda _{X(cc\bar{c}\bar{c},0^{++})}$ with variation of the energy scale $\mu$ from Eqs. (29, 30)

4 Conclusion

In this article, we study the $J^{PC}=0^{++}$ and $2^{++}$ $QQ\bar{Q}\bar{Q}$ tetraquark states with the QCD sum rules by constructing the diquark–antidiquark type currents and calculating the contributions of the vacuum condensate up to dimension 4 in the operator product expansion. We obtain the predictions $M_{X(cc\bar{c}\bar{c},0^{++})} =5.99\pm 0.08\,\mathrm {GeV}$, $M_{X(cc\bar{c}\bar{c},2^{++})} =6.09\pm 0.08\,\mathrm {GeV}$, $M_{X(bb\bar{b}\bar{b},0^{++})} =18.84\pm 0.09\,\mathrm {GeV}$, $M_{X(bb\bar{b}\bar{b},2^{++})} =18.85\pm 0.09\,\mathrm {GeV}$, which can be confronted to the experimental data in the future. Furthermore, we illustrate that the diquark–antidiquark type tetraquark state can be taken as a special superposition of a series of meson–meson pairs and embodies the net effects. We can search for the $J^{PC}=0^{++}$ and $2^{++}$ $QQ\bar{Q}\bar{Q}$ tetraquark states in the mass spectrum of $\mu ^+\mu ^- \mu ^+\mu ^-$.

Appendix

The explicit expressions of the QCD spectral densities $\rho _{S/T}(s)$ are

$$\begin{aligned}&\rho _S(s,z,t,r)\\&\quad = \frac{3m_Q^4}{8\pi ^6} ( s-\overline{m}_Q^2 )^2+\frac{t z m_Q^2}{8\pi ^6} ( s-\overline{m}_Q^2 )^2 ( 5s-2\overline{m}_Q^2 )\\&\quad +\,\frac{rtz(1-r-t-z)}{1-t-z} \frac{1}{32\pi ^6} (s-\overline{m}_Q^2 )^3 ( 3s-\overline{m}_Q^2 ) \\&\quad +\frac{rtz(1-r-t-z)}{1-z} \frac{1}{32\pi ^6} ( s-\overline{m}_Q^2 )^3\\&\quad \times ( 3s-\overline{m}_Q^2 )\Big [5-\frac{t}{1-t-z} \Big ] \\&\quad -\frac{rtz^2(1-r-t-z)}{1-z} \frac{3}{16\pi ^6} (s-\overline{m}_Q^2 )^4 \\&\quad +rtz(1-r-t-z) \frac{3s}{8\pi ^6} (s-\overline{m}_Q^2 )^2\nonumber \\&\quad \Big [ 2s-\overline{m}_Q^2-\frac{z}{1-z} ( s-\overline{m}_Q^2 )\Big ] \\&\quad +m_Q^2\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \left\{ -\frac{1}{r^3} \frac{m_Q^4}{6\pi ^4}\delta ( s-\overline{m}_Q^2 ) \right. \nonumber \\&\quad -\frac{1-r-t-z}{r^2} \frac{m_Q^2}{12\pi ^4} [2+s \delta ( s-\overline{m}_Q^2 ) ] \\&\quad -\frac{tz}{r^3} \frac{m_Q^2}{12\pi ^4} [2+s \delta ( s-\overline{m}_Q^2 ) ] \nonumber \\&\quad -\frac{tz(1-r-t-z)}{r^2(1-t-z)} \frac{1}{12\pi ^6} ( 3s-2\overline{m}_Q^2 ) \\&\quad -\frac{tz(1-r-t-z)}{r^2(1-z)} \frac{1}{12\pi ^4} ( 3s-2\overline{m}_Q^2 ) \\&\quad \times \left[ 5-\frac{t}{1-t-z} \right] \\&\quad +\frac{tz^2(1-r-t-z)}{r^2(1-z)} \frac{1}{\pi ^4} ( s-\overline{m}_Q^2 ) \\&\quad -\frac{tz(1-r-t-z)}{r^2} \frac{1}{2\pi ^4}\left[ s+\frac{s^2}{3}\delta ( s-\overline{m}_Q^2)-\frac{z}{1-z}s\right] \\&\quad \left. +\frac{1}{r^2} \frac{m_Q^2}{2\pi ^4} +\frac{tz}{r^2} \frac{1}{4\pi ^4} ( 3s-2\overline{m}_Q^2 )- \frac{1}{16\pi ^4} ( 3s-2\overline{m}_Q^2) \right\} \end{aligned}$$

$$\begin{aligned}&\quad +\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \left\{ \frac{1}{rz} \frac{m_Q^4}{6\pi ^4} +\frac{t}{r} \frac{m_Q^2}{6\pi ^4} ( 3s-2\overline{m}_Q^2) \right. \nonumber \\&\quad +\frac{t(1-r-t-z)}{(1-t-z)} \frac{1}{12\pi ^4} ( s-\overline{m}_Q^2 ) ( 2s-\overline{m}_Q^2 ) \nonumber \\&\quad +\frac{t(1-r-t-z)}{(1-z)} \frac{1}{12\pi ^4} ( s-\overline{m}_Q^2 ) ( 2s-\overline{m}_Q^2 )\nonumber \\&\quad \times \left[ 2-\frac{t}{1-t-z} \right] \nonumber \\&\quad -\frac{tz(1-r-t-z)}{(1-z)} \frac{1}{4\pi ^4} ( s-\overline{m}_Q^2 )^2\nonumber \\&\quad +t(1-r-t-z) \frac{1}{12\pi ^4}s\bigg [ 4s-3\overline{m}_Q^2\nonumber \\&\quad -\frac{z}{1-z}3 ( s-\overline{m}_Q^2)\bigg ]\bigg \} , \end{aligned}$$

(31)

$$\begin{aligned}&\rho _T(s,z,t,r)\\&\quad = \frac{3m_Q^4}{16\pi ^6} ( s-\overline{m}_Q^2 )^2\\&\quad +\frac{t z m_Q^2}{8\pi ^6} ( s-\overline{m}_Q^2 )^2 ( 4s-\overline{m}_Q^2 )\\&\quad +\frac{rtz(1-r-t-z)}{1-t-z} \\&\quad \times \frac{1}{320\pi ^6} ( s-\overline{m}_Q^2 )^3 ( 17s-5\overline{m}_Q^2 )\\&\quad +\frac{rtz(1-r-t-z)}{1-z} \frac{1}{320\pi ^6} ( s-\overline{m}_Q^2 )^3\\&\quad \times \left[ ( 21s-5\overline{m}_Q^2)-\frac{t}{1-t-z} ( 17s-5\overline{m}_Q^2) \right] \\&\quad -\frac{rtz^2(1-r-t-z)}{1-z} \frac{1}{32\pi ^6} ( s-\overline{m}_Q^2 )^4 \\&\quad +rtz(1-r-t-z) \frac{s}{80\pi ^6} ( s-\overline{m}_Q^2 )^2\\&\quad \times \left[ 28s-13\overline{m}_Q^2-\frac{z}{1-z}7 ( s-\overline{m}_Q^2)\right] \\&\quad +m_Q^2\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \left\{ -\frac{1}{r^3} \frac{m_Q^4}{12\pi ^4}\delta ( s-\overline{m}_Q^2 )\right. \\&\quad \left. -\frac{1-r-t-z}{r^2} \frac{m_Q^2}{12\pi ^4} [1+s \delta ( s-\overline{m}_Q^2 ) ]\right. \\&\quad -\frac{tz}{r^3} \frac{m_Q^2}{12\pi ^4} [1+s \delta ( s-\overline{m}_Q^2 ) ] \\&\quad -\frac{tz(1-r-t-z)}{r^2(1-t-z)} \frac{1}{12\pi ^6} ( 2s-\overline{m}_Q^2 ) \\&\quad -\frac{tz(1-r-t-z)}{r^2(1-z)} \frac{1}{12\pi ^4} ( 2s-\overline{m}_Q^2 )\\&\quad \times \left[ 1-\frac{t}{1-t-z} \right] \\&\quad +\frac{tz^2(1-r-t-z)}{r^2(1-z)} \frac{1}{6\pi ^4} ( s-\overline{m}_Q^2 ) \\&\quad -\frac{tz(1-r-t-z)}{r^2} \frac{1}{6\pi ^4}\\&\quad \times \left[ s+\frac{s^2}{2}\delta ( s-\overline{m}_Q^2 )-\frac{z}{1-z}s\right] \\&\quad \left. +\frac{1}{r^2} \frac{m_Q^2}{4\pi ^4} +\frac{tz}{r^2} \frac{1}{4\pi ^4} ( 2s-\overline{m}_Q^2 ) \right\} \end{aligned}$$

$$\begin{aligned}&\quad +\langle \frac{\alpha _sGG}{\pi }\rangle \bigg \{- \frac{m_Q^2}{48\pi ^4} ( 4s-3\overline{m}_Q^2 ) \nonumber \\&\quad -\frac{r(1-r-t-z)}{1-t-z}\frac{1}{32\pi ^4} ( s-\overline{m}_Q^2) ( 3s-\overline{m}_Q^2 )\nonumber \\&\quad -\frac{r(1-r-t-z)}{1-z}\frac{1}{480\pi ^4} ( s-\overline{m}_Q^2 )\nonumber \\&\quad \times \bigg [ ( 17s-5\overline{m}_Q^2 )-\frac{t}{1-t-z}15 ( 3s-\overline{m}_Q^2 )\bigg ]\nonumber \\&\quad +\frac{rz(1-r-t-z)}{1-z}\frac{1}{24\pi ^4} ( s-\overline{m}_Q^2 )^2 \nonumber \\&\quad -r(1-r-t-z)\frac{1}{240\pi ^4}s\nonumber \\&\quad \times \bigg [ ( 14s-9\overline{m}_Q^2 )-\frac{z}{1-z}21 ( s-\overline{m}_Q^2)\bigg ]\nonumber \\&\quad -\frac{1}{rz} \frac{m_Q^4}{36\pi ^4} -\frac{t}{r} \frac{m_Q^2}{18\pi ^4} ( 2s-\overline{m}_Q^2 )\nonumber \\&\quad -\frac{t(1-r-t-z)}{(1-t-z)} \frac{1}{72\pi ^4} ( s-\overline{m}_Q^2 ) ( 4s-\overline{m}_Q^2 ) \nonumber \\&\quad -\frac{t(1-r-t-z)}{(1-z)} \frac{1}{72\pi ^4} ( s-\overline{m}_Q^2 ) \nonumber \\&\quad \times \bigg [2 ( 2s-\overline{m}_Q^2)-\frac{t}{1-t-z}( 4s-\overline{m}_Q^2) \bigg ] \nonumber \\&\quad +\frac{tz(1-r-t-z)}{(1-z)} \frac{1}{24\pi ^4} ( s-\overline{m}_Q^2)^2\nonumber \\&-t(1-r-t-z) \frac{1}{72\pi ^4}s\nonumber \\&\Big [ 7s-5\overline{m}_Q^2-\frac{z}{1-z}5 ( s-\overline{m}_Q^2 )\Big ]\Big \} , \end{aligned}$$

(32)

where

$$\begin{aligned} \overline{m}_Q^2= & {} \frac{m_Q^2}{r}+\frac{m_Q^2}{t}+\frac{m_Q^2}{z}+\frac{m_Q^2}{1-r-t-z} . \end{aligned}$$

(33)