1 Introduction

The gauge/string duality [1–3] provides a powerful tool to analyze the dynamics of the strongly coupled quark–gluon plasma (QGP). For example, the gauge/string duality has been applied to various topics in heavy ion collisions, e.g., drag force [4–8], photon production [9–11], elliptic flow [12], and jet quenching [13–18]. Among these we mainly study anisotropy jet quenching [19–34]. The experiments conducted at the Relativistic Heavy Ion Collider (RHIC) [35, 36] and at the Large Hadron Collider (LHC) [37, 38] demonstrate that the QGP is anisotropic and far from equilibrium during a short period of time after the collision. After that, the system becomes locally isotropic. In Refs. [24–34], the authors constructed a new black brane solution of IIB supergravity, aiming to describe the QGP at intermediate times \(\tau _{out}< \tau <\tau _{iso}\) with an intrinsically anisotropic hydrodynamical picture. This gravity solution is dual to a spatially anisotropic \({\mathcal {N}}=4\) super Yang–Mills plasma at finite temperature [39, 40]. A R-charged version of the anisotropic black brane was also obtained by one of us [19, 20]. Those static solutions, possessing a regular, anisotropic horizon, can be viewed as a renormalization group flow from an AdS geometry in the ultraviolet to a Lifshitz-like geometry in the infrared.

In this paper, we wish to extend previous calculations of the jet quenching parameter to a more general Lifshitz-like geometry [13]. A natural realization of the AdS/CFT correspondence with Lifshitz-fixed points is described by the following anisotropic spacetime [41–48]:

$$\begin{aligned} \mathrm{d}s^2=r^2\left( -\mathrm{d}t^2+\sum ^p_{i=1}\mathrm{d}x^2_i\right) +r^{\frac{2}{z}} \sum ^\mathrm{d}_{i=p+1}\mathrm{d}y^2_j+{\frac{\mathrm{d}r^2}{r^2}}, \end{aligned}$$
(1)

which is invariant under the scaling transformation \((t,x_i,y_j,r)\rightarrow (\lambda t, \lambda x_i, \lambda ^{\frac{1}{z}} y_j, r/\lambda )\). Note that the \(y_j\)-direction corresponds to the Lorentz symmetry violation and anisotropy. The simplest case with \(p=0\) represents non-relativistic fixed points with dynamical critical exponent z, which is very well known in quantum critical systems in condensed matter physics. Other cases with \(1\le p\le \mathrm{d}-1\) are interpreted as space-like Lifshitz fixed point and cannot be simply regarded as a generalization of \(p=0\). The black brane solution is given in Refs. [19, 20, 39], corresponding to the case \(z=3/2\). One of the main purposes of this paper is to calculate jet quenching parameters along the longitudinal direction and transverse plane.

Another purpose of this paper is to take the effect of a non-zero chemical potential into account on calculating the jet quenching parameter. In general, in the quark–gluon plasma produced in RHIC, the escaped quark is surrounded by high density quarks fluids liberated from the nucleons of the heavy ions and then some of the jets are quenched by the surrounding medium. In such a setting, the baryon density of the quark–gluon plasma is relevant and the chemical potential must be taken into account.

The structure of this paper is as follows. In Sect. 2 we build up a general setting. In Sect. 3, we consider the jet quenching in spatially anisotropic black brane background with a chemical potential. The jet quenching parameter in a spatially anisotropic black brane with a chemical potential at the quark moving along the longitudinal direction is discussed in Sect. 3.1. The cases of the transverse plane are then discussed in Sect. 3.2. The jet quenching parameter in an anisotropic black blane background as the quark is moving along the longitudinal direction is given in Sect. 4.1. The situation for the quark moving in the transverse plane is discussed in Sect. 4.2. We end with conclusions in Sect. 5.

2 General setup

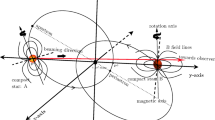
In order to compute the jet parameter \(\hat{q}\) for an ultra-relativistic quark, we need to consider the worldsheet of a string whose endpoints move at the speed of light along a given boundary direction and are separated a small distance l along an orthogonal direction. As noted in [15], the jet quenching parameter depends on how these directions are oriented with respect to the longitudinal and transverse directions in the plasma. For simplicity, we refer to z-axis as the longitudinal direction and to the xy-plane as the transverse directions.

As illustrated in Fig. 1, we assume that the direction of motion is contained in the xz-plane, which will be denoted Z. We use \(\theta \) for the angle between the Z- and the z-axis. We choose one of the two independent orthogonal directions to Z to be denoted by X, located within the xz-plane and the other one, Y, coincides with the y-axis. We denote by \(\varphi \) the polar angle in the XY-plane with respect to the Y-axis. The relation between the XYZ-coordinate and the xyz-coordinate is provided through the following transformation:

$$\begin{aligned} {\left\{ \begin{array}{ll} z=Z\cos \theta -X\sin \theta ,\\ x=Z\sin \theta +X\cos \theta ,\\ y=Y. \end{array}\right. } \end{aligned}$$
(2)

If \(p_\varphi \) is called the momentum component in the direction in the XY-plane specified by \(\varphi \), then clearly

$$\begin{aligned} p_\varphi =p_Y \cos \varphi +p_X\sin \varphi . \end{aligned}$$
(3)
Fig. 1
figure 1

Schematic plot on relative orientation between the anisotropic direction z, the direction of motion of the quark, and the direction in which the momentum is measured \( \bigtriangleup p\)

Full size image

We consider Eq. (3) as the differential treatment, then we square and average both sides of the equation instead. Because \(\Delta p_Y \Delta p_X=0 \), the result is

$$\begin{aligned}<\Delta p_\varphi ^2>=<\Delta p_Y^2>{\cos ^2\varphi }+<\Delta p_X^2>{\sin ^2\varphi }. \end{aligned}$$
(4)

The definition of the jet quenching parameter \(\hat{q}\) is the average momentum squared acquired by the quark through the medium at a unit distance [50–52]. So we obtain

$$\begin{aligned} \hat{q}_{\theta ,\varphi }=\cos ^2\varphi \hat{q}_{\theta ,0}+\sin ^2\varphi \hat{q}_{\theta ,{\frac{\pi }{2}}}. \end{aligned}$$
(5)

3 Spatially anisotropic black brane with a chemical potential

In this section, we calculate the jet quenching parameter in the spatially anisotropic black brane background with a chemical potential [6, 19, 20]. We adopt the light-cone metric and use coordinates of \(\sigma ^\alpha (\tau ,\sigma )\) to parameterize the worldsheet. Note that the action is invariant under a change. Then we calculate the jet quenching by the Nambu–Goto action. Afterwards we figure out the jet quenching parameter through the non-perturbative definition of \(\hat{q}\). Finally, we examine the effect of the charge Q and the anisotropic parameter a by comparing results on varying Q and a. In the beginning, we mainly consider the anisotropic action as follows:

$$\begin{aligned} I= & {} {\frac{1}{2\kappa ^2}}\int \mathrm{d}^5x\sqrt{-g}\left( R+12-{\frac{1}{2}}(\partial \phi )^2 \right. \nonumber \\&\left. - {\frac{1}{2}}e^{2\alpha \phi }(\partial \chi )^2-{\frac{1}{4}}F_{\mu \nu }F^{\mu \nu }\right) +S_{GH}, \end{aligned}$$
(6)

where we have set \(\kappa ^2=4\pi ^2/N_c^2\) and \(S_{GH}\) is the Gibbons–Hawking boundary term. We obtain the metric as

$$\begin{aligned} ds_5^2= & {} {\frac{L^2}{u^2}}\left( -{\mathcal {F}}{\mathcal {B}}\mathrm{d}t^2+\mathrm{d}x^2+\mathrm{d}y^2+{\mathcal {H}}\mathrm{d}z^2+{\frac{\mathrm{d}u^2}{\mathcal {F}}}\right) \nonumber \\&+\,L^2e^{\frac{1}{2}\phi }\mathrm{d}\Omega _5^2,\end{aligned}$$
(7)
$$\begin{aligned} A= & {} A_t(u)\mathrm{d}t,\chi =az, \phi =\phi (u), \end{aligned}$$
(8)

where L is the AdS radius and the event horizon is located at \(u=u_H\). The functions \(\mathcal {F}\), \(\mathcal {B}\), and \({\mathcal {H}}\) can be found in [20]. The Hawking temperature is as follows:

$$\begin{aligned} T= & {} -\frac{\mathcal {F}'(u_H)\sqrt{\mathcal {B}_H}}{4\pi }\nonumber \\= & {} \sqrt{B_H}[\frac{e^{-\frac{\phi _H}{2}}}{16\pi u_H}(16+a^2e^{7\frac{\phi _H}{2}}u_H^2)-\frac{e^{2\phi _H}Q^2u_H^5}{24\pi }].\nonumber \\ \end{aligned}$$
(9)

According to the Bekenstein–Hawking entropy formula, the entropy density goes as

$$\begin{aligned} s={\frac{A_H}{4GV_3}}=\frac{N_c^2e^{-\frac{5}{4}\phi _H}}{2\pi u_H^3}, \end{aligned}$$
(10)

where \(V_3\) is the volume of the black brane horizon.

3.1 Motion along the longitudinal direction

Using light-cone coordinates

$$\begin{aligned} z^\pm ={\frac{t\pm z}{\sqrt{2}}}, \end{aligned}$$
(11)

we can obtain the transformed metric as follows:

$$\begin{aligned} \mathrm{d}S_5^2= & {} {\frac{L^2}{u^2}}\left[ {\frac{1}{2}}({\mathcal {H}}-{\mathcal {FB}})(\mathrm{d}z^+)^2+{\frac{1}{2}}({\mathcal {H}} -{\mathcal {FB}})(\mathrm{d}z^-)^2 \right. \nonumber \\&\left. -\,({\mathcal {H}}+{\mathcal {FB}})\mathrm{d}z^+\mathrm{d}z^-+\mathrm{d}x^2+\mathrm{d}y^2+{\frac{\mathrm{d}u^2}{\mathcal {F}}}\right] . \end{aligned}$$
(12)

We consider a quark moving along \(z^-\). The xy-plane is rotational symmetric and we can set \(y=0\) without loss of generality. Then we take the static gauge by identifying \((z^-,x)=(\tau ,\sigma )\). We specify the string embedding through one function \(u=u(x)\) subject to the boundary conditions \(u(\pm l/2)=0\). On this occasion the Nambu–Goto action takes the form

$$\begin{aligned} S=-{\frac{1}{2\pi {\alpha }^{'}}}{\int } \mathrm{d}{\tau }\mathrm{d}\sigma \sqrt{-det g_{ind}}. \end{aligned}$$
(13)

Since we have

$$\begin{aligned} \det g_{ind}=\det g_{\alpha {\beta }}={\frac{L^4}{2u^4}}(\mathcal {H}-\mathcal {FB})\left( 1+\frac{u'^2}{\mathcal {F}}\right) , \end{aligned}$$
(14)

and \(L^-\gg L\), where \(L^-\) is the long side of the Wilson loop, the action now reads

$$\begin{aligned} S=\frac{iL^2L^-}{\pi {\alpha }'}\int _0^{l/2}\mathrm{d}x\frac{1}{u^2}\sqrt{\frac{1}{2}(\mathcal {H}-\mathcal {FB})\left( 1+\frac{u'^2}{\mathcal {F}}\right) }. \end{aligned}$$
(15)

We use the Euler–Lagrange equation to deal with the integration. The x-independence of the Lagrangian results in a conserved quantity \(\Pi _x\) and we just take the first-order term, which is

$$\begin{aligned} u'^2=\frac{\mathcal {F}}{2\Pi _x^2u^4}\left[ (\mathcal {H}-\mathcal {FB})-2\Pi _x^2u^4\right] . \end{aligned}$$
(16)

Since \(u'=\partial _\sigma u\) and \(\int _0^{l/2}\mathrm{d}\sigma =l/2\), one finds

$$\begin{aligned} {\frac{l}{2}}={\sqrt{2}{\Pi }}_x{\int }_0^{u_H}\mathrm{d}u{\frac{u^2}{\sqrt{\mathcal {F}}\sqrt{({\mathcal {H}}-{\mathcal {FB}})-2{\Pi }_x^2u^4}}}. \end{aligned}$$
(17)

Note that, as expected, \(l\rightarrow 0\) as \(\Pi _x\rightarrow 0\), so in this limit we obtain

$$\begin{aligned} l=2{\sqrt{2}{\Pi }}_x{\mathcal {I}}_x+{\mathcal {O}}({{\Pi }_x}^2), \end{aligned}$$
(18)

where

$$\begin{aligned} {\mathcal {I}}_x\equiv {\int }_0^{u_H}\mathrm{d}u{\frac{u^2}{\sqrt{\mathcal {F}}{\sqrt{\mathcal {H}-\mathcal {FB}}}}}. \end{aligned}$$
(19)

Substituting Eq. (16) into Eq. (15), one obtains

$$\begin{aligned} S={\frac{iL^2L^-}{\sqrt{2}{\pi }{\alpha '}}}{\int }_0^{u_H}{\frac{\mathrm{d}u}{u^2}} {\frac{\mathcal {H}-{\mathcal {FB}}}{\sqrt{\mathcal {F}}\sqrt{({\mathcal {H}}-{\mathcal {FB}})-2{{\Pi }_x}^2u^4}}}. \end{aligned}$$
(20)

The action diverges because the integration near \(u=0\). This can be seen by use of Maclaurin expansion in powers of \({\Pi }_x\), and we obtain the recast action

$$\begin{aligned} S={\frac{iL^2L^-}{\sqrt{2}{\pi }\alpha '}{\int }_0^{u_H}}\mathrm{d}u {\frac{\sqrt{\mathcal {H}-{\mathcal {BF}}}}{u^2\sqrt{\mathcal {F}}}}+{\frac{iL^2L^-l^2}{8\sqrt{2}{\pi }{\mathcal {I}}_x\alpha '}}+{\mathcal {O}}(l^4).\nonumber \\ \end{aligned}$$
(21)

Substituting Eq. (18) into the above equation, and we have

$$\begin{aligned} S={\frac{iL^2L^-}{\sqrt{2}{\pi }\alpha '}}\left[ \int _0^{u_H}{\frac{\mathrm{d}u}{u^2}} {\frac{\sqrt{\mathcal {H}-{\mathcal {FB}}}}{\sqrt{\mathcal {F}}}+{\mathcal {I}}_x{{\Pi }_x}^2+{\mathcal {O}}}({{\Pi }_x}^4)\right] .\nonumber \\ \end{aligned}$$
(22)

The jet quenching parameter can be obtained from the finite \(l^2\)-term which does not require any renormalization. It then follows that \(\hat{q}\) is not sensitive to the presence of the anomaly. The relation between the action and the jet quenching parameter is given by [14, 49]

$$\begin{aligned} e^{i2S}=<W^A({\mathcal {C}})>\approx e^{-{\frac{L^-l^2}{4\sqrt{2}}{\hat{q}}}}, \end{aligned}$$
(23)

where S signifies the finite part of the action.

Comparing the \(l^2\) term in (21) with that in (23), we obtain

$$\begin{aligned} {\hat{q}}_z={\hat{q}}_{0,\varphi }={\frac{L^2}{\pi \mathcal {I}_x\alpha '}}={\frac{\sqrt{\lambda }}{\pi \mathcal {I}_x}}, \end{aligned}$$
(24)

where \( \sqrt{\lambda }=L^2/\alpha '\) is the coupling parameter.

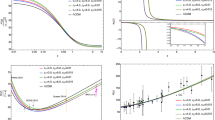
For Eq. (24), we can solve the value of \({\hat{q}}_z\) by giving values of Q and a. When Q equals zero, the case will recover the situation of [15]. We have numerically determined \({\hat{q}}_z\) as a function of a / T for various values of Q. In Fig. 2, we show the relation between the ratio of jet quenching parameter \({\hat{q}}_z\) to isotropic jet quenching parameter \({\hat{q}}_{iso}^{Q=0}\) and a / T for \(Q=0, 0.5, 1, 3, 5\). We find that the jet quenching parameter is generally enhanced as the chemical potential increases. We can easily observe that the behavior of longitudinal jet quenching for large chemical potential is different from the small chemical potential case. For large chemical potential the jet quenching parameter is growing much faster than the small one at large a / T.

Fig. 2
figure 2

The function of the anisotropy of jet quenching parameter \({\hat{q}}_z\) for a quark moving along the longitudinal z-direction. a The ratio of \({\hat{q}}_{z}\) to \({\hat{q}}_{iso}^{Q=0}\) for \(Q=0\) (blue), \(Q=0.5\) (red) and \(Q=1\) (green). b Large Q cases show results for \(Q=3\) and \(Q=5\) by a blue line and red line, respectively

Full size image

3.2 Motion in the transverse plane

Then we discussed the situation where the string motion is in the transverse plane. Due to the rotational symmetry in xy-plane, we can simply choose the string moving in the x-direction. This situation corresponds to the case \({\theta }={\pi }/2\). In the same way as in the previous example, it is convenient to compute with suitable light-cone coordinates,

$$\begin{aligned} x^{\pm }=\frac{t\pm x}{\sqrt{2}}. \end{aligned}$$
(25)

The metric (7) now takes the form

$$\begin{aligned} \mathrm{d}S_5^2= & {} \frac{L^2}{u^2}\left[ \frac{1}{2}(1-\mathcal {FB})(\mathrm{d}x^+)^2+\frac{1}{2}(1-\mathcal {FB})(\mathrm{d}x^-)^2\right. \nonumber \\&\left. -\,(1+\mathcal {FB})\mathrm{d}x^+\mathrm{d}x^-+\mathrm{d}y^2+\mathcal {H}\mathrm{d}z^2+\frac{\mathrm{d}u^2}{\mathcal {F}}\right] . \end{aligned}$$
(26)

In this situation, we fix the static gauge by identifying \((x^-,u)=(\tau ,\sigma )\). At the same time, \(x^+=constant\), and the string projection in the xy-plane can be specified as follows:

$$\begin{aligned} y\rightarrow \cos \varphi y(u), \quad z\rightarrow \sin \varphi z(u). \end{aligned}$$
(27)

One obtains the following result by using the Nambu–Goto action (13):

$$\begin{aligned} S= & {} {\frac{iL^2}{\pi \alpha '}}\int \mathrm{d}x \int _0^{u_H}\mathrm{d}u \nonumber \\&\times \, {\frac{1}{u^2}}\sqrt{{\frac{1}{2}} (1-\mathcal {FB})\left( {\frac{1}{\mathcal {F}}}+y'^2\cos ^2\varphi +\mathcal {H}z'^2\sin ^2\varphi \right) }.\nonumber \\ \end{aligned}$$
(28)

Similarly, since the Lagrangian does not depend on y, z explicitly, we find that

$$\begin{aligned} y'={\frac{\sqrt{2\mathcal {H}}u^2{\Pi }_y}{{\sqrt{\mathcal {F}}}\sqrt{\mathcal {H} (1-{\mathcal {FB}})-2u^4\left( {\mathcal {H}}{\Pi }_y^2\cos ^2\varphi +{\Pi }_z^2\sin ^2\varphi \right) }}},\nonumber \\ \end{aligned}$$
(29)
$$\begin{aligned} z'={\frac{\sqrt{2}u^2{\Pi }_z}{\sqrt{\mathcal {HF}} \sqrt{\mathcal {H}(1-{\mathcal {FB}})-2u^4\left( {\mathcal {H}}{\Pi }_y^2\cos ^2\varphi +{\Pi }_z^2\sin ^2\varphi \right) }}},\nonumber \\ \end{aligned}$$
(30)

where \({\Pi }_y\) and \({\Pi }_z\) are conserved quantities. Because of \(y'=\partial _\sigma y\), \(z'=\partial _\sigma z\), and \({\int }_0^{l/2} d\sigma =l/2 \), following a similar procedure to the previous section, we obtain

$$\begin{aligned} \frac{l}{2}= & {} \int \nolimits _{0}^{{u_{H} }} {\text {d}}u \nonumber \\&\times \frac{{\sqrt{2{\mathcal {H}}} u^{2} \Pi _{y} }}{{\sqrt{\mathcal {F}} \sqrt{{\mathcal {H}}(1 - {\mathcal {F}\mathcal {B}}) - 2u^{4} \left( {{\mathcal {H}}\Pi _{y}^{2} \cos ^{2} \varphi + \Pi _{z}^{2} \sin ^{2} \varphi } \right) } }}, \end{aligned}$$
(31)
$$\begin{aligned} \frac{l}{2}= & {} \int _{0}^{{u_{H} }} {\text {d}} u\nonumber \\&\times \frac{{\sqrt{2} u^{2} \Pi _{z} }}{{\sqrt{{\mathcal {H}\mathcal {F}}} \sqrt{{\mathcal {H}}(1 - {\mathcal {F}\mathcal {B}}) - 2u^{4} \left( {{\mathcal {H}}\Pi _{y}^{2} \cos ^{2} \varphi + \Pi _{z}^{2} \sin ^{2} \varphi } \right) } }}. \end{aligned}$$
(32)

Expanding the above two equations in the limit \(\Pi _y\rightarrow 0\) and \({\Pi }_z\rightarrow 0\), respectively,

$$\begin{aligned} l=2\sqrt{2}\Pi _y{\mathcal {I}}_{xy}+{\mathcal {O}}({\Pi }^2), \end{aligned}$$
(33)
$$\begin{aligned} l=2\sqrt{2}{\Pi }_z{\mathcal {I}}_{xz}+{\mathcal {O}}(\Pi ^2), \end{aligned}$$
(34)

with

$$\begin{aligned} {\mathcal {I}}_{xy}\equiv \int _0^{u_H}\mathrm{d}u{\frac{u^2}{\sqrt{\mathcal {F}}(1-{\mathcal {FB}})}}, \end{aligned}$$
(35)
$$\begin{aligned} {\mathcal {I}}_{xz}\equiv {\int }_0^{u_H}\mathrm{d}u\frac{u^2}{\mathcal {H}\sqrt{\mathcal {F}(1-{\mathcal {FB})}}}, \end{aligned}$$
(36)

which are convergent integrals. Substituting Eq. (29) and Eq. (30) into Eq. (28), we can obtain

$$\begin{aligned} S= & {} \frac{iL^2L^-}{\sqrt{2}\pi \alpha '}\int _0^{u_h}du \nonumber \\&\times \frac{\sqrt{\mathcal {H}}(1-\mathcal {FB})}{u^2\sqrt{\mathcal {F}}(\mathcal {H}(1-\mathcal {FB})- 2u^4(\mathcal {H}\Pi _y^2\cos ^2\varphi +\Pi _z^2\sin ^2\varphi ))^\frac{1}{2}}.\nonumber \\ \end{aligned}$$
(37)

Again, we can expand the action in powers of \(\Pi _y\) and \(\Pi _z\), and obtain the result to the second order:

$$\begin{aligned} S= & {} {\frac{iL^2L^-}{\sqrt{2}\pi \alpha '}}{\int }_0^{u_H}\mathrm{d}u{\frac{\sqrt{1-{\mathcal {FB}}}}{u^2\sqrt{\mathcal {F}}}} \nonumber \\&+{\frac{iL^2L^-}{\sqrt{2}\pi \alpha '}}{\int }_0^{u_H}du\frac{u^2{\mathcal {H}}\cos ^2\varphi {\Pi }_y^2+u^2\sin ^2\varphi {\Pi }_z^2}{\mathcal {H}\sqrt{\mathcal {F}}\sqrt{1-{\mathcal {FB}}}}. \end{aligned}$$
(38)

Similarly, we only take out the second item. Because \({\Pi }_y=l/{2\sqrt{2}{\mathcal {I}}_{xy}}\) and \({\Pi }_z=l/{2\sqrt{2}{\mathcal {I}}_{xz}}\), the action becomes

$$\begin{aligned} S={\frac{iL^2L^-l^2}{8\sqrt{2}\pi \alpha '}}\left( {\frac{\cos ^2\varphi }{\mathcal {I}_{xy}}}+{\frac{\sin ^2\varphi }{\mathcal {I}_{xz}}}\right) . \end{aligned}$$
(39)

Following the prescription Eq. (23), the transverse jet quenching parameter is given by

$$\begin{aligned} {\hat{q}}_{xy}={\hat{q}}_{\frac{\pi }{2},0}=\frac{L^2}{{\pi } \alpha '{\mathcal {I}}_{xy}}, {\hat{q}}_{xz}={\hat{q}}_{\frac{\pi }{2},{\frac{\pi }{2}}}={\frac{L^2}{\pi \alpha '{\mathcal {I}}_{xz}}}. \end{aligned}$$
(40)

Hence

$$\begin{aligned} {\hat{q}}_{\frac{\pi }{2},\varphi }={\hat{q}}_{xy}\cos ^2\varphi +{\hat{q}}_{xz}\sin ^2\varphi . \end{aligned}$$
(41)

In Fig. 3, we find that, for a small chemical potential, there exists a peak in \(\hat{q}_{xy}\) at low anisotropy a / T, then \({\hat{q}}_{xy}\) decreases and becomes lower than the isotropic case at large anisotropy a / T. But when the chemical potential is larger, \({\hat{q}}_{xy}\) behaves different from the small chemical potential case. It always increases and grows fast as the anisotropy a / T increases.

In Fig. 4, we show the jet quenching parameter \({\hat{q}}_{xz}\) for a quark moving in the transverse xy plane. In contrast to \({\hat{q}}_{xy}\), \({\hat{q}}_{xz}\) always increases whether the chemical potential is large or not. In addition, we have plotted \({\hat{q}}_{\frac{\pi }{2},\varphi }\) to \({\hat{q}}_{iso}^{Q=0}\) for various values of \(\varphi \) in Fig. 5.

The drag force calculated in [16] shows that the jet quenching increases with the increasing charge Q. Comparing with the jet quenching computed in [6], we find that the jet quenching is also increasing as the charge density Q increases.

Fig. 3
figure 3

Functions of the anisotropic jet quenching parameter \({\hat{q}}_{xy}\) for a quark moving along the vertical direction of the XY-plane. The Y-axis is the ratio of the jet quenching parameter \({\hat{q}}_{xy}\) to \({\hat{q}}_{iso}^{Q=0}\), the X-axis is the ratio of parameter a to temperature T. a Lines show results for \(Q=0\) (blue), \(Q=0.5\) (red) and \(Q=1\) (green). b Blue line and red line describe results for \(Q=3\) and \(Q=5\) respectively

Full size image
Fig. 4
figure 4

Functions of the anisotropic jet quenching parameter \({\hat{q}}_{xz}\) for a quark moving along the parallel direction of the XY-plane. The vertical coordinate is the ratio of the jet quenching parameter \({\hat{q}}_{xz}\) to \({\hat{q}}_{iso}^{Q=0}\), the horizontal coordinate is the ratio of parameter a to temperature T. a Lines show results for \(Q=0\) (blue), \(Q=0.5\) (red) and \(Q=1\) (green). b Blue line and red line describe results for \(Q=3\) and \(Q=5\), respectively

Full size image
Fig. 5
figure 5

a The transverse jet quenching parameter \({\hat{q}}_{{\pi }/2,\varphi }\) for \(Q=0\), from top to bottom, with \(\varphi ={\pi }/2, {\pi }/3, {\pi }/4, \pi /6, 0\). b The transverse jet quenching parameter \(\hat{q}_{{\pi }/2,\varphi }\) for \(Q=1\), from top to bottom, corresponds to \(\varphi ={\pi }/2, {\pi }/3, {\pi }/4, {\pi }/6, 0\), respectively. c The transverse jet quenching parameter \({\hat{q}}_{\pi /2,\varphi }\) for \(Q=2\), from top to bottom, with \(\varphi =\pi /2, \pi /3, \pi /4, \pi /6, 0\). d The transverse jet quenching parameter \({\hat{q}}_{\pi /2,\varphi }\) for \(Q=3\), from top to bottom, with \(\varphi =\pi /2, \pi /3, \pi /4, \pi /6, 0\)

Full size image

4 Anisotropic black brane in the IR region

In this section, we will consider the jet quenching in the Einstein–dilaton–axion model discussed in [53]. The Einstein–dilaton–axion action is given by

$$\begin{aligned} S=\frac{1}{2\kappa ^{2}}\int {\mathrm{d}^{5}x\sqrt{-g}\left( R+12\Lambda -\frac{1}{2}(\partial \phi )^{2}-\frac{1}{2}e^{2\alpha \phi }(\partial \chi )^{2}\right) }.\nonumber \\ \end{aligned}$$
(42)

Here \(2\kappa ^{2}=16\pi G\) is the gravitational coupling and G is the Newton constant in 5 dimensions. The parameter \(\alpha \) enters in the dilaton dependence of axion kinetic term. Earlier work in [39] considered the case with \(\alpha =1\), and the case \(\alpha =-1\) has SL(2, R) invariance. It is easy to see there exists a near-extremal solution whose near horizon limit at small temperature \(T\ll \rho \) is given by

$$\begin{aligned}&\mathrm{d}s^2=\frac{R^2}{u^2}\left[ -\mathcal {F}\mathrm{d}t^2+\frac{\mathrm{d}u^2}{\mathcal {F}}+\mathrm{d}x^2+\mathrm{d}y^2+\mathcal {H}\mathrm{d}z^2\right] ,\end{aligned}$$
(43)
$$\begin{aligned}&\mathcal {F}=1-\left( \frac{u}{u_h}\right) ^p,\quad \mathcal {H}=\rho ^2u^{\frac{2}{1+2\alpha ^2}},\quad R^2=\frac{3+8\alpha ^2}{4+8\alpha ^2}, \end{aligned}$$
(44)
$$\begin{aligned}&p=\frac{3+8\alpha ^2}{1+2\alpha ^2},\quad \chi =c_1\rho z,\end{aligned}$$
(45)
$$\begin{aligned}&\phi =-\frac{2\alpha }{1+2\alpha ^2}\log (u),\quad c_1=\frac{\sqrt{2(3+8\alpha ^2)}}{(1+2\alpha ^2)}. \end{aligned}$$
(46)

The metric is a special case of the metric (1), which corresponds to \(z=1/2\alpha ^2+1\). The black hole horizon is at \(u=u_h\) and the boundary is at \(u=0\). The Hawking temperature is given by

$$\begin{aligned} T=\frac{p^2}{16\pi u_h}. \end{aligned}$$
(47)

This solution breaks rotational invariance along the z-direction due to the linearly varying axion, and \(\rho \) is the mass scale which characterizes the breaking of anisotropy.

4.1 Motion along the longitudinal direction

To compute the jet quenching parameter along the longitudinal direction, we use the light-cone coordinate so that

$$\begin{aligned} z^{\pm }=\frac{t\pm z}{\sqrt{2}}, \end{aligned}$$
(48)

and we can recast the metric as

$$\begin{aligned} \mathrm{d}S^2=&\frac{R^2}{u^2}\left[ \frac{1}{2}(\mathcal {H}-\mathcal {F})(\mathrm{d}z^+)^2+\frac{1}{2}(\mathcal {H}-\mathcal {F}) (\mathrm{d}z^-)^2\right. \nonumber \\&\left. -(\mathcal {H}+\mathcal {F})\mathrm{d}z^+\mathrm{d}z^-+\mathrm{d}x^2+\mathrm{d}y^2+\frac{\mathrm{d}u^2}{\mathcal {F}}\right] . \end{aligned}$$
(49)

Now we consider a quark moving along the \(z^-\)-direction. The xy-plane is symmetric and we can set \(y=0\) without loss of generality. Then we fix the static gauge by ascertaining \((z^-,x)=(\tau ,\sigma )\), and assign the string embedding through one function \(u=u(x)\), which is subjected to the boundary condition \(u(\pm l/2)=0\). Note that the Nambu–Goto action is given by

$$\begin{aligned} S=-\frac{1}{2\pi {\alpha }^{'}}\int \mathrm{d}\tau \mathrm{d}\sigma \sqrt{-det g_{ind}}. \end{aligned}$$
(50)

Because of

$$\begin{aligned} \det g_{\alpha \beta }=\frac{R^4}{2u^4}(\mathcal {H}-\mathcal {F})\left( 1+\frac{u'^2}{\mathcal {F}}\right) ,\quad L^-\gg L, \end{aligned}$$
(51)

the action takes the form

$$\begin{aligned} S={\frac{iR^2L^-}{\pi {\alpha }'}}\int _0^{l/2}dx{\frac{1}{u^2}}\sqrt{\frac{1}{2}({\mathcal {H}}-{\mathcal {F}})\bigg (1+{\frac{u'^2}{\mathcal {F}}\bigg )}}. \end{aligned}$$
(52)

Following the same procedure, noting that the Lagrangian does not depend on x explicitly leads to a conserved quantity \(\mathcal {E}_x\), and we take the first-order term, that is to say:

$$\begin{aligned} u'^2={\frac{\mathcal {F}}{2{{\mathcal {E}}}_{x}^{2}u^4}}[({\mathcal {H}}-{\mathcal {F}})-2{\mathcal {E}}_x^2u^4]. \end{aligned}$$
(53)

Since \(u'=\partial _{\sigma } u\) and \({\int }_0^{l/2}\mathrm{d}{\sigma }=l/2\), one finds

$$\begin{aligned} {\frac{l}{2}}=\sqrt{2}{\mathcal {E}}_x{\int }_0^{u_h}\mathrm{d}u{\frac{u^2}{\sqrt{\mathcal {F}}\sqrt{({\mathcal {H}}-{\mathcal {F}})-2{\mathcal {E}}_x^2u^4}}}. \end{aligned}$$
(54)

Note that \(l\rightarrow 0\) as \({\mathcal {E}}_x\rightarrow 0\), so in this limit we can obtain

$$\begin{aligned} l=2\sqrt{2}{\mathcal {E}}_x{\mathcal {K}}_x+{\mathcal {O}}({\mathcal {E}_x}^2), \end{aligned}$$
(55)

where

$$\begin{aligned} {\mathcal {K}}_x\equiv {\int }_0^{u_h}\mathrm{d}u{\frac{u^2}{\sqrt{\mathcal {F}}\sqrt{\mathcal {H}-{\mathcal {F}}}}}. \end{aligned}$$
(56)

We substitute Eq. (53) into Eq. (52), then we obtain the equation as follows:

$$\begin{aligned} S={\frac{iR^2L^-}{\sqrt{2}\pi \alpha '}}\int _0^{u_h}{\frac{\mathrm{d}u}{u^2}} {\frac{\mathcal {H}-{\mathcal {F}}}{\sqrt{\mathcal {F}}\sqrt{({\mathcal {H}}-{\mathcal {F}})-2{\mathcal {E}_x}^2u^4}}}. \end{aligned}$$
(57)

We expand the integrand and use Eqs. (55) and (56) to get

$$\begin{aligned} S={\frac{iR^2L^-}{\sqrt{2}\pi \alpha '}}\int _0^{u_h}\mathrm{d}u {\frac{\sqrt{\mathcal {H}-{\mathcal {F}}}}{u^2\sqrt{\mathcal {F}}}}+{\frac{iR^2L^-l^2}{8\sqrt{2}\pi {\mathcal {K}}_x\alpha '}}+{\mathcal {O}}(l^4).\nonumber \\ \end{aligned}$$
(58)

As we have

$$\begin{aligned} e^{i2S}=<W^A({\mathcal {C}})>\approx exp[-{\frac{L^-l^2}{4\sqrt{2}}}{\hat{q}}], \end{aligned}$$
(59)

this leads to

$$\begin{aligned} {\hat{q}}_z={\hat{q}}_{0,\varphi }={\frac{L^2}{\pi {\mathcal {K}}_x\alpha '}}={\frac{\sqrt{\lambda }}{\pi {\mathcal {K}}_x}}, \end{aligned}$$
(60)

where \( \sqrt{\lambda }={R^2}/\alpha '\).

Figure 6 shows the jet quenching parameter \({\hat{q}}_{z}\) as a function of \(\alpha \). It is found that as \(\alpha \) increases, the ratio increases and approaches a fixed value at large \(\alpha \).

Fig. 6
figure 6

The vertical coordinate is the ratio of the jet quenching parameter of anisotropic black brane to the isotropic one. The horizontal co ordinate is \(\alpha \), which can be used to describe the change of the geometry near horizon

Full size image

4.2 Motion in the transverse plane

Next we discuss the situation where the motion is in the transverse plane. We set the rotational symmetry in the xy-plane and choose the motion in x-direction. That is \(\theta =\pi /2\) in Fig. 1. In the y-direction and z-direction, there is no rotational symmetry, so in this situation the result will be dependent of \(\varphi \). In the same way as in the previous example, we consider the light-cone coordinates,

$$\begin{aligned} x^{\pm }={\frac{t\pm x}{\sqrt{2}}}. \end{aligned}$$
(61)

The metric (7) becomes

$$\begin{aligned} \mathrm{d}S^2= & {} {\frac{R^2}{u^2}}\left[ {\frac{1}{2}}(1-\mathcal {F})(\mathrm{d}x^+)^2+{\frac{1}{2}}(1-{\mathcal {F}})(dx^-)^2 \right. \nonumber \\&\left. - (1+{\mathcal {F}})\mathrm{d}x^+\mathrm{d}x^-+\mathrm{d}y^2+{\mathcal {H}}\mathrm{d}z^2+{\frac{\mathrm{d}u^2}{\mathcal F}}\right] . \end{aligned}$$
(62)

In this situation, we fix the static gauge by identifying \((x^-,u)=({\tau },\sigma )\). At the same time, \(x^+=const.\), and we specify the string projection in the xy-plane as follows:

$$\begin{aligned} y\rightarrow \cos \varphi y(u) ,z\rightarrow \sin \varphi z(u). \end{aligned}$$
(63)

One can get the following result by using (50)

$$\begin{aligned} S= & {} {\frac{iR^2}{\pi \alpha '}}{\int } \mathrm{d}x \int _0^{u_h}\mathrm{d}u \nonumber \\&\times \,{\frac{1}{u^2}}\sqrt{\frac{1}{2}(1-\mathcal {F})\left( \frac{1}{\mathcal {F}}+y'^2\cos ^2\varphi +{\mathcal {H}}z'^2{\sin }^2\varphi \right) }.\nonumber \\ \end{aligned}$$
(64)

The fact that the Lagrangian does not have explicit an y, z dependence leads to

$$\begin{aligned} y'=\frac{\sqrt{2\mathcal {H}}u^2\mathcal {E}_y}{\sqrt{\mathcal {F}}\sqrt{\mathcal {H}(1-\mathcal {F})-2u^4(\mathcal {H}\mathcal {E}_y^2\cos ^2\varphi +\mathcal {E}_z^2\sin ^2\varphi )}},\nonumber \\ \end{aligned}$$
(65)

and

$$\begin{aligned} z'=\frac{\sqrt{2}u^2\mathcal {E}_z}{\sqrt{\mathcal {HF}}\sqrt{\mathcal {H}(1-\mathcal {F})-2u^4(\mathcal {H}\mathcal {E}_y^2\cos ^2\varphi +\mathcal {E}_z^2\sin ^2\varphi )}},\nonumber \\ \end{aligned}$$
(66)

where \({\mathcal {E}}_y\) and \(\mathcal {E}_z\) are conserved quantities. Because \(y'=\mathrm{d}y/\mathrm{d}u\) and \(z'=\mathrm{d}z/\mathrm{d}u\), \(\int _0^{l/2}\mathrm{d}y=l/2\) and \(\int _0^{l/2}\mathrm{d}z=1/2\), one has

$$\begin{aligned} \frac{l}{2}= & {} \sqrt{2}\mathcal {E}_y\int _0^{u_h}\mathrm{d}u\nonumber \\&\times \,\frac{\sqrt{\mathcal {H}}u^2}{\sqrt{\mathcal {F}}\sqrt{\mathcal {H}(1-\mathcal {F})-2u^4(\mathcal {H}\mathcal {E}_y^2\cos ^2\varphi +\mathcal {E}_z^2\sin ^2\varphi )}},\nonumber \\ \end{aligned}$$
(67)
$$\begin{aligned} \frac{l}{2}= & {} \sqrt{2}\mathcal {E}_z\int _0^{u_h}\mathrm{d}u\nonumber \\&\times \frac{u^2}{\sqrt{\mathcal {HF}}\sqrt{\mathcal {H}(1-\mathcal {F})-2u^4(\mathcal {H}\mathcal {E}_y^2\cos ^2\varphi +\mathcal {E}_z^2\sin ^2\varphi )}}.\nonumber \\ \end{aligned}$$
(68)

We expand the above two equations in the limit \(\mathcal {E}_y\rightarrow 0\) and \(\mathcal {E}_z\rightarrow 0\), respectively,

$$\begin{aligned} l=2\sqrt{2}\mathcal {E}_y\mathcal {K}_xy+\mathcal {O}(\mathcal {E}^2), \end{aligned}$$
(69)
$$\begin{aligned} l=2\sqrt{2}\mathcal {E}_z\mathcal {K}_xz+\mathcal {O}(\mathcal {E}^2), \end{aligned}$$
(70)

with

$$\begin{aligned} \mathcal {K}_{xy}\equiv \int _0^{u_h}\mathrm{d}u\frac{u^2}{\sqrt{\mathcal {F}(1-\mathcal {F})}}, \end{aligned}$$
(71)
$$\begin{aligned} \mathcal {K}_{xz}\equiv \int _0^{u_h}\mathrm{d}u\frac{u^2}{\mathcal {H}\sqrt{\mathcal {F}(1-\mathcal {F})}}. \end{aligned}$$
(72)

Take Eqs. (65) and (66) into Eq. (64),

$$\begin{aligned} S= & {} \frac{iR^2L^-}{\sqrt{2}\mathcal {E} \alpha '}\int _0^{u_h}\mathrm{d}u\frac{\sqrt{\mathcal {H}}(1-{\mathcal {FH}})}{u}^2 \nonumber \\&\times \,\left[ \frac{\mathcal {F}}{\mathcal {H}(1-{\mathcal {F}}) -2u^4({\mathcal {E}_y}^2\cos ^2\varphi +{\mathcal {E}}_z^2\sin ^2\varphi )}\right] ^{\frac{1}{2}}.\nonumber \\ \end{aligned}$$
(73)

We expand the integrand and rearrange the above equation, and we obtain

$$\begin{aligned} S= & {} \frac{iR^2L^-}{\sqrt{2}\pi \alpha '}\int _0^{u_h}\mathrm{d}u\frac{\sqrt{1-{\mathcal {F}}}}{u^2\sqrt{\mathcal {F}}} \nonumber \\&+\,\frac{iR^2L^-}{\sqrt{2}\pi \alpha '}\int _0^{u_h}\mathrm{d}u\frac{u^2{\mathcal {H}}\cos ^2\varphi {\mathcal {E}}_y^2+u^2\sin ^2\varphi {\mathcal {E}}_z^2}{\mathcal {H}\sqrt{\mathcal {F}}\sqrt{1-{\mathcal {F}}}}. \end{aligned}$$
(74)

We only take out the second item, then

$$\begin{aligned} S={\frac{iR^2L^-}{\sqrt{2}\pi \alpha '}}(\cos ^2{\mathcal {E}}_y^2{\mathcal {K}}_{xy}+\sin ^2{\mathcal {E}}_z^2{\mathcal {K}}_{xz}), \end{aligned}$$
(75)

and because \({\mathcal {E}}_y=l/{2\sqrt{2}{\mathcal {K}}_{xy}}\) and \({\mathcal {E}}_z=l/{2\sqrt{2}{\mathcal {K}}_{xz}}\), this yields

$$\begin{aligned} S={\frac{iR^2L^-l^2}{8\sqrt{2}\pi \alpha '}}\left( \frac{\cos ^2\varphi }{\mathcal {K}_{xy}}+\frac{\sin ^2\varphi }{\mathcal {K}_{xz}}\right) \end{aligned}$$
(76)

and

$$\begin{aligned} \hat{q}_\perp =\hat{q}_{\frac{\pi }{2},0}=\frac{R^2}{\pi \alpha '\mathcal {K}_{xy}}, \quad \hat{q}_L=\hat{q}_{\frac{\pi }{2},\frac{\pi }{2}}=\frac{R^2}{\pi \alpha '\mathcal {K}_{xz}}. \end{aligned}$$
(77)

As a result,

$$\begin{aligned} \hat{q}_{\frac{\pi }{2},\varphi }=\hat{q}_\perp \cos ^2\varphi +\hat{q}_L\sin ^2\varphi . \end{aligned}$$
(78)

From Fig. 7, we find the same situation as for the longitudinal direction, values of the ratio rising with the increasing of \(\alpha \). When it reaches one value, it stops rising, in spite of the growth of \(\alpha \). We know the values of the ratio are reduced as the angle \(\varphi \) decreases.

Fig. 7
figure 7

\(\hat{q}_z\) as a function of \(\alpha \) with different \(\varphi \). From top to bottom, the curves represent \(\varphi =\pi /2,\pi /3,\pi /6,0\) relative to the y-axis

Full size image

We find that our results are consistent with results in [14, 15]. We know the jet quenching parameter as the temperature increases from [14, 15]. In our case, the parameter \(\alpha ^2\) is proportional to the temperature so that our result is consistent with [14, 15].

5 Summary

The jet quenching parameter \(\hat{q}\) describes the momentum broadening of a highly relativistic parton moving through a non-Abelian plasma. We have considered two cases, one is a R-charged version of the anisotropic black brane [19, 20] and the other is an anisotropic black brane in the IR region [39, 40]. Both are in the coordinate system, where there exists rotational symmetry in the x, y-directions but not in the z-direction. In the context of heavy ion collisions the former x, y symmetric directions and the latter z asymmetric direction would correspond to the transverse plane and beam direction, respectively. There are some factors that affect the jet quenching parameter as follows: (1) the relative orientation between these directions, (2) the movement direction of the parton, (3) the direction of the measured momentum broadening, and (4) the charge density Q or, equivalently, the chemical potential. We mainly discuss the quark moving in the longitudinal direction and the transverse plane, namely we study the cases \(\theta =0\) and \(\theta =\pi /2\).

In Sect. 3, we compute the jet quenching parameter in the background of a charged anisotropic black brane. We find that for small enough anisotropy the jet quenching parameter is always larger than that in an isotropic plasma at the same temperature, regardless of the directions of motion and momentum broadening. As the anisotropy increase, the momentum broadening for the moving quark will depend on the direction of the momentum broadening. In other words, at small a / T the momentum broadening is larger for quarks propagating along the beam axis z, while it is larger for quarks propagating in the transverse plane for large a / T (unless the momentum broadening is measured very close to the orthogonal direction within the transverse plane). On the other hand, the jet quenching parameter is always enhanced by the charge density Q, and the jet quenching parameter has different behaviors for small charge density and large charge density. When the charge density is small, the jet quenching parameter in the longitudinal direction will increase as a / T increases and possibly approaches some constant at large a / T. But when the charge density is large, the jet quenching parameter in the longitudinal direction will increase fast at large a / T. As the quark is moving in the transverse plane, the jet quenching parameter has a similar behavior to the longitudinal case, i.e., it is always enhanced by the charge density and has different behaviors for small and large charge density. However, for the transverse case, the jet quenching parameter will depend on the direction of momentum broadening.

In Sect. 4, we compute the jet quenching parameter in the background in the IR region of a spatially anisotropic black hole in Einstein–dilaton–axion theory. For this case, we also conclude that the jet quenching parameter increases as the anisotropy \(\alpha \) and tends to saturate at large anisotropy \(\alpha \).

According to the above discussion, we can conclude that: (1) The jet quenching parameter of the anisotropic systems increases as the anisotropic parameter a or \(\alpha \) goes up. (2) The jet quenching parameter of the anisotropic systems also increases as the charge Q goes up. (3) The jet quenching parameter increases with the increasing angle \(\phi \). (4) When the Q is small (\(Q\le 1\)), the jet quenching parameter increases with increasing a or \(\alpha \) until to some fixed value. It illustrates that a and \(\alpha \) only impact the parameter at small value.