Higgs coupling measurements at the LHC

Abstract

Due to the absence of tantalising hints for new physics during the LHC’s Run 1, the extension of the Higgs sector by dimension-six operators will provide the new phenomenological standard for searches of non-resonant extensions of the Standard Model. Using all dominant and subdominant Higgs production mechanisms at the LHC, we compute the constraints on Higgs physics-relevant dimension-six operators in a global and correlated fit. We show in how far these constraints can be improved by new Higgs channels becoming accessible at higher energy and luminosity, both through inclusive cross sections as well as through highly sensitive differential distributions. This allows us to discuss the sensitivity to new effects in the Higgs sector that can be reached at the LHC if direct hints for physics beyond the SM remain elusive. We discuss the impact of these constraints on well-motivated BSM scenarios.

1 Introduction

Since the Higgs boson’s discovery in 2012 [1, 2], ATLAS and CMS have quickly established a picture of consistency with the Standard Model (SM) expectation of the Higgs sector [3, 4]. By now, a multitude of constraints have been formulated across many dominant and subdominant Higgs production modes [5]. All these measurements, as well as the absence of a direct hint for new physics from exotics searches, seem to suggest that the scale of new physics is well separated from the electroweak scale. This motivates¹ the extension of the Higgs sector by dimension-six operators [7–11]

$$\begin{aligned} \mathcal{{L}}_{\text {Higgs}} = \mathcal{{L}}_{\text {Higgs}}^{\text {SM}} + \sum _i { c_i \over \Lambda ^2} O_i \end{aligned}$$

(1)

to capture new interactions beyond the Standard Model (BSM) in a model-independent way—within the generic limitations of effective field theories. Constraints on these operators from a series of Run 1 and other measurements have been provided [12–29].

A question that arises at this stage in the LHC programme is the ultimate extent to which we will be able to probe the presence of such interactions. Or stated differently: what are realistic estimates of Wilson coefficient constraints that we can expect after Run 2 or the high-luminosity phase if direct hints for new physics will remain elusive? With a multitude of additional Higgs search channels as well as differential measurements becoming available, the complexity of a fit of the relevant dimension-six operators becomes immense.

It is the purpose of this work to provide these estimates. Using the Gfitter [30–33] and Professor [34] frameworks, we construct predictions of fully differential cross sections, evaluated to the correct leading-order expansion in the dimension-six extension $\hbox {d}\sigma =\hbox {d}\sigma ^{\text {SM}} + \hbox {d}\sigma ^{\{O_i\}}/\Lambda ^2$. We derive constraints on the Wilson coefficients in a fit of the dimension-six operators relevant for the Higgs sector, inputting a multitude of present as well as projections of future LHC Higgs measurements.

This paper is outlined as follows. In Sect. 2 we introduce our approach in more detail. In particular, we discuss the involved Higgs production and decay processes and review our interpolation methods in the dimension-six operator space, as well as introduce the key elements of our fit procedure. In Sect. 3 we give an overview of the statistical setup used. Our results using LHC Run 1 data are compared to existing and related work in Sect. 4. This sets the stage for the extrapolation to 14 TeV LHC centre-of-mass energy in Sect. 5, where we detail the assumptions made when extrapolating to higher luminosities. Our results are presented in Sect. 6, where we give estimates of the sensitivity that can be expected at the LHC for the operators considered in this work. An example on how the EFT constraints can be used in the context of a well-defined BSM model is given in Sect. 7. We give a discussion of our results and conclude in Sect. 8.

Throughout this work we will use the so-called strongly interacting light Higgs basis [9] adopting the “bar notation” (this choice is not unique and can be related to other bases [35]), and constrain deviations from the SM with leading-order electroweak precision. A series of publications have extended the dimension-six framework to next-to-leading order [36–45]. The impact of these modified electroweak corrections can in principle be large in phase space regions where SM electroweak corrections are known to be sizable and should be treated on a case-by-case basis. However, this is not the main objective of this analysis and we consider higher-order electroweak effects beyond the scope of this work.

2 Framework and assumptions

We perform a global fit within a well-defined Higgs boson EFT framework assuming SM gauge and global symmetries and a SM field content. We focus on the phenomenology of the Higgs boson that can be cast into narrow width approximation calculations,

$$\begin{aligned} \sigma (pp\rightarrow H \rightarrow X) = \sigma (pp\rightarrow H) {\text {BR}}(H\rightarrow X)\,. \end{aligned}$$

(2)

Therefore, we can divide the simulation of the underlying dimension six phenomenology into production and decay of the Higgs boson. We discuss our approach to these parts in the following.

We consider the set of operators known as the strongly interacting light Higgs Lagrangian in bar convention (for details see Refs. [9, 11, 46, 47])

$$\begin{aligned} \mathcal{L}_{\text {SILH}}= & {} \frac{\bar{c}_H}{2v^2}\partial ^\mu ( H^\dagger H)\partial _\mu (H^\dagger H)\nonumber \\&+\,\frac{\bar{c}_T}{2v^2}(H^\dagger {\overleftrightarrow { D^\mu }} H )(H^\dagger {\overleftrightarrow D}_\mu H)- \frac{\bar{c}_6\lambda }{v^2}(H^\dagger H)^3 \nonumber \\&+ \left( \frac{\bar{c}_{u,i} y_{u,i}}{v^2}H^\dagger H {\bar{u}}_L^{(i)} H^c u^{(i)}_R +{\text {h.c.}}\right) \nonumber \\&+ \left( \frac{\bar{c}_{d,i} y_{d,i}}{v^2}H^\dagger H {\bar{d}}_L^{(i)} H d^{(i)}_R+{\text {h.c.}}\right) \nonumber \\&+\,\frac{i\bar{c}_Wg}{2m_W^2}(H^\dagger \sigma ^i \overleftrightarrow {D^\mu } H)( D^\nu W_{\mu \nu })^i\nonumber \\&+\,\frac{i\bar{c}_Bg'}{2m_W^2}(H^\dagger \overleftrightarrow {D^\mu } H)(\partial ^\nu B_{\mu \nu }) \nonumber \\&+\,\frac{i\bar{c}_{HW} g}{m_W^2} (D^\mu H)^\dagger \sigma ^i(D^\nu H)W_{\mu \nu }^i\nonumber \\&+\,\frac{i\bar{c}_{HB}g'}{m_W^2} (D^\mu H)^\dagger (D^\nu H)B_{\mu \nu } \nonumber \\&+\,\frac{\bar{c}_\gamma {g'}^2}{m_W^2}H^\dagger H B_{\mu \nu }B^{\mu \nu } +\frac{\bar{c}_g g_S^2}{m_W^2}H^\dagger H G_{\mu \nu }^a G^{a\mu \nu }.\nonumber \\ \end{aligned}$$

(3)

While this basis is not complete [40, 47], it is sufficient for the purposes of this paper. In particular we assume flavour-diagonal dimension-six effects and in order to directly reflect the oblique correction subset of LEP measurements of S, T we decrease the number of degrees of freedom in the fit by identifying (see also [9, 11, 24, 48])

$$\begin{aligned} \bar{c}_T=0,\quad \bar{c}_W + \bar{c}_B =0. \end{aligned}$$

(4)

We do not include anomalous triple gauge vertices to our fit [24, 49–51].

Fig. 1

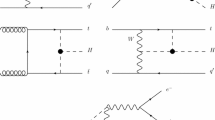
Comparison of parton-level $pp\rightarrow HZ$ and $pp\rightarrow H+\text {j}$ for large partonic centre-of-mass energy $\sqrt{\hat{s}}$ and a particular value of $\bar{c}_g$. The Higgs branching ratios are rescaled to have the correct SM signal strength in gluon fusion, leading to normalisation differences or enhancements at large momentum transfers. Normalisation effects from flat K factors as well as different acceptances are included to illustrate the relative importance of different production modes as signal channels

2.1 Higgs production and decay

To simulate the Higgs boson phenomenology, we employ the narrow width approximation

$$\begin{aligned}&\sigma ^{{d=6}}(pp\rightarrow H \rightarrow X) \nonumber \\&\quad = \sigma (pp\rightarrow H,\{c_i\}) {\text {BR}}(H\rightarrow X,\{c_i\}) \end{aligned}$$

(5)

where we linearise both parts in the Wilson coefficients. This factorisation is motivated from being able to extract the Higgs as the pole of the full amplitude, which is possible to all orders of perturbation theory [52]. We detail the production and decay parts in the following.

2.1.1 Production

For the production we rely on an implementation of dimension-six operators analogous to [53], which we have cross checked and introduced in [54]. The Monte-Carlo integration of the Higgs production processes is performed with a modified version of Vbfnlo [55] that interfaces FeynArts, FormCalc, and LoopTools [56, 57] using a model file output by FeynRules [58–60] and we only consider “genuine” dimension-six effects that arise from the interference of the dimension-six amplitude with the SM. Writing

$$\begin{aligned} \mathcal{{M}}=\mathcal{{M}}_{\text {SM}}+\mathcal{{M}}_{d=6}, \end{aligned}$$

(6)

we obtain a squared matrix element of the form

$$\begin{aligned} |\mathcal{{M}} |^2 = | \mathcal{{M}}_{\text {SM}} |^2 + 2\, \text {Re} \{ \mathcal{{M}}_{\text {SM}} \mathcal{{M}}_{d=6}^*\} + \mathcal{{O}}(1/\Lambda ^4), \end{aligned}$$

(7)

and we consistently neglect the dimension eight contributions that arise from squaring the dimension-six effects. Similar to higher-order electroweak or QCD calculations, the differential cross sections are not necessarily positive definite in this expansion, but negative bin entries provide a means to judge the validity of the Wilson coefficient and the dimension-six approach in general.

For parameter choices close to the SM, including $|\mathcal{{M}}_{d=6}|^2$ is typically not an issue and the parameters $c_i^2$ are often numerically negligible for inclusive observables such as signal strengths. However, to obtain an inclusive measurement, we marginalise over a broad range of energies at the LHC and a positive theoretical cross section might be misleading as momentum dependencies of some dimension-six operators violate a naive scaling $c_i E^2/\Lambda ^2 <c_i^2 E^4/\Lambda ^4$ in the tails of momentum-dependent distributions, where E denotes the respective and process-relevant energy scale. For this reason, we choose to calculate cross sections to the exact order ${\sim } 1/\Lambda ^2$ and later reject Wilson coefficient choices that lead to a negative differential cross section for integrated bins of a given LHC setting when this part of the phase space is resolved; such negative cross sections signal bigger contributions of the $d=6$ terms than we expect in the SM, and we cannot justify limiting our analysis to dimension-six operators if new physics becomes as important as the SM in observable phase space regions. This provides a conservative tool to gauge the validity of our approach, but care has to be taken by interpreting the results when connecting to concrete physics scenarios. In strongly interacting scenarios, it can be shown that the squared $d=6$ terms are important, for small Wilson coefficients they are negligible. The latter avenue should be kept in mind for our results.

2.1.2 Included production modes and operators

We consider the production modes $pp\rightarrow H$, $pp \rightarrow H+{\text {j}}$, $pp \rightarrow t\bar{t} H$, $p p \rightarrow WH$, $p p \rightarrow ZH$ and $p p\rightarrow H+2{\text {j}}$ (via gluon fusion and weak-boson fusion) in a fully differential fashion by including the differential Higgs transverse momentum distributions to setting constraints. As we demonstrate, including energy-dependent differential information whenever possible, is key to setting most stringent constraints on the dimension-six extension by including the information of the distributions’ shapes beyond the total cross section, especially when probing blind directions in the signal strength, as shown in Fig. 1a. Note that for the underlying $2\rightarrow 2$ and $2\rightarrow 3$ processes in the regions of detector acceptance, the Higgs transverse momentum is highly correlated with the relevant energy scales that probe the new interactions, Fig. 1b, and therefore is a suitable observable to include in this first step towards a fully differential Higgs fit. Expanding the cross sections to linear order in the Wilson coefficients as done in this work is not a mere technical twist, but allows us to obtain a description of the high-$p_T$ cross sections within our approximations.

The operator $(H^\dagger H)^3$ and off-shell Higgs production in the EFT framework [54, 61, 62] deserve additional comments. Dihiggs production is the only process which provides direct sensitivity to $\bar{c}_6$ [63] and factorises from the global fit, at least at leading order. Hence, the $\bar{c}_6$ can be separated from the other directions to good approximation. While Higgs pair production process can serve to lift $y_t$-degeneracies in the dimension-six extension [64, 65], the sensitivity to $\bar{c}_6$ is typically small when we marginalise over $\bar{c}_{u3}$. The latter can be constrained either in $pp \rightarrow \bar{t} t H$, $pp\rightarrow ZZ$ in the Higgs off-shell regime [54, 61, 62, 66, 67] or $pp\rightarrow H+{\text {j}}$ [68–71], however, only the former of these processes provides direct sensitivity to $\bar{c}_{u3}$ without significant limitations due to marginalisation over the other operator directions. Current recast analyses place individual constraints in the range of $|\bar{c}_{u3}|\lesssim 5$ and $|\bar{c}_g|\lesssim 10^{-3}$ [70] for the 8 TeV data set.

While the expected sensitivity to $pp\rightarrow HH(+{\text {jets}})$ still remains experimentally vague at this stage in the LHC programme [72, 73], the potential to observe $pp\rightarrow \bar{t} t H$ is consensus. We therefore do not include $pp\rightarrow HH$ to our projections and also omit off-shell Higgs boson production, since experimental efficiencies during the LHC high-luminosity phase will significantly impact the sensitivity in these channels. We leave a more dedicated discussion of these channels to future work [74].

Due to the small Yukawa couplings of first and second generation quarks and leptons, we limit ourselves to modified top–Higgs and bottom–Higgs couplings throughout and neglect modifications of the lepton–Higgs system too. An overview of the tree-level sensitivity of the production channels considered in this work is given in Table 1.

Table 1 Tree-level sensitivity of the various production mechanisms

Fig. 2

Variation of Higgs branching ratios as a function of $\bar{c}_\gamma$ normalised to the SM values

2.1.3 Branching ratios

For the branching ratios, we rely on eHdecay to include the correct Higgs branching ratios in the dimension-six extended Standard Model, which is detailed in [75] and implements a linearisation in the Wilson coefficients. The branching ratios are therefore sensitive to all Wilson coefficients affecting single Higgs physics. An example for the variation of the branching ratios as a function of $\bar{c}_\gamma$ is shown in Fig. 2.

We sample a broad range of dimension-six parameter choices and interpolate them using the Professor method detailed in the Appendix A. This also allows us to identify already at this stage a reasonable Wilson coefficient range with a positive-definite Higgs decay phenomenology that limits the validity (i.e. the positive definiteness) of our narrow width approximation. We find an excellent interpolation of the eHdecay output (independent of the interpolated sample’s size and choice) and we typically obtain per mille-level accuracy of the Higgs partial decay widths and branching ratios, which is precise enough for the limits we can set. Interpolation using Professor is key to performing the fit in the high dimensional space of operators and observables in a very fast and accurate way.

3 Statistical analysis

The Gfitter software is used for calculating the likelihood and the estimation of the sensitivity of data. The data include correlated experimental systematic uncertainties, implemented in the form of a covariance matrix. These uncertainties either come from measurements at the LHC or from pseudo-data, as explained in detail below. The theoretical uncertainties are taken into account as nuisance parameters. The negative log-likelihood $-2 \ln \mathcal {L}= \chi ^2$ is constructed as

$$\begin{aligned} \chi ^2 = (\varvec{x} - \varvec{t}(c_i, \delta _k))^T \varvec{V}^{-1} (\varvec{x} - \varvec{t}(c_i, \delta _k)) + \sum _k \delta _k^2 \end{aligned}$$

(8)

where $\varvec{x}$ denotes the vector of measurements, $\varvec{t}(\bar{c}_i, \delta _k)$ the theory predictions depending on the Wilson coefficients $c_i$ and theoretical uncertainties implemented as nuisance parameters $\delta _k$ and $\varvec{V}$ is the covariance matrix. The covariance matrix is given by

$$\begin{aligned} \varvec{V} = \varvec{V}_{\text {stat}} + \varvec{V}_{\text {syst}}, \end{aligned}$$

(9)

consisting of an uncorrelated statistical part $\varvec{V}_{\text {stat}}$ and a correlated experimental systematic uncertainty $\varvec{V}_{\text {syst}}$. The sensitivity on the coefficients $\bar{c}_i$ is calculated by scanning the likelihood as a function of a given set of Wilson coefficients. For each point of this scan the likelihood is profiled over the other dimension-six coefficients and the nuisance parameters $\delta _k$ corresponding to the theoretical uncertainties. The profiling is performed by a multi-dimensional fit. Each of these fits include up to 32 free parameters. Out of those, 24 are due to nuisance parameters of the theoretical uncertainties and the other eight parameters are the dimension-six coefficients themselves.

4 Results for Run 1

In the following we will evaluate the status of the effective Lagrangian Eq. (3) in light of available Run 1 analyses. Similar analyses have been performed by a number of groups; see e.g. [22, 24, 26]. Comparing the above fit-procedure to these results not only allows us to validate the highly non-trivial fitting procedure against other approaches, but also to extend these results by including additional measurements which have become available in the meantime. We include Run 1 experimental analyses using HiggsSignals v1.4 [76, 77], based on HiggsBounds v4.2.1 [78–81], which calculates $\chi ^2$ given in Eq. (8) taking into account experimental and theoretical correlations, as well as signal acceptances.

Specifically, we include the following analyses. Higgs decays to bosons have been measured in the channels $H\rightarrow \gamma \gamma$ [82, 83], $H\rightarrow ZZ^{(*)} \rightarrow 4l$ [84, 85] and $H\rightarrow WW^{(*)} \rightarrow 2l 2\nu$ [86–89]. These analyses have sensitivity to the gluon-fusion, $H+2{\text {j}}$ and VH production modes. The coupling to leptons has been probed in the $H\rightarrow \tau ^+\tau ^-$ channel [90, 91], with some evidence for $H\rightarrow b\bar{b}$ in VH production [92, 93] and a search for $H\rightarrow \mu ^+ \mu ^-$ [94]. The coupling to top quarks has been addressed through $t\bar{t}H$ production in the $H\rightarrow b\bar{b}$ decay [95, 96] and in leptonic decays, sensitive to the $H\rightarrow ZZ^{(*)}$, $H\rightarrow WW^{(*)}$ and $H\rightarrow \tau ^+\tau ^-$ channels [96, 97]. This results in a total of 78 measurements included in the fit. All measurements used are listed in Appendix B, together with the values of $\mu$, the uncertainties and details on the signal acceptances. Correlations between the measurements are introduced due to the acceptance of a given experimental measurement to a number of production and decay modes and the overall luminosity measurement. Also, the theoretical uncertainties from the normalisation of the signal strength measurements to the SM prediction, as included in the experimental results, are taken to be fully correlated among the experimental measurements [76, 77]. Correlations due to theory uncertainties in the calculations with dimension-six effects are included as well.

Fig. 3

Confronting the Lagrangian Eq. (3) with the 8 TeV LHC Run 1 measurements. Solid lines correspond to a fit with theoretical uncertainties included, dashed lines show results without theoretical uncertainties, the band shows the impact of these. Grey lines and bands denote the individual constraints on a given parameter, and blue refers to the marginalised results. For details see the main text

Fig. 4

Confronting the Lagrangian Eq. (3) with the 14 TeV LHC measurements with $L=300$ (green) and $3000~\text {fb}^{-1}$ (orange). We only take signal strength measurements into account. Solid lines correspond to a fit with theoretical uncertainties included, dashed lines show results without theoretical uncertainties, the band shows the impact of these. For details see the text

Fig. 5

Confronting the Lagrangian Eq. (3) with the 14 TeV LHC measurements with $L=300$ (green) and $3000~\text {fb}^{-1}$ (orange). We include the full $p_{T,H}$ distribution and the signal strength measurement for $pp\rightarrow H$ production in the limit setting procedure. Solid lines correspond to a fit with theoretical uncertainties included, dashed lines show results without theoretical uncertainties, the band shows the impact of these

The results are shown in Fig. 3 and are in good agreement with the results obtained in Refs. [24, 28]. Numerical values are given below in Table 5. Small differences can be understood from working under different assumptions (specifically the strict linearisation of dimension-six effects) as well as including more analyses. It should be noted that our choice of limiting the range of Wilson coefficient values (necessary for the positive definiteness of differential distributions) is necessitated by our extrapolation and inclusion of differential distributions. Consequently, we cannot set a limit on many operators in the light of Run 1 measurements within our approximations. However, the direct comparison to the Figs. 4 and 5 will allow us to see how these can be improved when going to higher centre-of-mass energy and luminosity. Relaxing these constraints will lead to increased Wilson coefficient intervals for the marginalised scans over the 8 TeV signal strength measurements (for a recent fit without limited coefficient ranges see Ref. [51]).

The fit converges with a minimum value of $\chi ^2$ of 87.7 for 70 degrees of freedom $(n_{\text {dof}})$, corresponding to a p-value of about 0.07. Without theory uncertainties the value of $\chi ^2$ increases to 96.5. The goodness-of-fit is slightly worse than the result of a $\chi ^2$ test of the SM hypothesis, which gives a minimum value of $\chi ^2 / n_{\text {dof}} = 91.3 / 78 = 1.17$, or a p-value of 0.14. The smaller p-value for the dimension-six fit with respect to the SM result can be understood because of the addition of free parameters not needed to describe the data, in other words, some dimension-six coefficients are not constrained by the current data. Two coefficients, $\bar{c}_{g}$ and $\bar{c}_{\gamma }$, can be reliably constrained at 95 % confidence level (CL) within the range of Wilson coefficient values considered. We find the allowed 95 % CL ranges

$$\begin{aligned}&\bar{c}_{g} \in [-0.64, \, 0.43] \times 10^{-4} \nonumber \\&\bar{c}_{\gamma } \in [-7.8, \, 4.3] \times 10^{-4}. \end{aligned}$$

(10)

These constraints are somewhat tighter than the ones obtained by the ATLAS collaboration, $\bar{c}_{g} \in [-0.7, \, 1.3] \times 10^{-4}$ and $\bar{c}_{\gamma } \in [-7.4, \, 5.7] \times 10^{-4}$ [28], because the ATLAS values are derived using only the ATLAS $H\rightarrow \gamma \gamma$ measurement.

Let us compare these limits to the SM to get an estimate of how big these constraints are if we move away from the bar convention. The limits on, e.g., $\bar{c}_g\lesssim 0.4\times 10^{-4}$ can be compared for instance against the effective ggH operator that arises from integrating out the top quark in the limit $m_t\rightarrow \infty$. The effective operator for this limit, using low energy effective theorems [98–100] reads

$$\begin{aligned} \frac{\alpha _s}{12\pi } G_{\mu \nu }^a G^{a\mu \nu } \log ( 1+ H/v) \simeq \frac{ \alpha _s}{12\pi v} G_{\mu \nu }^a G^{a\mu \nu } H + \cdots \nonumber \\ \end{aligned}$$

(11)

Matching this operator onto SILH convention of Eq. (3), we obtain $|\bar{c}_g({\text {effective SM}})|\simeq 0.2\times 10^{-3}$. So in this sense, new physics is constrained to a $\mathcal{{O}}(10~\%)$ deviation relative to the SM from inclusive observables. The relative deviations in the tails of the Higgs transverse momentum distributions that are induced by this operator can easily be as big as factors of two (see e.g. [54, 61, 62]), which highlights the necessity to resolve this deviation with energy or momentum-dependent observables during Run 2 and the high-luminosity phase to best constrain the presence of non-resonant physics using high momentum transfers.

5 Projections for 14 TeV and the high-luminosity phase

Throughout our analysis we normalise our results to the recommendation of the Higgs cross section working group [101–103]. Predicted rates are using the narrow width approximation of Eq. (2). We construct pseudo-measurements to asses the sensitivity of the LHC with a centre-of-mass energy of 14 TeV to the set of operators considered in this work. The theoretically predicted number of events for a specific final state $N_{\text {th}}$ is obtained by multiplying by additional branching ratios if necessary and the luminosity L of the particular analysis:

$$\begin{aligned} N_{\text {th}}= & {} \sigma (H+X) \times \text {BR}(H\rightarrow YY) \nonumber \\&\times \, L \times \text {BR}(X,Y\rightarrow \text {{final~state}}). \end{aligned}$$

(12)

This number is then multiplied by the efficiency to measure the production channel $\epsilon _p$ and the efficiency to measure the decay products $\epsilon _d$, to obtain the measured number of events

$$\begin{aligned} N_{\text {ev}} = \epsilon _p \epsilon _d N_{\text {th}}. \end{aligned}$$

(13)

The relative statistical uncertainty for a given pseudo-measurement is estimated to be $\sqrt{N_{\text {ev}}}$. For the efficiency to reconstruct a specific final state, we rely on experimental results from Run 1, where available. The efficiencies used are $\epsilon _{p,{\mathrm{t}\bar{\mathrm{t}}\mathrm{h}}} = 0.10$ [95, 96, 104, 105], $\epsilon _{p,\text {ZH}} = 0.12$, $\epsilon _{p,\text {WH}} = 0.04$, $\epsilon _{p,\text {VBF}} = 0.30$ [4, 82, 83, 92]. We assume a value of $\epsilon _{p,\text {H+j}} = 0.5$ [106] (see also [67, 107, 108]) where no experimental results targeting this production mode are available so far. In order to simplify the assumptions and the background estimates, we consider only leptonic channels for the VH and $t\bar{t}H$ production modes. Here only final states with electrons and muons are used. These are, however, allowed to originate from $\tau$-decays. In case of the gluon-fusion production mode, analyses targeting different final states have different reconstruction efficiencies. We use the following efficiencies for the process $pp\rightarrow H$: $\epsilon _{p,\text {GF}} = 0.4$ for $H\rightarrow \gamma \gamma$ [82, 83], $\epsilon _{p,\text {GF}} = 0.01$ for $H\rightarrow \tau ^+ \tau ^-$ [90, 91], $\epsilon _{p,\text {GF}} = 0.25$ for $H\rightarrow 4l$ [4, 84], $\epsilon _{p,\text {GF}} = 0.10$ for $H\rightarrow 2l 2\nu$ [86, 88], $\epsilon _{p,\text {GF}} = 0.10$ for $H\rightarrow Z \gamma$ [109, 110], and $\epsilon _{p,\text {GF}} = 0.50$ for $H\rightarrow \mu \mu$ [94, 111]. The $H\rightarrow b\bar{b}$ decay is not considered for the gluon-fusion production mode. Taking a conservative approach we assume the same reconstruction efficiencies for measurements at 14 TeV, independent of the Higgs transverse momentum.

In the reconstruction of the Higgs boson we include reconstruction and identification efficiencies of the final state objects:

$H\rightarrow \mathrm {b}\bar{b}$::

We assume a flat b-tagging efficiency of $60~\%$, i.e. $\epsilon _{d,b\bar{b}}=0.36$.

$H\rightarrow \gamma \gamma$::

For the identification and reconstruction of isolated photons we assume, respectively, an efficiency of $85~\%$. Hence, we find $\epsilon _{d,\gamma \gamma } \simeq 0.72$.

$H\rightarrow \tau ^+ \tau ^-$::

We consider $\tau$-decays into hadrons ($\text {BR}_{\text {had}}=0.648$) or leptons, i.e. an electron ($\text {BR}_{e}=0.178$) or muon ($\text {BR}_{\mu }=0.174$). For the reconstruction efficiency of the hadronic $\tau$ we assume a value of $50~\%$ and for the electron and muon we use $95~\%$. Thus, the total reconstruction efficiency is $\epsilon _{d,\tau \tau } \simeq 0.433$.

$H\rightarrow ZZ^* \rightarrow 4l$::

We consider Z decays into electrons and muons only, also taking into account $\tau$ decays into lighter leptons. For each lepton we assume a reconstruction efficiency of $95~\%$, which gives a total reconstruction efficiency of $\epsilon _{d,4l} \simeq 0.815$.

$H\rightarrow WW^* \rightarrow 2l 2\nu$::

Only lepton decays into electrons and muons are considered and for each visible lepton we include a $95~\%$ reconstruction efficiency, i.e. $\epsilon _{d,2l 2\nu } = 0.9025$

$H\rightarrow Z \gamma$::

Again, we include separately an $85~\%$ identification and reconstruction efficiency for isolated photons and a $95~\%$ reconstruction efficiency for each electron and muon. As a result we find $\epsilon _{d,Z\gamma } \simeq 0.767$.

$H\rightarrow \mu ^+ \mu ^-$::

Each muon is assumed to have a reconstruction efficiency of $95~\%$, resulting in $\epsilon _{d,\mu \mu }=0.9025$.

Owing to the different selections made in the various experimental analyses, each channel has a unique background composition, resulting in different additional systematic uncertainties on the measurements. We approximate those by adding uncorrelated systematic uncertainties for each production and decay channel in quadrature. The uncertainties used are given in Table 2 and are assumed to be flat in $p_{T,H}$. The uncertainties are taken from experimental Run 1 analyses [3, 4, 82–88, 90, 91, 94, 95, 109–112], where publicly available. In cases where these uncertainties are not explicitly given they are approximated to reproduce the total experimental uncertainties. The total uncorrelated uncertainty is obtained by adding the systematic uncertainty from background processes to the statistical uncertainty from signal events in quadrature.

Table 2 Relative systematic uncertainties due to background processes for each production and decay channel in $\%$

Table 3 Relative systematic uncertainties for each production times decay channel in $\%$

Beyond identification and reconstruction efficiencies for production channels and Higgs decays, each channel is plagued by individual experimental systematic uncertainties. We adopt flat systematic uncertainties in $p_{T,H}$ for the individual channels. The numerical values are based on the results from experimental Run 1 analyses [3, 4, 82–88, 90, 91, 94, 95, 109–112], see Table 3. In channels where no measurement has been performed or no information is publicly available, e.g. $pp\rightarrow H+2\text {j}, H\rightarrow Z \gamma$, we choose a conservative estimate of systematic uncertainties of 100 %. In addition to the uncertainties listed in Table 3, we include a systematic uncertainty of 30 % for the $H\rightarrow 2l 2\nu$ channel for differential cross sections. This uncertainty is due to the inability of reconstructing the Higgs transverse momentum accurately.

During future runs, experimental uncertainties are likely to improve with the integrated luminosity. Hence for our results at 14 TeV we use the 8 TeV uncertainties as a starting point, as displayed in Tables 2 and 3, and we rescale them by $L_8/L_{14}$ for a given integrated luminosity at 14 TeV $L_{14}$. This results in a reduction of statistical and experimental systematic uncertainties by a factor of about 0.3 for $L_{14}=300~\text {fb}^{-1}$ and about 0.1 for $L_{14}=3000~\text {fb}^{-1}$. This simplified procedure has also been adopted by the ATLAS and CMS collaborations to extrapolate the sensitivity of experimental analyses to future runs [113–116]. We use this extrapolation for ease of comparison and reproducibility.

We only consider measurements with more than five signal events after the application of all efficiencies and a total uncertainty smaller than 100 %. The pseudo-data are constructed using the SM hypothesis, i.e. all Wilson coefficients are set to zero. We construct expected signal strength measurements for all accessible production and decay modes. Additionally, differential cross sections as a function of the Higgs transverse momentum are simulated with a bin size of 100 GeV. In $2\rightarrow 3$ processes like ttH other differential distributions might provide higher sensitivity than $p_{T,H}$, but at this point we restrict the analysis to include $p_{T,H}$ distributions only, as these are likely to be provided as unfolded distributions by the experimental collaborations. We leave studies on the sensitivity of additional kinematic variables in a global fit to future work [74].

Comparing our predictions for the uncertainties on the signal strength measurements for 14 TeV using an integrated luminosity of $L_{14}=300~\text {fb}^{-1}$ and $L_{14}=3000~\text {fb}^{-1}$, with the expectations published by ATLAS [113, 114] and CMS [115, 116], we find good quantitative agreement with the publicly available channels.

Table 4 Theoretical uncertainties for each production and decay channel in $\%$

Table 5 Constraints at 95 % CL on dimension-six operator coefficients (first column) from LHC Run 1 data, considering only one operator in the fit (second column) and all operators simultaneously (third column). The results obtained using pseudo-data are shown in the last two columns, with signal strengths measurements only (fourth column) and including differential distributions (fifth column). In case no constraints can be derived within the parameter ranges considered in this work, the lower and upper limits are indicated to lie outside this range

Theory uncertainties included in the fit are listed in Table 4 and have been obtained by the Higgs cross section working group [101–103] (see also [117] about their role in Higgs fits). We assume the same size of theory uncertainties for the SM predictions as for calculations using the EFT framework. The theory uncertainties are not scaled with luminosity and retain the values given in Table 4 throughout this work.

Systematic uncertainties are crucial limiting factors of a coupling extraction and the scaling we choose in the present paper are unlikely to be realistic, but provide a clean extrapolation picture for potential progress over the next decades. In summary, the assumptions chosen to get our estimate are

• the above luminosity scaling of experimental uncertainties,

• a clean separation of the measurements of all production and decay channels (no cross talk between channels),

• flat experimental systematic uncertainties as a function of $p_{T,H}$,

• flat theory uncertainties as a function of $p_{T,H}$ as quoted in Table 4, which we assume to be independent of the Wilson coefficients.

A more detailed investigation of systematics beyond the approximations chosen in this work can provide a guideline for future precision efforts, this work is currently ongoing [74].

6 Predicted constraints

The projected measurements of the Higgs signal strengths and the Higgs transverse momentum ($p_{T,H}$) distributions are used to test the sensitivity to the dimension-six operators that can be obtained with the LHC. In all fits theory uncertainties are included as nuisance parameters with Gaussian constraints. The constraints on individual Wilson coefficients are obtained by a marginalisation over the remaining coefficients and the nuisance parameters related to the theory uncertainties.

In order to test this approach, we first generate pseudo-data for 8 TeV following the procedure detailed above. The integrated luminosity is chosen to be $L_8$, i.e. $25~\text {fb}^{-1}$ per experiment which corresponds to the full Run 1 data. With this setting no luminosity scaling of experimental uncertainties is performed. Besides statistical uncertainties, the generated 8 TeV data have systematic uncertainties corresponding to the values given in Tables 2 and 3. We compare the constraints obtained with these pseudo-data with the ones obtained from the Run 1 analysis in Table 5. Similar to the constraints derived in Sect. 4 no reliable constraints at 95 % CL on coefficients other than $\bar{c}_{g}$ and $\bar{c}_{\gamma }$ can be derived within the parameter ranges considered in this work. We observe that the constraints using pseudo-data are considerably weaker than the ones from the existing Run 1 measurements. This is no surprise, as the simplified approach outlined above cannot reflect the complexity of real analyses, where a number of signal regions are used to disentangle different production modes. This picture does not change when including differential distributions (last column of Table 5) which results in slightly better constraints at 8 TeV compared to the fit with signal strengths only. We note that although the constraints obtained with pseudo-data are generally weaker, they are very similar to the ones using current Run 1 experimental data. We therefore trust our method and proceed to derive the expected sensitivity of the LHC.

In Fig. 4 we show in how far the limits from the LHC Run 1 with 8 TeV extrapolate to 14 TeV at luminosities of $300~\text {fb}^{-1}$, as well as after the high-luminosity phase with $3000~\text {fb}^{-1}$. In these fits we only include expected signal strength measurements. With these statistics, more production and decay channels become observable at smaller statistical and systematic uncertainties, which leads to a more constrained fit. The fit for the $300~\text {fb}^{-1}$ scenario uses 36 signal strength measurements, and 46 measurements are used for the scenario with $3000~\text {fb}^{-1}$. All details of the pseudo-data used in performing these extrapolations can be found in the appendix, where also the luminosity-scaling of systematic uncertainties is depicted. Specifically the constraints on operators that modify associated Higgs production and weak-boson fusion benefit from the increased centre-of-mass energy and luminosity. In the scenario for the high luminosity phase the theoretical uncertainties become dominant in some cases.

Fig. 6

Contours of 68, 95 and 99 % CL (from dark to light), obtained from a marginalised fit using the expected signal strength modifiers only (grey) and the $p_{T,H}$ measurements (orange) for 14 TeV with a luminosity of $3000~\text {fb}^{-1}$. All coefficients have been multiplied by a factor of $10^{3}$

Table 6 Predicted constraints at 95 % CL on dimension-six operator coefficients (first column) for the LHC with 14 TeV with an integrated luminosity of $300~\text {fb}^{-1}$ (LHC-300) and $3000~\text {fb}^{-1}$ (LHC-3000). In the second and third columns results are given using signal strength measurements only, in the last two columns results including differential $p_{T,H}$ measurements are shown. In case no constraints can be derived within the parameter ranges considered in this work, the lower and upper limits are indicated to lie outside this range

In a second step, we include the differential $p_{T,H}$ measurements from all production modes, except $pp\rightarrow H$. For the $pp\rightarrow H$ production mode we include six signal strength measurements (see the Appendix), as no transverse momentum of the Higgs boson is generated on tree-level. This results in $82+6$ independent measurements included for the fit with $300~\text {fb}^{-1}$ and $117+6$ for $3000~\text {fb}^{-1}$. In a given production and decay channel, experimental systematic uncertainties are included as correlated uncertainties among bins in $p_{T,H}$. Comparing the above constraints with those expected from including the differential distributions, Fig. 5, we see a tremendous improvement. The improvement compared to the constraints presented in Fig. 4 is solemnly due to the inclusion of differential distributions, as no new channels are added in this step. We also observe a reduction of the impact of theoretical uncertainties. Two-dimensional contours of the expected constraints are shown in Fig. 6 for the scenario with $3000~\text {fb}^{-1}$. The fits using signal strength measurements only (grey) reveal a series of flat directions which cannot be amended by a different operator choice. Several flat directions are resolved with the fit using information from the differential $p_{T,H}$ measurements. While the improvement on the exact numerical constraints can be somewhat compromised by larger systematic uncertainties, the general feature of lifting flat directions still remains [74]. Even with $3000~\text {fb}^{-1}$ it is not possible to constrain $\bar{c}_{u3}$ and $\bar{c}_{g}$ or $\bar{c}_{HW}$ and $\bar{c}_{HB}$ simultaneously using signal strength modifiers only. Using information from the differential $p_{T,H}$ measurements, which are systematically under sufficient control, effectively allows one to constrain all coefficients simultaneously. Elements of studying differential distributions to effective Higgs dimension-six framework have been investigated with similar findings in the literature [24, 26, 118], but, to our knowledge, Figs. 5 and 6 provide the first consistent fit of all single-Higgs relevant operators in a fully differential fashion, in particular with extrapolations to 14 TeV. The numerical values of the 95 % CL intervals for the different scenarios are given in Table 6.

A series of dimension-six operators, on which no constraints can be formulated at this stage of the LHC programme or by only including signal strength measurements, can eventually be constrained with enough data and differential distributions. The reason behind this is that differential measurements ipso facto increase the number of (correlated) measurements by number of bins, leading to a highly over-constrained system. Also, since the impact of many operators is most significant in the tails of energy-dependent distribution, the relative statistical pull is decreased by only considering inclusive quantities.

7 Interpretation of constraints

The whole purpose of interpreting data in terms of an effective field theory is to use this framework as a means of communication between a low-scale measurement at the LHC and a UV model defined at a high scale, out of reach of the LHC. This way, the EFT framework allows us to limit a large class of UV models.

For a well-defined interpretation using effective operators, we assume that the operators, induced by the UV theory, only directly depend on the SM particle and symmetry content, and we also need to assume that the UV theory is weakly coupled to the SM sector. The last condition is necessary to justify the truncation of the effective Lagrangian at dimension six. After establishing limits on Wilson coefficients of the effective theory, as performed in Sects. 4–6, we can now address the implications for a specific UV model.

Two popular ways of addressing the Hierarchy problem are composite Higgs models and supersymmetric theories. Let us quickly investigate in how far these constraints are relevant once we match the EFT expansion to a concrete UV scenario.

In the strongly interacting Higgs case, from the power-counting arguments of Refs. [9, 119, 120], one typically expects

$$\begin{aligned} \overline{c}_g \sim \frac{ m_W^2 }{16\pi ^2 f^2 } \frac{y_t^2}{g_\rho ^2}, \end{aligned}$$

(14)

where $g_\rho \lesssim 4\pi$ and the compositeness scale is set by $\Lambda \sim g_\rho f$. So our predicted constraint on $\bar{c}_g$ including information from the differential Higgs $p_T$ distribution translates into $\Lambda \gtrsim 2.8$ TeV, which falls outside the effective kinematic coverage of the Higgs phenomenology at the LHC. This means that new composite physics with a fundamental scale $\Lambda \gtrsim 2.8$ TeV can naively not be probed in the Higgs sector alone. However, new contributions, such as narrow resonances around this mass can be discovered in different channels such as weak-boson fusion [121] or Drell–Yan production [122].

Matching, say, the MSSM stop contribution on the $\bar{c}_g$ operator, we have (see e.g. [70, 123, 124] for a more detailed discussion)

$$\begin{aligned} \overline{c}_g= & {} {m_W^2 \over (4\pi )^2} {1\over 24} \bigg ( {h_t^2 - g_1^2c_{2\beta }/6 \over m_{\tilde{Q}}^2 } + {h_t^2 + g_1^2 c_{2\beta }/3 \over m_{\tilde{t}_R}^2} -\, {h_t^2 X_t^2\over m_{\tilde{Q}}^2 m_{\tilde{t}_R}^2}\bigg ),\nonumber \\ \end{aligned}$$

(15)

where $h_t \equiv y_t s_\beta$, $X_t \equiv A_t - \mu \cot \beta$ and $m_{\tilde{Q}}$ and $m_{\tilde{t}_R}$ denote the soft masses of the left- and right-handed stops, respectively. To ensure the validity of our EFT approach based on differential distributions, we have to make the strong assumption that all supersymmetric particles are heavier than the momentum transfer probed in all processes that are involved in of our fit [44, 125] (see also [54, 127] for discussions of (non-)resonant signatures in BSM scenarios and EFT). For convenience, we additionally assume that all supersymmetric particles except the lightest stop $\tilde{t}_1$ are very heavy and decouple from $\overline{c}_g$. The largest value for $p_{T,H}$ we expect to probe during the LHC high-luminosity runs, based on our leading-order theory predictions is 500 GeV in the SM. We can therefore trust the effective field theory approach for $m_{\tilde{t}_1} > 600$ GeV in our limit setting procedure that inputs SM pseudo-data. For instance, fixing the soft masses $m_{\tilde{Q}}=m_{\tilde{t}}=m$, $\mu =200~\text {GeV}$ and $\tan \beta =30$ we can understand the constraints on $\overline{c}_g$ as constraints in the $A_t-m$ plane, Fig. 7. Similar interpretations are, of course, possible with the other Wilson coefficients.

Fig. 7

Matching the constraints on $|\bar{c}_g|\lesssim 5\times 10^{-6}$ of Fig. 5 onto stop contributions using Eq. (15) for identified soft masses $m_{\tilde{Q}}=m_{\tilde{t}}=m$. The EFT approach is valid only for parameter combinations (red area) that result in stop masses that do not directly impact the Higgs transverse momentum distribution directly (e.g. through thresholds). For further details see text

8 Discussion, conclusions and outlook

Even though current measurements as performed by ATLAS and CMS show good agreement with the SM hypothesis for the small statistics collected during LHC Run 1, the recently discovered Higgs boson remains one of the best candidates that could be a harbinger of physics beyond the SM. If new physics is heavy enough, modifications to the Higgs boson’s phenomenology from integrating out heavy states can be expressed using effective field theory methods.

In this paper we have constructed a scalable fitting framework, based on adapted versions of Gfitter, Professor, Vbfnlo, and eHdecay and have used an abundant list of available single-Higgs LHC measurements to constrain new physics in the Higgs sector for the results of Run 1. In these fits we have adopted the leading-order strongly interacting light Higgs basis assuming vanishing tree-level T and S parameters and flavour universality of the new physics sector. Our results represent the latest incarnation of fits at 8 TeV, and update results from the existing literature. The main goal of this work, however, is to provide an estimate of how these constraints will improve when turning to high energy collisions at the LHC with large statistics in light of expected systematics. In this sense our work represents a first step towards an ultimate Higgs sector fit, which is not limited to inclusive measurements, but uses highly sensitive differential distributions throughout.

Using extrapolations to 14 TeV, we find a major improvement of the expected constraints, in particular when differential information is included to the limit setting procedure. A summary of the current and expected constraints is given in Fig. 8; these are of immediate relevance for the expected sensitivity of the Higgs sector to concrete UV physics in the limit of large scale separations and unresolved new physics at the LHC.

Fig. 8

Marginalised 95 % CL constraints for the dimension-six operator coefficients for current data (blue), the LHC at 14 TeV with an integrated luminosity of $300~\text {fb}^{-1}$ (green) and $3000~\text {fb}^{-1}$ (orange). The expected constraints are centred around zero by construction, since the pseudo-data are generated by using the SM hypothesis. The left panel shows the constraints obtained using signal strength measurements only, and on the right differential $p_{T,H}$ measurements are included. The inner error bar depicts the experimental uncertainty, the outer error bar shows the total uncertainty, given the assumptions detailed in the text

It is interesting to see that including differential information at the LHC, we can expect the limits on certain operators to become competitive with measurements at a future FCC-ee [127, 128]. This is not entirely unexpected since the high $p_{T,H}$ cross sections, especially for hadronic channels, are sensitive probes of BSM physics. A major limiting factor, however, are the involved theoretical uncertainties, especially when moving to differential distributions at large statistics. Obviously, electroweak precision constraints provide a complementary avenue to constrain the presence of higher dimensional operators [24, 51, 129, 130] and are guaranteed to improve the sensitivity. We reserve a dedicated discussion for the future.

Appendices

Appendix A: Interpolation with Professor

Running a Monte-Carlo event generator and a subsequent analysis tool to fill a bin of a histogram can be thought of as a CPU-expensive evaluation of a function, $f_\text {MC}(\mathbf {p})$, at a certain point in a P-dimensional parameter space, $\mathbf {p}$. The Professor method [34] is an approach that reduces the time to evaluate $f_\text {MC}$ dramatically using P-dimensional polynomial parametrisations.

The key idea is to treat each bin of a histogram as an independent function of the parameter space as iterated above. The parametrisations ${f_\text {MC}(\mathbf {p})}$ all together provide a fast pseudo-generator that yields an approximate response in milliseconds rather than hours. Further, due to the usage of polynomials, the response function is steady. These properties make ${f_\text {MC}(\mathbf {p})}$ suitable for numeric applications.

So far it has been applied with great emphasis and success to the problem of Monte-Carlo generator tuning—essentially a numerical minimisation of a goodness-of-fit measure between real data and ${f_\text {MC}(\mathbf {p})}$. When facing the problem of hypothesis testing of a Monte-Carlo prediction as it is done in this work, the same principle can be applied. The difference being that the axes of the parameter space in this case are the theoretically well-motivated Wilson coefficients which are to be set limits for. In its latest incarnation a C++ version of the core functionality of Professor, i.e. the parametrisation, has been added. It uses Eigen3 to perform the SVD and calculate the approximate ${f_\text {MC}(\mathbf {p})}$.

Table 7 Signal strengths measurements $\mu$ from the ATLAS collaboration used in the Run 1 analysis. In the last five columns the signal compositions are given in terms of efficiencies for production channels assuming a SM Higgs boson

Table 8 Signal strengths measurements $\mu$ from the CMS collaboration used in the Run 1 analysis. In the last five columns the signal compositions are given in terms of efficiencies for production channels assuming a SM Higgs boson

The lowest-order polynomial to incorporate parameter correlations is of second order. For a certain bin, b, at a point $\mathbf {p}$ in parameter space, this can be written as

$$\begin{aligned} \text {MC}_b(\mathbf {p})\approx & {} f^{(b)}(\mathbf {p}) \nonumber \\= & {} \alpha ^{(b)}_0 + \sum _i \beta ^{(b)}_i \, p_i + \sum _{i \le j} \gamma ^{(b)}_{ij} \, p_i \, p_j \end{aligned}$$

(A1)

with the coefficients to be determined ${\alpha _0,\beta _i,\gamma _{ij}}$. The Professor approach to determine the latter is to construct an over-constrained system of equations using the ensemble of bin contents $v^{(b)}_a,\,a\in [1,N]$ obtained when running the MC generator with the parameter settings $\mathbf {p}_a = (x_a, y_a),\,a\in [1,N]$ (“anchors” of the parametrisation).

Fig. 9

Relative uncertainty of the interpolation for the Higgs branching ratios as well as the total width in the dimension six extension of the SM in percent, including uncertainties. Note that due to the dependence on the total width this interpolation is highly non-linear

With the system being overconstrained, the matrix $\tilde{P}$ can be (pseudo-) inverted using the functionality of eigen3. With the pseudo-inverse, ${\tilde{P}}^{-1}$, at hand, the coefficients, $\mathbf {c}^{(b)}$ can be solved for easily by calculating ${\tilde{P}}^{-1}\cdot \mathbf {v}_a$ and the approximation $f^{(b)}(\mathbf {p})$ can be calculated according to Eq. (A1). The fast pseudo-generator is then simply a collection of coefficients $\mathbf {c}^{(b)}$ for all bins, b, of interest.

$$\begin{aligned} \underbrace{ \begin{pmatrix} v_1 \\ v_2 \\ \vdots \\ v_N \end{pmatrix} }_{v^{(b)}_a} = \underbrace{ \begin{pmatrix} 1 &{}\quad x_1 &{}\quad y_1 &{}\quad x^2_1 &{}\quad x_1y_1 &{}\quad y^2_1 \\ 1 &{}\quad x_2 &{}\quad y_2 &{}\quad x^2_2 &{}\quad x_2y_2 &{}\quad y^2_2 \\ &{} &{} &{} \quad \vdots &{} &{} \\ 1 &{}\quad x_N &{}\quad y_N &{}\quad x^2_N &{}\quad x_Ny_N &{}\quad y^2_N \end{pmatrix} }_{\tilde{P}} \underbrace{ \begin{pmatrix} \alpha _0 \\ \beta _x \\ \beta _y \\ \gamma _{xx} \\ \gamma _{xy} \\ \gamma _{yy} \end{pmatrix} }_{\mathbf {c}^{(b)}}\nonumber \\ \end{aligned}$$

(A2)

To show the accuracy with which this procedure works, we show the interpolation of the Higgs branching ratios in Fig. 9, which due to its non-linear character is the most complicated interpolation involved in this work. We reproduce the branching ratios at the per mille level.

Appendix B: LHC Run 1 measurements

The signal strength measurements used in the Run 1 analysis (Sect. 4) are listed in Tables 7 and 8. The values of $\mu$ are given with their total uncertainties, where statistical, systematic and theoretical uncertainties have been added in quadrature. Signal acceptances are given for the production channels gluon fusion (ggH), vector boson fusion (VBF), WH, ZH and $t\bar{t}H$ production.

Appendix C: Pseudo-data used for 14 TeV studies

A summary is given in Figs. 10 and 11 of the pseudo-data used for the evaluation of the LHC’s sensitivity to the set of dimension-six operators considered in this work. The pseudo-data is obtained using the assumptions detailed in Sect. 5. The pseudo-data for 8 TeV has been generated to validate the assumptions made.

Fig. 10

Pseudo-data for the production modes gluon fusion $pp\rightarrow H$ (GF), $W^-H$, $W^+H$, ZH VBF, $t\bar{t}H$ and $pp\rightarrow H+\text {j}$ (from top to bottom) and for the decay channels $H\rightarrow \gamma \gamma$, $H\rightarrow ZZ^* \rightarrow 4l$, $H\rightarrow WW^* \rightarrow 2l2\nu$ and $H\rightarrow \tau ^+\tau ^-$ (from left to right). The pseudo-data for 8 TeV with $L=25~\text {fb}^{-1}$ are shown in blue, the 14 TeV scenarios with $L=300~\text {fb}^{-1}$ and $L=3000~\text {fb}^{-1}$ are shown in green and orange. The inner error bar illustrates the statistical uncertainty and the outer error bar shows the total uncertainty

Fig. 11

Pseudo-data for the production modes gluon fusion ($pp\rightarrow H)$, $W^-H$, $W^+H$, VBF, $t\bar{t}H$ and $pp\rightarrow H+\text {j}$ (from top to bottom) and for the decay channels $H\rightarrow b\bar{b}$, $H\rightarrow \mu ^+\mu ^-$ and $H\rightarrow Z \gamma$ (from left to right). The pseudo-data for 8 TeV with $L=25~\text {fb}^{-1}$ are shown in blue, the 14 TeV scenarios with $L=300~\text {fb}^{-1}$ and $L=3000~\text {fb}^{-1}$ are shown in green and orange. The inner error bar illustrates the statistical uncertainty and the outer error bar shows the total uncertainty