1 Introduction

The gauge/gravity duality contains interesting gravity theories. One of these is known as Lifshitz gravity, which can be dual to scale-invariant field theories, not being conformally invariant. In this context, interesting properties are found when the gauge/gravity duality is generalized to non-relativistic situations [1–13], with the Lifshitz holographic superconductor being one of the best studied systems. Such theories exhibit the anisotropic scale invariance \(t\rightarrow \chi ^{z}t\), \(x\rightarrow \chi x\), with \(z\ne 1\), where z is the relative scale dimension of time and space. Systems with such behavior appear, for instance, in the description of strongly correlated electrons.

In [12] the Lifshitz spacetime at any dimension D was obtained coupling the Proca field to Einstein gravity with a negative cosmological constant; however, it was impossible to construct black holes. On the other hand, electrically charged black holes with massless Maxwell fields are very known at any dimension but these gauge fields are incompatible with the Lifshitz asymptotic. The solution to the problem of constructing charged asymptotically Lifshitz black holes was solved adding the Maxwell action to the described Proca system [14]. In this work, only configurations for the dynamical exponent \(z=2(D-2)\) were found; however, in [15] these configurations were extended to a much more general charged black holes for any value of the dynamical exponent \(z>1\) by considering nonlinear electrodynamics. Very recently, in [16], analytic topological Lifshitz black holes with constant curvature horizon in the presence of a power-law Maxwell field in four and higher dimensions were constructed.

In this work, we consider a matter distribution outside the event horizon of the topological nonlinear charged Lifshitz black hole in 4 dimensions with a spherical and plane transverse section and dynamical exponent z [16]. The matter is parameterized by scalar fields minimally coupled to gravity. Then we obtain numerically the quasinormal frequencies (QNFs) for scalar fields by using the improved AIM [17], which is an improved version of the method proposed in [18, 19] and which has been applied successfully in the context of quasinormal modes (QNMs) for different black hole geometries (see for instance [17, 20–27]). Then we study their stability under scalar perturbations. We focus our study on the dependence of the dynamical exponent, the nonlinear exponent, the angular momentum, and the mass of the scalar field in obtaining overdamped and non-overdamped quasinormal frequencies, mainly, motivated by a recent work, where the authors showed that for \(d > z+1\), at zero momenta, the modes are non-overdamped, whereas for \(d \le z + 1\) the system is always overdamped [24]. This is contrary to other Lifshitz black holes where the QNFs show the absence of a real part [28–34].

On the gravity side of the gauge/gravity duality the QNFs [35–40] provide information as regards the stability of black holes under matter fields that evolve perturbatively in their exterior region; these fields are considered mere test fields, with no backreaction over the spacetime itself. Recently, a study of the stability of a non-Schwarzschild black hole in quadratic gravity was performed in [41]. Also, QNMs have been shown to be related to the area and entropy spectrum of the black hole horizon. Besides, the QNFs determine how fast a thermal state in the boundary theory will reach thermal equilibrium [42] according to the gauge/gravity duality [43], where the relaxation time of a thermal state is proportional to the inverse of the smallest imaginary part of the QNFs of the dual gravity background, which was established due to the QNFs of the black hole being related to the poles of the retarded correlation function of the corresponding perturbations of the dual conformal field theory [44].

The paper is organized as follows. In Sect. 2 we give a brief review of the topological nonlinear charged Lifshitz black holes that we will consider as background. In Sect. 3 we calculate the QNFs of scalar perturbations numerically by using the improved AIM. Finally, our conclusions are in Sect. 4.

2 Topological nonlinear charged Lifshitz black holes

The topological nonlinear charged Lifshitz black holes that we consider are solutions to the Einstein–dilaton gravity in the presence of a power law and two linear Maxwell electromagnetic fields [16]. The action is given by

$$\begin{aligned}&S=-\frac{1}{16\pi }\int _M d^4x\sqrt{-g}\nonumber \\&\quad \times \left( R -2(\nabla \phi )^2-2\Lambda _4+(-e^{-2\lambda _1\phi }F)^p-\sum _{i=2}^3 e^{-2\lambda _i\phi }H_i\right) ,\nonumber \\ \end{aligned}$$
(1)

where R is the Ricci scalar on the manifold M, \(\phi \) is the dilaton field, \(\Lambda _4\) is the cosmological constant, \(\lambda _i\) are constants. F and \(H_i\) are the Maxwell invariants of electromagnetic fields \(F_{\mu \nu }=\partial _{[\mu }A_{\nu ]}\) and \((H_i)_{\mu \nu }=\partial _{[\mu }(B_i)_{\nu ]}\), where \(A_\mu \) and \((B_i)_\mu \) are the electromagnetic potentials. The following metric is the solution for the equations of motion of the theory defined by the action (1):

$$\begin{aligned} \mathrm{d}s^2=-\frac{r^{2z}}{l^{2z}}f(r)\mathrm{d}t^2+\frac{l^2}{r^2}\frac{\mathrm{d}r^2}{f(r)}+r^2\mathrm{d}\Omega _k^2, \end{aligned}$$
(2)

where \(\mathrm{d}\Omega _k^2\) is the metric of the spatial 2-section, which can have positive curvature, \(k=1\), negative curvature, \(k=-1\), or zero curvature, \(k=0\), and

$$\begin{aligned} f(r)=1+\frac{kl^2}{r^2z^2}-\frac{m}{r^{z+2}}+\frac{q^{2p}}{r^{\Gamma _4+z+2}}, \end{aligned}$$
(3)

if the constant \(\Lambda _4\) is

$$\begin{aligned} \Lambda _4=-\frac{(z+1)(z+2)}{2l^2}. \end{aligned}$$
(4)

The gauge field is given by

$$\begin{aligned} F_{rt}=\frac{q_{1}b^{2(z-1)}}{r^{\Gamma _{4}+1}}, \end{aligned}$$
(5)

and the gauge potential by

$$\begin{aligned} A_{t}=-\frac{q_{1}b^{2(z-1)}}{\Gamma _{4}r^{\Gamma _{4}}}, \end{aligned}$$
(6)

where

$$\begin{aligned} q^{2p}=\frac{(2p-1)b^{2(z-1)}}{2\Gamma _4 l^{-2p(z-1)-2}}(2q_1^2)^p, \end{aligned}$$
(7)
$$\begin{aligned} \Gamma _4=z-2+\frac{2}{(2p-1)}, \end{aligned}$$
(8)

with \(q_1\) and b being constants. Also, in order to have a finite mass, \(\Gamma _4\) should be positive, which imposes the following restrictions on p and z:

  • for \(p<1/2\), \(z-1>(3-2p)/(1-2p)\),

  • for \(1/2<p\le 3/2\), all \(z (\ge 1)\) values are allowed,

  • for \(p>3/2\), \(z-1>(2p-3)/(2p-1)\).

3 Quasinormal modes

The Klein–Gordon equation for a scalar field minimally coupled to curvature is

$$\begin{aligned} \frac{1}{\sqrt{-g}}\partial _{\mu }\left( \sqrt{-g}g^{\mu \nu }\partial _{\nu }\right) \psi =m_s^{2}\psi , \end{aligned}$$
(9)

where \(m_s\) is the mass of the scalar field \(\psi \). Thus, the QNMs of scalar perturbations in the background of a four-dimensional topological nonlinear charged Lifshitz black hole are given by the scalar field solution of the Klein–Gordon equation with appropriate boundary conditions. Now, by means of the following ansatz:

$$\begin{aligned} \psi =e^{-i\omega t}R(r)Y(\theta ,\phi ), \end{aligned}$$
(10)

where \(Y(\theta ,\phi )\) is a normalizable harmonic function on the two-sphere which satisfies the eigenvalues equation \(\nabla ^{2}Y(\theta ,\phi )=-QY(\theta ,\phi )\), where \(Q=\ell (\ell +1)\) \(\ell =0,1,2, \ldots \), the Klein–Gordon equation yields

$$\begin{aligned}&\frac{1}{r^{z+3}}\partial _{r}\left[ r^{z+3}f(r)\partial _{r}R\right] \nonumber \\&\quad +\left[ \left( \frac{l}{r}\right) ^{2(z+1)}\frac{\omega ^{2}}{f(r)}-\left( \frac{l}{r}\right) ^{2}\frac{Q}{r^{2}}-\left( \frac{l}{r}\right) ^{2}m_s^{2}\right] R(r)=0.\nonumber \\ \end{aligned}$$
(11)

Also, defining R(r) as

$$\begin{aligned} R(r)=\frac{K(r)}{r}, \end{aligned}$$
(12)

and by using the tortoise coordinate \(r_{*}\) given by

$$\begin{aligned} \mathrm{d}r_{*}=\frac{l^{z+1}\mathrm{d}r}{r^{z+1}f(r)}, \end{aligned}$$
(13)

the Klein–Gordon equation can be written as a one- dimensional Schrödinger equation,

$$\begin{aligned} \frac{d^{2}K(r_{*})}{\mathrm{d}r_{*}^{2}}+\left[ \omega ^{2}-V(r)\right] K(r_{*})=0, \end{aligned}$$
(14)

where the effective potential V(r),

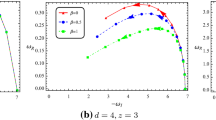
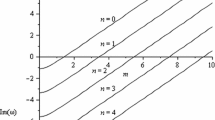
$$\begin{aligned} V(r)=\left( \frac{r}{l}\right) ^{2z}f(r)\left( \frac{(z+1)}{l^2}f(r)+\frac{r}{l^2}f^{\prime }(r)-\frac{Q}{r^2}-m_s^{2}\right) , \end{aligned}$$
(15)

diverges at spatial infinity; see Fig. 1. Therefore, we will consider that the field vanishes at the asymptotic region as a boundary condition or a Dirichlet boundary condition. In Fig. 2 we plot the behavior of the effective potential near the horizon for different values of Q.

Fig. 1
figure 1

The behavior of V(r) with \(l=1\), \(m=1\), \(q_1=0.1\), \(m_s=0.1\), \(b=1\), \(z=2\), \(p=2\), and \(Q=2\)

Full size image
Fig. 2
figure 2

The behavior of V(r) with \(l=1\), \(m=1\), \(q_1=0.1\), \(m_s=0.1\), \(b=1\), \(z=2\), \(p=2\), and \(Q=0, 2, 6, 12, 20\)

Full size image

It is worth mentioning that it is not trivial to find analytical solutions to Eq. (11). Therefore, we will perform numerical studies by using the improved AIM [17]. In order to implement the improved AIM we make the change of variables \(u=1-r_H/r\) in Eq. (9). Then the Klein–Gordon equation yields

$$\begin{aligned}&r_H^{z+1}(1-u)^{1-z}f(u)\partial ^2_uR(u)+r_H^{z+1}(1-u)^{2}\nonumber \\&\quad \times \left( \frac{f^{\prime }(u)}{(1-u)^{1+z}}+\frac{f(u)(1+z)}{(1-u)^{z+2}}\right) \partial _uR(u)\nonumber \\&\quad +\left( \frac{l^{2(z+1)}\omega ^2(1-u)^{z-1}}{r_H^{z-1}f(u)}+\frac{r_H^{z-1}l^2Q}{(1-u)^{z-1}}-\frac{m_s^2r_H^{z+1}l^2}{(1-u)^{z+1}}\right) \nonumber \\&\quad \times R(u)=0. \end{aligned}$$
(16)

Now, in order to propose an ansatz for the scalar field, we must consider its behavior on the event horizon and at spatial infinity. Accordingly, on the horizon, \(u\rightarrow 0\), its behavior is given by

$$\begin{aligned} R\left( u\rightarrow 0\right) \sim C_{1}u^{i\frac{l^{z+1}\omega }{r_H^z f^{\prime }(0)}}+C_{2}u^{-i\frac{l^{z+1}\omega }{r_H^z f^{\prime }(0)}}. \end{aligned}$$
(17)

So, if we consider only ingoing waves on the horizon, we must impose \(C_{1}=0\). Also, asymptotically, from Eq. (16), the scalar field behaves as

$$\begin{aligned}&R \left( u\rightarrow 1\right) \sim D_{1}\left( 1-u\right) ^{1/2(1+(1+z)-\sqrt{(2+z)^2+4m^2l^2})}\nonumber \\&\quad +\,D_{2}\left( 1-u\right) ^{1/2(1+(1+z)+\sqrt{(2+z)^2+4m^2l^2})}. \end{aligned}$$
(18)

So, in order to have a null field at infinity, we must impose \(D_{1}=0 \). Therefore, taking into account these behaviors we define

$$\begin{aligned} R\left( u\right) =u^{-i\frac{l^{z+1}\omega }{r_H^z f^{\prime }(0)}}\left( 1-u\right) ^{1/2(1+(1+z)+\sqrt{(2+z)^2+4m^2l^2})} \end{aligned}$$
(19)

as ansatz. Then, by inserting these fields into Eq. (16), we obtain the homogeneous linear second-order differential equation for the function \(\chi (z)\)

$$\begin{aligned} \chi ^{\prime \prime }=\lambda _{0}(z)\chi ^{\prime }+s_{0}(z)\chi , \end{aligned}$$
(20)

where

$$\begin{aligned}&\lambda _{0}(u)=-\frac{r_H^{-z}}{A_1(-1 + u) u f(u)}\nonumber \\&\quad \times \,(\sqrt{(1+A_2)^2 - 4 B_2}A_1 r_H^z u f(u) - 2i l^{(1 + z)} (u-1) \omega f(u)\nonumber \\&\quad +\, A_1 r_H^z u ((A_2 - z) f(u) + (u-1) f^{\prime }(u))), \end{aligned}$$
(21)
$$\begin{aligned}&s_{0}(z) =-\frac{r_H^{-2(1+z)}}{2 A_1^2 (u-1)^2 u^2 f(u)^2}\nonumber \\&\quad \times (2 A_1^2 l^{2 + 2 z} r_H^2 (1 - u)^{2z} u^2 \omega ^2-2 l^{2 + 2 z} (u-1)^2 \omega ^2\nonumber \\&\quad - 2 i A_1 l^{1 + z} r_H^ z (u-1) \omega \nonumber \\&\quad \times (1 + u (-1 + A_2 + \sqrt{(1 + A_2)^2 - 4 B_2} - z))\nonumber \\&\quad -1-\sqrt{(1 + A_2)^2-4B_2}-2B_2A_2\nonumber \\&\quad +\sqrt{(1+A_2)^2-4B_2}(A_2-z)-z)f(u)^2\nonumber \\&\quad +2 A_1 l^2 r_H^z (-m^2 r_H^2 + Q (u-1)^2) u \nonumber \\&\quad +(r_H^2 (u-1)((1+A_2 +\sqrt{(1+A_2)^2-4B_2}) \nonumber \\&\quad \times A_1 r_H^z u - 2 i l^{1+z} (u-1) \omega ) f^{\prime }(u))), \end{aligned}$$
(22)

where

$$\begin{aligned} A_1=f^{\prime }(0),\quad A_2=1+z,\quad B_2 = -m^2l^2. \end{aligned}$$
(23)

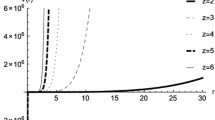
This can be solved numerically (see [27] for more details). So, we choose the parameters \(l=1\), \(m=1\), \(q_1=0.01\), and \(b=1\). Then, in Table 1, we show the fundamental quasinormal frequency and the first overtone for a massive scalar field \(m_s=0.1\) and for a massless scalar field \(m_s=0\) with \(z=2\), \(p=2\), and different values of the angular momentum Q. We can observe that the modes are non-overdamped at zero momenta. Otherwise, the system is always overdamped. Then, in Table 2, we set \(Q=0\) and we show some of the lowest QNFs for \(p=2\), and different values of z for a massive scalar field \(m_s=0.1\) and for a massless scalar field \(m_s=0\). We observe that there is a limit on the dynamical exponent z (\(z\approx 2.3\)), above which the system is always overdamped. Additionally, in Table 3 we show some fundamental QNFs, for \(z=2\), \(Q=0\), and different values of the nonlinear exponent p for a massive scalar field \(m_s=0.1\), and for a massless scalar field \(m_s=0\), where we can observe that the behavior of the modes (overdamped or non-overdamped) do not depend on p. It is worth mentioning that in all the cases analyzed, we observe that the modes have a negative imaginary part, which ensures the stability of four-dimensional topological nonlinear charged Lifshitz black holes with spherical transverse section under scalar perturbations.

Table 1 QNFs for a massive scalar field \(m_s=0.1\) and for a massless scalar field \(m_s=0\) with \(l=1\), \(m=1\), \(q_1=0.1\), \(b=1\), \(z=2\), \(p=2\), and different values of Q
Full size table
Table 2 QNFs for a massive scalar field \(m_s=0.1\) and for a massless scalar field \(m_s=0\) with \(l=1\), \(m=1\), \(q_1=0.1\), \(b=1\), \(p=2\), \(Q=0\), and different values of z
Full size table
Table 3 QNFs for a massive scalar field \(m_s=0.1\) and for a massless scalar field \(m_s=0\) with \(l=1\), \(m=1\), \(q_1=0.1\), \(b=1\), \(z=2\), \(Q=0\), and different values of p
Full size table
Table 4 QNFs for a massive scalar field \(m_s=0.1\) and for a massless scalar field \(m_s=0\) with \(l=1\), \(m=1\), \(q_1=0.1\), \(b=1\), \(z=2\), \(p=2\), and different values of Q. Plane transverse section
Full size table
Table 5 QNFs for a massive scalar field \(m_s=0.1\) and for a massless scalar field \(m_s=0\) with \(l=1\), \(m=1\), \(q_1=0.1\), \(b=1\), \(p=2\), \(Q=0\), and different values of z. Plane transverse section
Full size table
Table 6 QNFs for a massive scalar field \(m_s=0.1\) and for a massless scalar field \(m_s=0\) with \(l=1\), \(m=1\), \(q_1=0.1\), \(b=1\), \(z=2\), \(Q=0\), and different values of p. Plane transverse section
Full size table

The results obtained previously can be generalized for a plane transverse section. The effective potential has a similar behavior on the horizon and at the asymptotic region to the case of a spherical transverse section. Now, in Tables 4, 5, and 6 we show the QNFs for some cases analyzed for the spherical transverse section. Here, in all the cases analyzed, we observe that the system is overdamped with a negative imaginary part, which ensures the stability of four-dimensional topological nonlinear charged Lifshitz black holes with a plane transverse section under scalar perturbations.

4 Concluding comments

In this work we calculated numerically the QNFs of scalar field perturbations for four-dimensional topological nonlinear charged Lifshitz black holes with spherical and plane transverse sections. Then we studied the stability of these black holes under massive and massless scalar field perturbations and we have shown that for all the cases analyzed, the modes have a negative imaginary part, which ensures the stability of four-dimensional topological nonlinear charged Lifshitz black holes with spherical and plane transverse sections under scalar perturbations. Also, it was found that the modes are overdamped, depending heavily on the dynamical exponent and the angular momentum of the scalar field for a spherical transverse section. However, the modes of a four-dimensional topological nonlinear charged Lifshitz black hole with a plane transverse section are always overdamped.