Analysis of the strong coupling constant $G_{D_{s}^{*}D_{s}\phi }$ and the decay width of $D_{s}^{*}\rightarrow D_{s}\gamma$ with QCD sum rules

Abstract

In this article, we calculate the form factors and the coupling constant of the vertex $D_{s}^{*}D_{s}\phi$ using the three-point QCD sum rules. We consider the contributions of the vacuum condensates up to dimension 7 in the operator product expansion. And all possible off-shell cases are considered, $\phi$, $D_{s}$ and $D_{s}^{*}$, resulting in three different form factors. Then we fit the form factors into analytical functions and extrapolate them into time-like regions, which giving the coupling constant for the process. Our analysis indicates that the coupling constant for this vertex is $G_{D_{s}^{*}D{_{s}}\phi }=4.12\pm 0.70\,\mathrm{GeV}^{-1}$. The results of this work are very useful in the other phenomenological analysis. As an application, we calculate the coupling constant for the decay channel $D_{s}^{*}\rightarrow D_{s}\gamma$ and analyze the width of this decay with the assumption of the vector meson dominance of the intermediate $\phi (1020)$. Our final result about the decay width of this decay channel is $\Gamma =0.59\pm 0.15\,\mathrm{keV}$.

1 Introduction

In relativistic heavy ion collisions $J/\psi$ suppression has been recognized as an important tool to identify the possible phase transition to quark–gluon plasma [1]. The dissociation of $J/\psi$ in the quark–gluon plasma due to color screening can lead to a reduction of its production. People usually explained this phenomenon as a process of the $J/\psi$ absorption by $\pi$, $\rho$ or $\phi$ mesons in a meson-exchange model [2–6]. And we can calculate the absorption cross sections based on the interractions among the quarkonia and mesons, where the hadronic coupling constants are basic input parameters. For example, $G_{D_{s}^{*}D_{s}\phi }$ will be used in the absorption process $J/\psi +\phi \rightarrow D_{s}^{*+}+D_{s}^{-}$. A detailed knowledge of this coupling constant is of great importance in understanding the effects of heavy quarkonium absorptions in hadronic matter. Besides, the hadronic coupling constants about the heavy-light mesons can also help us understanding the final-state interactions in the heavy quarkonium decays [7–10]. Furthermore, some exotic mesons have been detected in recent years [11–13], which are beyond the usual quark-model description as $q\overline{q}$ pairs. And people interpret them as quark–gluon hybrids ($q\overline{q}g$), tetraquark states ($q\overline{q}q\overline{q}$), molecular states of two ordinary mesons, glueballs, states with exotic quantum numbers and many others [14–22]. The form factors and coupling constants play an important role in understanding the nature of these exotic mesons. For example, the coupling constants $G_{D_{s}^{*}D_{s}\phi }$ will be used in the analysis about the process $Y(4140)\rightarrow D_{s}^{*-}D_{s}^{+}\rightarrow J/\psi \phi$.

However, the strong coupling constant used in the above questions can not be explained by perturbative theories, because the associate interactions lie in the low energy region. It is fortunate that the QCDSR approach can help us to solve the difficulty. The QCDSR is one of the most powerful non-perturbative methods, which is also independent of model parameters. In recent years, numerous research articles have been reported about the precise determination of the strong form factors and coupling constants via QCDSR, light-cone QCDSR or lattice calculation [23–37]. And many strong coupling constants have been determined by different groups, for example, $D^{*}D_{s}K$, $D{s}^{*}DK$, $B_{c}^{*}B_{c}\Upsilon$, $B_{c}^{*}B_{c}\psi$, $B_{s}^{*}BK$, $J/\psi D_{s}^{*}D_{s}$, $J/\psi D_{s}D_{s}$, $J/\psi D_{s}^{*}D_{s}^{*}$, $D_{s}^{*}D_{s}\eta '$ [23–29, 38–43]. In this work, we use the QCDSR formalism to obtain the coupling constant of the meson vertice $D_{s}^{*}D_{s}\phi$, where the contributions of the vacuum condensates up to dimension 7 in the OPE are considered. The results of this work are very useful in these phenomenological analysis mentioned above.

It is indicated by the BaBar collaboration that $\Gamma (D_{s}^{*})<1.9\,\mathrm{MeV}$ and $\frac{\Gamma (D_{s}^{*}\rightarrow D_{s}\gamma )}{\Gamma _\mathrm{total}}\approx 0.94$ [44]. However, the exact value of the decay width have yet not been determined. A more exact result can help us understanding the nature of the meson and testing the validity of the theoretical model. As an application, we also give an analysis about the decay $D_{s}^{*}\rightarrow D_{s}\gamma$ in the end of this paper, where the electromagnetic coupling constant $G_{D_{s}^{*}D_{s}\gamma }$ will be used. This coupling constant can be easily obtained, when we set $Q^{2}=0$ in the analytical function of coupling constant $G_{D^{*}_{s}D_{s}\phi }(Q^2)$ in Sect. 3.

The outline of this paper is as follows. In Sect. 2, we study the $D_{s}^{*}D_{s}\phi$ vertices using the three-point QCDSR. In order to reduce the uncertainties of the result, we calculate the three-point correlation functions: one with the vector meson $\phi$ off-shell, another with the pseudoscalar meson $D_{s}$ off-shell, and a third one with the vector meson $D^{*}_{s}$ off-shell. Besides of the perturbative contribution, we also consider the contribution of $\langle q\overline{q}\rangle$, $\left\langle \overline{q}g\sigma .Gq\right\rangle$, $\langle g^2G^2\rangle$, $\langle f^3G^3\rangle$, $\langle q\overline{q} \rangle ^2$ and $\langle q\overline{q}\rangle \langle GG\rangle$ at OPE side. In Sect. 3, we present the numerical results and discussions, and Sect. 4 is reserved for our conclusions.

2 QCD sum rules for the $D_{s}^{*}D_{s}\phi$

In this work, the $D_{s}^{*}D_{s}\phi$ is a vector-pseudoscalar-vector (VPV) vertex. With each meson off-shell, we write down the three-point correlation functions:

$$\begin{aligned} \Pi _{\mu \nu }^{\phi }(p,p^{\prime })= & {} i^{2}\int \mathrm{d}^{4} x\mathrm{d}^{4}y\mathrm{e}^{ip^{\prime }.x+i(p-p^{\prime }).y}\nonumber \\&\times \langle 0|T\{J_{5}(x)j_{\mu }(y)J_{\nu }^{\dagger }(0)\}|0\rangle \end{aligned}$$

(1)

$$\begin{aligned} \Pi _{\mu \nu }^{D_{s}}(p,p^{\prime })= & {} i^{2}\int \mathrm{d}^{4}x\mathrm{d}^{4}y\mathrm{e}^{ip^{\prime }.x+i(p-p^{\prime }).y}\nonumber \\&\times \langle 0|T\{J_{\nu }(x)J_{5}(y)j_{\mu }^{\dagger }(0)\}|0\rangle \end{aligned}$$

(2)

$$\begin{aligned} \Pi _{\mu \nu }^{D^{*}_{s}}(p,p^{\prime })= & {} i^{2}\int \mathrm{d}^{4} x\mathrm{d}^{4}y\mathrm{e}^{ip^{\prime }.x+i(p-p^{\prime }).y}\nonumber \\&\times \langle 0|T\{j_{\mu }(x)J_{\nu }(y)J_{5}^{\dagger }(0)\}|0\rangle \end{aligned}$$

(3)

where T is the time ordered product and $J_{\nu }^{\dagger }(x)$, $J_{5}(x)$ and $j_{\mu }(x)$ are the interpolating currents of the mesons $D_{s}^{*}$, $D_{s}$ and $\phi$ respectively:

$$\begin{aligned}&J_{\nu }^{\dagger }(x)=\bar{s}(x)\gamma _{\nu }c(x) \end{aligned}$$

(4)

$$\begin{aligned}&J_{5}(x)=\bar{c}(x)i\gamma _{5}s(x) \end{aligned}$$

(5)

$$\begin{aligned}&j_{\mu }(x)=\bar{s}(x)\gamma _{\mu }s(x) \end{aligned}$$

(6)

According to the QCDSR, these correlation functions can be calculated in two different ways: using hadron degrees of freedom, called the phenomenological side, or using quark degrees of freedom, called the OPE side. In the following we will obtain the sum rule according to above formulations.

2.1 The phenomenological side

We insert a complete set of intermediate hadronic states with the same quantum numbers as the current operators $J_{\nu }^{\dagger }(x)$, $J_{5}(x)$ and $j_{\mu }(x)$ into the correlation functions $\Pi _{\mu \nu }^{\phi }(p,p^{\prime })$, $\Pi _{\mu \nu }^{D_{s}}(p,p^{\prime })$ and $\Pi _{\mu \nu }^{D^{*}_{s}}(p,p^{\prime })$ to obtain the phenomenological representations. After isolating the ground-state contributions, we get the following functions for the mesons $\phi$, $D_{s}$ and $D^{*}_{s}$ off-shell cases.

$$\begin{aligned}&\Pi _{\mu \nu }^{\mathrm{phen}(\phi )}=\frac{-CG_{D_{s}^{*}D_{s}\phi }^{(\phi )} (q^{2})p^{\alpha }p^{\prime \beta }\varepsilon _{\mu \nu \alpha \beta }}{(m_{D_{s}^{*}}^{2}-p^{2})(m_{\phi }^{2}-q^{2})(m_{D_{s}}^{2}-p^{\prime 2})}+h.r.\end{aligned}$$

(7)

$$\begin{aligned}&\Pi _{\mu \nu }^{\mathrm{phen}(D_{s})}=\frac{-CG_{D_{s}^{*}D_{s}\phi }^{(D_{s})} (q^{2})p^{\alpha }p^{\prime \beta }\varepsilon _{\mu \nu \alpha \beta }}{(m_{\phi }^{2}-p^{2})(m_{D_{s}}^{2}-q^{2})(m_{D_{s}^{*}}^{2}-p^{\prime 2})}+h.r. \nonumber \\\end{aligned}$$

(8)

$$\begin{aligned}&\Pi _{\mu \nu }^{\mathrm{phen}(D_{s}^{*})}=\frac{-CG_{D_{s}^{*}D_{s}\phi } ^{(D_{s}^{*})}(q^{2})p^{\alpha }p^{\prime \beta }\varepsilon _{\mu \nu \alpha \beta }}{(m_{D_{s}}^{2}-p^{2})(m_{D_{s}^{*}}^{2}-q^{2})(m_{\phi }^{2}-p^{\prime 2})}+h.r.\nonumber \\ \end{aligned}$$

(9)

where $C=\frac{f_{D_{s}}m_{D_{s}}^{2}f_{D_{s}^{*}}m_{D_{s}^{*} }f_{\phi }m_{\phi }}{(m_{s}+m_{c})}$ and h.r. stand for the contributions of higher resonances and continuum states of each meaon. And in the derivation, we have used the following effective Lagrangian $\pounds$ and definitions for the decay constants $f_{D_{s}^{*}}$, $f_{D_{s}}$ and $f_{\phi }$:

$$\begin{aligned}&\pounds =G_{D_{s}^{*}D_{s}\phi }\varepsilon _{\alpha \beta \lambda \tau }(\partial ^{\alpha }D_{s}^{*+ \beta }D_{s}^{-}\partial ^{\lambda }+\partial ^{\alpha }D_{s}^{*- \beta }D_{s}^{+}\partial ^{\lambda })\phi ^{\tau } \nonumber \\\end{aligned}$$

(10)

$$\begin{aligned}&\langle 0|J_{\nu }(0)|D_{s}^{*}(p)\rangle =f_{D_{s}^{*} }m_{D_{s}^{*}}\zeta _{\nu }\end{aligned}$$

(11)

$$\begin{aligned}&\langle 0|J_{5}(0)|D_{s}(p^{\prime })\rangle =f_{D_{s}}m_{D_{s} }^{2}/(m_{s}+m_{c})\end{aligned}$$

(12)

$$\begin{aligned}&\langle 0|j_{\mu }(0)|\phi (q)\rangle =f_{\phi }m_{\phi }\xi _{\mu } \end{aligned}$$

(13)

where $\zeta _{\nu }$ and $\xi _{\mu }$ are the polarization vectors:

$$\begin{aligned} \xi _{\mu }\xi ^{\tau }=-g_{\mu \tau }+\frac{q_{\mu }q_{\tau }}{ q^{2}}\end{aligned}$$

(14)

$$\begin{aligned} \zeta _{\nu }\zeta ^{\beta }=-g_{\nu \beta }+\frac{p_{\nu }p_{\beta }}{p^{2}} \end{aligned}$$

(15)

From Eqs. (8)–(10), we can see that there is only one tensor structure to work within the formalism of the QCDSR.

2.2 The OPE side

Now, we briefly outline the operator product expansion for the correlation functions Eqs. (1)–(3). Firstly, we contract the quark fields in the correlation functions with Wich’s theorem.

$$\begin{aligned}&\Pi _{\mu \nu }^{(\phi ) }=-i^{2}\int \mathrm{d}^{4}x\mathrm{d}^{4}y\mathrm{e}^{ip^{\prime }x+i(p-p^{\prime })y}\mathrm{tr}\nonumber \\&\qquad \quad \times \{i\gamma _{5}s^{mn}(x-y)\gamma _{\mu }s^{nk}(y-0)\gamma _{\nu }c^{km}(0-x)\} \end{aligned}$$

(16)

$$\begin{aligned}&\Pi _{\mu \nu }^{(D_{s})}=-i^{2}\int \mathrm{d}^{4}x\mathrm{d}^{4}y\mathrm{e}^{ip^{\prime }x+i(p-p^{\prime })y}\mathrm{tr}\nonumber \\&\qquad \quad \times \{\gamma _{\nu }c^{mn}(x-y)i\gamma _{5}s^{nk}(y-0)\gamma _{\mu }s^{km}(0-x)\} \end{aligned}$$

(17)

$$\begin{aligned}&\Pi _{\mu \nu }^{(D_{s}^{*})}=-i^{2}\int \mathrm{d}^{4}x\mathrm{d}^{4}y\mathrm{e}^{ip^{\prime }x+i(p-p^{\prime })y} \mathrm{tr}\nonumber \\&\qquad \quad \times \{\gamma _{\mu }s^{mn}(x-y)\gamma _{\nu }c^{nk}(y-0)i\gamma _{5}s^{km}(0-x)\} \end{aligned}$$

(18)

Then, we replace the c and s quark propagators $c^{ij}(x)$ and $s^{ij}(x)$ with the corresponding full propagators [45–47],

$$\begin{aligned} S_{ij}(x)= & {} \frac{i\delta _{ij}x \!\!\!/}{2\pi ^{2}x^{4}}-\frac{\delta _{ij}m_{s}}{ 4\pi ^{2}x^{4}}-\frac{\delta _{ij}\langle \overline{s}s\rangle }{ 12}+\frac{i\delta _{ij}x\!\!\!/ m_{s}\langle \overline{s}s\rangle }{48}\nonumber \\&-\frac{\delta _{ij}x^{2}\langle \overline{s}g_{s}\sigma Gs\rangle }{192}+\frac{i\delta _{ij}x^{2}x\!\!\!/ m_{s}\langle \overline{s}g_{s}\sigma Gs\rangle }{1152}\nonumber \\&-\frac{ig_{s}G_{\alpha \beta }^{a}t_{ij}^{a}(x\!\!\!/ \sigma ^{\alpha \beta }+\sigma ^{\alpha \beta }x\!\!\!/)}{32\pi ^{2}x^{2}}-\frac{i\delta _{ij}x^{2}x\!\!\!/g_{s}^{2}\langle \overline{s}s\rangle ^{2}}{7776}\nonumber \\&-\frac{\delta _{ij}x^{4}\langle \overline{s}s\rangle \langle g_{s}^{2}GG\rangle }{27648}-\frac{\langle \overline{s}_{j}\sigma ^{\mu \nu }s_{i}\rangle \sigma _{\mu \nu }}{8}\nonumber \\&-\frac{\langle \overline{s}_{j}\gamma ^{\mu }s_{i}\rangle \gamma _{\mu }}{4}+\cdots , \end{aligned}$$

(19)

$$\begin{aligned} C_{ij}(x)= & {} \frac{i}{(2\pi )^{4}}\int \mathrm{d}^{4}k\mathrm{e}^{-ik.x}\nonumber \\&\times \left\{ \frac{\delta _{ij}}{ k-m_{c}}-\frac{g_{s}G_{\alpha \beta }^{n}t_{ij}^{n}}{4}\frac{\sigma ^{\alpha \beta }(k\!\!\!/+m_{c})+(k\!\!\!/+m_{c})\sigma ^{\alpha \beta }}{(k^{2}-m_{c}^{2})^{2}}\right. \nonumber \\&+\frac{g_{s}D_{\alpha }G_{\beta \lambda }^{n}t_{ij}^{n}(f^{\lambda \beta \alpha }+f^{\lambda \alpha \beta })}{3(k^{2}-m_{c}^{2})^{4}}\nonumber \\&\left. -\frac{g_{s}^{2}(t^{a}t^{b})_{ij}G_{\alpha \beta }^{a}G_{\mu \nu }^{b}(f^{\alpha \beta \mu \nu }\!+\!f^{\alpha \mu \beta \nu }+f^{\alpha \mu \nu \beta })}{4(k^{2}\!-\!m_{c}^{2})^{5}}\!+\!\cdot \cdot \cdot \right\} ,\nonumber \\ \end{aligned}$$

(20)

(21)

(22)

where $\langle g^{2}_{s}GG \rangle =\langle g^{2}_{s}G^{n}_{\alpha \beta }G^{n\alpha \beta } \rangle$, $t^{n}=\frac{\lambda ^{n}}{2}$, the $\lambda ^{n}$ is the Gell–Mann matrix, $D_{\alpha }=\partial _{\alpha }-ig_{s}G^{n}_{\alpha }t^{n}$, and the i, j are color indices. Then we compute the integrals both in the coordinate and momentum spaces, and obtain the correlation functions. Finally, the correlation functions can be divided into two parts:

$$\begin{aligned} \Pi _{\mu \nu }^{\mathrm{OPE}(M)}=\Pi _{\mu \nu }^{\mathrm{pert}(M)}+\Pi _{\mu \nu }^{\mathrm{non}{\text {-}}\mathrm{pert}(M)} \end{aligned}$$

(23)

where M is the off-shell meson ($M=\phi ,D_{s},D^{*}_{s}$). Using dispersion relations, the perturbative term for a given meson M off-shell can be written in the following form:

$$\begin{aligned}&\Pi _{\mu \nu }^{\mathrm{pert}(M)}(p,p^{\prime })\nonumber \\&\quad =-\frac{1}{4\pi ^{2}}\int _{s_{1}}^{s_{0}} \int _{u_{1}}^{u_{0}}\frac{\rho _{\mu \nu }^{\mathrm{pert}(M)}(s,u,q^{2})}{(s-p^{2} )(u-p^{\prime 2})}\mathrm{d}s\mathrm{d}u \end{aligned}$$

(24)

Fig. 1

The perturbative contributions for $\phi$, $D_{s}$ and $D_{s}^{*}$ off-shell. The dashed lines denote the Cutkosky cuts

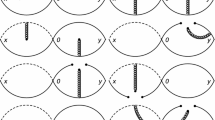
and the quantities $s=p^{2}$, $u=p'^2$ and $q=p-p'$. We put all quark lines on mass shell using Cutkosky’s rules (Fig.1a, b) and obtain the spectral density $\rho _{\mu \nu }^{pert(M)}(s,u,q^{2})$

$$\begin{aligned}&\rho _{\mu \nu }^{\mathrm{pert}(\phi )}(s,u,q^{2})\nonumber \\&\quad =-\frac{3}{\sqrt{\lambda }}\left[ (m_{c} \!-\!m_{s})\frac{q^{2}(s\!+\!u\!-\!q^{2}\!+\!2m_{s}^{2}\!-\!2m_{c}^{2})}{\lambda (s,u,q^{2})} \!-\!m_{s}\right] \nonumber \\&\qquad \times \varepsilon _{\mu \nu \alpha \beta }p^{\alpha }p^{\prime \beta } \end{aligned}$$

(25)

$$\begin{aligned}&\rho _{\mu \nu }^{\mathrm{pert}(D_{s})}(s,u,q^{2})=-\frac{3}{\sqrt{\lambda }}\left[ (m_{c} -m_{s})\right. \nonumber \\&\qquad \left. \times \frac{(u-q^{2})(s+u-q^{2})-2s(u+m_{c}^{2}-m_{s}^{2})}{\lambda (s,u,q^{2})}-m_{c}\right] \nonumber \\&\qquad \times \varepsilon _{\mu \nu \alpha \beta }p^{\alpha }p^{\prime \beta }\end{aligned}$$

(26)

$$\begin{aligned}&\rho _{\mu \nu }^{\mathrm{pert}(D_{s}^{*})}(s,u,q^{2})=-\frac{3}{\sqrt{\lambda }}\bigg [(m_{c}-m_{s})\nonumber \\&\qquad \times \frac{u(s\!+\!u\!-\!q^{2})\!-\!2u(m_{c}^{2}\!-\!m_{s}^{2}\!+\!u\!-\!q^{2})}{\lambda (s,u,q^{2})}\!-\!m_{s}\bigg ]\varepsilon _{\mu \nu \alpha \beta }p^{\alpha } p^{\prime \beta }\nonumber \\ \end{aligned}$$

(27)

Fig. 2

Contributions of the condensate parts $\langle g^2G^2\rangle$ and $\langle f^3G^3\rangle$ for $\phi$ off-shell case

where $\lambda (s,u,q^{2})=(s+u-q^{2})^{2}-4su$. As to the non-perturbative contributions, we take into account the contribution of $\langle s\overline{s}\rangle$, $\left\langle \overline{s}g\sigma .Gs\right\rangle$, $\langle g^2G^2\rangle$, $\langle f^3G^3\rangle$, $\langle s\overline{s} \rangle ^2$ and $\langle s\overline{s}\rangle \langle GG\rangle$, which are showed explicitly in Figs. 2 and 3. It should be noticed that as the consequence of the use of the double Borel transform, the $\phi$ off-shell case has only the contributions of $\langle g^2G^2\rangle$ and $\langle f^3G^3\rangle$ (Fig. 2). Full expressions for these contributions of Figs. 2 and 3 for $\phi$, $D_{s}$ and $D^{*}_{s}$ off-shell cases can be found in Appendix A, B and C, where the following representations will be used:

$$\begin{aligned}&N_{m_{1}m_{2}m_{3}}^{abc}=\frac{(-1)^{a+b+c}\pi ^{2}i}{\Gamma (a)\Gamma (b)\Gamma (c)(M_{1}^{2})^{b}(M_{2}^{2})^{c}(M^{2})^{a-2}}\nonumber \\&\quad \times \int _{0}^{\infty }\mathrm{d}\tau (\tau +1)^{a+b+c-4}\tau ^{1-b-c} \exp \left\{ -\frac{1}{\tau }\frac{Q^{2}}{M_{1}^{2}+M_{2}^{2}}\right. \nonumber \\&\quad \left. -\,\frac{(\tau \!+\!1)m_{1}^{2}}{M^{2}}\!-\!\frac{(\tau \!+\!1)m_{2}^{2}}{\tau M_{1}^{2}}\!-\!\frac{(\tau \!+\!1)m_{3}^{2}}{\tau M_{2}^{2}}\right\} \end{aligned}$$

(28)

$$\begin{aligned}&I_{m_{1}m_{2}m_{3}}^{abc}=\frac{(-1)^{a+b+c}\pi ^{2}i}{\Gamma (a)\Gamma (b)\Gamma (c)(M_{1}^{2})^{b}(M_{2}^{2})^{c+1}(M^{2})^{a-3}}\nonumber \\&\quad \times \int _{0}^{\infty }\mathrm{d}\tau (\tau +1)^{a+b+c-5}\tau ^{1-b-c}\exp \left\{ -\frac{1}{\tau }\frac{Q^{2}}{M_{1}^{2}+M_{2}^{2}}\right. \nonumber \\&\quad \left. -\frac{(\tau +1)m_{1}^{2}}{M^{2}}\right. \left. -\frac{(\tau +1)m_{2}^{2}}{\tau M_{1}^{2}}-\frac{(\tau +1)m_{3}^{2}}{\tau M_{2}^{2}}\right\} \end{aligned}$$

(29)

$$\begin{aligned}&\widetilde{I}_{m_{1}m_{2}m_{3}}^{abc}=\frac{(-1)^{a+b+c}\pi ^{2}i}{\Gamma (a)\Gamma (b)\Gamma (c)(M_{1}^{2})^{b+1}(M_{2}^{2})^{c}(M^{2})^{a-3}}\nonumber \\&\quad \times \int _{0}^{\infty }\mathrm{d}\tau (\tau +1)^{a+b+c-5}\tau ^{1-b-c}\exp \left\{ -\frac{1}{\tau }\frac{Q^{2}}{M_{1}^{2}+M_{2}^{2}}\right. \nonumber \\&\quad \left. -\frac{(\tau +1)m_{1}^{2}}{M^{2}}\right. \left. -\frac{(\tau +1)m_{2}^{2}}{\tau M_{1}^{2}}-\frac{(\tau +1)m_{3}^{2}}{\tau M_{2}^{2}}\right\} \end{aligned}$$

(30)

Fig. 3

Contributions of the non-perturbative parts for $D_{s}(D_{s}^{*})$ off-shell case

2.3 The coupling constant and the meson decay

We make the change of variables $p^{2}\rightarrow -P^{2}$,$p'^{2}\rightarrow -P'^{2}$ and $q^{2}\rightarrow -Q^{2}$ and perform a double Borel transform [48] to the physical as well as the OPE sides, which involves the transformation: $P^{2}\rightarrow M_{1}^{2}$ and $P'^{2}\rightarrow M_{2}^{2}$, where $M_{1}$ and $M_{2}$ are the Borel parameters. Then, we equate the phenomenological and OPE sides, invoking the quark-hadron duality from which the sum rule is obtained.

In order to eliminate the h.r. terms from the phenomenological side in Eqs. (8)–(10), two continuum threshold parameters $s_{0}$ and $u_{0}$ in the OPE side are introduced. These parameters fulfill the following relations: $m_{i}^{2}<s_{0}<m_{i}'^{2}$ and $m_{o}^{2}<u_{0}<m_{o}'^{2}$, where $m_{i}$ and $m_{o}$ are the masses of the incoming and out-coming mesons respectively and $m'$ is the mass of the first excited state of these mesons. After these performations, the form factors can be written as:

$$\begin{aligned} G_{D_{s}^{*}D_{s}\phi }^{\phi }(Q^{2})= & {} \frac{-\frac{1}{4\pi ^{2}M_{1}^{2}M_{2}^{2}}\int _{s_{1}}^{s_{0}}\int _{u_{1}}^{u_{0}}\rho ^{\mathrm{pert}(\phi )}(s,u,Q^{2})\mathrm{e}^{-\frac{s}{M_{1}^{2}}}\mathrm{e}^{-\frac{u}{M_{2}^{2}} }\mathrm{d}s\mathrm{d}u+\fancyscript{BB}[\Pi ^{\mathrm{non}{\text {-}}\mathrm{pert}(\phi )}]}{\frac{C}{(Q^{2}+m_{\phi }^{2})M_{1}^{2}M_{2}^{2}}\mathrm{e}^{-m_{D_{s}^{*}}^{2}/M_{1}^{2}}\mathrm{e}^{-m_{D_{s}}^{2}/M_{2}^{2}}},\end{aligned}$$

(31)

$$\begin{aligned} G_{D_{s}^{*}D_{s}\phi }^{D_{s}}(Q^{2})= & {} \frac{-\frac{1}{4\pi ^{2}M_{1}^{2}M_{2}^{2}}\int _{s_{1}}^{s_{0}}\int _{u_{1}}^{u_{0}}\rho ^{\mathrm{pert}(D_{s})}(s,u,Q^{2})\mathrm{e}^{-\frac{s}{M_{1}^{2}}}\mathrm{e}^{-\frac{u}{M_{2}^{2}} }\mathrm{d}s\mathrm{d}u+\fancyscript{BB}[\Pi ^{\mathrm{non}{\text {-}}\mathrm{pert}(D_{s})}]}{\frac{C}{ (Q^{2}+m_{D_{s}}^{2})M_{1}^{2}M_{2}^{2}}\mathrm{e}^{-m_{\phi }^{2}/M_{1}^{2}}\mathrm{e}^{-m_{D_{s}^{*}}^{2}/M_{2}^{2}}},\end{aligned}$$

(32)

$$\begin{aligned} G_{D_{s}^{*}D_{s}\phi }^{D_{s}^{*}}(Q^{2})= & {} \frac{-\frac{1}{4\pi ^{2}M_{1}^{2}M_{2}^{2}}\int _{s_{1}}^{s_{0}}\int _{u_{1}}^{u_{0}}\rho ^{\mathrm{pert}(D_{s}^{*})}(s,u,Q^{2})\mathrm{e}^{-\frac{s}{M_{1}^{2}}}\mathrm{e}^{-\frac{u}{ M_{2}^{2}}}\mathrm{d}s\mathrm{d}u+\fancyscript{BB}[\Pi ^{\mathrm{non}{\text {-}}\mathrm{pert}(D_{s}^{*})}]}{\frac{C}{ (Q^{2}+m_{D_{s}^{*}}^{2})M_{1}^{2}M_{2}^{2}} \mathrm{e}^{-m_{D_{s}}^{2}/M_{1}^{2}}\mathrm{e}^{-m_{\phi }^{2}/M_{2}^{2}}}, \end{aligned}$$

(33)

where $\fancyscript{BB}[\;\;]$ stands for the double Borel transform. Now, we can calculate the form factors in the space-like region according to these above equations. However, in order to obtain the coupling constants, it is necessary to extrapolate these results into physical regions $(Q^{2}<0)$, which is realized by fit the form factors into suitable analytical functions. It is indicated that we should get the same values for the coupling constants $G^{\phi }_{D_{s}^{*}D_{s}\phi }$, $G^{D_{s}}_{D_{s}^{*}D_{s}\phi }$ and $G^{D_{s}^{*}}_{D_{s}^{*}D_{s}\phi }$ [49], when we take $Q^{2}=-m_{\phi }^{2}$, $Q^{2}=-m_{D_{s}}^{2}$ and $Q^{2}=-m_{D_{s}^{*}}^{2}$ separately. This above procedure is used to minimize the uncertainties in the calculation of the coupling constant, which will be quite clear in the following section.

With the assumption of the vector meson dominance($\phi (1020)$), the radiative decays $D_{s}^{*}\rightarrow D_{s}\gamma$ can be described by the following electromagnetic lagrangian $\pounds '$,

$$\begin{aligned} \pounds '=-eQ_{s}\overline{s}\gamma _{\mu }sA^{\mu } \end{aligned}$$

(34)

where the $A_{\mu }$, $Q_{s}$ are the electromagnetic field and the charge number. From the lagrangian $\pounds '$, we can obtain the decay amplitude [50, 51],

$$\begin{aligned}&\langle D_{s}(p)\gamma (q,\varepsilon )|D_{s}^{*}(p^{\prime },\xi )\rangle \nonumber \\&\quad =\langle \gamma (q,\varepsilon )|\phi (q,\eta )\rangle \frac{i}{ q^{2}-m_{\phi }^{2}}\langle D_{s}(p)\phi (q,\eta )|D_{s}^{*}(p^{\prime },\xi )\rangle \nonumber \\&\quad =\langle D_{s}(p)\phi (q,\eta )|D_{s}^{*}(p^{\prime },\xi )\rangle \frac{i}{q^{2}\!-\!m_{\phi }^{2}}f_{\phi }m_{\phi }eQ_{s}(-i)\varepsilon _{\mu }^{*}\eta ^{\mu }\nonumber \\&\quad =G_{D_{s}^{*}D_{s}\gamma }\epsilon ^{\alpha \beta \lambda \tau }p_{\alpha }^{\prime }q_{\lambda }\xi _{\beta }\eta _{\tau }^{*}\frac{i}{q^{2}-m_{\phi }^{2}}f_{\phi }m_{\phi }eQ_{s}(-i)\varepsilon _{\mu }^{*}\eta ^{\mu }\nonumber \\ \end{aligned}$$

(35)

The parameters $G_{D_{s}^{*}D_{s}\gamma }$ and $f_{\phi }$ are the coupling constant and the weak decay constant, respectively. $p_{\alpha }'$ and $q_{\lambda }$ are the four momenta of the $D_{s}$ and $\gamma$. $\eta ^{\mu }$, $\varepsilon ^{*}_{\mu }$ and $\xi _{\beta }$ are the polarization vectors of the $\phi$, $\gamma$ and $D^{*}_{s}$, respectively. The strong coupling constant $G_{D_{s}^{*}D_{s}\gamma }$ can be related to the effective coupling constant in the heavy quark effective Lagrangian by Eq. (10) in this paper.

3 Results and discussions

Present section is devoted to the numerical analysis of the sum rules for the coupling constants. The decay constants and hadronic parameters used in this work are taken as $f_{\phi }=0.229\pm 0.003$ [52], $f_{D_{s}}=0.257\pm 0.006$ [52], $f_{D_{s}^{*}}=0.301\pm 0.013$ [52], $m_{\phi }=1.019\pm 0.020\,\mathrm{GeV}$ [52], $m_{D_{s}}=1.968\pm 0.00032\,\mathrm{GeV}$ [52], $m_{D_{s}^{*}}=2.112\pm 0.0005\,\mathrm{GeV}$ [52]. The vacuum condensates are taken to be the standard values $\langle \overline{s}s\rangle =-(0.8\pm 0.1)\times (0.24\pm 0.01\,\mathrm{GeV})^3$ [48, 53], $\langle \overline{s}g_{s}\sigma Gs\rangle =m_{0}^{2}<\overline{s}s>$ [48, 53], $m_{0}^{2}=(0.8\pm 0.1)\,\mathrm{GeV}^2$, $\langle g_{s}^{2}GG \rangle =(0.022\pm 0.004)\,\mathrm{GeV}^4$ [54–56], $\langle f^3G^3 \rangle =(8.8\pm 5.5)\,\mathrm{GeV}^{2}\langle g_{s}^{2}GG\rangle$ [54–56]. And we also take the masses of quark $m_{c}=(1.275\pm 0.025)\,\mathrm{GeV}$, $m_{s}=0.095\pm 0.005\,\mathrm{GeV}$ from the Particle Data Group [52].

From Eqs. (31)–(33), we also know that the value of the form factor $G_{D_{s}^{*}D_{s}\phi }$ is the function of the input parameters, including the Borel parameters $M_{1}^{2}$ and $M_{2}^{2}$, the continuum thresholds $s_{0}$ and $u_{0}$, the momentum $Q^2$. The working regions for the $M_{1}^{2}$ and $M_{2}^{2}$ are determined by requiring not only that the contributions of the higher states and continuum be effectively suppressed, but also that the contributions of the higher-dimensional operators are small. In other words, we should find a good plateau which will ensure OPE convergence and the stability of our results [48]. The plateau is often called “Borel window”. In addition, the continuum parameters, $s_{0}=(m_{i}+\bigtriangleup _{i})^{2}$ and $u_{0}=(m_{o}+\bigtriangleup _{o})^{2}$ are employed to include the pole and to suppress the h.r. contributions for the cases of $\phi$, $D_{s}$ and $D_{s}^{*}$ mesons off-shell. The values for $\triangle _{\phi }$, $\triangle _{D_{s}}$ and $\triangle _{D_{s}^{*}}$ can not be far from the experimental value of the distance between the pole and the first excited state [48]. In general, these two continuum thresholds $s_{0}$ and $u_{0}$ are determined by the relations $s_{0}\sim (m_{i}+0.5\,\mathrm{GeV})^{2}$ and $u_{0}\sim (m_{o}+0.5\,\mathrm{GeV})^{2}$.

Fig. 4

The strong form factor, $G_{D_{s}^{*}D_{s}\phi }$ on Borel parameter $M_{2}^{2}$, in the different values of $s_{0}$ and $u_{0}$, for the off-shell $\phi$ meson

Fig. 5

Pole and continuum contributions for the $\phi$ off-shell, on Borel parameter $M_{1}^{2}$ (a) and $M_{2}^{2}$ (b)

The form factor $G^{\phi }_{D_{s}^{*}D_{s}\phi }$ on Borel parameter $M_{2}^{2}$ in the different values of $s_{0}$ and $u_{0}$ for the off-shell $\phi$ meson are shown in Fig.  4. It can be seen that the results have more stability with $s_{0}=6.9\,\mathrm{GeV}^2$($\bigtriangleup _{D_{s}^{*}}\approx 0.5\,\mathrm{GeV}$) and $u_{0}=6.1\,\mathrm{GeV}^2$($\bigtriangleup _{D_{s}}\approx 0.5\,\mathrm{GeV}$). In Fig.  5 we show also the relative continumm versus pole contribution, from where we clearly see that the pole contribution is bigger than the continuum contribution for $M^2<6.3\,\mathrm{GeV}^2$. Thus, we use the Borel region $5.0\le M_{1}^{2}\le 7.0\,\mathrm{GeV}^2$ and $5.0\le M_{2}^{2}\le 7.0\,\mathrm{GeV}^2$ ($Q^2=3.0\,\mathrm{GeV}^2$) for $\phi$ off-shell. According to the same analysis with $\phi$ off-shell, we choose the Borel window $6.0\le M_{1}^{2}\le 8.0\,\mathrm{GeV}^2$ and $6.0\le M_{2}^{2}\le 8.0\,\mathrm{GeV}^2$ ($Q^2=1.0\,\mathrm{GeV}^2$) for $D_{s}$ and $D_{s}^{*}$ off-shell with $\bigtriangleup _{\phi }= \bigtriangleup _{D_{s}}=\bigtriangleup _{D_{s}^{*}}=0.5\,\mathrm{GeV}$.

Fig. 6

The contributions of different condensate terms in the OPE with variations of the Borel parameters $M_{1}^{2}$ and $M_{2}^{2}$ for $\phi$ (a, b), $D_{s}$ (c, d) and $D_{s}^{*}$ (e, f) off-shell, where A–H denote the perturbative term,$\langle g^2G^2\rangle$, $\langle f^3G^3\rangle$, $\langle s\overline{s}\rangle$, $\langle \overline{s}g\sigma .Gs\rangle$, $\langle s\overline{s} \rangle ^2$, $\langle s\overline{s}\rangle \langle GG\rangle$ and total contributions

In Fig.  6, we show explicitly the contributions of different condensate terms in the OPE with variations of the Borel parameters $M_{1}^{2}$ and $M_{2}^{2}$ for $\phi$, $D_{s}$ and $D_{s}^{*}$ off-shell. From the figure, we can see that the values are rather stable with variations of the Borel parameters, it is reliable to extract the form factors. Besides of the perturbative term, we can also see that $\langle s\overline{s}\rangle$ give a considerable contribution for $D_{s}$ and $D_{s}^{*}$ off-shell cases (Fig.6c–f). And the contributions of the other condensate terms are small ($<1\,\%$). To the case of $\phi$ off-shell, condensate parts $\langle g^2G^2\rangle$ and $\langle f^3G^3\rangle$ make up $1{-}2\,\%$ of the total contributions. It should be noticed that although these condensates terms, all except for the perturbative term and $\langle s\overline{s}\rangle$, give small contributions to the form factors, they have a significant influence on the following analytical functions (Eqs. (36)–(38)), which are obtained by numerical fitting. Thus, these condensates contributions should not be neglected in the calculation.

Fig. 7

Form factors of the $D_{s}^{*}D_{s}\phi$ vertex for $\phi$ off-shell (a), $D_{s}$ off-shell (b) and $D_{s}^{*}$ off-shell (c)

The form factors $G^{\phi }_{D_{s}^{*}D_{s}\phi }$, $G^{D_{s}}_{D_{s}^{*}D_{s}\phi }$ and $G^{D_{s}^{*}}_{D_{s}^{*}D_{s}\phi }$ are shown explicitly in Fig. 7 and are fitted into the following analytical functions:

$$\begin{aligned}&G^{\phi }_{D_{s}^{*}D_{s}\phi }=A\mathrm{exp}(-BQ^2),\end{aligned}$$

(36)

$$\begin{aligned}&G^{D_{s}}_{D_{s}^{*}D_{s}\phi }=\frac{C}{1+DQ^2}\mathrm{exp}(-EQ^2),\end{aligned}$$

(37)

$$\begin{aligned}&G^{D^{*}_{s}}_{D_{s}^{*}D_{s}\phi }=\frac{C'}{1+D'Q^2}\mathrm{exp}(-E'Q^2), \end{aligned}$$

(38)

where $A=2.964\pm 0.089\,\mathrm{GeV}^{-1},$ $B=0.1621\pm 0.0077\,\mathrm{GeV}^{-2}$, $C=2.755\pm 0.008,$ $D=-0.1944\pm 0.0186,$ $E=0.256\pm 0.0265,$ $C^{'}=2.825\pm 0.012\,\mathrm{GeV}^{-1},$ $D^{'}=-0.1855\pm 0.0171\,\mathrm{GeV}^{-2},$ $E'=0.2593\pm 0.0257$,

Considering uncertainties of all the input parameters, such as quark and mesons masses, decay constants and the values of different condensates terms, we plot the upper and lower bounds of the form factors in Fig.  7. We can see that although the uncertainties are large (about $20{-}30\,\%$ of the central values), the fitted functions can reproduce the central values of the form factors well. Thus, it is reliable for us to extrapolate the $Q^2$ to the physical region $Q^2<0$ for $\phi$, $D_{s}$ and $D_{s}^{*}$ off-shell cases to obtain the coupling constant for the vertex $D_{s}^{*}D_{s}\phi$. Substituting $Q^{2}=-m_{\phi }^{2}$, $Q^{2}=-m_{D_{s}}^{2}$ and $Q^{2}=-m_{D_{s}^{*}}^{2}$ separately in Eqs. (36)–(38), we obtain the values for $G^{\phi }_{D_{s}^{*}D_{s}\phi }$, $G^{D_{s}}_{D_{s}^{*}D_{s}\phi }$ and $G^{D_{s}^{*}}_{D_{s}^{*}D_{s}\phi }$:

$$\begin{aligned} G^{\phi }_{Ds*Ds\phi }=3.51\pm 0.11\,\mathrm{GeV}^{-1}\end{aligned}$$

(39)

$$\begin{aligned} G^{Ds}_{Ds*Ds\phi }=4.24\pm 0.47 \,\mathrm{GeV}^{-1}\end{aligned}$$

(40)

$$\begin{aligned} G^{Ds*}_{Ds*Ds\phi }=4.61\pm 0.51\,\mathrm{GeV}^{-1} \end{aligned}$$

(41)

Although the values for each off-shell case are different, they are roughly compatible when the uncertainties are taken into account, where the uncertainties in Eqs. (39)–(41) originate from the uncertainties of the fitted parameters $\delta A$, $\delta B$, $\delta C$, $\delta D$, $\delta E$, $\delta C'$, $\delta D'$ and $\delta E'$. Taking the mean values between the numbers presented above, we obtain the strong coupling constant for $G_{Ds*Ds\phi }$:

$$\begin{aligned} G_{Ds*Ds\phi }=4.12\pm 0.70\,\mathrm{GeV}^{-1} \end{aligned}$$

(42)

In Ref. [57], Z.G.Wang studied the $D^{*}DV$ vertex with the light-cone QCD sum rules. Most of the results in this work is analyzed to be much smaller than others [57]. And the coupling constant $G_{Ds*Ds\phi }$ is estimated to be about $0.82\pm 0.16\,\mathrm{GeV}^{-1}$ which is also much smaller than our result. This difference is most probably due to the different input parameters and the different methods employed. In Reference [42, 43], it is indicated that the value of $G_{Ds*Ds\phi }$ is $4.07\pm 0.71\,\mathrm{GeV}^{-1}$ in the framework of the three-point QCD sum rules. Besides of the perturbative part, the contributions of quark–quark, gluon–gluon, and quark–gluon condensate are considered in this work. It is clearly that our result is compatible well with that of Refs. [42, 43], which indicates to some extent the reliability of our result.

As to the coupling constant $G_{D_{s}^{*}D_{s}\gamma }$ in the decay $D_{s}^{*}\rightarrow D_{s}\gamma$ in Eq. (35), we can easily obtain its value by setting $Q^2=0$ in the analytical function (Eq. 36):

$$\begin{aligned} G_{Ds*Ds\gamma }=2.96\pm 0.09\,\mathrm{GeV}^{-1} \end{aligned}$$

(43)

Now, it is time for us to give an analysis of electromagnetic decay $D_{s}^{*}\rightarrow D_{s}\gamma$. As to its decay width, it can be written as the following representation:

$$\begin{aligned} \Gamma =\frac{1}{2J+1}\sum \frac{p}{8\pi M_{i}^{2}}\left| T\right| ^{2} \end{aligned}$$

$$\begin{aligned} p=\frac{\sqrt{(M_{i}^{2}-(M_{f}^{2}+m^{2})^{2})(M_{i}^{2}-(M_{f}^{2}-m^{2})^{2})}}{2M_{i}} \end{aligned}$$

(44)

where the i and f denote the initial and final state mesons, respectively, the J is the total angular momentum of the initial meson, the $\sum$ denotes the summation of all the polarization vectors, and the T denotes the scattering amplitudes.

With the Eqs. (35) and (44), the decay width of $D_{s}^{*}\rightarrow D_{s}\gamma$ can be expressed as:

$$\begin{aligned} \Gamma =\alpha G_{D_{s}^{*}D_{s}\gamma }^{2}\left[ \frac{f_{\phi }}{m_{\phi }}Q_{s}\right] ^{2}\frac{\left| p\right| ^{3}}{ 3M_{D_{s}^{*}}^{2}}\left[ \frac{M_{D_{s}^{*}}^{2}+M_{D_{s}}^{2}}{ 2M_{D_{s}^{*}}}\right] ^{2} \end{aligned}$$

(45)

with $Q_{s}=\frac{1}{3}$, $\alpha =\frac{1}{137}$. Considering all the uncertainties of the input parameters, we finally get the decay width of the process $D_{s}^{*}\rightarrow D_{s}\gamma$:

$$\begin{aligned} \Gamma =0.59\pm 0.15\,\mathrm{keV} \end{aligned}$$

It is indicated by the Babar collaboration that the decay width of $\Gamma (D_{s}^{*})<1.9\,\mathrm{MeV}$. And the ratio of the decay channel $D_{s}^{*}\rightarrow D_{s}\gamma$ is about $94.2\,\%$ of the total width. This means that our result is compatible with the experimental data. Besides, Donald et al. predicted the value of this decay channel is $\Gamma (D_{s}^{*}\rightarrow D_{s}\gamma )=0.066\pm 0.026\,\mathrm{keV}$ in Full Lattice QCD [58], which is much smaller than our result. Although these results are all compatible with the experimental data, it needs to be further testified by more experiments and theoretical calculations because of this difference.

4 Conclusions

In this article, we have calculated the form factors $G^{\phi }_{D_{s}^{*}D_{s}\phi }$, $G^{D_{s}}_{D_{s}^{*}D_{s}\phi }$ and $G^{D_{s}^{*}}_{D_{s}^{*}D_{s}\phi }$ in the space-like regions with $\phi$, $D_{s}$ and $D_{s}^{*}$ off-shell cases by three different QCD sum rules. Then we fit the form factors into analytical functions, extrapolated them into the time-like regions, and obtained the strong coupling constant $G_{Ds*Ds\phi }$. This procedure help us to reduce the errors related to the method, leading to compatible coupling constants, as seen Eqs. (39)–(41). In addition, we also obtained the coupling constant $G_{Ds*Ds\gamma }$ with the analytical function. With this coupling constant, we calculated the decay width of the electromagnetic decay $D_{s}^{*}\rightarrow D_{s}\gamma$ and compared our result with those of other groups.

Appendices

Appendix A: Full expressions of the $\langle g^{2}G^{2}\rangle$ and $\langle f^{3}G^{3}\rangle$ contributions for $\phi$ off-shell case

$$\begin{aligned} \Pi _{\mu \nu }^{\langle g^{2}G^{2}\rangle (\phi )}= & {} \frac{i\left\langle \frac{g^{2}G^{2}}{4\pi ^{2}}\right\rangle }{4\pi ^{2}} \left\{ -m_{c}\left[ \widetilde{I}_{m_{c}m_{s}m_{s}}^{311}+m_{c}^{2}\widetilde{I} _{m_{c}m_{s}m_{s}}^{411}+I_{m_{c}m_{s}m_{s}}^{311}\right. \right. \nonumber \\&\left. +m_{c}^{2}I_{m_{c}m_{s} m_{s}}^{411}+N_{m_{c}m_{s}m_{s}}^{311} +m_{c}^{2}N_{m_{c}m_{s}m_{s}}^{411}\right] \nonumber \\&+\,m_{c}^{2} m_{s}\left[ \widetilde{I}_{m_{c}m_{s}m_{s}}^{411}+m_{c}^{2}I_{m_{c}m_{s}m_{s}} ^{411}\right] +m_{s}I_{m_{c}m_{s}m_{s}}^{131}\nonumber \\&+\,m_{s}^{2}(m_{s}-m_{c})\left[ I_{m_{c}m_{s}m_{s} }^{141}+\widetilde{I}_{m_{c}m_{s}m_{s}}^{141}\right] \nonumber \\&-\,m_{c}m_{s}^{2}N_{m_{c} m_{s}m_{s}}^{141}-m_{s}^{2}(m_{c}-m_{s})\nonumber \\&\times \left[ I_{m_{c}m_{s}m_{s}}^{114} +\widetilde{I}_{m_{c} m_{s}m_{s}}^{114}\right] \nonumber \\&+m_{s}\widetilde{I}_{m_{c}m_{s}m_{s}}^{113}-m_{c}m_{s}^{2}N_{m_{c}m_{s}m_{s}}^{114}\nonumber \\&+\frac{1}{6}\left[ (m_{c}-m_{s})I_{m_{c}m_{s}m_{s}}^{122}\right. \nonumber \\&\left. +\,(m_{c}-m_{s})\widetilde{I}_{m_{c}m_{s}m_{s}}^{122}+m_{c}N_{m_{c}m_{s}m_{s}}^{122}\right] \nonumber \\&+\,\frac{1}{6}\left[ (m_{c}-m_{s})I_{m_{c}m_{s}m_{s}}^{221}+(m_{c}-m_{s})\widetilde{I}_{m_{c}m_{s}m_{s}}^{221}\right. \nonumber \\&\left. +\,m_{c}N_{m_{c}m_{s}m_{s}}^{221}\right] +\frac{1}{6}\left[ 3(m_{s}-m_{c})\widetilde{I}_{m_{c}m_{s}m_{s}}^{212}+(m_{s}\right. \nonumber \\&\left. \left. -\,3m_{c})I_{m_{c}m_{s}m_{s}}^{212}-3m_{c}N_{m_{c}m_{s}m_{s}}^{212}\right] \right\} p_{\alpha }p_{\beta }^{\prime }\varepsilon ^{\mu \nu \alpha \beta }\nonumber \\ \end{aligned}$$

(46)

$$\begin{aligned} \Pi _{\mu \nu }^{\langle f^{3}G^{3}\rangle (\phi )}= & {} \frac{ i\langle f^{3}G^{3}\rangle }{32\pi ^{4}}\left\{ \frac{m_{c}}{6} \left[ N_{m_{c}m_{s}m_{s}}^{321}+2m_{c}^{2}N_{m_{c}m_{s}m_{s}}^{421}\right. \right. \nonumber \\&-\,3\widetilde{I}_{m_{c}m_{s}m_{s}}^{321}-3I_{m_{c}m_{s}m_{s}}^{321}-2m_{c}^{2}\widetilde{I} _{m_{c}m_{s}m_{s}}^{421}\nonumber \\&\left. -2m_{c}^{2}I_{m_{c}m_{s}m_{s}}^{421}\right] \nonumber \\&+\frac{m_{c}}{6} \left[ 11N_{m_{c}m_{s}m_{s}}^{312}+\,11m_{c}^{2}N_{m_{c}m_{s}m_{s}}^{412}\right. \nonumber \\&-2I_{m_{c}m_{s}m_{s}}^{402}+I_{m_{c}m_{s}m_{s}}^{312} +\,m_{c}^{2}I_{m_{c}m_{s}m_{s}}^{412}+\,9\widetilde{I}_{m_{c}m_{s}m_{s}}^{312}\nonumber \\&\left. +6m_{c}^{2}\widetilde{I} _{m_{c}m_{s}m_{s}}^{412}\right] \nonumber \\&-\frac{m_{c}}{3}\left[ I_{m_{c}m_{s}m_{s}}^{132}+\widetilde{I} _{m_{c}m_{s}m_{s}}^{132}+N_{m_{c}m_{s}m_{s}}^{132}\right] \nonumber \\&-\frac{m_{c}}{6} \left[ I_{m_{c}m_{s}m_{s}}^{231}+\widetilde{I}_{m_{c}m_{s}m_{s}}^{231} +N_{m_{c}m_{s}m_{s}}^{231}\right] \nonumber \\&-\frac{m_{c}}{6}\left[ I_{m_{c}m_{s}m_{s}}^{123}+\widetilde{I} _{m_{c}m_{s}m_{s}}^{123}+N_{m_{c}m_{s}m_{s}}^{123}\right] \nonumber \\&+\,m_{c}\left[ I_{m_{c}m_{s}m_{s}}^{213}+ \widetilde{I}_{m_{c}m_{s}m_{s}}^{213}+N_{m_{c}m_{s}m_{s}}^{213}\right] \nonumber \\&+\,\frac{1}{2}\left[ (6m_{s}-m_{c})\left( \widetilde{I}_{m_{c}m_{s}m_{s}}^{411}-I_{m_{c}m_{s}m_{s}}^{411}\right) \right. \nonumber \\&+\,8m_{s}^{2}(m_{s}-m_{c})\left( \widetilde{I}_{m_{c}m_{s}m_{s}}^{511}-I_{m_{c}m_{s}m_{s}}^{511}\right) \nonumber \\&+\,(m_{s}-m_{c})\left( I_{m_{c}m_{s}m_{s}}^{411}+8m_{s}^{2}I_{m_{c}m_{s}m_{s}}^{511}\right) \nonumber \\&\left. -\,6m_{s}N_{m_{c}m_{s}m_{s}}^{411}-8m_{s}^{3}N_{m_{c}m_{s}m_{s}}^{511}\right] \nonumber \\&+\,\frac{1}{2}\left[ (m_{s}-6m_{c})I_{m_{c}m_{s}m_{s}}^{411}+8m_{c}^{2}(m_{s}-m_{c})I_{m_{c}m_{s}m_{s}}^{511}\right. \nonumber \\&-\,(m_{s}-6m_{c}) \widetilde{I}_{m_{c}m_{s}m_{s}}^{411}-8m_{c}^{2}(m_{s}-m_{c})\widetilde{I} _{m_{c}m_{s}m_{s}}^{511}\nonumber \\&\left. -\,6m_{c}N_{m_{c}m_{s}m_{s}}^{411} -8m_{c}^{3}N_{m_{c}m_{s}m_{s}}^{511}\right] \nonumber \\&+\frac{1}{2}\left[ (m_{s}-m_{c})\left( \widetilde{I}_{m_{c}m_{s}m_{s}}^{141}-\,I_{m_{c}m_{s}m_{s}}^{141}+9m_{s}^{2}\widetilde{I} _{m_{c}m_{s}m_{s}}^{151}\right. \right. \nonumber \\&\left. -9m_{s}^{2}I_{m_{c}m_{s}m_{s}}^{151}\right) +\,(m_{s}-m_{c})\nonumber \\&\times \,\left( I_{m_{c}m_{s}m_{s}}^{141}+9m_{s}^{2}I_{m_{c}m_{s}m_{s}}^{151}\right) \nonumber \\&+5m_{s}\left( I_{m_{c}m_{s}m_{s}}^{141}-m_{s}^{2}I_{m_{c}m_{s}m_{s}}^{151}\right) \nonumber \\&\left. +\,m_{s}\left( N_{m_{c}m_{s}m_{s}}^{141}+9m_{s}^{2}N_{m_{c}m_{s}m_{s}}^{151}\right) \right] \nonumber \\&\left. -\,\frac{m_{c}}{6}\left[ I_{m_{c}m_{s}m_{s}}^{222}+\widetilde{I} _{m_{c}m_{s}m_{s}}^{222}+N_{m_{c}m_{s}m_{s}}^{222}\right] \right\} p_{\alpha }p_{\beta }^{\prime }\varepsilon ^{\mu \nu \alpha \beta }\nonumber \\ \end{aligned}$$

(47)

Appendix B: Full expressions about the condensate terms for $D_{s}$ off-shell case

$$\begin{aligned}&\Pi _{\mu \nu }^{\langle \overline{s}s\rangle (D_{s})}=\frac{ \langle \overline{s}s\rangle }{2}\left\{ -\frac{m_{s}^{2}}{(p^{\prime 2}-m_{c}^{2})(p^{2}-m_{s}^{2})^{2}}\right. \nonumber \\&\quad \left. +\frac{m_{c}m_{s}}{(p^{\prime 2}-m_{c}^{2})^{2}(p^{2}-m_{s}^{2})} +\frac{2}{(p^{\prime 2}-m_{c}^{2})(p^{2}-m_{s}^{2})}\right\} \nonumber \\&\quad \times p_{\alpha }p_{\beta }^{\prime }\varepsilon ^{\mu \nu \alpha \beta }\end{aligned}$$

(48)

$$\begin{aligned}&\Pi _{\mu \nu }^{\left\langle \overline{s}g\sigma .Gs\right\rangle (D_{s})} =\left\langle \overline{s}g\sigma .Gs\right\rangle \left\{ \frac{1}{12}\left[ \frac{1}{(p^{\prime 2}-m_{c}^{2})^{2}(p^{2}-m_{s}^{2})}\right. \right. \nonumber \\&\quad \left. \left. +\frac{1}{(p^{\prime 2}-m_{c}^{2})(p^{2}-m_{s}^{2})^{2}}\right] \right. \nonumber \\&\quad -\frac{1}{96}\left[ -2m_{s}^{2}\left( \frac{12}{ (p^{\prime 2}-m_{c}^{2})(p^{2}-m_{s}^{2})^{3}}\right. \right. \nonumber \\&\quad +\frac{24m_{s}^{2}}{(p^{\prime 2}-m_{c}^{2})(p^{2}-m_{s}^{2})^{4}}+\frac{2}{(p^{\prime 2}-m_{c}^{2})^{2}(p^{2}-m_{s}^{2})^{2}}\nonumber \\&\quad \left. +\frac{8m_{c}^{2}}{ (p^{\prime 2}\!-\!m_{c}^{2})^{3}(p^{2}\!-\!m_{s}^{2})^{2}}\right) \!+\!2m_{c}m_{s}\left( \frac{12}{ (p^{\prime 2}\!-\!m_{c}^{2})^{3}(p^{2}\!-\!m_{s}^{2})}\right. \nonumber \\&\quad +\frac{24m_{c}^{2}}{(p^{\prime 2}-m_{c}^{2})^{4}(p^{2}-m_{s}^{2})}+\frac{2}{(p^{\prime 2}-m_{c}^{2})^{2}(p^{2}-m_{s}^{2})^{2}}\nonumber \\&\quad \left. +\frac{ 8m_{s}^{2}}{(p^{\prime 2}-m_{c}^{2})^{2}(p^{2}-m_{s}^{2})^{3}}\right) +6\left( \frac{2}{(p^{\prime 2}-m_{c}^{2})(p^{2}-m_{s}^{2})^{2}}\right. \nonumber \\&\quad +\frac{8m_{s}^{2}}{(p^{\prime 2}-m_{c}^{2})(p^{2}-m_{s}^{2})^{3}}+\frac{2}{(p^{\prime 2}-m_{c}^{2})^{2}(p^{2}-m_{s}^{2})}\nonumber \\&\quad \left. \left. \left. +\frac{8m_{c}^{2}}{(p^{\prime 2}-m_{c}^{2})^{3}(p^{2}-m_{s}^{2})}\right) \right] \right\} p_{\alpha }p_{\beta }^{\prime }\varepsilon ^{\mu \nu \alpha \beta } \end{aligned}$$

(49)

$$\begin{aligned}&\Pi _{\mu \nu }^{\left\langle \overline{s}s\right\rangle ^{2}(D_{s})}=\left\{ \frac{2\left\langle \overline{s}s\right\rangle ^{2}m_{c}}{ 27(p^{2}-m_{s}^{2})(p^{\prime 2}-m_{c}^{2})^{3}}\right. \nonumber \\&\quad -\frac{\left\langle \overline{s}s\right\rangle ^{2}}{162(p^{2}-m_{s}^{2})(p^{\prime 2}-m_{c}^{2})}\left[ \frac{3m_{s}}{(p^{2}-m_{s}^{2})^{2}}+\frac{2m_{s}^{3}}{ (p^{2}-m_{s}^{2})^{3}}\right. \nonumber \\&\quad -\frac{m_{c}}{(p^{\prime 2}-m_{c}^{2})(p^{2}-m_{s}^{2}) }+\frac{2m_{c}m_{s}^{2}}{(p^{\prime 2}-m_{c}^{2})(p^{2}-m_{s}^{2})^{2}}\nonumber \\&\quad +\frac{m_{s}}{(p^{\prime 2}-m_{c}^{2})(p^{2}-m_{s}^{2})}+\frac{2m_{s}m_{c}^{2}}{ (p^{\prime 2}-m_{c}^{2})^{2}(p^{2}-m_{s}^{2})}\nonumber \\&\quad \left. \left. -\frac{3m_{c}}{(p^{\prime 2}-m_{c}^{2})^{2}}-\frac{2m_{c}^{3}}{(p^{\prime 2}-m_{c}^{2})^{3}}\right] \right\} p_{\alpha }p_{\beta }^{\prime }\varepsilon ^{\mu \nu \alpha \beta } \end{aligned}$$

(50)

$$\begin{aligned}&\Pi _{\mu \nu }^{\langle \overline{s}sGG\rangle (D_{s})}=\frac{ \langle g^{2}\overline{s}sGG\rangle }{72}\left\{ -\frac{3m_{s}^{2}}{ (p^{\prime 2}-m_{c}^{2})^{2}(p^{2}-m_{s}^{2})^{3}}\right. \nonumber \\&\quad +\frac{3m_{c}m_{s}}{ (p^{\prime 2}-m_{c}^{2})^{3}(p^{2}-m_{s}^{2})^{2}}+\frac{1}{(p^{\prime 2}-m_{c}^{2})^{2}(p^{2}-m_{s}^{2})^{2}}\nonumber \\&\quad +\frac{2}{(p^{\prime 2}-m_{c}^{2})^{2}(p^{2}-m_{s}^{2})^{2}}+\frac{4m_{s}^{2}}{(p^{\prime 2}-m_{c}^{2})^{2}(p^{2}-m_{s}^{2})^{3}}\nonumber \\&\quad +\frac{4m_{c}^{2}}{(p^{\prime 2}-m_{c}^{2})^{3}(p^{2}-m_{s}^{2})^{2}}+\frac{4m_{s}^{2}m_{c}^{2}}{(p^{\prime 2}-m_{c}^{2})^{3}(p^{2}-m_{s}^{2})^{3}}\nonumber \\&\quad +\frac{3}{(p^{\prime 2}-m_{c}^{2})(p^{2}-m_{s}^{2})^{3}}+\frac{12m_{s}^{2}}{(p^{\prime 2}-m_{c}^{2})(p^{2}-m_{s}^{2})^{4}}\nonumber \\&\quad +\frac{4m_{s}^{4}}{(p^{\prime 2}-m_{c}^{2})(p^{2}-m_{s}^{2})^{5}}+\frac{3}{(p^{\prime 2}-m_{c}^{2})^{3}(p^{2}-m_{s}^{2})}\nonumber \\&\quad +\frac{12m_{c}^{2}}{(p^{\prime 2}-m_{c}^{2})^{4}(p^{2}-m_{s}^{2})}+ \frac{4m_{c}^{4}}{(p^{\prime 2}-m_{c}^{2})^{5}(p^{2}-m_{s}^{2})}\nonumber \\&\quad +\frac{m_{s}^{2}m_{c}m_{s}}{2(p^{\prime 2}-m_{c}^{2})^{2}(p^{2}-m_{s}^{2})^{4}}-\frac{m_{s}^{4}}{2(p^{\prime 2}-m_{c}^{2})(p^{2}-m_{s}^{2})^{5}}\nonumber \\&\quad -\frac{m_{s}^{2}}{2(p^{\prime 2}-m_{c}^{2})(p^{2}-m_{s}^{2})^{4}}+\frac{m_{c}^{2}m_{c}m_{s}}{2(p^{\prime 2}-m_{c}^{2})^{5}(p^{2}-m_{s}^{2})}\nonumber \\&\quad -\frac{m_{c}^{2}m_{s}^{2}}{2(p^{\prime 2}-m_{c}^{2})^{4}(p^{2}-m_{s}^{2})^{2}}+\frac{3m_{c}m_{s}}{2(p^{\prime 2}-m_{c}^{2})^{4}(p^{2}-m_{s}^{2})}\nonumber \\&\quad \left. +\frac{2m_{c}^{2}}{2(p^{\prime 2}-m_{c}^{2})^{4}(p^{2}-m_{s}^{2})}\right\} p_{\alpha }p_{\beta }^{\prime }\varepsilon ^{\mu \nu \alpha \beta } \end{aligned}$$

(51)

$$\begin{aligned}&\Pi _{\mu \nu }^{\langle g^{2}G^{2}\rangle (D_{s})}=\frac{ i\left\langle \frac{g^{2}G^{2}}{4\pi ^{2}}\right\rangle }{4\pi ^{2}} \left\{ -m_{s}\left[ (m_{s}^{2}-m_{s}m_{c})\widetilde{I}_{m_{s}m_{s}m_{c}}^{411}\right. \right. \nonumber \\&\quad +\,\widetilde{I}_{m_{s}m_{s}m_{c}}^{311}+N_{m_{s}m_{s}m_{c}}^{311}+m_{s}^{2}N_{m_{s}m_{s}m_{c}}^{411}\left. +\,I_{m_{s}m_{s}m_{c}}^{311}\right] \nonumber \\&\quad +\,m_{s}\left[ m_{s}(m_{c}-m_{s})\widetilde{I} _{m_{s}m_{s}m_{c}}^{141}-\,m_{s}^{2}N_{m_{s}m_{s}m_{c}}^{141}+I_{m_{s}m_{s}m_{c}}^{131}\right] \nonumber \\&\quad +m_{c}\left[ \widetilde{I}_{m_{s}m_{s}m_{c}}^{113}\right. \left. \!+\!\,(m_{c}^{2}-m_{s}m_{c})\widetilde{I} _{m_{s}m_{s}m_{c}}^{114}-m_{s}m_{c}N_{m_{s}m_{s}m_{c}}^{114}\right] \!\!\nonumber \\&\quad +\,\frac{1}{6}\left[ (3m_{c}-m_{s})\widetilde{I} _{m_{s}m_{s}m_{c}}^{122}+2m_{s}I_{m_{s}m_{s}m_{c}}^{122}\left. -\,m_{s}N_{m_{s}m_{s}m_{c}}^{122}\right] \right. \nonumber \\&\quad + \frac{1}{6}\left[ (m_{s}-m_{c})\widetilde{I} _{m_{s}m_{s}m_{c}}^{221}+m_{s}N_{m_{s}m_{s}m_{c}}^{221}\right] \nonumber \\&\quad \left. +\,\frac{1}{6}\left[ (m_{s}-m_{c})\widetilde{I}_{m_{s}m_{s}m_{c}}^{212}+m_{s}N_{m_{s}m_{s}m_{c}}^{212}\right] \right\} p_{\alpha }p_{\beta }^{\prime }\varepsilon ^{\mu \nu \alpha \beta }\nonumber \\ \end{aligned}$$

(52)

$$\begin{aligned}&\Pi _{\mu \nu }^{\langle f^{3}G^{3}\rangle (D_{s})}=\frac{ i\left\langle f^{3}G^{3}\right\rangle }{32\pi ^{4}}\left\{ \frac{m_{c}}{6} \widetilde{I}_{m_{s}m_{s}m_{c}}^{321}+\frac{m_{c}}{3}\widetilde{I} _{m_{s}m_{s}m_{c}}^{312}\right. \nonumber \\&\quad -m_{c}\widetilde{I}_{m_{s}m_{s}m_{c}}^{132}+\frac{ m_{c}}{6}\widetilde{I}_{m_{s}m_{s}m_{c}}^{231}+\frac{m_{c}}{6}\left[ -5\widetilde{I} _{m_{s}m_{s}m_{c}}^{123}\right. \nonumber \\&\quad \left. +2I_{m_{s}m_{s}m_{c}}^{123}+2I_{m_{s}m_{s}m_{c}}^{114}\right. -2m_{c}^{2} \widetilde{I}_{m_{s}m_{s}m_{c}}^{124}+2(m_{s}^{2}+m_{c}^{2}\nonumber \\&\quad \left. +q\,{\hat{}}\, 2)I_{m_{s}m_{s}m_{c}}^{124}\right] +\frac{m_{c}}{6} \left[ 4N_{m_{s}m_{s}m_{c}}^{213}+4m_{c}^{2}N_{m_{s}m_{s}m_{c}}^{214}\right. \nonumber \\&\quad \left. +\widetilde{I}_{m_{s}m_{s}m_{c}}^{213}+2\widetilde{I}_{m_{s}m_{s}m_{c}}^{114}\right] +m_{c}\left[ 3\widetilde{I}_{m_{s}m_{s}m_{c}}^{114}+4m_{c}^{2}\widetilde{I} _{m_{s}m_{s}m_{c}}^{115}\right] \nonumber \\&\quad +\frac{m_{c}}{2}\widetilde{I} _{m_{s}m_{s}m_{c}}^{411} +\frac{1}{2}\left[ m_{c}\widetilde{I}_{m_{s}m_{s}m_{c}}^{141}+8m_{s}^{2}m_{c} \widetilde{I}_{m_{s}m_{s}m_{c}}^{151}\right. \nonumber \\&\quad \left. -6m_{s}I_{m_{s}m_{s}m_{c}}^{141}-8m_{s}^{3}I_{m_{s}m_{s}m_{c}}^{151}\right] +\frac{1}{6}\left[ (m_{c}-m_{s})\widetilde{I} _{m_{s}m_{s}m_{c}}^{222}\right. \nonumber \\&\quad \left. \left. -m_{s}N_{m_{s}m_{s}m_{c}}^{222}\right] \right\} p_{\alpha }p_{\beta }^{\prime }\varepsilon ^{\mu \nu \alpha \beta } \end{aligned}$$

(53)

Appendix C: Full expressions about the condensate terms for $D_{s}^{*}$ off-shell case

$$\begin{aligned}&\Pi _{\mu \nu }^{\langle \overline{s}s\rangle (D_{s}^{*})}=\frac{\langle \overline{s}s\rangle }{2}\left\{ \frac{m_{s}^{2}}{ (p^{\prime 2}-m_{s}^{2})^{2}(p^{2}-m_{c}^{2})}\right. \nonumber \\&\quad \left. -\frac{m_{c}m_{s}}{(p^{\prime 2}-m_{s}^{2})(p^{2}-m_{c}^{2})^{2}}+\frac{2}{(p^{\prime 2}-m_{s}^{2})(p^{2}-m_{c}^{2})}\right\} \nonumber \\&\quad _{\alpha }p_{\beta }^{\prime }\varepsilon ^{\mu \nu \alpha \beta } \end{aligned}$$

(54)

$$\begin{aligned}&\Pi _{\mu \nu }^{\langle \overline{s}s\rangle ^{2}(D_{s}^{*})}=\left\{ \frac{2\langle \overline{s}s\rangle ^{2}}{ 27(p^{2}-m_{c}^{2})(p^{\prime 2}-m_{s}^{2})}\left[ \frac{m_{c}}{ (p^{2}-m_{c}^{2})^{2}}\right. \right. \nonumber \\&\quad \left. +\frac{m_{s}}{(p^{\prime 2}-m_{s}^{2})^{2}}\right] -\frac{\left\langle \overline{s}s\right\rangle ^{2}}{162(p^{2}-m_{c}^{2})(p^{\prime 2}-m_{s}^{2})}\nonumber \\&\quad \times \left[ \frac{3m_{c}}{(p^{2}-m_{c}^{2})^{2}}+\frac{2m_{c}^{3}}{ (p^{2}-m_{c}^{2})^{3}}\right. \nonumber \\&\quad -\frac{m_{s}}{(p^{\prime 2}-m_{s}^{2})(p^{2}-m_{c}^{2}) }-\frac{2m_{s}m_{c}^{2}}{(p^{\prime 2}-m_{s}^{2})(p^{2}-m_{c}^{2})^{2}}\nonumber \\&\quad +\frac{m_{c}}{(p^{\prime 2}-m_{s}^{2})(p^{2}-m_{c}^{2})}+\frac{ 2m_{c}m_{s}^{2}}{(p^{\prime 2}-m_{s}^{2})^{2}(p^{2}-m_{c}^{2})}\nonumber \\&\quad \left. \left. -\frac{3m_{s}}{(p^{\prime 2}-m_{s}^{2})^{2}}-\frac{2m_{s}^{3}}{(p^{\prime 2}-m_{s}^{2})^{3}}\right] \right\} p_{\alpha }p_{\beta }^{\prime }\varepsilon ^{\mu \nu \alpha \beta } \end{aligned}$$

(55)

$$\begin{aligned}&\Pi _{\mu \nu }^{\left\langle \overline{s}g\sigma .Gs\right\rangle (D_{s}^{*})}=\left\langle \overline{s}g\sigma .Gs\right\rangle \nonumber \\&\quad \times \left\{ \frac{1}{12}\left[ \frac{1}{(p^{\prime 2}-m_{s}^{2})^{2}(p^{2}-m_{c}^{2})}-\frac{3}{ (p^{\prime 2}-m_{s}^{2})(p^{2}-m_{c}^{2})^{2}}\right] \right. \nonumber \\&\quad -\frac{1}{24}\left[ -m_{s}^{2}\left( \frac{3}{(p^{\prime 2}-m_{s}^{2})^{3}(p^{2}-m_{c}^{2})}\right. \right. \nonumber \\&\quad +\frac{2m_{s}^{2}}{(p^{\prime 2}-m_{s}^{2})^{4}(p^{2}-m_{c}^{2})}+\frac{1}{ (p^{\prime 2}-m_{s}^{2})^{2}(p^{2}-m_{c}^{2})^{2}}\nonumber \\&\quad \left. +\frac{2m_{c}^{2}}{ (p^{\prime 2}-m_{s}^{2})^{2}(p^{2}-m_{c}^{2})^{3}}\right) +m_{c}m_{s}\left( \frac{3}{ (p^{\prime 2}-m_{s}^{2})(p^{2}-m_{c}^{2})^{3}}\right. \nonumber \\&\quad +\frac{2m_{c}^{2}}{(p^{\prime 2}\!-\!m_{s}^{2})(p^{2}\!-\!m_{c}^{2})^{4}}\!+\!\frac{1}{(p^{\prime 2}\!-\!m_{s}^{2})^{2}(p^{2}\!-\!m_{c}^{2})^{2}}\nonumber \\&\quad \left. +\frac{ 2m_{s}^{2}}{(p^{\prime 2}-m_{s}^{2})^{3}(p^{2}-m_{c}^{2})^{2}}\right) +3\left( \frac{1}{(p^{\prime 2}-m_{s}^{2})(p^{2}-m_{c}^{2})^{2}}\right. \nonumber \\&\quad +\frac{2m_{c}^{2}}{(p^{\prime 2}-m_{s}^{2})(p^{2}-m_{c}^{2})^{3}}+\frac{1}{(p^{\prime 2}-m_{s}^{2})^{2}(p^{2}-m_{c}^{2})}\nonumber \\&\quad \left. \left. \left. +\frac{2m_{s}^{2}}{(p^{\prime 2}-m_{s}^{2})^{3}(p^{2}-m_{c}^{2})}\right) \right] \right\} p_{\alpha }p_{\beta }^{\prime }\varepsilon ^{\mu \nu \alpha \beta } \end{aligned}$$

(56)

$$\begin{aligned}&\Pi _{\mu \nu }^{\langle \overline{s}sGG\rangle (D_{s}^{*})} =\frac{\langle g^{2}\overline{s}sGG\rangle }{72}\left\{ -\frac{ m_{s}^{2}}{2(p^{\prime 2}-m_{s}^{2})^{3}(p^{2}-m_{c}^{2})^{2}}\right. \nonumber \\&+\frac{m_{c}m_{s}}{2(p^{\prime 2}-m_{s}^{2})^{2}(p^{2}-m_{c}^{2})^{3}}+\frac{1}{(p^{\prime 2}-m_{s}^{2})^{2}(p^{2}-m_{c}^{2})^{2}}\nonumber \\&\quad +\frac{2}{(p^{\prime 2}-m_{s}^{2})^{2}(p^{2}-m_{c}^{2})^{2}}+\frac{4m_{s}^{2}}{(p^{\prime 2}-m_{s}^{2})^{2}(p^{2}-m_{c}^{2})^{3}}\nonumber \\&\quad +\frac{4m_{c}^{2}}{(p^{\prime 2}-m_{s}^{2})^{3}(p^{2}-m_{c}^{2})^{2}}+\frac{4m_{s}^{2}m_{c}^{2}}{(p^{\prime 2}-m_{s}^{2})^{3}(p^{2}-m_{c}^{2})^{3}}\nonumber \\&\quad +\frac{3}{(p^{\prime 2}-m_{s}^{2})(p^{2}-m_{c}^{2})^{3}}+\frac{12m_{s}^{2}}{(p^{\prime 2}-m_{s}^{2})(p^{2}-m_{c}^{2})^{4}}\nonumber \\&\quad +\frac{4m_{s}^{4}}{(p^{\prime 2}-m_{s}^{2})(p^{2}-m_{c}^{2})^{5}}+\frac{3}{(p^{\prime 2}-m_{s}^{2})^{3}(p^{2}-m_{c}^{2})}\nonumber \\&\quad +\frac{12m_{c}^{2}}{(p^{\prime 2}-m_{s}^{2})^{4}(p^{2}-m_{c}^{2})}+\frac{4m_{c}^{4}}{(p^{\prime 2}-m_{s}^{2})^{5}(p^{2}-m_{c}^{2})}\nonumber \\&\quad \times \frac{m_{c}^{2}}{(p^{\prime 2}-m_{s}^{2})(p^{2}-m_{c}^{2})^{4}}-\frac{ 3m_{c}m_{s}}{2(p^{\prime 2}-m_{s}^{2})(p^{2}-m_{c}^{2})^{4}}\nonumber \\&\quad -\frac{m_{s}m_{c}^{3}}{2(p^{\prime 2}-m_{s}^{2})(p^{2}-m_{c}^{2})^{5}}+\frac{m_{s}^{2}m_{c}^{2}}{2(p^{\prime 2}-m_{s}^{2})^{2}(p^{2}-m_{c}^{2})^{4}}\nonumber \\&\quad -\frac{m_{c}m_{s}^{3}}{2(p^{\prime 2}-m_{s}^{2})^{4}(p^{2}-m_{c}^{2})^{2}}+ \frac{m_{s}^{4}}{2(p^{\prime 2}-m_{s}^{2})^{5}(p^{2}-m_{c}^{2})}\nonumber \\&\quad \left. +\frac{5m_{s}^{2}}{2(p^{\prime 2}-m_{s}^{2})^{4}(p^{2}-m_{c}^{2})}\right\} p_{\alpha }p_{\beta }^{\prime }\varepsilon ^{\mu \nu \alpha \beta } \end{aligned}$$

(57)

$$\begin{aligned}&\Pi _{\mu \nu }^{\langle g^{2}G^{2}\rangle (D_{s}^{*})}=\frac{i\left\langle \frac{g^{2}G^{2}}{4\pi ^{2}}\right\rangle }{4\pi ^{2}} \left\{ -m_{s}\left[ (m_{s}^{2}-m_{s}m_{c})I_{m_{s}m_{c}m_{s}}^{411}\right. \right. \nonumber \\&\quad +I_{m_{s}m_{c}m_{s}}^{311}+N_{m_{s}m_{c}m_{s}}^{311}+m_{s}^{2}N_{m_{s}m_{c}m_{s}}^{411}\left. +\widetilde{I}_{m_{s}m_{c}m_{s}}^{311}\right] \nonumber \\&\quad +m_{c}\left[ m_{c}(m_{c}-m_{s})I_{m_{s}m_{c}m_{s}}^{141}-m_{s}m_{c}N_{m_{s}m_{c}m_{s}}^{141}\right. \nonumber \\&\quad \left. +I_{m_{s}m_{c}m_{s}}^{131}\right] +m_{s}\left[ \widetilde{I}_{m_{s}m_{c}m_{s}}^{113}+m_{s}(m_{c}-m_{s})I_{m_{s}m_{c}m_{s}}^{114}\right. \nonumber \\&\quad \left. -m_{s}^{2}N_{m_{s}m_{c}m_{s}}^{114}\right] +\frac{1}{6}\left[ (m_{s}-m_{c})I_{m_{s}m_{c}m_{s}}^{122}+m_{s}N_{m_{s}m_{c}m_{s}}^{122}\right] \!\!\!\nonumber \\&\quad +\frac{1}{6}\left[ 3(m_{c}-m_{s})I_{m_{s}m_{c}m_{s}}^{221}-2m_{s} \widetilde{I}_{m_{s}m_{c}m_{s}}^{221}-3m_{s}N_{m_{s}m_{c}m_{s}}^{221}\right] \nonumber \\&\quad \left. +\frac{1}{6}\left[ (m_{s}-m_{c})I_{m_{s}m_{c}m_{s}}^{212}+m_{s}N_{m_{s}m_{c}m_{s}}^{212}\right] \right\} p_{\alpha }p_{\beta }^{\prime }\varepsilon ^{\mu \nu \alpha \beta }\nonumber \\ \end{aligned}$$

(58)

$$\begin{aligned} \Pi _{\mu \nu }^{\langle f^{3}G^{3}\rangle (D_{s}^{*})}= & {} \frac{i\langle f^{3}G^{3}\rangle m_{c}}{32\pi ^{4}} \left\{ -I_{m_{s}m_{c}m_{s}}^{321}+\frac{1}{6}I_{m_{s}m_{c}m_{s}}^{312}\right. \nonumber \\&+\frac{1}{2}I_{m_{s}m_{c}m_{s}}^{132}+\frac{1}{3}\left[ \widetilde{I} _{m_{s}m_{c}m_{s}}^{231}+I_{m_{s}m_{c}m_{s}}^{231}\right] \nonumber \\&+\frac{1}{3}I_{m_{s}m_{c}m_{s}}^{123}+\frac{1}{6}I_{m_{s}m_{c}m_{s}}^{213}+ \frac{1}{2}I_{m_{s}m_{c}m_{s}}^{114}\nonumber \\&+\frac{1}{2}I_{m_{s}m_{c}m_{s}}^{411}+3I_{m_{s}m_{c}m_{s}}^{141}-2m_{c}^{2}I_{m_{s}m_{c}m_{s}}^{151}\nonumber \\&\left. +\frac{1}{6}I_{m_{s}m_{c}m_{s}}^{222}\right\} p_{\alpha }p_{\beta }^{\prime }\varepsilon ^{\mu \nu \alpha \beta } \end{aligned}$$

(59)