Higgs mass bounds from renormalization flow for a Higgs–top–bottom model

Abstract

We study a chiral Yukawa model mimicking the Higgs–top–bottom sector of the standard model. We re-analyze the conventional arguments that relate a lower bound for the Higgs mass with vacuum stability in the light of exact results for the regularized fermion determinant as well as in the framework of the functional renormalization group. In both cases, we find no indication for vacuum instability nor meta-stability induced by top fluctuations if the cutoff is kept finite but arbitrary. A lower bound for the Higgs mass arises for the class of standard bare potentials of $\phi ^4$ type from the requirement of a well-defined functional integral (i.e., stability of the bare potential). This consistency bound can, however, be relaxed considerably by more general forms of the bare potential without necessarily introducing new metastable minima.

1 Introduction

Long before the recent discovery of a comparatively light standard-model Higgs boson [1, 2], estimates and bounds on this mass parameter have been derived from renormalization arguments [3–9]. Assuming the validity of the standard model over a wide range of scales up to an ultraviolet (UV) cutoff scale $\Lambda$, together with mild assumptions on the microscopic action at the scale $\Lambda$, typically leads to a finite range of possible low-energy values for the Higgs mass, the so-called infrared (IR) window [6, 10]. Similar arguments can also be applied to models beyond the standard model of particle physics [11–17]. It has been suggested that Higgs masses below the lower bound necessarily require the effective potential of the standard model to develop a further minimum beyond the electroweak minimum [18–24]. Since the measured value of the Higgs mass near $m_{\text {H}}=125$ GeV appears to be near if not below the lower bound, the standard-model vacuum could be unstable or at least metastable. In the latter case, the metastability has to be sufficiently long-lived compared to the age of the universe to allow for our existence [25–34].

While the occurrence of the vacuum instability is often attributed to the fluctuation of the top quark (and therefore sensitively depends on the top mass), the conventional perturbative analysis of determining the instability has been questioned by non-perturbative methods. Within the toy model of a top–Higgs–Yukawa system with discrete symmetry, lattice simulations have revealed that the full effective potential in this model with the cutoff kept finite does not develop an instability [35–37]. By contrast, the perturbative treatment of the same model in the limit $\Lambda \rightarrow \infty$ exhibits an instability in disagreement with the simulation results. Within the same model and using functional methods, the occurrence of the erroneous instability has been traced back to an implicit renormalization condition that contradicts the underlying assumption of a well-defined functional integral [38–40].

In a series of recent lattice simulations using chiral Higgs–Yukawa models, imposing the criterion of a stable bare potential (typically of $\phi ^4$ type) has lead to a number of quantitative results for the lower bound on the Higgs mass [37, 41–44] without the need to require low-energy stability. The same line of argument can in fact be used to put strong constraints on the existence of a fourth generation of flavor in the light of the Higgs boson mass measurement [45–49]. These results have also been substantiated by conventional analytical methods [50].

In a recent work, we have been able to show that the sole consideration of bare potentials of $\phi ^4$ type is actually too restrictive [51]. In fact, if the standard model is viewed as a low-energy effective theory, there is no reason to exclude higher-dimensional operators from the bare potential. Their occurrence is actually expected. Whereas Wilsonian renormalization group (RG) arguments of course suggest that low-energy observables remain almost completely unaffected by the higher-dimensional operators, we have demonstrated that Higgs-mass bounds can in fact exhibit a significant dependence on the bare potential. This may seem counter-intuitive at first sight, since the Higgs mass is clearly an IR observable. However, a Higgs-mass bound formulated in terms of a function of the cutoff, $m_{\text {H}}{}_{,\text {bound}}(\Lambda )$, can be strongly influenced by a non-trivial RG running of the couplings near the cutoff. In [51], we have identified a simple RG mechanism that leads to a lowering of the conventional lower bound for the case of a $\mathbb {Z}_2$-symmetric Yukawa toy model.

Our findings of a “lowering” of the lower bound have been confirmed in the chiral Yukawa models studied on the lattice [52] as well as in a model involving an additional dark-matter scalar [53].

In view of the latent controversy about the (non-)existence of a top-fluctuation induced vacuum in-/meta- stability of the electroweak vacuum, the purpose of this work is twofold: first, we demonstrate on the basis of exact results for the fermion determinant in the presence of a scalar vacuum expectation value that the interaction part contribution to the effective potential is positive if the UV cutoff is kept finite but arbitrary. By contrast, a removal of the cutoff by taking the naive limit $\Lambda \rightarrow \infty$ makes the fermionic contribution to the effective potential unstable. Second, we generalize our results of [51] to the chiral Yukawa model, which is also used in lattice simulations. Using the functional RG, we demonstrate that the conventional lower bound can be relaxed considerably by more general forms of the bare potential without necessarily introducing new metastable minima.

The paper is organized as follows: in Sect. 2, we introduce our model and all relevant notation. Section 3 is devoted to an analysis of exact properties of the fermion determinant in order to explore the origin of the apparent instability of the standard-model vacuum. The non-perturbative RG flow equations of the present model are summarized in Sect. 4. These are used in Sect. 5 to compute the Higgs-mass bounds of the model non-perturbatively for various bare potentials. Conclusions are presented in Sect. 6.

2 Chiral Higgs–top–bottom model

In order to illustrate our main points in a transparent fashion, we investigate a chiral Higgs–Yukawa model forming a self-contained subset of the standard model. The field content consists of a scalar field which is a complex SU$(2)$-doublet

$$\begin{aligned} \phi = \frac{1}{\sqrt{2}} \begin{pmatrix} \phi _1+i\phi _2\\ \phi _4+i\phi _3 \end{pmatrix}, \end{aligned}$$

(1)

and two Dirac fermions which represent the top and bottom quark. The left-handed components of the bottom and top transform as a doublet under SU(2) while the right-handed components are singlets.

$$\begin{aligned} \psi _{\text {L}} = \begin{pmatrix} t_{\text {L}}\\ b_{\text {L}} \end{pmatrix}, \quad t_{\text {R}}, \quad b_{\text {R}}. \end{aligned}$$

The classical euclidean action of the model is given by

$$\begin{aligned} S&= \! \int \mathrm{d}^4x \left[ \partial _{\mu }\phi ^{\dagger }\partial ^{\mu }\phi + U(\bar{\rho })\right. \nonumber \\&\quad + i\bar{\psi }_{\text {L}}/\!\!{\partial }\psi _{\text {L}} + i\bar{t}_{\text {R}}/\!\!{\partial }t_{\text {R}} + i\bar{b}_{\text {R}}/\!\!{\partial }b_{\text {R}} \nonumber \\&\quad + i\bar{h}_{\text {b}}(\bar{\psi }_{\text {L}}\phi b_{\text {R}} + \bar{b}_{\text {R}}\phi ^{\dagger }\psi _{\text {L}}) \nonumber \\&\quad \left. + i\bar{h}_{\text {t}}(\bar{\psi }_{\text {L}}\phi _{\mathcal {C}} t_{\text {R}} + \bar{t}_{\text {R}}\phi _{\mathcal {C}}^{\dagger }\psi _{\text {L}}) \right] . \end{aligned}$$

(2)

where $\phi _{\mathcal {C}}=i\sigma _2\phi ^*$ denotes the charge conjugated scalar. The scalar field couples to the fermions via a chiral Yukawa interaction where $\bar{h}_{\text {t}}$ and $\bar{h}_{\text {b}}$ are the (bare) Yukawa couplings for the top and bottom respectively. Furthermore, we include scalar self-interactions encoded in the scalar potential which depends on the field invariant

$$\begin{aligned} \bar{\rho }= \phi ^{\dagger }\phi . \end{aligned}$$

(3)

The action (2) is invariant under the following global symmetry transformations:

$$\begin{aligned} \phi \rightarrow e^{i\alpha ^i\frac{\sigma ^i}{2}}\phi , \quad \psi _{\text {L}} \rightarrow e^{i\alpha ^i\frac{\sigma ^i}{2}}\psi _{\text {L}}, \quad t_{\text {R}} \rightarrow t_{\text {R}}, \quad b_{\text {R}} \rightarrow b_{\text {R}}, \end{aligned}$$

where $\sigma ^i$ are the Pauli matrices acting on the SU(2) doublet structure and

$$\begin{aligned} \begin{aligned}&\phi \rightarrow e^{i\beta _{\text {s}}}\phi , \\&\psi _{\text {L}} \rightarrow e^{i\beta _{\text {L}}}\psi _{\text {L}}, \end{aligned} \qquad \begin{aligned} t_{\text {R}}&\rightarrow e^{i\beta _{\text {R}}^\text {t}}t_{\text {R}}, \\ b_{\text {R}}&\rightarrow e^{i\beta _{\text {R}}^\text {b}}b_{\text {R}}. \end{aligned} \end{aligned}$$

Here, the $\beta$ angles are related to a single angle by the usual hypercharge assignments, $\beta _{\text {s}}\,{=}\,\frac{1}{2} \beta$, $\beta _{\text {L}}\,{=}\,\frac{1}{6}\beta$, $\beta _{\text {R}}^{\text {t}} \,{=}\, \frac{2}{3} \beta$, and $\beta _{\text {R}}^{\text {b}} \,{=}\, -\frac{1}{3} \beta$. Thus, the model has a global SU(2)$\times$U(1) symmetry. The symmetry can be spontaneously broken down to a global U(1) by a nonzero vacuum expectation value of the scalar field $\phi \rightarrow v$, giving rise to Dirac masses for the fermions and the Higgs boson mass.

The classical action is already equipped with a potential for the scalar field $U(\bar{\rho })$. Symmetry breaking in the quantum theory occurs, if the corresponding renormalized potential $U$ develops a nonvanishing minimum $\bar{\rho }_0$. In this case, we can write the masses¹ in terms of this minimum and the renormalized Yukawa couplings $h_{\text {t}}$ and $h_{\text {b}}$,

$$\begin{aligned} \begin{aligned}&v = \sqrt{2}Z_{\phi }^{\frac{1}{2}}\left<\phi \right> = \sqrt{Z_{\phi }\bar{\rho }_0}, \\&m_{\text {H}}^2 = v^2\frac{U''(\bar{\rho }_0)}{Z_{\phi }^2}, \end{aligned} \quad \begin{aligned} m_{\text {t}}^2&= \frac{1}{2}v^2h_{\text {t}}^2, \\ m_{\text {b}}^2&= \frac{1}{2}v^2h_{\text {b}}^2, \end{aligned} \end{aligned}$$

where we already accounted for a wave function renormalization $Z_{\phi }$ to be defined together with the other renormalized quantities below.

Apart from the missing further matter and flavor content, our model also ignores the gauge sectors of the standard model. This avoids not only technical complications and subtle issues arising from the gauge-Higgs interplay [54–56] in the standard model. But it will, of course, also lead to decisive differences to standard-model properties, which will be commented on in the course of this work. Nevertheless, the gauge sector is less important for the main points of the present work. In order to make closer contact with the standard-model language, we fix $v=246$ GeV, $m_{\text {t}}=173$ GeV and $m_{\text {b}}=4.2$ GeV for illustrative purposes, but leave the Higgs mass as a free parameter for the moment.

For the following discussion it is important to note that the standard model in its conventional form (as well as the present model) may not be extendible to arbitrarily high momentum scales. The problem of triviality [57–63]–where substantial evidence has been accumulated for $\phi ^4$-type theories–is likely to extend to the full chiral-Yukawa sector as well. If so, the definition of the model unavoidably requires a UV cutoff $\Lambda$ which physically plays the role of the scale of maximum UV extent up to which a quantum field theory description is appropriate. If the cutoff scale is sufficiently large, Wilsonian renormalization guarantees that the IR physics essentially depends only on a finite number of relevant and marginal parameters, rendering the theory predictive (in spite of our ignorance about the physics beyond $\Lambda$).

In fact, the strategy of perturbative renormalization manifestly allows one to implicitly or explicitly take the limit $\Lambda \rightarrow \infty$ for certain physical observables. For the general definition of the theory, it is, however, important to accept the fact that the cutoff $\Lambda$ may unavoidably have to be kept finite.²

Fixing physical parameters such as $v,m_{\text {t}}$, and $m_{\text {b}}$ is technically implemented by renormalization conditions. Phenomenologically, it is useful to fix these conditions at observational IR scales. Conceptually, however, it is equally well possible to impose suitable renormalization conditions at the UV cutoff $\Lambda$. A perturbative study of possible Higgs-mass values for partly randomized UV initial conditions at the Planck scale has, for instance, been performed for the standard model in [64]. For the present model, we can fix $h_{\text {t}}$, $h_{\text {b}}$, and the scalar potential $U$ in terms of their bare quantities at the cutoff, $h_{\text {t}}{}_{\Lambda }=\bar{h}_{\text {t}}$, $h_{\text {b}}{}_{\Lambda }=\bar{h}_{\text {b}}$, and $U_{\Lambda }$. In practice, the fixing can be done such that the constraints set by the physical values of $v,m_{\text {t}}$, and $m_{\text {b}}$ are satisfied.

From this viewpoint, the Higgs boson mass as the remaining free parameter becomes a function of the unconstrained combinations of the UV couplings. Now, bounds on the Higgs boson mass arise, if all permissible choices of UV couplings result in a finite range of Higgs boson masses. Examples for such finite ranges of possible Higgs masses, so-called IR windows, are shown in Figs. 1 and 2. Before we derive these results from the functional RG, let us specifically pay attention to the lower bound that has been associated with vacuum stability.

Fig. 1

Higgs mass $m_{\text {H}}$ as a function of the bare quartic coupling $\lambda _{2,\Lambda }$ for fixed cutoff $\Lambda =10^7$ GeV for various approximations. Dashed lines depict leading order results in the derivative expansion while solid lines show the next-to-leading order. Also the convergence of the polynomial truncation of the scalar potential is illustrated. Red lines with squares arise from $N_{\text {p}}=2$ whereas blue lines with circles are derived for $N_{\text {p}}=4$

Fig. 2

Higgs mass $m_{\text {H}}$ as a function of the cutoff $\Lambda$ for various bare quartic couplings. The black solid line represents a lower mass bound ($\lambda _{2,\Lambda }=0$) within $\phi ^4$ theory. Dashed lines depict Higgs masses for $\lambda _{2,\Lambda }=1$ (red), 10 (blue), 100 (green) from bottom to top

3 Fermion determinant and (in-)stability

The current state of the art is a next-to-next-to-leading order analysis of the standard-model effective potential, in order to study its stability properties; see, e.g., [31, 65–67]. However, the stability issue is already visible at one-loop order. In a nutshell, the argument goes as follows; see, e.g., [68]. First, standard renormalization conditions on the effective potential are imposed in such a way that a first non-trivial minimum occurs at $v\simeq 246$ GeV. This involves in particular to choose the counterterm $\sim \phi ^\dagger \phi$ appropriately. Then one assumes based on RG-improvement arguments that the effective potential for large field values $\phi \gg v$ is well approximated by³

$$\begin{aligned} U_{\text {eff}}(\rho )\simeq \frac{\lambda (\mu )}{2} \rho ^2, \quad \rho = \phi ^\dagger \phi , \end{aligned}$$

(4)

where the RG scale $\mu$ then should be identified with the field amplitude $\mu \simeq |\phi |$. The dependence of the $\phi ^4$ coupling on the scale $\mu$ can be computed by integrating its $\beta$ function from the IR (where the boundary condition is fixed in terms of the Higgs mass) upwards to higher scales. For the present model, the $\beta$ function reads,

$$\begin{aligned} \beta _\lambda = \frac{1}{4 \pi ^2} \left[ - h_{\text {t}}^4 - h_{\text {b}}^4 + \lambda (h_{\text {t}}^2 +h_{\text {b}}^2) + 3\lambda ^2 \right] . \end{aligned}$$

(5)

(This agrees with the corresponding standard-model sectors if a color factor of $N_{\mathrm {c}}$ is included for each fermion loop.) Obviously, the pure fermion-loop contributions $\sim h_{\text {t}}^4,h_{\text {b}}^4$ come with a negative sign, implying that they tend to deplete $\lambda$ towards the UV. In particular for a heavy top (large $h_{\text {t}}$) and a light Higgs (small $\lambda$), the integrated coupling $\lambda (\mu )$ can drop below zero at high scales. Identifying $\mu$ with $|\phi |$ and inserting this result into Eq. (4) leads us to the standard conclusion that the effective potential seems to develop an instability towards large field values. (NB: In the present model, this line of argument actually results in an effective potential being unbounded from below for $|\phi | \rightarrow \infty$. In the full standard model, electroweak fluctuations eventually stabilize this effective potential again by turning $\lambda (\mu )$ back to positive values for scales typically far above the Planck scale; see, e.g. [69]).

With hindsight, the arguments underlying Eq. (4) rely on the assumption that the field amplitude $\phi$ provides for the only relevant scale at large values. It is precisely this assumption that fails in the presence of a finite cutoff independently of the size of the cutoff. In order to see this, let us start from the (for simplicity Euclidean) generating functional for the scalar correlation functions of the model

$$\begin{aligned} Z[J]= \int _\Lambda \mathcal {D}\phi \mathcal {D} \bar{\psi }\mathcal {D} \psi e^{-S[\phi ,\bar{\psi },\psi ]+\int J \phi }, \end{aligned}$$

(6)

where the appearance of $\Lambda$ at the functional integral shall remind us of the fact that the theory requires a regularization procedure as part of its definition. As the action is a quadratic form in the fermion fields, the corresponding fermionic integral can be carried out and yields

$$\begin{aligned} Z[J]&= \int _\Lambda \mathcal {D}\phi \, \text {det}_\Lambda (\mathcal {L}(\phi )) e^{-S_{\text {B}}[\phi ]+\int J \phi } \nonumber \\&= \int _\Lambda \mathcal {D}\phi \, e^{-S_{\text {B}}[\phi ]-S_{\text {F},\Lambda }[\phi ] +\int J\phi }, \end{aligned}$$

(7)

where $S_{\text {B}}$ is the purely bosonic part of the action and $\mathcal {L}(\phi )$ denotes the Dirac operator in the presence of the scalar field. In the second line of Eq. (7), we have introduced the effective action $S_{\text {F},\Lambda }[\phi ]$ arising from integrating out the fermion fluctuations. As the fermion determinant and thus also $S_{\text {F},\Lambda }$ corresponds already to a loop-integration, it suffices for the present purpose to investigate its properties for a homogeneous mean field $\phi$. Deviations from this mean field contribute to the full effective potential only in terms of fluctuations at higher-loop order. Therefore, we concentrate on the fermion-fluctuation induced contribution to the effective potential

$$\begin{aligned} U_{\text {F}}(\rho ) = - \frac{1}{\Omega } \ln \text {det}_{\Lambda } (\mathcal {L}(\phi )), \end{aligned}$$

(8)

where $\Omega =\int \mathrm{d}^4x$ denotes the spacetime volume, and where we have used the fact that the dependence on $\phi$ must occur in terms of the SU(2) invariant variable $\rho$. Incidentally, Eq. (8) corresponds to the leading contribution to the effective potential at large $N_{\mathrm {f}}$.

Upon a global SU(2) rotation, the mean field can be rotated into the $\phi _4$ component of the scalar field. The Dirac operator then becomes block diagonal in top-bottom space, reading $\mathcal {L}_a(\phi ) = i /\!\!{\partial } + i \frac{1}{\sqrt{2}} h_a \phi _4$ where $a=\{\text {t},\text {b}\}$ in the top or bottom subspace respectively. Because of the hermiticity of $\gamma _5$, $i/\!\!{\partial }$ is isospectral to $-i/\!\!{\partial }$, which allows us to write

$$\begin{aligned} U_{\text {F}}(\rho ) = - \frac{1}{2\Omega }\sum _{a=\{\text {t},\text {b}\}} \ln \frac{\text {det}_{\Lambda } ( -\partial ^2 +h_a^2 \rho )}{\text {det}_{\Lambda } ( -\partial ^2)}, \end{aligned}$$

(9)

where $\rho =\frac{1}{2} \phi _4^2$ for our choice of mean field. In proceeding from Eq. (8) to Eq. (9), we also used the freedom of choosing the normalization of the generating functional such that the fermion-induced effective potential is normalized to the zero-field limit, i.e., $U_{\text {F}}(\rho =0)=0$. This resulting ratio of determinants can be evaluated straightforwardly, once a regularization procedure has been chosen. The final result will of course depend on the regularization for any finite value of the cutoff $\Lambda$. As argued above, we should not expect that the cutoff can be sent to infinity, since our model is likely to have a scale of maximum UV extent. In order to understand this regulator dependence, it is therefore instructive to compute Eq. (9) for different choices of the regularization.

3.1 Sharp cutoff

As the contributions from both quarks are formally identical up to a different value of the Yukawa coupling, it is sufficient to study $U_{\text {F},a}$ and take the sum over ${a=\{\text {t},\text {b}\}}$ afterward. A straightforward regularization is provided by a sharp cutoff in momentum space, such that Eq. (9) translates into

$$\begin{aligned} U_{\text {F},a}(\rho ) = - 2 \int _\Lambda \frac{\mathrm{d}^4p}{(2\pi )^4} \ln \left( 1+ \frac{h_a^2\rho }{p^2} \right) , \end{aligned}$$

(10)

where we have used the fact that we work here with 4-component Dirac spinors. As expected, the integral contains quadratic and logarithmic “divergencies”, which can be made explicit by writing the analytic exact result of the integral as

$$\begin{aligned} U_{\text {F},a}(\rho )&= -\frac{\Lambda ^2}{8\pi ^2} h_a^2 \rho \end{aligned}$$

(11)

$$\begin{aligned}&+ \frac{1}{16\pi ^2} \left[ h_a^4\rho ^2 \ln \left( \! 1+ \frac{\Lambda ^2}{h_a^2\rho }\! \right) +h_a^2\rho \Lambda ^2 \right. \nonumber \\&\left. - \Lambda ^4 \ln \left( \! 1+ \frac{h_a^2\rho }{\Lambda ^2}\! \right) \right] . \end{aligned}$$

(12)

Here observe that the quadratic divergence $\sim \Lambda ^2$ has been isolated in the first line. The remaining term in square brackets contains only logarithmic divergencies $\sim \ln \Lambda$. It is, however, more important to note that the first line also isolates the only term proportional to $\rho \sim \phi ^\dagger \phi$ and thus contributes to the mass parameter of the scalar field. The remaining terms represent the interacting part of the fermion-induced effective potential.

Most importantly: whereas the contribution to the mass term is negative, as it should be, since fermion fluctuations tend to induce chiral symmetry breaking, the whole interaction part in square brackets is strictly positive for all $\rho >0$. This follows immediately from the inequality $\ln (1+x)<x$ (for $x>0$) applied to the last term. Similarly, it can be shown that also the derivative of the interacting part with respect to $\rho$ is strictly positive for any finite value of $\rho$, $h_a$, and $\Lambda$.

We conclude that the fermion determinant–apart from its contribution to the scalar mass term–is strictly positive and monotonically increasing in its interacting part. Therefore, once the scalar mass term has been fixed by a renormalization condition, the remaining contributions from the top fluctuations to the interacting part of the bosonic potential are strictly positive. This excludes the possibility that an instability beyond the electroweak vacuum is induced by fermionic fluctuations. This can also be phrased in terms of a more rigorous statement: if the potential of the purely bosonic part $S_\text {B}$ of the action in Eq. (7) is bounded from below by a function of the form $U_{\text {B}}(\rho )> c_1 + c_2 \rho ^{1+\epsilon }$ with an arbitrary finite constant $c_1$ and finite positive constants $c_2,\epsilon >0$, then also the full potential including the fermionic fluctuations is bounded from below.

This result is in obvious direct disagreement with the standard perturbative reasoning outlined above, cf. Eqs. (4) and (5). Nevertheless, it is in fact possible to “rediscover” this seeming instability of the standard reasoning from the stable contribution (12) by trying to take the limit $\Lambda \rightarrow \infty$. The leading-order terms in this limit read

$$\begin{aligned} U_{\text {F},a}(\rho )&= -\frac{\Lambda ^2}{8\pi ^2} h_a^2 \rho + \frac{1}{16\pi ^2} \left[ h_a^4 \rho ^2 \ln \frac{\Lambda ^2}{h_a^2\rho } \right. \nonumber \\&\left. + \frac{h_a^4\rho ^2}{2} + \mathcal {O}\left( \frac{(h_a^2\rho )^3}{\Lambda ^2} \right) \right] . \end{aligned}$$

(13)

From this, it is tempting to isolate the divergencies $\sim \Lambda ^2$ and $\ln \Lambda$, combine them with the bare scalar mass and $\phi ^4$ coupling parameters, and trade them for renormalized parameters $m_\phi ^2(\mu _0)$ and $\lambda (\mu _0)$. Here $\mu _0$ is some arbitrary (typically low-energy) renormalization scale. Ignoring the mass term for a moment, the renormalized interaction contribution to the effective potential would then read

$$\begin{aligned} U_{\text {F},a}(\rho ) \mathop {\rightarrow }\limits ^{\text {?}} - \frac{1}{16\pi ^2} h_a^4 \rho ^2 \left( \ln \frac{h_a^2\rho }{\mu _0^2} +\text {const.} \right) , \end{aligned}$$

(14)

where the constant depends on the details of the renormalization scheme. This is precisely the fermion-loop contribution to the effective action, which we would obtain from integrating the first two terms of the $\beta _\lambda$ function (5) from $\mu _0$ to $\mu$ and identifying $\mu ^2 \sim \rho$. Hence, we have “rederived” the contribution with the characteristic minus sign that seems to indicate the presence of an instability at large values of $\rho$, while the cutoff $\Lambda$ seems to have disappeared completely.

The problem of this line of argument becomes obvious once we go back to the cutoff-dependent leading order terms in Eq. (13). It is straightforward to work out that also these leading-order terms seem to have an instability: the interaction part of the potential in square brackets first develops a maximum and then eventually turns negative for large fields $\rho$. However, the location of the maximum is in fact at $h_a^2\rho = \Lambda ^2$. In other words, these seeming instability features appear precisely at those field values, where the expansion in terms of the parameter $\frac{h_a^2\rho }{\Lambda ^2}\ll 1$ breaks down. We conclude that the instability “discovered” in Eq. (14) is an artifact of having tried to send the cutoff to infinity $\Lambda \rightarrow \infty$ together with a problematic choice of the renormalization conditions. In fact, it has been shown in [38–40] for the $\mathbb {Z}_2$-Yukawa model that the renormalization conditions needed to arrive at Eq. (14) require an unstable bare bosonic potential with negative bare $\phi ^4$ coupling, $\lambda (\Lambda )<0$.

Some additional comments are in order:

• (1) Our conclusions are identical to those of [35, 36], where essentially the same results have been found for the $\mathbb {Z}_2$-Yukawa model. In these works, fully non-perturbative lattice simulations have been compared with the one-loop effective potential with a cutoff kept finite, matching the lattice data almost perfectly. By contrast, the effective potential with the cutoff removed à la Eq. (14) shows an artificial instability in strong disagreement with the non-perturbative simulation. This work has been criticized [68, 70] also because it is generically difficult on the lattice to bridge wide ranges of scales, in particular to separate the cutoff from the long-range mass scales by many orders of magnitude. As is clear from the above discussion, this problem does not exist for the present line of argument; the cutoff can be arbitrarily large in the above discussion of the fermion determinant. As long as it is finite, the interaction part of the determinant does not induce any instability.

• (2) For the above discussion and the comparison to the standard line of arguments at one-loop order, it has been sufficient to evaluate the determinant for a homogeneous mean field. Though this does not interfere with our argument, one might ask whether the determinant behaves qualitatively differently for non-homogeneous fields. Some exact results are known for $d=1+1$ dimensional determinants, where the Peierls instability at a finite chemical potential can lead to inhomogeneous ground states with lower free energy [71, 72]. However, the vacuum ground state is generically homogeneous as no mechanism exists that can “pay” for the higher cost in kinetic energy. Absolute lower and upper bounds for fermion determinants have been found, e.g., for QED [73].

• (3) The fact that the interaction part of the fermion contribution to the scalar potential is positive does not imply that the full theory cannot have further potentially (meta-) stable vacua. The conclusion rather is that such further vacua have to be provided by the bosonic sector. In particular, the bare bosonic potential $U_{\text {B}}$ can in principle be chosen such that it has several vacua.⁴ As a further special case, it is even possible to construct somewhat special examples such that the bare bosonic potential has one minimum, but the sum of $U_{\text {B}}$ and $U_{\text {F}}$ has two minima. This is still very different from the perturbative reasoning which for the present model seems to suggest a global instability due to the fermionic fluctuations, whereas a global instability of $U_{\text {B}}+U_{\text {F}}$ in our analysis would have to be seeded from the choice of $U_{\text {B}}$. The fact a second global minimum of the effective potential could be generated by physics in the UV has also been emphasized in [70]. To summarize, our arguments do not exclude that our electroweak vacuum is unstable, but they suggest that such an in/meta-stability would have to be provided by the microscopic underlying theory; see [74] for a specific example from string phenomenology. In this case, however, the Higgs-mass bounds from metastability as well as the life-time estimates of the electroweak vacuum would be very different from the conventional estimates; see e.g. [75].

• (4) As mentioned above, the result for the fermion determinant is regulator dependent, as long as the cutoff is kept finite. The preceding results have been derived for a sharp cutoff in momentum space. These results in fact generalize to arbitrary smooth cutoff shape functions in momentum space as they can be implemented straightforwardly within the functional RG framework; see below and Appendix B. Though this is not an issue for the present model, one might be concerned about the fact that such regularizations are not gauge invariant. Hence a gauge-invariant regularization is studied in the remainder of this section.

3.2 $\zeta$ function regularization

It is illustrative to study the fermion determinant also using $\zeta$ function regularization which can be used to interpolate between proper-time and dimensional regularization. For this, we write $U_{\text {F}}$ of Eq. (9) for one of the quark flavors as

$$\begin{aligned} U_{\text {F},a}(\rho ) = \frac{1}{2\Omega } \int _{1/\Lambda ^2}^\infty \frac{\mathrm{d}T}{T} \left( e^{-h_a^2 \rho T}-1 \right) \, \text {Tr}\, e^{\partial ^2 T}, \end{aligned}$$

(15)

where $T$ is a proper-time parameter, being introduced via Frullani’s formula for a representation of the logarithm. Here the lower bound of the $T$ integral serves as a (gauge-invariant) momentum cutoff. Furthermore, we now evaluate the momentum trace in $d$ dimensions and introduce an arbitrary dimensionful scale $\mu _0$ in order to implement the correct dimensionality of the potential, $\text {Tr} \rightarrow \text {tr}_\gamma \Omega \int \frac{\mathrm{d}^4 p}{(2\pi )^4} \rightarrow \text {tr}_\gamma \frac{\Omega }{\mu _0^{d-4}} \int \frac{\mathrm{d}^d p}{(2\pi )^d}$. We obtain,

$$\begin{aligned} U_{\text {F},a}(\rho ) = \frac{2\mu _0^{4-d}}{(4\pi )^{d/2}} \int _{1/\Lambda ^2}^\infty \frac{\mathrm{d}T}{T^{1+(d/2)}} \left( e^{-h_a^2 \rho T}-1 \right) . \end{aligned}$$

(16)

In the limit $d\rightarrow 4$, we have the standard proper-time regularization, whereas in the limit $\Lambda \rightarrow \infty$, we end up with dimensional regularization. Separating the mass term $\sim \rho$ as before, we get

$$\begin{aligned} U_{\text {F},a}(\rho )&= - \frac{4\mu _0^{4-d}}{(d-2)(4\pi )^{d/2}} h_a^2 \rho \Lambda ^{d-2}\end{aligned}$$

(17)

$$\begin{aligned}&+\frac{2\mu _0^{4-d}}{(4\pi )^{d/2}} \!\!\int _{\!1/\Lambda ^2}^\infty \!\! \frac{\mathrm{d}T}{T^{1+(d/2)}} \left( e^{-h_a^2 \rho T} +h_a^2\rho T -1 \right) .\nonumber \\ \end{aligned}$$

(18)

Again, we observe that the mass term (first line) contributes with the minus sign as expected, whereas the interaction part (second line) is a strictly positive function for all finite values of $\Lambda ,h_a,\rho ,d>0$. The conclusions are therefore identical to the ones for the sharp cutoff. Incidentally, the proper-time integration can be carried out analytically, the result can be written in terms of an incomplete $\Gamma$ function with the positivity properties of course remaining unchanged.

As the mass term will become part of the renormalized scalar mass term by means of a renormalization condition, let us now focus on the interaction part Eq. (18). In order to take the limit towards dimensional regularization, we first take the limit $\Lambda \rightarrow \infty$, and then expand about $d=4-\epsilon$, as is standard. We then find for the interaction part

$$\begin{aligned} U_{\text {F},a}(\rho )&\rightarrow \frac{2\mu _0^{4-d}}{(4\pi )^{d/2}} (h_a^2 \rho )^{d/2} \Gamma (-d/2)\end{aligned}$$

(19)

$$\begin{aligned}&= \frac{h_a^4 \rho ^2}{8\pi ^2} \frac{1}{\epsilon } \nonumber \\&- \frac{h_a^4 \rho ^2}{16\pi ^2}\left( \ln \frac{h_a^2 \rho }{\mu _0^2} + \text {const.}\right) + \mathcal {O}(\epsilon ). \end{aligned}$$

(20)

Following the standard recipes, we would absorb the positive $1/\epsilon$ divergence in the bare $\phi ^4$ term by means of a renormalization condition. The finite part in Eq. (20) is identical to that of the sharp cutoff in Eq. (14) in the limit $\Lambda \rightarrow \infty$ (apart from the scheme-dependent constants), seemingly indicating an instability at large field values. With dimensional regularization, we would therefore arrive at the standard conclusion that fermionic fluctuations can induce an instability of the vacuum at large fields.

Whereas for the sharp cutoff, this was an obvious artifact of the $\Lambda \rightarrow \infty$ limit, the failure is less obvious here. Nevertheless, as we have derived this misleading result of a negative contribution from a strictly positive expression given in Eq. (18), it is clear that the standard strategies of dimensional regularization fail to describe the global behavior of the fermion determinant properly. The reason is that dimensional regularization is not only a regularization but at the same time a projection solely onto the logarithmic divergencies. It has in fact long been known that the use of dimensional regularization in the presence of large fields can become delicate; procedures to deal with this problem typically suggest to go back to the dimensionally continued proper-time/$\zeta$-function representation that we started out with [76, 77].

There is another perspective that explains why the standard perturbative argument of integrating the $\beta$ function of the $\phi ^4$ theory is misleading as far as vacuum stability is concerned: the $\beta$ functions are typically derived in mass-independent regularization schemes (though mass-dependent schemes have recently also been studied [78]), and it is implicitly assumed that the discussion can be performed in the deep Euclidean region where all mass scales are much smaller than any of the involved momentum scales of the fluctuations. The latter assumption is in fact not valid, as both scales the value of the field as well as the cutoff $\Lambda$ can interfere non-trivially with each other. This is illustrated rather explicitly in the sharp-cutoff calculation given above.

4 Renormalization flow

Independently of the validity of the perturbative arguments about vacuum stability, the comparatively small mass of the observed Higgs boson [1, 2] poses a challenge: the fermionic fluctuations (dominated by top loops) contribute to the curvature of the effective potential which determines the Higgs boson mass. Even in the absence of any bosonic interactions, this appears to lead to a lower bound on the value of the Higgs mass which are in tension with the measured value. This line of argument has been used in quantitative lattice studies [37, 41–44]. For rendering simulations on a Euclidean lattice well defined, the bosonic action has to be bounded from below; in practice, lower bounds on the Higgs mass thus arise in the limit of the bare $\phi ^4$ coupling approaching zero, $\bar{\lambda }\rightarrow 0_+$.

While it is debatable whether this criterion could be relaxed for a Minkowskian functional integral in the continuum, we have already provided first examples in the $\mathbb {Z}_2$-symmetric Yukawa toy model that these conventional lower bounds can be relaxed by allowing for more general forms of the bare potential [51]. These results have recently been confirmed in lattice simulations [52]. In particular, no state of meta-/instability is required for relaxing the lower bound. In the following, we generalize these results to the chiral top–bottom–Higgs Yukawa model.

For this, we use the functional RG as a non-perturbative tool. Though our results for the lower Higgs-mass bound can in principle also be derived within a perturbative framework, the functional RG allows one to discuss weak-coupling limits (lower bounds) as well as the large-coupling region (upper bounds) in a unified setting. Also, more generalized bare actions can be dealt with more conveniently, the preceding fermion determinant results arise in a specific limit, and higher-loop effects as well as RG improvement are automatically included. Starting from a bare microscopic action $S$ defined at a UV cutoff $\Lambda$ (which may or may not be sent to infinity), the RG flow of a corresponding scale-dependent action $\Gamma _k$ is determined by the Wetterich equation [79],

$$\begin{aligned} \partial _t\Gamma _k = \frac{1}{2} \text {STr}\Big [ \frac{\partial _tR_k}{\Gamma _k^{(2)}+R_k} \Big ], \quad t=\ln \frac{k}{\Lambda }, \end{aligned}$$

(21)

which interpolates smoothly between microscopic physics, $\Gamma _{k=\Lambda }=S$, and the full quantum effective action, $\Gamma _{k=0}=\Gamma$. $\Gamma _k^{(2)}$ in Eq. (21) denotes the second derivative of $\Gamma _k$ with respect to the fluctuating fields ($\phi _a$, $t_{\text {L}}$, $\bar{t}_{\text {L}}$, $\ldots$) and the supertrace includes a minus sign for fermionic degrees of freedom. The regulator $R_k$ in the denominator acts as an IR cutoff for modes with momenta smaller than $k$. The derivative $\partial _tR_k$ at the same time provides for a UV regularization. For instance, for a suitable choice of $R_k$ in terms of a sharp cutoff, taking only the fermion loops of Eq. (21) into account reproduces the fermion determinant results given above. For detailed reviews of the functional RG, see [80–86].

We compute the effective average action at next-to-leading order (NLO) in a derivative expansion, corresponding to the following truncation:

$$\begin{aligned} \Gamma _k&= \int _x \left[ Z_{\phi }|\partial _{\mu }\phi |^2 + U(\phi ^{\dagger }\phi ) + Z_{\text {L}}\bar{\psi }_{\text {L}}i/\!\!{\partial }\psi _{\text {L}} + Z_{\text {R}}^{\text {t}}\bar{t}_{\text {R}}i/\!\!{\partial }t_{\text {R}} \right. \nonumber \\&\quad + Z_{\text {R}}^{\text {b}}\bar{b}_{\text {R}}i/\!\!{\partial }b_{\text {R}} + i\bar{h}_{\text {b}} (\bar{\psi }_{\text {L}}\phi b_{\text {R}} + \bar{b}_{\text {R}}\phi ^{\dagger }\psi _{\text {L}}) \nonumber \\&\quad \left. + i\bar{h}_{\text {t}} (\bar{\psi }_{\text {L}}\phi _{\mathcal {C}} t_{\text {R}} + \bar{t}_{\text {R}}\phi _{\mathcal {C}}^{\dagger }\psi _{\text {L}}) \right] . \end{aligned}$$

(22)

Here the scalar potential, both Yukawa couplings and the wave function renormalizations $Z_{\phi }$, $Z_{\text {L}}$, and $Z_{\text {R}}^{\text {t,b}}$ for the fields depend on the RG scale $k$ ($U=U_k$, $h_{\text {t}}=h_{\text {t},k}$, $\ldots$). For compactness of notation, this dependence is suppressed.

Inserting this truncation into the Wetterich equation leads to the $\beta$ functions, i.e., the flow equations for the effective potential, the Yukawa couplings as well as for the wave function renormalizations. The latter will be encoded in the anomalous dimensions of the fields,

$$\begin{aligned} \eta _i = -\partial _t\ln {Z_i}, \end{aligned}$$

where $i$ labels the different fields. Furthermore, it is useful to define dimensionless renormalized quantities, such as

$$\begin{aligned}&\rho = Z_{\phi }k^{2-d}\phi ^{\dagger }\phi \\&h_{\text {t}}^2 = Z_{\phi }^{-1}Z_{\text {L}}^{-1}{Z_{\text {R}}^{\text {t}}}^{-1}k^{d-4}\, \bar{h}_{\text {t}}^2, \\&h_{\text {b}}^2 = Z_{\phi }^{-1}Z_{\text {L}}^{-1}{Z_{\text {R}}^{\text {b}}}^{-1}k^{d-4}\, \bar{h}_{\text {b}}^2. \end{aligned}$$

Here and in the following, we work in $d$ dimensional spacetime for reasons of generality. Accordingly, the dimensionless potential simply reads

$$\begin{aligned} u = k^{-d} U. \end{aligned}$$

In the following, we list the flow equations for the various quantities, as they follow from the Wetterich equation, using standard calculation techniques; see, e.g., [87]. The flow equation for the potential can be written as

$$\begin{aligned} \partial _tu&= -\mathrm{d}u + (d-2+\eta _{\phi })\rho u' \nonumber \\&\quad + v_d \left( 3l_0^{d}(u') + l_0^{d}(u'+2\rho u'')\right) \nonumber \\&\quad - d_{\text {W}}v_{d}\left( l_{0\, \text {L}}^{(\text {F})d}(h_{\text {t}}^2\rho ) + l_{0\, \text {L}}^{(\text {F})d}(h_{\text {b}}^2\rho ) \right. \nonumber \\&\quad \left. + l_{0\, \text {R}_{\text {t}}}^{(\text {F})d}(h_{\text {t}}^2\rho ) + l_{0\, \text {R}_{\text {b}}}^{(\text {F})d}(h_{\text {b}}^2\rho ) \right) , \end{aligned}$$

(23)

where primes denote derivatives with respect to $\rho$. The threshold functions $l_0^d$, $l_{0\, \text {L}}^{(\text {F})d}$, $l_{0\, \text {R}_{\text {t}}}^{(\text {F})d}$, and $l_{0\, \text {R}_{\text {b}}}^{(\text {F})d}$ governing the decoupling of massive modes can be found in the appendix for the convenient choice of a linear regulator. Here, $v_d^{-1}=2^{d+1}\pi ^{d/2}\Gamma (d/2)$ and $d_{\text {W}}$ is the dimension of the spinor representation of the Weyl fermions. We will specialize to $d=4$ and $d_{\text {W}}=2$ for quantitative calculations. The flow equations for the Yukawa couplings are

$$\begin{aligned} \partial _th_{\text {t}}^2&= (d-4+\eta _{\phi }+\eta _{\text {L}}+\eta _{\text {R}}^{\text {t}})h_{\text {t}}^2 \nonumber \\&- 4v_d h_{\text {t}}^4 \Big [ (6\kappa u''+4\kappa ^2u''') l_{1,2}^{(\text {FB})d}(h_{\text {t}}^2\kappa ,u'+2\kappa u'')\nonumber \\&- 2\kappa u'' l_{1,2}^{(\text {FB})d}(h_{\text {t}}^2\kappa ,u') \nonumber \\&+ 2h_{\text {t}}^2\kappa \big ( l_{2,1}^{(\text {FB})d}(h_{\text {t}}^2\kappa ,u'+2\kappa u'') \nonumber \\&- l_{2,1}^{(\text {FB})d}(h_{\text {t}}^2\kappa ,u') \big ) - l_{1,1}^{(\text {FB})d}(h_{\text {t}}^2\kappa ,u'+2\kappa u'') \nonumber \\&+ l_{1,1}^{(\text {FB})d}(h_{\text {t}}^2\kappa ,u') \Big ] \nonumber \\&- 8v_d h_{\text {t}}^2h_{\text {b}}^2 \Big [ - 2\kappa u'' l_{1,2}^{(\text {FB})d}(h_{\text {b}}^2\kappa ,u')\nonumber \\&- 2h_{\text {b}}^2\kappa \, l_{2,1}^{(\text {FB})d}(h_{\text {b}}^2\kappa ,u') + \, l_{1,1}^{(\text {FB})d}(h_{\text {b}}^2\kappa ,u') \Big ] \Big |_{\rho =\kappa },\nonumber \\ \partial _th_{\text {b}}^2&= (d-4+\eta _{\phi }+\eta _{\text {L}}+\eta _{\text {R}}^{\text {b}})h_{\text {b}}^2 \nonumber \\&- 4v_d h_{\text {b}}^4 \Big [ (6\kappa u''+4\kappa ^2u''') l_{1,2}^{(\text {FB})d}(h_{\text {b}}^2\kappa ,u'+2\kappa u'')\nonumber \\&- 2\kappa u'' l_{1,2}^{(\text {FB})d}(h_{\text {b}}^2\kappa ,u') \nonumber \\&\quad + 2h_{\text {b}}^2\kappa \big ( l_{2,1}^{(\text {FB})d}(h_{\text {b}}^2\kappa ,u'+2\kappa u'')\nonumber \\&- l_{2,1}^{(\text {FB})d}(h_{\text {b}}^2\kappa ,u') \big ) - l_{1,1}^{(\text {FB})d}(h_{\text {b}}^2\kappa ,u'+2\kappa u'')\nonumber \\&+ l_{1,1}^{(\text {FB})d}(h_{\text {b}}^2\kappa ,u') \Big ] \nonumber \\&- 8v_d h_{\text {b}}^2h_{\text {t}}^2 \Big [ - 2\kappa u'' l_{1,2}^{(\text {FB})d}(h_{\text {t}}^2\kappa ,u')\nonumber \\&- 2h_{\text {t}}^2\kappa \, l_{2,1}^{(\text {FB})d}(h_{\text {t}}^2\kappa ,u') \!+\! l_{1,1}^{(\text {FB})d}(h_{\text {t}}^2\kappa ,u') \Big ] \Big |_{\rho =\kappa }, \end{aligned}$$

(24)

where $\kappa$ denotes the minimum of the potential. Finally, the anomalous dimensions are given by

$$\begin{aligned} \eta _{\phi }&= \frac{8v_d}{d}\kappa \big [ 3u''m_{22}^d(u') + (3u''+2\kappa u''')^2 m_{22}^d(u'+2\kappa u'') \big ] \nonumber \\&-\frac{8d_{\text {W}}}{d}v_d \Big [ \kappa h_{\text {t}}^4 m_2^{(\text {F})d}(h_{\text {t}}^2\kappa ) - h_{\text {t}}^2 m_4^{(\text {F})d}(h_{\text {t}}^2\kappa ;\eta _{\text {t}})\nonumber \\&+ \kappa h_{\text {b}}^4 m_2^{(\text {F})d}(h_{\text {b}}^2\kappa ) - h_{\text {b}}^2 m_4^{(\text {F})d}(h_{\text {b}}^2\kappa ;\eta _{\text {b}}) \Big ] \Big |_{\rho =\kappa },\nonumber \\ \eta _{L}&= \frac{4v_d}{d} \Big [ h_{\text {t}}^2\Big ( m_{1,2}^{(\text {FB})d}(\kappa h_{\text {t}}^2,u') + m_{1,2}^{(\text {FB})d}(\kappa h_{\text {t}}^2,u'+2\kappa u'') \Big ) \nonumber \\&+ 2h_{\text {b}}^2 m_{1,2}^{(\text {FB})d}(\kappa h_{\text {b}}^2,u') \Big ] \Big |_{\rho =\kappa }, \nonumber \\ \eta _{\text {R}}^{\text {t}}&= \frac{4v_d}{d}h_{\text {t}}^2 \big [ m_{1,2}^{(\text {FB})d}(h_{\text {t}}^2\kappa ,u')+m_{1,2}^{(\text {FB})d}(h_{\text {t}}^2\kappa ,u'+2\kappa u'')\nonumber \\&+ 2m_{1,2}^{(\text {FB})d}(h_{\text {b}}^2\kappa ,u') \big ] \Big |_{\rho =\kappa }, \nonumber \\ \eta _{\text {R}}^{\text {b}}&= \frac{4v_d}{d}h_{\text {b}}^2 \big [ m_{1,2}^{(\text {FB})d}(h_{\text {b}}^2\kappa ,u')+m_{1,2}^{(\text {FB})d}(h_{\text {b}}^2\kappa ,u'+2\kappa u'') \nonumber \\&+ 2m_{1,2}^{(\text {FB})d}(h_{\text {t}}^2\kappa ,u') \big ] \Big |_{\rho =\kappa }. \end{aligned}$$

(25)

Again, the definition of the threshold functions can be found in the appendix. Furthermore it is useful to define anomalous dimensions of the top and bottom quark via

$$\begin{aligned} \eta _{\text {t}} = \frac{1}{2} (\eta _{\text {L}} + \eta _{\text {R}}^{\text {t}}), \quad \eta _{\text {b}} = \frac{1}{2} (\eta _{\text {L}} + \eta _{\text {R}}^{\text {b}}). \end{aligned}$$

(26)

The flow equations agree with those for the $\mathbb {Z}_2$-symmetric Yukawa model [51, 88] in the limit of a vanishing bottom sector, $h_{\text {b}}=0$, and ignoring the terms arising from the additional scalar contributions.⁵ The reliability of the derivative expansion can be monitored with the aid of the anomalous dimension, providing a rough measure for the importance of the higher-derivative terms. In practice, we study the convergence of the derivative expansion by comparing leading-order results ($\eta _i=0$) to the full NLO calculation; see below.

5 Non-perturbative Higgs-mass bounds

The flow equations listed above enable us to take a fresh look at Higgs boson mass bounds possibly arising from the RG flow of the model. For this, it is useful to think of the RG flow as a mapping from a microscopic theory defined at some high scale $\Lambda$ onto the effective long-range theory governing the physics observed in collider experiments. For this mapping, we use the standard-model-type parameters $v=246$ GeV, $m_{\text {t}}=173$ GeV and $m_{\text {b}}=4.2$ GeV as constraints. The range of all possible Higgs boson masses resulting from the remaining UV parameters for a given cutoff then defines the IR window and correspondingly puts bounds on the Higgs boson mass as a function of the cutoff scale $\Lambda$.

In full generality, constructing this mapping is a complex problem, since the microscopic theory at scale $\Lambda$ is a priori unconstrained to a large extent. At first sight, it seems natural to allow only the renormalizable terms in the bare action. For the present model, this has been successfully implemented in extensive lattice simulations [37, 41–46] yielding quantitative results for the Higgs-mass bounds. In particular, the lower bound arises from the lowest possible value for the Higgs selfinteraction $\bar{\lambda }\phi ^4$, i.e., $\bar{\lambda }\rightarrow 0$, for which the lattice theory remains well defined. The resulting bounds should therefore not be viewed as vacuum stability bounds, but as consistency bounds arising from the requirement that the underlying lattice partition function is well defined.

However, there is no need at all to confine the bare theory to just the renormalizable operators. On the contrary, generic underlying theories (UV completions) are expected to produce all terms allowed by the symmetries, such that the search for Higgs-mass bounds corresponds to finding extrema of a function (the Higgs mass) depending on infinitely many variables (the bare action). Formulated in terms of this generality, it is actually unclear whether these extrema and thus a universal consistency bound would exist at all. We therefore confine our study to a much simpler question: given the lower mass bound arising within the conventional class of $\phi ^4$ potentials, can we find more general bare potentials, which (a) lower the mass bounds and (b) do not show an instability towards a different vacuum neither in the UV nor in the IR? While (a) is obviously inspired by the fact that the measured Higgs boson mass seems to lie below the conventional lower bound, an answer to (b) can serve as an illustration that no meta-stability is required in order to relax the lower bound.

While these two questions have been answered in the affirmative for the $\mathbb {Z}_2$-Yukawa model in [51] with functional RG methods as well as for the present chiral model with lattice simulations up to cutoff scales on the order of several TeV [52], the present flow equation study can elucidate the underlying RG mechanisms in more detail and can bridge a wide range of scales. Furthermore, it is straightforward to deal with two distinct quark masses, $h_{\text {t}}\ne h_{\text {b}}$, in our functional approach, whereas simulations with the physical ratio $m_{\text {t}}/m_{\text {b}}\simeq 40$ would be rather expensive on the lattice.

Before we turn to a quantitative analysis of the RG flow, we have to cure a deficiency of the chiral Yukawa model in comparison with the full standard-model top–bottom–Higgs sector. Since chiral symmetry breaking in the present model breaks a global symmetry, our present model has massless Goldstone bosons in the physical spectrum. This is different from the standard model where the would-be Goldstone bosons due to their interplay with the gauge sector are ultimately absent from the physical spectrum, the latter finally containing massive vector excitations. In order to make contact with the standard-model physics, we therefore have to modify our chiral Yukawa model, otherwise the massless Goldstone modes have the potential to induce an IR behavior which is very different from that of the standard model. This modification of the model is not unique and could be done in various ways. For instance on the lattice, the influence of the unwanted Goldstone bosons is identified by their strong finite volume effects and subtracted accordingly [41–46]. Similarly, we could study the onset of Goldstone dynamics in the limit $k\rightarrow 0$ and perform a similar subtraction.

In the present work, we model the decoupling of Goldstone bosons more physically as inspired by the Higgs mechanism in the fully gauged version of the theory: generically all dependencies on the particle masses and their decoupling is contained in the threshold functions of the flow equations. For the linear regulators used below, this dependence occurs in the form

$$\begin{aligned} \frac{k^2}{k^2+m^2} \end{aligned}$$

(27)

to some power. For $k\rightarrow 0$, all these functions vanish for finite particle masses $m$, whereas massless modes such as Goldstone modes with $m=m_{\text {G}}=0$ contribute equally on all scales $k$. (For other regulators, the functional dependence on $k$ and $m$ may look differently, but behaves analogously in the various limits.) The Goldstone modes can therefore directly be identified in our flow equations. They contribute to those threshold functions that contain an argument $\sim u'(\rho )$ in the SSB regime. As soon as we enter the broken regime, the corresponding mass argument $m_{\text {G}}^2/k^2 \sim u'(\kappa )$ vanishes at the running minimum $\kappa$ of the potential. We thus can dynamically remove the Goldstone modes by the replacement

$$\begin{aligned} \frac{k^2}{k^2+m_{\text {G}}^2} \rightarrow \frac{k^2}{k^2+m_{\text {G}}^2 + g\frac{v_k^2}{2}} \mathop {=}\limits ^{m_{\text {G}}=0} \frac{k^2}{k^2 + g\frac{v_k^2}{2}}, \end{aligned}$$

in the broken regime. Here, $v_k$ is the running vacuum expectation value approaching $v_k\rightarrow v$ in the long-range limit $k\rightarrow 0$, and $g$ is an a priori free parameter. Inspired by the decoupling of massive vector bosons in the full standard model, we choose $g$ in such a way that the resulting masses for the Goldstone bosons have the same order of magnitude as the $W$ boson mass scale, e.g. $g=2(80/246)^2$. It turns out that the result for the lower Higgs-mass bound is only slightly affected by different choices of $g$, as well as different choices of removing the Goldstone mode contributions, cf. Appendix C.

As a result, all fluctuations acquire a mass in the regime of spontaneous symmetry breaking (SSB) and the whole flow freezes out, similarly to the $\mathbb {Z}_2$ Yukawa model and as expected in the full standard model.

Now that we have amended our model with a dynamical removal of the unwanted Goldstone bosons, the RG flow of the model is technically similar to the simpler $\mathbb {Z}_2$ invariant Yukawa model extensively studied in [51]. In the following, we therefore focus on the new features induced by the additional degrees of freedom of the chiral model such as the bottom quark and the three additional real scalar fields. Further technical details follow those of [51].

The relevant information to compute Higgs-mass bounds can be extracted from the shape of the scalar effective potential near its minimum. We extract this information from a power series expansion of the potential about this flowing minimum. In the symmetric (SYM) regime, we expand about the zero field amplitude

$$\begin{aligned} u = \sum _{n=1}^{N_{\text {p}}} \frac{\lambda _n}{n!} \rho ^n \end{aligned}$$

in which $\lambda _1$ is a mass term and $\lambda _2$ the quartic coupling. $N_{\text {p}}$ defines the order of this polynomial expansion. In practice, all results studied in this work converge rather rapidly in this expansion. The expansion point in the SSB regime is set by the nonvanishing vev

$$\begin{aligned} u = \sum _{n=2}^{N_{\text {p}}} \frac{\lambda _n}{n!} (\rho -\kappa )^n. \end{aligned}$$

The flow equations for the couplings $\lambda _1,\ldots ,\lambda _{N_P}$ (SYM) or $\kappa$, $\lambda _2,\ldots ,\lambda _{N_P}$ (SSB) can be read off from Eq. (23).

5.1 Bare potentials of $\phi ^4$ type

First, we determine mass bounds for the Higgs boson arising from microscopic bare potentials of $\phi ^4$ type,

$$\begin{aligned} u_{\Lambda }&= \lambda _{1,\Lambda }\rho + \frac{\lambda _{2,\Lambda }}{2}\rho ^2&\mathrm {(SYM)}\end{aligned}$$

(28)

$$\begin{aligned} u_{\Lambda }&= \frac{\lambda _{2,\Lambda }}{2}(\rho -\kappa _{\Lambda })^2&\mathrm {(SSB)}. \end{aligned}$$

(29)

For small $\lambda _{2,\Lambda }$ a physical flow typically starts in the SYM regime. Near the electroweak scale the system is driven into the SSB regime by fermionic fluctuations. Mathematically speaking, we switch from the flow equation for the SYM to the SSB couplings at the scale, where $\lambda _1$ crosses zero. In the SSB regime a nonzero vev builds up, inducing masses for all particles in the theory including the would-be Goldstone bosons as discussed above. This results in a decoupling of all modes in the IR and therefore all dimensionful quantities freeze out.

By contrast: for large $\lambda _{2,\Lambda }$, the theory already starts in the SSB regime with a small value for $\kappa _{\Lambda }$. The flow still runs over many scales, depending on the initial conditions, until $\kappa$ eventually grows large near the electroweak scale. As a result, all modes decouple and we can read off the long-range observables.

The flow equation provide us with a map of the UV parameters to physical parameters such as the mass of the Higgs, the top or the bottom quark. In the following, we fine tune either $\lambda _{1,\Lambda }$ if we start in the SYM regime or $\kappa _{\Lambda }$ in the SSB regime, in order to arrive at a vev of $v_{k\rightarrow 0}=246$ GeV in the IR. Further, we vary the bare top $h_{t,\Lambda }$ and bottom $h_{b,\Lambda }$ Yukawa coupling such that we obtain the desired top and bottom quark mass, $m_{\text {t}}\simeq 173$ GeV and $m_{\text {b}}\simeq 4.2$ GeV. For this reduced class of bare $\phi ^4$ potentials, the Higgs mass is only a function of the bare quartic coupling $\lambda _{2,\Lambda }$ for a fixed cutoff. In order to start with a well-defined theory in the UV, $\lambda _{2,\Lambda }$ must be strictly nonnegative.

We find that the Higgs mass is a monotonically increasing function of the bare quartic coupling, which can be seen in Fig. 1. Here, the Higgs mass $m_{\text {H}}$ is plotted as a function of the bare quartic coupling $\lambda _{2,\Lambda }$ for a fixed cutoff $\Lambda =10^7$ GeV. The lower bound is approached for $\lambda _{2,\Lambda }\rightarrow 0$, where the Higgs mass becomes rather independent of $\lambda _{2,\Lambda }$. This was also shown in lattice simulations for the $\mathbb {Z}_2$ model [35] as well as for a chiral Yukawa theory [41–44]. For large bare quartic couplings the Higgs mass reaches a region of saturation.

To test the convergence of our expansion and truncation, we plotted the Higgs mass in various approximations in Fig. 1. The derivative expansion is tested by comparing leading-order (LO) (dashed lines) to NLO results (solid lines). At LO, we drop the running of the kinetic terms in Eq. (22), achieved by setting the anomalous dimensions to zero in the flow equation (23) and (24). These differ by at most $12\,\%$ for small as well as for large couplings. The difference for small couplings is somewhat larger than in the $\mathbb {Z}_2$-symmetric Yukawa model because of the larger number of fluctuating scalar components.

Furthermore, we varied $N_{\text {p}}$ to check the convergence of the polynomial expansion of the potential. The simplest non-trivial order is given by $N_{\text {p}}=2$ and plotted as red lines with squares in Fig. 1. For $N_{\text {p}}=4$ (blue lines with circles) there are only small deviations for small $\lambda _{2,\Lambda }$ ($\sim 2$ GeV) and deviations of $5\,\%$ for large $\lambda _{2,\Lambda }$ compared to $N_{\text {p}}=2$. Beyond this, we find no deviations between the Higgs masses for $N_{\text {p}}=4,5,6,8,10$ within our numerical accuracy, demonstrating the remarkable convergence of the polynomial truncation for the present purpose.

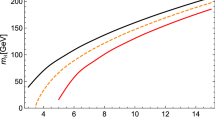
In Fig. 2, the resulting Higgs masses are plotted as a function of the UV cutoff for different bare quartic couplings for a wide range of cutoff values $\Lambda =10^3,\ldots ,10^9$ GeV. The lower black line is derived for $\lambda _{2,\Lambda }=0$ and indicates a lower bound for $m_{\text {H}}$ within the $\phi ^4$ type bare potentials. Incidentally, it agrees comparatively well with the results of a simple mean-field (“large-$N_{\mathrm {f}}$”) calculation sketched in the appendix. Dashed lines depict upper Higgs-mass bounds if one restricts the bare quartic coupling to $\lambda _{2,\Lambda }\le 1,10,100$ (from bottom to top). Artificially restricting the coupling $\lambda _{2,\Lambda }$ to the perturbatively accessible domain, say, $\lambda _{2,\Lambda }\lesssim 1$, the upper bound is obviously significantly underestimated.

By comparing the chiral Yukawa model to the $\mathbb {Z}_2$ Yukawa model, we are able to study the influence of the additional standard-model degrees of freedom on the Higgs-mass bounds. As expected, the bottom quark has no significant influence on the Higgs-mass values, due to its substantially smaller Yukawa coupling. Higgs-mass values only differ by less than $1$ GeV if one neglects the coupling of the bottom to the Higgs. The main new contributions to the scalar potential and thus to the Higgs mass are induced by the additional scalar degrees of freedom. For the lower bound $\lambda _{2,\Lambda }=0$ the scalar sector is weakly coupled, hence the Higgs mass is mainly build up by top fluctuations (apart from mutual RG backreactions). Therefore, the deviations between the two models are small for the lower Higgs-mass bounds. For a strongly coupled scalar sector in the UV, $\lambda _{2,\Lambda }>1$, the situation is different. There, the additional scalar degrees of freedom have a significantly larger impact. This results in smaller Higgs masses, since scalar fluctuations generically tend to drive the system into the SYM regime. The consequence of this is a flattening of the scalar potential near its minimum and hence a smaller value for the Higgs mass, which is visualized in Fig. 3.

Fig. 3

Higgs mass $m_{\text {H}}$ as a function of the cutoff $\Lambda$ for the chiral Higgs–Yukawa model (black solid lines) as well as for the simple $\mathbb {Z}_2$-symmetric Higgs–Yukawa theory (red dashed lines) as studied in [51]. For the lower mass bound no significant difference is observed between the two models. By contrast, a strongly coupled scalar sector ($\lambda _{\Lambda }=100$) leads to significantly lower masses in the present model which is a consequence of the additional scalar degrees of freedom in the chiral model; see main text

Finally, we should emphasize once more that the use of standard-model-like parameters is only for the purpose of illustration. The quantitative difference becomes obvious, e.g., from Fig. 2 where the “channel” of Higgs mass values that allow for a large cutoff is centered near $m_{\text {H}}\simeq 200$ GeV. The same channel-like behavior in the full standard model occurs near $m_{\text {H}}\simeq 130$ GeV. This quantitative difference is mainly due to the influence of the gauge sectors, in particular the strong interactions. But also the electroweak gauge sector can take a conceptually (if not quantitatively) important influence on mass bounds: e.g., recent non-perturbative lattice simulations of the Yang–Mills–Higgs system suggest that the Higgs mass has to be larger than the weak gauge-boson masses in certain parameter regimes, otherwise the electroweak sector would rather be in a QCD-like domain [94].

5.2 Generalized bare potentials

Motivated by previous continuum calculations in the $\mathbb {Z}_2$ model [51] and by lattice studies in the chiral version [52], we study whether more general bare potentials can modify the phenomenologically relevant lower Higgs-mass bound. The main purpose of this study is to demonstrate that the lower bound can be relaxed without the occurrence of an in- or metastability of the potential. An analysis of all conceivable bare potentials is a numerically challenging problem and beyond the scope of this work.

In fact, already the simplest extension including a $\phi ^6$ term in the bare potential,

$$\begin{aligned} u_{\Lambda } = \lambda _{1,\Lambda }\rho + \frac{\lambda _{2,\Lambda }}{2}\rho ^2 + \frac{\lambda _{3,\Lambda }}{6}\rho ^3, \end{aligned}$$

(30)

suffices to illustrate our main point. Here, negative values for the bare quartic coupling $\lambda _{2,\Lambda }$ are permissible if the potential is stabilized by a positive $\lambda _{3,\Lambda }$. Precisely choices of this type indeed lead to the desired features.

In Fig. 4 we illustrate this generic feature by a simple example. The black dashed line depicts the lower bound within $\phi ^4$ theory ($\lambda _{2,\Lambda }=\lambda _{3,\Lambda }=0$), whereas the red solid line shows Higgs masses for the initial data $\lambda _{2,\Lambda }=-0.1$ and $\lambda _{3,\Lambda }=3$. This example flow shows that the lower Higgs-mass bound can be significantly relaxed if the restriction to bare potentials of $\phi ^4$ type is dropped. We emphasize that this restriction to renormalizable operators is meaningless for the bare action as Wilsonian renormalizability arguments do not apply to the bare field theory action that might be generated from an unknown underlying UV complete theory.

Fig. 4

Higgs mass $m_{\text {H}}$ as a function of the cutoff $\Lambda$. The black dashed curve again corresponds to the lower bound derived within the class of $\phi ^4$-type bare potential. The red solid line shows an example of Higgs boson mass values derived from a more general class of bare potentials of Eq. (30) with the initial UV values $\lambda _{2,\Lambda }=-0.1$ and $\lambda _{3,\Lambda }=3$. This demonstrates both that the lower bound can be significantly relaxed and that no in- or metastability is required to occur for Higgs masses below the conventional lower bound

Similarly to the $\mathbb {Z}_2$ invariant model, this phenomenon of a relaxed bound as a consequence of a modified bare theory can be understood by the RG flow itself [51]. First note that the parameters for the generalized bare potential are chosen in such a way that the potential is initially in the SYM regime; this is also true for the lower bound within $\phi ^4$ theory. In the present case of the generalized bare potential, the negative quartic coupling $\lambda _2$ flows quickly to positive values whereas $\lambda _3$ becomes small as expected in the vicinity of the Gaußian fixed point. Therefore, the system essentially flows back into the class of $\phi ^4$-type potentials. In other words, the system defined for a fixed cutoff $\Lambda$ with $\lambda _{2,\Lambda }<0$ and $\lambda _{3,\Lambda }>0$ can be mapped to a system with $\lambda _{2,\Lambda }>0$ and $\lambda _{3,\Lambda }\approx 0$ for an effectively smaller cutoff $\tilde{\Lambda }<\Lambda$. Roughly speaking some RG time is required to flow from the beyond-$\phi ^4$-type potentials back to the class of standard $\phi ^4$-type potentials. Thereby, the red dashed line can be interpreted as a horizontally shifted variant of the Higgs mass curve derived from $\phi ^4$ potentials for effectively larger cutoffs.

We emphasize that the effective potential is stable at all scales with one well-defined minimum for the present choice of parameters.⁶ Finally, we would like to point out that the non-perturbatively computed effective potential for a finite cutoff is of course regularization scheme dependent much in the same way as the fermion determinant presented above. Choosing different regulator shape functions would also lead to (typically slightly) different Higgs mass curves in Figs. 1, 2, 3 and 4. We expect that this scheme change could be compensated for by a corresponding change of the bare action. Hence, it suffices to vary only the bare action for a fixed regulator in order to illustrate our main points.

6 Conclusions

6.1 Summary

We have analyzed a chiral Yukawa model featuring the interactions of a scalar SU(2) Higgs field with a chiral top-bottom quark sector similar to the Higgs sector of the standard model. We have critically re-examined conventional perturbative arguments that relate a lower bound for the Higgs mass with the stability of the effective potential. Based on exact results for the regularized fermion determinant, we have shown that the interacting part of the fermion determinant contributes strictly positively to the effective scalar potential for any finite field value – as long as the UV cutoff $\Lambda$ is kept finite. We have shown that this result holds for a variety of regularization schemes including the sharp momentum cutoff as well as (gauge-invariant) $\zeta$-function/proper-time regularization schemes.

Furthermore, we have shown that the conventional perturbative conclusion of a vacuum in-/metastability of the effective potential due to top fluctuations can be rediscovered if the cutoff is forced to approach infinity together with standard ad hoc recipes to project onto the finite parts. For the example of the sharp cutoff, we have shown explicitly that this corresponds to an illegitimate order of limits, as the resulting instability occurs at scalar field values where the supposedly small expansion parameter of the $\Lambda \rightarrow \infty$ limit is actually of order 1. A similar failure occurs for dimensional regularization where the standard procedures of projecting onto the finite parts violate the positivity properties of the interacting part of the effective potential. Our findings corroborate earlier results from non-perturbative lattice simulations [35, 36], but in addition allow for a large separation of the UV cutoff from the Fermi scale and an analytic control of the corresponding limits.

Because of the presumable triviality of the present model as well as the Higgs sector of the full standard model, the cutoff most likely cannot be removed from the theory – at least not within a straightforward manner. The cutoff as well as a corresponding regularization scheme should rather be viewed as part of the definition of our particle physics models that parametrize the embedding of this field-theory description into a possibly UV complete theory. Still, as long as the cutoff is large compared to the Fermi scale, Wilsonian renormalization arguments guarantee that the low-energy observables are largely insensitive to the details of this embedding. We have demonstrated that a counter-example to this generic rule is given by bounds on the mass of the Higgs boson.

In this work, we have not performed an exhaustive analysis of different bare actions or potentials, but simply focused on a constructive example that leads to Higgs boson masses below the conventional lower bound. Most importantly, this example exhibits no vacuum in-/metastability.

This together with our basic line of argument involving exact results for the fermion determinant demonstrate that there is no reason for concern arising from top-quark fluctuations as far as false vacuum decay in our universe is concerned, despite the comparatively light value of the measured Higgs mass. This does not mean that there might be no reason for concern at all. For instance, if the bare scalar potential itself features an instability induced by the underlying UV complete theory, our standard model could still live in an un- or metastable vacuum. Our arguments only exclude instabilities caused by the fluctuations of the fermionic matter fields within the standard model.

6.2 Vacuum stability vs. consistency bounds

Our results suggest a revision of the standard picture of Higgs mass bounds as a function of the UV cutoff. Depending on the implicit assumptions made to derive mass bounds, this revision might be more or less significant.

From our results on fermion determinants, it is clear that the conventional interpretation that top-quark fluctuations induce a vacuum instability is not tenable; this interpretation is a result of taking an inconsistent $\Lambda \rightarrow \infty$ limit. Still, the top-quark fluctuations play, of course, a decisive role for the value of the Higgs mass. In order to reconcile these observations, we propose a UV-to-IR viewpoint: the Higgs-mass bounds should be understood as a mapping from initial conditions set at the UV cutoff given in terms of a microscopic bare action $S_\Lambda$ onto all IR values accessible by the RG flow of the system, $m_{\text {H}}=m_{\text {H}}[\Lambda ;S_\Lambda ]$. In this manner, Higgs-mass bounds arise from consistency conditions imposed on the bare action. For instance, in order to start from a well-defined (Euclidean) partition function, the action needs to be bounded from below.

The conventional vacuum stability bounds then are approximately equivalent to such a consistency bound arising within a restricted class of bare actions, e.g., bare potentials of $\phi ^4$ type; here, the bare $\phi ^4$ coupling is required to be positive for consistency of the generating functional. However, as the bare action is not at our disposal but generally a result of the underlying UV embedding, there is no reason to make such restrictive assumptions. Already for slightly more general bare actions, we have been able to show that the conventional lower mass bounds can be substantially relaxed in the present chiral Yukawa model. The reason is that a more general bare action can modify the RG flow near and below the cutoff. As a result, the consistency bound lies below the vacuum stability bound. In particular, we have given an explicit example with a Higgs boson mass below the “stability bound” but an in fact stable effective potential on all scales; our results are in agreement with lattice simulations [52] and extend them to a much wider range of scales.

Determining the consistency bound remains an open problem, the solution of which requires further assumptions. One natural but not necessary assumption could be that the effective action should feature a unique minimum on all scales. The consistency bound would then arise from a complicated extremization problem in the space of all consistent bare actions subject to the unique-minimum constraint (to be satisfied on all scales). Even in this case, it seems unclear whether the bound remains finite. Therefore, it appears reasonable to add another physical assumption: since the bare action is expected to be provided by an underlying (UV complete) theory at scale $\Lambda$, it is natural to assume (in the absence of any concrete knowledge about the underlying theory) that the couplings of all possible operators are of order $\mathcal {O}(1)$ if measured in terms of $\Lambda$. For future studies, it is one of the most pressing questions to quantitatively estimate the resulting consistency bound under such a set of assumptions.

Of course, it appears equally legitimate to give up the criterion of a unique minimum at all scales, but instead allow for further minima in the bare action. If the resulting IR effective action turns out to have one unique minimum again (to be identified with the electroweak minimum), such bare actions can lead to a further relaxation of the consistency bound described above. In the general case, it should be possible to construct bare actions with multiple local minima such that the full effective action has a global minimum different from the local electroweak minimum. Since such bare actions are less constrained than those of the preceding scenarios, we expect the resulting lower Higgs mass consistency bounds to be even more relaxed to smaller values. Again, a quantitative estimate of such consistency bounds including metastable scenarios remains an urgent question.

Comparing the conventional stability bounds with the present consistency bounds, the overall picture seems to be qualitatively similar. The primary main difference is of quantitative nature, since the unique-minimum consistency bound lies below the stability bound. Wilsonian RG arguments, however, suggest that this difference could become small for large UV cutoffs, as is also reflected by the example of Fig. 4. Nevertheless, the size of this quantitative difference substantially depends on the assumptions imposed on the size of the couplings in the bare action. Also, the consistency bound is necessarily regularization scheme dependent. As the regularization actually should model the details of the embedding into the underlying UV completion, this dependence has a physical meaning. Even larger differences are expected between the conventional meta-stability bound and the consistency bound including metastable scenarios. The reason is that the metastable features are expected to arise from the bare action and thus are largely unknown. The size of the metastable region and corresponding life-time estimates will be even more subject to assumptions on the bare action.

6.3 Outlook

Independently of whether the measured value of the Higgs boson mass eventually turns out to lie slightly above or below the conventional lower bound, it is remarkable that the Higgs- and top-mass parameters appear to lie close to a region in the IR parameter space that can be connected to a bare UV effective potential that could exhibit almost vanishing scalar self-interactions. In this sense, a precise measurement of these mass parameters is relevant beyond the pure goal of precision data. These measurements can impose requirements that any UV embedding has to satisfy. The viewpoint of consistency bounds presented above provides a means to quantify these requirements. Therefore, a comprehensive quantitative exploration of these bounds appears most pressing.

One scenario appears particularly interesting: if the Higgs mass eventually turns out to be exactly compatible with a UV flat potential (apart from a possible mass term), a corresponding embedding would have to explain this rather particular feature. It is interesting to note that such scenarios exist even within purely quantum field theory approaches as, for instance, in models with asymptotically safe gravity [95, 96].

Recently, an asymptotically safe/free scenario in a gauged chiral Yukawa model has been identified [93], the UV limit of which corresponds to a flat scalar potential also allowing for comparatively light Higgs masses in the IR. In order to explore this option of a UV complete limit, we perform an RG fixed-point search also within this model along the lines of [89, 90] in Appendix E. However, in this ungauged model, we find no reliable indication for the existence of a non-Gaußian fixed point. Still, our present findings should serve as a strong motivation to further search for asymptotically free gauged chiral models with viable low-energy properties.

Appendices

Appendix A: Threshold functions

The threshold functions $l,m$ in the flow equations for the various couplings parametrize the decoupling of massive modes. As a function of their mass-type arguments, they approach zero in the limit of large masses and tend to a constant value in the zero-mass limit. The explicit form of these threshold functions depends on the regulator, characterizing the details of the momentum–shell integration. In this work, we use the linear regulator [97, 98] which allows one to work out the threshold functions analytically. For the bosonic modes, this regulator is given by

$$\begin{aligned} R_k(p)= Z_{\phi } p^2 \, r(p^2/k^2) = Z_{\phi }(k^2-p^2)\theta (k^2-p^2). \end{aligned}$$

The corresponding chirally symmetric fermionic regulator $R_k(p)=Z_{\psi } p\!\!\!/ r_{\text {F}}(p^2/k^2)$ is chosen such that $p^2(1+r)=p^2(1+r_{\text {F}})^2$. For reasons of completeness, we list the threshold functions appearing in the main text for the linear regulator:

$$\begin{aligned} l_n^d(\omega )&= \frac{4(\delta _{n,0}+n)}{d}\frac{1-\frac{\eta _{\phi }}{d+2}}{(1+\omega )^{n+1}}, \\ l_{0\, \text {L}}^{(\text {F})d}(\omega )&= \frac{4(\delta _{n,0}+n)}{d} \frac{1-\frac{\eta _{L}}{d+1}}{(1+\omega )^{n+1}}, \\ l_{0\, \text {R}_{\text {t/b}}}^{(\text {F})d}(\omega )&= \frac{4(\delta _{n,0}+n)}{d} \frac{1-\frac{\eta _{R}^{t/b}}{d+1}}{(1+\omega )^{n+1}}, \\ l_{n_1,n_2}^{(\text {FB})d}(\omega _1,\omega _2;\eta _{\psi },\eta _{\phi })&= \frac{2}{d}\frac{1}{(1+\omega _1)^{n_1}}\frac{1}{(1+\omega _2)^{n_2}} \\&\quad \times \left[ \frac{n_1 \left( 1\!\!-\!\!\frac{\eta _{\psi }}{d\!+\!1}\right) }{1+\omega _1} \!+\! \frac{n_2 \left( 1\!-\!\frac{\eta _{\phi }}{d\!+\!2}\right) }{1+\omega _2} \right] , \\ m_{n_1,n_2}^d(\omega _1,\omega _2)&= \frac{1}{(1+\omega _1)^{n_1}(1+\omega _2)^{n_2}}, \\ m_2^{(\text {F})d}(\omega )&= \frac{1}{(1+\omega )^4}, \end{aligned}$$

$$\begin{aligned} m_4^{(\text {F})d}(\omega ;\eta _{\psi })&= \frac{1}{(1+\omega )^4} + \frac{1-\eta _{\psi }}{d-2}\frac{1}{(1+\omega )^3} \\&\quad - \left( \frac{1-\eta _{\psi }}{2d-4} + \frac{1}{4} \right) \frac{1}{(1+\omega )^2}, \\ m_{n_1,n_2}^{(\text {FB})d}(\omega _1,\omega _2;\eta _{\psi },\eta _{\phi })&= \frac{1-\frac{\eta _{\phi }}{d+1}}{(1+\omega _1)^{n_1}(1+\omega _2)^{n_2}}. \end{aligned}$$

These threshold functions agree with those given in [99].

Appendix B: Mean-field effective potential

Let us generalize our results for the fermionic determinant obtained for a sharp cutoff in the main text to a wider class of regulator shape functions in this section. This corresponds to a mean-field analysis of the effective scalar potential for general momentum–space regularization schemes. More technically speaking we integrate Eq. (23) for fixed Yukawa couplings, $h_a \rightarrow h_{a,\Lambda }$ ($a=\{\text {t,b}\}$), as well as fixed wave function renormalizations, $Z_i \rightarrow 1$, where the subscript $i$ labels the different fields, from $k=\Lambda$ to $k=0$. In addition we also neglect the bosonic contributions on the right-hand side of Eq. (23). The resulting mean-field potential reads

$$\begin{aligned} U_k^{\text {MF}}(\rho ) \!=\! U_{\Lambda }(\rho ) \!+\! d_{\text {W}} \int _p \sum _{a\!=\!\{\text {t},\text {b}\}} \ln { \frac{p^2(1\!+\!r_{\text {F},\Lambda })^2 \!+\! h_{a,\Lambda }^2\rho }{p^2(1\!+\!r_{\text {F},k})^2 \!+\! h_{a,\Lambda }^2\rho } },\nonumber \\ \end{aligned}$$

(B.1)

where the regulator shape function $r_{\text {F}}$ depends on the momentum as well as on the RG scale, $r_{\text {F},k}=r_{\text {F}}(p^2/k^2)$. In order to provide for a regularization, $r_\text {F}(x)$ should vanish for large argument and diverge sufficiently fast to positive infinity for $x\rightarrow 0$. Apart from analyticity for all finite $x>0$, no further requirements on $r_{\text {F}}$ are needed; however, for an interpretation of a physical regularization, we assume $r_{\text {F}}$ to be positive for finite $x$. The second derivative of the mean-field effective potential with respect to $\rho$ encodes the fermionic contributions to the interacting part of the effective potential:

$$\begin{aligned}&{U_{k=0}^{\text {MF}}}''(\rho ) = U_{\Lambda }''(\rho ) + \frac{d_{\text {W}}}{8\pi ^2} \sum _{a=\{\text {t},\text {b}\}} h_{a,\Lambda }^4 \\&\times \!\! \int _0^{\infty }\!\!\! dp\, p^3 \frac{[p^2(1\!+\!r_{\text {F},\Lambda })^2\!-\!p^2][p^2(1\!+\!r_{\text {F},\Lambda })^2 \!+\! p^2 \!+\! 2h_{a,\Lambda }^2\rho ]}{[p^2(1\!+\!r_{\text {F},\Lambda })^2\!+\!h_{a,\Lambda }^2\rho ]^2 [p^2\!+\!h_{a,\Lambda }^2\rho ]^2}. \end{aligned}$$

The integrand is strictly positive for $r_{\text {F}}>0$ and so is the integral. This corroborates the conclusion in the main text that the interaction part of the fermion determinant is strictly positive for a wide class of regulators.

Furthermore it is instructive to calculate the Higgs boson mass in this simple approximation. For the linear regulator the mean-field effective potential for $k=0$ reads

$$\begin{aligned} U^{\text {MF}}&= U_{\Lambda } + \frac{d_{\text {W}}}{32\pi ^2}\\&\quad \times \sum _{a=\{\text {t},\text {b}\}} \left[ -h_{a,\Lambda }^2\rho \Lambda ^2 + (h_{a,\Lambda }^2\rho )^2 \ln {\left( 1+\frac{\Lambda ^2}{h_{a,\Lambda }^2\rho }\right) } \right] , \end{aligned}$$

where the decomposition into a negative mass-like term $\sim \rho$ and a positive interaction part is manifest. The Higgs boson mass is now given as the second derivative of the potential at the nonvanishing minimum $v=246$ GeV (${U^{\text {MF}}}'(v)=0$):

$$\begin{aligned} m_{\text {H}}^2&= 2\rho \frac{\partial ^2 U^{\text {MF}}}{\partial \rho ^2} \Bigg |_{\rho =v^2/2} \\&= \frac{m_{\text {t}}^4}{4\pi ^2v^2} \left[ 2\ln {\left( 1+\frac{\Lambda ^2}{m_{\text {t}}^2}\right) } - \frac{3\Lambda ^4+2\Lambda ^2m_{\text {t}}^2}{(\Lambda ^2+m_{\text {t}}^2)^2} \right] \\&\quad + \frac{m_{\text {b}}^4}{4\pi ^2v^2} \left[ 2\ln {\left( 1+\frac{\Lambda ^2}{m_{\text {b}}^2}\right) } - \frac{3\Lambda ^4+2\Lambda ^2m_{\text {b}}^2}{(\Lambda ^2+m_{\text {b}}^2)^2} \right] \\&\quad + v^2U_{\Lambda }''\Big (\frac{v^2}{2}\Big ), \end{aligned}$$

where we have used $d_{\text {W}}=2$ for 2-component Weyl fermions. Here it is obvious that the restricted class of quartic bare potentials ($U_{\Lambda }''=\lambda _\Lambda \ge 0$) gives rise to a lower bound for the Higgs mass for $\lambda _\Lambda =0$, nonetheless no instability is induced by the fermionic fluctuations.

Appendix C: Cutoff mechanism for the Goldstone modes

In the main text, we have amended the chiral Yukawa model with a dynamical mechanism that effectively removes the Goldstone bosons from the low-energy spectrum by providing them with a mass of the order of the gauge-boson mass in the full standard model. Conceptually, this mechanism can be viewed as an IR deformation of our model and is neither universal nor unique. Here, we explore the sensitivity of our results for the Higgs boson mass on the details of this mechanism.

Within our deformation, let us vary the parameter $g$, which controls the size of the effective mass for the Goldstone bosons proportional to the vev, $m_{\text {G}}^2 = (1/2) g v_k^2$. Figure 5 shows the Higgs mass depending on the effective Goldstone mass at $\Lambda =10^7$ GeV. For a weakly coupled scalar sector, $\bar{\lambda }_{\Lambda }=0$ (blue squares), the impact of $g$ on $m_{\text {H}}$ is insignificant. Even if the Goldstone mass changes by an order of magnitude the influence on the Higgs mass is less than 2 GeV. The situation is different for a strong scalar coupling, e.g., $\bar{\lambda }_{\Lambda }=10$ (red circles). For large effective Goldstone masses ($m_{\text {G}}>m_{\text {H}}$), we observe again only small deviations from the case $m_{\text {G}}=80$ GeV. This is because the Goldstone modes decouple roughly at the same scale as the top and the Higgs. However, if we choose smaller values of $m_{\text {G}}$ the deviations become larger, e.g., we observe a deviation of $20\,\%$ for $m_{\text {G}}=20$ GeV compared to the case of $m_{\text {G}}=80$ GeV. Now, the Goldstone modes contribute over a wider range of scales to the flow equations than the Higgs or the top quark. This results in a smaller Higgs mass. For vanishing $m_{\text {G}}$ we observe a log-like running of $\lambda _2$ (which is presumably an artifact of our definition of this coupling in terms of a Cartesian field decomposition). As a result, $m_{\text {H}}$ approaches smaller and smaller values in the limit $g\rightarrow 0$.

Of course, beyond the deformation of the model chosen in this work, other methods are conceivable to effectively remove the massless Goldstone bosons to mimic the physics of the fully gauged standard model. One option is to choose an arbitrary scale $k_{\text {nG}}$ within the SSB regime of the flow, below which all Goldstone boson contributions to the flow equations for RG scales smaller than $k_{\text {nG}}$. This corresponds to switching on a source at $k_{\text {nG}}$, which gives the Goldstone modes an infinitely large mass and leads to an ad hoc decoupling. Another possibility is to introduce a source term $J^a\phi ^a$ on the level of the Lagrangian. This would leave the flow equations unchanged because only the Hessian of the effective average action $\Gamma _k^{(2)}$ contributes to the Wetterich equation. Still, the shape of the scalar potential would be changed by this explicit symmetry breaking term. As a result, source-dependent mass terms for all scalar degrees of freedom are induced, and also the vev as well as the couplings become source dependent, $\kappa =\kappa (J)$, $\lambda _n=\lambda _n(J)$. In any case, each of these different IR deformations of the model leads to similar results. They parametrize a decoupling of the Goldstone modes removing the contamination of the IR flow by particle degrees of freedom which would not be present in the standard model.

Fig. 5

Higgs mass $m_{\text {H}}$ as a function of the modeled mass of the would-be Goldstone bosons for a weakly coupled ($\lambda _{2,\Lambda }=0$, blue squares) as well as for a strongly coupled ($\lambda _{2,\Lambda }=10$, red circles) scalar sector. The filled characters mark the Higgs masses computed for the value $m_G=80$ GeV, which we have used in the main text to derive our quantitative results

Appendix D: Impact of the top-quark mass on Higgs mass values

The top mass plays an important role in the study of the lower Higgs mass bound within $\phi ^4$ theory. Within the perturbative line of reasoning, a change of the top mass by 1 GeV goes along with a change of the Higgs-mass bound by approximately 2 GeV in standard-model calculations. As the Higgs mass is near (or presumably below) the conventional lower bound, an accurate determination of the mass of the top quark in the appropriate renormalization scheme [32] is crucial for a discussion of the consequences of this “near criticality” [34].

In this appendix, we study the values for the Higgs boson mass for a given initial bare potential of $\phi ^4$ as a function of the top quark mass in order to analyze the top-quark mass dependence in the present model. Within our truncation of the effective action, our top-mass IR parameter automatically coincides with the pole mass, the latter being the phenomenologically relevant quantity. Differences (straightforwardly computable) between these mass parameters only arise at next-to-next-to-leading order in the derivative expansion.

For the class of $\phi ^4$-type bare potentials, Table 1 summarizes our results for the Higgs mass for the lower mass bound ($\lambda _{2,\Lambda }=0$) as well as for a strongly coupled scalar sector ($\lambda _{2,\Lambda }=10$) as a function of the top-quark mass for $\Lambda = 10^7$ GeV. For the weakly coupled scalar sector, $\lambda _{2,\Lambda }=0$, the Higgs mass is generated essentially through top-quark fluctuations. Therefore, the resulting Higgs mass values are most sensitive to the precise mass of the top quark. In the present model, the Higgs mass is shifted by approximately 3 GeV for a change in the top mass by 2 GeV using a cutoff of $\Lambda =10^7$ GeV. With increasing cutoff the deviation of the Higgs mass is larger. This phenomenon is illustrated in Fig. 6 where the spread of the lower bound for larger cutoff scales is shown.

Table 1 Higgs masses for the lower bound ($\lambda _{2,\Lambda }=0$) and for a strongly interacting scalar sector ($\lambda _{2,\Lambda }=10$) for a cutoff of $\Lambda =10^7$ GeV as a function of the top-quark mass. Bold numbers indicate the standard top mass of 173 GeV

By contrast, we find only a slight impact of the top mass on the Higgs mass for the case of a strongly coupled scalar sector. This illustrates that the Higgs mass is rather dominated by scalar fluctuations in this regime.

Fig. 6

Higgs mass $m_{\text {H}}$ as a function of the cutoff $\Lambda$ for different values of $m_{\text {t}}$. The black solid line is the lower bound for $m_{\text {t}}=173$ GeV using $\lambda _{2,\Lambda }=0$ for a $\phi ^4$-type bare potential. In addition lower Higgs-mass bounds for $m_{\text {t}}=163$ GeV (red dashed lower curve) and $m_{\text {t}}=183$ GeV (blue dotted upper line) are plotted

Appendix E: Fixed-point structure

As the flow equation provides us with information about the system beyond perturbative limitations, we can explore the properties of the model also at stronger coupling. In particular, it is worthwhile to search for possible RG fixed points at finite values of the couplings (non-Gaußian fixed points), as these offer the chance to evade the triviality problem. Pure field-theory UV completions are possible within the asymptotic safety scenario, where the UV limit $\Lambda \rightarrow \infty$ can be taken safely by means of a UV stable RG fixed point [100], as is even explored for quantum gravity [101–106]; see [107–109] for reviews and examples. Provided such a fixed point exists and has suitable properties the theory remains interacting (non-trivial) in the long-range limit and has predictive power.

The search for such fixed points in Yukawa systems has recently been revived with systematic studies in the framework of the functional renormalization group. A general mechanism for inducing asymptotic safety in such systems has been identified in [88], relying on a dynamical balance between boson and fermion fluctuations. Chiral Yukawa models have successively been studied in this context [89, 90] providing hints for the possible existence of such fixed points, but also indicating that fully gauged models may be required for a stable asymptotic safety scenario of standard-model like theories. Gauged models indeed appear to offer different routes to UV complete theories either in the weak-coupling asymptotically free limit [93], at fully interacting fixed points (including the loss of asymptotic freedom) [110], or even in combination with quantum gravity [111–113]. In fact, asymptotic safety has become a viable concept of consistently quantizing gravity in the recent years. Also nonlinear chiral models have been explored along this direction [114].

Here, we concentrate again on the pure chiral Yukawa sector, performing an analysis much in the spirit of [89, 90], paying particular attention to the additional bottom quark degree of freedom.

1.1 E.1 Symmetric regime

Whereas the mechanism identified in [88] operates in the regime of spontaneous symmetry breaking, it is instructive to start the fixed-point search in the symmetric regime, where the flow equations are less complex.

The flow equations for the Yukawa couplings using the linear regulator read in this regime

$$\begin{aligned} \partial _th_{\text {t}}^2&= h_{\text {t}}^2 \Bigg [ \eta _{\phi }+2\eta _{\text {t}} \\&\quad \qquad \quad - h_{\text {b}}^2\frac{16v_d}{d}\left( \frac{1-\frac{\eta _{\text {t}}}{d+1}}{1+\lambda _1}+\frac{1-\frac{\eta _{\phi }}{d+2}}{(1+\lambda _1)^2} \right) \Bigg ], \\ \partial _th_{\text {b}}^2&= h_{\text {b}}^2 \Bigg [ \eta _{\phi }+2\eta _{\text {b}} \\&\quad \qquad \quad - h_{\text {t}}^2\frac{16v_d}{d} \left( \frac{1-\frac{\eta _{\text {b}}}{d+1}}{1+\lambda _1}+\frac{1-\frac{\eta _\phi }{d+2}}{(1+\lambda _1)^2} \right) \Bigg ], \end{aligned}$$

where $\lambda _1\ge 0$ corresponds to the mass-like term in the effective potential in the SYM regime. Let us start with resolving the fixed-point conditions $\partial _th_{\text {t}}^2=0$ and $\partial _th_{\text {b}}^2=0$ in leading order in the derivative expansion: for $\eta _i=0$, both conditions can be satisfied for either $h_{\text {b}}=0$ and $h_{\text {t}}$ arbitrary or vice versa. Without loss of generality, let us assume that $h_{\text {b}}=0$, leaving us with a free parameter $h_{\text {t}}^*$, labeling a potential line of fixed points. Now it is easy also to solve the fixed-point condition for the effective potential, $\partial _tu = 0$, cf. Eq. (23), with an arbitrarily chosen value for $h_{\text {t}}^*$ at least within a polynomial expansion of $u(\rho )$. We do not pursue this any further, since this line of fixed points does not exist beyond leading order.

At next-to leading order it is necessary to include the equations for the anomalous dimensions, which read for the linear regulator in the SYM regime

$$\begin{aligned} \eta _{\phi }&= \frac{8v_d}{d}\big [ h_{\text {t}}^2(4-\eta _{\text {t}})+h_{\text {b}}^2(4-\eta _{\text {b}}) \big ], \\ \eta _{\text {t}}&= \frac{4v_d}{d}\frac{3h_{\text {t}}^2+h_{\text {b}}^2}{(1+\lambda _1)^2}\Big (1-\frac{\eta _{\phi }}{d+1}\Big ), \\ \eta _{\text {b}}&= \frac{4v_d}{d}\frac{h_{\text {t}}^2+3h_{\text {b}}^2}{(1+\lambda _1)^2}\Big (1-\frac{\eta _{\phi }}{d+1}\Big ). \end{aligned}$$

It is useful to study a linear combination of the two fixed-point conditions, $0 = \frac{1}{h_{\text {t}}^2}\partial _th_{\text {t}}^2 - \frac{1}{h_{\text {b}}^2}\partial _th_{\text {b}}^2$, assuming that $h_{\text {t}}\ne 0 \ne h_{\text {b}}$,

$$\begin{aligned} 0&= \frac{1}{h_{\text {t}}^2}\partial _th_{\text {t}}^2 - \frac{1}{h_{\text {b}}^2}\partial _th_{\text {b}}^2 \nonumber \\&= 2(\eta _{\text {t}}+\eta _{\text {b}}) - \frac{16v_d}{d} \left[ \frac{1-\frac{\eta _{\text {b}}}{d+1}}{1+\lambda _1}+\frac{1-\frac{\eta _\phi }{d+2}}{(1+\lambda _1)^2} \right] (h_{\text {t}}^2-h_{\text {b}}^2) \nonumber \\&= \!-\frac{8v_d}{d}\! \left[ 2\frac{1\!-\!\frac{\eta _{\text {t}}}{d\!+\!1}}{1\!+\!\lambda _1} \!+\! \frac{1\!-\!\frac{d\eta _{\phi }}{(d\!+\!2)(d\!+\!1)}}{(1+\lambda _1)^2} \right] (h_{\text {t}}^2-h_{\text {b}}^2). \end{aligned}$$

(E.1)

In order to justify the use of the derivative expansion of the effective action, we demand for the anomalous dimensions $\eta _i$ to remain sufficiently small also at a possible fixed point, $\eta _i^*\lesssim 1$. As a consequence, the term in the square bracket of Eq. (E.1) is positive. This condition can only be solved by $h_{\text {t}}^2=h_{\text {b}}^2$. Therefore the system of algebraic fixed-point equations reduces to

$$\begin{aligned} 0&= \eta _{\phi }+2\eta _{\text {t}} - \frac{16v_d}{d}h_{\text {t}}^2\left[ \frac{1-\frac{\eta _{\text {t}}}{d+1}}{1+\lambda _1}+\frac{1-\frac{\eta _{\phi }}{d+2}}{(1+\lambda _1)^2}\right] , \nonumber \\ \eta _{\text {t}}&= \frac{16v_d}{d}h_{\text {t}}^2\frac{1-\frac{\eta _{\phi }}{d+1}}{(1+\lambda _1)^2}, \nonumber \\ \eta _{\phi }&= \frac{16v_d}{d} h_{\text {t}}^2(4-\eta _{\text {t}}). \end{aligned}$$

(E.2)

The constraints on the anomalous dimensions $\eta _i<1$ imply that also $\eta _i> 0$ holds, as the negative terms linear in $\eta _i$ on the right-hand sides of Eq. (E.2) remain subdominant compared with the positive terms. Expressing the constraints $0<\eta _{\phi }<1$ and $0<\eta _{t}<1$ through a constraint on the top Yukawa coupling via the last two lines of Eq. (E.2) leads to a constraint on $h_{\text {t}}^2$: $0\le h_{\text {t}}^2 \le 4\pi ^2[5(1+\lambda _1)^2-\sqrt{5}\sqrt{(1+\lambda _1)^4-(1+\lambda _1)^2}]$ for $d=4$. Within this constraint, a solution for the fixed-point equation (first line of Eq. (E.2)) does not exist independently of any permissible value of $\lambda _1$. Hence, we do not find a non-trivial fixed point within our present truncation in the symmetric regime in four spacetime dimensions.

1.2 E.2 SSB regime

Because of the couplings of the fluctuating fields to the condensate the structure of the flow equations in the SSB regime is much richer than in the symmetric case. As a starting point we analyze the beta functions to leading order in the derivative expansion and expand the potential to the lowest non-trivial order in the field invariant, $u=\frac{\lambda _2}{2}(\rho -\kappa )^2$. Therefore, we have to solve the following nonlinear system of equations:

$$\begin{aligned}&\partial _t\kappa = \beta _{\kappa }(\kappa ^*,\lambda _2^*,h_{\text {t}}^*,h_{\text {b}}^*) = 0,\\&\partial _t\lambda _2 = \beta _{\lambda _2}(\kappa ^*,\lambda _2^*,h_{\text {t}}^*,h_{\text {b}}^*) = 0,\\&\partial _th_{\text {t}}= \beta _{h_{\text {t}}}(\kappa ^*,\lambda _2^*,h_{\text {t}}^*,h_{\text {b}}^*) = 0,\\&\partial _th_{\text {b}}= \beta _{h_{\text {b}}}(\kappa ^*,\lambda _2^*,h_{\text {t}}^*,h_{\text {b}}^*) = 0, \end{aligned}$$

where the flow equations can be read off from Eqs. (23) and (24). For the linear regulator, this system can be solved analytically resulting in two inequivalent fixed points for admissible physical parameters ($\kappa >0$, $h_{\text {t}}^2\ge 0$, $h_{\text {b}}^2\ge 0$, $\lambda _2>0$). The values of the fixed-point couplings are listed in Table 2. First of all note that there are two additional fixed points by exchanging the numerical values for $h_{\text {t}}^*$ and $h_{\text {b}}^*$ due to the fact that the flow equations are symmetric under an exchange of the Yukawa couplings. Of course, these additional fixed points are physically equivalent to those given in Table 2, corresponding to a mere renaming of the couplings.

Table 2 Fixed-point values for the various parameters in the SSB regime to leading order in the derivative expansion

Furthermore, the flow equations of the Yukawa couplings are proportional to the Yukawa couplings themselves, $\partial _th_a^2 \propto h_a^2$, which leads to a decoupling of the bottom quark at all scales. Therefore the system reduces to that studied in [89, 90].

In order to check if these fixed points persist beyond the leading order, we have to include the anomalous dimensions of the fields. As long as these quantities, which measure the influence of higher-derivative terms in our truncation, remain small, the derivative expansion appears legitimate. For a first impression of the size of the anomalous dimensions, we insert the leading order fixed-point values listed in Table 2 into the right-hand sides of Eqs. (25)–(26). Similar to the results of [89, 90] the anomalous dimensions of the fields at the fixed points are large, especially $\eta _{\text {t}}$ is much larger than 1 ($\eta _{\text {t}}\simeq 22$ for the first fixed point and $\eta _{\text {t}}\simeq 4$ for the second one). This casts serious doubts on the existence of these fixed points in the full theory. In fact, it has been shown numerically in [89, 90] that the fixed points do not persist as soon as back-reactions of the anomalous dimensions are included. This can be traced back to large contributions of massless modes, such as the Goldstone and bottom quark modes near the would-be fixed point.

To summarize, we find no indications that the present chiral model in its pure form supports physically acceptable fixed points within the validity domain of the derivative expansion of the effective action.