Financial price dynamics and phase transitions in the stock markets

Abstract

Price dynamics in stock market is modelled by a statistical physics systems: Ising model. A comparative analysis of the historical dynamics of stock returns between the US, UK, and French markets is given. Since the Ising model requires binary inputs, the effect of binarization is studied. Then, using the TAP approximation method, external fields and coupling strengths are calculated. The fluctuation cycles of coupling strengths have a remarkable corresponding relationship with the important period of the financial market. The highlight of this paper is to verify the phase transition can also occur in the stock market and it reveals the transformation of the market state. The numerical solution in this paper is consistent with the exact solution obtained by Lars Onsager. Our findings can help to discover the economic cycles and provide more possibilities for studying financial markets using physical models.

Graphic abstract

1 Introduction

The research on modeling financial price dynamics is complex and attractive. In recent years, considerable attention from academia has been paid to this area. Many scientists have applied physical theories and methods to empirical research in economical phenomena. One of the popular approaches is to consider a financial market as a complex system. The complex system is mostly used to describe the changing process of a system, such as market price fluctuations. For example, the stock market is a typical feedback system, in which the interaction between stocks has been taking place. The most famous example of a complex system is the Ising model which was used to explain the phase transition of ferromagnetic materials initially.

Fig. 1

The flowchart of our paper

Nowadays, as a famous statistical physics system, the Ising model can also be adopted to explain and model the interaction mechanism of financial market [2,3,4,5,6, 8,9,10, 12,13,14, 16, 18, 22,23,24, 26, 28,29,30]. The Ising model is popularly applied in the stock market [2,3,4,5,6, 8,9,10, 12,13,18, 20,21,24, 26,27,30] and also be used in the study of financial crash [12,13,14, 26]. For example, Borysov analyzed the historical behavior of the parameters inferred using exact and approximate learning algorithms within Boltzmann learning framework. Properties of distributions of external fields and couplings were studied for different historical dates and moving window sizes [2]. Bury provided empirical evidence that the financial network is accurately described by a statistical model which can be thought of as an Ising model on a complex graph with scaled interaction strengths [4]. Zhang described interacting micromechanism for the formation of the price and various properties of logarithmic returns for the financial model were investigated by some statistical analyses [29]. Some novel mathematical methods are also utilized in explaining and analyzing the stock market, such as the minimal spanning tree [21, 27, 28] and cross-correlation matrix [8, 10, 15, 21, 24, 27, 29, 30]. Moreover, the Ising model allows the identification of phase transitions as a simplified model of reality, and phase transitions are also observed in financial research [14, 21, 26, 27].

In this paper, the stock market is treated as the Ising model and parameters in the model are learned from the real stock return time series. The Ising model contains a large number of interacting spins and we consider the pairwise interaction of the Ising model. These spins can be expressed in two states (1 or $-1$), which represent the state of stock at a certain time. The flowchart of our paper is shown in Fig. 1. Since the Ising model requires binary inputs, the first four moments of the distribution of average binarized versus raw and standardized returns are compared. The stock data come from the US, UK, and French markets. Then, using the TAP approximation method, external fields and coupling strengths are calculated. We are interested in describing financial markets in terms of physical quantities, so statistical analysis about external fields and coupling strengths is performed. At last, the phase transition in the stock market is studied. When using stock data, the phase transition can occur. Furthermore, phase transition points marked on the price curve can point out the state transition of stock price. The numerical solution in this paper is consistent with the exact solution obtained by Lars Onsager in 1944.

The main contributions of this paper are the following four points: First, using different mathematical tools, namely the correlation matrix, the covariance matrix, and the eigenvalues, the first four moments of the distribution of average binarized versus raw and standardized returns are compared. The presented results show that binarized returns behave similarly to raw and standardized returns, and binarization preserves the correlation structure of the market. Second, novel financial price dynamics are established by Ising model, where the Ising model is applied to define the price interacting micromechanism between different stocks and we only consider the pairwise interaction of the Ising model. Some physical quantities, such as the coupling strength and the external field are introduced to provide a new perspective to observe the price dynamics. Third, it is remarkable that we transform stock data into two dimensions and obtain its critical temperature. To exhibit the phenomenon of phase transition, the 2D Ising model is solved based on the Metropolis algorithm. Three temperature expressions for the stock market are constructed. It is the first time to simulate the Ising model in 2D based on the stock data using the Metropolis algorithm and we characterize the stock market temperature in a reasonable way. The conclusion is that phase transitions can occur in the stock market. Fourth, the phase transition points are marked on the price curve, which reveals the transformation of the market state. This makes the phase transition phenomenon have practical significance in the financial market and it is one of the innovations of our paper. This is the first work to find the phase transition point of stock prices.

The rest of this paper is organized as follows. In Sect. 2, data, basic statistical analysis, approximation method, and the Metropolis Hastings algorithm for solving the 2D Ising Model are presented. Section 3 lays out experimental results. The effect of binarization of stock returns is discussed. Some physical quantities, such as the coupling strength and the external field are calculated. Further, phase transitions in stock markets are explored. Section 4 concludes the main findings.

2 Data and methodology

2.1 Data and basic statistical analysis

We study the historical dynamics of three major stock indexes in the world: S &P500 (the United States), FTSE100 (the United Kingdom), and CAC40 (France). All stock markets apply the time series of daily closing prices, $P_i(t)$, $i=1,\dots , N$. Here $P_i(t)$ represents the price of stock i on trading day t, and N is equal to 500, 100, and 40 respectively for three different countries. The data span the period from Jan 1, 2006 to July 1, 2021, during which the global capital markets witnessed a sharp rise and steep fall, providing sufficient samples for research. The stock prices are converted to logarithmic returns.

$$\begin{aligned} s_{i}^{\text{ raw } }(t)=\ln \left[ P_{i}(t) / P_{i}(t-1)\right] . \end{aligned}$$

(1)

Next, we define some operations, and the average stock return is defined.

$$\begin{aligned} {\bar{s}}(t)=1 / N \sum _{i=1}^{N} s_{i}(t). \end{aligned}$$

(2)

Here $s_{i}(t)$ can be $s_{i}^{\text{ raw } }(t)$ which is defined above. It can also be $s_{i}^{\text{ std } }(t)$ or $s_{i}^{\text{ bin } }(t)$, which is defined later. To extract long-term trends from the time series, a simple moving window (SMA) approach is employed. It functions as a low-pass filter, averaging out high-frequency components. Within the SMA approach, the time series data is divided into multiple windows of size T. For each set of chunks, one can denote averaging over time (historical values).

$$\begin{aligned} \left\langle s_{i}\right\rangle =\frac{1}{T} \sum _{t=0}^{T-1} s_{i}\left( t\right) . \end{aligned}$$

(3)

Fig. 2

Differences between $\left\langle s_{i}\right\rangle$ and ${\bar{s}}(t)$. The former averages the prices of one stock over multiple days and it is used to calculate the covariance matrix. While the latter averages the prices of multiple stocks within a day, whose role is to describe the situations in the stock market (see Fig. 5)

Let $s=\{s_1,s_2,\dots ,s_N \}$, here $s_{i}$ is the return series of each stock. Different statistical characteristics such as covariance matrix, ${{\textbf {C}}} (N\times N)$ is used with the elements, $c_{ij}$ is the element in covariance matrix ${{\textbf {C}}}$, $i,j=1,\dots , N$.

$$\begin{aligned} C=(c_{ij})_{N\times N}=\text {Cov}(s_i,s_j). \end{aligned}$$

(4)

The covariance matrix must be positive definite, so $T \ge N$. In this case, correlation matrix ${{\textbf {Q}}} (N\times N)$, is a normalized covariance matrix with the elements, $q_{ij}$ is the element in covariance matrix ${{\textbf {Q}}}$, $i,j=1,\dots , N$.

$$\begin{aligned} Q=(q_{ij})_{N\times N}=\frac{c_{i j}}{\sigma _{i} \sigma _{j}}, \end{aligned}$$

(5)

where $\sigma$ denotes standard deviation or volatility in finance. Furthermore, to measure the asymmetry and tailedness of the probability distribution, higher-order moments such as skewness and kurtosis are denoted as follows.

$$\begin{aligned} \text { Skew }\left( s_{i}\right)= & {} \left\langle \left( \frac{s_{i}-\left\langle s_{i}\right\rangle }{\sigma _{i}}\right) ^{3}\right\rangle , \end{aligned}$$

(6)

$$\begin{aligned} {\text {Kurt}}\left( s_{i}\right)= & {} \frac{\left\langle \left( s_{i}-\left\langle s_{i}\right\rangle \right) ^{4}\right\rangle }{\sigma _{i}^{4}}-3. \end{aligned}$$

(7)

As mentioned in Abstract, the Ising model requires binary inputs. Thus, the binarized version of the returns is defined as follows.

$$\begin{aligned} s_{i}^{\textrm{bin}}(t)={\text {sign}}\left( s_{i}^{\textrm{raw}}(t)\right) . \end{aligned}$$

(8)

Another common approach to deal with data is standardization.

$$\begin{aligned} s_{i}^{\textrm{std}}(t)=\frac{s_{i}^{\textrm{raw}}(t)-\left\langle s_{i}^{\textrm{raw}}\right\rangle }{\sigma _{i}} \end{aligned}$$

(9)

2.2 Definition of the problem

In this paper, the stock market is treated as the Ising model and parameters in the model are learned from the real stock return time series. The Ising model contains a large number of interacting spins that can simulate the investors and the flow of information among them. These spins can be expressed in two states ($+$1 or −1), and there are two common ways to represent entities in the financial market as spins. The first case appeared in Ref. [2,3,4, 30] is that we consider a set of N market indices or N stocks with binary states $s_i(t)$ ($s_i(t) = 1$ for all $i=1,\dots ,N$). Here $s_i(t)$ is the state of stock i at time t. Therefore, the system configuration will be described by a vector $s = (s_1,\dots ,s_N)$. The binary variables $s_i(t)$ will be equal to $+$1 if the closeing price today is larger than (or equal to) yesterday’s price and equal to −1 if not. In ref. [5, 8, 10, 12, 13, 16, 17, 23, 24, 29], the spin can simulate the investor or the trader. The stock market consists of N traders and each of them can share one of two investment attitudes, buyer or seller. The investment attitude $s_i(t)$ is defined as follows: if trader i buy the stock at a timestep t, then $s_i(t) = +1$. If trader i, in contrast, is the seller of the stock at a timestep t, then $s_i(t) = -1$.

Our work take the first way. After these spins are expressed in two states (1 or $-1$), denoting spin up or down, they are arranged according to a certain rule to form a lattice. The adjacent spins influence each other, and the interactions are determined by the coupling strength. Note that we only consider the pairwise interaction of the Ising model. The 3-spin interaction and the 4-spin interaction shown in ref. [1, 7] are not used. In the pairwise case, the objective is to have a model capable of reproducing statistical observables based on time series for a particular historical period. The expression for the objective is as follows.

$$\begin{aligned} \left\langle s_{i}\right\rangle _{\text{ data } }=\left\langle s_{i}\right\rangle _{\text{ model }}, \quad \left\langle s_{i} s_{j}\right\rangle _{\textrm{data}}=\left\langle s_{i} s_{j}\right\rangle _{\text{ model }},\nonumber \\ \end{aligned}$$

(10)

where $i=1, \ldots , N$ and angular brackets denote statistical averaging over time.

As mentioned before, spins in the Ising model $s_i(t)$ is the state of stock i at time t. It is defined as follows. The state sequence $s_i(t)$ is then used to infer the Ising model interaction strengths and external fields.

$$\begin{aligned} \begin{aligned} s_i(t) = s_{i}^{\textrm{bin}}(t)=\left\{ \begin{array}{rl} 1, &{} s_{i}^{\textrm{raw}}(t) \ge 0 \\ 0, &{} s_{i}^{\textrm{raw}}(t) < 0 \end{array}\right. . \end{aligned} \end{aligned}$$

(11)

After the state of the stock is defined, an analogy between the financial system and Ising model is proposed. The binarized states of each stock in three stock markets will be mapped to a two-state Ising spin model which leads to a pairwise interaction model.

The Ising model with N binary spin variables ${s_i = \pm 1}$ ($i=1,\dots ,N$) is constructed. The pairwise couplings $J_{i j}$ determine the interactions between two adjacent spins. Also a spin i has an external magnetic field $h_i$ interacting with it. In the equilibrium case, the energy of a configuration ${s_i}$ is given by the Hamiltonian function,

$$\begin{aligned} H_{\textbf{J}, \textbf{h}}(\textbf{s})=-\sum _{\langle i, j\rangle } J_{i j} s_{i} s_{j}-\mu \sum _{i} h_{i} s_{i}. \end{aligned}$$

(12)

The notation $\langle i, j\rangle$ indicates that sites i and j are nearest neighbors and $\sum \nolimits _{\langle i, j\rangle }$ represents the sum of nearest neighbors. The magnetic moment is given by $\mu$.

2.3 TAP approximation

Next, two methods reconstructing the interaction strength and external fields of Ising model are introduced. The first-order approximation within the mean-field theory (nMF) gives,

$$\begin{aligned}{} & {} \textbf{J}^{\textrm{nMF}}=\textbf{A}^{-1}-\textbf{C}^{-1}\end{aligned}$$

(13)

$$\begin{aligned}{} & {} h_{i}^{\textrm{nMF}}=\tanh ^{-1}\left\langle s_{i}\right\rangle -\sum _{j=1}^{N} J_{i j}^{\textrm{nMF}}\left\langle s_{i}\right\rangle , \end{aligned}$$

(14)

where $A_{i j}=\left( 1-\left\langle s_{i}\right\rangle ^{2}\right) \delta _{i j}$ and $\delta _{i j}$ is the Kronecker delta. To improve accuracy of the approximation, the diagonal element $J_{ii}$ which is usually discarded and participates in the calculation of corresponding $h_i$. It is known as the diagonal-weight trick [25]. We abbreviate the external fields with the diagonal element as $h\_diag$.

Furthermore, to obtain the second-order correction to the nMF approximation, the Thouless-Anderson-Palmer (TAP) equations need to be solved. In 1977, Thouless, Anderson, and Palmer (TAP) added a term to the Gibbs free energy [18]. Thus, the covariance matrix is revised,

$$\begin{aligned} \left( \textbf{C}^{-1}\right) _{i j}=-J_{i j}^{\textrm{TAP}}-2\left( J_{i j}^{\textrm{TAP}}\right) ^{2}\left\langle s_{i}\right\rangle \left\langle s_{j}\right\rangle . \end{aligned}$$

(15)

Then, the coupling strength and external field is calculated as follows,

$$\begin{aligned} J_{i j}^{\textrm{TAP}}= & {} \frac{-2\left( \textbf{C}^{-1}\right) _{i j}}{1+\sqrt{1-8\left( \textbf{C}^{-1}\right) _{i j} s_{i} s_{j}}}, \end{aligned}$$

(16)

$$\begin{aligned} h_{i}^{\textrm{TAP}}= & {} h_{i}^{\textrm{nMF}}-\left\langle s_{i}\right\rangle \sum _{j=1}^{N}\left( J_{i j}^{\textrm{TAP}}\right) ^{2}\left( 1-\left\langle s_{j}\right\rangle ^{2}\right) .\nonumber \\ \end{aligned}$$

(17)

In this paper, we use the TAP approximation to calculate the coupling strengths and external fields.

2.4 Market temperature

To measure the investment enthusiasm in the stock market, three formulas of market temperature, namely $\mathrm {T_{sum}}$, $\mathrm {T_{std}}$, and $\mathrm {T_{max}}$ are proposed as follows. $P_i(t)$ represents the price of stock i on trading day t, $i=1,\dots , N$, and N is the total number of stocks.

$$\begin{aligned} T_{sum}(t)= & {} \sum _{i=1}^{N}(P_{i}(t) - P_{i}(t-1)), \end{aligned}$$

(18)

$$\begin{aligned} T_{std}(t)= & {} \sqrt{\frac{\sum _{i=1}^{N}\left( P_{i}(t) - P_{i}(t-1)-T_{sum}(t)/N\right) ^{2}}{N}}, \end{aligned}$$

(19)

$$\begin{aligned} T_{max}(t)= & {} \max \{P_{i}(t) - P_{i}(t-1)\}. \end{aligned}$$

(20)

As a result, the daily temperature of the market T is defined in three ways based on the sum, standard deviation, and maximum value of daily returns. It should be noted that Eq. 18 and Eq. 20 allow sub-zero temperatures. In fact, the normalized operation on temperature data is carried out in Algorithm.1, ensuring that the temperature data entered into the Metropolis Hastings algorithm are all positive.

Fig. 3

2-dimentional lattice. The red arrows show the spin direction. On each lattice point, there is an atom whose spin, $s_i$, can be pointed either upward ($s_i$ = $+$1) or downward ($s_i$ = −1). Parallel spins ($\uparrow \uparrow$) have less energy than spins with opposite orientation ($\uparrow \downarrow$). Links between nearest neighbours are seen as lines connecting sites and periodic boundaries are shown for this small lattice. Note, for illustration purposes the links across the boundary are not shown here but do exist

2.5 Solutions to the 2D Ising model

The one dimensional (1D) Ising model does not exhibit the phenomenon of phase transition while higher dimensions do. We now consider the two-dimensional Ising model and an example are shown in Fig. 3. The self-consistent equation is defined to obtain the solution of the two-dimensional Ising model [11].

$$\begin{aligned} {\bar{s}}=\tanh \left( \frac{\mu h}{k T}+\frac{z J}{k T} {\bar{s}}\right) , \end{aligned}$$

(21)

where ${\bar{s}}$ is the average of the lattice spins, tanh is the hyperbolic tangent function, k is the Boltzmann constant, T is the temperature, $\mu$ is the magnetic moment, h is the external field, J is the coupling strength, z is the number of neighbors of particle i. Consider the case of no external magnetic field, i.e. $h = 0$ and let $T_c=\frac{z J}{k}$. Equation 21 reduces to,

$$\begin{aligned} {\bar{s}}=\tanh \left( \frac{T_c}{T} \cdot {\bar{s}}\right) . \end{aligned}$$

(22)

To solve Eq. 22, first plot an image of functions $y=x$ and $y=tanh(ax), a\in R$ for observation. For $\frac{z J}{k T}<1$, $T>T_c$, Eq. 22 has a unique solution ${\bar{s}}=0$. The system is in a disordered or the paramagnetic state. In this case, there are no long-range correlations between the spins. For $\frac{z J}{k T}>1$, $T<T_c$, Eq. 22 has three solutions ${\bar{s}}=0, {\bar{s}}=\pm {\bar{s}}_{0}$, where ${\bar{s}} = \pm {\bar{s}}_{0} \ne 0$. The system magnetizes, and the state is called the ferromagnetic or the ordered state. This amounts to a globally ordered state due to the presence of local interactions between the spin. The system undergoes a second-order phase transition at $T_{c}$. It can be concluded that $T_c$ is the critical temperature of ferromagnetic-to-paramagnetic phase transition.

Fig. 4

An illustration of solving Eq. 22. ‘$a<1$’ corresponds to $T>T_c$. ‘$a>1$’ corresponds to $T<T_c$

In the case where the Ising model is two-dimensional, it can be deduced that $T_c=\frac{4J}{k}$ based on the mean-field approximation. Lars Onsager obtained the exact solution for the two dimensional Ising model in zero field in 1944 [19], that is,

$$\begin{aligned} T_c=\frac{2.269J}{k}. \end{aligned}$$

(23)

Fig. 5

a Historical dynamics of the first four temporal moments of the distribution of mean market return. Top-bottom: temporal mean, standard deviation, skewness and kurtosis calculated using SMA window of 20 days (approximately one trading year) for the raw (${\bar{s}}^{\textrm{raw}}$, blue), standardized (${\bar{s}}^{\textrm{std}}$, green) and binarized (${\bar{s}}^{\textrm{bin}}$, red) returns of S &P500 stocks. b Correlations between binarized returns and other two returns have been around 1. Binarized returns behave similar to raw and standardized returns over time

Fig. 6

a Historical dynamics of the first four temporal moments of the distribution of mean market return of FTSE100 stocks. b Correlations between binarized returns and other two returns have been around 1. Binarized returns are similar to raw and standardized returns apart from years in 2009

Fig. 7

a Historical dynamics of the first four temporal moments of the distribution of mean market return of CAC 40 stocks. b Correlations between binarized returns and other two returns have been around 1. Binarized returns behave similar to raw and standardized returns

Fig. 8

a Historical dynamics of the first four moments of the distribution of off-diagonal elements of covariance ($\textbf{C}^{\text{ raw }}$, blue) and correlation ($\textbf{Q}^{\text{ raw }}$, red) matrices of raw returns, and covariance matrix of binarized returns ($\textbf{C}^{\text{ bin }}$, green) of S &P500 stocks calculated using SMA window of 20 days. Top-bottom: mean, standard deviation, skewness, and kurtosis of the off-diagonal elements of the matrices. The similarity between $\textbf{Q}^{\text{ raw }}$ and $\textbf{C}^{\text{ bin }}$ is very high. Binarization makes scovariance matrix similar to the correlation matrix of raw returns. b The correlation between $\textbf{Q}^{\text{ raw }}$ and $\textbf{C}^{\text{ bin }}$ is around 1 except in 2008

Fig. 9

a Historical dynamics of the four largest eigenvalues of the correlation matrix of raw returns (green) and covariance matrix of binarized returns (red) of S &P500 stocks calculated using SMA window of 20 days. The eigenvalues of $\textbf{Q}^{\text{ raw }}$ and $\textbf{C}^{\text{ bin }}$ also maintain a high degree of coincidence. Binarization preserves the market mode, which corresponds to the largest eigenvalue. b The correlation between the eigenvalues of $\textbf{Q}^{\text{ raw }}$ and $\textbf{C}^{\text{ bin }}$ is also around 1 except in 2017

2.6 The Metropolis–Hastings algorithm

If the total number of sites on the lattice is N, since every spin site has $\pm 1$ spin, there are $2^N$ different states that are possible. This motivates us to simulate the Ising model using Monte Carlo methods. The Metropolis–Hastings algorithm is the most commonly used Monte Carlo algorithm to calculate Ising model estimations.

The one-dimensional (1D) Ising model does not exhibit the phenomenon of phase transition while higher dimensions do. Using the Metropolis algorithm, the Ising model in 2D can be simulated. The main steps of Metropolis algorithm are,

• (1) Prepare an initial configuration of N spins.

• (2) Flip the spin of a randomly chosen lattice site, and calculate the change in energy $\varDelta E$.

• (3) If $\varDelta E < 0$, accept the move. Otherwise, accept the move with probability $e^{-\varDelta E/kT}$.

• (4) Repeat 2–3, until ensuring a final equilibrium state. So far, the energy, magnetization, specific heat, and susceptibility of the system have been estimated.

3 Results and discussion

The experiments and results are divided into three steps and are organized as follows. In Sect. 3.1, the effect of binarization of raw sequences is explored since the inputs of the Ising model are binarized states. Section 3.2 calculates the coupling strength and the external field, and their properties are studied. Section 3.3 shows phase transitions can also occur in the stock market.

Before all the experiments, four important periods in financial markets are selected to observe changes and they are highlighted with the light green background:

• (1) the global financial crisis from Sept 1, 2007 to Dec 31, 2008, the U.S. housing bubble and the bankruptcy of Lehman Brothers occurred at that time.

• (2) European sovereign debt crisis (from Dec 1, 2009 to Apr 1, 2012). During this period, the euro area, and the IMF continued to provide economic assistance to Greece and other countries.

• (3) Geopolitical turmoil in 2018. On June 26, 2018, the Queen approved the Brexit, allowing the United Kingdom to leave the European Union. On August 23, 2018, the 16 billion tax list between China and the United States came into effect.

• (4) Covid-19 (from Jan 1, 2020 to Jul 1, 2021).

3.1 Effect of binarization

From Eq. 11, the inputs of the Ising model are binarized states, so whether the information about the market trends in the binarized time series is preserved is worth exploring. The mapping defined by Eq. 8 will certainly affect information contained in the time series. With this aim, the historical evolution of the first four moments of the distribution of average binarized versus raw and standardized returns are compared.

As shown in Figs. 5a, 6a, and  7a, four temporal moments concerning three countries are demonstrated and the evolution of stock indexes in different countries is vividly displayed. In the highlight regions, for example, during the Covid-19 period, the second-order moment (the standard deviation) fluctuates extremely. In Figs. 5b, 6b, and 7b, correlations between binarized returns and other two returns are also calculated. Overall correlations have been maintained near 1, indicating that binarized returns behave similar to raw and standardized returns. The results presented in the three figures indicate that the binarized returns behave similarly to the raw and standardized returns, preserving dynamics of the first two moments and less so about the third moment, while information about kurtosis is lost for all periods. Furthermore, signatures of economic cycles and frequency of market crashes are preserved in the binarized time series.

Fig. 10

The first four moments of the couplings are about S &P500. Four moments of the couplings fluctuate extremely in the highlight regions. The fluctuation cycles of coupling strengths have a remarkable corresponding relationship with the important period of financial market

The binarized returns need to be compared to the raw and standardized returns further. Therefore, the covariance matrix and correlation matrix of the raw returns and the covariance matrix of binarized returns are calculated. The first four moments of the elements in these matrices are shown in Fig. 8. Only US data is used here as a representative. It can be inferred that the covariance matrix of the binarized returns becomes similar to the correlation matrix of the raw returns. Indeed, their off-diagonal elements follow similar distributions with a very high correlation between their means. However, the covariance matrix of the raw returns is less correlated by comparison. For higher-order moments, the correlation is not so strong.

Studying the eigenvalue distribution of correlation matrices for the original and transformed time series is another way to explore effects of the binarization procedure since it is well-known that for a random correlation matrix, the distribution of eigenvalues is quite different. So along with the results in Fig. 8, there is a strong correlation between the correlation matrix of raw returns and the covariance matrix of binarized returns, the historical dynamic of the four largest eigenvalues is compared in Fig. 9. All four values are well preserved and the largest one, corresponding to the “market mode”, is in remarkable agreement even if binarization is performed.

To summarize the content of this section, the first four moments of the distribution of average binarized versus raw and standardized returns are compared based on three mathematical tools, namely the correlation matrix, the covariance matrix, and the eigenvalues. By comparison, binarized time series capture statistical properties and historical behavior of the original time series well, laying a foundation for establishing the Ising model.

3.2 Analysis of inferred parameters

Fig. 11

The first four moments of the external fields about S &P500. The standard deviation of the external field changes significantly in special periods

Fig. 12

The first four moments of the external fields with the diagonal element about S &P500. The mean value and standard deviation vary apparently in highlight regions

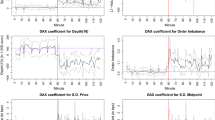
Following the SMA approach with T = 20 trading days (approximately one trading month), the historical evolution of the coupling strength, external field, and external field with the diagonal element, that is J, h, and $h\_diag$ are calculated for three markets. The methodology is the TAP approximate learning methods described in the previous section. Four temporal moments are shown in Figs. 10, 11, and . In the special financial period, such as the global financial crisis in 2008, the mean and variance of the three physical quantities show relatively large fluctuations. Therefore, the fluctuation periods of the three physical quantities J, h, and $h\_diag$ correspond to important periods in financial markets remarkably, helping to discover the economic cycles and market crashes.

Next, two-step analysis for the three physical quantities themselves are performed, which are observing their distribution histograms and implementing the Anderson–Darling test on the distribution, and calculating the Hurst exponent.

3.2.1 Distribution of inferred parameters and A–D test

Fig. 13

The distributions of physical quantities for three different markets. The red columns represent the distribution of physical quantities, while the black curve fits a standard normal distribution. In these distributions, the distribution of external fields of FTSE100 is the closest to the Gaussian (see Figure (e)). All these distributions do not possess heavy tails which is common in financial time series

Table 1 Results of A–D test

Fig. 14

Hurst exponent of physical quantities for three different markets

As shown in Fig. 13, the coupling strength J for three markets are all peaked, in which almost all J for the French market are positive. Distributions of the external field h for three markets are stacked near 0. In addition, h for the UK market has a relatively wider and flatten distribution, and it seems to be close to the normal distribution. The bulks of the diagonal element $h\_diag$ for three markets are also distributed concentratedly.

For further understanding of the difference between Gaussian distribution, the Anderson–Darling (A–D) test is applied to the three quantities. The A–D test is a modification of the Kolmogorov–Smirnov test to verify if the data is from the normal distribution. The Anderson-Darling test is defined as $H_0:$ The data follow a Gaussian distribution. $H_1:$ The data do not follow the Gaussian distribution. The results of the A–D test are demonstrated in Table 2.

From A–D test results, there is a clear view that all p-values are so close to 0. If the p-value is smaller than 0.05, the null hypothesis can be rejected. Therefore, three physical quantities including the coupling strength, external field, and external field with the diagonal element do not follow the Gaussian distribution. In the financial market, many returns do not satisfy the normal distribution but show the characteristics of sharp peaks and fat tails. The physical quantity we get is the same as the return rate, and it does not satisfy the normal distribution.

3.2.2 The Hurst exponent

The Hurst exponent is referred to as the index of dependence. It quantifies the relative tendency and characterizes the long-term memory of a time series. If $0<H<0.5$, it is well known that these data in time series have negative long-term memory properties, that is, they have anti-persistence. A single high value will probably be followed by a low value and the value after that will tend to be high, with this tendency to switch between high and low values lasting a long time into the future. If $H=0.5$, the data are completely independent, and their correlation coefficient is 0, where the time series can be considered as a Brownian motion. If $0.5<H<1$, the data in the time series will have persistent long-term memory property. A high value in the series will probably be followed by another high value and the values a long time into the future will also tend to be high.

To get the dynamic Hurst exponent, the rolling-window based approach is applied to investigate the evolution of long-term memory property of the physical quantities and the rolling-window is set as 20 days and moves forward in one-day intervals. Figure 14 demonstrates the plots of dynamic Hurst exponent values of the S &P500, FTSE100, and CAC40 over time, showing the cyclical phenomenon behavior, namely, the Hurst exponent will decrease continuously after a continuous increase, and conversely, it will increase continuously after continuous decrease. It is also observed that all H-curves are above 0.5 horizons, indicating that the data in the time series will have persistent long-term memory properties.

3.3 Phase transition in stock market

Phase transitions are common in nature. The 1D Ising model does not exhibit the phenomenon of phase transition while higher dimensions do. The 2D Ising model in this paper is solved based on the Metropolis algorithm. We are interested in two points: 1. Whether phase transitions can occur in the stock market. 2. Whether the critical point can be obtained if phase transitions exist. To perform the Metropolis algorithm, the FTSE100 index in the UK is selected as the dataset. The data span the period from Jan 1, 2019 to Jan 1, 2021. Excluding the missing data, there are 89 stocks and 507 trading days in total. Steps of implementing the Metropolis algorithm are as follows. Algorithm 1 shows the process of obtaining the coupling strength and initial matrix according to the sliding of the window over time. An example of sliding window is shown in Fig. 15.

Fig. 15

An example of sliding window. The data in matrix format contains information on trading days and stocks. The element such as ‘S1D1’, represents the price status (1 or $-1$) of the first stock on the first day. Here the length of the sliding window is 2. On day 3, the data of the past two days are used to calculate the coupling strength J

The calculation of market temperature is one of the highlights of this paper. In terms of the temperature required by the Metropolis algorithm, we apply three different formulas, which are defined in three ways based on the sum, standard deviation, and maximum value. The market temperatures and the index price of the FTSE100 are shown in Fig. 16. In March 2020, due to the impact of covid-19, stock index prices fell significantly, and temperature fluctuations during this period were also very large. Further, there are two-time points of sharp rise. In May 26, 2020, TUIT soared 52.02%, thanks to the collective rise of the Travel & Leisure sector in Euro Stoxx. In Nov 9, 2020, Rolls-Royce rose 43.76% with a modest rise of 4.67% in FTSE100 on the back of the news that a potential Covid-19 vaccine, being developed Pfizer and BioNTech, revealed a success rate of over 90% in its late-stage trials. Therefore, three formulas Eqs. 18, 19, and 20 can reflect the situation and sentiment of the market.

Fig. 16

Top to Bottom: the index price of FTSE100, the temperature calculated by three formulas, and the coupling strength J. In May 26, 2020, TUIT soared 52.02%. In Nov 9, 2020, Rolls-Royce rose 43.76%. In these two moments, the temperature data fluctuated greatly

Table 2 Summary of three experiments

Fig. 17

Histograms of the temperature data based on three different formulas

Fig. 18

Scatter graphs describing the relationship between temperature and coupling strength. The red horizontal line indicates $J=1$

Note that in Fig. 11, the J of S &P500 is extremely close to zero, indicating that the coupling strength of the financial time series is relatively small. And in Sect. 2.5, there is a proportional relationship between the critical temperature and the coupling strength. In addition, due to the existence of absolute zero in thermodynamics, all calculations should be carried out above zero, so the coupling strength should be greater than zero as much as possible. In Algorithm 1, $J^{\prime }=J+1$, and J is replaced by $J^{\prime }$. It’s a simple calculation, but it is significant. Since $J^{\prime }$ is used as the coupling strength value as an alternative, interference from absolute zero can be avoided.

Fig. 19

Experiment 1. Temperatures are obtained by the sum of the intraday increase of each stock. When $T = 2.3$, the phase transition is obvious

Fig. 20

Experiment 2. Because the data distribution is sparse near the critical temperature point, the phase transition is not very obvious

Fig. 21

Experiment 3. When $T = 2.3$, the phase transition is not obvious

Three experiments are carried out according to the three temperature expressions. Histograms of the temperature data based on different formulas are shown in Fig. 17 and Scatter graphs between temperature $\textrm{T}$ and coupling strength J are presented in Fig. 18. In the range from 1 to 3, the temperature data calculated by using $\mathrm {T_{sum}}$ is more uniform, similar to a normal distribution. While the data calculated using $\mathrm {T_{std}}$ and $\mathrm {T_{max}}$ is very concentrated around 1. For each J, there is a corresponding T, pairs of (J, T) are considered. So Fig. 18 indicates the feedback between T and J, and their values are measured simultaneously.

The algorithm performs calculations at different temperatures. Figure 19 shows the results in Experiment 1. There are four subgraphs, showing energy, magnetization, specific heat, susceptibility changes according to different temperatures in the order from left to right, top to bottom. By repeating the algorithm and continuous heating, the system reaches thermal equilibrium at temperature $T_c$. In this way, by calculating the average magnetization and specific heat of the system, the curie temperature point of the system can be received.

• (1) The energy increases monotonically with temperature. As the temperature increases, the energy increases (see Fig. 19a).

• (2) Let the external field $h=0$, when $T \rightarrow 0$, in order to keep the energy lowest, all lattice points tend to the same direction, the whole system is either downward or upward. The system is in the ferromagnetic phase and the magnetization is not zero. When $T \rightarrow +\infty$, the thermal motion of the system dominates, the direction of the lattice points is random. The system as a whole is non-magnetic. The magnetization is 0. The system is in the paramagnetic phase and the system exhibits symmetry. Now consider that when the temperature T gradually decreases from $+\infty$, then the system must have a certain temperature $T_c$. Above this temperature, the system is non-magnetic, and below this temperature, the system’s magnetism gradually strengthens. At temperature $T_c$, the system transforms from a symmetric magnet to an asymmetric one, and this is the Symmetry-Breaking. Since this breaking is not caused by an external magnetic field, it is also called Spontaneous Symmetry Breaking. Figure 19b shows this Spontaneous Symmetry Breaking exists near the temperature of 2.3.

• (3) The specific heat is the first derivative of the temperature and changes significantly near the critical temperature $T_c$. When the temperature $T<T_c$, the specific heat increases with the increase of the temperature, and when $T>T_c$, the specific heat decreases with the increase of the temperature. According to observations, $T_c \approx 2.3$ (see Fig. 19c).

• (4) $T_c$ is the critical point of phase transition. Before the phase transition, the magnetic susceptibility is almost 0, but after the phase transition, the magnetic susceptibility increases rapidly until saturation, which is the spontaneous magnetization caused by the Spontaneous Symmetry Breaking (see Fig. 19d).

Fig. 22

The panels show situations of the lattice when the Monte Carlo sweeps steps reach 1024. Two different colors indicate the up and down states of the spins. These results are based on different temperature conditions, ranging from 1.6 to 3.0

Fig. 23

Subgraphs A through F report the results of the energy versus time under different temperatures. In each subgraph, the energy converges to $-1$

Fig. 24

Subgraphs A through F report the results of the magnetization versus time under different temperatures. In each subgraph, the magnetization converges to 1

Fig. 25

The phase transition points are marked on the price curve of the FTSE100. Top to Bottom: Results obtained by three formulas $\mathrm {T_{sum}}$, $\mathrm {T_{std}}$, and $\mathrm {T_{max}}$. After the phase transition point, the stock price rise

Compared with Experiment 1 (see Fig. 19), the results of the phase transition in Experiment 2 (see Fig. 20) and Experiment 3 (see Fig. 21) are similar. The difference between the three experiments lies in the distribution of temperature points. Because the data distribution is sparse near the critical temperature point, the phase transition is not very obvious in Experiment 2 and Experiment 3. The conclusion of these experiments is consistent, that is, phase transitions can occur in the stock market. According to the numerical simulation of this system, the critical temperature is around 2.3 for a thermodynamic system when the mean value of coupling strength $J^{\prime }$ is around 1. Therefore, the Eq. 24 is established.

$$\begin{aligned} T_c=\frac{2.3J^{\prime }}{k}. \end{aligned}$$

(24)

Therefore, the numerical solution Eq. 24 based on the Metropolis–Hastings algorithm for the two-dimensional Ising model in zero field is almost consistent with the exact solution Eq. 23 obtained by Lars Onsager in 1944.

3.4 Further discussion on phase transition

In the previous section, we identify that the phase transition can occur in the stock market and Spontaneous Symmetry Breaking exists near the temperature of 2.3, indicating that the critical point $T_c \approx 2.3$. In this section, we discuss the thermodynamic equilibrium of stocks, and at which time the phase transition occurs.

3.4.1 Thermodynamic equilibrium

The Ising model describes a magnet in a state of thermodynamic equilibrium, i.e., we are dealing here with equilibrium phase transition. To confirm that the system reaches an equilibrium level in the three experiments in Sect. 3.3, we perform two steps as follow.

First, we select different temperature conditions to simulate the two-dimensional Ising model and the equilibrium states are shown in Fig. 22. The Monte Carlo sweeps steps is set to ‘1024’ and the temperature ranges from 1.6 to 3.0. When the temperature is lower than 2.2, all spins are aligned in the same direction. When the temperature exceeds 2.2, the equilibrium state gradually changes. The situations where not all spins are equally oriented are shown. In conclusion, an increase in temperature will affect the state of thermodynamic equilibrium. The phase transition point is near 2.2, and there is no hysteresis, which is consistent with the three experimental results in Sect. 3.3.

Second, to check whether the system reaches thermodynamic equilibrium, two physical quantities the magnetization and energy are examined. We start with an initial configuration, flip the spin of a randomly chosen lattice site, and then display the average magnetization and average energy of each lattice site at the specified temperature, as the system coarsens to its equilibrium state. The number of Monte Carlo sweeps steps is set to ‘1024’. As steps increase, the energy decreases gradually and finally converges to -1 (see Fig. 23). When the temperature is low (see Fig. 23a), the energy will converge quickly; on the contrary, when the temperature is high (see Fig. 23f), the energy will not converge easily. In Fig. 24, the situations are similar. The magnetization increases gradually at all temperatures, eventually converging to 1. In conclusion, both the energy and the magnetization reach the plateaus and we can assume that the system reaches the state of statistical equilibrium.

Note that what we give here is the analytical solution of the convergence of magnetization and energy with time, not an exact solution. This check is meaningful sinces it shows how the magnetization and energy of the system relaxes.

3.4.2 Phase transition points

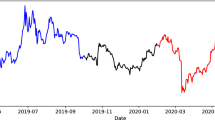
According to the exact solution shown in Eq. 23, a phase transition will occur at temperatures around 2.269. When using the formula $\mathrm {T_{sum}}$, we choose the date whose temperature is the closest to 2.269 as the phase transition point and mark this specific date on the price curve using red dots (see Fig. 25). For the formula $\mathrm {t_{std}}$ and $\mathrm {t_{max}}$, we mark these dates in the same way.

The results shown in Fig. 25 are very consistent. The phase transition points marked by the three temperature expressions are all between March and May 2020, during which the market sentiment goes up, and the stock price ushers in a continuous rise in the following period of time. It can be concluded that the phase transition of the stock market reveals the process of stock prices changing from low to high and market sentiment transforming from cold to warm.

4 Conclusion

Since the Ising spin states require binary variables with $\pm 1$, the return time series of three major stock markets are transformed using the sign function. The first four moments of the distribution of average binarized versus raw and standardized returns are compared. Results show the binary operation preserve the statistical properties and historical behavior of the original time series well. The couplings and external fields are calculated using TAP approximate algorithms. If the diagonal-weight trick is used, the external fields with the diagonal elements are also obtained. Distinctions and specific characteristics between different markets can be demonstrated through the distributions of couplings, external fields, and external fields with the diagonal element. The fluctuation periods of couplings and external fields correspond to important periods in financial markets remarkably, helping to discover the economic cycles and market crashes. Properties of physical quantities are researched. From the A–D test, these physical quantities do not follow the Gaussian distribution. The analogy between the Ising model and the stock market has revealed the non-Gaussian properties of the stock market interactions. Through Hurst exponents, physical quantities’ series have persistent long-term memory properties.

The highlight of our paper is that phase transition in the stock market is studied. The Ising model is an attempt to model phase transition behavior in ferromagnets and the model allows the identification of phase transitions as a simplified model of reality. The 2D square-lattice Ising model is one of the simplest statistical models to show a phase transition. So Metropolis algorithm is implemented for the 2D Ising model. We verify phase transitions can also occur in the stock market and the critical temperature is around 2.3 for our thermodynamic system. The numerical solution solved in stock markets is consistent with the exact solution obtained by Lars Onsager in 1944. Furthermore, the phase transition points are marked on the price curve, which reveals the transformation of the market state and the process of stock prices changing from low to high. This makes the phase transition phenomenon have practical significance in the financial market. In the future, more research about phase transitions can be explored.