Dispersion corrections to elastic electron–nucleus scattering

Abstract

Calculations of the elastic scattering of polarized and unpolarized electrons from spin-zero nuclei within the recoil-modified phase-shift analysis are supplemented with the dispersion correction estimated within the second-order Born approximation. For the $^{12}$C nucleus, three strong transient nuclear excitations are taken into account, for which not only Coulombic, but also magnetic transitions are considered. Dispersion effects of up to 10% in the differential cross section near the first diffraction minimum, resulting largely from Coulombic transitions at the higher collision energies, are in qualitative agreement with experimental findings. Below 300 MeV, dispersion is greatly influenced by magnetic scattering. Investigations of the spin asymmetry for perpendicularly polarized electrons indicate that it is strongly affected by dispersion, predominantly at small scattering angles.

1 Introduction

The deviation of the measured elastic scattering cross section, corrected for multiple scattering and QED effects, from calculations based on the phase-shift analysis, occurring in the vicinity of the diffraction minima, is commonly attributed to the transient excitation of the target nucleus during the scattering process [1,2,3,4,5]. This dispersion effect was originally investigated by Schiff [6] and Lewis [7], and later by Friar and Rosen [8], specifying to a carbon nucleus. However, their use of a closure approximation, based on a fixed excitation energy for all nuclear states, strongly underpredicts dispersion at the higher collision energies [4, 5].

The results presented in this contribution improve on the Friar-Rosen theory in two respects. First, instead of applying closure, a few dominant nuclear excitations are explicitly considered, using experimental excitation energies and nuclear transition densities calculated from the quasiparticle-RPA theory [9]. Second, not only transitions induced by the charge-charge coupling between projectile and nucleus are accounted for, but also those from the magnetic current-current coupling, which can be quite important in nuclear excitation processes. Such magnetic transitions have commonly been neglected in the context of dispersion, since an early investigation [10] indicated that they should be of no importance.

A related topic of current interest is the influence of dispersion on the beam-normal spin asymmetry in the case of perpendicularly polarized beam electrons. The precise knowledge of this spin asymmetry, termed Sherman function, is required for monitoring the degree of beam polarization during a measurement with the help of Mott polarimeters [11]. Moreover, it contributes to the background in parity violation experiments if the beam is contaminated by a small fraction of perpendicularly polarized electrons [12]. From a theoretical point of view, the Sherman function is very sensitive to the employed models since it probes exclusively the higher-order effects such as Coulomb distortion or dispersion. If calculated with the phase-shift analysis the measured spin asymmetry is severely underpredicted for electrons at moderate collision energies and large scattering angles [13] or at ultrahigh (GeV) energies and small angles [14]. For such small angles, most of the experimental data [15, 16] can be reconciled by handling the transient nuclear excitations by means of the experimentally known Compton scattering cross section, to which the forward dispersion amplitude can be related [14, 17].

At impact energies in the MeV region, the experiments can well be explained by the phase-shift theory for the Sherman function [18, 19]. Advancing to collision energies between $50-100$ MeV and to a higher measurement precision, as considered for the forthcoming experiments at the MAMI facility [19], the influence of dispersion is studied in this work. Arbitrarily large scattering angles are taken into account where it is not possible to extract any information from measured Compton scattering data.

2 Dispersion theory

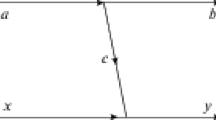
The dispersion effect is represented by the Feynman box diagram shown in Fig. 1.

Fig. 1

Feynman box diagram. The single line represents the electron with initial, intermediate and final momenta $k_i,\;p$ and $k_f$, respectively, and the double line represents the nucleus which is in an intermediate excited state $N^*$. The virtual photon momenta are denoted by $q_1$ and $q_2$

The corresponding transition amplitude is given (in atomic units, $\hbar =m=e=1$) by [8]

(2.1)

where $E_i$ and $E_f$ are the initial and final electron energies, respectively, $t_{\mu \nu }$ is the electronic transition matrix element with the electron four-momentum in its intermediate state, and $T^{\mu \nu }$ is the nuclear transition matrix element (involving an excited state with angular momentum L, magnetic quantum number M and energy $\omega _L$).

Making use of gauge invariance, each of the two photon propagators $(q_i^2+i\epsilon )^{-1},\;i=1,2,$ can be decomposed according to [10]

(2.2)

where $g^{\mu \nu }$ is the metric tensor and . The insertion into (2.1) leads to four contributions, a purely Coulombic one (with $\mu =\nu =0$, i.e. proportional to ), and three magnetic ones (arising from $\mu =m,\;\nu =n$ with $m,n=1,2,3$).

To lowest order in the dispersion correction, the differential cross section for elastic electron scattering is given by [8, 20]

(2.3)

where $f_\textrm{coul}$ is the transition amplitude from the phase-shift analysis. Recoil is accounted for by a reduced collision energy $\bar{E}=\sqrt{(E_i-c^2)(E_f-c^2)}$ [21] in $f_\textrm{coul}$, as well as by the recoil factor $f_\textrm{rec}$ [20]. and are the initial and final electron momenta, respectively, and the sum runs over the spin projections $\sigma _i$ and $\sigma _f$ of the electron.

From the cross section $d\sigma _\textrm{box}/d\Omega$, the dispersion correction $\Delta \sigma _\textrm{box}$ is obtained by means of

$$\begin{aligned} \Delta \sigma _\textrm{box}\,=\, \frac{d\sigma _\textrm{box}/d\Omega }{d\sigma _\textrm{coul}/d\Omega }\,-\,1, \end{aligned}$$

(2.4)

where $d\sigma _\textrm{coul}/d\Omega$ is the phase-shift result (the first term in (2.3)).

For perpendicularly polarized electrons, the Sherman function S is defined as the relative cross section change when the initial spin of the electron is flipped. Including dispersion, one has

(2.5)

where the denominator is twice the unpolarized (spin-averaged) cross section from (2.3).

The relative change of the phase-shift result $S_\textrm{coul}$ by dispersion is conventionally defined by

$$\begin{aligned} d S_\textrm{box}\;=\;\frac{S_\textrm{box} -S_\textrm{coul}}{S_\textrm{coul}}. \end{aligned}$$

(2.6)

Alternatively, one may use the difference

$$\begin{aligned} \Delta S_\textrm{box}\,=\, S_\textrm{box}-S_\textrm{coul}=d S_\textrm{box}\cdot S_\textrm{coul} \end{aligned}$$

(2.7)

for representing the dispersion effects. This quantity has the advantage that it is well-defined even when $S_\textrm{coul}$ approaches zero due to diffraction. Moreover, $\Delta S_\textrm{box}$ turns into the dispersive Sherman function in the limit of the Born approximation,

$$\begin{aligned} S_\textrm{box}^\textrm{Born}\,=\,\frac{\sum _{\sigma _f} 2\hbox { Re}\,\{(f^{*B1} A_{fi}^\textrm{box})(\uparrow )\,-\,(f^{*B1} A_{fi}^\textrm{box})(\downarrow )\}}{2 \sum _{\sigma _f}\,|f^\textrm{B1}|^2},\nonumber \\ \end{aligned}$$

(2.8)

where $f^{B1}$ is the scattering amplitude from the first-order Born approximation. This formula results from (2.5) by replacing in (2.3) $f_\textrm{coul}$ with $f^{B1}$ and noting that $|f^{B1}|^2$ does not depend on the electron spin because of time-reversal invariance.

If the dispersive changes of the cross section are very small (well below 1%, which is the case for low impact energies), the respective contributions from each of the nuclear excited states can simply be added,

$$\begin{aligned} S_\textrm{box}\,\approx & {} \,\sum _{L,\omega _L} S_\textrm{box}(L,\omega _L) -(N_L-1)\,S_\textrm{coul}, \nonumber \\ d S_\textrm{box}\;\approx & {} \;\sum _{L,\omega _L} d S_\textrm{box}(L,\omega _L), \end{aligned}$$

(2.9)

where $N_L=3$ is the number of considered excited states.

3 Cross section results

For obtaining the phase-shift results the Coulombic potential is derived from the $^{12}$C ground-state charge density distribution [22], and the Dirac equation is solved with the help of the Fortran code RADIAL [23]. For dispersion, two strong excitations in the giant dipole resonance region (at $\omega _L=23.5$ MeV and 17.7 MeV) and the lowest quadrupole excitation (at $\omega _L=4.439$ MeV) are considered. The form factors which enter into the nuclear transition matrix element $T^{\mu \nu }$ are calculated from the nuclear transition densities provided by Ponomarev [24] according to the prescription in [25]. The three-dimensional integral in (2.1) is performed numerically as described in [20]. Concerning the sum over $\sigma _f$ in (2.3) or (2.8), it turns out that the consideration of the magnetic contributions to $A_{fi}^\textrm{box}$ destroys the invariance of the dispersive cross-section modification when the final electron changes its helicity state.

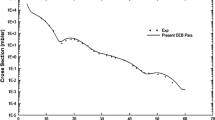
Figure 2 displays the angular dependence of the differential cross section for electron scattering from $^{12}$C at 238.1 MeV collision energy. It is seen that the consideration of recoil in the phase-shift theory is mandatory for obtaining agreement with the experimental data [4]. The inclusion of dispersion reproduces the data quite well near and beyond the first diffraction minimum. This feature is even more pronounced at a higher collision energy [20].

Fig. 2

Elastic scattering cross section for 238.1 MeV electrons colliding with $^{12}$C as a function of scattering angle $\theta$. Shown is $d\sigma _\textrm{coul}/d\Omega$ with ($----$) and without $(\cdots \cdots )$ the consideration of recoil in comparison with the measurements from Offermann et al. ($\blacksquare$, [4]). Included is $d\sigma _\textrm{box}/d\Omega$ from (2.3) (———-)

Fig. 3

Dispersion correction $\Delta \sigma _\textrm{box}$ for $e+^{12}$C collisions in the vicinity of the first diffraction minimum as a function of collision energy $E_i-c^2$. Shown is the result from (2.4) at $\theta _\textrm{min}$ (———-) in comparison with the spline-interpolated experimental data at $\theta _\textrm{min}\;\,(\blacksquare )$. Included is $\Delta \sigma _\textrm{box}$ from (2.4) at $\theta _\textrm{min}+1^\circ \;\,(-\cdot - \cdot -)$ and at $\theta _\textrm{min}-1^\circ \;\,(----)$ together with experimental data lying in the interval $[\theta _\textrm{min}-1^\circ ,\theta _\textrm{min}+1^\circ ]$ (open circles with error bars, [2,3,4]). Also shown is the Friar-Rosen result at $\theta _\textrm{min}\,\; (\cdots \cdots )$, calculated according to [26]

A systematic display of dispersion is given in Fig. 3 by comparing the cross-section change $\Delta \sigma _\textrm{box}$ with experiment as a function of collision energy. This is done by setting for each energy the scattering angle $\theta$ to its value $\theta _\textrm{min}$ at the first diffraction minimum of $d\sigma _\textrm{coul}/d\Omega$. The figure shows that $\Delta \sigma _\textrm{box}(\theta _\textrm{min})$ increases much stronger with energy than the Friar-Rosen result and is in satisfactory accord with the experimental findings, which are obtained by spline-interpolating the measured points in the vicinity of $\theta _\textrm{min}$ and relating them to $d\sigma _\textrm{coul}/d\Omega$ in correspondence to (2.4). Attaching average experimental error bars to these data points, the resulting reduced $\chi ^2$, defined by $\chi ^2=\frac{1}{n} \sum _{i=1}^n (\Delta \sigma ^{(i)}_\textrm{box,exp}-\Delta \sigma ^{(i)}_\textrm{box,theor})^2/l_i^2$ where $n=4$ is the number of points and $l_i$ is the half-length of the error bar of datum point i, is $\chi ^2=0.3$ (compared to $\chi ^2=6.8$ for the Friar-Rosen results) which emphasizes the superiority of the present theory.

Fig. 4

Dispersion correction $\Delta \sigma _\textrm{box}$ for 56 MeV $e + ^{12}$C collisions as a function of scattering angle $\theta$ (———). Also shown are its constituents from the individual transient excited states at 23.5 MeV $(-\cdot - \cdot -)$, 17.7 MeV $(\cdots \cdots )$ and 4.439 MeV $(----)$. Included is the Coulombic contribution to $\Delta \sigma _\textrm{box}\;\,(-\cdots -)$

Included in the figure are the measured data points which are closest to $\theta _\textrm{min}$, being located in an interval $[\theta _\textrm{min}-1^\circ ,\theta _\textrm{min}+1^\circ ]$. In order to show the corresponding variation of the theory, the dispersion results at the angles $\theta =\theta _\textrm{min}\pm 1^\circ$ are also provided. Except for the data near 300 MeV the experiments are mostly located within the region spanned by the three theoretical curves.

Magnetic scattering, although important for exciting each of the transient nuclear states, largely cancels when they are summed over, leaving a net effect below 10% at energies beyond 400 MeV [20]. However, the magnetic contribution to the cross-section change gains importance at the lower collision energies. This is quantified in Fig. 4, where the angular distribution for 56 MeV electron impact is shown. Indeed, $\Delta \sigma _\textrm{box}$ (comprising Coulombic and magnetic contributions and marked by ’tot’ in the figure) is not only much larger than its Coulombic part, but it differs even in shape. Also, while at the higher energies all transient nuclear states contribute in a similar way, it is the highest dipole state which largely dominates the dispersive cross-section change at the lower energies.

Fig. 5

Spin asymmetry S for perpendicularly polarized electrons colliding with $^{12}$C at 56 MeV as a function of scattering angle $\theta$. Shown are the results from the phase-shift analysis $(----)$, and including dispersion according to (2.5) (———)

4 Spin asymmetry results

The Sherman function for a collision energy of 56 MeV is displayed in Fig. 5 in the forward hemisphere, with and without the consideration of dispersion. Since this energy is well below the onset of any diffraction effects in $^{12}$C, S is monotonously decreasing up to scattering angles close to $180^\circ$. In order to quantify the influence of dispersion, Fig. 6a shows its change $d S_\textrm{box}$, including the separate contributions of the three transient nuclear states. It is seen that $d S_\textrm{box}$ strongly increases in modulus with decreasing scattering angle in the forward hemisphere, and, like for $\Delta \sigma _\textrm{box}$, the main contribution to $d S_\textrm{box}$ originates from the highest dipole state. It should be mentioned that for low momentum transfer ( there appears a logarithmic singularity in the differential cross section which leads to wiggles in $d S_\textrm{box}$ near the corresponding angles. This singularity is due to a coincidence of the poles from the electron propagator and from one of the photon propagators. The same behaviour is known from the second-order Born approximation to elastic scattering (when the nucleus remains in its ground state [8]), where the singularity can be removed by means of introducing a finite photon mass and proceeding to the third-order Born approximation which cancels the pathological contribution. With this in mind, the wiggles are smoothed in the sum over the three contributing states.

Fig. 6

a Relative change $dS_\textrm{box}$ of the spin asymmetry from 56 MeV $e+^{12}$C collisions as a function of scattering angle $\theta$. Shown are the contributions $dS_\textrm{box}(L,\omega _L)$ from the nuclear states at 23.5 MeV $(-\cdot - \cdot -)$, 17.7 MeV $(\cdots \cdots )$ and 4.439 MeV $(----)$ as well as their sum (———-). b is an enlarged vesion of a, including the Coulombic contribution to $dS_\textrm{box}\,\; (-\cdots -)$ as well as the Friar-Rosen result according to [26] $(\cdots \cdots )$

An enlarged account of the angular dependence between $55^\circ$ and $150^\circ$ is provided in Fig. 6b. In addition to $dS_\textrm{box}$, the Coulombic contribution to $dS_\textrm{box}$ is displayed, which is at most 0.5% and deviates considerably from $dS_\textrm{box}$. It follows that the magnetic scattering provides the dominant contribution to the dispersion correction of the spin asymmetry at this low energy. The Friar-Rosen result, which is based on mere Coulombic scattering [8], differs strongly in shape from both $dS_\textrm{box}$ and the Coulombic contribution to $dS_\textrm{box}$. However, it converges to the contribution from the quadrupole state to $dS_\textrm{box}$ at the backmost angles. We recall that for that state, magnetic scattering is small [20].

Figure 7 shows $d S_\textrm{box}$ at a higher energy of 100 MeV in the angular region beyond $30^\circ$, which is above the location of the logarithmic singularities. For angles larger than $120^\circ$, diffraction comes into play and $d S_\textrm{box}$ is no longer a suitable parameter. In fact, the vanishing of $S_\textrm{coul}$ at $140^\circ$ is already perceptible by means of the strong increase of $|dS_\textrm{box}|$ towards $120^\circ$. For angles beyond $90^\circ$, the two dipole transient nuclear excitations contribute similarly to the change in the spin asymmetry, in contrast to the lower energy where the 23.5 MeV state dominates at all angles. In the forward hemisphere $dS_\textrm{box}$ is above the one at 56 MeV, and the dispersion effects increase with energy beyond 100 MeV at fixed (forward) angle.

Fig. 7

Relative change $dS_\textrm{box}$ of the spin asymmetry from 100 MeV $e+^{12}$C collisions as a function of scattering angle $\theta$ (———-). Also shown are the contributions $dS_\textrm{box}(L,\omega _L)$ from the nuclear states at 23.5 MeV $(-\cdot -\cdot -)$, 17.7 MeV $(\cdots \cdots )$ and 4.439 MeV $(----)$

The dispersion correction for 56 MeV, now represented in terms of the difference $S_\textrm{box} -S_\textrm{coul}$, is depicted in Fig. 8 at small angles. Below $12^\circ$ the sum over the phase shifts converges poorly due to the convergence acceleration [27] which is necessary for such energetic collisions. Therefore, $\Delta S_\textrm{box}$ is supplemented by the Born approximation for the lower angles. From the comparison of $\Delta S_\textrm{box}$ with $S_\textrm{box}^\textrm{Born}$ it is seen that the Born theory provides the correct angular dependence at near-forward angles. The difference relates to the Coulomb distortion which amounts to 4–8% below $45^\circ$. Even for backward angles, the distortion effects are at most 5% at this energy for the $^{12}$C nucleus.

Fig. 8

Influence of dispersion on the spin asymmetry from 56 MeV $e+^{12}$C collisions as a function of scattering angle $\theta$. Shown is $\Delta S_\textrm{box}$ from (2.7) (———–) and $S_\textrm{box}^\textrm{Born}$ from (2.8) $(-\cdot - \cdot -)$. Included are the separate contribution from the 4.439 MeV state to $\Delta S_\textrm{box}$ $(----)$ and the Friar-Rosen result $(\cdots \cdots )$

Included in the figure is the Friar-Rosen result for $\Delta S_\textrm{box}$ in comparison with the contribution from the 4.439 MeV state. At very small angles this contribution and also the Friar-Rosen result behave approximately like $\sin ^3(\theta /2)$ as does $S_\textrm{coul}$, whereas $\Delta S_\textrm{box}$ increases much stronger, according to $\sin (\theta /2)$. This linear instead of cubic increase is due to the influence of magnetic scattering and agrees with the predictions from the relation to the experimental Compton scattering cross section [28].

5 Concluding remarks

By calculating the dispersion effect to lowest order in the Born approximation and allowing for three strong transient nuclear excitations, we have shown that the cross section modifications are small at energies below 100 MeV ($< 0.1\%$), but increase up to nearly 10% beyond 400 MeV. However, the influence of dispersion on the beam-normal spin asymmetry is considerably stronger in the investigated energy region 50–150 MeV. At forward angles where the Sherman function is very small, dispersion may lead to an increase of 100% or more, reducing to a few percent at intermediate angles. In contrast to the cross-section modifications where magnetic scattering is mostly of minor importance, it is dominant in case of the spin-asymmetry change, particularly at very small and very large angles. Due to the lack of experimental spin asymmetry data and due to the fact that the highest dipole excitation is largely dominant at most angles, it remains an open question whether high-lying transient states of multipolarity larger than one have to be considered as well.

As an outlook, one might further investigate the effect of dispersion on the scattering of positrons. In fact, spin-polarized positrons can now efficiently be generated from spin-polarized electrons with the help of circularly polarized bremsstrahlung produced when passing through thick high-Z targets [29].