Flavor-diagonal CP violation: the electric dipole moment

Abstract

The observed baryon asymmetry in the universe cannot be reconciled with the current form of the Standard Model (SM) of particle physics. The Standard Model breaks charge conjugation parity (CP) symmetry, but not in a sufficient amount to explain the observed matter-antimatter asymmetry. Historically one of the first systems to be studied in the search of symmetry breaking within the Standard Model is the electric dipole moment (EDM) of the neutron. The contribution to the neutron EDM coming from the SM is several order of magnitudes smaller than the current experimental bound, thus providing a unique, background-free window for potential discovery of physics Beyond the Standard Model (BSM). The strong CP-violating $\theta$ term can also contribute to the neutron EDM, as can all the CP-violating effective operators describing, at energies below the electro-weak scale, the contributions from BSM. To constrain all these contributions to the neutron EDM we need to precisely determine the hadronic matrix elements of the corresponding renormalized operators. After a brief introduction on baryon asymmetry and baryogenesis, I summarize the current stuatus for experiments in search of a neutron EDM. I then describe in more details the different CP-violating sources, and some results in Chiral Perturbation Theory precede a discussion on the current status of Lattice QCD calculations. I will in particular focus on the 2 main challenges for these type of calculations: the signal-to-noise ratio and the renormalization. I will discuss several improvement techniques trying to improve these two aspects of the calculation and I will conclude with an optimistic view into the future.

1 Matter-antimatter asymmetry

The equivalence of masses and decay widths between particle and antiparticles is a direct consequence of the CPT theorem. Observations contrast with the naive expectation that also the particle and antiparticle density are the same. The observed Universe is dominated by matter over antimatter and the antiprotons that are observed in cosmic rays are produced at a rate consistent with the antiprotons density $\sim 10^{-4}$ smaller than the proton density [1].

During the evolution of the Universe the baryon number density changes with the cosmological scale factor and it is advantageous to define

$$\begin{aligned} \eta = \frac{n_B}{n_\gamma }\,, \qquad n_B = n_b - n_{{\overline{b}}}\,, \end{aligned}$$

(1)

as a measure of the baryon asymmetry of the Universe, where $n_{b} (n_{\overline{b}})$ is the baryon (antibaryon) density and with $n_\gamma$ the photon density.

Fig. 1

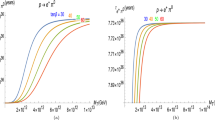
Primordial abundances of light nuclei, $^4$He, D, $^3$He and $^7$Li, shown as a function of the baryon-to-photon ratio $\eta$, as predicted by standard Big-Bang nucleosynthesis (BBN). Bands show $95\%$ of C.L. The results of the experimental observation are in the yellow bands and the vertical lines denote the measure of the cosmic baryon density from CMB (thin band labelled by CMB) and the so-called concordance range for the BBN including the D and the $^4$He (wide vertical band). Both with $95\%$ of C.L. Figure taken from Ref. [2]

The value of $\eta$ can be determined comparing the $\eta$ dependence of the light element abundances predicted by standard Big-Bang nucleosynthesis (BBN) and the corresponding observed abundances. Fixing the number of neutrinos, the standard BBN predicts the relative abundances of D, ${}^3$He, ${}^4$He, and ${}^7$Li as a function of $\eta$. In this way any experimental determination of the light nuclei abundance can be used to determine $\eta$. In Fig. 1 the relative abundances of the light nuclei predicted by the standard model of BBN are shown as a function of $\eta$ with colored bands representing $95\%$ CL range [3]. See Ref. [4] for a recent analysis after the latest release of the Planck data.

Excluding the Lithium abundance,¹ that leads to inconsistent values of $\eta$ with respect to the other abundances, the values of $\eta$ obtained using D/H and and $^4$He abundances lead to very consistent values for $\eta$. In particular using the very recent determination of the D/H abundance [5] one infers a value of $5.8 \times 10^{-10}< \eta < 6.5 \times 10^{-10}$ [2].

The prediction of the baryon density obtained by the standard model of BBN can be compared with a completely independent determination of $\eta$ from the Cosmic Microwave Background (CMB) angular power spectrum [6]. The most recent analysis of the Planck data [7] gives a value $\eta = \left( 6.12 \pm 0.04\right) \times 10^{-10}$ [2] perfectly consistent with the value obtained from the observed primordial abundances and standard model of BBN.

Independent of the particle physics theory responsible for the baryon asymmetry in the universe, a set of criteria, the Sakharov conditions [8], need to be satisfied by the responsible interaction: baryon number violation; C- and CP- violation; Universe out of thermal equilibrium to avoid the thermal average washing out the net baryon asymmetry.

2 Baryogenesis scenarios and CP-violation

The analysis of the 3 Sakharov conditions compared with the observed asymmetry between matter and antimatter, can shed some light on the baryogenesis mechanisms. In order to satisfy the last condition, i.e. to stay out of thermal equilibrium, Sakharov imagined that baryogenesis would start after the Big Bang, when most reactions would take place out of thermal equilibrium and at a temperature not much below the Planck scale [11].

An example of BSM theories providing baryon number violation combined with possible new sources of CP-violation are Grand Unified Theories (GUT) [10]. While GUT theories could in principle provide the necessary CP-violation with some extra heavy-particles they have to face a few difficulties. The first one is that all the GUT theories, consistent with the current values of the SM parameters, have to rely on inflation to remove relics of particles generated at the GUT scale. As a result though any baryon asymmetry would be washed out as well and the temperature would be too low to restart any GUT process generating again a baryon asymmetry [11].

Another challenge for GUT scenarios is the fact that any mechanism generating a baryon asymmetry has to compete with the anomalous baryon number violation in the SM [12]. Analogously to what happens in QCD with the topological charge and the tunneling probability between topological sectors, in the SM the baryon number is violated with a probability proportional to $\sim \exp \left( -4\pi /\alpha _W\right)$, where $\alpha _W$ is the weak coupling [12, 13]. While at a relatively low temperature the probability to all practical purposes vanishes, at high temperature, around and above $\sim 100$ GeV, the anomalous baryon violation can compensate any baryon violation [14]².

Another possibility is to actually make use of the anomalous baryon number violation to generate a baryon asymmetry. The mechanism to be out of equilibrium at the electro-weak scale is provided by a first-order weak phase transition at the electro-weak scale, $\sim 100$ GeV. The main mechanism for electroweak baryogenesis is that after the Big Bang no baryon asymmetry is generated at temperatures above 100 GeV. When the temperature reaches the electroweak scale the $SU(2)_L \times U(1)_Y$ SM symmetry is broken spontaneously generating a non zero expectation value for the Higgs field. The requirement of having a first order electroweak phase transition, implies that bubbles, or regions, would form, where the expectation value of the Higgs field is non-zero. A non-zero net baryon number is generated at the boundaries of these regions where the CP- and C-violating interaction convert 3 baryons (anti-baryons) in 3 antileptons (leptons), preserving though B-L. These baryon number violating transitions are mediated by so-called sphaleron field configurations, just as instanton configurations are responsible for the change of the topological charge, even though with a different mechanism [15]. Eventually the regions with non-zero Higgs condensate will expand and blend in the universe we know today with a net baryon asymmetry and a non-vanishing Higgs vacuum expectation value. For reviews on electroweak baryogenesis or baryogenesis in general [16,17,18] should be consulted.

The problem with this mechanism is that the current value of the Higgs mass, $m_H = 125.10 \pm 0.14$ GeV, heavier than $\sim 70$ GeV, prevents the phase transition from being first order [19]. Even if the transition could be first order, the amount of CP-violation from the Cabibbo–Kobayashi–Maskawa (CKM) matrix [20, 21] would not be sufficient to generate the correct baryon asymmetry [22, 23]. And this is the main reason to study BSM baryogenesis scenarios (see Ref. [11] for a review). The CP-violation from the CKM matrix amounts to a product of mixing angles resulting in a factor of order $10^{-20}$ or less [22,23,24], which is difficult to reconcile with the baryon asymmetry inferred from experiment. All these considerations bring to the conclusion that BSM physics is required in order to explain the current baryon asymmetry in the Universe.

A measurement of the intrinsic Electric Dipole Moment of elementary particles and more complex systems, provides a measure of Parity (P) and charge conjugation parity (CP) symmetries violation. In Sect. 5 we will see that several BSM sources can induce a non-zero Electric Dipole Moment (EDM), providing a natural probe for the BSM energy scale $\varLambda _{\text {BSM}}$. The constraints provided by the EDM cannot disentangle between $\varLambda _{\text {BSM}}$ and the CP-violating phases. One can combine though the determination from a BSM theory for the matter-antimatter asymmetry, with the constraints coming from an experimental determination of the EDM. As an example we show the result of the analysis of Ref. [9] within the Minimal Supersymmetric Standard Model (MSSM). In Fig. 2, taken from Ref.  [9], the green band represents the prediction for the MSSM parameters, the bino mass parameter, $M_1$, and CP-violating phase factor, $\sin \varPhi _1$, consistent with the observed baryon asymmetry. The black curves represent the values of the neutron EDM (nEDM) within the same model. The current experimental bound on the nEDM, in Eq. (5), does not constrain any region of the MSSM parameters consistent with the observed baryon asymmetry. The next generation of experiments, although not conclusive for this particular model, might push the limit down to $10^{-27} e$ cm. While present and future pp collider experiments can shed a light on these new interactions, the search for a permanent EDM still remains one of the most promising tools to discover new sources of CP-violation.

Fig. 2

MSSM parameters plot with the bino mass $M_1$ on the x-axis and its phase $\varPhi _1$. The green band represent the values of the MSSM parameters consistent with the observed baryon asymmetry. The black curves are the prediction for the nEDM within the same model. Fig. published with permission from the authors of Ref. [9]

3 Electric Dipole Moment

The original motivation to search for a permanent intrinsic neutron Electric Dipole Moment (nEDM) was the investigation of possible violation of parity (P) symmetry [25]. Only later it was recognized that a non-zero EDM would also signal time-reversal (T) symmetry violation [26, 27].

Assuming locality, Lorentz invariance and Hermiticity of the fundamental quantum field theory describing the dynamics of elementary particles, then the theory is invariant under the combined CPT symmetry, where C is the charge-conjugation symmetry [28, 29]. This implies that if we measure a non-vanishing intrinsic EDM then we would be probing a CP-violating interaction.

The intrinsic EDM thus is a natural quantity to measure any source of CP-violation, whether coming from the Standard Model (SM) or from a Beyond the Standard Model (BSM) source. This is particularly important in view of the fact that the source of CP-violation in the SM, the CKM matrix, is not able to generate the sufficient amount of CP-violation to induce the currently observed matter-antimatter asymmetry as we have discussed in the previous sections.

Following the Wigner-Eckart theorem, the intrisic EDM, $\mathbf{d}$, of a system has to be proportional to its average angular momentum $\mathbf{d}= d \left\langle \mathbf{J}\right\rangle$. We can describe the interaction of a particle with spin 1/2, with field $\psi$, and the electromagnetic field, $F_{\mu \nu } = \partial _\mu A_\nu -\partial _\nu A_\mu$, with the Lagrangian in Minkowski space [30]

$$\begin{aligned} {{\mathcal {L}}}= - \mu \overline{\psi }\sigma ^{\mu \nu }F_{\mu \nu }\psi - i d \overline{\psi }\gamma _5 \sigma ^{\mu \nu }F_{\mu \nu }\psi \, \end{aligned}$$

(2)

where $\mu$ is the magnetic moment. The form of the interaction in the second term, the EDM term, of Eq. (2) makes evident the violation of P and T-symmetry. In the non-relativistic limit the Hamiltonian

$$\begin{aligned} H = -\mu ~\mathbf{J}\cdot \mathbf{B}- d~\mathbf{J}\cdot \mathbf{E}\,, \end{aligned}$$

(3)

shows that while the magnetic moment, $\mu$, term is even under P- and T-symmetry ($\mathbf{B}$ and $\mathbf{J}$ are even under P- and odd under T-symmetry), the EDM, d, term is odd under both P- and T-symmetry ($\mathbf{E}$ is even under T- and odd under P-symmetry).

The first experimental attempt to measure an intrinsic EDM was with the neutron [31], because a neutral system would avoid the loss of control over the particles in a strong electric field. To measure the nEDM the idea is to measure the frequency of the spin precession of the polarized neutrons

$$\begin{aligned} \nu _\pm = \mu B \pm d E\,, \end{aligned}$$

(4)

where the configurations of the magnetic, B, and electric, E , fields are parallel and antiparallel. One would then extract the nEDM from the difference of the measured frequencies, $d = (\nu _+-\nu -)/2E$.

To have an idea on the type of control needed on the magnetic field, an nEDM of $d_n \sim 10^{-26}e$ cm will generate a signal (the spin precession frequency) $10^{8}$ smaller than the signal of the magnetic moment, using typical values for B and E [32]. Given that the nEDM signal comes from the fine cancellation of parallel and antiparallel configurations for the electric and magnetic field, the factor $10^8$ is the minimal required accuracy in the control of the magnetic field.

This challenging measurement can be achieved only if the magnetic field is very well under control, if we have large enough number of neutrons and if we extend, as much as possible, the time-duration of the interaction between the the spin of the neutrons and the electric field.

In the first experiments the neutrons were produced in trasversely polarized beams deriving a bound for the nEDM of $3 \times 10^{-24}~e$ cm. The sources were thermal neutrons with a typical interaction time with the electric field of $\sim 1$ ms. This experimental technique had several limitations [19] and it was overtaken when new techniques, based on ultra-cold neutrons (UCNs) [33, 34], were developed, pushing the limit of the nEDM to $1.2 \times 10^{-25}~e$ cm with $95 \%$ confidence level (C.L.) [35].

A big advantage of this technique is that UCNs have such a small kinetic energy, that they can be stored in traps, reflecting completely when colliding with the walls. The experiment performed at Institut Laue-Langevin (ILL) [36] succeeded in having an interaction time of $\sim 100$ seconds and a bound on the nEDM $|d_n| < 3.0 \times 10^{-26} e$ cm ($90\%$ C.L.). The main limiting factor in these most recent searches for a nEDM is still the statistical uncertainty.

Future nEDM experiments will take advantage of UCN source with increased intensity. For example the latest analysis of the data obtained at the PSI UCN source has given us the new best bound for the nEDM [37]

$$\begin{aligned} \left| d_n \right| < 1.8 \times 10^{-26}~e~{\text {cm}}\,, \quad 90\%{\text {C.L.}} \end{aligned}$$

(5)

In Table 1 I provide a summary, taken from Ref. [32], with a list of the ongoing efforts towards better nEDM experiments  [38,39,40,41,42,43,44]. The experiments have different timelines but they all promise an improvement of a factor $10-100$ by 2030.

Table 1 Ongoing experimental nEDM projects around the world. Columns indicate: the experiment, neutron source, main experimental technique and reference. Table reproducing Table 1 of Ref. [32]

The neutron is not the only system studied to determine an intrinsic EDM. Atoms and molecules can also provide experimental systems to probe CP-violations. Paramagnetic systems, where one or more electrons are unpaired, are mainly probes for the electron EDM³. To probe hadronic CP-violating term, diamagnetic systems are used, such as $^{129}$Xe, $^{199}$Hg and $^{225}$Ra. Charged particles in storage rings can also be used to search for EDMs. An example is the experiment with ${H\!f\!F}^+$ cation to extract the electron EDM [45]. Another example is the Storage Ring COSY that plans to keep confined proton and deuteron [46] for EDM measurements. A summary of the recent experimental bounds on the EDM for other systems can be found in Ref. [19].

4 Standard Model and $\theta$ term

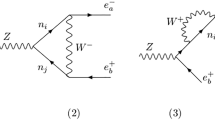
The CKM matrix phase factor and the $\theta$ term (see next Sect. 4.1) in the QCD Lagrangian are the only 2 CP-violating parameters in the SM. The CKM matrix induces an EDM to the quarks starting at 2-loops [47, 48]. The contribution of the CKM matrix to the neutron EDM comes from a $\varDelta S=1$ CP violating strong penguin diagram, see left graph of Fig. 3. The CP-violating $\varDelta S=1$ interaction is then combined with a CP-conserving one and the EDM is a 1-loop effect enhanced by chiral logs, see right graph in Fig. 3.

Fig. 3

Left: $\varDelta S=1$ penguin diagram. Right: The $\varDelta S=1$ coupling combines together with a $\varDelta S=1$ CP-even coupling. The circle with a cross indicates the effective operator corresponding to the penguin diagram on the left. This diagram describes the contribution to the nEDM from the CKM matrix

The latest determination of the nEDM [49] from the CKM matrix is $d_n^{\text {CKM}} = 1-6 \times 10^{-32} e$ cm. The variation of the result covers the hadronic uncertainties in the calculation. This range of values lies 6 order of magnitudes below the current experimental bounds for the nEDM that we have discussed in Sect. 3, Eq. (5). Thus any nEDM experimental determination in the near future will be a background free window into physics Beyond the Standard Model.

4.1 The $\theta$ term

The EDM induced by the CKM matrix is suppressed, because of the flavor non-diagonal nature of the CP-violating interaction. A natural CP-violating source of an EDM is the flavor-diagonal CP-odd $\theta$ term. In Minkowski space the QCD Lagrangian,including the $\theta$ term, for $N_f=3$ quark flavors with a diagonal mass matrix M is

(6)

where $D_\mu$ is the usual covariant derivative, the quark fields are collected in $\psi = (u,d,s)^T$ and the gluon field tensor by $G^a_{\mu \nu }, \quad a=1,\ldots ,8$. $\epsilon ^{0123}=+1$ is the completely antisymmetric tensor and the CP-violating operator is multiplied by the coupling ${\bar{\theta }}$, also called the $\theta$ term.

The $\theta$ term is denoted with ${\bar{\theta }}$ to remind us the specific choice of basis. The quark mass matrix, in general complex, can be made real by reabsorbing the complex phase into a modified coupling ${\bar{\theta }}= \theta + \mathrm {arg}\,\mathrm {det}(M)$ with a redefinition of the quark fields phases. In this basis the $\theta$ term is proportional to the CP-violating pure gauge operator. This is a basis very popular within Lattice QCD (LQCD) calculation.

If we now start from the Lagrangian in Eq. (6) using a $U(1)_A$ chiral rotation [50, 51] and enforcing the stability of the vacuum, one can “rotate” the $\theta$ term proportional to the topological charge density into a pseudoscalar mass term

$$\begin{aligned} {{\mathcal {L}}}_{{\bar{\theta }}} \rightarrow m_* {\bar{\theta }}i \overline{\psi }\gamma _5 \psi \,, \end{aligned}$$

(7)

where $m_*$ is the reduced mass that in the case of $N_f=3$ flavors reads

$$\begin{aligned} m_* = \left( \frac{1}{m_u} + \frac{1}{m_d} + \frac{1}{m_s} \right) ^{-1} = \frac{{\overline{m}}\left( 1 - \epsilon ^2\right) }{2} + O(\frac{{\overline{m}}}{m_s})\,,\quad \end{aligned}$$

(8)

where

$$\begin{aligned} {\overline{m}}= \frac{m_u + m_d}{2}\,, \quad \epsilon = \frac{m_d - m_u}{m_d+m_u}\,. \end{aligned}$$

(9)

This basis is particularly advantageous for calculations in chiral perturbation theory ($\chi$PT). If the $\theta$ term is mapped into the mass term, it allows a straightforward mapping of the CP-violating interaction term into the chiral effective Lagrangian. We discuss CP-violating terms in $\chi$PT in Sect. 6.

In Euclidean space the QCD Lagrangian for $N_f=3$ flavors in Eq. (6) becomes

(10)

which is invariant under the global group transformation

$$\begin{aligned} U(3)_L \otimes U(3)_R \simeq SU(3)_L \otimes SU(3)_R \otimes U(1)_V \otimes U(1)_A\,. \end{aligned}$$

(11)

The standard assumption is that the non-singlet part of the chiral group, $SU(3)_L \times SU(3)_R$, is broken spontaneously in the massless limit, while the remaining $U(1)_A$ sector is still apparently a symmetry of the theory. If true, this would imply the existence of a parity partner for each Goldstone boson.

The absence of light scalar mesons seem to indicate that the $U(1)_A$ cannot be a symmetry, but it also cannot be spontaneously broken, because the corresponding Goldstone boson should have a mass lighter than $\sqrt{3} m_\pi$ [52]. Neither the $\eta$ nor the $\eta '$ meson masses fulfill the Weinberg bound. This apparent paradox is resolved by ’tHooft [12, 13] showing that non-perturbative effects can be responsible for a violation of the axial charge conservation. As a consequence the associated pseudo-scalar meson must remain massive even in the chiral limit.

For lattice practitioners it is more familiar to understand the breaking of $U(1)_A$ symmetry as a result of the non-invariance of the fermion integration measure in the functional integral formulation of QCD [53]. The lack of invariance of the functional integral under a $U(1)_A$ symmetry transformation, explains the anomalous breaking of the Ward identity in the chiral limit for $N_f$ flavors

$$\begin{aligned} \partial _\mu \sum _{f=1}^{N_f} \overline{\psi }_f(x)\gamma _\mu \gamma _5 \psi _f(x) = i 2 N_f q(x)\,, \end{aligned}$$

(12)

where

$$\begin{aligned} q(x) = \frac{1}{32 \pi ^2}G^a_{\mu \nu }(x){\widetilde{G}}^a_{\mu \nu }(x)\,, \quad {\widetilde{G}}^a_{\mu \nu }(x) = \frac{1}{2} \varepsilon _{\mu \nu \rho \sigma }G^a_{\rho \sigma }(x), \end{aligned}$$

(13)

is the topological charge density. To connect this result with the violation of the axial charge conservation one should notice that, despite being a total derivative, the topological charge density can still be integrated over space-time to obtain a net non-vanishing value, exactly because of non-perturbative effects parametrized by “instanton” configurations.⁴

The fact that a $U(1)_A$ rotation modifies the integration measure by a factor proportional to the topological charge density can be used to rotate away the $\theta$ term in the action. Before doing so one should also pay attention to the mass term. The quark mass matrix is in general complex, because it originates from the symmetry breaking of the electroweak vacuum with interactions that violate both P and CP⁵.

The mass term of the QCD Lagrangian in Eq. (10) can be written as

$$\begin{aligned} \overline{\psi }M \psi = \sum _{f=1}^{N_f} m_f \left( \overline{\psi }_f\right) _L \left( \overline{\psi }_f\right) _R + m_f^* \left( \overline{\psi }_f\right) _R \left( \overline{\psi }_f\right) _L\,, \end{aligned}$$

(14)

where $m_f$ are the diagonal entries of the mass matrix and

$$\begin{aligned} \psi _R = \frac{1}{2}(1+\gamma _5) \psi \,, \quad \psi _L = \frac{1}{2}(1-\gamma _5) \psi \,. \end{aligned}$$

(15)

Under the following U(1) transformation

$$\begin{aligned} \psi \rightarrow {\mathrm{e}}^{i \alpha _f \gamma _5} \psi \,, \end{aligned}$$

(16)

the mass term transforms as

$$\begin{aligned} m_f \rightarrow m_f{\mathrm{e}}^{2 i \alpha _f}\,. \end{aligned}$$

(17)

This implies that if we start in a basis, such as the one in Eq. (10), with a real mass term, a $U(1)_A$ rotation (16) will remove the $\theta$ term, because of the shift from the integration measure, but it will render the mass complex. As a result the P and CP violating $\theta$ term is “rotated” into the mass term, such as Eq. (7). If one of the quark masses vanishes then the $\theta$ term in Eq. (7) vanishes.

5 Beyond the standard model source for CP-violation and EDM

We have argued in Sects. 2 and 3, that the SM does not provide a sufficient amount of CP-violation to explain the baryon asymmetry in the Universe. Beside the possibility of a $\theta$ term in the QCD Lagrangian there is always the possibility to consider an unspecified BSM theory with new heavy particles above the energy scale $\varLambda _{\text {BSM}}$. Below the energy scale $\varLambda _{\text {BSM}}$ we can integrate out the heavy degrees of freedom and describe their effects as local effective operators made of the fundamental degrees of freedom of the SM. Such operators, if not already present in the SM, are represented by higher dimensional operators suppressed by powers of $1/\varLambda _{\text {BSM}}^{D-4}$, where D is the dimension of the effective operator. We now concentrate only on the operators that contribute to the EDM, but a complete list of CP-violating higher dimensional operators can be found in Ref. [54].

Considering only the dimension 6 operators we have

$$\begin{aligned} {{\mathcal {L}}}_{\text {BSM}}^{\text {eff}} = \frac{1}{\varLambda _{\text {BSM}}^2} \sum _i C_i^{(6)} {{\mathcal {O}}}_i^{(6)}\,, \end{aligned}$$

(18)

where we have labelled generically with i all the local operators of dimension 6 and with $C_i^{(6)}$ the corresponding Wilson coefficients. The complete list of the these operators can be found for example in Ref. [55]. To get to the form of operators amenable to a lattice QCD calculation, we still have to go below the Electro-Weak symmetry breaking scale and “substitute” the Higgs field with its vacuum expectation value.

Among the resulting operators a subset have been estimated to give the dominant contributions to the EDM [56]: the quark-gluon operators, the 3-gluon operator, or so called the Weinberg operator [57], and 4-fermion operators. The quark-gluon operator, also called, quark-chromo EDM (qCEDM) operator is given by

$$\begin{aligned} {{\mathcal {O}}}_{qC}(x) = -i \sum _f \overline{\psi }_f(x) \gamma _5 \sigma ^{\mu \nu } G_{\mu \nu } \psi _f(x)\,, \end{aligned}$$

(19)

where $G_{\mu \nu } = \sum _{a=1}^8 G_{\mu \nu }^a T^a$ is the gluon field tensor and $\psi _f$ represents the fermion field associated with the flavor f.

The Weinberg operator is given by the expression

$$\begin{aligned} W(x) = \frac{1}{3} f^{ABC} {\widetilde{G}}^{A,\mu \nu } G_{\mu \rho }^B G_{\nu }^{C,\rho }\,, \end{aligned}$$

(20)

where ${\widetilde{G}}_{\mu \nu } = 1/2 \varepsilon _{\mu \nu \alpha \beta }G^{\alpha \beta }$ is the dual of the gluon field tensor and $\varepsilon _{0123}= +1$.

The 4-fermion operators are usually divided in semi-leptonic, containing 2 lepton and 2 quark fields and the hadronic ones containing 4 quark fields. At the time of writing there are no lattice QCD (LQCD) results about these 4-fermion operators so we will not consider them further.

The goal of LQCD calculations is to provide the renormalized hadronic matrix elements of the CP-violating operators. Those matrix elements represent the key input to constrain and disentangle the different contributions to any future experimental measurement of a non-zero EDM. Following Ref. [55] we can parametrize the nucleon EDM from different sources as follows

$$\begin{aligned} d_{\text {N}}= M_{\text {N}}^{\theta } {\bar{\theta }}+ \left( \frac{v}{\varLambda _{\text {BSM}}} \right) ^2 \sum _i M_{\text {N}}^{(i)} {\widetilde{d}}_i\,, \end{aligned}$$

(21)

where $M_{\text {N}}^{(i)}$ and $M_{\text {N}}^\theta$ represent respectively the LQCD hadronic matrix elements of the CP-violating operators ${{\mathcal {O}}}_i$ and the topological charge, v is the Higgs field vacuum expectation value and the ${\widetilde{d}}_i$ generically represents the contributions from the Wilson coefficients of the corresponding CP-violating operator ${{\mathcal {O}}}_i$.

While the latter can be calculated in perturbation theory (for a review see [54]) we focus on the non-perturbative calculation of the hadronic quantities $M_{\text {N}}^{(i,\theta )}$. Before discussing how such calculations are performed in LQCD, I will briefly summarize results obtained in Chiral Perturbation Theory ($\chi$PT), because this will also serve the purpose to introduce the $\chi$PT formulæ which are used to analyse LQCD data.

6 Chiral perturbation theory

In Sect. 3 we have briefly summarized the history of the experimental search for the nEDM in the last 60 years from the first search in 1957 [25, 31] to the most recent bound [36, 37, 58] $d_n<1.8\times 10^{-26} e$ cm ($90\%$ C.L.).

The experimental bound on the nEDM provides a bound on the value of ${\bar{\theta }}$ if, for example, we are able to determine in QCD the relation between the nEDM and the ${\bar{\theta }}$ parameter. After the first estimates [50, 51] based on chiral symmetry arguments, the ${\bar{\theta }}$ dependence of the nEDM has been determined using LQCD and Chiral Perturbation Theory ($\chi$PT). We will discuss in the following Sects. 7, 8 and 9 LQCD calculations for EDM with several CP-violating sources. Here I try to summarize a few interesting results obtained in $\chi$PT, that can serve also in discussing the pion mass dependence of the LQCD calculations.

A $\chi$PT calculation of the nEDM is usually performed mapping the CP-violating interactions into suitable CP-violating fields built of pion and nucleons. As we have seen in Sect. 4.1 the fermion basis can be chosen to have the $\theta$ term given by the pseudoscalar mass term in Eq. (7).

The chiral Lagrangian of Heavy Baryon Chiral Perturbation Theory (HB$\chi$PT) [59] is augmented with all possible interaction terms transforming as the corresponding CP-violating operators transform [56, 60]. We retain only the terms that are relevant for this discussion with low-energy-constants (LECs) ${\overline{g}}_0$, ${\overline{g}}_1$ and ${\overline{g}}_2$. Those are the couplings of the iso-scalar, -vector and -tensor nucleon-pion CP-odd interactions

(22)

where N is the 2-component nucleon doublet, $\tau ^a$ are the isospin Pauli matrices, $\pi ^a$ is the pion triplet and $F_\pi \simeq 92.4$ MeV. The choice made in Eq. (22) makes the couplings ${\overline{g}}_i$ dimensionless.⁶ Calculations are done in the nucleon rest frame where $v_\mu = (1,\mathbf{0})$ and $S_\mu = (0,\sigma _k$), where now $\sigma _k$ denote the Pauli matrices acting on the spin degrees of freedom. The first terms, ${\overline{d}}_0$ and ${\overline{d}}_1$, are called in jargon “short-range” LECs contributing to the nucleon EDM and, as we will see below, these terms play the role of counterterms when renormalizing the chiral expansion.

Chiral symmetry and dimensional arguments already give us a rough estimate for the values of the nucleon EDM. For example for the $\theta$-term contribution one estimates [61] that

$$\begin{aligned} d_{\text {N}}^{\theta } = M_M^\theta {\bar{\theta }}\simeq e {\bar{\theta }}\frac{m_\pi ^2}{\varLambda _\chi ^3} \sim 2-4.5 \times 10^{-3} {\bar{\theta }}e~\text {fm}\,, \end{aligned}$$

(23)

where $\varLambda _\chi$ is an hadronic scale that we take in the range between the nucleon mass $m_N$ and $4 \pi F_\pi$. This estimate combined with the current experimental bound (5) already tells us that ${\bar{\theta }}\sim 10^{-10}$.

A similar estimate can be done for the qCEDM and Weinberg operators. In this case the increased dimensionality of the operators implies that the matrix element for the qCEDM $M_{\text {N}}^{(qC)}$ is of O(1) while the matrix element for the Weinberg operator is $M_{\text {N}}^{(W)} \sim \varLambda _\chi$. The dimensionality of the nEDM is carried, in the case of the $D=5$⁷ qCEDM operator completely by the coupling ${\widetilde{d}}_{qC} \sim \frac{m_q}{\varLambda _{\text {BSM}}^2}$ while for the Weinberg operator it is obtained by combining the LQCD matrix element with the coupling ${\widetilde{d}}_W \sim \frac{1}{\varLambda _{\text {BSM}}^2}$. We observe that while the suppression toward the chiral limit for the $\theta$-term EDM is naturally carried by the LQCD matrix element, for the qCEDM is actually a consequence of the Yukawa coupling and the EWSB. The Weinberg operator being of dimension $D=6$ and chirally invariant is enhanced by a hadronic scale factor of $\varLambda _\chi$ and naturally suppressed like any $D=6$ operator by a power of $1/\varLambda _{\text {BSM}}^2$.

These rather crude estimates are a good starting point to better address the pitfalls of more precise calculations in LQCD. To make these estimates more robust, one can systematically perform an expansion in HB$\chi$PT obtaining in this way an expression for the CP-violating form factors and corresponding EDM in terms of the LECs and counterterms in Eq. (22). Many calculations have been performed in the two-flavor [50, 56, 62,63,64,65,66] and in the three-flavor case [64, 67,68,69]. In general the expressions determined in $\chi$PT for the CP-odd form factors and the corresponding EDM depend on the LECs and consequently the LECs depend on the CP-violating source. In the case of the $\theta$-term we separate the iso-scalar and iso-vector case and the expressions up to NLO are

$$\begin{aligned} d_0^{\theta }= & {} {\overline{d}}_0^{\theta } - \frac{e g_A {\overline{g}}_0}{16\pi F_\pi } \frac{3 m_\pi }{M_N}\,, \end{aligned}$$

(24)

$$\begin{aligned} d_1^{\theta }= & {} {\overline{d}}_1^{\theta }(\mu ) + \delta _1(\mu ) + \frac{e g_A {\overline{g}}_0}{4\pi ^2 F_\pi }\left[ \ln \frac{m_\pi ^2}{m_N^2} - \frac{5\pi m_\pi }{4m_N}\right] \,, \end{aligned}$$

(25)

where we have neglected isospin violations. The equivalent expressions for the qCEDM of Eqs. (24,25) would contain an additional analytic term at NLO proportional to ${\overline{g}}_1$.

The renormalization scale dependence of $\delta _1(\mu )$, which is the result of the regulated loop integral, is reabsorbed by the scale dependence of the counter-term. The common argument to explain the dominance of the logarithmic term over the counter-term, is that choosing a renormalization scale around the nucleon mass $\mu \simeq m_N$, will capture most of the logarithmic dependence from the loop integral, thus relegating the counter-term to a a sub-leading contribution with respect to the chiral log. In Sect. 7 we show that first lattice QCD results, even though with rather poor precision, seem to confirm these expectations.

Beside the EDM, $\chi$PT can also provide a direct estimate of the CP-violating LECs, ${\overline{g}}_i$. One interesting approach is based on the observation that the $\theta$ term, once rotated in the basis where CP-violation is embedded in the mass term (see Sect. 4.1), it has definite transformation under the chiral symmetry group.

Probably a good way to understand how the method works, is to analyze the chiral Lagrangian of HB$\chi$PT and compare the leading CP-violating coupling, for example the ${\overline{g}}_0$ term, with the expansion of the mass term modified by the presence of the $\theta$ term. The mass and the terms appear in the chiral Lagrangian of HB$\chi$PT [59] only at O($p^2$) and, if we neglect the decuplet terms, for the SU(3) chiral Lagrangian we have

$$\begin{aligned}&{{\mathcal {L}}}_{{\text {HB}}\chi {\text {PT}}}^{(2)} \supset b_0 {{\mathrm{Tr}}}\left( {\overline{B}}B\right) {{\mathrm{Tr}}}\chi _+ + (b_D+b_F) {{\mathrm{Tr}}}\left( {\overline{B}}\chi _+ B\right) \nonumber \\&\, \, + (b_D-b_F){{\mathrm{Tr}}}\left( {\overline{B}}B \chi _+ \right) \,, \end{aligned}$$

(26)

where B represent the octet baryon field

$$\begin{aligned} B= \begin{pmatrix} \frac{1}{\sqrt{2}} \varSigma ^0 + \frac{1}{\sqrt{6}}\varLambda &{} \varSigma ^+ &{} p \\ \varSigma ^- &{} -\frac{1}{\sqrt{2}} \varSigma ^0 + \frac{1}{\sqrt{6}}\varLambda &{} n \\ \varXi ^- &{} \varXi ^0 &{} -\frac{2}{\sqrt{6}} \varLambda \\ \end{pmatrix} \end{aligned}$$

(27)

and

$$\begin{aligned} \chi _+ = u^\dagger \chi u^\dagger + u \chi ^\dagger u\,, \quad u^2(x) = \exp {\left( \frac{2 i \pi (x)}{F} \right) }\,, \end{aligned}$$

(28)

where $\chi$ the quark mass term augmented by the presence of the $\theta$ term

$$\begin{aligned} \chi = 2 B \left( {{\mathcal {M}}}+ i m_* {\bar{\theta }}\right) \,. \end{aligned}$$

(29)

Expanding the mass terms at leading order the terms proportional to $b_D$ and $b_F$ are responsible for the nucleon mass splitting

$$\begin{aligned} m_N - m_P = \left( \varDelta M_N\right) _{\text {QCD}} = - 8 B \epsilon \overline{m} (b_F + b_D)\,. \end{aligned}$$

(30)

At the following order, because of the presence of the $\theta$ term in the mass term (28), the 1-pion contribution, i.e. the $\overline{N}N\chi _+$ terms, in Eq. (26) does not vanish and, equating it with the ${\overline{g}}_0$ term of the CP-violating chiral Lagrangian (22), one obtains

$$\begin{aligned} {\overline{g}}_0= & {} 4 B \frac{b_D + b_F}{F_\pi } m_* {\bar{\theta }}= - \frac{\left( \varDelta M_N\right) _{\text {QCD}}}{2F_\pi } \frac{m_*{\bar{\theta }}}{\overline{m}\epsilon } \nonumber \\= & {} - \left( \varDelta M_N\right) _{\text {QCD}} \left( \frac{1 - \epsilon ^2}{4 F_\pi \epsilon }\right) {\bar{\theta }}+ \text {O}(\frac{\overline{m}}{m_s})\,. \end{aligned}$$

(31)

The important observation [70] is that the leading order relation (31), known since some time [50, 55, 60], receives small corrections from higher order contributions in the chiral expansion, allowing the direct determination of the LEC ${\overline{g}}_0$ from the study of the QCD isospin splitting in a CP-conserving vacuum. Using lattice QCD determinations of the QCD nucleon mass splitting [71, 72], one obtains the estimate [70]

$$\begin{aligned} {\overline{g}}_0= -14.7 (2.3)\times 10^{-3} {\bar{\theta }}\,. \end{aligned}$$

(32)

One can now use the $\chi$PT expressions (24,25), and the known values of $g_A, {\overline{g}}_0, F_\pi , m_\pi , M_N$, to estimate the chiral log contributions, i.e. the logarithmic term of Eq. (25), of the nucleon EDMs

$$\begin{aligned} d_n(\theta )= & {} {{\bar{d}}}_n-2.1(3)\times 10^{-3}\,{\bar{\theta }}\,e\,\mathrm {fm}\, ,\nonumber \\ d_p(\theta )= & {} {\bar{d}}_p+2.5(3)\times 10^{-3}\,{\bar{\theta }}\,e\,\mathrm {fm}\,, \end{aligned}$$

(33)

but a reliable estimate for the nEDM still needs the determination of the counter-term. While the complete determination of the nucleon EDM requires the LQCD calculations of the relevant hadronic matrix elements, the determination of ${\overline{g}}_0$ from Eq. (31) allows a comparison with the pion mass dependence of the LQCD results for the nucleon EDM. This is a strong consistency check of very different determinations of the same CP-violating LEC, ${\overline{g}}_0$.

The scope of the lattice QCD calculations is to provide a robust and complete determination of the neutron EDM without any assumptions about the log dominance, but rather trying to confirm or disprove it.

A complete determination of the nEDM is important for systems that are particularly sensitive to the iso-singlet linear combination $d_n+d_p$ where the contributions coming from the one-loop terms cancel each other out almost exactly. One example of such system is the deuteron EDM that is the target of the experimental effort in the Storage Ring COSY at the Forschungszentrum in Jülich [46], where the charged particles (proton, deuteron and maybe ${}^3$He) are kept confined in a storage ring. This example emphasize not only the importance of a LQCD calculation, but also the importance to have experimental efforts focusing on different systems which are sensitive to different sources of CP-violation.

An interesting application of the determination of the nEDM, is the estimate of EDM of light nuclei. It is possible to relate the EDM of light nuclei with a linear combination of terms containing the single-nucleon EDM and the CP-violating pion-nucleon couplings [73] ${\overline{g}}_i$. We have applied those relations in Ref. [74] and obtained the estimate

$$\begin{aligned} d_{{}^2\mathrm {H}}({\bar{\theta }})= & {} 0.2(1.2)\times 10^{-3}\,{\bar{\theta }}\,e\,\mathrm {fm}\, ,\nonumber \\ d_{{}^3\mathrm {H}}({\bar{\theta }})= & {} 3.2(1.0)\times 10^{-3}\,{\bar{\theta }}\,e\,\mathrm {fm}\, ,\nonumber \\ d_{{}^3\mathrm {He}}({\bar{\theta }})= & {} -2.5(0.8)\times 10^{-3}\,{\bar{\theta }}\,e\,\mathrm {fm}\,. \end{aligned}$$

(34)

The deuteron has a large uncertainty because is dominated by the isoscalar nucleon EDM. For $^3$H the situation is more favorable because the contribution to the uncertainties quoted, is roughly equally shared between the uncertainty of the nEDM and the uncertainty of the LECs.

7 Strong CP violation and $\theta$ term

In the previous section we have emphasized the role of LQCD in the determination of the nEDM. To calculate the $\theta$ term contribution to the nEDM, the most obvious approach is to treat the ${\bar{\theta }}$ parameter small, as the current experimental bound [37] of the nEDM suggests, ${\bar{\theta }}\sim 10^{-10}$ (see Sects. 3, 6), and treat the topological charge as an insertion in the hadron correlators. The EDM is then directly related to the CP-odd form factor describing the nucleon matrix element of the electromagnetic current in a CP-odd background.

In Minkowski space with mostly-negative (or West-coast) metric, $\eta ^{\mu \nu } = \text {diag}\left( 1,-1,-1,-1)\right)$, the form factor decomposition of the electromagnetic current $J^\mu = \sum _f q_f \overline{\psi }_f \gamma ^\mu \psi _f$ between on-shell nucleon states with momentum p ($p'$) and polarization s ($s'$) is given by [75]⁸

(35)

where

$$\begin{aligned} \varGamma ^{\mu }(Q^2) = \gamma ^\mu F_1(Q^2) + \left( F_2(Q^2) + i \gamma _5 F_3(Q^2)\right) \frac{i \sigma ^{\mu \nu }q_\nu }{2m_N}\,. \end{aligned}$$

(36)

The spinor $u_{s}(\mathbf{p})$ represents the nucleon with spin s and momentum $\mathbf{p}$. Beside the usual Dirac and Pauli form factors $F_{1,2}$ that are functions of $Q^2 = -q^2$, $q=p'-p$, there is an extra form factor parametrizing the CP-odd part of the hadronic matrix element. To relate the CP-odd form factor to the nucleon EDM one can evaluate the matrix element of the interaction Hamiltonian

$$\begin{aligned} H_{\text {int}} = e \int d^3x A_\mu J^\mu \,, \end{aligned}$$

(37)

where the $e>0$ is the charge of the proton and $A_\mu$ is the electromagnetic potential to be evaluated between 2 nucleon states. To identify the EDM we can, in the non-relativistic limit, associate the term proportional to the electric field $\mathbf {E}$ with the EDM and relate it to CP-odd part of the matrix element of the electromagnetic current. Performing the non-relativistic limit of Eq. (35), or in other words, retaining only the leading terms in an expansion in small momenta ($|\mathbf{p}|, |\mathbf{p}'| \rightarrow 0$) together with the positive frequency contributions of the fermion field, one obtains (see for example Ref. [75])

$$\begin{aligned} \varDelta E_{\text {s',s}}^{LO} = \left\langle \mathbf{p}',s'| H_{\text {int}} | \mathbf{p},s\right\rangle = - \mu _N \mathbf{H}\cdot \mathbf {\varSigma }_{s',s} - d_N \mathbf {E}\cdot \mathbf {\varSigma }_{s',s}\,,\nonumber \\ \end{aligned}$$

(38)

where $\mathbf{H}$ and $\mathbf {E}$ are the magnetic and electric fields and $\varSigma _{s,s'}^k$ is the matrix element of the 3 Pauli matrices, $\sigma ^k$, between the solutions of the Dirac equation at rest $\xi _s = \left( 1,0\right) ^T$ ($\xi _s = \left( 0,1\right) ^T$ for $s=-1/2$), i.e. $\varSigma ^k_{s,s'} = \xi ^\dagger _{s'} \sigma ^k \xi _{s}$. The magnetic, $\mu _N$, and electric dipole, $d_N$, moments take the usual form

$$\begin{aligned} \mu _N = \frac{e G_M(Q^2=0)}{2m_N}\,, \quad d_N = \frac{e F_3(Q^2=0)}{2m_N}\,. \end{aligned}$$

(39)

We note here that in the literature different signs appear in front of the EDM definition in Eq. (39), depending on the sign in front of the $F_3$ term in the form factor decomposition in Eq. (36). We also notice that once we rotate to Euclidean space and we specifically use certain representations of the Dirac matrices, while intermediate results might have different signs, depending on the intermediate conventions, the final result should be unambiguous.

The analysis above shows us that to determine the EDM we need to calculate the CP-odd form factor $F_3$ at $Q^2=0$ in the presence of a CP-odd source. To calculate the form factor in Euclidean space in presence of the $\theta$ term we need to calculate nucleon, N(x), 2-point and 3-point functions with the insertion of the topological charge

$$\begin{aligned} Q = a^4 \sum _z q(z)\,, \end{aligned}$$

(40)

where q(z) is the topological charge density in Eq. (13)

$$\begin{aligned}&a^3 \sum _{\mathbf{x}} {\mathrm{e}}^{-i \mathbf{p}\mathbf{x}} \left\langle N(\mathbf{x},x_4) {\overline{N}}(0) Q \right\rangle \,, \end{aligned}$$

(41)

$$\begin{aligned}&a^6 \sum _{\mathbf{x},\mathbf{y}} {\mathrm{e}}^{-i \mathbf{p}\mathbf{x}} \left\langle N(\mathbf{x},x_4) J_\mu (\mathbf{y},y_4) {\overline{N}}(0) Q \right\rangle \,. \end{aligned}$$

(42)

To renormalize the correlation functions above, beside the normalization of the vector current, one needs to address the issue of the definition of the topological charge in LQCD. With chirally symmetric [76, 77] lattice QCD formulations, such as Domain Wall [78, 79] or Neuberger Fermions [80, 81], it is in principle possible to determine the topological charge Q from the index theorem definition [82, 83]. A different, and perhaps more convenient definition, applicable for any LQCD action, is based on the gradient flow. We discuss in Sect. 7.1 more details about the gradient flow and in Sect. 7.2 results obtained following the strategy outlined above, where the $\theta$ term is treated perturbatively.

An alternative way to determine the EDM is to use a different fermion basis. The strategy of [84, 85] is to perform a calculation at imaginary ${\bar{\theta }}$ in the fermion basis of Eq. (7), causing the $\theta$ term to be real and thus amenable to be included directly in the gauge ensembles. Effectively ${\bar{\theta }}$ becomes an external parameter of the simulation, that tunes the strength of the CP-violating term of the action. Several gauge ensembles can be generated at several values of ${\bar{\theta }}$ and an extrapolation, at fixed lattice spacing, to ${\bar{\theta }}\rightarrow 0$ allows to determine the linear response proportional to ${\bar{\theta }}$ and thus the nEDM. As noted some time ago [86], in the fermion basis of (7) only the disconnected contractions of the pseudo-scalar density contribute to the EDM.

A subtlety has to be taken into account when the LQCD action breaks chiral symmetry. The ${\bar{\theta }}$ needs to be renormalized by the ratio of the singlet scalar, $Z_S^S$, and pseudo-scalar, $Z_P$, renormalization constants $Z_S^S/Z_P$. The values of $Z_S^S/Z_P$ can vary depending on the lattice action and it has to be taken into account in the extrapolation. In this respect the use of chirally invariant fermions could be beneficial.

Another important aspect to take into consideration in the extrapolation to ${\bar{\theta }}\rightarrow 0$, is the need to stay at rather large values if ${\bar{\theta }}$, i.e. ${\bar{\theta }}\sim O(1)$, in order to have a significant improvement on the signal to noise ratio, since the signal vanishes when ${\bar{\theta }}=0$.⁹ This requires a rather large extrapolation in ${\bar{\theta }}$ where higher-than-the-linear terms in ${\bar{\theta }}$ need to be included [85].

7.1 Gradient flow

The gradient flow [87, 88] (GF) is a differential operator that modifies the fields at short distances with a renormalizable smoothing procedure. The new flowed gauge and fermion fields are a complicated non-linear function of the original degrees of freedom which are the initial conditions of the GF evolution. The GF equation for the gauge fields [89] is given by

$$\begin{aligned} \partial _t B_{\mu }=D_{\nu ,t}G_{\nu \mu }\,, \quad \left. B_\mu \right| _{t=0} = A_\mu \,, \end{aligned}$$

(43)

where

$$\begin{aligned} G_{\mu \nu }=\partial _{\mu }B_{\nu }-\partial _{\nu }B_{\mu }+[B_{\mu },B_{\nu }]\,, \qquad D_{\mu ,t}=\partial _{\mu }+[B_{\mu },\,\cdot \;]\,, \end{aligned}$$

(44)

and the flow-time t has the dimensions of length squared. In this review the flow time is sometimes also labelled with $t_f$ or $t_\text {WF}$, to be consistent with figures taken from the literature. The use of t to indicate the flow time should not generate confusion from the context when we talk about Euclidean time separation. The fundamental gluon field $A_\mu (x)$, not to be confused with the electromagnetic field of the previous sections, represents the initial condition, at $t=0$, for the flowed field $B_\mu (x;t)$. We introduce and discuss the GF for fermion fields in Sect. 9, where we discuss its use to renormalize fermion higher dimensional operators.

The smoothing procedure induced by the GF has mainly 2 advantages. The first one is that, when applied to topological objects, such as the charge Q, it provides a quantum theoretical definition of the charge, equivalent to the one based on chirally symmetric LQCD actions [87, 90]. The second advantage, is that it allows, at least in principle, to define multiplicatively renormalized higher dimensional operators, with no mixing with lower dimensional operators [91].

For pure gauge operators it is possible to show to all orders in perturbation theory that, once the theory at $t=0$, QCD, is renormalized no additional renormalization are needed to remove the regulator. To all order in perturbation theory correlators involving flowed fields $B_\mu (x;t)$ are finite [87, 92] after we renormalize QCD.

This is particular advantageous if the connections between correlation functions evaluated at $t \ne 0$ with the “physical” correlation functions at $t=0$ is calculable.

Here we want to mainly focus on the $\theta$ term and thus on the property of flow-time indpendence of the topological charge. Following Polyakov (see Sect. 6.2 of Ref. [93]) one can show, that a small continuous deformation of the gauge field, induces a variation of the topological charge density proportional to the divergence of a gauge invariant vector field [90]. The GF acting on the gauge field, as in Eq. (43), effectively performs a continuous deformation on the gauge field. If one defines the topological charge density with gauge fields, $B_\mu (x,t)$ at non-zero flow time

$$\begin{aligned} q(x,t) = \frac{1}{64\pi ^2} \epsilon _{\mu \nu \rho \sigma } G_{\mu \nu }^a(x,t)G_{\rho \sigma }^a(x,t)\,, \end{aligned}$$

(45)

the variation in continuum QCD is calculable

$$\begin{aligned} \partial _t q(x;t) = \partial _\mu w_\mu (x,t)\,. \end{aligned}$$

(46)

The exact form of the dimension 5 vector field $w_\mu$ can be found in [90]. What is important is that the vector $w_\mu$ is gauge invariant and once we integrate both sides of Eq. (46) in $d^4x$, $\partial _t Q(t)=0$. In the continuum the topological charge $Q(t) = \int d^4z q(z,t)$ is independent of the flow time and it gives a definition for correlation functions containing any power of the topological charge.

Fig. 4

Flow-time dependence (the flow time in this figure is denoted by $t_f$) of the topological charge for 3 different ensembles, see text, at 3 different pion masses. For a flow-time radius of $\sqrt{8 t_f} \gtrsim 3-4 a$ the susceptibility is practically flow-time independent. We also observe the expected suppression of the susceptibility when lowering the pion mass

Fig. 5

Continuum extrapolation and chiral interpolation of the topological susceptibility for $N_f=2$ non-perturbative clover improved fermions. Fig. published with permission from the authors of Ref. [94]

In Fig. 4 I show the example of the topological susceptibility $\chi = V^{-1}\left\langle Q^2 \right\rangle$ obtained using $N_f=2+1$ non-perturbatively clover improved Wilson fermions at 3 different pion masses [74]. We see the presence of the contact term¹⁰ around $t=0$ and cutoff effects for $\sqrt{8t} \lesssim 3-4 a$ (in Fig. 4 the flow time is denoted with $t_f$). For larger flow times the susceptibility is essentially flow-time independent and finite when we perform the continuum limit. Cutoff effects for correlators containing only flowed gauge fields are parametrically of O($a^2$) as for the standard pure gauge theory, but different higher dimensional operators might change the strength of the cutoff effects [95]. See for example Refs. [96] for a discussion of cutoff effects for flowed gauge correlators. A study of cutoff effects, up to O($a^8$), of a finite volume gauge coupling [97], has also shown the importance of removing tree-level cutoff effects when performing the continuum limit.

As always, only studying the scaling violations numerically, we can have confirmation on the control of the cutoff effects in a given quantity. In Fig. 5 I show the results published in Ref. [94] where a combined chiral and continuum analysis is performed. See also Refs. [98, 99] for other determinations of the topological susceptibility. The main 2 features we notice is that the susceptibility does not vanish in the chiral limit at fixed lattice spacing, but it does after we perform the continuum limit. We will come back to this topic in Sect. 6 when we discuss the chiral extrapolation of the EDM.

When determining the statistical uncertainty of a lattice QCD calculation, one should consider the autocorrelation between data along the same Markov Chain Monte Carlo (MCMC). This is particularly true for quantities such the topological charge and susceptibility, as well as for the EDM induced by the $\theta$ term, because these quantities are notoriously very slow to decorrelate along a MCMC [101]. A measure of the autocorrelation function and of the integrated autocorrelation time, $\tau _\mathrm{int}$, [100], reveals potential underestimation of statistical errors.

Defining the topological charge with the GF is also beneficial in the proper assessment of the integrated autocorrelation time. In Fig. 6 I show the integrated autocorrelation time for the topological charge as a function of flow time from Ref. [74]. The first observation is that $\tau _\mathrm{int}$ is deceptively small at small flow time, but at larger flow times $\tau _\mathrm{int}$ increases and it stabilizes at $\sqrt{8 t} \simeq 0.2$ fm, $\sim 2-3 \times a$. Removing the short distance fluctuations with the GF, allows a better estimate of the statistical uncertainty [94, 102].

Fig. 6

Integrated autocorrelation time $\tau _\mathrm{int}$ of Q as a function of the flow-time radius $\sqrt{8 t_f}$. In this figure the flow time is denoted by $t_f$. Results are for ensembles at different lattice spacings. The sea lattice action if non-perturbatively O(a) improved clover fermions. The uncertainty on $\tau _\mathrm{int}$, as well as, the optimal window $W_{\text {opt}}$, are chosen following [100]

The second observation is that decreasing the lattice spacing, $\tau _\mathrm{int}$ increases. This is also expected [101, 102], because at finer spacings the probability of tunneling between different topological sectors decreases. This observation is important when Ginsparg-Wilson fermions are used. The lattice chiral symmetry of the lattice action disfavors, along the MCMC, changes of topological sectors at very fine lattice spacings. An example of this effect, with Domain Wall (DW) fermions, can be observed in the last row of Fig. 1 of Ref. [103] where the MC history of the topological charge, Q, is shown from left to right at at $a \simeq 0.11, 0.062, 0.083$ fm. It clearly shows an increase towards the finer lattice spacing of $\tau _\mathrm{int}$, which is estimated to be for topological charge Q, of the order of 460 Molecular Dynamics Time Units (MDTU) in Ref. [103].

In the calculation of the nEDM induced by the $\theta$ term, numerical evidence shows that the problem of the very large value of $\tau _\mathrm{int}$ is milder than with pure gauge observables. Nevertheless, in all the results discussed in this review the autocorrelation along the MCMC is taken into account by either estimating the proper value of $\tau _\mathrm{int}$, or blocking the data, or skipping enough trajectories to completely decorrelate the data.

7.2 EDM from the $\theta$ term

Given the GF properties we just introduced, it is natural to define the EDM induced by ${\bar{\theta }}$ with the GF [104, 105]. One defines the nEDM inserting the topological charge in the hadron correlator at a fixed value of the flow time. The value of the flow time should be large enough to avoid short distance cutoff effects. A value of the flow time corresponding for example to the plateau region in Fig. 4 is usually chosen. The real challenge in the nEDM calculation induced by the $\theta$ term is the very poor signal-to-noise ratio (SNR) ratio of the CP-odd form factor. The poor SNR is caused by multiple reasons. There is the standard increase of noise towards the chiral limit of baryon correlation functions. This will combine with the increase of the fluctuations of the topological charge for increasing volumes, $\varDelta Q \sim \left\langle Q^2 \right\rangle$ and the loss of signal when the topological charge density is mainly located in “lumps” which are localized in space-time regions away from the dominant contribution of the fermionic part of the correlation function. All the noise-reduction techniques adopted nowadays are based on the observation that it might be beneficial to restrict the space-time regions where to sum the topological charge density in order to maximize the signal and neglect the space-time regions that only add noise. For the nEDM this observation dates back to Ref. [106], where it was suggested to integrate the topological charge density only on space-time slabs with the inclusion of increasingly more time-slices. Another technique is based on cluster decomposition [107] that achieves around a factor 2–3 gain in the total uncertainty. In Ref. [107] the analysis is focused on the strange quark disconnected contribution and the topological charge insertion in nucleon 2-point functions. The idea is to truncate the $\int d^4x$ integration of the topological charge density in a $4-D$ sphere with radius R centered in the sink location of the nucleon 2-point function

(47)

(48)

where $\varPi =\varPi _+=(1+\gamma _4)/2$ is in this case the parity projector.

Fig. 7

CP-violating phase $\alpha _N$ as a function of the summation radius R, see text. We observe a saturation of the signal for $R \simeq 20$ with a reduction in the statistical uncertainty. Fig. taken from Ref. [107]

In Fig. 7 we see the CP-violating phase in the nucleon sector

$$\begin{aligned} \alpha _{N} = \frac{G^{(Q)}_{2}({\mathbf{p}}^{\, \prime }= \mathbf{0},x_4,\gamma _{5}\varPi _{+},t)}{G_{2}({\mathbf{p}}^{\, \prime }=\mathbf{0},t,\varPi _{+})}\,, \end{aligned}$$

(49)

as a function of the $4-$dimensional sphere radius R, i.e. the integration region of the topological charge density at fixed value of $x_4$. Figure is taken from Ref. [107]. It is evident that the truncation to a value of R smaller than the extent of the whole lattice, allows one to capture completely the signal and minimize the uncertainty.

Fig. 8

Effective CP-violating phase for the nucleon as a function of the source- sink separation. The different colors correspond to different values from $\varDelta t_Q=2a$, blue, to $\varDelta t_Q=32a$, green. Excluding $\varDelta t_Q=2a$ and $\varDelta t_Q=4a$ (red data points), for $\varDelta t_Q \gtrsim 8 a$ the signal is saturated. The 2 plots refer to 2 different summation regions in the spatial direction. Figs. taken from Ref. [108]

Another proposal in this direction is to integrate on a cylinder with a spatial radial extent $r_Q$ centered in the source location [108]. For the temporal extent, the topological charge density is first summed over all the time slices between the sink and the source and then the summation is continued outside this region by an amount $\varDelta t_Q$. In Fig. 8 are shown the results from Ref. [108, 109] for $\alpha _N$ as a function of Euclidean time (not to be confused with the flow time here) obtained for 2 different radii $r_Q$ and several time summation windows $\varDelta t_Q$. While there is an early saturation of the signal for $\varDelta t_Q \gtrsim 8a$, the saturation in the radial direction is slower and reached when the integration radius $r_Q > L/2$, thus reducing the effectiveness of the method, at least for small volumes.

In Refs. [74, 110] we have proposed a truncation based on spectral decomposition for the CP-odd form factor and $\alpha _N$. We first sum the topological charge density over the 3-dimensional space

(50)

Fig. 9

Left plot: CP-violating phase $\alpha _N$ as a function of the summation window $t_s$. In the figure t refers to the fixed source-sink time separation between the 2 nucleon interpolators and not the flow time. The arrows indicate respectively from left to right the choice for $t=t_s = 7a$ for the ensemble $A_2$ (blue data point) and $t=t_s = 10a$ for the larger volume ensemble $M_3$ (green data points). Right plot: the ratio in Eq. (49) as a function of the source sink separation t at fixed summation window $t_s$. The 2 colors refer to the standard (red) and improved (blue) determination. Fig.  taken from Ref. [74]

and then we sum along the Euclidean time direction, $\tau _Q$, symmetrically around the parity projector location (source or sink) by $t_s$ time slices. The spectral decomposition shows that the summed correlator becomes independent of $t_s$, for large enough $t_s$, with corrections which are exponentially suppressed. We tested numerically this result and in Fig. 9 is shown the dependence on $t_s$ of $\alpha _N$ for 2 different ensembles corresponding to 2 different volumes at very similar lattice spacings and fixed source-sink separation. We see a clear saturation of the signal for $t_s$ around the source-sink separation. We note though that it does not mean that we are summing only between the source and the sink because we are summing symmetrically in both direction around the source (or sink) location. We have applied the same technique for the 3-point function with the insertion of the topological charge. Our numerical experiments show an improvement of a factor 2–3 in the SNR for the CP-odd form factor $F_3(Q^2)$.

Fig. 10

CP-violating phase $\alpha _N$ for the nucleon as a function of the summation window $R_T$. See main text for a more detailed explanation. Plot for 3 different ensembles at 3 different pion masses, $m_\pi \simeq 130,~220,~310$ MeV (red, yellow and green data points), a single lattice spacing $a\simeq 0.09$ fm, and fixed flow time, here denoted as $t_{WF}$. Fig. taken from Ref. [111]

The method just described [74], has been tested at lighter pion masses [111]. In Fig. 10 it is shown $\alpha _{N}$ calculated in Ref. [112] with clover valence fermions on HISQ sea quarks [113]. We observe that, while at around $m_\pi \simeq 300$ MeV the method seems to work well with a gain of a factor 2, if we truncate the summation around $R_T/a\simeq 20$, the truncation becomes less and less effective towards the physical point. $R_T$ here is the same as $t_s$ of Ref. [74] and in Fig. 9. The reason lies, most likely, in the reduced gap with the excited states contamination towards the chiral limit. Possibly an analysis including the excited states could improve this determination, but given the strong correlation of the data along the summation window, it seems unlikely to further reduce the noise in this way.

Despite all these noise-reduction techniques, the determination of the CP-odd form factor is still very challenging. It is thus of utmost importance to have several collaborative efforts using different lattice actions and different noise reduction techniques to try to pin down the systematics of such an important calculation. The numerical experience accumulated seems to indicate that to determine the EDM induced by the $\theta$ term at the physical point with a relative precision of $10-20\%$, we most likely need at least $O(10^7)$ measurements, depending a little on the volume and lattice spacing under consideration. In this respect it would be maybe beneficial to either have better noise-reduction techniques or not determine the EDM from the CP-odd form factor $F_3$. When discussing the chiral extrapolation I will argue that one could still learn from the pion mass dependence of the nEDM at heavier pion masses where possibly the cost of the determination of the nEDM is less exorbitant.

Another way to determine the EDM is based on the observation [114] that in a constant and small electric field $\mathbf {E}$ the energies of nucleons with opposite spin $\mathbf{S}$ are different

$$\begin{aligned} E_N(\mathbf {E},\mathbf{S}) - E_N(\mathbf {E},-\mathbf{S}) = 2 d_N \mathbf{S}\cdot \mathbf {E}+ O(|\mathbf {E}|^3)\,, \end{aligned}$$

(51)

when calculated with a $\theta$ term, or any other CP-violating source. The construction of a constant electric field on a periodic lattice is non-trivial [75, 115,116,117] and it needs to satisfy the quantization condition

$$\begin{aligned} |\mathbf {E}| = \frac{2 \pi n}{q L T}\,,\quad n \in \mathbb {Z}\,, \end{aligned}$$

(52)

where q is the charge of the quark coupled to the electric field.

While the determination of the EDM with an external electric field did not show in the past to be superior to the form factor determination, recently an improved determination has been proposed [109]. The determination of the energy difference in Eq. (51) can be improved by summing , defined in Eq. (50), only between source and sink and neglecting the “outside” regions. A spectral decomposition then shows that, similarly as for standard 2-point functions, the corrections are exponentially small.

Certainly one clear difference between the form factor and the electric field methods is that the former requires an extrapolation to $Q^2 \rightarrow 0$. While the extrapolation is potentially another source of systematics, the knowledge of $F_3(Q^2)$ contains more information than the EDM alone. The CP-odd form factor can be calculated in HB$\chi$PT [62, 65] and up to NLO the result can be parametrized as

$$\begin{aligned} \frac{F^{N}_{3}(Q^{2})}{2 M_N} = d_N - S_N Q^2 + H_N(Q^2)\,, \end{aligned}$$

(53)

where N denotes either nucleons. Beside the EDM, $d_N$, the linear term in $Q^2$ is the so-called nucleon Schiff moment, $S_N$, and the remaining $Q^2$ dependence is described by the function $H_N$. The detailed expressions for these functions can be found in the original references [62, 65]. At LO in HB$\chi$PT the expression for the Schiff moment contains only the isovector part

$$\begin{aligned} S_p=- S_n= -\frac{eg_A\bar{g}_0}{24 \pi ^2 m_{\pi }^2} = 1.7(3)\times 10^{-4}\,{\bar{\theta }}\,e\,\mathrm {fm}^3\,, \end{aligned}$$

(54)

where I have used the estimate of ${\overline{g}}_0$ in Eq. (32). The NLO corrections [65] provide a rather substantial shift to the isovector contribution, while providing a small contribution to the isoscalar, $S_n +S_p \sim 10^{-5} {\bar{\theta }}e \text {fm}^3$. The conclusion of the HB$\chi$PT analysis is that up to small corrections the Schiff moments of proton and neutron are the same but opposite in sign. The form factor expression (53), for example for the neutron, can be evaluated in the limit $Q^2\ll m_\pi ^2$

$$\begin{aligned} \frac{F^{n}_{3}(Q^2\ll m_\pi ^2)}{2 M_N} = d_n - \frac{eg_A\bar{g}_0}{24 \pi ^2} \left( \frac{Q^2}{m_{\pi }^2}+ \dots \right) \,, \end{aligned}$$

(55)

showing that an extrapolation to $Q^2 \rightarrow 0$ at fixed pion mass, is dominated by the Schiff moment. The determination of the slope provides an independent determination for the CP-violating coupling ${\overline{g}}_0$. The expression in Eq. (55) cannot be used to study the chiral limit of the $Q^2$ dependence. In fact already a dimensional analysis shows us that because $d_n \sim {\overline{g}}_0\sim m_\pi ^2 {\bar{\theta }}$ vanishes in the chiral limit, the form factor $F_3$ does not vanish in the chiral limit as it should. The correct expression to study the chiral limit is

$$\begin{aligned} \frac{F^{n}_{3}(Q^2\gg m_\pi ^2)}{2 M_N} = d_n + \frac{eg_A\bar{g}_0}{4 \pi ^2 } \left( 2 + \ln \frac{m_\pi ^2}{Q^2} \right) \,, \end{aligned}$$

(56)

where now the form factor vanishes in the chiral limit. The current lattice data are not precise enough to determine the Schiff moments, but first estimates [74]

$$\begin{aligned} S_p= & {} 0.50(59) \times 10^{-4} {\bar{\theta }}e \mathrm {fm}^3\,, \end{aligned}$$

(57)

$$\begin{aligned} S_n= & {} -0.10(43) \times 10^{-4} {\bar{\theta }}e \mathrm {fm}^3\,, \end{aligned}$$

(58)

seem to indicate that their ratio is in the right ballpark of the expected NLO results (54). To make a more quantitative statement, perhaps even more than for the EDM, we need to increase by at least a factor $10^2-10^3$ the current number of measurements bringing it to the order of $10^8$.

Fig. 11

Left plot: CP-odd form factor for the neutron as a function of $Q^2$ and $m_\pi \simeq 410$ MeV. The blue and red data refer respectively to the noise-reduction improved and unimproved analyses described in Ref. [74]. The shaded bands are linear fits in $Q^2$. Right plot: nEDM results for 6 ensembles, 3 pion masses and 3 lattice spacings at the heaviest pion. The red band represents the chiral fit including O($a^2$) discretization effects. The blue band is a chiral interpolation using the formula in Eq. (59). The cross are the fit results at the physical point. For details on the analysis see Ref. [74]

In the left plot of Fig. 11 I show an example of extrapolation to $Q^2 \rightarrow 0$ from Ref. [74]. We immediately notice the difficulty to determine a statistically significant slope in $Q^2$ and the importance of noise-reduction techniques. The extrapolated values to $Q^2 \rightarrow 0$ can now be analyzed as functions of the pion mass and the lattice spacing. In Ref. [74] we have computed the EDM for 3 values of the pion mass and 3 lattice spacings at the heaviest pion mass available. The ensembles, made available via the ILDG [118], are generated by JLQCD and PACS-CS. Details on the ensembles can be found in Refs. [119, 120].

In the right plot of Fig. 11 I show the neutron EDM, $d_n$, as a function of the pion mass for 6 ensembles. The NLO results from HB$\chi$PT theory suggest an extrapolation using the expression

$$\begin{aligned} d_{p/n}(m_{\pi }) = C_1\ m_{\pi }^{2} + C_2\ m_{\pi }^{2}\ln (\frac{m_{\pi }^{2}}{m_{N}^{2}})\,, \end{aligned}$$

(59)

where the fit parameters are $C_1$ and $C_2$ and they are directly related to the counter-term ${\bar{d}}_n$ and the other LECs, ${\overline{g}}_0$, $g_A$ and $F_\pi$. For the nucleon mass, $m_N$, we take the physical neutron mass. This fit function constrains the chiral extrapolation to have a vanishing nEDM at zero pion mass. We have already discussed this property of the $\theta$ term in Sects. 7,6. The fact that the EDM induced by ${\bar{\theta }}$ vanishes in the chiral limit, is a consequence of chiral symmetry. The chiral rotation connecting the ${\bar{\theta }}$ term to the complex mass term, does not leave the remainder of the action invariant, if the action presents some additional sources of chiral symmetry breaking. If the lattice QCD action breaks chiral symmetry, it is not guaranteed for the EDM to vanish in the chiral limit. We have already encountered this phenomenon in the topological susceptibility in Fig. 4 from Ref. [94]. In Ref. [74] we have used a non-perturbatively improved Wilson lattice action and we have parametrized the cutoff effects, in our chiral and continuum limit analysis, with an additional O($a^2$) term. While potentially there could be additional O($am_q$) effects, they vanish though in the chiral limit. It goes without saying that a precise continuum extrapolation analysis can be done only with more precise data and having under control other systematics, such as the excited state contamination. The chiral-continuum analysis shows that even introducing a free parameter fit for the O($a^2$) effects, the chirally extrapolated EDM, still vanishes within error bars. This gives us some confidence that the cutoff effects are under control, within the current statistical accuracy, and we can perform a chiral interpolation including the $m_\pi =0$ point. We emphasize again that the continuum limit becomes extremely important to improve the chiral analysis of the EDM. Imposing the constraint that the EDM vanishes in the chiral limit improves substantially what is now a chiral interpolation.

Fig. 12

Left plot: The green band represents the fit result to the LQCD data using the $\chi$PT expression in Eq. (59). The red band represents only the log contribution, while the blu band the counter-term. Right plot: The green band represents the fit result to the LQCD data using a quadratic polynomial in $m_\pi ^2$, see main text. The red band represents the $m_\pi ^4$ term, while the blu band the $m_\pi ^2$

The chiral interpolation in Fig. 11, while indicating a good consistency with the expectations of $\chi$PT, is still based on LQCD data with rather large statistical uncertainties that can possibly still be described by a different functional form.

An important consistency check is comparing the ${\overline{g}}_0$ determination from the coefficient of the chiral log extracted from the LQCD data and the determination using Eq. (31). The coefficient $C_2$ from the chiral fit (59) is related to ${\overline{g}}_0$

$$\begin{aligned} {\bar{g}}_0 = - \frac{8\pi ^2 F_\pi }{g_A} \frac{C_2 m_\pi ^2}{e}\,, \end{aligned}$$

(60)

which at the physical pion mass gives

$$\begin{aligned} {\bar{g}}_0 = -12.8(6.4)\times 10^{-3}\,{\bar{\theta }}\,. \end{aligned}$$

(61)

In Sect. 6 we have explained how it is possible to extract ${\overline{g}}_0$ from the calculation of the neutron-proton mass splitting only induced by QCD isospin-violating effects [50, 60, 70]. The estimate in Eq. (32) is perfectly consistent with Eq. (61). This gives a rather robust consistency check of the LQCD data description using $\chi$PT.

To test another functional dependence, one can perform a polynomial fit $d_n(m_\pi ) = C_1 m_\pi ^2 + C_2 m_\pi ^4$ to the EDM LQCD data. In Fig. 12 are shown the separate contributions of the $\chi$PT chiral interpolation formula (59) and the ones of the polynomial fit. The data are from Ref. [74]. A simple comparison of the $\chi ^2$ obtained by the 2 different fits, $\chi ^2_{\chi {\text {PT}}} = 1.8(1.5)$ and $\chi ^2_{\text {poly}} = 1.7(1.4)$, shows that the data are described by the 2 fit functions equally well. The uncertainties on the $\chi ^2$ are determined with the bootstrap samples.

Table 2 Summary table of unquenched results for the nEDM $|d_n|$ induced by the $\theta$ term

In Sect. 6 we have mentioned the general expectation of the log-dominance in comparison with the counter-term [50]. The $\chi$PT fit of our data is consistent with this expectation. On the other side the polynomial fit contains quadratic and quartic terms in the pion mass of similar size and with opposite signs, an indicator of a poorly behaved expansion. The results of the 2 analysis read

$$\begin{aligned} \left[ d_n\right] _{\chi PT}= & {} - 1.52(71) \times 10^{-3} \overline{\theta }~e~\text {fm}\,, \end{aligned}$$

(62)

$$\begin{aligned} \left[ d_n\right] _{\text {poly}}= & {} - 0.64(25) \times 10^{-3} \overline{\theta }~e~\text {fm}\,. \end{aligned}$$

(63)

In Ref. [74] we quoted the result from the $\chi$PT in Eq. (62) as the final result, because the $\chi$PT interpolation formula is physically more motivated and because the values of ${\overline{g}}_0$ determined with the pion mass dependence of the EDM and with the QCD neutron-proton mass splitting, as discussed above, are perfectly consistent.

It is clear though, that it is desirable to have results with better precision and closer to the physical point. A new determination at the physical point, $m_\pi \simeq 139$ MeV, has been recently obtained by ETMC [121]. Using $N_f=2+1+1$ Wilson twisted mass fermions [122,123,124,125,126]. At $a \simeq 0.08$ the final result is

$$\begin{aligned} |d_n| = 9(24) \times 10^{-4} \overline{\theta }~e~\text {fm}\,. \end{aligned}$$

(64)

This result shows how challenging is to perform the determination of the nEDM directly at the physical point. In Table 2 I summarize the few recent results for the nEDM from the $\theta$ term. It is clear that more determinations are needed and that a simple increase of measurements to O($10^7$) might not be sufficient, without better variance reduction techniques.

It could be beneficial to make use of the fact that the EDM induced by the $\theta$ term vanishes in the chiral limit. A possible strategy would be to have few determinations of the EDM for pion masses slightly above the physical point, perhaps in the range $180 \lesssim m_\pi \lesssim 300$, combined with an interpolation at $m_\pi =0$: it will slightly increase the signal and reduce the noise thus it should help reduce the uncertainties at the physical point. To proceed in this way one should make sure that $\chi$PT is matched at those pion masses. In this respect an independent determination of ${\overline{g}}_0$, like the one discussed above, provides a strong check.

We repeat that the use of the fact that the EDM vanishes in the chiral limit is only justified in the presence of chiral symmetry. This implies that a LQCD determination of the nEDM with any kind of Wilson-type fermions, can use the $m_\pi =0$ constraint only after performing the continuum limit, or at least, given the current statistical accuracy of the LQCD data, have some control over the cutoff effects. In the short-term this might be a viable way, at least, to better understand the pion mass dependence of the nEDM induced by the $\theta$ term.

8 CP-odd chromo-magnetic operator

The quark-chromo EDM defined in Eq. (19) is a dimension 5 operator potentially contributing to the EDM of the neutron and other systems. In discussing the challenges of the $\theta$-term nEDM we have emphasized the degradation of the SNR towards the chiral and infinite volume limit. For the qCEDM the real challenge, compared with the $\theta$ term, is the rather complicated renormalization pattern.

In Sect. 7 we have discussed the advantage of using the GF to define the topological charge at finite lattice spacing. Here we discuss a second application of the gradient flow. The renormalization pattern of local operators can be ameliorated at finite flow time. The connection to QCD at $t=0$ can be done either perturbatively in the continuum [127,128,129,130,131,132,133,134], or non-perturbatively using Ward identities [88, 135, 136]. Below we discuss the matching to QCD in the context of the short flow-time expansion (SFTE).

In the pure gauge theory we do not need to renormalize the flowed gauge field [92]. Any correlation function containing a gauge field at finite flow time is finite, once we renormalize the Yang-Mills theory at $t=0$. If we decide to flow also the fermion fields the situation is different. We consider here the GF for fermions proposed in Ref. [88]

$$\begin{aligned} \partial _t\chi= & {} D_\mu D_\mu \chi \,, \nonumber \\ \chi (x;t=0)= & {} \psi (x)\,, \end{aligned}$$

(65)

where $B_\mu$ is the flowed gauge field according to Eq. (43). We can now consider correlation functions containing gauge and fermion fields at $t=0$ and gauge and fermion fields at $t>0$. While the flowed gauge fields do not require renormalization, the fermion fields however do [88]. The renormalization constant of the flowed fermion fields is denoted by $Z_\chi$. The divergent part has been calculated at 1-loop [88, 127, 131] and 2-loop [133]. The renormalization of fermion local operators, e.g. a bilinear or a 4-fermion operator (see Ref. [134] for a study of $B_K$), is still greatly simplified because it renormalizes multiplicatively depending on the number of fermion fields, i.e. with $Z_\chi$ and its powers we renormalize any fermion local operator at $t>0$ [88]. This implies that flowed fermion local composite fields have no power divergences. To understand where the power divergence is gone, it is convenient to study the behavior at short flow time of the composite fields. The short flow time expansion is an operator product expansion around $t=0$, with Wilson coefficients which can be computed in perturbation theory containing the flow-time dependence [91]. Once we take care of the renormalization of the flowed fermion fields we can relate the flowed operators with the operators at $t=0$ using a SFTE. Performing the continuum limit at non-vanishing flow time can be advantageous because then the SFTE can be performed in the continuum, and the symmetries of the continuum theory can be used to classify the operators contributing to the SFTE.

The SFTE can be used to remove the power divergences of higher dimensional operators. In the SFTE the power divergences appear as powers of 1/t and can be subtracted either perturbatively, calculating the appropriate Wilson coefficient, or non-perturbatively with an appropriate non-perturbative condition at finite flow time.

Fig. 13

Feynman diagrams contributing to $c_{CP}(t)$ at leading order in $g^2$. The qCEDM at non-zero flow time t is denoted by a box vertex with a t in it. The O(g) vertex coming from the GF is denoted by Y and the double lines refer to the use of the heat kernel for the fermion flow

Power divergences can be calculated also in the RI-MOM scheme  [137,138,139,140,141] and using the coordinate space method [109, 142,143,144].

To address the leading behavior at small flow time it is advantageous to use an operator product expansion at short flow time, a short flow-time expansion (SFTE). The SFTE for a renormalized gauge-invariant local operator, $\left( {{\mathcal {O}}}_i\right) _R(t)$, is [91]

(66)

where the operators contributing are classified according to the symmetries of the theory. The Wilson coefficients, or expansion coefficients, $c_{ij}(t)$, can be determined in perturbation theory. The operators on the r.h.s of the SFTE (66) are classified based on their naive dimension and the lowest dimensional operators dominate the behavior at small flow time. The same SFTE is valid if we insert the local operator $\left( {{\mathcal {O}}}_i\right) _R(t)$ in a correlation function, as far as we avoid contact terms on the r.h.s of the SFTE. This gives us the freedom to probe the OPE in many different ways, isolating the contribution from each operator of the r.h.s. of Eq. (66).

As we have seen in Sect. 5 CP-violating higher dimensional operators describe, at the hadronic scale, BSM contributions to the EDM. The renormalization on the lattice of the qCEDM operator is complicated because, not only it mixes with operators of the same dimension, but also with lower dimensional operators [140]. The classification of these operators depend on the lattice action used. If the lattice action satisfies the Ginsparg-Wilson relation the number of these operators is reduced. Independent of the choice of the lattice action though, the lowest dimensional operator contributing a $1/a^2$ divergence is the pseudoscalar density, P(x). Potentially there is also a dimension 4 operator proportional to the topological charge density. This term comes with a 1/a divergent coefficient if the lattice action breaks chiral symmetry, or with a single power of the quark mass, if the regulator respects chiral symmetry. This is a direct consequence of the chiral transformation properties of the qCEDM.

The use of the GF circumvents this problem because at fixed finite flow time, up to a renormalization of the fermion field $Z_\chi$, the continuum limit does not require additional renormalization. Thus also in this case the topological charge does not contribute a 1/a power divergence. If we perform the SFTE in the continuum we can classify the contributing operators based on the symmetries of the continuum theory and for example the topological charge density will not contribute to the SFTE, if not a logarithmic term proportional to the quark mass. We have checked in the continuum in perturbation theory that the leading contribution at finite flow time is indeed given by the pseudoscalar density and that the topological charge contributes a logarithmic divergence multiplied by a single power of the quark mass [145].

We consider in Euclidean space the qCEDM (67)

$$\begin{aligned} {{\mathcal {O}}}_C(t)=\overline{\chi }(t)\sigma _{\mu \nu }G_{\mu \nu }(t)\chi (t)\,, \end{aligned}$$

(67)

at small flow time t, $\left( {{\mathcal {O}}}_C\right) _R(t)$

(68)

where

$$\begin{aligned} {{\mathcal {O}}}_q = \frac{1}{4}\epsilon _{\mu \nu \rho \sigma } G_{\mu \nu }^aG_{\rho \sigma }^a\,, \end{aligned}$$

(69)

and the dots indicate operators of dimension 5 or higher. To determine the expansion coefficients $c_{CP}(t)$ and $c_{Cq}(t)$ we probe the qCEDM with different external states [146]. We use 2 external quarks to determine, $c_{CP}(t)$, and 2 external gluons to determine, $c_{Cq}(t)$. Technical details of the calculations and all the Feynman rules needed, together with a sample calculation, can be found in Ref. [145].

To determine $c_{CP}(t)$ we consider correlation functions of the local operators, ${{\mathcal {O}}}$, between 2 quark fields

$$\begin{aligned} \varGamma _{\psi \mathcal {O}\bar{\psi }}(x,y;t)= \left\langle \psi (x)\mathcal {O}(t)\bar{\psi }(y)\right\rangle \,, \end{aligned}$$

(70)

while to determine $c_{Cq}(t)$ between 2 gauge fields

$$\begin{aligned} \varGamma _{A\mathcal {O}A}(x,y;t)_{\alpha \beta }^{ab}= \left\langle A_\alpha ^a(x)\mathcal {O}(t)A_\beta ^b(y)\right\rangle \,, \end{aligned}$$

(71)

Applying the SFTE (66) to Eq. (70) we obtain

$$\begin{aligned} \varGamma ^R_{\psi \mathcal {O}_C\bar{\psi }}(x,y;t)= & {} c_{CP}(t)\varGamma ^R_{\psi P \bar{\psi }}(x,y;0) \nonumber \\&+ c_{Cq}(t)\varGamma ^R_{\psi {{\mathcal {O}}}_q \bar{\psi }}(x,y;0)+\cdots \end{aligned}$$

(72)

and an analogous SFTE can be written for Eq. (71).

Fig. 14

Feynman diagrams contributing to $c_{Cq}(t)$ at leading order in $g^2$. The qCEDM at non-zero flow time t is denoted by a box vertex with a t in it. The O(g) vertex coming from the GF is denoted by Y and the double lines refer to the use of the heat kernel for the fermion flow

At tree-level one obtains that the values of the expansion coefficient vanish, $c_{CP}^{(0)}(t) = 0$ and $c_{Cq}^{(0)}(t) = 0$. With some additional algebra at the next order O($g^2$) one obtains

$$\begin{aligned} \varGamma ^{(1)}_{\psi \mathcal {O}_C\bar{\psi }}(x,y;t)&= c_{CP}^{(1)}(t)\varGamma ^{(0)}_{\psi P\bar{\psi }}(x,y;0)\,, \end{aligned}$$

(73a)

$$\begin{aligned} \varGamma ^{(1)}_{A\mathcal {O}_CA}(x,y;t)&= c_{Cq}^{(1)}(t)\varGamma ^{(0)}_{A Q A}(x,y;0)\,. \end{aligned}$$

(73b)

where the labels (0) and (1) refers to the coefficients of the expansion of O($g^0$) and O($g^2$). We can now determine $c_{CP}^{(1)}(t)$ evaluating $\varGamma ^{(1)}_{\psi \mathcal {O}_C\bar{\psi }}(x,y;t)$.

The calculation of $\varGamma ^{(1)}_{\psi \mathcal {O}_C\bar{\psi }}(x,y;t)$ requires the calculation of the Feynman diagrams in Fig. 13. It turns out that only the first diagram in Fig. 13 contribute to $\varGamma ^{(1)}_{\psi \mathcal {O}_C\bar{\psi }}(x,y;t)$ [145]. The calculation brings the following expression

$$\begin{aligned} c_{CP}^{(1)}(t)=6ig^2\frac{C_2(F)}{(4\pi )^2}\frac{1}{t}\,, \end{aligned}$$

(74)

which confirms the expectation that the leading contribution at small t to the qCEDM is given by the pseudoscalar density with a linearly divergent in 1/t expansion coefficient. We denote with g the renormalized coupling and with $C_2(F) = (N^2-1)/2N$ for SU(N).

To calculate $c_{Cq}(t)$, as we have done for $c_{CP}(t)$, we calculate $\varGamma ^{(1)}_{A\mathcal {O}_CA}(x,y;t)$ from the Feynman diagrams in Fig. 14. We defer for the technical aspects of this calculation to Ref. [145].

The final result for the expansion coefficient reads

$$\begin{aligned} c_{Cq}^{(1)}(t)=4ig^2\frac{m}{(4\pi )^2}\left[ \log (2p^2t)+\gamma _E-1\right] \,, \end{aligned}$$

(75)

where we confirm again the expectation from chiral symmetry considerations. Chiral symmetry of continuum QCD enforces a power of the quark mass to multiply the topological charge density and thus we are left with a logarithmic divergence in the flow time.

8.1 Towards a determination of the qCEDM

The calculation of the bare nEDM induced by the qCEDM operator proceeds in a similar fashion as the nEDM induced by the $\theta$ term discussed in Sect. 7. As for the $\theta$ term we can calculate the bare CP-violating phase factor for a nucleon induced by the qCEDM. The 2-point function with the insertion of the qCEDM operator

(76)

(77)

defines

$$\begin{aligned} \alpha _{N}^{qC} = \frac{G^{(qC)}_{2}({\mathbf{p}}^{\, \prime }= \mathbf{0},x_4,\gamma _{5}\varPi _{+},t)}{G_{2}({\mathbf{p}}^{\, \prime }=\mathbf{0},x_4,\varPi _{+})}\,, \,. \end{aligned}$$

(78)

To renormalize the bare CP-violating phase $\alpha _{N}^{qC}$ we clearly need to renormalize the qCEDM. In the previous section we have introduced the GF as a tool to renormalize the qCEDM and we have determined in PT the dominant contribution at small flow time.

Fig. 15

Up-quark contribution of the CP-violating phases $\alpha _N^{qC}$ (in the plot simply denoted as $\alpha _N$) as a function of the flow-time radius $\sqrt{8t_f}$. Different colors represent different lattice spacings $a=0.1095, 0.0936,0.0684$ fm. Fig. taken from Ref. [147]

In Fig. 15 is shown the flow-time dependence of $\alpha _{N}^{qC}$ determined in [147]. The flow-time evolution shows a rapid decrease with increasing flow time. This flow time dependence is most likely related to the 1/t divergence we have discussed in this section above and that has been calculated in PT in Ref. [145]. The scope of the SFTE is to connect the renormalized matrix element calculated at $t > 0$ with the renormalized ones at $t=0$.

Results for the CP-odd form factor, $F_3$, induced by the qCEDM, have been presented in Refs. [75, 108, 112].

Fig. 16

Light quarks, u and d, contributions to the CP-odd form factors $F_{3p,n}(Q^2)$ for the proton or neutron. Different colors correspond to different nucleon source-sink separation: blue, $t=8a$, red, $t=9a$ and green, $t=10a$. Fig. taken from Ref. [108]

As we have discussed above the qCEDM operator mixes with pseudoscalar density, thus the determination of the nEDM requires the determination of the CP-odd form factor induced by the pseudoscalar density. In Fig. 16 is shown the CP-odd form factor $F_3(Q^2)$ induced by the pseudoscalar density determined in Ref. [108]. A rather clean signal is seen for each quark contribution.

About the calculation of Ref. [112] it is interesting to mention 2 technical aspects. The first is the use of a variance-reduced correlator obtained by subtracting from the physical observable $\left\langle {{\mathcal {O}}}_{\text {ph}} \right\rangle$ another observable, $\left\langle {{\mathcal {O}}}_0 \right\rangle =0$, with 0 expectation value $\left\langle {{\mathcal {O}}}_{\text {ph}} \right\rangle - \left\langle {{\mathcal {O}}}_0 \right\rangle$, but highly correlated with $\left\langle {{\mathcal {O}}}_{\text {ph}} \right\rangle$. The choice of Ref. [112] is to subtract from the CP-odd form factor $F_3$ the same form factor evaluated in a QCD background, i.e. without a $\theta$ term. In this way the expectation value vanishes, but hopefully the correlation between the two $F_3$s can reduce the variance of the physical observable. The results of Fig. 17 from Ref. [112] indicate a rather dramatic improvement.

The second aspect to mention is the use of Machine Learning (ML) algorithms [148] in the evaluation of lattice correlators. The intent is to “learn” the relation between observables of different computational costs and which are correlated. While the cost reduction seems modest in the case studied, the method is rather general. It is possible that a better choice of correlated observables or better ML algorithms would improve the cost reduction.

Fig. 17

CP-odd bare form factor $F_3$ at fixed value of $Q^2$ as a function of the electromagnetic current insertion time. Different colors represent different nucleon source-sink separation. Before (left plot) and after (right plot) a variance reduction technique, see main text. Fig. taken from Ref.  [112]

Fig. 18

Feynman diagrams contributing to $\varGamma ^{(1)}_{A\mathcal {O}_WA}$. The squared vertex, containing t, represents the Weinberg operator at flow time t. The vertex labelled with X is the first order vertex term coming from the expansion of the GF and the double curly line is the gluonic kernel

9 Weinberg operator

In Sect. 5 we have seen that the dimension $d=6$ Weinberg operator

$$\begin{aligned} {{\mathcal {O}}}_W=\text {Tr}\left\{ \left[ G_{\mu \rho },G_{\nu \rho }\right] {\tilde{G}}_{\mu \nu }\right\} \, \end{aligned}$$

(79)

can potentially induce a big contribution to the nEDM, because chiral symmetry does not suppress its matrix element with powers of the quark mass. As for the qCEDM, the Weinberg operator has a rather complicated renormalization pattern. In an off-shell scheme the renormalization mixing pattern of the Weinberg operator has been recently studied in Ref. [141].

The conclusion of Ref. [141] is that the Weinberg operator mixes with 3 dimension 4 operators and, for $N_f \ge 3$ there is also 1 dimension 5 operator. The mixing with this operator starts at O($g^4$). The mixing continues with 30 dimension 6 operators, 20 of which are nuisance operators and it is possible to define an RI-$\tilde{\text {S}}$MOM scheme [141] with 34 renormalization conditions. The implementation of this program on the lattice seems rather challenging. In Ref. [141] is investigated the possibility to use a background-field method [149] to probe the Weinberg operator. This reduces the number of renormalization conditions to impose and could be a promising tool for the study of renormalization of higher dimensional operators.

The GF is another approach that can be used to disentangle the short-distance behavior of the Weinberg operator. The SFTE of the Weinberg operator contains contribution of the CP-odd operators with $d=6$ or less that can be classified following [141].

As a first step into the renormalization of the Weinberg operator we have computed [145, 150] in perturbation theory to O($g^2$) the power divergent mixing coefficient. The only dimension 4 operator contributing to the power divergences at O($g^2$) is the topological charge density. Any fermionic bilinear with a power of mass or derivative will contribute at higher order in the coupling, because to probe such mixing one needs 2 external quark fields, and the correlation function between the Weinberg operator and 2 quark fields is of O($g^4$).

If we retain only the leading term the SFTE of the Weinberg operators

(80)

where we neglect not only higher dimensional operators but also operators contributing at O($g^4$). We probe the Weinberg operator with 2 external gluons, $\varGamma _{A\mathcal {O}_WA}(x,y;t)$, and expanding in powers of the coupling we obtain that the tree-level of the expansion coefficient vanishes, $c_{Wq}^{(0)}=0$, while at O($g^2$) we obtain

$$\begin{aligned} \varGamma ^{(1)}_{A\mathcal {O}_WA}(x,y;t) = c_{Wq}^{(1)}(t)\varGamma ^{(0)}_{A\mathcal {O}_qA}(x,y;0)\,. \end{aligned}$$

(81)

The O($g^2$) Feynman diagrams contributing to $\varGamma ^{(1)}_{A\mathcal {O}_WA}$ are depicted in Fig. 18. The Feynman rules and the technical details of the calculation can be found in Ref. [145]. The result of the calculation leads to a power divergence proportional to the topological charge density with expansion coefficient

$$\begin{aligned} c_{Wq}^{(1)}(t) = \frac{45}{8} g^2 \frac{C_2(A)}{(4\pi )^2}\frac{1}{t}\,. \end{aligned}$$

(82)

where $C_2(A) = N$ for SU(N). This result confirms again the expectation that the Weinberg operator at small flow time receives contributions from the lowest dimensional operators with the same symmetries preserved by the theory. At this order in the strong coupling, the only operator is the topological charge density.

9.1 First numerical results for the Weinberg operator

The difficulty to renormalize the Weinberg operator has until now discouraged any serious attempt to determine the nEDM. Nevertheless exploratory studies have been performed. In Ref. [151] we have explored for example the flow-time dependence of the correlation functions containing one Weinberg and one topological charge

$$\begin{aligned} \chi _{QW}(t) = \frac{1}{V}\int d^4 x \int d^4 y \left\langle {{\mathcal {O}}}_W(x;t) {{\mathcal {O}}}_q(y;t) \right\rangle \,. \end{aligned}$$

(83)

In Fig. 19 is shown the correlator, $\chi _{QW}(t)$, as a function of flow time. We observe a non-trivial flow-time dependence that should be explained by the flow time dependence of the Weinberg operator. These type of correlators could provide conditions to determine the mixing of the Weinberg operator with the topological charge.

10 A look into the future

The Electric Dipole Moment is a prime quantity to probe CP-violation within the Standard Model and Beyond. Several sources can contribute to the EDM and it is important to address those sources theoretically to estimate how each of them contributes to the EDM. Even if experimentally no intrinsic EDM has been observed yet, technical advances promise to bring the bound on the neutron EDM (nEDM) down by $1-2$ order of magnitudes within the next 10 years. This imposes a serious attempt to determine the hadronic contribution of each single CP-violating source.

Fig. 19

Flow-time dependence of the mixed correlator in Eq. (83) for 2 different pion masses. The ensembles are $N_f=2+1$ non-perturbatively improved clover fermions at $a = 0.0905$ fm

The challenges to overcome in this program are the bad signal-to-noise ratio (SNR) for the $\theta$ term, and the renormalization for the higher dimensional operators. For the $\theta$ term contribution, I have discussed several improvement techniques to tame the SNR problem. Despite the variance-reduction techniques applied, the calculation of the nEDM remains challenging. Even if first lattice QCD results seem to be consistent with NLO Chiral Perturbation Theory ($\chi$PT), clearly better improvements are needed. If we want to improve the accuracy of the nEDM induced by the $\theta$ term to a $10\%-20\%$ directly at the physical point, we need to increase by $1-2$ order of magnitudes the amount of lattice measurements. Most likely a new level of variance reduction techniques are needed to determine more precisely the nEDM induced by the $\theta$ term.

Perhaps a better strategy, at least for the short term, would be to perform simulations at pion masses slightly higher than the physical point and then do a chiral interpolation including the constraint in the chiral limit, $d_n(m_\pi =0)=0$. This procedure would work if we make sure we have properly matched $\chi$PT. In this respect the direct calculation of CP-violating couplings, such as ${\overline{g}}_0$, provides a strong check.

Higher dimensional operators, such as the quark-chromo and the Weinberg operators, can also contribute to the nEDM as to the EDM of other systems. The challenge to determine the hadronic matrix element of these CP-violating operators is the renormalization. The mixing pattern of both the qCEDM and the Weinberg is now known also for off-shell schemes. The power divergences in the lattice spacing and the plethora of operators contributing to the mixing make the renormalization using off-shell schemes challenging. Alternative schemes have been proposed based on on the Gradient Flow and on the coordinate space method. First results in perturbation theory with the Gradient Flow have been obtained towards the renormalization of the qCEDM and the Weinberg, but we are still not close to a complete non-perturbative renormalization. Efforts in this direction are ongoing and we emphasize the importance, for future developments, to attempt the renormalization using different techniques.

CP-violation physics has always been gentle in the past, gifting us with windows over new phenomena. Future experiments in search of a non-zero EDM, should be accompanied by a vigorous theoretical effort to disentangle all the CP-violating sources. The current statistical and systematic uncertainties in LQCD calculations call for larger numerical investments and better methodologies to improve the SNR and disentangle the renormalization mixing. Despite the difficult challenges ahead of us, I will not be surprised if CP-violation once again teaches us something about fundamental interactions.