Viscous coefficients and thermal conductivity of a $\pi K N$ gas mixture in the medium

Abstract

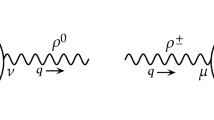
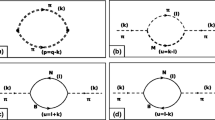
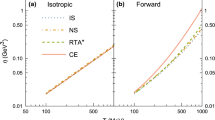
The temperature and density dependence of the relaxation times, thermal conductivity, shear viscosity and bulk viscosity for a hot and dense gas consisting of pions, kaons and nucleons have been evaluated in the kinetic theory approach. The in-medium cross-sections for $\pi \pi$, $\pi K$ and $\pi N$ scatterings were obtained by using complete propagators for the exchanged $\rho$, $\sigma$, $K^*$ and $\Delta$ excitations derived using thermal field theoretic techniques. Notable deviations can be observed in the temperature dependence of $\eta$, $\zeta$ and $\lambda$ when compared with corresponding calculations using vacuum cross-sections usually employed in the literature. The value of the specific shear viscosity $\eta /s$ is found to be in agreement with available estimates.

Appendices

Appendix A: Thermodynamic quantities

The thermodynamic quantities like energy density, number density, pressure and enthalpy of the three component system consisting of pions, kaons and nucleons can be expressed in terms of the sum of series of Bessels function as $S_n^\alpha (z_\pi )$, $R_n^\alpha (z_K)$ and $T_n^\alpha (z_N)$, where $z_\pi =m_\pi /T$, $z_K=m_K /T$ and $z_N=m_N /T$. These quantities are given as:

$$\begin{aligned} n_\pi= & {} g_\pi \int \frac{d^3p_\pi }{(2\pi )^3} f_\pi ^{(0)} (p_\pi )= \left( \frac{g_\pi }{2 \pi ^2}\right) z_\pi ^2 T^3 S_2^1 (z_\pi ), \nonumber \\\end{aligned}$$

(A1)

$$\begin{aligned} P_\pi= & {} g_\pi \int \frac{d^3p_\pi }{(2\pi )^3} \frac{\vec {p_\pi }^2}{3E_{p_\pi }} f_\pi ^{(0)} (p_\pi )\nonumber \\= & {} \left( \frac{g_\pi }{2 \pi ^2}\right) z_\pi ^2 T^4 S_2^2 (z_\pi ), \end{aligned}$$

(A2)

$$\begin{aligned} n_\pi e_\pi= & {} g_\pi \int \frac{d^3p_\pi }{(2\pi )^3} E_{p_\pi } f_\pi ^{(0)}(p_\pi )\nonumber \\= & {} \left( \frac{g_\pi }{2 \pi ^2}\right) z_\pi ^2 T^4 \left[ z_\pi S_3^1(z_\pi )-S_2^2(z_\pi )\right] , \end{aligned}$$

(A3)

$$\begin{aligned} n_\pi h_\pi= & {} n_\pi z_\pi \frac{S_3^1(z_\pi )}{S_2^1(z_\pi )} \end{aligned}$$

(A4)

where $E_{p_\pi }=\sqrt{\vec {p}_\pi ^2+m_\pi ^2}$ and $f_\pi ^{(0)}(p_\pi )=[e^{\beta (E_{p_\pi }-\mu _\pi )}-1]^{-1}$. Making use of the formula

$$\begin{aligned} {[}a-1]^{-1}=\sum _{n=1}^{\infty }~(a^{-1})^n~~~\text {for}~~ \left| a\right| <1, \end{aligned}$$

(A5)

the distribution function can be expanded, so that the three momentum integrals in the above equations could be analytically performed and expressed in terms of the following infinite series

$$\begin{aligned} S_n^\alpha (z_\pi )=\sum _{k=1}^{\infty }~e^{{k\mu _\pi }/T}~k^{-\alpha }~K_n(kz_\pi ) \end{aligned}$$

(A6)

where $K_n(x)$ is the modified Bessel function of order n whose integral representation is

$$\begin{aligned} K_n(x)=\frac{2^n n!}{(2n)!~x^n}\int _{x}^{\infty }d\tau (\tau ^2-x^2)^{n-\frac{1}{2}}e^{-\tau } \end{aligned}$$

(A7)

or

$$\begin{aligned} K_n(x)=\frac{2^n n! (2n-1)}{(2n)!x^n}\int _{x}^{\infty }\tau ~ d\tau (\tau ^2-x^2)^{n-\frac{3}{2}}~e^{-\tau }. \end{aligned}$$

(A8)

The expression for thermodynamic quantities mentioned above will be similar for kaons and nucleons except the term $S_n^\alpha (z_\pi )$ will be replaced by $R_n^\alpha (z_K)$ for kaons and $T_n^\alpha (z_N)$ for nucleons where

$$\begin{aligned} R_n^\alpha (z_K)=\sum _{k=1}^{\infty }~e^{{k\mu _K}/T}~k^{-\alpha }~K_n(kz_K) \end{aligned}$$

(A9)

and

$$\begin{aligned} T_n^\alpha (z_N)=\sum _{k=1}^{\infty }~(-1)^{k-1}~e^{{k\mu _N}/T}~k^{-\alpha }~K_n(kz_N). \end{aligned}$$

(A10)

Appendix B: Useful expressions

The transport equation for each species is given by

$$\begin{aligned} p^\mu \partial _\mu f_k^{(0)}(x,p)=-\frac{\delta f(x,p)}{\tau _k} E_k \end{aligned}$$

(B1)

where on the right hand side of the equation, we have made use of relaxation time approximation. The time and space derivatives (in the local rest frame) present in the left hand side of the above equation will be replaced by the derivatives of the thermodynamics parameters. The equation then reduces to

$$\begin{aligned}&(p_k\cdot u)\left[ \frac{p_k\cdot u}{T^2}DT + D\left( \frac{\mu _k}{T}\right) ~-~\frac{p_k^\mu }{T}Du_\mu \right] \nonumber \\&\qquad + p^\mu \left[ \frac{p_k\cdot u}{T^2} \nabla _\mu T + \nabla _\mu \left( \frac{\mu _k}{T}\right) -\frac{p_k^\nu }{T}\nabla _\mu u_\nu \right] \nonumber \\&\quad =-\frac{\delta f(x,p)}{\tau _k} E_k. \end{aligned}$$

(B2)

The conservation equations

$$\begin{aligned} \partial _\mu N_k^\mu= & {} 0,~~~ Dn_k=-n_k \partial _\mu u^\mu ~~\text {and}~~ \sum _{k} n_k De_k \nonumber \\= & {} -\sum _{k}P_k\partial _\mu u^\mu \end{aligned}$$

(B3)

with $N^\mu =n U^\mu$ and total $P=p_\pi +p_K+p_N$ can be expanded in terms of the derivative with respect to temperature and chemical potential over temperature as

$$\begin{aligned}&\frac{\partial n_\pi }{\partial T} DT + \frac{\partial n_\pi }{\partial (\mu _\pi /T)}D\left( \frac{\mu _\pi }{T}\right) + \frac{\partial n_K}{\partial (\mu _K/T)}D\left( \frac{\mu _K}{T}\right) \nonumber \\&\quad + \frac{\partial n_N}{\partial (\mu _N/T)}D\left( \frac{\mu _N}{T}\right) =-n_\pi ~\partial _\mu u^\mu ~, \end{aligned}$$

(B4)

$$\begin{aligned}&\frac{\partial n_K}{\partial T} DT + \frac{\partial n_\pi }{\partial (\mu _\pi /T)}D\left( \frac{\mu _\pi }{T}\right) ~+~\frac{\partial n_K}{\partial (\mu _K/T)}D\left( \frac{\mu _K}{T}\right) \nonumber \\&\quad + \frac{\partial n_N}{\partial (\mu _N/T)}D\left( \frac{\mu _N}{T}\right) = -n_K~\partial _\mu u^\mu ~, \end{aligned}$$

(B5)

$$\begin{aligned}&\frac{\partial n_N}{\partial T} DT+\frac{\partial n_\pi }{\partial (\mu _\pi /T)}D\left( \frac{\mu _\pi }{T}\right) +\frac{\partial n_K}{\partial (\mu _K/T)}D\left( \frac{\mu _K}{T}\right) \nonumber \\&\quad + \frac{\partial n_N}{\partial (\mu _N/T)}D\left( \frac{\mu _N}{T}\right) = -n_N~\partial _\mu u^\mu ~, \\&\quad \left[ n_\pi \frac{\partial e_\pi }{\partial T}+n_K\frac{\partial e_K}{\partial T}+n_N\frac{\partial e_N}{\partial T} \right] +n_\pi \frac{\partial e_\pi }{\partial (\mu _\pi /T)} D\left( \frac{\mu _\pi }{T}\right) \nonumber \\&\quad + n_K\frac{\partial e_K}{\partial (\mu _K/T)}D\left( \frac{\mu _K}{T}\right) +n_N\frac{\partial e_N}{\partial (\mu _N/T)}D\left( \frac{\mu _N}{T}\right) = -P\partial _\mu u^\mu ~.\nonumber \end{aligned}$$

(B6)

Making use of the expressions obtained in Appendix A in the above equations and then solving for DT, $D\left( \frac{\mu _\pi }{T}\right)$, $D\left( \frac{\mu _K}{T}\right)$ and $D\left( \frac{\mu _N}{T}\right)$ we get

$$\begin{aligned}&DT = T~(1-\gamma ')~\partial _\mu u^\mu ~, \end{aligned}$$

(B7)

$$\begin{aligned}&TD\left( \frac{\mu _\pi }{T}\right) = [(\gamma _\pi ''-1)-T\gamma _\pi ''']~\partial _\mu u^\mu ~, \end{aligned}$$

(B8)

$$\begin{aligned}&TD\left( \frac{\mu _K}{T}\right) = [(\gamma _K''-1)-T\gamma _K''']~\partial _\mu u^\mu ~, \end{aligned}$$

(B9)

$$\begin{aligned}&TD\left( \frac{\mu _N}{T}\right) = {[}(\gamma _N''-1)-T\gamma _N''']~\partial _\mu u^\mu \end{aligned}$$

(B10)

where

$$\begin{aligned} \gamma '= & {} \frac{1}{X}\Bigg [g_\pi \left\{ z_\pi ^3\left( 4R_2^0S_2^0T_2^0S_3^1+R_2^0T_2^0S_3^0S_2^1\frac{}{}\right) \right. \nonumber \\&\left. +\, z_\pi ^4\left( R_2^0T_2^0(S_2^0)^2-R_2^0T_2^0(S_3^0 )^2\frac{}{}\right) \right\} \nonumber \\&+g_K\left\{ z_K^3\left( 4R_2^0S_2^0T_2^0R_3^1+S_2^0T_2^0R_3^0R_2^1\frac{}{}\right) \right. \nonumber \\&\left. +\, z_K^4\left( S_2^0T_2^0(R_2^0)^2-S_2^0T_2^0(R_3^0)^2 \frac{}{}\right) \right\} \nonumber \\&+\, g_N\left\{ z_N^3\left( 4R_2^0S_2^0T_2^0T_3^1+R_2^0S_2^0T_3^0T_2^1\frac{}{}\right) \right. \nonumber \\&\left. +\, z_N^4\left( R_2^0S_2^0(T_2^0)^2-R_2^0S_2^0(T_3^0)^2\frac{}{}\right) \right\} \Bigg ], \end{aligned}$$

(B11)

$$\begin{aligned} \gamma _\pi ''= & {} \frac{1}{X}\Bigg [g_\pi \left\{ -5z_\pi ^2R_2^0T_2^0(S_2^1)^2+z_\pi ^3\left( 3R_2^0S_2^0T_2^0S_3^1+3R_2^0T_2^0S_3^0S_2^1\frac{}{}\right) \right. \nonumber \\&\left. +\, z_\pi ^4\left( R_2^0T_2^0(S_2^0)^2-R_2^0T_2^0(S_3^0)^2\frac{}{}\right) \right\} \nonumber \\&+g_K\left\{ -z_K^2S_2^0T_2^0(R_2^1)^2 +\, z_K^3\left( 3R_2^0S_2^0T_2^0R_3^1+2R_3^0S_2^0T_2^0R_2^1\frac{}{}\right) \right. \nonumber \\&\left. +\, z_K^4\left( S_2^0T_2^0(R_2^0)^2-S_2^0T_2^0(R_3^0)^2\frac{}{}\right) \right\} \nonumber \\&+\, g_N\left\{ -z_N^2R_2^0S_2^0(T_2^1)^2+z_N^3\left( 3R_2^0S_2^0T_2^0T_3^1+2R_2^0S_2^0T_3^0T_2^1\frac{}{}\right) \right. \nonumber \\&\left. +\, z_N^4\left( R_2^0S_2^0(T_2^0)^2-R_2^0S_2^0(T_3^0)^2\frac{}{}\right) \right\} \Bigg ], \end{aligned}$$

(B12)

$$\begin{aligned} \gamma _\pi '''= & {} \frac{1}{X}\Bigg [g_\pi \left\{ z_\pi ^4R_2^0T_2^0S_2^0S_2^1\frac{}{}\right\} +\, g_K\left\{ z_K^3\left( 4R_2^0T_2^0S_2^1R_3^1+T_2^0R_3^0R_2^1S_2^1\frac{}{}\right) \right. \nonumber \\&\left. +\, z_K^4\left( T_2^0S_2^1(R_2^0)^2-T_2^0S_2^1(R_3^0)^2 \frac{}{}\right) \right. \nonumber \\&\left. -z_\pi z_K^2T_2^0S_3^0(R_2^1)^2 +z_\pi z_K^3\left( R_3^0S_3^0T_2^0R_2^1-R_2^0S_3^0T_2^0R_3^1\frac{}{}\right) \right\} \nonumber \\&+\, g_N\left\{ z_N^3\left( 4R_2^0T_2^0S_2^1T_3^1+R_2^0T_3^0S_2^1T_2^1\frac{}{}\right) \right. \nonumber \\&\left. +\, z_N^4\left( R_2^0S_2^1(T_2^0)^2-R_2^0S_2^1(T_3^0)^2\frac{}{}\right) -z_\pi z_N^2R_2^0S_3^0(T_2^1)^2 \right. \nonumber \\&\left. +\, z_\pi z_N^3\left( R_2^0S_3^0T_3^0T_2^1-R_2^0S_3^0T_2^0T_3^1\frac{}{}\right) \right\} \Bigg ] , \end{aligned}$$

(B13)

$$\begin{aligned} \gamma _K''= & {} \frac{1}{X}\Bigg [g_\pi \left\{ -z_\pi ^2R_2^0T_2^0(S_2^1)^2+z_\pi ^3\left( 3R_2^0S_2^0T_2^0S_3^1+2R_2^0T_2^0S_3^0S_2^1\frac{}{}\right) \right. \nonumber \\&\left. +\, z_\pi ^4\left( R_2^0T_2^0(S_2^0)^2-R_2^0T_2^0(S_3^0)^2\frac{}{}\right) \right\} \nonumber \\&+\, g_K\left\{ -5z_K^2S_2^0T_2^0(R_2^1)^2 +z_K^3\left( 3R_2^0S_2^0T_2^0R_3^1+3R_3^0S_2^0T_2^0R_2^1\frac{}{}\right) \right. \nonumber \\&\left. +\, z_K^4\left( S_2^0T_2^0(R_2^0)^2-S_2^0T_2^0(R_3^0)^2\frac{}{}\right) \right\} \nonumber \\&+\, g_N\left\{ -z_N^2R_2^0S_2^0(T_2^1)^2+z_N^3\left( 3R_2^0S_2^0T_2^0T_3^1+2R_2^0S_2^0T_3^0T_2^1\frac{}{}\right) \right. \nonumber \\&\left. +\, z_N^4\left( R_2^0S_2^0(T_2^0)^2-R_2^0S_2^0(T_3^0)^2\frac{}{}\right) \right\} \Bigg ] , \end{aligned}$$

(B14)

$$\begin{aligned} \gamma _K'''= & {} \frac{1}{X}\Bigg [g_\pi \left\{ z_\pi ^3\left( 4T_2^0S_2^0R_2^1S_3^1+T_2^0S_3^0R_2^1S_2^1\frac{}{}\right) \right. \nonumber \\&\left. +\, z_\pi ^4\left( T_2^0R_2^1(S_2^0)^2 -T_2^0R_2^1(S_3^0)^2\frac{}{}\right) -z_Kz_\pi ^2T_2^0R_3^0(S_2^1)^2 \right. \nonumber \\&\left. +\, z_Kz_\pi ^3\left( T_2^0R_3^0S_3^0S_2^1 - T_2^0R_3^0S_2^0S_3^1\frac{}{}\right) \right\} +g_K\left\{ z_k^4S_2^0T_2^0R_2^0R_2^1\frac{}{}\right\} \nonumber \\&+\, g_N\left\{ z_N^3\left( 4T_2^0S_2^0R_2^1T_3^1+S_2^0T_3^0R_2^1T_2^1\frac{}{}\right) \right. \nonumber \\&+\, z_N^4\left( S_2^0R_2^1(T_2^0)^2-S_2^0R_2^1(T_3^0)^2\frac{}{}\right) -z_K z_N^2S_2^0R_3^0(T_2^1)^2\nonumber \\&\left. +\, z_Kz_N^3\left( S_2^0R_3^0T_3^0T_2^1-S_2^0R_3^0T_2^0T_3^1\frac{}{}\right) \right\} \Bigg ] , \end{aligned}$$

(B15)

$$\begin{aligned} \gamma _N''= & {} \frac{1}{X}\Bigg [g_\pi \left\{ -z_\pi ^2R_2^0T_2^0(S_2^1)^2+z_\pi ^3\left( 3R_2^0S_2^0T_2^0S_3^1+2R_2^0T_2^0S_3^0S_2^1\frac{}{}\right) \right. \nonumber \\&\left. +\, z_\pi ^4\left( R_2^0T_2^0(S_2^0)^2-R_2^0T_2^0(S_3^0)^2\frac{}{}\right) \right\} \nonumber \\&+\, g_K\left\{ -z_K^2S_2^0T_2^0(R_2^1)^2 +z_K^3\left( 3R_2^0S_2^0T_2^0R_3^1+2R_3^0S_2^0T_2^0R_2^1\frac{}{}\right) \right. \nonumber \\&\left. +\, z_K^4\left( S_2^0T_2^0(R_2^0)^2-S_2^0T_2^0(R_3^0)^2\frac{}{}\right) \right\} \nonumber \\&+\, g_N\left\{ -5z_N^2R_2^0S_2^0(T_2^1)^2+z_N^3\left( 3R_2^0S_2^0T_2^0T_3^1+3R_2^0S_2^0T_3^0T_2^1\frac{}{}\right) \right. \nonumber \\&\left. +\, z_N^4\left( R_2^0S_2^0(T_2^0)^2-R_2^0S_2^0(T_3^0)^2\frac{}{}\right) \right\} \Bigg ] , \end{aligned}$$

(B16)

$$\begin{aligned} \gamma _N'''= & {} \frac{1}{X}\Bigg [g_\pi \left\{ z_\pi ^3\left( 4S_2^0R_2^0T_2^1S_3^1+R_2^0S_3^0T_2^1S_2^1\frac{}{}\right) \right. \nonumber \\&\left. +\, z_\pi ^4\left( R_2^0T_2^1(S_2^0)^2 -R_2^0T_2^1(S_3^0)^2\frac{}{}\right) -z_Nz_\pi ^2R_2^0T_3^0(S_2^1)^2 \right. \nonumber \\&\left. +\, z_Nz_\pi ^3\left( R_2^0S_3^0T_3^0S_2^1 - R_2^0S_2^0T_3^0S_3^1\frac{}{}\right) \right\} \nonumber \\&+\, g_N\left\{ z_N^4S_2^0T_2^0R_2^0T_2^1\frac{}{}\right\} +g_K\left\{ z_K^3\left( 4R_2^0S_2^0T_2^1R_3^1+R_3^0S_2^0R_2^1T_2^1\frac{}{}\right) \right. \nonumber \\&+\, z_K^4\left( (R_2^0)^2S_2^0T_2^1 -(R_3^0)^2S_2^0T_2^1\frac{}{}\right) -z_Nz_K^2S_2^0T_3^0(R_2^1)^2\nonumber \\&\left. +\, z_Nz_K^3\left( S_2^0R_3^0T_3^0R_2^1-R_2^0S_2^0T_3^0R_3^1\frac{}{}\right) \right\} \Bigg ], \end{aligned}$$

(B17)

and the term X appearing in the above expressions of $\gamma$’s is given by

$$\begin{aligned} X= & {} g_\pi \left[ -z_\pi ^2R_2^0T_2^0(S_2^1)^2+z_\pi ^3\left( 3R_2^0S_2^0T_2^0S_3^1+2R_2^0T_2^0S_3^0S_2^1\frac{}{}\right) \right. \nonumber \\&\left. +\, z_\pi ^4\left( R_2^0T_2^0(S_2^0)^2-R_2^0T_2^0(S_3^0)^2\frac{}{}\right) \right] \nonumber \\&+\, g_K\Big [-z_K^2S_2^0T_2^0(R_2^1)^2 \nonumber \\&+\, z_K^3\left( 3R_2^0S_2^0T_2^0R_3^1+2R_3^0S_2^0T_2^0R_2^1\frac{}{}\right) \nonumber \\&+\, z_K^4\left( S_2^0T_2^0(R_2^0)^2-S_2^0T_2^0(R_3^0)^2\frac{}{}\right) \Big ] \nonumber \\&+\, g_N \Big [-z_N^2R_2^0S_2^0(T_2^1)^2\nonumber \\&+\, z_N^3\left( 3R_2^0S_2^0T_2^0T_3^1+2R_2^0S_2^0T_3^0T_2^1\frac{}{}\right) \nonumber \\&+\, z_N^4\left( R_2^0S_2^0(T_2^0)^2-R_2^0S_2^0(T_3^0)^2\frac{}{}\right) \Big ]~. \end{aligned}$$

(B18)