The shear viscosity of parton matter under anisotropic scatterings

Abstract

The shear viscosity $\eta$ of a quark–gluon plasma in equilibrium can be calculated analytically using multiple methods or numerically using the Green–Kubo relation. It has been realized, which we confirm here, that the Chapman–Enskog method agrees well with the Green–Kubo result for both isotropic and anisotropic two-body scatterings. We then apply the Chapman–Enskog method to study the shear viscosity of the parton matter from a multi-phase transport model. In particular, we study the parton matter in the center cell of central and midcentral Au + Au collisions at 200A GeV and Pb + Pb collisions at 2760A GeV, which is assumed to be a plasma in thermal equilibrium but partial chemical equilibrium. As a result of using a constant Debye mass or cross section $\sigma$ for parton scatterings, the $\eta /s$ ratio increases with time (as the effective temperature decreases), contrary to the trend preferred by Bayesian analysis of the experimental data or pQCD results that use temperature-dependent Debye masses. At $\sigma =3$ mb that enables the transport model to approximately reproduce the elliptic flow data of the bulk matter, the average $\eta /s$ of the parton matter in partial equilibrium is found to be very small, between one to two times $1/(4\pi )$.

1 Introduction

In ultra-relativistic heavy ion collisions at the Relativistic Heavy Ion Collider (RHIC) and the Large Hadron Collider (LHC), a quark–gluon plasma (QGP) has been created [1, 2]. The comparisons [3,4,5] between the experimental measurements of the anisotropic flows and theoretical models such as hydrodynamics suggest that the QGP behaves like a near-perfect fluid with a very small $\eta /s$ (shear viscosity to entropy density) ratio, not too far from the lower bound $1/(4\pi )$ from the conformal field theory [6].

Similar to hydrodynamics models, transport models can also describe the large observed elliptic flow in high energy heavy ion collisions once parton interactions are included [7,8,9,10]. In these transport models, the interactions among partons are typically represented by the interaction cross section(s), including the magnitude and angular distribution, which then determine the plasma properties including the shear viscosity $\eta$ and the heavy quark spatial diffusion coefficient $D_s$. Unlike hydrodynamics models, where the $\eta /s$ ratio (including its possible temperature dependence) is an input parameter, transport model calculations can only be related to the QGP shear viscosity or $\eta /s$ after applying the relation between the parton cross section(s) and shear viscosity [8, 10,11,12].

The shear viscosity of a parton matter at a given temperature can be calculated analytically or numerically. Analytical methods include the Israel–Stewart (IS), Navier–Stokes (IS), relaxation time approximation (RTA), and Chapman–Enskog (CE) [13, 14] methods. They often give different results, especially for anisotropic scatterings. The shear viscosity can also be numerically calculated with the Green–Kubo relation [15,16,17]. An earlier study [18] has found that for two-body anisotropic scatterings the Chapman–Enskog method agrees well with the Green-Kubo result while the relaxation time approximation (even a modified version RTA$^*$) does not.

In this study, we first examine the four analytical methods (IS, NS, RTA$^*$, CE) in comparison with the Green–Kubo numerical results on the shear viscosity and $\eta /s$ ratio for massless partons in equilibrium under isotropic or anisotropic two-body scatterings. We then apply the CE method to the parton matter in the string melting version of a multi-phase transport (AMPT) model [19], which we assume as a QGP in partial equilibrium. In particular, we study the time evolution of $\eta$ and $\eta /s$ of the center cell of the parton matter in high energy Au + Au and Pb + Pb collisions. After some discussions, we then summarize our findings.

2 Methods

In addition to the isotropic scattering cross section, we also consider the forward-angle scattering cross section, which is based on the perturbative QCD (pQCD) $gg\rightarrow gg$ cross section and implemented in the ZPC [20] and AMPT [21] models. The differential cross section for forward scattering is given by [21]

$$\begin{aligned} \frac{d\sigma }{d\hat{t}}=\frac{9\pi \alpha _s^2}{2} \left( 1+\frac{\mu ^2}{\hat{s}}\right) \frac{1}{(\hat{t}-\mu ^2)^2}, \end{aligned}$$

(1)

where ${\hat{s}}$ and ${\hat{t}}$ are the standard Mandelstam variables, $\alpha _s$ is the strong-coupling constant, and $\mu$ is the Debye screening mass. The factor $(1+\mu ^2/{{\hat{s}}})$ is used to make the total cross section energy independent (i.e., independent of ${\hat{s}}$):

$$\begin{aligned} \sigma = \frac{9\pi \alpha _s^2}{2\mu ^2}. \end{aligned}$$

(2)

The transport cross section, defined as [22]

$$\begin{aligned} \sigma _{\mathrm {tr}}=\int d\sigma \sin ^2\theta _{\mathrm {cm}}, \end{aligned}$$

(3)

where $\theta _{\mathrm {cm}}$ is the scattering angle in the two-parton center of mass frame, often appears in the viscosity expressions because the shear viscosity depends on the effectiveness of momentum transfer of the parton scatterings. For the above forward cross section, one gets [18, 22]

$$\begin{aligned} \sigma _{\mathrm {tr}}=4 a (1+a) \left[ (1+2a) \ln \left( 1+\frac{1}{a} \right) -2 \right] \sigma \equiv h(a) \; \sigma , \nonumber \\ \end{aligned}$$

(4)

where $a=\mu ^2/\hat{s}$. As $a \rightarrow 0$, the cross section becomes more forward-peaked and $h(a) \rightarrow 0$. On the other hand, as $a \rightarrow \infty$, the differential cross section of Eq. (1) becomes isotropic and $h(a) \rightarrow 2/3$. Also note that the h(a) function increases monotonously with a. Therefore, h(a) is directly related to the anisotropy of the scattering cross section. Since the transport cross section depends on ${\hat{s}}$ even if the total cross section does not, we take its thermal average [23] when considering a parton matter at a given temperature T:

$$\begin{aligned} \langle \sigma _{\mathrm {tr}}\rangle= & {} \frac{\sigma }{32}\int _0^\infty du~ h\! \left( \frac{w^2}{u^2} \right) \nonumber \\&\times \left[ u^4K_1(u)+2u^3K_2(u)\right] \equiv \sigma g_0(w). \end{aligned}$$

(5)

In the above, $w=\mu /T, u=\sqrt{{\hat{s}}}/T$ is the integration variable, $K_n$ is the modified Bessel function of the second kind, and Boltzmann statistics is used for the thermal distribution. The $g_0(w)$ function defined above is just the thermal average of h(a), it thus approaches 0 as $w \rightarrow 0$ but approaches 2/3 as $w \rightarrow \infty$.

Next we examine four analytical methods and the numerical Green-Kubo method for calculating the shear viscosity of a parton matter under isotropic or forward scatterings. Note that we only consider a massless QGP. Therefore, the entropy density is given by $s=4 g_{\mathrm{B}}T^3/\pi ^2$, where $g_{\mathrm{B}}=4(4 + 3N_f )$ is the total degeneracy factor of the QGP with Boltzmann statistics, and $N_f$ is the number of relevant quark flavors.

2.1 Israel–Stewart and Navier–Stokes Methods

The Israel–Stewart [24, 25] and Navier–Stokes [14] expressions for shear viscosity can be written respectively as

$$\begin{aligned} \eta ^{\,\mathrm {IS}}=\frac{6~T}{5~\sigma }, ~\eta ^{\,\mathrm {NS}}\simeq 1.2654 \frac{T}{\sigma } \end{aligned}$$

(6)

for isotropic scatterings, where $\sigma _{\mathrm {tr}}=2\sigma /3$. They can be generalized to anisotropic scatterings as [26]

$$\begin{aligned} \eta ^{\,\mathrm {IS}}=\frac{4~T}{5\langle \sigma _{\mathrm {tr}}\rangle }, ~\eta ^{\,\mathrm {NS}}\simeq 0.8436\frac{T}{\langle \sigma _{\mathrm {tr}}\rangle }. \end{aligned}$$

(7)

2.2 The modified relaxation time approximation

The relaxation time approximation is widely used in kinetic theory, where one approximates the collision integral in the Boltzmann equation as ${\mathcal {C}}[f]\propto -(f-f_{eq})/\tau$. Here f is the particle distribution function with $f_{eq}$ being the one in equilibrium, and $\tau$ is the relaxation time. With Boltzmann statistics, the RTA expression for the shear viscosity is given by [27]

$$\begin{aligned} \eta ^{\mathrm {RTA}}=\frac{4~T}{5~\sigma }. \end{aligned}$$

(8)

In the modified RTA method (denoted as RTA$^*$ in this study) [18], Eq.(8) is changed to the following:

$$\begin{aligned} \eta ^{\mathrm {RTA^*}}=\frac{4~T}{5\langle \sigma _{\mathrm {tr}} v_{\mathrm {rel}}\rangle }. \end{aligned}$$

(9)

In the above, $v_{\mathrm {rel}}=\sqrt{ {{\hat{s}}} ({{\hat{s}}}-4m^2)} /(2E_1E_2)$ is the relative velocity between the two colliding partons, where $E_1$ and $E_2$ represent respectively the energy of the two partons (each with mass m); for massless partons one has $\langle v_{\mathrm {rel}}\rangle =1$. Note that for isotropic scatterings this modification gives $\eta ^{\mathrm {RTA^*}}=6T/(5\sigma )$, which fails to reproduce the original RTA result of Eq. (8); however, it agrees with the Israel–Stewart (and Chapman–Enskog) expression. For anisotropic scatterings, it differs from the Israel–Stewart expression by a $v_{\mathrm {rel}}$ term, with the thermal average given by [18, 28]

$$\begin{aligned} \langle \sigma _{\mathrm {tr}}v_{\mathrm {rel}} \rangle= & {} \frac{8z}{K_2^2(z)}\int _1^\infty dy~y^2(y^2-1)K_1(2zy)\nonumber \\&\times \int d\sigma \sin ^2\theta _{\mathrm {cm}}, \end{aligned}$$

(10)

where $z=m/T$ and $y=\sqrt{\hat{s}}/(2m)$. For massless partons and the AMPT differential cross section of Eq. (1), we obtain

$$\begin{aligned} \langle \sigma _{\mathrm {tr}}v_{\mathrm {rel}} \rangle =\frac{\sigma }{16}\int _0^\infty du~ h\!\left( \frac{w^2}{u^2}\right) u^4K_1(u) \equiv \sigma g_1(w), \end{aligned}$$

(11)

where $g_1(w)$ is effectively another thermal average of h(a).

2.3 The Chapman–Enskog method

The Chapman–Enskog method solves the Boltzmann equation by applying a series expansion on the distribution function [13]. The first-order result for the general case of massive particles under an anisotropic cross section is given by [29]

$$\begin{aligned} \eta ^{\mathrm {CE}}=\frac{T}{10}\frac{\gamma _0^2}{c_{00}}, \end{aligned}$$

(12)

where $\gamma _0=-10K_3(z)/K_2(z)$, and

$$\begin{aligned} \frac{c_{00}}{\gamma _0^2}= & {} \frac{4z^3}{25K_3^2(z)}\int _1^\infty dy~(y^2-1)^3\left[ \left( y^2+\frac{1}{3z^2} \right) K_3(2zy)\right. \nonumber \\&\left. -\frac{y}{z}K_2(2zy)\right] \int d\sigma \sin ^2\theta _{\mathrm {cm}}. \end{aligned}$$

(13)

For the special case of massless partons and the AMPT differential cross section of Eq. (1), we then obtain [30]

$$\begin{aligned} \frac{c_{00}}{\gamma _0^2}= & {} \frac{\sigma }{51200}\int _{0}^\infty du~ h\!\left( \frac{w^2}{u^2} \right) u^6 \left[ \left( \frac{u^2}{4} +\frac{1}{3} \right) K_3(u)\right. \nonumber \\&\left. -\frac{u}{2}K_2(u) \right] \equiv \frac{\sigma }{8} g_2(w). \end{aligned}$$

(14)

For isotropic scatterings, $g_2(w)=2/3$ and $\eta ^{\mathrm {CE}}=\eta ^{\mathrm {IS}}$. For anisotropic scattering in general, we have

$$\begin{aligned} \eta ^{\mathrm {CE}}=\frac{4~T}{5~\sigma g_2(w)}. \end{aligned}$$

(15)

Comparing to $\eta ^{\mathrm {IS}}$ in Eq. (7), we see that $\sigma g_2(w)$ in the CE method serves the role of $\langle \sigma _{\mathrm {tr}}\rangle$ in the IS method, and $g_2(w)$ is another thermal average of h(a) similar to $g_0(w)$ in Eq. (5) and $g_1(w)$ in Eq. (11).

The $\eta$ expressions in Eqs. (12) and (13) for the general case of massive partons were given earlier [18, 29], while Eqs. (14) and (15) for the special massless case were shown later [30]. Note that there is a typo in Eq.(35) and Eq. (38) of Ref. [18], which give the $\eta$ result for the modified RTA and Chapman–Enskog methods respectively, where $h(2zy{\bar{a}})$ in the two equations should be $h(a)=h(1/(2zy{\bar{a}})^2)$ since $2zy{\bar{a}}=\sqrt{{\hat{s}}}/\mu \ne a$ with ${\bar{a}} \equiv T/\mu$ [18].

2.4 The Green–Kubo relation

The Green–Kubo relation [31, 32] can be used to numerically calculate the shear viscosity at or near equilibrium [15,16,17]. In an earlier work [33], we have calculated the shear viscosity of a massless gluon gas in equilibrium in a box under isotropic or anisotropic two-body scatterings according to the following form of the Green–Kubo relation [15]:

$$\begin{aligned} \eta =\frac{V}{T} \int _{0}^{\infty }dt \, \langle \bar{\pi }^{xy}(t+t^\prime )\,\bar{\pi }^{xy}(t^\prime ) \rangle . \end{aligned}$$

(16)

In the above, V is the volume of the gluon gas, and the bracket represents the time ($t^\prime$) and ensemble average. The term $\bar{\pi }^{xy}(t)$ represents the volume-averaged xy-component of the energy-momentum tensor at time t: $\bar{\pi }^{xy}(t)=\sum (p_{i}^{x}p_{i}^{y}/p^{0}_{i})/V$ [33]. The correlation function in the above relation is known to damp exponentially with time [15, 16]:

$$\begin{aligned} \langle \bar{\pi }^{xy}(t+t^\prime )\,\bar{\pi }^{xy}(t^\prime ) \rangle =\langle \bar{\pi }^{xy}(t^\prime )\,\bar{\pi }^{xy}(t^\prime ) \rangle ~e^{-t/\tau }, \end{aligned}$$

(17)

where $\tau$ is the corresponding relaxation time. In addition, the average variance of $\bar{\pi }^{xy}$ in equilibrium is given by $\langle \bar{\pi }^{xy}(t^\prime )\,\bar{\pi }^{xy}(t^\prime ) \rangle =4\epsilon \,T/(15V)$, where $\epsilon$ is the energy density of the partons in equilibrium. One then has

$$\begin{aligned} \eta =\frac{4}{15}\, \epsilon \,\tau . \end{aligned}$$

(18)

In practice, we first extract the relaxation time $\tau$ from the numerical calculation of the correlation function in Eq. (17) using the ZPC parton cascade [20, 33] and then obtain the shear viscosity from the above relation.

3 Results for gluons in a box

In this section, we consider a gluon gas in a box at a given temperature with an elastic scattering cross section of $\sigma =2.6$ mb and $\alpha _s=\sqrt{2}/3$ [33], which corresponds to $\mu \simeq 0.69$ GeV. Figure 1 shows the shear viscosity versus temperature from the four analytical methods under isotropic scatterings in panel (a) and the AMPT forward scatterings in panel (b). We see in panel (a) that the viscosity for isotropic scatterings at a fixed cross section is linear in T for each method, and the results from the Israel–Stewart, modified relaxation time approximation, and the Chapman–Enskog methods are all the same. The results from the Navier–Stokes method is also very close, only about 5% higher.

For forward scatterings, however, we see in panel (b) that the viscosity results from the four methods are not the same. At high temperatures, the viscosity from the Chapman–Enskog method is much higher than results from the other three methods that are relatively close to each other. Also, the shear viscosity for forward scatterings is significantly higher than that for isotropic scatterings for every method; this is a result of the smaller transport cross section as $h(a)<2/3$ for forward scatterings. At low temperatures, the four methods give almost the same result because $a \gg 1$ there, which makes the forward scattering cross section of Eq. (1) almost isotropic. Note that the results shown in Fig. 1 apply not only to massless gluons but also to massless partons.

Fig. 1

The shear viscosity versus temperature from four analytical methods for massless partons under (a) isotropic scatterings or (b) forward-angle scatterings, both at $\sigma =2.6$ mb with $\alpha _s=0.47$. The methods include Israel–Stewart (IS), Navier–Stokes (NS), modified relaxation time approximation (RTA$^*$), and Chapman–Enskog (CE)

Fig. 2

The ratio of shear viscosity to entropy density versus the opacity parameter $\chi$ for massless gluons in equilibrium under (a) isotropic scatterings or (b) forward-angle scatterings of $\sigma =2.6$ mb with $\alpha _s=0.47$. Results from four analytical methods (curves) are compared with the numerical values from the Green–Kubo relation (circles)

Results of the $\eta /s$ ratio for the gluon gas are shown versus the opacity parameter for isotropic scatterings in Fig. 2a and the AMPT forward scatterings in Fig. 2b. The unitless opacity parameter is defined as [33, 34]

$$\begin{aligned} \chi =\sqrt{\frac{\sigma }{\pi } }/\lambda =n \sqrt{\frac{\sigma ^3}{\pi } }, \end{aligned}$$

(19)

where $\lambda$ is the mean free path, and n is the parton number density. For a gluon gas under isotropic scatterings, we then have

$$\begin{aligned} \left( \frac{\eta }{s}\right) ^{\mathrm {IS}} \simeq \frac{0.1744}{\chi ^{2/3}},~~ \left( \frac{\eta }{s}\right) ^{\mathrm {NS}}\simeq \frac{0.1839}{\chi ^{2/3}}. \end{aligned}$$

(20)

We see in Fig. 2a that the $\eta /s$ ratios from the four analytical methods are almost the same. They also agree well with the circles, which represent our previous numerical results [33] obtained from the Green–Kubo relation for four cases ($T=0.2$ GeV and $\sigma =2.6$ mb, $T=0.5$ GeV and $\sigma =2.6$ mb, $T=0.7$ GeV and $\sigma =5.2$ mb, $T=0.7$ GeV and $\sigma =10$ mb). Note that the Green–Kubo results shown in this section represent the results using parton subdivision with a subdivision factor $l=10^6$ [33] that essentially removes the causality violation in parton cascade calculations.

Figure 2b shows the $\eta /s$ results for forward scatterings. Results from the Chapman–Enskog method agree well with the previous numerical results from the Green–Kubo relation [33], while results from the other three analytical methods are too low. Note that the $\eta /s$ ratio for anisotropic scatterings is no longer only a function of the opacity parameter $\chi$; it also depends on the $\alpha _s$ value because the h(a) function leads to a dependence of $\eta$ on $\mu /T$, which is $\propto \alpha _s/\chi ^{1/3}$. At a fixed $\alpha _s$ value, which is the case for the calculations shown in Fig. 2, the $\eta /s$ ratio is still a function of $\chi$ only. Also note that it has been shown earlier [18] that the Chapman–Enskog method agrees well with the Green–Kubo results for forward scatterings. Therefore, we shall mostly use the Chapman–Enskog viscosity in the following.

4 Time evolution of $\eta$ and $\eta /s$ of the parton matter from the AMPT model

We now consider the parton matter in the string melting version of the AMPT model [21]. In an earlier study [19], we have calculated the time evolution of the parton energy density $\epsilon$, number density, mean transverse momentum $\langle p_T\rangle$, and mean energy in the center cell of central and midcentral Au+Au collisions at 200A GeV and Pb+Pb collisions at 2760A GeV. Note that the study used the parton scattering cross section given by Eq. (1) with $\sigma =3$ mb and $\alpha _s=0.33$. We then extracted from each of these quantities the effective temperature including $T_\epsilon$ and $T_{\langle p_T\rangle }$, which are found to be quite different; this also means that the parton matter is in partial (not full) equilibrium [19]. Partial chemical equilibrium can be characterized by the fugacity parameter $\exp (\phi /T)$, where $\phi$ is the chemical potential. The shear viscosity for distributions in thermal equilibrium but with a non-zero chemical potential has been calculated in the relaxation time approximation [29, 35], and the viscosity can be shown to be independent of the fugacity for Boltzmann distributions. Therefore, the $\eta$ expressions shown in the previous Section can be applied to a parton matter under partial chemical equilibrium.

Fig. 3

The time evolutions of the effective temperatures $T_\epsilon$ and $T_{\langle p_T\rangle }$ for the center cell in (a) Pb + Pb collisions at 2760A GeV and (b) Au + Au collisions at 200A GeV. (c) shows the time evolutions of the collision rates (in arbitrary units) for the center cell

Figure 3 shows the time evolutions of two effective temperatures obtained earlier [19] from the AMPT model for the center cell of central and midcentral Pb + Pb collisions at 2760A GeV in panel (a) and Au + Au collisions at 200A GeV in panel (b). Central and midcentral collisions at the RHIC energy refer to Au + Au events with $b<3$ fm and $b=7.3$ fm, respectively; while those at the LHC energy refer to Pb+Pb events with $b<3.5$ fm and $b=7.8$ fm, respectively. The center cell is the volume within mid-spacetime-rapidity in the center of the transverse plane within $|x|<1/2$ fm and $|y|<1/2$ fm. Note that we have plotted the time evolutions up to the time when the center cell reaches $T_\epsilon =155$ MeV, approximately the temperature of the QCD crossover transition at zero net-baryon density. The effective temperature $T_\epsilon$ is determined from the parton energy density [19] assuming that the parton matter is a QGP with massless gluons and (anti)quarks of three flavors under the Boltzmann statistics, i.e., using $\epsilon =3g_\mathrm{B}T_\epsilon ^4/\pi ^2$ with $g_{\mathrm{B}}=52$. On the other hand, temperature $T_{\langle p_T\rangle }$ is determined from the mean parton transverse momentum for massless partons under the Boltzmann statistics, i.e., using $\langle p_T\rangle =3\pi T_{\langle p_T\rangle }/4$. In full thermal and chemical equilibrium, these two temperature values are the same. However, we see from Fig. 3a and b that they are very different for the parton matter from the AMPT model, with $T_\epsilon >T_{\langle p_T\rangle }$ for the four collision systems. Note that in principle the parton matter is not in full thermal equilibrium because the pressures along different axes are not isotropic during the evolution of the parton matter in the AMPT model [19, 36]. This causes the effective temperatures extracted from ${\langle p_T\rangle }$, ${\langle p\rangle }$, and ${\langle p_T^2\rangle }$ to be different [19]. On the other hand, the difference between $T_\epsilon$ and $T_{\langle p_T\rangle }$ is typically much larger [19]. Therefore, in this section we approximate the parton matter in the center cell as a QGP in full thermal equilibrium (at temperature $T_{\langle p_T\rangle }$) but partial chemical equilibrium (with the energy density given by temperature $T_\epsilon$) so that we can apply the analytical expressions for the shear viscosity. Note that this corresponds to a QGP with the fugacity of $(T_\epsilon /T_{\langle p_T\rangle })^4$.

Fig. 4

The time evolutions of (a) the CE shear viscosity and (b) $\eta /s$ of the center cell in Pb + Pb collisions at 2760A GeV and Au + Au collisions at 200A GeV. Here the parton matter from the AMPT model is considered as a QGP in partial equilibrium, where the momentum distribution corresponds to temperature $T_{\langle p_T\rangle }$ but the energy density corresponds to temperature $T_\epsilon$. Circle on each curve represents the corresponding average $\eta /s$ weighed by the collision rate

Figure 4a shows the time evolutions of the shear viscosity from the CE method for the parton matter in the center cell in partial equilibrium. Since the shear viscosity is determined by the momentum transfer but not fugacity, it should be calculated with temperature $T_{\langle p_T\rangle }$ that represents the momentum distribution. As expected for a constant cross section, the shear viscosity decreases with time as the parton matter cools down. The time evolutions of $\eta /s$ are shown in Fig. 4b. Note that throughout this Section the entropy density for the parton matter from the AMPT model is taken as the full equilibrium value, $s_{eq}=4 g_\mathrm{B}T_{\epsilon }^3/\pi ^2$, i.e., the value when the parton matter is assumed to be a QGP in full equilibrium with energy density $\epsilon$. We see in Fig. 4b that the $\eta /s$ ratio strongly increases with time as the effective temperature decreases [12]. Also, the $\eta /s$ ratio is lower at the LHC energy than the RHIC energy and lower in central events than semicentral events. These features are mainly because of the higher entropy density at higher temperatures ($s \propto T^3$) and $\eta \propto T/g_2(w)$, where $1/g_2(w)$ grows with T slower than $\sim T^{1.4}$ within the relevant temperature range (as can be observed from the CE curves in Fig. 1). In addition, at very early times the $\eta /s$ values from the AMPT model are sometimes significantly below $1/(4\pi )$, the lower bound from the conformal field theory [6]. This is partly a result of the high parton density (or equivalently the high $T_{\epsilon }$) in the string melting AMPT model despite the small parton cross section.

The $\eta /s$ ratio in Fig. 4b decreases as the temperature increases; this temperature dependence is opposite to that preferred by the Bayesian analysis of heavy ion experimental data [37], where the preferred $\eta /s$ increases as the temperature increases. This “wrong” temperature dependence is a result of using a constant parton cross section. If we use in Eq. (1) a temperature-dependent Debye mass as $\mu \propto g T$ with g being the QCD gauge coupling, we would have $\sigma \propto \alpha _s/T^2$ and thus $\eta ^\mathrm{CE}/s \propto 1/(\alpha _s g_2)$ would increase with T. This would be qualitatively similar to earlier pQCD studies [38, 39] that used temperature-dependent Debye screening masses for $2\leftrightarrow 2$ and $1\leftrightarrow 2$ parton processes, which showed that the $\eta /s$ of the QGP increases with the temperature [40].

Our early study on the effective temperatures of the parton matter [19] found that $\sigma =3$ mb can roughly reproduce the bulk observables in the four collision systems, including the pion and kaon elliptic flows at low $p_T$. An effective $\eta /s$ value averaged over its time evolution is a good overall measure of the property of the parton matter. Since parton scatterings convert the initial spatial geometry into anisotropic flows including the elliptic flow [7, 41], we use the collision rate in the center cell as the weight in the average. From Fig. 3c, we see that the collision rate (i.e., the number of parton collisions per time in the center cell) rises at early times before it decreases; the rise is because a parton is only allowed to interact a finite formation time after it is produced from the collision of the two nuclei. The circle on each curve in Fig. 4b gives the average $\eta /s$ value, which is very small and ranges from just above $1/(4\pi )$ to about twice $1/(4\pi )$.

Fig. 5

Same as Fig. 4, but the parton matter is assumed to be a QGP in full equilibrium at temperature $T_\epsilon$

Because the AMPT model lacks inelastic parton processes such as $2 \leftrightarrow 3$ processes [42], its parton matter cannot approach chemical equilibrium. We thus also calculate the shear viscosity and $\eta /s$ by assuming that the parton matter is in full (chemical and thermal) equilibrium with the same energy density (i.e., at temperature $T_\epsilon$). Figure 5 shows the full equilibrium $\eta$ in panel (a) and the $\eta /s$ ratio in panel (b), where $\eta$ is calculated using temperature $T_\epsilon$ (instead of $T_{\langle p_T\rangle }$ for the partial equilibrium case). Compared to Fig. 4a, we see that the full equilibrium viscosity is significantly higher. This is because $T_\epsilon >T_{\langle p_T\rangle }$, and note that the increase of $\eta$ with temperature is faster than linear for anisotropic scatterings due to the $1/g_2(w)$ term in Eq. (15). Compared to the partial equilibrium case, the $\eta /s$ ratios for the full equilibrium case are significantly higher, and they are above $1/(4\pi )$ in all times for the four collision systems. As shown by the circles in Fig. 5, the averaged $\eta /s$ values are also significantly higher than the partial equilibrium case, around three times $1/(4\pi )$ for the four systems. Note that the partial equilibrium nature of the AMPT parton matter, particularly the low $T_{\langle p_T\rangle }$ relative to the high energy density, helps the model to reproduce the large observed elliptic flow [7, 43]; we now know that this is related to its lower shear viscosity and $\eta /s$ than the full equilibrium case.

5 Discussions

Since the CE viscosity of Eq. (15) contains the $g_2(w)$ function that involves an integral, we have fit it with the following to make the calculation of $\eta ^{\mathrm {CE}}$ easier for the parton cross section of Eq. (1):

$$\begin{aligned} g_2^{\mathrm {fit}}(w)= & {} h\!\left( \frac{w^2}{v^2} \right) , \mathrm{~~with~~}v=11.31\nonumber \\&-4.847\exp (-0.1378~w^{0.7338}). \end{aligned}$$

(21)

Figure 6 shows that the viscosity values using the fit function (dot-dashed curves) overlap with the exact CE results (solid curves) regardless of the cross section value.

The AMPT model results in Sect. 4 have been obtained at $\sigma =3$ mb, because this value enables the string melting version of the AMPT model to approximately reproduce the elliptic flow data at low $p_T$ [7, 19]. In the AMPT model with the new quark coalescence that allows a parton to have the freedom to form either a meson or a baryon [44], a smaller parton cross section of $\sigma =1.5$ mb is found to approximately reproduce the elliptic flow data. In that case, the shear viscosity would be higher (by a factor between one and two), as shown by the two solid curves in Fig. 6.

Fig. 6

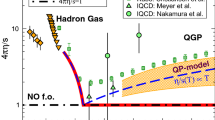
The shear viscosity versus temperature for a QGP in full equilibrium under forward-angle scatterings at $\sigma =3$ mb with $\alpha _s=0.33$. Results from the IS method, the CE method, and a fit of the CE result are shown, together with the estimated shear viscosity from Ref. [12] (long dashed curve) and the IS result (dashed curve) for $d\sigma ^\prime /d{{\hat{t}}}$. The CE results for $\sigma =1.5$ mb are also shown

An earlier study [12] used the IS method to estimate the shear viscosity and $\eta /s$ of the parton matter under forward scatterings of the AMPT model. A recent study [45] used the same estimates. They wrote the differential cross section as

$$\begin{aligned} \frac{d\sigma ^\prime }{d{{\hat{t}}}}=\frac{9\pi \alpha _s^2}{2} \frac{1}{({{\hat{t}}}-\mu ^2)^2}, \end{aligned}$$

(22)

i.e., the same as Eq. (1) except for the factor $(1+a)$. Note that the total cross section in this case would be given by $\sigma ^\prime =\sigma /(1+a)$ [21], which depends on energy or temperature. They further approximated the thermal average of the transport cross section as $\langle \sigma ^\prime h(a) \rangle \simeq \sigma ^\prime h(a) |_{a \rightarrow \mu ^2/\langle {{\hat{s}}} \rangle }$, where $\langle {{\hat{s}}} \rangle =18T^2$. The shear viscosity is then estimated as [12]

$$\begin{aligned} \eta ^\prime \simeq \frac{4~T^3}{5\pi \alpha _s^2\left[ \left( 1+\frac{\mu ^2}{9T^2} \right) \ln \left( 1+\frac{18T^2}{\mu ^2} \right) -2 \right] }. \end{aligned}$$

(23)

This estimated viscosity $\eta ^\prime$ for $\sigma =3$ mb and $\alpha _s=0.33$ is shown as the long dashed curve in Fig. 6. When we perform the proper thermal average of the transport cross section instead of approximating it with $a \rightarrow \mu ^2/\langle {{\hat{s}}} \rangle$, we get the IS viscosity for $d\sigma ^\prime /d{{\hat{t}}}$ as shown by the dashed curve in Fig. 6. We see that for $d\sigma ^\prime /d{{\hat{t}}}$ the estimated $\eta ^\prime$ is higher (or lower) than the IS curve at high (or low) temperatures, reflecting the inaccuracy of the approximation of the thermal average in $\eta ^\prime$. We also see that the IS curve for $d\sigma ^\prime /d{{\hat{t}}}$ approach the IS curve for $d\sigma /d{{\hat{t}}}$ of Eq. (1) (dotted curve) at high temperatures since $(1+\mu ^2/{{\hat{s}}}) \sim 1$ there, while at low temperatures $\eta ^{\mathrm {IS}}$ for $d\sigma ^\prime /d{{\hat{t}}}$ is much higher due to its smaller total cross section.

In this study we have only used the first-order Chapman–Enskog expression for the shear viscosity, which is $\eta ^{\mathrm {CE}}=(6/5)T/\sigma$ for isotropic scatterings. Higher-order CE terms have been derived earlier [29] and shown to only have a small effect. For example, for massless particles under isotropic scatterings, including the second-order term changes the $\eta ^{\mathrm {CE}}$ front coefficient from 6/5 to 1.256 while including terms up to the 16th order only changes the front coefficient to 1.268. Note that there is a typo in Eq. (25) of Ref. [29] for the second-order CE term, where $\gamma _0^2c_{00}$ should be $\gamma _0^2c_{11}$; this typo has been corrected in Ref. [18].

6 Conclusion

In this study, we investigate the shear viscosity and the $\eta /s$ ratio of a massless parton matter under isotropic or forward-angle two-body scatterings. We first compare the analytical results from the Israel–Stewart, Navier–Stokes, relaxation time approximation, and Chapman–Enskog methods with the numerical results from the Green–Kubo relation. We confirm the earlier finding that only the Chapman–Enskog method agrees well with the numerical results for anisotropic scatterings. We then apply the Chapman–Enskog method to calculate the time evolution of the shear viscosity and $\eta /s$ of the center cell of the parton matter from the string melting AMPT model for central and midcentral Au + Au collisions at 200A GeV and Pb + Pb collisions at 2760A GeV. We approximate the parton matter as a quark–gluon plasma in thermal equilibrium at effective temperature $T_{\langle p_T\rangle }$ but in partial chemical equilibrium, where the energy density corresponds to a higher effective temperature $T_\epsilon$. Due to the partial equilibrium nature, we use temperature $T_{\langle p_T\rangle }$ to calculate the shear viscosity, which has a lower value than the case if the parton matter were in full equilibrium at temperature $T_\epsilon$. For the AMPT model that approximately reproduces the elliptic flow data at low transverse momentum with a parton cross section $\sigma =3$ mb, the average $\eta /s$ for each of the four collision systems is found to be very small, between one to two times $1/(4\pi )$. If the parton matter were in full thermal and chemical equilibrium, the average $\eta /s$ would be higher, around three times $1/(4\pi )$. In addition, the $\eta /s$ ratio from the current model decreases as the temperature increases, contrary to pQCD results that use temperature-dependent Debye masses. This is a result of the AMPT model using a constant Debye mass for parton scatterings, which could be an area for future improvements.