Walsh’s Conformal Map Onto Lemniscatic Domains for Polynomial Pre-images II

Abstract

We consider Walsh’s conformal map from the exterior of a set $E=\bigcup _{j=1}^{\ell }E_j$ consisting of $\ell$ compact disjoint components onto a lemniscatic domain. In particular, we are interested in the case when E is a polynomial preimage of $[-1,1]$, i.e., when $E=P^{-1}([-1,1])$, where P is an algebraic polynomial of degree n. Of special interest are the exponents and the centers of the lemniscatic domain. In the first part of this series of papers, a very simple formula for the exponents has been derived. In this paper, based on general results of the first part, we give an iterative method for computing the centers when E is the union of $\ell$ intervals. Once the centers are known, the corresponding Walsh map can be computed numerically. In addition, if E consists of $\ell =2$ or $\ell =3$ components satisfying certain symmetry relations then the centers and the corresponding Walsh map are given by explicit formulas. All our theorems are illustrated with analytical or numerical examples.

1 Introduction

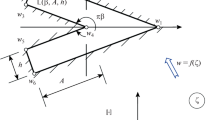
In his 1956 paper [23], Walsh obtained a canonical generalization of the Riemann mapping theorem from simply connected domains to multiply connected domains. In his construction, an $\ell$-connected domain in $\widehat{\mathbb {C}} \mathrel {\mathop :}=\mathbb {C}\cup \{ \infty \}$ is mapped onto the exterior of a generalized lemniscate, as indicated in the following theorem.

Theorem 1.1

Let $E_1, \ldots , E_\ell \subseteq \mathbb {C}$ be disjoint, simply connected, infinite compact sets and let

$$\begin{aligned} E = \bigcup _{j=1}^\ell E_j, \end{aligned}$$

(1.1)

that is, $E^{{\text {c}}} = \widehat{\mathbb {C}} \setminus E$ is an $\ell$-connected domain. Then there exists a unique compact set of the form

$$\begin{aligned} L \mathrel {\mathop :}=\{ w \in \mathbb {C}: \left| U(w)\right| \le {{\,\textrm{cap}\,}}(E) \}, \quad U(w) \mathrel {\mathop :}=\prod _{j=1}^\ell (w-a_j)^{m_j}, \end{aligned}$$

(1.2)

where $a_1, \ldots , a_\ell \in \mathbb {C}$ are distinct and $m_1, \ldots , m_\ell > 0$ are real numbers with $\sum _{j=1}^\ell m_j = 1$, and a unique conformal map

$$\begin{aligned} \Phi : E^{{\text {c}}} \rightarrow L^{{\text {c}}} \quad \text {with } \Phi (z) = z + \mathcal {O}\left( \frac{1}{z}\right) \text { at } \infty . \end{aligned}$$

(1.3)

If E is bounded by Jordan curves, then $\Phi$ extends to a homeomorphism from $\overline{E^{{\text {c}}}}$ to $\overline{L^{{\text {c}}}}$.

The compact set L in (1.2) consists of $\ell$ disjoint compact components $L_1, \ldots , L_\ell$, with $a_j \in L_j$ for $j = 1, \ldots , \ell$. The components $L_1, \ldots , L_\ell$ are labeled such that a Jordan curve surrounding $E_j$ is mapped by $\Phi$ onto a Jordan curve surrounding $L_j$. The centers $a_1, \ldots , a_\ell$ and the exponents $m_1, \ldots , m_\ell$ in Theorem 1.1 are uniquely determined. The domain $L^{{\text {c}}}$ is the exterior of the generalized lemniscate $\{ w \in \mathbb {C}: \left| U(w)\right| = {{\,\textrm{cap}\,}}(E) \}$ and is usually called a lemniscatic domain; see [5, p. 106]. Here, ${{\,\textrm{cap}\,}}(E)$ denotes the logarithmic capacity of E.

Walsh’s conformal map onto a lemniscatic domain is a canonical generalization of the Riemann map. Indeed, if $\ell = 1$ in Theorem 1.1, i.e., if E is simply connected, the exterior Riemann map $\mathcal {R}_E: E^{{\text {c}}} \rightarrow \overline{\mathbb {D}}^{{\text {c}}}$, uniquely determined by the normalization $\mathcal {R}_E(z) = d_1 z + d_0 + \mathcal {O}(1/z)$ at infinity with $d_1 > 0$, satisfies $\mathcal {R}_E(z) = d_1 \Phi (z) + d_0$, which follows from [23, Thm. 4]; see also [18, Rem. 1.2]. Thus, $\mathcal {R}_E$ and $\Phi$ are related by a simple linear transformation, and $L = \{ w \in \mathbb {C}: \left| w - a_1\right| \le {{\,\textrm{cap}\,}}(E) \}$ is a disk, where $a_1 = - d_0/d_1$ and ${{\,\textrm{cap}\,}}(E) = 1/d_1$.

The reason why we are interested in Walsh’s conformal map is that the lemniscatic domain $L^{{\text {c}}}$ in (1.2) has a very simple form and is in particular (the exterior of) a classical lemniscate if the exponents $m_1, \ldots , m_\ell$ in (1.2) are rational. In addition, as in the case of the Riemann map where the Green’s function for the complement of the unit disk is simply $\log \left| w\right|$, also the Green’s function for the complement of L in (1.2) has the simple form

$$\begin{aligned} g_L(w) = \log \left| U(w)\right| - \log ({{\,\textrm{cap}\,}}(E)) = \sum _{j=1}^\ell m_j \log \left| w - a_j\right| - \log ({{\,\textrm{cap}\,}}(E)) \end{aligned}$$

(1.4)

and $g_E(z) = g_L(\Phi (z))$ holds with $\Phi$ from Theorem 1.1. Moreover, Walsh’s conformal map allows the construction of Faber–Walsh polynomials on sets E with several components as in Theorem 1.1, generalizing the well-known Faber polynomials and the classical Chebyshev polynomials of the first kind; see Walsh’s original article [24], the book of Suetin [21], and the article [20].

After Walsh’s seminal paper [23], further existence proofs of Theorem 1.1 were published by Grunsky [3,4,5], Jenkins [6], and Landau [10]. The latter contains an iteration for computing Walsh’s map, but it requires knowledge of the harmonic measure of the boundary. None of these papers contain any explicit example, which might be the reason that Walsh’s map has not been widely used so far. However, in Walsh’s Selected Papers [25, pp. 374–377], Gaier recognizes Walsh’s conformal map onto lemniscatic domains as one of Walsh’s major contributions. The first explicit examples of Walsh’s map were derived in [19] and applied in [20] for polynomial approximation on disconnected compact sets. In [13], Nasser, Liesen and the second author obtained a numerical method for computing Walsh’s conformal map for sets E bounded by smooth Jordan curves. The method relies on solving a boundary integral equation (BIE) with the generalized Neumann kernel. This numerical algorithm also yields a method for the numerical computation of the logarithmic capacity of compact sets [11]. In [18], we obtained a characterization of the exponents $m_1, \ldots , m_\ell$ in terms of Green’s function and derived explicit formulas and examples of conformal maps onto lemniscatic domains for polynomial pre-images E.

One main objective is the actual computation of the lemniscatic domain L, that is, the computation of the exponents $m_j$ and the centers $a_j$, and of the conformal map $\Phi$. In this paper, we consider this question for sets E that are polynomial pre-images of ${[} {-1, 1} {]}$, i.e., $E = P^{-1}({[} {-1, 1} {]})$, where P is an algebraic polynomial of degree n. The set $P^{-1}({[} {-1, 1} {]})$ consists of $\ell$ components, $1 \le \ell \le n$, where each component consists of a certain number of analytic Jordan arcs [17]. In particular, the components $E_j$ of $P^{-1}({[} {-1, 1} {]})$ are not bounded by Jordan curves and thus the BIE method for computing $\Phi$ and L from [13] does not apply here.

This paper is the second of a series of papers. In the first part [18], we characterized the exponents as $m_j = n_j/n$, where $n_j$ is the number of zeros of the polynomial P in the component $E_j$ and n is the degree of the polynomial P. Moreover, we derived some general characterizations for the centers $a_1, \ldots , a_\ell$ and considered the cases $\ell = 1$ and $\ell = 2$ in more detail.

Building on these results, the main contributions in this paper are the following.

(1) In Sect. 3, we consider sets E consisting of $\ell = 2$ real intervals, or, more generally, of two components that are symmetric with respect to the real line. For these sets, we have explicit formulas for the centers $a_1, a_2$ (Theorem 3.1). If, in addition, the set E is symmetric with respect to the origin then the corresponding Walsh map $\Phi$ can be given explicitly; see Theorem 3.3 and the following two examples.

(2) In Sect. 4, we consider sets E consisting of $\ell = 3$ real intervals. In this case, the centers $a_1, a_2, a_3$ are the solution of a non-linear system of three equations, which can be solved numerically. This is illustrated in Example 4.1 considering a two-parameter family of three intervals. If, in addition, the set E is symmetric with respect to the origin then $a_1, a_2, a_3$ can be given by an explicit formula. In either case, the conformal map $\Phi$ can be computed numerically by solving a polynomial equation and using the mapping properties of $\Phi$ in Theorem 2.1.

(3) In Sect. 5, we propose an iterative method for the computation of $a_1, \ldots , a_\ell$ for sets E consisting of an arbitrary number $\ell \ge 1$ of real intervals, or, more generally, of $\ell$ components symmetric with respect to the real line. The key idea is that $a_1, \ldots , a_\ell$ are the zeros of a certain polynomial with prescribed critical values but unknown critical points, with an additional constraint on $a_1, \ldots , a_\ell$. Once the centers $a_j$ of L are computed, the conformal map $\Phi$ can be evaluated numerically. The iterative method for the computation of $a_1, \ldots , a_\ell$ works for an arbitrary number of intervals. In all our numerical examples, the method converges in very few iteration steps (at most 7 steps for up to 20 intervals) and returns highly accurate approximations of $a_1, \ldots , a_\ell$. In all examples where $a_1, \ldots , a_\ell$ are known explicitly, the computed values have an error of the order of the machine precision. In those examples, where the exact values of $a_1, \ldots , a_\ell$ are not known explicitly, the values obtained with our new method agree to order $10^{-14}$ with those obtained by a modification of the BIE method from [13]. This suggests that both methods are very accurate.

In Sect. 2, we first collect results on Walsh’s conformal map $\Phi$ and the lemniscatic domain for general compact sets E with certain symmetries. Second, we recall known important facts on sets E which are polynomial pre-images. In Appendix A, a rather general result concerning symmetric sets is proven, which is needed for the proofs in Sects. 3 and 4.

2 General Compact Sets and Polynomial Pre-Images

2.1 Results for General Compact Sets

For a set $K \subseteq \widehat{\mathbb {C}}$, we denote as usual $K^* \mathrel {\mathop :}=\{ \overline{z}: z \in K \}$ and $-K \mathrel {\mathop :}=\{ -z: z \in K \}$. If $K \subseteq \mathbb {C}$ is compact then the Green’s function (with pole at infinity) of $K^{{\text {c}}}$ is denoted by $g_K$. If $E = E_1 \cup \cdots \cup E_\ell$ and $E_j^* = E_j$ for all components of E then we label the components “from left to right”: By [18, Lem. A.2], each $E_j \cap \mathbb {R}$ is a point or an interval, and we label $E_1, \ldots , E_\ell$ such that $x \in E_j \cap \mathbb {R}$ and $y \in E_{j+1} \cap \mathbb {R}$ implies $x < y$ for all $j = 1, \ldots , \ell -1$. As a first result, let us collect some mapping properties of $\Phi$ if the set E has certain symmetries.

Theorem 2.1

Let the notation be as in Theorem 1.1.

• (i) If $E^* = E$, then $\Phi (z) = \overline{\Phi (\overline{z})}$, $\Phi (\mathbb {R}{\setminus } E) = \mathbb {R}{\setminus } L$, and $\Phi$ maps the upper (lower) half-plane without E bijectively onto the upper (lower) half-plane without L.

• (ii) If $E = -E^*$, i.e., E is symmetric with respect to the imaginary axis, then $\Phi (z) = -\overline{\Phi (-\overline{z})}$, $\Phi ( {{\text {i}}}\mathbb {R}{\setminus } E) = {{\text {i}}}\mathbb {R}{\setminus } L$, and $\Phi$ maps the left (right) half-plane without E bijectively onto the left (right) half-plane without L.

• (iii) If $E^* = E$ and $E = -E$, then $\Phi (\mathbb {R}^{\pm } {\setminus } E) = \mathbb {R}^{\pm } {\setminus } L$, $\Phi ( {{\text {i}}}\mathbb {R}^{\pm } {\setminus } E) = {{\text {i}}}\mathbb {R}^{\pm } {\setminus } L$, and $\Phi (z)$ is in the same quadrant as z.

• (iv) Assume that $E_j^* = E_j$ for $j = 1, \ldots , \ell$. Let $\mathbb {R}\setminus E = I_0 \cup \cdots \cup I_\ell$ with open intervals $I_j$ ordered from left to right, and let similarly $\mathbb {R}{\setminus } L = J_0 \cup \cdots \cup J_\ell$ with open intervals $J_j$ ordered from left to right. Then $\Phi$ maps $I_j$ onto $J_j$, that is $\Phi (I_j) = J_j$ for $j = 0, \ldots , \ell$, and $\Phi$ is strictly increasing on $\mathbb {R}\setminus E$, and in particular on each interval $I_j$.

• (v) Assume that $E_j^* = E_j$ for $j = 1, \ldots , \ell$. Then the Green’s function $g_E$ has $\ell -1$ critical points $z_1, \ldots , z_{\ell -1} \in \mathbb {C}{\setminus } E$. These are simple and satisfy $z_j \in I_j$ for $j = 1, \ldots , \ell -1$. Moreover, $\Phi (z_j) = w_j \in J_j$ are the critical points of $g_L$. In particular, if $z \in I_j$ with $z < z_j$ (resp. $z > z_j$) then $w = \Phi (z) \in J_j$ with $w < w_j$ (resp. $w > w_j$), and

  $$\begin{aligned} a_1< w_1< a_2< w_2< \ldots< w_{\ell -1} < a_\ell . \end{aligned}$$

  (2.1)

Proof

(i) Since $E^* = E$, we have $\Phi (z) = \overline{\Phi (\overline{z})}$ for $z \in \mathbb {C}\setminus E$ by [19, Lem. 2.2], hence $\Phi (z) \in \mathbb {R}$ if and only if $z \in \mathbb {R}$. Then the normalization $\Phi (z) = z + \mathcal {O}(1/z)$ at infinity implies that ${{\,\textrm{Im}\,}}(\Phi (z)) > 0$ for $z \in \mathbb {C}{\setminus } E$ with ${{\,\textrm{Im}\,}}(z) > 0$, and ${{\,\textrm{Im}\,}}(\Phi (z)) < 0$ for $z \in \mathbb {C}{\setminus } E$ with ${{\,\textrm{Im}\,}}(z) < 0$. (ii) Since $E = -E^*$, we have $\Phi (z) = -\overline{\Phi (-\overline{z})}$ for $z \in \mathbb {C}{\setminus } E$ by [19, Lem. 2.2], and (ii) now follows similarly to (i). (iii) follows from (i) and (ii). The assertions (iv) and (v) follow from [18, Thm. 2.8] and its proof. $\square$

In the next theorem, we consider sets E that are symmetric with respect to the origin and investigate the effect on the exponents $m_j$ and the centers $a_j$ of the lemniscatic domain.

Theorem 2.2

Let $E = \bigcup _{j=1}^\ell E_j$ be as in Theorem 1.1 with centers $a_1, \ldots , a_\ell$ and exponents $m_1, \ldots , m_\ell$ of L. If $E = -E$ and if $j_1, j_2$ are such that $E_{j_2} = - E_{j_1}$, then $m_{j_2} = m_{j_1}$ and $a_{j_2} = -a_{j_1}$. In particular, if $E_j = - E_j$, then $a_j = 0$. Moreover, the set of critical points of $g_E$ is symmetric with respect to zero.

Proof

If $E = -E$ then $\Phi (-z) = -\Phi (z)$ by [19, Lem. 2.2] or [18, Lem. 2.6], and $g_E(-z) = g_E(z)$ since $g_E(z)$ and $g_E(-z)$ both satisfy the properties of the Green’s function, hence, in particular, $(\partial _z g_E)(-z) = - (\partial _z g_E)(z)$. This shows that the set of critical points of $g_E$ is symmetric with respect to zero. Next, let $\gamma$ be a smooth closed curve in $\mathbb {C}{\setminus } E$ with ${{\,\textrm{wind}\,}}(\gamma ; z) = \delta _{j_1,k}$ for $z \in E_k$, then $-\gamma$ surrounds the component $-E_{j_1} = E_{j_2}$. We use [18, Thm. 2.3] and the substitution $z = -u$ to obtain

$$\begin{aligned} m_{j_2}&= \frac{1}{2 \pi {{\text {i}}}} \int _{-\gamma } 2 (\partial _z g_E)(z) \, {{\text {d}}}z = -\frac{1}{2 \pi {{\text {i}}}} \int _\gamma 2 (\partial _z g_E)(-u) \, {{\text {d}}}u \\&= \frac{1}{2 \pi {{\text {i}}}} \int _\gamma 2 (\partial _z g_E)(u) \, {{\text {d}}}u = m_{j_1}. \end{aligned}$$

Similarly,

$$\begin{aligned} m_{j_2} a_{j_2}&= \frac{1}{2 \pi {{\text {i}}}} \int _{-\gamma } \Phi (z) 2 (\partial _z g_E)(z) \, {{\text {d}}}z = -\frac{1}{2 \pi {{\text {i}}}} \int _\gamma \Phi (-u) 2 (\partial _z g_E)(-u) \, {{\text {d}}}u \\&= - \frac{1}{2 \pi {{\text {i}}}} \int _\gamma \Phi (u) 2 (\partial _z g_E)(u) \, {{\text {d}}}u = - m_{j_1} a_{j_1}, \end{aligned}$$

hence $a_{j_2} = - a_{j_1}$. $\square$

2.2 Results for Polynomial Pre-Images of an Interval

We consider polynomial pre-images of ${[} {-1, 1} {]}$, that is,

$$\begin{aligned} E \mathrel {\mathop :}=P^{-1}({[} {-1, 1} {]}) = \bigcup _{j=1}^\ell E_j, \end{aligned}$$

(2.2)

where P is a polynomial of degree $n \ge 1$ with complex coefficients of the form

$$\begin{aligned} P(z) = \sum _{j=0}^n p_j z^j = p_n z^n + p_{n-1} z^{n-1} + \cdots + p_0 \quad \text {with } p_n \ne 0. \end{aligned}$$

(2.3)

Each component $E_j$ consists of a certain number of analytic Jordan arcs, see [17] for details, and $E^{{\text {c}}}$ is connected; see [18, Thm. A.4] or [17, Lem. 1 (viii)]. All zeros of P are in E and each $E_j$ contains at least one zero of P, compare [18, Thm. 3.1]. By [15, Proof of Thm. 5.2.5], the Green’s function of $E^{{\text {c}}}$ is given by

$$\begin{aligned} g_E(z) = \frac{1}{n} \log \bigl |P(z) + \sqrt{P(z)^2-1} \bigr |, \quad z \in \mathbb {C}\setminus E, \end{aligned}$$

(2.4)

where $\sqrt{P(z)^2 - 1}$ has a branch cut along E and behaves as P(z) at $\infty$; compare also the beginning of [18, Sect. 3]. Note that the critical points of $g_E$ are the critical points of P in $\mathbb {C}\setminus E$. Again by [15, Thm. 5.2.5], the logarithmic capacity of E is

$$\begin{aligned} {{\,\textrm{cap}\,}}(E) = \frac{1}{\root n \of {2 \left| p_n\right| }}. \end{aligned}$$

(2.5)

In the next theorem, we summarize results from [18] that are needed in the sequel.

Theorem 2.3

Let E be a polynomial pre-image as in (2.2).

• (i) The set E has $\ell$ connected components if and only if P has exactly $\ell -1$ critical points $z_1, \ldots , z_{\ell -1}$ (counting multiplicities) for which $P(z_k) \notin {[} {-1, 1} {]}$ for $k = 1, \ldots , \ell -1$.

• (ii) The exponents $m_j$ in Theorem 1.1 are given by

  $$\begin{aligned} m_j = \frac{n_j}{n}, \quad j = 1, \ldots , \ell , \end{aligned}$$

  (2.6)

  where $n_j \ge 1$ is the number of zeros of P in $E_j$.

• (iii) For $z \in E^{{\text {c}}}$, we have

  $$\begin{aligned} Q(\Phi (z)) = P(z) + \sqrt{P(z)^2 - 1} \end{aligned}$$

  (2.7)

  with the polynomial

  $$\begin{aligned} Q(w) \mathrel {\mathop :}=\frac{{{\text {e}}}^{{{\text {i}}}\arg (p_n)}}{{{\,\textrm{cap}\,}}(E)^n} U(w)^n = 2 p_n \prod _{j=1}^\ell (w-a_j)^{n_j}. \end{aligned}$$

  (2.8)

  Moreover,

  $$\begin{aligned} L = \{ w \in \mathbb {C}: \left| Q(w)\right| \le 1 \}, \end{aligned}$$

  (2.9)

  compare (1.2).

• (iv) A point $z \in \mathbb {C}\setminus E$ is a critical point of P if and only if $w = \Phi (z)$ is a critical point of Q in $\mathbb {C}{\setminus } L$, and

  $$\begin{aligned} Q(w) = P(z) + \sqrt{P(z)^2 - 1}. \end{aligned}$$

  (2.10)

• (v) The polynomial Q has $\ell -1$ critical points in $\mathbb {C}\setminus L$ and these are the zeros of

  $$\begin{aligned} \sum _{k=1}^\ell n_k \prod _{\begin{array}{c} j=1 \\ j \ne k \end{array}}^\ell (w - a_j). \end{aligned}$$

  (2.11)

Proof

The exterior Riemann map of ${[} {-1, 1} {]}$ is ${{\,\mathrm{\mathcal {R}}\,}}: {[} {-1, 1} {]}^{{\text {c}}} \rightarrow \overline{\mathbb {D}}^{{\text {c}}}$, ${{\,\mathrm{\mathcal {R}}\,}}(z) = z + \sqrt{z^2 - 1}$, where $\sqrt{z^2 - 1}$ has a branch cut along ${[} {-1, 1} {]}$ and behaves as z at $\infty$. Then (i) follows from [18, Thm. 3.1], (ii) from [18, Thm. 3.2], (iii) from [18, Thm. 3.3], (iv) and (v) from [18, Lem. 3.5]. $\square$

Since the exponents $m_j$ are determined in Theorem 2.3 (ii), let us turn our attention to the determination of the centers $a_j$. If all components $E_j$ of E are symmetric with respect to the real line, we know that $a_1, \ldots , a_\ell$ are the solution of a certain non-linear system of equations.

Theorem 2.4

Let P be a polynomial of degree $n \ge 1$ such that $E = P^{-1}({[} {-1, 1} {]}) = E_1 \cup \cdots \cup E_\ell$ with $E_j^* = E_j$ for $j = 1, \ldots , \ell$. Then $a_1, \ldots , a_\ell$ are real with $a_1< \ldots < a_\ell$, the polynomial Q(w) in (2.8) has exactly $\ell -1$ critical points $w_1, \ldots , w_{\ell -1} \in \mathbb {C}{\setminus } L$, and these are real, simple with $a_1< w_1< a_2< w_2< a_3< \ldots < a_\ell$. Similarly, P has $\ell -1$ critical points $z_1, \ldots , z_{\ell -1}$ in $\mathbb {C}\setminus E$, these are real, simple and satisfy

$$\begin{aligned} \max (E_j \cap \mathbb {R})< z_j < \min (E_{j+1} \cap \mathbb {R}), \quad j = 1, \ldots , \ell -1. \end{aligned}$$

(2.12)

Moreover, $a_1, \ldots , a_\ell$ satisfy the system of equations

$$\begin{aligned} Q(w_j)&= P(z_j) + \sqrt{P(z_j)^2 - 1}, \qquad j = 1, \ldots , \ell -1, \end{aligned}$$

(2.13)

$$\begin{aligned} \sum _{j=1}^\ell n_j a_j&= - \frac{p_{n-1}}{p_n}. \end{aligned}$$

(2.14)

Proof

The first part follows immediately from Theorem 2.1 (v). In particular, $\Phi (z_j) = w_j$ for $j = 1, \ldots , \ell -1$. Then, (2.13) follows from Theorem 2.3 (iv), and (2.14) follows from [18, Thm. 3.3]. $\square$

Equations (2.13)–(2.14) are a non-linear system of equations for $a_1, \ldots , a_\ell$, provided that the critical points $w_1, \ldots , w_{\ell -1}$ of Q outside L can be expressed explicitly in terms of $a_1, \ldots , a_\ell$; see (2.11). This is possible for $\ell = 2$ and $\ell = 3$, and we consider these cases in Sects. 3 and 4. For larger $\ell$, this is no longer practical. In Sect. 5, we develop a numerical method to compute $a_1, \ldots , a_\ell$ for arbitrary $\ell \ge 1$.

Before we start this investigation, let us conclude this section with a theorem which gives a necessary and sufficient condition for a union of real intervals to be a polynomial pre-image of ${[} {-1, 1} {]}$, and which follows from [14, Lem. 2.1]; see also [16, Lem. 1].

Theorem 2.5

The set

$$\begin{aligned} E \mathrel {\mathop :}={[} {c_1, c_2} {]} \cup {[} {c_3, c_4} {]} \cup {[} {c_5, c_6} {]} \cup \cdots \cup {[} {c_{2n-1}, c_{2n}} {]} \end{aligned}$$

(2.15)

with

$$\begin{aligned} c_1< c_2 \le c_3< c_4 \le c_5< c_6 \le \ldots \le c_{2n-1} < c_{2n} \end{aligned}$$

(2.16)

is the pre-image of ${[} {-1, 1} {]}$ under a polynomial P of degree n, that is, $E = P^{-1}({[} {-1, 1} {]})$, if and only if $c_1, \ldots , c_{2n}$ satisfy the following system of equations:

$$\begin{aligned}{} & {} c_1^k - (c_2^k + c_3^k) + (c_4^k + c_5^k) - (c_6^k + c_7^k) {\pm } \cdots + (-1)^{n-1} (c_{2n-2}^k + c_{2n-1}^k) \nonumber \\{} & {} \quad + (-1)^n c_{2n}^k = 0 \end{aligned}$$

(2.17)

for $k = 1, 2, \ldots , n-1$.

Remark 2.6

• (i) The set E in Theorem 2.5 is the union of $\ell$ disjoint intervals, where $\ell \in \{ 1, 2, \ldots , n \}$, that is, E has $\ell -1$ gaps.

• (ii) With the help of $c_1, \ldots , c_{2n}$ satisfying (2.17), the corresponding polynomial P of degree n (unique up to sign) can be given by

  $$\begin{aligned} \begin{aligned} P(z)&= 1 - 2 \frac{(z-c_1) (z - c_4) (z - c_5) (z - c_8) (z - c_9) \cdots }{(c_2 - c_1) (c_2 - c_4) (c_2 - c_5) (c_2 - c_8) (c_2 - c_9) \cdots } \\&= -1 + 2 \frac{(z-c_2) (z - c_3) (z - c_6) (z - c_7) (z - c_{10}) (z - c_{11}) \cdots }{(c_1-c_2) (c_1 - c_3) (c_1 - c_6) (c_1 - c_7) (c_1 - c_{10}) (c_1 - c_{11}) \cdots }. \end{aligned}\nonumber \\ \end{aligned}$$

  (2.18)

  Note that P(z) and $-P(z)$ generate the same pre-image E.

• (iii) Figure 1 shows the real graph of a polynomial of degree $n = 7$ whose pre-image consists of the $\ell = 4$ disjoint intervals $E = {[} {c_1, c_4} {]} \cup {[} {c_5, c_6} {]} \cup {[} {c_7, c_{12}} {]} \cup {[} {c_{13}, c_{14}} {]}$, which has been computed with the help of (2.17) and (2.18).

Fig. 1

Real graph of a polynomial P of degree $n = 7$ whose pre-image of ${[} {-1, 1} {]}$ consists of $\ell = 4$ intervals; see Example 5.4 for the explicit formula of P

3 Sets with Two Components

If the polynomial pre-image $E = P^{-1}({[} {-1, 1} {]})$ has two components that are symmetric with respect to the real line, the centers $a_1, a_2$ are given explicitly in Theorem 3.1, which follows from the more general result in [18, Cor. 3.10]. This covers the important case that E consists of two real intervals, that is, $E = {[} {b_1, b_2} {]} \cup {[} {b_3, b_4} {]}$ with $b_1< b_2< b_3 < b_4$.

Theorem 3.1

Let P be a polynomial of degree $n \ge 1$ as in (2.3) with either real or purely imaginary coefficients such that $E = P^{-1}({[} {-1, 1} {]}) = E_1 \cup E_2$ with $E_1^* = E_1$ and $E_2^* = E_2$. Let $n_1, n_2$ be the number of zeros of P in $E_1$, $E_2$, respectively, and let $z_1$ be the critical point of P in $\mathbb {C}\setminus E$. Then the points $a_1, a_2$ are real with $a_1 < a_2$ and are given by

$$\begin{aligned} \begin{aligned} a_1&= - \frac{p_{n-1}}{n p_n} - \bigg ( \left( \frac{n_2}{n_1} \right) ^{n_1} \frac{(-1)^{n_2}}{2 p_n} \Big ( P(z_1) + \sqrt{P(z_1)^2 - 1} \Big ) \bigg )^{1/n},\\ a_2&= - \frac{p_{n-1}}{n p_n} + \bigg ( \left( \frac{n_1}{n_2} \right) ^{n_2} \frac{(-1)^{n_2}}{2 p_n} \Big ( P(z_1) + \sqrt{P(z_1)^2 - 1} \Big ) \bigg )^{1/n}, \end{aligned} \end{aligned}$$

(3.1)

with the positive real n-th root in (3.1).

In the following example for a one-parameter family of two intervals, we apply the formulas of Theorem 3.1 in order to obtain the lemniscatic domain and compute the corresponding conformal map $\Phi$.

Example 3.2

For $0< \alpha < 1$, consider the polynomial

$$\begin{aligned} P(z) = 1 + \frac{(z-1) (2 z + 1 + \alpha ^2)^2}{(1-\alpha ^2)^2} = \frac{4 z^3 + 4 \alpha ^2 z^2 + (\alpha ^4 - 2 \alpha ^2 + 3) z - 4 \alpha ^2}{(1-\alpha ^2)^2} \end{aligned}$$

of degree $n = 3$. It is easy to see that $E = P^{-1}({[} {-1, 1} {]}) = [-1, b_2] \cup [b_3, 1]$, where $b_2 = (1 - \alpha ^2)/2 - \alpha$, $b_3 = (1 - \alpha ^2)/2 + \alpha$. We have $n_1 = 2$, $n_2 = 1$, $p_3 = 4/(1-\alpha ^2)^2$, $p_2 = 4 \alpha ^2/(1-\alpha ^2)^2$, and the critical point of P outside E is $z_1 = (3 - \alpha ^2)/6$. Then, using the correct branch of the square root as indicated after (2.4), we obtain

$$\begin{aligned} P(z_1) + \sqrt{P(z_1)^2 - 1}&= - \frac{2 \alpha ^6 - 9 \alpha ^4 + 108 \alpha ^2 + 27 + 2 \alpha (9 - \alpha ^2) (3 + \alpha ^2)^{3/2}}{27 (1 - \alpha ^2)^2}. \end{aligned}$$

By (3.1), the centers are

$$\begin{aligned} a_1&= - \frac{\alpha ^2}{3} - \frac{1}{6 \root 3 \of {4}} \Big ( 2 \alpha ^6 - 9 \alpha ^4 + 108 \alpha ^2 + 27 + 2 \alpha (9 - \alpha ^2) (3 + \alpha ^2)^{3/2} \Big )^{1/3}, \\ a_2&= - \frac{\alpha ^2}{3} + \frac{1}{3 \root 3 \of {4}} \Big ( 2 \alpha ^6 - 9 \alpha ^4 + 108 \alpha ^2 + 27 + 2 \alpha (9 - \alpha ^2) (3 + \alpha ^2)^{3/2} \Big )^{1/3}. \end{aligned}$$

By Theorem 2.3 (iii), we have $L = \{ w \in \mathbb {C}: \left| w - a_1\right| ^2 \left| w - a_2\right| \le (1-\alpha ^2)^2/8 \}$. In order to compute $w = \Phi (z)$ for $z \in \mathbb {C}{\setminus } E$, we solve the equation

$$\begin{aligned} 2 p_n (w - a_1)^2 (w - a_2) = P(z) + \sqrt{P(z)^2 - 1}, \end{aligned}$$

Fig. 2

Illustration of the Walsh map $\Phi$ for $E = {[} {-1, b_2} {]} \cup {[} {b_3, 1} {]}$ with $b_2 = (1 - \alpha ^2)/2 - \alpha$ and $b_3 = (1 - \alpha ^2)/2 + \alpha$ for $\alpha = 0.1, 0.05, 0.01$ (from top to bottom); see Example 3.2. Left: Original domain with intervals (black) and a grid. Right: $\partial L$ (black) and image of the grid under $\Phi$

see Theorem 2.3 (iii). We use the mapping properties of $\Phi$ established in Theorem 2.1 to determine the correct value of w. The image of $z_1$ is $w_1=(n_2 a_1 + n_1 a_2)/n$. For real z, if $z > 1$ then $w \in \mathbb {R}$ with $w > a_2$, if $z_1< z < b_3$ then $w_1< w < a_2$, if $b_2< z < z_1$ then $a_1< w < w_1$, and if $z < -1$ then $w < a_1$. If ${{\,\textrm{Im}\,}}(z) > 0$, we choose w with ${{\,\textrm{Im}\,}}(w) > 0$ that is closest to z. For the lower half-plane, we use $\Phi (\overline{z}) = \overline{\Phi (z)}$.

In the limiting case $\alpha \rightarrow 1$, we have $b_2 \rightarrow -1$, $b_3 \rightarrow 1$, E degenerates to the set $\{ -1, 1 \}$, and $a_1 \rightarrow -1$, $a_2 \rightarrow 1$. In the other limiting case $\alpha \rightarrow 0$, we have $b_2 \rightarrow 1/2$ and $b_3 \rightarrow 1/2$, so that E tends to the interval ${[} {-1, 1} {]}$, while $a_1 \rightarrow - 1/(2 \root 3 \of {4}) =\mathrel {\mathop :}a_1(0)$ and $a_2 \rightarrow 1/\root 3 \of {4} =\mathrel {\mathop :}a_2(0)$, so that the corresponding set L “converges” to $\{ w \in \mathbb {C}: |w + 1/(2 \root 3 \of {4})|^2 |w - 1/\root 3 \of {4}| \le 1/8 \}$, which is an “eight” self-intersecting at $w_1 = (n_2 a_1(0) + n_1 a_2(0))/n = 1/(2\root 3 \of {4})$, compare Fig. 2. However, the centers $a_1, a_2$ of L do not converge to the center $a_1 = 0$ of the lemniscatic domain $L = \{ w \in \mathbb {C}: \left| w\right| \le 1/2 \}$ corresponding to $E = {[} {-1, 1} {]}$. This shows that a discontinuity in the connectivity (in our example from $\ell = 2$ components to $\ell = 1$ component) leads to a discontinuity in the centers.

If the polynomial P is real and even, then $E = P^{-1}({[} {-1, 1} {]})$ is symmetric with respect to the real line as well as symmetric with respect to the origin, and we obtain an explicit formula for the conformal map $\Phi$.

Theorem 3.3

Let the polynomial $P(z) = \sum _{j=0}^n p_j z^j$ with $p_n \ne 0$ be real, even and assume that P has exactly one critical point $z_1$ with critical value $P(z_1) \notin {[} {-1, 1} {]}$ and $z_1$ is a simple zero of $P'$, that is $z_1 \notin E \mathrel {\mathop :}=P^{-1}({[} {-1, 1} {]})$ while the other $n-2$ critical points are in E. Then the following assertions hold:

• (i) The set E consists of two components, $E = E_1 \cup E_2$, where $E_1, E_2$ are simply connected disjoint infinite compact sets with $E_1 = - E_2$, and $E = -E$, $E^* = E$, and $0 \notin E$. In particular, only the following two cases can occur: $E_1^* = E_1$, $E_2^* = E_2$ (case 1), and $E_1^* = E_2$ (case 2).

• (ii) If $E_1^* = E_1$, $E_2^* = E_2$, then

  $$\begin{aligned} a_2 = \left( \frac{(-1)^{n/2}}{2 p_n} \left( p_0 + \sqrt{p_0^2 - 1} \right) \right) ^{1/n} > 0 \end{aligned}$$

  (3.2)

  and if $E_1^* = E_2$ then

  $$\begin{aligned} a_2 = {{\text {i}}}\left( \frac{1}{2 p_n} \left( p_0 + \sqrt{p_0^2 - 1} \right) \right) ^{1/n}, \end{aligned}$$

  (3.3)

  with the positive real n-th root in both cases. For $\sqrt{p_0^2 - 1}$, the positive branch is taken if $p_0 > 1$ and the negative branch if $p_0 < -1$. Moreover, in both cases, $a_1 = - a_2$ and

  $$\begin{aligned} L = \{ w \in \mathbb {C}: |w^2 - a_2^2|^{1/2} \le {{\,\textrm{cap}\,}}(E) = (2 \left| p_n\right| )^{-1/n} \}. \end{aligned}$$

  (3.4)

• (iii) The Walsh map of E is $\Phi : E^{{\text {c}}} \rightarrow L^{{\text {c}}}$,

  $$\begin{aligned} \Phi (z) = \sqrt{a_2^2 + \left( \frac{P(z)}{2 p_n} + \sqrt{\left( \frac{P(z)}{2 p_n} \right) ^2 - \frac{1}{4 p_n^2}} \right) ^{2/n}} \end{aligned}$$

  with that branch of the n-th root and of the outer square root which yields positive real values of $\Phi (z)$ for sufficiently large z on the positive real line.

Proof

(i) The fact that E has $\ell = 2$ components is an immediate consequence of Theorem 2.3 (i) since P has exactly one critical point outside E. Thus, $E = E_1 \cup E_2$ with disjoint, simply connected, infinite compact sets $E_1, E_2$. Since P is real and even, we have $E^* = E$ and $E = -E$. By Theorem A.1 (ii) and Corollary A.2, assertion (i) follows.

(ii) and (iii): The number of zeros of P in $E_1$ and in $E_2$ is the same, i.e., $n_1 = n_2 = n/2$. Since P is even, $z = 0$ is a critical point of P. Since $0 \notin E$, we have $z_1 = 0$ and thus $p_0 = P(0) \in \mathbb {R}{\setminus } {[} {-1, 1} {]}$.

We consider the two cases pointed out in (i).

Case 1: If $E_1^* = E_1$ and $E_2^* = E_2$ then (ii) is a direct consequence of Theorem 3.1 (where $p_{n-1} = 0$ since P is even). By (2.8), $Q(w) = 2 p_n (w^2 - a_2^2)^{n/2}$ and (iii) follows from Theorem 2.3 (iii). Note that $P(z)/(2 p_n)$ is a real polynomial with positive leading coefficient 1/2. Therefore, the complex roots have to be taken as indicated in the theorem.

Case 2: $E_1^* = E_2$. We reduce this case to case 1 as follows. The polynomial $\widetilde{P}(z) \mathrel {\mathop :}=P({{\text {i}}}z)$ also satisfies the assumptions of the theorem, and the set $\widetilde{E} = \widetilde{P}^{-1}({[} {-1, 1} {]}) ) = - {{\text {i}}}E$ falls under case 1, so that the corresponding set $\widetilde{L}$ and conformal map $\widetilde{\Phi }:\widetilde{E}^{{\text {c}}} \rightarrow \widetilde{L}^{{\text {c}}}$ are determined by the formulas in case 1. By [19, Lem. 2.3], we have $a_2 = {{\text {i}}}\widetilde{a}_2$ and $\Phi (z) = {{\text {i}}}\widetilde{\Phi }(- {{\text {i}}}z)$, which yields after a short calculation the formulas in case 2. $\square$

Remark 3.4

• (i) In Theorem 3.3, the following equivalence holds: E contains a real point if and only if $E_1^* = E_1$ and $E_2^* = E_2$, which follows from [18, Lem. A.2]. In more detail: If $x \in E \cap \mathbb {R}$, then without loss of generality, $x \in E_1$ and hence $x \in E_1^*$, hence $E_1 = E_1^*$. Conversely, if $E_1^* = E_1$ and $E_2^* = E_2$, both $E_1$ and $E_2$ contain at least one real point [18, Lem. A.2].

• (ii) If $E_1^* = E_1$, $E_2^* = E_2$ in Theorem 3.3 then $\partial L \cap \mathbb {R}$ consists of the four points $c_1< c_2< 0< c_3 < c_4$ with $c_1 = - c_4$, $c_2 = - c_3$ and

  $$\begin{aligned} c_{3,4} = \left( a_2^2 {\mp } (2 \left| p_n\right| )^{-2/n} \right) ^{1/2}. \end{aligned}$$

  Denote $E_1 \cap \mathbb {R}= {[} {b_1, b_2} {]}$ and $E_2 \cap \mathbb {R}= {[} {b_3, b_4} {]}$ with $b_1 \le b_2< 0 < b_3 \le b_4$; see [18, Lem. A.2]. Since $E_1 = -E_2$, we have $b_1 = -b_4$, $b_2 = -b_3$. Then, by Theorem 2.1 (iv) and (v), $\Phi ({]} {-\infty , b_1} {[}) = {]} {-\infty , c_1} {[}$, $\Phi ({]} {b_2, 0} {[}) = {]} {c_2, 0} {[}$, $\Phi ({]} {0, b_3} {[}) = {]} {0, c_3} {[}$, $\Phi ({]} {b_4, \infty } {[}) = {]} {c_4, \infty } {[}$. In addition, $\Phi$ satisfies $\Phi (0) = 0$, $\Phi ({{\text {i}}}\mathbb {R}^-) = {{\text {i}}}\mathbb {R}^-$, $\Phi ({{\text {i}}}\mathbb {R}^+) = {{\text {i}}}\mathbb {R}^+$.

• (iii) If $E_1^* = E_2$, the roles of $\mathbb {R}$ and ${{\text {i}}}\mathbb {R}$ in (ii) switch.

Let us consider two illustrative examples for Theorem 3.3.

Example 3.5

(Two symmetric real intervals) For $0< \alpha < \beta$, consider the polynomial

$$\begin{aligned} P(z) = \frac{2}{\beta ^2 - \alpha ^2} (z^2 - \beta ^2) + 1, \end{aligned}$$

of degree $n = 2$. Then $E = P^{-1}({[} {-1, 1} {]}) = {[} {-\beta , -\alpha } {]} \cup {[} {\alpha , \beta } {]}$, and $n_1 = n_2 = 1$. The critical point of P is $z_1 = 0 \notin E$, so that P satisfies the assumptions in Theorem 3.3. Since $p_0 = - (\beta ^2 + \alpha ^2)/(\beta ^2 - \alpha ^2) < -1$, we have $p_0 + \sqrt{p_0^2 - 1} = - (\beta + \alpha )/(\beta - \alpha )$. Hence, by (3.2), $a_2 = (\beta + \alpha )/2$ and $a_1 = -a_2$, so that $L = \big \{ w \in \mathbb {C}: |w - a_2^2|^{1/2} \le \sqrt{(\beta ^2 - \alpha ^2)/4} \big \}$. Since

$$\begin{aligned} P(z) + \sqrt{P(z)^2 - 1} = \frac{1}{\beta ^2 - \alpha ^2} \Big ( 2 z^2 - \alpha ^2 - \beta ^2 + 2 \sqrt{(z^2 - \alpha ^2)(z^2 - \beta ^2)} \Big ), \end{aligned}$$

we obtain

$$\begin{aligned} \Phi (z) = \frac{1}{\sqrt{2}} \sqrt{z^2 + \alpha \beta + \sqrt{(z^2 - \alpha ^2)(z^2 - \beta ^2)}} \end{aligned}$$

which is in accordance with [19, Cor. 3.3]. Figure 3 shows the sets E and L and the image of a grid under $\Phi$. For the numerical evaluation of $\Phi (z)$ we use the modified formula

$$\begin{aligned} \Phi (z) = z \sqrt{\frac{1}{z^2}{\left( a_2^2 + \frac{P(z) + \sqrt{P(z)^2 - 1}}{2p_n} \right) }}, \quad z \in \mathbb {C}\setminus E, z \ne 0, \end{aligned}$$

with the main branch of the square root, and $\Phi (0) = 0$; compare to [19, Thm. 3.1].

Fig. 3

$E = P^{-1}({[} {-1, 1} {]}) = {[} {-2, -0.2} {]} \cup {[} {0.2, 2} {]}$ in Example 3.5. Left: E (black) and a grid. Right: $\partial L$ (black), $a_1, a_2$ (black dots), and the image of the grid under $\Phi$

Example 3.6

Consider the polynomial

$$\begin{aligned} P(z) = (z^2 - \alpha ^2)^2 \end{aligned}$$

of degree $n=4$ with parameter $\alpha > 1$ and $E = P^{-1}({[} {-1, 1} {]})$. The critical points of P are $z_1 = 0$ and $z_{2,3} = {\pm } \alpha$ with the critical values $P(z_1) = \alpha ^4 > 1$ and $P(z_{2,3}) = 0$, hence $z_1 = 0 \notin E$ and $z_{2,3} \in E$ and the assumptions of Theorem 3.3 are satisfied. Since ${\pm } \alpha \in E$, by Theorem 3.3 and Remark 3.4 (i), we have the case $E_1^* = E_1$, $E_2^* = E_2$. Note that $E_1 = - E_2$. The component $E_2$ is the union of the interval ${[} {\sqrt{\alpha ^2 - 1}, \sqrt{\alpha ^2 + 1}} {]}$ and of a Jordan arc symmetric with respect to the real line with endpoints $b_3 = \sqrt{\alpha ^2 + {{\text {i}}}}$ and $b_4 = \overline{b}_3 = \sqrt{\alpha ^2 - {{\text {i}}}}$ (where ${{\,\textrm{Re}\,}}(b_3) > 0$) intersecting the interval at the critical point $\alpha$; see [17, Thm. 1]. By (3.2), the points $a_1, a_2$ are given by

$$\begin{aligned} a_2 = \left( \frac{1}{2} \bigl ( \alpha ^4 + \sqrt{\alpha ^8 - 1} \bigr ) \right) ^{1/4}, \quad a_1 = - a_2. \end{aligned}$$

The conformal map is given by

$$\begin{aligned} \Phi (z) = \frac{1}{2^{1/4}} \sqrt{\Bigl ( \alpha ^4 + \sqrt{\alpha ^8 - 1} \Bigr )^{1/2} + \Bigl ( (z^2 - \alpha ^2)^2 + \sqrt{(z^2 - \alpha ^2)^4 -1} \Bigr )^{1/2}}. \end{aligned}$$

See Fig. 4 for an illustration.

Fig. 4

Pre-image $E = P^{-1}({[} {-1, 1} {]})$ in Example 3.6 with $\alpha = 1.01$. Left: E (black lines) and a grid. Right: $\partial L$ (black curves), $a_1, a_2$ (black dots), and the image of the grid under $\Phi$

4 Sets with Three components

Let the polynomial P be given as in (2.3) and assume that E given in (2.2) has $\ell = 3$ components, that is, $E = P^{-1}({[} {-1, 1} {]}) = E_1 \cup E_2 \cup E_3$. Then Q(w) in (2.8) has the form

$$\begin{aligned} Q(w) = 2 p_n (w - a_1)^{n_1} (w - a_2)^{n_2} (w - a_3)^{n_3} \end{aligned}$$

(4.1)

with $n_1 + n_2 + n_3 = n$. Moreover, Q has two critical points $w_{1,2}$ in $\mathbb {C}\setminus L$ which are the solutions of

$$\begin{aligned} n_1 (w - a_2) (w - a_3) + n_2 (w - a_1) (w - a_3) + n_3 (w - a_1) (w - a_2) = 0, \end{aligned}$$

(4.2)

see Theorem 2.3 (v). A short computation shows that

$$\begin{aligned} \begin{aligned} w_{1,2}&= \frac{1}{2 n} \bigg ( (n_2 + n_3) a_1 + (n_1 + n_3) a_2 + (n_1 + n_2) a_3 \\&{\mp } \sqrt{ \bigl ( (n_2 + n_3) a_1 + (n_1 + n_3) a_2 + (n_1 + n_2) a_3 \bigr )^2 - 4 n (n_3 a_1 a_2 + n_2 a_1 a_3 + n_1 a_2 a_3)} \Big ). \end{aligned} \end{aligned}$$

(4.3)

If all three components $E_1, E_2, E_3$ of E are symmetric with respect to $\mathbb {R}$, then $a_1, a_2, a_3$ are the solution of the non-linear system of equations (2.13)–(2.14) in Theorem 2.4, which can be solved numerically; see the following example.

Example 4.1

Let us construct a polynomial pre-image $E = P^{-1}({[} {-1, 1} {]})$ consisting of three real intervals. By Theorem 2.5, the set

$$\begin{aligned} E = {[} {-1, \gamma _1 - \alpha } {]} \cup {[} {\gamma _1 + \alpha , \gamma _2 - \beta } {]} \cup {[} {\gamma _2 + \beta , 1} {]}, \end{aligned}$$

(4.4)

is the polynomial pre-image of a polynomial P of degree $n = 3$ if and only if $\alpha , \beta , \gamma _1, \gamma _2$ satisfy the equations

$$\begin{aligned} (-1)^k - (\gamma _1 - \alpha )^k - (\gamma _1 + \alpha )^k + (\gamma _2 - \beta )^k + (\gamma _2 + \beta )^k - 1^k = 0 \end{aligned}$$

(4.5)

for $k=1$ and $k=2$. Simplifying this system gives

$$\begin{aligned} \gamma _1 = \frac{1}{2} (\alpha ^2 - \beta ^2 - 1) \quad \text {and} \quad \gamma _2 = \frac{1}{2} (\alpha ^2 - \beta ^2 + 1). \end{aligned}$$

(4.6)

Hence, for $\alpha , \beta > 0$, $\alpha + \beta < 1$, and $\gamma _1, \gamma _2$ given by (4.6), the set (4.4) is a polynomial pre-image. By (2.18), the polynomial of degree $n=3$ (unique up to sign) with $E = P^{-1}({[} {-1, 1} {]})$ is given by

$$\begin{aligned} \begin{aligned} P(z)&= -1 - \frac{\bigl ((z - \gamma _1)^2 - \alpha ^2 \bigr ) (z - 1)}{(1 + \gamma _1)^2 - \alpha ^2} \\&= -\frac{z^3 + (\beta ^2 - \alpha ^2) z^2 + (\gamma _1^2 - \beta ^2 - 1) z + \alpha ^2 - \beta ^2}{(1+\gamma _1)^2 - \alpha ^2}. \end{aligned} \end{aligned}$$

In particular,

$$\begin{aligned} p_3 = - \frac{1}{(1 + \gamma _1)^2 - \alpha ^2}, \quad p_2 = - \frac{\beta ^2 - \alpha ^2}{(1 + \gamma _1)^2 - \alpha ^2}. \end{aligned}$$

The critical points of P are given by

$$\begin{aligned} z_{1,2} = \frac{1}{6} \bigl ( 2 \alpha ^2 - 2 \beta ^2 {\mp } \sqrt{\alpha ^4 - 2 \alpha ^2 (\beta ^2 - 3) + (\beta ^2 + 3)^2} \bigr ). \end{aligned}$$

Next, we compute $a_1, a_2, a_3$ for the set in (4.4). Note that $n_1 = n_2 = n_3 = 1$. Using (4.1) and (4.3), we can solve the system (2.13)–(2.14) numerically for $a_1$, $a_2$, $a_3$. Choosing numerical values, say $\alpha = 0.05$ and $\beta = 0.3$, yields

$$\begin{aligned} E = [ -1, -\tfrac{19}{20}] \cup [-\tfrac{79}{20}, \tfrac{5}{32}] \cup [\tfrac{121}{160}, 1] \end{aligned}$$

and

$$\begin{aligned} a_1 = -0.7751\ldots , \quad a_2 = -0.1648\ldots , \quad a_3 = 0.8525\ldots . \end{aligned}$$

The Mathematica command NSolve returns six distinct triples $(a_1, a_2, a_3)$, which are permutations of each other, where only one satisfies $a_1< a_2 < a_3$. Figure 5 illustrates the conformal map $\Phi$. We compute $w = \Phi (z)$ by solving $Q(w) = P(z) + \sqrt{P(z)^2 - 1}$ and determine the correct solution w (out of the $n = 3$ solutions) using the mapping properties of $\Phi$ in Theorem 2.1.

Fig. 5

Left: The set E in Example 4.1 with $\alpha = 0.05$ and $\beta = 0.3$ in black and a grid. Right: Corresponding lemniscatic domain ($\partial L$ in black), the points $a_1, a_2, a_3$ (black dots), and the image of the grid under $\Phi$

If E has “double symmetry”, that is, E is symmetric with respect to zero and each component is symmetric with respect to $\mathbb {R}$, then the centers $a_1$, $a_2$, $a_3$ can be given explicitly.

Theorem 4.2

Let $E = P^{-1}({[} {-1, 1} {]}) = E_1 \cup E_2 \cup E_3$ with $E = -E$ and $E_j^* = E_j$ for $j = 1, 2, 3$. Let $z_1 < z_2$ be the critical points of P in $\mathbb {R}\setminus E$. Then, $z_2 = -z_1$, $n_1 = n_3$, $a_1< a_2 = 0 < a_3$ with $a_1 = -a_3$ and

$$\begin{aligned} a_3 = \sqrt{n} \root n \of { \frac{\left| P(z_2) + \sqrt{P(z_2)^2 - 1}\right| }{2 \left| p_n\right| n_2^{n_2/2} (2n_3)^{n_3}} } \end{aligned}$$

(4.7)

with the positive real n-th root. In (4.7), $z_2$ can also be replaced by $z_1$.

Proof

By Theorem A.1, $E_1 = -E_3$ and $E_2 = -E_2$. By Theorem 2.2, $z_2 = -z_1$, $n_1 = n_3$, $a_1 = -a_3$ and $a_2 = 0$. By Theorem 2.1 (v), we have $a_1< a_2 = 0 < a_3$. Therefore, by (4.1), $Q(w) = 2 p_n w^{n_2} (w^2 - a_3^2)^{n_3}$, and, by (4.3), $w_{1,2} = {\mp } a_3 \sqrt{n_2/n}$, and

$$\begin{aligned} Q(w_{1,2}) = 2 p_n \left( {\mp } \sqrt{\frac{n_2}{n}} \right) ^{n_2} \left( - \frac{2 n_3}{n} \right) ^{n_3} a_3^n. \end{aligned}$$

Since $Q(w_{1,2}) = P(z_{1,2}) + \sqrt{P(z_{1,2})^2 - 1}$, see Theorem 2.4, and $a_3 > 0$, we obtain

$$\begin{aligned} a_3 = \root n \of {\left( \sqrt{\frac{n}{n_2}} \right) ^{n_2} \left( \frac{n}{2 n_3} \right) ^{n_3} \frac{1}{2 \left| p_n\right| } \left| P(z_2) + \sqrt{P(z_2)^2 - 1}\right| }, \end{aligned}$$

which implies (4.7). $\square$

Example 4.3

Let us construct a polynomial P of degree $n=3$ with a pre-image consisting of three symmetric intervals $E = [-1,-\beta ] \cup [-\alpha ,\alpha ] \cup [\beta ,1]$ with $0< \alpha< \beta < 1$. By Theorem 2.5, E is a polynomial pre-image if and only (2.17) holds, which is equivalent to $\beta = 1-\alpha$. This implies $0< \alpha < 1/2$. By Remark 2.6 (ii),

$$\begin{aligned} P(z) = -1 + 2 \frac{(z + 1)(z - \alpha ) (z - (1 - \alpha ))}{(-\beta +1) (-\beta -\alpha ) (-\beta - (1 - \alpha ))} = \frac{z^3 - (1-\alpha +\alpha ^2) z}{\alpha (1-\alpha )}\nonumber \\ \end{aligned}$$

(4.8)

satisfies $P^{-1}([-1,1]) = E = [-1,-(1-\alpha )]\cup [-\alpha ,\alpha ]\cup [1-\alpha ,1]$ with $n_1 = n_2 = n_3 = 1$. The critical points of P are $z_{1,2} ={\mp }\sqrt{(1-\alpha +\alpha ^2)/3}$. We have $a_2 = 0$, $a_1 = - a_3$ and, by (4.7),

$$\begin{aligned} a_3 = \sqrt{3} \root 3 \of { \frac{\alpha (1-\alpha )}{4} \Bigl |P(z_2) + \sqrt{P(z_2)^2 -1} \Bigr |}, \end{aligned}$$

where a short calculation shows

$$\begin{aligned} P(z_2) + \sqrt{P(z_2)^2 - 1} = \frac{2}{3 \sqrt{3}} \frac{(1-\alpha + \alpha ^2)^{3/2}}{\alpha (1-\alpha )} + \frac{2 - 3 \alpha - 3 \alpha ^2 + 2 \alpha ^3}{3 \sqrt{3} \alpha (1-\alpha )}. \end{aligned}$$

This yields the explicit formula

$$\begin{aligned} a_3 = \root 3 \of {\frac{1}{2} (1 - \alpha + \alpha ^2)^{3/2} + \frac{1}{4} (2 - 3 \alpha - 3 \alpha ^2 + 2 \alpha ^3)}, \end{aligned}$$

with positive real roots. Since $a_2 = 0$, $a_1 = - a_3$, and $n_1 = n_2 = n_3 = 1$, we have explicitly determined the canonical domain $L^{{\text {c}}}$.

In the limiting case $\alpha \rightarrow 0$, the set E degenerates to $\{ -1, 0, 1 \}$ and $a_3 \rightarrow 1$. In the other limiting case $\alpha \rightarrow 1/2$, the set E tends to the interval ${[} {-1, 1} {]}$ and

$$\begin{aligned} \lim _{\alpha \rightarrow 1/2} a_3 = \frac{\sqrt{3}}{2 \root 3 \of {2}} = 0.6874\ldots . \end{aligned}$$

Thus, the set L “converges” to $\{ w \in \mathbb {C}: \left| w\right| \cdot \left| w^2 - 3 \cdot 2^{-8/3}\right| \le 1/8 \}$, whose boundary is a double figure eight self-intersecting at ${\pm } 2^{-4/3}$. As observed in Example 3.2, the centers of L do not converge to the center 0 of the lemniscatic domain $\{ w \in \mathbb {C}: \left| w\right| \le 1/2 \}$ corresponding to ${[} {-1, 1} {]}$. This shows again that a discontinuity in the connectivity (in this example from $\ell = 3$ components to $\ell = 1$ component) leads to a discontinuity of the centers.

Figure 6 illustrates the sets E and L, and the conformal map $\Phi$ for several values of $\alpha$. For $z \in \mathbb {C}\setminus E$, we determine $w = \Phi (z)$ by solving the polynomial equation $Q(w) = P(z) + \sqrt{P(z)^2 - 1}$, where the correct value is determined with the help of the mapping properties of $\Phi$ in Theorem 2.1.

Fig. 6

Set E in Example 4.3 with $\alpha = 0.2, 0.4, 0.49$ (from top to bottom). Left: E (black lines) and grid. Right: $\partial L$ (black curves), $a_1, a_2, a_3$ (black dots), and the image under $\Phi$ of the grid

5 Several Intervals

In this section, we consider the case that $E = P^{-1}({[} {-1, 1} {]})$ consists of $\ell$ components, each symmetric with respect to the real line. This includes in particular the important case when E consists of $\ell$ real intervals.

For a given polynomial P with critical points $z_1, \ldots , z_{\ell -1} \in \mathbb {C}{\setminus } E$, we want to compute the centers $a_1< \cdots < a_\ell$ of L with the help of (2.13) and (2.14) in Theorem 2.4. In other words, we are looking for the polynomial

$$\begin{aligned} Q(w) = 2 p_n (w - a_1)^{n_1} \cdots (w - a_\ell )^{n_\ell }, \end{aligned}$$

where $n_1, \ldots , n_\ell$ are known (these are the number of zeros of P in $E_1, \ldots , E_\ell$, see Theorem 2.3 (ii)), such that the critical values of Q at the critical points $w_1, \ldots , w_{\ell -1} \in \mathbb {C}{\setminus } L$ are given; see (2.13). Additionally, $a_1, \ldots , a_\ell$ must satisfy (2.14).

In his 1961 paper [7], Kammerer considered a similar problem and gave an algorithm for computing the (real) polynomial of degree n with $n-1$ prescribed oscillating critical values (and additionally two interpolatory conditions). Existence and uniqueness of such a polynomial has been proved in [2]; see also [1, 8, 9, 12, 22] for further results on polynomials with prescribed critical values. In [14, Sect. 6], Peherstorfer and the first author provided a modification of Kammerer’s algorithm for computing a polynomial pre-image consisting of $\ell$ intervals. In the following, we modify Kammerer’s algorithm for the computation of Q, that is, for the computation of $a_1, \ldots , a_\ell$. For the sake of simplicity, let us concentrate first on the case of $\ell$ real intervals.

Let the polynomial P be as in (2.3) and such that

$$\begin{aligned} E=P^{-1}([-1,1])=[b_1,b_2]\cup [b_3,b_4]\cup \cdots \cup [b_{2\ell -1},b_{2\ell }] \end{aligned}$$

(5.1)

with $b_1<b_2<\cdots <b_{2\ell }$. Let $n_j$ be the number of zeros of P in $E_j \mathrel {\mathop :}=[b_{2j-1},b_{2j}]$, $j=1,\ldots ,\ell$, and let $z_1, \ldots , z_{\ell -1}$ be the critical points of P outside E which satisfy $b_{2j}< z_j < b_{2j+1}$, $j = 1, \ldots , \ell -1$; see Theorem 2.1 (v). The following algorithm gives a procedure for numerically computing the critical points $w_1,\ldots ,w_{\ell -1}$ of Q and the centers $a_1, \ldots , a_{\ell }$ of L satisfying (2.13) and (2.14) in Theorem 2.4.

Algorithm 5.1

Initial values:

$$\begin{aligned} \begin{aligned} a_j^{[0]}&=\tfrac{1}{2}(b_{2j-1}+b_{2j}), \qquad j=1,\ldots ,\ell \\ w_j^{[0]}&=\tfrac{1}{2}(b_{2j}+b_{2j+1}), \qquad j=1,\ldots ,\ell -1 \end{aligned} \end{aligned}$$

FOR $k = 0, 1, 2, \ldots$ DO

• 1. Using $a_1^{[k]}, \ldots , a_{\ell }^{[k]}$ as initial values, compute $a_1^{[k+1]},\ldots ,a_{\ell }^{[k+1]}$ such that

  $$\begin{aligned} Q^{[k+1]}(w_j^{[k]})&= P(z_j)+\sqrt{P^2(z_j)-1}, \quad j = 1, \ldots , \ell -1, \\ \sum _{j=1}^{\ell }n_ja_j^{[k+1]}&= -\frac{p_{n-1}}{p_n}, \end{aligned}$$

  where

  $$\begin{aligned} Q^{[k+1]}(w) = 2p_n\bigl (w-a_1^{[k+1]}\bigr )^{n_1}\cdots \bigl (w-a_{\ell }^{[k+1]} \bigr )^{n_{\ell }}. \end{aligned}$$

• 2. Compute the solutions $w_1^{[k+1]},\ldots ,w_{\ell -1}^{[k+1]}$ of the equation

  $$\begin{aligned} \sum _{i=1}^\ell n_i \prod _{\begin{array}{c} j=1 \\ j \ne i \end{array}}^\ell \bigl ( w-a_j^{[k+1]} \bigr ) = 0. \end{aligned}$$

ENDFOR

Remark 5.2

The algorithm also works for more general sets $E = \bigcup _{j=1}^n E_j$ with $E_j^* = E_j$ for $j = 1, \ldots , \ell$. In this case, let us define $b_1, \ldots , b_{2\ell }$ by

$$\begin{aligned} E_j \cap \mathbb {R}= {[} {b_{2j-1}, b_{2j}} {]}, \quad j = 1, \ldots , \ell . \end{aligned}$$

(5.2)

Note that $E_j \cap \mathbb {R}$ is indeed a point or an interval; see [18, Lem. A.2]. In particular, $b_1 \le b_2< b_3 \le b_4< \ldots < b_{2\ell -1} \le b_{2 \ell }$. Then the algorithm works with the same initial values.

In our MATLAB implementation of the above algorithm, we solve the non-linear system of equations for $a_1^{[k+1]}, \ldots$, $a_\ell ^{[k+1]}$ in Step 1 using a Newton iteration, and compute the new values $w_1^{[k+1]}, \ldots , w_{\ell -1}^{[k+1]}$ in Step 2 using MATLAB’s roots command. We stop the iteration when

$$\begin{aligned} \left| a_j^{[k+1]} - a_j^{[k]}\right| < {\text {abstol}} + {\text {reltol}} \cdot \left| a_j^{[k]}\right| \quad \text {for all } j = 1, \ldots , \ell , \end{aligned}$$

where we have chosen ${\text {abstol}} = {\text {reltol}} = 10^{-13}$. We performed the following experiments in MATLAB R2014b.

Example 5.3

We apply our algorithm to all previous examples. Table 1 lists the number of iteration steps in our algorithm until convergence. For those sets where $a_1, \ldots , a_\ell$ are known explicitly, also the maximal error $\max _{j=1, \ldots , \ell } |a_j^{[k]} - a_j|$ in the final step is reported. We observe that in all examples the algorithm converges in very few iteration steps. Moreover, in the examples where $a_j$ are known explicitly, the algorithm terminates with an error close to machine precision, which suggests that the algorithm is highly accurate. In Example 3.5, the initial guess is already the exact solution and the iteration stops in its first step. Figure 7 shows the error curves $|{a_j^{[k]} - a_j}|$ for Example 3.2 and Example 4.3.

In Example 4.1, the exact values of $a_1$, $a_2$, $a_3$ are not known. For a comparison, we first map $E^{{\text {c}}}$ onto a region bounded by Jordan curves (through the successive application of inverse Joukowski maps to the intervals) and then apply the numerical boundary integral equation (BIE) method from [13], which computes the centers $a_1, \ldots , a_\ell$, the exponents $m_1, \ldots , m_\ell$, the capacity ${{\,\textrm{cap}\,}}(E)$ and the conformal map $\Phi$. The difference between the values $a_j$ computed by the two methods is close to machine precision, suggesting that both methods are very accurate.

Table 1 Number of iteration steps until convergence and final maximal error between the computed and exact values of $a_1, \ldots , a_\ell$, where available; see Example 5.3

Fig. 7

Error curves $\left| a_j^{[k]} - a_j\right|$ for the sets E from Example 3.2 (left) and 4.3 (right). Missing dots mean that the error is exactly zero

Example 5.4

The polynomial P shown in Fig. 1 is

$$\begin{aligned} P(z)&= -75.60176146228515 z^7 -6.112631353464664 z^6 + 130.38101983617594 z^5 \\&\quad + 7.91625847587283 z^4 - 63.44786532361087 z^3 - 1.793124210064775 z^2 \\&\quad + 7.668606949720056 z -0.010502912343433701. \end{aligned}$$

The set $E = P^{-1}({[} {-1, 1} {]})$ consists of $\ell = 4$ intervals while $n = \deg (P) = 7$. The numbers of zeros of P in the intervals are $n_1 = 2$, $n_2 = 1$, $n_3 = 3$, $n_4 = 1$, which can also be seen from Fig. 1. Our algorithm converges after 5 iteration steps to the values

$$\begin{aligned} a_1&= -0.807906463544657&a_3&= 0.341284084426686 \\ a_2&= -0.367217238438923&a_4&= 0.878324884021925. \end{aligned}$$

For comparison, we compute $a_1, \ldots , a_4$ by adapting the BIE method from [13] as described in Example 5.3. The difference of the computed values is of order $10^{-15}$, suggesting that both methods are very accurate.

With the obtained values $a_1, \ldots , a_4$, the conformal map $w = \Phi (z)$ is evaluated as follows. We solve the polynomial equation $Q(w) = P(z) + \sqrt{P(z)^2 - 1}$, see Theorem 2.3 (iii), and determine the correct value of w using the mapping properties of $\Phi$ given in Theorem 2.1. Figure 8 shows the sets E and L and also illustrates the image of a grid under the conformal map $\Phi$.

Fig. 8

Left: Polynomial pre-image $E = P^{-1}({[} {-1, 1} {]})$ with $\ell = 4$ intervals (black) and $\deg (P) = 7$ from Example 5.4 and a grid. Right: $\partial L$ (black curves), $a_1, \ldots , a_4$ (black dots), and the image of the grid under the conformal map $\Phi$

Example 5.5

Consider the polynomial

$$\begin{aligned} P(z) = 26 z^5 + 5 z^4 - 32 z^3 - 5 z^2 + 7 z + \frac{1}{2}, \end{aligned}$$

for which $E = P^{-1}({[} {-1, 1} {]})$ consists of $\ell = 5$ intervals; see Fig. 9. Here, $n_1 = \ldots = n_5 = 1$. The centers $a_1, \ldots , a_5$ of L are not known explicitly. Our algorithm converges in 4 steps to the values

$$\begin{aligned} a_1&= -0.957893296657925,&a_4&= 0.464367835203743, \\ a_2&= -0.570567929561560,&a_5&= 0.951037765762270. \\ a_3&= -0.079252067054220, \end{aligned}$$

For comparison, we compute $a_1, \ldots , a_5$ also by adapting the BIE method from [13] as described in Example 5.3. The difference of the computed results is of the order $10^{-14}$, i.e., both results agree up to almost machine precision.

The computed values $a_1, \ldots , a_5$ are used to compute numerically the conformal map $\Phi$ as described in Example 5.4. Figure 9 illustrates the conformal map. The difference of the values of $\Phi$ on the grid computed by this method and by the BIE method from [13] is of the order $10^{-14}$. We have again a very good agreement between both methods, which suggests that both methods are very accurate.

Fig. 9

Left: Polynomial pre-image $E = P^{-1}({[} {-1, 1} {]})$ with $\ell = 5$ intervals (black) from Example 5.5 and a grid. Right: $\partial L$ (black curves), $a_1, \ldots , a_5$ (black dots), and the image of the grid under the conformal map $\Phi$

Example 5.6

Let $P(z) = \alpha T_{10}(z)$, where $\alpha = 1.05$ and $T_{10}$ is the Chebyshev polynomial of the first kind of degree $n = 10$. Then $E = P^{-1}({[} {-1, 1} {]})$ consists of $\ell = 10$ intervals; see Fig. 10. Similarly to Example 5.5, we compute $a_1, \ldots , a_{10}$ with our algorithm, which converged in 5 iteration steps. In addition, we compute the conformal map $\Phi$, illustrated in Fig. 10. We repeated the same numerical experiment with $P(z) = \alpha T_{20}(z)$ with $\alpha = 1.05$, for which $E = P^{-1}({[} {-1, 1} {]})$ consists of 20 intervals. Our algorithm for computing $a_1, \ldots , a_{20}$ converged in 6 steps.

Fig. 10

Left: Polynomial pre-image $E = P^{-1}({[} {-1, 1} {]})$ with $\ell = 10$ intervals (black) from Example 5.6 and a grid. Right: $\partial L$ (black curves), $a_1, \ldots , a_{10}$ (black dots), and the image of the grid under the conformal map $\Phi$

A Appendix

Given a set $E = \bigcup _{j=1}^\ell E_j$ with certain symmetries, we characterize the possible relations between the components $E_1, \ldots , E_\ell$. In this section, unlike in the previous parts of the paper, the components $E_j$ are allowed to shrink to points, and we require that the $E_j$ are non-empty simply connected compact sets. Note that if $E_j$ has at least two points, then it is an infinite compact set.

Theorem A.1

Let $E = \bigcup _{j=1}^\ell E_j$ with $E = -E$ and disjoint, simply connected non-empty compact sets $E_1, \ldots , E_\ell$.

• (i) If $\ell = 1$ then $0 \in E$.

• (ii) If $\ell = 2$ then $E_1 = -E_2$ and $0 \notin E$.

• (iii) If $\ell = 3$ then there exists $j_0, j_1, j_2$ with $\{ j_0, j_1, j_2 \} = \{ 1, 2, 3 \}$ with $0 \in E_{j_0} = -E_{j_0}$ and $E_{j_1} = -E_{j_2}$.

• (iv) If $\ell = 2k$ is even then $\{ 1, \ldots , \ell \}$ is partitioned into k pairs $(j_1, j_2)$ with $E_{j_1} = -E_{j_2}$, and $0 \notin E$.

• (v) If $\ell = 2k+1$ is odd then $\{ 1, \ldots , \ell \}$ is partitioned into $\{ j_0 \}$ with $0 \in E_{j_0} = -E_{j_0}$ and k pairs $(j_1, j_2)$ with $E_{j_1} = -E_{j_2}$.

Proof

First, let $\ell = 1$, i.e., let E be a simply connected non-empty compact set with $E = -E$. If E consists of a single point then $E = -E$ implies $E = \{ 0 \}$. Otherwise, E is an infinite compact set (since E is simply connected with at least two distinct points), and we can apply Theorem 1.1 to E. The symmetry $E = -E$ implies that $L = \{ w \in \mathbb {C}: \left| w\right| \le {{\,\textrm{cap}\,}}(E) \}$ since $a_1 = 0$ by Theorem 2.2, and that $\Phi$ is odd. The assumption $0 \in E^{{\text {c}}}$ leads to the contradiction $0 = \Phi (0) \in L^{{\text {c}}}$. This shows that $0 \in E$ and concludes the proof of (i).

Let $\ell \ge 2$ and $E = \bigcup _{j=1}^\ell E_j$ with $E = -E$. The function $f(z) = -z$ satisfies $f(E) = E$. For $j \in \{ 1, 2, \ldots , \ell \}$, the set $f(E_j)$ is connected and, since $f(E_j) \subseteq E$, there exists $k_j \in \{ 1, \ldots , \ell \}$ with $f(E_j) \subseteq E_{k_j}$. Define $\sigma : \{ 1, \ldots , \ell \} \rightarrow \{ 1, \ldots , \ell \}$, $j \mapsto k_j$. We show that $\sigma$ is a permutation. Suppose it is not, then there exists $k_0 \in \{ 1, \ldots , \ell \}$ such that $f(E_j) \not \subseteq E_{k_0}$ for all j, which implies $E = f(E) = \bigcup _{j=1}^\ell f(E_j) \subseteq \bigcup _{j=1, j \ne k_0}^\ell E_j \subsetneq E$, a contradiction. Thus $\sigma$ is a permutation. Since $f(E) = E$, we also have $f(E_j) = E_{k_j}$ for all $j \in \{ 1, \ldots , \ell \}$.

We write the permutation $\sigma$ as a product of disjoint cycles. Since f is an involution, i.e., $f(f(z)) = z$, we have $\sigma ^2 = {{\,\textrm{id}\,}}$, which shows that the cycles have length 1 or 2 (transpositions). A cycle of length 1, say (j), corresponds to a set with $-E_j = f(E_j) = E_j$, which satisfies $0 \in E_j$ by (i). Since the sets $E_1, \ldots , E_\ell$ are disjoint, there can be no other cycle of length 1. Thus, $\sigma$ is the product of (disjoint) transpositions and possibly one cycle of length 1.

The remaining assertions now follow easily. If $\ell = 2$ then $\sigma = (1, 2)$ and $f(E_1) = E_2$, i.e., $E_1 = -E_2$. More generally, if $\ell = 2k$ is even, $\sigma$ is a product of k (disjoint) transpositions and there are k pairs $(j_1, j_2)$ which partition $\{ 1, \ldots , 2k \}$, such that $E_{j_1} = -E_{j_2}$. In particular, $0 \notin E$, since otherwise $0 \in E_{j_1} = -E_{j_2}$ implies $0 \in E_{j_1} \cap E_{j_2}$, a contradiction. If $\ell = 3$ then $\sigma = (j_0) (j_1, j_2)$ with $\{ j_0, j_1, j_2 \} = \{ 1, 2, 3 \}$, that is $E_{j_1} = -E_{j_2}$ and $E_{j_0} = -E_{j_0}$ with $0 \in E_{j_0}$. More generally, if $\ell = 2k+1$ is odd, $\sigma$ is a product of one cycle of length 1 and k (disjoint) transpositions, i.e., there is one $j_0 \in \{ 1, \ldots , 2k+1 \}$ with $0 \in E_{j_0} = - E_{j_0}$ and k pairs $E_{j_1} = -E_{j_2}$. $\square$

The method of proof of Theorem A.1 yields an analogous statement for sets that are symmetric with respect to the real line.

Corollary A.2

Let $E = \bigcup _{j=1}^\ell E_j$ with $E^* = E$ and disjoint, simply connected non-empty compact sets $E_1, \ldots , E_\ell$. Then $\{ 1, 2, \ldots , \ell \}$ is partitioned into sets $\{ j_0 \}$ with one element, for which $E_{j_0}^* = E_{j_0}$, and sets $\{ j_1, j_2 \}$ with two distinct elements, for which $E_{j_1}^* = E_{j_2}$.

In the special case $\ell = 2$, i.e., $E = E_1 \cup E_2$ with $E^* = E$, then either $E_1^* = E_1$ and $E_2^* = E_2$, or $E_1^* = E_2$.

Proof

Let $f(z) = \overline{z}$ and $f(E) = E^* = E$, for which $f(f(z)) = z$ for all $z \in \mathbb {C}$. Proceeding as in the proof of Theorem A.1, we obtain that $f(E_j) = E_{\sigma (j)}$ with a permutation $\sigma$, which decomposes into cycles of length 1 or 2. Hence the components of E are either symmetric ($E_j^* = E_j$, corresponding to a cycle (j)) or come in pairs $E_{j_1}^* = E_{j_2}$ (corresponding to a cycle $(j_1, j_2)$ of length 2). $\square$

Remark A.3

The method of proof of Theorem A.1 can be generalized to $E = \bigcup _{j=1}^\ell E_j$ with disjoint, simply connected non-empty compact sets $E_1, \ldots , E_\ell$, and a continuous function $f: E \rightarrow E$ with $f(E) = E$ and $f^k = f \circ \cdots \circ f = {{\,\textrm{id}\,}}$ for some integer $k \ge 2$ (where k is minimal with this property). Then $\sigma$ defined as in the proof of Theorem A.1 is a permutation that satisfies $\sigma ^k = {{\,\textrm{id}\,}}$. In particular, $\sigma$ can be written as a product of disjoint cycles, where the length of each cycle divides k. Indeed, $\sigma ^k = {{\,\textrm{id}\,}}$ implies $c^k = {{\,\textrm{id}\,}}$ for every cycle c of $\sigma$, hence a cycle c has length $l(c) \le k$. Write $k = q l(c) + r$ with $0 \le r < l(c)$. Then ${{\,\textrm{id}\,}}= c^k = c^r$, which implies $r = 0$ since $r < l(c)$ and l(c) is the smallest positive exponent with $c^{l(c)} = {{\,\textrm{id}\,}}$. Hence, l(c) divides k.