1 Introduction

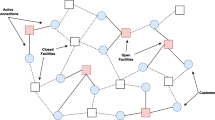
The facility location problem (FLP), originally introduced by Stollsteimer (1961) and Balinski (1966), involves deciding the position of an undetermined number of facilities (each associated with a decision variable) to minimize the sum of: (i) the setup cost of these facilities and (ii) the cost related to serving the customers from them. Most versions of the problem assume that the alternative sites where the facilities can be located are predetermined, and also that all inputs (e.g., the demand associated with each customer and the service costs) are deterministic in the sense that they are known in advance. Usually, decisions on facility location are difficult to reverse due to the fixed costs associated with opening a facility. In this regard, the FLP is useful to model allocation problems in very diverse application fields, from logistics and inventory planning (e.g., where to allocate distribution or retailing centers in a supply chain) to telecommunication and computing networks (e.g., where to allocate cloud service servers in a distributed network, cabinets in optical fiber networks, etc.). A simple example of a FLP instance is shown in Figure 1, where each customer (circle) is assigned via an active connection to its closest open facility (dark square).

The uncapacitated version of the FLP (UFLP) assumes that the capacity of each facility is virtually unlimited or, at least, far beyond the expected demand. According to Verter (2011), the UFLP variant is considered to be the simplest version of the FLP. Nevertheless, even without the capacity constraint, the FLP has been proved to be NP-hard (Cornuejols et al, 1990).

Figure 1
figure 1

Illustrative example of the facility location problem

Full size image

More formally, the UFLP is defined over an undirected graph \(G = (F, C, E)\), where F is a non-empty subset of facilities (each of them with unlimited capacity), C is a non-empty set of customers to be served, and E is a set of edges connecting each customer \(j \in C\) with some of the facilities in F (Figure 1). Delivering a customer \(j\in C\) throughout a facility \(i \in F\) has a service cost \(c_{ij} \ge 0\). Also, each facility \(i \in F\) has a fixed opening cost \(f_i \ge 0\). Let X be the decision variable denoting the set of open facilities, with \(\emptyset \subset X \subseteq F\). Let \(\sigma : C \rightarrow F\) be a function assigning to each customer \(j \in C\) a facility \(\sigma (j) \in F\) satisfying \(c_{\sigma (j),j} = \min _{i \in X} \{ c_{ij}\}\). Under these circumstances, the UFLP consists in minimizing the total cost of providing service to all customers, i.e., \(\text {minimize} \sum _{i \in X} f_i + \sum _{j \in C} c_{\sigma (j),j}\).

In the literature, the UFLP is also called the simple facility location problem, the simple warehouse location problem, or the simple plant location problem. Realistic applications of the UFLP can be found, for instance, in the lube oil industry (Brahimi and Khan, 2014), in the bank account location (Cornuejols et al, 1977), in the self-configuration of wireless sensor networks (Frank and Römer, 2007), in computer vision (Lazic et al, 2009), or in health care (Maric et al, 2015). Having a wide range of applications, the UFLP has been studied for several decades now (Mallette and Francis, 1972; Hansen, 1976). However, to the best of our knowledge, methods that provide robust solutions taking into account uncertainty conditions are not reported in the literature. This stochastic environment appears, for example, when inputs such as the customers’ demands or the service costs are random variables instead of constant values.

To partially close this gap, we introduce here a novel simheuristic algorithm (Juan et al, 2015) designed to deal with the stochastic version of the UFLP (SUFLP). First, the optimal values for all the classical UFLP benchmark instances are obtained using the Gurobi commercial solver. This is achieved after implementing the mixed integer programming (MIP) model of the UFLP into a Python script. As far as we know, this is the first time that these optimal values are reported. Then, since obtaining the optimal solution for a large-sized instance might take several hours in a standard computer, we propose a savings-based heuristic for the deterministic UFLP. This heuristic is able to generate reasonably good solutions in milliseconds. Next, we integrate this constructive heuristic inside an iterated local search (ILS) metaheuristic framework. The resulting algorithm allows generating near-optimal solutions for the UFLP in short time. Finally, once the quality of this approach has been tested in the deterministic version of the UFLP, we extend it to a simheuristic algorithm in order to deal with the SUFLP, when optimization goals other than the minimum expected cost should be considered. In effect, notice that in a stochastic environment one could be interested in solutions that offer a good trade-off between total expected cost and risk or variability.

In this regard, our simheuristic approach is able to generate several alternative solutions, each of them offering different values for each of the parameters considered. In particular, for any given instance of the SUFLP we focus on finding: (i) the solution with minimum expected cost; (ii) the solution which minimizes the third quartile of the cost values obtained when it is run multiple times; and (iii) solutions offering a good trade-off between expected cost and standard deviation of the cost values obtained when they are run multiple times (i.e., among those solutions with low expected costs, we are interested in identifying the ones showing a relatively low variability or risk).

Accordingly, the remainder of this paper is structured as follows: Section 2 reviews the literature on the UFLP, enumerating the solution approaches available to this problem. Then, Section 3 reviews the literature on the SUFLP, detailing previous works that have dealt with this particular problem. Section 4 explains our implementation of the Erlenkotter (1978) model for the UFLP and discusses the need for heuristic and metaheuristic approaches to shorten computing times in some real-life applications. Section 5 describes our savings-based heuristic for the UFLP. Section 6 explains how this heuristic can be integrated into a metaheuristic framework to generate an efficient algorithm. Section 7 discusses the quality of the proposed approaches for solving the UFLP. Section 8 describes how the metaheuristic algorithm can be extended into a simheuristic one for the SUFLP, and analyzes some numerical examples of application. Finally, Section 9 highlights the main conclusions of this paper and points out some open research lines.

2 Literature review on the UFLP

This section presents a review of the different approaches to the UFLP. For a more extensive literature review on the FLP, the reader is addressed to Drezner (1995), Snyder (2006), and Fotakis (2011). The FLP was introduced by Stollsteimer (1961) and Balinski (1966), originally referred to as the plant location problem. In general, the FLP has been studied from the perspectives of worst-case analysis, probabilistic analysis, polyhedral combinatory and empirical heuristics (Cornuejols et al, 1990). In the existing literature, we can also find exact algorithms for the problem, but its NP-hard nature makes heuristics a more suitable tool to quickly obtain solutions for larger and realistic instances.

One of the first works on the FLP was a branch-and-bound algorithm developed by Efroymson and Ray (1966). They used a compact formulation of the FLP to take advantage of the fact that its linear programming relaxation can be solved by inspection. However, this linear programming relaxation is known to be weak and therefore does not provide tight lower bounds. Another of the early approaches proposed for the problem is the direct search or implicit enumeration method proposed by Spielberg (1969). The author defined two different algorithms based on the same directed search, one considering the facilities initially open and another one considering the facilities initially closed. Later, Schrage (1975) presented a tight linear programming formulation for the FLP different from the one defined by Efroymson and Ray (1966). Schrage applied to this formulation a specialized linear programming algorithm for variable upper bound constraints. Beginning with this tight linear programming formulation, Erlenkotter (1978) presented a dual-based procedure, differing from previous approaches by considering a dual objective function. An improved version of this original algorithm was presented by Körkel (1989). The main drawback of exact approaches is the difficulties solving large real instances in short times.

Regarding the use of approximation algorithms for this problem, one of the earliest was the greedy algorithm proposed by Hochbaum (1982). In the 1990s, the first constant factor approximation emerged by the hand of Shmoys et al (1997), and it was later improved by Chudak (1998), being both of these algorithms based on LP-rounding and therefore having high running times. In order to reduce these running times, Jain and Vazirani (1999) proposed a primal-dual algorithm adapted for solving several related problems. This same algorithm was later enhanced in Jain et al (2003), obtaining better results. More recently, Li (2013) outperformed the former results by reducing the approximation ratio of the previous approximation algorithms. Approximation algorithms are very valuable for a theoretical analysis of the problem. However, these algorithms are outperformed in practice by more straightforward heuristics with no performance guarantees.

Constructive algorithms and local search methods have been used for decades, starting with Kuehn and Hamburger (1963). The authors presented one of the earliest models for the problem and a heuristic procedure for solving it. Their heuristic comprised two main phases: first a constructive phase is considered as the main program, followed by a second, improvement phase which evaluates the profit implications of dropping individual warehouses or of shifting them from one location to another. Following this work, more sophisticated heuristics have been applied to the FLP. Alves and Almeida (1992) proposed a simulated annealing algorithm. Kratica et al (2001) presented a genetic algorithm outperforming previous works. Ghosh (2003) presented a neighborhood search heuristic for the problem, using tabu search as local search and obtaining competitive solutions in very low computational times, compared to exact algorithms. Michel and Van Hentenryck (2004) defined a simple tabu search algorithm, which demonstrated to be robust, efficient, and competitive when compared with previous genetic algorithms applied to the problem. The tabu search algorithm used a linear neighborhood, which flipped a single facility at each iteration. Resende and Werneck (2006) proposed an algorithm based on the GRASP metaheuristic. This algorithm combined a greedy construction phase with a local search procedure and path relinking. It obtained results very close to the lower bound values for a wide range of different instance sets. More recently, Lai et al (2010) presented a hybrid algorithm based on the Benders’ decomposition algorithm (Benders, 1962) and using a genetic algorithm instead of the costly branch-and-bound method, to obtain good-quality solutions. According to the computational results reported, the algorithm seems to be efficient. However, the author only compared its performance with the Benders’ original algorithm.

Concerning the use of parallel computing techniques, Wang et al (2008) presented an adaptive version of a parallel multi-population particle swarm optimization algorithm. The implementation obtained an important improvement in terms of execution times, while obtaining competitive results using a standard computer. However, they only solved small- and medium-sized instances of the problem. To the best of our knowledge, there are not approaches in the literature that optimally solve large instances (between 500 and 3000 facilities) under a real-time setting, i.e., a few seconds using a standard computer.

Regardless of the solution method, many variants of the basic FLP have been studied in the literature. An important source of variations is due to considering uncertainty in the problem (Snyder, 2006). This is typically taken into consideration by introducing a wide variance on any of the parameters of the problem (cost, demands, or distances). The goal in these problems is to find a solution that performs well under any possible realization of the random variables, i.e., a robust solution. The random variables can be either continuous or discrete. As an example, Balachandran and Jain (1976) presented a FLP model with piecewise linear production costs that need be neither concave nor convex. Demands are random and continuous, described by some joint probability distributions. In this kind of problems, only the first-stage decisions are available, so there are no recourse decisions. Thus, once the locations are set, they cannot be changed after the uncertainty is resolved. The objectives therefore include the expected recourse costs. In this paper, we consider the UFLP with random customers’ demands, which affect the assignment costs of customers to facilities. Therefore, it can be considered to involve stochastic costs. An analysis of this uncertainty is provided as explained in the next sections.

In reference to applications of the FLP in real-time environments, some examples can be found in the literature. These examples are usually related to environments with high mobility, dynamism, or uncertainty. For instance, Gendreau et al (2001) described a system for the real-time re-allocation of ambulances to maintain cover after an ambulance responds to a call. Similarly, Kolesar and Walker (1974) considered the redeployment of fire companies in New York City while some of them are responding to a call. An example in digital network design problems is the equipment allocation for video on demand (VoD) network deployments (Thouin and Coates, 2008). VoD services are complex and resource demanding, so deployments involve careful design of many mechanisms where content attributes and usage should be taken into account. The high bandwidth requirements motivate distributed architectures with replication of content. An important and complicated task during the network-planning phase of these distributed architectures is resource allocation. An example of such a distributed infrastructure is the Guifi Net network (www.guifi.net), an open, free, and neutral telecommunication network whose infrastructure is completely supported by its users. In fact, the growth of peer-to-peer networks and the use of mobile devices for accessing the contents have made the problem even more complex.

Another example can be found in Lee and Murray (2010). These authors introduce an approach for survivable network design of citywide wireless broadband based on the FLP model. They address two issues: how to locate the wi-fi equipment to maximally cover the given demand and how to connect wi-fi equipment to ensure survivable networking on a real case scenario in the city of Dublin (Ohio, USA). An online FLP (Meyerson, 2001) is encountered when modeling a network design problem in which several servers need to be purchased and each client has to be connected to one of the servers. Once the network has been constructed, it may be necessary to add additional clients to the network. In this case, additional costs will be incurred; e.g., the cost of connecting a new customer to the cluster, or the cost of installing additional servers whenever the current capacity cannot accommodate the increase in demand. Finally, in the telecommunication sector, a real-time environment that could require the quick solution of UFLP concerns the future 5G cellular networks. The research community, together with standardization organizations, has posed the need for the densification of the radio access network, so that the current set of deployed base stations will be complemented with a tier of small cells to provide high capacity (Bartelt et al, 2015; Wang et al, 2015). The right location and activation of these small cells according to the customers behavior could involve large energy and monetary savings.

3 Literature review on stochastic location problems

This section presents a review of some approaches to the different variants of the SUFLP. Usually the values that can take the inputs of combinatorial optimization problems are not deterministic in real life. In the case of the UFLP, a variety of sources of uncertainty may appear. In this regard, Snyder (2006) reviewed the FLP with stochasticity, illustrating both the rich variety of approaches for optimization under uncertainty that have appeared in the literature and their application to facility location problems. Later, Arabani and Farahani (2012) reported some aspects and characteristics of the dynamics of FLPs, dedicating a section to the probabilistic, fuzzy, and stochastic versions of the problem in the literature. Recently, Correia and da Gama (2015) discussed different modeling frameworks for the facility location under uncertainty, distinguishing between robust optimization, stochastic programming, and chance-constrained models. None of these three surveys are specifically devoted to review the UFLP, but the different variants of the FLP, dealing with the UFLP in some marginal parts. Here, we will focus on the stochasticity in the UFLP and some of its most interesting variants.

Our proposal solves the UFLP where service costs are considered stochastic. A similar stochastic variant of the problem is tackled by Verma et al (2010), who adopt fuzzy theory for dealing with the uncertainty. However, only very small instances of the problem can be solved with their approach due to the complexity of the problem. Although other approaches in the literature dealt with the UFLP under stochastic environments, they work with other features and variants of the uncapacitated version. Thus, for instance, Ravi and Sinha (2004) formulated the problem in the framework of two-stage stochastic optimization so that the demand of each customer in the UFLP is not known at the first stage. In each scenario, a customer has a demand which may be zero. Each facility has a first-stage opening cost and recourse costs in other scenarios. These may be infinity, reflecting the unavailability of the facilities in various scenarios. These authors provided a nearly tight approximation algorithm to solve it.

Disruptions are other features incorporated in some UFLP. Drezner (1987) introduced them in some FLPs for the first time. One interesting recent research in this line was developed in Lu et al (2015). In their work, authors used a model that allows disruptions to be correlated with an uncertain joint distribution, and they applied distributionally robust optimization to minimize the expected cost under the worst-case distribution with given marginal disruption probabilities.

Another variant of the problem with uncertainty is the competitive FLP, used for commercial facilities, e.g., shops and stores. In this case, the objective of a decision maker is mainly to obtain as many demands for his/her facilities as possible. Uno et al (2010) presented a fuzzy method to address this problem with stochastic demands. The demands for facilities are represented as fuzzy random variables. For a review of competitive location models, see the book by Drezner (1995), and the review by Eiselt et al (1993).

In Contreras et al (2011), the uncapacitated hub location problem is addressed. In this variant of the problem, it is assumed that flows originating at the same node but having different destination points can be routed through different sets of hub nodes, i.e., a multiple assignment pattern applies. This way the objective is to minimize the sum of the hub fixed costs and demand routing costs. These authors demonstrate that the stochastic problems with uncertain demands or dependent transportation costs are equivalent to their associated deterministic expected value problem in which random variables are replaced by their expectations. In the case of uncertain independent transportation costs, the corresponding stochastic problem is not equivalent and specific solution methods need to be developed.

In order to incorporate the level of risk aversion into the decision-making process, some works use a mean–variance objective function. Thus, Jucker and Carlson (1976) used it in a stochastic formulation of the UFLP in which selling price (and hence demand) may be random. Later, Hodder and Jucker (1985) extended this model to allow for correlation among random prices. Wagner et al (2009) provided an exact method for a problem where demands are probabilistic and correlated. It is a mean–variance approach that balances two often conflicting objectives: profit and associated uncertainty. The objective of locating the facilities is to maximize the lower limit of future earnings based on a stated confidence level.

Finally, some papers place constraints on the maximum regret that may be attained by the solution (Kouvelis et al, 1992). The term of p-robustness to measure it was introduced by Snyder and Daskin (2006). In Snyder et al (2007), they combined the minimum-expected-cost and p-robustness measures for the UFLP with the aim of finding the minimum-expected-cost solution that is p-robust. They solved their models using Lagrangian decomposition.

Notice that none of these works in the literature dealing with variants of the stochastic UFLP applied the combination of simulation and metaheuristics proposed in this work, which means that our approach is novel in this field.

4 Optimal solutions for the UFLP

In order to evaluate the quality of the results provided by heuristic algorithms, different authors have used lower bound values of the optimal values as a reference. However, to the best of our knowledge, the optimal values for some of the largest instances in the literature have not been reported so far. Therefore, another contribution of this paper is the publication of these optimal values, for all the classical benchmarks, through the application of a MIP model which uses the Gurobi state-of-the-art solver (see Table 1). In order to use this solver, we have implemented the MIP model into a Python script. By comparing against optimal values instead of lower bounds, we can assess more accurately the quality of the solutions obtained via approximate methods.

A mathematical model for the UFLP was provided by Erlenkotter (1978). The set of clients is I, and the set of possible locations for the facilities is J. Costs \(f_j\) are the fixed costs for installing facility j, and \(c_{ij}\) are the costs incurred if customer i is served from facility j. Binary variables \(y_j\) will be 1 if location j is used, and 0 otherwise, for \(j\in J\). Variables \(x_{ij}\), also binary, take the value of 1 if customer i is served from facility j, and 0 otherwise, for \(i\in I, j\in J\). The objective (1a) is to minimize the sum of both fixed and variable costs. Constraints (1b) state that all the customers must be satisfied by exactly one facility. Constraints (1c) impose that if a facility is used to serve some customer, then it must be opened.

$${\text{ minimize }} \quad \sum _{j\in J} f_j y_j +\sum _{i\in I} \sum _{j\in J} c_{ij} x_{ij}$$
(1a)
$${\text{ subject }} {\text{ to: }} \quad \sum _{i\in I} x_{ij} = 1 \quad \forall {i\in I} $$
(1b)
$$x_{ij} \le y_j \quad\forall {i\in I,\, j \in J} $$
(1c)
$$x_{ij} \in \{ 0,1 \} \quad \forall {i\in I,\, j \in J} $$
(1d)
$$y_j \in \{ 0,1 \} \quad \forall {j \in J} $$
(1e)

We have developed a Python-based implementation of this mathematical model ready to be used in the Gurobi commercial solver. As it will be shown in the experimental section, for some of the largest instances several hours of computation are required in order to obtain the optimal value. In some real-life UFLP applications (e.g., in the telecommunication or computing sectors), a solution might be required after a few milliseconds or seconds. These applications justify the need for fast heuristics. Additionally, these heuristics can be further extended to simheuristics in order to account for the uncertainty behavior that characterizes most real-life applications.

5 A savings-based heuristic for the UFLP

As the initial stage in the process of developing a simheuristic algorithm is able to deal with the SUFLP, we have designed a novel constructive heuristic for the deterministic UFLP. Unlike the few heuristics available in the UFLP literature (Hoefer, 2014), our heuristic is relatively easy to understand. Also, as shown in Table 1, it offers an outstanding performance in terms of computing times, providing quite competitive results even for the largest instances in the literature (average gap around 3% with respect to the optimal solutions) in just a few milliseconds. Thus, this heuristic constitutes a good alternative for real-life UFLP applications in which real-time solutions might be required.

Notice that, in general, closing a facility is computationally less expensive than opening a facility. Indeed, if an open facility is closed, only the customers that were assigned to it need to be re-allocated to alternative open facilities. On the contrary, if a closed facility is open, then all customers in the system need to be evaluated in order to decide which of them should be assigned to it. Accordingly, the proposed heuristic is based on the concept of cost savings associated with closing a given facility in the current configuration of open facilities. The savings of closing a given facility can be either a positive or a negative value. In particular, the savings related to closing a facility in the current configuration are computed as follows: the cost of opening the facility, plus the assignment cost of its customers, minus the re-allocation cost of its customers to alternative facilities. For each customer, its best alternative facility is the open facility with a minimum re-allocation cost in case its current facility is closed. Thus, for example, in Figure 2, customers c1, c2, and c3 are assigned to facility F1, but if F1 is closed they will be assigned to F2 and F3, respectively. In this case, we would save the opening cost of F1, as well as the assignment cost of c1, c2, and c3 to F1; however, we would have to account for the re-allocation cost of c1 and c3 to F3, as well as the re-allocation cost of c2 to F2.

Figure 2
figure 2

Best and best alternative assignments for a customer

Full size image

Our constructive heuristic works as follows (Figure 3). Given an UFLP instance, we consider an initial system configuration in which all the facilities are open. Then, using this initial configuration as a reference, we compute the cost savings associated with closing each individual facility while keeping all the others open. This way, we obtain a list of possible closures, which is then sorted by decreasing savings value. This is henceforth called the savings list. Afterward, starting from the initial system configuration (the one with all facilities open), the savings list is iteratively traversed from the beginning and until no more positive savings are obtained. At each iteration, the corresponding facility is closed and the savings list is updated according to the new configuration of open facilities. In order to make the savings re-computation process efficient, every customer keeps updated information about its best alternative facility in case the currently assigned one gets closed. Thus, every time an open facility F is closed, the customers directly affected (i.e., the customers that were assigned to F) are quickly re-allocated to their best alternative facilities. Additionally, the customers indirectly affected (i.e., those customers that had F as their best alternative facility) update the information about their best alternative open facility. This way, the savings only need to be re-computed for a reduced set of facilities, the ones associated with the affected customers, which speeds up the computation.

Figure 3
figure 3

Flow chart of the proposed heuristic approach

Full size image

6 Combination with a metaheuristic framework

In this section, we describe how the previous heuristic is integrated into a metaheuristic framework. This allows improving the quality of the generated solution whenever more computing time is allowed. In this paper, the ILS metaheuristic has been chosen. This selection is based on the following criteria: (i) it offers a well-balanced combination of efficiency and relative simplicity (Juan et al, 2014; Dominguez et al, 2016) and (ii) it can be easily extended to a simheuristic (Grasas et al, 2016). Being an algorithm with few parameters, our ILS-based approach represents an interesting alternative to other state-of-the-art approaches.

The proposed ILS-based approach is detailed in Algorithm 1. It receives the following input parameters: (i) the facilities and customers of the instance; (ii) the limits for the percentage of facilities to be deleted from the current base solution during the perturbation phase; and (iii) a stopping criterion (maximum number of iterations to run). The algorithm works as follows: first, the savings list is created and sorted (line 1). Then, an initial solution is generated using our savings-based heuristic (line 2) or, alternatively, a biased-randomized version of it as described in Juan et al (2011b) (this option might be preferred if parallel computing strategies are required). A local search procedure is applied to refine this initial solution (line 3). This procedure combines closing and opening movements. The solution generated will be used by the ILS framework as the initial base solution. During the ILS iterative process (lines 7–19), the current base solution is perturbated in order to generate a new feasible solution. After a local search process, this new solution is compared against the current base solution and if the former is better or an acceptance criterion is met, then the latter is updated to resume the search from a more promising point in the solution space. At any time, the best solution found so far is also saved, since this is the solution that will be returned at the end. Notice that during the perturbation stage, a random percentage of the current base solution is destroyed (i.e., a random percentage of closed facilities are opened) and then reconstructed (by closing some facilities) to generate a new solution. Also, notice that the acceptance criterion is based on the concept of credit. Whenever the current base solution is improved, a credit is assigned by the algorithm. This credit has the same value of the improvement, and it poses a limit on the quantity that the current base solution could be worsened during the next iteration.

figure a
figure b
figure c
figure d

For implementation purposes, the pseudocodes of the auxiliary methods employed by the approach are included and briefly explained next. The createSavingsList method (Algorithm 2) is used to create and sort the list of savings. The genInitSol method (Algorithm 3) is responsible for generating the initial solution, which serves as a starting point for the algorithm. The perturbate method (Algorithm 4) implements the perturbation operator used within the main loop of the algorithm. First, it starts a destruction phase, so that a set of new facilities are randomly chosen to be included in the current base solution. Their number is determined by the minimum destruction percentage and the maximum destruction percentage. Finally, a reconstruction phase is applied, using the pathRelinking procedure. Path relinking was originally proposed in the context of the tabu search metaheuristic (Glover, 1997), and it is based on the generation of new solutions by exploring trajectories that connect high-quality solutions. Here, the pathRelinking method (Algorithm 5) applies a simple form of path relinking between two solutions. The localSearch method (Algorithm 6) relies on a loop structured in two different blocks that are kept running consecutively until a non-improving iteration is reached. In the first block, an open facility is tentatively removed from the solution to search for an improvement in total cost. In the second block, a closed facility is tentatively incorporated to the configuration of open facilities.

figure e
figure f

7 Computational experiments for the UFLP

To evaluate and assess the performance of the proposed algorithms, several computational experiments were performed. The proposed algorithms have been implemented as Java\(^\circledR \) 7SE applications. All tests have been executed on a standard desktop computer with an Intel\(^\circledR \) Core\(^{\mathrm{TM}}\) i5 at 2.4 GHz and 8 GB RAM running on Windows 7. The largest instances in the UFLP literature have been used, since they are the most challenging ones. To the best of our knowledge, the results of these instances have not been improved from 2006  (Resende and Werneck, 2006). Therefore, they are the perfect benchmarks to test the quality of our algorithm. This set of instances is called MED. They were originally proposed for the p-median problem by Ahn et al (1988) and later used in the context of the UFLP by Barahona and Chudak (1999). Each instance is a set of n points picked uniformly at random in the unit square. A point represents both a user and a facility, and the corresponding Euclidean distance determines connection costs. The set consists of six different subsets, each with a different number of facilities and customers (500, 1000, 1500, 2000, 2500, and 3000), and three different opening cost schemes for each subset (\(\sqrt{n}/10, \sqrt{n}/100\), and \(\sqrt{n}/1000\) corresponding to 10, 100, and 1000 instance suffixes, respectively). In order to introduce customer demands in these instances (since they will be used later during the stochastic experiments), we have divided the assignment costs of each customer to each facility by the expected customer demand, so that the assignment cost per unit is obtained.

As mentioned before, our MIP model implementation has been run in order to generate the optimal solutions for this set of instances. Afterward, we have executed the proposed savings-based heuristic for each problem instance. Finally, our ILS-based approach has been run. In particular, each instance has been run 30 times, each time employing a different seed for the pseudorandom number generator. Both the best and average solutions found by our algorithm are reported jointly with the average time for the 30 runs. Table 1 depicts all these results using the benchmarks mentioned above. Each row corresponds to a single instance. The first two columns show the Gurobi results, the next three columns depict the savings-based heuristic results, five columns are used for the ILS-based approach results, and finally Resende and Werneck (2006) results are in the last three columns. Times are shown in seconds and gaps are calculated as follows:

$$Gap (Cost,Cost_{Optimal}) = 100\left( \frac{Cost - Cost_{Optimal}}{Cost_{Optimal}}\right) $$
(2)

Notice that our savings-based heuristic approach provides reasonably good solutions in just a few milliseconds, with and average gap of 3.15% with respect to the optimal values. Additionally, our ILS-based approach provides near-optimal solutions (average gap of 0.26% with respect to the optimal values). Also, notice that the best and the average costs provided are quite similar, which supports the idea that our algorithm is quite robust in that sense.

Thus, although the performance of the algorithm proposed by Resende and Werneck (2006) is still somewhat superior, the difference of performance with respect to our ILS-based approach seems to be small, which allows us to use it as a base for our simheuristic approach.

Table 1 Efficiency of the proposed heuristic and ILS-based approach for the UFLP
Full size table

8 Extending to a simheuristic for the SUFLP

Once it has been verified that our ILS-based approach is able to provide competitive solutions in short computing times (average gap below 1% after a few seconds in a standard computer), it can be extended to a simheuristic algorithm for solving the SUFLP, when solutions offering a good trade-off between total expected cost and variability or risk might be desirable. Now, instead of considering a deterministic service cost \(d_i\) for a customer \(i (\forall i \in \{1, 2, \ldots , |C|\})\), this service cost will be modeled as a random variable \(D_i\) with \(E[D_i] = d_i\).

As discussed in Juan et al (2015), one natural way to extend heuristic algorithms, so they can deal with stochastic versions of combinatorial optimization problems, is by integrating simulation inside the metaheuristic framework. In the case of an ILS metaheuristic framework, a detailed discussion of this hybridization process can be found in Grasas et al (2016). Accordingly, in this paper we have integrated our ILS-based approach with Monte Carlo simulation (MCS). The MCS does not only provide estimates to the expected cost associated with the solutions generated by the approach, but it also reports feedback to the stochastic search process. Indeed, the selection of the current base solution is driven by the results of the MCS.

Algorithm 7 depicts our simheuristic proposal. On the one hand, the detCost routine returns the deterministic cost of a solution, i.e., the solution cost using the deterministic service costs specified by the UFLP instance. On the other hand, the stochCost routine returns the average cost of the simulations performed over that solution (i.e., an estimate of its expected cost). Observe that, after considering that a new solution is better than the current base solution in the deterministic environment (lines 11–12 with deltaDet storing the difference), a fast simulation is performed (line 13) in order to check its goodness in the stochastic environment (lines 14–15 with deltaStoch storing the difference).

In case the new solution is better in the stochastic environment, the current base solution is updated (line 16) and a credit is fixed (line 17). The best-found solution is also updated if the new solution improves its performance in the stochastic environment (lines 18–19). A pool of best-found solutions (poolBestSol) is kept in order to analyze them later (line 20). If the new solution is not better than the current base solution in terms of deterministic cost, we can still consider the degradation of the current base solution. This allows the algorithm to escape from stagnation (line 21). In order to avoid a degradation after another, the credit is reestablished to zero each time it is used (line 23). Finally, larger simulations are performed over a reduced set of the best-found solutions. This allows to obtain more accurate estimates of the different parameters associated with the stochastic costs generated by each of these solutions, e.g., standard deviation, quartiles, etc. (lines 25–26).

figure g

In order to test our simheuristic algorithm in the SUFLP environment, we have extended the deterministic benchmark instances by employing the log-normal probability distribution for modeling the stochastic service costs. In a real-world application, historical data could be used to model each service cost by a different probability distribution. As discussed in Juan et al (2011a), the log-normal distribution is a more natural choice than the normal distribution when modeling nonnegative random variables. The log-normal has two parameters, namely: the location parameter, \(\mu _i\), and the scale parameter, \(\sigma _i\). According to the properties of the log-normal distribution, these parameters will be given by the following expressions:

$$ \mu _i= \ln (E[D_i]) - \frac{1}{2} \ln \left( 1 + \frac{Var[D_i]}{E[D_i]^2}\right) \sigma _i= \left| \sqrt{\ln \left( 1 + \frac{Var[D_i]}{E[D_i]^2}\right) }\right| $$

As stated before, \(E[D_i] = d_i, \forall i \in \{1, 2, \ldots , |C|\}\). For computational experiments, we have considered a variance level (uncertainty) \(Var[D_i] = 50 d_i\). Observe that the original UFLP instances are a particular case of these new instances when \(Var[D_i] = 0, \forall i \in \{1, 2, \ldots , |C|\}\).

During the stochastic searching process, only simulations with a reduced number of runs (5000 in our experiments) are employed. This way, we avoid the simulation to jeopardize the computing time of the ILS-based approach. Once a reduced set of promising solutions for the SUFLP has been selected, a simulation with more runs (100,000 in our case) is employed to obtain more accurate estimates of the different parameters associated with the stochastic costs generated by each of these solutions. Actually, simulation is not only used here to generate estimates of the expected cost associated with each solution and to guide the searching process of the heuristic component, but it is also employed to generate observations on the stochastic behavior of each solution. As suggested in Juan et al (2015), these observations can then be analyzed to perform a risk analysis on each of these promising solutions.

Notice that, in the basic SUFLP with a linear objective function, the solution minimizing the total expected cost will be the same as the optimal solution for the deterministic UFLP (this property will not hold if, for instance, a nonlinear penalty cost is added in the SUFLP objective function to account for facilities with a total demand higher than a threshold, etc.). Nevertheless, even in this basic SUFLP variant, the decision maker will be interested not only in the solution that minimizes the total expected cost but also in other solutions that might offer a better trade-off between total expected cost and ‘robustness’ (in terms of assuming a reasonably low variability or risk). For this purpose, our approach is able to generate several alternative solutions, each of them offering different values for each of the parameters considered. In particular, for any given instance of the SUFLP we are interested in obtaining: (i) det, the optimal solution for the deterministic UFLP when applied to the stochastic environment (as discussed before, for the basic linear version of the SUFLP this solution will be also the one with the minimum expected cost); (ii) min-avg, the solution with minimum expected cost found by the simheuristic algorithm (for validation purposes, it might be useful to compare min-avg with det); (iii) min-q3, the solution with minimum third quartile, where the third quartile refers to the observed costs after multiple executions of a solution; and (iv) min-dev, a solution offering a good trade-off between expected cost and standard deviation, i.e., among those solutions with a low expected cost, we are interested in identifying the ones also offering low variability or risk.

For the 1000_10 instance, Figure 4 depicts the aforementioned four solutions in a radar-like graph. Notice that each solution offers different values in each of the three dimensions considered. In particular, (i) the min-avg solution and the det solution are overlapping, which contributes to validate our approach; and (ii) both the min-avg and the det solutions offer a poor performance, in terms of standard deviation and third quartile, when compared with min-dev and min-q3, respectively.

Figure 4
figure 4

Comparison of solutions for instance 1000_10

Full size image

As mentioned before, once the simheuristic approach has found the solutions with best performance for each dimension, simulation with more runs (100,000 in our case) is employed in the last step to obtain more accurate values. Therefore, we can develop a multiple boxplot comparison of the cost obtained through this large simulation for the aforementioned four solutions. Figure 5 shows this multiple boxplot comparison for the 1500-10 instance. For each boxplot, it also includes the number of facilities open in the corresponding solution.

Again, it can be observed that solution min-avg is quite similar to solution det, both in average cost and variability as well as in number of open facilities. However, solution min-q3 seems completely different: by accepting a somewhat higher expected cost, it offers less variability (risk). In particular, 75% of the times it is applied will provide cost levels that are considerably lower than the third quartile associated with the det solution. Notice that this reduction in risk is achieved by increasing the number of open facilities: by increasing this number, the network becomes more 'resilient’ to high demands that could significantly increase service costs if only a few facilities were open. Finally, the min-dev solution illustrates how it is possible to find alternative solutions combining different cost variability and expected cost levels. According to the results, it seems that in order to reduce the cost variability more facilities are needed, thus reducing the expected service cost (although increasing somewhat the opening cost and, eventually, the total expected cost).

Figure 5
figure 5

Comparison of the solutions obtained by the simheuristic approach

Full size image

9 Conclusions

In this paper, a simheuristic algorithm for solving the stochastic uncapacitated facility location problem (SUFLP) has been developed. In the SUFLP, service costs are assumed to be random variables. The simheuristic development process is based on the following logic: first, we have obtained optimal solutions for the large-sized instances of the deterministic version of the problem (UFLP). To the best of our knowledge, these optimal values had never been reported before in the UFLP literature. Unfortunately, obtaining optimal values for large-sized instances requires computing times that are beyond the available times in some practical applications of the UFLP. For that reason, we have also developed a fast savings-based heuristic able to provide reasonably good solutions in a few milliseconds. This heuristic might be useful in some real-life applications whenever instantaneous solutions are required. Then, this heuristic has been extended to a competitive ILS-based approach, which is able to provide near-optimal solutions in short time. Finally, we have built a simheuristic algorithm for the SUFLP by integrating the metaheuristic with Monte Carlo simulation techniques. The simulation stage is not only used to estimate the stochastic behavior of the solutions generated by the ILS-based approach, but its feedback is used by the approach to drive the stochastic search process.

As illustrated with several examples, even in the case of basic versions of the SUFLP with linear objective functions, our simheuristic approach can be used to provide alternative solutions to the one with the minimum expected cost, e.g., the solution that minimizes a given percentile, or solutions with different trade-off levels of expected cost and variability. The methodology can also be applied to more advanced versions of the SUFLP with nonlinear penalty costs and/or probabilistic constraints, where the optimal solution to the deterministic UFLP might provide a suboptimal value for the minimum expected cost.

This work can be extended in several directions. In first place, other more advanced variants of the SUFLP could be analyzed. Also, similar approaches to the one introduced in this paper could be used to solve stochastic versions of: (i) the capacitated facility location problem; (ii) the p-median problem; or (iii) the location routing problem, where also vehicle routing plans need to be accounted for.