Robust controlling of chaotic behavior in supply chain networks

Abstract

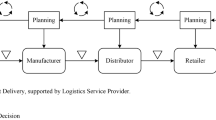
The supply chain network is a complex nonlinear system that may have a chaotic behavior. This network involves multiple entities that cooperate to meet customers demand and control network inventory. Although there is a large body of research on measurement of chaos in the supply chain, no proper method has been proposed to control its chaotic behavior. Moreover, the dynamic equations used in the supply chain ignore many factors that affect this chaotic behavior. This paper offers a more comprehensive modeling, analysis, and control of chaotic behavior in the supply chain. A supply chain network with a centralized decision-making structure is modeled. This model has a control center that determines the order of entities and controls their inventories based on customer demand. There is a time-varying delay in the supply chain network, which is equal to the maximum delay between entities. Robust control method with linear matrix inequality technique is used to control the chaotic behavior. Using this technique, decision parameters are determined in such a way as to stabilize network behavior.

Appendices

Appendix 1: Proof of Theorem 1

Consider the following Lyapunov–Krasovskii functional candidate for the system (22):

$$ V(t) = \sum\limits_{i = 1}^{5} {V_{i} (t)} , $$

(39)

where

$$ V_{1} (t) = y^{T} (t)Py(t), $$

(40)

$$ V_{2} (t) = \sum\limits_{i = t - \tau (t)}^{t - 1} {y^{T} (i)Qy(i)} , $$

(41)

$$ V_{3} (t) = \sum\limits_{{j = t - \tau_{2} + 1}}^{{t - \tau_{1} }} {\sum\limits_{i = j}^{t - 1} {y^{T} (i)Qy(i)} } , $$

(42)

$$ V_{4} (t) = \sum\limits_{{i = t - t_{2} }}^{t - 1} {y^{T} (i)Ry(i)} , $$

(43)

$$ V_{5} (t) = \tau_{2} \sum\limits_{{j = - \tau_{2} }}^{ - 1} {\sum\limits_{i = t + j}^{t - 1} {\eta^{T} (i)Z} } \eta (i),\begin{array}{*{20}c} {} \\ \end{array} \eta (t) = y(t + 1) - y(t). $$

(44)

Define ΔV(t) = V(t + 1) − V(t). Then, along the solution of system (20), it is obtained

$$ \Delta V(t) = \sum\limits_{i = 1}^{5} {\Delta V_{i} (t)} , $$

(45)

where

$$ \begin{aligned} \Delta V_{1} (t) & = y^{T} (t + 1)Py(t + 1) - y^{T} (t)Py(t) \\ & = y^{T} (t)(A^{T} PA - P)y(t) + 2y^{T} (t)A^{T} PBg(y(t)) + 2y^{T} (t)A^{T} PCg_{d} (y(t - \tau (t)) \\ & \quad + g^{T} (y(t))B^{T} PBg(y(t)) + 2g^{T} (y(t))B^{T} PCg_{d} (y(t - \tau (t)) \\ & \quad + g_{d}^{T} (y(t - \tau (t))C^{T} PCg_{d} (y(t - \tau (t)), \\ \end{aligned} $$

(46)

$$ \begin{aligned} \Delta V_{2} (t) & = \sum\limits_{i = t + 1 - \tau (t + 1)}^{t} {y^{T} (i)Qy(i)} - \sum\limits_{i = t - \tau (t)}^{t - 1} {y^{T} (i)Qy(i)} \\ & = \sum\limits_{i = t + 1 - \tau (t + 1)}^{{t - \tau_{1} }} {y^{T} (i)Qy(i)} + \sum\limits_{{i = t - \tau_{1} + 1}}^{t - 1} {y^{T} (i)Qy(i)} + y^{T} (t)Qy(t) \\ & \quad - \sum\limits_{i = t - \tau (t) + 1}^{t - 1} {y^{T} (i)Qy(i)} - y^{T} (t - \tau (t))Qy(t - \tau (t)) \\ & \le \sum\limits_{i = t + 1 - \tau (t + 1)}^{{t - \tau_{1} }} {y^{T} (i)Qy(i)} + y^{T} (t)Qy(t) - y^{T} (t - \tau (t))Qy(t - \tau (t)) \\ & \le \sum\limits_{{i = t + 1 - \tau_{2} }}^{{t - \tau_{1} }} {y^{T} (i)Qy(i)} + y^{T} (t)Qy(t) - y^{T} (t - \tau (t))Qy(t - \tau (t)), \\ \end{aligned} $$

(47)

$$ \begin{aligned} \Delta V_{3} (t) & = \sum\limits_{{i = t - \tau_{2} + 2}}^{{t + 1 - \tau_{1} }} {\sum\limits_{i = j}^{t} {y^{T} (i)Qy(i)} } - \sum\limits_{{j = t - \tau_{2} + 1}}^{{t - \tau_{1} }} {\sum\limits_{i = j}^{t - 1} {y^{T} (i)Qy(i)} } \\ & = (\tau_{2} - \tau_{1} )y^{T} (t)Qy(t) - \sum\limits_{{i = t - \tau_{2} + 1}}^{{t - \tau_{1} }} {y^{T} (i)Qy(i)} , \\ \end{aligned} $$

(48)

$$ \Delta V_{4} (t) = y^{T} (t)Ry(t) - y^{T} (t - \tau_{2} )Ry(t - \tau_{2} ), $$

(49)

$$ \begin{aligned} \Delta V_{5} (t) & = \tau_{2} \sum\limits_{{j = - \tau_{2} }}^{ - 1} {[\eta^{T} (t)Z\mu (t) - } \eta^{T} (t + j)Z\eta (t + j)] \\ & = \tau_{2}^{2} \mu^{T} (t)Z\eta (t) - \tau_{2} \sum\limits_{{j = t - \tau_{2} }}^{t - 1} {\eta^{T} (j)Z\eta (j)} \\ & \le \tau_{2}^{2} \eta^{T} (t)Z\eta (t) - \sum\limits_{{j = t - \tau_{2} }}^{t - 1} {\eta^{T} (j)Z} \sum\limits_{{j = t - \tau_{2} }}^{t - 1} {\eta (j)} \\ & = \tau_{2}^{2} \eta^{T} (t)Z\eta (t) + \left[ {\begin{array}{*{20}c} {y(t)} \\ {y(t - \tau_{2} )} \\ \end{array} } \right]^{T} \left[ {\begin{array}{*{20}c} { - Z} & Z \\ * & { - Z} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {y(t)} \\ {y(t - \tau_{2} )} \\ \end{array} } \right]. \\ \end{aligned} $$

(50)

Substituting (46)–(50) into (45) leads to

$$ \Delta V(t) \le \zeta^{T} (t)\varXi_{1} \zeta (t), $$

(51)

where

$$ \zeta (t) = \left[ {\begin{array}{*{20}c} {y^{T} (t)} & {y^{T} (t - \tau (t))} & {y^{T} (t - \tau_{2} )} & {g^{T} (y(t))} & {g_{d}^{T} (y(t - \tau (t))} \\ \end{array} } \right], $$

$$ \varXi_{1} = \left[ {\begin{array}{*{20}c} { - P + (\tau_{2} - \tau_{1} + 1)Q + R - Z} & 0 & Z & 0 & 0 \\ * & { - Q} & 0 & 0 & 0 \\ * & * & { - R - Z} & 0 & 0 \\ * & * & * & 0 & 0 \\ * & * & * & * & 0 \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} A \\ 0 \\ 0 \\ {B^{T} } \\ {C^{T} } \\ \end{array} } \right]P\left[ {\begin{array}{*{20}c} A \\ 0 \\ 0 \\ {B^{T} } \\ {C^{T} } \\ \end{array} } \right]^{T} + \left[ {\begin{array}{*{20}c} {A - I} \\ 0 \\ 0 \\ {B^{T} } \\ {C^{T} } \\ \end{array} } \right](\tau_{2}^{2} Z)\left[ {\begin{array}{*{20}c} {A - I} \\ 0 \\ 0 \\ {B^{T} } \\ {C^{T} } \\ \end{array} } \right]^{T} . $$

From (23) and (24), it follows that

$$ [g_{i} (y_{i} (t)) - u_{i}^{ - } y_{i} (t)][g_{i} (y_{i} (t)) - u_{i}^{ + } y_{i} (t)] \le 0,\quad i = 1,2, \ldots ,n, $$

(52)

$$ [g_{{d_{i} }} (y_{i} (t)) - v_{i}^{ - } y_{i} (t)][g_{{d_{i} }} (y_{i} (t)) - v_{i}^{ + } y_{i} (t)] \le 0,\quad i = 1,2, \ldots ,n. $$

(53)

which are equivalent to

$$ \left[ {\begin{array}{*{20}c} {y(t)} \\ {g(y(t))} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {u_{i}^{ - } u_{i}^{ + } e_{i} e_{i}^{T} } & { - \frac{{u_{i}^{ - } + u_{i}^{ + } }}{2}e_{i} e_{i}^{T} } \\ { - \frac{{u_{i}^{ - } + u_{i}^{ + } }}{2}e_{i} e_{i}^{T} } & {e_{i} e_{i}^{T} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {y(t)} \\ {g(y(t))} \\ \end{array} } \right] \le 0,\quad i = 1,2, \ldots ,n, $$

(54)

$$ \left[ {\begin{array}{*{20}c} {y(t - \tau (t))} \\ {g_{d} (y(t - \tau (t)))} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {v_{i}^{ - } v_{i}^{ + } e_{i} e_{i}^{T} } & { - \frac{{v_{i}^{ - } + v_{i}^{ + } }}{2}e_{i} e_{i}^{T} } \\ { - \frac{{v_{i}^{ - } + v_{i}^{ + } }}{2}e_{i} e_{i}^{T} } & {e_{i} e_{i}^{T} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {y(t - \tau (t))} \\ {g(y(t - \tau (t)))} \\ \end{array} } \right] \le 0,\quad i = 1,2, \ldots ,n, $$

(55)

where e _i is the unit column vector having one element on its ith row and zeros elsewhere.

Letting D = diag{d ₁, d ₂, …, d _n } ≻ 0 and H = diag{h ₁, h ₂, …, h _n } ≻ 0, it follows from (51), (54), and (55) that

$$ \begin{aligned} & \Delta V(t) \le \zeta^{T} (t)\varXi_{1} \zeta (t) \\ & \quad - \sum\limits_{i = 1}^{n} {d_{i} } \left[ {\begin{array}{*{20}c} {y(t)} \\ {g(y(t))} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {u_{i}^{ - } u_{i}^{ + } e_{i} e_{i}^{T} } & { - \frac{{u_{i}^{ - } + u_{i}^{ + } }}{2}e_{i} e_{i}^{T} } \\ { - \frac{{u_{i}^{ - } + u_{i}^{ + } }}{2}e_{i} e_{i}^{T} } & {e_{i} e_{i}^{T} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {y(t)} \\ {g(y(t))} \\ \end{array} } \right] \\ & \quad - \sum\limits_{i = 1}^{n} {h_{i} } \left[ {\begin{array}{*{20}c} {y(t - \tau (t))} \\ {g_{d} (y(t - \tau (t)))} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {v_{i}^{ - } v_{i}^{ + } e_{i} e_{i}^{T} } & { - \frac{{v_{i}^{ - } + v_{i}^{ + } }}{2}e_{i} e_{i}^{T} } \\ { - \frac{{v_{i}^{ - } + v_{i}^{ + } }}{2}e_{i} e_{i}^{T} } & {e_{i} e_{i}^{T} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {y(t - \tau (t))} \\ {g(y(t - \tau (t)))} \\ \end{array} } \right] \\ & \quad = \eta^{T} (t)\varXi_{1} \eta (t) \\ & \quad - \left[ {\begin{array}{*{20}c} {y(t)} \\ {g(y(t))} \\ \end{array} } \right]^{T} \left[ {\begin{array}{*{20}c} {U_{1} D} & { - U_{2} D} \\ * & D \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {y(t)} \\ {g(y(t))} \\ \end{array} } \right] \\ & \quad - \left[ {\begin{array}{*{20}c} {y(t - \tau (t))} \\ {g_{d} (y(t - \tau (t)))} \\ \end{array} } \right]^{T} \left[ {\begin{array}{*{20}c} {V_{1} H} & { - V_{2} H} \\ * & H \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {y(t - \tau (t))} \\ {g_{d} (y(t - \tau (t)))} \\ \end{array} } \right] \\ & \quad = \zeta^{T} (t)\varXi_{2} \zeta (t), \\ \end{aligned} $$

(56)

where

$$ \varXi_{2} = \left[ {\begin{array}{*{20}c} {\varPi_{1} } & 0 & Z & {U_{2} D} & 0 \\ * & {\varPi_{2} } & 0 & 0 & {V_{2} H} \\ * & * & {\varPi_{3} } & 0 & 0 \\ * & * & * & { - D} & 0 \\ * & * & * & * & { - H} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {A^{T} } \\ 0 \\ 0 \\ {B^{T} } \\ {C^{T} } \\ \end{array} } \right]P\left[ {\begin{array}{*{20}c} {A^{T} } \\ 0 \\ 0 \\ {B^{T} } \\ {C^{T} } \\ \end{array} } \right]^{T} + \left[ {\begin{array}{*{20}c} {A - I} \\ 0 \\ 0 \\ {B^{T} } \\ {C^{T} } \\ \end{array} } \right](\tau_{2}^{2} Z)\left[ {\begin{array}{*{20}c} {A - I} \\ 0 \\ 0 \\ {B^{T} } \\ {C^{T} } \\ \end{array} } \right]^{T} . $$

with Π ₁, Π ₂, and Π ₃ defined in (33), (34), and (35). According to the research of Zhengguang et al (2009), Ξ is equivalent to Ξ ₂, and we have

$$ \Delta V(t) \le \zeta^{T} (t)\varXi \zeta (t). $$

(57)

It is clear from Ξ ≺ 0 that there exists a small scalar ɛ ₀ ≻ 0 such that

$$ \varXi + \varepsilon_{0} diag\{ I_{n \times n} ,0\} \prec 0. $$

(58)

From (57) and (58), it follows that

$$ \Delta V(t) \le - \varepsilon_{0} \left\| {y(t)} \right\|^{2} . $$

(59)

Therefore, the Lyapunov stability for the supply chain network (20) is achieved.

The exponential stability analysis of the network (20) is almost similar to the researches of Song and Wang (2007), Zhang et al (2008), Wang et al (2009) that is omitted to save pages. This completes the proof.

Appendix 2: Proof of Theorem 2

Construct the same Lyapunov–Krasovskii functional candidate V(t) as in Theorem 1. According to (36) and (37), a similar calculation as in Theorem 1 leads to

$$ \varXi (t) = \varXi + \Delta \varXi (t) \prec 0, $$

(60)

where

$$ \Delta \varXi (t) = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 & {(MF(t)N_{a} )^{T} P} & {\tau_{2} (MF(t)N_{a} )^{T} Z} \\ * & 0 & 0 & 0 & 0 & 0 & 0 \\ * & * & 0 & 0 & 0 & 0 & 0 \\ * & * & * & 0 & 0 & {(MF(t)N_{b} )^{T} P} & {\tau_{2} (MF(t)N_{b} )^{T} Z} \\ * & * & * & * & 0 & {(MF(t)N_{c} )^{T} P} & {\tau_{2} (MF(t)N_{c} )^{T} Z} \\ * & * & * & * & * & 0 & 0 \\ * & * & * & * & * & * & 0 \\ \end{array} } \right]. $$

It can be written as

$$ \varXi (t) = \varXi + \varGamma F(t)\varPsi^{T} + \varPsi F^{T} (t)\varGamma^{T} \prec 0. $$

(61)

By Lemma 1, (61) holds for any F(t) satisfying (37) if and only if there exists a scalar ɛ ≻ 0 such that

$$ \varXi + \varepsilon^{ - 1} \varGamma \varGamma^{T} + \varepsilon \varPsi \varPsi^{T} \prec 0. $$

(62)

By applying Schur complement (Zhengguang et al, 2009), (62) is equivalent to (38). Exponential stability analysis is exactly the same as Theorem 1.