1 Introduction

Business enterprises must have an efficient supply chain strategy that corresponds with their strategic planning and goals. Supply chain management (SCM) comprises the companies and the business activities needed to design, make, deliver and use a product or service. In essence, the supply chain network is a nonlinear dynamical system which includes multiple constituents incorporating business activities of shipping goods and adding values from the raw material stage to the delivery stage. Moreover, efficient supply chain management will directly affect the entire logistics networks of modern enterprises in terms of business performance, operation risks and profits. One of the motivations for pursuing network efficiency is anchored in the ability of supply chains to secure longstanding business survival or sustainability, resilience and competitiveness. Simultaneous management optimization across multi-echelon supply network is essential in providing high system performance, reliability and operation in a challenging business world with extensive network uncertainties. Then the optimized system can maximize resource utilization efficiency, minimize operation risks and maximize the profits.

So far, many researchers have investigated conceptual supply chain model from the perspective of system dynamics, and specifically described its constituent elements and dynamic characteristics [1,2,3,4]. The ‘Forrester’ supply chain model reveals the existence of the bullwhip effect in the production–distribution system [5, 6]. By using Forrester system as a target model, Naim et al. [7] put forward an analogical reasoning method to identify the origins of the bullwhip effect, which is also known as Forrester effect or demand amplification and distortion from end customers to manufacturers or even raw material suppliers. On the other hand, in references [8, 9], the automatic pipeline feedback order-based production control system (APIOBPCS) is utilized to illustrate the bullwhip effect in the multi-echelon supply chains. Moreover, the impact of retail prices on bullwhip effect in an energy-efficient air conditioning supply chain is discussed in reference [10]. Hasanov et al. [11] proposed a four-level supply chain model with remanufacturing processes and investigated the production and inventory policies that minimize total costs. However, the practical supply chain systems always show series of unpredictable dynamical behaviours caused by its constituent uncertainty. Generally, chaos in supply chain management can be observed. Chaos is a specific behaviour of nonlinear dynamical systems described by deterministic equations, exhibiting sensitive dependence on initial conditions. Chaotic behaviours have encompassed the dynamical phenomena related to ubiquitous irregularity of engineering, physical, biological, financial management, and other systems. In fact, chaotic behaviour widely exists in the fields of many natural systems and some systems with artificial components, including fluid flow, weather, climate, stock market and road traffic. In addition, chaotic dynamics have been displayed by passive walking biped robots [12]. Cryptography has also benefited from applications of chaos theory. Chaos and nonlinear dynamics have been used to design a large number of cryptographic primitives, which including image encryption algorithms, hash functions, secure pseudo-random number generators, stream ciphers, and watermarking [13]. In economics, chaos can be detected by means of recurrence quantification analysis. Chaos theory can help model economic operations and embedding shocks caused by external events, such as COVID-19 [14]. Compared with traditional analysis methods, chaos theory, which is considered as a feasible method on dealing with supply chain management issues [15, 16], provides more efficient methods to deal with complex dynamical behaviours. Chaos synchronization and control have been widely studied in various fields such as physics, secure communication, chemical reactor, biological networks, and artificial neural networks, just to name a few. Chaos synchronization is significant to adapt its unpredictable dynamical behaviour in the real market [17, 18]. The synchronization algorithm facilitates today’s supply chains to react quickly to changes in demand and in product design. In the view of business management, it will help the policymakers to prevent the supply chain system from being on an undesirable volatility and eventually make company very profitable. To date, many control theories have been introduced in synchronization scheme of chaotic systems [19,20,21,22] and even chaotic supply chain management [23,24,25,26,27,28,29]. Specially, a set of three-echelon Lorenz-like differential equations have been used to describe chaos behaviour of the supply chain system and synchronization scheme [26,27,28,29]. However, a three-echelon system has limitations in providing insights into more complex behaviours. A more general supply chain model composed of additional participants is necessary to describe market demand fluctuations and instability in reality.

In this study, a new four-echelon model is proposed for chaotic supply chain system, where system uncertainties and exogenous disturbances can significantly deteriorate achievable closed-loop system performance. Then the synchronization algorithm is realized by novel fractional order sliding mode control (FO-SMC) algorithm with adaptation mechanism. Sliding mode control (SMC) has been emerged as a robust control method to handle parametric uncertainties and exogenous disturbances which are inevitable in most of the practical systems [30]. An adaptive algorithm can be utilized to update the control gain to ensure satisfactory performance when the supply chain network suffers from sudden changes caused by tumultuous real market. Moreover, fractional order (FO) calculus allows greater degree of freedom for handling diverse problems in mathematics, engineering and management. Many researchers have presented SMC method with utilizing FO calculus for modelling and regulating of various systems [20, 31,32,33]. Hajipour et al. [34] presented a hyperchaotic fractional financial system and analysed its dynamical behaviour, and then two FO systems are synchronized using adaptive SMC technique. Dumlu [32] proposed a FO adaptive SMC to realize the tracking control of robotic manipulator, and the designed controller gives well tracking performance and faster convergence compared with the classical integral SMC counterpart. However, to the best of author’s knowledge, there is no result available in the existing literature to explore multi-stage supply chains with abovementioned control synthesis. The existing literature regarding the applications of system dynamics and chaos theory to modelling and control algorithms for chaotic supply chain optimization problems are listed in Table 1. The corresponding abbreviations are explained as follows: RBFNN (radial basis function neural network); ANFIS (adaptive neuro-fuzzy inference system); ANN (artificial neural network); ASMC (adaptive sliding mode control); ASTW SMC (adaptive super-twisting sliding mode control); FO-ASMC (fractional order adaptive sliding mode control).

Table 1 Modelling and optimization of the chaotic supply chain system
Full size table

In fact, the control algorithms in the existing literature suffer from the following drawbacks: the low efficiency of simple linear feedback controller, and the chattering and high initial energy consumption of the control input for the integer-order SMC controller. To copy with these critical issues, the comprehensive FO-ASMC method is proposed from the unified point of view. A new four-echelon supply chain strategy can provide fast finite-time tracking convergence with ensuring robustness and accuracy. From the management perspective, this work might help business companies better understand the chaotic supply chains affected by the bullwhip effect. The decision-makers can make rapid and informed demand predictions based on real-time data from across the advanced network management software. Eventually, the leaders in business decision make their plan to bring together all supply chain data, and manage all logistics needs from door to door across land, ocean and air. In addition, synchronization scheme can maximise business profits by ensuring that supply chain management is robust against sudden changes in price, availability and quality. The overall structure of this article is as follows. In Sect. 2, a new four-echelon supply chain is formulated. Section 3 introduces the fractional order adaptive sliding mode control (FO-ASMC) method to realise chaos synchronization. The stability of the controlled system is proved based on Lyapunov theorem. The numerical simulation results are demonstrated in Sect. 4. Finally, Sect. 5 includes the conclusions and further research discussions.

2 System description and problem formulation

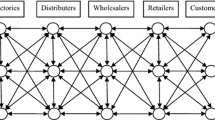
The supply chain system is the coordination and management of complex network of activities. As illustrated in Fig. 1, a complete supply chain usually consists of six members: raw materials supplier, manufacturer, distributor, retailer, end customer, and their logistics service provider. The key supply chain activities are explained as flows. Retailers develop their order plans by evaluating the potential demand of customers, and send them to distributors. Based on the received retailers’ orders, distributors can provide the products to retailers or vendors from their inventory warehouse, and release the orders to the upstream manufacturers by assessing their inventory level which the demand can be satisfied. For the production process, manufacturers make the production program when the orders come, after that, the raw materials purchasing plan can be decided. All transportation processes are supported by several third-party logistics service providers. The inventory can be seen as a buffer to ensure the operation of the factory even some unpredictable fluctuations of orders occur. In particular, inventory level will affect order policy and production decision and further affect product benefits and costs. If the demand orders and inventory of each echelon are observed, it can be found that the amplified demand variability and information distortion occur throughout the whole supply chain network from ultimate customer to raw materials supplier, which is the so-called bullwhip effect or the magnification of demand fluctuations. Along the supply chains involving multiple entities encompassing all business activities, there exist various types of uncertainties in demand, production, and delivery in the real market. Active management of supply chain activities are intended to maximize customer value and achieve a sustainable competitive advantage.

Fig. 1
figure 1

Classical supply chain activity

Full size image

To reveal the existence of bullwhip effect from the point of actual demand to the point of origin, a set of differential equations have been used to construct a chaotic supply chain model. Three-echelon equations are discussed in previous researches [26, 27, 29]. For more practical dynamic model, the entire supply chain activity usually composes of more than three echelons. In this study, new four-echelon differential equations of supply chain system are described as

$$ \left\{ {\begin{array}{*{20}l} {\dot{x}_{{1}} = - \left( {x_{{2}} + nx_{{1}} } \right)} \hfill \\ {\dot{x}_{{2}} = mx_{{3}} - \left( {n + 1} \right)x_{{2}} + cx_{{1}} } \hfill \\ {\dot{x}_{{3}} = rx_{{2}} - x_{{3}} - x_{{2}} x_{{4}} } \hfill \\ {\dot{x}_{{4}} = x_{{2}} x_{{3}} - \left( {1 - k} \right)x_{{4}} } \hfill \\ \end{array} } \right. $$
(1)

where the state variables \(x_{{1}}\), \(x_{{2}}\), \(x_{{3}}\) and \(x_{{4}}\) (\(\in {\mathbf{\mathbb{R}}}\)) are actual demand of customer, the retailer’s demand order, inventory level of distributor and produced quantity by manufacturer, respectively. Particularly, the negative values of state variables can be described as follows: \(x_{{1}} < 0\) presents the situation of supply more than demand in the market; \(x_{{2}} < 0\) means the backlog in retailer; the critical information distortion occurs in \(x_{{3}} < 0\) and there is no need to adjust the inventory level; \(x_{{4}} < 0\) indicates the case of overstock or return. Moreover, the system parameters are defined as follows: \(c\), \(m\), \(n\), \(r\) and \(k\) denote the contingency reserve coefficient, the delivery efficiency of distributor, the rate of customer demand, the rate of information distortion and safety stock coefficient, respectively. The chaotic behaviour can potentially explain fluctuations in sales markets and order decisions which appear to be unpredictable. In fact, the specific system parameters will be considered in Eq. (1) that the supply chain model can exhibit the chaotic complex behaviours. Additionally, real supply chain systems are often affected by parametric variations and exogenous disturbances. And these variations caused by disruptions are often stochastic or at least nonlinear in real operation process of a supply chain network. To this end, the nonlinear supply chain system with uncertain parameters is proposed as follows:

$$ \left\{ {\begin{array}{*{20}l} {\dot{x}_{{1}} = - \left( {x_{{2}} + \tilde{n}x_{{1}} } \right) + d_{1} } \hfill \\ {\dot{x}_{{2}} = \tilde{m}x_{{3}} - \left( {\tilde{n} + 1} \right)x_{{2}} + \tilde{c}x_{{1}} + d_{2} } \hfill \\ {\dot{x}_{{3}} = \tilde{r}x_{{2}} - x_{{3}} - x_{{2}} x_{{4}} + d_{3} } \hfill \\ {\dot{x}_{{4}} = x_{{2}} x_{{3}} - \left( {1 - \tilde{k}} \right)x_{{4}} + d_{4} } \hfill \\ \end{array} } \right. $$
(2)

where the perturbed parameters are described by \(\tilde{c}\),\(\tilde{m}\),\(\tilde{n}\),\(\tilde{r}\) and \(\tilde{k}\). These parameters are assumed to be uncertain, with a nominal value, and a wide range of variations, which allow these parameters to vary randomly with time. Specially, the parametric variations are given by

$$ \tilde{c} = \overline{c}\left( {1 + 0.1\delta_{c} } \right),\;\tilde{m} = \overline{m}\left( {1 + 0.{05}\delta_{m} } \right)\;\tilde{n} = \overline{n}\left( {1 + 0.{05}\delta_{n} } \right)\;\tilde{r} = \overline{r}\left( {1 + 0.1\delta_{r} } \right)\;{\text{and}}\,\tilde{k} = \overline{k}\left( {1 + 0.1\delta_{k} } \right) $$

where \(\delta_{c}\), \(\delta_{m}\), \(\delta_{n}\), \(\delta_{r}\) and \(\delta_{k}\)\(\left( { \in {\mathbb{R}}} \right)\) are arbitrary variables changing within the range of \(\left[ { - 1,\;1} \right]\). It is noted that this represents 10% uncertainty in \(\tilde{c}\), 5% in \(\tilde{m}\), 5% in \(\tilde{n}\), 10% in \(\tilde{r}\) and 10% in \(\tilde{k}\) with respect to nominal values (\(\overline{c}\), \(\overline{m}\), \(\overline{n}\), \(\overline{r}\) and \(\overline{k}\)), respectively. More realistic supply chain model can quickly generate results so a decision-maker can adjust targets frequently to respond to changing demand and supply conditions against parametric uncertainty.

3 Adaptive fractional order control synthesis

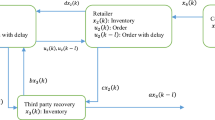
With the wide application of control theory in global logistics, many enterprises are committed to establishing an efficient supply chains to identify and weaken the impact of the bullwhip effect, so as to reduce waste and save cost. Chaos theory concerns deterministic systems whose behaviour can be predicted by control action. Generally, chaos phenomena can be observed in complex supply chain networks. The active control of chaotic supply chain is one of challenging open problems in the field of robust supply chain management to improve its efficiency. Therefore, in order to achieve the desirable chaotic trajectory of the system, it is necessary to design a suitable synchronization controller which can guarantee the synchronization errors stable or asymptotically stable. The synchronization algorithm facilitates today’s supply chains to react quickly to changes in demand and in product design. This scheme is particularly suitable in just-in-time supply chain management. Synchronization scheme can eliminate the asymmetrical risks and overcome the uncertain information distortions in supply chain activity. In this context, the fractional-order (FO) adaptive sliding mode control (ASMC) is utilized to implement the synchronization of the perturbed supply chain system. The work principle of synchronization scheme is shown briefly in Fig. 2.

Fig. 2
figure 2

Synchronization scheme of FO-ASMC algorithm for supply chain system

Full size image

3.1 Synchronization system

For the master–slave configuration, the master (or drive) system is used as supply chain reference model and the slave (or response) system is driven to follow the chaotic dynamics of the master. A pair of chaotic systems is considered for this dynamical analysis. Consider a nominal supply chain model as a master system with the state variable vector \(x_{m} = \left[ {x_{m1} ,x_{m2} ,x_{m3} ,x_{m4} } \right]^{T}\)(\(\in {\mathbf{\mathbb{R}}}^{4}\)),

$$ \dot{x}_{m} = A_{m} x_{m} + f_{m} \left( {x_{m} } \right) $$
(3)

where

$$ A_{m} = \left[ {\begin{array}{*{20}c} { - \overline{n}} & { - 1} & 0 & {0} \\ {\overline{c}} & { - \left( {\overline{n} + 1} \right)} & {\overline{m}} & 0 \\ 0 & {\overline{r}} & { - 1} & 0 \\ 0 & 0 & 0 & { - \left( {1 - \overline{k}} \right)} \\ \end{array} } \right],\;f_{m} \left( {x_{m} } \right) = \left[ {\begin{array}{*{20}c} 0 \\ {0} \\ { - x_{{m{2}}} x_{{m{4}}} } \\ {x_{{m{2}}} x_{{m{3}}} } \\ \end{array} } \right] $$

In this model, the nonlinear system can be split into a linear \(A_{m} x_{m}\) and nonlinear part \(f_{m} \left( {x_{m} } \right)\). From Eq. (2), the slave system with state vector \(x = \left[ {x_{1} ,x_{2} ,x_{3} ,x_{4} } \right]^{T}\)(\(\in {\mathbf{\mathbb{R}}}^{4}\)) is described as

$$ \dot{x} = \tilde{A}x + f\left( x \right) + d + u $$
(4)

where

$$ \tilde{A} = \left[ {\begin{array}{*{20}c} { - \tilde{n}} & { - 1} & 0 & 0 \\ {\tilde{c}} & { - \left( {\tilde{n} + 1} \right)} & {\tilde{m}} & 0 \\ 0 & {\tilde{r}} & { - 1} & 0 \\ 0 & 0 & 0 & { - \left( {1 - \tilde{k}} \right)} \\ \end{array} } \right]\;,f\left( x \right) = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ { - x_{2} x_{4} } \\ {x_{2} x_{3} } \\ \end{array} } \right] $$

In Eq. (4), the input signals include \(d = \left[ {d_{1} ,d_{2} ,d_{3} ,d_{4} } \right]^{T}\)(\(\in {\mathbf{\mathbb{R}}}^{4}\)) as exogenous disturbances, and \(u = \left[ {u_{1} ,u_{2} ,u_{3} ,u_{4} } \right]^{T}\)(\(\in {\mathbf{\mathbb{R}}}^{4}\)) as active control actions which are implemented by the nonlinear controller such that two chaotic systems can be synchronized. In this formation, the master system determines the synchronized behaviour of the slave system. The synchronization scheme reduces to find the active controller \(u\) such that the master and slave can be synchronized under system uncertainties. Specifically, the tracking error (\(e = x - x_{m}\)) for asymptotic stability should satisfy such that the following synchronization objective is achieved, or \(\mathop {\lim }\limits_{t \to \infty } \left\| e \right\| = 0\), where ∥ ∥ is the Euclidean norm. Euclidean norm (or L2-norm) of vector in a coordinate space \(\Re^{n}\) is the square root of the sum of the squares of its the vector coordinates, or \(\left\| e \right\| = \left\| e \right\|_{2} = \sqrt {e_{1}^{2} + \cdots + e_{n}^{2} }\). In Euclidean space, it is one of the most frequently cited norms to measure the magnitude or length of vectors. This norm is used to ensure that the tracking error of the state variables is sufficiently small or even zero under control activities.

This proves that the slave system can follow the master system in a stable synchronization way. From Eqs. (3) and (4), the synchronization error dynamics \(\dot{e}\) (\(\in {\mathbf{\mathbb{R}}}^{4}\)) can be obtained as

$$ \begin{aligned} \dot{e}_{1} & = - \left( {e_{2} + \overline{n}e_{1} } \right) + \xi_{1} \left( x \right) + d_{1} + u_{1} \\ \dot{e}_{2} & = \overline{m}e_{3} - (\overline{n} + 1)e_{2} + \overline{c}e_{1} + \xi_{2} \left( x \right) + d_{2} + u_{2} \\ \dot{e}_{3} & = \overline{r}e_{2} - e_{3} - \left( {x_{2} x_{4} - x_{m2} x_{m4} } \right) + \xi_{3} \left( x \right) + d_{3} + u_{3} \\ \dot{e}_{4} & = \left( {x_{2} x_{3} - x_{m2} x_{m3} } \right) - (1 - \overline{k})e_{4} + \xi_{4} \left( x \right) + d_{4} + u_{4} \\ \end{aligned} $$
(5)

In this formulation, the uncertainty related to system parameters is lumped as the vector form \(\Delta = \left[ {\xi_{1} \left( x \right),\xi_{2} \left( x \right),\xi_{3} \left( x \right),\xi_{4} \left( x \right)} \right]^{T}\), or more precisely, \(\xi_{1} \left( x \right) = 0.05\overline{n}\delta_{n} x_{1}\), \(\xi_{2} \left( x \right) = 0.05\overline{n}\delta_{n} x_{2} + 0.05\overline{m}\delta_{m} x_{3} + 0.1\overline{c}\delta_{c} x_{1}\),\(\xi_{3} \left( x \right) = 0.1\overline{r}\delta_{r} x_{2}\) and \(\xi_{4} \left( x \right) = 0.1\overline{k}\delta_{k} x_{4}\).

It is assumed that the parameter uncertainty \(\Delta\) and the exogenous disturbance \(d\) are bounded in magnitudes. Then a new term \(\Theta = \left[ {\theta_{1} ,\theta_{2} ,\theta_{3} ,\theta_{4} } \right]^{T}\)\(\in {\mathbb{R}}^{4}\) is defined to represent all general uncertainties, including parameter variations and external disturbances, or \(\Theta = \Delta + d\). Hence, for the unknown bounded perturbations \(\Theta\), there exit a constant vector \(\left[ {\rho_{1} ,\rho_{2} ,\rho_{3} ,\rho_{4} } \right]^{{\text{T}}}\) such that

$$ \left| {\theta_{i} } \right| = \left| {\xi_{i} \left( x \right) + d_{i} } \right| < \rho_{i} ,\;i = 1,2,3,4,\;\forall t \in \left[ {0,\infty } \right). $$
(6)

3.2 Fractional order sliding mode control with adaptive law

The theories of fractional calculus (fractional derivative plus fractional integral) have provided a natural framework for the discussion of various kinds of real problems described by the aid of fractional derivative, particularly system analysis, control theory, and signal processing. A fractional order calculus has been presented to capture more details of the dynamical phenomena and attributes of the systems which are ignored by integer-order model. For the operator \(D^{\alpha }\) with a fractional order \(\alpha \in {\mathbb{R}}^{ + }\)(positive real numbers), the Caputo derivative of function \(x\left( t \right)\) can be defined as

$$ D_{t}^{\alpha } x\left( t \right){ = }\frac{1}{{\Gamma \left( {\upsilon - \alpha } \right)}}\int_{0}^{t} {\left( {t - \tau } \right)^{\upsilon - \alpha - 1} x^{\left( \upsilon \right)} \left( \tau \right)d\tau } $$
(7)

where \(\upsilon - 1 < \alpha < \upsilon ,\;\upsilon \in {\mathbb{Z}}^{ + }\)(positive integers), and \(\Gamma\) is the Euler Gamma function. When \(\upsilon = \alpha\), the derivatives are defined to be the usual \(\upsilon\)th order derivatives. If \(x\left( t \right) \in C^{\upsilon } \left[ {0,\infty } \right)\) with \(\upsilon - 1 < \alpha < \upsilon \in {\mathbb{Z}}^{ + }\), is the space of functions having \(\upsilon\)th derivatives absolutely continuous, the following properties can be listed [35] just for reference:

  • \(D_{t}^{\alpha } b = 0\), where b an arbitrary constant.

  • \(D_{t}^{\alpha } D_{t}^{ - \alpha } x\left( t \right) = x\left( t \right)\), for \(\upsilon = 1\)

  • \(D_{t}^{\alpha } D_{t}^{n} x\left( t \right) = D_{t}^{\alpha + n} x\left( t \right)\), \(n \in {\mathbb{N}}\) (natural numbers)

The sliding surface \(s = \left[ {s_{1} ,s_{2} ,s_{3} ,s_{4} } \right]^{T}\)(\(\in {\mathbf{\mathbb{R}}}^{{4}}\)) is defined by using FO calculus

$$ s = D_{t}^{\alpha } \left\{ {e\left( t \right)} \right\} + \lambda e\left( t \right) $$
(8)

where \(\lambda\) is the coefficient matrix, or \(\lambda = {\text{diag}}\left( {\lambda_{1} ,\lambda_{2} ,\lambda_{3} ,\lambda_{4} } \right)\) with \(\lambda_{i}\) (\(\in {\mathbb{R}}^{ + }\)). Taking the time derivative of FO sliding surface into consideration leads to

$$ \dot{s} = D_{t}^{\alpha + 1} \left\{ {e\left( t \right)} \right\} + \lambda \dot{e}\left( t \right) $$
(9)

Noting that the error dynamics in sliding mode, the asymptotic synchronization can be further realised if the following conditions are satisfied: \(\mathop {\lim }\limits_{t \to \infty } \left\| s \right\| = 0\) and \(\mathop {\lim }\limits_{t \to \infty } \left\| {\dot{s}} \right\| = 0\). The active control synthesis consists of two parts for ensuring robust control system against uncertainties: the equivalent control law (\(u_{eq}\)) and the switching control law (\(u_{sw}\)). The corresponding FO-SMC is designed as

$$ u = u_{eq} + u_{sw} $$
(10)

The equivalent control law \(u_{eq}\) in the following equation derives the error dynamics to reach to the sliding surface. In this regard, the equivalent control law \(u_{eq} = \left[ {u_{eq1} ,u_{eq2} ,u_{eq3} ,u_{eq4} } \right]^{T}\) can be calculated as

$$ \left\{ {\begin{array}{*{20}l} {u_{eq1} = e_{2} + \overline{n}e_{1} - \frac{1}{{\lambda_{1} }}D_{t}^{\alpha + 1} e_{1} } \hfill \\ {u_{eq2} = - \overline{m}e_{3} + (\overline{n} + 1)e_{2} - \overline{c}e_{1} - \frac{1}{{\lambda_{2} }}D_{t}^{\alpha + 1} e_{2} } \hfill \\ {u_{eq3} = - \overline{r}e_{2} + e_{3} + \left( {x_{2} x_{4} - x_{m2} x_{m4} } \right) - \frac{1}{{\lambda_{3} }}D_{t}^{\alpha + 1} e_{3} } \hfill \\ {u_{eq4} = - \left( {x_{2} x_{3} - x_{m2} x_{m3} } \right) + (1 - \overline{k})e_{4} - \frac{1}{{\lambda_{4} }}D_{t}^{\alpha + 1} e_{4} } \hfill \\ \end{array} } \right. $$
(11)

As mentioned above, the system uncertainties and disturbances leading to instabilities are the main obstacles that face the efficient logistics and supply chain management. Thus, the equivalent control is not enough to manage the perturbed system with disturbances. In the reaching phase where \(s(t) \ne 0\) and in order to satisfy the sliding condition another correction term \(u_{sw}\), will be added to modify the control law (switching function). Therefore, substituting Eqs. (5) and (11) into Eq. (9), the time derivative of FO-SMC surface can be rewritten in the following form:

$$ \dot{s} = \Theta + \lambda u_{sw} $$
(12)

The switching control law \(u_{sw} = \left[ {u_{sw1} ,u_{sw2} ,u_{sw3} ,u_{sw4} } \right]^{{\text{T}}}\) can be selected as

$$ u_{sw} = - \rho sgn\left( s \right) $$
(13)

where \(\rho\) is positive switching gain, and sgn (s) denotes the signum function of the sliding surface \(s\). Specifically, the signum function or sgn(s) is defined as

$$ sgn(s) = \left\{ {\begin{array}{*{20}c} {1,\;if\;s > 0} \\ { - 1,\;if\;s < 0} \\ \end{array} } \right. $$

The switching control law is designed to ensure the system trajectory on the sliding surface for all further time even if the system is subject to the parametric perturbations and disturbances. The speed of convergence and the magnitude of trajectory can be determined by the switching gain \(\rho\). In other words, if a proper \(\rho\) is given to consider the upper bound of the perturbation \(\Theta\), the controlled system will be robust stable. On the other hand, if the switching gain \(\rho\) is too large to exceed the limit value, the strong chattering will occur in sliding variables. Especially, chattering phenomenon may disrupt the production decision and increase the supply chain risk and reduce performance. To fix these, the switching gain can be estimated by adaption algorithm.

Theorem 1.

Consider the system error dynamics subjected to the parameter uncertainties and exogenous disturbances for any initial conditions. Then the trajectory of synchronization error will converge asymptotically to zero by the following FO-ASMC control algorithm:

$$ \hat{u} = u_{eq} - \hat{\rho }sgn\left( s \right) $$
(14)

and the proposed update law by adaptation is given by

$$ \dot{\hat{\rho }} = \left[ {\begin{array}{*{20}c} {\eta_{{1}} \left| {s_{{1}} } \right|} & 0 & 0 & 0 \\ 0 & {\eta_{2} \left| {s_{2} } \right|} & 0 & 0 \\ 0 & 0 & {\eta_{3} \left| {s_{3} } \right|} & 0 \\ 0 & 0 & 0 & {\eta_{4} \left| {s_{4} } \right|} \\ \end{array} } \right] $$
(15)

where \(\hat{\rho }\) is the estimated value of the switching gain \(\rho\), and \(\eta_{i}\) is a positive constant.

Proof.

The stability properties of the error dynamics can be investigated by using Lyapunov theory. First, a quadratic Lyapunov candidate, which is a positive definite function, is defined as.

$$ V = \frac{1}{2}s^{T} s + \frac{1}{2}\tilde{\rho }^{T} Q\tilde{\rho } $$
(16)

where \(Q\) is given in any positive definite matrix, or \(Q = {\text{diag}}\left( {{{1} \mathord{\left/ {\vphantom {{1} {\eta_{1} }}} \right. \kern-\nulldelimiterspace} {\eta_{1} }},{{1} \mathord{\left/ {\vphantom {{1} {\eta_{2} }}} \right. \kern-\nulldelimiterspace} {\eta_{2} }},{{1} \mathord{\left/ {\vphantom {{1} {\eta_{3} }}} \right. \kern-\nulldelimiterspace} {\eta_{3} }},{{1} \mathord{\left/ {\vphantom {{1} {\eta_{4} }}} \right. \kern-\nulldelimiterspace} {\eta_{4} }}} \right)\); \( \tilde{\rho } = \left[ {\hat{\rho }_{{1}} - \overline{\rho }_{{1}} \;\hat{\rho }_{{2}} - \overline{\rho }_{{2}} \;\hat{\rho }_{{3}} - \overline{\rho }_{{3}} \;\hat{\rho }_{{4}} - \overline{\rho }_{{4}} } \right]^{T}\) is the estimation error vector of the gain vector \(\rho\); \(\overline{\rho }\) is the nominal value of the estimated value \(\hat{\rho }\). Then the derivative of estimation error \(\tilde{\rho }\) can be defined as \( \dot{\tilde{\rho }} = \left[ {\eta_{{1}} \left| {s_{1} } \right|\;\eta_{2} \left| {s_{2} } \right|\;\eta_{3} \left| {s_{3} } \right|\;\eta_{4} \left| {s_{4} } \right|} \right]^{T}\). Thus, its time derivative \(\dot{V}\) can be calculated as

$$ \dot{V} = s^{T} \dot{s} + \tilde{\rho }^{T} Q\dot{\tilde{\rho }} $$
(17)

Substituting Eq. (12) into (17) leads to

$$ \dot{V} = \sum\limits_{i = 1}^{4} {\left\{ {s_{i} \left( {\theta_{i} - \lambda_{i} \hat{\rho }_{i} {\text{sgn}} \left( {s_{i} } \right)} \right) + \frac{{\lambda_{i} }}{{\eta_{i} }}\tilde{\rho }_{i} \dot{\hat{\rho }}_{i} } \right\}} $$
(18)

Using the property \(\left| s \right| = s{\text{sgn}} \left( s \right)\) and adaptive update law (15), one can obtain,

$$ \begin{aligned} \dot{V} & = \sum\limits_{i = 1}^{4} {\left( {s_{i} \theta_{i} - \lambda_{i} \hat{\rho }_{i} \left| {s_{i} } \right| + \lambda_{i} \hat{\rho }_{i} \left| {s_{i} } \right| - \lambda_{i} \overline{\rho }_{i} \left| {s_{i} } \right|} \right)} \\ & \le \sum\limits_{i = 1}^{4} {\left( {\left| {s_{i} } \right|\left| {\theta_{i} } \right| - \lambda_{i} \overline{\rho }_{i} \left| {s_{i} } \right|} \right)} \\ \end{aligned} $$
(19)

Then \(\dot{V}\) can be a negative definite function when the switching gain \(\rho_{i}\) satisfies

$$ \overline{\rho }_{i} > \frac{1}{{\lambda_{i} }}\left| {\theta_{i} } \right| $$
(20)

Note that the inequality (20) holds under Eq. (6). The proof of Theorem 1 is completed.

In general, the sliding mode control utilizing sign function or \({\text{sgn}} \,( \cdot )\) in Eq. (13) will exhibit undesirable phenomenon of oscillations having finite frequency and amplitude, which is known as chattering. To avoid this phenomenon, the discontinuous sign function is replaced with the continuous saturation function, or \({\text{sat}} \;( \cdot )\). Finally, the new FO-ASMC algorithm can be proposed as

$$ \hat{u} = u_{eq} - \hat{\rho }sat\left( {s,\varepsilon } \right) $$
(21)

where \(\varepsilon\)(\(\in {\mathbf{\mathbb{R}}}^{ + }\)) is a free (small) parameter which can be chosen arbitrarily by the designer to guarantee the smooth switching control structure. Meanwhile saturation function is defined as follows: \(sat\left( {s,\varepsilon } \right) = s/(\left| s \right| + \varepsilon )\). It is worth mentioning that a fractional order control strategy is proposed to achieve synchronization behaviours in the supply chains, for which the stability of synchronization errors is verified using Lyapunov theory.

4 Numerical simulation

In this section, extensive numerical simulations are carried out to validate the effectiveness and feasibility of the proposed control theory for chaotic synchronization of supply chain network. First, to demonstrate the chaotic behaviours of perturbed supply chain system, the system parameters are presented in Table 2. In practical situations, many chaotic systems are inevitably disturbed by model uncertainties and exogenous disturbances. The exogenous disturbances in supply chain systems are caused by a variety of factors, such as volatile customer demand, forecasting deviation, fluctuant inventory and shortages, and some natural and/or man-made disasters, which are incorporated as

$$ \left( {d_{{1}}, d_{2} , d_{3}, d_{4} } \right) = \left( {3\cos \left( {2t} \right),0.56\cos \left( {3t} \right),\;10\cos \left( {5t} \right),\;20\cos \left( {10t} \right)} \right). $$
Table 2 Parameter values of the chaotic supply chain system
Full size table

Particularly, for the given initial conditions, the time series of perturbed supply chain behaviours are shown in Fig. 3, in which each state variable shows chaotic behaviour. Besides, the bullwhip effect occurs throughout various stages of the supply chain, in other words, growing or waning customer demand directly impacts a business’ inventory. The magnitudes of customer demand \(x_{1}\) through order \(x_{2}\) and inventory \(x_{3}\) to production quantity \(x_{4}\) are progressively largely fluctuating. For synchronization of chaotic supply chain system, the decision-makers can also update targets more often so they always reflect current market realities. The initial conditions for the master and salve system are selected as \(x_{m} \left( 0 \right) = \left[ {3,\;1,\;5,\;9} \right]^{T}\) and \(x\left( 0 \right) = \left[ {0,\;5,\;3,\;2} \right]^{T}\). Moreover, set the initial adaptive gain \(\rho \left( 0 \right)\) starting from origin. To realize synchronization, the specific control parameters are selected as

$$ \alpha = 0.1,\;\eta_{1} = 1,\eta_{2} = 0.8,\eta_{3} = 0.8,\eta_{4} = 1.8,\;\varepsilon_{{1}} { = 8,}\varepsilon_{2} { = 10,}\varepsilon_{3} { = 5,}\varepsilon_{4} { = 8,}\sigma { = 0}{\text{.0001,}}\lambda = {\text{diag}}\left( {100,100,100,100} \right) $$
Fig. 3
figure 3

Time series of state variables of perturbed chaotic supply chain without control: a \(x_{1}\), b \(x_{{2}}\), c \(x_{{3}}\), and d \(x_{{4}}\)

Full size image

To better observe the control performance, the active controllers are activated after \(t = 15\) (time periods). The synchronization performance and tracking error of each state variable have been shown in Figs. 4 and 5. For the controlled chaotic systems, the two chaotic systems will approach synchronization for any initial condition by the proposed control scheme. It can be seen that the synchronization errors converge to zero rapidly. Clearly, the proposed FO-ASMC algorithm provides faster and smoother responses when compared to the general integer ASMC counterpart. Also, the control actions for both controllers have been shown in Fig. 6. On the premise of achieving similar synchronization performance, the proposed controllers (FO-ASMC) exhibit smoother and relatively small control activity signals, while the control input signal of the general integer order controller (ASMC) becomes large at the beginning and then shows even overshoot. All of which led to a huge waste of energy and undesirable behaviours in supply chain management, which are related to negative impacts, and thus deteriorate the resilience and sustainability in supply chains. Furthermore, the performance indices, including integral of the absolute error (IAE) values of tacking error and integral of root mean square values (IRMSV) of the tracking error and control signal, have been calculated by Eqs. (22) and (23) to evaluate the efficiency of the designed control algorithm. As shown in Figs. 7 and 8, the performance evaluation index works when the control action is activated. Specifically, two types of performance criteria have been exploited to compare the amount of synchronization by

$$ IAE = \int_{{0}}^{T} {\left| {e_{i} \left( t \right)} \right|dt} $$
(22)
$$ IRMSV = \left[ {\frac{1}{T}\int_{{0}}^{T} {\left\{ {e_{i} \left( t \right)^{2} \sigma u_{i} \left( t \right)} \right\}dt} } \right]^{\frac{1}{2}} $$
(23)
Fig. 4
figure 4

Synchronization trajectory of each state variable when the controllers are activated at \(t = 15\) (time periods): a \(x_{1}\), b \(x_{{2}}\), c \(x_{{3}}\), and d \(x_{{4}}\)

Full size image
Fig. 5
figure 5

Synchronization error of the state variables when the controllers are activated at \(t = 15\) (time periods): a \(e_{1}\), b \(e_{{2}}\), c \(e_{{3}}\), and d \(e_{{4}}\)

Full size image
Fig. 6
figure 6

Control action signals of active controllers: a \(u_{1}\), b \(u_{{2}}\), c \(u_{{3}}\), and d \(u_{{4}}\)

Full size image
Fig. 7
figure 7

Performance index on integral of absolute error (IAE): a \(x_{1}\), b \(x_{{2}}\), c \(x_{{3}}\), and d \(x_{{4}}\)

Full size image
Fig. 8
figure 8

Performance index on integral of root mean square values (IRMSV): a \(x_{1}\), b \(x_{{2}}\), c \(x_{{3}}\), and d \(x_{{4}}\)

Full size image

where \(T\) is the measured time when the controller is activated, and \(\sigma\) is the gain to determine the weight of the control activity signal. Both indices describe the deviation from synchronisation during a time-interval of length T. In fact, there is inherent intention to minimize error in any feedback control system and hence minimization of performance measure will ensure the minimization of error. By means of selecting the appropriate weighting coefficient, the values of the performance indices can be clearly detected. Figure 7 presents the accumulation of the total error of the synchronization scheme for both proposed control algorithms over time. It is shown that the accumulation of synchronization errors realized by FO-ASMC algorithm is lower than that effected by ASMC. It can be concluded that the synchronization performance of the chaotic supply chain can be improved by implementing control algorithm of FO-ASMC. When considering the combined effect of synchronization errors and corresponding control inputs, Fig. 8 displays the accumulation of the control inputs and errors while ensuring efficient system performance. Then it can be concluded that both the cumulative errors and control activity of the chaotic supply chain system under FO-ASMC strategy are less than those of the system under ASMC scheme. In summary, it can be readily seen from the trajectories of IAE and IRMSV that the FO-ASMC has smaller error values and lower energy consumption of control signals. This implies a better synchronization performance, ensuring less waste and lower cost for supply chain management. Therefore, the control performances of designed FO-ASMC scheme in terms of synchronization error, and control action are better than the general integer order ASMC counterpart against model imprecision and uncertainties.

In this numerical simulation, synchronizing two chaotic systems is intended to utilize the state variable trajectories of the drive system to control the state trajectories of the response system so that the state trajectories of the slave system track the state trajectories of the master system. The simulation results indicate that the slave system is driven to asymptotically follow the chaotic dynamics of the master one. In addition, the chaos synchronization is considered to be global due to the free choice of the initial states of the master and slave systems. The control synthesis based fractional order calculus will gain more and more interests for their ability to improve the system performances and robustness against uncertainties. Based on synchronization scheme, the leaders in business decision can meet their service goals for specific products and customers and modify inventory levels to reflect demand and supply uncertainties.

5 Conclusions

Business of managing and marketing as a chaotic system is always too complex to analyse completely in reality. Chaos theory is apparently involved in random or unpredictable behaviour but synchronisation scheme could help predict the state of a chaotic supply chain management ahead of time. This paper deals with an adaptive FO sliding mode controller for chaos synchronization of supply chain system against market disruptions. First, a four-echelon nonlinear supply chain system is built to describe the complex dynamical behaviours. Chaotic behaviours in supply chain management are described with bullwhip effect. This phenomenon can be well mitigated with appropriate control methods for supply chain management and optimization. Next, active controllers are applied for chaos synchronization. The synchronization has been considered as one of the critical methods on dealing with the complex chaotic systems in a challenging business world with extensive uncertainties. The multi-stage supply chain planning optimization problem for chaotic systems is implemented by the adaptive sliding mode control with fractional order calculus. The stability and robustness of the closed-loop management system has been proved using Lyapunov theory. Then, the comparative numerical simulations have been demonstrated to verify the performance of controlled system. New FO-ASMC algorithm can provide better and efficient decision-making policy compare to conventional integer-order ASMC counterpart. Based on chaotic synchronization, realistic supply chain management can quickly generate results so that a decision-maker can adjust targets frequently to respond to changing demand and supply conditions against uncertainty. Then, the supply chain manager can make better planning and execution decisions with the advanced management software to maximize business profitability in a challenging business world. Finally, this study provides significant contributions to in-depth analysis of the operation mechanism of chaotic supply chain networks and ensuring more efficient management optimization algorithm.