Introduction

Artificial neural networks (ANNs) have become an industry of great impact on society, with continuous growth and improved state-of-the-art achieved through the development of new algorithms and better learning techniques1. However, despite the current impressive applications of ANNs, there is still much to be explored in the field of cognitive computing, as the mechanisms behind intelligence and the brain itself remain largely unknown. Neuroscientists are constantly making new discoveries that have the potential to improve the implementation of ANNs, and vice versa, as engineering feedback sheds light on biological questions2,3,4. As such, the interdisciplinary relationship between neuroscience and engineering continues to be of utmost importance for advancing the field of artificial intelligence.

Astrocytes, abundant glial cells in the brain, have emerged as a subject of interest in recent researches. Over the last few decades, studies have revealed that astrocytes play a crucial role in neural network communication and modulation5,6,7. They form networks that are believed to be as important as the neural networks themselves. Research also suggests that astrocytes are involved in memory formation and possibly neurodegenerative disorders7,8,9.

The encoding and transfer of information between astrocytes and other cells are achieved through intra and intercellular Ca2+ oscillations, which are modulated by synaptic activity and, in turn, regulate these activities by releasing gliotransmitters such as glutamate, ATP, or adenosine in the synaptic cleft10,11,12,13,14.There are two types of Ca2+ oscillations: neurotransmitter-evoked and spontaneous14.

Neurotransmitter-evoked Ca2+ oscillations refer to oscillations that are generated as a response to synaptic activity14. During the synaptic transmission, the presynaptic neuron releases neurotransmitters that act upon both the postsynaptic neuron and the astrocyte. The result of this interaction is the generation of Ca2+ oscillations in the astrocyte6,15. The majority of the work about neuro-glia interaction refer to this type of oscillations, including mathematical models, and digital and analog neuromorphic implementations.

The main mathematical models for neurotransmitter-evoked Ca2+ include the Li-Rinzel model16, the Postnov model10 and the De Pittà model11. These models have been previously implemented as neuromorphic circuits. Nazari et al.17, Gomar et al.18, Hayati et al.19, Faramarzi et al.20, and Haghiri et al.21 are some examples of a digital implementation of these models. Analog neuromorphic implementations examples include Ahmadi et al.22, Ranjbar et al.23, and Khosravi et al.24.

Unlike the neurotransmitter-evoked oscillations, the spontaneous Ca2+ oscillations occur in the absence of external stimuli, being initiated by small variations in the cytosolic Ca2+ concentration ([Ca2+]cyt)25,26,27. Spontaneous Ca2+ oscillations are a common phenomenon observed in various cell types, including pituitary cells28 and cardiomyocytes29. Notably, such type of oscillations have also been detected in the cytosol of astrocytes25,26,27,30.

Recent studies have suggested that spontaneous oscillations in astrocytes may play an important role in astro-neural networks by initiating the process that leads to neural signaling26,30. However, the current mainstream paradigm in artificial neural network (ANN) applications assumes that astro-neural communication always starts with the neuron. This assumption provides an opportunity for further exploration of the potential contributions of astrocytes to the generation of neuronal signaling.

Some research in this area includes mathematical models for spontaneous oscillations26,27,31,32 and digital neuromorphic circuit implementations33,34. However, there is currently no proposal for an analog neuromorphic circuit capable of generating spontaneous Ca2+ oscillations.

Information is represented by relative values of analog signals in biological systems, making analog circuits a logical approach for the implementation of ANNs. It is possible to design very efficient neuromorphic circuits by defining an adequate representation of the biological variables, such that the physical principles and basic operations of analog devices match those of their biological counterparts. The advantages of an analog neuromorphic implementation include, but are not limited to, large-scale adaptivity, robustness to system failure and degradation, and low power consumption35 when compared to digital or non neuromorphical implementations.

This paper presents an analog neuromorphic circuit implementation of spontaneous Ca2+ oscillations based on the Lavrentovich-Hemkin (LH) model26. The LH model takes into account the mechanisms of inositol cross-coupling (ICC) and calcium-induced calcium release (CICR), as well as the independent production and degradation of inositol (1,4,5)-triphosphate (IP3). It assumes that a small change in cytosolic Ca2+ concentration due to the influx of calcium ions through the astrocyte’s membrane acts as the trigger for spontaneous oscillations.

While the LH model26 has previously been implemented as digital circuits33,34, this work proposes an analog neuromorphic system that aims to take advantage of the physical principles and VLSI properties of transistor-based circuits. Section “Spontaneous Ca2+ oscillations model” describes the LH mathematical model, while Section “Proposed circuit” presents the design and implementation of the model as circuits. The simulation and analysis of the circuits are discussed in Section “Results”, and the paper concludes in Section “Conclusion”.

Methods

Spontaneous Ca\(^{2+}\) oscillations model

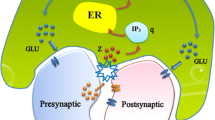
The Lavrentovich-Hemkin model26 describes the dynamic interactions of three variables: cytosolic Ca2+ concentration ([Ca2+]cyt), endoplasmic reticulum Ca2+ concentration ([Ca2+]ER), and cytosolic IP3 concentration ([IP3]cyt). The model considers the endoplasmic reticulum (ER) as the only Ca2+ storage unit and assumes the presence of a single type of receptor channel protein, the IP3 receptor (IP3R), with three binding sites: one for IP3, one for activating Ca2+, and one for deactivating Ca2+ (see Fig. 1).

Figure 1
figure 1

Schematic illustration of the mathematical model, showing paths 1 and 2 for the positive feedback loop and paths 3 and 4 for the negative feedback loop.

Full size image

The oscillation process is initiated by a small change in the concentration of Ca2+ in the cytosol ([Ca2+]cyt), which is a result of the influx of calcium ions through the astrocyte’s membrane from the extracellular space. The change in [Ca2+]cyt levels triggers the production of inositol 1,4,5-trisphosphate (IP3) by the enzyme phospholipase C\(\delta\)1 (PLC\(\delta\)1). The IP3 then binds to the IP3 receptor (IP3R) on the endoplasmic reticulum (ER) membrane, causing the channel to open and allowing the flow of calcium ions from the ER into the astrocyte’s cytosol (path 1 in Fig. 1).

The channel opening is also regulated by the binding of Ca2+ to the activating binding site on IP3R, through a process known as calcium-induced calcium release (CICR) mechanism (depicted as path 2 in Fig. 1). The channel opening by the binding of both IP3 and Ca2+ initiates a positive feedback loop, leading to an increase in the concentration of Ca2+ in the cytosol.

Low concentrations of Ca2+ in the cytosol promote the activation of the IP3 receptor’s binding site. However, high concentrations of calcium ions inhibit the IP3 receptors by binding to the deactivating site, which results in the closure of the channel and the cessation of the Ca2+ flux from the ER into the cytosol (illustrated as path 3 in Fig. 1).

During this process, calcium ions are sequestered back into the ER through a mechanism known as the sarco(endo)plasmic calcium ATPase (SERCA) pump, thus decreasing the cytosolic calcium concentration (path 4 in Fig. 1). Both the Ca2+ deactivating binding and SERCA pumps generate a negative feedback loop. The interaction of the coupled positive and negative feedback loops perpetuates the Ca2+ oscillation mechanism. The system dynamics are described by three ordinary differential equations (1–3), where \(X=[Ca^{2+}]_{cyt}\), \(Y=[Ca^{2+}]_{ER}\), and \(Z=[IP_3]_{cyt}\).

$$\begin{aligned}{} & {} \frac{dX}{dt} = V_{in}-k_{out}X+V_{CICR}-V_{SERCA} +k_f(Y-X) \end{aligned}$$
(1)
$$\begin{aligned}{} & {} \frac{dY}{dt} =V_{SERCA}-V_{CICR}-k_f(Y-X) \end{aligned}$$
(2)
$$\begin{aligned}{} & {} \frac{dZ}{dt} =V_{PLC}-k_{deg}Z \end{aligned}$$
(3)

The three main nonlinear terms in Eqs. (1–3) are described as follows:

  • VSERCA represents the Ca2+ flux from the cytosol to the ER due to the SERCA pumps (Eq. 4).

  • VPLC describes the formation of IP3 as a result of PLC\(\delta\)1 stimulation by calcium ions (Eq. 5).

  • VCICR describes the Ca2+ flow from the ER to the cytosol mediated by the IP3R (Eq. 6).

$$\begin{aligned}{} & {} V_{SERCA} =v_{M2}\left( \frac{X^2}{X^2+k_2^2}\right) \end{aligned}$$
(4)
$$\begin{aligned}{} & {} V_{PLC} =v_p\left( \frac{X^2}{X^2+k_p^2}\right) \end{aligned}$$
(5)
$$\begin{aligned}{} & {} V_{CICR} =\, 4v_{M3} \left( \frac{k_{CaA}^nX^n}{(X^n+k_{CaA}^n)(X^n+k_{CaI}^n)}\right) \times \left( \frac{Z^m}{Z^m+k_{ip3}^m}\right) (Y-X) \end{aligned}$$
(6)

The parameters’ values for these six equations can be obtained from the original work26 and are listed in Table 1. They are briefly explained below:

  • Vin—Ca2+ flux from the extracellular space into the astrocyte;

  • vM2—maximum flux of Ca2+ through the SERCA pumps;

  • vM3—maximum flux of Ca2+ into the cytosol from the ER;

  • vp—maximum rate of IP3 formation;

  • k2—Ca2+ concentration that achieves 50% of vM2’s maximum velocity;

  • kCaA—IP3R activating affinity with Ca2+;

  • kCaI—IP3R inhibiting affinity with Ca2+;

  • kip3—IP3 concentration that gives rise to 50% of vM3’s maximum velocity;

  • kp—Ca2+ concentration that gives rise to 50% of vp’s maximum velocity;

  • kdegZ—rate of degradation of IP3;

  • koutX—rate of calcium efflux from the cytosol to the extracellular space;

  • kf(Y-X)—leak flux from the ER into the cytosol;

  • n and m—Hill coefficients.

Table 1 Parameter’s values for the spontaneous Ca2+ oscillations model26.
Full size table

The ability of spontaneous oscillations to modulate synaptic activity can be demonstrated by applying the relationships established in Eqs. (7) and (8) to the LH model26. These equations, which describe the release of glutamate (Gm) and ATP (Ga) from astrocytes into the tripartite synapse, were obtained from the Postnov et al. model10 and are Ca2+ oscillations dependent. Glutamate depolarizes the postsynaptic neuron, whereas ATP hyperpolarizes it via adenosine. Table 2 lists the parameter values for Eqs. (7) and (8), obtained from the Postnov et al. work10.

$$\begin{aligned}{} & {} \tau _{Gm}\frac{dG_m}{dt} =[1+tanh(S_{Gm}(X-h_{Gm}))]\times (1-G_m)-\frac{G_m}{d_{Gm}} \end{aligned}$$
(7)
$$\begin{aligned}{} & {} \tau _{Ga}\frac{dG_a}{dt} =[1+tanh(S_{Ga}(X-h_{Ga}))]\times (1-G_a)-\frac{G_a}{d_{Ga}} \end{aligned}$$
(8)
Table 2 Parameter’s values for glutamate (7) and ATP (8) equations10.
Full size table

The parameters in Table 2 are briefly explained below, and the flow of glutamate and ATP release by the spontaneous oscillations is presented in Fig. 2:

  • \(\tau _{Gm}\)—controls the time scale for the glutamate process;

  • SGm—steepness of activation for the Gm function;

  • hGm—threshold parameter for the activation of glutamate release;

  • dGm—controls the deactivation rate of glutamate release;

  • \(\tau _{Ga}\)—controls the time scale for the ATP process;

  • SGa—steepness of activation for the Ga function;

  • hGa—threshold parameter for the activation of ATP release;

  • dGa—controls the deactivation rate of ATP release.

Figure 2
figure 2

Release flux of glutamate and ATP as modulated by spontaneous Ca2+ oscillations.

Full size image
Figure 3
figure 3

Proposed block diagram for [Ca2+]cyt, VX.

Full size image
Figure 4
figure 4

Proposed block diagram for [Ca2+]ER, VY.

Full size image

Proposed circuit

This section details the design of an analog circuit that implements the spontaneous oscillations model. To convert a mathematical model into an analog circuit, the first step is to establish a correspondence between biological and electronic variables. Subsequently, fundamental circuit principles can be used to analyze the relationships between these variables.

LH’s mathematical model is a detailed codification of the behavior of spontaneous oscillations and the variables involved in their generation. This biological to electronic variable mapping is quite interesting for electronic circuit implementations, in which it is necessary to know the influence of each variable on the desired result. Therefore, as an initial approach, the implementation based on the mathematical model was adopted, observing the effect of each variable and the device and/or physical quantity that could physically approximate it. In further work still based on the LR model, some adjustments can be made to the circuit architecture in order to achieve oscillations closer to those provided by the mathematical equation. The idea is to minimize discrepancies as much as possible. For example, the linear part of the hyperbolic tangent can be optimized, some subcircuits that act as filters can be added to improve circuit performance, or even more precise current source subcircuits can be used. Additionally, a design strategy for spontaneous oscillation circuits can be formulated according to the interaction to be performed.

Subsection “General structure of the circuit” defines the corresponding representation between biological and electrical variables, and Eqs. (1–3) are rewritten accordingly. Kirchhoff’s current law (KCL) is then applied to the new equations to obtain the general structure of the model’s circuit.

The design of the circuits for the nonlinear terms SERCA, PLC, and CICR is discussed in Subsection “SERCA, PLC, and CICR modules”. These circuits are constructed by approximating the sigmoidal nonlinear terms with the hyperbolic tangent function, which can be implemented using a differential pair, a building block of analog electronics.

Figure 5
figure 5

Proposed block diagram for [IP3]cyt, VZ.

Full size image

General structure of the circuit

The design of a neuromorphic circuit should take into consideration the device’s inherent physics capabilities and fundamental circuit laws. In an initial analysis, we observe that Eqs. (1) to (3) are composed of the sum of various terms. Kirchhoff’s laws state that the algebraic sum of either voltage or current is zero. Additionally, the current of a capacitor is given by the derivative of the voltage with respect to time, leading to the natural application of Kirchhoff’s current law (KCL) to the model. Thus, we introduce the following representation to rewrite the mathematical model as Eqs. (9) to (11):

  1. 1.

    Elements that represent concentration of ions or molecules are considered as differences in potential (voltage).

  2. 2.

    Elements that represent flux of ions or molecules are considered as current.

Figure 6
figure 6

Bipolar differential pair schematic.

Full size image
$$\begin{aligned}{} & {} c_X\frac{dV_X}{dt} =I_{in}-I_X+I_{CICR}-I_{SERCA}+I_{YX} \end{aligned}$$
(9)
$$\begin{aligned}{} & {} c_Y\frac{dV_Y}{dt} =I_{SERCA}-I_{CICR}-I_{YX} \end{aligned}$$
(10)
$$\begin{aligned}{} & {} c_Z\frac{dV_Z}{dt} =I_{PLC}-I_Z \end{aligned}$$
(11)

VX, VY, and VZ represent the primary variables X, Y, and Z as voltages, while their multiplying parameters kout, kf, and kdeg are transformed into conductances. The terms VCICR, VSERCA, and VPLC are relabeled as ICICR, ISERCA, and IPLC, respectively, to indicate that the solutions to Eqs. (4) to (6) are viewed as output currents by the system. Because of their nonlinear nature, the circuits implementing these equations are designed as separate modules in the subsequent subsection.

To define capacitance, we introduce capacitor elements cX, cY, and cZ in the equations. Their values are assumed to be unit, thereby preserving the original equations. Finally, applying KCL to Eqs. (9), (10), and (11) produces the block diagrams presented in Figs. 3, 4, and 5, respectively.

SERCA, PLC, and CICR modules

The SERCA, PLC, and CICR modules implement the nonlinear functions given by Eqs. (4), (5), and (6), which consist of Hill equations and are sigmoidal in nature. The Hill equation can be approximated by the hyperbolic tangent function, which can be easily implemented using a transistor differential pair.

The aim of this study is to present a preliminary investigation into the feasibility of the electronic implementation of spontaneous oscillations using simple devices and architectures. Building upon the previous representations stated as 1 and 2, the output signals of the proposed circuits are currents. Hence, for the initial approach, bipolar junction transistors (BJTs) were chosen as they are well-suited for low-current-driven circuits36,37. BJTs are current-controlled devices where the collector-emitter current is regulated by the base-emitter current.

The circuit design phase was initiated by selecting the parameters to be adjusted. It was decided to choose the parameters from the large-signal model of the BJT to construct a simple Spice model based on these values. The selected parameters were Is (saturation current), V\(_{AF}\) (forward Early voltage), and \(\beta _F\) (forward current gain). Initially, simulations were performed with typical values for these parameters. Subsequently, some empirical adjustments were made until the circuit provided oscillations that were as close as possible to the LH model. The parameters’ final values are in Tables 3 and 4. More parameters, like physical and geometrical ones, will be included in future work to adjust the circuit operation and make it closer to the reality of physical implementation. These parameters will encompass non-idealities inherent to transistor operation. Additionally, a parameter tuning technique for circuit optimization will be proposed. Figure 6 shows a schematic diagram of the differential pair based on bipolar junction transistors (BJTs). The differential current output is given by Eq. (12), where:

Figure 7
figure 7

Differential pair schematics for (left panel) SERCA and (right panel) PLC modules.

Full size image

  • Ic1, Ic2—collector current of transistors Q1 and Q2, respectively;

  • \(\alpha\)—common base current gain;

  • IEE—current source;

  • Vb1, Vb2—base voltage of transistors Q1 and Q2, respectively;

  • VT—thermal voltage.

$$\begin{aligned} I_{c1}-I_{c2}=\alpha \, I_{EE} \, tanh\left( \frac{V_{b1}-V_{b2}}{2V_T}\right) \end{aligned}$$
(12)

Both SERCA and PLC equations are functions of one Hill equation each, thus presenting a similar module design. Using Eq. (12) to approximate Eqs. (4) and (5), we obtain Eqs. (13) and (14), respectively. These equations are used to design the differential pairs with active load modules depicted in Fig. 7. The following BJT parameters were adjusted: saturation current, forward Early voltage, and forward beta. The proposed circuit parameters are presented in Table 3.

$$\begin{aligned}{} & {} I_{SERCA}\approx tanh(5X-0.065) \end{aligned}$$
(13)
$$\begin{aligned}{} & {} I_{PLC}\approx tanh(1.78X-0.045) \end{aligned}$$
(14)
Table 3 Parameter’s values for SERCA and PLC circuits.
Full size table

The CICR module presents a more complex equation than the SERCA and PLC modules, as it contains a rational function and two Hill equations. To design the CICR module, its function was decomposed into three separate equations. The equations dependent on X are called FX1 (16) and FX2 (17), and the equation dependent on Z is named FZ (18). Also, the term \((Y-X)\) from the original Eq. (6) is replaced by \(\frac{I_{YX}}{k_f}\).

$$\begin{aligned}{} & {} I_{CICR}=4v_{M3}\,F_{X1}\, F_{X2}\,F_Z\,\frac{I_{YX}}{k_f} \end{aligned}$$
(15)
$$\begin{aligned}{} & {} F_{X1}=\frac{k_{CaA}^n}{X^n+k_{CaA}^n} \end{aligned}$$
(16)
$$\begin{aligned}{} & {} F_{X2}=\frac{X^n}{X^n+k_{CaI}^n} \end{aligned}$$
(17)
$$\begin{aligned}{} & {} F_Z=\frac{Z^m}{Z^m+k_{ip3}^m} \end{aligned}$$
(18)
Figure 8
figure 8

Circuit schematic for CICR module.

Full size image

The equation FX1 can be approximated by the negative hyperbolic tangent (Eq. 20), which is an odd function that can be expressed as Eq. (19) by simply taking its negative. We approximate FX1 using Eq. (20), and the current addition of 1.08 in Eq. (20) can be implemented using an independent current source. In contrast, FX2 is a regular Hill equation and can be implemented without alterations to the differential pair circuit. The hyperbolic tangent approximation equation for FX2 is shown in Eq. (21).

$$\begin{aligned}{} & {} I_{c2}-I_{c1}=\alpha \, I \, tanh\left( \frac{V_{B2}-V_{B1}}{2V_T}\right) \end{aligned}$$
(19)
$$\begin{aligned}{} & {} F_{X1}\approx tanh(0.22-5.5X)+1.08 \end{aligned}$$
(20)
$$\begin{aligned}{} & {} F_{X2}\approx 4\,tanh(3.9X-0.07) \end{aligned}$$
(21)

Similarly, FZ (as given by Eq. 18) is also a regular Hill equation and can be approximated using the hyperbolic tangent function, as shown in Eq. (22).

$$\begin{aligned} F_Z\approx 5\,tanh(2.5Z-0.03) \end{aligned}$$
(22)
Figure 9
figure 9

Output from SERCA, PLC, and CICR modules. The original model is shown in solid red lines and circuit simulation result in dotted blue lines.

Full size image
Figure 10
figure 10

Graph showing [Ca2+]cyt, [Ca2+]ER, and [IP3]cyt variables for the mathematical model (red line) and the circuit simulation (blue dotted line).

Full size image
Figure 11
figure 11

Phase space diagram comparison of mathematical model (red line) and the circuit (blue line).

Full size image

Finally the ICICR complete module’s circuit is shown in Fig. 8. The full circuit includes the differential pairs for the three nonlinear functions and a current mirror (transistors Q13 and Q14) that inputs \(I_{YX}\) as the differential pair current source. The resistance R is added at the circuit output to supply the term \(4\,v_{M3}\,\frac{1}{k_f}\), making the equation complete. The circuit parameters are given in Table 4.

Table 4 Parameter’s values for CICR circuit.
Full size table

Results

The circuits depicted in Figs. 7 and 8 were simulated using the LTspice simulator with a bias voltage of \(\pm 1.5\) V. The simulation results were compared with the dynamics of the spontaneous Ca2+ oscillations model (Eqs. 1–6), which were simulated in Python using NumPy38 and Matplotlib39. The simulations of the circuits shown in Figs. 7 and 8 are presented in Fig. 9 and are compared with the mathematical model. The proposed circuit shows a good output match with the original mathematical model.

Figure 10 shows the time evolution of the variables [Ca2+]cyt, [Ca2+]ER, and [IP3]cyt from both the circuit and mathematical models. The Ca2+ oscillations obtained in the circuit closely match the theoretical model, demonstrating the high accuracy of the astrocyte circuit. Figure 11 presents the phase space portrait for both the model and circuit, which exhibit similar dynamics and stability, indicating that the circuit is a good representation of the biological model dynamics.

Figure 12
figure 12

Output from SERCA, PLC, and CICR modules for ideal inouts and noisy inputs. The ideal outputs are shown in solid red lines and noisy result is in solid blue lines.

Full size image
Figure 13
figure 13

[Ca2+]cyt, [Ca2+]ER, and [IP3]cyt variables for ideal inputs (red line) and noisy inputs (blue line).

Full size image
Figure 14
figure 14

Ca2+ oscillations for different values of Vin. The red solid line represents the mathematical model, and the blue dotted line represents the proposed circuit.

Full size image
Figure 15
figure 15

Period of oscillations as a function of Vin for the neuromorphic circuit. The red dots represent the mathematical model, and the blue dots represent the proposed circuit.

Full size image
Figure 16
figure 16

Gm and Ga release in the tripartite synapse due to Ca2+. The red solid line represents the mathematical model, and the blue dotted line represents the proposed circuit.

Full size image

Random noise was added to the input signals of the proposed circuit to evaluate its robustness. The added noise did not exceed 10\(\%\) of the maximum magnitude of the input signal. As can be seen in Fig. 12, the SERCA and PLC signals generated by the proposed circuit clearly exhibited the effects of the input noise. However, the CICR signal was hardly affected by it and remained very close to the ideal value. The circuit architecture of this subcircuit has several hyperbolic tangent modules, which likely absorbed the effects of small input variations due to noise.

On the other hand, [Ca2+]cyt, [Ca2+]ER, and [IP3]cyt (Fig. 13)exhibited subtle effects from the presence of noise. This can also be explained by the filtering effect of the resistive and capacitive elements in the output modules of each oscillation.

The circuit was also simulated with different values of Vin to investigate the astrocyte’s ability to form spontaneous oscillations in different scenarios of extracellular calcium ion flow. Figure 14 shows the results for the values of 0.04, 0.08, and 0.12 for Vin. The graph shows a discrepancy between the original model and the circuit, specially in relation to the frequency for Vin. Figure 15 shows how the period of oscillations changes as a function of Vin for the neuromorphic circuit. Despite the tendency of slightly higher frequency for the circuit, these results generally agree with the findings of Parri et al.30 regarding the spontaneous oscillations dependency of Vin. Because it is still not known how exactly the astrocytes signalling, specially the spontaneous ones, affects behaviour and cognition, it is hard to estimate what effect this discrepancy would have on a neural network. However, the circuit still presents itself as a good tool to further study these oscillations.

Despite neural communication in Spiking Neural Networks being carried out in the form of noise-robust spikes, the feedback network formed by astrocytes is expected to enhance the robustness of neuron-astrocyte circuits. Furthermore, design techniques aimed at reducing noise are being considered. These techniques include the use of low collector current values, high \(\beta\) values, and the application of filters and other appropriate techniques as needed40.

As the primary focus of this study is to demonstrate the possibility of generating spontaneous oscillations using electronic circuits, a preliminary estimation of the dissipated power was conducted. The simulation results indicate that the dissipation is approximately 40 μW. The circuit proposed in this work exhibits power dissipation on the same order of magnitude as the values presented for neurotransmitter-evoked Ca2+ oscillation24. Future improvements in this value are expected by employing low-power transistors, such as CMOS or carbon nanotube transistors, instead of the chosen BJTs. It should be noted, however, that the desired modulation characteristics of astrocytes may require implementations with mixed technologies.

Finally, Fig. 16 compares the release of glutamate and ATP in the tripartite synapse between the mathematical model and the proposed circuit. The Ca2+ oscillations generated by the proposed circuit is able to trigger a release response of glutamate and ATP that is very similar to that of the original mathematical model, achieving the main goal of this study.

Conclusion

In this work, we proposed and successfully implemented an analog neuromorphic circuit capable of spontaneous Ca2+ oscillations. This circuit exhibits similar dynamic behavior compared to the original biological model, even when subjected to noisy inputs. It is important to highlight that the proposed analog solution is simpler and easier to use in certain applications, as it does not require FPGA programming for implementing oscillations, unlike some previous digital circuit proposals. Another point to be highlighted is that the proposed architecture is capable for reproducing the similar dynamics of the biological model in reasonable accuracy.

The initial goal has been successfully achieved. As a first approach, bipolar transistor technology was chosen, but it is not limited to this device type. The SERCA, PLC, and CICR equations can be implemented with other devices that generate a hyperbolic tangent output, such as CMOS technology operating in the weak inversion zone. Some modules of the proposed circuit can be improved, and others can be added to enhance performance. The proposed circuit can be implemented in specific tasks to analyze self-repair properties, such as in robotics-related applications.

Moving forward, the objective is to further enhance the proposed implementation with a focus on large-scale integration. Parameters such as power consumption and robustness will be taken into account to optimize the proposed architecture. Additionally, a comprehensive methodology for designing spontaneous oscillation circuits can be proposed and used based on the required astrocyte-neuron interaction.