Pathfinder experiments with atom interferometry in the Cold Atom Lab onboard the International Space Station

Abstract

Deployment of ultracold atom interferometers (AI) into space will capitalize on quantum advantages and the extended freefall of persistent microgravity to provide high-precision measurement capabilities for gravitational, Earth, and planetary sciences, and to enable searches for subtle forces signifying physics beyond General Relativity and the Standard Model. NASA’s Cold Atom Lab (CAL) operates onboard the International Space Station as a multi-user facility for fundamental studies of ultracold atoms and to mature space-based quantum technologies. We report on pathfinding experiments utilizing ultracold ⁸⁷Rb atoms in the CAL AI. A three-pulse Mach–Zehnder interferometer was studied to understand the influence of ISS vibrations. Additionally, Ramsey shear-wave interferometry was used to manifest interference patterns in a single run that were observable for over 150 ms free-expansion time. Finally, the CAL AI was used to remotely measure the Bragg laser photon recoil as a demonstration of the first quantum sensor using matter-wave interferometry in space.

Introduction

NASA’s Cold Atom Lab (CAL) was launched to the International Space Station (ISS) in 2018 as a multi-user facility for fundamental physics investigations with ultracold atoms enabled by a persistent microgravity environment. The flight instrument incorporates a toolbox of capabilities for flight Principal Investigators (PIs) to pursue space-enabled studies with interacting quantum gases¹. Initial commissioning efforts for the flight instrument used laser and evaporative cooling of rubidium gases to produce Bose-Einstein Condensates (BECs) in orbit and characterized these quantum gases after freefall times exceeding 1 s². Subsequent science demonstrations by the CAL investigators included enhanced techniques for cooling, manipulation, and control for quantum gases such as decompression cooling via adiabatic relaxation³, shortcut to adiabaticity and delta-kick collimation techniques for preparing atoms with effective temperatures as low as 52 picokelvin⁴, as well as the development of RF-dressed potentials and the study of ultracold rubidium gases in bubble-shaped geometries⁵. Recently, sympathetic cooling of bosonic potassium using evaporated ⁸⁷Rb gases as a reservoir has also been utilized in CAL to produce ultracold gases of either ⁴¹K or ³⁹K and coexisting and interacting BECs of ⁴¹K and ⁸⁷Rb⁶.

Accommodation of CAL on the ISS not only provides the unique infrastructure, support, and effective real-time download of science data needed for daily operations, but also allows for on-orbit repair and upgrades by the resident astronaut crew. Notably, a replacement science module (SM-3) was launched to ISS onboard the commercial resupply services mission SpaceX-19 and was installed into CAL by astronauts Christina Koch and Jessica Meir. SM-3 was equipped with an optical beam path to enable experiments with atom interferometry. This article details the initial pathfinder experiments by CAL investigators utilizing matter-wave interferometry with ultracold ⁸⁷Rb gases in orbit.

Precision metrology based on light-pulse atom interferometry is a quintessential utilization of the wave-like nature of matter that is at the heart of quantum mechanics. Here, pulses of laser light generate a superposition of motional states of atoms whose momenta differ by discrete units of the photon recoil. Subsequent laser pulses then induce the components of the atomic wave functions to recombine and constructively or destructively interfere (see “Methods” for more details). The final result is an interference pattern that provides a phase-sensitive readout of effects such as accelerations, rotations, gravity, and subtle forces that could signify new physics acting on matter. Due to the quantum nature of ultracold atomic gases and the phase sensitivity of matter waves in extended freefall, atom interferometry can enable unprecedented applications for both applied and fundamental physics⁷. Such applications include gravimetry^8,9,10,11,12 and gravity gradiometry^13,14,15, investigating gravity at microscopic scales¹⁶, tests of the universality of free fall (UFF) with quantum matter^17,18,19 and measurement of relativistic effects with delocalized quantum superpositions^{20,21,22,23,24,25,26}, measurements of fundamental constants^{27,28,29,30,31}, realization of an optical mass reference³², tests of contemporary dark matter³³ and dark energy^34,35 candidates, and tests of theories of modified gravity^36,37.

On Earth, atom interferometers of various designs have been studied to capitalize on the favorable quadratic scaling of inertial-force sensitivities with matter-wave evolution times between the interferometry light pulses. Notably, high-precision measurements of UFF have been achieved with atom interferometers utilizing 10-meter-tall atomic fountains operating in Stanford University¹⁸ and the Wuhan Institute of Physics and Mathematics¹⁷. Further, long-baseline interferometers using alkaline earth metals are under construction at the Leibniz University of Hanover³⁸ and Stanford University³⁹ for precision fundamental physics experiments. Quantum gas experiments at the 100-meter drop tower in Bremen Germany have provided an enabling platform for developing cooling protocols and demonstrating atom interferometry in microgravity^40,41,42. The Einstein Elevator and the GraviTower Pro expand this capability with greater than 100 drops per day providing 4 and 2.5 s of freefall, respectively^43,44. Experiments have also been conducted in suborbital parabolic flights to detect inertial effects⁴⁵ and to test the UFF with a dual-species atom interferometer in microgravity⁴⁶. Finally, the 100-meter-long MAGIS interferometer³⁹, the MIGA large scale atom interferometer⁴⁷, and the AION interferometer network⁴⁸ are being developed for gravitational wave detection. Such work is expected to continue in multiple terrestrial facilities dedicated to the fundamental study of ultracold gases in microgravity conditions.

Developing matter-wave interferometry to operate in a space environment can address similar goals with significant advantages, including: (1) access to essentially unlimited freefall time in a compact instrument, (2) enabling novel schemes such as extreme adiabatic cooling and delta-kick collimation for achieving ultra-low effective temperatures in atomic gases^2,3,4, and (3) implementation and maturation of this quantum technology on a flight platform to support upcoming space missions where high-precision inertial sensing will be needed, including Earth observers and missions to test fundamental physics^{36,49,50,51,52}. Even for trapped atom interferometers, which have demonstrated unprecedented coherence times for interferometry and provide localized gravity measurements⁵³, microgravity can be beneficial since the need for a relatively strong potential to support the atoms against gravity is no longer a constraint. In 2017, the MAIUS sounding rocket mission provided a seminal demonstration of cold atom technologies by operating for 6 min in-space flight and achieved the production of BEC of ⁸⁷Rb atoms along with Bragg splitting and matter-wave interferometry^52,54. As part of the commissioning efforts for SM-3 in the CAL instrument, a dual-species atom interferometer in space was also recently demonstrated using simultaneously interrogated ⁴¹K and ⁸⁷Rb atoms with a single-laser atom interferometer beam⁶.

We report on a series of seminal experiments in which CAL investigators performed pathfinding investigations with single-species ⁸⁷Rb BECs to mature atom interferometry and quantum sensing on an Earth orbiting platform. Our results include (1) the demonstration of high-visibility Mach–Zehnder interferometry (MZI) at relatively short times, (2) signatures of atom interferometer sensitivities and visibility degradation due to the ISS vibration environment, (3) the use of shear-Ramsey atom interferometry to extract contrast and phase shifts in a single experimental run, (4) observation of interference fringes persisting for greater than 150 ms during freefall in the compact CAL science cell, and (5) the use of the CAL AI to perform a photon recoil measurement to demonstrate its utility as the first quantum matter-wave sensor in space.

Results

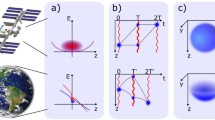
The CAL AI permits sensing of inertial forces onboard the ISS and is intended as a technology demonstrator for future space-borne fundamental physics experiments. Figure 1a gives an overview of the interior layout within the physics package at the heart of SM-3. This atom-interferometer-capable science module is based on the original CAL design^1,2. Primary upgrades are a redesigned atom chip and the inclusion of a laser beam, which propagates from the atom interferometer platform above the science cell, through the center of a 3-mm diameter on-chip window (and through a set of atom-chip wires separated by 2 mm), and is retro-reflected from an in-vacuum mirror at the bottom of the science cell. The CAL AI utilizes Bragg diffraction laser pulses^11,55 operating at 785 nm for matter-wave beam splitters and mirrors. The Bragg beam waist is approximately 0.5 mm (1/e²) within the science cell, and propagates at a 4° angle off the normal to the atom chip such that the laser wave vector k is nominally aligned with Earth’s gravity vector along z. Specifics of the design and implementation of the CAL AI were given previously⁶, with additional details in the “Methods” section.

Fig. 1: Atom interferometer set up onboard the ISS.

a Cut of the upper region of the physics package of SM-3 to expose the interior components and the path of the retro-reflected Bragg beam (red) inside the vacuum system. The expanded region shows the beam entering the vacuum chamber through a window and between pairs of Z- and U-traces (blue) and H-traces (yellow) on the atom chip. Dimensions of the upper vacuum cell are given to illustrate the compactness of the science region accommodating our AI experiments. Note that the entire CAL payload occupies only 0.4 m³ on the ISS with a mass of approximately 230 kg. b Space-time diagram of an ideal Mach–Zehnder interferometer, where three retro-reflected laser pulses (red) are applied in a sequence of $\frac{\pi }{2}$-π-$\frac{\pi }{2}$ pulses, with pulse separation times T, to create a superposition and then recombination of the initial atom cloud into two motional states ($\left| {p}_{+}\right\rangle$ and $\left| {p}_{0}\right\rangle$ given by blue and yellow clouds respectively). c Ramsey atom interferometer diagram using a sequence of $\frac{\pi }{2}$-$\frac{\pi }{2}$ pulses to explore shear-wave atom interferometry at long time-of-flight t_TOF. For sufficiently short T, used for photon recoil measurements, the outputs are similar to that of the MZI.

For all experiments described in this article, ultracold gases of bosonic ⁸⁷Rb are produced in the flight system using an atom-chip-based BEC source, producing up to 10⁴ degenerate atoms approximately once per minute^1,2,6. Thereafter, a multi-stage transport protocol is used to quasi-adiabatically displace the magnetic trap minimum to position the atoms near the center of the Bragg beam, approximately 1 mm below the on-chip window. After transport, atoms in the $\left| F=2,\, {m}_{F}=2\right\rangle$ internal state are confined in a nearly harmonic potential with measured trap frequencies (ω_x, ω_y, ω_z) = 2π × (13.8, 23.4, 18.8) Hz, characterized using dual-axis absorption imaging. Atoms rapidly released from this center trap serve as the starting point for the following atom-interferometer experiments.

Mach–Zehnder interferometer

A three-pulse MZI⁸, illustrated in Fig. 1b, was first demonstrated in Earth’s orbit including eight repeated measurement campaigns over a span of 38 days. Here, ⁸⁷Rb atoms were prepared and released from the center trap such that the cloud expands to less than 100 μm FWHM over 100 ms of freefall, and moves with the center-of-mass velocity v = p/m = (v_x, v_y, v_z) = (2.0, 1.0, 7.8) mm/s. The relatively large initial velocity (p₀/m = v₀ ≈ v_z) along the laser wave vector k was intentionally applied so that the Bragg transitions to $\left| {p}_{\pm }\right\rangle \equiv \left| {p}_{0}\pm 2\hslash k\right\rangle$ are nondegenerate, as this choice simplifies the interferometer operation and suppresses double diffraction⁵⁶ (see “Methods” for details on the relevant Bragg processes). For this demonstration, the Bragg laser contains two frequencies separated by δ = 34.82 kHz to compensate for the Doppler shift of the ⁸⁷Rb atoms along the direction of the beam. During the first 17 ms of freefall, atoms were transferred to the magnetically-insensitive $\left| F=2,\, {m}_{F}=0\right\rangle$ state via Adiabatic Rapid Passage, leaving no atoms detected in any of the unwanted m_F ≠ 0 levels (see “Methods”). Thereafter, three square pulses of the Bragg laser approximating (π/2, π, π/2) transitions were applied for (0.13 ms, 0.25 ms, 0.13 ms), respectively, with T = 0.5 ms pulse separation times.

The phase difference ϕ between the two paths of a MZI is sensitive to external perturbations on the atoms, including accelerations a, rotations Ω, and the Bragg laser phase⁵⁷. In leading order, ϕ can be expressed by:

$$\phi=\left[{{{{\boldsymbol{k}}}}}_{{{{\bf{eff}}}}}\cdot {{{\boldsymbol{a}}}}+2({{{{\boldsymbol{k}}}}}_{{{{\bf{eff}}}}}\times {{{\boldsymbol{v}}}})\cdot {{{\mathbf{\Omega }}}}\right]{T}^{2}+{\phi }_{{{{\rm{laser}}}}},$$

(1)

where k_eff is the effective two-photon wave vector with amplitude ≈ 2k that defines the transferred momentum during diffraction. To map out an interference fringe, the differential phase of two simultaneous frequency tones in the final Bragg laser pulse ϕ_laser was varied between 0 and 360°. After the final Bragg pulse, the atoms were allowed to propagate freely for t_TOF = 15 ms so that the different momentum components, constituting the exit ports of the atom interferometer, could separate in position. The populations of atoms N₀ and N₊, occupying the $\left| {p}_{0}\right\rangle$ and $\left| {p}_{+}\right\rangle$ output momentum states, respectively, were then measured using absorption imaging as shown in the lower inset of Fig. 2. Note that a small population in the spurious exit port N₋, corresponding to atoms driven toward the atom chip via off-resonant transitions into the $\left| {p}_{-}\right\rangle$ state, was also produced as a result of the finite cloud temperature, moderate two-frequency detunings of the Bragg laser, and hardware limitations that practically inhibited the use of smooth (e.g., Gaussian-shaped) pulses^52,54,56. Figure 2 shows the characteristic sinusoidal variation of the excitation fraction N₊/N_tot with ϕ_laser (see “Methods” Eq. (7)), providing a clear and repeatable signature of matter-wave interference with visibility V = 0.36(2).

Fig. 2: Mach–Zehnder interferometry and the influence of vibrations on the ISS.

The main plot shows the relative population of rubidium atoms in the $\left| {p}_{+}\right\rangle$ state after a Mach–Zehnder pulse sequence with T = 0.5 ms duration between Bragg pulses. Scanning the phase ϕ_laser of the traveling wave for the final laser pulse reveals a corresponding sinusoidal variation of N₊/N_tot. Eight independent data sets were analyzed, with up-to eight repetitions for each set. To increase the signal-to-noise ratio, the repeated images in each phase set were first summed, and the corresponding averaged images were fit to Thomas–Fermi profiles as described in “Methods”. The data plotted in light blue then yield the average N₊/N_tot for each ϕ_laser, with error bars given by the standard deviations. (Lower Inset) The first set of averaged absorption images after MZI, showing atoms oscillating between the $\left| {p}_{+}\right\rangle$ and $\left| {p}_{0}\right\rangle$ momentum states as ϕ_laser is increased. A small population occupying the $\left| {p}_{-}\right\rangle$ state can also be seen. (Upper Inset) The influence of ISS vibrations is modeled (see “Methods”), with 2 ms granularity, to illustrate limitations to the atom-interferometer visibility for single-source ⁸⁷Rb BECs at larger T. Data for the acceleration a_z in the z-direction from the SAMS 121F04 accelerometer on the ISS was used for each day during which the MZI experiments were conducted, with dashed lines to guide the eye. Experimental results for T = 0.5 ms and 10 ms are included (orange triangles) for comparison.

The limited visibility of the interferometer with short T can be attributed to two effects: (1) Condensates released from the trap expand due to mean-field interactions, leading to a Thomas–Fermi velocity spread along the k-direction of Δv₀ ≈ 1.6 mm/s. Both the Bragg pulse efficiencies and the phases developed during free evolution depend on the atomic velocity. (2) Analysis of the Bragg pulse efficiencies suggests that the atoms experience a relative spread in Bragg beam intensity of approximately ±25%. This variation is significantly larger than the approximately 5% variation expected from the spatial inhomogeneity of the Bragg beam if it had an ideal Gaussian profile. However, optical simulations indicate that the collimation lens used in the Bragg beam fiber coupler produces an imperfect Gaussian with substantial wings at large radii. The wings are clipped by the 2-millimeter aperture given by the atom-chip traces (see “Methods”) and the resulting diffraction pattern produces significant intensity modulation. We confirmed this effect by applying long-duration pulses of Bragg light to a ⁸⁷Rb BEC and observing the transverse motional excitation produced by the BEC propagating through this diffraction pattern.

Increasing T from 0.5 ms to 10 ms causes the interferometer visibility to drop to a value consistent with zero. However, the effective contrast at longer T was determined by fitting the histograms of the excitation fractions at T = 0.5 ms and T = 10 ms with a Probability Distribution Function (PDF) for a double-peaked distribution indicative of a sinusoidal excitation fraction with Gaussian noise (given by Eq. (9)). The effective contrast decreases by approximately 30% as T is increased from 0.5 ms to 10 ms, signifying that phase noise is still dominating the signal at T = 10 ms⁵⁸, but other sources of visibility degradation are also growing as T is increased. The rising influence of phase noise with T is consistent with the simulated T-dependent visibility degradation, shown in the upper inset of Fig. 2, which was modeled using ISS-SAMS 121F04 accelerometer data measured along the z direction. Details of the PDF fits and the visibility degradation simulation due to ISS vibrations are given in the “Methods” section.

Shear-wave atom interferometry

In Fig. 1c, a two-pulse Ramsey interferometer geometry⁵⁹ is illustrated. Here, two π/2 pulses of the Bragg laser beam are applied in relatively rapid succession so that the atomic wave functions split from the first laser pulse still sufficiently overlap as to interfere and reveal a spatially resolved interference pattern at imaging. Depending on the expansion energy of the atoms and the freefall time after the second pulse t_TOF, as well as the timings of the interferometer sequence and ϕ_laser, such shear-wave interferometers⁶⁰ can provide direct information about both the atoms and the experimental apparatus. In particular, the spatially resolved interference pattern can in general be a very useful tool for diagnosing phase shifts that vary across the atom cloud as for instance induced by optical dipole forces from the Bragg beam or further diffraction from stray laser light⁵².

For this interferometer arrangement, sufficient t_TOF is implemented after the pulse sequence so that spatial fringes are visible in a single experimental shot, as shown in Fig. 3. The fringes persist for over 150 ms time of flight, which would be challenging to observe in a similarly compact terrestrial instrument. Here, two π/2 Bragg laser pulses, each with a square-pulse time distribution lasting 0.16 ms and separated by 1 ms, are applied 2 ms after release of the BEC from the trap. Approximately 60 ms after the second pulse, weak stripe patterns emerge in both the undiffracted cloud ($\left| {p}_{0}\right\rangle$ state) and the cloud that was diffracted by the Bragg beam toward the atom chip (defined here as the $\left| {p}_{+}\right\rangle$ state). A weak third cloud, not shown in Fig. 3, consists of atoms off-resonantly excited to the $\left| {p}_{-}\right\rangle$ state. The images cannot be reliably analyzed for times greater than 150 ms because atoms in the $\left| {p}_{+}\right\rangle$ state propagate into the region near the chip which exhibits degraded signal quality and, eventually the ultracold cloud is destroyed as the atoms come into contact with the chip itself. Due to resolution limits of the detection system and the size of the BEC being smaller than the fringe spacing for very short times, the nonlinear behavior of the fringe spacing shown in Fig. 3 could not be resolved. However, there is promise in exploring this nonlinear regime with greater resolution in the future.

Fig. 3: Single shot shear-Ramsey interference in orbit.

a Fringe spacing λ_fr of a shear-Ramsey interferometer aboard CAL as a function of the free-evolution time t_TOF of the BEC after release from the magnetic trap. The BEC is split coherently with two π/2 Bragg pulses each lasting 0.16 ms with a separation of 1.0 ms between them to achieve the characteristic interference pattern for both exit ports within a single experimental run. The measured fringe spacings (blue dots for data and dashed line for the fit) show excellent agreement with the theoretical prediction (purple line) based on the expansion dynamics of the BEC in the Thomas–Fermi regime and a proper treatment of the finite pulse duration as expressed by Eq. (2). Exemplary 2D-density distributions for two different expansion times are shown in the top row (189 × 189 μm² area, with densities normalized for each image individually) with the integrated 1D densities (black lines) displayed below together with the fit results (red lines). b The contrast of the interference fringes (green dots) increases with expansion time and saturates at a maximum of around 45%. Error bars represent 1-sigma confidence bounds of fitting the density distributions.

Fits to extract the contrast and fringe spacing for the two primary clouds were obtained by first integrating the density distribution of the clouds along a direction parallel to the stripes, and then fitting each cloud to a Gaussian distribution with sinusoidal oscillations and a constant phase difference of π. Figure 3 gives the measured fringe spacing λ_fr and contrast as a function of t_TOF. Each point represents data from a single experimental run with error bars given by the fit uncertainty. A theoretical prediction for the fringe spacing (purple line) with no adjustable parameters shows excellent agreement with the fringe spacing data. The model, which takes into account the expansion dynamics of a BEC in the time-dependent Thomas–Fermi approximation, gives the following result for the fringe spacing⁶¹:

$${\lambda }_{{{{\rm{fr}}}}}({t}_{{{{\rm{TOF}}}}})=\frac{\pi }{k}\frac{R({t}_{{{{\rm{TOF}}}}})}{{T}_{{{{\rm{eff}}}}}\dot{R}({t}_{{{{\rm{TOF}}}}})}$$

(2)

Here, R(t_TOF) is the Thomas–Fermi radius, which follows from the scaling approach⁶². The asymptotic constant expansion rate is determined by the initial trap frequencies and the number of atoms and T_eff, the effective time separation of the two Bragg pulses taking into account the finite duration of each pulse. We calculated T_eff by solving the Schrödinger equation in the presence of the Bragg optical potential, giving a value of T_eff = 1.204 ms. When instead we fit the data to determine T_eff, we obtain a value of 1.21(1) ms, in excellent agreement with the calculated value.

Because the shear-Ramsey interferometer yields an interference pattern in a single run, it is not sensitive to dephasing by vibrational phase noise. The ability to observe the pattern after long freefall times illustrates the potential for exploring long-time interference effects in microgravity. A similar terrestrial experiment, limited to expansion times of a few milliseconds, illustrated the effects of atomic interactions on the fringe patterns⁶³. For our weak initial trap and low atom numbers, however, interactions between the two clouds can be safely neglected.

Photon recoil measurement

The two-pulse Ramsey interferometer configuration described in the previous section can also be used to perform a proof-of-principle recoil frequency measurement. Notably, in between the two Bragg pulses, the atomic wave packets develop a phase difference that depends on the recoil frequency ω_r ≡ ℏk²/2m. High-precision terrestrial measurements of ω_r are used to determine the fine structure constant^28,29. These efforts could be supported in microgravity by the availability of long interrogation times and low atom-cloud expansion rates. Many systematic errors are reduced for atoms remaining in a fixed position relative to the apparatus, and the impact of errors that impart a fixed phase shift (including laser phase errors⁶⁴) is reduced at longer interrogation times where the recoil phase is larger. Alternatively, even low-precision recoil frequency measurements could provide a useful method to calibrate the Bragg wave number k in a space environment where no conventional wavemeter instrument is available.

The phase evolution of a free atom is governed by its kinetic energy p²/2m. The interferometer is sensitive to the phase difference between wave packets with momenta p_± and p₀, which results in ϕ_atom = −(4ω_r ± 2kv₀)T for pulse separation time T (see “Methods” Eq. (5)). In addition, the laser phase evolves as δT + ϕ₀, where δ is the difference between frequencies in the Bragg laser and ϕ₀ is the phase offset of the second Bragg pulse. The measured phase (from “Methods” Eq. (8)) is therefore:

$$\phi=-(4{\omega }_{r}\pm 2k{v}_{0})T+\delta T+{\phi }_{0}.$$

(3)

In order to interferometrically determine both ω_r and v₀, we measure ϕ as a function of T for both signs of the Bragg momentum kick.

In these experiments v₀ ≈ 2.5 mm/s, so for the $\left| {p}_{0}\right\rangle \to \left| {p}_{+}\right\rangle$ transition away from the atom chip we set δ = 2π × 21 kHz and for $\left| {p}_{0}\right\rangle \to \left| {p}_{-}\right\rangle$ we set δ = 2π × 9 kHz. The net phase was determined by scanning ϕ₀, as shown in the inset of Fig. 4. The data are fit to a sinusoidal function to extract ϕ_atom at various values of T, with results shown in the main plot of Fig. 4. From the slopes of these lines, we find ω_r = 2π × 3.77(6) kHz and v₀ = 2.4(1) mm/s. The recoil frequency is consistent with the expected value of 3.72 kHz, and the initial velocity is consistent with time-of-flight measurements.

Fig. 4: Recoil frequency measurement in a Ramsey interferometer.

Accumulated phase difference of the atomic wave packets as a function of interrogation time T. Circled points are obtained by fitting interference fringes as shown in the inset, and error bars represent the estimated fit uncertainties. The lines are linear fits for the Bragg transition $\left| {p}_{0}\right\rangle \to \left| {p}_{+}\right\rangle$ with frequency δ = 2π × 21 kHz and $\left| {p}_{0}\right\rangle \to \left| {p}_{-}\right\rangle$ with 2π × 9 kHz. The phases for the two cases differ at T = 0 because of different couplings to their respective off-resonant momentum states.

The precision of these measurements is low due to the limited interrogation time. At the maximum usable time of T = 0.75 ms, the interference visibility has dropped to about 0.07 which is consistent with the expected coherence time R₀/v_B ≈ 0.7 ms. Here, R₀ ≈ 8 μm is the initial condensate size in the trap and v_B ≡ 2ℏk/m = 11.7 mm/s denotes the Bragg recoil velocity. Longer interaction times could be achieved by starting with atoms in a weaker trap, but a more effective method would be to use a closed interferometer configuration such a three-pulse contrast interferometer⁶⁵.

Discussion

In this article, we reported on three pathfinding experiments based on matter-wave interference of ultracold rubidium gases in orbital microgravity, which were each found to be robust and repeatable over timescales spanning months. We utilized the long freefall times available for atoms in space within the relatively compact CAL apparatus and compared the atom interferometer performance with ISS environmental data to gain insight into the high-frequency vibration environment experienced by the instrument. We further employed shear-wave interferometry to demonstrate the effects of matter-wave interference that are clearly visible in a single experimental run for more than 150 ms of freefall. Additionally, photon recoil measurements served to provide characterizations of the Bragg wave number using only the atomic feedback resulting from interferometer sequences, demonstrating the utility of CAL as the first quantum matter-wave sensor in space.

These efforts and findings serve as important milestones for maturing space-based atom interferometry for numerous mission concepts. Notably, observation of high-contrast interference fringes after long freefall times and within a single experimental run, as demonstrated here with shear-wave interferometry, is a technique that can be utilized for precision sensors³⁶, allowing for shot-to-shot determination of AI contrast and phase shifts. AI-based measurements of the photon recoil in space is also promising for multiple applications. Experiments to determine the fine structure constant^28,29 are expected to benefit from the extended freefall environment of microgravity for higher precision and reduced systematic errors by achieving long T in a relatively compact and freely-falling apparatus. Additionally, measuring the frequency of the AI laser via atomic feedback, as directly demonstrated in this article, will enable characterization and control over leading systematics for future missions and can remove the need for launching dedicated wave meters for the AI lasers. Finally, understanding the influence of ISS vibrations to the Rb-based AI allows researchers to understand limitations and optimize near-term experiments using differential interferometry for fundamental physics investigations on the ISS.

Significant advancements and new sensing capabilities are expected to arise as differential interferometry (using either spatially-separated atom interferometers with the same atomic species in a gradiometer configuration or simultaneous interrogation of two distinct atomic species) is further explored with CAL⁵⁸. The CAL AI is designed for precision dual-species simultaneous interferometry with ⁸⁷Rb and ³⁹K or ⁴¹K, interrogated via absorption imaging for phase-sensitive measurements with two dissimilar quantum test masses. The operating frequency of the Bragg laser at 785 nm is near the magic wavelength where the two-photon Rabi frequencies are essentially identical for Rb and K species³⁶. Hence, differential atom interferometer measurements in CAL are expected to be minimally impacted by common-mode noise sources including vibrations and laser noise. Initial experiments⁶ on CAL demonstrating differential atom interferometry with ⁸⁷Rb and ⁴¹K quantum gases at short T are particularly promising for PI-led efforts aiming to extend the capabilities of space-based dual-species differential atom interferometry.

A replacement for SM-3 on the ISS is already designed for reduced scattering of the beam before it enters the science cell and, hence, minimizing wavefront degradation. As a CAL follow-on, the BECCAL mission⁴⁹ is also expected to include numerous mechanisms to optimize visibility and allow long interrogation times with differential atom interferometers, including using relatively large beams and employing rotation compensation schemes to counter the effects of the ISS rotation as it orbits the Earth.

The experiments detailed in this article therefore serve as pathfinders for proposed space missions relying on sustained matter-wave interferometry with unprecedented sensitivity to inertial and fundamental physical forces, including tests of the Einstein Equivalence Principle^36,51,66, gravitational wave detectors^39,48,67, direct detection of dark matter and dark energy candidates^34,36, Earth and planetary sciences including geodesy, seismology, and sub-surface mapping^15,50,68, and advanced navigation and drag-free referencing^69,70. With the successful utilization of CAL SM-3 for seminal, long-term PI-led studies of atom interferometry in Earth’s orbit, this first-of-its kind instrument has brought quantum sensing via atom interferometry into the list of technologies matured and flight-qualified by NASA toward expanding our fundamental understanding and exploration of the cosmos.

Methods

Upgraded Cold Atom Lab facility

The CAL AI is designed to be sensitive to the force of Earth’s gravity, rotations of the ISS, and also to utilize differential measurements from atom interferometers consisting of simultaneously interrogated rubidium and potassium gases. To this end, the on-orbit upgraded SM-3 includes four primary changes from the original CAL design to enable atom interferometry⁶, the first three of which are illustrated in Fig. 1a. (1) Light from the Bragg laser system was delivered into the SM-3 via polarization maintaining optical fibers and routed to the atom interferometer platform, which is the optical bench used to shape and direct the beam as part of the upgraded physics package provided by ColdQuanta. (2) The atom chip was upgraded to allow the beam to propagate through the center of the 3-mm diameter window on the atom chip, which also serves as the top surface of the evacuated science cell. Passing the beam through the chip, as opposed to passing through the cell windows horizontal to the chip, was necessary to accommodate the desired orientation of the Bragg beam with respect to gravity. Providing clearance for the laser required the atom chip traces to be moved away from the center of the window, resulting in two pairs of in-vacuum traces (Z- and U-traces respectively), separated by approximately 2 mm along the x-axis, and a pair of wires on the atmospheric side of the chip (H-traces), separated by approximately 3 mm and oriented along the y-axis. (3) An in-vacuum mirror was mounted in the science cell on the side opposite to the atom chip, slightly off center and oriented at a 4° angle to allow retro-reflection of the Bragg beam while assuring clearance for the push beam and atom flux from the 2D MOT². (4) The optical path for the through-chip imaging system was rerouted to accommodate detection through the chip window in combination with the atom interferometer platform.

The fiber-coupled Bragg laser was included as part of the original CAL flight system in anticipation of SM-3. Coherent light is provided by a single-wavelength external cavity diode laser operating at nominally 785 nm, which exhibits a narrow linewidth (<200 kHz) and continuous output of tens of milliwatts. The light is directed via optical fibers from the single locker to the quad-locker² where it is amplified using a Tapered Amplifier (TA). The TA input is shared between the 785 nm and 780 nm seed lasers and the output is directed either to the cooling light or atom interferometer beam paths via optical switches. Before the 785-nm light is directed into SM-3, it is passed through an acousto-optic modulator, operating at approximately 79 MHz as controlled by an arbitrary waveform generator (National Instruments PXI-5422). This design allows multiple frequency components to be written onto the Bragg laser. A narrow bandpass optical filter (Semrock Laser Clean-up MaxLine 785/3) on the atom interferometer platform passes 785-nm light while suppressing residual light near 780 nm by over three orders of magnitude, in order to avoid resonant scattering. The resultant Bragg beam was approximately collimated within the CAL science cell and retroreflected by the in-vacuum mirror with overlap of the incident and reflected beam, measured before launch to the ISS, better than 0.1 mm.

Source control and detection

Transfer of ⁸⁷Rb atoms from the magnetically sensitive $\left| F=2,\, {m}_{F}=2\right\rangle$ state (within the ²S_1/2 manifold) to the magnetically insensitive $\left| F=2,\,m_F=0\right\rangle$ state is achieved with high-field adiabatic rapid passage (ARP)⁷¹. Here, the second-order Zeeman shift is made to be much larger than the Rabi frequency for RF coupling of atoms among magnetic sublevels, breaking the degeneracy that would otherwise arise when attempting to drive atoms among the five m_F -levels in the F = 2 manifold. At an applied bias field of 29.2 G, the splitting between the sublevels is approximately 20 MHz, and the second-order Zeeman shift is 120 kHz. In comparison, the RF Rabi frequency for the $\left| F=2,\,m_F=2\right\rangle \to \left| F=2,\,m_F=1\right\rangle$ transitions is approximately 9 kHz. The atoms are initially released from the center-trap and allowed to freefall for 5.2 ms while a B_x ≈ 31 G bias field along the x-axis is applied and allowed to stabilize. Single-tone RF at 20.4 MHz is then pulsed on for 5 ms while B_x is linearly ramped down to approximately 29.2 G. Using this method, an ultracold rubidium gas is transferred from the $\left| F=2,\,m_F=2\right\rangle$ to the $\left| F=2,\,m_F=0\right\rangle$ state with no detectable signal remaining in other m_F states. Thereafter, B_x was turned off and a 10 mG magnetic field was applied along the y direction to maintain a field quantization axis throughout the freefall and atom interferometer stages.

Atomic density distributions are measured via one of two absorption imaging systems, which are nearly identical to those of the original CAL science module², aside from the change to the through-chip imaging path discussed above. Here, the horizontal imaging system is used for detection of interference as it images the x–z plane. The vertical imaging system observes the atoms in the x–y plane through the atom chip and was used to help position atoms in the Bragg beam. At T = 0.5 ms atom interferometer interrogation time, the average signal variation at a fixed ϕ_laser = 0° is σ = 0.06, approximately an order of magnitude larger than the expected quantum projection-noise limit⁷² for an ensemble of N_tot ~ 5 × 10³ atoms. In comparison, the influence of detection noise and instabilities in the Bragg-pulse amplitudes was measured using an imbalance in timing between MZI pulses, with T₁ = 10 ms and T₂ = 8 ms so that the interferometer would not close at the final AI pulse, giving a mean excitation fraction of 0.53 with σ = 0.03.

Bragg atom interferometry

The principles of light-pulse atom interferometry have been reviewed in detail elsewhere^8,59,73. Here, we summarize the related theory for understanding the phases-shifts and fringes observed in Figs. 2–4. For simplicity, we consider the ideal first-order Bragg process driven by a light pulse with two frequency components ω₁ and ω₂, counter-propagating wave vectors k₁ and k₂, and frequency difference δ ≡ ω₁ − ω₂. For small detunings relevant to this study, k₁ ≃ k₂ = k. The Bragg light pulse coherently couples atoms occupying an initial momentum state $\left| {p}_{0}\right\rangle$ to the final states $\left| {p}_{\pm }\right\rangle \equiv \left| {p}_{0}\pm 2\hslash k\right\rangle$. Neglecting additional inertial forces, the evolution of the quantum state $\left| {{\Psi }}(t)\right\rangle$ can be expressed in terms of time-dependent coefficients c₀ and c_± by:

$$\left| {{\Psi }}(t)\right\rangle={c}_{0}(t)\, \left| {p}_{0}\right\rangle \exp \left[-\frac{i}{\hslash }\frac{{p}_{0}^{2}}{2m}t\right]+{c}_{\pm }(t)\, \left| {p}_{\pm }\right\rangle \exp \left[-\frac{i}{\hslash }\frac{{({p}_{0}\pm 2\hslash k)}^{2}}{2m}t\right]$$

(4)

which, up to an overall phase, is equivalent to:

$$\left| {{\Psi }}(t)\right\rangle={c}_{0}(t)\, \left| {p}_{0}\right\rangle+{c}_{\pm }(t)\, \left| {p}_{\pm }\right\rangle {e}^{-i(4{\omega }_{r}\pm 2k{v}_{0})t},$$

(5)

with recoil frequency ω_r ≡ ℏk²/2m and initial velocity v₀ = p₀/m along k. If the two levels are coupled by a pulse with duration τ, Rabi frequency Ω, and frequency δ, then the detuning is Δ_± = 4ω_r ± 2kv₀ − δ and the probability of finding an atom in the $\left| {p}_{\pm }\right\rangle$ state reads:

$$| {c}_{\pm }(\tau ){| }^{2}=\frac{{{{\Omega}}}^{2}}{{{{\Omega}}}^{2}+{{{\Delta }}}_{\pm }^{2}}{\sin^2 \left(\frac{\sqrt{{{{\Omega}}}^{2}+{{{\Delta }}}_{\pm }^{2}}}{2}\tau \right)}.$$

(6)

For the resonant case Δ_± = 0, an equal superposition of $\left| {p}_{0}\right\rangle$ and $\left| {p}_{\pm }\right\rangle$ states is prepared for a π/2 pulse, where Ωτ = π/2 and atoms are fully transferred between states for a π pulse, when Ωτ = π.

Matter-wave interference can be observed by applying a series of π/2 and π pulses, with pulse separation time T, as illustrated in Fig. 1. For each geometry, the output phase of the atom interferometer is observable from the population of atoms (N₀ or N₊) occupying one of two final momentum states ($\left| {p}_{0}\right\rangle$ or $\left| {p}_{+}\right\rangle$, respectively) as:

$$\frac{{N}_{0}}{{N}_{{{{\rm{tot}}}}}}=\frac{{N}_{{{{\rm{mean}}}}}}{{N}_{{{{\rm{tot}}}}}}(1+V\cos \phi )$$

(7)

where N₀ + N₊ = N_tot, N_mean is the number of atoms occupying N₀ averaged over all interferometer phases ϕ, and V gives the atom interferometer visibility. Therefore, observing the fraction of atoms in each final momentum state allows us to extract the accumulated phase modulo 2π. The measured phase can be decomposed into contributions from the Bragg laser and the atomic wave function evolution⁵⁷:

$$\phi={\phi }_{{{{\rm{laser}}}}}+{\phi }_{{{{\rm{atom}}}}}$$

(8)

These contributions depend on the environment and forces experienced by the atoms, the frequency stability of the laser pulses, geometric topological phase shifts, and the geometry of the atom interferometer itself ⁵⁹.

Fringe detection and data analysis

All interferometer data are acquired via absorption imaging, which yields the spatial distribution of the atoms at the end of the experimental sequence. Images with no atoms or other obvious errors are discarded. For the Mach–Zehnder and recoil measurements, images are cropped to a region of interest around the expected position of each output cloud, and the clouds are fit to independent Thomas–Fermi profiles in order to extract the atom number. All fits are confirmed visually. For the shear Ramsey atom interferometer measurements, absorption images were first processed using a principal component analysis of the whole data set to remove background imaging noise⁷⁴. The resulting density profiles were then fitted to the Ramsey fringe model described in the main text.

For the recoil frequency measurements, data sets of about 50 points are acquired by scanning the Bragg phase ϕ₀ from 0 to 2π. The resulting curves are fit to the form of Eq. (7), where here ϕ_atom = −4(ω_r ± 2kv₀)T and ϕ_laser = δT + ϕ₀. Uncertainty in ϕ is determined by the bounds for doubling the quality-of-fit parameter χ². The uncertainty ranges from about 0.5 rad at small T up to as much as 2 rad for large T, which is consistent with the reduction in atom interferometer visibility at larger T. In comparison, uncertainties in ϕ₀, δ and T are negligible.

Analysis of Mach–Zehnder interferometer output

To understand whether the loss of visibility observed at T = 10 ms is attributed to phase noise (e.g., induced by ISS vibrations) or from other factors such as dipole forces across the atom cloud, the histograms for the excitation fractions for both T = 0.5 ms and T = 10 ms, shown in Fig. 5, were fit to the probability density function (PDF) for a pure sine wave (double-peaked distribution with amplitude A and offset P₀) convoluted with a Gaussian noise distribution with standard deviation σ_P⁴⁵:

$$F(x)=N\int_{\!\!\!{P}_{0}-A}^{{P}_{0}+A}\,dx^{\prime} {\left[1-{\left(\frac{{P}_{0}-x^{\prime} }{A}\right)}^{2}\right]}^{-1/2}\times \frac{1}{{\sigma }_{P}\sqrt{2\pi }}\exp \left(-\frac{{(x-x^{\prime} )}^{2}}{2{\sigma }_{P}^{2}}\right),$$

(9)

with normalization factor N. This model is well suited for distinguishing the influence of phase noise, which will wash out the sinusoidal dependence of N₊/N_tot vs. ϕ_laser but will maintain the double-peaked density distribution, compared to other sources of noise or visibility loss that would also reduce A or increase σ_P in the PDF.

Fig. 5: Histogram analysis of Mach–Zehnder interferometer signals.

The relative population of rubidium atoms in the excited state after Mach–Zehnder pulse sequences: (left-hand side) with respect to ϕ_laser and the corresponding histograms (right-hand side). For both (a) T = 0.5 ms, and (b) T = 10 ms, N₊/N_tot was determined by fitting the images to Gaussian profiles for each experimental run and the fitting errors, shown for each N₊/N_tot, were propagated to the corresponding histogram errors using a Monte Carlo simulation. The histograms were fit with a PDF, described by Eq. (9), corresponding to a double-peaked distribution with amplitude A and offset P₀ and broadened into a nearly flat-top distribution by Gaussian noise with amplitude σ_P (red curves). Although the characteristic sinusoidal dependence of N₊/N_tot with respect to ϕ_laser is not observable for the T = 10 ms data, a reasonable fit of the histogram with the double-peaked PDF, giving C = 0.24 and SNR = 2.4, signifies that phase-noise is a major cause of the loss of AI visibility as T is increased to 10 ms for the CAL single-species ⁸⁷Rb atom interferometer.

For each data set, the histogram errors were extracted from N₊/N_tot fitting errors using Monte Carlo error propagation⁷⁵. The fitted PDF parameters for the T = 0.5 ms data are P₀(0.5 ms) = 0.476(8), A(0.5 ms) = 0.163(8), and σ_P(0.5 ms) = 0.055(9). It is evident that the T = 10 ms data does not exhibit the characteristic sinusoidal dependence of the excitation fraction with ϕ_laser that is clearly seen for the T = 0.5 ms data, indicating a visibility at T = 10 ms consistent with zero. However, the T = 10 ms histogram still exhibits a flat-top profile that agreed well with a PDF fit with P₀(10 ms) = 0.50(1), A(10 ms) = 0.12(1), and σ_P(10 ms) = 0.05(1). For both data sets, a reasonable signal-to-noise ratio (SNR = A/σ_P) and effective contrast (C = A/P₀) are found, signifying that phase noise is a major contributor to the loss of visibility as T is increased for the single-species (⁸⁷Rb) CAL AI. It must be noted, however, that the decrease of effective contrast by ~30% compared to the T = 0.5 ms data also shows that MZI noise (e.g., additive or offset noise⁷⁶) or sources of visibility degradation other than phase noise are also growing with T.

Phase noise can arise from acceleration noise (e.g., ISS vibrations as described in the next section) or from laser phase noise, which is highly suppressed in CAL by design. The two frequencies for Bragg AI are produced within a single acousto-optic modulator driven by the amplified multi-tone signal from the arbitrary waveform generator with phase stability better than −100 dBc/Hz⁷⁷. This implementation removes differential path lengths for the two Bragg frequencies, and makes laser phase noise contributions arising from both the AWG noise and from environmental perturbations on the laser negligible⁷⁶. To confirm this, the linewidth of the optical beatnote between two frequencies written onto the Bragg laser by the AOM, driven at 79 MHz and 79.035 MHz respectively, was measured to be below 10 Hz during the pre-launch checkout of CAL. Hence, the influence of ISS vibrations are found to be a leading source of visibility degradation for the (⁸⁷Rb) CAL AI at T = 10 ms.

ISS vibrations study

Our analysis of the impact of the ISS vibrations on the atom interferometer visibility is based on a_z data from the SAMS 121F04 three-axis accelerometer, which are provided publicly over NASA’s Principal Investigator Microgravity Services (PIMS)⁷⁸. The accelerometer is located on the front panel of the CAL Instrument in front of SM-3. It has a sample rate of 500 sps and a bandwidth of 200 Hz. The Physics Package is attached via a flexure mount inside the science module which modifies the acceleration spectrum. However, we expect no major impact in the frequency range of interest and use the unmodified accelerometer data in our analysis for simplicity.

The SAMS accelerometer provides discrete measurements a_z,i every Δt = 2 ms, giving a total of n = ⌊2T/Δt⌋ measurements at our disposal for each Mach–Zehnder interferometer sequence. Equations for calculating the accumulated MZI phase from a_z, k_eff and the sensitivity function g_s(t)⁷⁹ were discretized to utilize the PIMS data sets. The durations of the Bragg laser pulses were ignored since they are short compared to the overall atom interferometer interrogation time. We obtain:

$${{\Phi }}(T)\, \approx \, {k}_{{{{\rm{eff}}}}}\,{({{\Delta }}t)}^{2}{{\sum}_{j=1}^{2n}}{g}_{j}{{\sum}_{i=1}^{j}}{a}_{z,i},$$

(10)

with the discretized sensitivity function:

$${g}_{j}\equiv \left\{\begin{array}{ll}-1\quad &{{{\rm{for}}}}\,1\le j\le n\\+1\quad &{{{\rm{for}}}}\,n \, < \, j\le 2n\end{array}\right..$$

(11)

Although it was not feasible to correlate accelerometer measurements to individual atom interferometer experiments, the impact of vibrations was estimated for each day that MZI data was collected. Specifically, the accelerometer data set from a representative time frame of 2–4 h for each day was divided into blocks of n measurements. We then calculated the accumulated phase Φ(T) for each block at T = 2 ms, 4 ms, …, 30 ms. The phases follow Gaussian distributions (see Fig. 6b, inset) with standard deviations σ_Φ shown as a function of T in the main frame of Fig. 6b.

Fig. 6: Influence of the ISS vibrations on the accumulated atom interferometer phase.

a The spectra of the accelerations in z direction from the SAMS 121F04 accelerometer are compared to simulated Gaussian white noise spectra for different standard deviations σ_z. The accelerometer spectra are averaged over relevant time frames of 2–4 h for days during which atom interferometer experiments were conducted (see legend). b The standard deviation (σ_Φ) of the distribution of accumulated phases is depicted as a function of T. Distributions were obtained by calculating and binning the accumulated phases after dividing the acceleration data in blocks corresponding to the respective times T. (inset) Two examples of these distributions are given for T = 4 ms and T = 20 ms. Deviations of σ_Φ from the expected T²-scaling for ISS data are attributed to deviations of the accelerometer spectra from that of ideal Gaussian white noise as shown.

The impact of the vibrational phase noise on the atom interferometer visibility was modeled using simulated data for an ideal fringe. For each T, Gaussian-distributed noise with the previously calculated σ_Φ was added to the phase ϕ of ideal interferometer fringes. Fitting the resulting signals to Eq. (7) yielded the expected visibility shown in the upper inset of Fig. 2. While the ISS vibration spectra remained similar over the roughly 3-month time span over which the MZI experiments were conducted, differences in the day-to-day vibrations are noticeable at larger T.

For short T, σ_Φ due to ISS vibrations is larger than σ_Φ from simulated Gaussian white noise. However, the behavior inverts for larger T, as shown in Fig. 6b. A likely explanation for the deviation from the expected T²-behavior is that the harmonics in the real ISS vibration spectra are important for short T. The influence of small n for T = 2 ms are also found to lead to slight deviations from an ideal Gaussian distribution even with simulated Gaussian white noise. However, for larger T, low frequency harmonics are less impactful and can essentially only contribute a maximum phase.

Source data

Source Data