1 Introduction


Consider the general bond-pricing equation

$$\begin{aligned} \frac{\partial }{\partial t}u(x,t)+ \frac{1}{2} \rho ^2 x^{2 \gamma } \frac{\partial ^2}{\partial x\, \partial x}u(x,t)+\left( \kappa -\lambda \rho x^{\gamma }+\beta x\right) \frac{\partial }{\partial x}u(x,t) -x u(x,t)=0, \end{aligned}$$
(1)

where \(\kappa , \beta , \rho , \lambda \) (the market price of risk) and \(\gamma \) are constants, t is time, x is the stock price or instantaneous short-term interest rate at current time t and u(x, t) is the current value of the bond.


This model, like many other related bond-pricing models, exhibits a terminal condition, namely

$$\begin{aligned} u(x,T)= {\left\{ \begin{array}{ll} x-k \quad \quad \text {if} \quad x>k\\ 0 \quad \quad \quad \,\,\text {if} \quad x\le k, \end{array}\right. } \end{aligned}$$
(2)

where k is the strike price and T is the time of expiry of the option. The terminal condition is continuous but not smooth at \(x=k\).

Bond-pricing originated in the remarkable paper by Bachelier [1] that connected stock prices to Brownian motion. This later led to major developments by Merton and Black and Scholes [2, 3] in mathematical finance. Equation (1) is a linear parabolic partial differential equation (PDE), that is formulated from stochastic differential equations. Various modified versions of equations of this type exist, for example, the Vasicek model (\(\gamma = 0\)), Cox-Ingersoll model (\(\gamma = 1/2\), \(\lambda =0\)) and Dothan model (\(\kappa = \beta = 0, \gamma = 1\)), see [4,5,6,7]. In [8], the above model was considered in order to render it into Lie canonical forms and obtain solutions. The key difference with this paper is that the invariant surface condition (ISC) is invoked to find a symmetry generator that incorporates a transformed version of the terminal condition. This itself is a nontrivial task and it is the first time that symmetry invariant solutions that satisfy the terminal condition are presented for the model under study. Additionally, we consider novel transformations and different cases of the model that yield unique boundary conditions and hence new solutions.

The theory of Lie’s classification of linear second-order PDEs, translated in English, can be found in Ibragimov’s remarkable contribution [9]. Subsequently, Ibragimov showed that the Black-Scholes model, which has a similar symmetry group to the heat equation, is then included in Lie’s classification, via equivalence transformation formulae [10]. Lie’s formulae may then be extended to any model that satisfies these classification properties.

The model in this paper is first transformed and then its initial value problem is derived. The method of Lie symmetries plays a pivotal role in constructing solutions to the initial conditions. We emphasize that symmetries are not at the forefront when solving initial or boundary conditions. This method is categorically avoided for PDEs with nonsmooth boundary conditions, where derivatives may not exist at certain points and/or the imposed conditions result in asymptotic behaviour. However we show how to engage with such problems in light of the equation under study.

The plan of the paper follows. In Sect. 2, we introduce the parameters and transformations required to manipulate the model into the classical heat equation. Section 3 contains the main results, whereby we detail certain features of the boundary condition, and go on, to provide exact solutions of the model subject to the condition (2). Finally, we conclude in Sect. 4.

2 Transformations

In this section, we establish successive transformations that convert the model (1) to the well-known heat equation. The change of variables is necessary to apply some of the forthcoming initial value results to the model (1). It turns out that this model is transformable under precise forms of its arbitrary parameters. Hence we prove the following result.

Theorem 1


The option pricing model Eq. (1), is reducible to the heat equation

$$\begin{aligned} \omega _{\hat{t}} -\omega _{yy}=0, \quad \end{aligned}$$
(3)

where \(\omega =\omega (y,\hat{t})\), under the following specific parameter settings.

  1. (a)

    Case I: \(\gamma = 2, \quad \kappa =\beta = 0, \quad \lambda = -\frac{1}{\rho }, \quad \text {and} \quad \rho \quad \text {is arbitrary}\). The transformations are

    $$\begin{aligned} \hat{t}= & {} -t, \end{aligned}$$
    (4)
    $$\begin{aligned} y= & {} -\frac{\sqrt{2}}{x\cdot \rho }. \end{aligned}$$
    (5)
  2. (b)

    Case II: \(\gamma = \frac{1}{2}, \quad \kappa = \frac{\rho ^2}{4}, \quad \beta = \sqrt{2} i \rho , \quad \rho =i \quad \text {and} \quad \lambda =0\). The transformations are

    $$\begin{aligned} \hat{t}= & {} -t, \end{aligned}$$
    (6)
    $$\begin{aligned} y= & {} \frac{2 \sqrt{2} \sqrt{x}}{\rho }. \end{aligned}$$
    (7)

Proof


For Case I, an invertible change of the independent variables of the form y and \( \hat{t}\), reduces Eq. (1) to the form

$$\begin{aligned} {a}(y,\hat{t} ) u_y+{c}(y,\hat{t} ) u+u_{\hat{t}}-u_{yy}=0, \end{aligned}$$
(8)

where \(u(y,\hat{t})\), \({a}(y,\hat{t} )=\displaystyle {y\left( -\frac{2}{y^2} -\frac{\sqrt{2}}{y\cdot \rho }\right) }\) and \({c}(y,\hat{t} )=\displaystyle {-\frac{\sqrt{2}}{y\cdot \rho }}\).


Thereafter, under another transformation, the dependent variable \(u(y,\hat{t})\) undergoes a transformation, viz.

$$\begin{aligned} u(y,\hat{t})=\omega (y, \hat{t})\cdot e^{-\phi (y, \hat{t})}, \end{aligned}$$
(9)

where

$$\begin{aligned} \phi (y, \hat{t} )=\frac{y}{\sqrt{2}\cdot \rho }+\frac{\hat{t}}{2\rho ^2 }+\ln |y|. \end{aligned}$$
(10)

This transformation procedure converts Eq. (8) to the heat Eq. (3).

The proof for Case II is analogous, but where \({a}(y,\hat{t} )=\displaystyle {-\frac{\beta y}{2 }}\) and \({c}(y,\hat{t} )=\displaystyle {\frac{\rho ^2 y^2}{8}}\).

Similarly, we define the transformation (9), wherein this case admits the function

$$\begin{aligned} \phi (y, \hat{t} )=-\frac{\hat{t} }{2 \sqrt{2}}-\frac{y^2}{4 \sqrt{2}}. \end{aligned}$$
(11)

Naturally, the above result gives rise to the following lemma. \(\square \)

Lemma 2

The corresponding terminal condition (2) is transformed into a boundary condition of the heat equation, viz.

$$\begin{aligned} \omega (y,\hat{t}) = \text {max}\Big \{-e^{\frac{y}{\sqrt{2}\cdot \rho }+\frac{\hat{t}}{2\rho ^2 }+\ln |y|}\left( \frac{\sqrt{2}}{y\cdot \rho }+k\right) , 0\Big \}, \end{aligned}$$
(12)

for Case I, and

$$\begin{aligned} \omega (y,\hat{t}) = \text {max}\Big \{\left( -k-\frac{y^2}{8}\right) e^{-\frac{\hat{t} }{2 \sqrt{2}}-\frac{y^2}{4 \sqrt{2}}}, 0\Big \}, \end{aligned}$$
(13)

for Case II.

Proof

The terminal condition (2) may be expressed as \(u={max}\{x-k,0\}\), and with the application of the transformations (4), (5), (9) and (10) from Theorem (1), a boundary condition for the heat equation follows for Case I. Similarly, the transformations (6), (7), (9) and (11) yield a boundary condition for Case II. \(\square \)

3 The Initial Value Problem

The heat equation is often bench-marked as one of the most useful PDEs. It admits the Gaussian function as a fundamental solution, which leads to several analytical applications. We note that many studies of parabolic PDEs involve the heat equation, we refer the reader to [11,12,13,14,15,16,17,18]. In our context, we showcase that the heat equation is an easy facilitator of boundary conditions.

From Lemma 2, we construct the initial value problem for the heat equation

$$\begin{aligned} {\left\{ \begin{array}{ll} \omega _{\hat{t}} -\omega _{yy}=0, &{}~ \text {in}~{\mathbb {R}}\times (0,\infty ),\\ \omega (y,0)=F(y),&{} ~ \text {on}~{\mathbb {R}}\times \{\hat{t}=0\}.\end{array}\right. } \end{aligned}$$
(14)

In particular, we have the initial conditions

$$\begin{aligned} Case I: \omega (y,0)= & {} -e^{\frac{y}{\sqrt{2}\cdot \rho }+\ln |y|}\left( \frac{\sqrt{2}}{y\cdot \rho }+k\right) , \end{aligned}$$
(15)
$$\begin{aligned} Case II: \omega (y,0)= & {} e^{-\frac{y^2}{4 \sqrt{2}}}\left( -k-\frac{y^2}{8}\right) . \end{aligned}$$
(16)

Note that these initial conditions need not be smooth. To proceed, we consider the well known symmetries of (3), viz.

$$\begin{aligned} X = \xi (y,\hat{t},\omega )\frac{\partial }{\partial y}+\eta (y,\hat{t},\omega )\frac{\partial }{\partial \hat{t}}+\phi (y,\hat{t},\omega )\frac{\partial }{\partial \omega }, \end{aligned}$$
(17)

or, equivalently

$$\begin{aligned} X= & {} \left( 4c_1\hat{t}^2+2c_2\hat{t}+c_6 \right) \frac{\partial }{\partial \hat{t}}+ \left( 4c_1y\hat{t}+c_2y+2c_3\hat{t}+c_4 \right) \frac{\partial }{\partial y}\nonumber \\{} & {} \left( \left( c_1(-2\hat{t}-y^2)-c_3y+c_5 \right) \omega +\alpha (y,\hat{t}) \right) \frac{\partial }{\partial \omega }, \end{aligned}$$
(18)

where \(\alpha (y,\hat{t})\) is an arbitrary solution of the heat equation, i.e. \( \alpha _{ \hat{t}} = \alpha _{yy}. \)

We apply the ISC

$$\begin{aligned} \xi (y,\hat{t},\omega )\omega _y + \eta (y,\hat{t},\omega )\omega _{\hat{t}} -\phi (y,\hat{t},\omega )=0, \end{aligned}$$
(19)

which holds at the boundary where we impose \(\hat{t}=0\) and \(\omega (y,0)\), to obtain the condition [19]

$$\begin{aligned} \frac{\phi (y,0,F(y))-\xi (y,0,F(y))F'(y)}{\eta (y,0,F(y))}=\omega _{yy}(y,0). \end{aligned}$$
(20)

From condition (20), we have that

$$\begin{aligned} \alpha (y,0)=\left( c_1y^2+c_3y-c_5\right) F(y)+\left( c_2y+c_4\right) F'(y)+c_6F''(y). \end{aligned}$$
(21)

Equation (21) is an ordinary differential equation which when solved yields the most general initial condition. This condition gives less restrictive conditions on the initial conditions such that they be defined by a particular symmetry. We shall demonstrate several special conditions and solutions below. Now, the known fundamental solution of the heat equation is

$$\begin{aligned} A(y,\hat{t} ):={\left\{ \begin{array}{ll} \frac{1}{\sqrt{4\pi \hat{t} }}e^{-\frac{y^2}{4\hat{t} }}, &{} (y\in {\mathbb {R}}, \hat{t} >0),\\ 0,&{} (y\in {\mathbb {R}}, \hat{t} <0)\end{array}\right. } \end{aligned}$$
(22)

which is singular at the point (0,0). The knowledge of \(A(y,\hat{t})\) allows the construction of a solution to the initial value problem of the heat equation. Since \(A(y-m,\hat{t} )\) is also a solution for each fixed \(y\in {\mathbb {R}},\) then consequently the convolution [20]

$$\begin{aligned} \omega (y,\hat{t} )=\int _{{\mathbb {R}}}A(y-m,\hat{t} )\omega (m,0)dm\quad (y\in {\mathbb {R}}, \hat{t} >0), \end{aligned}$$
(23)

is a solution to the one dimensional heat equation as well.

Next, we apply the theory above to explore various solutions to the heat equation and subsequently, the general bond-pricing equation. All solutions are subject to the initial conditions given above, while solutions to the general bond-pricing equation is subject to the terminal condition (2).

To start, consider Case I. For simplicity, let \(c_4=1,c_1=c_2=c_3=c_5=c_6=0\). Therefore \( \alpha (y,0)=F'(y), \) and the symmetry we apply is \(X=\frac{\partial }{\partial y}+\alpha (y,\hat{t}) \frac{\partial }{\partial \omega }\). Hence, with the ISC (19), we find that the solution to the heat equation is \(\omega (y,\hat{t} )=\int \alpha (y,\hat{t})dy+H(\hat{t}).\) Without loss of generality, we let \(H(\hat{t})=0,\) and we are now faced with the challenge of finding \(\alpha (y,\hat{t})\). Since \(\alpha (y,\hat{t})\) is a solution to the heat equation, it will also satisfy the convolution property (23). Thus by integration with Maple, we obtain

$$\begin{aligned} \alpha (y,\hat{t})= & {} -\frac{1}{4 \sqrt{\pi } \rho ^2}e^{-\frac{y^2}{4 \hat{t} }} \Bigg (2 \sqrt{2} k \rho \sqrt{\hat{t} }+e^{\frac{\left( y \rho +\sqrt{2} \hat{t} \right) ^2}{4 \rho ^2 \hat{t} }} \sqrt{\pi } \left( 2+\sqrt{2} k y \rho +2 k \left( \rho ^2+\hat{t} \right) \right) \nonumber \\{} & {} +e^{\frac{\left( y \rho +\sqrt{2} \hat{t} \right) ^2}{4 \rho ^2 \hat{t} }} \sqrt{\pi } \left( 2+\sqrt{2} k y \rho +2 k \left( \rho ^2+\hat{t} \right) \right) \text {Erf}\left[ \frac{y \rho +\sqrt{2} \hat{t} }{2 \rho \sqrt{\hat{t} }}\right] \Bigg ). \end{aligned}$$
(24)

We integrate again to find

$$\begin{aligned} \omega (y,\hat{t} )= & {} -\frac{1}{4 \sqrt{\pi } \rho ^2}\Bigg (4 e^{-\frac{y^2}{4 \hat{t} }} k \rho ^2 \sqrt{\hat{t} }+2 e^{\frac{\sqrt{2} y \rho +\hat{t} }{2 \rho ^2}} \sqrt{\pi } \rho \left( \sqrt{2}+k y \rho +\sqrt{2} k \hat{t} \right) \nonumber \\{} & {} -2 \sqrt{2 \pi } \rho \text {Erf}\left[ \frac{y}{2 \sqrt{\hat{t} }}\right] +e^{\frac{\sqrt{2} y \rho +\hat{t} }{2 \rho ^2}} \sqrt{2 \pi } \rho \left( 2+\sqrt{2} k y \rho +2 k \hat{t} \right) \nonumber \\{} & {} \text {Erf}\left[ \frac{y \rho +\sqrt{2} \hat{t} }{2 \rho \sqrt{\hat{t} }}\right] \Bigg ), \end{aligned}$$
(25)

which is a solution to the heat Eq. (3).

Now recall the transformations from Theorem 1 to reverse the substitutions and yield the solution to the general bond-pricing model (1), viz.

$$\begin{aligned}{} & {} u(x,t)=\frac{1}{4 \sqrt{2 \pi } \rho }e^{\frac{t}{2 \rho ^2}+\frac{1}{x \rho ^2}} x \Bigg (2 e^{\frac{-t-\frac{2}{x}}{2 \rho ^2}} \sqrt{\pi } \left( \sqrt{2}-\sqrt{2} k t-\frac{\sqrt{2} k}{x}\right) \rho +4 e^{\frac{1}{2 t x^2 \rho ^2}} k \sqrt{-t} \rho ^2\nonumber \\{} & {} \quad +e^{\frac{-t-\frac{2}{x}}{2 \rho ^2}} \sqrt{2 \pi } \left( 2-2 k t-\frac{2 k}{x}\right) \rho \text {Erf} \,\left[ \frac{-\sqrt{2} t-\frac{\sqrt{2}}{x}}{2 \sqrt{-t} \rho }\right] +2 \sqrt{2 \pi } \rho \text {Erf}\left[ \frac{1}{\sqrt{2} \sqrt{-t} x \rho }\right] \Bigg ). \end{aligned}$$
(26)

Similarly, suppose, we set \(c_1=c_2=c_3=c_4=c_5=0\), \(c_6=1\) to obtain the symmetry \(X=\frac{\partial }{\partial \hat{t}}+\alpha (y,\hat{t}) \frac{\partial }{\partial \omega }\) and function \( \alpha (y,0)=F''(y). \) Thus, with (19), the solution to the heat equation is \(\omega (y,\hat{t} )=\int \alpha (y,\hat{t})d\hat{t}+H(y)\). Once again we let the arbitrary function vanish, i.e. \(H(y)=0\) and by integration we obtain

$$\begin{aligned} \alpha (y,\hat{t} )= & {} -\frac{1}{4 \sqrt{\pi } \rho ^3}e^{-\frac{y^2}{4 \hat{t} }} \Bigg (2 k \rho \sqrt{\hat{t} }+e^{\frac{\left( y \rho +\sqrt{2} \hat{t} \right) ^2}{4 \rho ^2 \hat{t} }} \sqrt{\pi } \left( \sqrt{2}+k y \rho +\sqrt{2} k \left( 2 \rho ^2+\hat{t} \right) \right) \nonumber \\{} & {} +e^{\frac{\left( y \rho +\sqrt{2} \hat{t} \right) ^2}{4 \rho ^2 \hat{t} }} \sqrt{\pi } \left( \sqrt{2}+k y \rho +\sqrt{2} k \left( 2 \rho ^2+\hat{t} \right) \right) \text {Erf}\left[ \frac{y \rho +\sqrt{2} \hat{t} }{2 \rho \sqrt{\hat{t} }}\right] \Bigg ), \end{aligned}$$
(27)

followed by

$$\begin{aligned} \omega (y,\hat{t} )= & {} -\frac{1}{4 \sqrt{\pi } \rho ^3}\Bigg (-4 e^{-\frac{y^2}{4 \hat{t} }} \rho \sqrt{\hat{t} }+2 e^{\frac{\sqrt{2} y \rho +\hat{t} }{2 \rho ^2}} \sqrt{\pi } \rho ^2 \left( \sqrt{2}+k y \rho +\sqrt{2} k \hat{t} \right) \nonumber \\{} & {} -2 \sqrt{\pi } y \rho \text {Erf}\left[ \frac{y}{2 \sqrt{\hat{t} }}\right] -2 \sqrt{2 \pi } \rho ^2 \text {Erf}\left[ \frac{y}{2 \sqrt{\hat{t} }}\right] -2 k \sqrt{\pi } y \rho ^3 \text {Erf}\left[ \frac{y}{2 \sqrt{\hat{t} }}\right] \nonumber \\{} & {} +2 e^{\frac{\sqrt{2} y \rho +\hat{t} }{2 \rho ^2}} \sqrt{\pi } \rho ^2 \left( \sqrt{2}+k y \rho +\sqrt{2} k \hat{t} \right) \text {Erf}\left[ \frac{y \rho +\sqrt{2} \hat{t} }{2 \rho \sqrt{\hat{t} }}\right] \Bigg ). \end{aligned}$$
(28)

Therefore, the solution to the original equation in this scenario is:

$$\begin{aligned} u(x,t)= & {} \frac{1}{4 \sqrt{2 \pi } \rho ^2}e^{\frac{t}{2 \rho ^2}+\frac{1}{x \rho ^2}} x \Bigg (-4 e^{\frac{1}{2 t x^2 \rho ^2}} \sqrt{-t} \rho +2 e^{\frac{-t-\frac{2}{x}}{2 \rho ^2}} \sqrt{\pi } \left( \sqrt{2}-\sqrt{2} k t-\frac{\sqrt{2} k}{x}\right) \rho ^2\nonumber \\{} & {} +2 e^{\frac{-t-\frac{2}{x}}{2 \rho ^2}} \sqrt{\pi } \left( \sqrt{2}-\sqrt{2} k t-\frac{\sqrt{2} k}{x}\right) \rho ^2 \text {Erf} \,\left[ \frac{-\sqrt{2} t-\frac{\sqrt{2}}{x}}{2 \sqrt{-t} \rho }\right] \nonumber \\{} & {} \quad -\frac{2 \sqrt{2 \pi } \text {Erf}\left[ \frac{1}{\sqrt{2} \sqrt{-t} x \rho }\right] }{x}\nonumber \\{} & {} +2 \sqrt{2 \pi } \rho ^2 \text {Erf}\left[ \frac{1}{\sqrt{2} \sqrt{-t} x \rho }\right] -\frac{2 k \sqrt{2 \pi } \rho ^2 \text {Erf}\left[ \frac{1}{\sqrt{2} \sqrt{-t} x \rho }\right] }{x}\Bigg ). \end{aligned}$$
(29)

As a solution for Case II, suppose we let \(c_3=\frac{1}{2}\) and \(c_1=c_2=c_4=c_5=c_6=0\), so that \(X=\hat{t}\frac{\partial }{\partial y}+(-y\omega /2+\alpha (y,\hat{t})) \frac{\partial }{\partial \omega }\) and from the ISC, the solution to the heat equation is

$$\begin{aligned} \omega (y,\hat{t})=\left( \int \frac{\alpha (y,\hat{t})}{\hat{t}}e^{\frac{y^2}{4\hat{t}}}dy +H(\hat{t})\right) e^{-\frac{y^2}{4\hat{t}}}. \end{aligned}$$
(30)

Hence, from the same procedure as described above, we have the functions

$$\begin{aligned} \alpha (y,\hat{t})= & {} \frac{\sqrt{\hat{t}} y e^{-\frac{y^2}{4 \left( \hat{t}+\sqrt{2}\right) }} \left( 4 k \left( \hat{t} \left( \hat{t}^2+3 \sqrt{2} \hat{t}+6\right) +2 \sqrt{2}\right) +\hat{t} \left( 3 \hat{t} \left( \sqrt{2} \hat{t}+4\right) +y^2\right) +\sqrt{2} \left( 6 \hat{t}+y^2\right) \right) }{\sqrt{-\hat{t}} \left( \sqrt{2} (-\hat{t})-2\right) ^{9/2}}, \end{aligned}$$
(31)
$$\begin{aligned} \omega (y,\hat{t})= & {} \frac{e^{-\frac{y^2}{4 \hat{t}}}}{\sqrt{-\hat{t}^2} \left( \sqrt{2} (-\hat{t})-2\right) ^{9/2}} \Bigg (\hat{t} \left( \sqrt{2} \hat{t}+2\right) \nonumber \\{} & {} e^{\frac{y^2}{2 \sqrt{2} \hat{t}^2+4 \hat{t}}} \left( 4 k \left( \hat{t}^3+3 \sqrt{2} \hat{t}^2+6 \hat{t}+2 \sqrt{2}\right) +\sqrt{2} \hat{t}^3+4 \hat{t}^2+\hat{t} \left( y^2+2 \sqrt{2}\right) +\sqrt{2} y^2\right) \Bigg ), \end{aligned}$$
(32)

and it follows that the solution to the original equation is

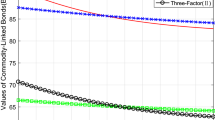
$$\begin{aligned} u(x,t)= & {} \frac{ \left( \sqrt{2}-t\right) \rho e^{\frac{2 x}{\sqrt{2}-t}-\frac{t}{2 \sqrt{2}}-\sqrt{2} x}}{\left( \sqrt{2} t-2\right) ^{9/2}}\nonumber \\{} & {} \left( 4 k \left( -\sqrt{2} t^3+6 t^2-6 \sqrt{2} t+4\right) -2 t^3+4 \sqrt{2} t^2-t \left( 4-8 \sqrt{2} x\right) -16 x\right) .\nonumber \\ \end{aligned}$$
(33)

We plot the solution of (33) in Fig. 1 and see that this solution, at a strike price of one, predicts a sudden drop in bond-value within a short time. We remark that by convention, one may rewrite all of the above solutions for the general bond-pricing model as \(u(x,\tau )\) where \(\tau =T-t\), and thereafter, if we let \(T=t\), it is obvious that the terminal condition (2) is satisfied.

Fig. 1
figure 1

Graphical 3D illustration of the analytical solution (33) with \(k=1\)

Full size image

4 Conclusion

A general equation linked to bond-pricing has been solved subject to its terminal condition, for several parameter values. We have transferred the problem of solving this equation to a different problem corresponding to the heat equation. Specifically, we have employed symmetry generators to solve for invariant solutions that satisfy some resulting initial values. In fact, the analytical solutions at the boundary involved the nontrivial computations of functions that solve the heat equation. Note that these conditions may be badly behaved but the technique used is up to the challenge. In the wider context of other applications, one may encounter integration difficulties for the solutions itself.

The heat equation possesses other well-known solutions aside from (22). As an example, take the infinite series solution [21]. However, such solutions also admit other boundary conditions. Hence, we remark that in principle, it is the fundamental solution or heat kernel defined above that fits perfectly when we transform the terminal condition into a specific initial condition, and thereby set up the convolution and any ensuing integrations required to solve the equation.

For nonlinear equations, it is possible to apply the above approach, in one of two ways, namely: either by first linearising the equation and then constructing transformations to the 1+1 heat equation, or secondly if one can find direct transformations to the heat equation. Both scenarios would certainly pose interesting challenges to pursue.