1 Introduction

Thermosolutal convection [1, 2] refers to the behavior of liquid stream induced by concentration and temperature gradients. It is a commonly observed occurrence in various usual and practical applications [3,4,5,6,7,8,9]. This occurrence arises due to buoyancy forces resulting from concurrent variations in concentration and temperature [10,11,12]. The Dufour effect [13, 14] describes the temperature caused by concentration gradients, while the Soret outcome [15, 16] refers to the concentration caused by temperature gradients. In situations where large temperature and concentration gradients exist, the cross-diffusion effects participate a vital task in natural and industrial processes, including combustion, materials processing, and biological systems. These effects are fundamental aspects studied in the field of transport phenomena and fluid dynamics [14,15,16].

Many researchers have conducted investigations on the impact of cross diffusion coefficients on natural thermohaline convection in different scenarios. For instance, Nithyadevi and Yang [17] examined the influence of these coefficients on the usual convection of water in a partially heated area. The study of thermohaline convection with cross diffusion effects involved the utilization of the lattice Boltzmann method [18]. Mahanthesh et al. [19] directed their attention towards investigating effect of cross diffusion on marangoni convection in non-Newtonian liquid flow. Xu et al. [20] conducted lattice Boltzmann simulations to analyze the cross-diffusion effects on thermohaline convection. Recently by Mohammadi and Nassab [9] explored thermohaline convection flow with cross diffusion effects in an asymmetrical geometry. Additionally, Li et al. [21] developed a mathematical model to replicate the behavior of a solutal gradient solar pond, incorporating the cross-diffusion effects on thermohaline convection.

In practical applications, many liquids show non-Newtonian behavior, which can drastically influence flow appearances, as well as thermohaline properties [22]. The Casson liquid model is usually used to define the rheological behavior of various materials such as food products, paints, and blood [23]. Unlike Newtonian fluids, Casson fluids possess a yield stress below which they do not flow and exhibit a non-linear relationship between shear stress and shear rate. In the Casson fluid model, there are two key parameters: the yield stress and the Casson viscosity. According to the Casson fluid model, the shear rate at the fluid's surface is zero when the shear stress is below the capitulate stress, and it increases linearly with the shear stress when it surpasses the yield stress [24]. Aktharet al. [25] utilized a Casson fluid model to analyze the peristaltic flow in an elliptical duct with double diffusion effects through a mathematical investigation. In their research, Roy and Saha [26] found that the flow of a Cassondusty fluid over a permeable stretching pane is subject to significant changes based on different physical parameters. They also discovered that these parameters can be adjusted and utilized to manipulate the flow and heat transfer characteristics. The study by Pushpalatha et al. [27] involved using numerical methods to analyse the behaviour of chemically reacting Casson fluid as it flows unsteadily past a surface that is being stretched. Mahdya [28] is studied effect of cross diffusion terms on non-Newtonian fluid permeable layer.

Non-Newtonian fluids and double diffusive flows are of great interest in the study of the cross-diffusion effects, which can have important practical information in fields such as materials science and medicine. Janaiah and Reddy [29] performed a study on the impacts of cross diffusion terms on ferromagnetic Casson fluid flow. The study utilized numerical solutions to model thermal diffusion effects and presented the findings graphically. In a study conducted by Majeed et al. [30], the impacts of cross diffusion terms on second grade fluid flow were investigated in the context of a stretching cylinder with thermal radiation. Mustafa et al. [31] examined double diffusive fourth grade peristaltic fluid flow in the presence of cross diffusion terms. Reddy [32] is theoretically analysed Casson fluid flow over an inclined porous layer.

An internal heat source is a process that generates heat within a material or system. This can be due to a variety of sources, including chemical reactions, nuclear reactions, or electrical resistance [33]. The heat generated by the internal source can cause a temperature increase within the system and alter its thermal behaviour. Internal heat sources play a crucial role in both natural and industrial processes. For example, in nuclear reactors, the heat generated by nuclear reactions is used to generate electricity. In combustion engines, the heat generated by fuel combustion drives the engine. In materials processing, such as welding and casting, heat generated by electrical resistance or chemical reactions is used to melt and join materials. The heat generated by the internal source can create a temperature gradient, which can cause thermal stresses and material deformation. Therefore, understanding the behavior of internal heat sources is essential in designing and optimizing processes that involve heat generation, such as energy production and materials processing, to ensure the safety and effectiveness of the systems. Fluid flow problems with internal heat source has been investigated extensively [34,35,36].

Overall, the learn of double-diffusive non-Newtonian fluid flow with the influence of internal heat source and the cross diffusion effects is a complex and challenging problem in fluid mechanics. It is very difficult to solve highly non-linear fluid flow problems by using analytically. Hence, the analysis of such flows requires the use of advanced mathematical and numerical techniques, and it can provide valuable insights into the behaviour of non-Newtonian fluids under different thermal and concentration gradients. There are various types of numerical methods available in the literature, and we consider one such wavelet numerical method. The study of wavelets is a relatively new and developing field in mathematics. It has found applications in various technical fields. However, numerical wavelets have established to be highly effective in signal examination, especially in representing and segmenting waveforms, performing time–frequency analysis, and implementing quick algorithms in a straightforward manner [37]. Wavelets allow a wide range of functions and operators to be accurately represented [38, 39] and also provide a relationship with quick numerical methods [40]. Very interesting liquid flow trouble are examined with the help of various numerical wavelet schemas [41,42,43,44,45]. Many problems [46,47,48,49] have been studied in current years with aid of numerical Bernoulli wavelet method. We consider the cross-diffusion effects on non-Newtonian Casson fluid with internal heat source and solved by using a new numerical technique- Bernoulli wavelet technique. The results are validated and found to be highly convergent. Graphical analysis is used to study the behaviour of temperature, velocity, and concentration profiles.

2 Formulation

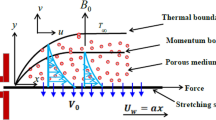
Consider an incompressible Casson liquid flow with an internal heat source that occurs connecting two parallel plates that are kept at a distance \(h(t) = l(1 - \alpha t)^{\frac{1}{2}}\). Additionally, if \(\alpha > 0\) causes the plates to squeeze together until they touch at \(t = \frac{1}{\alpha }\), but \(\alpha < 0\) causes plates to bear a receding and dilating motion. The density \(\rho\) is influenced by two distinct stratifying agents with varying molecular diffusivities. Additionally, the flux of one species is impacted by the solutal concentration gradient of the other, indicating the consideration of cross-diffusion. The governing equations are [50,51,52,53,54,55]

$$\frac{\partial u}{{\partial x}} + \frac{\partial v}{{\partial y}} = 0$$
(1)
$$\frac{\partial u}{{\partial t}} + u\frac{\partial u}{{\partial x}} + v\frac{\partial u}{{\partial y}} + \frac{1}{\rho }\frac{\partial p}{{\partial x}} - \nu \left( {1 + \frac{1}{\beta }} \right)\left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial y^{2} }}} \right) = 0$$
(2)
$$\frac{\partial v}{{\partial t}} + u\frac{\partial v}{{\partial x}} + v\frac{\partial v}{{\partial y}} + \frac{1}{\rho }\frac{\partial p}{{\partial y}} - \nu \left( {1 + \frac{1}{\beta }} \right)\left( {\frac{{\partial^{2} v}}{{\partial x^{2} }} + \frac{{\partial^{2} v}}{{\partial y^{2} }}} \right) = 0$$
(3)
$$\frac{\partial T}{{\partial t}} + u\frac{\partial T}{{\partial x}} + v\frac{\partial T}{{\partial y}} - D_{11} \left( {\frac{{\partial^{2} T}}{{\partial x^{2} }} + \frac{{\partial^{2} T}}{{\partial y^{2} }}} \right) - D_{12} \left( {\frac{{\partial^{2} C}}{{\partial x^{2} }} + \frac{{\partial^{2} C}}{{\partial y^{2} }}} \right) - \frac{\nu }{{C_{p} }}\left( {4\left( {\frac{\partial u}{{\partial x}}} \right)^{2} + \left( {\frac{\partial u}{{\partial y}}} \right)^{2} } \right) - \frac{{Q^{*} }}{{\rho C_{p} }}T = 0$$
(4)
$$\frac{\partial C}{{\partial t}} + u\frac{\partial C}{{\partial x}} + v\frac{\partial C}{{\partial y}} - D_{21} \left( {\frac{{\partial^{2} T}}{{\partial x^{2} }} + \frac{{\partial^{2} T}}{{\partial y^{2} }}} \right) - D_{22} \left( {\frac{{\partial^{2} C}}{{\partial x^{2} }} + \frac{{\partial^{2} C}}{{\partial y^{2} }}} \right) + K_{1} (t)C = 0$$
(5)

where \(p\), \(T\), \(\rho\), \(C\), \(\mu\), \(\nu\), \(K_{1} (t) = \frac{{k_{1} }}{(1 - \alpha t)}\), \(c_{p}\), \(Q^{ * }\) are represents pressure, temperature, density, concentration, viscosity, kinematic viscosity, time-dependent reaction rate, specific heat, coefficient of heat source respectively. \(D_{11}\) is the thermal diffusivity and \(D_{22}\) is the solute analogue of \(D_{11}\), while \(D_{12}\) and \(D_{21}\) are the cross diffusion diffusivities, \(u\) and \(v\) are velocities in the \(x\) and \(y\) directions.

The relevant boundary conditions are

$$T={T}_{H },C={C}_{H },u=0, v=\frac{dh}{dt}={v}_{w } at y=h\left(t\right)$$
$$v=\frac{\partial u}{dy}=\frac{\partial T}{dy}=\frac{\partial C}{dy}=0 at y=0.$$
(6)

The following similarity transformations are presented by us

$$\begin{aligned} \eta & = \frac{y}{{l(1 - \alpha t)^{\frac{1}{2}} }},\,u = \frac{\alpha x}{{2(1 - \alpha t)}}f^{\prime}(\eta ),\,\,v = \frac{ - \alpha l}{{2(1 - \alpha t)^{\frac{1}{2}} }}f(\eta ),\,\, \\ \theta & = \frac{T}{{T_{H} }},\,\,\phi = \frac{C}{{C_{H} }},Q^{*} = \frac{{Q_{0}^{*} }}{1 - \alpha t}. \\ \end{aligned}$$
(7)

Removing the pressure term from Eqs. (2) and (3) by using Eq. (7) we have,

$$S\left( {f^{\prime}\,f^{\prime\prime} + 3\,f^{\prime\prime} + \eta \,f^{\prime\prime\prime} - f\,\,f^{\prime\prime\prime}} \right) - \left( {1 + \beta^{ - 1} } \right)f^{iv} = 0.$$
(8)

Substitute similarity transformations in Eqs. (4–5) and after some simplification we get coupled highly nonlinear normalized ordinary differential equations in the form

$$\theta^{\prime\prime} + Pr\,S\left( {f\theta^{\prime} - \eta \theta^{\prime}} \right) - \Pr \,Ec\left( {\left( {f^{\prime\prime}} \right)^{2} + 4\delta^{2} \left( {f^{\prime}} \right)^{2} } \right) + Hs\theta + \gamma_{12} \phi^{\prime\prime} = 0$$
(9)
$$\phi^{\prime\prime} + Sc\left( {f\phi^{\prime} - \eta \phi^{\prime}} \right)S - Sc\gamma \phi + \gamma_{21} \theta^{\prime\prime} = 0$$
(10)

where, \(S=\frac{\alpha {l}^{2}}{2\nu }\) is the squeeze quantity, \(\beta\) is the Casson fluid quantity, \(Pr=\frac{\mu {c}_{p}}{k}\) is the Prandtl quantity, \(Sc=\frac{\nu }{{D}_{22}}\) is the Schmidt quantity, \(\gamma =\frac{{l}^{2}}{\nu }\) is the chemical reaction quantity, \(Hs = \frac{{Q_{0}^{*} l^{2} }}{k}\) is the internal heat source, \({\gamma }_{21}=\frac{{D}_{21}}{{D}_{22}}\frac{{T}_{H}}{{C}_{H}}\) isthe Soret quantity, \({\gamma }_{12}=\frac{{C}_{H}}{{T}_{H}}\frac{{D}_{12}}{{D}_{11}}\) is the Dufour quantity, \(Ec = \frac{1}{{C_{p} T_{H} }}\left( {\frac{\alpha x}{{2\left( {1 - \alpha t} \right)}}} \right)^{2}\) is the Eckert number and \(\delta = \frac{l}{x}\). We noticed in the absence of cross diffusion terms, internal heat source, and Casson fluid the present problem coincide with Mustafa et al. [50].

The matching limits that apply are

$$f\left(0\right)={ \theta }{\prime}\left(0\right)={\phi }{\prime}\left(0\right)={f}^{{\prime}{\prime}}\left(0\right)={f}{\prime}\left(1\right)=0, \theta \left(1\right)=\upphi \left(1\right)=f\left(1\right)=1.$$
(11)

Calculating skin friction yields valuable insights, as it aids in estimating both the overall frictional drag imposed on a fluid and the rate of convectional heat transfer. Furthermore, it helps determine the thermal and solutal Nusselt numbers, which enumerate the extent of convectional mass and heat transfer. We calculate the thermal Nusselt number \(Nu_{\theta }\), skin friction \(C_{f}\), and the solute Nusselt number \(Nu_{\phi }\) can be expressed as \(Nu_{\theta } = - \theta^{\prime}\left( 1 \right)\),\(C_{f} = - f^{\prime\prime}\left( 1 \right)\), and \(Nu_{\phi } = - \phi^{\prime}\left( 1 \right)\).

3 Numerical Bernoulli wavelet technique

The basic of BWM is discussed [46, 47, 49, 56]

3.1 Solution of momentum equation

Now, assume highest derivative of \(f\) in the form

$$f^{iv} \left( x \right) - G^{T} \xi \left( x \right) = 0.$$
(12)

Integrate Eq. (12) w.r.t \(x\) and limit from 0 to \(x\),

$$f^{\prime\prime\prime}\left( x \right) - f^{\prime\prime\prime}\left( 0 \right) - G^{T} \left[ {\,\xi \left( x \right)A + \overline{\xi } \left( x \right)} \right] = 0.$$
(13)

For second time integrate Eq. (12) w.r.t \(x\) and limit from 0 to \(x\),

$$f^{\prime\prime}\left( x \right) - f^{\prime\prime}\left( 0 \right) - xf^{\prime\prime\prime}\left( 0 \right) - G^{T} \left[ {\xi \left( x \right)A^{\prime} + \overline{{\xi^{\prime}}} \left( x \right)} \right] = 0.$$
(14)

For third time integrate Eq. (12) w.r.t \(x\) and limit from 0 to \(x\),

$$f^{\prime}\left( x \right)\, - f^{\prime}\left( 0 \right)\, - \,x\,\,f^{\prime\prime}\left( 0 \right) - \frac{{x^{2} }}{2!}\,\,f^{\prime\prime\prime}\left( 0 \right) - G^{T} \left[ {\,\xi \left( x \right)A^{\prime\prime} + \overline{{\xi^{\prime\prime}}} \left( x \right)} \right] = 0.$$
(15)

For fourth timeintegrate Eq. (12) w.r.t \(x\) and limit from 0 to \(x\),

$$f\left( x \right) - f\left( 0 \right) - xf^{\prime}\left( 0 \right) - \frac{{x^{2} }}{2!}f^{\prime\prime}\left( 0 \right) - \frac{{x^{3} }}{3!}\,f^{\prime\prime\prime}\left( 0 \right) - G^{T} \left[ {\,\xi \left( x \right)A^{\prime\prime\prime} + \overline{{\xi^{\prime\prime\prime}}} \left( x \right)} \right] = 0.$$
(16)

Substitute \(f(0) = 0\) and \(f^{\prime\prime}(0) = 0\) in Eq. (16) we have,

$$f\left( x \right) = xf^{\prime}\left( 0 \right) + f^{\prime\prime\prime}\left( 0 \right)\frac{{x^{3} }}{3!} + G^{T} \left[ {\xi \left( x \right)A^{\prime\prime\prime} + \overline{{\xi^{\prime\prime\prime}}} \left( x \right)} \right].$$
(17)

Substitute \(f\left( 1 \right) = 1\) and \(f^{\prime}\left( 1 \right) = \,0\) in Eqs. (15) and (17). Further, we find \(f^{\prime\prime\prime}\left( 0 \right)\) and \(f^{\prime}\left( 0 \right)\) we have,

$$f^{\prime\prime\prime}\left( 0 \right) = - 3 + 3\,G^{T} \left[ {\,\xi \left( x \right)A^{\prime\prime\prime} + \overline{{\xi^{\prime\prime\prime}}} \,\left( x \right)} \right]_{x = 1} - 3G^{T} \left[ {A^{\prime\prime}\xi \left( {\,x} \right) + \overline{{\xi^{\prime\prime}}} \left( {\,x} \right)} \right]_{x = 1}$$
(18)
$$f^{\prime}\left( 0 \right) = - \frac{1}{2}\,f^{\prime\prime\prime}\left( 0 \right) - \,G^{T} \left[ {\,\xi \left( x \right)A^{\prime\prime} + \,\,\,\overline{{\xi^{\prime\prime}}} \left( {\,x} \right)} \right]_{x = 1} .$$
(19)

Substitute (18) and (19) in (17) we have

$$\begin{aligned} f\left( x \right) & = - \frac{x}{2}\,f^{\prime\prime\prime}\left( 0 \right) - \,G^{T} \left[ {\,\,\xi \left( x \right)A^{\prime\prime} + \,\,\overline{{\xi^{\prime\prime}}} \,\left( {\,x} \right)} \right]_{x = 1} - 3 + 3\,G^{T} \left[ {\xi \left( x \right)A^{\prime\prime\prime} + \overline{{\xi^{\prime\prime\prime}}} \,\left( x \right)} \right]_{x = 1} \\ & \quad - 3G^{T} \left[ {\,\xi \left( {\,x} \right)A^{\prime\prime} + \overline{{\xi^{\prime\prime}}} \left( {\,x} \right)} \right]_{x = 1} \frac{{x^{3} }}{3!} + G^{T} \left[ {\xi \left( x \right)A^{\prime\prime\prime} + \overline{{\xi^{\prime\prime\prime}}} \left( x \right)} \right]. \\ \end{aligned}$$
(20)

3.2 Solution of energy equation

At present, second derivative of temperature is assumed in the form.

$$\theta^{\prime\prime}\left( x \right) = B^{T} \xi \left( x \right).$$
(21)

Integrate Eq. (21) w.r.t \(x\) and limit from 0 to \(x\).

$$\theta^{\prime}(x) = \theta^{\prime}\left( 0 \right) + B^{T} \left[ {\xi \left( x \right)A + \overline{\xi } \left( x \right)} \right].$$
(22)

Again, integrate Eq. (22) w.r.t \(x\) and limit from 0 to \(x\).

$$\theta \left( {\,x} \right) = \theta \left( {\,0} \right) + x\,\theta^{\prime}\left( {\,0} \right) + B^{T} \left[ {\xi \left( x \right)A^{\prime} + \overline{{\xi^{\prime}}} \left( x \right)} \right].$$
(23)

Substituting \(\theta (1) = 1\), in above equation we get

$$\theta (0) = \,1 - \left. {B^{T} \left[ {\,\,\xi \left( x \right)A^{\prime} + \,\overline{{\xi^{\prime}}} \left( x \right)} \right]} \right|_{x = 1} .$$
(24)

Substituting (24) in (23), we get

$$\theta \left( {\,x} \right) = 1 - \left. {B^{T} \left[ {\,\xi \left( x \right)A^{\prime} + \,\xi^{\prime}\left( x \right)} \right]} \right|_{x = 1} + B^{T} \left[ {\xi \left( {\,x} \right)A^{\prime} + \overline{{\xi^{\prime}}} \left( x \right)\,} \right].$$
(25)

3.3 Solution of concentration equation

Now, assume that

$$\phi^{\prime\prime}\left( x \right) = C^{T} \xi \left( x \right).$$
(26)

Integrate Eq. (26) w.r.t \(x\) and limit from 0 to \(x\),

$$\phi^{\prime}(x) = \phi^{\prime}\left( 0 \right) + C^{T} \left[ {\xi \left( x \right)A + \overline{\xi } \left( x \right)} \right].$$
(27)

Further, integrate Eq. (27) w.r.t \(x\) and limit from 0 to \(x\).

$$\phi \left( {\,x} \right) = \phi \left( {\,0} \right) + x\,\phi^{\prime}\left( {\,0} \right) + C^{T} \left[ {\xi \left( x \right)A^{\prime} + \overline{{\xi^{\prime}}} \left( x \right)} \right].$$
(28)

By setting \(\phi (1) = 1\), we obtain

$$\phi (0) = \,1 - \left. {C^{T} \left[ {\,\,\xi \left( x \right)A^{\prime} + \,\overline{{\xi^{\prime}}} \left( x \right)} \right]} \right|_{x = 1} .$$
(29)

Substituting (29) for (28), we get

$$\phi \left( {\,x} \right) = 1 - \left. {C^{T} \left[ {\,\xi \left( x \right)A^{\prime} + \,\overline{{\xi^{\prime}}} \left( x \right)} \right]} \right|_{x = 1} + C^{T} \left[ {\xi \left( {\,x} \right)A^{\prime} + \overline{{\xi^{\prime}}} \left( x \right)\,} \right].$$
(30)

To collocate the equations, one can substitute values for \(f^{iv} ,f^{\prime\prime\prime},f^{\prime\prime},\theta^{\prime\prime},\phi^{\prime\prime},f^{\prime},\theta^{\prime},\phi^{\prime},\theta ,\phi ,f\), and follow the collocation steps using \(x_{i} = \frac{2\,i - 1}{N}\), where \(i = 1,\,\,2,\,\,3,\,\, \cdot \cdot \cdot ,\,\,N\). This process leads to a nonlinear system of algebraic equations then solved with help of suitable solver to obtain the unknown coefficients of the Bernoulli wavelets. Substitute these values in Eqs. (20, 25, 30) gives Bernoulli wavelet numerical results for Eqs. (8–10).

4 Results and implications

In this article, numerical Bernoulli wavelet technique is applied to find the new results of the Soret and Dufour effects on thermohaline non-Newtonian liquid flow with the influence of internal heat source. Convergence of the numerical Bernoulli wavelet technique can be seen in Table 1 for changed values of \(S\). Values of \(Nu_{\theta }\), \(C_{f}\), and \(Nu_{\phi }\) have been intended for several values of \(S\) in Table 1. From Table 1, it is clear that the outcomes obtained by the existing technique is excellent conformity with the outcomes in literature. Hence, we can fulfil that Bernoulli wavelet numerical technique is a technique for solving nonlinear differential Eqs. (8–10) that is more suitable than any other method found in the literature. The special properties of known physical parameters such as the squeeze number, Casson fluid quantity, Prandtl quantity, Schmidt quantity, chemical reaction quantity, internal heat source, Soret quantity, Dufour quantity and Eckert number are investigated.

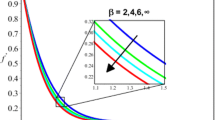
Table 1 Testing the accuracy of the Bernoulli wavelet method (BWM) by comparing it with Mustafa et al. [50]
Full size table

Figures 1, 2, 3, 4, 5 and 6 depict the property of parameter S on temperature and velocity variations. The values of S, whether negative or positive, are utilized to describe the approach or separation of surfaces. Analysis of Figs. 1 and 2 reveals a decrease in velocity as the value of S increases. This implies that when the surfaces come closer together (i.e., squeezing effect), the fluid is forced out of the channel, resulting in a slowdown of the velocity field. Figure 3 clearly demonstrates that rising positive values of S lead to a reduce in velocity. Conversely, Fig. 4 illustrates a rise in the velocity profile as S decreases towards negative values. Moreover, Fig. 5 shows that the control of S on the temperature field, indicating a decrease in temperature with rising values of S. Additionally, Fig. 6 represents that the values of parameter \(\beta\) increase as the function \(f(\eta )\) decreases.

Fig. 1
figure 1

Influence of \(S<0\) on \(f(\eta )\), with \(\beta =1\)

Full size image
Fig. 2
figure 2

Influence of \(S>0\) on \(f(\eta )\), with \(\beta =1\)

Full size image
Fig. 3
figure 3

Influence of \(S>0\) on \(f{\prime}(\eta )\), with \(\beta =1\)

Full size image
Fig. 4
figure 4

Influence of \(S<0\) on \(f{\prime}(\eta )\), \(\mathrm{with }\beta =1\)

Full size image
Fig. 5
figure 5

Influence of S on \(\theta (\eta )\)

Full size image
Fig. 6
figure 6

Influence of \(\beta\) on \(f(\eta )\), with S = 1

Full size image

An increase in Pr, leads to a reduction in the thermal diffusion of a viscous fluid, consequently elevating the flow temperature. The property of Pr on the temperature field is shown in Fig. 7, as Pr increases, the flow's temperature increases. When analysing fluid flow problem, changes to the internal heat source can impact the temperature outline of the fluid. The extent of this impact is influenced by several factors such as the fluid type, boundary conditions, and the problem's geometry. An increase in the internal heat source results in additional heat energy being supplied to the liquid. This additional energy can reason the fluid's temperature to increases, causing alterations to the temperature contour as indicated in Fig. 8. In some cases, an amplify in the heat source can also lead to a more uniform temperature profile across the fluid domain. This occurs because the heat source supplies energy more evenly across the fluid, reducing temperature variation.

Fig. 7
figure 7

Influence of Pr on \(\theta (\eta )\)

Full size image
Fig. 8
figure 8

Influence of Hs on \(\theta (\eta )\)

Full size image

Figure 9 shows the temperature for the involvement of \({\gamma }_{12}\) (Dufour effect) and temperature enrichment is essential for higher values of \({\gamma }_{12}\). Figure 10 illustrates how the variation of parameter Ec affects the temperature field, revealing a positive correlation between Ec enhancements and temperature increases. The phenomenon known as viscous dissipation refers to the heat generation affected by friction between liquid particles in a high-viscosity flow. Moreover, Fig. 11 demonstrates an increase in the values of parameter β as θ(η) decreases.

Fig. 9
figure 9

Influence of \({\gamma }_{12}\) on \(\theta (\eta )\)

Full size image
Fig. 10
figure 10

Influence of Ec on \(\theta (\eta )\)

Full size image
Fig. 11
figure 11

Influence of \(\beta\) on \(\theta (\eta )\)

Full size image

The impact of S on concentration as shown in Fig. 12, the concentration curve rises as S rises. Figure 13 depicted that the values of \(\beta\) increases with decrease in \(\phi (\eta )\). Figure 14 shows how the Sc affects the concentration field. Figure 15 explained that by rising \({\gamma }_{21}\)(Soret effect), the \(\phi (\eta )\) rises. The variation of concentration field with chemical reaction is shown in Fig. 16. For large levels of a unhelpful chemical reaction number, the concentration curves significantly drops. For the generative chemical reaction number, a discernible increase in the concentration field is shown. The steeper curves of the concentration function are a result of the severe reaction conditions that go along with high values of \(\gamma\).

Fig. 12
figure 12

Influence of S on \(\phi (\eta )\)

Full size image
Fig. 13
figure 13

Influence of \(\beta\) on \(\phi (\eta )\)

Full size image
Fig. 14
figure 14

Influence of Sc on \(\phi (\eta )\)

Full size image
Fig. 15
figure 15

Influence of \({\gamma }_{2}\) on \(\phi (\eta )\)

Full size image
Fig. 16
figure 16

Influence of \(\gamma\) on \(\phi (\eta )\)

Full size image

5 Conclusion

This article employed the Bernoulli wavelet technique to numerically solve the thermohaline Casson fluid flow with cross diffusion terms, incorporating an internal heat source. The results obtained using the Bernoulli wavelet numerical method demonstrate its effectiveness in solving non-linear differential equations, as evidenced by the presented figures and tables. The computed results obtained through Bernoulli wavelet numerical method closely approximates the numerical solution. Furthermore, the Bernoulli wavelet numerical method exhibits superior capabilities compared to other numerical methods for solving this particular model. The study investigated the impact of different factors, such as S, β, Pr, Ec, \(\gamma\), \({\gamma }_{12}, {\gamma }_{21},\) Hs and Sc, on concentration, velocity and temperature. The analysis of the results revealed several significant outcomes.

  • The velocity in the vicinity of the upper plate experiences an increment when the surfaces approach each other (S < 0), while it decreases when they move apart (S > 0).

  • Enhance in velocity and reduce in temperature as well as concentration for different values of \(\beta\).

  • An elevation of both Pr and Ec leads to an amplification in temperature and the rate of heat transfer.

  • An amplify in the internal heat source results in a higher amount of heat energy being introduced to the fluid, consequently leading to an elevation in the fluid's temperature.

  • The concentration profile decreases as the chemical reaction parameter increases.

  • The dimension of the local Sherwood number increases as \(\gamma\) increases.

  • Opposite effects on double diffusive rates are observed when the Dufour and Soret numbers are increased.