Nonadiabatic quantum dynamics of the coherent excited state intramolecular proton transfer of 10-hydroxybenzo[h]quinoline

Abstract

The photoinduced nonadiabatic dynamics of the enol-keto isomerization of 10-hydroxybenzo[h]quinoline (HBQ) are studied computationally using high-dimensional quantum dynamics. The simulations are based on a diabatic vibronic coupling Hamiltonian, which includes the two lowest $\pi \pi ^*$ excited states and a $n\pi ^*$ state, which has high energy in the Franck–Condon zone, but significantly stabilizes upon excited state intramolecular proton transfer. A procedure, applicable to large classes of excited state proton transfer reactions, is presented to parametrize this model using potential energies, forces and force constants, which, in this case, are obtained by time-dependent density functional theory. The wave packet calculations predict a time scale of 10–15 fs for the photoreaction, and reproduce the time constants and the coherent oscillations observed in time-resolved spectroscopic studies performed on HBQ. In contrast to the interpretation given to the most recent experiments, it is found that the reaction initiated by $1\pi \pi ^* \longleftarrow S_0$ photoexcitation proceeds essentially on a single potential energy surface, and the observed coherences bear signatures of Duschinsky mode-mixing along the reaction path. The dynamics after the $2\pi \pi ^* \longleftarrow S_0$ excitation are instead nonadiabatic, and the $n\pi ^*$ state plays a major role in the relaxation process. The simulations suggest a mainly active role of the proton in the isomerization, rather than a passive migration assisted by the vibrations of the benzoquinoline backbone.

Graphic Abstract

1 Introduction

Excited state proton or hydrogen transfer reactions are among the most ubiquitous and widely studied processes in photochemistry [1,2,3,4]. An important reason is that they are prototypical models to study fundamental acid-base chemistry, because the migration of the proton from a donor to an acceptor group can be initiated precisely and then followed in time. In addition, the mechanistic understanding of the proton transfer is crucial for the development of fluorescent sensors, sunscreen agents and optoelectronic devices [5,6,7]. In particular, excited state intramolecular proton transfers (ESIPT), which typically occur in molecules possessing an intramolecular hydrogen bond, are among the fastest reactions in chemistry, and can proceed on a time scale of few tens of femtoseconds [8,9,10,11].

The ultrafast reaction kinetics is the reason why, although evidence of ESIPT exists from the 50s, the detailed elucidation of the reaction mechanism relies on observations performed with modern time-resolved spectroscopic techniques. A variety of sophisticated spectroscopies, based on different sequences of laser pulses with variable delays and wavelengths, has allowed the monitoring of ultrafast ESIPT in the femtosecond time scale [10,11,12,13,14,15,16].

Given the relevance of this process and the complexity of such ultrafast measurements, theoretical approaches are needed to model the electronic structure of the involved chromophore, its nuclear and electronic photodynamics, and their manifestation in the spectroscopic observables. In particular, since the migrating proton can undergo tunneling and nonadiabatic effects might be operative [16,17,18,19], it is crucial to develop computational strategies where at least the H atom motion is treated quantum mechanically [20,21,22,23,24].

A prototypical molecule to investigate ultrafast ESIPT and explore the potentialities of new spectroscopic techniques is 10-hydroxybenzo[h]quinoline (HBQ), which undergoes the enol to keto photoisomerization depicted in Fig. 1.

Fig. 1

ESIPT reaction of HBQ

This photoreaction was first reported in Ref. [25] and studied by Chou et al. using transient absorption and fluorescence upconversion spectroscopy with a time resolution of 150–200 fs.[26] In that study, performed with cyclohexane as solvent, a time constant of $\sim 330\,\mathrm {fs}$ was attributed to a $S_2 \longrightarrow S_1$ internal conversion and, therefore, a nonadiabatic reaction mechanism was proposed. Subsequent transient absorption experiments of Takeuchi and Tahara [27] using pulses shorter than 30 fs estimated a proton transfer time of $25\pm 15\,\mathrm {fs}$ for HBQ in cyclohexane and revealed that the photoreaction is accompanied by coherences, which, once resolved in frequency, could be attributed to vibrational modes of the benzoquinoline skeleton in the frequency range 0–800 cm$^{-1}$. These coherences survive for more than 2 ps and were observed as well by Riedle and coworkers for HBQ and similar chromophores [28, 29], leading to the conclusion that the reaction actually proceeds on a single potential energy surface, because nonadiabatic processes lasting for hundreds of femtoseconds would lead to a rapid vibrational dephasing [27]. In addition, it was suggested [28, 29] that the proton transfer coordinate might have a rather passive role in the reaction, which might be driven by some skeletal vibrations which bring the hydroxyl group and the N heteroatom close to each other.

Joo and coworkers performed ultrafast time-resolved fluorescence experiments on HBQ and its deuterated form (DBQ) in methanol and cyclohexane solutions [11, 30], and found proton transfer times of $12\pm 6\,\mathrm {fs}$ for HBQ and $25\pm 5\,\mathrm {fs}$ for DBQ, with little dependence on the solvent. Since these time scales are compatible with the factor $\sqrt{2}$ expected for a ballistic proton migration, the authors suggested that it is the proton to have the active role in the reaction, whereas vibrational coherences form afterwards. Moreover, time-resolved fluorescence anisotropy measurements by Lee and Joo [31] revealed a component of $\approx 300\,\mathrm {fs}$ in the anisotropy decay, which was assigned to an internal conversion as initially suggested by Chou et al. [26]

The most recent transient absorption experiments performed for HBQ in ethanol had a time resolution of $\approx 10\,\mathrm {fs}$, which allowed the resolution of coherent oscillations in the spectroscopic signal with frequencies up to $3000\,\mathrm {cm}^{-1}$ [19]. The authors explained their observations using a nonadiabatic model based on two coupled harmonic potential energy surfaces, including Duschinsky rotations. Only assuming an internal conversion between the two surfaces they could reproduce the frequencies of the oscillations observed experimentally. Therefore, the coherences were interpreted as a signature of non-Born–Oppenheimer reaction dynamics.

In summary, different interpretations are still open for the rich amount of data provided by the numerous experimental studies. The extent to which nonadiabatic effects are involved in the ESIPT mechanism, the assignment of the observed coherences, and their connection to the active or passive role of the proton are still under debate. Surprisingly, the computational investigations of the electronic structure of HBQ are scarce and few example of dynamical simulations are available, based on two-dimensional quantum dynamics [28] or on classical trajectories [32], but limited to an isolated electronic excited state. The nonadiabatic effects invoked in the experimental works cited above have never been included in classical or quantum dynamical simulations based on ab initio potential energy surfaces.

This work has a double scope. In the first instance, it aims at interpreting the body of experimental results for the ultrafast excited state dynamics of HBQ, and clarify the debated questions mentioned above. This goal is pursued by constructing a multi-state multi-mode diabatic vibronic coupling Hamiltonian for HBQ, starting from quantum chemical calculations. This model is then used to simulate the photoreaction adopting a full quantum dynamical treatment based on the Gaussian-based multiconfigurational time-dependent Hartree method [33]. In this way the possible nonadiabatic processes and the motion of light atoms are treated in the most rigorous way as possible. The formulation of a general protocol for this task, applicable to large classes of ESIPT reactions, is the other objective of this work.

The rest of the paper is organized as follows: Sect. 2 describes the quantum chemical investigations of the electronic structure of HBQ in the enol and keto form, which are instrumental to the construction of the molecular diabatic Hamiltonian, explained in Sect. 3. Computational details are given in Sect. 4. Section 5 discusses the results of the quantum dynamical simulations initiated by photoexcitation to the first and second excited states. Section 6 summarizes the results and concludes.

2 Electronic structure of the enol and keto forms of 10-hydroxybenzo[h]quinoline

The electronic structure of HBQ was studied using density functional theory (DFT) and its time-dependent form (TDDFT) for the excited electronic states. The polarizable continuum model (PCM) was used to account for the effects of a non-polar solvent (cyclohexane). Five functionals were tested, which differ in the amount of exact exchange ($\alpha _\mathrm {HF}$) included in the total exchange functional. Although an extensive functional benchmark for HBQ is beyond the purpose of the present work, this investigation allows the identification of some general features of the electronic structure of the keto and enol form. In addition, the functional whose predictions agree most accurately with experimental data is then chosen to construct the diabatic vibronic coupling model used in the quantum dynamical simulations.

The results of the (TD)DFT study are reported in Table 1. The molecular geometry was optimized in the ground electronic state (for the enol form) and the first excited state (for the keto form), independently for each functional. A stable ground state keto isomer was not found. At both the optimized structures the four lowest singlet excited states include three states of $\pi \pi ^*$ character (their irrep is $A^\prime$ in $C_\mathrm {s}$ symmetry) and one state of $n\pi ^*$ character ($A^{\prime \prime }$).

Table 1 Energies of the ground and the four lowest electronic excited states of HBQ, evaluated at the optimized geometries of the enol and the excited keto isomers using different DFT functionals and the Def2-TZVP basis set

The $1\pi \pi ^*$ state ($S_1$) is the brightest state. The vertical excitation energy predicted by TDDFT for the enol isomer increases for increasing fraction of exact exchange, ranging from 3.24 eV for the TPSSh functional ($\alpha _\mathrm {HF} = 0.1$) to 3.76 eV for MN15 ($\alpha _\mathrm {HF} = 0.44$) and 3.94 eV for the range-separated $\omega$B97XD functional.

All tested functionals predict that the four excited states get stabilized upon ESIPT. For the two lowest $\pi \pi ^*$ states the energy difference between the enol and keto structures is very similar among all functionals and is $\approx 0.75\,\mathrm {eV}$ and $\approx 0.35\,\mathrm {eV}$ for the $1\pi \pi ^*$ and $2\pi \pi ^*$ states, respectively. Although these are “static” results, the fact that the energy separation between the lowest $\pi \pi ^*$ states increases upon photoisomerization suggests a mechanism involving a single Born–Oppenheimer surface, at least for long wavelength photoexcitation.

The five tested functionals agree in placing the dark $A^{\prime \prime }$ state as the fourth excited state in the enol region. According to TPSSh, B3LYP and PBE0, this is the state which gets mostly stabilized upon ESIPT, with an energy relaxation in the range of 0.9–1.2 eV. The reason can be found by inspecting the Kohn–Sham orbital of the keto isomer, depicted in Fig. 2. The dominant configuration in the $1n\pi ^*$ state (simply denoted $n\pi ^*$ hereafter) for the photoproduct is a transition from the (non-bonding) lone pair of the carbonyl oxygen atom, which becomes a bonding orbital at the enol structure and has therefore a lower energy. Although this state has been identified in previous theoretical investigations [28], its role in the dynamics of HBQ, induced by $S_1 \longleftarrow S_0$ and $S_2 \longleftarrow S_0$ excitations, has never been studied.

Fig. 2

Kohn–Sham orbitals involved in the most relevant excitations for the three lowest excited states of the keto isomer of HBQ, calculated at the optimized $S_1$ geometry at the TPSSh/Def2-TZVP level

The energy stabilization of the $n\pi ^*$ state upon proton transfer is higher for functionals with lower fraction of exact exchange. In particular, the TPSSh, B3LYP and PBE0 functionals predict that both the $2\pi \pi ^*$ and the $n\pi ^*$ state are in principle accessible upon vertical $1\pi \pi ^* \longleftarrow S_0$ excitation, even without taking their geometrical relaxation into account. In Sect. 5.1 this possibility is explicitly tested by dynamical simulations.

The calculated energies are compared with the available data obtained by the experimental absorption and fluorescence spectra of HBQ of Ref. [28]. The TPSSh functional gives the best agreement with the experiment, both for the vertical excitation energy, compared with absorption maximum, and the Stokes shift. Therefore, this functional is chosen for further modeling of the potential energy surfaces (PESs). On the other hand, the energy gaps between excited states and the oscillator strengths, which are key quantities to define the diabatic model of Sect. 3, are rather similar for different DFT functionals or as compared with coupled-cluster results [28]. Therefore, the findings obtained by the dynamical simulations described below are expected to be rather robust.

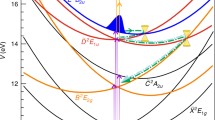
Figure 3 shows potential energy cuts of the ground and excited states of HBQ along a rectilinear dimensionless coordinate $Q_1$, (defined precisely in Sect. 3.1) which connects the minima of the enol and the excited state keto form, calculated at the TPSSh/Def2-TZVP level (full lines). This “straight line” reaction pathway is predicted to be barrierless for the reaction proceeding on $S_1$, in line with the observation that the ESIPT reaction occurs on an ultrafast time scale of $<20\,\mathrm {fs}$ [28]. A conical intersection between the states $2\pi \pi ^*$ and $n\pi ^*$, found at a structure intermediate between the reactant and the product, provides an electronic relaxation channel for a photoreaction initiated by the $2\pi \pi ^* \longleftarrow S_0$ excitation.

Fig. 3

Rigid (full lines) and relaxed (dashed lines) TPSSh/Def2-TZVP adiabatic potential energy scans of the lowest singlet states of HBQ along the dimensionless rectilinear coordinate $Q_1$ (defined in Sect. 3), which connects the minima of the $S_0$ and the $1\pi \pi ^*$ states. The sketch shows the Cartesian displacements associated with a distortion along $Q_1$ around the $S_0$ minimum

This work focuses on the dynamics initiated by the $1\pi \pi ^* \longleftarrow S_0$ and $2\pi \pi ^* \longleftarrow S_0$ photoexcitation. At all the investigated geometries the $3\pi \pi ^*$ state lies 0.5–1.0 eV above the $2\pi \pi ^*$ state. Therefore, even for dynamics initiated in the $2\pi \pi ^*$ surface, the $2\pi \pi ^* \longrightarrow 3\pi \pi ^*$ internal conversion is expected to be much less likely than the competing $2\pi \pi ^* \longrightarrow n\pi ^*$ and $2\pi \pi ^* \longrightarrow 1\pi \pi ^*$ processes. For this reason, and to make computations more easily feasible, the dynamical simulations of the present work only include the manifold of coupled $1\pi \pi ^*$, $2\pi \pi ^*$ and $n\pi ^*$ states.

3 Construction of a diabatic vibronic coupling model for HBQ

The preliminary exploration of the potential energy surfaces of HBQ suggests that the states $1\pi \pi ^*$, $2\pi \pi ^*$ and $n\pi ^*$ might be operative in the photodynamics initiated by light pulses with wavelengths in the range 320–380 nm [28]. To simulate the photoreaction quantum mechanically, a multimode diabatic vibronic coupling Hamiltonian is constructed using a protocol presented in this section and based on quantum chemical data, which, in this application, are obtained by TDDFT calculations using the TPSSh functional.

The diabatic electronic states are obtained by an orthogonal transformation between the adiabatic (Born–Oppenheimer) states [39, 40]. For ease of notation, in this and the subsequent Sections, the states $1\pi \pi ^*$, $2\pi \pi ^*$ and $n\pi ^*$, appropriately reordered, are also denoted $|1\rangle$, $|2\rangle$ and $|3\rangle$, respectively. The diabatic states $|\tilde{1}\rangle$, $|\tilde{2}\rangle$ and $|\tilde{3}\rangle$ are given as [40]

$$\begin{aligned} \left( \begin{array}{c} |\widetilde{1}\rangle \\ |\widetilde{2}\rangle \\ |\widetilde{3} \rangle \end{array} \right) = \mathbf {R}_z(\alpha ) \mathbf {R}_y(\beta ) \mathbf {R}_x(\gamma ) \left( \begin{array}{c} |1\rangle \\ |2\rangle \\ |3 \rangle \end{array} \right) , \end{aligned}$$

(1)

and are required to be associated with electronic wavefunctions which vary the least as possible as a function of the nuclear geometry. The matrices $\mathbf {R}_x(\gamma )$, $\mathbf {R}_y(\beta )$ and $\mathbf {R}_z(\alpha )$ are $3\times 3$ rotation matrices depending on the mixing angles $\alpha$, $\beta$ and $\gamma$,

$$\begin{aligned} \mathbf {R}_x(\gamma )= & {} \left( \begin{array}{ccc} 1 &{} 0 &{} 0 \\ 0 &{} \cos \gamma &{} \sin \gamma \\ 0 &{} -\sin \gamma &{} \cos \gamma \end{array}\right) , \nonumber \\ \mathbf {R}_y(\beta )= & {} \left( \begin{array}{ccc} \cos \beta &{} 0 &{} \sin \beta \\ 0 &{} 1 &{} 0 \\ -\sin \beta &{} 0 &{} \cos \beta \end{array}\right) , \nonumber \\ \mathbf {R}_z(\alpha )= & {} \left( \begin{array}{ccc} \cos \alpha &{} \sin \alpha &{} 0 \\ -\sin \alpha &{} \cos \alpha &{} 0 \\ 0 &{} 0 &{} 1 \end{array}\right) . \end{aligned}$$

(2)

The diabatic PESs are related to the adiabatic ones as

$$\begin{aligned} \left( \begin{array}{ccc} W_1 &{} W_{12} &{} W_{13} \\ W_{12} &{} W_2 &{} W_{23} \\ W_{13} &{} W_{23} &{} W_3 \end{array} \right)= & {} \mathbf {R}_z(\alpha ) \mathbf {R}_y(\beta ) \mathbf {R}_x(\gamma ) \nonumber \\&\times \left( \begin{array}{ccc} V_1 &{} 0 &{} 0 \\ 0 &{} V_2 &{} 0 \\ 0 &{} 0 &{} V_3 \end{array} \right) \nonumber \\&\times \mathbf {R}_x^T(\gamma ) \mathbf {R}_y^T(\beta ) \mathbf {R}_z^T(\alpha ), \end{aligned}$$

(3)

and are parametrized according to a predefined ansatz inspired by the reaction path formalism [41,42,43].

3.1 Reaction path Hamiltonian

The construction of the Hamiltonian starts with a frequency calculation performed at the optimized minimum of $S_0$, to obtain frequencies $\omega _i$ and (mass-weighted) normal modes $q_i^\prime$ (after projecting out translations and infinitesimal rotations); N dimensionless normal modes are obtained by frequency-weighting, $q_i = q_i^\prime \sqrt{\omega _i/\hbar }$. At the $S_0$ minimum HBQ has a $C_s$ geometry; the in-plane vibrations transform according to the irreducible representation $a^\prime$, whereas the out-of-plane distortions have $a^{\prime \prime }$ symmetry.

An effective dimensionless mode $Q_1$ is then constructed as a linear combination of the $q_i$s,

$$\begin{aligned} Q_1 = \sum _j q_j U_{j1}, \end{aligned}$$

(4)

where the coefficients $U_{j1}$ are defined in such a way that $Q_1$ connects rectilinearly the minima of $S_0$ and the $1\pi \pi ^*$ state, i.e. the equilibrium structures of the enol and keto isomers of HBQ. In practice, $Q_1$ coincides by more than 90% with the normal mode associated with the O–H stretch of HBQ. Given that the minimum of the $1\pi \pi ^*$ has also $C_s$ symmetry, the mode $Q_1$ is totally symmetric.

Normalizing the coefficients such that $\sum _j U_{j1}^2 = 1$, the vector $\{ U_{j1} \}$ is regarded as the first column of an orthogonal transformation matrix which connects the dimensionless normal modes to a new set of effective coordinates, among which a proton transfer mode $Q_1$—the “reaction coordinate”—is identified. Similarly, the remaining modes are given as $Q_r = \sum _j q_j U_{jr}$ and are regarded as “skeletal vibrations”. The precise definition of the remaining coefficients $U_{jr}$, with $r = 2,\ldots ,N$, is not necessary at the moment and is given in Sect. 3.3.

Having defined the reaction mode, relaxed potential energy scans are performed by optimizing the geometries of the adiabatic states $S_0$, $|1\rangle$, $|2\rangle$ and $|3\rangle$ along a grid of $Q_1$ values. The relaxed scans obtained at the TDDFT level for HBQ are shown in Fig. 3 and the optimization were performed imposing the $C_s$ symmetry, a feature that is helpful for the subsequent diabatization procedure.

$Q_1$-dependent reaction paths, $\mathbf {a}_s(Q_1) = \left( a_{s,2}(Q_1), \ldots , a_{s,N}(Q_1) \right)$, are thus obtained by collecting the optimized structures for each adiabatic electronic state s, including the ground state ($s=0$). The diagonal diabatic PES of Eq. (3) are approximated using a general quadratic reaction path potential,

$$\begin{aligned} W_s= & {} E_s(Q_1) + \mathbf {g}_s^T(Q_1) \left( \mathbf {Q}- \mathbf {a}_s(Q_1) \right) \nonumber \\&+ \frac{1}{2} \left( \mathbf {Q}- \mathbf {a}_s(Q_1) \right) ^T \mathbf {B}_s(Q_1) \left( \mathbf {Q}- \mathbf {a}_s(Q_1) \right) , \end{aligned}$$

(5)

where the (column) vector $\mathbf {Q}= (Q_2,\ldots ,Q_N)$ collects the skeletal modes, and $E_s(Q_1)$, $\mathbf {g}_s(Q_1)$ and $\mathbf {B}_s(Q_1)$ are the diabatic energy, gradient and Hessian along the adiabatic reaction path for each electronic state. In particular, this ansatz includes Duschinsky correlations between modes, which are believed to be important in proton transfer processes [44, 45]. The parameters of Eq. (5) are obtained from the corresponding adiabatic quantities (obtained ab initio) by differentiating the diagonal entries of Eq. (3) with respect to the skeletal modes [46] at the geometries on the reaction paths. This operation requires the knowledge of the derivatives of the mixing angles with respect to the coordinates $Q_r$, which are, in turn, obtained by differentiating the off-diagonal entries of Eq. (3), once the diabatic couplings $W_{12}$, $W_{13}$ and $W_{23}$ are known.

To this end, an ansatz is chosen for these functions. The coupling between the two $\pi \pi ^*$ states is simply taken as only dependent on $Q_1$, i.e. $W_{12}(Q_1,\mathbf {Q}) \equiv W_{12}(Q_1)$; the couplings between the $n\pi ^*$ state and the $\pi \pi ^*$ states are taken as linear functions of the out-of-plane skeletal modes, with $Q_1$-dependent coefficients,

$$\begin{aligned} W_{s3}(Q_1,\mathbf {Q}) = \sum _{\begin{array}{c} j \\ \varGamma (q_j) = a^{\prime \prime } \end{array}} \lambda _{s3,j}(Q_1) q_j , \quad s = 1,2. \end{aligned}$$

(6)

The diabatic couplings are parametrized according to the property-based approach described in Sect. 3.2. The lengthy operations to obtain the diagonal diabatic geometrical derivatives from the adiabatic ones are given in detail in the Supporting Information.

3.2 Property-based diabatization

The property-based diabatization [46] is based on the transition dipole moments between the $S_0$ and the excited states, and has strong similarities with the oscillator strength diabatization of Ref. [47] and the procedures used in Refs. [48, 49] to diabatize the $\pi \pi ^*/n\pi ^*$ intersections of nucleobases.

The structures along the reaction paths are planar and, due to this symmetry, the $n\pi ^* \longleftarrow S_0$ electric dipole transition is polarized perpendicularly to the molecular plane xy. This transition turns out to be essentially dark, with the oscillator strength lower than $10^{-4}$ in the keto region. The two $\pi \pi ^* \longleftarrow S_0$ transitions are polarized in parallel to the plane of the molecule, along nearly orthogonal directions.

Therefore, for the planar molecule the $\pi \pi ^*$ states are taken as uncoupled from the $n\pi ^*$ state, i.e. $\beta = \gamma = 0$ in Eqs. (1)–(3) at $C_s$ structures. This guarantees that the symmetry of the electronic states is not broken upon diabatization. Concerning the two $\pi \pi ^*$ states, to enforce an electronic structure that depends minimally on the geometry as possible, the electronic wavefunctions are mixed so to impose the orthogonality between the respective transition dipole moments,

$$\begin{aligned} \widetilde{\varvec{\mu }}_{01} \cdot \widetilde{\varvec{\mu }}_{02} = \langle S_0 | \varvec{\mu } | \widetilde{1} \rangle \cdot \langle S_0 |\varvec{\mu } | \widetilde{2} \rangle = 0, \end{aligned}$$

(7)

where $\varvec{\mu }$ is the dipole operator. This is the same strategy adopted in Ref. [47]. In principle, the condition of Eq. (7) can be applied at arbitrary geometries. In this work, to use a minimum number of quantum chemical calculations, it is applied only along the relaxed cut for the $2\pi \pi ^*$ state, i.e. at geometries where the two $\pi \pi ^*$ states are the closest and the internal conversion more likely. Replacing Eq. (1) into Eq. (7) the mixing angle along the reaction path is found by solving the equation

$$\begin{aligned} \left( \tan (2\alpha ) \right) _{\mathbf {Q}= \mathbf {a}_2(Q_1)} = \left( \frac{2 \varvec{\mu }_{01} \cdot \varvec{\mu }_{02}}{\mu _{01}^2 - \mu _{02}^2} \right) _{\mathbf {Q}= \mathbf {a}_2(Q_1)}, \end{aligned}$$

(8)

where $\varvec{\mu }_{01}$ and $\varvec{\mu }_{02}$ are the adiabatic transition dipole moments. The $1\pi \pi ^*/2\pi \pi ^*$ diabatic coupling is finally obtained from Eq. (3),

$$\begin{aligned} W_{12}(Q_1) = \left( \sin (2\alpha ) \frac{V_2 - V_1}{2} \right) _{\mathbf {Q}= \mathbf {a}_2(Q_1)}. \end{aligned}$$

(9)

Note that the fact that $\beta = \gamma = 0$ at $C_s$ structures significantly simplifies the derivation.

The $\pi \pi ^*/n\pi ^*$ couplings are found by forcing the polarization of the $n\pi ^* \longleftarrow S_0$ transition to be perpendicular to the molecular plane. Denoting $\hat{\mathbf {x}}$ and $\hat{\mathbf {y}}$ the unit vectors defining the plane, the condition

$$\begin{aligned} \langle S_0 | \varvec{\mu } \cdot \hat{\mathbf {x}} | \widetilde{3} \rangle = \langle S_0 | \varvec{\mu } \cdot \hat{\mathbf {y}} | \widetilde{3} \rangle = 0 \end{aligned}$$

(10)

is imposed not only at $C_s$ geometries but also for first order out-of-plane distortions around a selected reaction path. In this case it is convenient to choose the reaction path for the $n\pi ^*$ state $|3\rangle$. Using again Eq. (1) and evaluating the derivatives of Eq. (10) one obtains the system of equations

$$\begin{aligned} \left( \frac{\partial \varvec{\mu }_{03}}{\partial q_j} - \varvec{\mu }_{01} \frac{\partial \beta }{\partial q_j} - \varvec{\mu }_{02} \frac{\partial \gamma }{\partial q_j} \right) _{\mathbf {Q}= \mathbf {a}_3(q_1)} \cdot \hat{\mathbf {x}}= & {} 0, \nonumber \\ \left( \frac{\partial \varvec{\mu }_{03}}{\partial q_j} - \varvec{\mu }_{01} \frac{\partial \beta }{\partial q_j} - \varvec{\mu }_{02} \frac{\partial \gamma }{\partial q_j} \right) _{\mathbf {Q}= \mathbf {a}_3(q_1)} \cdot \hat{\mathbf {y}}= & {} 0, \end{aligned}$$

(11)

which allows the evaluation of the gradients of the mixing angles $\beta$ and $\gamma$ for $C_s$ geometries. Note that only distortions along non-totally symmetric modes make the in-plane components of $\partial \varvec{\mu }_{03}/\partial q_j$ different from zero, i.e. they induce intensity borrowing from the $\pi \pi ^*$ states. Solving for $\partial \beta /\partial q_j$ and $\partial \gamma / \partial q_j$ the parameters $\lambda _{s3,j}(Q_1)$ of Eq. (6) are finally obtained by differentiating the corresponding entries of Eq. (3),

$$\begin{aligned} \lambda _{13,j}\equiv & {} \left( \frac{\partial W_{13}}{\partial q_j} \right) _{\mathbf {Q}= \mathbf {a}_3(Q_1)} \nonumber \\= & {} \left( \cos \alpha \frac{\partial \beta }{\partial q_j} (V_3 - V_1) + \sin \alpha \frac{\partial \gamma }{\partial q_j} (V_3 - V_2) \right) _{\mathbf {Q}= \mathbf {a}_3(Q_1)} \ , \nonumber \\ \lambda _{23,j}\equiv & {} \left( \frac{\partial W_{23}}{\partial q_j} \right) _{\mathbf {Q}= \mathbf {a}_3(Q_1)} \nonumber \\= & {} \left( -\sin \alpha \frac{\partial \beta }{\partial q_j} (V_3 - V_1) + \cos \alpha \frac{\partial \gamma }{\partial q_j} (V_3 - V_2) \right) _{\mathbf {Q}= \mathbf {a}_3(Q_1)}, \end{aligned}$$

(12)

where the angle $\alpha$ is obtained using the pre-calculated function $W_{12}(Q_1)$ and Eq. (9) evaluated for $\mathbf {Q}= \mathbf {a}_3(Q_1)$. The gradients of the adiabatic transition dipole moment are available from Hessian calculations performed along the reaction path for the $n\pi ^*$ state, which need to be performed anyhow to parametrize the matrices $\mathbf {B}_s$ of Eq. (5), and are available analytically at the TDDFT level.

In summary, the ingredients needed from quantum chemistry to construct the diabatic electronic Hamiltonian of Eq. (3) (with some minor approximations described in the Supporting Information) are energies and force constants of the three electronic states evaluated each along the respective reaction path.

3.3 Reduced dimensionality model and anharmonic correction

To reduce the dimensionality of the Hamiltonian and speed up quantum dynamical calculations, the $\pi \pi ^*/n\pi ^*$ couplings are mainly concentrated into four effective coupling modes, constructed by orthonormalization of the modes $Q_2^\prime$, $Q_3^\prime$, $Q_4^\prime$, $Q_5^\prime$ given by the expressions [50, 51]

$$\begin{aligned} Q_r^\prime = \sum _{\begin{array}{c} j\\ \varGamma (q_j) = a^{\prime \prime } \end{array}} \lambda _{s3,j}\left( Q_1^* \right) q_j, \end{aligned}$$

(13)

where $s=1,2$ and $Q_1^* = 3, 7$ are two selected values for the reaction coordinate $Q_1$, corresponding to the keto product and a structure intermediate between the enol and the keto forms. The normalized modes $Q_2$, $Q_3$, $Q_4$ and $Q_5$ are then obtained by Gram–Schmidt orthogonalization of the coordinates of Eq. (13), which gives four more columns of the transformation matrix $U_{jr}$ defined in Sect. 3.1. The gradients of the coupling functions $W_{13}$ and $W_{23}$ along the remaining $a^{\prime \prime }$ modes turn out to be negligible for the whole range of $Q_1$ values; therefore, these modes are not included in the simulations of Sect. 5.

Since the effective modes are constructed as linear combinations of dimensionless normal modes, the kinetic energy operator contains kinematic couplings and takes the form [50, 51]

$$\begin{aligned} \hat{T} = - \frac{\hbar }{2} \sum _{rs} \varOmega _{rs} \frac{\partial ^2}{\partial Q_r \partial Q_s}, \end{aligned}$$

(14)

where $\varOmega _{rs} = \sum _j \omega _j U_{jr} U_{js}$. To minimize these couplings, the remaining effective modes are obtained by making the lower $(N-5)\times (N-5)$ block of the $\varvec{\varOmega }$ matrix diagonal. This uniquely defines the transformation matrix, which, using the chain rule, allows one to express the Cartesian coordinates, gradients and Hessians in terms of the effective modes, as required by Eq. (3). Since, for HBQ, the $Q_1$ modes mostly coincides with the normal mode associated to the O–H stretch, the $a^\prime$ effective modes are also very similar to the ground state normal modes.

The inspection of the vectors $\mathbf {a}_s(Q_1)$ along the reaction path reveals that most modes undergo little shifts from the $S_0$ equilibrium, within the validity of the harmonic approximation. Therefore, the dimensionality of the model is reduced by including only the modes whose displacement is larger than 0.3 for at least one point on the $Q_1$ grid. This results in a total of 30 modes in addition to $Q_1$, sketched in Fig. 4, which also reports the diagonal values of the $\varvec{\varOmega }$ matrix. The mode $Q_9$, corresponding to a low-frequency collective bending of the benzoquinoline rings, is the one with the largest displacement, reaching a maximum shift of $\approx 2$ for $Q_1 =3$. Therefore, the diabatic potentials are augmented with anharmonic terms of the form $c_3 Q_9^3 + c_4 Q_9^4$, parametrized by few additional quantum chemical computations, as explained in the Supporting Information.

Fig. 4

Atomic displacement vectors for the skeletal effective modes of HBQ included in the quantum dynamical simulations. For each mode, the diagonal element $\varOmega _{rr}$ of the metric matrix of Eq. (14) is given in parenthesis in $\mathrm {cm}^{-1}$. The proton transfer mode $Q_1$ is sketched in Fig. 3 and is associated with a kinematic frequency $\varOmega _{11} = 2696\,\mathrm {cm}^{-1}$

4 Computational details

The (TD)DFT geometry optimizations, frequency calculations and potential energy scans of the ground and excited states of HBQ were performed using the package Gaussian 16 [52]. For all calculations the Def2-TZVP basis set [53] was used. The continuum polarizable model (integral equation formalism) was used, with cyclohexane as solvent, to account for non-polar solvation effects. A brief comparison with excitation energies obtained for the molecule in vacuo is given in the Supplementary Information.

The relaxed potential energy cuts along the coordinate $Q_1$, which can be expressed as a linear combination of Cartesian coordinates, were performed exploiting the generalized internal coordinates (GIC) module implemented in Gaussian 16. $Q_1$ was scanned from $-3$ to 12 with unit steps. Using $C_s$ symmetry, planar stationary points were found along the reaction path. The frequency analysis showed that these structures are indeed stable minima for fixed $Q_1$, with the exception of few points for $Q_1 < 0$ (see Supporting Information). All $Q_1$-dependent quantities were computed on the $Q_1$ grid and interpolated via a quadratic spline.

4.1 Quantum dynamics using the G-MCTDH method

The dynamics of HBQ following the photoexcitation to the $1\pi \pi ^*$ and $2\pi \pi ^*$ states were simulated quantum mechanically on the 31-dimensional diabatic vibronic coupling model described in Sect. 3. The time-dependent Schrödinger equation

$$\begin{aligned} \mathrm {i}\hbar \frac{\partial |\varPsi ,t\rangle }{\partial t} = \hat{H} |\varPsi ,t\rangle \end{aligned}$$

(15)

was solved using the hybrid Gaussian-based multiconfigurational time-dependent Hartree (G-MCTDH) approach [33, 54, 55], which approximates the wave packets associated with different electronic states as a sum of Hartree products according to the ansatz

$$\begin{aligned} |\varPsi ,t\rangle= & {} \sum _s |s\rangle \sum _{\mathbf {J}} A_{\mathbf {J}}^{(s)}(t) \nonumber \\&\times \prod _{\kappa = 1}^M \varphi _{j_\kappa }^{(\kappa ,s)} \left( \mathbf {x}_\kappa ,t \right) \prod _{\kappa = M + 1}^N g_{j_\kappa }^{(\kappa )} \left( \mathbf {x}_\kappa ;\varvec{\xi }_{j_\kappa }^{(\kappa )}(t) \right) , \end{aligned}$$

(16)

where s refers to the electronic state and $\mathbf {J}$ is a multi-index $\mathbf {J} = (j_1,\ldots ,j_N)$. The coordinates are partitioned into N subsets (“combined modes”), each of which is associated with a prescribed number of single-particle functions. For M subsets of coordinates (the so called “primary modes” $\mathbf {x}_1, \ldots , \mathbf {x}_M$) accurate functions $\varphi _j^{(\kappa ,s)}$ are used, which are expanded on discrete variable representation (DVR) grids and are adapted to the different electronic states. In the present application the primary modes include the coordinates $Q_1,\ldots ,Q_5$, which refer to the large amplitude reaction coordinate and the diabatic coupling modes.

The dynamics of the remaining “secondary modes” (in this case the modes $Q_9,\ldots ,Q_{58}$ of Fig. 4) are approximated by a set of frozen Gaussian wave packets (GWPs) $g_j^{(\kappa )} \propto \exp \left( -\frac{1}{2} \mathbf {x}_\kappa ^T \varvec{\varSigma }_j^{(\kappa )} \mathbf {x}_\kappa + \mathbf {x}_\kappa ^T \varvec{\xi }_j^{(\kappa )}(t) \right)$, where $\varvec{\varSigma }_j^{(\kappa )}$ is a time-independent diagonal matrix of inverse standard deviations and $\varvec{\xi }_j^{(\kappa )}$ are complex-valued vectors containing the time-dependent parameters accounting for the motion of the GWPs in the phase space. All time-dependent quantities are propagated in time according to equations of motion derived from the time-dependent variational principle. To make the propagation more stable and save computation time, the same set of GWPs is used for all electronic states (single-set formalism in the MCTDH nomenclature [56]).

Gaussian wave packets have been already used successfully to simulate proton migration dynamics in the ground state [57]. The G-MCTDH approach is implemented in a self-developed code, whose details have been given in previous works [55, 58]. In the present calculations the G-MCTDH wavefunction was propagated using a second order constant mean field scheme, whereby the mean fields and the Hamiltonian matrix are updated on a coarse time grid instead of the dense integration grid. The accuracy of this approximation, which significantly speeds up the numerical propagation, was controlled as described in Refs. [33, 59]. The single particle functions, including the GWP parameters, were propagated using a fourth-order Runge–Kutta integrator with adaptive step size. The equations of motion for the configuration coefficients $A_\mathbf {J}^{(s)}(t)$, linear in the constant mean field scheme, were solved using a variable order Lanczos integrator [56].

Table 2 Details of the G-MCTDH wavefunctions used to simulate the dynamics initiated by $1\pi \pi ^* \longleftarrow S_0$ and $2\pi \pi ^* \longleftarrow S_0$ photoexcitation

The details of the structure of the G-MCTDH wavefunctions used in the calculation of Sects. 5.1 and 5.2 are given in Table 2. The secondary modes are grouped into two subsets, where the first one includes the five modes which undergo the largest shifts along the relaxed path. The initial state in the quantum dynamical simulations is the vibrational ground state of $S_0$ in the harmonic approximation, located in one of the $\pi \pi ^*$ states,

$$\begin{aligned} |\varPsi ,0\rangle = |s\rangle \exp \left( - \frac{1}{2} \sum _{r = 1}^{31} Q_r^2 \right) \ , \ s = 1\pi \pi ^*,2\pi \pi ^*. \end{aligned}$$

(17)

Note that the initial Gaussian wavefunction is invariant under orthogonal transformations between dimensionless normal modes.

5 Quantum dynamical simulations and discussion

5.1 $1\pi \pi ^* \longleftarrow S_0$ excitation

5.1.1 Reaction dynamics and time constants

The calculated electronic population dynamics after excitation to the lowest $\pi \pi ^*$ state is shown in Fig. 5a. Despite the presence of a coupling with the other $\pi \pi ^*$ state and four $a^{\prime \prime }$ modes inducing $\pi \pi ^*/n\pi ^*$ couplings, more than 95% of the wave packet remains in the initially populated electronic state. This is indeed expected, because the potential energy surface of the $1\pi \pi ^*$ state is energetically well separated from the other surfaces (see Fig. 3). In particular, no curve crossing involving this state is observed along the reaction pathway. This is in contrast with the interpretation given to the most recent ultrafast transient absorption experiments,$^{19}$ where the observed quantum beats were interpreted using a two-state nonadiabatic model. Even in some earlier time-resolved experiments a time constant around 300 fs was assigned to a nonadiabatic mechanism [26, 31].

Fig. 5

a Electronic population dynamics of HBQ following the initial $1\pi \pi ^* \longleftarrow S_0$ excitation; b oscillator-strength weighted energy gap (purple) and Gaussian-exponential background (orange); c wave packet broadening along the proton transfer coordinate $Q_1$. The insets in panels (b) and (c) highlight the short time dynamics

The present quantum dynamical simulations, based on a realistic molecular Hamiltonian, suggest instead a mechanism which does not substantially violate the Born–Oppenheimer approximation. To investigate whether these results are compatible with the experimental findings mentioned above, the vibrational coherences arising in the photoreaction are analyzed. These non-trivial quantities are usually investigated in the so called coherent vibrational spectrum [19] (CVS) which is obtained by resolving the quantum beats of the spectroscopic signals in frequency, via Fourier transform. A related observable is the time-dependent average excitation energy gap between ground and excited states, weighted by the oscillator strength,

$$\begin{aligned} \langle \varDelta E \rangle (t) = \frac{\sum _s f_s \langle \varPsi ,t | s\rangle \left( W_s - W_0 \right) \langle s |\varPsi ,t\rangle }{\sum _s f_s \langle \varPsi ,t | s\rangle \langle s |\varPsi ,t\rangle }, \end{aligned}$$

(18)

where the sums are over the electronic states and $W_0$ is the ground state adiabatic potential ($S_0$ is always considered isolated). This quantity can be taken as a measure of the average photon energy measured in transient stimulated emission or fluorescence upconversion spectra (with ideal time resolution), and oscillates with the same quantum beats of the spectroscopic signals. The factors $f_s$ are the oscillator strengths for the excited-to-ground state transitions. The calculations use the values $f_s = 0.146, 0.057$ and 0.0 for $1\pi \pi ^*$, $2\pi \pi ^*$ and $n\pi ^*$, respectively, which were obtained by the TDDFT calculations at the optimized geometries of the different excited states.

The calculated energy gap $\langle \varDelta E \rangle$ is plotted in Fig. 5b. According to Eq. (18), the initial value, $\langle \varDelta E \rangle (0) = 3.21\,\mathrm {eV}$ is the energy gap between $S_0$ and $1\pi \pi ^*$ averaged over the initial wave packet, and it is close the vertical excitation energy (see Fig. 3). $\langle \varDelta E\rangle$ decays to $\approx 2.07\,\mathrm {eV}$ in the first $\approx 10$ fs, indicating an initial ultrafast wave packet motion towards the keto region of the $1\pi \pi ^*$ PES. Although such ultrashort time constant is hard to measure experimentally, many time-resolved spectroscopic measurements agree on a mechanism where the photoisomerization occurs in less than 20 fs [11, 19, 27]. In particular, the time scale of the present simulations agrees well with the time constant of $12\pm 6\,\mathrm {fs}$ measured by Lee, Kim and Joo by time-resolved fluorescence [11, 30].

After this initial decay a slower rise on a time scale of few hundreds of fs is observed, accompanied by pronounced oscillations due to the molecular vibrations discussed below. After 500 fs $\langle \varDelta E\rangle$ oscillates around an average value of $\approx 2.15\,\mathrm {eV}$. The difference between the initial and the asymptotic value of $\langle \varDelta E\rangle$ is about $1.05\,\mathrm {eV}$ and compares well with the calculated and measured Stokes shift discussed in Sect. 2.

The initial decrease followed by a slight increase (or vice versa) has been observed, with similar time constants, in the pump-probe experiments of Refs. [27, 28, 31]. In most spectroscopic studies, a time constant of 300–350 fs was found for the slower step, which follows the proton transfer. It has been suggested [26, 31] that this might be an indication of an electronic relaxation from the $2\pi \pi ^*$ state, which, depending on the excitation wavelength, might be initially populated. However, the present simulation suggests that a purely intra-state process, namely the intramolecular vibrational redistribution, contributes, at least partially, to the observed time constant.

This is illustrated in Fig. 5c, which shows the width of the wave packet on the state $1\pi \pi ^*$ along the proton transfer mode $Q_1$, evaluated as

$$\begin{aligned} \left( \langle \varPsi |Q_1^2|\varPsi \rangle - \langle \varPsi | Q_1| \varPsi \rangle ^2 \right) ^{\frac{1}{2}}. \end{aligned}$$

Given that dimensionless units are used, the initial width is $1/\sqrt{2}$. Already the during initial reaction step (10–20 fs) the wave packet broadens by a factor 2.4 and the width reaches the value $\approx 1.7$. In the 200–300 fs time scale a slower relaxation takes place, due to the vibrational energy transfer to the skeletal modes. As shown in Fig. 3, the relaxed PES is rather shallow around the $1\pi \pi ^*$ minimum, so that the wave packet tends to broaden along $Q_1$ reaching a final width of $\approx 2.3$, more than three times the initial width on the ground state.

5.1.2 Vibrational coherences

The quantum dynamical simulations predict coherent oscillations during the whole dynamics. The oscillation amplitude only slightly decreases after the first picosecond; after this time other intra- or intermolecular motions, neglected in the simulation, are likely to lead to an increase of the dephasing rate. Nevertheless, the high dimensionality of the simulation is adequate to model the vibrational coherences. To extract the ultrafast time constant and resolve the coherences in frequency the oscillator strength-weighted energy gap $\langle \varDelta E \rangle$ is fitted to a sum of a Gaussian and an exponential,

$$\begin{aligned} F_\mathrm {decay}(t) = A_0 + A_1 \mathrm {e}^{- \frac{t^2}{2\tau _1^2}} + A_2 \mathrm {e}^{- \frac{t}{\tau _2}}. \end{aligned}$$

(19)

The result of the fit is shown in Fig. 5b. The Gaussian term, with the standard deviation $\tau _1$ fitted to 5.8 fs, accounts for the initial ultrafast decay of $\langle \varDelta E\rangle$, which is associated to the proton transfer. Taking $2\tau _1$ as a measure of the reaction time, the process is predicted to occur in less than 15 fs. The second time constant is associated to the vibrational broadening described in Sect. 5.1.1 and the value resulting from the fit is $\tau _2 = 149\pm 17\,\mathrm {fs}$, which is of the same order of magnitude of the 300–350 fs time constant observed in numerous experiments. Using various different fitting functions (e.g. only exponentials, three instead of two terms, etc.) values for $\tau _2$ in the range of 140–200 fs are obtained. Note, however, that the initial state in the dynamics corresponds to a wave packet created by an ideal $\delta$-pulse; the experimental finite duration pulses create wave packets that are narrower in energy and therefore could relax slightly more slowly.

Subtracting the decaying background from the energy gap function $\langle \varDelta E \rangle$ gives a residual trace which oscillates around zero. This trace was Fourier transformed after application of a Hann window to cure for the leakage due to finite time propagation [60]. The resulting coherent vibrational spectrum is shown in Fig. 6a. A number of vibrational peaks of different intensity are visible and their frequencies are reported in the figure. In the range of 0–700 cm$^{-1}$ the calculated sequence of peaks is in excellent agreement with the CVS obtained experimentally for HBQ in cyclohexane [11, 27, 28]. Although the experimental intensity pattern depends on parameters such as the duration and the carrier wavelength of the pulses, as well as the time resolution of the experiment, the intensity of the peak around $390\,\mathrm {cm}^{-1}$ is almost always dominant, as nicely reproduced in the calculation.

Fig. 6

a Coherent vibrational spectrum for the dynamics initiated by the $1\pi \pi ^* \longleftarrow S_0$ excitation of HBQ, calculated by Fourier transforming the oscillator strength-weighted energy gap of Fig. 5b after background subtraction; the frequencies of the main peaks are reported explicitly. b Fourier transform of the average wave packet trajectory along the $a^\prime$ modes included in the dynamics; the same normalization is used for all modes

Table 3 Calculated frequencies of the coherent vibrational spectrum of HBQ following the $1\pi \pi ^* \longleftarrow S_0$ and $2\pi \pi ^* \longleftarrow S_0$ photoexcitation, frequencies of the quantum beats observed in the time-resolved spectroscopic experiments of Refs. [27] (cyclohexane) and [19] (ethanol), and assignment in terms of the modes of Fig. 4

A high-resolution CVS has been recently obtained experimentally for HBQ dissolved in ethanol [19]. Despite the proticity and the higher polarity of the solvent, similar frequencies were reported for the quantum beats. A summary of the frequencies obtained in Refs. [19, 27] is reported in Table 3. The agreement between the experiments and the quantum chemical and quantum dynamical simulations is excellent and validates the present computational protocol. The experimental peaks observed around 392–$396\,\mathrm {cm}^{-1}$ and 543–550$\,\mathrm {cm}^{-1}$ are reproduced as doublets in the calculation, suggesting that more modes of similar frequency contribute to the peak. In the most recent experiment, with a time resolution of 11 fs, the same splittings were actually obtained by performing a linear prediction singular value decomposition of the spectroscopic signal (see the Supplementary Information of Ref. [19]).

Given the absence of strong nonadiabatic effects, this simulation proves that the vibrational coherences emerging in the ESIPT reaction of HBQ are perfectly explicable with a process occurring on a single potential energy surface. This agrees with the molecular dynamics simulations by Higashi and Saito, who obtained similar CVS frequencies, including just a single Born–Oppenheimer surface.

Therefore, the present results suggest that the two state nonadiabatic model proposed by Kim et al. in Ref. [19] has been probably over-interpreted. Their model uses two harmonic potential energy surfaces for the photoexcited HBQ, which refer to the enol and keto form. The normal modes of the two surfaces are displaced and rotated (Duschinsky mixing). Including a transition from the “enol” to the “keto” surface (and only in this case) the authors could successfully explain and assign the quantum beats observed in the transient absorption signal. Such two-state harmonic model is actually consistent with the present quantum dynamical simulation, where the wave packet evolves essentially on a single anharmonic surface. However, what the model actually captures is the Duschinsky rotation of the skeletal modes along a reaction path on a single electronic state, rather than a non-Born–Oppenheimer dynamics.

The quantum dynamical results allow the assignment of the peaks in the CVS in terms of the modes of Fig. 4. To this end, the expectation values of the skeletal coordinates, $\langle Q_r \rangle (t) = \langle \varPsi ,t | Q_r |\varPsi ,t\rangle$ are evaluated and resolved in frequencies (after exponential background subtraction and Hann-filtering). The Fourier transforms $\langle \widetilde{Q}_ r \rangle (\omega )$ are plotted in Fig. 6 for the most relevant modes, i.e. those having lower frequencies. The wave packet oscillates along the HBQ modes at the same frequencies observed in the CVS. In particular each of the peaks reported in Table 3 can be assigned to a small subset of coordinates, which in most cases includes a single mode. The fact that multiple modes can contribute to the same peak is a signature of the Duschinsky correlations along the reaction path, mentioned above.

The modes which mostly contribute to each peak are reported in Table 3. The modes $Q_9$, $Q_{12}$, $Q_{13}$, $Q_{16}$, $Q_{18}$ and $Q_{19}$, associated with the most intense peaks observed experimentally and theoretically, involve displacement of either the N or the O atom, or both (see Fig. 4). As shown in Fig. 2, this is expected since the initial $\pi \pi ^*$ excitation significantly alters the electron density at these atoms. Whether the vibrational coherences are formed after the reaction, or in a concerted way, is discussed in Sect. 5.3.

5.2 $2\pi \pi ^* \longleftarrow S_0$ excitation

The ESIPT dynamics of HBQ initiated on the second excited $\pi \pi ^*$ state have never been studied theoretically, although a few spectroscopic experiments using pump wavelengths lower than 360 nm, which can induce the $S_2 \longleftarrow S_0$ excitation, have been performed. Riedle and coworkers have also measured the ultrafast transient absorption spectrum and the CVS using a pump wavelength of 310 nm, which is near the $2\pi \pi ^*$ absorption maximum [28].

However, much less data are available for excitation of HBQ in shorter wavelength range, therefore, the simulations presented below have a rather predictive purpose and might serve as an indication to future experiments.

5.2.1 Reaction dynamics and time constants

Fig. 7

a Electronic population dynamics of HBQ following the initial $2\pi \pi ^* \longleftarrow S_0$ excitation; b oscillator-strength weighted energy gap (purple) and Gaussian-exponential background (orange); c wave packet broadening along the proton transfer coordinate $Q_1$. The insets in panels (b) and (c) highlight the short time dynamics

The electronic population dynamics following the excitation to the higher $\pi \pi ^*$ state are shown in Fig. 7a. In contrast to the long wavelength excitation of Sect. 5.1, the simulation predicts richer nonadiabatic effects when the reaction is induced by shorter wavelengths. A substantial fraction of the wave packet leaves the $2\pi \pi ^*$ state in the first 40–70 fs, with a minor amount (about 15%) relaxing directly to the lowest $\pi \pi ^*$ state in the first 20 fs. The short time population dynamics correlates well with the time scale of the proton transfer process, which is analyzed in more detail in Sect. 5.3. The major fraction of population, about 60%, is transferred to the dark $n\pi ^*$ state in 60–100 fs. In a second step, a slower $n\pi ^* \longrightarrow 1\pi \pi ^*$ internal conversion is observed and the lowest $\pi \pi ^*$ becomes the most populated state after $\approx 650\,\mathrm {fs}$. About 20% of the population remains trapped in the $2\pi \pi ^*$ state for the whole simulation time. This is in line with the higher energy gap predicted by TDDFT between the two $\pi \pi ^*$ states (see Fig. 3), which makes the $2\pi \pi ^* \longrightarrow 1\pi \pi ^*$ relaxation possible only in the reactant zone, and less likely after the ultrafast ESIPT. However, additional modes not included in the simulation (including solvent fluctuations) might induce an additional electronic relaxation after the first 0.5–1.0 ps.

Nevertheless, the $n\pi ^*$ state, whose potential energy surface crosses the one of the $2\pi \pi ^*$ state, turns out to play the major role in the relaxation process after the $2\pi \pi ^* \longleftarrow S_0$ excitation. Although this state was indicated as relatively stable by the calculations of Ref. [28], its role in the photodynamics has never been investigated. The present simulations suggest instead that the $n\pi ^*$ state should be taken into account in the study of the ESIPT initiated by wavelengths $<360\,\mathrm {nm}$ in HBQ or similar enol-keto molecules [61,62,63].

Fig. 8

a Coherent vibrational spectrum for the dynamics initiated by the $2\pi \pi ^* \longleftarrow S_0$ excitation of HBQ, calculated by Fourier transforming the oscillator strength-weighted energy gap of Fig. 7b after background subtraction; the frequencies of the main peaks are reported explicitly. b Fourier transform of the average wave packet trajectory along the $a^\prime$ modes included in the dynamics; the same normalization is used for all modes

The weighted energy gap $\langle \varDelta E\rangle$ resulting from the dynamics is plotted in Fig. 8b. This quantity decreases from the initial value of 3.70 eV, nearly coinciding with the vertical excitation energy of Table 1, to an asymptotic value of $\approx 2.40$ eV. In this case another exponential function, $A_3 \mathrm {e}^{-\frac{t}{\tau _3}}$ was added to Eq. (19) to fit the background. The decays constant resulting from the fit are $6.5 \pm 0.1$ fs, $45\pm 3$ fs and $681\pm 42$ fs and are assigned to the ultrafast proton transfer, the initial depopulation of the $2\pi \pi ^*$ state and the slower $n\pi ^* \longrightarrow 1\pi \pi ^*$ vibronic relaxation. As for the initial $1\pi \pi ^* \longleftarrow S_0$ transition, the latter process occurs concertedly with the broadening of the wave packet along the proton transfer coordinate, as illustrated in Fig. 7c. In this case, due to the larger total energy, the broadening is larger and, in the picosecond time scale, reaches a value of $\approx 2.6$, almost four times the initial wave packet width.

As written above, it is difficult to compare these theoretical data with experimental observations, because spectroscopic measurements with relatively short pump wavelengths are scarce. Moreover, since the $2\pi \pi ^* \longleftarrow S_0$ and $1\pi \pi ^* \longleftarrow S_0$ bands overlap, it is difficult to create optically an initial wave packet purely localized in the $2\pi \pi ^*$ state. However, the present results might serve to guide new experiments to address the reaction mechanism. In particular, it is worth to emphasize that the $n\pi ^*$ state is dark in emission; therefore, it might remain elusive in stimulated emission or fluorescence signals. In contrast, the novel techniques based on infrared probes might provide signatures of the transiently populated $n\pi ^*$ state [64].

5.2.2 Vibrational coherences

Compared to the case of initial $1\pi \pi ^* \longleftarrow S_0$ excitation, the coherent oscillations observed in Fig. 5b are much less pronounced. This is expected by the faster dephasing due to the higher density of states at the wave packet energy. However, given the large propagation time of 4 ps, it is still possible to resolve them into relatively narrow frequency peaks. The resulting CVS is plotted in Fig. 8a and displays very similar frequencies to those of Fig. 6a, with the highest intensity for the peaks at $391\,\mathrm {cm}^{-1}$ and $535\,\mathrm {cm}^{-1}$. As shown in Fig. 8b, the mode assignment is also the same.

This is in line with the experimental results of Ref. [28], where the CVS of HBQ in cyclohexane was found to be largely independent on the excitation wavelength when this was varied in the range of 310–380 nm. This observation was explained by assuming an ultrafast internal conversion to the lowest excited state. Indeed, the nonadiabatic quantum dynamics show that, already after 40 fs, the $1\pi \pi ^*$ state gives the dominant contribution to the energy gap $\langle \varDelta E\rangle$, as a consequence of its higher oscillator strength. After 100 fs the $1\pi \pi ^*$ state is the most populated emissive state. The fact that the PESs of the states $1\pi \pi ^*$ and $2\pi \pi ^*$ are nearly parallel is also likely to facilitate the conservation of the coherences to a good extent, despite the high dimensionality of the system.

5.3 Active or passive role of the proton?

The observation of the coherent vibrational motion in the ESIPT of HBQ and similar chromophores have stimulated a debate about the possibility that the proton might have a completely or partially passive role in the reaction. By this is meant that the skeletal vibrations bring the enol and the N heteroatom close to each other, so that the proton migration is a secondary reaction step [11]. In contrast, a mechanism with the active role of the proton would imply that the coherences form after the reaction has taken place, due to the dynamics induced in the HBQ skeleton by the changed potential energy landscape in the keto form.

A rather passive role for the proton was suggested by Riedle and coworkers on the basis of transient absorption experiments as well as theoretical calculations on HBQ, its deuterated form (DBQ) and the less rigid molecule 2-(2’-hydroxyphenyl)benzothiazole (HBT) [28, 29]. The faster time scale for the ESIPT in HBQ as compared to HBT was attributed to the generally higher frequencies of the HBQ backbone, which activates the reaction more rapidly. A semi-passive role for the proton was also reported by Higashi and Saito on the basis of molecular dynamics simulations [32].

In contrast, the time-resolved fluorescence measurements performed by Joo and coworkers on HBQ and DBQ support the active role of the proton [11, 30], because they find an ESIPT slower by factor $\approx \sqrt{2}$ upon deuteration, which is expected from a ballistic proton migration.

Although a rigorous definition of active vs. passive mechanism is hard to give, the role of the vibrations in assisting the reaction can be quantified, at the level of linear correlations, by monitoring the Pearson coefficient [65]

$$\begin{aligned} C_{1,r}(t) = \frac{\left\langle \varPsi ,t \left| \left( Q_1 - \langle Q_1\rangle _t \right) \left( Q_r - \langle Q_r\rangle _t \right) \right| \varPsi ,t\right\rangle }{\sqrt{ \left\langle \varPsi ,t \left| Q_1^2 - \langle Q_1\rangle _t^2 \right| \varPsi ,t\right\rangle \left\langle \varPsi ,t \left| Q_r^2 - \langle Q_r\rangle _t^2 \right| \varPsi ,t\right\rangle } } \end{aligned}$$

(20)

for the different modes during the proton transfer process. $C_{1,r}(t)$ varies between $-1$ and 1. If it is close to zero for a certain mode $Q_r$, then the mode can be reasonably regarded as a “spectator” of the photodynamics of the proton.

Fig. 9

a, a’ Vibrational distributions along the proton transfer mode $Q_1$ in the short time dynamics initiated by the $1\pi \pi ^* \longleftarrow S_0$ and $2\pi \pi ^* \longleftarrow S_0$ transitions. b–e, b’–e’ Time-dependent Pearson correlation coefficients between the proton transfer mode and the skeletal vibrations

Figure 9a, a’ reports the vibrational distributions along the proton transfer mode in the first 100 fs after the photoexcitation to the $1\pi \pi ^*$ and $2\pi \pi ^*$ states, respectively. They are obtained by integrating the squared wavefunctions over all remaining coordinates. The distributions are similar for the two cases, the main difference being a slightly larger broadening for the $2\pi \pi ^* \longleftarrow S_0$ excitation, due to the rapid population transfer to the other electronic states. In the first 15–20 fs the distributions move from $Q_1 \approx 0$ to $Q_1 \approx 6$, near the minima of the $\pi \pi ^*$ states (see Fig. 3). Note that the interplay between the $n\pi ^*$ and the $\pi \pi ^*$ states, described in Sect. 5.2, occurs when the wave packet is mostly in the keto region, where the $n\pi ^*$ state is more stable.

Figure 9b–e and b’–e’ reports the correlation coefficients of Eq. (20) for the 26 totally symmetric modes of the model for the two $\pi \pi ^* \longleftarrow S_0$ excitations. For almost all modes $|C_{1,r}|$ remains generally below 0.3 for the first 20 fs, during which the ESIPT takes place. The only notable exception is the mode $Q_{58}$, for which $C_{1,58}$ reaches a value of $\approx 0.5$ (see Fig. 9e, e’). This mode is a combination of the bending of the OH group and stretch of the neighboring aromatic C=C bond, which is strongly weakened by the $\pi \pi ^*$ transitions, as suggested by the orbitals of Fig. 2. The modes $Q_{13}$, $Q_{19}$, visible in the CVS spectra, and the mode $Q_{54}$ are the next in order of importance.

Despite these minor correlations, the analysis indicates that the proton mode itself is the most active coordinate in the ESIPT of HBQ, and receives just a minor assistance from the $Q_{58}$ mode, which has a frequency $\hbar \omega _{58} = 1710\,\mathrm {cm}^{-1}$. Indeed, the ultrashort time scale of the photoreaction is faster than the vibrational period of most other skeletal modes. On the other hand, as shown in Fig. 9b, b’, the lowest frequency modes preserve some correlation with $Q_1$ for some hundreds of fs, and therefore, mediate the earliest steps of vibronic relaxation of the keto product. In this time scale the mode most correlated to the proton transfer is, not unexpectedly, $Q_9$, which involves substantial distortion of the C–O group and the N atom (see Fig. 4). In contrast, the motion along most modes of higher frequency becomes rapidly uncorrelated with the proton transfer coordinate.

6 Conclusions

The coherent excited state intramolecular proton transfer dynamics of HBQ were simulated quantum mechanically for the molecule initially prepared in the $1\pi \pi ^*$ and the $2\pi \pi ^*$ states.

The simulations rely on a multimode diabatic vibronic coupling Hamiltonian which includes 31 vibrational modes, the lowest $\pi \pi ^*$ excited states, and a $n\pi ^*$ state which lies at high energy in the Franck–Condon zone, but stabilizes between the two $\pi \pi ^*$ upon proton transfer. The model is parametrized from first principles using time-dependent density functional theory calculations performed with the TPSSh functional, which gives the best agreement between the experimental and the theoretical Stokes shift, as well as the absolute vertical excitation and emission energies. The parametrization follows a protocol which is not specific for the HBQ molecule, but can be applied to general proton transfer processes that can be reasonably described using a large amplitude reaction coordinate and a harmonic bath for the molecular backbone [61, 62, 66].

The simulations predict a reaction time of 11–15 fs in agreement with the pump-probe spectroscopic experiments with the best time resolution performed so far. During this time the proton motion has little correlation with the vibrations of the benzoquinoline backbone. This excludes a primarily passive reaction mechanism guided by the skeletal vibrations, and suggests a rather active role of the proton.

The reaction initiated in the $1\pi \pi ^*$ state, which is reached with excitation wavelengths around 380 nm, mainly proceeds on a single potential energy surface, despite inter-state couplings being included, and leads to the formation of multimode vibrational coherences. Their calculated frequencies agree very well with the experimental values, proving that a nonadiabatic mechanism does not need to be invoked for their interpretation. Each coherent vibration is assigned dominantly to a subset of 1–3 modes and, to a lesser extent, to the other modes because of the Duschinsky correlation along the reaction path. In addition, the calculations suggest that the $\approx 300$ fs time constant measured in many pump-probe experiments is likely due to intramolecular vibrational relaxation, as initially proposed by Takeuchi and Tahara [27], and not to an internal conversion, as suggested in other works [26, 31].

The initial excitation to the $2\pi \pi ^*$ state, which is possible with wavelengths shorter than $\approx 360$ nm [28], leads to a nonadiabatic isomerization mechanism. 20% of the wave packet relaxes directly to the lowest $1\pi \pi ^*$ state in 15–30 fs; the majority of the wave packet follows the slower relaxation route $2\pi \pi ^* \longrightarrow n\pi ^* \longrightarrow 1\pi \pi ^*$, which occurs after the proton transfer and involves the $n\pi ^*$ state. The experimental observation of this path is challenging, because the $n\pi ^*$ state is dark in emission. The dynamics preserve less coherent oscillations, but their frequencies are the same of those obtained for the initial excitation to the $1\pi \pi ^*$ state, in agreement with the observations of Riedle and coworkers [28].

The role of the $n\pi ^*$ states was investigated in the excited state intramolecular hydrogen transfer of malonaldehyde [16], but never in hydroxyquinolines, which are an important class of compounds in sensing applications [7]. The present results suggest that future studies of excited state proton transfer reactions should address the energetic position of these states and their role in the proton transfer mechanisms. To this end, it will be valuable to use spectroscopies based on probes alternative to optical emission, such as excited state infrared absorption [64] or photoelectron emission [15].

Supplementary information The Supporting Information presents the equations to evaluate the geometrical derivatives of the diabatic potentials starting from the adiabatic ones.

The files of the potential parameters and a Python module which implements the evaluation of the full-dimensional diabatic potential energy surfaces are also provided. The basic usage of the module is described in the Supporting Information.