1 Introduction

Die forging processes for elongated forged parts of complex shapes are performed using billet material in the form of preforms. A preform is an axisymmetric solid with its shape being as close as possible to that of a forging, especially in terms of its profile in the parting plane. Individual cross-sections of a preform are equal to respective cross-sections of a forging increased by flash allowance. Numerous methods for forming preforms are used in industrial practice, including open-die forging, rotary swaging, electrical upsetting, machine forging, forging with the use of special devices (e.g. Tadeusz Rut’s method [1]), longitudinal rolling, and cross rolling [2].

The proper design of preform shape is necessary to implement the more and more popular precision forging method that allows significant reduction in material consumption [3]. Both numerical modelling and the use of optimization techniques play an important role in the design of forging processes. For example, Vasquez and Altan [4] proposed a preform design method based on numerical simulations using DEFORM-3D, in which a connecting rod was produced by flashless forging. Zhao et al. [5] used the same computer programme to optimize preform shape and thus minimize differences in strain distribution. Another objective function for preform optimization was employed by Sun et al. [6], who focussed on preventing defects in a half axle flange. Alimirzaloo et al. [7] optimized preform shape in the forging process of an airfoil blade, which made it possible to reduce flash volume (by 51%) and strain non-uniformity (by 42%).

Numerous research centres (e.g. Shanghai Jiao Tong University, Korea Advanced Institute of Science and Technology, Institut für Integrierte Produktion Hannover, and University of Ulsan) are conducting studies on preforms. These studies can be divided into two groups. The first one concerns the use of new methods for preform shape design, such as evolutionary structural optimization [8], electric field theory [9] and genetic algorithms [10]. The other group of research works relates to the development of new methods for preform production. Dombelsky et al. [11] investigated whether preforms welded by different methods, made of either the same or two different materials, could be used in the forging process. The best results were obtained using friction-welded preforms. Kim et al. [12] investigated the formation of Al-Si alloy tie-rod ends for the steering systems for automobiles, finding that preforms could be produced by casting. Li et al. [13] showed that in flashless forging of connecting rods one could use preforms obtained via powder metallurgy. Lis et al. [14] and Pater et al. [15] suggested that preforms could be produced by skew rolling in a CNC rolling mill, a method which is the subject-matter of this study.

Nowadays, the manufacturing industry is focussed on flexible manufacturing and just-in-time delivery. A major challenge for the flexible manufacturing system is to easily adapt to changes e.g. in production profile. In the forging industry rapid changes in production profile are not easy to implement, not to mention the fact that they generate very high costs related to machine retooling and making new instrumentation. The forging industry is today facing a serious problem due to rapid changes in production profiles. Another problem the forging industry is facing today is the fact that commissions received from e.g. the aerospace industry are related to the production of small batches of forgings. The metal forming industry is looking for new flexible manufacturing techniques. As far as sheet metal forming is concerned, one can observe a rapid development in sheet incremental forming techniques that enable flexible manufacturing of single batches of sheet metal products. As early as the 1980s, it was predicted that CNC programming would play an important role in the development of flexible manufacturing processes for sheet metal products [16]. Today it can be claimed that the predictions were true, as proved by the wide use of CNC techniques for sheet metal cutting [17] and bending [18], as well as for incremental forming products with non-developable surfaces [19]. At the same time it was thought that bulk forming processes such as forging, rolling and metal powder forming are considerably limited in terms of flexible manufacturing system implementation [16]. In the twenty-first century metal powder forming has become the most flexible manufacturing system for bulk products thanks to the implementation of selective laser sintering (SLS), a technique that is widely used in 3D printing [20]. Nevertheless, there still exist problems with flexible manufacturing systems for producing solid parts by processes such as forging and rolling. In recent years studies on CNC skew rolling have been undertaken [21]. This technique can make it possible to implement flexible production of axisymmetric parts such as preforms, and it addresses the needs of a flexible manufacturing system.

The main advantage of skew rolling using a CNC rolling mill is the method’s universality resulting from the fact that it allows for forming different parts with the use of only one set of tools (rolls) of a relatively simple shape. As a result, this forming method can be applied in piece production. Moreover, the rolling process is carried out with relatively low loads and torques, which means that rolling mills can be lightweight [22]. Given the shape of parts produced in a CNC rolling mill, it was assumed that the skew rolling method was suitable for manufacturing stepped axles and shafts. Early research works in this area focussed on this direction. Pater et al. [23, 24] used Simufact Forming to analyse numerically whether the skew rolling method could be used for producing solid axles and shafts. Pater et al. [25] then used a laboratory CNC rolling mill and produced solid rail axles (in a scale of 1:5) that had no external and internal defects. Xu and Shu [26] performed only numerical simulations and claimed that the method could also be used for manufacturing hollow rail axles. According to these authors, a long mandrel was necessary to determine the inside diameter of the axle.

This study focuses on forming preforms by skew rolling with a CNC rolling mill; the rolled preforms are then forged on forging presses. Considering the advantages of this rolling method, the focus was put on large-size forgings produced in short batches. Currently such forgings are manufactured using hammers (the use of these machines allows for forging preforms in the dies of auxiliary tools). The primary objective of the study was to demonstrate that the proposed rolling method makes it possible to manufacture such parts with the use of forging presses, which is beneficial for both employees and natural environment. The study involved performing numerical simulations of production processes for the analysed parts, these processes consisting of rolling a preform and forging a forged part on a press. In addition, experiments were performed in which—using a laboratory CNC rolling mill—preforms were produced (in a scale of 1: 2) for the analysed forging processes.

2 Principle of preform formation in a CNC rolling mill

A schematic diagram of the proposed preform forming process performed in a CNC rolling mill is shown in Fig. 1. In this process the workpiece is deformed simultaneously by three rolls of the same shape. The rolls are set askew at an angle θ relative to the axis of the workpiece, and they are rotated at the same number of revolutions nR. In addition to that, the rolls can move radially relative to the workpiece (with the velocity VR), which makes it possible to form steps with different diameters on the workpiece. One of the workpiece ends is fixed in a rotary chuck that moves axially with the velocity VC. Proper selection of the roll radial velocity VR and the chuck velocity VC makes it possible to produce axisymmetric parts with the required shape.

Fig. 1
figure 1

Schematic design of the 3-roll skew rolling process conducted in a CNC skew rolling mill; the most important parameters of this process are also marked in the figure

Full size image

Besides the afore-mentioned velocities nR, VR, VC, basic parameters of the skew rolling process include the following (Fig. 1): roll diameter D, forming angle α, sizing cylinder length b, exit angle β, and feed angle θ. It must, however, be remembered that the diameter of the roll used in this rolling process is limited and cannot exceed:

$${D}_{\mathrm{max}}=\frac{\sqrt{3}}{2-\sqrt{3}} {d}_{\mathrm{min}},$$
(1)

where Dmax is the maximum diameter of the roll, dmin is the minimum diameter of the workpiece.

A measure of strains generated in the analysed process is the reduction ratio δ, which is defined as:

$$\delta =\frac{{d}_{0}}{d},$$
(2)

where d0 is the diameter of the billet, d is the diameter of the rolled step.

3 Numerical analysis

The numerical analysis involved performing simulations of three forming processes using preforms produced in a CNC rolling mill. Forged parts for the analysis (scraper, hook, and connecting rod) were taken from the production profile of a Polish forging plant. Currently, such forgings are manufactured with the use of forging hammers. These particular preforms were selected from a group of preforms that can be manufactured by CNC skew rolling.

The numerical analysis was performed using the Forge® NxT v.2.0 simulation software for analysis of forming processes for solids. This programme has been widely employed to investigate cross and skew rolling processes [15, 27,28,29,30,31,32], and the numerical results obtained with this software solution were in good agreement with the results of validation experiments.

The analysed forgings were made of the same material, i.e. C45 steel. The billet was discretized using 3D tetrahedral finite elements. The size of the finite element mesh was 1.75 mm. Periodic remeshing was initiated every 20 time increments. The material model of this steel grade (taken from the material library database of the computer software) was described by the Hansel-Spittel equation having the form:

$${\sigma }_{F}=1521.3{e}^{-0.00269T}{\varepsilon }^{-0.12651}{e}^{-0.05957/\varepsilon }{\dot{\varepsilon }}^{0.14542},$$
(3)

where σF is the flow stress, ε is the effective strain, \(\dot{\varepsilon }\) is the strain rate, T is the temperature.

Friction on the material-tool contact surface was described by a constant friction model, according to which

$$\tau =m k,$$
(4)

where τ is the shear stress on contact surface, k is the pure shear yield stress (\(k={\sigma }_{F}/\sqrt{3}\)), and m is the friction factor. The friction factor was set to m = 0.8 in the skew rolling process [33], while for the forging process its value was set to m = 0.3 based on the Forge® database for water and graphite lubrication.

Thermal phenomena occurring during the forming process were considered in the simulations. The temperature of the tools (rolls and dies) was maintained constant at 250 °C. Under continuous production conditions, despite the use of water cooling, the temperature of the tools will become stable at about 250 °C. Therefore, based on practical observations, this temperature value was used in the numerical simulations. The coefficient of heat exchange between the workpiece and the tools was set to 10,000 W/m2K, this value taken from the Forge® database. The heat-air exchange coefficient responsible for heat convection and radiation was set to 20 W/m2K.

All preforms were formed using the same set of rolls described by the following parameters: D = 280 mm, α = 20°, b = 15 mm, β = 90°, θ = 5°. The rotational speed of the rolls was set to nR = 60 rev/min.

A serious limitation of skew rolling processes is material cracking in the form of longitudinal grooves, their shape depending on the number of rolls [34]. Material cracking in forming processes is modelled using different fracture criteria, the most frequently employed one being the normalized Cockcroft-Latham criterion (NCL). According to this criterion, the material cracks when the following condition is met

$${f}_{\mathrm{NCL}}={\int }_{0}^{\varepsilon }\frac{{\sigma }_{1}}{{\sigma }_{i}}d\varepsilon >C,$$
(5)

where fNCL is the damage function calculated according to the normalised Cockcroft-Latham ductile fracture criterion, σi is the effective stress, σ1 is the maximum principal stress, ε is the effective strain, C is the critical damage of material.

The critical damage C is determined experimentally through calibrating tests in which the stress state should reflect as close as possible that in the forming process under analysis. According to Pater et al. [35], when analysing the 3-roll skew rolling process one should use the critical damage values determined via the rotary compression in tool cavity test. The study conducted by Pater et al. [36] showed that for the C45 steel grade, the critical damage C depends on the temperature T and is described by the relationship:

$$C= 0.000692\bullet {e}^{0.00747 T}.$$
(6)

3.1 Scraper forging

A scraper is one of the main elements of scraper conveyors used in the mining industry. Figure 2 shows the forged scraper (and its overall dimensions) analysed in this study. Additionally, this figure shows the preform whose dimensions were calculated in a traditional way, i.e. based on the cross section size plus flash allowance. The designed preform has a symmetric shape that can be obtained with a relatively small cross-sectional reduction. The maximum reduction ratio δ is 1.37 and relates to the step in the central area of the preform. The weight of the forged part is 26.37 kg, while the preform weighs 28.97 kg. This means that material losses due to flash are only 9% in this forging process.

Fig. 2
figure 2

Forged scraper and the rolled preform

Full size image

Figure 3 shows the geometric model of the rolling process for a scraper preform, conducted in a CNC rolling mill. The model consists of three identical rolls and a cylindrical billet having the dimensions of Ø100 × 470 mm. To simplify the simulation, the chuck was omitted and its impact was simulated by fixing the end face of the workpiece (the nodes on this surface could only rotate relative to the axis of the workpiece) and making the rolls additionally move axially with their velocity equal to that of the chuck. Figure 4 shows the distributions of radial and axial velocities of the rolls ensuring the required preform shape.

Fig. 3
figure 3

Skew rolling of a scraper preform in a CNC rolling mill and the distribution of temperature in the workpiece (in °C)

Full size image
Fig. 4
figure 4

Distributions of linear velocities of the rolls during the forming process of a scraper preform

Full size image

The numerical results confirm that it is viable to form a preform with the required shape from a cylindrical billet having an initial temperature of 1200 °C (Fig. 3). As a result of contact with the rolls and air, the temperature of material on the preform’s surface decreased by about 140 °C. Despite a relatively long duration of the forming process, however, the temperature in the preform’s centre (Fig. 5) remains within the range of 1160–1200 °C, which is sufficient to perform the closed-die forging process of a scraper.

Fig. 5
figure 5

Distributions of temperature, effective strain and NCL damage function in the axial section of a scraper preform

Full size image

In the 3-roll skew rolling process, the material flows rapidly in a circumferential direction, which leads to high effective strains (Fig. 5). It is characteristic that the strains are arranged in layers, with their highest values located in the near-surface areas and the lowest in the axial zone. The observed strain distribution is typical of cross rolling processes [37].

The distribution of the NCL damage function shown in Fig. 5 demonstrates that the maximum values of material damage are lower than 0.9. Using Eq. (6) and assuming that the mean temperature of material inside the preform is approx. 1150 °C, it is possible to determine the critical damage C, its value being equal to approx. 3.7. A comparison of the two damage values reveals that material cracking will not occur during preform formation.

Interesting observations can be made regarding the distribution of loads in the skew rolling process of a scraper preform, shown in Fig. 6. The highest loads occur during the formation of the preform’s middle step having a diameter of 73 mm. The radial load acting on the roll does not exceed 110 kN, which is a relatively low value considering the dimensions of the workpiece. On the other hand, the maximum load of the chuck (defined as three times the value of the axial load acting on a single roll) is lower than 40 kN. It is worth noting that in the initial phase of the rolling process the chuck constrains axial displacement of the workpiece, as evidenced by the negative value of the load.

Fig. 6
figure 6

Loads acting on the roll and chuck in the skew rolling process of a scraper preform conducted in a CNC rolling mill

Full size image

Figure 7 shows the distribution of torque determined for one of the rolls. In terms of quality, the torque distribution is identical to the radial force distribution given in Fig. 6. The maximum torque on the roll does not exceed 3000 Nm, and it is equal to 0 at the moment when the rolls are moving apart (t ≈ 50 s).

Fig. 7
figure 7

Torque on one of the rolls in the skew rolling process of a scraper preform conducted in a CNC rolling mill

Full size image

To sum up, scraper preforms can easily be produced by rolling in a CNC rolling mill. Since the scraper is symmetric in shape, the produced preform can be defect-free. This claim is supported by the results of the analysis of the forging process for a scraper, shown in Fig. 8. The forging process is conducted in two stages: the first consists in flattening the preform and the other involves forging the scraper in the die cavity.

Fig. 8
figure 8

Numerical results of the forging process for a scraper, and the distribution of temperature in the workpiece (in °C)

Full size image

3.2 Connecting rod forging

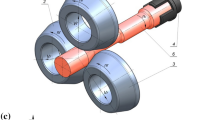
A connecting rod forging selected for analysis is shown in Fig. 9. The forged part consists of two heads connected by a thin shaft of considerable length, which is reflected in the rolled preform shape design. The weight of the forged connecting rod is 19.18 kg, while the weight of the preform is 24.71 kg. Thus, material losses in the proposed forming process amount to 22%.

Fig. 9
figure 9

Forged connecting rod and the rolled preform

Full size image

The diameter of the preform’s large head (equal to the diameter of the billet) is 110 mm, while the diameter of the smaller head is 70 mm and that of the shank is 44 mm. This means that the reduction ratio during shank formation is δ = 2.5. Such a high value of δ cannot be obtained in a single pass due to the risk of necking (rupture) of the step that is formed on the workpiece. Therefore, it was decided that the preform would be produced in two passes. In the first one, a middle step with a diameter of 70 mm would be rolled on the billet with the dimensions of Ø110 × 330 mm (Fig. 10). One end of the workpiece would remain underrolled due to the formation of a deep cavity on its end face. After that, the chuck and the workpiece would be retracted to the starting position, the second pass would be launched in which a 44 mm diameter shank would be formed (Fig. 11). For this case, the end of the workpiece is not subjected to forming, as a result of which the obtained preform head is smaller and has a diameter of 70 mm.

Fig. 10
figure 10

Scheme illustrating the first pass of the tools in the skew rolling process of a connecting rod preform conducted in a CNC rolling mill, and the distribution of temperature in the workpiece (in °C)

Full size image
Fig. 11
figure 11

Scheme illustrating the second pass of the tools in the skew rolling process of a connecting rod preform conducted in a CNC rolling mill, and the distribution of temperature in the workpiece (in °C)

Full size image

Figure 12 shows the distribution of velocities of the rolls in individual passes during the formation of a connecting rod. The maximum radial speed of the rolls on cutting into the material is 5.62 mm. In turn, the maximum axial velocity of the rolls (equal to the velocity of the chuck) is 15 mm/s.

Fig. 12
figure 12

Distribution of linear velocities of the rolls in the skew rolling process for a connecting rod preform

Full size image

Prior to rolling, the billet was thoroughly preheated to 1200 °C. In the first pass, which lasted about 24 s, the temperature of the workpiece dropped by about 50–60 °C (Fig. 9). However, as the rolls returned to their starting position to initiate the second pass, the temperature of the workpiece became stable. Following the second pass of the tools, which lasted 35 s, there was a further drop in the temperature of the workpiece (Fig. 11). According to the data given in Fig. 13, the highest temperature drop (to approx. 1050 °C) occurred in the preform shank. The temperature of material in both heads was approx. 100 °C higher, which bodes well for the closed-die forging process.

Fig. 13
figure 13

Distributions of temperature, effective strain and NCL damage function in the axial section of a forged connecting rod formed in two passes

Full size image

A very high reduction in the cross section of the preform shank resulted in very high strains. According to Fig. 13, the effective strain in this region of the workpiece is as high as 25. Rapid deformation of the material in the shank region was accompanied by the generation of large quantities of heat, which partially compensated for thermal losses resulting from the dissipation of heat to the much cooler tools. This phenomenon made it possible to maintain the temperature of the workpiece within the hot-working range despite a relatively long duration of the forming process. Another effect of rapid deformation of the material is that the damage function in the preform shank exceeds 2.5 (Fig. 13). The critical damage calculated from Eq. (6) is close to this value. Hence, the numerical results do not ensure that the rolled preform will be free of internal cracks. Thus, obtained preforms will have to be examined for cracks in the shank region.

Like in the case of a forged scraper, the distributions of force parameters were determined via numerical analysis, and the results are shown in Figs. 14 and 15. An analysis of the data in these figures demonstrates that much higher values of radial load (115 kN vs 55 kN), axial load (45 kN vs 25 kN) and torque (3200 Nm vs 1500 Nm) occur in the first pass. This undoubtedly results from a larger initial diameter (110 mm vs 70 mm), which leads to a considerably larger material-tool contact area in the first pass, which affects the force parameters during the rolling process [38]. Interestingly, the maximum force parameters are only slightly higher than those measured in the forming process of a scraper preform that was made from a smaller diameter billet. It seems that this results from the higher axial velocity of the rolls (15 mm/s vs 10 mm/s in scraper preform rolling). An increase in the axial velocity of rolls causes an increase in the strain rate, which causes an increase in the yield stress of materials.

Fig. 14
figure 14

Loads acting on the roll and chuck in the skew rolling process of a connecting rod preform conducted in a CNC rolling mill

Full size image
Fig. 15
figure 15

Torques on one of the rolls in the skew rolling of a connecting rod preform conducted in a CNC rolling mill

Full size image

Figure 16 shows the numerical results of the forging process for a connecting rod carried out in two operations: side pressing and die forging. The forged part has the correct shape, the flash is evenly distributed over the entire circumference of the part, and the material temperature is in the hot-working range. This proves that the connecting rod forging design was correct.

Fig. 16
figure 16

Numerical results of the forging process for a connecting rod, and the distribution of temperature in the workpiece (in °C)

Full size image

3.3 Hook forging

The third forging under analysis is the hook shown in Fig. 17. It is formed from a preform with the largest diameter of 115 mm and a weight of 37.93 kg. Taking into account that the forged part weighs 32.05 kg, material losses in the proposed forming process can be estimated at 16%.

Fig. 17
figure 17

Forged hook and a rolled preform

Full size image

The hook preform has a simple shape with a single narrowing of 65 mm in diameter. Given the diameter of the preform shank, the reduction ratio δ was set to δ = 1.77. This value can be obtained in one pass.

Figure 18 shows the model of skew rolling process for a hook preform that was performed in the same way as in the two previously described cases. In this process, a cylindrical billet with the dimensions of Ø115 × 467 mm was preheated to 1200 °C. The preform was formed at a constant axial velocity of the rolls (chuck) set to VC = 15 mm/s. The velocity of the rolls when cutting into the material in the initial stage of the rolling process (t = 0 ÷ 7.33 s) was VR = 3.41 mm/s, while the velocity of the roll exit from the workpiece in the final stage of the rolling process (t = 29.67 ÷ 34.35 s) was VR = -5.36 mm/s.

Fig. 18
figure 18

Rolling process of a hook preform conducted in a CNC rolling mill, and the distribution of temperature in the workpiece (in °C)

Full size image

The hook preform rolled in the CNC rolling mill has the required shape. During the rolling process, the temperature of the workpiece material is reduced by up to 150 °C. However, according to Fig. 19, the temperature drops only occur in the surface layers. The temperature in the preform core is high and amounts to approx. 1150 °C, which is sufficient to perform the closed-die forging operation.

Fig. 19
figure 19

Distributions of temperature, effective strain and NCL damage function in the axial section of a hook preform that was formed in two passes

Full size image

In the shank the strains are distributed in the form of annular layers and their highest values are located in the surface area (Fig. 19). The highest damage function is about 2, which is much lower than the permissible value that is estimated—as in the case of a scraper preform—at about 3.7. It can therefore be assumed that no material cracking will occur during the formation of a hook preform.

Among the three considered cases, the rolling process of a hook preform is characterized by the highest values of force parameters. The radial load on the roll reaches a value of 150 kN and the load on the chuck is 65 kN (Fig. 20). However, it should be noted that these values are very low given the dimensions of the rolled parts. A similar conclusion can be drawn with regard to torque (Fig. 21), its maximum value being approx. 4600 Nm. Assuming 50% of the torque margin, it is possible to estimate engine power for driving a single roll. This engine power is only 45 kW. Summing up, the CNC rolling mill used for preform forming will have a lightweight structure (due to low forming forces) and relatively low power drives.

Fig. 20
figure 20

Loads acting on the roll and chuck in the skew rolling process of a hook preform conducted in a CNC rolling mill

Full size image
Fig. 21
figure 21

Torque on one of the rolls in the skew rolling process of a hook preform conducted in a CNC rolling mill

Full size image

Figure 22 shows the numerical results of forging a hook from a rolled preform. In the first operation, the smaller head of the preform was subjected to side pressing while its larger head underwent bending from the longitudinal axis. In the second operation, the forging was subjected to die forging to form a hook with the required shape. The obtained distribution of flash around the forging proves that the forging design was correct.

Fig. 22
figure 22

Numerical results of the forging process for a hook, and the distribution of temperature in the workpiece (in °C)

Full size image

4 Experimental trials

Rolling tests were performed using a laboratory CNC rolling mill installed at the Lublin University of Technology. This rolling mill, described in detail in [39], was modernised. As a result of modernization, the drive for moving the rolls and chuck was changed from electromechanical to hydraulic. At the same time, the maximum operating loads were increased from 50 to 100 kN. The modernized rolling mill is shown in Fig. 23.

Fig. 23
figure 23

Laboratory CNC skew rolling mill used in the experiments

Full size image

Due to the technical capabilities of the rolling mill and the fact that it allows for manufacturing parts with the maximum dimensions of Ø60 × 1000 mm, it was decided that the preforms would be produced in a scale of 1:2. C45 steel billets were preheated to a temperature of 1150 °C in an electric chamber furnace. This temperature was lower than that used in the numerical analysis because the experiments were limited to rolling preforms, without performing the forging process. The preheated billets were mounted in the chuck of the rolling mill, and the rolling process was launched. The formation of individual preforms is shown in Fig. 24.

Fig. 24
figure 24

Formation of individual preforms under laboratory conditions, in a scale of 1:2

Full size image

Preforms obtained from the rolling tests are shown in Fig. 25. They have the required shape. Considering these shape, the manufacturing accuracy of the preforms formed in a CNC skew rolling mill should be regarded as good. On their outer surface, the rolled elements have shallow helical grooves. Nevertheless, according to the results presented in [15], these defects will not occur in forged parts produced via closed-die forging.

Fig. 25
figure 25

Preforms (in a scale of 1:2) obtained from experimental tests by skew rolling in a CNC rolling mill

Full size image

For the purpose of quality agreement assessment, the FEM and experimental force parameters are compared in Figs. 26 and 27. The experiment axial force on the chuck (Fig. 26) and the experiment torque (Fig. 27) were measured during the rolling process. The distributions of these force parameters qualitatively agree with the numerical results. It can also be observed that the axial forces on the chuck do not exceed 25 kN while the torque does not exceed 1150 Nm. Thus, it has been experimentally confirmed that the skew rolling process conducted in a CNC rolling mill is characterized by low loads, which is one of the main advantages of the discussed preform formation technique.

Fig. 26
figure 26

Distributions of axial load on the chuck in the skew rolling process conducted in a CNC rolling mill

Full size image
Fig. 27
figure 27

Distributions of torque in the skew rolling process conducted in a CNC rolling mill

Full size image

5 Discussion

Figure 28 shows preform dimensions selected for a comparative analysis of the geometrical accuracy of rolled preforms. The selected dimensions directly result from the rolling process. Numerical and experimental preform geometries as well as the dimensions of CAD-designed preforms are given in Table 1. The FEM preform dimensions very much agree with those of the CAD preforms. Small differences in the preform dimensions result from measurement errors. The experimental preform dimensions are definitely higher than the assumed dimensions (CAD) and those obtained by FEM. The differences in diameter do not exceed 1.5 mm, whereas the differences in length do not exceed 5 mm. The differences in the experimental preform geometries can result from mill stretch, slipping of the workpiece from the chuck, and measurement errors. Given the intended use of the preforms (billets for die forging), the obtained accuracy of these preforms can be considered satisfactory.

Fig. 28
figure 28

Dimensions selected for a comparative analysis of the geometrical accuracy of rolled preforms

Full size image
Table 1 Results of preform geometries
Full size table

Preforms for the die forging process should be free of internal cracks. The numerical results have shown that the greatest probability of material cracking occurs in the rolling process for producing a connecting rod preform. To detect any potential cracks in this preform, the smallest diameter step rolled in two tool passes was cut. An examination of the preform’s cross section C–C (Fig. 29) did not reveal the presence of internal cracks. In the other sections, the rolled preform does not show any cracks either.

Fig. 29
figure 29

Sections of steps in performs obtained by rolling according to Fig. 28

Full size image

Specimens for microstructural examination were taken from the preform areas that were subjected to rolling. These areas are marked in Fig. 28 as sections from A-A to E-E. Figure 29 shows test specimens that were mounted in resin and polished. They were etched with 2% nital. Microscopic examination was performed with the Keyence VHX-7000 digital microscope. The macroscopic and microscopic examination results did not show the presence of any cracks.

Figure 30 shows examples of images of the microstructure in the analysed areas. Figure 30f shows the original microstructure of C45 steel used in the experiments. It is a homogenous fine-grained ferrite-perlite structure. The original microstructure of C45 steel contains about 38.7% ferrite. The average grain size in the original microstructure is 9.8 μm.

Fig. 30
figure 30

Images showing the microstructure of rolled preforms in: a section A-A, b section B-B, c section C–C, d section D-D, e section E-E, f original microstructure

Full size image

Figure 30a shows the microstructure of a scraper preform in the A-A section. The microstructure in this area is inhomogeneous and contains small grains of reticular ferrite and large grains of lamellar perlite. The percentage of ferrite in the chemical composition of the examined microstructure is about 11.3%. The coarse-grained structure in this area results from low plastic strains and high temperature. The average grain size in the microstructure of a scraper perform in the A-A section is equal to 38.1 μm.

Figure 30b shows the microstructure of a scraper perform in the B-B section for the area that was deformed to the greatest extent. The microstructure is not homogenous and consists of large perlite grains and smaller grains of reticular ferrite. The percentage of ferrite in the chemical composition of the microstructure in the B-B section is higher than that in the A-A section and amounts to 17.4%. The average grain size in the microstructure of a scraper preform in the B-B section is 25.9 μm. The smaller grain size in the B-B section compared to that in the A-A section results from higher plastic strains due to higher cross-sectional reduction.

Figure 30c and d show images of the microstructure of a connecting rod perform in the sections C-C and D-D, respectively. The microstructure in the C-C section is homogenous. There is are no reticular ferrite grains around large perlite grains. The ferrite grains are not elongated; they have a more compact shape. The percentage of ferrite in the analysed area is 26.7%. The average grain size in the microstructure of a connecting rod perform in the C-C section is 14.7 μm. Compared to other examined areas, the grain size in the C-C section is definitely the smallest. The smallest grain size in this region results from very high plastic strains that reach 25. What is more, this area of the preform was deformed in two stages; as a result, the austenite grain was pre-refined prior to the other stage of the forming process. In addition, the cooling of the material during the first roll pass constrained austenite grain growth, the extent of which has a significant impact on microstructure quality after the rolling process. The microstructure of the D-D section of a connecting rod preform rolled in one pass is non-homogenous. In this area, the microstructure consists of large perlite grains and smaller elongated ferrite grains. The percentage of ferrite in this area amounts to 18.3%. The arrangement of ferrite grains is reticular in some areas. In other areas of the analysed structure one can, however, observe extensive agglomerations of ferrite grains with a small percentage of perlite grains. The average grain size in the microstructure of a connecting rod preform in the D-D section is 19.1 μm.

The microstructure of a hook preform is shown for the E-E section (Fig. 30e); this section was located in the central step that was the only one subjected to rolling. The microstructure in this area is not homogenous. One can observe the presence of large grains of perlite and smaller elongated grains of reticular ferrite. The percentage of ferrite in the analysed area amounts to 11.5%. The average grain size in the microstructure of a connecting rod preform in the E-E section is 25.4 μm.

The quality of the microstructure of rolled preforms varies and depends on many factors. The microstructure of a single preform can differ depending on its area. Given the fact that all preforms were rolled at the same temperature, it can be claimed that the microstructure is most significantly affected by plastic strains. Increase in plastic strains leads to grain size refinement and homogenization. As a result of the high temperature of the rolling process and relatively low plastic strains (due to preform geometry), one can observe the presence of Widmannstätten patterns in some cases, e.g. in the sections A-A, B-B and E-E. The presence of Widmannstätten patterns is proved by a small number of acicular ferrite grains. As far as preforms are concerned, structure homogenization and refinement can be achieved by final die forging and normalizing heat treatment.

6 Conclusions

The numerical and experimental results of this study lead to the following conclusions:

  • Elongated axisymmetric preforms can be produced by skew rolling in a CNC rolling mill;

  • A characteristic of forming preforms in a CNC rolling mill is that the rolling process is performed using the same set of tools (rolls); as a result, this method can be recommended for use in piece- and small-batch production;

  • Despite a relatively long duration of the forming process, the temperature of the preform is high enough for performing closed-die forging; the heat carried away to the environment and tools is compensated for by deformation and friction work;

  • Preforms produced with the use of a CNC rolling mill are characterized by high dimensional accuracy (diameter deviations do not exceed 1.5 mm), and they are free from internal cracks;

  • The rolled preforms have shallow helical grooves on their surface; these grooves do not, however, occur on the surface of the closed-die forged parts;

  • The process of rolling preforms in a CNC rolling mill is characterised by relatively low force parameters, which means that the rolling mill can be lightweight.

  • The microstructure of the rolled preforms is not homogenous.