1 Introduction

The stochastic modeling and analysis of a large number of realistic applications that include some kind of complementary services, i.e., when the total value of serving a customer depends on a set of smaller services, is carried out through the formation and study of networks of service systems. Such realistic applications occur either in service delivery systems, e.g., at the emergency department (ED) of a healthcare facility, or in make-to-order production systems. The queueing networks that represent such systems correspond to a variety of topologies, from relatively simple ones such as stations in tandem (when the service stages are predetermined and identical for all customers) to very complex ones (when the customers receive complementary services through alternative routes). In addition, most of these applications involve active customers who make individual decisions for maximizing their utility, taking into account the congestion of the system at any level of service and the available information. For example, patients who arrive at an ED and need to go through blood tests before a physical examination may balk due to excessive delays.

Therefore, the appropriate framework for the study of service systems with complementary services should involve the consideration of strategic customers. This area of queueing literature, mentioned as Queueing Games, deals with the analysis of customers’ decentralized behavior from an economic perspective and started with the pioneering work of Naor [1], who studied the join-or-balk dilemma when the customers observe the queue length before making their decisions (observable model). Subsequently, Edelson and Hilderbrand [2] studied the same problem, when the customers assess the expected congestion of the system only through its known parameters, but without observing the queue length (unobservable model). Since then, there has been a growing body of literature that extends in various directions.

For example, there are several papers dealing with various types of decisions (entry/exit, arrival time selection, reneging time selection, e.g., [3]), different types of systems (e.g., \(M/M^K/1\): [4], clearing systems: [5], M/M/1 with retrials: [6], M/M/1 with service vacations: [7,8,9]), system operation management (e.g., [10, 11]): dynamic control of service rate), or coordinating the system [12]. The corresponding studies on queueing networks have mostly focused on parallel queueing systems, i.e., on customer routing problems (e.g., [13]), or in telecommunications (e.g.,[14]). Other works emphasize that customers exhibit nonlinear aversion to delay, see, e.g., [15, 16]. For a comprehensive survey of queueing games, we refer to Hassin and Haviv [17] and Hassin [18].

In many cases, customers differ in their evaluation of excessive delays, since different customers value time differently. In fact, some customers are more patient and can wait for a long time to obtain service, while other customers are more sensitive to system congestion and could leave after a short time of waiting. Therefore, customers’ delay sensitivity is an important factor that plays an essential role not only in customers’ joining decisions but also in the operation of the system, especially in the case of complementary services where customers may abandon the system after completing some of the stages of service collecting a smaller service reward, before concluding their complete service. In applications, we observe this effect on ride-hailing platforms which are designed to offer different types of services based on the needs of customers that are more sensitive to service congestion. The effect of customers’ heterogeneity regarding delay sensitivity on their strategic behavior was studied in [19] for the M/M/1 queue under three different levels of available information upon customers’ arrival: no, partial, and full information. The authors identified special cases where more accurate delay information improves the performance of the system. On the other hand, Guo and Hassin [9] analyzed the case of heterogeneous customers facing the join/balk dilemma in a vacation queue and showed that there may exist multiple equilibria in such a system.

The present work focuses on a thread of research that studies the strategic customer behavior in tandem queues, see, e.g., [20, 21] and [22]. More specifically, in the present paper, we analyze strategic customer joining behavior in a Markovian tandem queueing system, where customers are heterogeneous in their delay sensitivity. Specifically, we consider two M/M/1 queues in series with strategic customers, who may enter the system only from the first queue and proceed to the second queue after completing their service in the first one. Customers are making joining decisions at the entrance of each queue, having the option to leave permanently the system before entering the second queue, and collecting the reward by the first service. In addition, we assume that both queues are unobservable; thus, customers’ join/balk decisions depend only on the operational and economic parameters of the system and not on the knowledge of the system state at their arrival instants, assuming different operational parameters and service values for each queue. As in the model by Burnetas [20] who analyzed customers’ strategic behavior for the join/balk dilemma considering a tandem system of N unobservable Markovian queues, customers’ decisions must take into account not only the trade-off between the acquired service value and the waiting cost in the current queue, but also the possibility that this loss may be compensated by joining the subsequent queue. In [20], the author determined the unique subgame perfect equilibrium of the problem by a backward recursion scheme.

The crucial difference from the model of Burnetas [20] is that in the present paper, we analyze the effect of customer heterogeneity in delay sensitivity on customers’ strategic behavior, which leads to the existence of equilibrium threshold strategies on their delay cost parameter. Since the complexity of the analysis increases significantly due to customers’ heterogeneity, the present model permits to obtain of comparative results between the cases of heterogeneous and homogeneous customers for several performance measures, especially for equilibrium arrival rates. Other significant works in this research thread are the papers in [21, 23], and [22].

D’Auria and Kanta [21] consider a tandem system with two queues where customers cannot balk in between, and they have to go through the whole system. The case where the arriving customers know the total number of customers in the system was studied by D’Auria and Kanta [23] who proved the existence of a unique strategic equilibrium. Finally, Ji et al. [22] investigate a tandem system of two M/M/1 queues where queue-length information is available at customers’ arrival and customers have the option to renege at any time. In the case where customers observe the state of the entire system and decide whether to join or not, they showed that customers’ equilibrium strategy is not necessarily a function of the total number of customers in the system and, also, that customers may balk in front of the second queue but never renege from the first queue. In all cases, customers are considered to be homogeneous.

The contribution of this paper is to enrich the literature in tandem Markovian queueing systems with strategic customers examining the more realistic case where customers differ on delay sensitivity. We show that equilibrium strategies are threshold-based in delay sensitivity, and we explicitly characterize the equilibrium in the whole range of the parameters. We have also applied our findings to situations where delay sensitivity parameters are uniformly or gamma-distributed and have conducted various numerical experiments under different operational and economic parameters to assess the impact of the variance on customers’ equilibrium behavior. The key takeaway from this study is that heterogeneity is significant and can be measured through our approach.

Specifically, there exists a set of critical values for the parameters where customer heterogeneity disappears and customers behave as almost homogeneous. In addition, as the second queue becomes more valuable for the customers or works faster, then, in equilibrium, fewer customers will join it as the variance of delay sensitivity increases. On the other hand, for low values of the fraction of the service values or the service rates, higher variance results in higher arrival rates. Therefore, there exist ideal sets of parameter values for which the information asymmetry can be controlled by the administrator of the system either by setting the service rates appropriately or by imposing an admission fee or a subsidy which in turn controls the fraction of the service values.

The rest of the paper is organized as follows: In Sect. 2, we describe the model, whereas in Sect. 3, we set up the strategy space, the equilibrium strategies, and the corresponding benefit functions. In Sect. 4, we establish the form of the unique symmetric equilibrium threshold strategy. In Sect. 5, we present numerical results on the comparison with the homogeneous case considering the equilibrium throughput and the equilibrium customers’ social welfare. Finally, in Sect. 6, we conclude and present possible extensions for future research. Some technical material and the notation are presented in the Appendix.

2 Model Description

We consider two M/M/1 tandem queues, namely, queues 1 and 2, where the service times are exponentially distributed with rates \(\mu _1\) and \(\mu _2\), respectively. Potential customers arrive at queue 1 according to a Poisson process with rate \(\Lambda\). We assume that both queues have infinite waiting spaces and that the service discipline is FCFS.

Customers are strategic, delay-sensitive, and risk-neutral optimizers. Their objective is to maximize their individual expected net benefit from their service in the system, taking into account that all customers have similar objectives and the same level of information. Each customer first decides whether to join or balk at queue 1 upon arrival. If she joins, she makes a second join/balk decision upon her arrival at the second queue.

The service values at queues 1 and 2 for an arbitrary customer are \(R_1\) and \(R_2\), respectively. To avoid trivialities, we assume that \(R_1, R_2>0\). A customer may choose either to balk upon arrival (in which case she receives 0 total service value), or to join the first queue and depart after finishing her service there (in which case her total service value is \(R_1\)), or to go through both queues (in which case her total service value is \(R_1+R_2\)).

Customers accumulate waiting costs as long as they stay in the system. Considering their delay sensitivity, we assume that they are heterogeneous in their valuations. Specifically, their valuation on the delay cost is linear on the waiting time with delay cost parameter C per unit time which is a customer-specific parameter indicating the importance of time. Furthermore, we assume that C is a non-negative continuous random variable with \(H(\cdot )\) being its cumulative distribution defined in an interval, i.e., \(C\sim H(c),\;c\in I\subseteq (0,\infty )\). For a tagged customer, we denote the realization of her delay sensitivity parameter by c. This is considered private information, not known to the other customers.

At their arrival instants, customers are not informed about the state of the queues, i.e., we consider the unobservable case of this model, but they know the operational and economic parameters of the system.

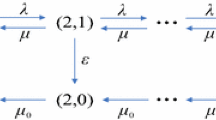
For convenience in the presentation, we assume that \(\Lambda <\min \{\mu _1,\mu _2\}\) in order to ensure the stability of the system even if all customers decide to go through both queues. In Fig. 1, we illustrate the tandem system along with the customers’ decisions and the operational and economic parameters.

Fig. 1
figure 1

Visualization of the setting

Full size image

3 Game Formulation

Since the expected benefit of an arriving customer at the system depends on the effective arrival rate at each queue, which in turn depends on the joining decisions of the population of customers, we have that the interaction among the customers can be viewed as a symmetric game (since they are a priori indistinguishable).

The system is unobservable, i.e., the customers are not aware of the system state at any queue upon their arrival instants. Therefore, a pure strategy of a customer with a given delay sensitivity c (in the following, we refer to her as a customer of type\(-c\)) is of the form \(\underline{x}(c)=(x_1(c),x_2(c))\) where \(x_n(c)\in \{0,1\}\), and \(x_n(c)=1\) if and only if the customer joins queue n. Note that if \(x_1(c)=0\), then \(x_2(c)=0\), because in case a customer balks after departing from queue 1, then at the same time she definitely departs from the system. Therefore, a customer’s pure strategy is a function

$$\begin{aligned} {X:I\rightarrow \{0,1\}^2:c\rightarrow (x_1(c),x_2(c)),} \end{aligned}$$
(1)

with \(X(c)=(x_1(c),x_2(c)) \in \{(0,0), (1,0), (1,1) \}\). Note that (0, 0) represents the decision that a type\(-c\) customer does not enter the system, (1, 0) refers to the decision of joining only the first queue and then leave the system, and, finally, (1, 1) stands for joining both queues.

Furthermore, we consider an equivalent definition of X which mirrors customers’ pure strategies to a partition of I, as follows:

$$\begin{aligned} \begin{aligned} V_{00}(X)&=\{c\in I:X(c)=(0,0)\},\\ V_{10}(X)&=\{c\in I:X(c)=(1,0)\},\\ V_{11}(X)&=\{c\in I:X(c)=(1,1)\}. \end{aligned} \end{aligned}$$
(2)

This partition of the interval I corresponds to the notion of pure strategies employed by customers of type\(-c\), since for any \(c\in V_{00}(X)\) customers will balk the system, for any \(c\in V_{10}(X)\) will join only the first queue, and for any \(c\in V_{11}(X)\) will definitely join both queues. Note that it would be equivalent to a threshold strategy if and only if there exist thresholds \(c_1\ge c_2\in I\) with \(c_1\ge c_2\), such that

$$\begin{aligned} \begin{aligned} V_{11}(X)&=\{c\in I: c\le c_2\},\\ V_{10}(X)&=\{c\in I: c_2<c\le c_1\},\\ V_{00}(X)&=\{c\in I: c> c_1\}. \end{aligned} \end{aligned}$$
(3)

In order to derive the effective arrival rates at each queue of the system, we note that \(V_{10}(X)\cup V_{11}(X)\) refers to those type\(-c\) customers who will join at least queue 1, whereas \(V_{11}(X)\) corresponds to those customers that will join at both queues 1 and 2. Letting \(V_1(X):=V_{10}(X)\cup V_{11}(X)\) and \(V_2(X):=V_{11}(X)\), then the corresponding effective arrival rates at queues 1 and 2, denoted by \(\lambda _1(X)\; \text{and}\; \lambda _2(X)\), respectively, can be defined as functions of X as

$$\begin{aligned} \lambda _1(X)=\Lambda P\left( V_1(X)\right) =\Lambda \int _{V_1(X)} dH(c), \end{aligned}$$
(4)
$$\begin{aligned} \lambda _2(X)=\Lambda P\left( V_2(X)\right) =\Lambda \int _{V_2(X)} dH(c). \end{aligned}$$
(5)

Note that \(\lambda _1(X)\ge \lambda _2(X)\), since we consider that queues 1 and 2 are in series and arrivals occur only at queue 1, and thus, the arrival rate at queue 2 cannot exceed the arrival rate of queue 1.

Therefore, under a given strategy X, the corresponding effective arrival rates at queues 1 and 2 are equal to \(\lambda _1(X)\) and \(\lambda _2(X)\), and thus, the expected sojourn time (delay) of any customer entering queue n is given by \(W_n(X)=\frac{1}{\mu _n-\lambda _n(X)}\) with \(\lambda _n(X)<\mu _n\).

Suppose that the population of customers follows a strategy X and let \(\lambda _n(X)\), \(n=1,2\), be the corresponding arrival rates. Then, the expected net benefit of a tagged customer with delay sensitivity parameter \(c'\) for joining queue n is

$$\begin{aligned} B_{n,c'}(X)=R_n-\frac{c'}{\mu _n-\lambda _n(X)},\;c'\in I,\;\lambda _n(X)<\mu _n. \end{aligned}$$
(6)

Therefore, the total expected utility of the tagged type\(-c'\) customer from following the decision \(Y(c')=\underline{y}(c')=(y_1(c'),y_2(c')),\; y_1,y_2\in \{0,1\}\), dictated by her strategy Y, when all others follow a strategy X, is

$$\begin{aligned} U_{c'}(Y;X)=y_1(c')\left( R_1-\dfrac{c'}{\mu _1-\lambda _1(X)}\right) +y_2(c')\left( R_2-\dfrac{c'}{\mu _2-\lambda _2(X)}\right) . \end{aligned}$$
(7)

Let \(Y^*(X)\) be her optimal response against X, which refers to the strategy that maximizes \(U_{c'}(Y; X)\) given that \(1\ge y_1(c')\ge y_2(c')\ge 0\), then a symmetric Nash equilibrium is defined as a strategy X such that \(Y^*(X)=X\), i.e., a best response against itself.

The best response \(Y^*(X)\) is determined by solving for all \(c'\) the following optimization problem:

$$\begin{aligned} B_{1,c'}(X)y_1^*+B_{2,c'}(X)y_2^*=\max _{y_1,y_2\in \{0,1\}}\{B_{1,c'}(X)y_1+B_{2,c'}(X)y_2\}. \end{aligned}$$
(8)

Note that the above maximization could be separated into the corresponding joining decisions at each queue considering the signs of \(B_{n,c'}\) and of their sum \(B_{1,c'}+B_{2,c'}\), as follows:

  1. (i)

    Customer of type\(-c'\) joins queue 1 \(\iff \max \{B_{1,c'},\;B_{1,c'}+B_{2,c'},\;0\} >0\),

  2. (ii)

    Customer of type\(-c'\) joins queue 2 \(\iff \max \{B_{2,c'},\;0\} >0\).

In Table 1, we present the feasible best responses of a tagged customer, according to the relevant signs of the above quantities.

Table 1 Feasible best responses of the tagged customer of type\(-c'\)
Full size table

Therefore, the tagged customer’s best response, \(\underline{y}^*(c')\), assumes the form

$$\begin{aligned} (y_1^*(c'),y_2^*(c'))=\left\{ \begin{array}{ll} (0,0),&{}\text { if } B_{1,c'}(X)\le 0\text { and }B_{1,c'}(X)+B_{2,c'}(X)\le 0 \\ (\{0,1\},0),&{} \text { if }B_{1,c'}(X)=0\text { and }B_{2,c'}(X)\le 0 \\ (1,0),&{} \text { if }B_{1,c'}(X)\ge 0\text { and }B_{2,c'}(X)\le 0\\ (1,\{0,1\}),&{} \text { if }B_{1,c'}(X)\ge 0\text { and }B_{2,c'}(X)=0\\ (1,1),&{} \text { if }B_{2,c'}(X)\ge 0\text { and }B_{1,c'}(X)+B_{2,c'}(X)\ge 0\\ (\{0,1\},\{0,1\}),&{}\text { if } B_{1,c'}(X)\le 0\text { and }B_{1,c'}(X)+B_{2,c'}(X)=0 \\ (\{0,1\},\{0,1\}),&{}\text { if } B_{n,c'}(X)=0,\text { for } n=1,2,\text { and }\\ {} &{} \;\;\;\;B_{1,c'}(X)+B_{2,c'}(X)=0 \end{array}\right. \end{aligned}$$

Furthermore, by (6), for any fixed X, \(B_{n,c'}(X)\) for \(n=1,2\), and \(B_{1,c'}(X)+B_{2,c'}(X)\) are strictly decreasing in \(c'\). Thus, by the best response function given above, when all others follow any fixed X, a customer of type\(-c'\) will not enter the system if \(c'>\max \{k_1,k_{12}\}\), will enter only queue 1 if \(k_2<c'<k_1\), and she will join both queues if \(c'\le \min \{k_2,k_{12}\}\), where

$$\begin{aligned} \begin{aligned} k_1&=R_1\left[ \mu _1-\lambda _1(X)\right] ,\\ k_2&=R_2\left[ \mu _2-\lambda _2(X)\right] ,\\ k_{12}&=\left( R_1+R_2\right) \left[ \dfrac{1}{\mu _1-\lambda _1(X)}+\dfrac{1}{\mu _2-\lambda _2(X)}\right] ^{-1}. \end{aligned} \end{aligned}$$

Therefore, depending on the values of the parameters, and the relative ordering of \(k_1,k_2\), and \(k_{12}\), it follows that there exist thresholds \(c_1\ge c_2\) such that the best response of the tagged customer of type\(-c'\)to be

$$\begin{aligned} (y_1^*(c'),y_2^*(c'))=\left\{ \begin{array}{ll} (0,0),&{} c'>c_1,\\ (1,0),&{} c_2< c' \le c_1,\\ (1,1),&{} c'\le c_2, \end{array}\right. \end{aligned}$$
(9)

with \(V_{11}(Y^*(X))=\{c'\in I:\; c'\le c_2\}\), \(V_{10}(Y^*(X))=\{c'\in I:\; c_2<c'\le c_1\}\), and \(V_{00}(Y^*(X))=\{c'\in I: \;c'> c_1\}\).

As we have noticed, due to the monotonicity of \(B_{n,c'}\) and \(B_{1,c'}+B_{2,c'}\) with respect to \(c'\), the best response of the tagged is specified by thresholds \(c_1,c_2\) for joining each queue, formulating a threshold-based strategy of the form \((c_1,c_2)\) where a customer of type\(-c\) will join queue n if and only if \(c\le c_n\). Therefore, the symmetric Nash equilibrium would also be a threshold strategy denoted by \((c_1^e,c_2^e)\).

In the following, we proceed with the equilibrium analysis which is restricted to the following set of threshold joining strategies:

$$\begin{aligned} TH=\{(c_1,c_2): c_1,c_2\in I,\;c_1\ge c_2\}. \end{aligned}$$

4 Equilibrium Analysis

We consider threshold joining strategies of the form \((c_1,c_2)\in TH\) as defined in (3) where a customer of type c joins queue 1 if and only if \(c \le c_1\), and queue 2 if and only if \(c \le c_2\). Since C is a non-negative continuous random variable taking values in the interval I representing the delay sensitivity of an arbitrary customer with distribution H(c), the corresponding joining probabilities are \(P(C \le c_1)\) for joining queue 1 and \(P(C \le c_2, C\le c_1 )\) for joining queue 2, respectively. But since only departures from queue 1 can be arrivals to queue 2, we can restrict our attention to the case where \(c_2\le c_1\). Therefore, the system corresponds to two M/M/1 queues in tandem with arrival rates \(\lambda _1=\Lambda H(c_1)\) and \(\lambda _2=\Lambda H(c_2)\). Note that there is a one-one correspondence between \(V_1(X), V_2(X)\), and the threshold strategies \(c_1,c_2\). The illustration of the system when all customers follow a threshold strategy \(\underline{c}=(c_1,c_2)\in TH\) can be seen in Fig. 2.

Fig. 2
figure 2

The tandem system in the framework of customer joining threshold strategies

Full size image

Therefore, letting \(\underline{\tilde{c}}=(\tilde{c}_1,\tilde{c}_2)\) be the threshold strategy followed by a tagged type-\(c'\) customer, and \(\underline{c}=(c_1,c_2)\) the one followed by the population of customers, her total expected net benefit in (8) can be written as

$$\begin{aligned} U_{c'}(\underline{\tilde{c}};\underline{c})=B_{1,c'}(\underline{c})\mathbb {1}_{\{c'\le \tilde{c}_1\}} +B_{2,c'}(\underline{c})\mathbb {1}_{\{c'\le \tilde{c}_2\}}, \end{aligned}$$
(10)

where \(B_{n,c'}(\underline{c})\) refers to customer’s expected net benefit from joining queue n.

Since the customer’s joining decision at each queue depends only on the corresponding threshold, we simplify \(B_{n,c'}(\underline{c})\) to the following:

$$\begin{aligned} B_{n,c'}(c_n)=R_n-\dfrac{c'}{\mu _n-\lambda (c_n)}=R_n-\dfrac{c'}{\mu _n-\Lambda H(c_n)},\; c'\in I,\; \lambda (c_n)<\mu _n. \end{aligned}$$
(11)

Similarly to (8), her optimal response is defined as the threshold strategy \(\underline{\tilde{c}}^*=(\tilde{c}^*_1,\tilde{c}^*_2)\) that maximizes her expected net benefit \(U_{c'}(\underline{\tilde{c}};\underline{c})\) when all others follow the threshold strategy \(\underline{c}=(c_1,c_2)\), and thus, it is the solution of the following optimization problem:

$$\begin{aligned} (\tilde{c}^*_1,\tilde{c}^*_2)=\arg \max _{\tilde{c}_1,\tilde{c}_2\in I:\tilde{c}_1\ge \tilde{c}_2} \{B_{1,c'}(c_1)\mathbb {1}_{\{c'\le \tilde{c}_1\}}+B_{2,c'}(c_2)\mathbb {1}_{\{c'\le \tilde{c}_2\}} \}. \end{aligned}$$
(12)

To match the optimal response analysis outlined in Sect. 3, we introduce two extended threshold values, namely, \(c_l\) and \(c_h\), such that

$$\begin{aligned} c_l=\sup \{\tilde{c}:\; H(\tilde{c})=0\}=\inf I,\;c_h=\inf \{\tilde{c}:\; H(\tilde{c})=1\}=\sup I, \end{aligned}$$
(13)

with the convention that \(\inf \emptyset =\infty\). These values describe situations where a type\(-c\) customer will either always refuse to join a queue for any \(c\in I\) or always choose to join a queue for any \(c\in I\), respectively. If the set I is closed, such as when C is uniformly distributed in \(I=[a,b]\), then \(c_l=a\) and \(c_h=b\). Additionally, if C follows a distribution with a support range of \(I=[0,\infty )\), e.g., an exponential distribution, then \(c_l=0\) and \(c_h=\infty\).

Therefore, in correspondence with the previous analysis in Sect. 3, the tagged customer’s optimal response is given:

$$\begin{aligned} (\tilde{c}_1^*,\tilde{c}_2^*)=\left\{ \begin{array}{ll} (c_l,c_l),&{} B_{1,c'}(c_1)\le 0\text { and }B_{1,c'}(c_1)+B_{2,c'}(c_2)\le 0 \\ (c_1,c_l),&{} B_{1,c'}(c_1)=0\text { and }B_{2,c'}(c_2)\le 0 \\ (c_h,c_l),&{} B_{1,c'}(c_1)\ge 0\text { and }B_{2,c'}(c_2)\le 0\\ (c_h,c_2),&{} B_{1,c'}(c_1)\ge 0\text { and }B_{2,c'}(c_2)=0\\ (c_h,c_h),&{} B_{2,c'}(c_2)\ge 0\text { and }B_{1,c'}(c_1)+B_{2,c'}(c_2)\ge 0\\ (c_1,c_1),&{} B_{1,c'}(c_1)\le 0\text { and }B_{1,c'}(c_1)+B_{2,c'}(c_2)=0 \\ (c_1,c_2),&{} B_{1,c'}=B_{2,c'}=B_{1,c'}+B_{2,c'}=0 \end{array}\right. , \end{aligned}$$
(14)

where \(\tilde{c}_1^*\; \text{and}\; \tilde{c}_2^*\) represent the optimal thresholds against the threshold strategy \((c_1,c_2)\) for joining queues 1 and 2, respectively, visualized in Fig. 3.

Fig. 3
figure 3

The best response of a type\(-c'\) customer in the \(B_1 B_2-\)plain

Full size image

Finally, for the equilibrium analysis, we let \(r_n\) be the unique roots of the equations \(B_{n,r_n}(r_n)=0 \iff R_n-\dfrac{r_n}{\mu _n-\lambda (r_n)}=0\), or equivalently,

$$\begin{aligned} r_n=R_n[\mu _n-\Lambda H(r_n). \end{aligned}$$
(15)

First, we consider the case where the support of H is the closed set \(I=[c_l,c_h]\) as in the case of a uniformly distributed delay sensitivity to explore all possible equilibria that can appear for the different values of the parameters. In this case, the extended thresholds \(c_l,c_h\) are finite and coincide with the boundaries of I.

In Theorem 1, we characterize the equilibrium threshold strategies \((c_1^e,c_2^e)\) for \(0< c_l\le c_2^e\le c_1^e\le c_h<\infty\) concerning the values of the economic and operational parameters of the model. Each of the seven areas (I, II, III, IV, V, VIa, VIb) in Fig. 4 refers to the corresponding case of Theorem 1.

Theorem 1

The equilibrium joining threshold strategies for the system of the two M/M/1 queues in tandem when customers’ delay sensitivity parameter takes values in the interval \(I=[c_l,c_h]\), are characterized as follows:

  1. (i)

    If \(R_1\le \dfrac{c_l}{\mu _1}\) and \(R_1+R_2\le \dfrac{c_l}{\mu _1}+\dfrac{c_l}{\mu _2}\), then the unique equilibrium threshold strategy is \((c_l,c_l)\), which implies \(\lambda _1^e=\lambda _2^e=0\).

  2. (ii)

    If \(R_1\ge \dfrac{c_h}{\mu _1-\Lambda }\) and \(R_2\le \dfrac{c_l}{\mu _2}\), then the unique equilibrium threshold strategy is \((c_h,c_l)\), which implies \(\lambda _1^e=\Lambda\) and \(\lambda _2^e=0\).

  3. (iii)

    If \(R_1+R_2 \ge \dfrac{c_h}{\mu _1-\Lambda }+\dfrac{c_h}{\mu _2-\Lambda }\) and \(R_2\ge \dfrac{c_h}{\mu _2-\Lambda }\), then the unique equilibrium threshold strategy is \((c_h,c_h)\), which implies \(\lambda _1^e=\lambda _2^e=\Lambda\).

  4. (iv)

    If \(\dfrac{c_l}{\mu _1}<R_1<\dfrac{c_h}{\mu _1-\Lambda }\) and \(R_2\le \dfrac{c_l}{\mu _2}\), then the unique equilibrium threshold strategy is \((c_1^e,c_l)\), with \(c_1^e=r_1\). In this case, \(\lambda _1^e=\Lambda H(r_1)\) and \(\lambda _2^e=0\).

  5. (v)

    If \(R_1\ge \dfrac{c_h}{\mu _1-\Lambda }\) and \(\dfrac{c_l}{\mu _2}<R_2<\dfrac{c_h}{\mu _2-\Lambda }\), then the unique equilibrium threshold strategy is \((c_h,c_2^e)\), with \(c_2^e=r_2\). In this case, \(\lambda _1^e=\Lambda\) and \(\lambda _2^e=\Lambda H(r_2)\).

  6. (vi)

    If \(\dfrac{c_l}{\mu _1}+\dfrac{c_l}{\mu _2}<R_1+R_2<\dfrac{c_h}{\mu _1-\Lambda }+\dfrac{c_h}{\mu _2-\Lambda }\), \(R_1<\dfrac{c_h}{\mu _1-\Lambda }\), and \(R_2>\dfrac{c_l}{\mu _2}\), then

    1. (a)

      If \(R_2 < \frac{r_1(R_1)}{\mu _1-\Lambda H(r_1(R_1))}\), the unique equilibrium threshold strategy is \((c_1^e,c_2^e)\), with \(c_1^e=r_1\) and \(c_2^e=r_2\), if \(r_1>r_2\). In this case, \(\lambda _1^e=\Lambda H(r_1)\) and \(\lambda _2^e=\Lambda H(r_2)\).

    2. (b)

      Otherwise, the unique equilibrium threshold strategy is \((c_1^e,c_1^e)\), with \(c_1^e=r\), where r is the solution of the following equation

      $$\begin{aligned} R_1-\dfrac{r}{\mu _1-\Lambda H(r)}+R_2-\dfrac{r}{\mu _2-\Lambda H(r)}=0. \end{aligned}$$
      (16)

      In this case, \(\lambda _1^e=\lambda _2^e=\Lambda H(r)\).

Proof

  1. (i)

    Consider that nobody joins the system, then all follow the threshold strategy \(c_1=c_2=c_l\). From the best response \((c_1^*,c_2^*)\) of the tagged\(-c'\) customer against \((c_l,c_l)\), it follows that \((c_l,c_l)\) would be an equilibrium if \(B_{1,c'}(c_l)\le 0\) and \(B_{1,c'}(c_l)+B_{2,c'}(c_l)\le 0\) for all \(c'\in [c_l,c_h]\). Since both are strictly decreasing in \(c'\), it suffices to assume that \(B_{1,c_l}(c_l)\le 0\) and \(B_{1,c_l}(c_l)+B_{2,c_l}(c_l)\le 0\). These imply by (11) that if \(R_1\le \dfrac{c_l}{\mu _1}\) and \(R_2+R_1 \le \dfrac{c_l}{\mu _1}+\dfrac{c_l}{\mu _2}\), then the unique equilibrium threshold strategy is \((c_l,c_l)\), and thus, in this case, nobody joins the system.

  2. (ii)

    Consider that all join the first queue and balk, i.e., all follow the threshold strategy \(c_1=c_h,\;c_2=c_l\). Once again by the best response function of a tagged\(-c'\) customer against \((c_h,c_l)\), it follows that in order \((c_h,c_l)\) to be an equilibrium strategy, then \(B_{1,c'}(c_h)\ge 0\) and \(B_{2,c'}( c_l)\le 0\) for all \(c'\in [c_l,c_h]\). Following that, and since \(B_{1,c'},\;B_{2,c'}\) are strictly decreasing in \(c'\), it suffices to assume that \(B_{1,c_h}(c_h)\ge 0\) and \(B_{2,c_l}(c_l)\le 0\). By substitution from (11), it follows that if \(R_1\ge \dfrac{c_h}{\mu _1-\Lambda }\) and \(R_2\le \dfrac{c_l}{\mu _2}\), then the unique equilibrium strategy is \((c_h,c_l)\).

  3. (iii)

    Consider that all join both queues, i.e., all follow the threshold strategy \(c_1=c_h,\;c_2=c_h\). From the best response of the tagged\(-c'\) customer against \((c_h,c_h)\), it follows that \((c_h,c_h)\) would be an equilibrium if \(B_{2,c'}(c_h)\ge 0\) and \(B_{1,c'}(c_h)+B_{2,c'}(c_h)\ge 0\) for all \(c'\in [c_l,c_h]\). Once again, since both are strictly decreasing in \(c'\), it suffices to consider \(B_{2,c_h}(c_h)\ge 0\) and \(B_{1,c_h}(c_h)+B_{2,c_h}(c_h)\ge 0\). Substituting the expressions for \(B_i\) considering (11), it follows that if \(R_2\ge \dfrac{c_h}{\mu _1-\Lambda }\) and \(R_2+R_1\ge \dfrac{c_h}{\mu _2-\Lambda }+\dfrac{c_h}{\mu _1-\Lambda }\), the unique equilibrium will be \((c_h,c_h)\).

  4. (iv)

    Consider that a fraction of customers join the first queue and then balk, then all follow a threshold strategy \((c_1,c_l)\), where \(c_1\in (c_l,c_h)\). By (14), \((c_1,c_l)\) would be best response of the tagged\(-c'\) customer against \((c_1,c_l)\), when

    $$\begin{aligned} \begin{array}{l} B_{1,c'}(c_1)\ge 0 \;\text {and}\; B_{2,c'}(c_l)\le 0 \text { for all } c'\le c_1, \text { and},\\ B_{1,c'}(c_1)\le 0 \;\text {and}\; B_{1,c'}(c_1)+B_{2,c'}(c_l)\le 0 \text { for all } c'> c_1. \end{array} \end{aligned}$$

    Since \(B_{1,c'}\) is strictly decreasing in \(c'\), \((c_1^e,c_l)\) with \(c_1^e\in (c_l,c_h)\) is an equilibrium strategy if and only if \(B_{1,c_1^e}(c_1^e)=0\), and, also,

    $$\begin{aligned} \begin{array}{r} B_{2,c'}(c_l)\le 0 \text { for all } c'\le c_1^e, \text { and},\\ B_{1,c'}(c_1^e)+B_{2,c'}(c_l)\le 0 \text { for all } c'\ge c_1^e. \end{array}{l} \end{aligned}$$

    Once again, due to the monotonicity of \(B_{2,c'}\) and \(B_{1,c'}+B_{2,c'}\) with respect to \(c'\), the above necessary conditions for equilibrium are equivalent to

    $$\begin{aligned} B_{2,c_l}(c_l)\le 0, \text { and } B_{1,c_1^e}(c_1^e)+B_{2,c_1^e}(c_l)\le 0, \end{aligned}$$
    (17)

    where \(c_1^e\) is the solution of the equation

    $$\begin{aligned} B_{1,c_1^e}(c_1^e)=0\Leftrightarrow R_1-\dfrac{c_1^e}{\mu _1-\Lambda H(c_1^e)}=0 \text { with } c_1^e\in (c_l,c_h). \end{aligned}$$
    (18)

    The latter coincides with \(r_1\) in (15). Substituting the expressions for \(B_n\) given in (11) in (17), it follows that \(R_2\le \dfrac{c_l}{\mu _2}\) and \(R_2\le \dfrac{c_1^e}{\mu _2}\). Since \(c_1^e\) lies in the interval \((c_l,c_h)\), we derive that \(R_2\le \dfrac{c_l}{\mu _2}\). In addition, the right part of \(R_1=\dfrac{c_1^e}{\mu _1-\Lambda H(c_1^e)}\) is increasing in \(c_1^e\in (c_l,c_h)\), thus \(\dfrac{c_l}{\mu _1}< R_1<\dfrac{c_h}{\mu _1-\Lambda }\). Therefore, if \(R_2\le \dfrac{c_l}{\mu _2}\) and \(\dfrac{c_l}{\mu _1}< R_1<\dfrac{c_h}{\mu _1-\Lambda }\), then the unique equilibrium strategy is \((c_1^e,c_l)\), where \(c_1^e=r_1\), the solution of (15) in \((c_l,c_h)\).

  5. (v)

    Consider that a fraction of customers join the second queue, whereas all have joined queue 1 at first, then all customers follow the threshold strategy \(c_1=c_h,\;c_2\in (c_l,c_h)\). By (14), \((c_h,c_2)\) would be the best response of the tagged\(-c'\) customer against \((c_h,c_2)\), when

    $$\begin{aligned} \begin{array}{l} B_{2,c'}(c_2)\ge 0 \;\text {and}\; B_{1,c'}(c_h)+B_{2,c'}(c_2)\ge 0 \text { for all } c'\le c_2, \text { and},\\ B_{1,c'}(c_h)\ge 0 \;\text {and}\; B_{2,c'}(c_2)\le 0 \text { for all } c'> c_2. \end{array} \end{aligned}$$

    Since \(B_{2,c'}\) is strictly decreasing in \(c'\), \((c_h,c_2^e)\) with \(c_2^e\in (c_l,c_h)\) is an equilibrium strategy if and only if \(B_{2,c_2^e}(c_2^e)=0\), and also,

    $$\begin{aligned} \begin{array}{r} B_{1,c'}(c_h)+B_{2,c'}(c_2)\ge 0 \text { for all } c'\le c_2^e, \text { and},\\ B_{1,c'}(c_h)\ge 0 \text { for all } c'\ge c_2^e. \end{array} \end{aligned}$$

    Once again, due to the monotonicity of \(B_{1,c'}\) and \(B_{1,c'}+B_{2,c'}\) with respect to \(c'\), the above equilibrium conditions are equivalent to

    $$\begin{aligned} B_{1,c_2^e}(c_h)+B_{2,c_2^e}(c_2^e)\ge 0, \text { and } B_{1,c_h}(c_h)\ge 0, \end{aligned}$$
    (19)

    where \(c_2^e\) is the solution of the equation

    $$\begin{aligned} B_{2,c_2^e}(c_2^e)=0\Leftrightarrow R_2-\dfrac{c_2^e}{\mu _2-\Lambda H(c_2^e)}=0 \text { with } c_2^e\in (c_l,c_h). \end{aligned}$$
    (20)

    The latter coincides with \(r_2\) the solution of equation (15) for \(n=2\). Substituting the expressions for \(B_n\) in (19), it follows that \(R_1\le \dfrac{c_2^e}{\mu _1-\Lambda }\) and \(R_1\ge \dfrac{c_h}{\mu _1-\Lambda }\). Since \(c_2^e\) lies in the interval \((c_l,c_h)\), it follows that \(R_1\ge \dfrac{c_h}{\mu _1-\Lambda }\). In addition, the right part of \(R_2=\dfrac{c_2^e}{\mu _2-\Lambda H(c_2^e)}\) is increasing in \(c_2^e\in (c_l,c_h)\), and thus, \(\dfrac{c_l}{\mu _2}< R_2<\dfrac{c_h}{\mu _2-\Lambda }\). Therefore, if \(R_1\ge \dfrac{c_h}{\mu _1-\Lambda }\) and \(\dfrac{c_l}{\mu _2}< R_2<\dfrac{c_h}{\mu _2-\Lambda }\), then the unique equilibrium strategy is \((c_h,c_2^e)\), where \(c_2^e=r_2\), the solution of (15) in \((c_l,c_h)\) for \(n=2\).

  6. (vi)

    Consider that a fraction of customers join both queues, which means that all customers adopt the joining thresholds \(c_1,c_2\) with \(c_1\ge c_2\) since \(\lambda _1\ge \lambda _2\). We consider the following two cases: (a) \(c_1>c_2\) and (b) \(c_1=c_2\).

    1. (a)

      For case (a), where \(c_1>c_2\), \((c_1,c_2)\) would the best response of a tagged type\(-c'\) customer against itself, when (14),

      $$\begin{aligned} \begin{array}{l} B_{2,c'}(c_2)\ge 0 \;\text {and}\; B_{1,c'}(c_1)+B_{2,c'}(c_2)\ge 0 \text { for all } c'\le c_2, \\ B_{1,c'}(c_1)\ge 0 \;\text {and}\; B_{2,c'}(c_2)\le 0 \text { for all } c_2\le c'\le c_1.\\ B_{1,c'}(c_1)\le 0 \;\text {and}\; B_{1,c'}(c_1)+B_{2,c'}(c_2)\le 0 \text { for all } c'\ge c_1. \end{array} \end{aligned}$$

      By the monotonicity of \(B_{n,c'}\), i.e., \(B_{1,c'} and B_{2,c'}\) are strictly decreasing in \(c'\), \((c_1^e,c_2^e)\) is an equilibrium strategy with \(c_l<c_2^e< c_1^e < c_h\) if and only if

      $$\begin{aligned} B_{2,c_2^e}(c_2^e)=0 \text { and } B_{1,c_1^e}(c_1^e)=0 \text { for } c_l< c_2^e< c_1^e<c_h, \end{aligned}$$
      (21)

      and in addition,

      $$\begin{aligned} \begin{array}{r} B_{1,c'}(c_1)+B_{2,c'}(c_2)\ge 0 \text { for all } c'\le c_2^e, \text { and},\\ B_{1,c'}(c_1)+B_{2,c'}(c_2)\le 0 \text { for all } c'\ge c_1^e. \end{array} \end{aligned}$$

      Once again, due to the monotonicity of \(B_{1,c'}+B_{2,c'}\) with respect to \(c'\), the above necessary equilibrium conditions are equivalent to

      $$\begin{aligned} B_{1,c_2^e}(c_1^e)+B_{2,c_2^e}(c_2^e)\ge 0, \text { and } B_{1,c_1^e}(c_1^e)+B_{2,c_1^e}(c_2^e)\le 0, \end{aligned}$$
      (22)

      where \(c_1^e and c_2^e\) satisfy the following equations

      $$\begin{aligned} B_{1,c_1^e}(c_1^e)=0 \Leftrightarrow R_1-\dfrac{c_1^e}{\mu _1-\Lambda H(c_1^e)}=0 \text { with } c_1^e\in (c_2^e,c_h), \end{aligned}$$
      (23)
      $$\begin{aligned} B_{2,c_2^e}(c_2^e)=0 \Leftrightarrow R_2-\dfrac{c_2^e}{\mu _2-\Lambda H(c_2^e)}=0 \text { with } c_2^e\in (c_l,c_1^e), \end{aligned}$$
      (24)

      which correspond to the roots \(r_n\) of (15) for \(n=1,2,\) respectively. Since \(B_{1,c_1^e}(c_1^e)=0, B_{2,c_2^e}(c_2^e)=0\), and by substitution of \(B_n\) in (22), it follows that

      $$\begin{aligned} B_{1,c_2^e}(c_1^e)\ge 0 \Leftrightarrow R_1\ge \dfrac{c_2^e}{\mu _1-\Lambda H(c_1^e)}, \end{aligned}$$
      (25)
      $$\begin{aligned} B_{2,c_1^e}(c_2^e)\le 0 \Leftrightarrow R_2\le \dfrac{c_1^e}{\mu _2-\Lambda H(c_2^e)}, \end{aligned}$$
      (26)

      which both are true if \(c_1^e=r_1>r_2=c_2^e\). Furthermore, by (23) and (24), it follows that \(R_1=\dfrac{c_1^e}{\mu _1-\Lambda H(c_1^e)}\) for \(c_1^e\in (c_2^e,c_h)\) and \(R_2=\dfrac{c_2^e}{\mu _2-\Lambda H(c_2^e)}\) for \(c_2^e\in (c_l,c_1^e)\). As in the proof of (v), the right part of \(R_1 and R_2\) is increasing in \(c_2^e\in (c_l,c_1^e)\) and \(c_1^e\in (c_2^e,c_h)\), respectively, thus \(\dfrac{c_2^e}{\mu _1-\Lambda H(c_2^e)}<R_1<\dfrac{c_h}{\mu _1-\Lambda }\) and \(\dfrac{c_l}{\mu _2}<R_2<\dfrac{c_1^e}{\mu _2-\Lambda H(c_1^e)}\). Taking into account the necessary conditions for equilibrium described by in (25) and (26), we derive that the point \((R_1,R_2)\) must lie in the region

      $$\begin{aligned} \left( \dfrac{c_2^e}{\mu _1-\Lambda H(c_1^e)},\dfrac{c_h}{\mu _1-\Lambda }\right) \times \left( \dfrac{c_l}{\mu _2},\dfrac{c_1^e}{\mu _2-\Lambda H(c_2^e)}\right) \end{aligned}$$
      (27)

      It is easy to show that the remaining area from the previous cases (i.e., VI in Fig. 4) is created from the set of equations,

      $$\begin{array}{l}R_1+R_2= \dfrac{c_l}{\mu _1}+\dfrac{c_l}{\mu _2},\\ R_1+R_2=\dfrac{c_h}{\mu _1-\Lambda }+\dfrac{c_h}{\mu _2-\Lambda },\\ R_1 = \dfrac{c_h}{\mu _1-\Lambda }, \text{ and } R_2=\dfrac{c_l}{\mu _2}.\end{array}$$

      Clearly, (27) is a sub-area of VI which corresponds to the area VI.a in Fig. 4 in which the unique equilibrium strategy is \((c_1^e,c_2^e)\), where \(c_n^e=r_n\), the solution of (15) in \((c_l,c_h)\) for \(i=1,2\).

    2. (b)

      The remaining area of IV corresponds to the pairs of \((R_1,R_2)\) which belong to VI but not in VI.a (the complement of VI.a). This takes place when (25) and (26) do not hold, i.e., \(c_1^e \le c_2^e\), which correspond to the equilibrium threshold strategy \((c_1^e,c_1^e)\). By using similar arguments, and based on the optimal response of the tagged customer in (14), in the area of VI.b the equilibrium strategy \((c_1^e, c_1^e)\) corresponds to (r, r) where r is the solution of \(B_{1,r}(r)+B_{2,r}(r)=0\), i.e., Eq. (16). Finally, regarding the red line in Fig. 4 that separates the areas VI.a and VI.b, we can derive its form as follows: We define the \(r_1,r_2\) solutions of Eq. (15) as functions of \(R_1\) and \(R_2\), respectively. Specifically,

      $$\begin{aligned} r_1(R_1)=R_1\left[ \mu _1-\Lambda H(r_1(R_1))\right] \Leftrightarrow R_1=\dfrac{r_1(R_1)}{\mu _1-\Lambda H(r_1(R_1))} \end{aligned}$$
      $$\begin{aligned} r_2(R_2)=R_2\left[ \mu _2-\Lambda H(r_2(R_2))\right] \Leftrightarrow R_2=\dfrac{r_2(R_2)}{\mu _2-\Lambda H(r_2(R_2))} \end{aligned}$$

      Cases (a) and (b) are distinguished by the ordering of \(r_1,r_2\), i.e., case (a) holds if \(r_1>r_2\), whereas case (b) holds if \(r_1\le r_2.\) In order to define this area explicitly with respect to the parameters \(R_1,R_2\), we need to derive the line which is defined by the equation \(r_1(R_1)=r_2(R_2)\). Substituting the expressions for \(r_1(R_1)\) and \(r_2(R_2)\), it follows that \(R_2=\dfrac{r_1(R_1)}{\mu _1-\Lambda H(r_1(R_1))}\). The latter coincides with the red curve in Fig. 4, and its shape depends on the distribution function H(c). Thus, the case where \(R_2<\dfrac{r_1(R_1)}{\mu _1-\Lambda H(r_1(R_1))}\), i.e., \(r_1>r_2\) corresponds to the VI.a area. Otherwise, \((R_1,R_2)\) pairs lie in the supplementary area VI.b.

Fig. 4
figure 4

Equilibrium thresholds in the \(R_2 R_1-\)plane

Full size image

As we have mentioned, the different cases stated in Theorem 1 characterize the equilibrium threshold strategies \((c_1^e,c_2^e)\) when the implemented customers’ delay sensitivity distribution takes values in a closed interval I. The latter corresponds to applications where the delay cost rate C is uniformly distributed in \([c_l,c_h]\) with \(0\le c_l\le c_2^e\le c_1^e\le c_h<\infty\). Following that, it is of interest to explore how the equilibrium threshold strategies \((c_1^e,c_2^e)\) described in Theorem 1 change, when \(c_l=0\) or \(c_h=\infty\), when other types of distributions are applied for C, e.g., an exponential or a gamma distribution.

Indeed, when \(c_l=0\) or \(c_h=\infty\), some of the extreme threshold strategies \((c_1^e,c_2^e)\in TH\) with \(c_1^e,c_2^e\in \{c_l,c_h\}\) are no longer equilibria. This causes the different cases of Theorem 1 to limit down. Specifically, Fig. 5 shows the equilibrium threshold strategies \((c_1^e,c_2^e)\) in the \(R_1 R_2\) plane depending on whether \(c_l=0\) or \(c_h=\infty\) and covers various types of distributions for the customers’ delay sensitivity parameter C. Specifically, Fig. 5a and c correspond to cases where \(c_l=0\), such as when C follows a uniform distribution in \([0,c_h]\) or an exponential distribution with rate \(\theta >0\), indicating that some customers are not sensitive to potential delays. In these cases, the threshold strategies \((c_l,c_l),\;(r_1,c_l),\) and \((c_h,c_l)\), which dictate that all customers will balk from a certain queue, cannot be equilibrium strategies because at least a small portion of customers will join both queues depending on the values of the parameters since they definitely acquire a positive expected net benefit. Thus, when \(c_l=0\), areas I, II, and IV of Fig. 4 disappear.

If \(c_h=\infty\), meaning the support I is unbounded above, such as in cases where C follows an exponential distribution with rate \(\theta\) or a gamma distribution with shape parameter \(n>0\) and rate parameter \(\theta >0\), and I is either \([0,\infty )\) or \((0,\infty )\), then there will be no threshold strategy in equilibrium dictating that all customers join at least the first queue. This is because some customers have a high delay sensitivity and their expected delay cost cannot be compensated by the potential benefit of joining the queue. Therefore, in this scenario, the areas II, III, and IV in Fig. 4 disappear, as shown in Fig. 5b and c. The proof regarding the corresponding cases in Theorem 1 when \(c_l=0\) or \(c_h=\infty\) is similar and follows the same steps. Finally, in the case where \(c_l=0\) and \(c_h=\infty\), where the different equilibrium threshold strategies are shown in Fig. 5c, the only valid case of Theorem 1 is (vi), and the different thresholds are distinguished only by the inequality \(R_2 < \frac{r_1(R_1)}{\mu _1-\Lambda H(r_1(R_1))}\) depending on whether \(r_1>r_2\) or not.

Fig. 5
figure 5

Equilibrium thresholds in the \(R_2 R_1-\)plane for the special case where a \(c_l=0\) and \(c_h<\infty\), b \(c_l>0\) and \(c_h=\infty\), c \(c_l=0\) and \(c_h=\infty\)

Full size image

5 The Impact of Heterogeneity on Customers’ Strategic Behavior: Numerical Experiments

As previously mentioned, the presence of customer heterogeneity regarding delay sensitivity is compatible with a number of situations that arise in several real-life applications, especially in the field of complementary services. These situations determine which parameters can be controlled by a decision-maker to improve the performance of a system. Our objective is to study the effect of customer heterogeneity with respect to delay sensitivity, considering several uniform distributions of different variances for the delay sensitivity C, and the case of homogeneous customers as a benchmark. The latter is approximated by considering a known distribution for C where its variance is almost 0.

Specifically, we perform extensive numerical experiments to obtain further insights on the effective arrival rates at each queue \((\lambda _1^e, \lambda _2^e)\), the corresponding joining double threshold strategy \((c_1^e,c_2^e)\), as well as the total expected customers’ benefit \(S^e\), in equilibrium, under different scenarios. We conducted two sets of numerical experiments. In the first set, we apply the uniform distribution for the delay sensitivity parameter C in the interval \([c_l, c_h]\) for given values of \(c_l,c_h\), whereas in the second set, we apply the Gamma distribution with the given shape parameter \(n\in \mathcal {N}\) and rate \(\theta >0\). In both cases, we consider distributions of the same mean value where we vary their variance. Specifically, for the case of the uniform, we considered distributions of mean value \(E(C)=\frac{c_l+c_h}{2}=4.5\), whereas for the case of the Gamma, we considered distributions of mean value \(E(C)=\dfrac{n}{\theta }=4\). Note that, in the latter case, the extended thresholds are \(c_l=0\) and \(c_h=\infty\), and the relative equilibrium strategies refer to the different cases shown in Fig. 5c.

The customers’ expected benefit from joining in equilibrium is given by the formula

$$\begin{aligned} \begin{aligned} S^e&= \Lambda \int _{c_l}^{c_h} \mathbb {1}_{\{c\le c_1^{e}\}} B_{1,c} (c_{1}^e) + \mathbb {1}_{\{c\le c_2^{e}\}} B_{2,c} (c_{2}^e) \,d H(c)\\&= \Lambda \left( \int _{c_l}^{c_2^{e}} ( B_{1,c} (c_{1}^e) + B_{2,c} (c_{2}^e)) \,d H(c) + \int _{c_2^{e}}^{c_1^{e}} B_{1,c} (c_{1}^e) \,d H(c)\right) , \end{aligned} \end{aligned}$$
(28)

which is finite for the considered distributions.

To represent the difference in variance, we use the terms almost zero, medium, and large variance, as a characteristic of each distribution for the delay cost rate C, since they all have the same mean value. The almost zero variance, which means that customers are almost identical, i.e., the case of almost homogeneous customers, is represented by the applications of \(C\sim U[c_l=4.45, c_h=4.55]\) in the first set of experiments and \(C\sim Gamma(n=256, \theta =64]\) in the second one. The latter applications are used as a benchmark for the analysis. The medium variance, with \(Var(C) \le 1\), is represented by \(C\sim U[c_l=3, c_h=6]\) with \(Var(C)=0.75\) and \(C\sim Gamma(n=16, \theta =4]\) with \(Var(C)=1\). Lastly, the large variance, with \(Var(C)\gg 1\), is represented by \(C\sim U[c_l=1, c_h=8]\) with \(Var(C)=\dfrac{49}{12}\) and \(C\sim Gamma(n=1, \theta =0.25)\equiv Exp(\theta =0.25)\) with \(Var(C)=16\).

The figures use dots, dashes, and continuous lines to represent almost zero, medium, and large variance, respectively. The black color represents the customers’ strategic behavior in queue 1, while red represents queue 2. The left panels show the equilibrium arrival rates \(\lambda _1^e,\lambda _2^e\), the middle panels show the corresponding equilibrium threshold strategy \((c_1^e,c_2^e)\), and the right panels show the plots of \(S^e\). The blue color is only used for the plots of \(S^e\) in the right panels.

5.1 Ratio of the Service Values

First, we study the effect on strategic customer behavior of the fraction of service valuation at each queueing system, \(R_2/R_1\), for different stochastic valuations of the customers’ delay sensitivity C, as we have analyzed above. We perform two numerical experiments considering different service speeds for the two queues, where queue 1 is faster with \(\mu _1=8\) than queue 2 where \(\mu _2=6\) in Figs. 6 and 8, and vice versa, in Figs. 7 and 9. This way, we have a clearer view of not only how customers differ in the evaluation of their delay, but also how their behavior is affected by the operation of the whole system. For both experiments, we fix \(\Lambda =5\) and \(R_1=1\). Therefore, as we increase \(R_2\) with respect to \(R_1\), we cover the following cases:

  1. 1.

    Queue 1 is faster and more valuable for customers than queue 2, i.e., Figs. 6 and 8 for \(R_2/R_1<1\).

  2. 2.

    Queue 1 is faster than queue 2 but less valuable for the customers, i.e., Figs. 6 and 8 for \(R_2/R_1>1\).

  3. 3.

    Queue 1 is slower than queue 2 but more valuable for the customers, i.e., Figs. 7 and 9 for \(R_2/R_1<1\).

  4. 4.

    Queue 1 is slower than queue 2 and less valuable for the customers, i.e., Figs. 7 and 9 for \(R_2/R_1>1\).

Our objective is to study the impact of customer heterogeneity along the four cases and whether there exists an ideal fraction of service values for which the information asymmetry can be controlled by the administrator of the system either by setting the service rates appropriately or by imposing an appropriate service fee. Note that, even though the above model formulation does not consider service fees explicitly, the service administrator could impose a service fee that decreases the corresponding service values at the desired levels.

Fig. 6
figure 6

Effective arrival rates, thresholds, and customers’ overall benefit, in equilibrium, with respect to service values ratio when \(\mu _1>\mu _2\) and \(C\sim Uniform[c_l,c_h]\) with \(E(C)=4.5\)

Full size image
Fig. 7
figure 7

Effective arrival rates, thresholds, and customers’ overall benefit, in equilibrium, with respect to service values ratio when \(\mu _1<\mu _2\) and \(C\sim Uniform[c_l,c_h]\) with \(E(C)=4.5\)

Full size image
Fig. 8
figure 8

Effective arrival rates, thresholds, and customers’ overall benefit, in equilibrium, with respect to service values ratio when \(\mu _1>\mu _2\) and \(C\sim Gamma(n,\theta )\) with \(E(C)=4\)

Full size image
Fig. 9
figure 9

Effective arrival rates, thresholds, and customers’ overall benefit, in equilibrium, with respect to service values ratio when \(\mu _1<\mu _2\) and \(C\sim Gamma(n,\theta )\) with \(E(C)=4\)

Full size image

Considering both Figs. 6 and 7 which refer to the different applications of the uniform distribution, we observe that both effective arrival rates, the corresponding thresholds at each queue, and the customers’ total benefit, in equilibrium, are non-decreasing in \(R_2/R_1\). Therefore, the more valuable the service in the second queue becomes, the more customers will join queue 2, as expected. A faster queue 2 will be more attractive for customers to join it even for smaller values of \(R_2/R_1\), since all plots in Fig. 7 are moved to the left with respect to those in Fig. 6. Also, in both figures, we identify a critical value of the fraction of the service values, \(R_2/R_1\approx 1.7\) in Fig. 6 and \(R_2/R_1\approx 0.65\) in Fig. 7, where the equilibrium threshold strategy changes from two distinct thresholds, i.e., \(c_1^e>c_2^e\), to equal ones. In addition, for very low values of \(R_2/R_1\), nobody joins the second queue, and the corresponding threshold strategy is \((r_1,c_l)\). This means that as the value of \(R_2/R_1\) increases, a portion of customers initially join the first queue and permanently leave the system after service, then they elaborate an equilibrium \((r_1,r_2)\) for intermediate values of \(R_2/R_1\), and, finally, when the benefit from joining the second queue becomes significantly higher, i.e., \(R_2>R_1\), they adopt the threshold strategy (r, r) and tend to join either both queues or none, since the service at the second queue will cover potential losses from the expected delays. Note that this critical point is lower when the service speed in queue 2 is higher. Therefore, there is a trade-off between service speed and the value of service. Indeed, when the second queue works faster, customers will adopt the same threshold for both queues if their service value \(R_2\) is above the \(60\%\) of \(R_1\). Finally, customers’ overall benefit will be slightly higher if queue 1 works faster. Observations in Figs. 8 and 9 are similar. However, there are some differences in the applications of the gamma distribution. In the gamma distribution, the equilibrium threshold \((r_1,0)\) does not occur as expected, and the equilibrium threshold \(c_2^e\) fluctuates when the customers are almost homogeneous, i.e., when \(Var(C)\approx 0\). This differs from the uniform distribution, where the equilibrium threshold \(c_2^e\) is always almost constant.

Considering the effect of the customers’ heterogeneity with respect to their delay sensitivity on the performance measures in equilibrium, we observe in Figs. 6 and 8, where \(\mu _1>\mu _2\), that lower variance always leads to a higher arrival rate at queue 1, while the opposite occurs for the second queue when \(R_2/R_1\) is less than a critical value of the ratio. Specifically, in the application of uniform distribution, there is a single critical value of \(R_2/R_1\approx 1.3\) (see Fig. 6), where all plots of \(\lambda _2^e\) intersect in a single point and the lower variance induces a higher arrival rate at queue 2 afterward. Similar behavior of \(\lambda _2^e\) occurs if the second queue is faster (see Figs. 7 and 9), but the critical point now moves to a lower value, i.e., when \(R_2/R_1\approx 1.1\) for the uniform, while for lower values of \(R_2/R_1\), the arrival rate at the first queue is higher as the variance of C increases. This fact changes after the critical value of \(R_2/R_1\). As in the previous case, lower variance induces a higher arrival rate for both queues, since \(\lambda _1^e=\lambda _2^e\).

When examining the gamma distribution, it is observed that \(\lambda _1^e\) and \(\lambda _2^e\) exhibit the same monotonicity in relation to variance for low or high values of the service reward ratio \(R_2/R_1\) as mentioned above. However, for certain intermediate values of the ratio \(R_2/R_1\), either the equilibrium arrival rate \(\lambda _2^e\) at queue 2 when \(\mu _1>\mu _2\) (as seen in Fig. 8 for \(R_2/R_1\in (1.25,1.5)\)) or the equilibrium arrival rate \(\lambda _1^e\) at queue 1 when \(\mu _1<\mu _2\) (as seen in Fig. 9 for \(R_2/R_1\in (1,1.4)\)) is not monotonic in this interval, unlike the previous application of the uniform distribution. This is due to the plots of the equilibrium arrival rates intersecting at different points when customers are heterogeneous and almost homogeneous, as opposed to a single intersection point that we had in the case of uniform distributions. Regardless of the above, both uniform and gamma applications indicate that when the fraction \(R_2/R_1\) is high, customer heterogeneity has a more negative impact on the resulting equilibrium arrival rates compared to low values of \(R_2/R_1\), which only occur if \(\mu _1>\mu _2\). Finally, in both numerical experiments, the intersection point of the different plots of equilibrium arrival rates also suggests a relative value of the corresponding rewards; at this point, customer heterogeneity disappears, and customers behave as if they were homogeneous in assessing their delays.

Regarding the threshold strategies in Fig. 6 or in Fig. 8, when the variance is large, we observe that the corresponding threshold is higher, while the arrival rate is lower. Although it seems counter-intuitive, it is quite reasonable in some cases, especially in the application of the uniform distribution, since the difference \(c_h-c_l\) is increasing in the variance. Therefore, it leads to a lower arrival rate (\(\lambda _1^e=\lambda H(c_1^e)\), where \(H(c)=\frac{c-c_l}{c_h-c_l}\)). In this example, for the large variance case, we obtain \(c_1^e=5.1\); thus, we have \(\lambda _1^e=5 \frac{5-1}{8-1}\approx 2.85\). On the other hand, for the medium variance case, we have that \(c_1^e=4.9\) which implies that \(\lambda _1^e=5 \frac{4.9-3}{6-3}\approx 3.16\). A similar effect is identified in the application of the gamma distribution because of the assumed parameters and the shape of the cumulated distribution.

Another impact of the variance concerns the threshold strategies. The numerical experiments suggest that the equilibrium threshold strategy at queue 1 is always higher for a larger variance in both applications when \(\mu _1>\mu _2\). This does not happen in queue 2, since for low values of \(R_2/R_1\), the lower variance leads to a higher threshold up to a point where \(R_2/R_1 \approx 1.3\) in Fig. 6, and the opposite takes place afterward. In both cases (medium and large variance) when the fraction becomes sufficiently large, the two thresholds \(c_1^e\) and \(c_2^e\) coincide, similarly to the effective arrival rates. In Figs. 7 and 9, in contrast to the previous case, the equilibrium threshold strategy for queue 1 is higher for low variance, whereas for higher values of \(R_2/R_1\), the two threshold strategies coincide again, and the higher variance leads to a higher threshold, independently of which queue is faster.

Regarding the customers’ overall benefit in equilibrium, we observe in Figs. 6, 7, 8, and 9 that it is always higher when the variance is high and non-decreasing at a high rate in all cases. For the case of almost zero variance which refers to the approximately homogeneous case, it tends to be zero in the application of uniform distribution, whereas it is positive in the application of gamma distribution, and coincides with the case where queue 2 is the faster one, as in Figs. 7 and 9. The latter indicates that in this case, the relative service speed between the two queues does not play any role regarding the effect of the variance on customers’ overall benefit.

In short, Figs. 6, 7, 8, and 9 illustrate the following:

  • The equilibrium arrival rates \((\lambda _1^e, \lambda _2^e)\), the corresponding thresholds \((c_1^e, c_2^e)\), and the customers’ overall benefit \(S^e\) are non-decreasing in \(R_2/R_1\).

  • The equilibrium arrival rates coincide above a critical value of \(R_2/R_1\), since the equilibrium thresholds become equal, and customers decide either to enter both queues or balk from the beginning. A faster queue 2 moves this point towards lower values of \(R_2/R_1\).

  • A faster queue 2 will impose a greater effective arrival rate at queue 1 as the variance increases, but lower for the same variance in the opposite case, whereas \(\lambda _2^e\) increases with respect to the variance for low values of \(R_2/R_1\) and decreases for greater ones. Equilibrium thresholds have the opposite behavior as the variance increases. There is a second critical point of \(R_2/R_1\), where the effective arrival rate at queue 2 becomes equal for any variance in the applications of the uniform distribution, and the heterogeneity effect seems to disappear. A higher variance will lead to greater customers’ overall benefit in equilibrium regardless of the relative service speed or the considered distribution for customers’ delay sensitivity.

5.2 Ratio of the Service Rates

In this subsection, we present the sensitivity analysis with respect to the ratio \(\mu _2/\mu _1\) for \(\Lambda =0.8, \mu _1=1\), when the service reward is higher on the first queue than the second one, i.e., \((R_1,R_2)=(9,1)\) in Fig. 10, and vice versa where \((R_1,R_2)=(1,9)\) in Fig. 11. Once again, as in Section 5.1, we consider the same three uniform and gamma distributions for customers’ delay sensitivity, presented at the beginning of Sect. 5.

We consider the four similar cases discussed in the previous subsection but now as a function of the ratio \(\mu _2/\mu _1\).

  1. 1.

    Queue 1 is faster and more valuable for customers than queue 2, i.e., Figs. 10 and 12 for \(\mu _2/\mu _1<1\).

  2. 2.

    Queue 1 is slower than queue 2 but more valuable for the customers, i.e., Figs. 10 and 12 for \(\mu _2/\mu _1>1\).

  3. 3.

    Queue 1 is faster than queue 2 but less valuable for the customers, i.e., Figs. 11 and 13 for \(\mu _2/\mu _1<1\).

  4. 4.

    Queue 1 is slower than queue 2 and less valuable for the customers, i.e., Figs. 11 and 13 for \(\mu _2/\mu _1>1\).

Once again, our objective is to study the impact of customer heterogeneity along the four cases and whether there exists an ideal fraction of service rates for which the information asymmetry can be controlled by the administrator of the system either by setting the service rates appropriately or by imposing an appropriate service fee.

In Fig. 10, as well as in Fig. 12, where the service reward for the first queue is very high, while is very low for the second queue, a large fraction of customers join the first queue, and in order to continue to the second queue, it requires a high increase in its service rate. Even in this case, only a very small portion of customers will continue to the second queue. The effect of the variance is very intense in the first queue since it leads fewer customers to decide to join when it is high. As in the previous experiments, for high values of \(\mu _2 / \mu _1\), the equilibrium effective arrival rates for both queues coincide, since the equilibrium thresholds become equal, and customers adopt a threshold to either join both queues or to balk. Also, with respect to the variance, the equilibrium arrival rates at queue 2 intersect at a certain value, and the effect of customer heterogeneity seems to disappear, making customers to be considered almost homogeneous in delay sensitivity. Furthermore, for lower values of \(\mu _2 / \mu _1\), greater variance results in a higher effective arrival rate but in a lower threshold, while greater values of the fraction of service rates lead the arrival rate to become increasing as the variance also increases. Finally, in terms of customers’ overall benefit, the higher variance reflects a higher overall benefit but at a very low increasing rate (almost constant) due to the devaluation of the second queue, and customers mainly benefit from the reward collected by the first queue.

On the other hand, in Fig. 11 where the service rewards are exchanged, making the service value of the first queue very low, we observe that customers will adopt the same threshold strategy at both queues, i.e., \(c_1^e=c_2^e\), since they are mainly interested to collect the high service reward from the second queue, and thus the arrival rates for both queues coincide. Note that, again, there is a critical point of the ratio \(\mu _2/ \mu _1\). For values of \(\mu _2/ \mu _1\) lower than this critical value, the arrival rate increases, and the threshold decreases as the variance increases. For values of \(\mu _2/ \mu _1\) that are higher than the critical value, the effect is reversed. Regarding the customers’ overall expected benefit, we observe again that regardless of the order of the service values, the higher variance induces a higher benefit, but at a greater rate now. Similar observations can be also made in Fig. 13.

Fig. 10
figure 10

Effective arrival rates, thresholds, and customers’ overall benefit, in equilibrium, with respect to service rates ratio when \(R_1>R_2\) and \(C\sim Uniform[c_l,c_h]\) with \(E(C)=4.5\)

Full size image
Fig. 11
figure 11

Effective arrival rates, thresholds, and customers’ overall benefit, in equilibrium, with respect to service rates ratio when \(R_1<R_2\) and \(C\sim Uniform[c_l,c_h]\) with \(E(C)=4.5\)

Full size image
Fig. 12
figure 12

Effective arrival rates, thresholds, and customers’ overall benefit, in equilibrium, with respect to service rates ratio when \(R_1>R_2\) and \(C\sim Gamma(n,\theta )\) with \(E(C)=4\)

Full size image
Fig. 13
figure 13

Effective arrival rates, thresholds, and customers’ overall benefit, in equilibrium, with respect to service rates ratio when \(R_1<R_2\) and \(C\sim Gamma(n,\theta )\) with \(E(C)=4\)

Full size image

In short, Figs. 10, 11, 12, and 13 illustrate the following:

  • The equilibrium arrival rates \((\lambda _1^e, \lambda _2^e)\), the corresponding thresholds \((c_1^e, c_2^e)\), and the customers’ overall benefit \(S^e\) are non-decreasing in \(\mu _2/\mu _1\).

  • The equilibrium arrival rates coincide above a critical value of \(\mu _2/\mu _1\) when \(R_1>R_2\). In the other case, where \(R_1=1<9=R_2\), the high difference in the service values forces customers to adopt a single threshold for either joining both queues or balking. In a more profitable queue 1, the almost homogeneous customers will impose a higher effective arrival rate which decreases as the corresponding variance increases.

  • Once again, there is a critical value of \(\mu _2/\mu _1\), where the effective arrival rates at queue 2 become equal for any variance, and the heterogeneity effect seems to disappear. A higher variance will lead to greater customers’ overall benefit in equilibrium at a much higher rate when queue 2 is more profitable.

6 Conclusion

In this paper, we considered a Markovian tandem system of two unobservable M/M/1 queues in series with strategic customers who are heterogeneous in their delay sensitivity when they make join/balk decisions when arriving in front of each queue. We identified the unique symmetric Nash equilibrium strategy which is threshold-based, and depending on the values of the parameters, it can dictate to customers either to join each queue under a different threshold or to use the same joining threshold for both queues. We performed several numerical experiments considering either uniformly distributed or gamma-distributed customers’ delay sensitivity to study the impact of customers’ heterogeneity on their strategic behavior, and we also compared it with the case of almost homogeneous customers.

The considered model is the first step towards a more thorough study of the impact of customers’ delay sensitivity heterogeneity on their strategic joining behavior in a network with queues in series. The current work can be extended in several directions to study the impact of customer heterogeneity on customer equilibrium behavior either considering a finite number of queues in series as in [20] or more general networks with feedback loops. Another approach in this direction could incorporate aspects of customers’ risk aversion who adopt a non-linear utility. Finally, studying the impact of customer heterogeneity in combination with the information disclosure of the number of customers in the system at any decision instant will provide managerial insights referring to even more realistic applications.